Abstract
Various real-time applications such as Human–Computer Interactions, Psychometric analysis, etc. use facial expressions as one of the important parameters. The researchers have used Action Units (AU) of the face as feature points and its deformation is compared with the reference points on the face to estimate the facial expressions. Among many parts of the face, features from the mouth contribute largely to all the well-known emotions. In this paper, the parabola theory is used to identify and mark various points on the lips. These points are considered as feature points to construct feature vectors. The Latus Rectum, Focal Point, Directrix, Vertex, etc. are also considered to identify the feature points of the lower lips and upper lips. The proposed approach is evaluated on benchmark datasets such as JAFFEE and Cohn–Kanade dataset and it is found that the performance is encouraging in understanding the facial expressions. The results are compared with contemporary methods and found that the proposed approach has given good classification accuracy in recognizing facial expressions.
Keywords: Facial expressions, Emotions, Parabola, Mouth, Lips
Introduction
The automated recognition of facial expressions is an important research topic as human emotion is used in many real-time applications. Human emotion is measured using different factors. Many research groups from academia and industry are actively engaged in research due to its wide-ranging applications. Facial expression recognition and emotional computing system plays a vital role in the area of Human–Computer Interaction (HCI). One can identify an individual’s emotional state through the feelings. As a result, information related to facial expressions is often used in automatic facial emotion recognition systems. Hence, automatic facial expression recognition has a demanding trend in the areas of gaming applications, criminal interrogations, psychiatry, animations, etc. In fact, Darwin (1872) proposed a theory on facial expressions in animals and humans in 1872. To provide evidence on this theory, Ekman and his colleagues in the early 1970s performed immense studies on human facial expressions (Ekman and Friesen 1978). These authors studied facial expressions in various cultures, even isolated or primitive, and provided results to prove the theory. These studies clarify that regardless of the differences imposed by social rules, the expression process and emotional recognition of face are common. Six basic categories of emotions such as happy, sad, surprise, anger, fear, and disgust are identified and are referred to as standard facial expressions. In general, facial expression recognition depends on two factors such as appearance and geometrical features. The shape of the face, forehead, eye, eyebrows, mouth, nose, and chin is considered and its geometrical feature is extracted. The texture of the face is extracted using furrows, wrinkles, etc. Ekman and Friesen built the Facial Action Coding System (FACS) framework, which is a popular framework for the researchers in the area of facial expression analysis. The framework use the muscle movements for analyzing facial expression known as facial Action Units (AUs). FACS uses still images of facial expression to manually describe the expression of the face. FACS uses this degree of deformation of the face in terms of features extracted. The framework is further used for feature extraction in combination with other state-of-art techniques such as Dynamic Bayesian Network (DBN) by Ko and Sim (2010), Local Binary Pattern (LBP) by Wang et al. (2015), Histograms of Oriented Gradients (HOG) by Dalal and Triggs (2005), Scale Invariant Feature Transform (SIFT) by Lowe (1999) for detecting and measuring the facial expressions.
Though much progress has been made, there are still issues and problems. In one hand, conventional feature extraction methods that are in use still rely on human experience and this leads to many computational complexities. Another issue with traditional approaches is that they cannot handle the big data and thus they perform poorly. The traditional approaches may not handle the real-time application requirements effectively. Illumination conditions and variations in head posture are some of the factors that affect the emotion recognition systems using cameras. Many techniques use handcrafted features for facial expression recognition and thus require increased efforts in terms of programming and computation cost. Based on the above discussion, the main objective of the paper is:
To propose the robust feature to handle the effect of illumination.
To propose a geometrical feature with scale, orientation and translation invariant.
To handle issues of hand crafted features to improve the accuracy of facial expression.
To improve the programming and computation cost.
As a result, the paper proposes a novel approach to extract geometric features from lips using the properties of the parabola. The proposed approach has various stages as given below:
The preprocessing is the first stage where the noise removal, lip localization, lip boundary processing, segmenting lower and upper lips, etc., are carried out.
In the second stage of the approach, the formation of pixel grid over lips, identifying the feature point, construction of feature vector is carried out.
In the third stage, n-fold cross-validation is performed on the dataset, classified the features using Support Vector Machine (SVM), Multi-Layer Perceptron (MLP) and Random Forest (RF) classifiers.
Thus, the novelty of the proposed approach is given below
-
(i)
There are a large number geometrical features proposed in recent times. The proposed approach extracts geometrical features from both upper and lower lips by using the properties and theory of the parabola. This is a novel concept, since it use a strong mathematics.
-
(ii)
The procedure of feature extraction is further substantiated with the theory presented in Sect. 3.2, which is novel concept.
-
(iii)
The features extracted using the parabolic theory is n-fold cross validated to create training and testing data sets for various machine learning algorithms, which is novel.
-
(iv)
The procedure for estimating the facial expression is also novel in the proposed approach.
The theory of feature extraction is validated with experiments and they are conducted on well-known benchmark datasets for calculating the classification accuracy. The performance of the proposed approach is good in classifying the facial expression and the results are compared with contemporary methods.
The rest of the paper is organized as follows. The review of recent literature is presented in the next section. The theory of Parabola and procedure of feature extraction is presented in Sect. 3. The performance of the proposed feature vector is validated and presented in Sect. 4 and the paper is concluded in the last section.
Literature review
Facial expression recognition plays a vital role in real-time applications such as pain detection, Human–Computer Interaction (HCI), driver fatigue detection, etc. In general, facial expression recognition can be dealt with in two ways such as processing with static images and processing with dynamic image sequences. In the first approach, the static image frame is considered to recognize the facial expressions keeping the neutral face image as a reference. The difference between the neutral face and the input face is compared to classify the expressions. However, it is stated that the recognition is difficult as very little information is available for classification (Ghimire and Lee 2014). The second approach deals with an image sequence that displays the temporal information dynamically to recognize facial expressions. The facial expression is recognized based on the difference between the initial image frame and the ith image frame that exhibits facial expression (Ghimire and Lee 2013). In general, the facial expression recognition system consists of two steps such as feature extraction and classification. The scheme of feature extraction is further divided into two categories such as geometric and appearance-based methods (Tian et al. 2005). The geometric based method uses the geometric shape of facial components. It tries to identify geometric relationships between facial components like eyes, eyebrows, mouth, nose, etc. (Pai and Chang 2011). The appearance-based method uses creases, wrinkles, furrows, and textures of facial images to recognize facial expressions. Filters are used either only on facial components or on a whole facial image considering as a single unit (Huang et al. 2012). The other scheme is based on the Action Unit (AU) that detects the fiducial/landmark points as the feature vectors on the face. The method identifies change that occur in their respective positions. The most commonly used feature extraction techniques are Principle Component Analysis (PCA) (Turk and Pentland 1991), Independent Component Analysis (ICA) (Bartlett et al. 2002), Gabor filters/wavelets (Lyons et al. 1999) and Local Binary Pattern (LBP) (Shan et al. 2009). Similarly, other feature extraction schemes are Local Direction Pattern (LDP) (Jabid et al. 2010), Histogram of Oriented Gradients (HOG) (Dalal and Triggs 2005), Active Appearance Model (AAM) (Cootes et al. 2001), Active Shape Model (ASM) (Huang and Huang 1997), etc. In addition, various classification algorithms such as Artificial Neural Networks (ANN) (Choi and Oh 2006), Support Vector Machines (SVM) (Cruz et al. 2014), Hidden Markov Model (HMM) (Siddiqi et al. 2013), Gaussian Mixture Model (GMM) (Schels and Schwenker 2010), and Deep Belief Network (DBN) (Liu et al. 2014) are widely used for classifying the facial expressions.
Shan et al. (2005) have proposed an approach to obtain complete and concise descriptive facial images by shifting sub-windows on input images. Lin (2006) has used PCA for extracting features from images and used Hierarchical Radial Basis Network (HRBFN) function for classifying the facial expressions. The PCA has segmented the facial data into small components to complement the feature extraction procedure. However, this approach has underperformed on still images compared to the video sequence as still image provides lesser information compared to video sequence. The Principle Component Analysis (PCA) has been used for analyzing facial expression by considering the contribution of various parts of the face such as nose, lips, etc. (Lekshmi et al. 2008). This method has considered both mouth and eye regions of the human face. It has been assumed that these portions of the face contribute to the facial expressions. Jeong et al. (2010) have proposed a pattern recognition method to address facial recognition problems. The important information from the facial data is extracted and constructed as a feature. The theory of both the Principal Component Analysis (PCA) and Singular Value Decomposition (SVD) have been used for extracting features (Kaur et al. 2010). The mean, standard deviation, variance, Covariance matrix and eigenvector have been calculated. The eigenvectors with the highest values are considered as the principle component. Khandait et al. (2011) have considered histogram equalizers to maintain image quality. Morphological image processing is applied to facial images to divide them into segments and the feature is extracted after handling the noise. The small segments are merged with neighboring larger segments based on threshold values. The Multi-Layer Perceptron (MLP) Neural Network with back propagation algorithm has been used for classifying the expression. The model proposed by Arumugam and Srinivasan (2011) has used a combined framework of Singular Value Decomposition (SVD), Radial Basis Function Network (RBFN) and Fisher’s Linear Discriminate (FLD) for recognizing facial expression and RBFN has been used for classification. The front posed facial images have been considered as reference and the facial expression has been recognized (Long et al. 2012). The Pseudo Zernike Moment Invariant (PZMI) and Radial Basis Function Network (RBFN) have been extracted and evaluated on the JAFFE database. The relation between facial features and the input space has been recognized by Choi et al. (2012) by applying discriminant analysis. The Pyramid of Local Binary Pattern (PLBP) has been used as a framework for facial expression recognition problems (Khan et al. 2013). The spatial layout of the facial images is extracted by tiling it in multiple resolutions, local texture information extracted for all the regions and linear combination of the local texture of all the regions are considered as a feature vector. Both the LBP and PCA are combined for extracting facial features from the facial images and SVM has been used as classifier (Yuan et al. 2013). An Adaptively Weighted Extended Local Binary Pattern Pyramid (AWELBPP) has been proposed by modifying LBP (Goa et al. 2013). The input facial image is divided into a group of horizontal sub images by applying Pyramid transformation. Sub-Extended Local Binary Pattern (ELBP) is calculated using information content of the sub-images. The feature vector is constructed from various ELBP belong to sub images as Pyramid structure and used for classification. Weber Local Descriptor (WLD) and LBP on Multi-scale based feature has been proposed and histograms at various levels are combined to have a feature vector (Yu et al. 2013). The Compound Local Binary Pattern (CLBP) has been used to capture local features (Ahmed et al. 2014). A two bit code is generated to capture sign and magnitude difference between them. The histogram is constructed with 16-bits and SVM has been used as classifier. The Binary Pattern Feature Descriptors has been proposed for recognizing Facial Expression (Kristensen et al. 2014). The blur invariance properties of the Local Frequency Descriptor have been exploited for feature extraction and classification. An Expression specific Local Binary Pattern (Es-LBP) has been proposed by Chao et al. (2015) for classifying facial expression. The locality information, facial points, and the relationship between facial features and expression class have been used. All the above mentioned approaches failed for high resolution facial images.
The local deformation, such as, wrinkles, textures, facial muscles contributes to the variation in the facial expression. Both Histograms of the Oriented Gradients (HOG) and LBP descriptor have been linearly combined by using decision level fusion and the facial expression is classified based on Sparse Representation (Ouyang et al. 2015). Carcagnì et al. (2015) have employed HOG and optimized for facial expression recognition and the SVM have been used as classifier. The spatial pyramid structure of HOG has been modified to get the dynamic and spatial information of facial expression (Fan and Tjahjadi 2015). The dense optical flow is integrated to generate spatial–temporal descriptor. Multimodal learning has been proposed and has used structured regularization to maintain robustness for recognizing facial expressions (Zhang et al. 2015). It has been argued that the combination of texture and landmark information has improved the classification accuracy. The author Al-Sumaidaee et al. (2015) have proposed Local Gabor Gradient Coding (LGC) for facial expression recognition. The orientation information is maintained using LGC codes and the performance has been evaluated on the JAFFE database. A framework has been proposed by Khan et al. (2015) for face detection with the help of histogram. The histogram is equalized to reduce its dimension to normalize the effect of illumination. The SVM has been used as the classifier and the performance has been evaluated on JAFFE database.
Spherical clustering fused with Online Sequential Extreme Learning Machine (OSELM) has been used for facial expression classification by Ucar et al. (2016). This approach has used both local curve let transform and statistical features. Wang et al. (2016) have proposed Sparse Local Fisher Discriminant Analysis (SLFDA) approach that uses the sparse property of Local Fisher Discriminant Analysis (LFDA) for recognizing facial expressions. The LBP features and Weber Local descriptor has been used for extracting micro information by Khan et al. (2016). A facial expression classification scheme is proposed to detect the driver fatigue detection on both high and low resolution images by Khan et al. (2018a, b). The information in the facial image is preserved by applying a Discrete Wavelet Transform (DWT) to get the down sampled version of the input image. It is further classified as informative and non-informative blocks by measuring the entropy and high variance as a feature for classification. Khan et al. (2018a, b) have proposed Weber Local Binary Image Cosine Transform (WLBI-CT) for classifying facial expressions. The frequency components of the facial images are extracted using both Weber local descriptor and local binary descriptor and it has been used for classifying the facial expressions. The performance of this approach has been evaluated on JAFEE, MMI and CK+ datasets and however, it has been noticed that it requires multiple feature sets with variable block sizes from different multi-scale images. Munir et al. (2018) fused Fast Fourier Transform, Contrast Limited Adaptive Histogram Equalization (FFT + CLAHE) and Merged Binary Pattern Code (MBPC) to recognize facial expression. For each pixel, a 16-bit code is created by using two bits of each neighborhood along with local feature. Though the above mentioned approaches handle facial expression recognition problem, some of these approaches will not work effectively for high dimension feature vector which increases computational cost and degrades the classification accuracy. Further, some approaches extract facial patches and salient features from the chosen landmarks which become computationally expensive. In the literature, many authors proposed hybrid approaches and the fusion of multiple features. Although, they increases the recognition rate but ends up generating redundant features that reduce the performance of facial expression recognition system.
The authors Chien and Choi (2000) have proposed an approach for extracting feature from mouth. The approach have considered grid-based and coordinate-based lips features such as width and height of outer and inner lips edges. The authors have used a single log-polar face template to identify face and its landmarks with varying scale and rotation parameters. The approach simulates the space-variant human visual system and supports in converting scale change and rotation of input image into a constant horizontal and cyclic vertical shift in the log-polar plane. Authors Su et al. (2010) have suggested geometrical and Gabor filter based face features fusion for better facial expression recognition. Here, the Gabor wavelet features of mouth and geometric characteristics of mouth are fused to achieve better performance. He et al. (2011) have proposed Modified Biologically Inspired Model (MBIM) of face features extraction, which utilizes more efficient pooling operation and boosting feature selection. The approach has used SVM for classification. Shan et al. (2009) have used the LBP method for extracting features in facial expression recognition system. The central pixel value is compared with its neighboring pixel values along with the radius. The greater neighboring pixel values are assigned 1 and lesser as 0. The generated binary number is transformed into a decimal number. All the above mentioned approaches, lack simplicity in detecting mouth lines and hardly extract simplified lips edges.
The authors Cheon and Kim (2008) have used Differential Active Appearance model Features (DAF) on the facial expression recognition framework. It is a person independent approach that calculates the difference between input face image and the neutral face image as the AAM parameter. The framework is extended to the temporal approach and used the K-Nearest Neighbor Sequence (K-NNS) classifier for recognizing the expressions. Lajevardi and Hussain (2009) have proposed a wrapper approach for feature selection as an initial step for facial expression recognition. Here, maximum intensity frames are detected and subjected to log-Gabor filters for feature generation. After the selection of features, Genetic Algorithm (GA) is applied to the features for optimization and the Naive base classifier is used for classification. Niu and Qiu (2010) have proposed an approach that used improved version of PCA for feature extraction and SVM classifier for facial expression recognition. It has used multi-featured Weighted Principal Component Analysis (WPCA) for extracting feature and reducing the dimension. The weights are determined using the Facial Action Code System (FACS). The method has used the Radial Basis Function (RBF)-SVM for classifying facial expressions. Jabid et al. (2010) have used LDP feature extraction method which is considered as illumination invariant method. The method has used Kirsch Mask technique to calculate the edge response values of the pixel. For eight masks, eight values either 0 or 1 are assigned for a pixel considering the highest value as 1. The binary number is then converted into a corresponding decimal number. The LDP generated code is considered as the LDP code of the image. Krizhevsky et al. (2012) have used Deep Convolution Neural Network (DCNN) framework for extracting features from facial images. DCNN uses several layers for accurate feature learning. The pre-learned features are used as filters and these filters convolve through the input image and produces the features which in turn are used by other layers of the network. The authors Wang et al. (2014) have proposed a framework for facial expression recognition using Active Shape Model (ASM) to align the faces and then extract the features using the LBP method. It has used SVM classifier to classify facial expressions.
Yun et al. (2013) have proposed an approach named parametric Kernel Eigenspace Method based on Class (PKEMC) feature. The approach is based on a combination of two methods such as the Parametric Eigenspace Method based on Class feature (PEMC) and Kernel Eigenspace Method based on Class features (KEMC). The approach has used the nearest neighbor classifier along with Euclidean distance for classifying facial expressions. Sadeghi et al. (2013) have proposed an appearance feature based approach for facial expression recognition. The method has given an importance to facial geometry and its components position in recognizing expressions. Before extracting the feature, this approach proceeds with facial geometric normalization to eliminate the geometric variability that occur during facial expressions. Standard geometric models for various expressions such as sad, surprise are used for geometric normalization. LBP is used for feature extraction and SVM classifier is used for classification. The authors, Elaiwat et al. (2014) exploit local feature based algorithms to extract salient points on the face region. The method used multi-scale local surface descriptors that separate unique peculiarities around located key points. The discrete curvelet transform uses Fast Discrete Curvelet Transform (FDCT) to decompose each image into a set of frequency and angle decomposition parts. A set of key focus is acquired and by contrasting these key focuses, dominant key points are chosen around the magnitude of decomposition components. Once the dominant key points are recognized, multi-scale local surface descriptors are separated around each of the key points. The main step is extracting sub patches. The patches are reordered utilizing circular shifts and a feature vector is fabricated. The authors Dosadia et al. (2015) have proposed a technique that utilizes both Gabor Filters with Discrete Cosine Transform (DCT) methods for feature extraction. Initially, Gabor equation on the facial image is used to generate the Gabor coefficient matrices. These matrices are averaged into a single average Gabor coefficient matrix and further subjected to DCT to have DCT coefficient matrix. The method retains only low frequency coefficients that contain the most useful information and others are discarded to reduce the redundancy. The constructed feature vector is used for classifying facial expressions.
Tong et al. (2014) have used the Local Gradient Code (LGC) method for feature extraction. The approach extracts the local information by comparing the neighboring pixels horizontally, vertically and diagonally. The HOG is considered as one of the methods to extract gradient-based feature (Jyoti et al. 2015). The gradient magnitude and angular orientation for each pixel is calculated. The gradient magnitude values are used for constructing histogram based on the angular orientation and the bins are arranged with 50% overlapping cells. The constructed feature vector is normalized to achieve a better illumination variance. The Haar Wavelet transformation has been used for extracting feature (Jyoti et al. 2015). The image is divided into four parts with different decomposition levels, say, LL, LH, HL and HH. Jyoti et al. (2016) have used both the LBP and the LGC, central pixel is compared with neighboring pixels, and the maximum of the two pixels is replaced as a new value. The resultant matrix is divided into blocks and the histogram of each block is constructed and linearly combined. Same authors again have used the HOG from the LDP image, and fused the HOG with the Wavelets. Xu et al. (2015) have proposed a model based on Deep Convolution Networks (DCN). The trained model extracts the high-level feature and the SVM classifies the facial expressions, which is six basic emotions and a neutral expression. Ghimire et al. (2015) have proposed an approach for recognizing facial expressions that use both appearance and geometric features. The face region is divided into grids to extract the appearance features. The region specific appearance features are further extracted by dividing whole face region as the domain specific local regions. The geometric features are also extracted from these regions and the SVM is used as classifier. Mistry et al. (2017) have proposed an approach for recognizing facial expression using both the horizontal and vertical Local Binary Pattern (hnvLBP). The facial feature is extracted by comparing horizontal and vertical neighborhood pixels. The micro Genetic Algorithm–embedded Particle Swarm Optimization (mGA-embedded PSO) is proposed for feature selection. It is known that many approaches consider the facial images from the same domain for testing and training. As a results, extracted feature vectors have the same marginal probability distribution (Zheng et al. 2018). This issue have been addressed and a method has been proposed that dealt with the cross domain for recognizing facial expression to achieve the considerable variation in the probability distribution of both the sets. Similarly, there are methods that combines the source domain labeled facial image set along with the target domain unlabeled auxiliary image set. The Transductive Transfer Regularized Least Squares Regression (TTRLSR) model is learned from the sets and the class labels are predicted using the SVM classifier for the auxiliary facial image set. Haq et al. (2019) have proposed an algorithm that can handle face pose, non-uniform illuminations, and low-resolution factors. The approach use sixty-eight points to locate the face and use the PCA to extract mean image. The AdaBoost and the LDA methods are used to extract facial features. In addition, there has been a study to group the emotions as combined emotions (Swaminathan et al. 2020). Further, a Deep Convolution Neural Networks (CNNs) is trained to analyze facial expressions explainable in a dimensional emotion model. This approach considers range of emotions along with subtle emotion intensities in addition to the conventional emotions. The facial expression is transformed from classification problem to regression (Zhou et al. 2020).
Based on the review, it is found that most of the approaches have used various features from the facial images. However, HCI applications require feature of the lips since it plays an important role in capturing human expression. As a result, we propose a method to capture the deformation of lips using the properties of Parabola. The entire mouth area is divided as upper and lower lip regions. A grid is superimposed on the regions and the pixels falling on the lip regions are categorized using the properties of the Parabola. The degree and type of emotion is mapped with the characteristics of parabolic curve. This approach is validated on various well-known benchmark datasets. The performance of the proposed approach is encouraging and estimates the facial expression effectively. In the next section, the proposed approach is presented in detail.
Proposed work
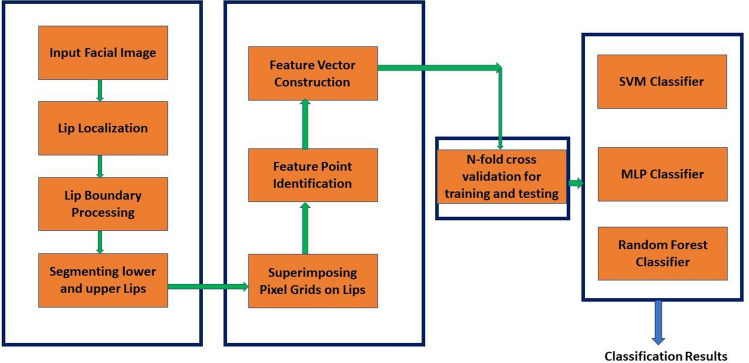
In this Section, the parabola theory and its properties, scheme of feature extraction, training and classification using various Machine Learning algorithms are presented. The block diagram of the proposed scheme is depicted below in Fig. 1. The first step is the pre-processing stage, where in the noise is removed from the input image and the lips portion of the facial image are localized. The boundary of the lips is segmented with a marking information as the upper and lower lip regions. Second stage of the scheme superimposes the pixel grids over the lip area of the input image. The pixels falling on the parabola (lip) are identified using the parabolic theory and properties. All the points satisfying the parabolic theory are considered as the feature points and the feature vector is constructed. Third stage classifies the expressions using the feature vector. The feature vector is extracted from all the facial images from different datasets and n-fold cross validation is used for making test and training datasets. The Support Vector Machine (SVM), Multi-Layer Perceptron (MLP) and Random Forest (RF) are used as classifiers. A detailed discussion on these algorithms are presented in Sect. 3.4. The properties of parabola and scheme of feature extraction are presented in subsequent sections.
Fig. 1.
Block diagram of the proposed approach
Properties of parabola
It is known that the parabola can be realized using multiple points in a plane such that all the points are equidistant from a fixed line and point in the respective plane. The fixed points are called focus and the fixed line is referred to as directrix. Similarly, the axis of the Parabola is the line through the focus and perpendicular to the directrix. The point of intersection of Parabola with the axis is called vertex. The concept is depicted in Fig. 2 and typical Parabola with focus and vertex is shown in Fig. 3 for better understanding.
Fig. 2.

Typical parabola with intersection points
Fig. 3.
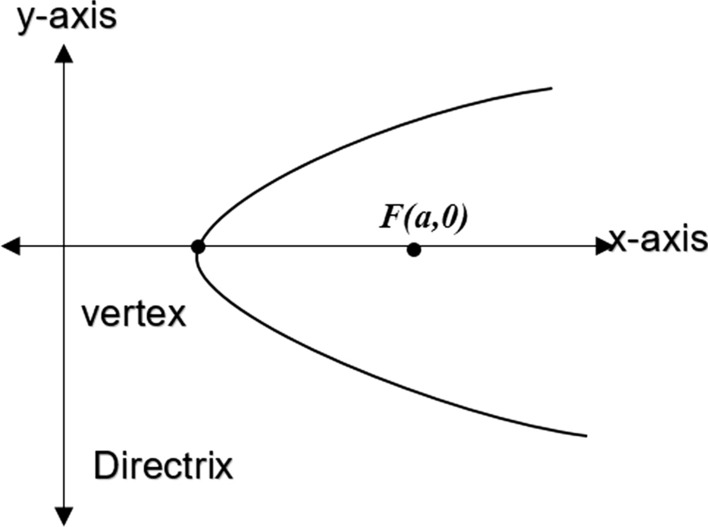
Typical parabola with Focus and Vertex
In Fig. 2, consider the points P1, P2, and P3 on the Parabola and all of them can be expressed as , and In addition, P1B1, P2B2 and P3B3 are perpendicular to the directrix. The distance between P1F, P2F and P3F can be calculated as given below:
| 1 |
| 2 |
| 3 |
Similarly, PB (P1B1, P2B2 and P3B3) can be written as follows:
| 4 |
The Eqs. (1–3) can be generalized as given in Eq. 5
| 5 |
It is known that PF = PB, hence
| 6 |
On squaring both LHS and RHS,
| 7 |
| 8 |
On solving Eq. (8),
| 9 |
Thus, if any point satisfies the condition as given in Eq. (9), the point in consideration is on the Parabola. In addition, if a point P(x, y) satisfies Eq. (9), the Parabola has Converse Property as given below in Eqs. (10–12)
| 10 |
| 11 |
| 12 |
As a result, it is further confirmed that any point P(x, y) satisfying Eq. (9) is on the Parabola. In addition, Eqs. (9) and (12) proves that equation of Parabola with vertex at the origin, focus at F(a, 0) and directrix x = − a is y2 = 4ax.
Based on the above discussion, the following points are highlighted:
Any point P(x, y), which satisfies Eq. (9) is a point on the parabola.
Based on the discussion above, all these properties can be used for modeling both the upper and lower lips of facial images to classify the facial expressions.
Observations on parabola
It is known that a Parabola is symmetric with its axis and the axis of symmetry depends on x and y terms in the Parabolic Equation derived in Sect. 3.1. Say, in case, the parabolic equation has y2 term, the axis of symmetry of parabola is along x-axis. Similarly, if the parabolic equation has x2, the symmetry of parabola is along y the axis. Using this observation on symmetry, a property named Latus Rectum is defined. Latus Rectum is a line segment perpendicular to the axis of the Parabola passing through the focal point. The endpoints of Latus Rectum lie on the Parabola as shown in Fig. 4. The length of the Rectums of Parabola is y2 = 4ax as given in Figs. 4 and 5.
Fig. 4.
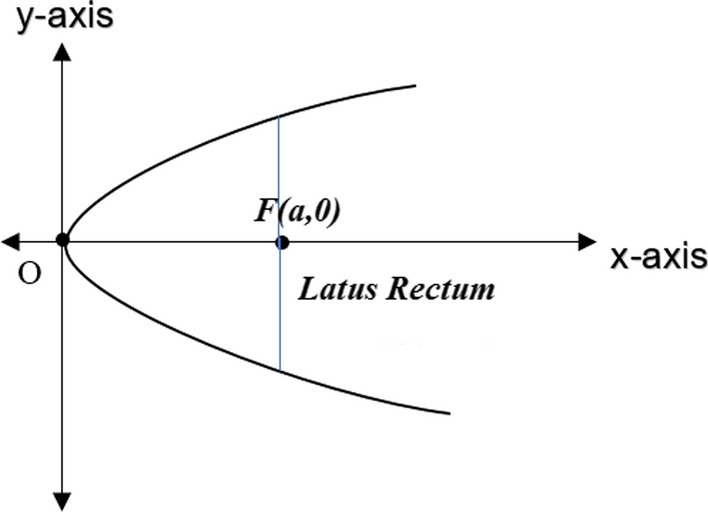
Latus Rectum in parabola
Fig. 5.
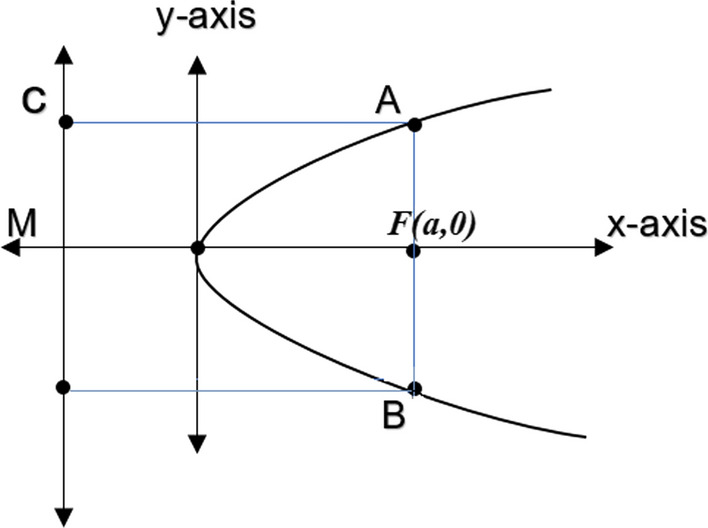
Multiple intersection points in parabola
By definition of Parabola, AF = AC. In Fig. 5, AC = FM as both AC and FM are perpendicular to directrix, AF is perpendicular to x-axis and FM = 2a. As a result, the length of the Rectum is given in Eq. (13).
| 13 |
Logical model of Lips using properties of parabola
Based on the discussion in Sects. 3.1 and 3.2, the procedure for extracting features by using the parabolic theory and the classifying the expressions from the human facial images is presented in this Section. The face is localized and processed with the face boundary detection. The approach proposed by Felzenszwalb et al. (2010) is applied to detect the face portion in the facial images. The boundary coordinates of the face portion is identified by applying Histogram of Oriented Gradients (HOG) and the facial area cropped. The noise present in the cropped facial image is removed by applying bilateral blurring algorithm by Tomasi and Manduchi (1998). The edge information is preserved by using suitable filter along with Gaussian blurring algorithm. All the points contributing to both upper and lower lip regions of the face is preserved using the edge information. The edge is mapped with various points on parabola (lips) as discussed in Sects. 3.1 and 3.2 and constraints are imposed on these points to satisfy the properties of Parabola. The nose of the images is considered as the reference point so that the resultant images are scale, rotation and translation invariant. The reason is that the preprocessing stage locates the face, nose, eyes, etc. In Fig. 6, we show parabola curve discussed in Sects. 3.1 and 3.2 on the facial image for better understanding the theory of the proposed approach. Similarly, the multiple points and multiple rectums are shown in Fig. 6a, b respectively for further understanding the proposed theory using the Parabola.
Fig. 6.
Parabola on lips. a Multiple points, b multiple rectums
In Fig. 7, the effect of variation in scale is shown. The Fig. 7a–d shows the 100%, 75%, 50% and 25% scaled facial images. Even though there is variation in the scale, various points on the lips can be extracted such that the extracted points satisfy the properties of the parabola. Thus, the proposed procedure scale invariant.
Fig. 7.
Scale invarient properties. a Full scale (100%), b 75% Scale, c 50% Scale, d 25% Scale
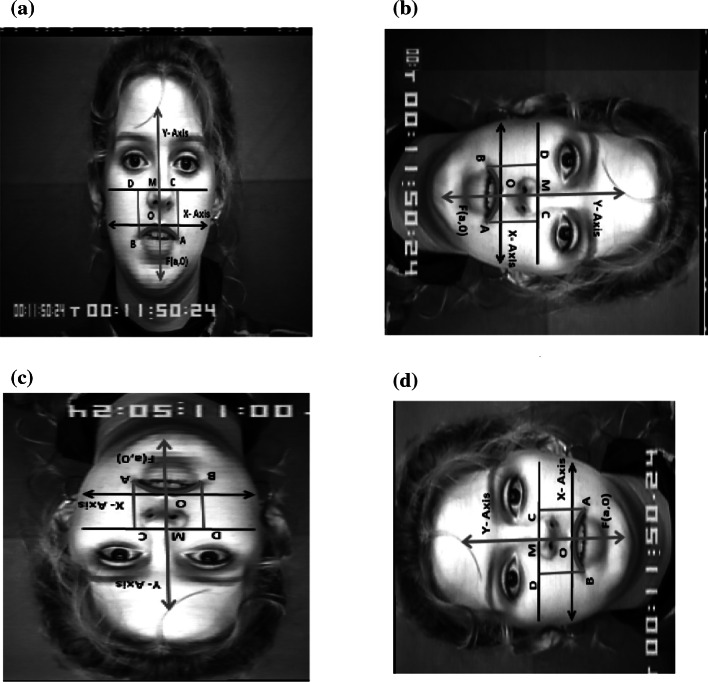
Similarly, in Fig. 8b–d, we show the facial images rotated in 90, 180 and 270 degrees. Since, the nose of the facial image is considered as reference points, even though the facial image is rotated, the points falling on the lip regions can be extracted by imposing the constraint to satisfy the properties of parabola. Thus, the proposed procedure is rotation invariant.
Fig. 8.
Ratation invarient properties a 0 Degree Roataed, b 90 Degree Rotated, c 180 Degree Rotated, d 270 Degree Rotated
In Fig. 9, we show the extracted lip region (Fig. 9a) along with superimposed grid on the lip regions (Fig. 9b). Since, nose is considered as the reference point, the scaled, rotated and translated facial images are pre-processed such that the normal view is restored and the grid is superimposed as shown in Fig. 9b.
Fig. 9.
Localized lip a Preprocessed lip area, b grid superimposed lip area
In Fig. 10 the mechanism of extracting and representing the feature vector is shown.
Fig. 10.

Lip region for extracting and representing feature points
The grid shown in above Fig. is considered as a two-dimensional matrix and the intersection point is considered as a pixel on the lip regions. In the above Fig, R1 and R2 represents upper and lower lip regions respectively and the pixels contributing to these regions are identified corresponding row (n) and column (m) of the grids of the regions. Let I be the super imposed matrix of size m × n. The coordinates of the super imposed matrix is denoted as (Ix, Iy) such that the value of Ix and Iy are within the range of m and n of respective regions (R1 and R2). The points contributing to various regions are represented as . Here, RR1 and RC1 are Maximum Row and Column of the superimposed matrix on Region 1 (R1). Similarly, the points contributing to . Here, RR2 and RC2 are Maximum Row and Column of the superimposed matrix on Region 2 (R2). As a result, each point on the super imposed grid of a region can be considered as feature point on the lip to construct the feature vector. In this paper, we are considering all the points on the lip area as feature points and its deformation is used for estimating the facial expression of human. Also, we impose a constraint on the points on the lip region that it has to satisfy the equation of parabola discussed in Sects. 3.1 and 3.1
Thus, all the points contributing to various regions are represented as:
| 14 |
| 15 |
In the above Eqs. ULRR1 and LLRR2 denotes the Upper and Lower Lips regions respectively. It is observed from Fig. 10 that all the pixel of ULRR1 and LLRR2 is not overlapping with the regions of the Lips. The points having blue colour background is out of lip region and the point with green colour background alone is falling on the lip region. As we have mentioned in Sects. 3.1 and 3.2, we can mathematically determine whether a pixel is falling on a lip region (parabola) or outside the lip region. Thus, if a pixel (point) satisfies Eq. (9), then the point is on the parabola along with the constraints given in Sects. 3.1 and 3.2. In Fig. 11, the parabolic curve is superimposed on the gridded lip regions for further understanding the feature extraction procedure.
Fig. 11.

Lip region with parabolic curve
Further, the points that are contributing to the expression of both the regions can be considered as predicate logic. It is known that a predicate is a Boolean-valued function , which is called a predicate on X. Thus, a predicate can be defined as given in Eq. 16 to find whether a point in Region R1 is satisfying the equation of parabola or not. If the predicate is true, the point is falling on the parabola otherwise it is not. In Eq. 16, X denotes the value of x, y, and F(a, 0) as per Eq. 9 and properties of parabola.
| 16 |
As a result, the predicate for R1 and R2 can be rewritten as given in Eqs. 17 and 18
| 17 |
| 18 |
In above Eqs. and are the points on the Region 1 and Region 2 respectively. and are the focal point in Region 1 and Region 2. Based on the predicates, we consider all the points for which the predicate is true. Thus, the feature vector is expressed as the linear combination and . These points are identified and extracted from facial images that belong to CK++ and JAFFE datasets and feature vector is constructed. The number of points which are falling on the parabola is not a constant and thus the dimension of feature vector is variable in size. The dimension of the feature vector is considered as the number of points forming the feature vector as per Eqs. (17) and (18).
Below, the algorithm for feature extraction is presented. The name of the algorithm is Lip_Feature_Extraction and takes LipGrid and row and col as arguments. The LipGrid is the rectangle sized grid superimposed on the lip regions. The algorithm presented along with the number of primitive operations of each step to analyze the run time complexity of the algorithm. The running time complexity of the algorithm is O(row*col) and the running time of each step is given along side.
Facial expression classification
This Subsection presents the procedure of incorporating points on the lips of human face into feature and then given as input to machine learning algorithms for classification. The approaches such as Support Vector Machine (SVM), Multi-Layer Perceptron (MLP) and Random Forest (RF) algorithms are used for classifying the facial expression based on lip features. The performance of each of the classifiers is presented below.
Support vector machine (SVM)
The SVM is one of the well-known machine learning algorithms. It addresses a binary pattern classification problem, which has a set of hyper plane in an infinite dimensional space. As a result, it is considered as the linear and nonlinear SVM. In SVM, the margin between various classes is minimized effectively while maintaining a minimum training set error. It is possible to find global minima very easily as the SVM are a convex quadratic programming method. However, it is important to set and tune various parameters for the SVM classifier. Some of the important parameters are penalty and smoothness of the Radial-Based Function. The feature database is trained by the SVM as given below. The training data set TS is represented as follows
| 19 |
In the above Eq. (19) both represent the points on the lips, is the corresponding emotional expression category and n is the size of the dataset. In the experiments Section, n-fold cross validation is used on the dataset for training the SVM. The approach used the multi-class binary SVM classifier to recognize basic six emotional expressions. The facial images from CK++ and JAFFE datasets are segregated into different known classes. Since it is a supervised learning method, the training set classes are labeled for each expression category. The SVM is a supervised classification model without any assumptions on the data distribution and it optimizes the location of the decision boundary between classes. The linear kernel function is used for training the classifier, where each input (xi, yi) has d attributes to denote its class cj = {Emotional Expressions}. The training data is in the form as shown in Eq. (19). Once the classification is learnt for an expression class, it is extended for all other possible classes. All the six possible emotional expressions are obtained along with discrimination accuracy as shown in below Fig. 12.
Fig. 12.

Sample multiclass output space of SVM
Multi-layer perceptron (MLP)
Let us consider the points on both the lower and upper lips. If it has m input data , it is called as m features. A feature, say one row of the feature database is considered as one variable, which influences a specific outcome of the emotional category. Each of the m features is multiplied with a weight (w1, w2, …, wm) and then summed them all together for obtaining a dot product as given below.
| 20 |
| 21 |
Here, m features are given as input in the form of (X, Y) to the input layers of the MLP as shown in Fig. 13. Suitable weights are determined during the training process such that the dot product is calculated between weights and inputs as shown in Eqs. (20) and (21). Similarly, the weights for each neuron in the hidden layers are also calculated. The dot product between the weights and input values of hidden layer similar to the input layer and as a result, the hidden layer is considered as yet another single layer perceptron.
Fig. 13.

Typical structure of multi-layer perceptron
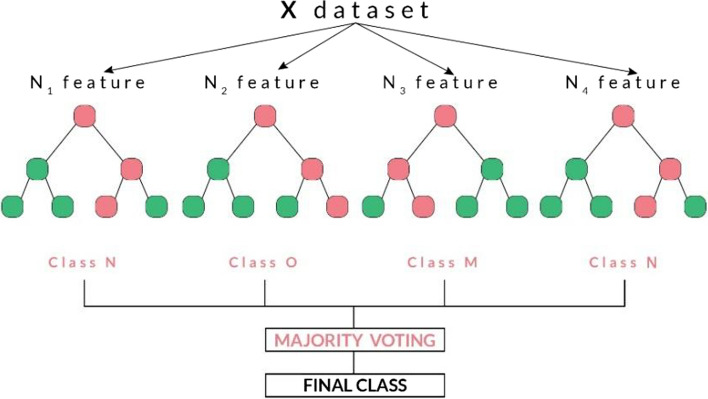
Random forest
Random Forest (RF) classifier consists of a large number of individual decision trees that operate as an ensemble. Each individual tree in the Random Forest spans a class prediction and the class with the most votes is prediction model. A typical structure of Random Forest is shown Fig. 14.
Fig. 14.
Typical structure of random forest
The procedure of training the Random Forest in the proposed approach is as follows. We considered the feature vector (P), extracted from each data sets and used for training the classifier.
| 22 |
| 23 |
In the above Eqs. (22–23), n is the number of data samples for training and m is number of emotional expression classes. Now, given the training set P, with responses Q, select a random sample to replace the training set by repeatedly performing bagging for B times. Once the training is over, the predictions on unseen samples can be estimated by averaging the predictions from all the individual regression tree on , which is given below Eq. (24).
| 24 |
The proposed approach minimizes the variance of the model given above to have strongly de-correlating trees. In addition, the uncertainty of prediction on sample can be written as follows.
| 25 |
In the above Eq. (25) B is the number of samples.
In all the classifiers, the training is n-fold cross-validated to ensure the participation of each sample in both training and testing for improving the classification accuracy. The performance of each classifier is presented in Sect. 4.
Experimental results
Details of dataset
The performance of the proposed approach in terms of classification accuracy is presented in this Section. As mentioned earlier, Cohn–Kanade Facial Expression (CK++) and Japanese Female Facial Expression (JAFFE) datasets are used for evaluation. The CK++ Facial Expression dataset consists of 593 images with 123 different subjects. The JAFFE dataset consists of 10 different subjects with 213 gray scale expression images with the resolutions of 256 × 256 pixels in crowning state. The dataset has different emotional category images such as 30 anger, 29 disgust, 31 happiness, 32 fear, 31 sad, 30 surprise and 30 neutral. The feature from all the images in the databases are extracted and built feature database. A tenfold cross validation with the Python’s stratified K-fold algorithm is applied on the feature dataset to have testing and training datasets.
Classification accuracy of proposed approach
As discussed earlier in Sect. 3.4, we use SVM, MLP, and RF algorithms for classifying the facial expressions. The Lib SVM classifier is used along with the Linear, Polynomial, Radial Basis Function (RBF) and Sigmoid as kernel in SVM. During the training stage, C and gamma values are set to 20 and 0.1 respectively in RBF to search the optical parameters automatically. Ensemble learning is used for evaluation and the learning rate for MLP model is set to 0.3, momentum as 0.2 and training time is set as 500. Two ensemble models such as Adaboost meta-algorithm with RF and Bagging with Hidden Markov Model (HMM) are used for training. In the RF tree, resampling technique is used to choose random subset of the dataset. The classification accuracy is presented for various classifiers on JAFFE and CK++ datasets.
Table 1 presents classification accuracy for JAFFE dataset with LibSVM and RBF. The values in the confusion matrix represent the number of images for a particular facial expression. For instance, in Table 1, out of 30 surprise facial expression samples, 25 are rightly classified as surprise and 5 are misclassified as anger, happy and disgust. The results show that the proposed approach correctly classifies 196 images out of 213 images, resulting for an accuracy of 92%. The classification accuracy for other expressions is also presented in Table 1.
Table 1.
Classification accuracy using Lib SVM (RBF) on JAFFE dataset
| Facial expressions | Classification accuracy (%) | |
|---|---|---|
|
Angry | 93.33 |
| Disgust | 93.10 | |
| Fear | 87.50 | |
| Happiness | 96.77 | |
| Neutral | 100 | |
| Sadness | 90.03 | |
| Surprise | 83.33 | |
| Overall Accuracy: 92% |
Below, the classification accuracy on JAFFE using MLP is presented in Table 2, classification accuracy using Bagging +HMM is presented in Table 3 and classification accuracy using the Adaboost + RF is presented in Table 4.
Table 2.
Classification Accuracy using MLP on JAFFE dataset
| Facial expressions | Rec. rate (%) | |
|---|---|---|
|
Angry | 96.67 |
| Disgust | 93.10 | |
| Fear | 87.50 | |
| Happiness | 100 | |
| Neutral | 100 | |
| Sadness | 93.54 | |
| Surprise | 90 | |
| Overall Accuracy: 94.40% |
Table 3.
Classification Accuracy using Bagging + HMM on JAFFE dataset
| Facial expressions | Rec. rate (%) | |
|---|---|---|

|
Angry | 100 |
| Disgust | 96.55 | |
| Fear | 90.62 | |
| Happiness | 100 | |
| Neutral | 100 | |
| Sadness | 93.54 | |
| Surprise | 96.67 | |
| Overall Accuracy: 96.76% |
Table 4.
Recognition Rate using Adaboost + RF on JAFFE dataset
| Facial expressions | Rec. rate (%) | |
|---|---|---|
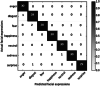
|
Angry | 100 |
| Disgust | 96.55 | |
| Fear | 87.50 | |
| Happiness | 96.77 | |
| Neutral | 100 | |
| Sadness | 96.77 | |
| Surprise | 96.67 | |
| Overall Accuracy: 96.32% |
It is observed that the highest classification accuracy is for happy expression. The misclassification rate is low for fear expression. The overall classification accuracy is 94.4%. The accuracy is improved for the combination Bagging + HMM. The classification accuracy of anger disgust, fear, etc. have increased to 96.76%. Similarly, Adaboost + RF has further improved the overall classification accuracy as 96.32% as shown in Table 4. It is observed from all the above results that the classification accuracy for angry and happy expressions is 100%.
In addition, the performance of the proposed approach is compared with the other competitive approaches on JAFFE and CK++ datasets. In Table 5, the performance comparison on JAFFE dataset is presented and the Adaboost + RF is used for classification. This is due to the fact that Adaboost + RF has given good results on JAFFE dataset. In all the experiments on JAFFE datasets, images having open mouth faces are considered. It is observed from the Table 5 that the performance of the proposed approach is encouraging compared to all other method presented. Similarly, the performance of the proposed approach on CK++ dataset is presented along with comparison in Table 6. The CK++ dataset contains exaggerated open mouth images and distinguishable from other emotional expression categories. As mentioned earlier on CK++ dataset, we have used Adaboost + RF combination for classification. The overall classification accuracy is encouraging. This is due to the fact that the proposed approach effectively captures the feature points. The procedure of converting the feature points as feature vector is more effective, such that the extracted feature vector is discriminative.
Table 5.
Performance comparison of proposed approach and other comparative approaches on JAFFE Dataset
| Approaches | Angry | Disgust | Fear | Happy | Sad | Surprise | Avg. accuracy (%) |
|---|---|---|---|---|---|---|---|
| Proposed approach | 100 | 96.55 | 87.50 | 96.77 | 96.77 | 96.67 | 96.32 |
| Tong et al. (2014) | 93.13 | 93.34 | 88.30 | 97.10 | 90.42 | 90.15 | 92.07 |
| Kahou et al. (2016) | 100 | 90.20 | 93.81 | 96.80 | 90.41 | 96.70 | 94.65 |
| Ghimire et al. (2015) | 90.21 | 92.02 | 91.01 | 96.30 | 92.40 | 96.11 | 93.05 |
| Shen et al. (2012) | 96.71 | 93.11 | 93.08 | 95.05 | 94.32 | 91.33 | 94.11 |
| Mistry et al. (2017) | 93.13 | 87.51 | 75.10 | 100 | 93.31 | 96.73 | 90.98 |
| Jyoti et al. (2016) | 96.72 | 90.50 | 93.08 | 93.16 | 93.06 | 90.10 | 92.77 |
| Swaminathan, et al. (2020) | 98.0 | 95.21 | 85.0 | 96.00 | 95.81 | 95.80 | 94.30 |
| Haq et al. (2019) | 98.10 | 95.00 | 85.0 | 95.00 | 94.81 | 95.00 | 93.81 |
| Zhou et al. (2020) | 98.1 | 95.51 | 85.5 | 96.50 | 96.21 | 96.30 | 94.68 |
Table 6.
Performance comparison of proposed approach and other comparative approaches on CK++ Database
| Approaches | Angry | Disgust | Fear | Happy | Sad | Surprise | Avg. Accuracy (%) |
|---|---|---|---|---|---|---|---|
| Proposed Approach | 96.11 | 93.13 | 95.15 | 100 | 98.77 | 95.02 | 96.36 |
| Tong et al. (2014) | 96.15 | 94.67 | 96.90 | 98.12 | 96.47 | 90.12 | 95.40 |
| Kahou et al. (2016) | 97.51 | 94.63 | 85.63 | 98.02 | 92.31 | 96.21 | 94.05 |
| Ghimire et al. (2015) | 92.12 | 98.17 | 93.12 | 96.66 | 94.51 | 95.72 | 94.55 |
| Shen et al. (2012) | 93.13 | 93.58 | 90.05 | 94.15 | 92.15 | 96.11 | 93.19 |
| Mistry et al. (2017) | 89.91 | 94.62 | 89.61 | 97.71 | 88.94 | 92.15 | 92.15 |
| Jyoti et al. (2016) | 90.18 | 94.43 | 93.13 | 94.26 | 96.48 | 87.51 | 92.66 |
| Swaminathan, et al. (2020) | 95.11 | 91.13 | 94.00 | 98.00 | 96.70 | 93.00 | 94.65 |
| Haq et al. (2019) | 94.90 | 90.00 | 93.00 | 96.80 | 95.30 | 92.88 | 93.81 |
| Zhou et al. (2020) | 94.80 | 90.10 | 92.80 | 96.10 | 94.90 | 93.00 | 93.61 |
The extracted feature vector is further trained using tenfold cross validation such that every data point in the dataset is participating in the training.
Based on the above experiment results, it is observed that the proposed approach achieves higher classification accuracy in recognizing the facial expressions which in turn maps the internal state of human emotions.
Conclusion
The facial expression is important in various computer science applications. The researchers in both academia and industry have concentrated on estimating all the well-known expression categories from the human face. In this work, we have considered features from the human facial images for categorizing the facial expressions. Since, the morphological structure of lip is very close to a Parabola, we have used the theory and properties of the parabola as reference exploited using vertex, symmetry, focal point, rectum, etc. The lip regions are localized, edge information is preserved, and a grid is superimposed on the lip regions and segmented as upper and lower regions. A predicate logic is used to find whether a point is falling on the lip region or not. All the points falling on the both the regions of the lips are considered as feature point and feature vector is constructed. The CK++ and JAFFE datasets are used for performance evaluation. The images of these datasets have different characteristics and thus we found these are suitable candidates for validating the proposed approach. In addition, various machine learning algorithms such as Support Vector Machine, Multilayer Perceptron and Random Forest are used for classification. We have used ensemble models with the all the above mentioned classification algorithms. The dataset is prepared for training and testing using a tenfold cross validation scheme. It is observed that the average classification accuracy of the proposed approach is 96.32%. The expressions such as anger and happiness are classified with 100% accuracy and achieve only 87.50% as classification accuracy for fear. However, overall, the performance of the parabolic based approach is good compared to the well-known, recently proposed approaches. In future, we will use the parabolic characteristics for eye and eye-brow features to improve the classification accuracy further.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
V. Suma Avani, Email: sumaavani2@gmail.com.
S. G. Shaila, Email: shaila-cse@dsu.edu.in
A. Vadivel, Email: vadivel.a@srmap.edu.in
References
- Ahmed F, Bari H, Hossain E. Person-independent facial expression recognition based on compound local binary pattern (CLBP) Int Arab J Inf Technol. 2014;11(2):195–203. [Google Scholar]
- Al-Sumaidaee SAM, Dlay SS, Woo WL, Chambers JA (2015) Facial expression recognition using local gabor gradient code-horizontal diagonal descriptor. In: 2nd IET international conference on intelligent signal processing (ISP), London, pp 1–6. 10.1049/cp.2015.1766
- Arumugam D, Srinivasan P. Emotion classification using facial expression. Int J Adv Comput Sci Appl. 2011;2:92–98. [Google Scholar]
- Bartlett MS, Movellan JR, Sejnowski TJ. Face recognition by independent component analysis. IEEE Trans Neural Netw. 2002;13(6):1450–1464. doi: 10.1109/TNN.2002.804287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carcagnì P, Coco M, Leo M, Distante C. Facial expression recognition and histograms of oriented gradients: a comprehensive study. SpringerPlus. 2015;4(1):645. doi: 10.1186/s40064-015-1427-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chao WL, Ding JJ, Liu JZ. Facial expression recognition based on improved local binary pattern and class-regularized locality preserving projection. J Sig Process. 2015;2:552–561. [Google Scholar]
- Cheon Y, Kim D (2008) A natural facial expression recognition using differential—AAM and k-NNs. In: Tenth IEEE international symposium on multimedia, Berkeley, pp 220–227
- Chien SI, Choi I. Face and facial landmarks location based on log-polar mapping. In: Lee SW, Bülthoff HH, Poggio T, editors. Biologically motivated computer vision (BMCV 2000) Berlin: Springer; 2000. pp. 379–386. [Google Scholar]
- Choi HC, Oh SY (2006) Real time facial expression recognition using active appearance model and multilayer perceptron. In: SICE-ICASE international joint conference, Busan, pp 5924–5927
- Choi S-I, Oh J, Choi C-H, Kim C. Input variable selection for feature extraction in classification problems. Sig Process. 2012;92(3):636–648. [Google Scholar]
- Cootes TF, Edwards GJ, Taylor CJ. Active appearance models. IEEE Trans Pattern Anal Mach Intell. 2001;23(6):681–685. [Google Scholar]
- Cruz AC, Bhanu B, Thakoor NS. Vision and attention theory based sampling for continuous facial emotion recognition. IEEE Trans Affect Comput. 2014;5(4):418–431. [Google Scholar]
- Dalal N, Triggs B (2005) Histograms of oriented gradients for human detection. In: IEEE computer society conference on computer vision and pattern recognition (CVPR ‘05), San Diego, CA, vol 1, pp 886–893
- Darwin C. The expression of the emotions in man and animals. London: John Murray; 1872. [Google Scholar]
- Dosadia P, Poonia A, Gupta SK, Agrwal SL (2015) New Gabor-DCT feature extraction technique for facial expression recognition. In: 5th international conference on communication systems and network technologies (CSNT), Gwalior, pp 546–549
- Ekman P, Friesen WV. Facial action coding system: a technique for the measurement of facial movement. Palo Alto: Consulting Psychologists Press; 1978. [Google Scholar]
- Elaiwat S, Bennamoun M, Boussaid F, El-Sallam A. 3-D Face recognition using curvelet local features. IEEE Signal Process Lett. 2014;21(2):172–175. [Google Scholar]
- Fan X, Tjahjadi T. A spatial-temporal framework based on histogram of gradients and optical flow for facial expression recognition in video sequences. Pattern Recogn. 2015;48:3407–3416. [Google Scholar]
- Felzenszwalb PF, Girshick RB, McAllester D, Ramanan D. Object detection with discriminatively trained part-based models. IEEE Trans Pattern Anal Mach Intell. 2010;32(9):1627–1645. doi: 10.1109/TPAMI.2009.167. [DOI] [PubMed] [Google Scholar]
- Ghimire D, Lee J. Geometric feature-based facial expression recognition in image sequences using multi-class AdaBoost and support vector machines. Sensors J. 2013;13(6):7714–7734. doi: 10.3390/s130607714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghimire D, Lee J. Extreme learning machine ensemble using bagging for facial expression recognition. J Inf Process Syst. 2014;10(3):443–458. [Google Scholar]
- Ghimire D, Jeong S, Yoon S, Choi J, Lee J (2015) Facial expression recognition based on region specific appearance and geometric features. In: 2015 Tenth International Conference on Digital Information Management (ICDIM), Jeju, pp 142–147
- Goa T, Fenga XL, Lub H, Zhaia JH. A novel face feature descriptor using adaptively weighted extended LBP pyramid. J Opt. 2013;124:6286–6291. [Google Scholar]
- Haq MU, Shahzad A, Mahmood Z, Shah AA. Boosting the face recognition performance of ensemble based LDA for Pose, non-uniform illuminations, and low-resolution images. KSII Trans Internet Inf Syst. 2019;13(6):3144–3166. [Google Scholar]
- He C, Mao H, Jin L. Realistic smile expression recognition using biologically inspired features. In: Wang D, Reynolds M, editors. Advances in artificial intelligence (AI 2011) Berlin: Springer; 2011. pp. 590–599. [Google Scholar]
- Huang CL, Huang YM. Facial expression recognition using model based feature extraction and action parameters classification. J Vis Commun Image Represent. 1997;8(3):278–290. [Google Scholar]
- Huang X, Zhao G, Zheng W, Pietikäinen M. Towards a dynamic expression recognition system under facial occlusion. Pattern Recogn Lett. 2012;33(16):2181–2191. [Google Scholar]
- Jabid T, Kabir MH, Chae O (2010) Facial expression recognition using Local Directional Pattern (LDP). In: 2010 IEEE international conference on image processing, Hong Kong, pp 1605–1608
- Jeong G-M, Ahn H-S, Choi S-I, Kwak N, Moon C. Pattern recognition using feature feedback: application to face recognition. J Control Autom Syst. 2010;8(1):141–148. [Google Scholar]
- Jyoti K, Rajesh R, Pooja KM. Facial expression recognition: a survey. Procedia Comput Sci. 2015;58:486–491. [Google Scholar]
- Jyoti K, Rajesh R, Abhinav K (2016) Fusion of features for the effective facial expression recognition. In: International conference on communication and signal processing (ICCSP), Melmaruvathur, India, pp 0457–0461
- Kahou SE, Bouthillier X, Lamblin P, et al. EmoNets: multimodal deep learning approaches for emotion recognition in video. J. Multimodal User Interfaces. 2016;10(2):99–111. doi: 10.1007/s12193-015-0195-2. [DOI] [Google Scholar]
- Kaur M, Vashisht R, Neeru N. Recognition of Facial Expressions with principal component analysis and singular value decomposition. Int J Comput Appl. 2010;9(12):0975–8887. [Google Scholar]
- Khan RA, Meyer A, Konik H, Bouakaz S. Framework for reliable, real-time facial expression recognition for low resolution images. Pattern Recogn Lett. 2013;34:1159–1168. [Google Scholar]
- Khan SA, Ansari NR, Akram S, Latif S. Facial expression recognition using computationally intelligent techniques. J Intell Fuzzy Syst. 2015;28:2881–2887. [Google Scholar]
- Khan SA, Hussain A, Usman M. Facial expression recognition on real world face images using intelligent techniques: a survey. Optik Int J Light Electron Opt. 2016;127(15):6195–6203. [Google Scholar]
- Khan SA, Hussain S, Xiaoming S, Yang S. An effective framework for driver fatigue recognition based on intelligent facial expressions analysis. IEEE Access. 2018;6:67459–67468. doi: 10.1109/ACCESS.2018.2878601. [DOI] [Google Scholar]
- Khan SA, Hussain A, Usman M. Reliable facial expression recognition for multi-scale images using weber local binary image based cosine transform features. Multimed Tools Appl. 2018;77:1133–1165. doi: 10.1007/s11042-016-4324-z. [DOI] [Google Scholar]
- Khandait SP, Thool RC, Khandait PD. Automatic facial feature extraction and expression recognition based on neural network. Int J Adv Comput Sci Appl. 2011;2:113–118. [Google Scholar]
- Ko KE, Sim KB. Emotion recognition in facial image sequences using a combination of AAM with FACS and DBN. In: Liu H, Ding H, Xiong Z, Zhu X, editors. Intelligent robotics and applications (ICIRA 2010) Berlin: Springer; 2010. pp. 702–712. [Google Scholar]
- Kristensen RL, Tan Z-H, Ma Z, Gou J (2014) Emotion recognition in blurred images with local features and machine learning. Master Thesis, pp 130.
- Krizhevsky A, Sutskever I, Hinton GE (2012) Imagenet classification with deep convolutional neural networks. In: Pereira FBurges C, Bottou L, Weinberger K (eds), Advances in neural information processing systems, Curran Associates, vol 25, pp 1097–1105
- Lajevardi SM, Hussain ZM (2009) Feature selection for facial expression recognition based on optimization algorithm. In: 2nd international workshop on nonlinear dynamics and synchronization, Klagenfurt, pp 182–185
- Lekshmi VP, Vidyadharan DS, Naveen S (2008) Analysis of facial expressions using PCA on half and full faces. In: Proceedings of international conference of audio, language and image processing (ICALIP), pp 1379–1383
- Lin DT. Facial expression classification using PCA and hierarchical radial basis function network. J Inf Sci Eng. 2006;22:1033–1046. [Google Scholar]
- Liu P, Han S, Meng Z, Tong Y (2014) Facial expression recognition via a boosted deep belief network. In: IEEE conference on computer vision and pattern recognition, Columbus, pp 1805–1812
- Long TB, Thai LH, Hanh T. Facial expression classification method based on pseudo-zernike moment and radial basis function network. Int J Mach Learn Comput. 2012;2(4):402–405. [Google Scholar]
- Lowe DG (1999) Object recognition from local scale-invariant features. In: Seventh IEEE international conference on computer vision, Kerkyra, Greece, vol 2, pp 1150–1157
- Lyons MJ, Budynek J, Akamatsu S. Automatic classification of single facial images. IEEE Trans Pattern Anal Mach Intell. 1999;21(12):1357–1362. [Google Scholar]
- Mistry K, Zhang L, Neoh SC, Lim CP, Fielding B. A microGA embedded PSO feature selection approach to intelligent facial emotion recognition. IEEE Trans Cybern. 2017;47(6):1496–1509. doi: 10.1109/TCYB.2016.2549639. [DOI] [PubMed] [Google Scholar]
- Munir A, Hussain A, Khan SA, Nadeem M, Arshid S. Illumination invariant facial expression recognition using selected merged binary patterns for real world images. Optik. 2018;158:1016–1025. [Google Scholar]
- Niu Z, Qiu X (2010) Facial expression recognition based on weighted principal component analysis and support vector machines. In: 3rd international conference on advanced computer theory and engineering (ICACTE), vol 3, pp V3-174–V3-178
- Ouyang Y, Sang N, Huang R. Accurate and robust facial expressions recognition by fusing multiple sparse representation based classifiers. J Neurocomput. 2015;149:71–78. [Google Scholar]
- Pai N-S, Chang S-P. An embedded system for real-time facial expression recognition based on the extension theory. Comput Math Appl. 2011;61(8):2101–2106. [Google Scholar]
- Sadeghi H, Raie AA, Mohammadi MR (2013) Facial expression recognition using geometric normalization and appearance representation. In: 8th Iranian conference on machine vision and image processing (MVIP), Zanjan, pp 159–163
- Schels M, Schwenker F (2010) A multiple classifier system approach for facial expressions in image sequence utilizing GMM Supervectors. In: 20th international conference on pattern recognition, Istanbul, pp 4251–4254
- Shan C, Gong S, Mc Owan PW (2005) Conditional mutual information based boosting for facial expression recognition. In: Clocksin WF, Fitzgibbon AW, Torr PHS (eds), Proceedings of the British machine conference (BMVC), pp 1–10. 10.5244/c.19.42
- Shan C, Gong S, McOwan PW. Facial expression recognition based on local binary patterns: a comprehensive study. Image Vis Comput. 2009;27(6):803–816. [Google Scholar]
- Shen X, Wu Qi FuX. Effects of the duration of expressions on the recognition of microexpressions. Journal of Zhejiang University Science B. 2012;13(3):221–30. doi: 10.1631/jzus.B1100063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siddiqi MH, Lee S, Lee Y-K, Khan AM, Truc PTH. Hierarchical recognition scheme for human facial expression recognition systems. Sensors J. 2013;13:16682–16713. doi: 10.3390/s131216682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su C, Deng J, Yang Y, Wang G. Expression recognition methods based on feature fusion. In: Yao Y, Sun R, Poggio T, Liu J, Zhong N, Huang J, editors. Brain informatics (BI 2010) Berlin: Springer; 2010. pp. 346–356. [Google Scholar]
- Swaminathan A, Vadivel A, Arock M. FERCE: facial expression recognition for combined emotions using FERCE algorithm. IETE J Res. 2020 doi: 10.1080/03772063.2020.1756471. [DOI] [Google Scholar]
- Tian YL, Kanade T, Cohn JF. Handbook of face recognition. New York: Springer; 2005. Facial expression analysis. [Google Scholar]
- Tomasi C, Manduchi R (1998) Bilateral filtering for gray and color images. In: Proceedings of the 1998 IEEE international conference on computer vision, Bombay, India
- Tong Y, Chen R, Cheng Y. Facial expression recognition algorithm using LGC based on horizontal and diagonal prior principle. Optik Int J Light Electron Opt. 2014;125(16):4186–4189. [Google Scholar]
- Turk MA, Pentland AP (1991) Face recognition using eigenfaces. In: IEEE computer society conference on computer vision and pattern recognition. Maui, HI, pp 586–591
- Ucar A, Demir Y, Guzelis C. A new facial expression recognition based on curvelet transform and online sequential extreme learning machine initialized with spherical clustering. Neural Comput Appl. 2016;27:131–142. [Google Scholar]
- Wang X, Liu X, Lu L, Shen Z (2014) A new facial expression recognition method based on geometric alignment and LBP features. In: IEEE 17th international conference on computational science and engineering, Chengdu, pp 1734–1737
- Wang L, Li RF, Wang K, Chen J. Feature representation for facial expression recognition based on FACS and LBP. Int J Autom Comput. 2015;11(5):459–468. [Google Scholar]
- Wang Z, Ruan Q, An G. Facial expression recognition using sparse local fisher discriminant analysis. Neurocomputing. 2016;174:756–766. [Google Scholar]
- Xu M, Cheng W, Zhao Q, Ma L, Xu F (2015) Facial expression recognition based on transfer learning from deep convolutional networks. In: 11th international conference on natural computation (ICNC), Zhangjiajie, pp 702–708
- Yu K, Wang Z, Zhuo L, Wang J, Chi Z, Feng D. Learning realistic facial expressions from web images. Pattern Recogn. 2013;46:2144–2155. [Google Scholar]
- Yuan LUO, Wu C, Zhang Y. Facial expression feature extraction using hybrid PCA and LBP. J China Univ Posts Telecommun. 2013;20(2):120–124. [Google Scholar]
- Yun W, Kim D, Park C, Kim J (2013) Multi-view facial expression recognition using parametric kernel Eigenspace method based on class features. In: IEEE conference on systems, man and cybernetics, Manchester, pp 2689–2693
- Zhang W, Zhang Y, Ma L, Guan J, Gong S. Multimodal learning for facial expression recognition. Pattern Recogn. 2015;48:3191–3202. [Google Scholar]
- Zheng W, Zong Y, Zhou X, Xin M. Cross-domain color facial expression recognition using transductive transfer subspace learning. IEEE Trans Affect Comput. 2018;9(1):21–37. [Google Scholar]
- Zhou F, Kong S, Fowlkes CC, Chen T, Lei B. Fine-grained facial expression analysis using dimensional emotion model. Neurocomputing. 2020;392(7):38–49. [Google Scholar]