A Machine Learning Classifier Improves Mortality Prediction Compared With Pediatric Logistic Organ Dysfunction-2 Score: Model Development and Validation

Supplemental Digital Content is available in the text.

Abstract

Objectives:

To determine whether machine learning algorithms can better predict PICU mortality than the Pediatric Logistic Organ Dysfunction-2 score.

Design:

Retrospective study.

Setting:

Quaternary care medical-surgical PICU.

Patients:

All patients admitted to the PICU from 2013 to 2019.

Interventions:

None.

Measurements and Main Results:

We investigated the performance of various machine learning algorithms using the same variables used to calculate the Pediatric Logistic Organ Dysfunction-2 score to predict PICU mortality. We used 10,194 patient records from 2013 to 2017 for training and 4,043 patient records from 2018 to 2019 as a holdout validation cohort. Mortality rate was 3.0% in the training cohort and 3.4% in the validation cohort. The best performing algorithm was a random forest model (area under the receiver operating characteristic curve, 0.867 [95% CI, 0.863–0.895]; area under the precision-recall curve, 0.327 [95% CI, 0.246–0.414]; F1, 0.396 [95% CI, 0.321–0.468]) and significantly outperformed the Pediatric Logistic Organ Dysfunction-2 score (area under the receiver operating characteristic curve, 0.761 [95% CI, 0.713–0.810]; area under the precision-recall curve (0.239 [95% CI, 0.165–0.316]; F1, 0.284 [95% CI, 0.209–0.360]), although this difference was reduced after retraining the Pediatric Logistic Organ Dysfunction-2 logistic regression model at the study institution. The random forest model also showed better calibration than the Pediatric Logistic Organ Dysfunction-2 score, and calibration of the random forest model remained superior to the retrained Pediatric Logistic Organ Dysfunction-2 model.

Conclusions:

A machine learning model achieved better performance than a logistic regression-based score for predicting ICU mortality. Better estimation of mortality risk can improve our ability to adjust for severity of illness in future studies, although external validation is required before this method can be widely deployed.

R isk of mortality is often used to stratify severity of illness for research and quality improvement  efforts in ICUs (1). In the PICU, more organ failure has been found to be associated with mortality, and few patients die without having multiple organ dysfunction syndrome (MODS) (2). The Pediatric Logistic Organ Dysfunction (PELOD) score was developed in 1999 and is based on ten variables measuring degree of organ failure across five organ systems (3). It is the most frequently used score to describe pediatric MODS, but its performance worsened over time as clinical presentations and practice, such as patient demographics, disease prevalence, monitoring, treatment, and mortality rates, have changed (1, 4–6). The PELOD score was updated to PELOD-2 to include mean arterial pressure (MAP) and lactatemia, which are also variably present in the Sequential Organ Failure Assessment (SOFA) (7), pediatric SOFA (8), and Pediatric MODS scores (9), and hepatic dysfunction was removed (1). The discrimination (as measured by area under the receiver operating characteristic curve [AUC]) of PELOD-2, which is a multivariable logistic regression model, for predicting mortality ranges from 0.773 to 0.934 in several PICU populations (1, 10–12). Logistic regression is among the most commonly used prediction methods in biomedicine because it converges on parameter estimates relatively easily, is familiar, and is easy to implement (13). However, machine learning methods often result in improved predictive accuracy, although interpretability of how each risk factor included in the model relates to the outcome may be more challenging (14–16).

One challenge related to using severity scores such as PELOD-2 is the time required to gather the necessary data (17). Sauthier et al (10) created an automatic algorithm to calculate PELOD-2 (called “aPELOD-2” by the authors) from the electronic health record (EHR) that was less labor intensive and had better discrimination for survival than the manually calculated score. This automated method enables researchers to use amounts of data that would be challenging for humans to process in a reasonable amount of time (10). We aimed to use the larger datasets enabled by aPELOD-2 to develop and validate machine learning models with improved prediction of PICU mortality. Our hypothesis was that, even when using the same variables as the traditional PELOD-2 score, a machine learning approach would demonstrate improved discrimination and calibration. By using the same input variables, we examined specifically the impact of a different modeling approach, as opposed to the effect of different data types, on our ability to predict mortality.

MATERIALS AND METHODS

Patients and Setting

We conducted a retrospective study of patients admitted to the Medical-Surgical ICU (MSICU) at Boston Children’s Hospital from 2013 to 2019. Patients in the MSICU represent the full spectrum of pediatric critical illness, excluding patients whose primary reason for admission relates to congenital or acquired pediatric heart disease. We included all patients admitted during the study period. Each ICU admission for patients admitted more than once was analyzed independently. Patients admitted from 2013 to 2017 were used for model training, and patients admitted from 2018 to 2019 were used for validation. The Boston Children’s Hospital Institutional Review Board approved the study with a waiver of informed consent (Protocol P00036084). We conducted the study in accordance with the principles described in the Transparent Reporting of a Multivariable Prediction Model for Individual Prognosis or Diagnosis (TRIPOD) guidelines (18) and the guidelines from the editors of Respiratory, Sleep, and Critical Care Journals (19). A TRIPOD checklist is provided in the Online Supplement (http://links.lww.com/CCX/A614).

Data

All data were extracted directly from the institutional data warehouse, which combines data from several source systems used for routine clinical and operational purposes. The primary outcome was PICU mortality. Independent variables were those used to calculate the PELOD-2 score: Glasgow Coma Scale score, pupillary reaction, lactate, MAP, creatinine, ratio of Pao₂ to Fio₂, Paco₂, whether invasive mechanical ventilation was used, WBC count, and platelet count. We used the method described by Sauthier et al (10) to calculate PELOD-2 score using EHR data. The most abnormal value—defined as in the original PELOD-2 score (1)—for each variable recorded within the first 24 hours of PICU admission was included.

The original PELOD-2 score used cut offs to transform continuous independent variables into categorical predictors because the log-linearity assumption was not verified (1). Because machine learning models are not constrained by this assumption, which results in simplification if not loss of data, we did not transform continuous variables in this manner. However, using continuous variables required additional modifications to the PELOD-2 model. Although age was not used separately as a predictor in PELOD-2, because normal MAP and creatinine vary with age, PELOD-2 used different age-specific cut offs for these variables, and thus age was implicitly included in the PELOD-2 model. We included age as an independent variable in our models because we did not create age-specific categorical variables for MAP and creatinine. PELOD-2 assumed that when certain values were not measured in the first 24 hours of ICU admission, they were normal. We similarly assigned normal values to Glasgow Coma Scale score and pupillary reaction and assumed there was no use of invasive ventilation when values for these variables were not recorded. However, for age-varying continuous variables, more complex imputation was required (PELOD-2 assigns a score of 0 for these variables, regardless of age). For MAP and creatinine, we used k-nearest neighbor (knn) imputation to assign values to missing data (19). Three nearest neighbors were used in order to avoid changing the original distribution of the data (20). The knn model was fit using training data only. This model was then applied to both the training and holdout validation data to impute missing values. For the remaining (not age-dependent) continuous physiologic and laboratory variables, we assigned a fixed normal value (Supplemental Table 1, http://links.lww.com/CCX/A614). We also compared model performance when assigning a random number from a continuous uniform distribution of normal values (Supplemental Table 1, http://links.lww.com/CCX/A614). Pao₂ was estimated from Fio₂, and Paco₂ using the alveolar gas equation (21).

Analysis

All continuous variables were centered and scaled. We explored performance of various classes of machine learning models: decision trees, Naïve Bayes, support vector machine, knn, boosted ensemble, and random forest. The outcome of interest was mortality during the index PICU admission.

All of the predictor variables were included in each model. Each model was trained using the training data. Hyperparameters were optimized for area under the precision-recall curve (AUPRC) using Bayesian optimization and five-fold cross-validation on the training data (22). The ranges of values tested for each hyperparameter are shown in Supplemental Table 2 (http://links.lww.com/CCX/A614). The AUPRC objective function was evaluated 30 times based on the expected-improvement-per-second-plus acquisition function that evaluates hyperparameters based on expected amount of improvement in the objective function while modifying behavior to reduce overexploitation (23). The classification thresholds were chosen to maximize F1, the harmonic mean of precision (positive predictive value [PPV]) and recall (sensitivity), for each model. Final performance was reported based on evaluation of each model on the holdout validation data. Risk of mortality using PELOD-2 (10) was also evaluated on the patients in the validation dataset for comparison. As a stronger baseline, we additionally relearned the PELOD-2 logistic regression model (using the same cut offs to create categorical variables as in the original PELOD-2 description [1]) in our training data and evaluate the retrained model on the holdout validation set. We report mean performance with 95% CIs calculated on 1,000 bootstrap replications of the validation dataset. We assessed discrimination using AUC, which is traditionally used to report discrimination for mortality risk models, as well as F1 and AUPRC, which better represent performance of models for rare events (24). We also report accuracy, sensitivity, specificity, PPV, and negative predictive value. AUC of the best performing model and the relearned PELOD-2 were compared using DeLong’s method (25). We evaluated the relationship between observed and predicted probabilities of death in the validation set with a calibration plot (26) using the loess algorithm (27). Overall fit was assessed with the scaled Brier score (28), and calibration was assessed with the Hosmer-Lemeshow goodness of fit test (29).

The PELOD-2 calculation and data preprocessing were performed using R Version 4.0.1 (R Foundation for Statistical Computing, Vienna, Austria). knn imputation was performed using the caret package Version 6.0-86 (30). DeLong’s test was performed using the pROC package Version 1.16.2 (31). Calibration curves were plotted using the ggplot2 package Version 3.3.2 (32). Hosmer-Lemeshow goodness of fit was performed using the ResourceSelection package Version 0.3-5 (33). All other analyses were performed using MATLAB Version 9.7 (Mathworks, Natick, MA).

RESULTS

A total of 10,194 admissions for 6,949 patients were included in the training data, and 4,043 admissions for 3,031 patients were included in the validation data (Table 1). Mortality was 3.0% in the training data and 3.4% in the validation data. PELOD-2 scores were similar in the training and validation cohorts. Frequency of missing data is reported in Table 1.

TABLE 1.

Patient Characteristics and Description of Missing Data

Variables	Training Set (n = 10,194)	Training Set Missing Data	Validation Set (n = 4,043)	Validation Set Missing Data
Male sex	5795 (56.8)	0 (0)	2,285 (56.5)	0 (0)
Diagnosis type		105 (1.0)		13 (0.3)
Bone marrow transplant/stem  cell transplant	225 (2.2)		121 (3.0)
Other medical	1,581 (15.5)		587 (14.5)
Neurology	4,025 (39.5)		1681 (41.6)
Oncology	1,014 (9.9)		475 (11.7)
Surgical	3,244 (31.8)		1,166 (28.8)
Died	302 (3.0)	0 (0)	136 (3.4)	0 (0)
Age at admission (mo)	81 (23–170)	0 (0)	76 (21–165)	0 (0)
Maximum Paco2 (mm Hg)	45.1 (39.8–52.1)	5,634 (55)	44.5 (39.5–51.5)	2,317 (57)
Maximum creatinine (mg/dL)	0.4 (0.2–0.6)	2,485 (24)	0.4 (0.2–0.6)	978 (24)
Minimum Glasgow Coma Scale score	14 (11–15)	85 (1)	14 (10–15)	54 (1)
Maximum lactate (mmol/L)	1.5 (1–2.5)	6,593 (65)	1.4 (1–2.3)	2,657 (66)
Minimum mean arterial pressure (mm Hg)	54 (47–61)	46 (0.5)	54 (47–61)	17 (0.4)
Minimum ratio of the Pao2 to Fio2	280 (176–391)	8,147 (80)	287 (183–399)	3,240 (80)
Minimum platelets (× 109/L)	217 (146–290)	3,397 (33)	206 (140–272)	1,397 (35)
Minimum WBC count (× 109/L)	9.2 (6.4–12.7)	3,396 (33)	9.2 (6.2–12.6)	1,397 (35)
Pupillary reaction: both fixed	180 (1.8)	48 (0.5)	63 (1.6)	17 (0.4)
Use of mechanical ventilation	3,049 (30)	0 (0)	1,236 (31)	0 (0)
Pediatric Logistic Organ Dysfunction-2 Score	3 (2–6)	0 (0)	3 (2–6)	0 (0)

Data shown are median (interquartile range) or n (%).

The optimized hyperparameters are shown in Supplemental Table 2 (http://links.lww.com/CCX/A614). The machine learning model with the best performance, as assessed by F1 score, was a random forest classifier, which we term PELOD_RF (Table 2). Additional performance metrics for the models are shown in Supplemental Table 3 (http://links.lww.com/CCX/A614). Performance of most models was worse when a random normal value was chosen from a range of plausible values as compared to using a single, fixed normal value for continuous variables (Supplemental Table 4, http://links.lww.com/CCX/A614). PELOD_RF showed higher AUC (0.867 [95% CI, 0.863–0.895]) than the PELOD-2 score (0.761 [95% CI, 0.713–0.81]) (Fig. 1). PELOD_RF also had higher AUPRC (0.327 [95% CI, 0.246–0.414]), which better reflects the performance for predicting the rare outcome of death (24), than PELOD-2 (0.239 [95% CI, 0.165–0.316]) (Fig. 2). After relearning coefficients for the PELOD-2 logistic regression model using our training data, AUC (0.827 [95% CI, 0.785–0.868]) of the PELOD-2 model remained lower than that of PELOD_RF (p = 0.003). Similarly, AUPRC of the relearned PELOD-2 model was lower (0.279 [95% CI, 0.204–0.360]) than that of PELOD_RF. PELOD_RF showed better calibration than PELOD-2, even after retraining the PELOD-2 model (Fig. 3). By the Hosmer-Lemeshow test, both PELOD-2 (p < 0.001) and relearned PELOD-2 (p < 0.001) showed poor calibration, whereas calibration of PELOD_RF was acceptable (p = 0.076). PELOD_RF showed higher overall fit by scaled Brier score (0.176 [95% CI, 0.126–0.230]) than PELOD-2 (0.010 [95% CI, –0.098 to 0.106]) and the relearned PELOD-2 (0.133 [95% CI, 0.057–0.201]).

TABLE 2.

Performance Metrics for Pediatric Logistic Organ Dysfunction-2 and Machine Learning Models

Models	F1	Area Under the Precision-Recall Curve	Area Under the Receiver Operating Characteristic Curve	Accuracy
Random forest	0.396 (0.321–0.468)	0.327 (0.246–0.414)	0.867 (0.836–0.895)	0.960 (0.954–0.966)
Random undersampling boosting	0.373 (0.294–0.453)	0.339 (0.260–0.431)	0.852 (0.814–0.886)	0.964 (0.958–0.969)
Support vector machine	0.342 (0.276–0.408)	0.263 (0.190–0.344)	0.785 (0.740–0.831)	0.950 (0.944–0.957)
Adaptive boosting	0.325 (0.272–0.379)	0.277 (0.202–0.357)	0.810 (0.766–0.851)	0.928 (0.920–0.935)
Naïve Bayes	0.308 (0.229–0.378)	0.220 (0.156–0.292)	0.798 (0.748–0.841)	0.960 (0.954–0.966)
PELOD-2	0.284 (0.209–0.360)	0.239 (0.165–0.316)	0.761 (0.713–0.810)	0.959 (0.953–0.965)
Tree	0.259 (0.211–0.305)	0.217 (0.155–0.285)	0.716 (0.673–0.759)	0.904 (0.895–0.912)
Relearned PELOD-2	0.241 (0.160–0.325)	0.279 (0.204–0.360)	0.827 (0.785–0.868)	0.966 (0.961–0.971)
Adaptive logistic regression	0.222 (0.187–0.262)	0.300 (0.219–0.385)	0.838 (0.801–0.874)	0.841 (0.829–0.852)
Gentle adaptive boosting	0.202 (0.171–0.233)	0.310 (0.230–0.394)	0.863 (0.831–0.894)	0.791 (0.779–0.802)

PELOD = Pediatric Logistic Organ Dysfunction.

Data shown are mean (95% CI).

Figure 1.

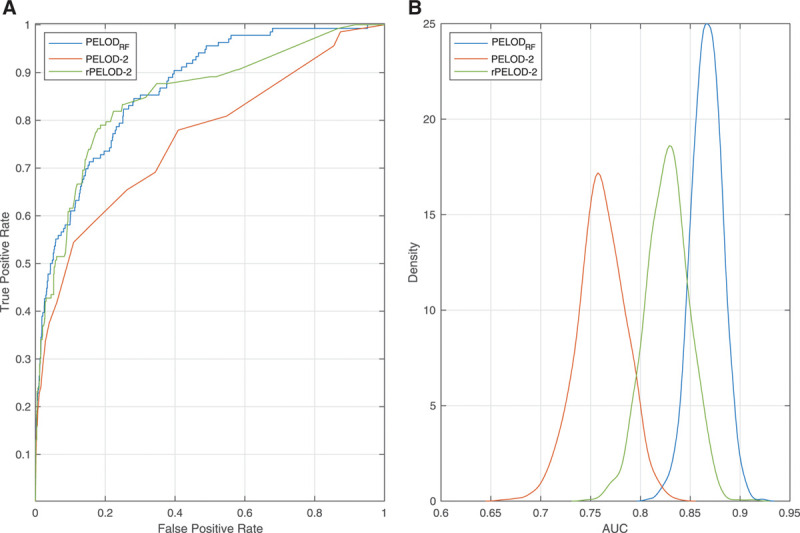
Discrimination performance of three models using receiver operating characteristic curves. A, Receiver operating characteristic curve comparing PELOD_RF, PELOD-2, and the PELOD-2 score relearned on local data (rPELOD-2). B, Density plot of area under the receiver operating characteristic curve (AUC) comparing the three models over 1,000 bootstrap replications. PELOD = Pediatric Logistic Organ Dysfunction.

Figure 2.

Discrimination performance of three models using precision-recall curves. A, Precision-recall curve comparing PELOD_RF, PELOD-2 and the PELOD-2 score relearned on local data (rPELOD-2). B, Density plot of area under the precision-recall curve (AUPRC) comparing the three models over 1,000 bootstrap replications. PELOD = Pediatric Logistic Organ Dysfunction.

Figure 3.

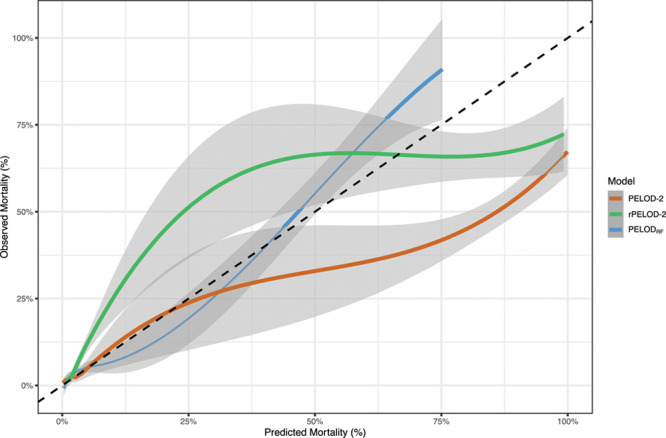
Calibration plot of PELOD_RF, PELOD-2, and the PELOD-2 score relearned on local data (rPELOD-2). Shaded bands represent 95% CIs. Dotted line represents ideal calibration. PELOD = Pediatric Logistic Organ Dysfunction.

DISCUSSION

PELOD_RF, a random forest-based classifier for predicting mortality using the same variables as the PELOD-2 score, had better discrimination and calibration than PELOD-2 for predicting PICU mortality. Although mortality scores are not typically used at the bedside due to complexity of data collection and chance of human error (10), they are essential for quality assessment and to control for severity of illness in clinical studies (1, 5, 6, 10). We found that most machine learning models had better performance than the logistic regression-based PELOD-2 model, even after relearning PELOD-2 model on local data. Although logistic regression is well recognized in ICU prognostic modeling for binary outcomes, machine learning models such as random forests are able to describe nonlinear and complex relationships among predictors and outcomes that are difficult to model accurately using traditional statistical methods (34–36).

Random forests use ensemble learning, which is able to improve classifier performance by aggregating predictions from trained weak learners (34). Ensemble learning techniques train several different classifiers and combine their decisions in order to increase accuracy of a single classifier (34). Previous studies of machine learning for predictions with healthcare data have shown that ensemble methods can perform better than standard classification methods such as logistic regression in accuracy and reproducibility (35). Bagging, also known as bootstrap aggregation, is the type of ensemble learning used in random forests that can avoid overfitting and enhance accuracy of decision tree models when random features are used (37). In the bagged ensemble method, bootstrap replicas of the data are created, and decision trees are grown on the replicas. The random forest method is used to randomly select predictors for each decision split in the tree (37). Fernández-Delgado et al (36) found that random forests are likely to perform best compared with other classifiers in their study of 179 classifiers tested on 121 datasets. We similarly found that a random forest classifier performed best for predicting PICU mortality.

A random undersampling boosting (RUS boost) model performed nearly as well as PELOD_RF in terms of F1 and AUC and in fact outperformed PELOD_RF in accuracy and AUPRC. RUS boost is designed for data with class imbalance and combines undersampling and boosting techniques (38). Undersampling removes examples from the majority class (in this case, the majority of patients who survived), and RUS boost uses adaptive boosting to improve the performance of weak classifiers by iteratively building an ensemble of models (38). Imbalanced data present a problem for many classification methods. If a positive outcome is rare, a classifier that attempts to maximize accuracy can often do so by predicting all cases to be negative rather than correctly classifying the rare outcome (34). RUS boost is designed to avoid favoring the majority class as traditional techniques do (38). Given RUS boost’s strong performance predicting ICU mortality, this model should be considered in future validation studies.

In classification tasks with imbalanced data (where one outcome is a lot more common than the other) and rare outcomes, accuracy, which is the most commonly used measure of classification performance, may not be the appropriate measure to use (34). AUC, another commonly used outcome metric, may appear similarly optimistic when used to describe performance for rare outcomes (24, 39). Mortality in the PICU is emblematic of this imbalanced data problem. Thus, we emphasize the importance of models that balance the tradeoff between precision (PPV) and recall (sensitivity). Although AUPRC reflects this tradeoff across the range of potential cutpoints at which a model may discriminate patients predicted to experience an event (in this case, death) from those predicted not to, F1 reflects this tradeoff at the chosen threshold probability at which predicted classes are dichotomized. PELOD_RF had better performance than the PELOD-2 model for all metrics except specificity, and five of eight machine learning models tested had higher F1 than PELOD-2. Although relearning the PELOD-2 model on local data improved AUPRC compared with using the base PELOD-2 score, F1 actually decreased, demonstrating that finding an optimal probability cut off to maximize both precision and recall was actually harder with the updated model, which showed poor calibration.

Studies have shown that the performance of a model on either a single training and testing set or models evaluated using cross-validation can result in inaccurate performance estimates (40). The use of resampling methods (with replacement) can be used to approximate model performance on unknown samples from the population (40). The results from our bootstrap replications show the variation in performance of our models given different test samples. Future studies of prediction and classification ought to report variation in performance using bootstrapping or other resampling methods. In addition, we use a temporal validation set, which is less prone to overoptimistic estimates of performance than traditional internal validation methods (41). In future work, we plan to perform a true external validation at other institutions.

This study has several limitations. Our data had frequent missing values, which is typical of most ICU databases (42). Of note, the original PELOD-2 publication does not clearly indicate the proportion of data that were missing (1). However, PELOD-2 assigns missing values a normal score based on the assumption that if a value is missing, it was not measured because the physician thought the variable was normal based on the patient’s clinical status (1). Given this, our final imputation method similarly assumed that missing values would be normal, and we assigned missing variables a fixed normal value. In order to test the robustness of this assumption, we compared this fixed normal value imputation method with the performance of machine learning models built using an imputation method with a range of normal values that would allow for natural variation in the missing data (43). This imputation method did not perform better than an imputation method that used a single fixed normal value for missing values, but future work should examine the assumption that missing data are normal. Although the PELOD-2 score has been shown to be insensitive to missing values (44), the impact of missingness on model performance needs to be validated for PELOD_RF. We limited our study to the predictors included in the PELOD-2 model in order to assess how machine learning models perform compared with the logistic regression model that is currently used, but additional predictors of mortality could be included in future models. We used the most abnormal value in the first 24 hours after PICU admission as is done in PELOD-2, but future studies could consider including additional measurements that are available in the EHR (1). For example, Kim et al (45) achieved higher accuracy and better discrimination in predicting PICU mortality compared with the Pediatric Index of Mortality 3 when incorporating changing vital signs of an individual rather than static physiologic variables in a predictive algorithm. There are also many other classification methods and variations of these machine learning models that could be investigated. Of note, PELOD-2 has a lower AUC in our population than in previously studied populations (1, 10, 11). Although we suspect that this difference is attributable to differences in patient populations, and performance of the PELOD-2 logistic regression model improved after retraining using local data, we cannot exclude other systematic biases in the current work.

CONCLUSIONS

A novel, random forest classifier achieved better performance than the standard logistic regression-based score for predicting ICU mortality. Future studies should include external validation of this model. As computational methods improve, machine learning models such as PELOD_RF should be given increased consideration when creating algorithms for risk stratification.