A Tutorial of Bland Altman Analysis in A Bayesian Framework

Abstract

There are two schools of thought in statistical analysis, frequentist, and Bayesian. Though the two approaches produce similar estimations and predictions in large-sample studies, their interpretations are different. Bland Altman analysis is a statistical method that is widely used for comparing two methods of measurement. It was originally proposed under a frequentist framework, and it has not been used under a Bayesian framework despite the growing popularity of Bayesian analysis. It seems that the mathematical and computational complexity narrows access to Bayesian Bland Altman analysis. In this article, we provide a tutorial of Bayesian Bland Altman analysis. One approach we suggest is to address the objective of Bland Altman analysis via the posterior predictive distribution. We can estimate the probability of an acceptable degree of disagreement (fixed a priori) for the difference between two future measurements. To ease mathematical and computational complexity, an interface applet is provided with a guideline.

1. Introduction

In exercise science and medical and clinical studies, researchers want a reliable method of measurement. When a new method of measurement is developed, it is compared to the current method (i.e. the gold standard). To test if the two methods of measurement have an acceptable degree of disagreement, a statistical method known as Bland Altman analysis is widely used (Bland & Altman, 1986; Hopkins, 2000; Spineli, 2019; Tytler & Seely, 1986). In a seminar paper, Bland and Altman (1986) proposed a statistical method (one that was later named Bland Altman analysis) in which researchers calculate the mean difference between two measurements and an interval which is referred to as the limits of agreement (LOAs). An overview and examples of reporting absolute agreement indices are provided in the literature (Giavarina, 2015; Looney, 2018).

There are two competing philosophies in statistics, frequentist and Bayesian (Bland & Altman, 1998). Despite the growing popularity of Bayesian analysis, nearly all (if not all) Bland Altman analysis has been implemented by a frequentist approach. A Bayesian approach is found in the literature but the focus was on repeated measurements (Schluter, 2009) which is more complex than the original Bland Altman analysis (which is cited more than 45,000 times as of April 2020). In this paper, we explore Bland Altman analysis in a Bayesian framework.

A reason why the frequentist approach may be more attractive than a Bayesian approach is due to its simple calculations. In the frequentist approach, approximate confidence intervals for the true mean difference and the true (population) LOAs have closed-form expressions. On the other hand, a Bayesian approach often does not have a closed-form expression for point and interval estimations. Instead, researchers must choose an appropriate model and follow three steps. First, they need to express their belief about the model parameters (e.g. the mean, μ, and variance, σ², of a normal distribution) through a probability model (called a prior). Then they need to express the likelihood of observing a sample given the model parameters. Finally, the prior belief and the likelihood are combined to update their belief about the model parameters (called a posterior). This Bayesian analysis often requires multivariate calculus, increasing computational difficulty. Another crucial challenge in Bayesian analysis is the specification of a prior (i.e., what model is appropriate for the prior). If a prior is not carefully chosen, it may lead to an unreasonable posterior, particularly in a small sample size.

One advantage of a Bayesian approach is the utilization of prior knowledge (because researchers must have some prior information to eliminate implausible parameter values), and experienced and knowledgeable researchers can benefit from Bayesian analysis particularly in a small-sample study. For instance, if timing gates and a stopwatch are compared to measure gait speeds of a 20-meter walk (Martin et al., 2019), researchers probably assume that the expected difference of the two measurements should not exceed one second or even one half of a second. Another advantage is the intuitive and natural interpretation of a result. Consider, for instance, a frequentist’s 95% confidence interval. Once a confidence interval is calculated from a sample, researchers cannot make a probabilistic statement (which is commonly done in an incorrect way). In a frequentist framework, a probability is interpreted as the proportion of times an event happens when the same experiment is repeated a large number of times (which is not realistic in practice). In a Bayesian framework, a probability can quantify the strength of one’s belief about an unknown parameter, and the probability can be updated after observing data (because a belief can react to new data). Therefore, a Bayesian 95% credible interval can be interpreted as “researchers believe that the true (unknown) parameter value is within the interval with a probability of 0.95 after observing data” which is a different interpretation of a frequentist’s 95% confidence interval. Though this subjective interpretation is intuitive, Bayesian analysis has not been used in the past due to computational complexity. However, computational challenges should not be an issue anymore given today’s advanced computing tools. In fact, Bland Altman analysis is a two-parameter problem, so it can be handled by various computational methods.

In the literature, Bayesian methods are not rare for complex statistical problems, but we cannot find any for the relatively simple Bland Altman analysis. Schluter (2009) wrote “Until now, there have been no published Bayesian methods focusing on measurement method comparison studies. This is perhaps surprising given the increased utilization of Bayesian techniques . . . ” The popular seminar paper of Bland and Altman (1986) was published 23 years before Schluter (2009), and since then, a Bayesian approach to Bland Altman analysis has not been formulated (to our best knowledge). It is probably due to a lack (or absence) of explanations of a Bayesian approach for researchers who use Bland Altman analysis. The aim of this article is to briefly review the frequentist approach for Bland Altman analysis (Section 3) and to outline the procedure for a Bayesian approach (Section 4) with an applied example (introduced in Section 2.1). In this article, we suggest assessing the degree of agreement between two methods of measurement via a posterior predictive distribution (e.g., calculation of the probability that the absolute difference will be within a fixed value in future observations) instead of a hypothesis test for the true (population) LOAs. Since the mathematical and computational contents can be heavy for some readers and practitioners, an interface R Shiny applet is developed (https://kalari.shinyapps.io/BBAA/) with a guideline in the Appendix.

There are tutorials of the Bland and Altman analysis in frequentist framework (Giavarina, 2015; Looney, 2018), and the LOAs have been widely used in the research of physical education and exercise science (Christmas et al., 2017; Kastelic & Šarabon, 2019; Mason et al., 2020; Kastelic & Monfort-Pañego & Miñana-Signes, 2020; Overstreet et al., 2016). As researchers become more experienced, they may be able (and willing) to express their knowledge before collecting data (i.e., prior information), and the Bayesian framework will provide a space to express their prior information in the statistical analysis. The intended contributions of this paper are (1) to provide a Bayesian perspective on comparing two methods of measurement, (2) to provide the Bayesian approach with a user-friendly computational applet with a guideline, and (3) to show how to elicit researchers’ prior knowledge in a tractable manner (which is to be combined with observed data in the Bayesian analysis).

2. Model assumptions

Suppose that we want to analyze the agreement of two measurement methods. Let D_i be the difference between the two outcomes when the i ^th subject was measured by each method for i = 1, 2, ..., n, where n is a fixed sample size. Assume D_1, ..., D_n are independent random variables (referred to as the independence assumption). In addition, assume each D_i follows a normal distribution with some true average difference μ and some true standard deviation σ (referred to as the normality assumption). The normality assumption is denoted D_i∼N(μ, σ²), and it is graphically presented in Figure 1. The independence assumption and the normality assumption are maintained throughout this paper, whether we use a frequentist approach (Section 3) or a Bayesian approach (Section 4).

Figure 1.

The normality assumption D_i∼N(μ,σ²).

2.1. Applied example

To illustrate both approaches we will be using the following example throughout the manuscript. Gait speed is a useful predictor of various health outcomes, and is something that clinicians can measure conveniently. (Martin et al., 2019). To measure gait speed, a patient is asked to walk a fixed distance (e.g., 20 meters), and the time is recorded in seconds. There are two methods of measuring gait speed (m/s), a timing gate and a stopwatch. A timing gate is known to be highly accurate and reliable, but it is relatively expensive when compared to a stopwatch. If the difference between the measurement by a timing gate and the measurement by a stopwatch is small, clinicians may prefer a stopwatch. For the purpose of demonstration, we consider a hypothetical example based on the estimates by Martin et al. (2019).

Suppose that a difference of δ = 0.1 seconds is practically negligible when a timing gate and a stopwatch are used to measure the time for a 20-meter walk (i.e. we are setting the acceptable limit to be δ = 0.1). A hypothetical sample of size n = 10 is given in Table 1. Let x_i and y_i denote the measurements by the timing gate and by the stopwatch, respectively, and (x_i, y_i) are observed from the i^th subject. The difference between the two measurements is calculated as d_i = y_i – x_i as shown in the table. The unknown average difference μ is estimated by the sample mean $\overline{d}=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{d}_i}$, the sum of n observed differences divided by n. The unknown variance σ² is estimated by the sample variance $s^2=\frac{1}{n-1}{\displaystyle {\sum }_{i=1}^n{\left(d_i-\overline{d}\right)}^2}$, the sum of square distances between d_i and $\overline{d}$ divided by n – 1. The unknown standard deviation σ is then estimated by $s=\sqrt{s^2}$. Given the data in Table 1, the resulting sample mean and sample standard deviation are $\overline{d}=0.066$ and s = 0.0237.

Table 1.

A hypothetical sample of size n = 10.

Subject i	Measurement by timing gate (xi)	Measurement by stopwatch (yi)	Difference di = yi − xi
1	12.01	12.05	0.04
2	11.87	11.96	0.09
3	12.41	12.46	0.05
4	11.82	11.92	0.10
5	12.25	12.32	0.07
6	11.87	11.92	0.05
7	12.19	12.27	0.08
8	12.41	12.47	0.06
9	12.30	12.39	0.09’
10	11.25	11.28	0.03

3. Frequentist approach

3.1. Limits of agreement and frequentist interpretation

By the empirical rule under the normality assumption, a random difference D_i (to be observed in the future) is between μ – 1.96σ and μ + 1.96σ with a probability of 0.95, and these limits are estimated by $l=\overline{d}-1.96s$ and $u=\overline{d}+1.96s$, respectively. Given the data in Table 1, the resulting 95% limits of agreement (95% LOAs) are l = 0.020 and u = 0.112, and the 95% LOAs would be typically interpreted as “a difference between two measurements will be between 0.020 and 0.112 seconds with a probability of 0.95.” This interpretation appears to be widely accepted in literature, but it sounds strange because data collected in another study will result in different values of 95% LOAs. An accurate frequentist interpretation is more cumbersome because the frequentist interpretation of a probability requires repeating the same experiment (e.g. collecting a sample of size n = 10) infinitely many times.

From the perspective of statistical theory, the resulting 95% LOAs (0.020, 0.112) are not intended to capture a future outcome of D_i with a probability of 0.95. If the sample size n is very large, the aforementioned interpretation of 95% LOAs is approximately correct. However, if researchers really intend to capture a future random variable D_n+1 with a probability of 0.95 (regardless of the sample size n), the interval $\overline{d}\pm t_{0.975,n-1}s\sqrt{1+\frac{1}{n}}$ should be used, where t_{0.975,n – 1} = 2.262 is the 97.5 ^th percentile of the T distribution with n – 1 degrees of freedom (e.g., t_0.975,9 = 2.262). Given the data in Table 1, the resulting interval would be (0.010, 0.122), and this is called the prediction interval (Geisser, 1993).

3.2. Hypothesis testing

Giavarina (2015) noted that “the best way to use the Bland Altman plot would be to define a priori the limits of maximum acceptable differences (limits of agreement expected), based on biologically and analytically relevant criteria, and then to obtain the statistics to see if these limits are exceeded, or not.” In this regard, two parameters of interest in the Bland and Altman analysis are θ₁ = μ – 1.96σ (lower limit) and θ₂ = μ + 1.96σ (upper limit), and approximate confidence intervals for these parameters can be calculated (Bland & Altman, 1986; Giavarina, 2015; Lu et al., 2016; Stöckl et al., 2004).

Lu et al. (2016) developed a sample size formula for hypothesis testing H₀: θ₁ < – δ or θ₂ > δ versus H₁: θ₁ ≥ – δ and θ₂ ≤ δ, where δ (acceptable limit) is fixed before observing data. At the significance level α = 0.05, the hypothesis test requires 95% confidence intervals for θ₁ and θ₂ given by

$$\left(l_1,u_1\right)=\overline{d}-1.96s\pm t_{0.975,n-1}\sqrt{\frac{3s^2}{n}}=(-0.010,0.049),$$

$$\left(l_2,u_2\right)=\overline{d}+1.96s\pm t_{0.975,n-1}\sqrt{\frac{3s^2}{n}}=(0.083,0.141),$$

respectively. Note that these intervals are to capture the unknown parameters θ₁ = μ – 1.96σ and θ₂ = μ + 1.96σ, respectively. According to Lu et al. (2016), the null hypothesis H₀ is rejected (i.e., H₁ is concluded) when – δ < l₁ < u₂ < δ. Given the data in Table 1, the resulting 95% confidence intervals are (l₁, u₁) = (–0.010, 0.049) for θ₁ and (l₂, u₂) = (0.083, 0.141) for θ₂, so H₀ is not rejected at α = 0.5 because u₂ = 0.141 is greater than δ = 0.1. In this context, we have a lack of evidence to conclude that the timing gate and the stopwatch are practically different.

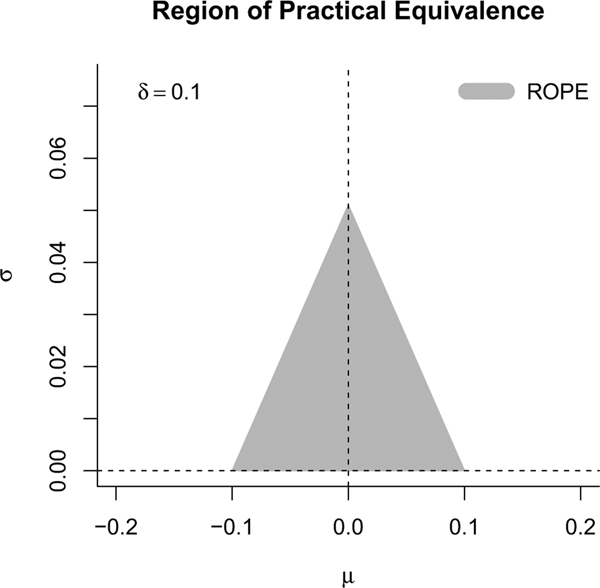
3.3. Region of practical equivalence

The idea of fixing the practically acceptable difference δ can be viewed as a region of practical equivalence (ROPE) in Bayesian inference. All possible values of (μ, σ) can be partitioned into two regions: (i) a small region where the two methods of measurement are practically the same (i.e., close enough) and (ii) elsewhere (not close enough). In the formulated hypothesis testing, H₁ represents the small region, and H₀ represents elsewhere. For example, if δ = 0.1 is the maximum acceptable difference between the two methods of agreement, H₁: θ₁ > – 0.1 and θ₂ < 0.1 can be expressed as μ – 1.96σ > – 0.1 and μ + 1.96σ < 0.1. These two inequalities are equivalent to σ < a + bμ and σ < a – bμ respectively, where $a=\frac{0.1}{1.96}$ and $b=\frac{1}{1.96}$. The two inequalities are represented by the shaded zone in Figure 2.

Figure 2.

The region of practical equivalence (ROPE).

We can calculate a credible interval and see if it covers a portion of ROPE (Kruschke, 2015). Since we have a two-dimensional ROPE for (μ, σ), we need to calculate a credible region (Note: the term “credible interval” is used for one parameter, and the term “credible region” is used for two or more parameters). Alternatively, we can calculate the posterior probability of H₁ to quantify the updated belief that the true parameter values are within the fixed ROPE.

3.4. Alternative perspective of acceptable agreement

Note that hypothesis testing and confidence intervals are used to make statements about unknown parameters (not future outcomes). Kim and Wand (2020) discussed a strange case in the hypothesis testing discussed in Section 3.2. For instance, let δ = 0.1, and assume the true parameter values are μ = 0.05 and σ = 0.03. In this case, θ₂ = μ + 1.96σ = 0.1088 exceeds δ = 0.1 (i.e., H₀ is true), but P(–δ < D_i < δ) = 0.9522 exceeds 0.95 (which may be an acceptable probability of agreement). The two statements “H₁: θ₁ ≥ −δ and θ₂ ≤ δ” and “P(–δ ≤ D_i ≤ δ) ≥ 0.95” are not equivalent (Kim & Wand, 2020). The former statement is regarding the two parameters θ₁ = μ – 1.96σ and θ₂ = μ + 1.96σ, and the latter statement is regarding the random variable D_i. The researcher’s perspective is crucial to determine the method of analysis. If we focus directly on D_i and its observed future value, an alternative perspective of the acceptable agreement should be based on the probability P(–δ ≤ D_i ≤ δ). Researchers who are more interested in answering the probabilistic question “What is the probability that the difference between two measurements (to be observed in future) is within (–δ, δ) = (–0.1, 0.1)” should use this alternative perspective. This question can be answered in a Bayesian approach (specifically at the end of Section 4.4).

4. Bayesian approach

In literature, the term “frequentist” has been rarely (or never) used for the current practice of Bland Altman analysis because a Bayesian approach has not been considered by many (and most) researchers. We believe that the frequentist approach gained popularity because of simple formulas and easy calculations. A Bayesian approach involves more mathematics and programming, but it is more flexible (in terms of addressing a research question) and easier to provide a probabilistic interpretation (as opposed to the frequentist interpretation of a probability which requires the hypothetical assumption of repeated experiments; Section 3.1).

For readers who are unfamiliar with Bayesian methods, van de Schoot et al. (2014) provided a gentle introduction to Bayesian analysis. Kruschke (2015) wrote a book about Bayesian analysis with concrete examples and programming codes. Bland and Altman (1998) wrote a short article to compare between frequentist and Bayesian analysis.

Under the normality assumption (Section 2), the model parameters are μ and σ which are unknown and to be estimated after observing data. For mathematical convenience, the standard deviation σ is transformed to $\tau =\frac{1}{{\sigma }^2}$ which is referred to as precision. Given the precision τ, the standard deviation is $\sigma =\frac{1}{\sqrt{\tau }}$. A greater precision means a smaller standard deviation (i.e. the two methods of measurement tend to agree more). In other words, τ is just an alternative way of quantifying uncertainty. A Bayesian inference for (μ, τ) requires three steps.

1. Model data, (d_1, ..., d_n) or simply $\overrightarrow{d}$. The probability model for $\overrightarrow{d}$ given the model parameters (μ, τ) is denoted by $f(\overrightarrow{d}\mid \mu ,\tau )$, and it is referred to as the likelihood function or simply likelihood (Section 4.1). It quantifies the likelihood of observing $\overrightarrow{d}$ if the values of the model parameters (μ, τ) are given.

2. Model researcher’s belief about (μ, τ) via a probability model f (μ, τ) prior to observing data (d_1, ..., d_n). The probability model f (μ, τ) is referred to as the prior distribution or the prior density function (Section 4.2). For example, if f (0, 4) = 0.2 and f(0, 1) = 0.1, the researcher is expressing that μ = 0 and τ = 4 (σ = 0.5) is twice more plausible than μ = 0 and τ = 1 (σ = 1). Since μ can be any real number and τ can be any positive real number, we need a mathematical function f (μ, τ) to model researcher’s belief efficiently.

3. Update the researcher’s belief about (μ, τ) given data $\overrightarrow{d}$. The updated probability model for (μ, τ) given $\overrightarrow{d}$ is denoted by $f(\mu ,\tau \mid \overrightarrow{d})$, and it is referred to as the posterior distribution or the posterior density function (Section 4.3). All statistical inferences are from the updated model $f(\mu ,\tau \mid \overrightarrow{d})$, and it is derived by combining the prior f (μ, τ) and the likelihood $f(\overrightarrow{d}\mid \mu ,\tau )$ (Note: they are combined using Bayes theorem, hence the name Bayesian inference).

4.1. Likelihood

Under the independence assumption and the normality assumption given μ and $\tau =\frac{1}{{\sigma }^2}$, the likelihood of observing $\overrightarrow{d}$ is quantified as

$$f(\overrightarrow{d}\mid \tau ,\mu )=\prod _{i=1}^n{\left(\frac{\tau }{2\pi }\right)}^{\frac{1}{2}}{e}^{-\frac{\tau {\left(d_i-\mu \right)}^2}{2}}\propto {\tau }^{\frac{n}{2}}{e}^{-\frac{\tau }{2}\left[nv+n{(\overline{d}-\mu )}^2\right]}$$ (1)

where $\overline{d}=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{d}_i}$ and $v=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{\left(d_i-\overline{d}\right)}^2}$. To quantify the likelihood, we do not need to know all individual values of $\overrightarrow{d}=\left(d_1,\dots ,d_n\right)$, and it is sufficient to summarize the data by the two statistics $\overline{d}$ and v (referred to as sufficient statistics). Note that the sample variance in the frequentist approach is $s^2=\frac{1}{n-1}{\displaystyle {\sum }_{i=1}^n{\left(d_i-\overline{d}\right)}^2}$, so $v=\frac{n-1}{n}{s}^2$.

4.2. Prior

A popular prior distribution for the normal model parameters (μ, τ) is the normal-gamma distribution which is given by

$$f(\mu ,\tau )\propto {\tau }^{a_0-\frac{1}{2}}{e}^{-b_0\tau }{e}^{\frac{-{\lambda }_0\tau {\left(\mu -{\mu }_0\right)}^2}{2}}$$ (2)

for – ∞ < μ < ∞ and τ > 0. The values of (a₀, b₀, μ₀, λ₀) are chosen to reflect the researcher’s state of knowledge about (μ, τ) before observing data $\overrightarrow{d}$. The value of μ₀ reflects the best guess of μ, and the value of λ₀ reflects the pseudo sample size (i.e. given τ, a larger value of λ₀ makes the prior belief about μ stronger). It will be shown (in Equation (6) of Section 4.3) that μ₀ and λ₀ are combined with $\overrightarrow{d}$ and n to determine a posterior estimate for μ, and λ₀ can be interpreted as the relative amount of information when μ is estimated by a weighted average of μ₀ and $\overrightarrow{d}$. The value of $\frac{a_0-0.5}{b_0}$ reflects the best guess of τ, and a smaller value of a₀ and a larger value of b₀ make the prior belief of τ stronger. However, a₀ and b₀ also affect the strength of the prior belief about μ, so it is not simple to accurately choose the values of (a₀, b₀, μ₀, λ₀) by trial and error. To specify the prior in a tractable manner, guidance is provided in Section 4.5. Note that Equation (2) is often denoted by

$$(\mu ,\tau )\sim \mathcal{N}\mathcal{G}\left(a_0,b_0,{\mu }_0,{\lambda }_0\right),$$

the subscript “0” is used to emphasize that these are the parameters of the prior distribution.

In practice, Bayesian analyses are commonly performed by “letting data speak out.” In other words, when researchers do not have useful prior information about (μ, τ), values of (a₀, b₀, μ₀, λ₀) may be chosen in a certain way such that the prior f(μ, τ) has negligible influence on the posterior $f(\mu ,\tau \mid \overrightarrow{d})$. In this case, the posterior $f(\mu ,\tau \mid \overrightarrow{d})$ would be dominated by the likelihood $f(\overrightarrow{d}\mid \tau ,\mu )$. For instance, if we are uninformed about (μ, τ), we may choose a₀ = 0.5, b₀ = 0.000001, μ₀ = 0, and λ₀ = 0.000001, and the prior distribution (modeled by the normal-gamma distribution in Equation (2)) becomes

$$f(\mu ,\tau )\propto e^{-0.000001\tau }{e}^{\frac{-0.000001\tau {(\mu )}^2}{2}}\doteq 1.$$

This prior distribution will not affect the posterior distribution. It is because the posterior inference is based on the product of the likelihood $f(\overrightarrow{d}\mid \tau ,\mu )$ and the prior f (μ, τ) (Equation ((3)) in Section 4.3). To this end, if f (μ, τ) = 1, the posterior will be dominated by the data (likelihood) only. When researchers want to incorporate substantive prior information about the parameters (μ, τ), appropriate values of (a₀, b₀, μ₀, λ₀) can be found by a tractable manner (see Section 4.5).

Note that the normal-gamma prior is not the only way of specifying a prior. There are many forms of f (μ, τ) that researchers may choose. For example, if researchers are finding it challenging to express their prior beliefs about μ and τ simultaneously, one can choose a prior model f (μ) for μ (often a normal model) and a prior model f (τ) for τ independently, and by the definition of independence in probability theory, one can let f (μ, τ) = f (μ) f (τ). In this case, the forms of f (τ) and f (μ) are flexible as long as they are legitimate probability models on the possible values of τ and μ (i.e. τ > 0 and 1< μ < ∞).

4.3. Posterior

The Bayesian inference follows the spirit of the Bayes’ theorem

$$f(\mu ,\tau \mid \overrightarrow{d})=\frac{f(\overrightarrow{d}\mid \mu ,\tau )f(\mu ,\tau )}{f(\overrightarrow{d})}\propto f(\overrightarrow{d}\mid \mu ,\tau )f(\mu ,\tau ),$$ (3)

where the likelihood $f(\overrightarrow{d}\mid \mu ,\tau )$ is in Equation (1) and the prior f (μ, τ) is in Equation (2). The function $f(\overrightarrow{d})$ is called the marginal likelihood, but it is not important for our purposes. Using Bayes’ theorem in Equation (3), the posterior distribution is given by

$$\begin{array}{c}f(\mu ,\tau \mid \overrightarrow{d})\propto f(\overrightarrow{d}\mid \mu ,\tau )f(\mu ,\tau )\\ \propto {\tau }^{\frac{n}{2}}{e}^{-\frac{\tau }{2}\left[nv+n{(\overline{d}-\mu )}^2\right]}{\tau }^{a_0-\frac{1}{2}}{e}^{-b_0\tau }{e}^{\frac{-{\lambda }_0\tau {\left(\mu -{\mu }_0\right)}^2}{2}}\\ \propto {\tau }^{a_1-\frac{1}{2}}{e}^{-b_1\tau }{e}^{\frac{-{\lambda }_1\tau {\left(\mu -{\mu }_1\right)}^2}{2},}\end{array}$$ (4)

where

$$\begin{array}{l}{a}_1=a_0+\frac{n}{2}\hfill \\ b_1=b_0+\frac{n}{2}\left(v+\frac{{\lambda }_0{\left(\overline{d}-{\mu }_0\right)}^2}{{\lambda }_0+n}\right)\hfill \\ {\mu }_1=\frac{{\lambda }_0{\mu }_0+n\overline{d}}{{\lambda }_0+n}\hfill \\ {\lambda }_1={\lambda }_0+n.\hfill \end{array}$$ (5)

The subscript “0” is used to signify a parameter of the prior distribution (as noted above) while the subscript “1” signifies a parameter for the posterior distribution. Note that the posterior distribution presented in Equation (4) is in the form of the normal-gamma model (compare to Equation (2)), and we denote the posterior distribution by

$$(\mu ,\tau )\mid \overrightarrow{d}\sim \mathcal{N}\mathcal{G}\left(a_1,b_1,{\mu }_1,{\lambda }_1\right).$$

In other words, the prior knowledge expressed via the normal-gamma model NG(a₀, b₀, μ₀, λ₀) is updated by the normal-gamma model NG(a₁, b₁, μ₁, λ₁) by updating the old values of (a₀, b₀, μ₀, λ₀) with the new values of (a₁, b₁, μ₁, λ₁) after observing a sample of size n. In Equation (5), note that μ₁ (referred to as the posterior mean of μ) can be expressed as

$${\mu }_1=\frac{{\lambda }_0}{{\lambda }_0+n}{\mu }_0+\frac{n}{{\lambda }_0+n}\overline{d}.$$ (6)

It is a weighted average of μ₀ (prior guess for μ) and $\overline{d}$ (sample mean to estimate μ) weighted by λ₀ and n, respectively. Therefore, λ₀ and n can be interpreted as the contribution of the prior and data, respectively, to the posterior inference for μ. To this end, researchers can gauge how strong their prior belief about μ was relative to the sample size n.

In summary, the Bayesian inference is based on the seven numbers (n, $\overline{d}$, v, a₀, b₀, μ₀, λ₀) which constitute (a₁, b₁, μ₁, λ₁). The analytic approach to the posterior $f(\mu ,\tau \mid \overrightarrow{d})$ requires some calculus. Without a background in calculus, the posterior $f(\mu ,\tau \mid \overrightarrow{d})$ still can be analyzed numerically using Gibbs sampling, and an example is given in Section 4.4. A more detailed explanation of the Gibbs sampling can be found in Supplemental Note 1.

4.4. Applied example

Consider the same data in Section 3.3, and suppose a prior is fixed at a₀ = 0.5, b₀ = 0.000001, μ₀ = 0, and λ₀ = 0.000001 to express very weak prior knowledge about (μ, τ) as discussed in Section 4.2. A sample R code for Gibbs sampling is given in Supplemental Note 2. The function named BA.Bayesian in the Supplemental Note 2 should be loaded in R, then the following lines can be submitted to input the data $\overrightarrow{d}=\left(d_1,\dots ,d_n\right)$ and to run the function.

### Input data (difference between two measurements) data = c(0.04, 0.09, 0.05, 0.1, 0.07, 0.05, 0.08, 0.06, 0.09, 0.03)

### Run BA.Bayesian function

BA.Bayesian(d = data, delta = 0.1, a0 = 0.5, b0 = 1e-6, mu0 = 0, lambda0 = 1e-6)

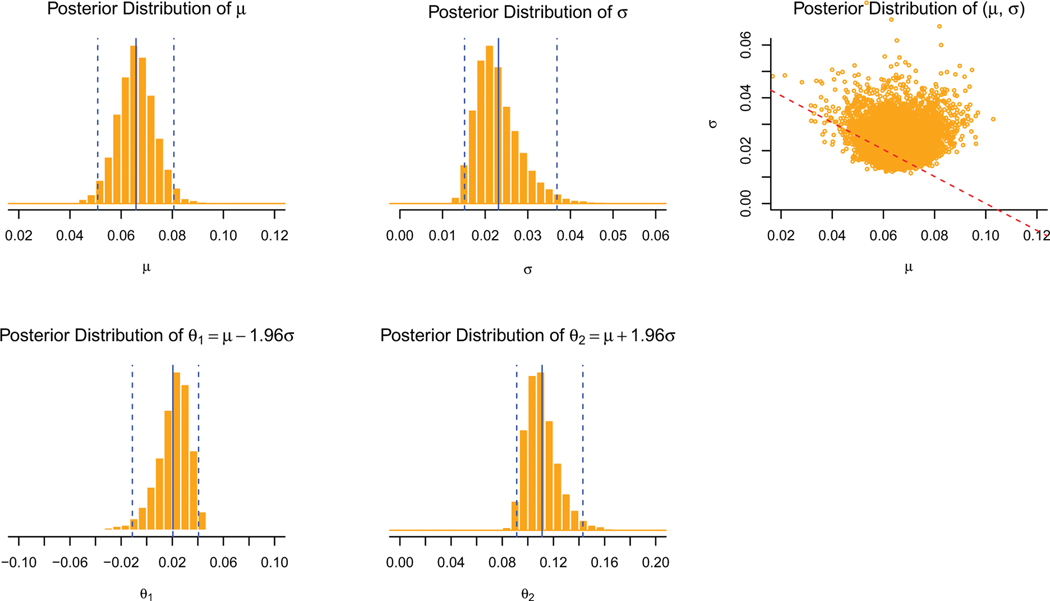
After running this code, R outputs the following posterior inference for (μ, σ, θ₁, θ₂) and the posterior distributions seen in Figure 3.

Figure 3.

Posterior distributions of (μ, σ, θ₁, θ₂).

$post

mean 2.5% 5% 25% 50% 75% 95% 97.5% mu 0.066 0.051 0.054 0.061 0.066 0.071 0.078 0.081 sigma 0.023 0.015 0.016 0.019 0.022 0.026 0.033 0.037 theta1 0.021 − 0.010 − 0.003 0.014 0.023 0.030 0.038 0.041

theta2 0.111 0.091 0.093 0.102 0.109 0.118 0.135 0.142 diff 0.066 0.016 0.026 0.051 0.066 0.081 0.105 0.115

$post.h1

[1] 0.1853

$post.pred.agree

[1] 0.9233

The posterior distributions in Figure 3 are interpreted as follows:

• Upper left panel: After observing the sample (d₁, ... , d_n) of size n = 10, we are 95% sure that μ is between 0.051 and 0.081 (vertical dashed lines), and the interval (0.051, 0.081) is called a 95% credible interval (CI) for μ. The posterior distribution of μ is centered at 0.066 (the vertical solid line, indicating the average of the posterior distribution), and 0.066 is called the posterior mean of μ.

• Upper middle panel: The posterior mean of σ is 0.023, and a 95% CI for σ is (0.015, 0.037).

• Upper right panel: The two parameters of interest are θ₁ = μ – 1.96σ and θ₂ = μ + 1.96σ, and θ₁ and θ₂ depend on the two model parameters μ and σ jointly. The scatter plot provides the joint posterior distribution of (μ, σ), and the dotted line represents the boundary between the null hypothesis H₀: θ₁ < – 0.1 or θ₂ > 0.1 and the alternative hypothesis H₁: θ₁ ≥ –0.1 and θ₂ ≤ 0.1. The inner zone represents H₁, and the proportion of (μ, σ) located inside the zone of H₁ is 0.183 which is called the posterior probability of H₁. After observing the data, we believe H₁ is true with a probability 0.183.

• Lower left panel: The posterior mean of θ₁ = μ – 1.96σ is 0.021, and a 95% CI for θ₁ is (–0.011, 0.041).

• Lower middle panel: The posterior mean of θ₂ = μ + 1.96σ is 0.111 with a 95% CI (0.091, 0.142).

Note that all, but one, of the observed differences d_1, ..., d₁₀ are within 0.1 seconds (with one boundary case d₄ = 0.1), and the posterior probability of H₁ is as low as 0.183.

There are infinitely many 95% CIs for a parameter. In the above results, a 95% CI is calculated by the 2.5 ^th percentile and the 97.5 ^th percentile of the posterior distribution, and it is referred to as the central CI. When the posterior distribution is unimodal (i.e. a single peak), we can find the shortest interval as follows (Section 25.2.2 of Kruschke, 2015). Note that the 1^st percentile and the 96^th percentile can serve as a 95% CI, and the 1.5 ^th percentile and the 96.5 ^th percentile can serve as another 95% CI. Among infinitely many 95% CIs, the shortest CI is called the highest (posterior) density interval (HDI), and it provides a more precise (shorter) interval estimation when the posterior distribution is skewed (e.g. for σ in Figure 3). See Table 2 to compare the length of the central 95% CI and the length of 95% HDI for each parameter. The lengths are the same for μ because the posterior distribution of μ is symmetric, and the length of HDI is slightly shorter for σ, θ₁, and θ₂, but the difference seems negligible (about 0.002–0.003 seconds). When the posterior distribution is multimodal (i.e. multiple peaks), a different method of finding HDI is needed according to the formal definition of an HDI (Section 4.3.4 of Kruschke, 2015).

Table 2.

The central 95% CI and the 95% HDI for μ, σ, θ₁, and θ₂

Parameter	Central 95% CI	length	95% HDI	Length	Lower %	Upper %
μ	(0.051, 0.081)	0.030	(0.051, 0.081)	0.030	2.5%	97.5%
σ	(0.015, 0.037)	0.022	(0.014, 0.034)	0.020	0.7%	95.7%
θ1	(−0.010, 0.041)	0.051	(−0.005, 0.043)	0.048	3.9%	98.9%
θ2	(0.091, 0.142)	0.051	(0.089, 0.137)	0.048	0.8%	95.8%

As mentioned in Section 3.4, the question of interest is the probability that the difference between the two measurements will be between (−δ, δ) = (−0.1, 0.1) in the future. In this regard, let $\tilde{D}$ be a random difference (comparing stopwatch to timing gates) to be observed in the future. The probability model of $\tilde{D}$ (informed by observed data $\overrightarrow{d}$) is referred to as the posterior predictive distribution, and it is shown in Figure 4 (generated by the R code in the Supplemental Note 2). As shown in the R outputs given earlier in this section, we are 95% sure that the difference will be between 0.016 and 0.115 (2.5% and 97.5% of the row named diff), and we believe that the difference will be within δ = 0.1 seconds with a probability of 0.9233 (post.pred.agree) which we denoted as $P(-\delta \le \tilde{D}\le \delta \mid \overrightarrow{d})=0.9233$.

Figure 4.

Posterior predictive distribution of $\tilde{D}$.

Recalling our applied example from section 2.1, if the probability of 0.9233 is an acceptable level of agreement (which should be judged based on practical significance), the stopwatch should be recommended rather than the more expensive timing gates. Otherwise, the stopwatch should not be recommended as a replacement for the timing gates.

According to Bayesian theory, the posterior predictive distribution of $\tilde{D}$ follows a scaled and shifted T distribution (Murphy, 2007). It can be generated from N(μ, σ) by using posterior samples of (μ, σ), and the posterior probability of $-\delta \le \tilde{D}\le \delta$ can be approximated numerically.

4.5. Prior specification

The Bayesian (posterior) inference is a combination of prior knowledge and empirical evidence (data). So far, we have considered the vague prior a₀ = 0.5, b₀ = 0.000001, μ₀ = 0, and λ₀ = 0.000001, which does not substantially influence the posterior inference. However, researchers are sometimes knowledgeable (or have a strong opinion) about the model parameters (μ, τ), where $\tau =\frac{1}{{\sigma }^2}$ (i.e., $\sigma =\frac{1}{\sqrt{\tau }}$). The most distinguishable feature of Bayesian inference (compared to frequentist inference) is the influence of prior, in our context the choice of (a₀, b₀, μ₀, λ₀). As aforementioned in Section 4.2, it is fairly challenging to specify (a₀, b₀, μ₀, λ₀) which properly reflects the researcher’s prior knowledge, so we introduce an induced prior specification in this section (Christensen et al., 2011).

For an induced prior specification on the parameters μ and $\sigma =\frac{1}{\sqrt{\tau }}$, researchers can be asked the following questions: (1) What is your best guess for σ? Call it $\widehat{\sigma }$. (2) What is the upper bound u_σ such that you (researcher) believe that P(σ ≤ u_σ) = 0.95? (3) What is the lower bound l_μ and upper bound u_μ for the mean difference μ such that you believe that P(l_μ ≤ μ ≤ u_μ) = 0.95?

For the purpose of demonstration, suppose a researcher (who has been involved in walk studies in the past) provided the following answers: (1) My best guess for the standard deviation σ (of the difference between two measurements) is $\widehat{\sigma }=0.05$ (estimated by the sample standard deviation of the previous study). (2) I am 95% sure that the standard deviation σ does not exceed u_σ = 0.1, that is P(σ < 0.1) = 0.95 (a guess based on previous experiences; unlikely that σ exceeds 0.1 seconds in a walk study). (3) I am 95% sure that the average difference μ is between l_μ = 0.5 and u_μ = 0.5 seconds, that is P(−0.5 ≤ μ ≤ 0.5) = 0.95 (a guess based on experience; quite certain that |μ| is within 0.5 seconds). By the specified values, $\widehat{\sigma }=0.05$, u_σ = 0.1, l_μ = −0.5, and u_μ = 0.5, we can find (a₀, b₀, μ₀, λ₀) = (2.71, 0.0093, 0, 0.086). A method of finding these values is described in the Supplemental Note 3 for readers who are interested in the thorough mathematics behind the scenes, but these calculations are automatically done in the interface R Shiny applet, so it is not required by users. Users are asked to input ($\widehat{\sigma }$, u_σ, l_μ, u_μ) as described in the Appendix. Otherwise, the uninformed (vague) prior used in Section 4.2 is implemented by default.

Using this informative prior and the same data, the posterior inference is as follows:

> BA.Bayesian(d = data, delta = 0.1, a0 = 2.71, b0 = 0.00093, mu0 = 0, lambda0 = 0.086)

$post

mean 2.5% 5% 25% 50% 75% 95% 97.5% mu 0.065 0.051 0.053 0.061 0.065 0.070 0.077 0.080 sigma 0.023 0.016 0.017 0.020 0.022 0.025 0.031 0.033 theta1 0.021 − 0.006 0.000 0.014 0.022 0.029 0.037 0.039 theta2 0.110 0.092 0.094 0.102 0.109 0.116 0.130 0.135 difference 0.065 0.017 0.025 0.049 0.065 0.081 0.104

0.113

$post.h1

[1] 0.1734

$post.pred.agree

[1] 0.9278

The above results are fairly close to the results with the vague prior in Section 4.4 because the amount of prior information λ₀ = 0.086 was relatively small (when compared to the sample size n = 10). As shown in Equation (6) of Section 4.3, the posterior mean of μ is

$$\begin{gathered} {\mu }_1=\frac{0:086}{0.086+10}(0)+\frac{10}{0.086+10}(0.066) \\ =0.0085(0)+0.9915(0.066)=\mathrm{0.065.} \end{gathered}$$

In words, the sample mean $\overline{d}=0.066$ is weighted by 0.9915 and the prior guess μ₀ = 0 is weighted by 0.0085 in the posterior estimation for μ.

The impact of a prior specification can be substantial particularly when λ₀ is large relative to n and a prior guess deviates from observed data. For the purpose of demonstrating this point, let us consider another prior given by $\widehat{\sigma }=0.1$, u_σ = 0.25, l_μ = 0.1, and u_μ = 0.1 which results in (a₀, b₀, μ₀, λ₀) = (1.68, 0.027, 0, 14.38) (using the R Shiny applet). This prior is fairly strong in a sense that λ₀ = 14.38 is greater than the sample size n = 10. Furthermore, the prior guess $\widehat{\sigma }=0.1$ with P(σ < 0.25) = 0.95 appears to be an overestimate relative to the observed sample standard deviation s = 0.0237. Given the same data presented in the previous example, this strong prior (which conflicts with the observed data) results in the following posterior inference.

$post

mean 2.5% 5% 25% 50% 75% 95% 97.5% mu 0.027 − 0.008 − 0.002 0.016 0.027 0.038 0.056 0.062 sigma 0.085 0.058 0.061 0.072 0.082 0.094 0.119 0.129 theta1 − 0.139 − 0.234 − 0.212 − 0.160 − 0.132 − 0.111 − 0.086- − 0.079

theta2 0.193 0.133 0.140 0.165 0.187 0.214 0.267 0.287 difference 0.028 − 0.146 − 0.116 − 0.029 0.027 0.086 0.172 0.202

$post.h1

[1] 0

$post.pred.agree

[1] 0.7311

In this case, the posterior mean for μ is calculated by the weighted average

$${\mu }_1=\frac{14.38}{14.38+10}(0)+\frac{10}{14.38+10}(0.066)=0.027$$

which is closer to the prior guess μ₀ = 0 rather than the data $\overline{d}=0.066$. In addition, the posterior mean 0.085 for σ is substantially closer to the prior guess $\widehat{\sigma }=0.1$ rather than the data s = 0.0237. Since this strong prior expressed relatively large σ (when compared to the previous prior), $P(-0.1\le \tilde{D}\le 0.1\mid \overrightarrow{d})=0.7311$ is substantially smaller than the previously resulting probability of 0.9278.

To critique the influence of a prior, it is recommended to revisit Equation (4) in Section 4.3. The posterior values (a₁, b₁, λ₁, μ₁) are determined by prior (a₀, b₀, λ₀, μ₀) and data (n, $\overline{d}$, v). In particular, a large value of λ₀ is highly influential when a prior guess μ₀ and an estimate $\overline{d}$ for μ are distant. In addition, the prior can be affected by the difference between a prior guess $\widehat{\sigma }$ and an estimate (s or $\sqrt{v}$) for σ. In practice, the posterior result from a strong prior and the posterior result from a vague prior (e.g. the prior first introduced in Section 4.4) are compared to critique the prior influence.

5. Discussion

Although Bland Altman analysis is not new to the literature, there is very little on Bland Altman analysis through a Bayesian lens. To this end, our goal was to provide researchers a Bayesian framework to complete Bland Altman analysis. We summarize this procedure as follows: (1) specify a normal-gamma prior on (μ, τ), where τ = 1/σ, (2) conduct Gibbs sampling for a posterior sample of (μ, τ), (3) summarize the posterior distribution of (μ, τ) and any combination of (μ, τ) such as μ ± 1.96σ, and (4) summarize the posterior predictive distribution for future outcomes to assess the degree of agreement between two different methods of measurement for a given threshold value of δ. To help researchers navigate a prior specification and reduce the technical challenges, an applet (https://kalari.shinyapps.io/BBAA/) is provided.

While the Bayesian approach is more computationally expensive, it has some benefits that the frequentist approach does not have. The Bayesian method allows researchers to incorporate their prior knowledge in their analysis. Researchers should have at least some knowledge to rule out implausible values of (μ, σ), and it is useful especially in a small-sample (pilot) study. In addition, the interpretation of the posterior probability $P(-\delta \le \tilde{D}\le \delta \mid \overrightarrow{d})$ is more intuitive and more reflective of what researchers seek (the probability of seeing an acceptable difference). It provides a simple probabilistic statement regarding the future difference between two measures in the Bayesian framework. In the frequentist framework, a resulting 95% LOAs (l, u) is also a statement about the future difference between two measures, but an accurate interpretation of the resulting (l, u) cannot be directly related to the probability of seeing an acceptable difference. According to the frequentist interpretation of probability, it requires the hypothetical assumption of repeating the same experiment (to calculate l and u) and repeating future observations (to see if the future difference is between l and u). As we repeat the same experiment, values of l and u will vary, so the interpretation of an observed (l, u) is not straightforward. In addition, resulting 95% confidence intervals (l₁, u₁) for θ₁ = μ – 1.96σ and (l₂, u₂) for θ₂ = μ 1.96σ are statements about the model parameters, and an accurate interpretation of (l₁, u₂) in the frequentist framework can be challenging for many practitioners. The interval (l₁, u₂) is intended to capture both parameters θ₁ and θ₂, and it does not make a direct statement about the probability of capturing the future difference between the two measures.

The choice of a prior can be impactful on the posterior result. It may be difficult to set a threshold to flag that a prior has a poor effect on the posterior analysis. If two priors (e.g., a prespecified prior and a vague prior) result in substantially different posterior results, it may signify that the sample size n is too small (relatively to the amount of prior information λ₀), so they may consider continuing data collection. The authors strongly believe that researchers should not change a prespecified prior after seeing the posterior result. The prior must be independent of observed data, and changing the prior after observing data is double-dipping the data (inflating the amount of information contained in the data). If researchers are concerned about the prior sensitivity, the vague prior (the default option in the R Shiny applet) would be a safe option.

While the frequentist approach to Bland Altman analysis is widely used and is fairly simple to implement, the Bayesian Bland Altman analysis can be advantageous in helping researchers better understand and interpret their results. With today’s advanced technology, performing Bayesian inference is no longer a labored task. The process of constructing an informative prior and assessing the agreement between two methods of measurement via a posterior predictive distribution can be an alternative criterion for researchers to determine one measurement method over the other.

Appendix: R Shiny Applet Guideline

In order to aid researchers with the computational complexity of Bayesian Bland Altman analysis, an R Shiny applet is developed. A user inputs (1) a value of δ, the acceptable degree of disagreement between the two methods of measurement, (2) $\overrightarrow{d}=\left(d_1,\dots ,d_n\right)$, the data of n differences, (3) a choice of prior described below, (4) a statistic for checking the normality assumption by the posterior predictive p-value, and (5) the size of a posterior sample (default: 10,000). To check the normality assumption, the posterior predictive p-value is used (Gelman et al., 2013). An extremely small or large p-value indicates deviation from the normality assumption. The app provides two options for a statistic: the proportion of – δ < d_i < δ and skewness. Since the proportion is more meaningful from the practical perspective, it is set as default. A researcher has the following six options for choosing a prior.

• Vague prior (set as default): a₀ = 0.5, b₀ = 0.000001, μ₀ = 0, and λ₀ = 0.000001 as described in Section 4.2 and applied in Section 4.4.

• Normal-gamma prior with a₀, b₀, μ₀, and λ₀: A user chooses values of a₀, b₀, μ₀, and λ₀ to reflect one’s prior knowledge.

• Normal-gamma prior with $\widehat{\sigma }$, u_σ, l_μ, and u_μ: A user chooses values of $\widehat{\sigma }$, u_σ, l_μ, and u_μ by answering the three questions in Section 4.5. The user does not need to find the values of a₀, b₀, μ₀, and λ₀. The applet does for the user.

• Independent normal and gamma priors with a₀, b₀, μ₀, and λ₀: This prior assumes μ∼N(μ₀, 1/λ₀) and τ∼Gamma(a₀, b₀) independently. A user chooses values of a₀, b₀, μ₀, and λ₀ to reflect one’s prior knowledge.

• Independent normal and gamma priors with $\widehat{\sigma }$, u_σ, l_μ, and u_μ: A user chooses values of $\widehat{\sigma }$, u_σ, l_μ, and u_μ by answering the three questions in Section 4.5. The user does not need to find the values of a₀, b₀, μ₀, and λ₀. The applet does for the user under the independent assumption μ∼N(μ₀, 1/λ₀) and τ∼Gamma(a₀, b₀).

• Independent uniform (flat) priors with l_σ, u_σ, l_μ, and u_μ. A user assumes that all possible values of (μ, σ) are equally plausible for l_μ < μ < u_μ and l_σ < σ < u_σ. In other words, the user specifies arbitrarily wide boundaries for μ and σ.

After receiving the user’s inputs, the applet produces posterior results, graphics seen in Figure 3 and Figure 4, and interpretations of some key posterior results. The figures for the posterior distributions can be saved by right clicking on the image and choosing “save image as.”