Diffusion Anisotropy Measurement of Brain White Matter Is Affected by Voxel Size: Underestimation Occurs in Areas with Crossing Fibers

Abstract

BACKGROUND AND PURPOSE: Voxel size/shape of diffusion tensor imaging (DTI) may directly affect the measurement of fractional anisotropy (FA) in regions where there are crossing fibers. The purpose of this article was to investigate the effect of voxel size/shape on measured FA by using isotropic and nonisotropic voxels.

MATERIALS AND METHODS: Ten healthy adult volunteers had MR imaging by using a 1.5T clinical imager. DTI was performed with 2 different voxel sizes: a 2-mm-section isotropic voxel (2 × 2 × 2 mm³) and a 6-mm-section nonisotropic voxel (2 × 2 × 6 mm³). Images were obtained by using a single-shot echo-planar imaging technique with motion-probing gradients in 15 orientations and a b-value of 1000 s/mm². FA and the apparent diffusion coefficient (ADC) were measured at different sites of the brain.

RESULTS: When smaller isotropic voxels were used, the FA was greater in areas with crossing fibers, including the superior longitudinal fasciculus, the thalamus, and the red nucleus; the FA was not significantly different in areas without crossing fibers, such as the corpus callosum, the posterior limb of the internal capsule, and the corticospinal tract at the level of the centrum semiovale (P > .05). The ADC values were not affected by voxel size/shape at any of the areas of the brain that were measured.

CONCLUSION: FA values that are measured in regions containing crossing fibers are underestimated when using nonisotropic DTI.

Diffusion-weighted MR imaging has enabled the in vivo estimation of the diffusivity of the water molecule¹; it is now being increasingly used as a routine clinical examination.^2–4 A further extension of this technique is the estimation of diffusion anisotropy, which is known as diffusion tensor imaging (DTI).^5–7 DTI is especially useful in evaluating the white matter of the brain, in which there is a significant degree of anisotropy caused by the presence of cellular structures that provide barriers to free diffusion.⁸

Diffusion anisotropy has been shown to be effective in assessing diseases such as multiple sclerosis (MS),^9–10 stroke,¹¹ and amyotrophic lateral sclerosis.¹² For example, the anisotropy measurements of otherwise normal-appearing white matter in patients with MS have been shown to be related to the degree of demyelination.⁹ Fractional anisotropy (FA) is one of the most commonly used quantitative measures of anisotropy¹³ because it provides a higher contrast-to-noise ratio when compared with other measures, such as the volume ratio and relative anisotropy.¹⁴

A typical DTI examination uses the single-shot echo-planar imaging (EPI) technique. Single-shot EPI is inherently limited in its through-plane resolution, which could be a potential source of partial volume averaging.^15–17 However, the usual through-plane resolution of a clinical EPI for DTI would be approximately 2 ± 0.4 mm, for a FOV of 230 ± 20 mm and phase-encoding steps of 98–128. Thus, a typical voxel of a clinical DTI examination would be approximately 2 × 2 × 6 mm³.^9–10,18 Given this situation, it is apparent that the partial volume effect is much more prone to occur due to section thickness and not through-plane resolution.

We hypothesized that if FA measurements are done by using nonisotropic voxels (2 × 2 × 6 mm³) placed in areas where crossing fibers are expected, the measured FA would be underestimated when compared with that measured by isotropic voxels with the same through-plane resolution (eg, 2 × 2 × 2 mm³). On the other hand, if the measurements are done in regions where the fiber bundles are aligned in a single orientation, underestimation would not occur. On the other hand, the apparent diffusion coefficient (ADC) would not be underestimated regardless of the location measured because it is rotationally invariant. To the best of our knowledge, this effect of voxel size/shape on the measurement of ADC and FA has not been fully examined previously.¹⁷ The purpose of this article was to investigate the effect of voxel size/shape on the measured FA by using isotropic and nonisotropic voxels. We also examined the potential impact of voxel size/shape on the fiber-tracking technique.

Materials and Methods

This study was approved by the institutional review board. Written informed consent was obtained from each subject.

Subjects

Ten healthy adult volunteers without a history of neurologic disease or head trauma were recruited; there were 6 men and 4 women, ranging from 20 to 52 years of age, with a mean age of 34.1 years ± 11.0.

Imaging Methods

All images were obtained by using a 1.5T whole-body scanner (Gyroscan Intera, Philips Medical Systems, Best, Netherlands). A single-shot EPI technique was used for DTI (TR = 11 359 ms, TE = 71 ms) with a motion-probing gradient in 15 orientations, an FOV of 256 mm, and a b-value of 0 and 1000 s/mm². Through-plane resolution was 128 × 128. The sections were 2 or 6 mm thick without intersection gaps. Because signal-to-noise ratio (SNR) is proportional to the square root of the number of acquisitions, the number of acquisitions for the 2-mm-section DTI must be 9 times higher than that for the 6-mm-section DTI to compensate for the difference in voxel size. Thus, the image averaging was 1 time for the 6-mm-section scans and 9 times for the 2-mm-section scans, respectively. To cover the major part of the brain, we obtained 42 sections. The scanning times were 27 minutes 50 seconds for the 2-mm-section images and 2 minutes 42 seconds for the 6-mm-section images.

Image Analysis

We transferred the DWI data to an off-line workstation for analysis. Before averaging, unwrapping of the eddy current effects on the diffusion-weighted MR images was performed as previously described.^19–20 Eigenvalues and eigenvectors of the tensor were calculated by using a Jacobi transformation.²¹ FA was calculated from the eigenvalues as described by Basser and Pierpaoli.¹³ The mean diffusivity was estimated by averaging the 15 eigenvalues.

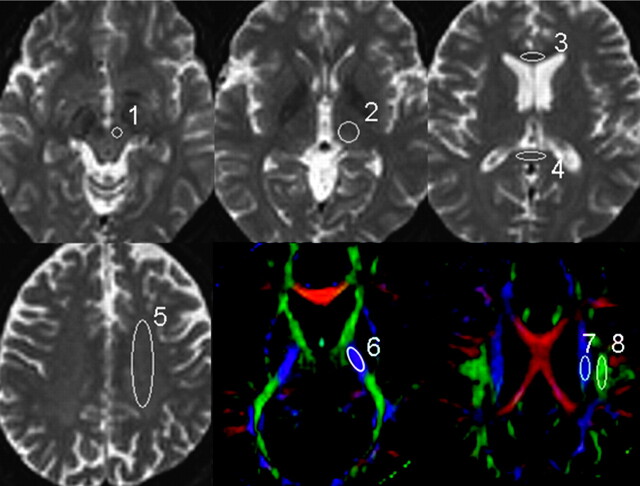
To evaluate the effect of section thickness on ADC and FA, we performed a region-of-interest analysis. Regions of interest were manually placed in characteristic gray and white matter structures on the b = 0 maps (thalamus, genu of the corpus callosum, splenium of the corpus callosum, centrum semiovale, and red nucleus [Fig 1]) and on the FA maps (posterior limb of the internal capsule, corticospinal tract [CST] at the level of centrum semiovale, and superior longitudinal fasciculus [SLF] [Fig 1]). All regions of interest were placed on the basis of the consensus of 2 skilled operators (K.Y., H.O.).

Fig 1.

The regions of interest used in the data analysis are superimposed on the transverse single-shot EPI performed with a b-value of 0 s/mm² and the FA maps. 1 indicates red nucleus; 2, thalamus; 3, genu of the corpus callosum; 4, splenium of the corpus callosum; 5, centrum semiovale; 6, posterior limb of the internal capsule; 7, CST; 8, SLF.

The regions of interest were initially placed on the 6-mm-thick images. These same regions of interest were then placed on the 2-mm-thick images for 3 contiguous sections. The averaged values from these 3 contiguous sections of the 2-mm-thick images were obtained.

Simulation Study

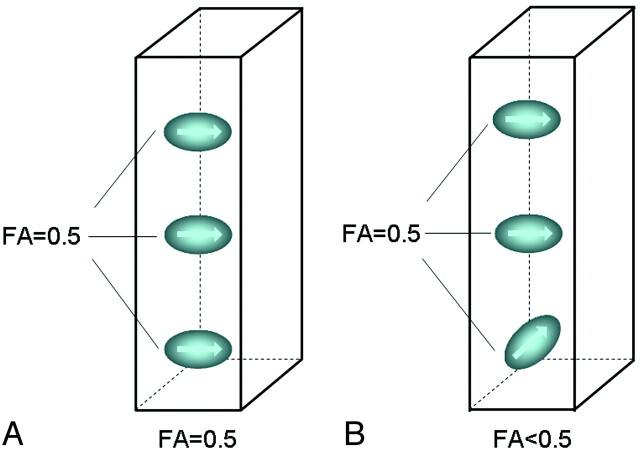
We performed a simulation that replicated the condition in which a nonisotropic voxel is placed in the brain white matter for FA measurement. We defined the baseline condition as 3 fiber bundles existing within the nonisotropic voxel, with the same eigenvector and with the same FA value (FA = 0.5). The condition in which 1 of these fiber bundles is not parallel to the other 2 was also simulated (Fig 2).

Fig 2.

FA measurement in a nonisotropic voxel. It was assumed that there are 3 fiber bundles traversing this voxel, each with an FA of 0.5. When all fibers are aligned in a single direction (A), the measured FA of the voxel is 0.5. When there is a crossing fiber within this voxel (B), then the measured FA of the voxel is <0.5.

Tractography

Tractography of the CST and the SLF was done for all subjects. We used PRIDE software (Philips Medical Systems) for the analysis. Detailed descriptions of the tracking methods are given elsewhere.²² The FA and ADC values of each fiber tract were also measured.

Statistical Analysis

The statistical significance of the ADC and FA values at each section thickness was assessed by paired t tests for each region of interest. The results were considered statistically significant at P < .05. All statistical analyses were performed by using a statistical software package (StatView, version 5.0; SAS Institute, Cary, NC).

Results

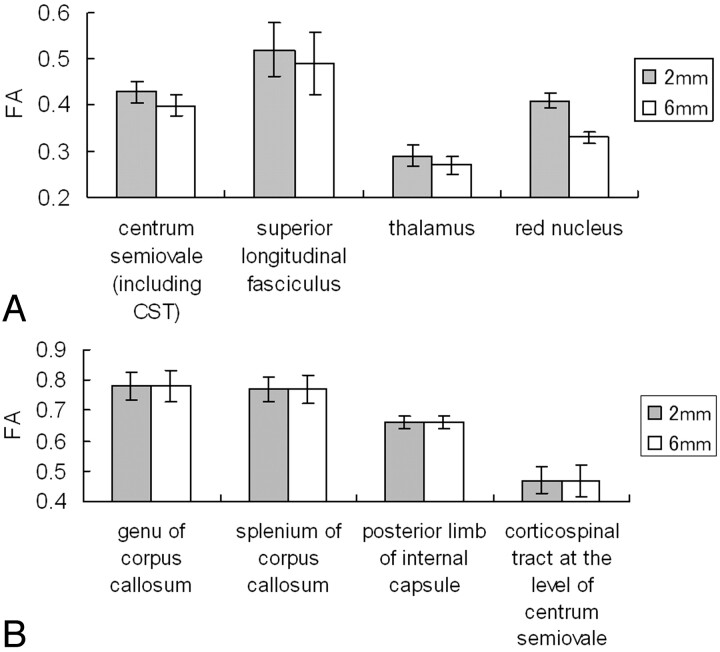
The mean FA and ADC values at each location are summarized in Figs 3 and 4, respectively. The areas with statistically significant FA differences between the isotropic and nonisotropic voxels are shown in Fig 3A, and the areas without significant differences are summarized in Fig 3B. Areas with statistically significant FA differences were located at the centrum semiovale, SLF, thalamus, and red nucleus. Areas without statistically significant differences were located at the genu of the corpus callosum, splenium of the corpus callosum, posterior limb of the internal capsule, and CST (P > .05). The ADC values obtained from different section thicknesses did not differ statistically for any of the measurements (P > .05).

Fig 3.

The graphs present the measured mean FA values in the nonisotropic voxel (2 × 2 × 6 mm³) and in the isotropic voxel (2 × 2 × 2 mm³).

A, Statistically significant FA differences were noted at the centrum semiovale (P < .0001), SLF (P < .0001), thalamus (P < .0001), and red nucleus (P < .0001).

B, The areas without statistically significant differences.

Fig 4.

Graph shows ADC measurements of the 2- and 6-mm-thick sections. The ADC values were not affected by voxel size/shape at any of the areas of the brain that were measured.

Tractography was done successfully in all subjects. The robustness of the CST was not substantially different between the 2- and 6-mm-section thicknesses. This finding was expected because the CST runs perpendicular to the section. The CST also appeared symmetric in all subjects.

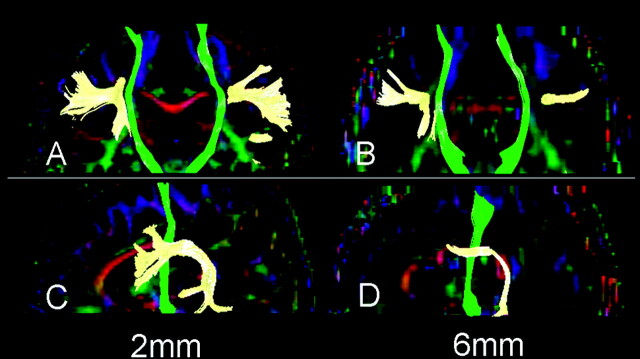
The SLF was also successfully depicted by using both 6- and 2-mm sections in most subjects. However, the depiction of the SLF was poor in 2 subjects, and there were 3 subjects who had substantial laterality when the 6-mm-section thickness was used. A representative example is shown in Fig 5.

Fig 5.

Fiber tracts of the CST (green) and SLF (yellow) are superimposed on the vector maps. Note that the SLFs obtained from 2-mm-section images (A, C) are more robust than those obtained by 6-mm-section images (B, D). Depiction of the CST did not substantially differ between 2- and 6-mm-section images.

A simulation study that replicated the condition in which a nonisotropic voxel was placed for FA measurement is presented in Fig 6. When all 3 bundles of fibers contained in this voxel were aligned in exactly the same direction (parallel to each other), the measured FA of this nonisotropic voxel (2 × 2 × 6 mm³) was similar to that measured by the isotropic voxel (2 × 2 × 2 mm³). When 1 of the 3 fiber bundles was not parallel to the other 2 bundles, the measured FA of the nonisotropic voxel was less than that of isotropic voxel.

Fig 6.

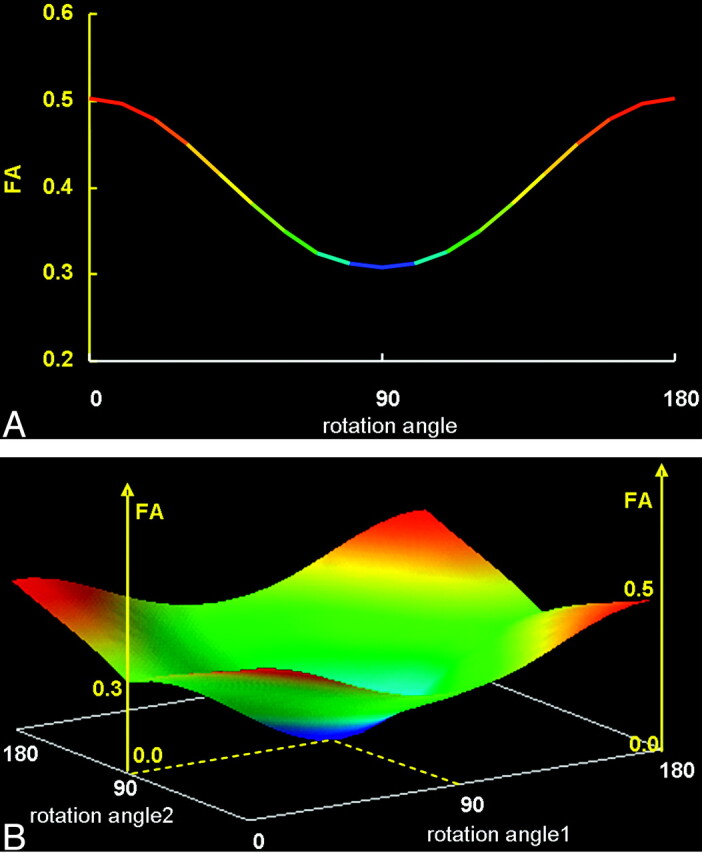
The graphs show the results of the simulation study in which 1 (A) or 2 (B) of the 3 fiber bundles contained within a nonisotropic voxel were rotated 180°.

A, When only 1 of the fiber bundles was rotated from its original location, FA underestimation occurred, which was lowest when the fiber bundle was oriented perpendicular (90°) to its original location.

B, Similarly, when 2 of 3 fiber bundles were rotated simultaneously, FA was underestimated to various degrees depending on the extent of the rotation, becoming zero when both bundles were perpendicular to each other (represented by the central part of this 3D graph).

The graphs show the results of rotating 1 (or 2) of the fiber bundles 180° from the original angle. The data indicate that the FA of the nonisotropic voxel was most underestimated when the bundles were aligned at 90°(perpendicular) to the original direction.

Discussion

To our knowledge, our study is the 1st systematic evaluation of the effect of voxel size/shape on measured FA. We have shown that measured FA may be affected by voxel size/shape in certain regions of the brain, but not in other regions. The areas in which measured FA did not depend on voxel size/shape included the corpus callosum and the CST. On the other hand, when using the nonisotropic voxel, statistically significant lower FA values were found in locations such as the SLF, the red nucleus, and the thalamus. For example, FA values from the 2 × 2 × 6 mm³ voxel at the SLF were lower by approximately 6% compared with those of the 2 × 2 × 2 mm³ voxel.

The difference between the regions with and without FA diversity appears to be related to the degree that crossing fibers were contained within the voxel of the DTI. For example, callosal fibers and the CST are both characterized by tightly packed fiber bundles that run in a similar direction. These areas did not have a lower FA for the nonisotropic voxel DTI, possibly because there was less of a crossing-fiber effect within each voxel. It is also noteworthy that this effect did not depend on fiber direction. Fibers within the corpus callosum run parallel to the transaxial sections, whereas CST fibers run perpendicular to the transaxial sections. Regardless of direction, there was no significant FA diversity using the nonisotropic-voxel DTI. However, when crossing fibers were present within a nonisotropic voxel, the measured FA was lower than the FA measured by an isotropic voxel. The mechanism of this difference in measured FA is illustrated in Fig 2, and the simulation results are illustrated in Fig 6.

This voxel size/shape dependency of the measured FA is of vast clinical importance because anisotropy measurements have captured the attention of investigators in various fields and have been used to study many different diseases, as well as healthy subjects.^9–12,18,23 In fact, there are studies that use the data not only to support the diagnosis of certain diseases but also to assess the treatment effect and to monitor a patient's condition at follow-up.^10,18,23 One of the most common FA measurement sites is the corpus callosum.^12,18 The results of our study show that the FA of these regions is not voxel size/shape–dependent, and the results are, therefore, comparable between different studies. Another common FA measurement site is the CST, which is commonly measured in studies of patients with amyotrophic lateral sclerosis.¹² Again, FA measurements at these regions will be reliable regardless of voxel size.

However, when using a nonisotropic voxel to measure FA values in regions with crossing fibers, one should expect a certain degree of voxel size/shape–dependent change. This unwanted effect will be larger as the section thickness increases because the voxel shape becomes distorted from the ideal isotropic (cubic) shape with increased thickness. Furthermore, the data from regions with crossing fibers obtained from different studies may not be directly comparable. Therefore, when one wishes to compare groups of patients, it is ideal to keep the DTI voxel size similar, or as close as possible, between studies. There have been a few previous reports comparing FA values obtained by using different section thicknesses^24–25; these reports may have contained a certain degree of error in their assessment of regions with crossing fibers. It is also important to note that previously published normative FA data²⁶ may not serve as a direct reference unless the voxel size/shape is almost identical.

Our data suggest that smaller voxel sizes likely present a more accurate picture of the true anisotropy measurement. Thus when a 1 × 1 mm² through-plane resolution is achieved by advances in MR imaging technique, the ideal section thickness will be 1 mm. The trade-off apparently is the SNR. The SNR of the obtained images would have a direct impact on the measured FA¹⁴; thus, it would not be ideal to lower the SNR below a certain level. Ultra-high-field MR imaging units may be able to solve part of this problem. Another advanced technique that could be used to circumvent the problem may be the high-angular-resolution diffusion imaging technique, which has the potential to resolve multiple fiber orientations within a single voxel.²⁷

It would be ideal if a simple coefficient could be defined that could correct for the difference in voxel size/shape. However, this is not thought to be possible because there is no a priori way of knowing what causes the low FA of a given voxel; a low FA could be due to voxel size/shape–dependent changes resulting from crossing fibers or due to the nature of the brain tissue contained within the voxel.

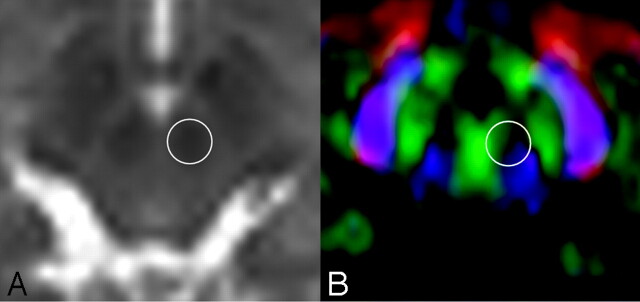
There was substantial FA change at the red nucleus, with approximately a 20% difference between the 2 × 2 × 2 mm³ and the 2 × 2 × 6 mm³ voxels. In Fig 6, the color map of this area shows that it contains various fibers running in different directions (Fig 7). Thus, an easy rule of thumb would be to avoid measuring FA in areas that contain different colors (directions). Therefore, when one is measuring FA, the use of a color map in conjunction with other imaging studies would be an ideal way to avoid bias.

Fig 7.

B = 0 (A) and color-coded FA maps (B) through the red nucleus are shown. The circles represent the location where the FA measurements were taken. Note that there are many different colors within this region of interest, indicating that there may be crossing fibers contained in this small area of the brain.

In this study, we have also shown that imaging with an isotropic voxel may be beneficial for fiber tracking. Tracking was more robust and symmetric when thinner sections were used. The effect was more prominent for fibers running parallel to the section (ie, SLFs). A similar effect would thus be expected when visualizing fibers such as the optic radiation or the callosal fibers.

This study has several limitations. First, the number of samples may be somewhat small. However, we were able to show statistically significant differences in FA between the areas with/without crossing fibers; thus, the number of subjects was sufficient to allow conclusions to be drawn. Second, the DTI in our study was done by using a motion-probing gradient in 15 orientations. Some studies have suggested that 30 or more directions would be optimal for accurate diffusion tensor estimation.²⁸ Therefore, additional studies may be needed to show that the changes in FA values occur even at higher angular DWI. Third, the study was done by using only a 1.5T MR imaging unit; therefore, we have no data using a higher field magnet, such as is used in a 3T machine. Although it may be apparent from the results of our study that a smaller voxel size achieved by a higher SNR by using 3T would be advantageous, this fact may have to be clarified by using healthy subjects scanned by magnets at different field strengths to emphasize the benefit of using higher field MR imaging units. At present, the acquisition time used for the 2 × 2 × 2 mm³ examination at 1.5T would be too long for any clinical application. Prolonged acquisition time would raise the potential for motion effects on the data. Thus, the use of a 3T machine may be able to solve this SNR issue.

In conclusion, voxel size/shape–dependent underestimation of the FA occurs in regions where there are crossing fibers. On the other hand, the FA measured in regions without crossing fibers (such as the corpus callosum and the CST) is not prone to underestimation and can, thus, be used for comparisons between studies. It would be ideal to obtain all images with an isotropic voxel, but this is not always possible. Thus, when measuring FA by using nonisotropic-voxel DTI, the following 3 rules would help avoid underestimation: First, the region of interest should not be placed in regions with a substantial degree of crossing fibers; color maps may help avoid such regions. Second, corpus callosum and CST measurements may serve as references because these regions are less affected by voxel size/shape. Third, when doing a prospective longitudinal follow-up study or a comparison of studies, it would be ideal to have an identical voxel size.