Prediction of the Jugular Venous Waveform Using a Model of CSF Dynamics

Abstract

BACKGROUND AND PURPOSE: We have previously reported a model of cerebral hydrodynamics in the form of an equivalent electrical circuit. The aim of this work was to demonstrate that the model could predict venous flow patterns seen in the superior sagittal sinus (SSS), straight sinus (STS), and jugular vein (JV) in normal volunteers.

MATERIALS AND METHODS: An electrical equivalence model of CSF and cerebral blood flow was fitted to measured arterial and CSF data from 16 healthy volunteers. Predictions of the venous outflow waveform derived from the model were compared with measured venous flows in the SSS, STS, and JV.

RESULTS: The model accurately predicted the measured jugular waveform. The measured waveforms from SSS and STS showed a less pronounced and delayed systolic peak compared with the predicted outflow. The fitted bulk model parameters provided relative values that correspond approximately to the impedance of arterial capillaries (1.0), cerebral aqueduct (≈0), venous capillaries (≈0), and arteries (0.01) and for the elastic capacitance of the ventricles (4.11), capillaries (≈0), and veins (271). The elastic capacitance of the major cerebral arteries was large and could not be accurately determined.

CONCLUSIONS: We have confirmed the ability of the model to predict the venous waveforms in healthy persons. The absence of any statistically significant component of the venous waveform not described by the model implies that measurements of venous flow could be used to constrain further the model-fitting process.

The Monro-Kellie hypothesis states that the sum of the brain, CSF, and intracranial blood volumes is constant if the skull is intact.¹ Electrocardiogram (ECG) gated MR phase imaging allows quantitative, high temporal-resolution imaging of CSF and blood flow within the skull during a single cardiac cycle. MR-based studies of these flows show that the constraints of the Monro-Kellie hypothesis result in a complex homeostatic hydrodynamic mechanism that compensates for the transient increases in cerebral blood volume and arterial blood pressure occurring during systole.^2,3 We refer to this as Monro-Kellie homeostasis to distinguish it from the mechanisms responsible for the maintenance of mean cerebral blood flow. Breakdown of Monro-Kellie homeostasis has been implicated in a number of disease processes.^2-10

Almost all previous MR imaging studies rely on phenomenologic observations, such as flow volume measurements or delay in the arteriovenous passage of the systolic pulse wave, or first-order derived variables describing more physiologic parameters, notably vascular compliance within the vascular tree feeding specific venous drainage territories.² Unfortunately, the complexity of the homeostatic mechanism, common variations in vascular anatomy,^2,11,12 variation in measurements and interpretation methods recommended by different groups,^3,5,6,13-15 and the limitations on the number of measurements available from MR imaging flow techniques combine to make these approaches increasingly unsatisfactory. There is a clear need for a quantitative physiologic model to act as a substrate for principled analysis of this type of data to support direct comparison between studies and, more importantly, to allow estimation of hydrodynamic parameters that cannot be measured directly with existing techniques.

We have recently reported a model that describes, using an electrical circuit analogy, the inter-relationships between arterial, capillary, and venous blood flow and movements of CSF between the cerebral ventricles, subarachnoid, and spinal CSF spaces.^16,17 When fitted to arterial and foramen magnum flow measurements, it allows direct proportional (but not absolute) estimation of 7 parameters that cannot be derived by direct measurement, corresponding approximately to arterial, brain, ventricular and venous compliances, and arterial, brain, and cerebral aqueduct impedances. The identification of additional localized, measurable inputs that can be used to drive the fitting process could provide more anatomic specificity. Fortunately, the existing model provides the ideal method to investigate the validity of such additional measurements because observed values can be directly compared with model-based predictions. The objective of this study is therefore to demonstrate that the model can predict venous flow patterns seen in the superior sagittal sinus (SSS), straight sinus (STS), and jugular vein (JV) in normal volunteers.

Materials and Methods

Electrical Equivalence Model

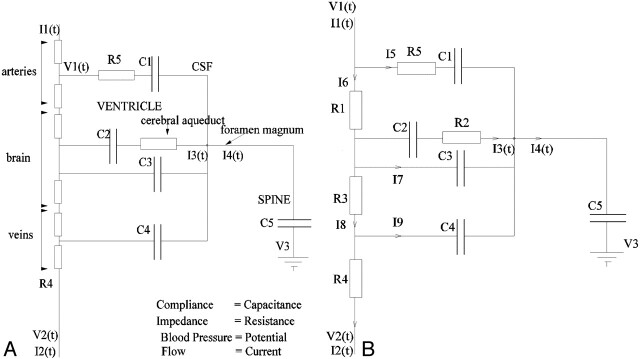
The electrical equivalence model has been presented previously.^16,17 In brief, it is based on the simplified anatomic construct illustrated in Fig 1. This idealized system is modeled, treating the impedance of flow paths as resistances, the compliance of thin boundaries as capacitances, pressure differences as voltages, and flows as currents. This results in the electrical equivalence model shown in Fig 2A. Analysis of this model illustrates redundancy of some components, supporting simplification to the final circuit demonstrated in Fig 2B. A series of functions that can be fitted using standard minimization approaches can then be derived (Appendix 1).

Fig 1.

The simplified anatomic model on which the electrical equivalence model is based. Boundaries identified by thin lines are considered compliant.

Fig 2.

A, The electrical equivalence model derived for the anatomic model shown in Fig 1.

B, The simplified equivalent circuit after removal of redundant components.

Subjects and MR Image Acquisition

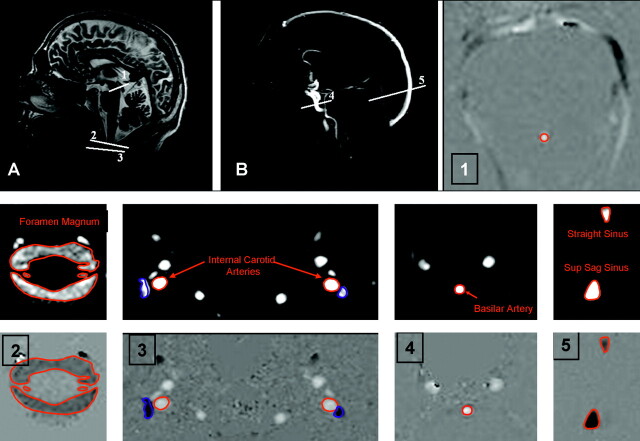
MR image volumes were acquired from 16 control subjects (14 men and 2 women; age, 32 ± 10 years) with no known abnormality. Written informed consent was obtained from all subjects and the local NHS (National Health Service) and University ethical committees approved the study. All subjects were scanned using a 3T whole-body imager (Acheiva, Philips Medical Systems, Best, the Netherlands). Sagittal T1-weighted images and phase-contrast (PC) angiography scout images were acquired to allow prescription of imaging planes perpendicular to the principal direction of flow (Fig 3). Velocity encoded PC-cine MR images were then obtained at 7 points: CSF flow at the cerebral aqueduct (AQ); CSF flow at the foramen magnum (FM); arterial blood flow in the basilar artery (BA) at the level of the midclivus; arterial blood flow in the internal carotid arteries (CA) immediately below the foramen lacerum; venous blood flow from the SSS 2–3 cm above the confluence of the sinuses; venous blood flow from the midpoint of the STS; venous blood flow from the JVs immediately below the base of skull. Two of the JV images exhibited motion artifacts, which prevented accurate location of the vessel, and so only 14 JV images were used in the subsequent analysis. Retrospective vector electrocardiographic gating was used to generate 16 pairs of images spanning the cardiac cycle for each subject. The first image was a flow modulus image showing the anatomic location of flow and the second a velocity-encoded image in which the intensity is linearly proportional to flow velocity (Fig 3). The imaging parameters were: flip angle, 10–15°; section thickness, 5–7 mm; repetition time, 8.82–22.13 ms; and echo time, 8.14–14.39 ms; velocity encoding (V_enc) was set at 10 cm/s for the AQ and FM, 90 cm/s for the BA and CA, and 60 cm/s for SSS, STS, and JV. Scan time was usually 2–4 minutes for each region depending on heart rate; total scanning time was 15–30 minutes.

Fig 3.

Anatomic (A) and arteriographic (B) scout images showing the location of the measurement planes. Subsequent images show the location of regions of interest for the cerebral aqueduct (1), foramen magnum (2), internal carotid arteries and jugular veins (3), basilar artery (4), and superior sagittal and straight sinuses (5).

Image Processing

To obtain a reliable estimation of the AQ flow, an approximate location for the center of the aqueduct was provided manually, and a quadratic function was fitted over the 9 voxels in a 3 × 3 region around it at each time point in the cardiac cycle. The area under this curve was then integrated for all positive values of the function. The BA, CA, FM, SSS, STS, and JV flows were estimated from the sum of flow values within the region of the vessels, defined by thresholding the modulus images to find the region of interest (ROI) as shown in Fig 3.

Data Analysis

Measured values from CA and BA were combined to produce an arterial input function (carotid and basilar artery [CAB]). The flow values from CAB, FM, and AQ were then used to fit the model allowing prediction of venous outflow currents corresponding to I8, I9, and I2 in Fig 2B. Measured flow values from SSS and STS were summed to derive an estimated total supratentorial venous output function (Ven). Measured values of flow in SSS, STS, Ven, and JV were compared with predicted values for venous outflow from the model (I2). Waveforms were compared using Wald-Wolfowitz runs test for mean values and Mann-Whitney test for comparison of group data at each individual heart phase. Pulsatility indices were calculated for SSS, ST, JV, I8, I9, and I2 by subtracting the end diastolic flow rate from the peak systolic flow rate and dividing by the average value.⁴ Pulsatility indices were compared using the Mann-Whitney test.

Results

Table 1 shows the range of measured values of flow in the CAB, SSS, STS, and JV and model-based predictions of I2, I8, and I9 for all 16 subjects. The measured SSS flow showed considerable variation from 34% to 75% of the combined CAB flows, reflecting the anatomic variation in prosencephalic venous drainage described by previous authors.¹² The total STS flow also showed significant but smaller variation from 11% to 21% of CAB, whereas the combined SSS and STS measurements accounted for between 46% and 92% of measured CAB. The combined JV measurements were also extremely variable, accounting for 48%–104% of the measured CAB in keeping with the observations of previous authors.¹² The presence of Ven flows equivalent to CAB presumably reflects the use of a BA measurement point distal to the inferior cerebellar and other inferior arterial branches within the infratentorial compartment. Likewise, the observation of JV flows in excess of the CAB presumably reflects the combination of this factor and contributions of the extracerebral circulation to jugular venous drainage.

Table 1:

The measured flow volumes and pulsatility indices (PI) from the superior sagittal sinus (SSS), straight sinus (STS), combined venous outflow (SSS + STS = Ven), jugular vein (JV), and arterial inflow (carotid + basilar arteries = CAB), the predicted flow volume for I2 (overall venous outflow in the model), and the predicted indices for I2, I8, and I9

	Volume (ml/min)	PI (mean ± SD)
SSS	305.79 ± 53.59	0.33 ± 0.057
STS	87.23 ± 16.61	0.28 ± 0.068
Ven	392 ± 61.4	0.31 ± 0.041
JV	312 ± 138	0.51 ± 0.045
CAB	536.21 ± 73.61	0.81 ± 0.21
I2	536.21 ± 71.14	0.45 ± 0.16
I8		0.0037 ± 0.0013
I9		1.91 ± 0.53

Comparison of the pulsatility indices of the observed and measured parameters (Table 1) showed that the measured values of SSS, STS, and Ven were significantly lower (0.33 ± 0.057, P < .05; 0.28 ± 0.068, P < .01; 0.31 ± 0.041, P < .05, respectively) than the predicted value for I2 (0.45 ± 0.16). The pulsatility index of JV (0.51 ± 0.045) was not significantly different from I2.

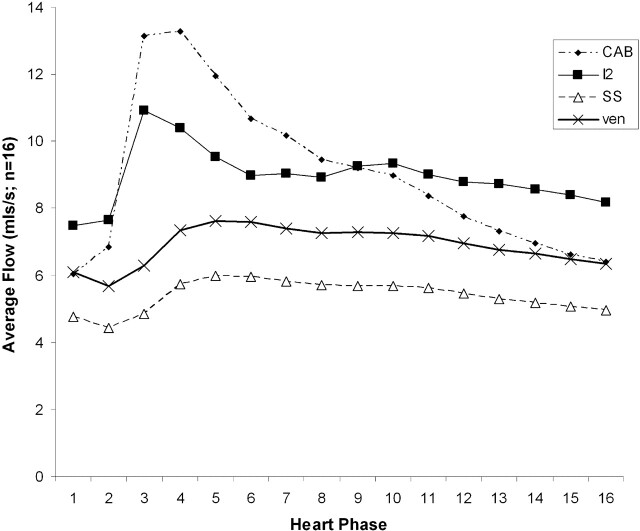
Figure 4 shows the time course curves from a single cardiac cycle for mean values of CAB, I2, SSS, and Ven. These represent the interactions occurring within the supratentorial compartment. It can be seen that SSS and Ven have identical curve shapes and represent approximately 70% of the predicted value of I2. In addition, there is a significant delay of approximately 12% of a cardiac cycle between the systolic peak of the CAB and I2 curves and the measured data from SSS and Ven.

Fig 4.

Measured flow rates for carotid and basilar arteries combined (CAB), superior sagittal sinus (SSS), and combined straight sinus (STS) and SSS venous outflow (Ven) averaged across 16 subjects compared with the predicted venous outflow I2.

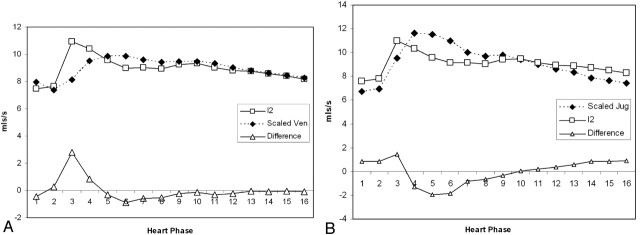
Figure 5A shows the time course of I2 and Ven (scaled to I2 [ie, equivalent bulk flow]), together with the calculated difference, and Fig 5B shows the same plot for comparison of I2 and the scaled measurements of JV. Figure 5A shows a clear large systolic peak in the difference graph, indicating poor conformance between the predicted and measured venous flows, whereas Fig 5B shows relatively good conformance.

Fig 5.

A, Comparison of the predicted venous outflow (I2) and the combined STS and SSS venous outflow (Ven). The venous outflow has been scaled to have the same integral as I2. The lower curve shows the difference in the waveforms. Note the prominent systolic peak in the difference.

B, Comparison of the predicted venous outflow (I2) and the jugular venous outflow (JV). The venous outflow has been scaled to have the same integral as I2. The lower curve shows the difference in the waveforms.

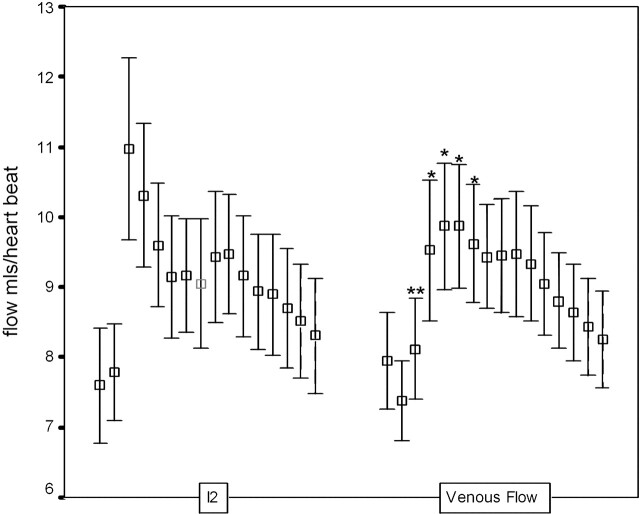
Figure 6 also compares the pulsatility profiles of the predicted venous outflow I2 and the scaled measures of supratentorial flow (Ven). The curves are significantly different (P < .05, Wald-Wolfowitz test) with intergroup differences (P < .05, Mann-Whitney test) at 5 of the 16 time points. Figure 7 shows the equivalent comparison between I2 and the scaled measurement of JV. There is a smaller delay between the peak of I2 and JV of approximately 6% of a cardiac cycle. A significant difference (P < .05, Mann-Whitney test) between the individual measurements is seen at only one time point.

Fig 6.

Mean and 95% confidence intervals for flow at each of 16 heart phases for the predicted venous outflow (I2) and the combined STS and SSS venous outflow (Ven). Asterisks indicate significant differences (∗, P < .05; ∗∗, P < .01).

Fig 7.

Mean and 95% confidence intervals for flow at each of 16 heart phases for the predicted venous outflow (I2) and the jugular venous outflow. Asterisks indicate significant differences (∗, P < .05).

Table 2 shows the calculated values of the 7 relative variables derived from the model. A measurement of pressure at some point within the cerebral vasculature would be required to set the scaling of the model and provide absolute values of the parameters. However, a pressure measurement could not be obtained noninvasively; therefore, the parameters are given as relative values, normalized to R1. As expected, the impedance values of the aqueduct, venous capillaries, and major arteries are very low, whereas the arterial capillaries (including the pial resistance arterioles) are high. Elastic capacitance in the cerebral arteries is extremely high and cannot be accurately estimated from the model because it tends to infinity, whereas the elastic capacitance of the ventricles and of the cerebral capillary bed is very low (consistent with 0). The capacitance of the draining veins is intermediate in value, approximately 50 times higher than the ventricles but far lower than the major arteries.

Table 2:

The estimated relative values for parameters R1–R5 and C1–C4 (Fig. 2) together with their approximate physiologic characteristics

Parameter	Physical Interpretation	Value	SE
R1	Impedance of arterial capillaries	1.0	0.0025
R2	Impedance of cerebral aqueduct	≈0.0
R3	Impedance of venous capillaries	≈0.0
R5	Impedance of arteries	0.01	8 × 1.8−3
C1	Elastic capacitance of arteries	≈Large
C2	Elastic capacitance of ventricles	4.11	0.11
C3	Elastic capacitance of capillaries	≈0.0	5 × 10−3
C4	Elastic capacitance of veins	271.017	18

Discussion

In healthy subjects, systolic expansion of the basal cerebral arteries produces a pressure wave within the subarachnoid CSF (which causes an outflow of CSF through the foramen magnum into the compliant spinal CSF space) equivalent to approximately 50% of the increase in intracerebral blood volume.^3,4 The pressure wave is also transmitted to the major dural venous sinuses by systolic expansion of the arachnoid granulations.^9,18,19 The effect of this is that the systolic pressure wave is dissipated into the formation of CSF and venous pulsatility and largely bypasses the cerebral circulation. In addition, elastic artery walls absorb part of the energy of the systolic pulse wave, which is then released during diastole, further flattening the arteriolar pressure profile to which the intracerebral circulation is exposed: this is known as the Windkessel effect. Constancy of cerebral perfusion pressure is also maintained by transient systolic increases in venous backpressure within the brain as a result of direct compression of cortical surface veins by the systolic pulse wave in the subarachnoid CSF space. This combination of processes maintains a constant perfusion pressure and flow in the cerebral capillary bed despite the major pressure changes seen between systole and diastole. Abnormalities of the mechanism have been described in a number of disease states, including communicating hydrocephalus,³ normal pressure hydrocephalus,^2,6 idiopathic intracranial hypertension,^5,20 secondary intracranial hypertension,⁵ ischemic white matter change (leukoariaosis),⁴ neurodegenerative and mixed dementias, cerebral atrophy, and vascular depression^7,21 (ie, geriatric depression associated with cerebrovascular disease). It is now believed that, in some of these disease states, abnormalities of this homeostatic mechanism form the major mechanism of injury, whereas in others, it is unclear whether abnormalities simply reflect secondary effects.

One of the main problems associated with MR flow studies of Monro-Kelly homeostasis is the diversity of methodology used to analyze the data; there are few examples of coherent analysis approaches even in consecutive studies from single research groups. This variance largely reflects continuing confusion concerning the actual mechanism and its modes of failure and the need to tailor analyses to specific disease states. Previous workers have described theoretic electrical equivalence models of intracranial hydrodynamics and have tested them with simulated datasets.^22,23 However, our previous study and the work presented here represent the first attempt to validate such a model with real data.

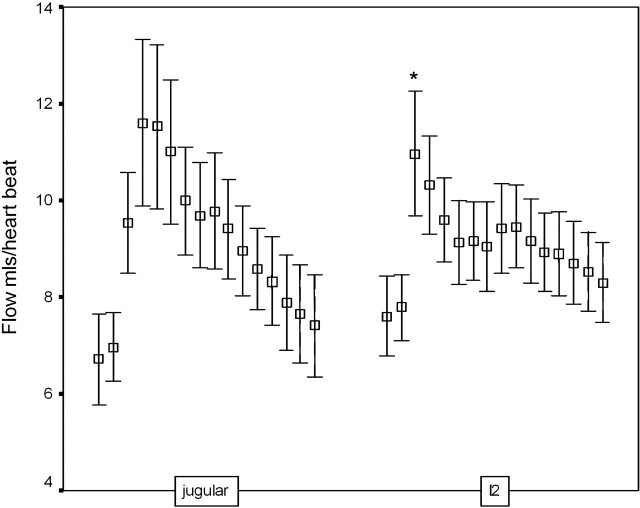
We have shown previously that the model describes the statistical variations observed in arterial and CSF waveforms in healthy persons.¹⁷ In this study, we have demonstrated that the model is capable of predicting the venous outflow waveform in the jugular vein with an acceptable level of accuracy, confirming the assumptions implicit in the simplified anatomic model (Fig 1) on which it is based. Nonetheless, a review of the literature indicates that it is likely to be overly simplistic for use in pathologic conditions.¹⁸ First, there is a clear functional dichotomy between the superficial and deep cerebral venous drainage territories, which are not represented separately in the model, in the way that they respond in different disease states.^2,6 Second, there is a need to understand the distribution of systolic pulse wave energy within the superficial venous system and major dural venous sinuses. Third, the variations in CSF flow in the supratentorial and infratentorial compartments may require explicit modeling. In this study, we showed that the major dural venous sinuses in the supratentorial compartment have a later and less pronounced systolic waveform than those predicted by the model and observed in the jugular venous outflow. This supports the observations of previous workers that the infratentorial CSF dynamics are characterized by an early outflow of CSF from the fourth ventricle.¹¹

Alperin et al²⁴ have identified a temporal discrepancy between the fluid inflow (arterial) and outflow (venous plus CSF), which indicates the existence of small temporal fluctuations in intracranial volume. They attribute these changes to inherent elastance in the brain substance and use the known relationships between pressure and flow to derive noninvasive estimates of intracranial pressure. We have also observed this discrepancy, which can be expressed as the difference between the scaled measurements of jugular venous outflow and the estimate (I2) provided by the model (Fig 5B). The shape and timing of this waveform are identical to that described by Alperin et al²⁴ (Fig 5), though the measured peak-to-peak values in this study are slightly larger than the values they described in 8 volunteers (3.8 mL/heartbeat change in intercranial volume versus 0.3–1.3 mL/heartbeat).

One potential shortcoming of the current study was the decision to measure flow patterns in the hindbrain circulation from the midportion of the basilar artery. This was done to ensure that the measured waveform was truly characteristic of the intracranial arterial tree, which may differ from that seen in the vertebral arteries. It was expected to lead to a systematic underestimation of the arterial blood flow volume, which was indeed evident in the comparisons of prosencephalic arterial and venous flow volume, where CAB was almost equivalent to Ven in some subjects. It may also underlie the minor differences in intracranial volume change described above. In practice, this can easily be corrected using the volume measurements from the vertebral arteries to scale the waveform from the basilar artery for use in the model.

Although the current study represents a validation of a simplified model in healthy subjects, it is clearly appropriate for the study of diseases in which the principal abnormalities lie in the arterial inflow waveform (such as hypertension, elevated pulse pressure), the arterial tree (such as arterial stenosis, vascular depression, vascular dementia, primary (idiopathic) intercranial hypertension [IICH]), or the compliance of the brain itself. The application of the model to these and similar disorders is likely to improve our understanding of the pathologic mechanisms involved through its ability to support statistical intergroup comparisons of physiologic variables that are currently not measurable (arterial compliance, brain compliance, ventricular compliance, overall venous compliance, arterial impedance, brain impedance, and the impedance of the cerebral aqueduct). However, although the model could be applied to the characterization and study of other disorders, such as venoocclusive diseases, it is unlikely to provide the desirable level of granularity to explore the underlying anatomic and physiologic mechanisms involved. There is therefore a need for further extension of the model to support such studies. Explicit modeling of the contributions of the supratentorial and infratentorial compartments is likely to be relatively straightforward as variations in the waveforms of the major supratentorial dural venous sinuses are directly measurable. The addition of a measurement of CSF flux through the incisura is straightforward, though the fourth ventricular outflow may have multiple outflow pathways. More importantly, it is possible to measure pulsatile venous flow at other sites in the venous system, including the straight sinus, sigmoid, and transverse sinuses, extracerebral jugular vein and major superficial cortical veins such as the Great Vein of Labbe, which represent the principal collateral venous flow mechanism from the prosencephalic cortex. The use of these measurements may support extension of the model to allow differentiation of the pressure effects on deep cerebral, superficial cortical, and dural veins, which have been proposed as etiologic factors in various disorders.^2,4-7

Conclusion

We have described a simplified anatomic model of Monro-Kellie homeostasis and presented an electrical equivalence model that allows derivation of values corresponding approximately to arterial, brain, ventricular, and venous compliance and arterial, brain, and cerebral aqueduct impedance. We have validated the model by showing its ability to predict jugular venous waveform in healthy subjects and have identified a number of potential applications in which the use of the model can be expected to improve our ability to understand the mode of failure of the homeostatic mechanism.

Appendix

This section describes the derivation of a minimal descriptive model for the circuit shown in Fig 2B and the fitting approach used to estimate individual parameters. The application of the Kirchoff laws leads to

Vertex Currents

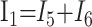1)

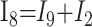2)

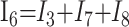3)

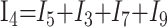4)

Voltage Loops

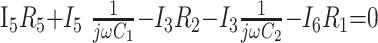5)

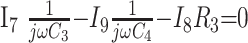6)

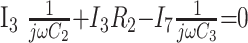7)

Point-to-Point Voltages

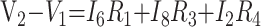8)

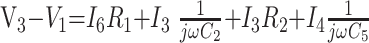9)

In these equations, ω is frequency and j is −1. We have introduced 5 new current variables (I₅ to I₉), and we have 9 equations, leaving 6 degrees of freedom. The point-to-point voltages require the equivalent of pressure measurements in the biologic system.

After eliminating unwanted variables, and by using the notational convention D_nω = 1/jωC_n, we have obtained 3 important equations to note: the Monro-Kellie Principle (eq. 10), which is simply a statement of volume preservation; the constraint equation (eq. 11) relating currents, which does not contain I₁, C₅, or R₄; and eq. 12, which scales the variables using mean potentials.

The Monro-Kellie Principle:

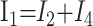10)

Constraint equation relating currents (flows):

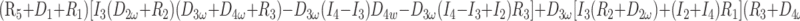11)

Using mean potentials (pressures) to scale variables:

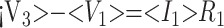12)

Parameter Estimation

A likelihood-based approach was adopted to estimate the parameters of the model. We can build a suitable likelihood function from eq. 11. Substituting eq. 10 and reorganizing terms, we obtain an equation of the form

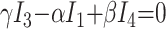13)

We can now make corrections to the flow variables ΔI_n to enforce the constraint equations, in a way that minimizes the change in the measurements consistent with the measurement errors

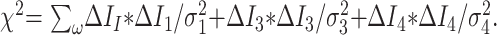14)