Machine Learning for the Diagnosis of Parkinson's Disease: A Review of Literature

Jie Mei; Christian Desrosiers; Johannes Frasnelli

doi:10.3389/fnagi.2021.633752

. 2021 May 6;13:633752. doi: 10.3389/fnagi.2021.633752

Machine Learning for the Diagnosis of Parkinson's Disease: A Review of Literature

Jie Mei ^1,^*, Christian Desrosiers ², Johannes Frasnelli ^1,³

PMCID: PMC8134676 PMID: 34025389

Abstract

Diagnosis of Parkinson's disease (PD) is commonly based on medical observations and assessment of clinical signs, including the characterization of a variety of motor symptoms. However, traditional diagnostic approaches may suffer from subjectivity as they rely on the evaluation of movements that are sometimes subtle to human eyes and therefore difficult to classify, leading to possible misclassification. In the meantime, early non-motor symptoms of PD may be mild and can be caused by many other conditions. Therefore, these symptoms are often overlooked, making diagnosis of PD at an early stage challenging. To address these difficulties and to refine the diagnosis and assessment procedures of PD, machine learning methods have been implemented for the classification of PD and healthy controls or patients with similar clinical presentations (e.g., movement disorders or other Parkinsonian syndromes). To provide a comprehensive overview of data modalities and machine learning methods that have been used in the diagnosis and differential diagnosis of PD, in this study, we conducted a literature review of studies published until February 14, 2020, using the PubMed and IEEE Xplore databases. A total of 209 studies were included, extracted for relevant information and presented in this review, with an investigation of their aims, sources of data, types of data, machine learning methods and associated outcomes. These studies demonstrate a high potential for adaptation of machine learning methods and novel biomarkers in clinical decision making, leading to increasingly systematic, informed diagnosis of PD.

Keywords: Parkinson's disease, machine learning, deep learning, diagnosis, differential diagnosis

Introduction

Parkinson's disease (PD) is one of the most common neurodegenerative diseases with a prevalence rate of 1% in the population above 60 years old, affecting 1–2 people per 1,000 (Tysnes and Storstein, 2017). The estimated global population affected by PD has more than doubled from 1990 to 2016 (from 2.5 million to 6.1 million), which is a result of increased number of elderly people and age-standardized prevalence rates (Dorsey et al., 2018). PD is a progressive neurological disorder associated with motor and non-motor features (Jankovic, 2008) which comprises multiple aspects of movements, including planning, initiation and execution (Contreras-Vidal and Stelmach, 1995).

During its development, movement-related symptoms such as tremor, rigidity and difficulties in initiation can be observed, prior to cognitive and behavioral alterations including dementia (Opara et al., 2012). PD severely affects patients' quality of life (QoL), social functions and family relationships, and places heavy economic burdens at individual and society levels (Johnson et al., 2013; Kowal et al., 2013; Yang and Chen, 2017).

The diagnosis of PD is traditionally based on motor symptoms. Despite the establishment of cardinal signs of PD in clinical assessments, most of the rating scales used in the evaluation of disease severity have not been fully evaluated and validated (Jankovic, 2008). Although non-motor symptoms (e.g., cognitive changes such as problems with attention and planning, sleep disorders, sensory abnormalities such as olfactory dysfunction) are present in many patients prior to the onset of PD (Jankovic, 2008; Tremblay et al., 2017), they lack specificity, are complicated to assess and/or yield variability from patient to patient (Zesiewicz et al., 2006). Therefore, non-motor symptoms do not yet allow for diagnosis of PD independently (Braak et al., 2003), although some have been used as supportive diagnostic criteria (Postuma et al., 2015).

Machine learning techniques are being increasingly applied in the healthcare sector. As its name implies, machine learning allows for a computer program to learn and extract meaningful representation from data in a semi-automatic manner. For the diagnosis of PD, machine learning models have been applied to a multitude of data modalities, including handwritten patterns (Drotár et al., 2015; Pereira et al., 2018), movement (Yang et al., 2009; Wahid et al., 2015; Pham and Yan, 2018), neuroimaging (Cherubini et al., 2014a; Choi et al., 2017; Segovia et al., 2019), voice (Sakar et al., 2013; Ma et al., 2014), cerebrospinal fluid (CSF) (Lewitt et al., 2013; Maass et al., 2020), cardiac scintigraphy (Nuvoli et al., 2019), serum (Váradi et al., 2019), and optical coherence tomography (OCT) (Nunes et al., 2019). Machine learning also allows for combining different modalities, such as magnetic resonance imaging (MRI) and single-photon emission computed tomography (SPECT) data (Cherubini et al., 2014b; Wang et al., 2017), in the diagnosis of PD. By using machine learning approaches, we may therefore identify relevant features that are not traditionally used in the clinical diagnosis of PD and rely on these alternative measures to detect PD in preclinical stages or atypical forms.

In recent years, the number of publications on the application of machine learning to the diagnosis of PD has increased. Although previous studies have reviewed the use of machine learning in the diagnosis and assessment of PD, they were limited to the analysis of motor symptoms, kinematics, and wearable sensor data (Ahlrichs and Lawo, 2013; Ramdhani et al., 2018; Belić et al., 2019). Moreover, some of these reviews only included studies published between 2015 and 2016 (Pereira et al., 2019). In this study, we aim to (a) comprehensively summarize all published studies that applied machine learning models to the diagnosis of PD for an exhaustive overview of data sources, data types, machine learning models, and associated outcomes, (b) assess and compare the feasibility and efficiency of different machine learning methods in the diagnosis of PD, and (c) provide machine learning practitioners interested in the diagnosis of PD with an overview of previously used models and data modalities and the associated outcomes, and recommendations on how experimental protocols and results could be reported to facilitate reproduction. As a result, the application of machine learning to clinical and non-clinical data of different modalities has often led to high diagnostic accuracies in human participants, therefore may encourage the adaptation of machine learning algorithms and novel biomarkers in clinical settings to assist more accurate and informed decision making.

Methods

Search Strategy

A literature search was conducted on the PubMed (https://pubmed.ncbi.nlm.nih.gov) and IEEE Xplore (https://ieeexplore.ieee.org/search/advanced/command) databases on February 14, 2020 for all returned results. Boolean search strings used are shown in Table 1. No additional filters were applied in the literature search. All retrieved studies were systematically identified, screened and extracted for relevant information following the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) guidelines (Moher et al., 2009).

Table 1.

Boolean search strings used for the retrieval of relevant publications on PubMed and IEEE Xplore databases.

Database	Boolean search string
PubMed	(“Parkinson Disease”[Mesh] OR Parkinson) AND (“Machine Learning”[Mesh] OR machine learn OR machine-learn* OR deep learn* OR deep-learn) AND (human OR patient) AND (“Diagnosis”[Mesh] OR diagnos OR detect* OR classif* OR identif*) NOT review[Publication Type]
IEEE Xplore	(Parkinson) AND (machine learn OR machine-learn* OR deep learn* OR deep-learn*) AND (human OR patient) AND (diagnosis OR diagnose OR diagnosing OR detection OR detect OR detecting OR classification OR classify OR classifying OR identification OR identify OR identifying)

Open in a new tab

Inclusion and Exclusion Criteria

Studies that satisfy one or more of the following criteria and used machine learning methods were included:

Classification of PD from healthy controls (HC),
Classification of PD from Parkinsonism (e.g., progressive supranuclear palsy (PSP) and multiple system atrophy (MSA)), and
Classification of PD from other movement disorders (e.g., essential tremor (ET)).

Studies falling into one or more of the following categories were excluded:

Studies related to Parkinsonism or/and diseases other than PD that did not involve classification or detection of PD (e.g., differential diagnosis of PSP, MSA, and other atypical Parkinsonian disorders),
Studies not related to the diagnosis of PD (e.g., subtyping or severity assessment, analysis of behavior, disease progression, treatment outcome prediction, identification, and localization of brain structures or parameter optimization during surgery),
Studies related to the diagnosis of PD, but performed analysis and assessed model performance at sample level (e.g., classification using individual MRI scans without aggregating scan-level performance to patient level),
Classification of PD from non-Parkinsonism (e.g., Alzheimer's disease),
Study did not use metrics that measure classification performance,
Study used organisms other than human (e.g., Caenorhabditis elegans, mice or rats),
Study did not provide sufficient or accurate descriptions of machine learning methods, datasets or subjects used (e.g., does not provide sample size, or incorrectly described the dataset(s) used),
Not original journal article or conference proceedings papers (e.g., review and viewpoint paper), and
In languages other than English.

Data Extraction

The following information is included in the data extraction table: (1) objectives, (2) type of diagnosis (diagnosis, differential diagnosis, sub-typing), (3) data source, (4) data type, (5) number of subjects, (6) machine learning method(s), splitting strategy and cross validation, (7) associated outcomes, (8) year, and (9) reference.

For studies published online first and archived in another year, “year of publication” was defined as the year during which the study was published online. If this information was unavailable, the year in which the article was copyrighted was regarded as the year of publication. For studies that introduced novel models and used existing models merely for comparison, information related to the novel models was extracted. Classification of PD and scans without evidence for dopaminergic deficit (SWEDD) was treated as subtyping (Erro et al., 2016).

Study Objectives

To outline the different goals and objectives of included studies, we have further categorized them based on the type of diagnosis and their general aim. From the perspective of diagnostics, these studies could be divided into (a) the diagnosis or detection of PD (which compares data collected from PD patients and healthy controls), (b) differential diagnosis (discrimination between patients with idiopathic PD and patients with atypical Parkinsonism), and (c) sub-typing (discrimination among sub-types of PD).

Included studies were also analyzed for their general aim: For studies with a focus on the development of novel technical approaches to be used in the diagnosis of Parkinson's disease, e.g., new machine learning and deep learning models and architectures, data acquisition devices, and feature extraction algorithms that haven't been previously presented and/or employed, we defined them as (a) “methodology” studies. Studies that validate and investigate (a) the application of previously published and validated machine learning and deep learning models, and/or (b) the feasibility of introducing data modalities that are not commonly used in the machine learning-based diagnosis of PD (e.g., CSF data), were defined as (b) “clinical application” studies.

Model Evaluation

In the present study, accuracy was used to compare performance of machine learning models. For each data type, we summarized the type of machine learning models that led to the per-study highest accuracy. However, in some studies, only one machine learning model was tested. Therefore, we define “model associated with the per-study highest accuracy” as (a) the only model implemented and used in a study or (b) the model that achieved the highest accuracy or that was highlighted in studies that used multiple models. Results are expressed as mean (SD).

For studies reporting both training and testing/validation accuracy, testing or validation accuracy was considered. For studies that reported both validation and test accuracy, test accuracy was considered. For studies with more than one dataset or classification problem (e.g., HC vs. PD and HC vs. idiopathic hyposmia vs. PD), accuracy was averaged across datasets or classification problems. For studies that reported classification accuracy for each group of subjects individually, accuracy was averaged across groups. For studies reporting a range of accuracies or accuracies given by different cross validation methods or feature combinations, the highest accuracies were considered. In studies that compared HC with diseases other than PD or PD with diseases other than Parkinsonism, diagnosis of diseases other than PD or Parkinsonism (e.g., amyotrophic lateral sclerosis) was not considered. Accuracy of severity assessment was not considered.

Results

Literature Review

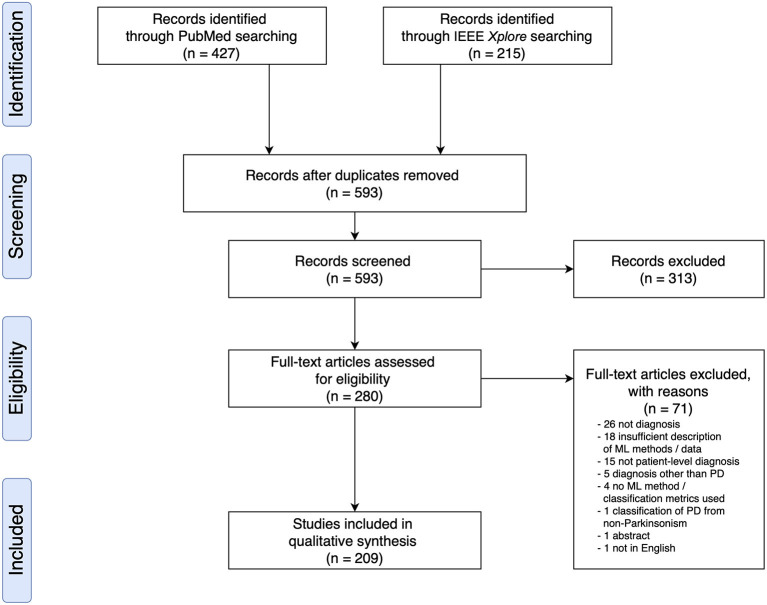
Based on the search criteria, we retrieved 427 (PubMed) and 215 (IEEEXplore) search results, leading to a total of 642 publications. After removing duplicates, we screened 593 publications for titles and abstracts, following which we excluded 313 based on the exclusion criteria and examined 280 full text articles. Overall, we included 209 research articles for data extraction (Figure 1 and see Supplementary Materials for a full list of included studies). All articles were published from the year 2009 onwards, and an increase in the number of papers published per year was observed (Supplementary Figure 1).

PRISMA Flow Diagram of Literature Search and Selection Process showing the number of studies identified, screened, extracted, and included in the review.

Data Source and Sample Size

In 93 out of 209 studies (43.1%), original data were collected from human participants. In 108 studies (51.7%), data used were from public repositories and databases, including University of California at Irvine (UCI) Machine Learning Repository (Dua and Graff, 2018) (n = 44), Parkinson's Progression Markers Initiative (Marek et al., 2011) (PPMI; n = 33), PhysioNet (Goldberger et al., 2000) (n = 15), HandPD dataset (Pereira et al., 2015) (n = 6), mPower database (Bot et al., 2016) (n = 4), and 6 other databases (Mucha et al., 2018; Vlachostergiou et al., 2018; Bhati et al., 2019; Hsu et al., 2019; Taleb et al., 2019; Wodzinski et al., 2019; Table 2).

Table 2.

Source of data of the included studies.

Data source/Database	Number of studies	Percentage
independent recruitment of human participants	93	43.06%
UCI Machine Learning Repository	44	20.37%
PPMI database	33	15.28%
PhysioNet	15	6.94%
HandPD dataset	6	2.78%
mPower database	4	1.85%
Other databases (1 PACS, 1 PaHaW, 1 PC-GITA database, 1 PDMultiMC database, 1 Neurovoz corpus, 1 The NTUA Parkinson Dataset)	6	2.78%
Collected postmortem	1	0.46%
Commercially sourced	1	0.46%
Acquired at another institution	1	0.46%
From another study	1	0.46%
From the author's institutional database	1	0.46%
Others (1 PPMI + Sheffield Teaching Hospitals NHS Foundation Trust; 1 PPMI + Seoul National University Hospital cohort; 1 UCI + collected from participants)	3	1.39%

Open in a new tab

PACS, Picture Archiving and Communication System; PaHaW, Parkinson's Disease Handwriting Database.

In 3 studies, data from public repositories were combined with data from local databases or participants (Agarwal et al., 2016; Choi et al., 2017; Taylor and Fenner, 2017). In the remaining studies, data were sourced (Wahid et al., 2015) from another study (Fernandez et al., 2013), collected at another institution (Segovia et al., 2019), obtained from the authors' institutional database (Nunes et al., 2019), collected postmortem (Lewitt et al., 2013), or commercially sourced (Váradi et al., 2019).

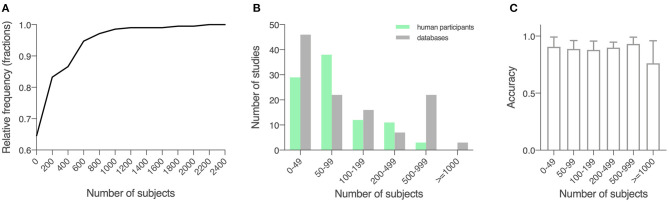
The 209 studies had an average sample size of 184.6 (289.3), with a smallest sample size of 10 (Kugler et al., 2013), and a largest sample size of 2,289 (Tracy et al., 2019; Figure 2A). For studies that recruited human participants (n = 93), data from an average of 118.0 (142.9) participants were collected (range: 10–920; Figure 2B). For other studies (n = 116), an average sample size of 238.1 (358.5) was reported (range: 30–2,289; Figure 2B). For a description of average accuracy reported in these studies in relation to sample size, see Figure 2C.

Sample size of the included studies. **(A)** Cumulative relative frequency graph depicting the frequency of the sample sizes studied. **(B)** Histogram depicting the frequency of a sample size of 0–50, 50–100, 100–200, 200–500, 500–100, and over 1,000 for studies using locally recruited human participants and studies using previously published open databases. Green, studies using locally recruited human participants; gray, studies using data sourced from public databases. **(C)** Model performance as measured by accuracy in relation to sample size, shown in means (SD).

Study Objectives

In included studies, although “diagnosis of PD” was used as the search criteria, machine learning had been applied for diagnosis (PD vs. HC), differential diagnosis (idiopathic PD vs. atypical Parkinsonism) and sub-typing (differentiation of sub-types of PD) purposes. Most studies focused on diagnosis (n = 168, 80.4%) or differential diagnosis (n = 20, 9.6%). Fourteen studies performed both diagnosis and differential diagnosis (6.7%), 5 studies (2.4%) diagnosed and subtyped PD, 2 studies (1.0%) included diagnosis, differential diagnosis, and subtyping.

Among the included studies, a total of 132 studies (63.2%) implemented and tested a machine learning method, a model architecture, a diagnostic system, a feature extraction algorithm, or a device for non-invasive, low-cost data acquisition that hasn't been established for the detection and early diagnosis of PD (methodology studies). In 77 studies (36.8%), previously proposed and validated machine learning methods were tested in clinical settings for early detection of PD, identification of novel biomarkers or examination of uncommonly used data modalities for the diagnosis of PD (e.g., CSF; clinical application studies).

Comparing Studies With Different Objectives

Source of Data

In the 132 studies that proposed or tested novel machine learning methods (i.e., methodology studies), a majority used data from publicly available databases (n = 89, 67.4%). Data collected from human participants were used in 41 studies (31.1%) and the two remaining studies (1.5%) used commercially sourced data or data from both existing public databases and local participants specifically recruited for the study. Out of the 77 studies that used machine learning models in clinical settings (i.e., clinical application studies), 52 (67.5%) collected data from human participants, 22 (28.6%) used data from public databases. Two (2.6%) studies obtained data from a database and a local cohort, and 1 (1.3%) study collected data postmortem.

Data Modality

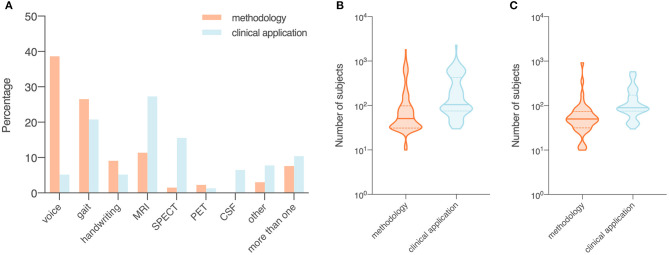
In methodology studies, the most commonly used data modalities were voice recordings (n = 51, 38.6%), movement (n = 35, 26.5%), and MRI data (n = 15, 11.4%). For studies on clinical applications, MRI data (n = 21, 27.3%), movement (n = 16, 20.8%), and SPECT imaging data (n = 12, 15.6%) were of high relevance. All studies using CSF features (n = 5) focused on validation of existing machine learning models in a clinical setting (Figure 3A).

Number of Subjects

The average sample size was 137.1 for the 132 methodology studies (Figure 3B). For 41 out of the 132 studies that used data from recruited human participants, the average sample size was 81.7 (Figure 3C). In the 77 studies on clinical applications, the average sample size was 266.2 (Figure 3B). For 52 out of the 77 clinical studies that collected data from recruited participants, the average sample size was 145.9 (Figure 3C).

Machine Learning Methods Applied to the Diagnosis of PD

We divided 448 machine learning models from the 209 studies into 8 categories: (1) support vector machine (SVM) and variants (n = 132 from 130 studies), (2) neural networks (n = 76 from 62 studies), (3) ensemble learning (n = 82 from 57 studies), (4) nearest neighbor and variants (n = 33 from 33 studies), (5) regression (n = 31 from 31 studies), (6) decision tree (n = 28 from 27 studies), (7) naïve Bayes (n = 26, from 26 studies), and (8) discriminant analysis (n = 12 from 12 studies). A small percentage of models used did not fall into any of the categories (n = 28, used in 24 studies).

On average, 2.14 machine learning models per study were applied to the diagnosis of PD. One study may have used more than one category of models. For a full description of data types used to train each type of machine learning models and the associated outcomes, see Supplementary Materials and Supplementary Figure 2.

Performance Metrics

Various metrics have been used to assess the performance of machine learning models (Table 3). The most common metric was accuracy (n = 174, 83.3%), which was used individually (n = 55) or in combination with other metrics (n = 119) in model evaluation. Among the 174 studies that used accuracy, some have combined accuracy with sensitivity (i.e., recall) and specificity (n = 42), or with sensitivity, specificity and AUC (n = 16), or with recall (i.e., sensitivity), precision and F1 score (n = 7) for a more systematic understanding of model performance. A total of 35 studies (16.7%) used metrics other than accuracy. In these studies, the most used performance metrics were AUC (n = 19), sensitivity (n = 17), and specificity (n = 14), and the three were often applied together (n = 9) with or without other metrics.

Table 3.

Performance metrics used in the evaluation of machine learning models.

Performance metric	Definition	Number of studies
Accuracy	$\frac{T P + T N}{T P + T N + F P + F N}$	174
Sensitivity (recall)	$\frac{T P}{T P + F N}$	110
Specificity (TNR)	$\frac{T N}{T N + F P}$	94
AUC	The two-dimensional area under the Receiver Operating Characteristic (ROC) curve	60
MCC	$\frac{T P \times T N - F P \times F N}{\sqrt{(T P + F P) (T P + F N) (T N + F P) (T N + F N)}}$	9
Precision (PPV)	$\frac{T P}{T P + F P}$	31
NPV	$\frac{T N}{T N + F N}$	8
F1 score	$2 \times \frac{p r e c i s i o n \times r e c a l l}{p r e c i s i o n + r e c a l l}$	25
Others (7 kappa; 4 error rate; 3 EER; 1 MSE; 1 LOR; 1 confusion matrix; 1 cross validation score; 1 YI; 1 FPR; 1 FNR; 1 G-mean; 1 PE; 5 combination of metrics)	N/A	28

Open in a new tab

TNR, true negative rate; AUC, Area under the ROC Curve; MCC, Matthews correlation coefficient; PPV, positive predictive value; NPV, negative predictive value; EER, equal error rate; MSE, mean squared error; LOR, log odds ratio; YI, Youden's Index; FPR, false positive rate; FNR, false negative rate; PE, probability excess.

Data Types and Associated Outcomes

Out of 209 studies, 122 (58.4%) applied machine learning methods to movement-related data, i.e., voice recordings (n = 55, 26.3%), movement data (n = 51, 24.4%), or handwritten patterns (n = 16, 7.7%). Imaging modalities analyzed including MRI (n = 36, 17.2%), SPECT (n = 14, 6.7%), and positron emission tomography (PET; n = 4, 1.9%). Five studies analyzed CSF samples (2.4%). In 18 studies (8.6%), a combination of different types of data was used.

Ten studies (4.8%) used data that do not belong to any categories mentioned above, such as single nucleotide polymorphisms (Cibulka et al., 2019) (SNPs), electromyography (EMG) (Kugler et al., 2013), OCT (Nunes et al., 2019), cardiac scintigraphy (Nuvoli et al., 2019), Patient Questionnaire of Movement Disorder Society Unified Parkinson's Disease Rating Scale (MDS-UPDRS) (Prashanth and Dutta Roy, 2018), whole-blood gene expression profiles (Shamir et al., 2017), transcranial sonography (Shi et al., 2018) (TCS), eye movements (Tseng et al., 2013), electroencephalography (EEG) (Vanegas et al., 2018), and serum samples (Váradi et al., 2019).

Given that studies used different data modalities and sources, and sometimes different samples of the same database, a summary of model performance, instead of direct comparison across studies, is provided.

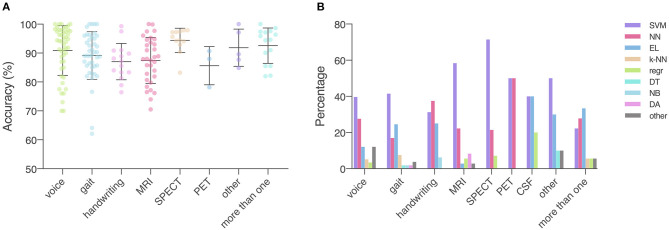
Voice Recordings (n = 55)

The 49 studies that used accuracy to evaluate machine learning models achieved an average accuracy of 90.9 (8.6) % (Figure 4A), ranging from 70.0% (Kraipeerapun and Amornsamankul, 2015; Ali et al., 2019a) to 100.0% (Hariharan et al., 2014; Abiyev and Abizade, 2016; Ali et al., 2019c; Dastjerd et al., 2019). In 3 studies, the highest accuracy was achieved by two types of machine learning models individually, namely regression or SVM (Ali et al., 2019a), neural network or SVM (Hariharan et al., 2014), and ensemble learning or SVM (Mandal and Sairam, 2013). The per-study highest accuracy was achieved with SVM in 23 studies (39.7%), with neural network in 16 studies (27.6%), with ensemble learning in 7 studies (12.1%), with nearest neighbor in 3 studies (5.2%), and with regression in 2 studies (3.4%). Models that do not belong to any given categories led to the per-study highest accuracy in 7 studies (12.1%; Figure 4B).

Data type, machine learning models applied, and accuracy. **(A)** Accuracy achieved in individual studies and average accuracy for each data type. Error bar: standard deviation. **(B)** Distribution of machine learning models applied per data type. MRI, magnetic resonance imaging; SPECT, single-photon emission computed tomography; PET, positron emission tomography; CSF, cerebrospinal fluid; SVM, support vector machine; NN, neural network; EL, ensemble learning; k-NN, nearest neighbor; regr, regression; DT, decision tree; NB, naïve Bayes; DA, discriminant analysis; other: data/models that do not belong to any of the given categories.

Voice recordings from the UCI machine learning repository were used in 42 studies (Table 4). Among the 42 studies, 39 used accuracy to evaluate classification performance and the average accuracy was 92.0 (9.0) %. The lowest accuracy was 70.0% and the highest accuracy was 100.0%. Eight out of 9 studies that collected voice recordings from human participants used accuracy as the performance metric, and the average, lowest and highest accuracies were 87.7 (6.8) %, 77.5%, and 98.6%, respectively. The 4 remaining studies used data from the Neurovoz corpus (n = 1), mPower database (n = 1), PC-GITA database (n = 1), or data from both the UCI machine learning repository and human participants (n = 1). Two out of these 4 studies used accuracy to evaluate model performance and reported an accuracy of 81.6 and 91.7%.

Table 4.

Studies that applied machine learning models to voice recordings to diagnose PD (n = 55).

Objectives	Type of diagnosis	Source of data	Number of subjects (n)	Machine learning method(s), splitting strategy and cross validation	Outcomes	Year	References
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	Fuzzy neural system with 10-fold cross validation	Testing accuracy = 100%	2016	Abiyev and Abizade, 2016
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	RPART, C4.5, PART, Bagging CART, random forest, Boosted C5.0, SVM	SVM:	2019	Aich et al., 2019
					Accuracy = 97.57%
					Sensitivity = 0.9756
					Specificity = 0.9987
					NPV = 0.9995
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	DBN of 2 RBMs	Testing accuracy = 94%	2016	Al-Fatlawi et al., 2016
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	EFMM-OneR with 10-fold cross validation or 5-fold cross validation	Accuracy = 94.21%	2019	Sayaydeha and Mohammad, 2019
Classification of PD from HC	Diagnosis	UCI machine learning repository	40; 20 HC + 20 PD	Linear regression, LDA, Gaussian naïve Bayes, decision tree, KNN, SVM-linear, SVM-RBF with leave-one-subject-out cross validation	Logistic regression or SVM-linear accuracy = 70%	2019	Ali et al., 2019a
Classification of PD from HC	Diagnosis	UCI machine learning repository	40; 20 HC + 20 PD	LDA-NN-GA with leave-one-subject-out cross validation	Training:	2019	Ali et al., 2019c
					Accuracy = 95%
					Sensitivity = 95%
					Test:
					Accuracy = 100%
					Sensitivity = 100%
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	NNge with AdaBoost with 10-fold cross validation	Accuracy = 96.30%	2018	Alqahtani et al., 2018
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	Logistic regression, KNN, naïve Bayes, SVM, decision tree, random forest, DNN with 10-fold cross validation	KNN accuracy = 95.513%	2018	Anand et al., 2018
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	MLP with a train-validation-test ratio of 50:20:30	Training accuracy = 97.86%	2012	Bakar et al., 2012
					Test accuracy = 92.96%
					MSE = 0.03552
Classification of PD from HC	Diagnosis	UCI machine learning repository	31 (8 HC + 23 PD) for dataset 1 and 68 (20 HC + 48 PD) for dataset 2	FKNN, SVM, KELM with 10-fold cross validation	FKNN accuracy = 97.89%	2018	Cai et al., 2018
Classification of PD from HC	Diagnosis	UCI machine learning repository	40; 20 HC + 20 PD	SVM, logistic regression, ET, gradient boosting, random forest with train-test split ratio = 80:20	Logistic regression accuracy = 76.03%	2019	Celik and Omurca, 2019
Classification of PD from HC	Diagnosis	UCI machine learning repository	40; 20 HC + 20 PD	MLP, GRNN with a training-test ratio of 50:50	GRNN:	2016	Çimen and Bolat, 2016
					Error rate = 0.0995 (spread parameter = 195.1189)
					Error rate = 0.0958 (spread parameter = 1.2)
					Error rate = 0.0928 (spread parameter = 364.8)
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	ECFA-SVM with 10-fold cross validation	Accuracy = 97.95%	2017	Dash et al., 2017
					Sensitivity = 97.90%
					Precision = 97.90%
					F-measure = 97.90%
					Specificity = 96.50%
					AUC = 97.20%
Classification of PD from HC	Diagnosis	UCI machine learning repository	40; 20 HC + 20 PD	Fuzzy classifier with 10-fold cross validation, leave-one-out cross validation or a train-test ratio of 70:30	Accuracy = 100%	2019	Dastjerd et al., 2019
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	Averaged perceptron, BPM, boosted decision tree, decision forests, decision jungle, locally deep SVM, logistic regression, NN, SVM with 10-fold cross-validation	Boosted decision trees:	2017	Dinesh and He, 2017
					Accuracy = 0.912105
					Precision = 0.935714
					F-score = 0.942368
					AUC = 0.966293
Classification of PD from HC	Diagnosis	UCI machine learning repository	50; 8 HC + 42 PD	KNN, SVM, ELM with a train-validation ratio of 70:30	SVM:	2017	Erdogdu Sakar et al., 2017
					Accuracy = 96.43%
					MCC = 0.77
Classification of PD from HC	Diagnosis	UCI machine learning repository	252; 64 HC + 188 PD	CNN with leave-one-person-out cross validation	Accuracy = 0.869	2019	Gunduz, 2019
					F-measure = 0.917
					MCC = 0.632
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	SVM, logistic regression, KNN, DNN with a train-test ratio of 70:30	DNN:	2018	Haq et al., 2018
					Accuracy = 98%
					Specificity = 95%
					sensitivity = 99%
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	SVM-RBF, SVM-linear with 10-fold cross validation	Accuracy = 99%	2019	Haq et al., 2019
					Specificity = 99%
					Sensitivity = 100%
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	LS-SVM, PNN, GRNN with conventional (train-test ratio of 50:50) and 10-fold cross validation	LS-SVM or PNN or GRNN:	2014	Hariharan et al., 2014
					Accuracy = 100%
					Precision = 100%
					Sensitivity = 100%
					specificity = 100%
					AUC = 100
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	Random tree, SVM-linear, FBANN with 10-fold cross validation	FBANN:	2014	Islam et al., 2014
					Accuracy = 97.37%
					Sensitivity = 98.60%
					Specificity = 93.62%
					FPR = 6.38%
					Precision = 0.979
					MSE = 0.027
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	SVM-linear with 5-fold cross validation	Error rate ~0.13	2012	Ji and Li, 2012
Classification of PD from HC	Diagnosis	UCI machine learning repository	40; 20 HC + 20 PD	Decision tree, random forest, SVM, GBM, XGBoost	SVM-linear:	2018	Junior et al., 2018
					FNR = 10%
					Accuracy = 0.725
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	CART, SVM, ANN	SVM accuracy = 93.84%	2020	Karapinar Senturk, 2020
Classification of PD from HC	Diagnosis	UCI machine learning repository	Dataset 1: 31; 8 HC + 23 PD Dataset 2: 40; 20 HC + 20 PD	EWNN with a train-test ratio of 90:10 and cross validation	Dataset 1: Accuracy = 92.9%	2018	Khan et al., 2018
					Ensemble classification accuracy = 100.0%
					Sensitivity = 100.0%
					MCC = 100.0%
					Dataset 2:
					Accuracy = 66.3%
					Ensemble classification accuracy = 90.0%
					Sensitivity = 93.0%
					Specificity = 97.0%
					MCC = 87.0%
Classification of PD from HC	Diagnosis	UCI machine learning repository	40; 20 HC + 20 PD	Stacked generalization with CMTNN with 10-fold cross validation	Accuracy = ~70%	2015	Kraipeerapun and Amornsamankul, 2015
Classification of PD from HC	Diagnosis	UCI machine learning repository	40; 20 HC + 20 PD	HMM, SVM	HMM:	2019	Kuresan et al., 2019
					Accuracy = 95.16%
					Sensitivity = 93.55%
					Specificity = 91.67%
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	IGWO-KELM with 10-fold cross validation	Iteration number = 100	2017	Li et al., 2017
					Accuracy = 97.45%
					Sensitivity = 99.38%
					Specificity = 93.48%
					Precision = 97.33%
					G-mean = 96.38%
					F-measure = 98.34%
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	SCFW-KELM with 10-fold cross validation	Accuracy = 99.49%	2014	Ma et al., 2014
					Sensitivity = 100%
					Specificity = 99.39%
					AUC = 99.69%
					F-measure = 0.9966
					Kappa = 0.9863
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	SVM-RBF with 10-fold cross validation	Accuracy = 96.29%	2016	Ma et al., 2016
					Sensitivity = 95.00%
					Specificity = 97.50%
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	Logistic regression, NN, SVM, SMO, Pegasos, AdaBoost, ensemble selection, FURIA, rotation forest Bayesian network with 10-fold cross-validation	Average accuracy across all models = 97.06% SMO, Pegasos, or AdaBoost accuracy = 98.24%	2013	Mandal and Sairam, 2013
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	Logistic regression, KNN, SVM, naïve Bayes, decision tree, random forest, ANN	ANN:	2018	Marar et al., 2018
					Accuracy = 94.87%
					Specificity = 96.55%
					Sensitivity = 90%
Classification of PD from HC	Diagnosis	UCI machine learning repository	Dataset 1: 31; 8 HC + 23 PD	KNN	Dataset 1 accuracy = 90%	2017	Moharkan et al., 2017
			Dataset 2: 40; 20 HC + 20 PD		Dataset 2 accuracy = 65%
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	Rotation forest ensemble with 10-fold cross validation	Accuracy = 87.1%	2011	Ozcift and Gulten, 2011
					Kappa error = 0.63
					AUC = 0.860
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	Rotation forest ensemble	Accuracy = 96.93%	2012	Ozcift, 2012
					Kappa = 0.92
					AUC = 0.97
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	SVM-RBF with 10-fold cross validation or a train-test ratio of 50:50	10-fold cross validation:	2016	Peker, 2016
					Accuracy = 98.95%
					Sensitivity = 96.12%
					Specificity = 100%
					F-measure = 0.9795
					Kappa = 0.9735
					AUC = 0.9808
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	ELM with 10-fold cross validation	Accuracy = 88.72%	2016	Shahsavari et al., 2016
					Recall = 94.33%
					Precision = 90.48%
					F-score = 92.36%
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	Ensemble learning with 10-fold cross validation	Accuracy = 90.6%	2019	Sheibani et al., 2019
					Sensitivity = 95.8%
					Specificity = 75%
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	GLRA, SVM, bagging ensemble with 5-fold cross validation	Bagging:	2017	Wu et al., 2017
					Sensitivity = 0.9796
					Specificity = 0.6875
					MCC = 0.6977
					AUC = 0.9558
					SVM:
					Sensitivity = 0.9252
					specificity = 0.8542
					MCC = 0.7592
					AUC = 0.9349
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	Decision tree classifier, logistic regression, SVM with 10-fold cross validation	SVM:	2011	Yadav et al., 2011
					Accuracy = 0.76
					Sensitivity = 0.9745
					Specificity = 0.13
Classification of PD from HC	Diagnosis	UCI machine learning repository	80; 40 HC + 40 PD	KNN, SVM with 10-fold cross validation	SVM:	2019	Yaman et al., 2020
					Accuracy = 91.25%
					Precision = 0.9125
					Recall = 0.9125
					F-Measure = 0.9125
Classification of PD from HC	Diagnosis	UCI machine learning repository	31; 8 HC + 23 PD	MAP, SVM-RBF, FLDA with 5-fold cross validation	MAP:	2014	Yang et al., 2014
					Accuracy = 91.8%
					Sensitivity = 0.986
					Specificity = 0.708
					AUC = 0.94
Classification of PD from other disorders	Differential diagnosis	Collected from participants	50; 30 PD + 9 MSA + 5 FND + 1 somatization + 1 dystonia + 2 CD + 1 ET + 1 GPD	SVM, KNN, DA, naïve Bayes, classification tree with LOSO	SVM-linear:	2016	Benba et al., 2016a
					Accuracy = 90%
					Sensitivity = 90%
					Specificity = 90%
					MCC = 0.794067
					PE = 0.788177
Classification of PD from other disorders	Differential diagnosis	Collected from participants	40; 20 PD + 9 MSA + 5 FND + 1 somatization + 1 dystonia + 2 CD + 1ET + 1 GPD	SVM (RBF, linear, polynomial, and MLP kernels) with LOSO	SVM-linear accuracy = 85%	2016	Benba et al., 2016b
Classification of PD from HC and assess the severity of PD	Diagnosis	Collected from participants	52; 9 HC + 43 PD	SVM-RBF with cross validation	Accuracy = 81.8%	2014	Frid et al., 2014
Classification of PD from HC	Diagnosis	Collected from participants	54; 27 HC + 27 PD	SVM with stratified 10-fold cross validation or leave-one-out cross validation	Accuracy = 94.4%	2018	Montaña et al., 2018
					Specificity = 100%
					Sensitivity = 88.9%
Classification of PD from HC	Diagnosis	Collected from participants	40; 20 HC + 20 PD	KNN, SVM-linear, SVM-RBF with leave-one-subject-out or summarized leave-one-out	SVM-linear:	2013	Sakar et al., 2013
					Accuracy = 77.50%
					MCC = 0.5507
					Sensitivity = 80.00%
					Specificity = 75.00%
Classification of PD from HC	Diagnosis	Collected from participants	78; 27 HC + 51 PD	KNN, SVM-linear, SVM-RBF, ANN, DNN with leave-one-out cross validation	SVM-RBF:	2017	Sztahó et al., 2017
					Accuracy = 84.62%
					Precision = 88.04%
					Recall = 78.65%
Classification of PD from HC and assess the severity of PD	Diagnosis	Collected from participants	88; 33 HC + 55 PD	KNN, SVM-linear, SVM-RBF, ANN, DNN with leave-one-subject-out cross validation	SVM-RBF:	2019	Sztahó et al., 2019
					Accuracy = 89.3%
					Sensitivity = 90.2%
					Specificity = 87.9%
Classification of PD from HC	Diagnosis	Collected from participants	43; 10 HC + 33 PD	Random forests, SVM with 10-fold cross validation and a train-test ratio of 90:10	SVM accuracy = 98.6%	2012	Tsanas et al., 2012
Classification of PD from HC	Diagnosis	Collected from participants	99; 35 HC + 64 PD	Random forest with internal out-of-bag (OOB) validation	EER = 19.27%	2017	Vaiciukynas et al., 2017
Classification of PD from HC	Diagnosis	UCI machine learning repository and participants	40 and 28; 20 HC + 20 PD and 28 PD, respectively	ELM	Training data:	2016	Agarwal et al., 2016
					Accuracy = 90.76%
					MCC = 0.815
					Test data:
					Accuracy = 81.55%
Classification of PD from HC	Diagnosis	The Neurovoz corpus	108; 56 HC + 52 PD	Siamese LSTM-based NN with 10-fold cross- validation	EER = 1.9%	2019	Bhati et al., 2019
Classification of PD from HC	Diagnosis	mPower database	2,289; 2,023 HC + 246 PD	L2-regularized logistic regression, random forest, gradient boosted decision trees with 5-fold cross validation	Gradient boosted decision trees:	2019	Tracy et al., 2019
					Recall = 0.797
					Precision = 0.901
					F1-score = 0.836
Classification of PD from HC	Diagnosis	PC-GITA database	100; 50 HC + 50 PD	ResNet with train-validation ratio of 90:10	Precision = 0.92	2019	Wodzinski et al., 2019
					Recall = 0.92
					F1-score = 0.92
					Accuracy = 91.7%

Open in a new tab

ANN, artificial neural network; AUC, area under the receiver operating characteristic (ROC) curve; CART, classification and regression trees; CD, cervical dystonia; CMTNN, complementary neural network; CNN, convolutional neural network; DA, discriminant analysis; DBN, deep belief network; DNN, deep neural network; ECFA, enhanced chaos-based firefly algorithm; EFMM-OneR, enhanced fuzzy min-max neural network with the OneR attribute evaluator; ELM, extreme Learning machine; ET, extra trees or essential tremor; EWNN, evolutionary wavelet neural network; FBANN, feedforward back-propagation based artificial neural network; FKNN, fuzzy k-nearest neighbor; FLDA, Fisher's linear discriminant analysis; FND, functional neurological disorder; FNR, false negative rate; FPR, false positive rate; FURIA, fuzzy unordered rule induction algorithm; GA, genetic algorithm; GBM, gradient boosting machine; GLRA, generalized logistic regression analysis; GPD, generalized paroxysmal dystonia; GRNN, general(ized) regression neural network; HC, healthy control; HMM, hidden Markov model; IGWO-KELM, improved gray wolf optimization and kernel(-based) extreme learning machine; KELM, kernel-based extreme learning machine; KNN, k-nearest neighbors; LDA, linear discriminant analysis; LOSO, leave-one-subject-out; LS-SVM, least-square support vector machine; LSTM, long short-term memory; MAP, maximum a posteriori decision rule; MCC, Matthews correlation coefficient; MLP, multilayer perceptron; MSA, multiple system atrophy; MSE, mean squared error; NN, neural network; NNge, non-nested generalized exemplars; NPV, negative predictive value; PD, Parkinson's disease; PNN, probabilistic neural network; RBM, restricted Boltzmann machine; ResNet, residual neural network; RPART, recursive partitioning and regression trees; SCFW-KELM, subtractive clustering features weighting and kernel-based extreme learning machine; SMO, sequential minimal optimization; SVM, support vector machine; SVM-linear, support vector machine with linear kernel; SVM-RBF, support vector machine with radial basis function kernel; XGBoost, extreme gradient boosting.

Movement Data (n = 51)

The 43 out of 51 studies using accuracy to assess model performance achieved an average accuracy of 89.1 (8.3) %, ranging from 62.1% (Prince and de Vos, 2018) to 100.0% (Surangsrirat et al., 2016; Joshi et al., 2017; Pham, 2018; Pham and Yan, 2018; Figure 4A). One study reported three machine learning methods (SVM, nearest neighbor and decision tree) achieving the highest accuracy individually (Félix et al., 2019). Out of the 51 studies, the per-study highest accuracy was achieved with SVM in 22 studies (41.5%), with ensemble learning in 13 studies (24.5%), with neural network in 9 studies (17.0%), with nearest neighbor in 4 studies (7.5%), with discriminant analysis in 1 study (1.9%), with naïve Bayes in 1 study (1.9%), and with decision tree in 1 study (1.9%). Models that do not belong to any given categories were associated with the highest per-study accuracy in two studies (3.8%; Figure 4B).

Among the 33 studies that collected movement data from recruited participants, 25 used accuracy in model evaluation, leading to an average accuracy of 87.0 (7.3) % (Table 5). The lowest and highest accuracies were 64.1% (Martínez et al., 2018) and 100.0% (Surangsrirat et al., 2016), respectively. Fifteen studies used data from the PhysioNet database (Table 5) and had an average accuracy of 94.4 (4.6) %, a lowest accuracy of 86.4% and a highest accuracy of 100%. Three studies used data from the mPower database (n = 2) or data sourced from another study (n = 1), and the average accuracy of these studies was 80.6 (16.2) %.

Table 5.

Studies that applied machine learning models to movement data to diagnose PD (n = 51).

Objectives	Type of diagnosis	Source of data	Number of subjects (n)	Machine learning method(s), splitting strategy and cross validation	Outcomes	Year	References
Classification of PD from HC	Diagnosis	Collected from participants	103; 71 HC + 32 PD	Ensemble method of 8 models (SVM, MLP, logistic regression, random forest, NSVC, decision tree, KNN, QDA)	Sensitivity = 96% Specificity = 97% AUC = 0.98	2017	Adams, 2017
Classification of PD, HC and other neurological stance disorders	Diagnosis and differential diagnosis	Collected from participants	293; 57 HC + 27 PD + 49 AVS + 12 PNP + 48 CA + 16 DN + 25 OT + 59 PPV	Ensemble method of 7 models (logistic regression, KNN, shallow and deep ANNs, SVM, random forest, extra-randomized trees) with 90% training and 10% testing data in stratified k-fold cross-validation	8-class classification accuracy = 82.7%	2019	Ahmadi et al., 2019
Classification of PD from HC	Diagnosis	Collected from participants	137; 38 HC + 99 PD	SVM with leave-one-out-cross validation	PD vs. HC accuracy = 92.3%	2016	Bernad-Elazari et al., 2016
					Mild vs. severe accuracy = 89.8%
					Mild vs. HC accuracy = 85.9%
Classification of PD from HC	Diagnosis	Collected from participants	30; 14 HC + 16 PD	SVM (linear, quadratic, cubic, Gaussian kernels), ANN, with 5-fold cross-validation	Classification with ANN:	2019	Buongiorno et al., 2019
					Accuracy = 89.4%
					Sensitivity = 87.0%
					Specificity = 91.8%
					Severity assessment with ANN:
					Accuracy = 95.0%
					sensitivity = 90.0%
					Specificity = 99.0%
Classification of PD from HC	Diagnosis	Collected from participants	28; 12 HC + 16 PD	NN with a train-validation-test ratio of 70:15:15, SVM with leave-one-out cross-validation, logistic regression with 10-fold cross validation	SVM: Accuracy = 85.71% Sensitivity = 83.5% Specificity = 87.5%	2017	Butt et al., 2017
Classification of PD from HC	Diagnosis	Collected from participants	28; 12 HC + 16 PD	Logistic regression, naïve Bayes, SVM with 10-fold cross validation	Naïve Bayes:	2018	Butt et al., 2018
					Accuracy = 81.45%
					Sensitivity = 76%
					Specificity = 86.5%
					AUC = 0.811
Classification of PD from HC	Diagnosis	Collected from participants	54; 27 HC + 27 PD	Naïve Bayes, LDA, KNN, decision tree, SVM-linear, SVM-RBF, majority of votes with 5-fold cross validation	Majority of votes (weighted) accuracy = 96%	2018	Caramia et al., 2018
Classification of PD, HC and PD, HC, IH	Diagnosis	Collected from participants	90; 30 PD + 30 HC + 30 IH	SVM, random forest, naïve Bayes with 10-fold cross validation	Random forest:	2019	Cavallo et al., 2019
					HC vs. PD:
					Accuracy = 0.950
					F-measure = 0.947
					HC + IH vs. PD:
					Accuracy = 0.917
					F-measure = 0.912
					HC vs. IH vs. PD:
					Accuracy = 0.789
					F-measure = 0.796
Classification of PD from HC and classification of HC, MCI, PDNOMCI, and PDMCI	Diagnosis, differential diagnosis and subtyping	Collected from participants	PD vs. HC:	Decision tree, naïve Bayes, random forest, SVM, adaptive boosting (with decision tree or random forest) with 10-fold cross validation	Adaptive boosting with decision tree:	2015	Cook et al., 2015
			75; 50 HC + 25 PD		PD vs. HC:
					Accuracy = 0.79
			Subtyping:		AUC = 0.82
			52; 18 HC + 16 PDNOMCI + 9 PDMCI + 9 MCI		Subtyping (HOA vs. MCI vs. PDNOMCI vs. PDMCI):
					Accuracy = 0.85
					AUC = 0.96
Classification of PD from HC	Diagnosis	Collected from participants	580; 424 HC + 156 PD	Hidden Markov models with nearest neighbor classifier with cross validation and train-test ratio of 66.6:33.3	Accuracy = 85.51%	2017	Cuzzolin et al., 2017
Classification of PD from HC	Diagnosis	Collected from participants	80; 40 HC + 40 PD	Random forest, SVM with 10-fold cross validation	SVM-RBF:	2017	Djurić-Jovičić et al., 2017
					Accuracy = 85%
					Sensitivity = 85%
					Specificity = 82%
					PPV = 86%
					NPV = 83%
Classification of PD from HC	Diagnosis	Collected from participants	13; 5 HC + 8 PD	SVM-RBF with leave-one-out cross validation	100% HC and PD classified correctly (confusion matrix)	2014	Dror et al., 2014
Classification of PD from HC	Diagnosis	Collected from participants	75; 38 HC + 37 PD	SVM with leave-one-out cross validation	Accuracy = 85.61%	2014	Drotár et al., 2014
					Sensitivity = 85.95%
					Specificity = 85.26%
Classification of PD from ET	Differential diagnosis	Collected from participants	24; 13 PD + 11 ET	SVM-linear, SVM-RBF with leave-one-out cross validation	Accuracy = 83%	2016	Ghassemi et al., 2016
Classification of PD from HC	Diagnosis	Collected from participants	41; 22 HC + 19 PD	SVM, decision tree, random forest, linear regression with 10-fold and leave-one-individual out (L1O) cross validation	SVM accuracy = 0.89	2018	Klein et al., 2017
Classification of PD from HC	Diagnosis	Collected from participants	74; 33 young HC + 14 elderly HC + 27 PD	SVM with 10-fold cross validation	Sensitivity = ~90%	2017	Javed et al., 2018
Classification of PD from HC and assess the severity of PD	Diagnosis	Collected from participants	55; 20 HC + 35 PD	SVM with leave-one-out cross validation	PD diagnosis:	2016	Koçer and Oktay, 2016
					Accuracy = 89%
					Precision = 0.91
					Recall = 0.94
					Severity assessment:
					HYS 1 accuracy = 72%
					HYS 2 accuracy = 77%
					HYS 3 accuracy = 75%
					HYS 4 accuracy = 33%
Classification of PD from HC	Diagnosis	Collected from participants	45; 20 HC + 25 PD	Naïve Bayes, logistic regression, SVM, AdaBoost, C4.5, BagDT with 10-fold stratified cross-validation apart from BagDT	BagDT: Sensitivity = 82% Specificity = 90% AUC = 0.94	2015	Kostikis et al., 2015
Classification of PD from HC	Diagnosis	Collected from participants	40; 26 HC + 14 PD	Random forest with leave-one-subject-out cross-validation	Accuracy = 94.6% Sensitivity = 91.5% Specificity = 97.2%	2017	Kuhner et al., 2017
Classification of PD from HC	Diagnosis	Collected from participants	177; 70 HC + 107 PD	ESN with 10-fold cross validation	AUC = 0.852	2018	Lacy et al., 2018
Classification of PD from HC	Diagnosis	Collected from participants	39; 16 young HC + 12 elderly HC + 11 PD	LDA with leave-one-out cross validation	Multiclass classification (young HC vs. age-matched HC vs. PD):	2018	Martínez et al., 2018
					Accuracy = 64.1%
					Sensitivity = 47.1%
					Specificity = 77.3%
Classification of PD from HC	Diagnosis	Collected from participants	38; 10 HC + 28 PD	SVM-Gaussian with leave-one-out cross validation	Training accuracy = 96.9%	2018	Oliveira H. M. et al., 2018
					Test accuracy = 76.6%
Classification of PD from HC	Diagnosis	Collected from participants	30; 15 HC + 15 PD	SVM-RBF, PNN with 10-fold cross validation	SVM-RBF:	2015	Oung et al., 2015
					Accuracy = 88.80%
					Sensitivity = 88.70%
					Specificity = 88.15%
					AUC = 88.48
Classification of PD from HC	Diagnosis	Collected from participants	45; 14 HC + 31 PD	Deep-MIL-CNN with LOSO or RkF	With LOSO:	2019	Papadopoulos et al., 2019
					Precision = 0.987
					Sensitivity = 0.9
					specificity = 0.993
					F1-score = 0.943
					With RkF:
					Precision = 0.955
					Sensitivity = 0.828
					Specificity = 0.979
					F1-score = 0.897
Classification of PD, HC and post-stroke	Diagnosis and differential diagnosis	Collected from participants	11; 3 HC + 5 PD + 3 post-stroke	MTFL with 10-fold cross validation	PD vs. HC AUC = 0.983	2017	Papavasileiou et al., 2017
Classification of PD from HC	Diagnosis	Collected from participants	182; 94 HC + 88 PD	LSTM, CNN-1D, CNN-LSTM with 5-fold cross-validation and a training-test ratio of 90:10	CNN-LSTM:	2019	Reyes et al., 2019
					Accuracy = 83.1%
					Precision = 83.5%
					Recall = 83.4%
					F1-score = 81%
					Kappa = 64%
Classification of PD from HC	Diagnosis	Collected from participants	60; 30 HC + 30 PD	Naïve Bayes, KNN, SVM with leave-one-out cross validation	SVM:	2019	Ricci et al., 2020
					Accuracy = 95%
					Precision = 0.951
					AUC = 0.950
Classification of PD, HC and IH	Diagnosis and differential diagnosis	Collected from participants	90; 30 HC + 30 PD + 30 IH	SVM-polynomial, random forest, naïve Bayes with 10-fold cross validation	HC vs. PD, naïve Bayes or random forest:	2018	Rovini et al., 2018
					Precision = 0.967
					Recall = 0.967
					Specificity = 0.967
					Accuracy = 0.967
					F-measure = 0.967
					HC + IH vs. PD, random forest:
					Precision = 1.000
					Recall = 0.933
					Specificity = 1.000
					Accuracy = 0.978
					F-measure = 0.966
					Multiclass classification, random forest:
					Precision = 0.784
					Recall = 0.778
					Specificity = 0.889
					Accuracy = 0.778
					F-measure = 0.781
Classification of PD, HC and IH	Diagnosis and differential diagnosis	Collected from participants	45; 15 HC + 15 PD + 15 IH	SVM-polynomial, random forest with 5-fold cross validation	HC vs. PD, random forest:	2019	Rovini et al., 2019
					Precision = 1.000
					Recall = 1.000
					Specificity = 1.000
					Accuracy = 1.000
					F-measure = 1.000
					Multiclass classification (HC vs. IH vs. PD), random forest:
					Precision = 0.930
					Recall = 0.911
					Specificity = 0.956
					Accuracy = 0.911
					F-measure = 0.920
Classification of PD from ET	Differential diagnosis	Collected from participants	52; 32 PD + 20 ET	SVM-linear with 10-fold cross validation	Accuracy = 1	2016	Surangsrirat et al., 2016
					Sensitivity = 1
					Specificity = 1
Classification of PD from HC	Diagnosis	Collected from participants	12; 10 HC + 2 PD	Naive Bayes, LogitBoost, random forest, SVM with 10-fold cross-validation	Random forest:	2017	Tahavori et al., 2017
					Accuracy = 92.29%
					Precision = 0.99
					Recall = 0.99
Classification of PD from HC	Diagnosis	Collected from participants	39; 16 HC + 23 PD	SVM-RBF with 10-fold stratified cross validation	Sensitivity = 88.9%	2010	Tien et al., 2010
					Specificity = 100%
					Precision = 100%
					FPR = 0.0%
Classification of PD from HC	Diagnosis	Collected from participants	60; 30 HC + 30 PD	Logistic regression, naïve Bayes, random forest, decision tree with 10-fold cross validation	Random forest:	2018	Urcuqui et al., 2018
					Accuracy = 82%
					False negative rate = 23%
					False positive rate = 12%
Classification of PD from HC	Diagnosis	PhysioNet	47; 18 HC + 29 PD	SVM, KNN, random forest, decision tree	SVM with cubic kernel:	2017	Alam et al., 2017
					Accuracy = 93.6%
					Sensitivity = 93.1%
					Specificity = 94.1%
Classification of PD from HC	Diagnosis	PhysioNet	34; 17 HC + 17 PD	MLP, SVM, decision tree	MLP:	2018	Alaskar and Hussain, 2018
					Accuracy = 91.18%
					Sensitivity = 1
					Specificity = 0.83
					Error = 0.09
					AUC = 0.92
Classification of PD from HC and assess the severity of PD	Diagnosis	PhysioNet	166; 73 HC + 93 PD	1D-CNN, 2D-CNN, LSTM, decision tree, logistic regression, SVM, MLP	2D-CNN and LSTM accuracy = 96.0%	2019	Alharthi and Ozanyan, 2019
Classification of PD from HC	Diagnosis	PhysioNet	146; 60 HC + 86 PD	SVM-Gaussian with 3- or 5-fold cross validation	Accuracy = 100%, 88.88%, and 100% in three test groups	2019	Andrei et al., 2019
Classification of PD from HC	Diagnosis	PhysioNet	166; 73 HC + 93 PD	ANN, SVM, naïve Bayes with cross validation	ANN accuracy = 86.75%	2017	Baby et al., 2017
Classification of PD from HC	Diagnosis	PhysioNet	31; 16 HC + 15 PD	SVM-linear, KNN, naïve Bayes, LDA, decision tree with leave-one-out cross validation	SVM, KNN and decision tree accuracy = 96.8%	2019	Félix et al., 2019
Classification of PD from HC	Diagnosis	PhysioNet	31; 16 HC + 15 PD	SVM-linear with leave-one-out cross validation	Accuracy = 100%	2017	Joshi et al., 2017
Classification of PD from HC	Diagnosis	PhysioNet	165; 72 HC + 93 PD	KNN, CART, decision tree, random forest, naïve Bayes, SVM-polynomial, SVM-linear, K-means, GMM with leave-one-out cross validation	SVM: Accuracy = 90.32% Precision = 90.55% Recall = 90.21% F-measure = 90.38%	2019	Khoury et al., 2019
Classification of ALS, HD, PD from HC	Diagnosis	PhysioNet	64; 16 HC + 15 PD + 13 ALS + 20 HD	String grammar unsupervised possibilistic fuzzy C-medians with FKNN, with 4-fold cross validation	PD vs. HC accuracy = 96.43%	2018	Klomsae et al., 2018
Classification of PD from HC	Diagnosis	PhysioNet	166; 73 HC + 93 PD	Logistic regression, decision trees, random forest, SVM-Linear, SVM-RBF, SVM-Poly, KNN with cross validation	KNN:	2018	Mittra and Rustagi, 2018
					Accuracy = 93.08%
					Precision = 89.58%
					Recall = 84.31%
					F1-score = 86.86%
Classification of PD from HC	Diagnosis	PhysioNet	85; 43 HC + 42 PD	LS-SVM with leave-one-out, 2- or 10-fold cross validation	Leave-one-out cross validation:	2018	Pham, 2018
					AUC = 1
					Sensitivity = 100%
					Specificity = 100%
					Accuracy = 100%
					10-fold cross validation:
					AUC = 0.89
					Sensitivity = 85.00%
					Specificity = 73.21%
					Accuracy = 79.31%
Classification of PD from HC	Diagnosis	PhysioNet	165; 72 HC + 93 PD	LS-SVM with leave-one-out, 2- or 5- or 10-fold cross validation	Accuracy = 100%	2018	Pham and Yan, 2018
					Sensitivity = 100%
					Specificity = 100%
					AUC = 1
Classification of PD from HC	Diagnosis	PhysioNet	166; 73 HC + 93 PD	DCALSTM with stratified 5-fold cross validation	Sensitivity = 99.10%	2019	Xia et al., 2020
					Specificity = 99.01%
					Accuracy = 99.07%
Classification of HC, PD, ALS and HD	Diagnosis and differential diagnosis	PhysioNet	64; 16 HC + 15 PD + 13 ALS + 20 HD	SVM-RBF with 10-fold cross validation	PD vs. HC:	2009	Yang et al., 2009
					Accuracy = 86.43%
					AUC = 0.92
Classification of PD, HD, ALS and ND from HC	Diagnosis	PhysioNet	64; 16 HC + 15 PD + 13 ALS + 20 HD	Adaptive neuro-fuzzy inference system with leave-one-out cross validation	PD vs. HC:	2018	Ye et al., 2018
					Accuracy = 90.32%
					Sensitivity = 86.67%
					Specificity = 93.75%
Classification of PD from HC and assess the severity of PD	Diagnosis	mPower database	50; 22 HC + 28 PD	Random forest, bagged trees, SVM, KNN with 10-fold cross validation	Random forest:	2017	Abujrida et al., 2017
					PD vs. HC accuracy = 87.03%
					PD severity assessment accuracy = 85.8%
Classification of PD from HC	Diagnosis	mPower database	1,815; 866 HC + 949 PD	CNN with 10-fold cross validation	Accuracy = 62.1%	2018	Prince and de Vos, 2018
					F1 score = 63.4%
					AUC = 63.5%
Classification of PD from HC	Diagnosis	Dataset from Fernandez et al., 2013	49; 26 HC + 23 PD	KFD-RBF, naïve Bayes, KNN, SVM-RBF, random forest with 10-fold cross validation	Random forest accuracy = 92.6%	2015	Wahid et al., 2015

Open in a new tab

ALS, amyotrophic lateral sclerosis; ANN, artificial neural network; AUC, area under the receiver operating characteristic (ROC) curve; AVS, acute unilateral vestibulopathy; BagDT, bootstrap aggregation for a random forest of decision trees; CA, anterior lobe cerebella atrophy; CART, classification and regression trees; DCALSTM, dual-modal with each branch has a convolutional network followed by an attention-enhanced bi-directional LSTM; DN, downbeat nystagmus syndrome; ESN, echo state network; FKNN, fuzzy k-nearest neighbor; GMM, Gaussian mixture model; HC, healthy control; HD, Huntington's disease; IH, idiopathic hyposmia; KFD, kernel Fisher discriminant; KNN, k-nearest neighbors; LDA, linear discriminant analysis; LOSO, leave-one-subject-out; LS-SVM, least-squares support vector machine; LSTM, long short-term memory; MCI, mild cognitive impairment; MIL, multiple-instance learning; MLP, multilayer perceptron; MTFL, multi-task feature learning; NN, neural network; NSVC, nu-support vector classification; OT, primary orthostatic tremor; PD, Parkinson's disease; PDMCI, PD participants who met criteria for mild cognitive impairment; PDNOMCI, PD participants with no indication of mild cognitive impairment; PNN, probabilistic neural network; PNP, sensory polyneuropathy; PPV, phobic postural vertigo; QDA, quadratic discriminant analysis; RkF, repeated k-fold; SVM, support vector machine; SVM-Poly, support vector machine with polynomial kernel; SVM-RBF, support vector machine with radial basis function kernel.

MRI (n = 36)

Average accuracy of the 32 studies that used accuracy to evaluate the performance of machine learning models was 87.5 (8.0) %. In these studies, the lowest accuracy was 70.5% (Liu L. et al., 2016) and the highest accuracy was 100.0% (Cigdem et al., 2019; Figure 4A). Out of the 36 studies, the per-study highest accuracy was obtained with SVM in 21 studies (58.3%), with neural network in 8 studies (22.2%), with discriminant analysis in 3 studies (8.3%), with regression in 2 studies (5.6%), and with ensemble learning in 1 study (2.8%). One study (2.8%) obtained the highest per-study accuracy using models that do not belong to any of the given categories (Figure 4B). In 8 of 36 studies, neural networks were directly applied to MRI data, while the remaining studies used machine learning models to learn from extracted features, e.g., cortical thickness and volume of brain regions, to diagnose PD.

Out of 17 studies that used MRI data from the PPMI database, 16 used accuracy to evaluate model performance and the average accuracy was 87.9 (8.0) %. The lowest and highest accuracies were 70.5 and 99.9%, respectively (Table 6). In 16 out of 19 studies that acquired MRI data from human participants, accuracy was used to evaluate classification performance and an average accuracy was 87.0 (8.1) % was achieved. The lowest reported accuracy was 76.2% and the highest reported accuracy was 100% (Table 6).

Table 6.

Studies that applied machine learning models to MRI data to diagnose PD (n = 36).

Objectives	Type of diagnosis	Source of data	Number of subjects (n)	Machine learning method(s), splitting strategy and cross validation	Outcomes	Year	References
Classification of PD from MSA	Differential diagnosis	Collected from participants	150; 54 HC + 65 PD + 31 MSA	SVM with leave-one-out-cross validation	MSA vs. PD:	2019	Abos et al., 2019
					Accuracy = 0.79
					Sensitivity = 0.71
					Specificity = 0.86
					MSA vs. HC:
					Accuracy = 0.79
					Sensitivity = 0.84
					Specificity = 0.74
					MSA vs. subsample of PD:
					Accuracy = 0.84
					Sensitivity = 0.77
					Specificity = 0.90
Classification of PD from MSA	Differential diagnosis	Collected from participants	151; 59 HC + 62 PD + 30 MSA	SVM with leave-one-out-cross validation	Accuracy = 77.17%	2019	Baggio et al., 2019
					Sensitivity = 83.33%
					Specificity = 74.19%
Classification of PD from HC	Diagnosis	Collected from participants	94; 50 HC + 44 PD	CNN with 85 subjects for training and 9 for testing	Training accuracy = 95.24%	2019	Banerjee et al., 2019
					Testing accuracy = 88.88%
Classification of PD from HC	Diagnosis	Collected from participants	47; 26 HC + 21 PD	SVM-linear with leave-one-out cross validation	Accuracy = 93.62%	2015	Chen et al., 2015
					Sensitivity = 90.47%
					Specificity = 96.15%
Classification of PD from PSP	Differential diagnosis	Collected from participants	78; 57 PD + 21 PSP	SVM with leave-one-out cross validation	Accuracy = 100%	2013	Cherubini et al., 2014a
					Sensitivity = 1
					Specificity = 1
Classification of PD, MSA, PSP and HC	Diagnosis and differential diagnosis	Collected from participants	106; 36 HC + 35 PD + 16 MSA + 19 PSP	Elastic Net regularized logistic regression with nested 10-fold cross validation	HC vs. PD/MSA-P/PSP:	2017	Du et al., 2017
					AUC = 0.88
					Sensitivity = 0.80
					Specificity = 0.83
					PPV = 0.82
					NPV = 0.81
					HC vs. PD:
					AUC = 0.91
					Sensitivity = 0.86
					Specificity = 0.80
					PPV = 0.82
					NPV = 0.89
					PD vs. MSA/PSP:
					AUC = 0.94
					Sensitivity = 0.86
					Specificity = 0.87
					PPV = 0.88
					NPV = 0.84
					PD vs. MSA:
					AUC = 0.99
					Sensitivity = 0.97
					Specificity = 1.00
					PPV = 1.00
					NPV = 0.93
					PD vs. PSP:
					AUC = 0.99
					Sensitivity = 0.97
					Specificity = 1.00
					PPV = 1.00
					NPV = 0.94
					MSA vs. PSP:
					AUC = 0.98
					Sensitivity = 0.94
					Specificity = 1.00
					PPV = 1.00
					NPV = 0.93
Classification of HC, PD, MSA and PSP	Diagnosis and differential diagnosis	Collected from participants	64; 22 HC + 21 PD + 11 MSA + 10 PSP	SVM-linear with leave-one-out cross validation	PD vs. HC:	2011	Focke et al., 2011
					Accuracy = 41.86%
					Sensitivity = 38.10%
					Specificity = 45.45%
					PD vs. MSA:
					Accuracy = 71.87%
					Sensitivity = 36.36%
					Specificity = 90.48%
					PD vs. PSP:
					Accuracy = 96.77%
					Sensitivity = 90%
					Specificity = 100%
					MSA vs. PSP:
					Accuracy = 76.19%
					MSA vs. HC:
					Accuracy = 78.78%
					Sensitivity = 54.55%
					Specificity = 90.91%
					PSP vs. HC:
					Accuracy = 93.75%
					Sensitivity = 90.00%
					Specificity = 95.45%
Classification of PD and atypical PD	Differential diagnosis	Collected from participants	40; 17 PD + 23 atypical PD	SVM-RBF with 10-fold cross-validation	Accuracy = 97.50%	2012	Haller et al., 2012
					TPR = 0.94
					FPR = 0.00
					TNR = 1.00
					FNR = 0.06
Classification of PD and other forms of Parkinsonism	Differential diagnosis	Collected from participants	36; 16 PD + 20 other Parkinsonism	SVM-RBF with 10-fold cross validation	Accuracy = 86.92%	2012	Haller et al., 2013
					TP = 0.87
					FP = 0.14
					TN = 0.87
					FN = 0.13
Classification of HC, PD, PSP, MSA-C and MSA-P	Diagnosis and differential diagnosis	Collected from participants	464; 73 HC + 204 PD + 106 PSP + 21 MSA-C + 60 MSA-P	SVM-RBF with 10-fold cross validation	PD vs. HC:	2016	Huppertz et al., 2016
					Sensitivity = 65.2%
					Specificity = 67.1%
					Accuracy = 65.7%
					PD vs. PSP:
					Sensitivity = 82.5%
					Specificity = 86.8%
					Accuracy = 85.3%
					PD vs. MSA-C:
					Sensitivity = 76.2%
					Specificity = 96.1%
					Accuracy = 94.2%
					PD vs. MSA-P:
					Sensitivity = 86.7%
					Specificity = 92.2%
					Accuracy = 90.5%
Classification of PD from HC	Diagnosis	Collected from participants	42; 21 HC + 21 PD	SVM-linear with stratified 10-fold cross validation	Accuracy = 78.33%	2017	Kamagata et al., 2017
					Precision = 85.00%
					Recall = 81.67%
					AUC = 85.28%
Classification of PD, PSP, MSA-P and HC	Diagnosis and differential diagnosis	Collected from participants	419; 142 HC + 125 PD + 98 PSP + 54 MSA-P	CNN with train-validation ratio of 85:15	PD:	2019	Kiryu et al., 2019
					Sensitivity = 94.4%
					Specificity = 97.8%
					Accuracy = 96.8%
					AUC = 0.995
					PSP:
					Sensitivity = 84.6%
					Specificity = 96.0%
					Accuracy = 93.7%
					AUC = 0.982
					MSA-P:
					Sensitivity = 77.8%
					Specificity = 98.1%
					Accuracy = 95.2%
					AUC = 0.990
					HC:
					Sensitivity = 100.0%
					Specificity = 97.5%
					Accuracy = 98.4%
					AUC = 1.000
Classification of PD from HC	Diagnosis	Collected from participants	65; 31 HC + 34 PD	FCP with 36 out of the 65 subjects as the training set	AUC = 0.997	2016	Liu H. et al., 2016
Classification of PD, PSP, MSA-C and MSA-P	Differential diagnosis	Collected from participants	85; 47 PD + 22 PSP + 9 MSA-C + 7 MSA-P	SVM-linear with leave-one-out cross validation	4-class classification (MSA-C vs. MSA-P vs. PSP vs. PD) accuracy = 88%	2017	Morisi et al., 2018
Classification of PD from HC	Diagnosis	Collected from participants	89; 47 HC + 42 PD	Boosted logistic regression with nested cross-validation	Accuracy = 76.2%	2019	Rubbert et al., 2019
					Sensitivity = 81%
					Specificity = 72.7%
Classification of PD, PSP and HC	Diagnosis and differential diagnosis	Collected from participants	84; 28 HC + 28 PSP + 28 PD	SVM-linear with leave-one-out cross validation	PD vs. HC:	2014	Salvatore et al., 2014
					Accuracy = 85.8%
					Specificity = 86.0%
					Sensitivity = 86.0%
					PSP vs. HC:
					Accuracy = 89.1%
					Specificity = 89.1%
					Sensitivity = 89.5%
					PSP vs. PD:
					Accuracy = 88.9%
					Specificity = 88.5%
					Sensitivity = 89.5%
Classification of PD, APS (MSA, PSP) and HC	Diagnosis and differential diagnosis	Collected from participants	100; 35 HC + 45 PD + 20 APS	CNN-DL, CR-ML, RA-ML with 5-fold cross-validation	PD vs. HC with CNN-DL:	2019	Shinde et al., 2019
					Test accuracy = 80.0%
					Test sensitivity = 0.86
					Test specificity = 0.70
					Test AUC = 0.913
					PD vs. APS with CNN-DL:
					Test accuracy = 85.7%
					Test sensitivity = 1.00
					Test specificity = 0.50
					Test AUC = 0.911
Classification of PD from HC	Diagnosis	Collected from participants	101; 50 HC + 51 PD	SVM-RBF with leave-one-out cross validation	Sensitivity = 92% Specificity = 87%	2017	Tang et al., 2017
Classification of PD from HC	Diagnosis	Collected from participants	85; 40 HC + 45 PD	SVM-linear with leave-one-out, 5-fold, 0.632-fold (1-1/e), 2-fold cross validation	Accuracy = 97.7%	2016	Zeng et al., 2017
Classification of PD from HC	Diagnosis	PPMI database	543; 169 HC + 374 PD	RLDA with JFSS with 10-fold cross validation	Accuracy = 81.9%	2016	Adeli et al., 2016
Classification of PD from HC	Diagnosis	PPMI database	543; 169 HC + 374 PD	RFS-LDA with 10-fold cross validation	Accuracy = 79.8%	2019	Adeli et al., 2019
Classification of PD from HC	Diagnosis	PPMI database	543; 169 HC + 374 PD	Random forest (for feature selection and clinical score); SVM with 10-fold stratified cross validation	Accuracy = 0.93	2018	Amoroso et al., 2018
					AUC = 0.97
					Sensitivity = 0.93
					Specificity = 0.92
Classification of PD, HC and prodromal	Diagnosis	PPMI database	906; 203 HC + 66 prodromal + 637 PD	MLP, XgBoost, random forest, SVM with 5-fold cross validation	MLP:	2020	Chakraborty et al., 2020
					Accuracy = 95.3%
					Recall = 95.41%
					Precision = 97.28%
					F1-score = 94%
Classification of PD from HC	Diagnosis	PPMI database	Dataset 1: 15; 6 HC + 9 PD	SVM with leave-one-out cross validation	Dataset 1:	2014	Chen et al., 2014
					EER = 87%
			Dataset 2: 39; 21 HC + 18 PD		Accuracy = 80%
					AUC = 0.907
					Dataset 2:
					EER = 73%
					Accuracy = 68%
					AUC = 0.780
Classification of PD from HC	Diagnosis	PPMI database	80; 40 HC + 40 PD	Naïve Bayes, SVM-RBF with 10-fold cross validation	SVM:	2019	Cigdem et al., 2019
					Accuracy = 87.50%
					Sensitivity = 85.00%
					Specificity = 90.00%
					AUC = 90.00%
Classification of PD from HC	Diagnosis	PPMI database	37; 18 HC + 19 PD	SVM-linear with leave-one-out cross validation	Accuracy = 94.59%	2017	Kazeminejad et al., 2017
Classification of PD, HC and SWEDD	Diagnosis and subtyping	PPMI database	238; 62 HC + 142 PD + 34 SWEDD	Joint learning with 10-fold cross validation	HC vs. PD:	2018	Lei et al., 2019
					Accuracy = 91.12%
					AUC = 94.88%
					HC vs. SWEDD:
					Accuracy = 94.89%
					AUC = 97.80%
					PD vs. SWEDD:
					accuracy = 92.12%
					AUC = 93.82%
Classification of PD and SWEDD from HC	Diagnosis	PPMI database	Baseline: 238; 62 HC + 142 PD + 34 SWEDD12 months: 186; 54 HC + 123 PD + 9 SWEDD 24 months: 127; 7 HC + 88 PD + 22 SWEDD	SSAE with 10-fold cross validation	HC vs. PD: Accuracy = 85.24%, 88.14%, and 96.19% for baseline, 12 m, and 24 mHC vs. SWEDD: Accuracy = 89.67%, 95.24%, and 93.10% for baseline, 12 m, and 24 m	2019	Li et al., 2019
Classification of PD from HC	Diagnosis	PPMI database	112; 56 HC + 56 PD	RLDA with 8-fold cross validation	Accuracy = 70.5%	2016	Liu L. et al., 2016
					AUC = 71.1
Classification of PD from HC	Diagnosis	PPMI database	60; 30 HC + 30 PD	SVM, ELM with train-test ratio of 80:20	ELM:	2016	Pahuja and Nagabhushan, 2016
					Training accuracy = 94.87%
					Testing accuracy = 90.97%
					Sensitivity = 0.9245
					Specificity = 0.9730
Classification of PD from HC	Diagnosis	PPMI database	172; 103 HC + 69 PD	Multi-kernel SVM with 10-fold cross validation		2017	Peng et al., 2017
					Accuracy = 85.78%
					Specificity = 87.79%
					Sensitivity = 87.64%
					AUC = 0.8363
Classification of PD from HC	Diagnosis and subtyping	PPMI database	109; 32 HC + 77 PD (55 PD-NC + 22 PD-MCI)	SVM with 2-fold cross validation	PD vs. HC:	2016	Peng et al., 2016
					Accuracy = 92.35%
					Sensitivity = 0.9035
					Specificity = 0.9431
					AUC = 0.9744
					PD-MCI vs. HC:
					Accuracy = 83.91%
					Sensitivity = 0.8355
					Specificity = 0.8587
					AUC = 0.9184
					PD-MCI vs. PD-NC:
					Accuracy = 80.84%
					Sensitivity = 0.7705
					Specificity = 0.8457
					AUC = 0.8677
Classification of PD, HC and SWEDD	Diagnosis and subtyping	PPMI database	831; 245 HC + 518 PD + 68 SWEDD	LSSVM-RBF with cross validation	Accuracy = 99.9% Specificity = 100% Sensitivity = 99.4%	2015	Singh and Samavedham, 2015
Classification of PD, HC and SWEDD	Diagnosis and differential diagnosis	PPMI database	741; 262 HC + 408 PD + 71 SWEDD	LSSVM-RBF with 10-fold cross validation	PD vs. HC accuracy = 95.37%	2018	Singh et al., 2018
					PD vs. SWEDD accuracy = 96.04%
					SWEDD vs. HC accuracy = 93.03%
Classification of PD from HC	Diagnosis	PPMI database	408; 204 HC + 204 PD	CNN (VGG and ResNet)	ResNet50 accuracy = 88.6%	2019	Yagis et al., 2019
Classification of PD from HC	Diagnosis	PPMI database	754; 158 HC + 596 PD	FCN, GCN with 5-fold cross validation	AUC = 95.37%	2018	Zhang et al., 2018

Open in a new tab

APS, atypical parkinsonian syndromes; AUC, area under the receiver operating characteristic (ROC) curve; CNN, convolutional neural network; CNN-DL, convolutional neural network with discriminative localization; CR-ML, contrast ratio classifier; EER, equal error rate; ELM, extreme learning machine; FCN, fully connected network; FCP, folded concave penalized (learning); FN, false negative; FNR, false negative rate; FP, false positive; FPR, false positive rate; GCN, graph convolutional network; HC, healthy control; JFSS, joint feature-sample selection; LSSVM, least-squares support vector machine; MLP, multilayer perceptron; MSA, multiple system atrophy; MSA-C, multiple system atrophy with a cerebellar syndrome; MSA-P, multiple system atrophy with a parkinsonian type; PD, Parkinson's disease; PD-MCI, PD participants who met criteria for mild cognitive impairment; PD-NC, PD participants with no indication of mild cognitive impairment; PSP, progressive supranuclear palsy; RA-ML, radiomics based classifier; ResNet, residual neural network; RFS-LDA, robust feature-sample linear discriminant analysis; RLDA, robust linear discriminant analysis; SSAE, stacked sparse auto-encoder; SVM, support vector machine; SVM-RBF, support vector machine with radial basis function kernel; SWEDD, PD with scans without evidence of dopaminergic deficit; TN, true negative; TNR, true negative rate; TP, true positive; TPR, true positive rate; XgBoost, extreme gradient boosting.

Handwriting Patterns (n = 16)

Fifteen out of 16 studies used accuracy in model evaluation and the average accuracy was 87.0 (6.3) % (Table 7). Among these studies, the lowest accuracy was 76.44% (Ali et al., 2019b) and the highest accuracy was 99.3% (Pereira et al., 2018; Figure 4A). The highest accuracy per-study was obtained with neural network in 6 studies (37.5%), with SVM in 5 studies (31.3%), with ensemble learning in 4 studies (25.0%), and with naïve Bayes in 1 study (6.3%; Figure 4B).

Table 7.

Studies that applied machine learning models to handwritten patterns, SPECT, PET, CSF, other data types and combinations of data to diagnose PD (n = 67).

Objectives	Type of diagnosis	Source of data	Type of data	Number of subjects (n)	Machine learning method(s), splitting strategy and cross validation	Outcomes	Year	References
Classification of PD from HC	Diagnosis	HandPD	Handwritten patterns	92; 18 HC + 74 PD	LDA, KNN, Gaussian naïve Bayes, decision tree, Chi2 with Adaboost with 5- or 4-fold stratified cross validation	Chi-2 with Adaboost: Accuracy = 76.44% Sensitivity = 70.94% Specificity = 81.94%	2019	Ali et al., 2019b
Classification of PD (PD + SWEDD) from HC	Diagnosis	PPMI database	More than one	388; 194 HC + 168 PD + 26 SWEDD	Ensemble method of several SVM with linear kernel with leave-one-out cross validation	Accuracy = 94.38%	2018	Castillo-Barnes et al., 2018
Classification of PD from HC	Diagnosis	PPMI database	More than one	586; 184 HC + 402 PD	MLP, BayesNet, random forest, boosted logistic regression with a train-test ratio of 70:30	Boosted logistic regression: Accuracy = 97.159% AUC curve = 98.9%	2016	Challa et al., 2016
Classification of tPD from rET	Differential diagnosis	Collected from participants	More than one	30; 15 tPD + 15rET	Multi-kernel SVM with leave-one-out cross validation	Accuracy = 100%	2014	Cherubini et al., 2014b
Classfication of PD, HC and atypical PD	Diagnosis, differential diagnosis and subtyping	PPMI database and SNUH cohort	SPECT imaging data	PPMI: 701; 193 HC + 431 PD + 77 SWEDD snuh: 82 PD	CNN with train-validation ratio of 90:10	PPMI: Accuracy = 96.0% Sensitivity = 94.2% Specificity = 100% SNUH: Accuracy = 98.8% Sensitivity = 98.6% Specificity = 100%	2017	Choi et al., 2017
Classification of PD from HC	Diagnosis	Collected from participants	Other	270; 120 HC + 150 PD	Random forest	Classification error = 49.6% (rs11240569) Classification error = 44.8% (rs708727) Classification error = 49.3% (rs823156)	2019	Cibulka et al., 2019
Classification of PD from HC	Diagnosis	HandPD	Handwritten patterns	92; 18 HC + 74 PD	Naïve Bayes, OPF, SVM with cross-validation	SVM-RBF accuracy = 85.54%	2018	de Souza et al., 2018
Classification of PD from HC	Diagnosis	PPMI database	More than one	1194; 816 HC + 378 PD	BoostPark	Accuracy = 0.901 AUC-ROC = 0.977 AUC-PR = 0.947 F1-score = 0.851	2017	Dhami et al., 2017
Classification of PD and HC, and PD + SWEDD and HC	Diagnosis	PPMI database	More than one	430; 127 HC + 263 PD + 40 SWEDD	AdaBoost, SVM, naïve Bayes, decision tree, KNN, K-Means with 5-fold cross validation	PD vs. HC (adaboost): Accuracy = 0.98954704 Sensitivity = 0.97831978 Specificity = 0.99796748 PPV = 0.99723757 NPV = 0.98396794 LOR = 10.0058805 PD + SWEDD vs HC (adaboost): Accuracy = 0.9825784 Sensitivity = 0.97560976 Specificity = 0.98780488 PPV = 0.98360656 NPV = 0.98181818 LOR = 8.08332861	2016	Dinov et al., 2016
Classification of PD from HC	Diagnosis	Collected from participants	CSF	Cohort 1: 160; 80 HC + 80 PD Cohort 2: 60; 30 HC + 30 PD	Elastic Net and gradient boosted regression with 10-fold cross validation	Ensemble of 60 decision trees identified with gradient boosted model: Sensitivity = 85% Specificity = 75% PPV = 77% NPV = 83% AUC = 0.77	2018	Dos Santos et al., 2018
Classification of PD from HC	Diagnosis	Collected from participants	Handwritten patterns	75; 38 HC + 37 PD	SVM-RBF with stratified 10-fold cross-validation	Accuracy = 88.13% Sensitivity = 89.47% Specificity = 91.89%	2015	Drotár et al., 2015
Classification of PD from HC	Diagnosis	Collected from participants	Handwritten patterns	75; 38 HC + 37 PD	KNN, ensemble AdaBoost, SVM	SVM: Accuracy = 81.3% Sensitivity = 87.4% Specificity = 80.9%	2016	Drotár et al., 2016
Classification of IPD, VaP and HC	Differential diagnosis	Collected from participants	More than one	45; 15 HC + 15 IPD + 15 VaP	MLP, DBN with 10-fold cross validation	IPD + VaP vs HC with MLP: Accuracy = 95.68% Specificity = 98.08% Sensitivity = 92.44% VaP vs. IPD with DBN: Accuracy = 75.33% Specificity = 72.31% Sensitivity = 79.18%	2018	Fernandes et al., 2018
Classification of PD from HC	Diagnosis	Collected from participants	More than one	75; 15 HC + 60 PD blood: 75; 15 HC + 60 PD FDOPA PET: 58; 14 HC + 44 PD FDG PET: 67; 16 HC + 51 PD	SVM-linear, random forest with leave-one-out cross validation	SVM AUC for FDOPA + metabolomics: 0.98 SVM AUC for FDG + metabolomics: 0.91	2019	Glaab et al., 2019
Classification of PD, HC and SWEDD	Diagnosis and subtyping	PPMI database	More than one	666; 415 HC + 189 PD + 62 SWEDD	EPNN, PNN, SVM, KNN, classification tree with train-test ratio of 90:10	EPNN: PD vs SWEDD vs HC accuracy = 92.5% PD vs HC accuracy = 98.6% SWEDD vs HC accuracy = 92.0% PD vs. SWEDD accuracy = 95.3%	2015	Hirschauer et al., 2015
Classification of PD from HC and assess the severity of PD	Diagnosis	Picture Archiving and Communication System (PACS)	SPECT imaging data	202; 6 HC + 102 mild PD + 94 severe PD	Linear regression, SVM-RBF with a train-test ratio of 50:50	SVM-RBF: Sensitivity = 0.828 Specificity = 1.000 PPV = 0.837 NPV = 0.667 Accuracy = 0.832 AUC = 0.845 Kappa = 0.680	2019	Hsu et al., 2019
Classification of PD from VP	Differential diagnosis	Collected from participants	SPECT imaging data	244; 164 PD + 80 VP	Logistic regression, LDA, SVM with 10-fold cross-validation	SVM: Accuracy = 0.904 Sensitivity = 0.954 Specificity = 0.801 AUC = 0.954	2014	Huertas-Fernández et al., 2015
Classification of PD from HC	Diagnosis	Collected from participants	SPECT imaging data	208; 108 HC + 100 PD	SVM, KNN, NM with 3-fold cross validation	SVM: Sensitivity = 89.02% Specificity = 93.21% AUC = 0.9681	2012	Illan et al., 2012
Classification of PD from HC	Diagnosis	Collected from participants	Handwritten patterns	72; 15 HC + 57 PD	CNN with 10-fold cross validation or leave-one-out cross validation	Accuracy = 88.89%	2018	Khatamino et al., 2018
Classification of PD from HC	Diagnosis	Collected from participants	Other	10; 5 HC + 5 PD	SVM with leave-one-subject-out cross validation	Sensitivity = 0.90 Specificity = 0.90	2013	Kugler et al., 2013
Classification of PD from HC	Diagnosis	UCI machine learning repository	Handwritten patterns	72; 15 HC + 57 PD	SVM-linear, SVM-RBF, KNN with leave-one-subject-out cross validation	SVM-linear: Accuracy = 97.52% MCC = 0.9150 F-score = 0.9828	2019	İ et al., 2019
Classification of PD from HC	Diagnosis	Collected postmortem	CSF	105; 57 HC + 48 PD	SVM with 10-fold cross validation	Sensitivity = 65% Specificity = 79% AUC = 0.79	2013	Lewitt et al., 2013
Classification of PD from HC	Diagnosis	Collected from participants	CSF	78; 42 HC + 36 PD	Random forest and extreme gradient tree boosting with 10-fold cross validation	Extreme gradient tree boosting: Specificity = 78.6% Sensitivity = 83.3% AUC = 83.9%	2018	Maass et al., 2018
Classification of PD from HC or NPH	Diagnosis and differential diagnosis	Collected from participants	CSF	157; 68 HC + 82 PD + 7 NPH	SVM with 10-fold cross validation or leave-one-out cross validation	Cohort 1, PD vs HC: AUC = 0.76 Cohort 2, PD vs HC: AUC = 0.78 Cohort 3, PD vs HC: AUC = 0.31 Cohort 4, PD vs NPH: AUC = 0.88	2020	Maass et al., 2020
Classification of PD from HC	Diagnosis	PPMI database	More than one	550; 157 HC + 342 PD + 51 SWEDD	SVM, random forest, MLP, logistic regression, KNN with nested cross-validation	Motor features, SVM: Accuracy = 78.4% AUC = 84.7% Non-motor features, KNN: Accuracy = 82.2% AUC = 88%	2018	Mabrouk et al., 2019
Classification of PD from HC	Diagnosis	PPMI database	SPECT imaging data	642; 194 HC + 448 PD	CNN (LENET53D, ALEXNET3D) with 10-fold stratified cross-validation	ALEXNET3D: Accuracy = 94.1% AUC = 0.984	2018	Martinez-Murcia et al., 2018
Classification of PD from HC	Diagnosis	Collected from participants	Handwritten patterns	75; 10 HC + 65 PD	MLP, non-linear SVM, random forest, logistic regression with stratified 10-fold cross-validation	MLP: Accuracy = 84% Sensitivity = 75.7% Specificity = 88.9% Weighted Kappa = 0.65 AUC = 0.86	2015	Memedi et al., 2015
Classification of PD from HC	Diagnosis	Parkinson's Disease Handwriting Database (PaHaW)	Handwritten patterns	69; 36 HC + 33 PD	Random forest with stratified 7-fold cross-validation	Accuracy = 89.81% Sensitivity = 88.63% Specificity = 90.87% MCC = 0.8039	2018	Mucha et al., 2018
Classification of PD, MSA, PSP, CBS and HC	Differential diagnosis	Collected from participants	SPECT imaging data	578; 208 HC + 280 PD + 21 MSA + 41 PSP + 28 CBS	SVM with 5-fold cross-validation	Accuracy = 58.4–92.9%	2019	Nicastro et al., 2019
Classification of PD from HC	Diagnosis	Collected from participants	Handwritten patterns	30; 15 HC + 15 PD	KNN, decision tree, random forest, SVM, AdaBoost with 3-fold cross validation	Random forest accuracy = 0.91	2018	Nõmm et al., 2018
Classification of HC, AD and PD	Diagnosis and differential diagnosis	The authors' institutional oct database	Other	75; 27 HC + 28 PD + 20 AD	SVM-RBF with 2-, 5- and 10-fold cross validation	Accuracy = 87.7% HC sensitivity = 96.2% HC specificity = 88.2% PD sensitivity = 87.0% PD specificity = 100.0%	2019	Nunes et al., 2019
Classification of idiopathic PD, atypical Parkinsonian and ET	Differential diagnosis	Collected from participants	Other	85; 50 idiopathic PD + 26 atypical PD + 9 ET	SVM, random forest with leave-one-out cross validation	SVM accuracy = 100% Random forest accuracy = 98.5%	2019	Nuvoli et al., 2019
Classification of PD from HC	Diagnosis	PPMI database	SPECT imaging data	654; 209 HC + 445 PD	SVM-linear with leave-one-out cross validation	Accuracy = 97.86% Sensitivity = 97.75% Specificity = 98.09%	2015	Oliveira and Castelo-Branco, 2015
Classification of PD from HC	Diagnosis	PPMI database	SPECT imaging data	652; 209 HC + 443 PD	SVM-linear, KNN, logistic regression with leave-one-out cross validation	SVM-linear: Accuracy = 97.9% Sensitivity = 98.0% Specificity = 97.6%	2017	Oliveira F. et al., 2018
Classification of PD and non-PD (ET, drug-induced Parkinsonism)	Differential diagnosis	Collected from participants	SPECT imaging data	90; 56 PD + 34 non-PD	SVM-RBF with leave-one-out or 5-fold cross validation	Accuracy = 95.6%	2014	Palumbo et al., 2014
Classification of PD from HC	Diagnosis	Collected from participants	Handwritten patterns	55; 18 HC + 37 PD	Naïve Bayes, OPF, SVM-RBF with 10-fold cross validation	Naïve Bayes accuracy = 78.9%	2015	Pereira et al., 2015
Classification of PD from HC	Diagnosis	HandPD	Handwritten patterns	92; 18 HC + 74 PD	Naïve Bayes, OPF, SVM-RBF with cross-validation	SVM-RBF recognition rate (sensitivity) = 66.72%	2016	Pereira et al., 2016a
Classification of PD from HC	Diagnosis	Extended handpd dataset with signals extracted from a smart pen	Handwritten patterns	35; 21 HC + 14 PD	CNN with cross validation with a train:test ratio of 75:25 or 50:50	Accuracy = 87.14%	2016	Pereira et al., 2016b
Classification of PD from HC	Diagnosis	HandPD	Handwritten patterns	92; 18 HC + 74 PD	CNN, OPF, SVM, naïve Bayes with train-test split = 50:50	CNN-Cifar10 accuracy = 99.30% Early stage accuracy with CNN-ImageNet = 96.35% or 94.01% for Exam 3 or Exam 4	2018	Pereira et al., 2018
Classification of PD from HC	Diagnosis	UCI machine learning repository	More than one	Dataset 1: 40; 20 HC + 20 PD dataset 2: 77; 15 HC + 62 PD	Random forest, KNN, SVM-RBF, ensemble method with 5-fold cross validation	Ensemble method: Accuracy = 95.89% Specificity = 100% Sensitivity = 91.43%	2019	Pham et al., 2019
Classification of PD from HC	Diagnosis	PPMI database	More than one	618; 195 HC + 423 PD	SVM-linear, SVM-RBF, classification tree with a train-test ratio of 70:30	SVM-RBF, test set: Accuracy = 85.48% Sensitivity = 90.55% Specificity = 74.58% AUC = 88.22%	2014	Prashanth et al., 2014
Classification of PD from HC	Diagnosis and subtyping	PPMI database	SPECT imaging data	715; 208 HC + 427 PD + 80 SWEDD	SVM, naïve Bayes, boosted trees, random forest with 10-fold cross validation	SVM: Accuracy = 97.29% Sensitivity = 97.37% Specificity = 97.18% AUC = 99.26	2016	Prashanth et al., 2017
Classification of PD from HC	Diagnosis	PPMI database	More than one	584; 183 HC + 401 PD	Naïve Bayes, SVM-RBF, boosted trees, random forest with 10-fold cross validation	SVM: Accuracy = 96.40% Sensitivity = 97.03% Specificity = 95.01% AUC = 98.88%	2016	Prashanth et al., 2016
Classification of PD from HC	Diagnosis	PPMI database	Other	626; 180 HC + 446 PD	Logistic regression, random forests, boosted trees, SVM with cross validation	Accuracy > 95% AUC > 95% Random forests: Accuracy = 96.20–97.14% (95% CI)	2018	Prashanth and Dutta Roy, 2018
Classification of PD from HC	Diagnosis	mPower database	More than one	133 out of 1,513 with complete source data; 46 HC + 87 PD	Logistic regression, random forests, DNN, CNN, Classifier Ensemble, Multi-Source Ensemble learning with stratified 10-fold cross validation	Ensemble learning: Accuracy = 82.0% F1-score = 87.1%	2019	Prince et al., 2019
Classification of PD from HC	Diagnosis	HandPD	Handwritten patterns	35; 21 HC + 14 PD	Bidirectional Gated Recurrent Units with a train-validation-test ratio of 40:10:50 or 65:10:25	The Spiral dataset: Accuracy = 89.48% Precision = 0.848 Recall = 0.955 F1-score = 0.897 The Meander dataset: Accuracy = 92.24% Precision = 0.952 Recall = 0.883 F1-score = 0.924	2019	Ribeiro et al., 2019
Classification of PD from HC	Diagnosis	Collected from participants	Handwritten patterns	130; 39 elderly HC + 40 young HC + 39 PD + 6 PD (validation set) + 6 HC (validation set)	KNN, SVM-Gaussian, random forest with leave-one-out cross validation	SVM for PD vs young HC: Accuracy = 94.0% Sensitivity = 0.94 Specificity = 0.94 F1-score = 0.94 SVM for PD vs elderly HC: Accuracy = 89.3% Sensitivity = 0.89 Specificity = 0.89 F1-score = 0.89 Random forest for validation set: Accuracy = 83.3% Sensitivity = 0.92 Specificity = 0.93 F1-score = 0.92	2019	Rios-Urrego et al., 2019
Classification of IPD from non-IPD	Differential diagnosis	Collected from participants	PET imaging	87; 39 IPD + 48 non-IPD (24 MSA + 24 PSP)	SVM with leave-one-out cross validation	Accuracy = 78.16% Sensitivity = 69.29% Specificity = 85.42%	2015	Segovia et al., 2015
Classification of PD from HC	Diagnosis	Dataset from “Virgen de la Victoria” hospital	SPECT imaging data	189; 94 HC + 95 PD	SVM with 10-fold cross validation	Accuracy = 94.25% Sensitivity = 91.26% Specificity = 96.17%	2019	Segovia et al., 2019
Classification of PD from HC	Diagnosis	Collected from participants	Other	486; 233 HC + 205 PD + 48 NDD	SVM-linear with leave-batch-out cross validation	Validation AUC = 0.79 Test AUC = 0.74	2017	Shamir et al., 2017
Classification of PD from HC	Diagnosis	Collected from participants	PET imaging	350; 225 HC + 125 PD	GLS-DBN with a train-validation ratio of 80:20	Test dataset 1: Accuracy = 90% Sensitivity = 0.96 Specificity = 0.84 AUC = 0.9120 Test dataset 2: Accuracy = 86% Sensitivity = 0.92 Specificity = 0.80 AUC = 0.8992	2019	Shen et al., 2019
Classification of PD from HC	Diagnosis	Collected from participants	Other	33; 18 HC + 15 PD	SMMKL-linear with leave-one-out cross validation	Accuracy = 84.85% Sensitivity = 80.00% Specificity = 88.89% YI = 68.89% PPV = 85.71% NPV = 84.21% F1 score = 82.76%	2018	Shi et al., 2018
Classification of PD from HC	Diagnosis	Collected from participants	More than one	Plasma samples: 156; 76 HC + 80 PD; CSF samples: 77; 37 HC + 40 PD	PLS, random forest with 10-fold cross validation with train-test ratio of 70:30	PLS: AUC (plasma) = 0.77 AUC (CSF) = 0.90	2018	Stoessel et al., 2018
Classification of PD from HC	Diagnosis	PPMI database	SPECT imaging data	658; 210 HC + 448 PD	Logistic Lasso with 10-fold cross validation	Test errors: FP = 2.83% FN = 3.78% Net error = 3.47%	2017	Tagare et al., 2017
Classification of PD from HC	Diagnosis	PDMultiMC	handwritten patterns	42; 21 HC + 21 PD	CNN, CNN-BLSTM with stratified 3-fold cross validation	CNN: Accuracy = 83.33% Sensitivity = 85.71% Specificity = 80.95% CNN-BLSTM: Accuracy = 83.33% Sensitivity = 71.43% Specificity = 95.24%	2019	Taleb et al., 2019
Classification of PD from HC	Diagnosis	PPMI database and local database	SPECT imaging data	Local: 304; 113 Non-PDD + 191 PD PPMI: 657; 209 HC + 448 PD	SVM with stratified, nested 10-fold cross-validation	Local data: Accuracy = 0.88 to 0.92 PPMI: Accuracy = 0.95 to 0.97	2017	Taylor and Fenner, 2017
Classification of PD from HC	Diagnosis	Collected from participants	CSF	87; 43 HC + 44 PD	Logistic regression	Sensitivity = 0.797 specIFICITy = 0.800 AUC = 0.833	2017	Trezzi et al., 2017
Classification of PD from HC	Diagnosis	Collected from participants	Other	38; 24 HC + 14 PD	SVM-RFE with repeated leave-one-out bootstrap validation	Accuracy = 89.6%	2013	Tseng et al., 2013
Classification of MSA and PD	Differential diagnosis	Collected from participants	More than one	85; 25 HC + 30 PD + 30 MSA-P	NN	AUC = 0.775	2019	Tsuda et al., 2019
Classification of PD from HC	Diagnosis	Collected from participants	Other	59; 30 HC + 29 PD	Logistic regression, decision tree, extra tree	Extra tree AUC = 0.99422	2018	Vanegas et al., 2018
Classification of PD from HC	Diagnosis	Commercially sourced	Other	30; 15 HC + 15 PD	Decision tree	Cross validation score = 0.86 (male) Cross validation score = 0.63 (female)	2019	Váradi et al., 2019
Classification of PD from HC	Diagnosis	Collected from participants	More than one	84; 40 HC + 44 PD	CNN with train-validation-test ratio of 80:10:10	Accuracy = 97.6% AUC = 0.988	2018	Vásquez-Correa et al., 2019
Classification of PD and Parkinsonism	Differential diagnosis	The NTUA Parkinson Dataset	More than one	78; 55 PD + 23 Parkinsonism	MTL with DNN	Accuracy = 0.91 Precision = 0.83 Sensitivity = 1.0 Specificity = 0.83 AUC = 0.92	2018	Vlachostergiou et al., 2018
Classification of PD from HC	Diagnosis	PPMI database	More than one	534; 165 HC + 369 PD	pGTL with 10-fold cross validation	Accuracy = 97.4%	2017	Wang et al., 2017
Classification of PD from HC	Diagnosis	PPMI database	SPECT imaging data	645; 207 HC + 438 PD	CNN with train-validation-test ratio of 60:20:20	Accuracy = 0.972 Sensitivity = 0.983 Specificity = 0.962	2019	Wenzel et al., 2019
Classification of PD from HC	Diagnosis	Collected from participants	PET imaging	Cohort 1: 182; 91 HC + 91 PD Cohort 2: 48; 26 HC + 22 PD	SVM-linear, SVM-sigmoid, SVM-RBF with 5-fold cross validation	Cohort 1: Accuracy = 91.26% Sensitivity = 89.43% Specificity = 93.27% Cohort 2: Accuracy = 90.18% Sensitivity = 82.05% Specificity = 92.05%	2019	Wu et al., 2019
Classification of PD, MSA and PSP	Differential diagnosis	Collected from participants	PET imaging	920; 502 PD + 239 MSA + 179 PSP	3D residual CNN with 6-fold cross validation	Classification of PD: Sensitivity = 97.7% Specificity = 94.1% PPV = 95.5% NPV = 97.0% Classification of MSA: Sensitivity = 96.8% Specificity = 99.5% PPV = 98.7% NPV = 98.7% Classification of PSP: Sensitivity = 83.3% Specificity = 98.3% PPV = 90.0% NPV = 97.8%	2019	Zhao et al., 2019

Open in a new tab

AD, Alzheimer's disease; AUC or AUC-ROC, area under the receiver operating characteristic (ROC) curve; AUC-PR, area under the precision-recall (PR) curve; BLSTM, bidirectional long short-term memory; CBS, corticobasal syndrome; CNN, convolutional neural network; CSF, cerebrospinal fluid; DBN, deep belief network; DNN, deep neural network; EPNN, enhanced probabilistic neural network; ET, essential tremor; FN, false negative; FP, false positive; GLS-DBN, group Lasso sparse deep belief network; HC, healthy control; IPD, idiopathic Parkinson's disease; KNN, k-nearest neighbors; LDA, linear discriminant analysis; LOR, log odds ratio; MCC, Matthews correlation coefficient; MLP, multilayer perceptron; MSA, multiple system atrophy; MSA-P, Parkinson's variant of multiple system atrophy; MTL, multi-task learning; NDD, neurodegenerative disease; NM, nearest mean; non-PDD, patients without pre-synaptic dopaminergic deficit; NPH, normal pressure hydrocephalus; NPV, negative predictive value; OPF, optimum-path forest; PD, Parkinson's disease; PET, positron emission tomography; pGTL, progressive graph-based transductive learning; PLS, partial least square; PNN, probabilistic neural network; PPV, positive predictive value; PSP, progressive supranuclear palsy; rET, essential tremor with rest tremor; SMMKL, soft margin multiple kernel learning; SPECT, single-photon emission computed tomography; SVM, support vector machine; SVM-RBF, support vector machine with radial basis function kernel; SVM-RFE, support vector machine-recursive feature elimination; SWEDD, PD with scans without evidence of dopaminergic deficit; tPD, tremor-dominant Parkinson's disease; VaP or VP, vascular Parkinsonism; YI, Youden's Index.

SPECT (n = 14)

Average accuracy of 12 out of 14 studies that used accuracy to measure the performance of machine learning models was 94.4 (4.2) % (Table 7). The lowest reported accuracy was 83.2% (Hsu et al., 2019) and 97.9% (Oliveira F. et al., 2018; Figure 4A). SVM led to the highest per-study accuracy in 10 out of 14 studies (71.4%). The highest per-study accuracy was obtained with neural networks in 3 studies (21.4%) and with regression in 1 study (7.1%; Figure 4B).

PET (n = 4)

All 4 studies used sensitivity and specificity (Table 7) in model evaluation while 3 used accuracy. Average accuracy of the 3 studies was 85.6 (6.6) %, with a lowest accuracy of 78.16% (Segovia et al., 2015) and a highest accuracy of 90.72% (Wu et al., 2019; Figure 4A). Half of the 4 studies (50.0%) obtained the highest per-study accuracy with SVM (Segovia et al., 2015; Wu et al., 2019) and the other half (50.0%) with neural networks (Figure 4B).

CSF (n = 5)

All 5 studies used AUC, instead of accuracy, to evaluate machine learning models (Table 7). The average AUC was 0.8 (0.1), the lowest AUC was 0.6825 (Maass et al., 2020) and the highest AUC was 0.839 (Maass et al., 2018), respectively. Two studies obtained the highest per-study AUC with ensemble learning, 2 studies with SVM and 1 study with regression (Figure 4B).

Other Types of Data (n = 10)

Only 5 studies used accuracy to measure the performance of machine learning models (Table 7). An average accuracy of 91.9 (6.4) % was obtained, with a lowest accuracy of 84.85% (Shi et al., 2018) and a highest accuracy of 100% (Nuvoli et al., 2019; Figure 4A). Out of the 10 studies, 5 (50%) used SVM to achieve the per-study highest accuracy, 3 (30%) used ensemble learning, 1 (10%) used decision trees and 1 (10%) used machine learning models that do not belong to any given categories (Figure 4B).

Combination of More Than One Data Type (n = 18)

Out of the 18 studies that used more than one type of data, 15 used accuracy in model evaluation (Table 7). An average accuracy of 92.6 (6.1) % was obtained, and the lowest and highest accuracy among the 15 studies was 82.0% (Prince et al., 2019) and 100.0% (Cherubini et al., 2014b), respectively (Figure 4A). The per-study highest accuracy was achieved with ensemble learning in 6 studies (33.3%), with neural network in 5 studies (27.8%), with SVM in 4 studies (22.2%), with regression in 1 (5.6%) study and with nearest neighbor (5.6%) in 1 study. One study (5.6%) used machine learning models that do not belong to any given categories to obtain the highest per-study accuracy (Figure 4B).

Discussion

Principal Findings

In this review, we present results from published studies that applied machine learning to the diagnosis and differential diagnosis of PD. Since the number of included papers was relatively large, we focused on a high-level summary rather than a detailed description of methodology and direct comparison of outcomes of individual studies. We also provide an overview of sample size, data source and data type, for a more in-depth understanding of methodological differences across studies and their outcomes. Furthermore, we assessed (a) how large the participant pool/dataset was, (b) to what extent new data (i.e., unpublished, raw data acquired from locally recruited human participants) were collected and used, (c) the feasibility of machine learning and the possibility of introducing new biomarkers in the diagnosis of PD. Overall, methodology studies that proposed and tested novel technical approaches (e.g., machine learning and deep learning models, data acquisition devices, and feature extraction algorithms) have repetitively shown that features extracted from data modalities including voice recordings and handwritten patterns could lead to high patient-level diagnostic performance, while facilitating accessible and non-invasive data acquisition. Nevertheless, only a small number of studies further validated these technical approaches in clinical settings using local human participants recruited specifically for these studies, indicating a gap between model development and their clinical applications.

A per-study diagnostic accuracy above chance levels was achieved in all studies that used accuracy in model evaluation (Figure 4A). Apart from studies using CSF data that measured model performance with AUC, classification accuracy associated with 8 other data types ranged between 85.6% (PET) and 94.4% (SPECT), with an average of 89.9 (3.0) %. Therefore, although the small number of studies of some data types may not allow for a generalizable prediction of how well these data types can help us differentiate PD from HC or atypical Parkinsonian disorders, the application of machine learning to a variety of data types led to high accuracy in the diagnosis of PD. In addition, an accuracy significantly above chance levels was achieved in all machine learning models (Supplementary Table 1), while SVM, neural networks and ensemble learning were among the most popular model choices, all yielding great applicability to a variety of data modalities. In the meantime, when compared with other models, they led to the per-study highest classification accuracy in >50% of all cases (50.7, 51.9, and 52.3%, respectively; Supplementary Table 1). Despite the high diagnostic accuracy and performance reported, in a number of studies, data splitting strategies and the use of cross validation were not specified. For data modalities such as 3D MRI scans, when 2D slices are extracted from 3D volumes, multiple slices could be generated for one subject. Having data from the same subject across training, validation and tests sets can lead to a biased data split (Wen et al., 2020), causing data leakage and overestimation of model performance, thus compromising reproducibility of published results.

As previously discussed (Belić et al., 2019), although satisfactory diagnostic outcomes could be achieved, sample size in few studies was extremely small (<15 subjects). The application of some machine learning models, especially neural networks, typically rely on a large dataset. Nevertheless, collecting data from a large pool of participants remains challenging in clinical studies, and data generated are commonly of high dimensionality and small sample size (Vabalas et al., 2019). To address this challenge, one solution is to combine data from a local cohort with public repositories including PPMI, UCI machine learning repository, PhysioNet and many others, depending on the type of data that have been collected from the local cohort. Furthermore, when a great difference in group size is observed (i.e., class imbalance problem), labeling all samples after the majority class may lead to an undesired high accuracy. In this case, evaluating machine learning models with other metrics including precision, recall and F-1 score is recommended (Jeni et al., 2013).

Even though high diagnostic accuracy of PD has been achieved in clinical settings, machine learning approaches have also reached high accuracy as shown in the present study, while models including SVM and neural networks are particularly useful in (a) diagnosis of PD using data modalities that have been overlooked in clinical decision making (e.g., voice), and (b) identification of features of high relevance from these data. For example, the use of machine learning models with feature selection techniques allows for assessing the relative importance of features of a large feature space in order to select the most differentiating ones, which is conventionally challenging using manual approaches. For the discovery of novel markers allowing for non-invasive diagnostic options with relatively high accuracy, e.g., handwritten patterns, a small number of studies have been conducted, mostly using data from published databases. Given that these databases generally included handwritten patterns from a small number of diagnosed PD patients, sometimes under 15, it would be of great importance to validate the use of handwritten patterns in early diagnosis of PD in clinical studies of a larger scale. In the meantime, diagnosing PD using more than one data modality has led to promising results. Accordingly, supplying clinicians with non-motor data and machine learning approaches may support clinical decision making in patients with ambiguous symptom presentations, and/or improve diagnosis at an earlier stage.

An issue observed in many included studies was the insufficient or inaccurate description of methods or results, and some failed to provide accurate information of the number and type of subjects used (for example, methodology studies on early diagnosis of PD missing a table summarizing the characteristics of subjects, therefore it was challenging to understand the stage of PD in recruited patients), or how machine learning models were implemented, trained and tested. Infrequently, authors skipped basic information such as number of subjects and their medical conditions and referred to another publication. Although we attempted to list model hyperparameters and cross-validation strategies in the data extraction table, many included studies did not make this information available in the main text, leading to potential difficulties in replicating the results. Apart from these, rounding errors or inconsistent reporting of results also exist. Furthermore, although we treated the differentiation of PD from SWEDD as subtyping, there is ongoing controversy regarding whether it should be considered as differential diagnosis or subtyping (Lee et al., 2014; Erro et al., 2016; Chou, 2017; Kwon et al., 2018). Given these limitations, clinicians interested in adapting machine learning models or implementing diagnostic systems based on novel biomarkers are advised to interpret published results with care. Further, in this context we would like to stress the need for uniform reporting standards in studies using machine learning.

In both machine learning research and clinical settings, appropriately interpreting published results and methodologies is a necessary step toward an understanding of state-of-the-art methods. Therefore, vagueness in reporting not only compromises the interpretation of results but makes further methodological developments based on published research unnecessarily challenging. Moreover, for medical doctors interested in learning how machine learning methods could be applied in their domains, insufficient description of methods may lead to incorrect model implementation and failure of replication.

To enable efficient replication of published results, detailed descriptions of (a) model and architecture (hyperparameters, number and type of layers, layer-specific parameter settings, regularization strategies, activation functions), (b) implementation (programming language, machine learning and deep learning libraries used, model training and testing, metrics and model evaluation, validation strategy, optimization), and (c) version numbers of software/libraries used for both preprocessing and model implementation, are often desirable, as newer software versions may lead to differences in pre-processing and model implementation stages (Chepkoech et al., 2016).

Due to the use of imbalanced datasets in medical sciences, reporting model performance with a confusion matrix may give rise to a more comprehensive understanding of the model's ability to discriminate between PD and healthy controls. In the meantime, due to costs associated with acquisition of patient data, researchers often need to expand data collected from a local cohort using data sourced from publicly available databases or published studies. Nevertheless, unclear description of data acquisition and pre-processing protocols in some published studies may lead to challenges in the integration of newly acquired data and previously published data. Taken together, to facilitate early, refined diagnosis of PD and efficient application of novel machine learning approaches in a clinical setting, and to allow for improved reproducibility of studies on machine learning-based diagnosis and assessment of PD, a higher transparency in reporting data collection, pre-processing protocols, model implementation, and study outcomes is required.

Limitations

In the present study, we have excluded research articles in languages other than English and results published in the form of conference abstracts, posters, and talks. Despite the ongoing discussion of advantages and importance of including conference abstracts in systematic reviews and reviews (Scherer and Saldanha, 2019), conference abstracts often do not report sufficient key information which is why we had to exclude them. However, this may lead to a publication and result bias. In addition, since the aim of the present review is to assess and summarize published studies on the detection and early diagnosis of PD, we noticed that few large-scale, multi-centric studies on subtyping or/and severity assessment of PD were therefore excluded. Given the current challenges in subtyping, severity assessment and prognosis of PD, a further step toward a more systematic understanding of the application of machine learning to neurodegenerative diseases would be to review these studies.

Moreover, due to the high inter-study variance in the data source and presentation of results, it was challenging to directly compare outcomes associated with each type of model across studies, as some studies failed to indicate whether model performance was evaluated using a test set, and/or results given by models that did not yield the best per-study performance. Results of published studies were discussed and summarized based on data and machine learning models used, and for data modalities such as PET (n = 4) or CSF (n = 5), the number of studies were too small despite the high total number of studies included. Therefore, it was improbable to assess the general performance of machine learning techniques when PET or CSF data are used.

Conclusions

To the best of our knowledge, the present study is the first review which included results from all studies that applied machine learning methods to the diagnosis of PD. Here, we presented included studies in a high-level summary, providing access to information including (a) machine learning methods that have been used in the diagnosis of PD and associated outcomes, (b) types of clinical, behavioral and biometric data that could be used for rendering more accurate diagnoses, (c) potential biomarkers for assisting clinical decision making, and (d) other highly relevant information, including databases that could be used to enlarge and enrich smaller datasets. In summary, realization of machine learning-assisted diagnosis of PD yields high potential for a more systematic clinical decision-making system, while adaptation of novel biomarkers may give rise to easier access to PD diagnosis at an earlier stage. Machine learning approaches therefore have the potential to provide clinicians with additional tools to screen, detect or diagnose PD.

Data Availability Statement

The original contributions generated for the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

JM conceived and designed the study, collected the data, performed the analysis, and wrote the paper. CD and JF supervised the research. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Dr. Antje Haehner for her comments on the manuscript. This work was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) and Québec Bio-Imaging Network.

Footnotes

Funding. JM was supported by the Québec Bio-Imaging Network Postdoctoral Fellowship (FRSQ—Réseaux de recherche thématiques; Dossier: 35450). JF was supported by FRQS (#283144), Parkinson Québec, Parkinson Canada (PPG-2020-0000000061), and CIHR (#PJT173514).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnagi.2021.633752/full#supplementary-material

Click here for additional data file.^{(997.8KB, docx)}

References

Abiyev R. H., Abizade S. (2016). Diagnosing Parkinson's diseases using fuzzy neural system. Comput. Mathe. Methods Med. 2016:1267919. 10.1155/2016/1267919 [DOI] [PMC free article] [PubMed] [Google Scholar]
Abos A., Baggio H. C., Segura B., Campabadal A., Uribe C., Giraldo D. M., et al. (2019). Differentiation of multiple system atrophy from Parkinson's disease by structural connectivity derived from probabilistic tractography. Sci. Rep. 9:16488. 10.1038/s41598-019-52829-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
Abujrida H., Agu E., Pahlavan K. (2017). Smartphone-based gait assessment to infer Parkinson's disease severity using crowdsourced data, in 2017 IEEE Healthcare Innovations and Point of Care Technologies (HI-POCT) (Bethesda, MD: ), 208–211. 10.1109/HIC.2017.8227621 [DOI] [Google Scholar]
Adams W. R. (2017). High-accuracy detection of early Parkinson's Disease using multiple characteristics of finger movement while typing. PLoS ONE 12:e0188226. 10.1371/journal.pone.0188226 [DOI] [PMC free article] [PubMed] [Google Scholar]
Adeli E., Shi F., An L., Wee C.-Y., Wu G., Wang T., et al. (2016). Joint feature-sample selection and robust diagnosis of Parkinson's disease from MRI data. NeuroImage 141, 206–219. 10.1016/j.neuroimage.2016.05.054 [DOI] [PMC free article] [PubMed] [Google Scholar]
Adeli E., Thung K.-H., An L., Wu G., Shi F., Wang T., et al. (2019). Semi-supervised discriminative classification robust to sample-outliers and feature-noises. IEEE Trans. Pattern Anal. Mach. Intell. 41, 515–522. 10.1109/TPAMI.2018.2794470 [DOI] [PMC free article] [PubMed] [Google Scholar]
Agarwal A., Chandrayan S., Sahu S. S. (2016). Prediction of Parkinson's disease using speech signal with Extreme Learning Machine, in 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT) (Chennai: ), 3776–3779. 10.1109/ICEEOT.2016.7755419 [DOI] [Google Scholar]
Ahlrichs C., Lawo M. (2013). Parkinson's disease motor symptoms in machine learning: a review. arXiv preprint arXiv:1312.3825. 10.5121/hiij.2013.2401 [DOI] [Google Scholar]
Ahmadi S. A., Vivar G., Frei J., Nowoshilow S., Bardins S., Brandt T., et al. (2019). Towards computerized diagnosis of neurological stance disorders: data mining and machine learning of posturography and sway. J. Neurol. 266(Suppl 1), 108–117. 10.1007/s00415-019-09458-y [DOI] [PubMed] [Google Scholar]
Aich S., Kim H., younga K., Hui K. L., Al-Absi A. A., Sain M. (2019). A supervised machine learning approach using different feature selection techniques on voice datasets for prediction of Parkinson's disease, in 2019 21st International Conference on Advanced Communication Technology (ICACT) (PyeongChang: ), 1116–1121. 10.23919/ICACT.2019.8701961 [DOI] [Google Scholar]
Alam M. N., Garg A., Munia T. T. K., Fazel-Rezai R., Tavakolian K. (2017). Vertical ground reaction force marker for Parkinson's disease. PLoS ONE 12:e0175951. 10.1371/journal.pone.0175951 [DOI] [PMC free article] [PubMed] [Google Scholar]
Alaskar H., Hussain A. (2018). Prediction of Parkinson disease using gait signals, in 2018 11th International Conference on Developments in eSystems Engineering (DeSE) (Cambridge: ), 23–26. 10.1109/DeSE.2018.00011 [DOI] [Google Scholar]
Al-Fatlawi A. H., Jabardi M. H., Ling S. H. (2016). Efficient diagnosis system for Parkinson's disease using deep belief network, in 2016 IEEE Congress on Evolutionary Computation (CEC) (Vancouver, BC: ), 1324–1330. 10.1109/CEC.2016.7743941 [DOI] [Google Scholar]
Alharthi A. S., Ozanyan K. B. (2019). Deep learning for ground reaction force data analysis: application to wide-area floor sensing, in 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE) (Vancouver, BC: )„ 1401–1406. 10.1109/ISIE.2019.8781511 [DOI] [Google Scholar]
Ali L., Khan S. U., Arshad M., Ali S., Anwar M. (2019a). A multi-model framework for evaluating type of speech samples having complementary information about Parkinson's disease, in 2019 International Conference on Electrical, Communication, and Computer Engineering (ICECCE) (Swat: ), 1–5. 10.1109/ICECCE47252.2019.8940696 [DOI] [Google Scholar]
Ali L., Zhu C., Golilarz N. A., Javeed A., Zhou M., Liu Y. (2019b). Reliable Parkinson's disease detection by analyzing handwritten drawings: construction of an unbiased cascaded learning system based on feature selection and adaptive boosting model. IEEE Access 7, 116480–116489. 10.1109/ACCESS.2019.2932037 [DOI] [Google Scholar]
Ali L., Zhu C., Zhang Z., Liu Y. (2019c). Automated detection of Parkinson's disease based on multiple types of sustained phonations using linear discriminant analysis and genetically optimized neural network. IEEE J. Transl. Eng. Health Med. 7, 1–10. 10.1109/JTEHM.2019.2940900 [DOI] [PMC free article] [PubMed] [Google Scholar]
Alqahtani E. J., Alshamrani F. H., Syed H. F., Olatunji S. O. (2018). Classification of Parkinson's disease using NNge classification algorithm, in 2018 21st Saudi Computer Society National Computer Conference (NCC) (Riyadh: ), 1–7. 10.1109/NCG.2018.8592989 [DOI] [Google Scholar]
Amoroso N., La Rocca M., Monaco A., Bellotti R., Tangaro S. (2018). Complex networks reveal early MRI markers of Parkinson's disease. Med. Image Anal. 48, 12–24. 10.1016/j.media.2018.05.004 [DOI] [PubMed] [Google Scholar]
Anand A., Haque M. A., Alex J. S. R., Venkatesan N. (2018). Evaluation of machine learning and deep learning algorithms combined with dimentionality reduction techniques for classification of Parkinson's disease, in 2018 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT) (Louisville, KY: ), 342–347. 10.1109/ISSPIT.2018.8642776 [DOI] [Google Scholar]
Andrei A., Tău?an A., Ionescu B. (2019). Parkinson's disease detection from gait patterns, in 2019 E-Health and Bioengineering Conference (EHB) (Iasi: ), 1–4. 10.1109/EHB47216.2019.8969942 [DOI] [Google Scholar]
Baby M. S., Saji A. J., Kumar C. S. (2017). Parkinsons disease classification using wavelet transform based feature extraction of gait data, in 2017 International Conference on Circuit, Power and Computing Technologies (ICCPCT) (Kollam: ), 1–6. 10.1109/ICCPCT.2017.8074230 [DOI] [Google Scholar]
Baggio H. C., Abos A., Segura B., Campabadal A., Uribe C., Giraldo D. M., et al. (2019). Cerebellar resting-state functional connectivity in Parkinson's disease and multiple system atrophy: characterization of abnormalities and potential for differential diagnosis at the single-patient level. NeuroImage. Clin. 22:101720. 10.1016/j.nicl.2019.101720 [DOI] [PMC free article] [PubMed] [Google Scholar]
Bakar Z. A., Ispawi D. I., Ibrahim N. F., Tahir N. M. (2012). Classification of Parkinson's disease based on Multilayer Perceptrons (MLPs) neural network and ANOVA as a feature extraction, in 2012 IEEE 8th International Colloquium on Signal Processing and its Applications) (Malacca: ), 63–67. 10.1109/CSPA.2012.6194692 [DOI] [Google Scholar]
Banerjee M., Chakraborty R., Archer D., Vaillancourt D., Vemuri B. C. (2019). DMR-CNN: a CNN tailored For DMR scans with applications to PD classification, in 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019) (Venice: ), 388–391. 10.1109/ISBI.2019.8759558 [DOI] [Google Scholar]
Belić M., Bobić V., BadŽa M., Šolaja N., Ã?urić-Jovičić M., Kostić V. S. (2019). Artificial intelligence for assisting diagnostics and assessment of Parkinson's disease–a review. Clin. Neurol. Neurosurg. 184:105442. 10.1016/j.clineuro.2019.105442 [DOI] [PubMed] [Google Scholar]
Benba A., Jilbab A., Hammouch A. (2016a). Discriminating between patients with Parkinson's and neurological diseases using cepstral analysis. IEEE Trans. Neural Syst. Rehab. Eng. 24, 1100–1108. 10.1109/TNSRE.2016.2533582 [DOI] [PubMed] [Google Scholar]
Benba A., Jilbab A., Hammouch A., Sandabad S. (2016b). Using RASTA-PLP for discriminating between different neurological diseases, in 2016 International Conference on Electrical and Information Technologies (ICEIT) (Tangiers: ), 406–409. 10.1109/EITech.2016.7519630 [DOI] [Google Scholar]
Bernad-Elazari H., Herman T., Mirelman A., Gazit E., Giladi N., Hausdorff J. M. (2016). Objective characterization of daily living transitions in patients with Parkinson's disease using a single body-fixed sensor. J. Neurol. 263, 1544–1551. 10.1007/s00415-016-8164-6 [DOI] [PubMed] [Google Scholar]
Bhati S., Velazquez L. M., Villalba J., Dehak N. (2019). LSTM siamese network for Parkinson's disease detection from speech, in 2019 IEEE Global Conference on Signal and Information Processing (GlobalSIP) (Ottawa, ON: ), 1–5. 10.1109/GlobalSIP45357.2019.8969430 [DOI] [Google Scholar]
Bot B. M., Suver C., Neto E. C., Kellen M., Klein A., Bare C., et al. (2016). The mPower study, Parkinson disease mobile data collected using ResearchKit. Sci. Data 3, 1–9. 10.1038/sdata.2016.11 [DOI] [PMC free article] [PubMed] [Google Scholar]
Braak H., Del Tredici K., Rüb U., De Vos R. A., Steur E. N. J., Braak E. (2003). Staging of brain pathology related to sporadic Parkinson's disease. Neurobiol. Aging 24, 197–211. 10.1016/S0197-4580(02)00065-9 [DOI] [PubMed] [Google Scholar]
Buongiorno D., Bortone I., Cascarano G. D., Trotta G. F., Brunetti A., Bevilacqua V. (2019). A low-cost vision system based on the analysis of motor features for recognition and severity rating of Parkinson's Disease. BMC Med. Inform. Decision Making 19(Suppl 9):243. 10.1186/s12911-019-0987-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
Butt A. H., Rovini E., Dolciotti C., Bongioanni P., De Petris G., Cavallo F. (2017). Leap motion evaluation for assessment of upper limb motor skills in Parkinson's disease. IEEE Int. Conf. Rehabil. Robot. 2017, 116–121. 10.1109/ICORR.2017.8009232 [DOI] [PubMed] [Google Scholar]
Butt A. H., Rovini E., Dolciotti C., De Petris G., Bongioanni P., Carboncini M. C., et al. (2018). Objective and automatic classification of Parkinson disease with Leap Motion controller. Biomed. Eng. Online 17:168. 10.1186/s12938-018-0600-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
Cai Z., Gu J., Wen C., Zhao D., Huang C., Huang H., et al. (2018). An intelligent Parkinson's disease diagnostic system based on a chaotic bacterial foraging optimization enhanced fuzzy KNN approach. Comp. Math. Methods Med. 2018:2396952. 10.1155/2018/2396952 [DOI] [PMC free article] [PubMed] [Google Scholar]
Caramia C., Torricelli D., Schmid M., Munoz-Gonzalez A., Gonzalez-Vargas J., Grandas F., et al. (2018). IMU-based classification of Parkinson's disease from gait: a sensitivity analysis on sensor location and feature selection. IEEE J. Biomed. Health Inf. 22, 1765–1774. 10.1109/JBHI.2018.2865218 [DOI] [PubMed] [Google Scholar]
Castillo-Barnes D., Ramírez J., Segovia F., Martínez-Murcia F. J., Salas-Gonzalez D., Górriz J. M. (2018). Robust ensemble classification methodology for I123-Ioflupane SPECT images and multiple heterogeneous biomarkers in the diagnosis of Parkinson's disease. Front. Neuroinf. 12:53. 10.3389/fninf.2018.00053 [DOI] [PMC free article] [PubMed] [Google Scholar]
Cavallo F., Moschetti A., Esposito D., Maremmani C., Rovini E. (2019). Upper limb motor pre-clinical assessment in Parkinson's disease using machine learning. Parkinsonism Relat. Disord. 63, 111–116. 10.1016/j.parkreldis.2019.02.028 [DOI] [PubMed] [Google Scholar]
Celik E., Omurca S. I. (2019). Improving Parkinson's disease diagnosis with machine learning methods, in 2019 Scientific Meeting on Electrical-Electronics & Biomedical Engineering and Computer Science (EBBT) (Istanbul: ), 1–4. 10.1109/EBBT.2019.8742057 [DOI] [Google Scholar]
Chakraborty S., Aich S., Kim H.-C. (2020). 3D textural, morphological and statistical analysis of voxel of interests in 3T MRI scans for the detection of Parkinson's disease using artificial neural networks. Healthcare 8:E34. 10.3390/healthcare8010034 [DOI] [PMC free article] [PubMed] [Google Scholar]
Challa K. N. R., Pagolu V. S., Panda G., Majhi B. (2016). An improved approach for prediction of Parkinson's disease using machine learning techniques, in 2016 International Conference on Signal Processing, Communication, Power and Embedded System (SCOPES) (Paralakhemundi: ), 1446–1451. 10.1109/SCOPES.2016.7955679 [DOI] [Google Scholar]
Chen Y., Storrs J., Tan L., Mazlack L. J., Lee J.-H., Lu L. J. (2014). Detecting brain structural changes as biomarker from magnetic resonance images using a local feature based SVM approach. J. Neurosci. Methods 221, 22–31. 10.1016/j.jneumeth.2013.09.001 [DOI] [PubMed] [Google Scholar]
Chen Y., Yang W., Long J., Zhang Y., Feng J., Li Y., et al. (2015). Discriminative analysis of Parkinson's disease based on whole-brain functional connectivity. PLoS ONE 10:e0124153. 10.1371/journal.pone.0124153 [DOI] [PMC free article] [PubMed] [Google Scholar]
Chepkoech J. L., Walhovd K. B., Grydeland H., Fjell A. M., Alzheimer's Disease Neuroimaging Initiative (2016). Effects of change in FreeSurfer version on classification accuracy of patients with Alzheimer's disease and mild cognitive impairment. Hum. Brain Mapp. 37, 1831–1841. 10.1002/hbm.23139 [DOI] [PMC free article] [PubMed] [Google Scholar]
Cherubini A., Morelli M., Nisticó R., Salsone M., Arabia G., Vasta R., et al. (2014a). Magnetic resonance support vector machine discriminates between Parkinson disease and progressive supranuclear palsy. Move. Disord. 29, 266–269. 10.1002/mds.25737 [DOI] [PubMed] [Google Scholar]
Cherubini A., Nisticó R., Novellino F., Salsone M., Nigro S., Donzuso G., et al. (2014b). Magnetic resonance support vector machine discriminates essential tremor with rest tremor from tremor-dominant Parkinson disease. Move. Disord. 29, 1216–1219. 10.1002/mds.25869 [DOI] [PubMed] [Google Scholar]
Choi H., Ha S., Im H. J., Paek S. H., Lee D. S. (2017). Refining diagnosis of Parkinson's disease with deep learning-based interpretation of dopamine transporter imaging. NeuroImage Clin. 16, 586–594. 10.1016/j.nicl.2017.09.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
Chou K. L. (2017). Diagnosis and Differential Diagnosis of Parkinson Disease. Waltham, MA: UpToDate. [Google Scholar]
Cibulka M., Brodnanova M., Grendar M., Grofik M., Kurca E., Pilchova I., et al. (2019). SNPs rs11240569, rs708727, and rs823156 in SLC41A1 do not discriminate between slovak patients with idiopathic parkinson's disease and healthy controls: statistics and machine-learning evidence. Int. J. Mol. Sci. 20:4688. 10.3390/ijms20194688 [DOI] [PMC free article] [PubMed] [Google Scholar]
Cigdem O., Demirel H., Unay D. (2019). The performance of local-learning based clustering feature selection method on the diagnosis of Parkinson's disease using structural MRI, in 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC) (Bari: ), 1286–1291. 10.1109/SMC.2019.8914611 [DOI] [Google Scholar]
Çimen S., Bolat B. (2016). Diagnosis of Parkinson's disease by using ANN, in 2016 International Conference on Global Trends in Signal Processing, Information Computing and Communication (ICGTSPICC) (Jalgaon: ), 119–121. 10.1109/ICGTSPICC.2016.7955281 [DOI] [Google Scholar]
Contreras-Vidal J., Stelmach G. E. (1995). Effects of Parkinsonism on motor control. Life Sci. 58, 165–176. 10.1016/0024-3205(95)02237-6 [DOI] [PubMed] [Google Scholar]
Cook D. J., Schmitter-Edgecombe M., Dawadi P. (2015). Analyzing activity behavior and movement in a naturalistic environment using smart home techniques. IEEE J. Biomed. Health Inf. 19, 1882–1892. 10.1109/JBHI.2015.2461659 [DOI] [PMC free article] [PubMed] [Google Scholar]
Cuzzolin F., Sapienza M., Esser P., Saha S., Franssen M. M., Collett J., et al. (2017). Metric learning for Parkinsonian identification from IMU gait measurements. Gait Posture 54, 127–132. 10.1016/j.gaitpost.2017.02.012 [DOI] [PubMed] [Google Scholar]
Dash S., Thulasiram R., Thulasiraman P. (2017). An enhanced chaos-based firefly model for Parkinson's disease diagnosis and classification, in 2017 International Conference on Information Technology (ICIT) (Bhubaneswar: ), 159–164. 10.1109/ICIT.2017.43 [DOI] [Google Scholar]
Dastjerd N. K., Sert O. C., Ozyer T., Alhajj R. (2019). Fuzzy classification methods based diagnosis of Parkinson's disease from speech test cases. Curr. Aging Sci. 12, 100–120. 10.2174/1874609812666190625140311 [DOI] [PubMed] [Google Scholar]
de Souza J. W. M., Alves S. S. A., Rebouças E. d,.S, Almeida J. S., Rebouças Filho P.P. (2018). A new approach to diagnose Parkinson's disease using a structural cooccurrence matrix for a similarity analysis. Comput. Intell. Neurosci. 2018:7613282. 10.1155/2018/7613282 [DOI] [PMC free article] [PubMed] [Google Scholar]
Dhami D. S., Soni A., Page D., Natarajan S. (2017). Identifying Parkinson's patients: a functional gradient boosting approach. Artif. Intell. Med. Conf. Artif. Intell. Med. 10259, 332–337. 10.1007/978-3-319-59758-4_39 [DOI] [PMC free article] [PubMed] [Google Scholar]
Dinesh A., He J. (2017). Using machine learning to diagnose Parkinson's disease from voice recordings, in 2017 IEEE MIT Undergraduate Research Technology Conference (URTC) (Cambridge, MA: ), 1–4. 10.1109/URTC.2017.8284216 [DOI] [Google Scholar]
Dinov I. D., Heavner B., Tang M., Glusman G., Chard K., Darcy M., et al. (2016). Predictive big data analytics: a study of parkinson's disease using large, complex, heterogeneous, incongruent, multi-source and incomplete observations. PLoS ONE 11:e0157077. 10.1371/journal.pone.0157077 [DOI] [PMC free article] [PubMed] [Google Scholar]
Djurić-Jovičić M., Belić M., Stanković I., Radovanović S., Kostić V. S. (2017). Selection of gait parameters for differential diagnostics of patients with de novo Parkinson's disease. Neurol. Res. 39, 853–861. 10.1080/01616412.2017.1348690 [DOI] [PubMed] [Google Scholar]
Dorsey E. R., Elbaz A., Nichols E., Abd-Allah F., Abdelalim A., Adsuar J. C., et al. (2018). Global, regional, and national burden of Parkinson's disease, 1990–2016: a systematic analysis for the Global Burden of Disease Study 2016. Lancet Neurol. 17, 939–953. 10.1016/S1474-4422(18)30295-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
Dos Santos M. C. T., Scheller D., Schulte C., Mesa I. R., Colman P., Bujac S. R., et al. (2018). Evaluation of cerebrospinal fluid proteins as potential biomarkers for early stage Parkinson's disease diagnosis. PLoS ONE 13:e0206536. 10.1371/journal.pone.0206536 [DOI] [PMC free article] [PubMed] [Google Scholar]
Dror B., Yanai E., Frid A., Peleg N., Goldenthal N., Schlesinger I., et al. (2014). Automatic assessment of Parkinson's disease from natural hands movements using 3D depth sensor, in 2014 IEEE 28th Convention of Electrical & Electronics Engineers in Israel (IEEEI) (Eilat: ), 1–5. 10.1109/EEEI.2014.7005763 [DOI] [Google Scholar]
Drotár P., Mekyska J., Rektorová I., Masarová L., Smékal Z., Faundez-Zanuy M. (2014). Analysis of in-air movement in handwriting: a novel marker for Parkinson's disease. Comp. Methods Progr. Biomed. 117, 405–411. 10.1016/j.cmpb.2014.08.007 [DOI] [PubMed] [Google Scholar]
Drotár P., Mekyska J., Rektorová I., Masarová L., Smékal Z., Faundez-Zanuy M. (2015). Decision support framework for Parkinson's disease based on novel handwriting markers. IEEE Trans. Neural Syst. Rehabil. Eng. 23, 508–516. 10.1109/TNSRE.2014.2359997 [DOI] [PubMed] [Google Scholar]
Drotár P., Mekyska J., Rektorová I., Masarová L., Smékal Z., Faundez-Zanuy M. (2016). Evaluation of handwriting kinematics and pressure for differential diagnosis of Parkinson's disease. Artif. Intell. Med. 67, 39–46. 10.1016/j.artmed.2016.01.004 [DOI] [PubMed] [Google Scholar]
Du G., Lewis M. M., Kanekar S., Sterling N. W., He L., Kong L., et al. (2017). Combined Diffusion tensor imaging and apparent transverse relaxation rate differentiate Parkinson disease and atypical Parkinsonism. Am. J. Neuroradiol. 38, 966–972. 10.3174/ajnr.A5136 [DOI] [PMC free article] [PubMed] [Google Scholar]
Dua D., Graff C. (2018). UCI Machine Learning Repository. Irvine, CA: University of California, School of Information and Computer Science. [Google Scholar]
Erdogdu Sakar B., Serbes G., Sakar C. O. (2017). Analyzing the effectiveness of vocal features in early telediagnosis of Parkinson's disease. PLoS ONE 12:e0182428. 10.1371/journal.pone.0182428 [DOI] [PMC free article] [PubMed] [Google Scholar]
Erro R., Schneider S. A., Stamelou M., Quinn N. P., Bhatia K. P. (2016). What do patients with scans without evidence of dopaminergic deficit (SWEDD) have? New evidence and continuing controversies. J. Neurol. Neurosurg. Psychiatry 87, 319–323. 10.1136/jnnp-2014-310256 [DOI] [PubMed] [Google Scholar]
Félix J. P., Vieira F. H. T., Cardoso Á. A., Ferreira M. V. G., Franco R. A. P., Ribeiro M. A., et al. (2019). A Parkinson's disease classification method: an approach using gait dynamics and detrended fluctuation analysis, in 2019 IEEE Canadian Conference of Electrical and Computer Engineering (CCECE) (Edmonton, AB: ), 1–4. 10.1109/CCECE.2019.8861759 [DOI] [Google Scholar]
Fernandes C., Fonseca L., Ferreira F., Gago M., Costa L., Sousa N., et al. (2018). Artificial neural networks classification of patients with Parkinsonism based on gait, in 2018 IEEE International Conference on Bioinformatics and Biomedicine (BIBM) (Madrid: ), 2024–2030. 10.1109/BIBM.2018.8621466 [DOI] [Google Scholar]
Fernandez K. M., Roemmich R. T., Stegemöller E. L., Amano S., Thompson A., Okun M. S., et al. (2013). Gait initiation impairments in both Essential Tremor and Parkinson's disease. Gait Posture 38, 956–961. 10.1016/j.gaitpost.2013.05.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
Focke N. K., Helms G., Scheewe S., Pantel P. M., Bachmann C. G., Dechent P., et al. (2011). Individual voxel-based subtype prediction can differentiate progressive supranuclear palsy from idiopathic Parkinson syndrome and healthy controls. Human Brain Mapp. 32, 1905–1915. 10.1002/hbm.21161 [DOI] [PMC free article] [PubMed] [Google Scholar]
Frid A., Safra E. J., Hazan H., Lokey L. L., Hilu D., Manevitz L., et al. (2014). Computational diagnosis of Parkinson's disease directly from natural speech using machine learning techniques, in 2014 IEEE International Conference on Software Science, Technology and Engineering (Ramat Gan: ), 50–53. 10.1109/SWSTE.2014.17 [DOI] [Google Scholar]
Ghassemi N. H., Marxreiter F., Pasluosta C. F., Kugler P., Schlachetzki J., Schramm A., et al. (2016). Combined accelerometer and EMG analysis to differentiate essential tremor from Parkinson's disease. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2016, 672–675. 10.1109/EMBC.2016.7590791 [DOI] [PubMed] [Google Scholar]
Glaab E., Trezzi J.-P., Greuel A., Jäger C., Hodak Z., Drzezga A., et al. (2019). Integrative analysis of blood metabolomics and PET brain neuroimaging data for Parkinson's disease. Neurobiol. Dis. 124, 555–562. 10.1016/j.nbd.2019.01.003 [DOI] [PubMed] [Google Scholar]
Goldberger A. L., Amaral L. A., Glass L., Hausdorff J. M., Ivanov P. C., Mark R. G., et al. (2000). PhysioBank, PhysioToolkit, and PhysioNet: components of a new research resource for complex physiologic signals. Circulation 101, e215–e220. 10.1161/01.CIR.101.23.e215 [DOI] [PubMed] [Google Scholar]
Gunduz H. (2019). Deep learning-based parkinson's disease classification using vocal feature sets. IEEE Access 7, 115540–115551. 10.1109/ACCESS.2019.2936564 [DOI] [Google Scholar]
Haller S., Badoud S., Nguyen D., Barnaure I., Montandon M. L., Lovblad K. O., et al. (2013). Differentiation between Parkinson disease and other forms of Parkinsonism using support vector machine analysis of susceptibility-weighted imaging (SWI): initial results. Eur. Radiol. 23, 12–19. 10.1007/s00330-012-2579-y [DOI] [PubMed] [Google Scholar]
Haller S., Badoud S., Nguyen D., Garibotto V., Lovblad K. O., Burkhard P. R. (2012). Individual detection of patients with Parkinson disease using support vector machine analysis of diffusion tensor imaging data: initial results. Am. J. Neuroradiol. 33, 2123–2128. 10.3174/ajnr.A3126 [DOI] [PMC free article] [PubMed] [Google Scholar]
Haq A. U., Li J., Memon M. H., Khan J., Din S. U., Ahad I., et al. (2018). Comparative analysis of the classification performance of machine learning classifiers and deep neural network classifier for prediction of Parkinson disease, in 2018 15th International Computer Conference on Wavelet Active Media Technology and Information Processing (ICCWAMTIP) (Chengdu: ), 101–106. [Google Scholar]
Haq A. U., Li J. P., Memon M. H., khan J., Malik A., Ahmad T., et al. (2019). Feature selection based on L1-Norm support vector machine and effective recognition system for Parkinson's disease using voice recordings. IEEE Access 7, 37718–37734. 10.1109/ACCESS.2019.2906350 [DOI] [Google Scholar]
Hariharan M., Polat K., Sindhu R. (2014). A new hybrid intelligent system for accurate detection of Parkinson's disease. Comput. Methods Programs Biomed. 113, 904–913. 10.1016/j.cmpb.2014.01.004 [DOI] [PubMed] [Google Scholar]
Hirschauer T. J., Adeli H., Buford J. A. (2015). Computer-aided diagnosis of Parkinson's disease using enhanced probabilistic neural network. J. Med. Syst. 39:179. 10.1007/s10916-015-0353-9 [DOI] [PubMed] [Google Scholar]
Hsu S.-Y., Lin H.-C., Chen T.-B., Du W.-C., Hsu Y.-H., Wu Y.-C., et al. (2019). Feasible classified models for Parkinson disease from (99m)Tc-TRODAT-1 SPECT imaging. Sensors 19:1740. 10.3390/s19071740 [DOI] [PMC free article] [PubMed] [Google Scholar]
Huertas-Fernández I., García-Gómez F. J., García-Solís D., Benítez-Rivero S., Marín-Oyaga V. A., Jesús S., et al. (2015). Machine learning models for the differential diagnosis of vascular parkinsonism and Parkinson's disease using [(123)I]FP-CIT SPECT. Eur. J. Nucl. Med. Mol. Imag. 42, 112–119. 10.1007/s00259-014-2882-8 [DOI] [PubMed] [Google Scholar]
Huppertz H.-J., Möller L., Südmeyer M., Hilker R., Hattingen E., Egger K., et al. (2016). Differentiation of neurodegenerative parkinsonian syndromes by volumetric magnetic resonance imaging analysis and support vector machine classification. Mov. Disord. 31, 1506–1517. 10.1002/mds.26715 [DOI] [PubMed] [Google Scholar]
I K., Ulukaya S., Erdem O. (2019). Classification of Parkinson's disease using dynamic time warping, in 2019 27th Telecommunications Forum (TELFOR) (Belgrade: ), 1–4 [Google Scholar]
Illan I. A., Gorrz J. M., Ramirez J., Segovia F., Jimenez-Hoyuela J. M., Ortega Lozano S. J. (2012). Automatic assistance to Parkinson's disease diagnosis in DaTSCAN SPECT imaging. Med. Phys. 39, 5971–5980. 10.1118/1.4742055 [DOI] [PubMed] [Google Scholar]
Islam M. S., Parvez I., Hai D., Goswami P. (2014). Performance comparison of heterogeneous classifiers for detection of Parkinson's disease using voice disorder (dysphonia), in 2014 International Conference on Informatics, Electronics & Vision (ICIEV) (Dhaka: ), 1–7. 10.1109/ICIEV.2014.6850849 [DOI] [Google Scholar]
Jankovic J. (2008). Parkinson's disease: clinical features and diagnosis. J. Neurol. Neurosurg. Psychiatry 79, 368–376. 10.1136/jnnp.2007.131045 [DOI] [PubMed] [Google Scholar]
Javed F., Thomas I., Memedi M. (2018). A comparison of feature selection methods when using motion sensors data: a case study in Parkinson's disease. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2018, 5426–5429. 10.1109/EMBC.2018.8513683 [DOI] [PubMed] [Google Scholar]
Jeni L. A., Cohn J. F., De La Torre F. (2013). Facing imbalanced data–recommendations for the use of performance metrics, in 2013 Humaine Association Conference on Affective Computing and Intelligent Interaction (Geneva: IEEE; ), 245–251. 10.1109/ACII.2013.47 [DOI] [PMC free article] [PubMed] [Google Scholar]
Ji W., Li Y. (2012). Energy-based feature ranking for assessing the dysphonia measurements in Parkinson detection. IET Signal Proc. 6, 300–305. 10.1049/iet-spr.2011.0186 [DOI] [Google Scholar]
Johnson S. J., Diener M. D., Kaltenboeck A., Birnbaum H. G., Siderowf A. D. (2013). An economic model of P arkinson's disease: implications for slowing progression in the United States. Move. Disord. 28, 319–326. 10.1002/mds.25328 [DOI] [PubMed] [Google Scholar]
Joshi D., Khajuria A., Joshi P. (2017). An automatic non-invasive method for Parkinson's disease classification. Comput. Methods Programs Biomed. 145, 135–145. 10.1016/j.cmpb.2017.04.007 [DOI] [PubMed] [Google Scholar]
Junior S. B., Costa V. G. T., Chen S., Guido R. C. (2018). U-healthcare system for pre-diagnosis of Parkinson's disease from voice signal, in 2018 IEEE International Symposium on Multimedia (ISM) (Taichung: ), 271–274. [Google Scholar]
Kamagata K., Zalesky A., Hatano T., Di Biase M. A., El Samad O., Saiki S., et al. (2017). Connectome analysis with diffusion MRI in idiopathic Parkinson's disease: evaluation using multi-shell, multi-tissue, constrained spherical deconvolution. NeuroImage. Clin. 17, 518–529. 10.1016/j.nicl.2017.11.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
Karapinar Senturk Z. (2020). Early diagnosis of Parkinson's disease using machine learning algorithms. Med. Hypoth. 138:109603. 10.1016/j.mehy.2020.109603 [DOI] [PubMed] [Google Scholar]
Kazeminejad A., Golbabaei S., Soltanian-Zadeh H. (2017). Graph theoretical metrics and machine learning for diagnosis of Parkinson's disease using rs-fMRI, in 2017 Artificial Intelligence and Signal Processing Conference (AISP) (Shiraz: ), 134–139. 10.1109/AISP.2017.8324124 [DOI] [Google Scholar]
Khan M. M., Mendes A., Chalup S. K. (2018). Evolutionary Wavelet Neural Network ensembles for breast cancer and Parkinson's disease prediction. PLoS ONE 13:e0192192. 10.1371/journal.pone.0192192 [DOI] [PMC free article] [PubMed] [Google Scholar]
Khatamino P., I C., Özyilmaz L. (2018). A deep learning-CNN based system for medical diagnosis: an application on Parkinson's disease handwriting drawings, in 2018 6th International Conference on Control Engineering & Information Technology (CEIT) (Istanbul: ), 1–6. 10.1109/CEIT.2018.8751879 [DOI] [Google Scholar]
Khoury N., Attal F., Amirat Y., Oukhellou L., Mohammed S. (2019). Data-driven based approach to aid Parkinson's disease diagnosis. Sensors 19:242. 10.3390/s19020242 [DOI] [PMC free article] [PubMed] [Google Scholar]
Kiryu S., Yasaka K., Akai H., Nakata Y., Sugomori Y., Hara S., et al. (2019). Deep learning to differentiate parkinsonian disorders separately using single midsagittal MR imaging: a proof of concept study. Eur. Radiol. 29, 6891–6899. 10.1007/s00330-019-06327-0 [DOI] [PubMed] [Google Scholar]
Klein Y., Djaldetti R., Keller Y., Bachelet I. (2017). Motor dysfunction and touch-slang in user interface data. Scientific reports 7:4702. 10.1038/s41598-017-04893-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
Klomsae A., Auephanwiriyakul S., Theera-Umpon N. (2018). String grammar unsupervised possibilistic fuzzy C-medians for gait pattern classification in patients with neurodegenerative diseases. Comput. Intell. Neurosci. 2018:1869565. 10.1155/2018/1869565 [DOI] [PMC free article] [PubMed] [Google Scholar]
Koçer A., Oktay A. B. (2016). Nintendo Wii assessment of Hoehn and Yahr score with Parkinson's disease tremor. Technol. Health Care 24, 185–191. 10.3233/THC-151124 [DOI] [PubMed] [Google Scholar]
Kostikis N., Hristu-Varsakelis D., Arnaoutoglou M., Kotsavasiloglou C. (2015). A smartphone-based tool for assessing Parkinsonian hand tremor. IEEE J. Biomed. Health Inf. 19, 1835–1842. 10.1109/JBHI.2015.2471093 [DOI] [PubMed] [Google Scholar]
Kowal S. L., Dall T. M., Chakrabarti R., Storm M. V., Jain A. (2013). The current and projected economic burden of Parkinson's disease in the United States. Move. Disord. 28, 311–318. 10.1002/mds.25292 [DOI] [PubMed] [Google Scholar]
Kraipeerapun P., Amornsamankul S. (2015). Using stacked generalization and complementary neural networks to predict Parkinson's disease, in 2015 11th International Conference on Natural Computation (ICNC) (Zhangjiajie: ), 1290–1294. 10.1109/ICNC.2015.7378178 [DOI] [Google Scholar]
Kugler P., Jaremenko C., Schlachetzki J., Winkler J., Klucken J., Eskofier B. (2013). Automatic recognition of Parkinson's disease using surface electromyography during standardized gait tests. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2013, 5781–5784. 10.1109/EMBC.2013.6610865 [DOI] [PubMed] [Google Scholar]
Kuhner A., Schubert T., Cenciarini M., Wiesmeier I. K., Coenen V. A., Burgard W., et al. (2017). Correlations between motor symptoms across different motor tasks, quantified via random forest feature classification in Parkinson's disease. Front. Neurol. 8:607. 10.3389/fneur.2017.00607 [DOI] [PMC free article] [PubMed] [Google Scholar]
Kuresan H., Samiappan D., Masunda S. (2019). Fusion of WPT and MFCC feature extraction in Parkinson's disease diagnosis. Technol. Health Care 27, 363–372. 10.3233/THC-181306 [DOI] [PubMed] [Google Scholar]
Kwon D.-Y., Kwon Y., Kim J.-W. (2018). Quantitative analysis of finger and forearm movements in patients with off state early stage Parkinson's disease and scans without evidence of dopaminergic deficit (SWEDD). Parkinsonism Related Disord. 57, 33–38. 10.1016/j.parkreldis.2018.07.012 [DOI] [PubMed] [Google Scholar]
Lacy S. E., Smith S. L., Lones M. A. (2018). Using echo state networks for classification: A case study in Parkinson's disease diagnosis. Artif. Intell. Med. 86, 53–59. 10.1016/j.artmed.2018.02.002 [DOI] [PubMed] [Google Scholar]
Lee M. J., Kim S. L., Lyoo C. H., Lee M. S. (2014). Kinematic analysis in patients with Parkinson's disease and SWEDD. J. Parkinsons Dis. 4, 421–430. 10.3233/JPD-130233 [DOI] [PubMed] [Google Scholar]
Lei H., Huang Z., Zhou F., Elazab A., Tan E.-L., Li H., et al. (2019). Parkinson's disease diagnosis via joint learning from multiple modalities and relations. IEEE J. Biomed. Health Inf. 23, 1437–1449. 10.1109/JBHI.2018.2868420 [DOI] [PubMed] [Google Scholar]
Lewitt P. A., Li J., Lu M., Beach T. G., Adler C. H., Guo L., et al. (2013). 3-hydroxykynurenine and other Parkinson's disease biomarkers discovered by metabolomic analysis. Move. Disord. 28, 1653–1660. 10.1002/mds.25555 [DOI] [PubMed] [Google Scholar]
Li Q., Chen H., Huang H., Zhao X., Cai Z., Tong C., et al. (2017). An enhanced grey wolf optimization based feature selection wrapped kernel extreme learning machine for medical diagnosis. Comput. Math. Methods Med. 2017:9512741. 10.1155/2017/9512741 [DOI] [PMC free article] [PubMed] [Google Scholar]
Li S., Lei H., Zhou F., Gardezi J., Lei B. (2019). Longitudinal and Multi-modal Data Learning for Parkinson's Disease Diagnosis via Stacked Sparse Auto-encoder, in 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019) (Venice: ), 384–387. 10.1109/ISBI.2019.8759385 [DOI] [Google Scholar]
Liu H., Du G., Zhang L., Lewis M. M., Wang X., Yao T., et al. (2016). Folded concave penalized learning in identifying multimodal MRI marker for Parkinson's disease. J. Neurosci. Methods 268, 1–6. 10.1016/j.jneumeth.2016.04.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
Liu L., Wang Q., Adeli E., Zhang L., Zhang H., Shen D. (2016). Feature selection based on iterative canonical correlation analysis for automatic diagnosis of Parkinson's disease. Med. Image Comput. Computer Assist. Interv. 9901, 1–8. 10.1007/978-3-319-46723-8_1 [DOI] [PMC free article] [PubMed] [Google Scholar]
Ma C., Ouyang J., Chen H.-L., Zhao X.-H. (2014). An efficient diagnosis system for Parkinson's disease using kernel-based extreme learning machine with subtractive clustering features weighting approach. Computat. Math. Methods Med. 2014:985789. 10.1155/2014/985789 [DOI] [PMC free article] [PubMed] [Google Scholar]
Ma H., Tan T., Zhou H., Gao T. (2016). Support Vector Machine-recursive feature elimination for the diagnosis of Parkinson disease based on speech analysis, in 2016 Seventh International Conference on Intelligent Control and Information Processing (ICICIP) (Siem Reap: ), 34–40. 10.1109/ICICIP.2016.7885912 [DOI] [Google Scholar]
Maass F., Michalke B., Leha A., Boerger M., Zerr I., Koch J.-C., et al. (2018). Elemental fingerprint as a cerebrospinal fluid biomarker for the diagnosis of Parkinson's disease. J. Neurochemistry 145, 342–351. 10.1111/jnc.14316 [DOI] [PubMed] [Google Scholar]
Maass F., Michalke B., Willkommen D., Leha A., Schulte C., Tönges L., et al. (2020). Elemental fingerprint: reassessment of a cerebrospinal fluid biomarker for Parkinson's disease. Neurobiol. Dis. 134:104677. 10.1016/j.nbd.2019.104677 [DOI] [PubMed] [Google Scholar]
Mabrouk R., Chikhaoui B., Bentabet L. (2019). Machine learning based classification using clinical and DaTSCAN SPECT imaging features: a study on Parkinson's disease and SWEDD. IEEE Trans. Rad. Plasma Med. Sci. 3, 170–177. 10.1109/TRPMS.2018.2877754 [DOI] [Google Scholar]
Mandal I., Sairam N. (2013). Accurate telemonitoring of Parkinson's disease diagnosis using robust inference system. Int. J. Med. Informatics 82, 359–377. 10.1016/j.ijmedinf.2012.10.006 [DOI] [PubMed] [Google Scholar]
Marar S., Swain D., Hiwarkar V., Motwani N., Awari A. (2018). Predicting the occurrence of Parkinson's disease using various classification models, in 2018 International Conference on Advanced Computation and Telecommunication (ICACAT) (Bhopal: ), 1–5. 10.1109/ICACAT.2018.8933579 [DOI] [Google Scholar]
Marek K., Jennings D., Lasch S., Siderowf A., Tanner C., Simuni T., et al. (2011). The parkinson progression marker initiative (PPMI). Progress Neurobiol. 95, 629–635. 10.1016/j.pneurobio.2011.09.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
Martínez M., Villagra F., Castellote J. M., Pastor M. A. (2018). Kinematic and kinetic patterns related to free-walking in Parkinson's disease. Sensors 18:4224. 10.3390/s18124224 [DOI] [PMC free article] [PubMed] [Google Scholar]
Martinez-Murcia F. J., Górriz J. M., Ramírez J., Ortiz A. (2018). Convolutional neural networks for neuroimaging in Parkinson's disease: is preprocessing needed? Int. J. Neural Syst. 28:1850035. 10.1142/S0129065718500351 [DOI] [PubMed] [Google Scholar]
Memedi M., Sadikov A., Groznik V., Žabkar J., Možina M., Bergquist F., et al. (2015). Automatic spiral analysis for objective assessment of motor symptoms in Parkinson's disease. Sensors 15, 23727–23744. 10.3390/s150923727 [DOI] [PMC free article] [PubMed] [Google Scholar]
Mittra Y., Rustagi V. (2018). Classification of subjects with Parkinson's disease using gait data analysis, in 2018 International Conference on Automation and Computational Engineering (ICACE) (Greater Noida: ), 84–89. 10.1109/ICACE.2018.8687022 [DOI] [Google Scholar]
Moharkan Z. A., Garg H., Chodhury T., Kumar P. (2017). A classification based Parkinson detection system, in 2017 International Conference On Smart Technologies For Smart Nation (SmartTechCon) (Bengaluru: ), 1509–1513. 10.1109/SmartTechCon.2017.8358616 [DOI] [Google Scholar]
Moher D., Liberati A., Tetzlaff J., Altman D. G. (2009). Preferred reporting items for systematic reviews and meta-analyses: the PRISMA statement. Ann. Inter. Med. 151, 264–269. 10.7326/0003-4819-151-4-200908180-00135 [DOI] [PubMed] [Google Scholar]
Montaña D., Campos-Roca Y., Pérez C. J. (2018). A Diadochokinesis-based expert system considering articulatory features of plosive consonants for early detection of Parkinson's disease. Comp. Methods Programs Biomed. 154, 89–97. 10.1016/j.cmpb.2017.11.010 [DOI] [PubMed] [Google Scholar]
Morisi R., Manners D. N., Gnecco G., Lanconelli N., Testa C., Evangelisti S., et al. (2018). Multi-class parkinsonian disorders classification with quantitative MR markers and graph-based features using support vector machines. Parkinsonism Relat. Disord. 47, 64–70. 10.1016/j.parkreldis.2017.11.343 [DOI] [PubMed] [Google Scholar]
Mucha J., Mekyska J., Faundez-Zanuy M., Lopez-De-Ipina K., Zvoncak V., Galaz Z., et al. (2018). Advanced Parkinson's disease dysgraphia analysis based on fractional derivatives of online handwriting, in 2018 10th International Congress on Ultra Modern Telecommunications and Control Systems and Workshops (ICUMT) (Moscow: ), 1–6. 10.1109/ICUMT.2018.8631265 [DOI] [Google Scholar]
Nicastro N., Wegrzyk J., Preti M. G., Fleury V., Van de Ville D., Garibotto V., et al. (2019). Classification of degenerative parkinsonism subtypes by support-vector-machine analysis and striatal (123)I-FP-CIT indices. J. Neurol. 266, 1771–1781. 10.1007/s00415-019-09330-z [DOI] [PMC free article] [PubMed] [Google Scholar]
Nõmm S., Bard,õš K., Toomela A., Medijainen K., Taba P. (2018). Detailed analysis of the Luria's alternating seriestests for Parkinson's disease diagnostics, in 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA) (Orlando, FL: ), 1347–1352. 10.1109/ICMLA.2018.00219 [DOI] [Google Scholar]
Nunes A., Silva G., Duque C., Januário C., Santana I., Ambrósio A. F., et al. (2019). Retinal texture biomarkers may help to discriminate between Alzheimer's, Parkinson's, and healthy controls. PLoS One 14:e0218826. 10.1371/journal.pone.0218826 [DOI] [PMC free article] [PubMed] [Google Scholar]
Nuvoli S., Spanu A., Fravolini M. L., Bianconi F., Cascianelli S., Madeddu G., et al. (2019). [(123)I]Metaiodobenzylguanidine (MIBG) cardiac scintigraphy and automated classification techniques in Parkinsonian disorders. Mol. Imaging Biol. 22, 703–710. 10.1007/s11307-019-01406-6 [DOI] [PubMed] [Google Scholar]
Oliveira F. P. M., Castelo-Branco M. (2015). Computer-aided diagnosis of Parkinson's disease based on [(123)I]FP-CIT SPECT binding potential images, using the voxels-as-features approach and support vector machines. J. Neural Eng. 12:026008. 10.1088/1741-2560/12/2/026008 [DOI] [PubMed] [Google Scholar]
Oliveira F. P. M., Faria D. B., Costa D. C., Castelo-Branco M., Tavares J. M. R. S. (2018). Extraction, selection and comparison of features for an effective automated computer-aided diagnosis of Parkinson's disease based on [(123)I]FP-CIT SPECT images. Eur. J. Nucl. Med. Mol. Imaging 45, 1052–1062. 10.1007/s00259-017-3918-7 [DOI] [PubMed] [Google Scholar]
Oliveira H. M., Machado A. R. P., Andrade A. O. (2018a). On the use of t-distributed stochastic neighbor embedding for data visualization and classification of individuals with Parkinson's disease. Comput. Math. Methods Med. 2018:8019232. 10.1155/2018/8019232 [DOI] [PMC free article] [PubMed] [Google Scholar]
Opara J., Brola W., Leonardi M., Błaszczyk B. (2012). Quality of life in Parkinsons disease. J. Med. Life 5:375. [PMC free article] [PubMed] [Google Scholar]
Oung Q. W., Hariharan M., Lee H. L., Basah S. N., Sarillee M., Lee C. H. (2015). Wearable multimodal sensors for evaluation of patients with Parkinson disease, in 2015 IEEE International Conference on Control System, Computing and Engineering (ICCSCE) (Penang: ), 269–274. 10.1109/ICCSCE.2015.7482196 [DOI] [Google Scholar]
Ozcift A. (2012). SVM feature selection based rotation forest ensemble classifiers to improve computer-aided diagnosis of Parkinson disease. J. Med. Syst. 36, 2141–2147. 10.1007/s10916-011-9678-1 [DOI] [PubMed] [Google Scholar]
Ozcift A., Gulten A. (2011). Classifier ensemble construction with rotation forest to improve medical diagnosis performance of machine learning algorithms. Comp. Methods Progr. Biomed. 104, 443–451. 10.1016/j.cmpb.2011.03.018 [DOI] [PubMed] [Google Scholar]
Pahuja G., Nagabhushan T. N. (2016). A novel GA-ELM approach for Parkinson's disease detection using brain structural T1-weighted MRI data, in 2016 Second International Conference on Cognitive Computing and Information Processing (CCIP) (Mysuru: ), 1–6. 10.1109/CCIP.2016.7802848 [DOI] [Google Scholar]
Palumbo B., Fravolini M. L., Buresta T., Pompili F., Forini N., Nigro P., et al. (2014). Diagnostic accuracy of Parkinson disease by support vector machine (SVM) analysis of 123I-FP-CIT brain SPECT data: implications of putaminal findings and age. Medicine 93:e228. 10.1097/MD.0000000000000228 [DOI] [PMC free article] [PubMed] [Google Scholar]
Papadopoulos A., Kyritsis K., Klingelhoefer L., Bostanjopoulou S., Chaudhuri K. R., Delopoulos A. (2019). Detecting Parkinsonian tremor from IMU data collected in-the-wild using deep multiple-instance learning. IEEE J. Biomed. Health Inform. 24, 2559–2569. 10.1109/JBHI.2019.2961748 [DOI] [PubMed] [Google Scholar]
Papavasileiou I., Zhang W., Wang X., Bi J., Zhang L., Han S. (2017). Classification of neurological gait disorders using multi-task feature learning, in 2017 IEEE/ACM International Conference on Connected Health: Applications, Systems and Engineering Technologies (CHASE) (Philadelphia, PA: ), 195–204. 10.1109/CHASE.2017.78 [DOI] [Google Scholar]
Peker M. (2016). A decision support system to improve medical diagnosis using a combination of k-medoids clustering based attribute weighting and SVM. J. Med. Syst. 40:116. 10.1007/s10916-016-0477-6 [DOI] [PubMed] [Google Scholar]
Peng B., Wang S., Zhou Z., Liu Y., Tong B., Zhang T., et al. (2017). A multilevel-ROI-features-based machine learning method for detection of morphometric biomarkers in Parkinson's disease. Neurosci. Lett. 651, 88–94. 10.1016/j.neulet.2017.04.034 [DOI] [PubMed] [Google Scholar]
Peng B., Zhou Z., Geng C., Tong B., Zhou Z., Zhang T., et al. (2016). Computer aided analysis of cognitive disorder in patients with Parkinsonism using machine learning method with multilevel ROI-based features, in 2016 9th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI) (Datong: ), 1792–1796. 10.1109/CISP-BMEI.2016.7853008 [DOI] [Google Scholar]
Pereira C. R., Pereira D. R., da Silva F. A., Hook C., Weber S. A., Pereira L. A., et al. (2015). A step towards the automated diagnosis of parkinson's disease: Analyzing handwriting movements, in 2015 IEEE 28th International Symposium on Computer-Based Medical Systems (Sao Carlos: IEEE; ), 171–176. 10.1109/CBMS.2015.34 [DOI] [Google Scholar]
Pereira C. R., Pereira D. R., Rosa G. H., Albuquerque V. H. C., Weber S. A. T., Hook C., et al. (2018). Handwritten dynamics assessment through convolutional neural networks: An application to Parkinson's disease identification. Artif. Intell. Med. 87, 67–77. 10.1016/j.artmed.2018.04.001 [DOI] [PubMed] [Google Scholar]
Pereira C. R., Pereira D. R., Silva F. A., Masieiro J. P., Weber S. A. T., Hook C., et al. (2016a). A new computer vision-based approach to aid the diagnosis of Parkinson's disease. Comp. Methods Progr. Biomed. 136, 79–88. 10.1016/j.cmpb.2016.08.005 [DOI] [PubMed] [Google Scholar]
Pereira C. R., Pereira D. R., Weber S. A., Hook C., de Albuquerque V. H. C., Papa J. P. (2019). A survey on computer-assisted Parkinson's disease diagnosis. Artif. Intell. Med. 95, 48–63. 10.1016/j.artmed.2018.08.007 [DOI] [PubMed] [Google Scholar]
Pereira C. R., Weber S. A. T., Hook C., Rosa G. H., Papa J. P. (2016b). Deep learning-aided Parkinson's disease diagnosis from handwritten dynamics, in 2016 29th SIBGRAPI Conference on Graphics, Patterns and Images (SIBGRAPI) (São Paulo: ), 340–346. 10.1109/SIBGRAPI.2016.054 [DOI] [Google Scholar]
Pham H. N., Do T. T. T., Chan K. Y. J., Sen G., Han A. Y. K., Lim P., et al. (2019). Multimodal detection of Parkinson disease based on vocal and improved spiral test, in 2019 International Conference on System Science and Engineering (ICSSE) (Dong Hoi: ), 279–284. 10.1109/ICSSE.2019.8823309 [DOI] [Google Scholar]
Pham T. D. (2018). Pattern analysis of computer keystroke time series in healthy control and early-stage Parkinson's disease subjects using fuzzy recurrence and scalable recurrence network features. J. Neurosci. Methods 307, 194–202. 10.1016/j.jneumeth.2018.05.019 [DOI] [PubMed] [Google Scholar]
Pham T. D., Yan H. (2018). Tensor decomposition of gait dynamics in Parkinson's disease. IEEE Trans. Bio-Med. Eng. 65, 1820–1827. 10.1109/TBME.2017.2779884 [DOI] [PubMed] [Google Scholar]
Postuma R. B., Berg D., Stern M., Poewe W., Olanow C. W., Oertel W., et al. (2015). MDS clinical diagnostic criteria for Parkinson's disease. Move. Disord. 30, 1591–1601. 10.1002/mds.26424 [DOI] [PubMed] [Google Scholar]
Prashanth R., Dutta Roy S. (2018). Early detection of Parkinson's disease through patient questionnaire and predictive modelling. In. J. Med. Inform. 119, 75–87. 10.1016/j.ijmedinf.2018.09.008 [DOI] [PubMed] [Google Scholar]
Prashanth R., Dutta Roy S., Mandal P. K., Ghosh S. (2016). High-accuracy detection of early Parkinson's disease through multimodal features and machine learning. Int. J. Med. Inform. 90, 13–21. 10.1016/j.ijmedinf.2016.03.001 [DOI] [PubMed] [Google Scholar]
Prashanth R., Roy S. D., Mandal P. K., Ghosh S. (2014). Parkinson's disease detection using olfactory loss and REM sleep disorder features, in Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2014, 5764–5767. 10.1109/EMBC.2014.6944937 [DOI] [PubMed] [Google Scholar]
Prashanth R., Roy S. D., Mandal P. K., Ghosh S. (2017). High-accuracy classification of Parkinson's disease through shape analysis and surface fitting in 123I-Ioflupane SPECT imaging. IEEE J. Biomed. Health Inform. 21, 794–802. 10.1109/JBHI.2016.2547901 [DOI] [PubMed] [Google Scholar]
Prince J., Andreotti F., Vos M. D. (2019). Multi-source ensemble learning for the remote prediction of Parkinson's disease in the presence of source-wise missing data. IEEE Trans. Biomed. Eng. 66, 1402–1411. 10.1109/TBME.2018.2873252 [DOI] [PMC free article] [PubMed] [Google Scholar]
Prince J., de Vos M. (2018). A deep learning framework for the remote detection of Parkinson's disease using smart-phone sensor data, in 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) (Honolulu, HI: ), 3144–3147. 10.1109/EMBC.2018.8512972 [DOI] [PubMed] [Google Scholar]
Ramdhani R. A., Khojandi A., Shylo O., Kopell B. H. (2018). Optimizing clinical assessments in Parkinson's disease through the use of wearable sensors and data driven modeling. Front. Comput. Neurosci. 12:72. 10.3389/fncom.2018.00072 [DOI] [PMC free article] [PubMed] [Google Scholar]
Reyes J. F., Montealegre J. S., Castano Y. J., Urcuqui C., Navarro A. (2019). LSTM and convolution networks exploration for Parkinson's diagnosis, in 2019 IEEE Colombian Conference on Communications and Computing (COLCOM) (Barranquilla: ), 1–4. 10.1109/ColComCon.2019.8809160 [DOI] [Google Scholar]
Ribeiro L. C. F., Afonso L. C. S., Papa J. P. (2019). Bag of samplings for computer-assisted Parkinson's disease diagnosis based on recurrent neural networks. Comp. Biol. Med. 115:103477. 10.1016/j.compbiomed.2019.103477 [DOI] [PubMed] [Google Scholar]
Ricci M., Lazzaro G. D., Pisani A., Mercuri N. B., Giannini F., Saggio G. (2020). Assessment of motor impairments in early untreated parkinson's disease patients: the wearable electronics impact. IEEE J. Biomed. Health Inform. 24, 120–130. 10.1109/JBHI.2019.2903627 [DOI] [PubMed] [Google Scholar]
Rios-Urrego C. D., Vásquez-Correa J. C., Vargas-Bonilla J. F., Nöth E., Lopera F., Orozco-Arroyave J. R. (2019). Analysis and evaluation of handwriting in patients with Parkinson's disease using kinematic, geometrical, and non-linear features. Comput. Methods Progr. Biomed. 173, 43–52. 10.1016/j.cmpb.2019.03.005 [DOI] [PubMed] [Google Scholar]
Rovini E., Maremmani C., Moschetti A., Esposito D., Cavallo F. (2018). Comparative motor pre-clinical assessment in parkinson's disease using supervised machine learning approaches. Annals Biomed. Eng. 46, 2057–2068. 10.1007/s10439-018-2104-9 [DOI] [PubMed] [Google Scholar]
Rovini E., Moschetti A., Fiorini L., Esposito D., Maremmani C., Cavallo F. (2019). Wearable sensors for prodromal motor assessment of parkinson's disease using supervised learning, in 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), 4318–4321. 10.1109/EMBC.2019.8856804 [DOI] [PubMed] [Google Scholar]
Rubbert C., Mathys C., Jockwitz C., Hartmann C. J., Eickhoff S. B., Hoffstaedter F., et al. (2019). Machine-learning identifies Parkinson's disease patients based on resting-state between-network functional connectivity. Br. J. Radiol. 92:20180886. 10.1259/bjr.20180886 [DOI] [PMC free article] [PubMed] [Google Scholar]
Sakar B. E., Isenkul M. E., Sakar C. O., Sertbas A., Gurgen F., Delil S., et al. (2013). Collection and analysis of a Parkinson speech dataset with multiple types of sound recordings. IEEE J. Biomed. Health Inform. 17, 828–834. 10.1109/JBHI.2013.2245674 [DOI] [PubMed] [Google Scholar]
Salvatore C., Cerasa A., Castiglioni I., Gallivanone F., Augimeri A., Lopez M., et al. (2014). Machine learning on brain MRI data for differential diagnosis of Parkinson's disease and progressive supranuclear palsy. J. Neurosci. Methods 222, 230–237. 10.1016/j.jneumeth.2013.11.016 [DOI] [PubMed] [Google Scholar]
Sayaydeha O. N. A., Mohammad M. F. (2019). Diagnosis of the Parkinson disease using enhanced fuzzy min-max neural network and OneR attribute evaluation method, in 2019 International Conference on Advanced Science and Engineering (ICOASE) (Zakho-Duhok: ), 64–69. 10.1109/ICOASE.2019.8723870 [DOI] [Google Scholar]
Scherer R. W., Saldanha I. J. (2019). How should systematic reviewers handle conference abstracts? A view from the trenches. Syst. Rev. 8:264. 10.1186/s13643-019-1188-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
Segovia F., Górriz J. M., Ramírez J., Levin J., Schuberth M., Brendel M., et al. (2015). Analysis of 18F-DMFP PET data using multikernel classification in order to assist the diagnosis of Parkinsonism, in 2015 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC) (San Diego, CA: ), 1–4. 10.1109/NSSMIC.2015.7582227 [DOI] [Google Scholar]
Segovia F., Górriz J. M., Ramírez J., Martínez-Murcia F. J., Castillo-Barnes D. (2019). Assisted diagnosis of Parkinsonism based on the striatal morphology. Int. J. Neural Syst. 29:1950011. 10.1142/S0129065719500114 [DOI] [PubMed] [Google Scholar]
Shahsavari M. K., Rashidi H., Bakhsh H. R. (2016). Efficient classification of Parkinson's disease using extreme learning machine and hybrid particle swarm optimization, in 2016 4th International Conference on Control, Instrumentation, and Automation (ICCIA) (Qazvin: ), 148–154. 10.1109/ICCIAutom.2016.7483152 [DOI] [Google Scholar]
Shamir R., Klein C., Amar D., Vollstedt E.-J., Bonin M., Usenovic M., et al. (2017). Analysis of blood-based gene expression in idiopathic Parkinson disease. Neurology 89, 1676–1683. 10.1212/WNL.0000000000004516 [DOI] [PMC free article] [PubMed] [Google Scholar]
Sheibani R., Nikookar E., Alavi S. E. (2019). An ensemble method for diagnosis of Parkinson's disease based on voice measurements. J. Med. Signals Sens. 9, 221–226. 10.4103/jmss.JMSS_57_18 [DOI] [PMC free article] [PubMed] [Google Scholar]
Shen T., Jiang J., Lin W., Ge J., Wu P., Zhou Y., et al. (2019). Use of overlapping group LASSO sparse deep belief network to discriminate Parkinson's disease and normal control. Front. Neurosci. 13:396. 10.3389/fnins.2019.00396 [DOI] [PMC free article] [PubMed] [Google Scholar]
Shi J., Yan M., Dong Y., Zheng X., Zhang Q., An H. (2018). Multiple kernel learning based classification of Parkinson's disease with multi-modal transcranial sonography, in 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) (Honolulu, HI: ), 61–64. 10.1109/EMBC.2018.8512194 [DOI] [PubMed] [Google Scholar]
Shinde S., Prasad S., Saboo Y., Kaushick R., Saini J., Pal P. K., et al. (2019). Predictive markers for Parkinson's disease using deep neural nets on neuromelanin sensitive MRI. NeuroImage. Clin. 22:101748. 10.1016/j.nicl.2019.101748 [DOI] [PMC free article] [PubMed] [Google Scholar]
Singh G., Samavedham L. (2015). Unsupervised learning based feature extraction for differential diagnosis of neurodegenerative diseases: a case study on early-stage diagnosis of Parkinson disease. J. Neurosci. Methods 256, 30–40. 10.1016/j.jneumeth.2015.08.011 [DOI] [PubMed] [Google Scholar]
Singh G., Samavedham L., Lim E. C.-H., Alzheimer's Disease Neuroimaging I., Parkinson Progression Marker I. (2018). Determination of imaging biomarkers to decipher disease trajectories and differential diagnosis of neurodegenerative diseases (DIsease TreND). J. Neurosci. Methods 305, 105–116. 10.1016/j.jneumeth.2018.05.009 [DOI] [PubMed] [Google Scholar]
Stoessel D., Schulte C., Teixeira Dos Santos M. C., Scheller D., Rebollo-Mesa I., Deuschle C., et al. (2018). Promising metabolite profiles in the plasma and CSF of early clinical Parkinson's disease. Front. Aging Neurosci. 10:51. 10.3389/fnagi.2018.00051 [DOI] [PMC free article] [PubMed] [Google Scholar]
Surangsrirat D., Thanawattano C., Pongthornseri R., Dumnin S., Anan C., Bhidayasiri R. (2016). Support vector machine classification of Parkinson's disease and essential tremor subjects based on temporal fluctuation. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2016, 6389–6392. 10.1109/EMBC.2016.7592190 [DOI] [PubMed] [Google Scholar]
Sztahó D., Tulics M. G., Vicsi K., Valálik I. (2017). Automatic estimation of severity of Parkinson's disease based on speech rhythm related features, in 2017 8th IEEE International Conference on Cognitive Infocommunications (CogInfoCom) (Debrecen: ), 000011–000016. 10.1109/CogInfoCom.2017.8268208 [DOI] [Google Scholar]
Sztahó D., Valálik I., Vicsi K. (2019). Parkinson's disease severity estimation on Hungarian speech using various speech tasks, in 2019 International Conference on Speech Technology and Human-Computer Dialogue (SpeD) (Timisoara: ), 1–6. 10.1109/SPED.2019.8906277 [DOI] [Google Scholar]
Tagare H. D., DeLorenzo C., Chelikani S., Saperstein L., Fulbright R. K. (2017). Voxel-based logistic analysis of PPMI control and Parkinson's disease DaTscans. NeuroImage 152, 299–311. 10.1016/j.neuroimage.2017.02.067 [DOI] [PubMed] [Google Scholar]
Tahavori F., Stack E., Agarwal V., Burnett M., Ashburn A., Hoseinitabatabaei S. A., et al. (2017). Physical activity recognition of elderly people and people with parkinson's (PwP) during standard mobility tests using wearable sensors, in 2017 International Smart Cities Conference (ISC2) (Wuxi: ), 1–4. 10.1109/ISC2.2017.8090858 [DOI] [Google Scholar]
Taleb C., Khachab M., Mokbel C., Likforman-Sulem L. (2019). Visual representation of online handwriting time series for deep learning Parkinson's disease detection, in 2019 International Conference on Document Analysis and Recognition Workshops (ICDARW) (Sydney, NSW: ), 25–30. 10.1109/ICDARW.2019.50111 [DOI] [Google Scholar]
Tang Y., Meng L., Wan C. M., Liu Z. H., Liao W. H., Yan X. X., et al. (2017). Identifying the presence of Parkinson's disease using low-frequency fluctuations in BOLD signals. Neurosci. Lett. 645, 1–6. 10.1016/j.neulet.2017.02.056 [DOI] [PubMed] [Google Scholar]
Taylor J. C., Fenner J. W. (2017). Comparison of machine learning and semi-quantification algorithms for (I123)FP-CIT classification: the beginning of the end for semi-quantification? EJNMMI Phys. 4:29. 10.1186/s40658-017-0196-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
Tien I., Glaser S. D., Aminoff M. J. (2010). Characterization of gait abnormalities in Parkinson's disease using a wireless inertial sensor system, in Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2010, 3353–3356. 10.1109/IEMBS.2010.5627904 [DOI] [PubMed] [Google Scholar]
Tracy J. M., Özkanca Y., Atkins D. C., Hosseini Ghomi R. (2019). Investigating voice as a biomarker: deep phenotyping methods for early detection of Parkinson's disease. J. Biomed. Inform. 104:103362. 10.1016/j.jbi.2019.103362 [DOI] [PubMed] [Google Scholar]
Tremblay C., Martel P. D., Frasnelli J. (2017). Trigeminal system in Parkinson's disease: a potential avenue to detect Parkinson-specific olfactory dysfunction. Parkinsonism Relat. Dis. 44, 85–90. 10.1016/j.parkreldis.2017.09.010 [DOI] [PubMed] [Google Scholar]
Trezzi J.-P., Galozzi S., Jaeger C., Barkovits K., Brockmann K., Maetzler W., et al. (2017). Distinct metabolomic signature in cerebrospinal fluid in early parkinson's disease. Mov. Disord. 32, 1401–1408. 10.1002/mds.27132 [DOI] [PubMed] [Google Scholar]
Tsanas A., Little M. A., McSharry P. E., Spielman J., Ramig L. O. (2012). Novel speech signal processing algorithms for high-accuracy classification of Parkinson's disease. IEEE Trans. Bio. Med. Eng. 59, 1264–1271. 10.1109/TBME.2012.2183367 [DOI] [PubMed] [Google Scholar]
Tseng P.-H., Cameron I. G. M., Pari G., Reynolds J. N., Munoz D. P., Itti L. (2013). High-throughput classification of clinical populations from natural viewing eye movements. J. Neurol. 260, 275–284. 10.1007/s00415-012-6631-2 [DOI] [PubMed] [Google Scholar]
Tsuda M., Asano S., Kato Y., Murai K., Miyazaki M. (2019). Differential diagnosis of multiple system atrophy with predominant parkinsonism and Parkinson's disease using neural networks. J. Neurol. Sci. 401, 19–26. 10.1016/j.jns.2019.04.014 [DOI] [PubMed] [Google Scholar]
Tysnes O.-B., Storstein A. (2017). Epidemiology of Parkinson's disease. J. Neural Trans. 124, 901–905. 10.1007/s00702-017-1686-y [DOI] [PubMed] [Google Scholar]
Urcuqui C., Castaño Y., Delgado J., Navarro A., Diaz J., Muñoz B., et al. (2018). Exploring Machine Learning to Analyze Parkinson's Disease Patients, in 2018 14th International Conference on Semantics, Knowledge and Grids (SKG) (Guangzhou: ), 160–166. 10.1109/SKG.2018.00029 [DOI] [Google Scholar]
Vabalas A., Gowen E., Poliakoff E., Casson A. J. (2019). Machine learning algorithm validation with a limited sample size. PLoS ONE 14:e0224365. 10.1371/journal.pone.0224365 [DOI] [PMC free article] [PubMed] [Google Scholar]
Vaiciukynas E., Verikas A., Gelzinis A., Bacauskiene M. (2017). Detecting Parkinson's disease from sustained phonation and speech signals. PLoS ONE 12:e0185613. 10.1371/journal.pone.0185613 [DOI] [PMC free article] [PubMed] [Google Scholar]
Vanegas M. I., Ghilardi M. F., Kelly S. P., Blangero A. (2018). Machine learning for EEG-based biomarkers in Parkinson's disease, in 2018 IEEE International Conference on Bioinformatics and Biomedicine (BIBM) (Madrid: ), 2661–2665. 10.1109/BIBM.2018.8621498 [DOI] [Google Scholar]
Váradi C., Nehéz K., Hornyák O., Viskolcz B., Bones J. (2019). Serum N-glycosylation in Parkinson's disease: a novel approach for potential alterations. Molecules 24:2220. 10.3390/molecules24122220 [DOI] [PMC free article] [PubMed] [Google Scholar]
Vásquez-Correa J. C., Arias-Vergara T., Orozco-Arroyave J. R., Eskofier B., Klucken J., Nöth E. (2019). Multimodal assessment of parkinson's disease: a deep learning approach. IEEE J. Biomed. Health Inform. 23, 1618–1630. 10.1109/JBHI.2018.2866873 [DOI] [PubMed] [Google Scholar]
Vlachostergiou A., Tagaris A., Stafylopatis A., Kollias S. (2018). Multi-task learning for predicting Parkinson's disease based on medical imaging information, in 2018 25th IEEE International Conference on Image Processing (ICIP) (Athens: ), 2052–2056. 10.1109/ICIP.2018.8451398 [DOI] [Google Scholar]
Wahid F., Begg R. K., Hass C. J., Halgamuge S., Ackland D. C. (2015). Classification of Parkinson's disease gait using spatial-temporal gait features. IEEE J. Biomed. Health Inform. 19, 1794–1802. 10.1109/JBHI.2015.2450232 [DOI] [PubMed] [Google Scholar]
Wang Z., Zhu X., Adeli E., Zhu Y., Nie F., Munsell B., et al. (2017). Multi-modal classification of neurodegenerative disease by progressive graph-based transductive learning. Med Image Anal. 39, 218–230. 10.1016/j.media.2017.05.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
Wen J., Thibeau-Sutre E., Diaz-Melo M., Samper-González J., Routier A., Bottani S., et al. (2020). Convolutional neural networks for classification of Alzheimer's disease: overview and reproducible evaluation. Med. Image Anal. 63:101694. 10.1016/j.media.2020.101694 [DOI] [PubMed] [Google Scholar]
Wenzel M., Milletari F., Krüger J., Lange C., Schenk M., Apostolova I., et al. (2019). Automatic classification of dopamine transporter SPECT: deep convolutional neural networks can be trained to be robust with respect to variable image characteristics. Eur. J. Nuclear Med. Mol. Imaging 46, 2800–2811. 10.1007/s00259-019-04502-5 [DOI] [PubMed] [Google Scholar]
Wodzinski M., Skalski A., Hemmerling D., Orozco-Arroyave J. R., Nöth E. (2019). Deep learning approach to Parkinson's disease detection using voice recordings and convolutional neural network dedicated to image classification, in 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) (Berlin: ), 717–720. 10.1109/EMBC.2019.8856972 [DOI] [PubMed] [Google Scholar]
Wu Y., Chen P., Yao Y., Ye X., Xiao Y., Liao L., et al. (2017). Dysphonic voice pattern analysis of patients in Parkinson's disease using minimum interclass probability risk feature selection and bagging ensemble learning methods. Comput. Math. Methods Med. 2017:4201984. 10.1155/2017/4201984 [DOI] [PMC free article] [PubMed] [Google Scholar]
Wu Y., Jiang J.-H., Chen L., Lu J.-Y., Ge J.-J., Liu F.-T., et al. (2019). Use of radiomic features and support vector machine to distinguish Parkinson's disease cases from normal controls. Ann. Transl. Med. 7:773. 10.21037/atm.2019.11.26 [DOI] [PMC free article] [PubMed] [Google Scholar]
Xia Y., Yao Z., Ye Q., Cheng N. (2020). A dual-modal attention-enhanced deep learning network for quantification of Parkinson's disease characteristics. IEEE Trans. Neural Syst. Rehab. Eng. 28, 42–51. 10.1109/TNSRE.2019.2946194 [DOI] [PubMed] [Google Scholar]
Yadav G., Kumar Y., Sahoo G. (2011). Predication of Parkinson's disease using data mining methods: a comparative analysis of tree, statistical, and support vector machine classifiers. Ind. J. Med. Sci. 65, 231–242. 10.4103/0019-5359.107023 [DOI] [PubMed] [Google Scholar]
Yagis E., Herrera A. G. S. D., Citi L. (2019). Generalization Performance of Deep Learning Models in Neurodegenerative Disease Classification, in 2019 IEEE International Conference on Bioinformatics and Biomedicine (BIBM) (San Diego, CA: ), 1692–1698. 10.1109/BIBM47256.2019.8983088 [DOI] [Google Scholar]
Yaman O., Ertam F., Tuncer T. (2020). Automated Parkinson's disease recognition based on statistical pooling method using acoustic features. Med. Hypoth. 135:109483. 10.1016/j.mehy.2019.109483 [DOI] [PubMed] [Google Scholar]
Yang J.-X., Chen L. (2017). Economic burden analysis of Parkinson's disease patients in China. Parkinson's Dis. 2017:8762939. 10.1155/2017/8762939 [DOI] [PMC free article] [PubMed] [Google Scholar]
Yang M., Zheng H., Wang H., McClean S. (2009). Feature selection and construction for the discrimination of neurodegenerative diseases based on gait analysis, in 2009 3rd International Conference on Pervasive Computing Technologies for Healthcare (London: ), 1–7. 10.4108/ICST.PERVASIVEHEALTH2009.6053 [DOI] [Google Scholar]
Yang S., Zheng F., Luo X., Cai S., Wu Y., Liu K., et al. (2014). Effective dysphonia detection using feature dimension reduction and kernel density estimation for patients with Parkinson's disease. PLoS ONE 9:e88825. 10.1371/journal.pone.0088825 [DOI] [PMC free article] [PubMed] [Google Scholar]
Ye Q., Xia Y., Yao Z. (2018). Classification of gait patterns in patients with neurodegenerative disease using adaptive neuro-fuzzy inference system. Computat. Math. Methods Med. 2018:9831252. 10.1155/2018/9831252 [DOI] [PMC free article] [PubMed] [Google Scholar]
Zeng L.-L., Xie L., Shen H., Luo Z., Fang P., Hou Y., et al. (2017). Differentiating patients with Parkinson's disease from normal controls using gray matter in the cerebellum. Cerebellum 16, 151–157. 10.1007/s12311-016-0781-1 [DOI] [PubMed] [Google Scholar]
Zesiewicz T. A., Sullivan K. L., Hauser R. A. (2006). Nonmotor symptoms of Parkinson's disease. Expert Rev. Neurother. 6, 1811–1822. 10.1586/14737175.6.12.1811 [DOI] [PubMed] [Google Scholar]
Zhang X., He L., Chen K., Luo Y., Zhou J., Wang F. (2018). Multi-view graph convolutional network and its applications on neuroimage analysis for Parkinson's disease. Annu. Symp. Proc. 2018, 1147–1156. [PMC free article] [PubMed] [Google Scholar]
Zhao Y., Wu P., Wang J., Li H., Navab N., Yakushev I., et al. (2019). A 3D deep residual convolutional neural network for differential diagnosis of Parkinsonian syndromes on 18F-FDG PET images, in 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), 3531–3534. 10.1109/EMBC.2019.8856747 [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file.^{(997.8KB, docx)}

Data Availability Statement

The original contributions generated for the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

[B1] Abiyev R. H., Abizade S. (2016). Diagnosing Parkinson's diseases using fuzzy neural system. Comput. Mathe. Methods Med. 2016:1267919. 10.1155/2016/1267919 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B2] Abos A., Baggio H. C., Segura B., Campabadal A., Uribe C., Giraldo D. M., et al. (2019). Differentiation of multiple system atrophy from Parkinson's disease by structural connectivity derived from probabilistic tractography. Sci. Rep. 9:16488. 10.1038/s41598-019-52829-8 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B3] Abujrida H., Agu E., Pahlavan K. (2017). Smartphone-based gait assessment to infer Parkinson's disease severity using crowdsourced data, in 2017 IEEE Healthcare Innovations and Point of Care Technologies (HI-POCT) (Bethesda, MD: ), 208–211. 10.1109/HIC.2017.8227621 [DOI] [Google Scholar]

[B4] Adams W. R. (2017). High-accuracy detection of early Parkinson's Disease using multiple characteristics of finger movement while typing. PLoS ONE 12:e0188226. 10.1371/journal.pone.0188226 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B5] Adeli E., Shi F., An L., Wee C.-Y., Wu G., Wang T., et al. (2016). Joint feature-sample selection and robust diagnosis of Parkinson's disease from MRI data. NeuroImage 141, 206–219. 10.1016/j.neuroimage.2016.05.054 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B6] Adeli E., Thung K.-H., An L., Wu G., Shi F., Wang T., et al. (2019). Semi-supervised discriminative classification robust to sample-outliers and feature-noises. IEEE Trans. Pattern Anal. Mach. Intell. 41, 515–522. 10.1109/TPAMI.2018.2794470 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B7] Agarwal A., Chandrayan S., Sahu S. S. (2016). Prediction of Parkinson's disease using speech signal with Extreme Learning Machine, in 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT) (Chennai: ), 3776–3779. 10.1109/ICEEOT.2016.7755419 [DOI] [Google Scholar]

[B8] Ahlrichs C., Lawo M. (2013). Parkinson's disease motor symptoms in machine learning: a review. arXiv preprint arXiv:1312.3825. 10.5121/hiij.2013.2401 [DOI] [Google Scholar]

[B9] Ahmadi S. A., Vivar G., Frei J., Nowoshilow S., Bardins S., Brandt T., et al. (2019). Towards computerized diagnosis of neurological stance disorders: data mining and machine learning of posturography and sway. J. Neurol. 266(Suppl 1), 108–117. 10.1007/s00415-019-09458-y [DOI] [PubMed] [Google Scholar]

[B10] Aich S., Kim H., younga K., Hui K. L., Al-Absi A. A., Sain M. (2019). A supervised machine learning approach using different feature selection techniques on voice datasets for prediction of Parkinson's disease, in 2019 21st International Conference on Advanced Communication Technology (ICACT) (PyeongChang: ), 1116–1121. 10.23919/ICACT.2019.8701961 [DOI] [Google Scholar]

[B11] Alam M. N., Garg A., Munia T. T. K., Fazel-Rezai R., Tavakolian K. (2017). Vertical ground reaction force marker for Parkinson's disease. PLoS ONE 12:e0175951. 10.1371/journal.pone.0175951 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B12] Alaskar H., Hussain A. (2018). Prediction of Parkinson disease using gait signals, in 2018 11th International Conference on Developments in eSystems Engineering (DeSE) (Cambridge: ), 23–26. 10.1109/DeSE.2018.00011 [DOI] [Google Scholar]

[B13] Al-Fatlawi A. H., Jabardi M. H., Ling S. H. (2016). Efficient diagnosis system for Parkinson's disease using deep belief network, in 2016 IEEE Congress on Evolutionary Computation (CEC) (Vancouver, BC: ), 1324–1330. 10.1109/CEC.2016.7743941 [DOI] [Google Scholar]

[B14] Alharthi A. S., Ozanyan K. B. (2019). Deep learning for ground reaction force data analysis: application to wide-area floor sensing, in 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE) (Vancouver, BC: )„ 1401–1406. 10.1109/ISIE.2019.8781511 [DOI] [Google Scholar]

[B15] Ali L., Khan S. U., Arshad M., Ali S., Anwar M. (2019a). A multi-model framework for evaluating type of speech samples having complementary information about Parkinson's disease, in 2019 International Conference on Electrical, Communication, and Computer Engineering (ICECCE) (Swat: ), 1–5. 10.1109/ICECCE47252.2019.8940696 [DOI] [Google Scholar]

[B16] Ali L., Zhu C., Golilarz N. A., Javeed A., Zhou M., Liu Y. (2019b). Reliable Parkinson's disease detection by analyzing handwritten drawings: construction of an unbiased cascaded learning system based on feature selection and adaptive boosting model. IEEE Access 7, 116480–116489. 10.1109/ACCESS.2019.2932037 [DOI] [Google Scholar]

[B17] Ali L., Zhu C., Zhang Z., Liu Y. (2019c). Automated detection of Parkinson's disease based on multiple types of sustained phonations using linear discriminant analysis and genetically optimized neural network. IEEE J. Transl. Eng. Health Med. 7, 1–10. 10.1109/JTEHM.2019.2940900 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B18] Alqahtani E. J., Alshamrani F. H., Syed H. F., Olatunji S. O. (2018). Classification of Parkinson's disease using NNge classification algorithm, in 2018 21st Saudi Computer Society National Computer Conference (NCC) (Riyadh: ), 1–7. 10.1109/NCG.2018.8592989 [DOI] [Google Scholar]

[B19] Amoroso N., La Rocca M., Monaco A., Bellotti R., Tangaro S. (2018). Complex networks reveal early MRI markers of Parkinson's disease. Med. Image Anal. 48, 12–24. 10.1016/j.media.2018.05.004 [DOI] [PubMed] [Google Scholar]

[B20] Anand A., Haque M. A., Alex J. S. R., Venkatesan N. (2018). Evaluation of machine learning and deep learning algorithms combined with dimentionality reduction techniques for classification of Parkinson's disease, in 2018 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT) (Louisville, KY: ), 342–347. 10.1109/ISSPIT.2018.8642776 [DOI] [Google Scholar]

[B21] Andrei A., Tău?an A., Ionescu B. (2019). Parkinson's disease detection from gait patterns, in 2019 E-Health and Bioengineering Conference (EHB) (Iasi: ), 1–4. 10.1109/EHB47216.2019.8969942 [DOI] [Google Scholar]

[B22] Baby M. S., Saji A. J., Kumar C. S. (2017). Parkinsons disease classification using wavelet transform based feature extraction of gait data, in 2017 International Conference on Circuit, Power and Computing Technologies (ICCPCT) (Kollam: ), 1–6. 10.1109/ICCPCT.2017.8074230 [DOI] [Google Scholar]

[B23] Baggio H. C., Abos A., Segura B., Campabadal A., Uribe C., Giraldo D. M., et al. (2019). Cerebellar resting-state functional connectivity in Parkinson's disease and multiple system atrophy: characterization of abnormalities and potential for differential diagnosis at the single-patient level. NeuroImage. Clin. 22:101720. 10.1016/j.nicl.2019.101720 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B24] Bakar Z. A., Ispawi D. I., Ibrahim N. F., Tahir N. M. (2012). Classification of Parkinson's disease based on Multilayer Perceptrons (MLPs) neural network and ANOVA as a feature extraction, in 2012 IEEE 8th International Colloquium on Signal Processing and its Applications) (Malacca: ), 63–67. 10.1109/CSPA.2012.6194692 [DOI] [Google Scholar]

[B25] Banerjee M., Chakraborty R., Archer D., Vaillancourt D., Vemuri B. C. (2019). DMR-CNN: a CNN tailored For DMR scans with applications to PD classification, in 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019) (Venice: ), 388–391. 10.1109/ISBI.2019.8759558 [DOI] [Google Scholar]

[B26] Belić M., Bobić V., BadŽa M., Šolaja N., Ã?urić-Jovičić M., Kostić V. S. (2019). Artificial intelligence for assisting diagnostics and assessment of Parkinson's disease–a review. Clin. Neurol. Neurosurg. 184:105442. 10.1016/j.clineuro.2019.105442 [DOI] [PubMed] [Google Scholar]

[B27] Benba A., Jilbab A., Hammouch A. (2016a). Discriminating between patients with Parkinson's and neurological diseases using cepstral analysis. IEEE Trans. Neural Syst. Rehab. Eng. 24, 1100–1108. 10.1109/TNSRE.2016.2533582 [DOI] [PubMed] [Google Scholar]

[B28] Benba A., Jilbab A., Hammouch A., Sandabad S. (2016b). Using RASTA-PLP for discriminating between different neurological diseases, in 2016 International Conference on Electrical and Information Technologies (ICEIT) (Tangiers: ), 406–409. 10.1109/EITech.2016.7519630 [DOI] [Google Scholar]

[B29] Bernad-Elazari H., Herman T., Mirelman A., Gazit E., Giladi N., Hausdorff J. M. (2016). Objective characterization of daily living transitions in patients with Parkinson's disease using a single body-fixed sensor. J. Neurol. 263, 1544–1551. 10.1007/s00415-016-8164-6 [DOI] [PubMed] [Google Scholar]

[B30] Bhati S., Velazquez L. M., Villalba J., Dehak N. (2019). LSTM siamese network for Parkinson's disease detection from speech, in 2019 IEEE Global Conference on Signal and Information Processing (GlobalSIP) (Ottawa, ON: ), 1–5. 10.1109/GlobalSIP45357.2019.8969430 [DOI] [Google Scholar]

[B31] Bot B. M., Suver C., Neto E. C., Kellen M., Klein A., Bare C., et al. (2016). The mPower study, Parkinson disease mobile data collected using ResearchKit. Sci. Data 3, 1–9. 10.1038/sdata.2016.11 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B32] Braak H., Del Tredici K., Rüb U., De Vos R. A., Steur E. N. J., Braak E. (2003). Staging of brain pathology related to sporadic Parkinson's disease. Neurobiol. Aging 24, 197–211. 10.1016/S0197-4580(02)00065-9 [DOI] [PubMed] [Google Scholar]

[B33] Buongiorno D., Bortone I., Cascarano G. D., Trotta G. F., Brunetti A., Bevilacqua V. (2019). A low-cost vision system based on the analysis of motor features for recognition and severity rating of Parkinson's Disease. BMC Med. Inform. Decision Making 19(Suppl 9):243. 10.1186/s12911-019-0987-5 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B34] Butt A. H., Rovini E., Dolciotti C., Bongioanni P., De Petris G., Cavallo F. (2017). Leap motion evaluation for assessment of upper limb motor skills in Parkinson's disease. IEEE Int. Conf. Rehabil. Robot. 2017, 116–121. 10.1109/ICORR.2017.8009232 [DOI] [PubMed] [Google Scholar]

[B35] Butt A. H., Rovini E., Dolciotti C., De Petris G., Bongioanni P., Carboncini M. C., et al. (2018). Objective and automatic classification of Parkinson disease with Leap Motion controller. Biomed. Eng. Online 17:168. 10.1186/s12938-018-0600-7 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B36] Cai Z., Gu J., Wen C., Zhao D., Huang C., Huang H., et al. (2018). An intelligent Parkinson's disease diagnostic system based on a chaotic bacterial foraging optimization enhanced fuzzy KNN approach. Comp. Math. Methods Med. 2018:2396952. 10.1155/2018/2396952 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B37] Caramia C., Torricelli D., Schmid M., Munoz-Gonzalez A., Gonzalez-Vargas J., Grandas F., et al. (2018). IMU-based classification of Parkinson's disease from gait: a sensitivity analysis on sensor location and feature selection. IEEE J. Biomed. Health Inf. 22, 1765–1774. 10.1109/JBHI.2018.2865218 [DOI] [PubMed] [Google Scholar]

[B38] Castillo-Barnes D., Ramírez J., Segovia F., Martínez-Murcia F. J., Salas-Gonzalez D., Górriz J. M. (2018). Robust ensemble classification methodology for I123-Ioflupane SPECT images and multiple heterogeneous biomarkers in the diagnosis of Parkinson's disease. Front. Neuroinf. 12:53. 10.3389/fninf.2018.00053 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B39] Cavallo F., Moschetti A., Esposito D., Maremmani C., Rovini E. (2019). Upper limb motor pre-clinical assessment in Parkinson's disease using machine learning. Parkinsonism Relat. Disord. 63, 111–116. 10.1016/j.parkreldis.2019.02.028 [DOI] [PubMed] [Google Scholar]

[B40] Celik E., Omurca S. I. (2019). Improving Parkinson's disease diagnosis with machine learning methods, in 2019 Scientific Meeting on Electrical-Electronics & Biomedical Engineering and Computer Science (EBBT) (Istanbul: ), 1–4. 10.1109/EBBT.2019.8742057 [DOI] [Google Scholar]

[B41] Chakraborty S., Aich S., Kim H.-C. (2020). 3D textural, morphological and statistical analysis of voxel of interests in 3T MRI scans for the detection of Parkinson's disease using artificial neural networks. Healthcare 8:E34. 10.3390/healthcare8010034 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B42] Challa K. N. R., Pagolu V. S., Panda G., Majhi B. (2016). An improved approach for prediction of Parkinson's disease using machine learning techniques, in 2016 International Conference on Signal Processing, Communication, Power and Embedded System (SCOPES) (Paralakhemundi: ), 1446–1451. 10.1109/SCOPES.2016.7955679 [DOI] [Google Scholar]

[B43] Chen Y., Storrs J., Tan L., Mazlack L. J., Lee J.-H., Lu L. J. (2014). Detecting brain structural changes as biomarker from magnetic resonance images using a local feature based SVM approach. J. Neurosci. Methods 221, 22–31. 10.1016/j.jneumeth.2013.09.001 [DOI] [PubMed] [Google Scholar]

[B44] Chen Y., Yang W., Long J., Zhang Y., Feng J., Li Y., et al. (2015). Discriminative analysis of Parkinson's disease based on whole-brain functional connectivity. PLoS ONE 10:e0124153. 10.1371/journal.pone.0124153 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B45] Chepkoech J. L., Walhovd K. B., Grydeland H., Fjell A. M., Alzheimer's Disease Neuroimaging Initiative (2016). Effects of change in FreeSurfer version on classification accuracy of patients with Alzheimer's disease and mild cognitive impairment. Hum. Brain Mapp. 37, 1831–1841. 10.1002/hbm.23139 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B46] Cherubini A., Morelli M., Nisticó R., Salsone M., Arabia G., Vasta R., et al. (2014a). Magnetic resonance support vector machine discriminates between Parkinson disease and progressive supranuclear palsy. Move. Disord. 29, 266–269. 10.1002/mds.25737 [DOI] [PubMed] [Google Scholar]

[B47] Cherubini A., Nisticó R., Novellino F., Salsone M., Nigro S., Donzuso G., et al. (2014b). Magnetic resonance support vector machine discriminates essential tremor with rest tremor from tremor-dominant Parkinson disease. Move. Disord. 29, 1216–1219. 10.1002/mds.25869 [DOI] [PubMed] [Google Scholar]

[B48] Choi H., Ha S., Im H. J., Paek S. H., Lee D. S. (2017). Refining diagnosis of Parkinson's disease with deep learning-based interpretation of dopamine transporter imaging. NeuroImage Clin. 16, 586–594. 10.1016/j.nicl.2017.09.010 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B49] Chou K. L. (2017). Diagnosis and Differential Diagnosis of Parkinson Disease. Waltham, MA: UpToDate. [Google Scholar]

[B50] Cibulka M., Brodnanova M., Grendar M., Grofik M., Kurca E., Pilchova I., et al. (2019). SNPs rs11240569, rs708727, and rs823156 in SLC41A1 do not discriminate between slovak patients with idiopathic parkinson's disease and healthy controls: statistics and machine-learning evidence. Int. J. Mol. Sci. 20:4688. 10.3390/ijms20194688 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B51] Cigdem O., Demirel H., Unay D. (2019). The performance of local-learning based clustering feature selection method on the diagnosis of Parkinson's disease using structural MRI, in 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC) (Bari: ), 1286–1291. 10.1109/SMC.2019.8914611 [DOI] [Google Scholar]

[B52] Çimen S., Bolat B. (2016). Diagnosis of Parkinson's disease by using ANN, in 2016 International Conference on Global Trends in Signal Processing, Information Computing and Communication (ICGTSPICC) (Jalgaon: ), 119–121. 10.1109/ICGTSPICC.2016.7955281 [DOI] [Google Scholar]

[B53] Contreras-Vidal J., Stelmach G. E. (1995). Effects of Parkinsonism on motor control. Life Sci. 58, 165–176. 10.1016/0024-3205(95)02237-6 [DOI] [PubMed] [Google Scholar]

[B54] Cook D. J., Schmitter-Edgecombe M., Dawadi P. (2015). Analyzing activity behavior and movement in a naturalistic environment using smart home techniques. IEEE J. Biomed. Health Inf. 19, 1882–1892. 10.1109/JBHI.2015.2461659 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B55] Cuzzolin F., Sapienza M., Esser P., Saha S., Franssen M. M., Collett J., et al. (2017). Metric learning for Parkinsonian identification from IMU gait measurements. Gait Posture 54, 127–132. 10.1016/j.gaitpost.2017.02.012 [DOI] [PubMed] [Google Scholar]

[B56] Dash S., Thulasiram R., Thulasiraman P. (2017). An enhanced chaos-based firefly model for Parkinson's disease diagnosis and classification, in 2017 International Conference on Information Technology (ICIT) (Bhubaneswar: ), 159–164. 10.1109/ICIT.2017.43 [DOI] [Google Scholar]

[B57] Dastjerd N. K., Sert O. C., Ozyer T., Alhajj R. (2019). Fuzzy classification methods based diagnosis of Parkinson's disease from speech test cases. Curr. Aging Sci. 12, 100–120. 10.2174/1874609812666190625140311 [DOI] [PubMed] [Google Scholar]

[B58] de Souza J. W. M., Alves S. S. A., Rebouças E. d,.S, Almeida J. S., Rebouças Filho P.P. (2018). A new approach to diagnose Parkinson's disease using a structural cooccurrence matrix for a similarity analysis. Comput. Intell. Neurosci. 2018:7613282. 10.1155/2018/7613282 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B59] Dhami D. S., Soni A., Page D., Natarajan S. (2017). Identifying Parkinson's patients: a functional gradient boosting approach. Artif. Intell. Med. Conf. Artif. Intell. Med. 10259, 332–337. 10.1007/978-3-319-59758-4_39 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B60] Dinesh A., He J. (2017). Using machine learning to diagnose Parkinson's disease from voice recordings, in 2017 IEEE MIT Undergraduate Research Technology Conference (URTC) (Cambridge, MA: ), 1–4. 10.1109/URTC.2017.8284216 [DOI] [Google Scholar]

[B61] Dinov I. D., Heavner B., Tang M., Glusman G., Chard K., Darcy M., et al. (2016). Predictive big data analytics: a study of parkinson's disease using large, complex, heterogeneous, incongruent, multi-source and incomplete observations. PLoS ONE 11:e0157077. 10.1371/journal.pone.0157077 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B62] Djurić-Jovičić M., Belić M., Stanković I., Radovanović S., Kostić V. S. (2017). Selection of gait parameters for differential diagnostics of patients with de novo Parkinson's disease. Neurol. Res. 39, 853–861. 10.1080/01616412.2017.1348690 [DOI] [PubMed] [Google Scholar]

[B63] Dorsey E. R., Elbaz A., Nichols E., Abd-Allah F., Abdelalim A., Adsuar J. C., et al. (2018). Global, regional, and national burden of Parkinson's disease, 1990–2016: a systematic analysis for the Global Burden of Disease Study 2016. Lancet Neurol. 17, 939–953. 10.1016/S1474-4422(18)30295-3 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B64] Dos Santos M. C. T., Scheller D., Schulte C., Mesa I. R., Colman P., Bujac S. R., et al. (2018). Evaluation of cerebrospinal fluid proteins as potential biomarkers for early stage Parkinson's disease diagnosis. PLoS ONE 13:e0206536. 10.1371/journal.pone.0206536 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B65] Dror B., Yanai E., Frid A., Peleg N., Goldenthal N., Schlesinger I., et al. (2014). Automatic assessment of Parkinson's disease from natural hands movements using 3D depth sensor, in 2014 IEEE 28th Convention of Electrical & Electronics Engineers in Israel (IEEEI) (Eilat: ), 1–5. 10.1109/EEEI.2014.7005763 [DOI] [Google Scholar]

[B66] Drotár P., Mekyska J., Rektorová I., Masarová L., Smékal Z., Faundez-Zanuy M. (2014). Analysis of in-air movement in handwriting: a novel marker for Parkinson's disease. Comp. Methods Progr. Biomed. 117, 405–411. 10.1016/j.cmpb.2014.08.007 [DOI] [PubMed] [Google Scholar]

[B67] Drotár P., Mekyska J., Rektorová I., Masarová L., Smékal Z., Faundez-Zanuy M. (2015). Decision support framework for Parkinson's disease based on novel handwriting markers. IEEE Trans. Neural Syst. Rehabil. Eng. 23, 508–516. 10.1109/TNSRE.2014.2359997 [DOI] [PubMed] [Google Scholar]

[B68] Drotár P., Mekyska J., Rektorová I., Masarová L., Smékal Z., Faundez-Zanuy M. (2016). Evaluation of handwriting kinematics and pressure for differential diagnosis of Parkinson's disease. Artif. Intell. Med. 67, 39–46. 10.1016/j.artmed.2016.01.004 [DOI] [PubMed] [Google Scholar]

[B69] Du G., Lewis M. M., Kanekar S., Sterling N. W., He L., Kong L., et al. (2017). Combined Diffusion tensor imaging and apparent transverse relaxation rate differentiate Parkinson disease and atypical Parkinsonism. Am. J. Neuroradiol. 38, 966–972. 10.3174/ajnr.A5136 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B70] Dua D., Graff C. (2018). UCI Machine Learning Repository. Irvine, CA: University of California, School of Information and Computer Science. [Google Scholar]

[B71] Erdogdu Sakar B., Serbes G., Sakar C. O. (2017). Analyzing the effectiveness of vocal features in early telediagnosis of Parkinson's disease. PLoS ONE 12:e0182428. 10.1371/journal.pone.0182428 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B72] Erro R., Schneider S. A., Stamelou M., Quinn N. P., Bhatia K. P. (2016). What do patients with scans without evidence of dopaminergic deficit (SWEDD) have? New evidence and continuing controversies. J. Neurol. Neurosurg. Psychiatry 87, 319–323. 10.1136/jnnp-2014-310256 [DOI] [PubMed] [Google Scholar]

[B73] Félix J. P., Vieira F. H. T., Cardoso Á. A., Ferreira M. V. G., Franco R. A. P., Ribeiro M. A., et al. (2019). A Parkinson's disease classification method: an approach using gait dynamics and detrended fluctuation analysis, in 2019 IEEE Canadian Conference of Electrical and Computer Engineering (CCECE) (Edmonton, AB: ), 1–4. 10.1109/CCECE.2019.8861759 [DOI] [Google Scholar]

[B74] Fernandes C., Fonseca L., Ferreira F., Gago M., Costa L., Sousa N., et al. (2018). Artificial neural networks classification of patients with Parkinsonism based on gait, in 2018 IEEE International Conference on Bioinformatics and Biomedicine (BIBM) (Madrid: ), 2024–2030. 10.1109/BIBM.2018.8621466 [DOI] [Google Scholar]

[B75] Fernandez K. M., Roemmich R. T., Stegemöller E. L., Amano S., Thompson A., Okun M. S., et al. (2013). Gait initiation impairments in both Essential Tremor and Parkinson's disease. Gait Posture 38, 956–961. 10.1016/j.gaitpost.2013.05.001 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B76] Focke N. K., Helms G., Scheewe S., Pantel P. M., Bachmann C. G., Dechent P., et al. (2011). Individual voxel-based subtype prediction can differentiate progressive supranuclear palsy from idiopathic Parkinson syndrome and healthy controls. Human Brain Mapp. 32, 1905–1915. 10.1002/hbm.21161 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B77] Frid A., Safra E. J., Hazan H., Lokey L. L., Hilu D., Manevitz L., et al. (2014). Computational diagnosis of Parkinson's disease directly from natural speech using machine learning techniques, in 2014 IEEE International Conference on Software Science, Technology and Engineering (Ramat Gan: ), 50–53. 10.1109/SWSTE.2014.17 [DOI] [Google Scholar]

[B78] Ghassemi N. H., Marxreiter F., Pasluosta C. F., Kugler P., Schlachetzki J., Schramm A., et al. (2016). Combined accelerometer and EMG analysis to differentiate essential tremor from Parkinson's disease. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2016, 672–675. 10.1109/EMBC.2016.7590791 [DOI] [PubMed] [Google Scholar]

[B79] Glaab E., Trezzi J.-P., Greuel A., Jäger C., Hodak Z., Drzezga A., et al. (2019). Integrative analysis of blood metabolomics and PET brain neuroimaging data for Parkinson's disease. Neurobiol. Dis. 124, 555–562. 10.1016/j.nbd.2019.01.003 [DOI] [PubMed] [Google Scholar]

[B80] Goldberger A. L., Amaral L. A., Glass L., Hausdorff J. M., Ivanov P. C., Mark R. G., et al. (2000). PhysioBank, PhysioToolkit, and PhysioNet: components of a new research resource for complex physiologic signals. Circulation 101, e215–e220. 10.1161/01.CIR.101.23.e215 [DOI] [PubMed] [Google Scholar]

[B81] Gunduz H. (2019). Deep learning-based parkinson's disease classification using vocal feature sets. IEEE Access 7, 115540–115551. 10.1109/ACCESS.2019.2936564 [DOI] [Google Scholar]

[B82] Haller S., Badoud S., Nguyen D., Barnaure I., Montandon M. L., Lovblad K. O., et al. (2013). Differentiation between Parkinson disease and other forms of Parkinsonism using support vector machine analysis of susceptibility-weighted imaging (SWI): initial results. Eur. Radiol. 23, 12–19. 10.1007/s00330-012-2579-y [DOI] [PubMed] [Google Scholar]

[B83] Haller S., Badoud S., Nguyen D., Garibotto V., Lovblad K. O., Burkhard P. R. (2012). Individual detection of patients with Parkinson disease using support vector machine analysis of diffusion tensor imaging data: initial results. Am. J. Neuroradiol. 33, 2123–2128. 10.3174/ajnr.A3126 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B84] Haq A. U., Li J., Memon M. H., Khan J., Din S. U., Ahad I., et al. (2018). Comparative analysis of the classification performance of machine learning classifiers and deep neural network classifier for prediction of Parkinson disease, in 2018 15th International Computer Conference on Wavelet Active Media Technology and Information Processing (ICCWAMTIP) (Chengdu: ), 101–106. [Google Scholar]

[B85] Haq A. U., Li J. P., Memon M. H., khan J., Malik A., Ahmad T., et al. (2019). Feature selection based on L1-Norm support vector machine and effective recognition system for Parkinson's disease using voice recordings. IEEE Access 7, 37718–37734. 10.1109/ACCESS.2019.2906350 [DOI] [Google Scholar]

[B86] Hariharan M., Polat K., Sindhu R. (2014). A new hybrid intelligent system for accurate detection of Parkinson's disease. Comput. Methods Programs Biomed. 113, 904–913. 10.1016/j.cmpb.2014.01.004 [DOI] [PubMed] [Google Scholar]

[B87] Hirschauer T. J., Adeli H., Buford J. A. (2015). Computer-aided diagnosis of Parkinson's disease using enhanced probabilistic neural network. J. Med. Syst. 39:179. 10.1007/s10916-015-0353-9 [DOI] [PubMed] [Google Scholar]

[B88] Hsu S.-Y., Lin H.-C., Chen T.-B., Du W.-C., Hsu Y.-H., Wu Y.-C., et al. (2019). Feasible classified models for Parkinson disease from (99m)Tc-TRODAT-1 SPECT imaging. Sensors 19:1740. 10.3390/s19071740 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B89] Huertas-Fernández I., García-Gómez F. J., García-Solís D., Benítez-Rivero S., Marín-Oyaga V. A., Jesús S., et al. (2015). Machine learning models for the differential diagnosis of vascular parkinsonism and Parkinson's disease using [(123)I]FP-CIT SPECT. Eur. J. Nucl. Med. Mol. Imag. 42, 112–119. 10.1007/s00259-014-2882-8 [DOI] [PubMed] [Google Scholar]

[B90] Huppertz H.-J., Möller L., Südmeyer M., Hilker R., Hattingen E., Egger K., et al. (2016). Differentiation of neurodegenerative parkinsonian syndromes by volumetric magnetic resonance imaging analysis and support vector machine classification. Mov. Disord. 31, 1506–1517. 10.1002/mds.26715 [DOI] [PubMed] [Google Scholar]

[B91] I K., Ulukaya S., Erdem O. (2019). Classification of Parkinson's disease using dynamic time warping, in 2019 27th Telecommunications Forum (TELFOR) (Belgrade: ), 1–4 [Google Scholar]

[B92] Illan I. A., Gorrz J. M., Ramirez J., Segovia F., Jimenez-Hoyuela J. M., Ortega Lozano S. J. (2012). Automatic assistance to Parkinson's disease diagnosis in DaTSCAN SPECT imaging. Med. Phys. 39, 5971–5980. 10.1118/1.4742055 [DOI] [PubMed] [Google Scholar]

[B93] Islam M. S., Parvez I., Hai D., Goswami P. (2014). Performance comparison of heterogeneous classifiers for detection of Parkinson's disease using voice disorder (dysphonia), in 2014 International Conference on Informatics, Electronics & Vision (ICIEV) (Dhaka: ), 1–7. 10.1109/ICIEV.2014.6850849 [DOI] [Google Scholar]

[B94] Jankovic J. (2008). Parkinson's disease: clinical features and diagnosis. J. Neurol. Neurosurg. Psychiatry 79, 368–376. 10.1136/jnnp.2007.131045 [DOI] [PubMed] [Google Scholar]

[B95] Javed F., Thomas I., Memedi M. (2018). A comparison of feature selection methods when using motion sensors data: a case study in Parkinson's disease. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2018, 5426–5429. 10.1109/EMBC.2018.8513683 [DOI] [PubMed] [Google Scholar]

[B96] Jeni L. A., Cohn J. F., De La Torre F. (2013). Facing imbalanced data–recommendations for the use of performance metrics, in 2013 Humaine Association Conference on Affective Computing and Intelligent Interaction (Geneva: IEEE; ), 245–251. 10.1109/ACII.2013.47 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B97] Ji W., Li Y. (2012). Energy-based feature ranking for assessing the dysphonia measurements in Parkinson detection. IET Signal Proc. 6, 300–305. 10.1049/iet-spr.2011.0186 [DOI] [Google Scholar]

[B98] Johnson S. J., Diener M. D., Kaltenboeck A., Birnbaum H. G., Siderowf A. D. (2013). An economic model of P arkinson's disease: implications for slowing progression in the United States. Move. Disord. 28, 319–326. 10.1002/mds.25328 [DOI] [PubMed] [Google Scholar]

[B99] Joshi D., Khajuria A., Joshi P. (2017). An automatic non-invasive method for Parkinson's disease classification. Comput. Methods Programs Biomed. 145, 135–145. 10.1016/j.cmpb.2017.04.007 [DOI] [PubMed] [Google Scholar]

[B100] Junior S. B., Costa V. G. T., Chen S., Guido R. C. (2018). U-healthcare system for pre-diagnosis of Parkinson's disease from voice signal, in 2018 IEEE International Symposium on Multimedia (ISM) (Taichung: ), 271–274. [Google Scholar]

[B101] Kamagata K., Zalesky A., Hatano T., Di Biase M. A., El Samad O., Saiki S., et al. (2017). Connectome analysis with diffusion MRI in idiopathic Parkinson's disease: evaluation using multi-shell, multi-tissue, constrained spherical deconvolution. NeuroImage. Clin. 17, 518–529. 10.1016/j.nicl.2017.11.007 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B102] Karapinar Senturk Z. (2020). Early diagnosis of Parkinson's disease using machine learning algorithms. Med. Hypoth. 138:109603. 10.1016/j.mehy.2020.109603 [DOI] [PubMed] [Google Scholar]

[B103] Kazeminejad A., Golbabaei S., Soltanian-Zadeh H. (2017). Graph theoretical metrics and machine learning for diagnosis of Parkinson's disease using rs-fMRI, in 2017 Artificial Intelligence and Signal Processing Conference (AISP) (Shiraz: ), 134–139. 10.1109/AISP.2017.8324124 [DOI] [Google Scholar]

[B104] Khan M. M., Mendes A., Chalup S. K. (2018). Evolutionary Wavelet Neural Network ensembles for breast cancer and Parkinson's disease prediction. PLoS ONE 13:e0192192. 10.1371/journal.pone.0192192 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B105] Khatamino P., I C., Özyilmaz L. (2018). A deep learning-CNN based system for medical diagnosis: an application on Parkinson's disease handwriting drawings, in 2018 6th International Conference on Control Engineering & Information Technology (CEIT) (Istanbul: ), 1–6. 10.1109/CEIT.2018.8751879 [DOI] [Google Scholar]

[B106] Khoury N., Attal F., Amirat Y., Oukhellou L., Mohammed S. (2019). Data-driven based approach to aid Parkinson's disease diagnosis. Sensors 19:242. 10.3390/s19020242 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B107] Kiryu S., Yasaka K., Akai H., Nakata Y., Sugomori Y., Hara S., et al. (2019). Deep learning to differentiate parkinsonian disorders separately using single midsagittal MR imaging: a proof of concept study. Eur. Radiol. 29, 6891–6899. 10.1007/s00330-019-06327-0 [DOI] [PubMed] [Google Scholar]

[B108] Klein Y., Djaldetti R., Keller Y., Bachelet I. (2017). Motor dysfunction and touch-slang in user interface data. Scientific reports 7:4702. 10.1038/s41598-017-04893-1 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B109] Klomsae A., Auephanwiriyakul S., Theera-Umpon N. (2018). String grammar unsupervised possibilistic fuzzy C-medians for gait pattern classification in patients with neurodegenerative diseases. Comput. Intell. Neurosci. 2018:1869565. 10.1155/2018/1869565 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B110] Koçer A., Oktay A. B. (2016). Nintendo Wii assessment of Hoehn and Yahr score with Parkinson's disease tremor. Technol. Health Care 24, 185–191. 10.3233/THC-151124 [DOI] [PubMed] [Google Scholar]

[B111] Kostikis N., Hristu-Varsakelis D., Arnaoutoglou M., Kotsavasiloglou C. (2015). A smartphone-based tool for assessing Parkinsonian hand tremor. IEEE J. Biomed. Health Inf. 19, 1835–1842. 10.1109/JBHI.2015.2471093 [DOI] [PubMed] [Google Scholar]

[B112] Kowal S. L., Dall T. M., Chakrabarti R., Storm M. V., Jain A. (2013). The current and projected economic burden of Parkinson's disease in the United States. Move. Disord. 28, 311–318. 10.1002/mds.25292 [DOI] [PubMed] [Google Scholar]

[B113] Kraipeerapun P., Amornsamankul S. (2015). Using stacked generalization and complementary neural networks to predict Parkinson's disease, in 2015 11th International Conference on Natural Computation (ICNC) (Zhangjiajie: ), 1290–1294. 10.1109/ICNC.2015.7378178 [DOI] [Google Scholar]

[B114] Kugler P., Jaremenko C., Schlachetzki J., Winkler J., Klucken J., Eskofier B. (2013). Automatic recognition of Parkinson's disease using surface electromyography during standardized gait tests. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2013, 5781–5784. 10.1109/EMBC.2013.6610865 [DOI] [PubMed] [Google Scholar]

[B115] Kuhner A., Schubert T., Cenciarini M., Wiesmeier I. K., Coenen V. A., Burgard W., et al. (2017). Correlations between motor symptoms across different motor tasks, quantified via random forest feature classification in Parkinson's disease. Front. Neurol. 8:607. 10.3389/fneur.2017.00607 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B116] Kuresan H., Samiappan D., Masunda S. (2019). Fusion of WPT and MFCC feature extraction in Parkinson's disease diagnosis. Technol. Health Care 27, 363–372. 10.3233/THC-181306 [DOI] [PubMed] [Google Scholar]

[B117] Kwon D.-Y., Kwon Y., Kim J.-W. (2018). Quantitative analysis of finger and forearm movements in patients with off state early stage Parkinson's disease and scans without evidence of dopaminergic deficit (SWEDD). Parkinsonism Related Disord. 57, 33–38. 10.1016/j.parkreldis.2018.07.012 [DOI] [PubMed] [Google Scholar]

[B118] Lacy S. E., Smith S. L., Lones M. A. (2018). Using echo state networks for classification: A case study in Parkinson's disease diagnosis. Artif. Intell. Med. 86, 53–59. 10.1016/j.artmed.2018.02.002 [DOI] [PubMed] [Google Scholar]

[B119] Lee M. J., Kim S. L., Lyoo C. H., Lee M. S. (2014). Kinematic analysis in patients with Parkinson's disease and SWEDD. J. Parkinsons Dis. 4, 421–430. 10.3233/JPD-130233 [DOI] [PubMed] [Google Scholar]

[B120] Lei H., Huang Z., Zhou F., Elazab A., Tan E.-L., Li H., et al. (2019). Parkinson's disease diagnosis via joint learning from multiple modalities and relations. IEEE J. Biomed. Health Inf. 23, 1437–1449. 10.1109/JBHI.2018.2868420 [DOI] [PubMed] [Google Scholar]

[B121] Lewitt P. A., Li J., Lu M., Beach T. G., Adler C. H., Guo L., et al. (2013). 3-hydroxykynurenine and other Parkinson's disease biomarkers discovered by metabolomic analysis. Move. Disord. 28, 1653–1660. 10.1002/mds.25555 [DOI] [PubMed] [Google Scholar]

[B122] Li Q., Chen H., Huang H., Zhao X., Cai Z., Tong C., et al. (2017). An enhanced grey wolf optimization based feature selection wrapped kernel extreme learning machine for medical diagnosis. Comput. Math. Methods Med. 2017:9512741. 10.1155/2017/9512741 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B123] Li S., Lei H., Zhou F., Gardezi J., Lei B. (2019). Longitudinal and Multi-modal Data Learning for Parkinson's Disease Diagnosis via Stacked Sparse Auto-encoder, in 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019) (Venice: ), 384–387. 10.1109/ISBI.2019.8759385 [DOI] [Google Scholar]

[B124] Liu H., Du G., Zhang L., Lewis M. M., Wang X., Yao T., et al. (2016). Folded concave penalized learning in identifying multimodal MRI marker for Parkinson's disease. J. Neurosci. Methods 268, 1–6. 10.1016/j.jneumeth.2016.04.016 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B125] Liu L., Wang Q., Adeli E., Zhang L., Zhang H., Shen D. (2016). Feature selection based on iterative canonical correlation analysis for automatic diagnosis of Parkinson's disease. Med. Image Comput. Computer Assist. Interv. 9901, 1–8. 10.1007/978-3-319-46723-8_1 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B126] Ma C., Ouyang J., Chen H.-L., Zhao X.-H. (2014). An efficient diagnosis system for Parkinson's disease using kernel-based extreme learning machine with subtractive clustering features weighting approach. Computat. Math. Methods Med. 2014:985789. 10.1155/2014/985789 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B127] Ma H., Tan T., Zhou H., Gao T. (2016). Support Vector Machine-recursive feature elimination for the diagnosis of Parkinson disease based on speech analysis, in 2016 Seventh International Conference on Intelligent Control and Information Processing (ICICIP) (Siem Reap: ), 34–40. 10.1109/ICICIP.2016.7885912 [DOI] [Google Scholar]

[B128] Maass F., Michalke B., Leha A., Boerger M., Zerr I., Koch J.-C., et al. (2018). Elemental fingerprint as a cerebrospinal fluid biomarker for the diagnosis of Parkinson's disease. J. Neurochemistry 145, 342–351. 10.1111/jnc.14316 [DOI] [PubMed] [Google Scholar]

[B129] Maass F., Michalke B., Willkommen D., Leha A., Schulte C., Tönges L., et al. (2020). Elemental fingerprint: reassessment of a cerebrospinal fluid biomarker for Parkinson's disease. Neurobiol. Dis. 134:104677. 10.1016/j.nbd.2019.104677 [DOI] [PubMed] [Google Scholar]

[B130] Mabrouk R., Chikhaoui B., Bentabet L. (2019). Machine learning based classification using clinical and DaTSCAN SPECT imaging features: a study on Parkinson's disease and SWEDD. IEEE Trans. Rad. Plasma Med. Sci. 3, 170–177. 10.1109/TRPMS.2018.2877754 [DOI] [Google Scholar]

[B131] Mandal I., Sairam N. (2013). Accurate telemonitoring of Parkinson's disease diagnosis using robust inference system. Int. J. Med. Informatics 82, 359–377. 10.1016/j.ijmedinf.2012.10.006 [DOI] [PubMed] [Google Scholar]

[B132] Marar S., Swain D., Hiwarkar V., Motwani N., Awari A. (2018). Predicting the occurrence of Parkinson's disease using various classification models, in 2018 International Conference on Advanced Computation and Telecommunication (ICACAT) (Bhopal: ), 1–5. 10.1109/ICACAT.2018.8933579 [DOI] [Google Scholar]

[B133] Marek K., Jennings D., Lasch S., Siderowf A., Tanner C., Simuni T., et al. (2011). The parkinson progression marker initiative (PPMI). Progress Neurobiol. 95, 629–635. 10.1016/j.pneurobio.2011.09.005 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B134] Martínez M., Villagra F., Castellote J. M., Pastor M. A. (2018). Kinematic and kinetic patterns related to free-walking in Parkinson's disease. Sensors 18:4224. 10.3390/s18124224 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B135] Martinez-Murcia F. J., Górriz J. M., Ramírez J., Ortiz A. (2018). Convolutional neural networks for neuroimaging in Parkinson's disease: is preprocessing needed? Int. J. Neural Syst. 28:1850035. 10.1142/S0129065718500351 [DOI] [PubMed] [Google Scholar]

[B136] Memedi M., Sadikov A., Groznik V., Žabkar J., Možina M., Bergquist F., et al. (2015). Automatic spiral analysis for objective assessment of motor symptoms in Parkinson's disease. Sensors 15, 23727–23744. 10.3390/s150923727 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B137] Mittra Y., Rustagi V. (2018). Classification of subjects with Parkinson's disease using gait data analysis, in 2018 International Conference on Automation and Computational Engineering (ICACE) (Greater Noida: ), 84–89. 10.1109/ICACE.2018.8687022 [DOI] [Google Scholar]

[B138] Moharkan Z. A., Garg H., Chodhury T., Kumar P. (2017). A classification based Parkinson detection system, in 2017 International Conference On Smart Technologies For Smart Nation (SmartTechCon) (Bengaluru: ), 1509–1513. 10.1109/SmartTechCon.2017.8358616 [DOI] [Google Scholar]

[B139] Moher D., Liberati A., Tetzlaff J., Altman D. G. (2009). Preferred reporting items for systematic reviews and meta-analyses: the PRISMA statement. Ann. Inter. Med. 151, 264–269. 10.7326/0003-4819-151-4-200908180-00135 [DOI] [PubMed] [Google Scholar]

[B140] Montaña D., Campos-Roca Y., Pérez C. J. (2018). A Diadochokinesis-based expert system considering articulatory features of plosive consonants for early detection of Parkinson's disease. Comp. Methods Programs Biomed. 154, 89–97. 10.1016/j.cmpb.2017.11.010 [DOI] [PubMed] [Google Scholar]

[B141] Morisi R., Manners D. N., Gnecco G., Lanconelli N., Testa C., Evangelisti S., et al. (2018). Multi-class parkinsonian disorders classification with quantitative MR markers and graph-based features using support vector machines. Parkinsonism Relat. Disord. 47, 64–70. 10.1016/j.parkreldis.2017.11.343 [DOI] [PubMed] [Google Scholar]

[B142] Mucha J., Mekyska J., Faundez-Zanuy M., Lopez-De-Ipina K., Zvoncak V., Galaz Z., et al. (2018). Advanced Parkinson's disease dysgraphia analysis based on fractional derivatives of online handwriting, in 2018 10th International Congress on Ultra Modern Telecommunications and Control Systems and Workshops (ICUMT) (Moscow: ), 1–6. 10.1109/ICUMT.2018.8631265 [DOI] [Google Scholar]

[B143] Nicastro N., Wegrzyk J., Preti M. G., Fleury V., Van de Ville D., Garibotto V., et al. (2019). Classification of degenerative parkinsonism subtypes by support-vector-machine analysis and striatal (123)I-FP-CIT indices. J. Neurol. 266, 1771–1781. 10.1007/s00415-019-09330-z [DOI] [PMC free article] [PubMed] [Google Scholar]

[B144] Nõmm S., Bard,õš K., Toomela A., Medijainen K., Taba P. (2018). Detailed analysis of the Luria's alternating seriestests for Parkinson's disease diagnostics, in 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA) (Orlando, FL: ), 1347–1352. 10.1109/ICMLA.2018.00219 [DOI] [Google Scholar]

[B145] Nunes A., Silva G., Duque C., Januário C., Santana I., Ambrósio A. F., et al. (2019). Retinal texture biomarkers may help to discriminate between Alzheimer's, Parkinson's, and healthy controls. PLoS One 14:e0218826. 10.1371/journal.pone.0218826 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B146] Nuvoli S., Spanu A., Fravolini M. L., Bianconi F., Cascianelli S., Madeddu G., et al. (2019). [(123)I]Metaiodobenzylguanidine (MIBG) cardiac scintigraphy and automated classification techniques in Parkinsonian disorders. Mol. Imaging Biol. 22, 703–710. 10.1007/s11307-019-01406-6 [DOI] [PubMed] [Google Scholar]

[B147] Oliveira F. P. M., Castelo-Branco M. (2015). Computer-aided diagnosis of Parkinson's disease based on [(123)I]FP-CIT SPECT binding potential images, using the voxels-as-features approach and support vector machines. J. Neural Eng. 12:026008. 10.1088/1741-2560/12/2/026008 [DOI] [PubMed] [Google Scholar]

[B148] Oliveira F. P. M., Faria D. B., Costa D. C., Castelo-Branco M., Tavares J. M. R. S. (2018). Extraction, selection and comparison of features for an effective automated computer-aided diagnosis of Parkinson's disease based on [(123)I]FP-CIT SPECT images. Eur. J. Nucl. Med. Mol. Imaging 45, 1052–1062. 10.1007/s00259-017-3918-7 [DOI] [PubMed] [Google Scholar]

[B149] Oliveira H. M., Machado A. R. P., Andrade A. O. (2018a). On the use of t-distributed stochastic neighbor embedding for data visualization and classification of individuals with Parkinson's disease. Comput. Math. Methods Med. 2018:8019232. 10.1155/2018/8019232 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B150] Opara J., Brola W., Leonardi M., Błaszczyk B. (2012). Quality of life in Parkinsons disease. J. Med. Life 5:375. [PMC free article] [PubMed] [Google Scholar]

[B151] Oung Q. W., Hariharan M., Lee H. L., Basah S. N., Sarillee M., Lee C. H. (2015). Wearable multimodal sensors for evaluation of patients with Parkinson disease, in 2015 IEEE International Conference on Control System, Computing and Engineering (ICCSCE) (Penang: ), 269–274. 10.1109/ICCSCE.2015.7482196 [DOI] [Google Scholar]

[B152] Ozcift A. (2012). SVM feature selection based rotation forest ensemble classifiers to improve computer-aided diagnosis of Parkinson disease. J. Med. Syst. 36, 2141–2147. 10.1007/s10916-011-9678-1 [DOI] [PubMed] [Google Scholar]

[B153] Ozcift A., Gulten A. (2011). Classifier ensemble construction with rotation forest to improve medical diagnosis performance of machine learning algorithms. Comp. Methods Progr. Biomed. 104, 443–451. 10.1016/j.cmpb.2011.03.018 [DOI] [PubMed] [Google Scholar]

[B154] Pahuja G., Nagabhushan T. N. (2016). A novel GA-ELM approach for Parkinson's disease detection using brain structural T1-weighted MRI data, in 2016 Second International Conference on Cognitive Computing and Information Processing (CCIP) (Mysuru: ), 1–6. 10.1109/CCIP.2016.7802848 [DOI] [Google Scholar]

[B155] Palumbo B., Fravolini M. L., Buresta T., Pompili F., Forini N., Nigro P., et al. (2014). Diagnostic accuracy of Parkinson disease by support vector machine (SVM) analysis of 123I-FP-CIT brain SPECT data: implications of putaminal findings and age. Medicine 93:e228. 10.1097/MD.0000000000000228 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B156] Papadopoulos A., Kyritsis K., Klingelhoefer L., Bostanjopoulou S., Chaudhuri K. R., Delopoulos A. (2019). Detecting Parkinsonian tremor from IMU data collected in-the-wild using deep multiple-instance learning. IEEE J. Biomed. Health Inform. 24, 2559–2569. 10.1109/JBHI.2019.2961748 [DOI] [PubMed] [Google Scholar]

[B157] Papavasileiou I., Zhang W., Wang X., Bi J., Zhang L., Han S. (2017). Classification of neurological gait disorders using multi-task feature learning, in 2017 IEEE/ACM International Conference on Connected Health: Applications, Systems and Engineering Technologies (CHASE) (Philadelphia, PA: ), 195–204. 10.1109/CHASE.2017.78 [DOI] [Google Scholar]

[B158] Peker M. (2016). A decision support system to improve medical diagnosis using a combination of k-medoids clustering based attribute weighting and SVM. J. Med. Syst. 40:116. 10.1007/s10916-016-0477-6 [DOI] [PubMed] [Google Scholar]

[B159] Peng B., Wang S., Zhou Z., Liu Y., Tong B., Zhang T., et al. (2017). A multilevel-ROI-features-based machine learning method for detection of morphometric biomarkers in Parkinson's disease. Neurosci. Lett. 651, 88–94. 10.1016/j.neulet.2017.04.034 [DOI] [PubMed] [Google Scholar]

[B160] Peng B., Zhou Z., Geng C., Tong B., Zhou Z., Zhang T., et al. (2016). Computer aided analysis of cognitive disorder in patients with Parkinsonism using machine learning method with multilevel ROI-based features, in 2016 9th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI) (Datong: ), 1792–1796. 10.1109/CISP-BMEI.2016.7853008 [DOI] [Google Scholar]

[B161] Pereira C. R., Pereira D. R., da Silva F. A., Hook C., Weber S. A., Pereira L. A., et al. (2015). A step towards the automated diagnosis of parkinson's disease: Analyzing handwriting movements, in 2015 IEEE 28th International Symposium on Computer-Based Medical Systems (Sao Carlos: IEEE; ), 171–176. 10.1109/CBMS.2015.34 [DOI] [Google Scholar]

[B162] Pereira C. R., Pereira D. R., Rosa G. H., Albuquerque V. H. C., Weber S. A. T., Hook C., et al. (2018). Handwritten dynamics assessment through convolutional neural networks: An application to Parkinson's disease identification. Artif. Intell. Med. 87, 67–77. 10.1016/j.artmed.2018.04.001 [DOI] [PubMed] [Google Scholar]

[B163] Pereira C. R., Pereira D. R., Silva F. A., Masieiro J. P., Weber S. A. T., Hook C., et al. (2016a). A new computer vision-based approach to aid the diagnosis of Parkinson's disease. Comp. Methods Progr. Biomed. 136, 79–88. 10.1016/j.cmpb.2016.08.005 [DOI] [PubMed] [Google Scholar]

[B164] Pereira C. R., Pereira D. R., Weber S. A., Hook C., de Albuquerque V. H. C., Papa J. P. (2019). A survey on computer-assisted Parkinson's disease diagnosis. Artif. Intell. Med. 95, 48–63. 10.1016/j.artmed.2018.08.007 [DOI] [PubMed] [Google Scholar]

[B165] Pereira C. R., Weber S. A. T., Hook C., Rosa G. H., Papa J. P. (2016b). Deep learning-aided Parkinson's disease diagnosis from handwritten dynamics, in 2016 29th SIBGRAPI Conference on Graphics, Patterns and Images (SIBGRAPI) (São Paulo: ), 340–346. 10.1109/SIBGRAPI.2016.054 [DOI] [Google Scholar]

[B166] Pham H. N., Do T. T. T., Chan K. Y. J., Sen G., Han A. Y. K., Lim P., et al. (2019). Multimodal detection of Parkinson disease based on vocal and improved spiral test, in 2019 International Conference on System Science and Engineering (ICSSE) (Dong Hoi: ), 279–284. 10.1109/ICSSE.2019.8823309 [DOI] [Google Scholar]

[B167] Pham T. D. (2018). Pattern analysis of computer keystroke time series in healthy control and early-stage Parkinson's disease subjects using fuzzy recurrence and scalable recurrence network features. J. Neurosci. Methods 307, 194–202. 10.1016/j.jneumeth.2018.05.019 [DOI] [PubMed] [Google Scholar]

[B168] Pham T. D., Yan H. (2018). Tensor decomposition of gait dynamics in Parkinson's disease. IEEE Trans. Bio-Med. Eng. 65, 1820–1827. 10.1109/TBME.2017.2779884 [DOI] [PubMed] [Google Scholar]

[B169] Postuma R. B., Berg D., Stern M., Poewe W., Olanow C. W., Oertel W., et al. (2015). MDS clinical diagnostic criteria for Parkinson's disease. Move. Disord. 30, 1591–1601. 10.1002/mds.26424 [DOI] [PubMed] [Google Scholar]

[B170] Prashanth R., Dutta Roy S. (2018). Early detection of Parkinson's disease through patient questionnaire and predictive modelling. In. J. Med. Inform. 119, 75–87. 10.1016/j.ijmedinf.2018.09.008 [DOI] [PubMed] [Google Scholar]

[B171] Prashanth R., Dutta Roy S., Mandal P. K., Ghosh S. (2016). High-accuracy detection of early Parkinson's disease through multimodal features and machine learning. Int. J. Med. Inform. 90, 13–21. 10.1016/j.ijmedinf.2016.03.001 [DOI] [PubMed] [Google Scholar]

[B172] Prashanth R., Roy S. D., Mandal P. K., Ghosh S. (2014). Parkinson's disease detection using olfactory loss and REM sleep disorder features, in Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2014, 5764–5767. 10.1109/EMBC.2014.6944937 [DOI] [PubMed] [Google Scholar]

[B173] Prashanth R., Roy S. D., Mandal P. K., Ghosh S. (2017). High-accuracy classification of Parkinson's disease through shape analysis and surface fitting in 123I-Ioflupane SPECT imaging. IEEE J. Biomed. Health Inform. 21, 794–802. 10.1109/JBHI.2016.2547901 [DOI] [PubMed] [Google Scholar]

[B174] Prince J., Andreotti F., Vos M. D. (2019). Multi-source ensemble learning for the remote prediction of Parkinson's disease in the presence of source-wise missing data. IEEE Trans. Biomed. Eng. 66, 1402–1411. 10.1109/TBME.2018.2873252 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B175] Prince J., de Vos M. (2018). A deep learning framework for the remote detection of Parkinson's disease using smart-phone sensor data, in 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) (Honolulu, HI: ), 3144–3147. 10.1109/EMBC.2018.8512972 [DOI] [PubMed] [Google Scholar]

[B176] Ramdhani R. A., Khojandi A., Shylo O., Kopell B. H. (2018). Optimizing clinical assessments in Parkinson's disease through the use of wearable sensors and data driven modeling. Front. Comput. Neurosci. 12:72. 10.3389/fncom.2018.00072 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B177] Reyes J. F., Montealegre J. S., Castano Y. J., Urcuqui C., Navarro A. (2019). LSTM and convolution networks exploration for Parkinson's diagnosis, in 2019 IEEE Colombian Conference on Communications and Computing (COLCOM) (Barranquilla: ), 1–4. 10.1109/ColComCon.2019.8809160 [DOI] [Google Scholar]

[B178] Ribeiro L. C. F., Afonso L. C. S., Papa J. P. (2019). Bag of samplings for computer-assisted Parkinson's disease diagnosis based on recurrent neural networks. Comp. Biol. Med. 115:103477. 10.1016/j.compbiomed.2019.103477 [DOI] [PubMed] [Google Scholar]

[B179] Ricci M., Lazzaro G. D., Pisani A., Mercuri N. B., Giannini F., Saggio G. (2020). Assessment of motor impairments in early untreated parkinson's disease patients: the wearable electronics impact. IEEE J. Biomed. Health Inform. 24, 120–130. 10.1109/JBHI.2019.2903627 [DOI] [PubMed] [Google Scholar]

[B180] Rios-Urrego C. D., Vásquez-Correa J. C., Vargas-Bonilla J. F., Nöth E., Lopera F., Orozco-Arroyave J. R. (2019). Analysis and evaluation of handwriting in patients with Parkinson's disease using kinematic, geometrical, and non-linear features. Comput. Methods Progr. Biomed. 173, 43–52. 10.1016/j.cmpb.2019.03.005 [DOI] [PubMed] [Google Scholar]

[B181] Rovini E., Maremmani C., Moschetti A., Esposito D., Cavallo F. (2018). Comparative motor pre-clinical assessment in parkinson's disease using supervised machine learning approaches. Annals Biomed. Eng. 46, 2057–2068. 10.1007/s10439-018-2104-9 [DOI] [PubMed] [Google Scholar]

[B182] Rovini E., Moschetti A., Fiorini L., Esposito D., Maremmani C., Cavallo F. (2019). Wearable sensors for prodromal motor assessment of parkinson's disease using supervised learning, in 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), 4318–4321. 10.1109/EMBC.2019.8856804 [DOI] [PubMed] [Google Scholar]

[B183] Rubbert C., Mathys C., Jockwitz C., Hartmann C. J., Eickhoff S. B., Hoffstaedter F., et al. (2019). Machine-learning identifies Parkinson's disease patients based on resting-state between-network functional connectivity. Br. J. Radiol. 92:20180886. 10.1259/bjr.20180886 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B184] Sakar B. E., Isenkul M. E., Sakar C. O., Sertbas A., Gurgen F., Delil S., et al. (2013). Collection and analysis of a Parkinson speech dataset with multiple types of sound recordings. IEEE J. Biomed. Health Inform. 17, 828–834. 10.1109/JBHI.2013.2245674 [DOI] [PubMed] [Google Scholar]

[B185] Salvatore C., Cerasa A., Castiglioni I., Gallivanone F., Augimeri A., Lopez M., et al. (2014). Machine learning on brain MRI data for differential diagnosis of Parkinson's disease and progressive supranuclear palsy. J. Neurosci. Methods 222, 230–237. 10.1016/j.jneumeth.2013.11.016 [DOI] [PubMed] [Google Scholar]

[B186] Sayaydeha O. N. A., Mohammad M. F. (2019). Diagnosis of the Parkinson disease using enhanced fuzzy min-max neural network and OneR attribute evaluation method, in 2019 International Conference on Advanced Science and Engineering (ICOASE) (Zakho-Duhok: ), 64–69. 10.1109/ICOASE.2019.8723870 [DOI] [Google Scholar]

[B187] Scherer R. W., Saldanha I. J. (2019). How should systematic reviewers handle conference abstracts? A view from the trenches. Syst. Rev. 8:264. 10.1186/s13643-019-1188-0 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B188] Segovia F., Górriz J. M., Ramírez J., Levin J., Schuberth M., Brendel M., et al. (2015). Analysis of 18F-DMFP PET data using multikernel classification in order to assist the diagnosis of Parkinsonism, in 2015 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC) (San Diego, CA: ), 1–4. 10.1109/NSSMIC.2015.7582227 [DOI] [Google Scholar]

[B189] Segovia F., Górriz J. M., Ramírez J., Martínez-Murcia F. J., Castillo-Barnes D. (2019). Assisted diagnosis of Parkinsonism based on the striatal morphology. Int. J. Neural Syst. 29:1950011. 10.1142/S0129065719500114 [DOI] [PubMed] [Google Scholar]

[B190] Shahsavari M. K., Rashidi H., Bakhsh H. R. (2016). Efficient classification of Parkinson's disease using extreme learning machine and hybrid particle swarm optimization, in 2016 4th International Conference on Control, Instrumentation, and Automation (ICCIA) (Qazvin: ), 148–154. 10.1109/ICCIAutom.2016.7483152 [DOI] [Google Scholar]

[B191] Shamir R., Klein C., Amar D., Vollstedt E.-J., Bonin M., Usenovic M., et al. (2017). Analysis of blood-based gene expression in idiopathic Parkinson disease. Neurology 89, 1676–1683. 10.1212/WNL.0000000000004516 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B192] Sheibani R., Nikookar E., Alavi S. E. (2019). An ensemble method for diagnosis of Parkinson's disease based on voice measurements. J. Med. Signals Sens. 9, 221–226. 10.4103/jmss.JMSS_57_18 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B193] Shen T., Jiang J., Lin W., Ge J., Wu P., Zhou Y., et al. (2019). Use of overlapping group LASSO sparse deep belief network to discriminate Parkinson's disease and normal control. Front. Neurosci. 13:396. 10.3389/fnins.2019.00396 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B194] Shi J., Yan M., Dong Y., Zheng X., Zhang Q., An H. (2018). Multiple kernel learning based classification of Parkinson's disease with multi-modal transcranial sonography, in 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) (Honolulu, HI: ), 61–64. 10.1109/EMBC.2018.8512194 [DOI] [PubMed] [Google Scholar]

[B195] Shinde S., Prasad S., Saboo Y., Kaushick R., Saini J., Pal P. K., et al. (2019). Predictive markers for Parkinson's disease using deep neural nets on neuromelanin sensitive MRI. NeuroImage. Clin. 22:101748. 10.1016/j.nicl.2019.101748 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B196] Singh G., Samavedham L. (2015). Unsupervised learning based feature extraction for differential diagnosis of neurodegenerative diseases: a case study on early-stage diagnosis of Parkinson disease. J. Neurosci. Methods 256, 30–40. 10.1016/j.jneumeth.2015.08.011 [DOI] [PubMed] [Google Scholar]

[B197] Singh G., Samavedham L., Lim E. C.-H., Alzheimer's Disease Neuroimaging I., Parkinson Progression Marker I. (2018). Determination of imaging biomarkers to decipher disease trajectories and differential diagnosis of neurodegenerative diseases (DIsease TreND). J. Neurosci. Methods 305, 105–116. 10.1016/j.jneumeth.2018.05.009 [DOI] [PubMed] [Google Scholar]

[B198] Stoessel D., Schulte C., Teixeira Dos Santos M. C., Scheller D., Rebollo-Mesa I., Deuschle C., et al. (2018). Promising metabolite profiles in the plasma and CSF of early clinical Parkinson's disease. Front. Aging Neurosci. 10:51. 10.3389/fnagi.2018.00051 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B199] Surangsrirat D., Thanawattano C., Pongthornseri R., Dumnin S., Anan C., Bhidayasiri R. (2016). Support vector machine classification of Parkinson's disease and essential tremor subjects based on temporal fluctuation. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2016, 6389–6392. 10.1109/EMBC.2016.7592190 [DOI] [PubMed] [Google Scholar]

[B200] Sztahó D., Tulics M. G., Vicsi K., Valálik I. (2017). Automatic estimation of severity of Parkinson's disease based on speech rhythm related features, in 2017 8th IEEE International Conference on Cognitive Infocommunications (CogInfoCom) (Debrecen: ), 000011–000016. 10.1109/CogInfoCom.2017.8268208 [DOI] [Google Scholar]

[B201] Sztahó D., Valálik I., Vicsi K. (2019). Parkinson's disease severity estimation on Hungarian speech using various speech tasks, in 2019 International Conference on Speech Technology and Human-Computer Dialogue (SpeD) (Timisoara: ), 1–6. 10.1109/SPED.2019.8906277 [DOI] [Google Scholar]

[B202] Tagare H. D., DeLorenzo C., Chelikani S., Saperstein L., Fulbright R. K. (2017). Voxel-based logistic analysis of PPMI control and Parkinson's disease DaTscans. NeuroImage 152, 299–311. 10.1016/j.neuroimage.2017.02.067 [DOI] [PubMed] [Google Scholar]

[B203] Tahavori F., Stack E., Agarwal V., Burnett M., Ashburn A., Hoseinitabatabaei S. A., et al. (2017). Physical activity recognition of elderly people and people with parkinson's (PwP) during standard mobility tests using wearable sensors, in 2017 International Smart Cities Conference (ISC2) (Wuxi: ), 1–4. 10.1109/ISC2.2017.8090858 [DOI] [Google Scholar]

[B204] Taleb C., Khachab M., Mokbel C., Likforman-Sulem L. (2019). Visual representation of online handwriting time series for deep learning Parkinson's disease detection, in 2019 International Conference on Document Analysis and Recognition Workshops (ICDARW) (Sydney, NSW: ), 25–30. 10.1109/ICDARW.2019.50111 [DOI] [Google Scholar]

[B205] Tang Y., Meng L., Wan C. M., Liu Z. H., Liao W. H., Yan X. X., et al. (2017). Identifying the presence of Parkinson's disease using low-frequency fluctuations in BOLD signals. Neurosci. Lett. 645, 1–6. 10.1016/j.neulet.2017.02.056 [DOI] [PubMed] [Google Scholar]

[B206] Taylor J. C., Fenner J. W. (2017). Comparison of machine learning and semi-quantification algorithms for (I123)FP-CIT classification: the beginning of the end for semi-quantification? EJNMMI Phys. 4:29. 10.1186/s40658-017-0196-1 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B207] Tien I., Glaser S. D., Aminoff M. J. (2010). Characterization of gait abnormalities in Parkinson's disease using a wireless inertial sensor system, in Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2010, 3353–3356. 10.1109/IEMBS.2010.5627904 [DOI] [PubMed] [Google Scholar]

[B208] Tracy J. M., Özkanca Y., Atkins D. C., Hosseini Ghomi R. (2019). Investigating voice as a biomarker: deep phenotyping methods for early detection of Parkinson's disease. J. Biomed. Inform. 104:103362. 10.1016/j.jbi.2019.103362 [DOI] [PubMed] [Google Scholar]

[B209] Tremblay C., Martel P. D., Frasnelli J. (2017). Trigeminal system in Parkinson's disease: a potential avenue to detect Parkinson-specific olfactory dysfunction. Parkinsonism Relat. Dis. 44, 85–90. 10.1016/j.parkreldis.2017.09.010 [DOI] [PubMed] [Google Scholar]

[B210] Trezzi J.-P., Galozzi S., Jaeger C., Barkovits K., Brockmann K., Maetzler W., et al. (2017). Distinct metabolomic signature in cerebrospinal fluid in early parkinson's disease. Mov. Disord. 32, 1401–1408. 10.1002/mds.27132 [DOI] [PubMed] [Google Scholar]

[B211] Tsanas A., Little M. A., McSharry P. E., Spielman J., Ramig L. O. (2012). Novel speech signal processing algorithms for high-accuracy classification of Parkinson's disease. IEEE Trans. Bio. Med. Eng. 59, 1264–1271. 10.1109/TBME.2012.2183367 [DOI] [PubMed] [Google Scholar]

[B212] Tseng P.-H., Cameron I. G. M., Pari G., Reynolds J. N., Munoz D. P., Itti L. (2013). High-throughput classification of clinical populations from natural viewing eye movements. J. Neurol. 260, 275–284. 10.1007/s00415-012-6631-2 [DOI] [PubMed] [Google Scholar]

[B213] Tsuda M., Asano S., Kato Y., Murai K., Miyazaki M. (2019). Differential diagnosis of multiple system atrophy with predominant parkinsonism and Parkinson's disease using neural networks. J. Neurol. Sci. 401, 19–26. 10.1016/j.jns.2019.04.014 [DOI] [PubMed] [Google Scholar]

[B214] Tysnes O.-B., Storstein A. (2017). Epidemiology of Parkinson's disease. J. Neural Trans. 124, 901–905. 10.1007/s00702-017-1686-y [DOI] [PubMed] [Google Scholar]

[B215] Urcuqui C., Castaño Y., Delgado J., Navarro A., Diaz J., Muñoz B., et al. (2018). Exploring Machine Learning to Analyze Parkinson's Disease Patients, in 2018 14th International Conference on Semantics, Knowledge and Grids (SKG) (Guangzhou: ), 160–166. 10.1109/SKG.2018.00029 [DOI] [Google Scholar]

[B216] Vabalas A., Gowen E., Poliakoff E., Casson A. J. (2019). Machine learning algorithm validation with a limited sample size. PLoS ONE 14:e0224365. 10.1371/journal.pone.0224365 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B217] Vaiciukynas E., Verikas A., Gelzinis A., Bacauskiene M. (2017). Detecting Parkinson's disease from sustained phonation and speech signals. PLoS ONE 12:e0185613. 10.1371/journal.pone.0185613 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B218] Vanegas M. I., Ghilardi M. F., Kelly S. P., Blangero A. (2018). Machine learning for EEG-based biomarkers in Parkinson's disease, in 2018 IEEE International Conference on Bioinformatics and Biomedicine (BIBM) (Madrid: ), 2661–2665. 10.1109/BIBM.2018.8621498 [DOI] [Google Scholar]

[B219] Váradi C., Nehéz K., Hornyák O., Viskolcz B., Bones J. (2019). Serum N-glycosylation in Parkinson's disease: a novel approach for potential alterations. Molecules 24:2220. 10.3390/molecules24122220 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B220] Vásquez-Correa J. C., Arias-Vergara T., Orozco-Arroyave J. R., Eskofier B., Klucken J., Nöth E. (2019). Multimodal assessment of parkinson's disease: a deep learning approach. IEEE J. Biomed. Health Inform. 23, 1618–1630. 10.1109/JBHI.2018.2866873 [DOI] [PubMed] [Google Scholar]

[B221] Vlachostergiou A., Tagaris A., Stafylopatis A., Kollias S. (2018). Multi-task learning for predicting Parkinson's disease based on medical imaging information, in 2018 25th IEEE International Conference on Image Processing (ICIP) (Athens: ), 2052–2056. 10.1109/ICIP.2018.8451398 [DOI] [Google Scholar]

[B222] Wahid F., Begg R. K., Hass C. J., Halgamuge S., Ackland D. C. (2015). Classification of Parkinson's disease gait using spatial-temporal gait features. IEEE J. Biomed. Health Inform. 19, 1794–1802. 10.1109/JBHI.2015.2450232 [DOI] [PubMed] [Google Scholar]

[B223] Wang Z., Zhu X., Adeli E., Zhu Y., Nie F., Munsell B., et al. (2017). Multi-modal classification of neurodegenerative disease by progressive graph-based transductive learning. Med Image Anal. 39, 218–230. 10.1016/j.media.2017.05.003 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B224] Wen J., Thibeau-Sutre E., Diaz-Melo M., Samper-González J., Routier A., Bottani S., et al. (2020). Convolutional neural networks for classification of Alzheimer's disease: overview and reproducible evaluation. Med. Image Anal. 63:101694. 10.1016/j.media.2020.101694 [DOI] [PubMed] [Google Scholar]

[B225] Wenzel M., Milletari F., Krüger J., Lange C., Schenk M., Apostolova I., et al. (2019). Automatic classification of dopamine transporter SPECT: deep convolutional neural networks can be trained to be robust with respect to variable image characteristics. Eur. J. Nuclear Med. Mol. Imaging 46, 2800–2811. 10.1007/s00259-019-04502-5 [DOI] [PubMed] [Google Scholar]

[B226] Wodzinski M., Skalski A., Hemmerling D., Orozco-Arroyave J. R., Nöth E. (2019). Deep learning approach to Parkinson's disease detection using voice recordings and convolutional neural network dedicated to image classification, in 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) (Berlin: ), 717–720. 10.1109/EMBC.2019.8856972 [DOI] [PubMed] [Google Scholar]

[B227] Wu Y., Chen P., Yao Y., Ye X., Xiao Y., Liao L., et al. (2017). Dysphonic voice pattern analysis of patients in Parkinson's disease using minimum interclass probability risk feature selection and bagging ensemble learning methods. Comput. Math. Methods Med. 2017:4201984. 10.1155/2017/4201984 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B228] Wu Y., Jiang J.-H., Chen L., Lu J.-Y., Ge J.-J., Liu F.-T., et al. (2019). Use of radiomic features and support vector machine to distinguish Parkinson's disease cases from normal controls. Ann. Transl. Med. 7:773. 10.21037/atm.2019.11.26 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B229] Xia Y., Yao Z., Ye Q., Cheng N. (2020). A dual-modal attention-enhanced deep learning network for quantification of Parkinson's disease characteristics. IEEE Trans. Neural Syst. Rehab. Eng. 28, 42–51. 10.1109/TNSRE.2019.2946194 [DOI] [PubMed] [Google Scholar]

[B230] Yadav G., Kumar Y., Sahoo G. (2011). Predication of Parkinson's disease using data mining methods: a comparative analysis of tree, statistical, and support vector machine classifiers. Ind. J. Med. Sci. 65, 231–242. 10.4103/0019-5359.107023 [DOI] [PubMed] [Google Scholar]

[B231] Yagis E., Herrera A. G. S. D., Citi L. (2019). Generalization Performance of Deep Learning Models in Neurodegenerative Disease Classification, in 2019 IEEE International Conference on Bioinformatics and Biomedicine (BIBM) (San Diego, CA: ), 1692–1698. 10.1109/BIBM47256.2019.8983088 [DOI] [Google Scholar]

[B232] Yaman O., Ertam F., Tuncer T. (2020). Automated Parkinson's disease recognition based on statistical pooling method using acoustic features. Med. Hypoth. 135:109483. 10.1016/j.mehy.2019.109483 [DOI] [PubMed] [Google Scholar]

[B233] Yang J.-X., Chen L. (2017). Economic burden analysis of Parkinson's disease patients in China. Parkinson's Dis. 2017:8762939. 10.1155/2017/8762939 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B234] Yang M., Zheng H., Wang H., McClean S. (2009). Feature selection and construction for the discrimination of neurodegenerative diseases based on gait analysis, in 2009 3rd International Conference on Pervasive Computing Technologies for Healthcare (London: ), 1–7. 10.4108/ICST.PERVASIVEHEALTH2009.6053 [DOI] [Google Scholar]

[B235] Yang S., Zheng F., Luo X., Cai S., Wu Y., Liu K., et al. (2014). Effective dysphonia detection using feature dimension reduction and kernel density estimation for patients with Parkinson's disease. PLoS ONE 9:e88825. 10.1371/journal.pone.0088825 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B236] Ye Q., Xia Y., Yao Z. (2018). Classification of gait patterns in patients with neurodegenerative disease using adaptive neuro-fuzzy inference system. Computat. Math. Methods Med. 2018:9831252. 10.1155/2018/9831252 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B237] Zeng L.-L., Xie L., Shen H., Luo Z., Fang P., Hou Y., et al. (2017). Differentiating patients with Parkinson's disease from normal controls using gray matter in the cerebellum. Cerebellum 16, 151–157. 10.1007/s12311-016-0781-1 [DOI] [PubMed] [Google Scholar]

[B238] Zesiewicz T. A., Sullivan K. L., Hauser R. A. (2006). Nonmotor symptoms of Parkinson's disease. Expert Rev. Neurother. 6, 1811–1822. 10.1586/14737175.6.12.1811 [DOI] [PubMed] [Google Scholar]

[B239] Zhang X., He L., Chen K., Luo Y., Zhou J., Wang F. (2018). Multi-view graph convolutional network and its applications on neuroimage analysis for Parkinson's disease. Annu. Symp. Proc. 2018, 1147–1156. [PMC free article] [PubMed] [Google Scholar]

[B240] Zhao Y., Wu P., Wang J., Li H., Navab N., Yakushev I., et al. (2019). A 3D deep residual convolutional neural network for differential diagnosis of Parkinsonian syndromes on 18F-FDG PET images, in 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), 3531–3534. 10.1109/EMBC.2019.8856747 [DOI] [PubMed] [Google Scholar]

PERMALINK

Machine Learning for the Diagnosis of Parkinson's Disease: A Review of Literature

Jie Mei

Christian Desrosiers

Johannes Frasnelli

Abstract

Introduction

Methods

Search Strategy

Table 1.

Inclusion and Exclusion Criteria

Data Extraction

Study Objectives

Model Evaluation

Results

Literature Review

Figure 1.

Data Source and Sample Size

Table 2.

Figure 2.

Study Objectives

Comparing Studies With Different Objectives

Source of Data

Data Modality

Figure 3.

Number of Subjects

Machine Learning Methods Applied to the Diagnosis of PD

Performance Metrics

Table 3.

Data Types and Associated Outcomes

Voice Recordings (n = 55)

Figure 4.

Table 4.

Movement Data (n = 51)

Table 5.

MRI (n = 36)

Table 6.

Handwriting Patterns (n = 16)

Table 7.

SPECT (n = 14)

PET (n = 4)

CSF (n = 5)

Other Types of Data (n = 10)

Combination of More Than One Data Type (n = 18)

Discussion

Principal Findings

Limitations

Conclusions

Data Availability Statement

Author Contributions

Conflict of Interest

Acknowledgments

Footnotes

Supplementary Material

References

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases