Deep active learning for interictal ictal injury continuum EEG patterns

Abstract

Objectives:

Seizures and seizure-like electroencephalography (EEG) patterns, collectively referred to as “ictal interictal injury continuum” (IIIC) patterns, are commonly encountered in critically ill patients. Automated detection is important for patient care and to enable research. However, training accurate detectors requires a large labeled dataset. Active Learning (AL) may help select informative examples to label, but the optimal AL approach remains unclear.

Methods:

We assembled >200,000 h of EEG from 1,454 hospitalized patients. From these, we collected 9,808 labeled and 120,000 unlabeled 10-second EEG segments. Labels included 6 IIIC patterns. In each AL iteration, a Dense-Net Convolutional Neural Network (CNN) learned vector representations for EEG segments using available labels, which were used to create a 2D embedding map. Nearest-neighbor label spreading within the embedding map was used to create additional pseudo-labeled data. A second Dense-Net was trained using real- and pseudo-labels. We evaluated several strategies for selecting candidate points for experts to label next. Finally, we compared two methods for class balancing within queries: standard balanced-based querying (SBBQ), and high confidence spread-based balanced querying (HCSBBQ).

Results:

Our results show: 1) Label spreading increased convergence speed for AL. 2) All query criteria produced similar results to random sampling. 3) HCSBBQ query balancing performed best. Using label spreading and HCSBBQ query balancing, we were able to train models approaching expert-level performance across all pattern categories after obtaining ~7000 expert labels.

Conclusion:

Our results provide guidance regarding the use of AL to efficiently label large EEG datasets in critically ill patients.

1. Introduction

EEG monitoring in critical care has grown dramatically over the past 20 years with the discovery that a large proportion of ICU patients suffer from potentially harmful subclinical seizures and seizure-like electrical events, often collectively called “ictal-interictal-injury continuum” (IIIC) patterns, detectable only by electroencephalography (EEG) (Zafar et al., 2020; Koren et al., 2016). Besides seizures, clinically-important IIIC patterns include seizure-like patterns designated Lateralized Periodic Discharges (LPDs), Generalized Periodic Discharges (GPDs), Lateralized Rhythmic Delta Activity (LRDA) and Generalized Rhythmic Delta Activity (GRDA) (Newey et al., 2017; Rubinos et al., 2018; Sivaraju and Gilmore, 2016). The growth in ICU EEG monitoring has created a clinical need for more rapid and accurate EEG interpretation. IIIC patterns have the potential to damage the brain and contribute to permanent neurologic disability, yet detection by visual review is typically not possible to conduct in real time. Automated identification of these patterns would allow targeted treatment (and prevention of iatrogenically harmful treatments where they were not warranted). There is a critical unmet need for automated EEG monitoring for IIIC patterns (Bajaj and Pachori, 2011; Pohlmann-Eden and Newton, 2008; Temko et al., 2011).

Prior work on seizure and IIIC labeling and classification includes (Jing et al., 2018), in which our group applied unsupervised machine learning methods to achieve efficient pre-clustering of NCS and IIIC patterns in prolonged EEG recordings into a small number of clusters; the present work is an outgrowth of this approach. Others have explored deep learning approaches for seizure detection or prediction either directly from the raw EEG signal (Thodoroff et al., 2016) or from images (Jana et al., 2019). The latter reference used a Dense Convolutional Network (Dense-Net), similar to the model architecture we use in the present work. However, these prior efforts focused on relatively small data sets.

To develop an automated monitoring system for IIIC patterns, an adequately large set of labeled training data for supervised machine learning models must be developed first. For this purpose, we have collected over 200,000 h of EEG signals from > 1000 patients, comprising over 350 million EEG Segments. Our goal is ultimately to obtain a label every 2-second segment of EEG data from multiple experts. However, our dataset contains 350 million 2-second EEG segments corresponding to 200,000 h of EEG. Human experts cannot feasibly label all these EEG segments. Thus, we sought to design Active Learning (AL) schemes to select which EEG segments are most valuable to ask experts to label (Settles, 2009; Osugi et al., 2005; Dasgupta and Hsu, 2008).

Many different AL approaches have been proposed for various tasks involving EEG data, although none of them completely fits our present task. Among these Wu et al. (2016) used a technique called enhanced batch-mode active learning, in which the method improved reliability, representativeness, and diversity of the selected samples in driver drowsiness estimation based on EEG signals. Lawhern et al. (2015) used AL to improve the reliability of existing EEG artifact classifiers with minimal user interaction. Yang et al. (2012) applied AL to classify motor imagery from EEG signals in a brain computer interface. Gupta et al. (2017) developed methods that use sparse recovery and AL techniques for near real-time artifact identification and removal in EEG recordings. Macas et al. (2018) demonstrated that for semiautomatic annotation of sleep EEG signals, an AL strategy leads to statistically significantly smaller mean class error than a simple random sampling strategy. Joao et al. (2018) proposed a heuristic AL process that improves the performance of a previously developed epileptic seizure prediction algorithm. Yang et al. (2016) investigated the effectiveness of using an active learning algorithm to automatically annotate a large EEG for seizure and some of IIIC patterns. Karuppiah Ramachandran et al. (2018) proposed an active learning-based prediction framework that aims to improve the accuracy of the seizure prediction with a minimum amount of labelled data. Balakrishnan and Syed (2012) described an active learning framework for patient-specific seizure onset detection in continuous EEG signals.

However, several novel challenges arise for our IIIC pattern labeling and pattern classification problem that prior AL studies have not considered:

• Inter-Rater Agreement (IRA): In our labeling efforts, each EEG segment is labeled by multiple human experts. Experts frequently disagree regarding the correct label for an EEG segment.

• Imbalance: EEG datasets from hospitalized patients commonly exhibit substantial class imbalance, with most segments belonging to an “other” category, consisting of neither seizures nor IIIC patterns.

• Learning from raw EEGs: Optimal features for IIIC pattern classification are not known, therefore a data-driven method that discovers suitable features is desirable.

• Leveraging unlabeled data: As only a small amount of EEG data can be manually labeled, it is advantageous to design label spreading schemes to generate high-quality pseudo-labels to augment the size and diversity of the training data. Label spreading means assigning labels samples that have not been labeled by experts, to augment the training data. Methods for creating pseudo-labels are described below.

In this paper we present several AL methods to address each of these challenges. We evaluate how quickly and how well the labels provided by each proposed AL labeling scheme enable a deep learning model to learn to classify IIIC patterns in a large and representative EEG dataset.

2. Methods

2.1. Data

We selected 10-second EEG segments from 1435 patients from the Massachusetts General Hospital (MGH) EEG Archive from 2012 to 2017. All data was collected as part of routine clinical care. Retrospective analysis of the data was approved by the local Institutional Review Board (IRB), which waived the need for written informed consent. These data were labeled as part of an ongoing effort to develop automated seizure and IIIC pattern detectors. So far, we have collected 88,341 labels for 9,808 EEG segments from 25 human experts from 12 hospitals. The median number of labels gathered from each expert was 4015, and the range was 1005–6813.

2.2. Seizure and Interictal Ictal Injury Continuum (IIIC) pattern definitions

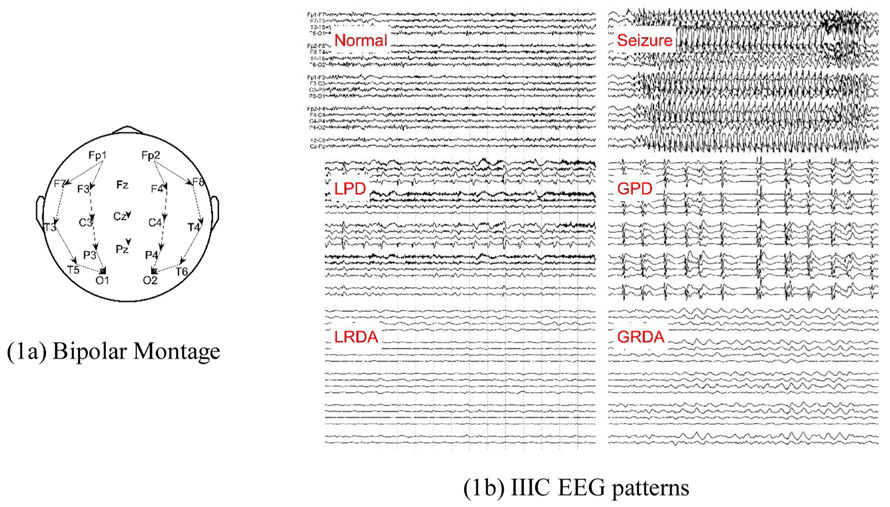
In this work, we study Active Learning for efficiently annotating seizures and IIIC patterns in continuous EEG recordings from critically ill and acutely hospitalized patients. All EEGs were recorded using the 10–20 system, an internationally standardized method for the placement of scalp electrodes (Fig. 1a) (Homan et al., 1987). The events of interest, seizures and IIIC patterns (LPD, GPD, LRDA, GRDA), are defined according to standardized American Clinical Neurophysiology Society (ACNS) nomenclature and the Salzburg criteria; (Hirsch et al., 2013; Beniczky et al., 2013; Leitinger et al., 2015) samples that do not fall into any of the preceding patterns were labeled as “other”. Definitions of IIIC patterns are available at ANON (2021a). Example images of these patterns are shown in Fig. 1.

Fig. 1.

Bipolar Montage and IIIC EEG patterns.

ACNS terminology also defines BIPDs (bilaterally independent periodic discharges), which are similar to GPDs except that the discharges on the left and right sides are not synchronous. BiPDs is a rare pattern, therefore we did not create a separate category for this pattern. Instead, experts were instructed to label any instances of BiPDs as GPDs.

2.3. Seizures and IIIC dataset

The 9,808 labeled EEG segments were obtained in a balanced manner, such that approximately half belonged to IIIC categories. Nevertheless, the proportion of the IIIC pattern data per unit time is lower in most ICU EEGs. Thus, we add 29,551 samples from EEGs reported as containing no IIIC patterns, and assigned these a label of “Other”, to yield 39359 samples for the AL experiments.

We divided data into a training dataset (70 %), validation dataset (10 %) and test dataset (20 %). Data was separated at the patient level, such that any given patient’s EEG data appeared in only one of the subsets, as summarized in Table 1.

Table 1.

Dataset for Seizures and IIIC.

	Number of patients	Number of segments	Percentage
Training	1003	26752	~70 %
Validation	144	3666	~10 %
Test	288	8941	~20 %
Total	1435	39359	100%

The samples were imbalanced across the six pattern categories, as shown in Table 2.

Table 2.

Number of EEG segments in different pattern categories.

	Other	Seizure	LPD	GPD	LRDA	GRDA
Training	23691(89 %)	247 (1 %)	1171 (4 %)	931 (3 %)	273 (1 %)	439 (2 %)
Validation	3051 (83 %)	53 (1 %)	212 (6 %)	229 (6 %)	73 (2 %)	48 (1 %)
Test	7961 (89 %)	57 (1 %)	353 (4 %)	331 (4 %)	66 (1 %)	173 (2 %)

2.4. Vector representation for EEG segments

EEG signals were recorded with 19 electrodes (FP1, F3, C3, P3, F7, T3, T5, O1, FZ, CZ, PZ, FP2, F4, C4, P4, F8, T4, T6, O2; see Fig. 1a). The sampling rate was 256 or 512 Hz; all signals were resampled to 200 Hz. EEG signals were arranged into bipolar montage, consisting of 16 channels formed by taking differences involving the following pairs of spatially adjacent channels: "FP1-F7", "F7-T3", "T3-T5", "T5-O1", "FP2-F8", "F8-T4", "T4-T6", "T6-O2", "FP1-F3", "F3-C3", "C3-P3", "P3-O1", "FP2-F4", "F4-C4", "C4-P4", "P4-O2". For purposes of annotation, EEG signals were divided into 2-second EEG segments. Each 2-second segment was provided with a 4-second context signal on both sides. Thus each 2-second segment was represented as a 16 channels x 2000-samples (10 s) signal. Here, ‘samples’ refers to digital data points. The sampling rate is 200 Hz, hence the number of samples in each 10 s signal segment is 2000.

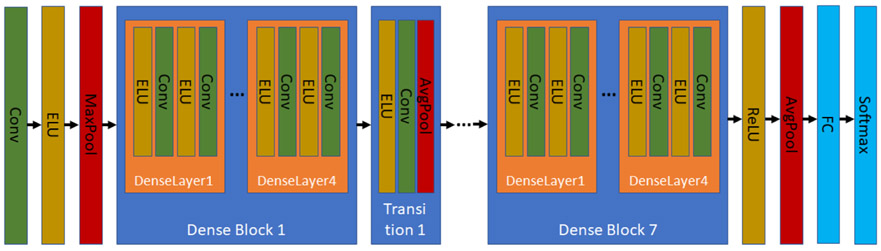
Dense-Net, a type of Convolutional Neural Network, was used to learn a vector representation of each 16 × 2000 EEG segment (Huang et al., 2017). The structure of the Dense-Net used is illustrated in Fig. 2. The Dense-Net includes 7 Dense Blocks. Each Dense Block includes 4 Dense-Layers. Each Dense Layer includes 2 Convolutional layers and 2 exponential linear unit (ELU) activations. Additionally, there are 6 transition blocks among the 7 Dense Blocks, where each transition block includes ELU activation, a convolutional layer, and an average pooling layer. We extracted the vectors (256 dimensions) from the second-to-last Fully Connected (FC) layer as the vector representation for EEG segments.

Fig. 2.

Structure of the Dense-Net CNN.

2.5. Embedding map for seizure and IIIC patterns

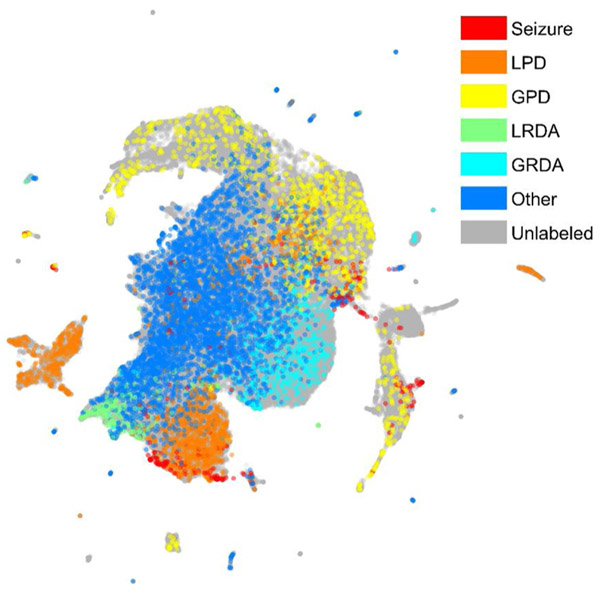
After mapping EEG segments into a high-dimensional vector representation using the Dense-Net model, we used the Uniform Manifold Approximation and Projection (UMAP) algorithm to reduce data dimensionality and visualize similarity relationships between segments (McInnes et al., 2018). In subsequent sections, we describe how the 2D UMAP visualization, hereafter referred to as a “UMAP”, is used to facilitate active learning. Fig. 3 shows an example of a UMAP for our data after 10 rounds of AL. The colored points have been labeled; the grey points are unlabeled points.

Fig. 3.

The UMAP for Seizure and IIIC.

2.6. Active learning

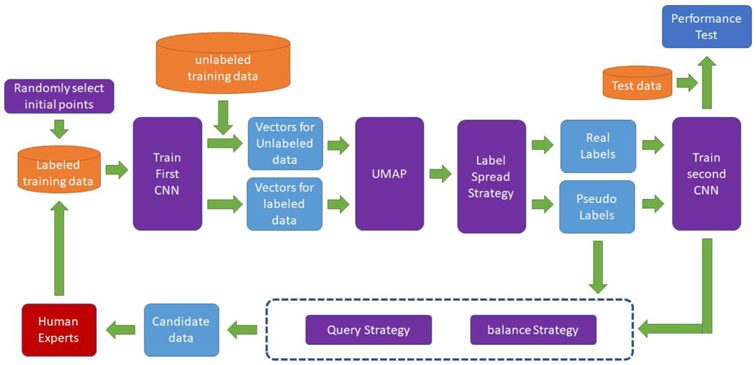
Our AL framework is illustrated in Fig. 4. The steps are as follows:

Fig. 4.

Our framework for Active Learning.

• Step 0: Randomly select EEG segments for human experts to label as initial seed points.

• Step 1: Use labeled data to train a first CNN.

• Step 2: Use the first CNN to process labeled and unlabeled data to obtain embeddings.

• Step 3: Use the EEG segment embeddings to create a 2D UMAP.

• Step 4: Use label spreading strategies to assign pseudo-labels to unlabeled data.

• Step 5: Use labeled data and pseudo-labeled data to train a second CNN.

• Step 6: Use query and balance strategies to select the most informative unlabeled data in the current iteration as candidate segments for expert labeling.

• Step 7: Ask multiple human experts to label the new candidate segments. Add the labeling results to the labeled dataset. Repeat steps 1-7.

In addition to the steps above, the second CNN is used to evaluate performance on a test dataset in each iteration.

In the following, we introduce details of the label propagation, query, and balance strategies explored in our AL scheme. We denote the number of label categories as M. In each iteration, the number of labeled EEG segments is K, and the k-th labeled EEG segment is denoted b_k, where 1 ≤ k ≤ K. The number of unlabeled EEG segments is N, and the n-th unlabeled point is denoted a_n, where 1 ≤ n ≤ N.

2.6.1. Label spread strategies

The goal of label spreading is to propagate labels from labeled EEG segments to similar unlabeled EEG segments. Label spreading generates pseudo-labels for unlabeled data to increase the number of training samples. In this work we propagate labels using the embedding map (UMAP), as follows. In each iteration of AL, unlabeled samples receive pseudo-labels from neighboring labeled points, as follows.

Let us denote segments that have been labeled as b_k, and their labels as $L_k=\left[l_1^k,\cdots ,l_m^k,\cdots ,l_M^k\right]$; where M = 6, and the 6 patterns are Seizure, LPD, GPD, LRDA, GRDA, Other. The numbers $l_m^k$ represent the number of votes received from experts for sample k belonging to pattern m. We assign a pseudo-label vector for unlabeled EEG segment a_n by spreading labels to it from neighboring labeled samples,

$${\widehat{L}}_n=\left[{\widehat{l}}_{{}_1}^{{}^n},\cdots ,{\widehat{l}}_{{}_m}^{{}^n},\cdots ,{\widehat{l}}_{{}_M}^{{}^n}\right]=\sum _{b_k\in D}(w_{n,k}\cdot L_k),$$ (1)

Where D is a neighborhood surrounding the unlabeled example a_n, and

$$w_{n,k}=exp\left(-\eta \cdot \Vert a_n-b_k{\Vert }^2\right)$$ (2)

Where ∥ ·∣ ∣² is the squared Euclidean distance, and η is a decay coefficient. The normalized pseudo-label for the unlabeled example a_n is ${\overline{L}}_n=\left[{\overline{l}}_1^n,\cdots ,{\overline{l}}_m^n,\cdots ,{\overline{l}}_M^n\right]$, where

$${\overline{l}}_{{}_m}^{{}^n}=\frac{{\widehat{l}}_{{}_m}^{{}^n}}{\sum _{m^{’}=1}^M{\widehat{l}}_{{}_{m^{’}}}^{{}^n}}$$ (3)

If there is no labeled EEG segment in D, a uniform label distribution is used for the pseudo-label, representing no prior label knowledge. In this way, each EEG segment is assigned a “soft label”, where the percentage of votes assigned to each class serves as an estimate of the probability of that class.

2.6.2. Query strategies

The goal of the query strategy is to select the most informative unlabeled EEG segment for labeling. We considered six query strategies: three are model-based, including confidence sampling, margin sampling and entropy sampling; three are model-free, including random sampling, density sampling and diversity sampling. These strategies are described as follows:

a). Random sampling:

In each iteration, unlabeled EEG segments are chosen at random with equal probability.

b). Confidence sampling:

(Settles, 2011) The feature of the n-th unlabeled EEG segment a_n is denoted x_n, where 1 ≤ n ≤ N. The label of a_n is denoted as y_n,m, where 1 ≤ m ≤ M is the index of the IIIC pattern. The classifier in the previous iteration is used to calculate the label probabilities for a_n denoted as p_n,m = Pr(y_n,m∣x_n), where ${\sum }_{m=1}^M{p}_{n,m}=1$, 1 ≤ n ≤ N. The confidence score for a_n is then represented as the maximum difference between one and any of the class probabilities,

$$s_n=\underset{m}{\max }(1-p_{n,m})$$ (4)

In each iteration, the normalized probability of sampling the n-th unlabeled EEG segment a_n is

$$p_n^{\text{sample}}=\frac{exp(s_n)}{\sum _{n=1}^{N}exp(s_n)}$$ (5)

c). Margin sampling:

(Settles, 2011) The margin score of the n-th unlabeled EEG segment a_n is represented as

$$s_n=\frac{1}{\underset{m}{\max }{p}_{n,m}-\underset{{}_{m,m\ne }\widehat{{}_m}}{\max }{p}_{n,m}}$$ (6)

Where $\widehat{m}=\underset{m}{\text{argmax}}{p}_{n,m}$. The normalized probability of sampling the n-th unlabeled EEG segment a_n is calculated via Eq. (5). The denominator represents the difference (margin) between the most and second most probable labels, and margin sampling favors data points where this margin is small.

d). Entropy sampling:

(Settles, 2011) The entropy of the n-th unlabeled EEG segment a_n is represented as

$$s_n=-\sum _{m=1}^M(p_{n,m}\cdot \log p_{n,m})$$ (7)

The normalized probability of sampling the n-th unlabeled EEG segment a_n is calculated via Eq. (5).

e). Density sampling:

In the embedding map, the similarity between unlabeled EEG segment a_n and labeled EEG segment b_k is represented as

$$\text{Similarity}(a_n,b_k)=\frac{1}{\Vert a_n-b_k{\Vert }^2}$$ (8)

The density for unlabeled EEG segment a_n is defined as (Hu et al., 2010)

$$s_n=\text{Density}(a_n)=\sum _{b_k\in \Omega }\text{Similarity}(a_n,b_k)$$ (9)

Where

$$\Omega =\{b_k\mid \text{Similarity}(a_n,b_k)\ge \gamma \}$$ (10)

Where γ is a threshold that defines the neighborhood of a_n. The normalized probability to sample the n-th unlabeled EEG segment a_n is calculated via Eq. (5).

f). Diversity Sampling:

The diversity for the unlabeled EEG segment a_n is defined as (Hu et al., 2010)

$$s_n=\text{Diversity}(a_n)=\frac{1}{\underset{1\le k\le K}{\max }\text{Similarity}(a_n,b_k)}=\underset{1\le k\le K}{\text{min}}\Vert a_n-b_k{\Vert }^2$$ (11)

The normalized probability to sample the n-th unlabeled EEG segment a_n is calculated via Eq. (5).

2.6.3. Balance strategies

Class imbalance is a common problem in training machine learning models, and leads models to prefer classes with greater numbers of samples. The goal of balancing schemes is to balance the selected unlabeled EEG segments queried across IIIC patterns. As seizures and IIIC patterns in our data are imbalanced, querying without a balancing scheme is likely to select a class-imbalanced collection of unlabeled EEG segments, which may be detrimental to classifier training for underrepresented categories (e.g. seizures). We explored two balancing strategies: spread-based, and spread-based with high confidence.

A). Standard spread-based balanced querying (SSBBQ):

Based on the label propagation schemes described above, we assign a pseudo label to each unlabeled EEG segment. These pseudo labels can be used to balance queries of new EEG segments. Namely, if the number of EEG segments to be queried is Q, we select (based on pseudo-labels) Q/M EEG segments from each of the M categories to query.

B). High confidence spread-based balanced querying (HCSBBQ):

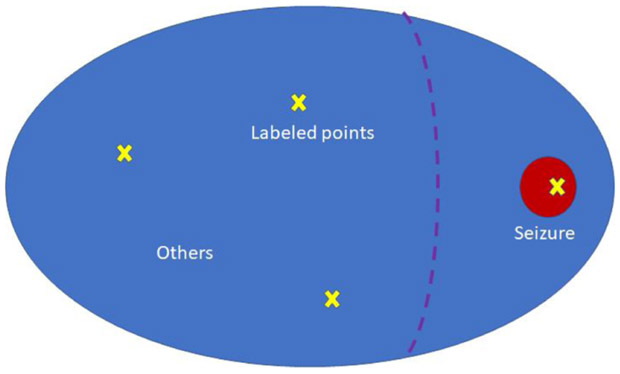
In the standard spread-based balancing scheme (A), pseudo-labels are derived by spreading based on votes and distances in the UMAP to balance query points across categories. However, this scheme is potentially problematic due to the extreme class imbalance of our dataset, as illustrated in Fig. 5. In this example, the blue area represents the majority category (“Other”), and the red area represents the minority category (“Seizure”). The yellow crosses are labeled points, namely three “Other” points and one “Seizure” point. Based on the label propagation scheme, the separation for pseudo-labels “Other” and “Seizure” might be the purple dashed line; that is, suppose points to the left of this line are pseudo-labeled “Other” and those to the right are pseudo-labeled “Seizure”. In balancing scheme (A), most sampled points in the “Seizure” pseudo-label region area are actually “Other” points rather than “Seizure” points. Thus, in balancing scheme (B), an area of high confidence is considered for the minority categories. If we assume a high confidence threshold of φ, the high confidence area is defined as the points x_n such that $Pr(y_{n,\widehat{m}}\mid x_n)\ge \phi$, where $\widehat{m}$ is the target minority category. The balancing scheme B samples Q/M points for each category as follows: Q/2M points are sampled using balancing scheme (A), and Q/2M are sampled from high confidence areas.

Fig. 5.

Illustration of the balance problem. The blue region represents the majority class (“Other”). The red region represents the minority class (“Seizure”). Yellow x’s represent labeled points within each region. Labels spreading would correctly assign pseudo-labels as “Other” to points left of the purple dashed line, but would incorrectly pseudo-label as “Seizure” most points to the right of the line. To the right of the dashed line, only those in the red circle are actually seizures.

2.6.3.1. Division of data into training, validation, and test sets.

We divided the total data (39,359 samples) into a training dataset (26,752, 70 %), validation dataset (3,666, 10 %) and test dataset (8,941, 20 %), such that data from any one patient occurred in only one of these sets. We analyzed results over 10 iterations of AL. In each iteration we selected 200 new query EEG segments from the training dataset, obtained labels for these from the group of experts, and added their labels to the training dataset. In each iteration of AL we used the updated labeled dataset to train new models, used the validation dataset to tune hyperparameters, and tested model performance on the test dataset.

2.7. Evaluation

Labels for EEG segments were obtained as votes from human experts. We denote the number of human experts as I, the number of labeled EEG segments as K, and the number of label categories as M. We denote the vote of the i -th human expert for the k -th EEG segment as v_i,k, where v_i,k ∈ {NA, 1, 2, ⋯ M}, and NA means that the i -th human expert didn’t cast a vote for the k -th EEG segment. Thus, the k -th EEG segment is given a label vector, containing the number of votes received for each pattern class across all experts, denoted L_k = [l_k,1, l_k,2, ⋯, l_k,M], where

$$l_{k,m}=\sum _{i=1}^I\mathbb{I}(v_{i,k},m),\mathbb{I}(v_{i,k},m)=\{\begin{array}{c}1if{v}_{i,k}=m\hfill \\ 0otherwise\hfill \end{array}\phantom{\}}$$ (12)

We also define the normalized label vector for the k -th EEG segment as ${\tilde{L}}_k=\left[{\tilde{l}}_{k,1},{\tilde{l}}_{k,2},\cdots ,{\tilde{l}}_{k,M}\right]$, where

$${\tilde{l}}_{k,m}=\frac{l_{k,m}}{\sum _{i=1}^M{l}_{k,i}}$$ (13)

The goal in training the deep learning model is that the predicted labels should be close to the labels given by human experts. To formalize this goal, we used two evaluation methods: KL divergence and pairwise agreement between human experts and model.

2.7.1. KL divergence

KL divergence is used to measure the distance between the label distribution from human experts vs the trained CNN (DenseNet) model. We denote the predicted normalized score vector from the model as ${\widehat{L}}_k=\left[{\widehat{l}}_{k,1},{\widehat{l}}_{k,2},\cdots ,{\widehat{l}}_{k,M}\right]$. The KL divergence between the normalized expert label vector ${\tilde{L}}_k$ and the normalized predicted label vector ${\widehat{L}}_k$ is defined as

$$K{L}_{average}=\frac{1}{K}\sum _{k=1}^{K}KL\left({\tilde{L}}_k,{\widehat{L}}_k\right)=\frac{1}{K}\sum _{k=1}^K\sum _{m=1}^M\left[{\tilde{l}}_{k,m}\cdot \log \frac{{\tilde{l}}_{k,m}}{{\widehat{l}}_{k,m}}\right]$$ (14)

2.7.2. Pairwise agreement

Pairwise agreement is used to measure agreement between human and human (model) for each category. The pairwise agreement between the i-th expert and the j-th expert for the m-th category is defined as

$$A_{i,j}=\frac{1}{2}\left\{\frac{\sum _{i=1}^I{\sum }_{j=1}^I\left[\mathbb{I}(v_{i,k},m)\cdot \mathbb{I}(v_{j,k},m)\right]}{\sum _{i=1}^I\mathbb{I}(v_{i,k},m)}+\frac{\sum _{i=1}^I{\sum }_{j=1}^I\left[\mathbb{I}(v_{i,k},m)\cdot \mathbb{I}(v_{j,k},m)\right]}{\sum _{j=1}^I\mathbb{I}(v_{j,k},m)}\right\}$$ (15)

The average agreement between experts, called expert-expert agreement (EEA), is defined as

$$EEA=\frac{1}{I(I-1)}\sum _{i=1}^I\sum _{j=1,j\ne i}^I{A}_{i,j},$$

The average agreement between the algorithm and experts, called expert-algorithm agreement (EAA), is defined as

$$EAA=\frac{1}{I}\sum _{i=1}^I{A}_{i,\text{model}}$$ (16)

2.8. Hyper parameter tuning

Hyper-parameters for CNN training were as follows. Batch size was set to 256. Each EEG segment included 16 channels, where each channel consisted of a 10-second EEG signal. As the EEG sampling rate was set to 200 Hz, the dimensions of the input tensor for the CNN were (256, 16, 2000). The dimensions of the representation vector in the second to last layer was set to be (255,1). The objective function was the weighted Kullback-Leibler divergence. Adam (an algorithm for first-order gradient-based optimization of stochastic objective functions, based on adaptive estimates of lower-order moments) was used as the optimizer for the CNN (Kingma and Ba, 2014). The initial learning rate was 0.0001 and weight decay was 0.001. Dropout was used as regularization, with a dropout rate of 0.2. The python libraries we used included pytorch, sklearn, scipy, numpy.

Hyper-parameters for UMAP were set as follows (ANON, 2021b). The dimensions of the output map were set to (2,1), to allow plotting in 2D. The size of the local neighborhood was set 15. The minimum distance apart that EEG segments can be in the low dimensional representation was set to 0.1. The distance metric was set to be Euclidean Distance. The initial embedding positions assignment was set to be random.

3. Results

3.1. Patient characteristics

Demographics and the presenting medical and neurologic problems leading to hospital admission for the 1435 patients are summarized in Table 3. Note that some patients had more than one presenting problem, resulting in a total greater than 1435.

Table 3.

Primary neurologic and medical problems leading to hospital admission.

Diagnosis
Diagnosis Neuro	Counts	Diagnosis Systemic	Counts
Brain tumor/primary or mets	123	Dermatological/Musculoskeletal	9
CNS infection/inflammation	111	Endocrine emergency	23
Hypoxic ischemic encephalopathy/Anoxic brain injury	142	Gastrointestinal non-hemorrhagic	24
Other TBI (including SAH)	18	Genitourinary	43
Other neurosurgical (non tumor/trauma) (eg EVD/VPS etc)	10	Immunological	5
Other structural-degenerative diseases	35	Liver disorders	49
Primary psychiatric disorder	39	Malignancy (solid tumors/hematologic)	84
SAH	160	Non head trauma (including spine)	13
SDH	103	Other post operative (eg CT surgery, transplant)	7
SDH + other TBI (including SAH)	52	Primary hematological disorder	22
Seizures/status epilepticus	387	Renal failure	96
Spells (behavioral events suspicious for seizures)	6	Respiratory disorders	393
Toxic metabolic encephalopathy	161	Systemic hemorrhage	9
hemorrhagic stroke	137	cardiovascular disorders	251
ischemic stroke	91	Total	1028
Epilepsy/suspected Epilepsy (EEG)	252
Total	1827

Abbreviations: mets = metastases; CNS = central nervous system; TBI = traumatic brain injury; EVD = external ventricular drain; VPS = ventriculoperitoneal shunt; SAH = subarachnoid hemorrhage; SDH = subdural hematoma; EEG = electroencephalography; EMU = epilepsy monitoring unit; CT = cardiothoracic surgery.

3.2. Comparison of AL schemes

We performed two types of experiments. In the first, we used only labeled data (9,808 labeled EEG segments + 29,551 “Other” EEG segments); this allowed us to compare the various AL schemes in detail. In the second, we added 120,000 unlabeled EEG segments to the 9,808 examples, to for AL schemes, to allow more intensive use of label spreading to improve model performance. These experiments were designed to examine the degree to which AL can help make it feasible for models to achieve expert-algorithm agreement that approaches expert-expert agreement.

1). Comparison of Query and Label Propagation schemes

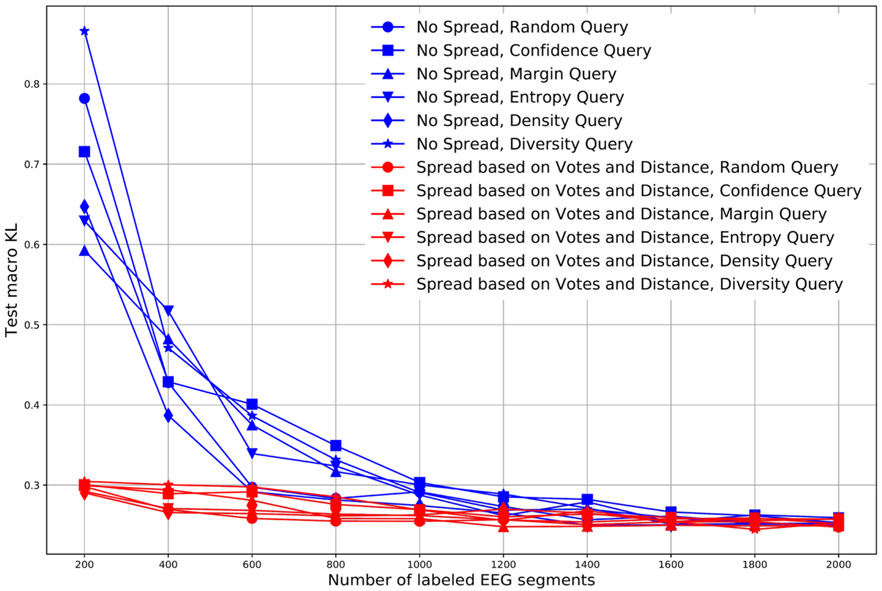
Fig. 6 compares the KL divergence for the test dataset using different query and label propagation schemes. In these experiments, we select 200 new query EEG segments in each AL iteration, and test performance of the different AL schemes over ten iterations. Accordingly, the number of labeled data points available for training is 200 in iteration 1, 400 in iteration 2, 600 in iteration 3, etc, until reaching 2000 in iteration 10. In Fig. 6, the blue lines are for the AL scheme without label spread, and the red lines are the KL divergences in the AL scheme with label spread. Different marker shapes indicate the different query schemes.

Fig. 6.

Comparison between AL with label spread and AL without label spread.

From this figure, we see that schemes with label spread are substantially better than schemes without label spread over the first five iterations (up to 1000 labels); results for the schemes with vs without spread become close after obtaining 1000 labels. This suggests that the pseudo-labels obtained by label spreading do enhance the model training when the number of available labels is low.

We also see from the figure that there is no clear difference among the different query schemes. In particular, given more than 200 segments, none of the query methods appreciably outperforms the simplest method of selecting query points at random.

2). Comparison of Query Balancing Schemes

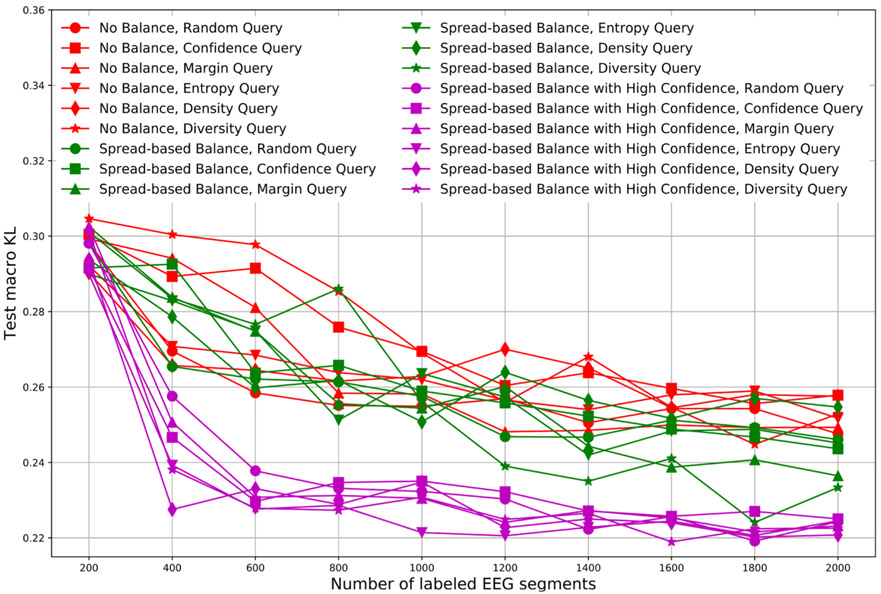
Fig. 7 compares the KL divergence for test data using different balancing schemes. In these experiments, we similarly used 10 iterations and selected 200 new query EEG segments to have their labels revealed in each iteration. Label spreading based on votes and distance were used in all schemes.

Fig. 7.

Comparison of different balancing schemes.

In Fig. 7, red lines indicate KL divergences for AL schemes without balancing, green lines are for schemes with standard spread-based balancing (SSBBQ), and purple lines are for schemes with high confidence spread-based balanced querying (HCSBBQ).

There is no clear difference between AL schemes without balance (red) and AL schemes with SSBBQ (green). This is attributable to the problem illustrated in Fig. 5. By contrast, AL schemes with HCSBBQ (purple) achieve the best (lowest) KL divergences. This is attributable to the highly class-imbalanced nature of the data, and that the confidence-based balance scheme better samples the minority class.

KL divergences for the different query schemes were all similar. In particular, no scheme was substantially better than selecting queries randomly.

3). Agreement between Models and Human Experts

We performed experiments to compare agreement between Models and Human Experts, as follows. We collected 9,808 labeled EEG segments and divided them into a training dataset (6974, 70 %), validation dataset (967, 10 %) and test dataset (1867, 20 %) at the patient level. 120 K unlabeled EEG segments were added to the training data to enhance the ability of label spreading to assist model training, as shown in Fig. 4. We performed 7 AL iterations. The numbers of EEG segments in these 7 iterations were (100, 200, 400, 800, 1600, 3200, 6974). In each iteration, if an unlabeled EEG segment was selected, the closest labeled EEG segment to it in the embedding map was utilized to replace it, to approximate being able to obtain a label for selected segment from an expert.

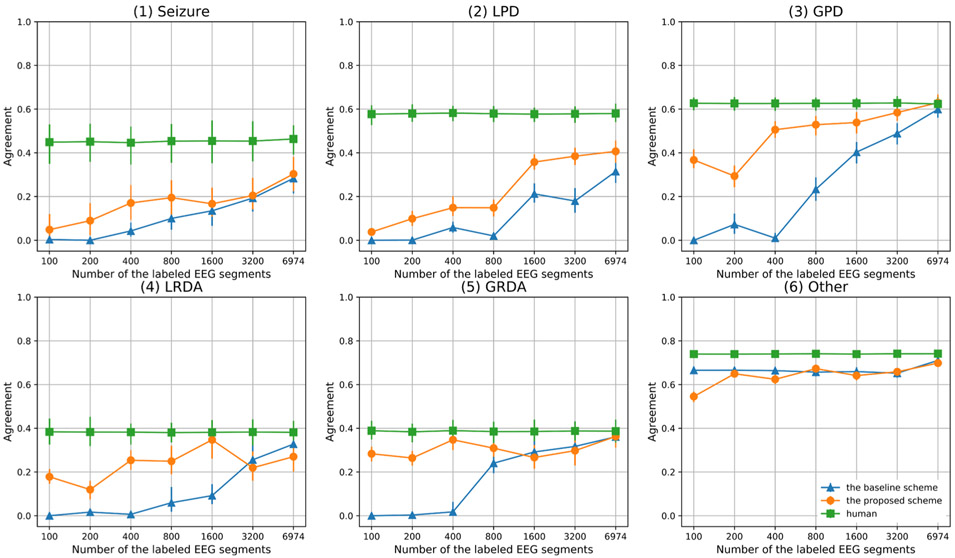
Fig. 8 compares pairwise agreements between the algorithm and human experts (EAA) with pairwise agreement among experts (EEA) for each of the six pattern categories. In the figure, the blue line is the average agreement between the algorithm and experts (EAA) using random query to obtain training labels, without label spreading or balancing; the orange line is the average agreement between the algorithm and experts (EAA) using the best-performing AL scheme (diversity query, label spread based on votes and distance, and high confidence spread-based balanced querying, HCSBBQ). The green line is the average agreement between pairs of experts (EEA). From this figure, we make the following observations.

Fig. 8.

Agreement Comparison.

a) In “Seizure”, “LPD”, “GPD”, “LRDA” and “GRDA” categories, agreement for the proposed AL scheme is initially higher than the baseline AL scheme, suggesting that label spreading and data balancing are beneficial.

b) For the “Other” category, agreement for the proposed AL scheme is initially lower than the baseline AL scheme, which can be ascribed to the fact that the baseline scheme without balancing selects more “other” data (the dominant class).

c) The baseline AL scheme eventually approaches the proposed AL scheme, because they select the same 6974 labeled EEG segments in our experimental setup. After reaching this number of labeled examples, the model is able to label “GPD” patterns as well as human experts. A small performance gap remains for “LRDA”, “GRDA” and “Other”. Relatively large gaps remain for “Seizure” and “LPD” patterns, suggesting that acquisition of additional expert labels is needed to achieve expert-algorithm agreement (EAA) equal to expert-expert agreement (EEA).

4. Discussion

In this work, we compared a wide variety of AL schemes for developing algorithms that automatically label seizure and IIIC patterns in electroencephalography data from critically ill patients. Based on the experimental results, we reached the following conclusions. First, AL label spreading is beneficial. Specifically, label spreading based on expert votes and distance in an embedding map converged faster, with fewer human labels needed, than AL without label spread. Second, in obtaining new labels from experts, balancing the queries based on label confidence is beneficial. Specifically, HCSBBQ (high confidence spread based balanced querying) performs substantially better than SSBBQ (standard spread based balanced querying). Third, all six query criteria produced similar results. Specifically, after choosing a label spreading and query balancing scheme, it did not matter which metric was used to select new samples for labeling: random sampling, confidence sampling, margin sampling, entropy sampling, density sampling, and diversity sampling all produced similar results. We conclude that random sampling, because it is the simplest, is the preferred strategy. Thus, in future work, in which we aim to use AL to obtain labels for 200,000 h EEG data from 25 human experts, we plan to combine 1) label spreading based on expert votes and embedding map distances, 2) high confidence spread based balanced querying (HCSBBQ), and 3) random sampling.

We were surprised that random query works approximately as well as any other scheme. In our experiments, we compared random query with five other query strategies including three model-based strategies (confidence, margin, entropy), and two model-free strategies (density and diversity). The model-based strategies prefer to select uncertain examples based on the model output which are usually located at category boundaries. The model-free strategies prefer to select examples based on data distribution information such as density or diversity. We believe two reasons may help explain this finding. The first is the problem of imperfect inter-rater agreement among experts regarding seizure and IIIC patterns. The uncertain EEG samples at boundaries between these categories may not be the best points to query from the standpoint of improving model performance, since these are likely to be labeled in a noisier manner by experts. The second reason is dataset imbalance. As most examples are “Other” and only a small amount of labeled data is available to estimate category boundaries to balance AL sampling, boundary estimation is noisy. Consequently, most queries find samples in the “other” category, which largely cancels the advantages of both model based and model-free query strategies.

Three prior studies used AL for developing automated methods to detect seizure or IIIC EEG patterns, such as (a) (Yang et al., 2016), (b) (Karuppiah Ramachandran et al., 2018), (c) (Balakrishnan and Syed, 2012). For the classification category, (b) and (c) only considered seizures, (a) considered two IIIC patterns namely LPDs and GPDs, whereas our work considers seizure and four IIIC patterns namely LPD, GPD, LRDA and GRDA. Regarding features, (a) (b) (c) use handcrafted features to train classifiers, while our work extracts features from raw EEG via a CNN. For the AL schemes, (a) used what is essentially a semi-supervised learning scheme, and (b) used the Bernoulli-Gaussian Mixture model which is essentially a model-based query scheme, (c) used a Distance and Diversity combined query scheme based on an SVM model. Our work considers a broader range of query strategies including three model-based strategies (confidence, margin, entropy), and three model-free strategies (random, density and diversity), and combined these with label spreading schemes.

Our study has important limitations. First, our data was from a single site. Second, our data set is highly imbalanced, which likely influences the experimental results for the AL strategies evaluated. Our results may not generalize to other datasets with less extreme data imbalance. Second, we assumed a standard CNN architecture, DenseNet, and held this fixed throughout all experiments. We believe that this was justified by high degree of flexibility afforded by the DenseNet architecture, and by our desire to focus the work on evaluating competing design choices for AL schemes proposed in the literature. Nevertheless, although we consider it unlikely, it is possible that other CNN architectures could lead to qualitatively different results. Thus optimization of the core deep learning model model architecture for use in AL remains an important unexplored topic.

Third, not all EEG segments were labeled by all 25 human experts. Further, we only consider 10-second EEG segments to train the classifier, whereas human experts were allowed to review larger contextual EEG windows when labeling. In the future work, we plan to explore varying levels of context, and to explore using Recurrent Neural Networks to learn temporal dependencies in the EEG to improve classification, particularly for seizures. Finally, given the imperfect levels of interrater agreement for seizure and IIIC patterns among experts, it is possible that these categories could benefit from further refinement. In fact, using data-driven approaches such as deep learning to delineate new EEG patterns is an exciting area for future research. Possible approaches might include data-driven identification of EEG features that facilitate higher levels of inter-rater agreement among experts. Alternatively, data-driven pattern discovery seek to identify EEG patterns that are highly predictive of neurologic outcomes (e.g. level of disability or death). These approaches contrast with the approach we have followed here, which takes expert-defined EEG pattern categories as given.

The experimental results and label spreading and query balancing methods presented herein provide valuable guidance for active learning involving multiple experts and large EEG datasets. By using these methods to obtain labels for over 200,000 h of EEG from critically ill patients from over 25 human experts, we expect to soon be able to create deep learning algorithms that are able to identify seizures and IIIC patterns with a level of reliability equivalent to human experts.