Assessing Toxicokinetic Uncertainty and Variability in Risk Prioritization

Abstract

High(er) throughput toxicokinetics (HTTK) encompasses in vitro measures of key determinants of chemical toxicokinetics and reverse dosimetry approaches for in vitro-in vivo extrapolation (IVIVE). With HTTK, the bioactivity identified by any in vitro assay can be converted to human equivalent doses and compared with chemical intake estimates. Biological variability in HTTK has been previously considered, but the relative impact of measurement uncertainty has not. Bayesian methods were developed to provide chemical-specific uncertainty estimates for two in vitro toxicokinetic parameters: unbound fraction in plasma (f_up) and intrinsic hepatic clearance (Cl_int). New experimental measurements of f_up and Cl_int are reported for 418 and 467 chemicals, respectively. These data raise the HTTK chemical coverage of the ToxCast Phase I and II libraries to 57%. While the standard protocol for Cl_int was followed, a revised protocol for f_up measured unbound chemical at 10, 30, and 100% of physiologic plasma protein concentrations, allowing estimation of protein binding affinity. This protocol reduced the occurrence of chemicals with f_up too low to measure from 44% to 9.1%. Uncertainty in f_up was also reduced, with the median coefficient of variation dropping from 0.4 to 0.1. Monte Carlo simulation was used to propagate both measurement uncertainty and biological variability into IVIVE. The uncertainty propagation techniques used here also allow incorporation of other sources of uncertainty such as in silico predictors of HTTK parameters. These methods have the potential to inform risk-based prioritization based on the relationship between in vitro bioactivities and exposures.

Introduction

Recent investments in high-throughput assays to address toxicity data gaps for thousands of chemicals in commerce have resulted in the availability of in vitro bioactivity measures across multiple pathways and endpoints for close to 10,000 chemicals (Kavlock et al., 2012; Tice et al., 2013). To provide context for these measurements, parallel efforts have explored the incorporation of in vitro measures of chemical toxicokinetics (Shibata et al., 2002; Waters et al., 2008) and reverse dosimetry approaches (Tan et al., 2006), known as high-throughput toxicokinetics (HTTK), to relate in vitro concentrations to external exposures required to achieve these concentrations systemically (Rotroff et al., 2010; Sipes et al., 2017; Tonnelier et al., 2012; Wambaugh et al., 2015; Wetmore et al., 2015; Wetmore et al., 2012). These efforts rely on simple toxicokinetic (TK) models and in vitro TK data to predict in vivo behaviors using a process known as in vitro-in vivo extrapolation (IVIVE) (Bell et al., 2018; Coecke et al., 2013; Rostami-Hodjegan, 2012; Wambaugh et al., 2018). The focus of this study is to develop methodology for estimation and propagation of TK uncertainty as a means of potentially informing chemical health risk decision-making.

Both statistical uncertainty and biological variability play important roles in chemical TK and IVIVE (Barton et al., 2007; Bell, et al., 2018; Bernillon et al., 2000). The World Health Organization distinguishes between uncertainty and variability such that: “Uncertainty relates to ‘lack of knowledge’ that, in theory, could be reduced by better data, whereas variability relates to an existing aspect of the real world that is outside our control” (World Health Organization, 2018). HTTK offers significant advances in throughput when compared to traditional efforts that are reliant on in vivo studies and more complex multi-compartment physiologically-based toxicokinetic (PBTK) modeling. Despite this, full implementation of HTTK as a tool is limited by concerns over the lack of an adequate understanding of the uncertainty and variability surrounding the resulting TK predictions (FIFRA SAP, 2014) as well as assay limitations. Even when the in vitro assays are restricted to measurement of plasma protein binding for the unbound fraction in plasma (f_up) and intrinsic hepatic clearance (Cl_int), the limits on the speed of mass spectrometry (MS) sample analysis can hinder efficiency (Wetmore, et al., 2015; Wetmore, et al., 2012). Further, detection limits are frequently exceeded for highly bound proteins during plasma protein binding assessments, a key parameter in predicting chemical TK behavior (Wambaugh, et al., 2015). Identification of strategies to rectify these issues and an understanding of the impact of some of these experimental uncertainties could lead to a broader understanding and acceptance of these HTTK approaches.

What is often desired in assessing the contribution of biological variability to the public health risk posed by chemical hazard is characterization of susceptibility (Zeise et al., 2013). Susceptibility can be the quantitative difference in toxic dose between the average individual and a sensitive population (Gundert-Remy et al., 2002). Monte Carlo (MC) simulation allows PBTK models to be coupled to distributions representing variation in human physiology (for example, body weight, cardiac output) to simulate the impact of human variability on TK (Cronin et al., 1995; Gearhart et al., 1993; Thomas et al., 1996). Since physiological parameters are correlated (for example, the shortest person is seldom the heaviest) various strategies have been developed, such as drawing correlated sets of biometrics (for example, the height, weight, age, ethnicity, gender of specific individuals) from large scale surveys such as the U.S. Centers for Disease Control and Prevention (CDC) National Health and Nutrition Examination Survey (NHANES) (Price et al., 2003; Ring et al., 2017; U.S. Centers for Disease Control and Prevention, 2012) followed by regression models to infer PBTK tissue volumes and blood flows (Bosgra et al., 2012; McNally et al., 2014). This variability in TK has been used to determine quantitative population distributions, the 95^th percentile of which may be thought of as a “susceptible population” which has higher systemic chemical concentrations for the same daily exposure (Ring, et al., 2017; Rotroff, et al., 2010; Sipes, et al., 2017; Wetmore, et al., 2015; Wetmore, et al., 2012). The use of the 95^th percentile in chemical risk assessment has a long history (Paustenbach, 1995) with respect to individuals receiving higher exposure (Cullen et al., 1999) and those with higher plasma levels as a result of a combination of both exposure and TK (Aylward et al., 2013).

While biological variability has been partially addressed, a 2014 review of the use of HTTK for chemical prioritization by the U.S. Endocrine Disruptor Screening Program identified that greater assessment of the “quality and accuracy of (and hence error associated with) the data” was needed (FIFRA SAP, 2014). Comparisons of HTTK predictions with in vivo data have found that roughly half of non-pharmaceuticals are predicted within a factor of three, while other chemicals are much more divergent (Wambaugh, et al., 2018; Wambaugh, et al., 2015; Wang, 2010; Yoon et al., 2014). Reasons for these discrepancies that have been investigated in the past and include the role of active cellular transporters and heterogeneity within the in vivo evaluation data (Wambaugh, et al., 2018; Wambaugh, et al., 2015). However, while the precision of a given in vitro TK measurement is known to vary from chemical to chemical, this uncertainty has not been previously quantified and propagated into chemical risk predictions.

In this study, we present the development of Bayesian methods that provide chemical-specific uncertainty estimates for parameters (i.e., f_up and Cl_int) used in IVIVE and modeling to predict chemical TK. These models are developed using new experimental measurements across 496 chemicals to improve understanding of the impact of experimental and analytic variability on estimates intended to inform risk prioritization efforts. A new protein binding measurement protocol was developed and applied to reduce uncertainty and allow insight into protein binding kinetics. Finally, the impacts of these experimental uncertainties are considered in conjunction with population variability to clarify the relative contribution of each, thus identifying key areas to target for future refinement of HTTK methods.

Methods

HTTK was performed using the modeling approaches described in Pearce et al. (2017b). All analyses were performed in R version 3.5.1. The in vitro data and TK models used in this analysis were made publicly available with the release of R package httk version 1.10 (https://cran.r-project.org/package=httk). We use capitalization to distinguish between “HTTK” and “httk”. Here, “HTTK” refers to the broader scientific methodology of combining in vitro TK assays and generic TK models to make rapid, chemical-specific predictions of TK for IVIVE. We use “httk” to refer to the specific implementation of HTTK provided by the R package “httk”. All supplemental materials are available online: https://doi.org/10.5061/dryad.nf40jb4

Test Chemical Selection and Stock Preparation.

Chemicals were selected for this study based on: 1) availability of ToxCast assay bioactivity data; 2) high estrogen receptor (ER) Interaction scores as previously described (Judson et al., 2015); 3) availability of NHANES biomonitoring data (U.S. Centers for Disease Control and Prevention, 2012); and/or 4) a lack of in vitro pharmacokinetic data (i.e., plasma protein binding and hepatocyte clearance data). Chemicals were selected from the ToxCast screening library (Richard et al., 2016), which was obtained commercially and distributed by Evotec (South San Francisco, CA). Chemical library information including structures can be found at http://epa.gov/ncct/dsstox/sdf_toxcst.html.

Physico-Chemical Properties

Structures, formula, and molecular weight were obtained from the U.S. EPA’s CompTox Chemicals dashboard (https://comptox.epa.gov/dashboard) (Williams et al., 2017). Hydrophobicity as characterized by logarithmic n-octanol/water partition coefficients (logP_ow) was predicted for each structure using the OPERA tool (Mansouri et al., 2018). OPERA is a suite of modern quantitative structure-activity relationships (QSARs) based upon the PHYSPROP database (U.S. Environmental Protection Agency, 2014a) constructed according to Organisation for Economic Co-operation and Development guidelines (OECD, 2007) and including a domain of applicability analysis (Weaver et al., 2008). OPERA predicts more than a dozen physicochemical and environmental fate properties from chemical structure. Literature values for membrane affinity (that is, the likelihood of partitioning into a lipid bi-layer) were used where available or otherwise were predicted from a regression (Pearce et al., 2017a). Chemical ionization equilibria (dissociation constants or pk_a) were predicted using ChemAxon (Cambridge, MA, USA) as reported in Strope et al. (2018). The distribution coefficient (D_ow) for the chemicals (that is, the ionization-dependent distribution into lipids) was calculated using the httk R package according to (Pearce, et al., 2017b):

$$D_{ow}=P_{ow}*f_{neutral}+0.001\times f_{charged}+f_{Zwittter}$$

where f_neutral, f_charged, and f_Zwitter are the neutral, charged, and Zwitterionic fractions of the total chemical number at a given pH (plasma is assumed to be pH 7.4).

Experimental Plasma Protein Binding Assessments.

Experiments were performed at Cyprotex (Watertown, MA). Measurements of plasma protein binding, as characterized by the fraction unbound in plasma (f_up), were collected using a rapid equilibrium dialysis (RED) procedure (Banker et al., 2008; Waters, et al., 2008) with slight modification: in addition to performing the RED assay using the typical 100% physiological plasma concentration (the normal condition), additional replicate experiments were conducted at 30% and 10% of the physiologic concentration.

One of the main challenges with plasma protein binding assessments is that often, for highly bound chemicals, the levels in the protein free, phosphate buffered saline (PBS) chamber will be at or below the limits of detection (LOD), resulting in f_up values that are zero or even negative (i.e., the area of the analyte peak in the mass spectrometry (MS) is similar to the blank, A_PBS ~ A_blank,). With the protein titration, described below, there is greater opportunity to detect f_up using a rapidly developed MS method. In the previous work when the free fraction was below the limit of quantification, f_up was assigned a value equal to half the average limit of quantification (i.e., 0.005) (Rotroff, et al., 2010; Wetmore, et al., 2015; Wetmore, et al., 2012) or was treated as a censored observation (Wambaugh, et al., 2015).

Human (mixed gender) plasma was obtained using the anti-coagulant K₂EDTA and stored at −80°C. Prior to use, the plasma was thawed at 37 °C using a water bath and diluted in PBS (to 30% and 10% of physiologic plasma protein (PPP) concentrations) in polypropylene microcentrifuge tubes. All plasma protein concentrations (i.e., 100%, 30%, and 10%) were pH adjusted to pH 7.4 ±0.1 using a concentrated stock solution of either NaOH or HCl.

Chemical solutions were prepared by creating stock solutions of neat chemical in DMSO. For each assay, stock solutions were further diluted in DMSO to 100x the final concentration (i.e., 500 μM for a 5 μM final concentration). The chemical solutions were then diluted into plasma, 5 μM final concentration, where the DMSO assay concentration did not exceed 1%. The assay was initiated with the addition of 500 μL PBS containing 1% DMSO in the white chamber and 300 μL of the chemical-spiked plasma in the red chamber of the RED device, samples were run in duplicate. The RED device plate was then sealed and incubated in a 37 °C incubator with gentle rotating shaking for 4 hours.

The recovery determination plate, or T0, was immediately prepared after the start of the 4-hour incubation. For recovery determination, 20 μL of the initial non-incubated plasma was transferred to a 96-well plate and mixed with 50 μL blank PBS containing 1% DMSO followed by the addition of 150 μL cold methanol containing internal standard (1 μM bucetin and 1 μM diclofenac). Blanks were prepared for background subtraction and run in duplicate and prepared by quenching 20 μL plasma containing 1% DMSO and 50 μL PBS containing 1% DMSO into 150 μL internal standard. The quench plate was kept on ice for 10 minutes then centrifuged at 6102 relative centrifugal force (RCF) at 4 °C for 20 minutes. The supernatant ----was then transferred to a liquid and gas chromatography mass spectrometry (LC-/GC-MS) vial for analysis.

After the 4-hour incubation, each well was mixed and 200 μL aliquoted to a transfer plate. From the transfer plate, 20 μl of each plasma sample and 50 μL of each PBS sample were aliquoted into a 96-well quench plate. The samples were matrix matched (i.e., 50 μL PBS containing 1% DMSO were mixed with plasma samples and 20 μL plasma containing 1% DMSO were mixed with PBS samples). The samples in the quench plate all received 150 μL cold methanol containing internal standard. The quench plate was kept on ice for 10 minutes then centrifuged at 6102 RCF at 4 °C for 20 minutes. The supernatant was then transferred to a LC-MS/MS plate or GCMS vial for analysis. Each assay was run with propranolol and warfarin as controls.

The measurements of ${\text{f}}_{\text{up}}$ were adjusted (f_{up, adjusted}) to account for differential distribution of highly lipophilic chemicals both in vitro and in vivo using the D_OW at pH 7.4 ($D_{ow,pH=7.4}$):

$$f_{up,adjusted}=\frac{1}{D_{ow,pH=7.4}*F_l+\frac{1}{f_{up,invitro}}}$$

where $F_l$ is the lipid fraction of the plasma (Pearce, et al., 2017a; Poulin et al., 2012).

Additional description of the plasma protein binding assay is available as supplemental materials.

Materials Used

The reference chemicals and reagents used were Warfarin (Sigma, Part A2250), (±)-propranolol hydrochloride (Sigma, Part P0884), bucetin (Fluka, Part B4027), diclofenac sodium salt (Sigma, Part D6899), DMSO (Fisher Scientific, Part D128), acetonitrile (Fisher Scientific, Part A955), water (Fisher Scientific, Part W6), methanol (Fisher Scientific, Part A456), Potassium phosphate buffer pH7.4 (Corning, Part 451201), hydrochloric acid 1N (Fisher Scientific, Part SA48), sodium hydroxide (Fisher Scientific, Part SS266), and Human plasma K₂EDTA (BioIVT, Part HUMANPLK2PNN). RED device inserts (Part 89809) and reusable base plate (Part 89811) were obtained from Thermo Scientific.

Hepatic Clearance Measurements.

The rate of hepatic clearance of the parent chemical was conducted as previously described with some modification (Rotroff, et al., 2010; Wetmore, et al., 2015; Wetmore, et al., 2012): Vials containing cryopreserved hepatocytes of 10 mixed gender donors were removed from liquid nitrogen storage and thawed in a 37 °C water bath until the ice was almost entirely melted. As soon as the contents were thawed, each vial was resuspended into a 50 mL conical vial containing 48 mL of warmed media. After dilution, the cells were centrifuged at 50 RCF for 5 minutes at room temperature. The resulting pellet was resuspended in 2 mL of warmed media per 50 mL conical vial and pooled if multiple vials used. Viability and cell counting were determined based on Trypan blue exclusion method. The correct volume of incubation medium was added to the hepatocyte suspension to a final cell count at 2x the final concentration (i.e., 1 million viable cells per ml for a final concentration of 0.5 million cells per mL) in warmed media. Viable and non-viable cells were counted using a hemocytometer. The cells were diluted using 20 μL Trypan Blue, 20 μL media, and 10 μL cell suspension.

The clearance assay was initiated upon the addition of an equal volume of hepatocytes, 250 μL, into the incubation plate. Samples were collected 15, 30, 60 and 120 minutes; a 100 μL aliquot from the incubation plate was precipitated into a quench plate containing an equal volume of cold methanol containing internal standard (1 μM bucetin, 1 μM propranolol, and 1 μM diclofenac). An “initial” (time 0) sample was separately prepared by aliquoting 50 μL of hepatocytes into a quench plate containing 100 μL internal standard followed by the addition of 50 μL from the chemical plate. Blanks were prepared for background subtraction and run in duplicate and prepared by quenching 50 μL of hepatocytes and 50 μL of media into a 100 μL internal standard. The quench plates were kept on ice for 10 minutes then centrifuged at 6102 RCF at 4 °C for 20 minutes. The supernatant was then transferred to a LC-MS/MS plate or GCMS vial for analysis. Each assay was run with verapamil, midazolam, and 7-OH 4-trifluoromethyl coumarin as controls.

Measured clearance rates were corrected using the predicted chemical fraction unbound in the hepatocyte assay according to the method of (Kilford et al., 2008). Additional description of the hepatic clearance assay is available as supplemental materials.

Materials Used

The reference chemicals and reagents used were 7-Hydroxy-4 (trifluoromethyl) coumarin (Acros, Part RJF00002DA), midazolam hydrochloride (Lipomed, Part MID-111-HC-100), (±)-verapamil hydrochloride (Sigma, Part V4629), (±)-propranolol hydrochloride (Sigma, Part P0884), bucetin (Fluka, Part B4027), diclofenac sodium salt (Sigma, Part D6899), Dimethyl sulfoxide (Fisher Scientific, Part D128), acetonitrile (Fisher Scientific, Part A955), water (Fisher Scientific, Part W6), methanol (Fisher Scientific, Part A456), Williams media (Gibco, Part A12176–01), Hepes (Sigma, Part H4034), L-glutamine (Hyclone, Part SH30034.01), and human hepatocytes 10 donor mixed gender (BioIVT, Part X008001).

Incubation media consisted of 500 mL of William’s E medium, 5 mL of 200 mM L Glutamine (final concentration 2 mM), and 3 g of HEPES (final concentration 25 mM). The media was mixed by inversion, warmed to 37 °C, and adjusted to pH 7.4 before each use.

Chemical solutions were prepared by diluting the chemical from a DMSO (or other appropriate solvent) stock solution into incubation media at 2x the final concentration (i.e., 10 μM for a 5 μM final concentration and 2 μM for a 1 μM final concentration). The chemical solutions were aliquoted, 250 μL, in triplicate into appropriate wells of an incubation plate and kept at 37 °C in the incubator.

Chemical Analysis

The in vitro methods for both f_up and Cl_int require the development of chemical-specific analysis methods to determine relative concentration. This requirement is in contrast to many assays used for in vitro assays in which a single reporter, such as bioluminescence, allows rapid analysis of the degree of perturbation across many chemicals (Hertzberg et al., 2000). Method development was attempted using LC- and GC-MS. For some chemicals, peaks could be identified in the hepatocyte incubation media, but could not be separated from the background caused by the presence of plasma protein in the assay for f_up. In this work, evaluation was restricted to chemicals for which a method could be developed to quantify the purity of the standard. Supplemental Table 1 identifies the method used for each chemical.

Statistical Analysis of In Vitro Assay Data

The MS peak areas for the samples drawn from the in vitro experiments are available in Supplemental Table 2 and 3 for f_up and Cl_int, respectively. In previous analyses, the measured peak areas from the experimental plasma protein binding and hepatic clearance assay samples were used to determine “point estimates” (single values) for f_up and Cl_int. In addition to calculating point estimates, two separate Bayesian models were used to analyze the protein binding data. The first model for f_up was a “base” model representing a Bayesian version of traditional methods for outlining data from a RED experiment, while the second model for f_up was an “affinity” model that used the data from the plasma protein titration to estimate a binding affinity. A third Bayesian model was used to analyze hepatic clearance data. Each of the three Bayesian models consisted of using two sub-models: a model for the in vitro experiment and a model for the measurement of chemical concentration using MS. The chemical concentration MS sub-model was the same in all three Bayesian models.

Bayesian analyses were conducted via Markov Chain Monte Carlo (MCMC) implemented with the JAGS software v4.3 (Plummer, 2003) and interfaced through the runjags (v2.0.4–2) and rjags (v4–6) R packages. The JAGS-language model descriptions and R scripts for analyzing the data are available as Supplemental Materials. Five Markov chains were run until the Gelman-Rubin convergence diagnostic (Gelman et al., 1992) achieved a value of <1.1 for all parameters. Note that MCMC differs from MC in that MCMC is a numerical integration technique to determine the posterior distribution combining data, prior information, and models; while MC is a numerical technique for drawing random samples from a distribution.

The results of the MCMC are reported in two ways. First, the median and lower and upper limits of the 95% credible interval are reported in Supplemental Table 4. Additionally, 1000 samples from the converged Markov Chains are saved in the R software “.RData” format object available upon request.

Chemical Concentration Mass Spectrometry Bayesian Model

MS was modeled consistently across all experimental analyses because MS is an analytical chemistry method. The observed peak areas were modeled as normally distributed about predicted, concentration-dependent peak areas with a standard deviation σ. A chemical-specific, heteroscedastic standard deviation ($\sigma$) for analytical chemistry measurements (Rocke et al., 1995) was used, as shown below:

$$\sigma =k_1+k_2\left[x\right]$$

where k₁ and k₂ are constants and [x] is the concentration (observed peak area) of chemical x. The logarithm base 10 of the constant term, k₁, was estimated using a normal prior that was centered at −2 with precision 0.1. A logarithm base 10 of a second term, k₂, that multiplied the concentration (i.e., heteroscedasticity) was estimated using a factor that was normally distributed, centered at 1, with precision 0.1, and multiplied by k₁ such that k₁ could be identifiable in instances where k₂ was not.

The peak area (A) measured by MS was assumed to 1) involve a threshold below which the chemical could not be detected and 2) be related by a linear calibration to actual chemical concentration such that:

$$A=\theta \left(\left[x\right]-t\right)\times \left(\left[x\right]-t\right)*m+b$$

where θ(x) is the Heaviside step function which is valued 1 for x ≥ 0 and 0, otherwise; t is the threshold for detection (units of concentration), m is the calibration (units of pixels per concentration) and b is the background noise (units of pixels). Since each of the three plasma protein concentrations used was analyzed on separate days, three different backgrounds, thresholds, and calibrations are estimated, one set for each of the concentrations.

The weakly informative prior on the threshold (t) assumed that t was uniformly distributed between 0 and the total concentration of chemical administered to the in vitro well. The weakly informative prior on the log of the calibration (m) was a normal distribution centered at 0 with precision 0.1 (that is, a Gaussian distribution with mean of zero and standard deviation of$\sqrt{10}$). The weakly informative prior on the background (b) was a uniform distribution constrained between 0 and 1000.

Protein Binding Bayesian Models

F_up was calculated using the peak areas measured for blank (no chemical) samples and for samples drawn from both the plasma protein and PBS chambers of the RED plates after incubation and equilibration (Banker, et al., 2008). Equilibrium samples from the PBS side of the double-well were diluted by a factor of 2 prior to analysis, while the time zero and equilibrium samples from the plasma side were diluted by a factor of 5 due to greater background interference from the plasma:

$$f_{up}=\frac{2\times A_{PBS}-A_{blank}}{5\times A_{plasma}-A_{blank}}$$

where A_PBS is the MS peak area for the PBS side, A_plasma is the area for the plasma side, and A_blank is the area for the blank samples. All areas are measured in units of pixels. Run in duplicate, the point estimates of f_up for each replicate was calculated individually and then averaged.

Two models were used for Bayesian analysis of the RED data. The base model used only the data from the 100% PPP experiments, and the affinity model used a protein binding model to make use of data from all three protein concentration experiments. Both the base and affinity models for plasma binding assumed that the true value for f_up could be below the limit of quantification of the analytical method. However, both analyses also included the above model for chemical analysis that constrained the observed data by a chemical-specific limit of a quantification.

In both models the measurements of blank (i.e., not treated with chemical) PBS were taken to be observations of the background (i.e., [x] = 0). Time zero measurements of the plasma protein solution treated with chemical were taken to be measurements of the total administered concentration (C_nominal) [x]= C_nominal =5 μM. Measurements drawn from the plasma protein (C_plasma) and PBS (non-plasma protein, C_PBS) sides of the membrane after equilibration, were treated as measurements of concentrations that depended on unknown values for unbound chemical concentration C_u, and bound chemical concentration (C_b) (Banker, et al., 2008; Toutain et al., 2002). RED assumes that, after equilibration, $\frac{C_{PBS}}{C_{plasma}}=\frac{C_u}{C_b+C_u}=f_{up}$, which gives:

$$C_b=\frac{1-f_{up}}{f_{up}}{C}_u$$

In the base model, the logarithm of f_up was estimated to be constrained between −5 and 0, (i.e., 0.00001 < f_up < 1).

We further assume that some amount of chemical is missing, (for example, non-specifically bound to membrane or well walls, C_missing). C_missing was constrained to be between zero and C_nominal. We then assumed that:

$$C_{nominal}=C_{missing}+C_{plasma}+C_{PBS}=C_{missing}+2*C_u+C_b$$

The expression for C_b can then be used to determine C_u from the estimated ($f_{up}$ and $C_{missing}$) and given ($C_{nominal}$) parameters:

$$C_u=\left(C_{nominal}-C_{missing}\right)$$

In the titration assay we measure the free concentration of chemical at three different protein concentrations. We jointly analyze these data by assuming that the free concentration is a function of both the chemical-specific dissociation constant and the protein concentration. A dissociation constant k_d (Toutain, et al., 2002) was assumed such that:

$$k_d=\frac{C_u{C}_{protein}^u}{C_b}$$

Where $C_{protein}^u\approx C_{protein}$ is the total (micromolar) concentration of protein (either 100%, 30% or 10% of 1053 μM (converted from a range of 60–80 g/L given by Berg et al. (2011), assuming all protein had roughly the same weight as albumin ~66.5 kDa). The log of k_d was assumed to be uniformly distributed between −4 and 5. The unbound and bound concentrations were determined as:

$$C_u=\left(C_{nominal}-C_{missing}\right)\times \frac{k_d}{2k_d+C_{protein}}$$

$$C_b=\left(C_{nominal}-C_{missing}\right)\times \frac{C_{protein}}{2k_d+C_{protein}}$$

Hepatic Clearance Bayesian Model

Cl_int point estimates were calculated similarly to the approach used in earlier work (Rotroff, et al., 2010; Wetmore, et al., 2015; Wetmore, et al., 2012). Concentration-time course data measuring percent chemical remaining over time was analyzed separately for the two concentrations (1 and 10 μM). A least squares best fit line was determined, and if the p-value relative to the mean of all data for the concentration (i.e., no change with time) was below 0.05, then the slope was assumed proportional to Cl_int.

The Bayesian analysis of clearance used the same chemical concentration model as for plasma protein binding, but with a separate model for exponential decay with time: $C\left(t\right)=C_o{e}^{-mt}$. The 1 and 10 μM data were analyzed simultaneously, with both concentrations potentially having the same $C{l}_{int}$. Two Boolean (1 or 0) indicator variables, $B_{decreases}$ and $B_{saturates}$, were estimated. $B_{decreases}$indicated whether the concentration decreased with time. $B_{saturates}$ indicated whether there was a lower clearance at 10 μM. The rate constant $m=B_{decreases}*r$ at 1 μM and $m=B_{decreases}*r*\left(1-B_{saturates}*F_{saturates}\right)$ at 10 μM, where $F_{saturates}$ is a fraction between 0 and 1. Rate constant r (1/h) is related to $C{l}_{int}=r*\frac{1h}{60min}*\frac{1000uL}{1mL}*\frac{mL}{0.5{10}^{6}hepatoctytes}$ such that $C{l}_{int}$ has units of μL/min/10⁶ hepatocytes.

Supplemental Figure 3 provides a chemical by chemical examination of the fitting results.

TK Model and Population Variability Simulation.

The mean values and units of the parameters used are provided in Table 1. Steady-state plasma concentration was predicted using an empirical, three-compartment model (Pearce, et al., 2017b) that is very similar to the model used previously for reverse dosimetry (Wetmore, et al., 2015; Wetmore, et al., 2012). Parameters were varied to simulate population variability as described by Ring, et al. (2017). In short, we have made use of the HTTK-pop module (Ring, et al., 2017) of the R package httk, which draws biometrics of individuals within CDC NHANES (U.S. Centers for Disease Control and Prevention, 2012). Individuals are sampled by NHANES such that there is a statistical weight allowing reconstruction of cohort representing the modern U.S. population. HTTK-pop uses regressions (McNally, et al., 2014) to translate the CDC NHANES biometrics into internal TK parameters such as liver volume and cardiac output. C_ss is calculated for 1000 simulated individuals and the upper 95^th percentile C_ss among the 1000 individuals is used as a surrogate for sensitive individuals.

Table 1.

Physiological and Other Parameters Used

Parameter	Description	Units	Mean Value (*Varied by HTTK-pop (Ring, et al., 2017))	Reference
Qliverc	Total blood flow to the liver (arterial and gut)	L/h/kg body weight	3.6*	Davies et al. (1993)
QGFR	Flow to the glomerulus (glomerular filtration rate)	L/h/kg body weight	0.32*	Davies, et al. (1993)
$n_{celldensity}$	Hepatocellularity	Millions of cells per gram liver	110*	Carlile et al. (1997)
$V_{liverc}$	Volume of the liver	L/kg body weight	0.0245*	Davies, et al. (1993)
$d_{liver}$	Liver density	g/mL	1.05*	International Commission on Radiological Protection (1975)
hematocrit	Fraction of blood that is red blood cells	Fraction	0.43*	(Davies, et al., 1993)
Cprotein	Concentration of protein used in fup assay	μM	5	Methods

A key revision of the three-compartment model that was used here accounts for the fraction of oral doses that undergo first pass metabolism through the liver. The hepatic bioavailability fraction (Rowland et al., 2011) was calculated according to:

$$f_{hepatic,bioavailability}=\frac{Q_{liver}}{Q_{liver}+\frac{C{l}_{hepatic}}{R_{blood:plasma}}}$$

where Q_liver is the total liver blood flow, R_blood:plasma is the chemical concentration ratio between blood and plasma, and the hepatic clearance is:

$$C{l}_{hepatic}=n_{celldensity}*V_{liverc}*d_{liver}*C{L}_{int}$$

is the hepatic clearance, scaled by hepatocellularity (10⁶ hepatocytes / g liver), the volume of liver per (kg body weight)^0.75, and d_liver is the density of liver (Pearce, et al., 2017b). Experimental values for R_blood:plasma were available in some cases, but typically a calibrated red blood cell:plasma partition coefficient was predicted (Pearce, et al., 2017a). Effective whole liver clearance Cl_liver is then calculated according to the well-stirred model (Yang, 2009):

$$C{l}_{liver}=\frac{Q_{liver}*f_{up}*C{l}_{hepatic}}{Q_{liver}+f_{up}*\frac{C{l}_{hepatic}}{R_{blood:plasma}}}$$

The steady state plasma concentration C_ss is calculated for a dose rate of 1 mg/kg body weight/day according to (Wilkinson et al., 1975) with the dose scaled for first pass metabolism (Rowland, et al., 2011):

$$C_{ss}=\frac{doserate*f_{hepatic,bioavailability}}{C{l}_{liver}+Q_{GFR}*f_{up}}$$

where Q_GFR is the glomerular filtration “rate” (which is actually a scaled flow in units of L/h/kg body weight) and Q_GFR * f_up represents passive renal clearance.

Monte Carlo Simulations for Comparing Uncertainty and Variability

Three separate MC simulations were performed: variability only, uncertainty only, and both uncertainty and variability.

This first MC simulation represented changes due to variability alone. Differences in one thousand simulated human individuals reflected biological variability with respect to physiology as well as variability in f_up and Cl_int around their median estimates (Ring, et al., 2017). This first simulation corresponds the default httk MC simulation in versions 1.9.2 (calc_mc_css). The distribution for f_up assumes that measured values of zero or 0.005 are censored below an assumed 1% limit of detection. The distribution for Cl_int includes a fraction of the population who are ultra-low metabolizers (Ring, et al., 2017).

A second MC simulation of uncertainty only for both f_up and Cl_int, was used to draw 1000 values of those two parameters that were consistent with the median and upper and lower bounds of the 95% credible interval. The Cl_int values were assumed to be distributed log-normally, while the adjusted f_up values (which are constrained to be between 0 and 1) were assumed to be distributed according to a beta distribution. Since some measurements of f_up resulted in very low values, a minimum of 0.0001 (corresponding to half the lowest measured value from the literature) was set. A single, default physiology was used for all 1000 draws, corresponding to httk function parameterize_steadystate.

A third MC simulation of both uncertainty and variability was conducted for 1000 samples. In the third simulation, uncertainty is first simulated using the same methods as the uncertainly only (second) MC simulation to determine a different “true” experimental value for f_up and Cl_int in each sample. Then, the full population variability model from the variability alone (first) M simulation is used, including simulating biological variability in f_up and Cl_int. This new simulation has replaced calc_mc_css as the default simulation in httk v 1.10 and is therefore used by calc_mc_oral_equiv for IVIVE oral equivalent doses. For chemicals from other studies (for example, Wetmore, et al. (2012)) without a 95% credible interval on Cl_int and f_up the median CVs of those parameters observed in this study are used to calculate credible intervals.

The three MC simulations were used to assess the relative contribution of population variability and chemical-specific measurement uncertainty when identifying the 95^th percentile most sensitive individuals who get higher plasma concentrations from the same dose.

In Vitro Bioactivity Data.

The ToxCast and Tox21 research programs employ batteries of high throughput assays to assess chemical bioactivity in vitro (Kavlock, et al., 2012; Tice, et al., 2013). Not every chemical is tested through every assay (Richard, et al., 2016). Most assays are conducted in concentration response, and each corresponding assay endpoint is analyzed statistically to determine if there is a concentration-dependent response or “hit” using the ToxCast Pipeline (Filer et al., 2016). Most assay endpoint-chemical combinations are non-responsive. Here, only the hits are treated as potential indicators of bioactivity. While biological models can be used to make predictions of toxicity based on in vitro data, here we simply used the 10^th percentile of the μM potencies (50% active concentration or AC₅₀) among all hits for each chemical. We are assuming that the 10^th percentile represents a low concentration for activating multiple assays (assuming ten or more bioactive assays were observed for a given chemical). However, this bioactivity does not have a direct toxicological interpretation. The October 2015 release (invitrodb_v2) of the ToxCast and Tox21 data (https://www.epa.gov/chemical-research/toxicity-forecaster-toxcasttm-data) were used for this analysis.

Reverse Dosimetry

As in previous HTTK chemical risk prioritizations, bioactivity IVIVE was performed using reverse dosimetry (Rotroff, et al., 2010; Wetmore, et al., 2015; Wetmore, et al., 2012). Here, the 10^th percentile bioactive concentration (μM) was divided by the C_ss (μM / 1 mg * kg bodyweight * day) to determine the mg / kg body weight / day dose needed to cause a plasma concentration equal to the bioactive dose. This calculation is possible because the HTTK model used is linear with dose (Pearce, et al., 2017b). The default HTTK v1.10 settings were used, for example, metabolic clearance was modeled as “restrictive” (Wetmore, et al., 2012).

Exposure Predictions

Because most chemicals lack measured data characterizing population intake rates (mg / kg body weight / day) (Egeghy et al., 2012), a consensus exposure prediction was used (Ring et al., 2018). Where there were intake rates that could be inferred from NHANES urine biomonitoring data (Ring, et al., 2017; Wambaugh et al., 2014) those rates were used. In all other cases, the Systematic Empirical Evaluation of Models (SEEM) approach was used to calibrate various exposure predictors (for example, production volume (U.S. Environmental Protection Agency, 2017)) and models (for example, the high throughput Stochastic Human Exposure Dose Simulator (Isaacs et al., 2014)) to reproduce the intake rates inferred from NHANES urine and serum biomonitoring. The SEEM approach aggregates exposure predictors based upon chemical-structure derived predictions of the relevant exposure pathways (Ring, et al., 2018). The SEEM exposure forecasts (i.e., ExpoCast) are uncertain, and the upper boundary of the 95% credible interval is used here. Although a 95% credible interval is calculated, this reflects uncertainty but not variability – the (Ring, et al., 2018) model predicts population median exposure rates for the U.S. population.

Results

New Data for High Throughput Toxicokinetics

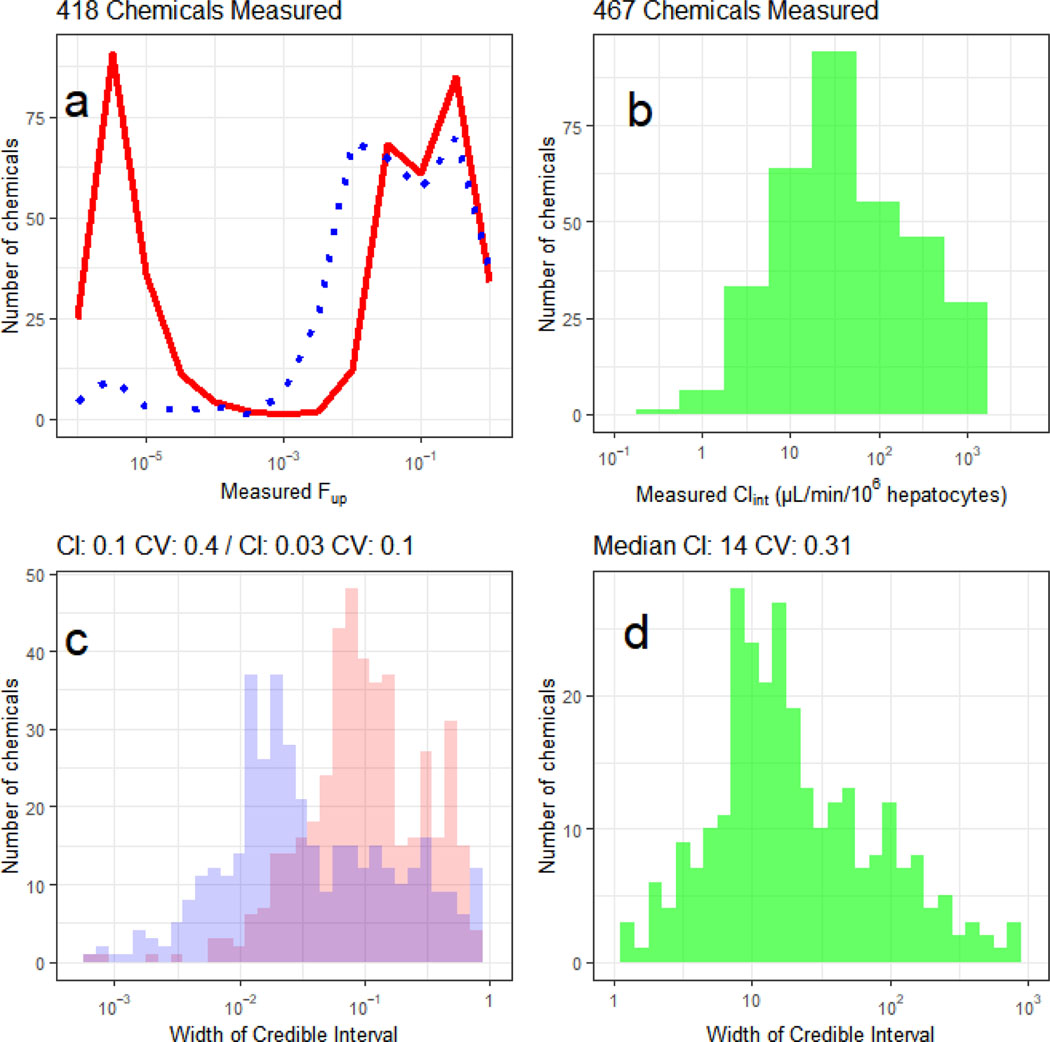
Experiments were attempted for 496 chemical samples. Of these, plasma protein binding was successfully measured for 418 chemicals and hepatocyte-mediated clearance was successfully measured for 467 chemicals, giving a total of 389 unique chemicals with both parameters. Both parameters are needed to parameterize an HTTK reverse dosimetry model. The release of these data bring the total number of chemicals within the ToxCast Phase I and II (ph1_v2; ph2; (Richard, et al., 2016) that have been assessed for TK to 608/1061 (57%). Review of the frequency distributions of the datasets show that many chemicals are relatively highly bound to protein (median f_up = 0.037, Figure 1a). Of the chemicals with successful clearance measurements, 142 showed no evidence of hepatic clearance over four hours, while for the others a broad range of clearance rates were observed, median Cl_int = 14 μL/min/10⁶ hepatocytes (Figure 1b).

Figure 1:

Histograms depicting the median measured values (a, b) and 95% credible intervals (c, d) for fraction unbound in plasma (f_up, a,c) and intrinsic hepatic clearance (Cl_int, b,d). In panel a, the distribution of estimated f_up for the single protein concentration assay (solid line) is compared with the protein titration (three concentrations) method (dotted) line. In panel b, the median estimated Cl_int is shown. In panel c, the distribution with larger credible intervals corresponds to the single protein concentration assay, with a median credible interval is 0.1, corresponding to a precision of roughly ±0.05. When data from the protein titration are jointly analyzed (smaller credible intervals), the certainty is increased to a median credible interval of 0.029, or roughly ±0.015. The width of the credible interval is a measure of the certainty in an estimate, i.e., a smaller credible interval indicates greater certainty. For the f_up values, a credible interval approaching 1 indicates that all possible values are consistent with the data – that is, the data do not help identify f_up since f_up must be between 0 and 1. In panel d the distribution of credible intervals for Cl_int is shown.

All new measured data are made available in Supplemental Table 4 and on-line at https://doi.org/10.5061/dryad.nf40jb4.

A New Protocol for Plasma Binding

A recurring challenge in the experimental f_up measurement is the ability to detect unbound chemical for those chemicals that are highly bound to plasma proteins or difficult to resolve relative to background. The f_up assay failed for 38.6 % of 239 chemicals in Wetmore, et al. (2012) and 11.5 % of 163 chemicals in Wetmore, et al. (2015). In the absence of a measured value, a default value of 0.5% was assumed (Rotroff, et al., 2010). To address this challenge, we used a new protocol consisting of RED assays performed with varied concentrations of plasma protein (10, 30 and 100% of physiologic levels), as opposed to using only a single, 100% physiologic plasma protein concentration as in previous efforts.

In this study, when the single concentration protocol of previous studies was used for f_up, 44% of the assays failed to provide a certain estimate (coefficient of variation (CV) < 0.5). Using the new protocol, only 9.1% of the assays returned uncertain values. While there were 234 chemicals for which f_up could be quantified using the original protocol, the new protein titration protocol boosted this number to 380 successfully measured chemicals, with only 38 chemicals where uncertainty was large (CV > 0.5). The median free fraction of the chemicals that were only measurable with the titration protocol was 0.0041, indicating that many of these chemicals were highly bound. However, the f_up values ranged from a low of 9.5×10⁻⁹ (the lower limit of the Bayesian prior distribution, i.e., effectively zero) to as high as 0.95. In the case of chemicals with large free fractions at 100% PPP we believe that the use of additional data and a model of binding affinity may have made the estimates more precise. The signal to noise ratio of the assays is chemical dependent, and so it is unsurprising that there are some cases of chemicals that are not highly bound but still uncertain when only 100% PPP is used. The median estimated f_up of 0.0041 was surprisingly similar to the previously used default assumption of 0.005 (Rotroff, et al., 2010).

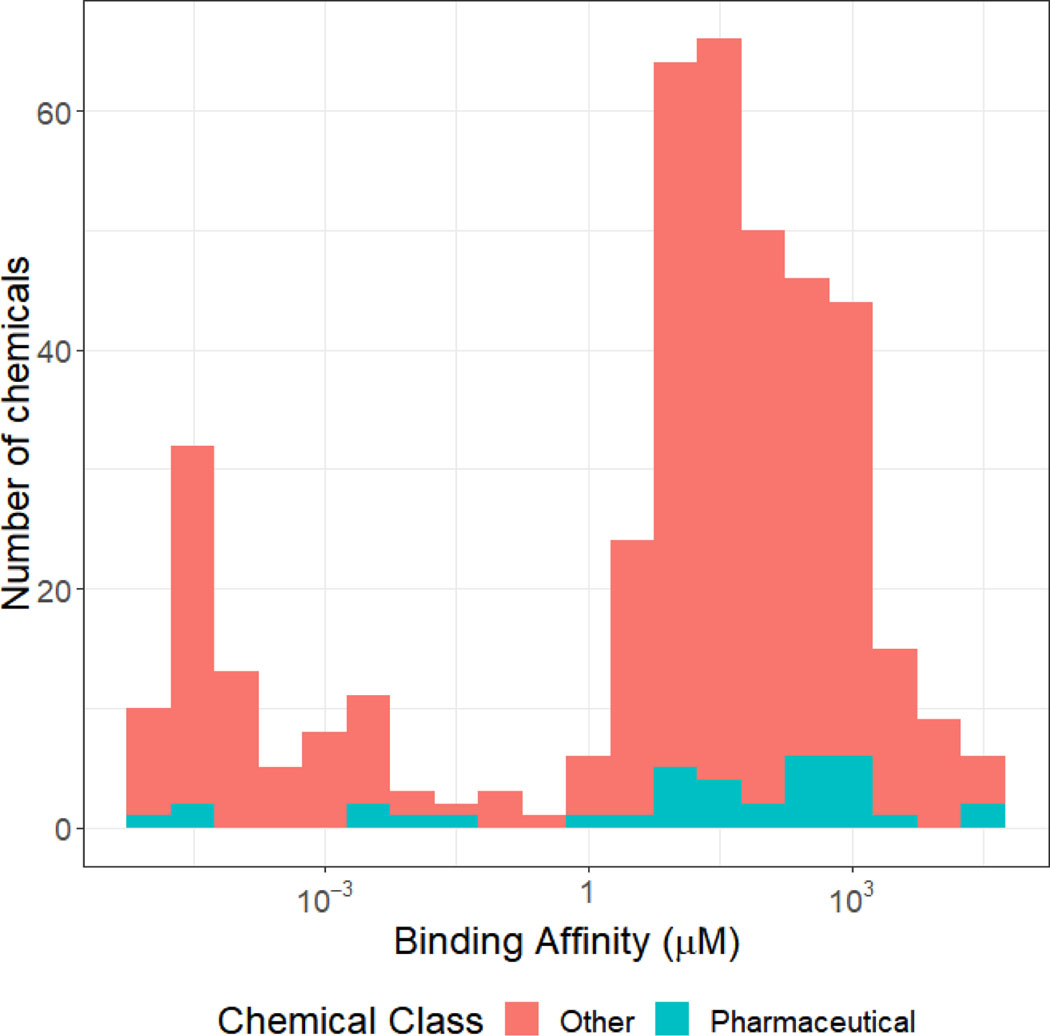
An additional benefit to the protein titration method of estimating f_up is that the binding affinity (characterized by dissociation constant k_d) can be estimated. In Figure 2, we show that the median of the estimated binding affinities ranges over many orders of magnitude, with a peak in the tens of μM. Although the distribution appears bimodal, the lower peak reflects those chemicals where k_d was very small but could not be identified from the data (Cobelli et al., 1980). There has been some debate in the literature as to whether pharmaceuticals are highly bound (i.e., “restrictive clearance”) and non-pharmaceuticals are weakly bound (i.e., “non-restrictive clearance”) (Toutain, et al., 2002; Wetmore, et al., 2012; Yoon et al., 2013) but the data in Figure 2 do not show a clear difference between pharmaceutical and non-pharmaceutical chemicals with the exception that most of the very weakly bound (near-zero k_d) chemicals are non-pharmaceuticals.

Figure 2.

Distribution of Binding Affinities Employed in Bayesian f_up Estimations. To jointly analyze the data from the RED assay conducted at three protein concentrations, a model for binding to protein with an dissociation constant (i.e., binding affinity) must be assumed. Although the specific binding protein (for example, hemoglobin) and the stoichiometry are unknown, this number provides a rough estimate for each chemical of how much that chemical would be expected to be impacted by the presence of plasma binding.

Since the estimated k_d is for an unspecified protein or proteins within the plasma, quantitative interpretation of this value is not possible; however, the breadth of the distribution (see Figure 2) illustrates that some chemicals are more greatly affected by the presence of a plasma protein. In in vitro screening batteries such as ToxCast, the amount of plasma protein varies depending upon the specific assay, so variation in plasma binding may make some chemicals more discordant between assays than others.

Twenty (20) chemicals were duplicated in a blinded fashion to test the reproducibility of the protein binding protocol. Although the medians were more concordant for f_up > 0.01, when the confidence intervals were considered all chemicals were consistent (Supplemental Figure 3).

Uncertainty Analysis

Across the chemical dataset, Bayesian methods were developed to assess the uncertainties inherent to experimental and analytical variability on a per chemical basis. These methods were used to assign a chemical-specific estimate of uncertainty to the in vitro f_up and Cl_int estimates. The joint analysis of the three protein concentrations used in the new f_up measurement protocol was made possible with the Bayesian framework. The Bayesian estimates include a 95% credible interval.

The credible interval around an estimate characterizes the certainty in that estimate – 95% of the values that are consistent with the prior information, the new data, and the model used lie within the 95% credible interval. In Figure 1c we compare the size of the credible intervals for chemicals analyzed using 100% physiological protein alone, with the joint analysis of three concentrations. Unsurprisingly, the uncertainties are reduced through the addition of new data. The median credible interval decreases from 0.1 (i.e., 95% chance of being within ±0.05) to 0.029. This indicates that even for chemicals where f_up was measurable at 100% PPP, there is a significant reduction in uncertainty about the value of f_up with the new method.

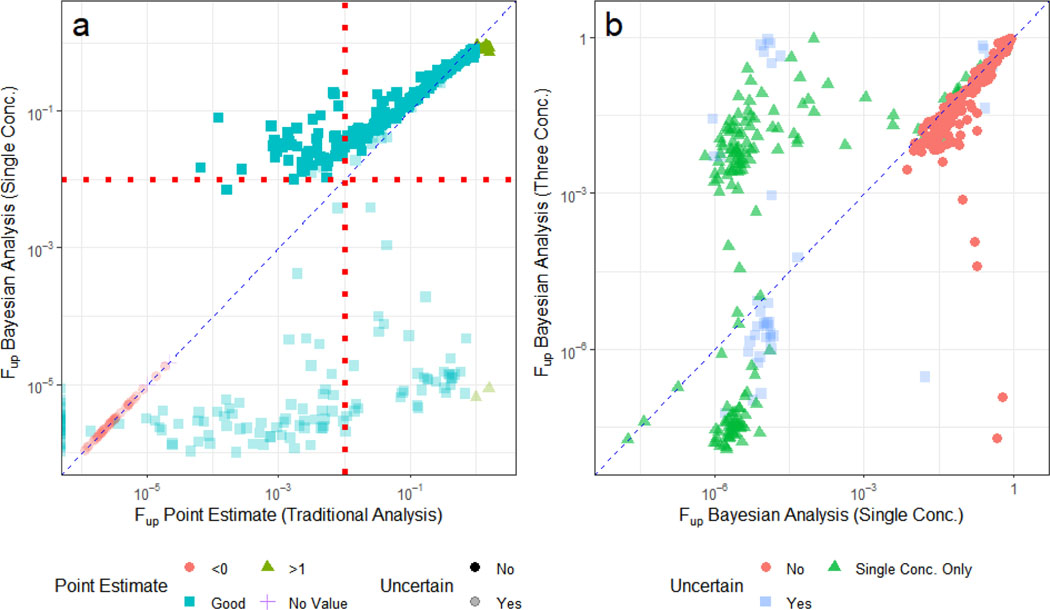
In Figure 3a, we observe that several chemicals for which there were erroneous point estimates (for example, f_up > 100% or f_up < 0%), the f_up estimates have been corrected. Most chemicals in Figure 3a have an f_up above 0.01 (the assumed limit of detection (Rotroff, et al., 2010)) have small credible intervals, while the more highly bound chemicals (i.e., f_up below 0.01) have uncertain estimates (CV>0.5). There are several chemicals where we would have estimated f_up = 0 because the point estimate reported negative values, but that have non-zero, albeit uncertain estimates with the Bayesian approach.

Figure 3.

Comparison of Bayesian f_up and Uncertainty Estimations to Experimental Point Estimates. Two separate Bayesian analyses were performed: one including only those data collected at 100% PPP, and a second that used a binding model to relate data collected at 10%, 30%, and 100% PPP. In (A), f_up point estimates <0 are plotted on the y-axis. These values are considered “good” if they lie between 0 and 1. The Bayesian median f_up values (x-axis) derived from the 100% PPP data and the associated uncertainty estimates (vertical lines) were correlated with point estimates. Bayesian model estimates were constrained to be greater than zero and less than 1;. The red dotted line (at 1%) represents a previously assumed generic limit of quantification (Wetmore, et al., 2015; Wetmore, et al., 2012). In (B), the medians from the two Bayesian analyses are compared. In both plots, the diagonal dashed line indicates the identity line (“perfect predictions”). In both panels the Bayesian estimates are “uncertain” (semi-solid) if the CV was larger than 0.5 and certain (solid) otherwise.

In Figure 3b, we compare the protocol with only 100% PPP with the results of the approach using protein titration (three concentrations). Many of the chemicals with uncertain estimates in Figure 3a become more certain in Figure 3b, with a group of the chemicals being estimated to have f_up between 0.001 and 0.01, and a second group being confidently estimated to have very small f_up (i.e., <10⁻⁴). Previously all these chemicals would have been treated as having an f_up of 0.005.

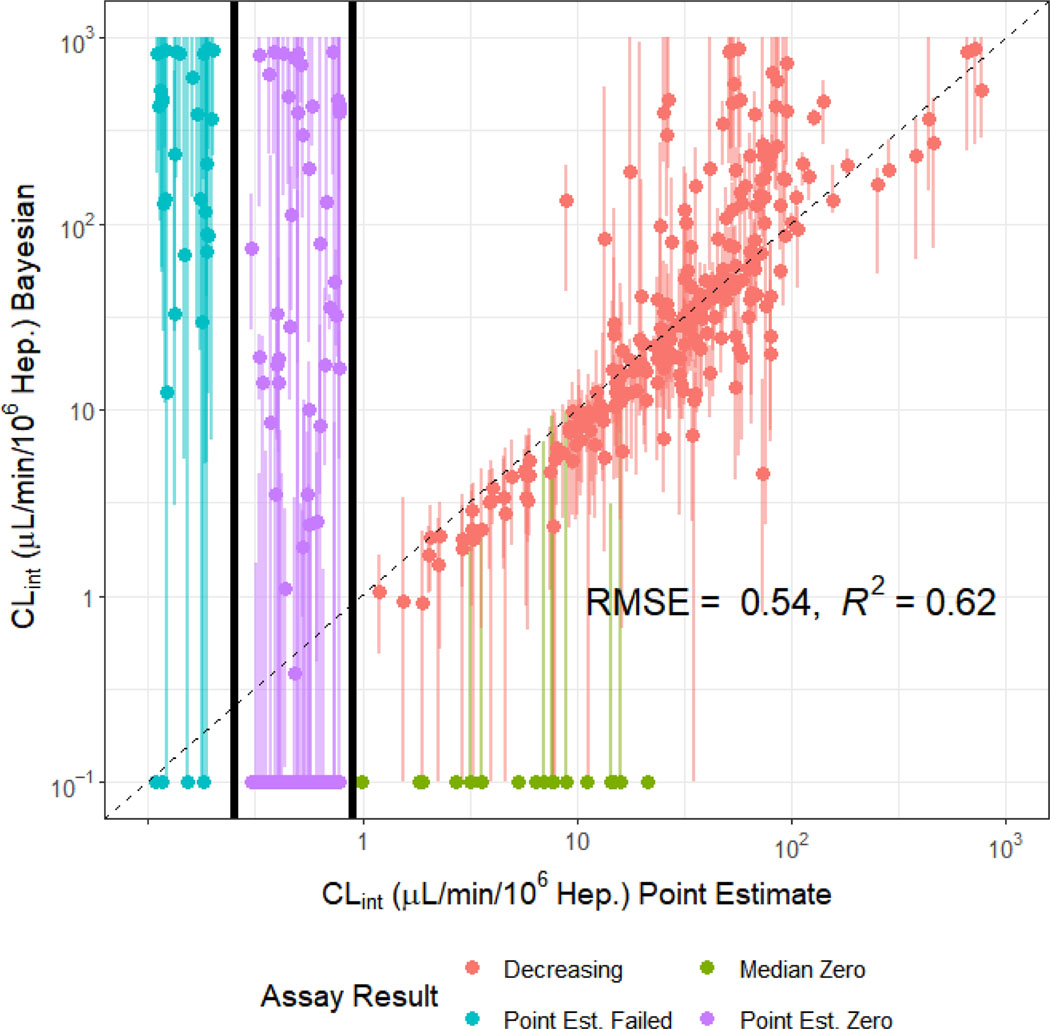
The in vitro intrinsic hepatic clearance assay data were also analyzed using Bayesian methodology. The Bayesian analysis jointly analyzed the data from the 1 and 10 μM experiments for disappearance of chemical due to hepatocyte metabolism. In Figure 4, we compare the 1 μM clearance rate derived from the previous, point estimate method with the Bayesian estimate. Two hundred and fifty-five chemicals had non-zero valued median Bayesian posterior estimates where the point estimate was also non-zero. We observe concordance (R² ~ 0.62) for chemicals where the point estimate was greater than 1.0 μl/min/10⁶ hepatocytes. Also in Figure 4, we examine Bayesian estimates of clearance for chemicals where the point estimate could not be made (far left) or the point estimate was zero (middle). In general, these estimates are much more uncertain but often the median estimate is statistically different from zero, consistent with cases where the chemical could be quantitated only at early time points.

Figure 4.

Comparison of Bayesian Cl_int and Uncertainty Estimations to Experimental Point Estimates. Cl_int estimate for 1 μM chemical concentration displayed, though 1 and 10 μM were fit jointly. The size of the credible interval varies significantly from chemical to chemical, especially for the lower clearance rates. Plots of individual fits are provided as supplemental material.

Within Figure 4 we identify seven overall groups of chemicals where the Bayesian analysis and point estimates were either concordant or discordant. Chemicals fall into a class depending upon their concentration vs. time course, which are plotted for each chemical in Supplemental Figures 4. The first two groups are consistent between the Bayesian and point estimates and contain a total of 322 chemicals. In group 1 we have 219 chemicals along the diagonal of Figure 4 where the non-zero valued median Bayesian posterior estimate was on the order (within ±3.2 times) of the point estimate for clearance. For example, the plot for o,p’-DDT in Supplemental Figures 4 shows that the median Bayesian estimate is very similar to the clearance data. Group 2 contains 103 chemicals where both the Bayesian and point estimates are zero. For example, 2,2’-Methylenebis(ethyl-6-tert-butylphenol) shows flat (unchanging) concentration with time.

We identify five inconsistent groups in Figure 4: Group 3 consists of 29 non-zero-valued median Bayesian posterior estimates where the estimate was greater than 3.2 times the point estimate. For example, the supplemental plot for Clodinafop-propargyl shows that the chemical concentration appears to quickly fall below the limit of quantitation. While the Bayesian estimate for Group 3 interprets the later points as non-detects, and therefore estimates rapid clearance, the point estimate uses all points to estimate a slower clearance. Group 4 includes 17 zero-valued Bayesian estimates for chemicals where the point estimate was non-zero. For example, the plot for 17alpha-Ethinylestradiol in Supplemental Tables 4 shows a very weak trend that is comparable to the noise in the data. While the point estimate still finds a weak, slope, the Bayesian method assigns only a 7% probability to decreasing. However, this non-zero probability of clearance is propagated when uncertainty is considered in subsequent analyses. Group 5 includes 43 chemicals where the Bayesian estimate was non-zero despite a zero point estimate (that is, p-value > 0.05 for linear regression). For example, the plot for Phenolphthalin in Supplemental Figures 4 shows a very slight decrease over time, but that decrease is consistent at both the 1 and 10 μM concentrations, lending greater confidence to the estimate than the point estimates found by analyzing the two concentrations separately. Group 6 contains 29 chemicals where a point estimate could not be made, but the Bayesian approach found a non-zero value. For example, the plot for Pentachloropyridine shows that the Bayesian model estimated that the chemical was rapidly metabolized at 1 μM, but that metabolism was completely saturated by 10 μM. The estimated clearance is highly uncertain, with a 95% credible interval ranging from 0.115 to 20.8 μL/min/10⁶ hepatocytes. Finally, Group 7 is the smallest – containing only five chemicals where a point estimate could not be made, and the Bayesian estimate was zero. For example, shows a scattered, noisy signal where all the values for the 1 μM were below the limit of quantitation. The Bayesian analysis assumes that there is most likely no clearance, although the upper limit of the 95% credible interval includes the possibility of clearance as fast as 2.21 μL/min/10⁶ hepatocytes.

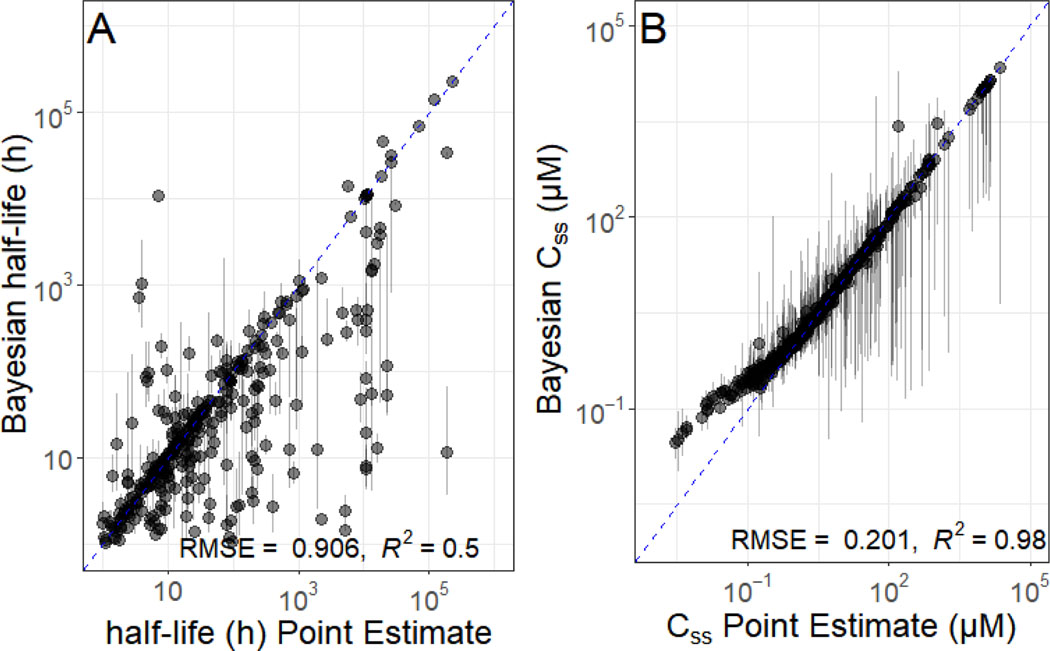
In Figure 5, we examine the impact of quantifying uncertainty on two key TK parameters. In Figure 5A we examine the chemical half-life. The half-life based upon the point estimate for f_up and Cl_int is somewhat concordant with the median of the Bayesian estimate (R² ~ 0.5), there is chemical-to-chemical variability in the confidence of the half-life estimate. In Figure 5B we examine steady-state plasma concentration (C_ss), which is used for high throughput “reverse dosimetry” (Wetmore, et al., 2015). We observe concordance (R2 ~0.98), but again there is variability from chemical to chemical in the breadth of the credible interval, with a handful of chemicals being extremely uncertain.

Figure 5.

Uncertainty Assessment for TK Quantities half-life and C_ss. The impact of uncertainty on estimated values for f_up and Cl_int could in turn affect additional TK quantities, for example elimination half-life (t_1/2, shown in panel A) and steady-state serum concentration (C_ss, shown in panel B). In both plots, the x-axis indicates the value that would have been estimated with previous methods, while the y-axis indicates the median and 95% credible interval for values calculated with our Bayesian method. Chemicals plotted with triangles are those that could be estimated with the previous, point estimate methods, while chemicals plotted with circles could not. The dashed line indicates the identity (perfect predictor) line. Chemicals that had no point estimate are plotted on the identity line.

Comparing Uncertainty and Variability

Quantification of uncertainty allows for analysis of the relative importance of uncertainty and biological variability in applications such as reverse dosimetry. Previous work (Ring, et al., 2017; Wetmore, et al., 2015; Wetmore, et al., 2012) has analyzed the impact of inter-individual human physiologic variability on TK, and especially the C_ss value. This variability has been characterized using the 95^th percentile C_ss, corresponding to the individuals who are predicted to have C_ss values higher than 95% of the population for the same steady-state dose. When converting in vitro bioactive concentrations to equivalent human doses, those individuals with higher C_ss values need smaller doses to achieve plasma concentrations equal to the bioactive concentration and are therefore considered more sensitive.

We performed three MC simulations to determine the C_ss upper 95^th percentile group. The first MC simulation was for biological variability alone. We have used both a preexisting population variability MC simulator based on CDC NHANES biometrics (Ring, et al., 2017). As in previous work, this first simulation varies physiological quantities such as liver flow and metabolic rate to reflect differences between individuals (Ring, et al., 2017; Rotroff, et al., 2010; Wetmore, et al., 2015; Wetmore, et al., 2012). The second MC simulation was for uncertainty alone: a single physiology was used for all individuals but different estimates of f_up and Cl_int were used, consistent with the estimated measurement uncertainty. The third MC simulation included both uncertainty and variability.

In Figure 6 we compare the 95^th percentile “sensitive individual” C_ss to the “median individual” C_ss for all three MC simulations (variability alone, uncertainty alone, and both). The ratio of the C_ss for the 95^th percentile to the median indicates the difference in doses needed between the median and more sensitive person to achieve the same plasma concentration – larger ratios indicate greater sensitivity. A ratio of 1 (horizontal dashed line in Figure 6) indicates that the 95^th percentile individuals are no more sensitive, while a ratio of 10 indicates that the 95^th percentile individuals would achieve bioactive concentrations in their blood at exposures ten times lower than the median individual. Comparing these ratios for the three MC simulations gives the relative contribution of uncertainty and variability.

Figure 6.

Relative contributions of uncertainty and variability to differences between the 95^th percentile and median C_ss. Monte Carlo analysis of both variability (triangles) and uncertainty (circles) give distributions that can be characterized by a 95^th percentile C_ss for which individuals achieve a higher C_ss for the same fixed dose rate – these individuals can be considered more “sensitive” to chemical exposure. Uncertainty and variability can be combined (squares) to estimate a 95^th percentile reflecting both factors. For most chemicals, variability contributes more than uncertainty to the difference between the Css predicted for the median Cl_int and f_up values.

In Figure 6 we observe that the ratio of the C_ss 95^th percentile for “variability” to the C_ss for median parameter values is roughly constant (median value of 6.27). The variability distribution is driven by constant CVs for f_up and Cl_int equal to 0.3, as well as five percent of the population being characterized as low-metabolizers with a mean clearance ten times lower than the mean for the rest of the population. Meanwhile, the ratio for the uncertainty distributions is, for many chemicals, smaller (median 2.32). This indicates that for most chemicals that population variability drives the difference between the median and the 95^th percentile. However, there are chemicals on the right-hand side of Figure 6 that have larger contributions due to uncertainty – in some cases as much as a hundred-fold difference between the 95^th percentile and the prediction made using the median values. For these chemicals it may be that the current HTTK data are insufficient and new measurements or methods are necessary. On the left-hand side of Figure 6 there are a few chemicals where the median and 95^th percentile for uncertainty alone do not differ – for these chemicals the median of the measured f_up was below the assumed minimum of 0.0001. When uncertainty and variability are both considered, we observe that the distributions are narrower than the previous “variability only” distribution. However, for chemicals measured previously with only a single protein concentration the combined uncertainty and variability would be greater than variability alone. For the Wetmore et al. (2012, 2015) chemicals the median shift in C_ss between the calculation in those analyses and the new method is an increase of 9.5 times.

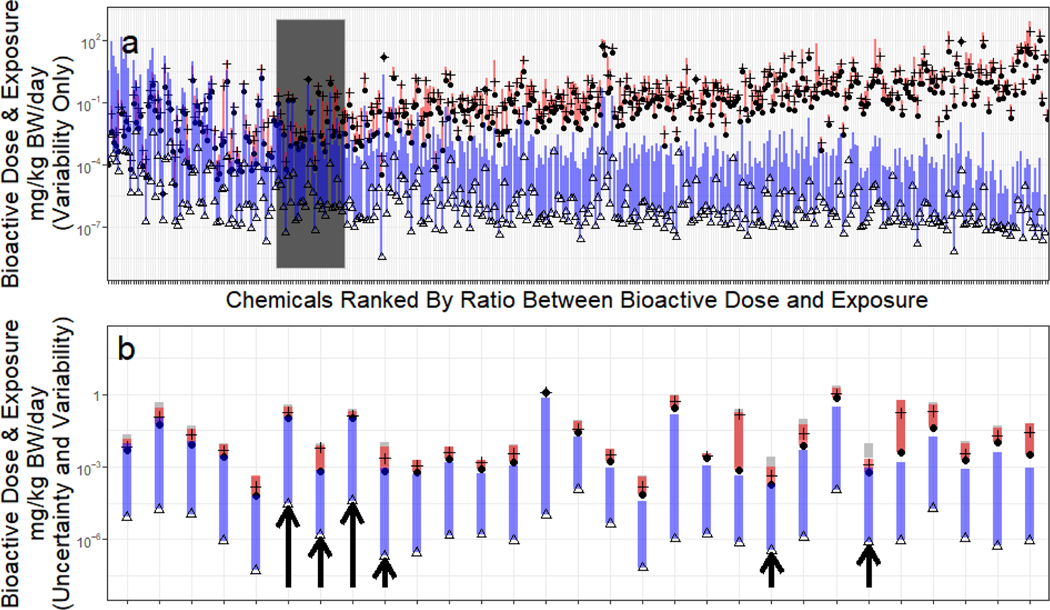
Finally, in Figure 7, we use the HTTK data reported here to prioritize future chemical research. We do this by comparing in vitro bioactive concentrations from the U.S. EPA toxicity forecasting (ToxCast) project (Judson et al., 2009; Kavlock, et al., 2012) with predicted exposures from the U.S. EPA exposure forecasting (ExpoCast) (Ring, et al., 2018). Each chemical in Figure 7 has been tested in concentration-response format through a batter y of ToxCast assays. When a systematic response as a function of chemical concentration was observed (a “hit”), the concentration needed to cause activity more than the assay background (activity concentration at cutoff or ACC) was determined. Since ACC has units of in vitro concentration (μM), the μM C_ss for a dose rate of 1 mg/kg/day was used to convert the in vitro hit ACC’s to dose rates that would cause bioactive concentrations. The range of bioactive dose rates for each chemical are indicated by the red vertical line in Figure 7. The median value is indicated by a horizontal hash, and the 10^th percentile dose rate in indicated by a round plot point for each chemical.

Figure 7:

High throughput risk-based prioritization can be conducted by using doses predicted to cause bioactivity identified by high throughput screening. High throughput exposure estimates have large uncertainty, indicated by the triangles (median of distribution) and vertical bar (upper 95^th percentile range). There are many in vitro activities identified for each chemical, the 80% interval of equivalent dose rates is indicated by the vertical red bar, with a horizontal slash indicating the median and the circle plot points indicating the 10^th percentile of the bioactive concentration. Anywhere the entire exposure bar is below the bioactivity circle there is 95% probability that the median exposure will not cause a dose sufficient to cause the 10^th percentile in vitro bioactivity. Chemicals are sorted from left-to-right by the margin between the 10^th percentile bioactivity (small circle) and the upper 95^th percentile limit on estimated median intake rate. In panel A, all chemicals for which C_ss could be calculated are shown using only variability. In panel B, the shaded region of panel A is shown, using both variability and uncertainty to calculate the bioactive dose. Arrows in panel B identify six chemicals where exposure and 10^th percentile bioactivity potentially overlap that would have been missed as priority chemicals if uncertainty analysis was not performed. Two overlapping bars are shown for each chemical’s bioactive doses – the upper one is for variability alone (as in Panel A), the lower is for uncertainty and variability together.

Chemicals in Figure 7 are sorted from left-to-right by the ratio of the 10^th percentile dose rate (mg/kg-bodyweight (bw)/day) to the upper 95^th percentile on the credible interval for predicted geometric mean U.S. population exposure rate (mg/kg-bw/day). Thus, the chemicals at the left-hand side may be considered higher priority chemicals since the putative margin between bioactivity and exposure is smaller. Given the large uncertainties involved, particularly with respect to exposure, the margins represent only a rapid estimate of relative priority for additional research based upon potential risk to the human population.

In Figure 7 we examine the impact of uncertainty analysis by comparing the prioritization using population variability alone (Figure 7a) with prioritization including both variability and uncertainty (Figure 7b). There are 78 chemicals with bioactive doses potentially overlapping with exposure in Figure 7a (Supplemental Table 5). In Figure 7b the dark grey region of Figure 7a has been expanded, and there are six chemicals (indicated by arrows, listed in Table 2) where the exposures overlap with the 10^th percentile dose rate only when uncertainty is considered in addition to variability. Thus, there are at least six chemicals with greater priority that are only identified through uncertainty analysis.

Table 2.

Chemicals where Uncertainty in Data Changed Bioactivity:Exposure Ratio to be less than One

Chemical	DSSTox Substance ID	Clint (μL / min / 106 hepatocytes)	fup	In vitro Assays 10th Quantile (μM)	Equivalent Dose - Variability Only (mg / kg body weight / day)	Equivalent Dose - Uncertainty and Variability (mg / kg body weight / day)	Exposure Upper 95th (mg /kg body weight / day)
2’,4’,5’,7’-Tetrabromofluorescein	DTXSID3044590	0	3.00E-03	0.66	9.99E-04	6.17E-04	8.82E-04
2-Chloro-4-phenylphenol	DTXSID0022353	49.2	1.17E-08	2.49	2.34E-03	5.61E-04	9.05E-04
3-Phenoxybenzoic acid	DTXSID1038321	0	7.16E-03	0.56	7.72E-04	6.48E-04	7.09E-04
Dodecyltrimethylammonium chloride	DTXSID1026900	16.2	3.64E-02	1.66	1.21E-01	9.91E-02	1.14E-01
N,N-Dimethyldodecan-1-amine	DTXSID1026906	34.2	6.99E-03	3.84	1.21E-01	9.92E-02	1.08E-01
Tamoxifen	DTXSID1034187	0	1.65E-03	0.92	4.25E-04	1.76E-04	1.82E-04

Discussion

Within the United States, a tapestry of laws cover how and to what extent chemicals are assessed for risk (Breyer, 2009). Except for pharmaceuticals, pesticide active ingredients, and food additives, most of the thousands of chemicals in commerce do not have public toxicological, toxicokinetic, or exposure data, be it human or animal (Egeghy, et al., 2012; Judson et al., 2008); Wetmore, et al. (2012). The 2017 National Academies of Sciences, Engineering, and Medicine report “Using 21^st Century Science to Improve Risk-Related Evaluations” stated that “Recent advances in high-throughput toxicity assessment, notably the ToxCast and Tox21 programs […], and in high-throughput computational exposure assessment […] have enabled first-tier risk-based rankings of chemicals on the basis of margins of exposure—the ratio of exposures that cause effects (or bioactivity) to measured or estimated human exposures (Shin et al., 2015; Wambaugh et al., 2013; Wambaugh, et al., 2014; Wetmore et al., 2014; Wetmore, et al., 2012)” (National Academies of Sciences, 2017). These “first-tier” tools can be used to identify chemicals for which additional research is most likely to be impactful (Thomas et al., 2013). Here we have reported on complete, chemical-specific HTTK measurements for 389 chemicals. We have further quantified chemical-specific measurement uncertainty, allowing for the first time a comparison between human variability and methodological uncertainty in chemical risk prioritization.

A key advancement presented here is both the quantification of chemical-specific uncertainty (Garcia et al., 2015) and the propagation of that uncertainty into prioritizations with the potential to inform chemical risk assessment (Chiu et al., 2009). The refined MC simulator now includes both human variability (Ring, et al., 2017) and propagation of uncertainty and is available in the public R package “httk” (Pearce, et al., 2017b) v1.10. For chemicals from previous studies (for example, Wetmore, et al. (2012)) where chemical-specific 95% credible intervals are unavailable, we propose that the chemicals studied here are similar enough (both sets are from the ToxCast library) to use the median CVs from this study as defaults for measurements from past studies. Out of the 933 chemicals available in v1.10.0 of HTTK, only 389 have complete HTTK data provided from this paper, leaving 544 chemicals for which default CV values must be used.

While uncertainty has been estimated and propagated for f_up and Cl_int, there are many human physiological parameters (Table 1) used here for which we are currently unable to assess uncertainty. Though population variability is simulated for each of these parameters, sensitivity analyses, literature reviews, and, potentially, new experiments may be needed to properly characterize the uncertainty in these parameters.

Estimating parameters for a non-linear model (as in the affinity binding model) from noisy data can be quite difficult. It can be hard to recognize when parameters are statistically non-identifiable, i.e., not informed by the available data. Garcia, et al. (2015) suggested that a Bayesian analysis allows a thorough, and perhaps the only defensible, analysis method. Without great care, alternative methods (i.e., frequentist statistics) may yield specific estimates of parameter values when in fact the data and model are insensitive (i.e., produce the same result) for a wide range of parameter values. Parameter non-identifiability is especially dangerous when models are to be used for extrapolation (Bernillon, et al., 2000). Bayesian analysis addresses parameter identifiability, as well as allowing the benefit of credible intervals for uncertainty quantification and propagation. However, we are currently assuming f_up and Cl_int, and their errors, are uncorrelated. This may not be true due to chemical-specific issues with analytical chemistry (for example, a chemical that cannot be well quantitated might both have a higher than observed f_up and is less likely to have rapidly disappeared from the hepatocyte assay).

The uncertainty propagation framework is developed here for experimental measurement uncertainty, but the same framework can also be used to combine disparate data types in general. For example, for literature measurements where chemical-specific measures of uncertainty are unavailable we can use estimates of the median uncertainty. The estimates could potentially vary from source-to-source or method-to-method. In addition, the uncertainty propagation framework could be applied to values predicted using in silico quantitative structure-property relationships (QSPR) (Ingle et al., 2018; Pradeep et al., 2018; Sipes, et al., 2017) – for example, the uncertainty estimated using the external evaluation data set might be propagated into risk priority predictions.

When uncertainty and variability are considered jointly we observe that most often biological variability is a greater driver of the breadth of the distributions (i.e., the differences between the mean and extreme quantiles). Through estimation and comparisons of the relative impact of uncertainty and variability on TK predictions, this study affirms the importance of characterizing population variability in chemical prioritization efforts intended to inform public health risk (Abdo et al., 2015). However, the in vitro HTTK data for some chemicals are very uncertain. HTTK data should not be used without uncertainty analysis – for the small subset of chemicals in Figure 6 where the uncertainty dwarfs the variability, failure to consider the uncertainty would have produced significantly higher predicted doses than should be used because of data quality issues. Previous efforts have relied on p-values and manual curation of data (Wetmore, et al., 2015; Wetmore, et al., 2012). As these assessments mature across more chemicals, establishment of best practices for assessing uncertainty could be helpful in identifying needs for follow-up studies.

We have characterized population variability with respect to toxicokinetics (Ring, et al., 2017), but not exposure (Ring, et al. (2018) gives medians) or hazard (ToxCast can be thought of as reflecting a “generic” human).To determine potentially bioactive doses, IVIVE was performed on nominal in vitro bioactivity concentration-response data with no accounting for in vitro distribution (Groothuis et al., 2015). There are models for predicting this that could be considered if sufficiently evaluated (Armitage et al., 2014; Fischer et al., 2017). Additionally, uncertainty in the in vitro bioactivity data has not been considered. New tools are being developed to allow this uncertainty to be assessed (Watt et al., 2018) and that uncertainty could similarly be propagated with MC methods.

With our new protocol for assessing plasma protein binding, we have estimated binding affinity (a ratio between on- and off-binding events). This information may allow us to determine whether a chemical should be modeled with “restrictive” or “non-restrictive” clearance in the liver (i.e., does the f_up limit the rate of metabolism) (Toutain, et al., 2002; Wetmore, et al., 2012; Yoon, et al., 2013). If a data set of known chemicals that do and do not follow restrictive clearance set were available, it might be analyzed to predict this aspect of metabolism. Unfortunately, no such public data set has yet been developed.

A key advantage of the new protocol for f_up is that we have reduced the uncertainty in estimates from a median of ±0.05 to ±0.015. This allows more precise prediction of toxicokinetics, including tissue partitioning. Quantitative uncertainty analysis augments the default CVs of 0.3 assumed for both f_up and Cl_int in previous work (Jamei et al., 2009; Rotroff, et al., 2010; Wetmore, et al., 2015; Wetmore, et al., 2012). In those studies, the CV of 0.3 was considered to describe as variability alone. Coincidentally, the median CV for uncertainty for Cl_int for the chemicals studied here was 0.31. The effective CV is larger than 0.3 for simulating Cl_int uncertainty and variability in HTTK. The CV for f_up using the single concentration protocol was 0.4, though for the titration protocol this has been reduced to 0.1. In HTTK v1.10 when chemical-specific estimates of uncertainty are unavailable 0.31 is now used for Cl_int and 0.4 is used for f_up values generated using a single protein concentration (e.g., Wetmore, et al. (2015) for example, Wetmore, et al. (2015)). This assumption, in part, increases the C_ss predicted for the Wetmore et al. (2012, 2015) chemicals by a median fold-change of 9.5 times. Remeasuring f_up for chemicals from previous studies using the protein titration protocol would be expected to reduce the uncertainty in the predictions for those chemicals.

The steady-state TK model included in “httk” v1.9 and later includes first pass metabolism by the liver, which reduces the amount of chemical that is available systemically following an oral dose (this process was previously included in the physiologically-based TK model of “httk”) (Honda et al., 2019). In order to account for first pass metabolism, the blood to plasma partition coefficient (R_blood:plasma) is needed. Although in silico predictors exist for this property (Pearce, et al., 2017a), measurement of this partitioning in vitro should be possible and might be considered as part of a standard suite of HTTK assays.

Additionally, the parameters for the analytical chemistry model were estimated assuming the analysis of the two Cl_int concentrations and three F_up concentrations were performed separately. If the concentrations from the respective experiments and chemical analysis were performed jointly there would be greater statistical power and lesser uncertainty.

The U.S. EPA’s “Strategic Plan to Promote the Development and Implementation of Alternative Test Methods Within the TSCA (Toxic Substances Control Act) Program” states that “TK is essential for translating in vitro-derived potency values into an external administered dose required to achieve internal concentrations equivalent to these potency values” (U.S. Environmental Protection Agency, 2018). The HTTK approach for IVIVE has been previously described (Rotroff, et al., 2010; Wetmore, et al., 2015; Wetmore, et al., 2012), but here we have expanded upon that approach in two ways: first, we have added new chemical-specific data for 496 chemicals, bringing the total to 933 substances, and second, we have quantified uncertainty in the data and introduced a framework for propagating that uncertainty into chemical risk prioritizations. HTTK based upon in vitro data is a new approach methodology with the potential to inform 21^st century chemical risk assessments (Kavlock et al., 2018; U.S. Environmental Protection Agency, 2014b, c).