Global Patterns of Recombination across Human Viruses

Abstract

Viral recombination is a major evolutionary mechanism driving adaptation processes, such as the ability of host-switching. Understanding global patterns of recombination could help to identify underlying mechanisms and to evaluate the potential risks of rapid adaptation. Conventional approaches (e.g., those based on linkage disequilibrium) are computationally demanding or even intractable when sequence alignments include hundreds of sequences, common in viral data sets. We present a comprehensive analysis of recombination across 30 genomic alignments from viruses infecting humans. In order to scale the analysis and avoid the computational limitations of conventional approaches, we apply newly developed topological data analysis methods able to infer recombination rates for large data sets. We show that viruses, such as ZEBOV and MARV, consistently displayed low levels of recombination, whereas high levels of recombination were observed in Sarbecoviruses, HBV, HEV, Rhinovirus A, and HIV. We observe that recombination is more common in positive single-stranded RNA viruses than in negatively single-stranded RNA ones. Interestingly, the comparison across multiple viruses suggests an inverse correlation between genome length and recombination rate. Positional analyses of recombination breakpoints along viral genomes, combined with our approach, detected at least 39 nonuniform patterns of recombination (i.e., cold or hotspots) in 18 viral groups. Among these, noteworthy hotspots are found in MERS-CoV and Sarbecoviruses (at spike, Nucleocapsid and ORF8). In summary, we have developed a fast pipeline to measure recombination that, combined with other approaches, has allowed us to find both common and lineage-specific patterns of recombination among viruses with potential relevance in viral adaptation.

Introduction

The high diversity in viruses enables their adaptability to new hosts; it could also drive immune evasion and lead to genetic-based therapeutic resistance. One of the main mechanisms of increasing viral genetic diversity is the generation of new viruses by mixing genomic material from existing viral strains. These chimeras are generated when different viruses coinfect the same cell, producing a new virus with a mosaic genome containing genomic information from the coinfecting parents. Some viruses with segmented genomes, such as influenza, can mix genomic information through reassortment, a process by which whole-genome segments are exchanged. Recombination generates mosaic genomes containing genomic material from different viruses, and it can occur within the same (homologous) or different (nonhomologous) sites from the parental strains (Pérez-Losada et al. 2015). Nonhomologous recombination events could be deleterious (Hanada et al. 2000).

Homologous recombination is a major, widespread evolutionary mechanism. In some cases, like in HIV, recombination has been reported to occur even more frequently than point mutations (Shriner et al. 2004; Vos and Didelot 2009). Recombination has also been associated with the emergence of new viral lineages able to cause zoonotic diseases. This is the case of SIVcpz, the ancestor of HIV (Bailes et al. 2003).

Negative single-stranded viruses (RNA−) may recombine less frequently than positive single-stranded viruses (RNA+) (Worobey and Holmes 1999; Chare et al. 2003). It has also been suggested that nonstructural genes as well as RNA secondary structures may be more prone to be targets of recombination (Lefeuvre et al. 2009; Simon-Loriere et al. 2010). However, it is noteworthy that although the occurrence of recombination in viruses has been previously assessed, these individual studies have relied on a limited number of viral species, sequences (usually, <30), or single-gene segments (e.g., Chare et al. 2003).

Recombinant viruses resemble different ancestors across different genomic regions as delimited by recombination breakpoints. Thus, specific recombination events are usually detected through analyses that test for phylogenetic incongruences along a sequence alignment (Pérez-Losada et al. 2015). Inferring the frequency at which a population recombines (population recombination rate, ρ) is usually performed using approaches based on linkage disequilibrium (LD), where the association between allele frequencies along a genome segment decays proportionally to the genome distance between loci (Awadalla et al. 1999). There also exist approaches aiming to create “ancestral recombination graphs,” detailed representations of the history of recombination and mutation that characterize a population (Arenas 2013; Rasmussen et al. 2014).

These widely used approaches to study recombination are computationally demanding, becoming slow, or precluding the analysis of hundreds of sequences. Topological data analysis, specifically persistent homology (PH), has been found to be a faster alternative to infer recombination rates (Camara, Rosenbloom, et al. 2016). The main idea behind topological data analysis is to capture the global structure of data by studying the properties of a set of nested simplicial complexes, a generalization of a network. PH captures the topological properties of these simplicial complexes, including the structure of connected components, the formation of loops, and the formation of voids in data. In the absence of recombination, data can be represented as a tree, and inferred pairwise genetic distances (PWDs) satisfy tree inequalities (Chan et al. 2013; Camara et al. 2016). It has been found that all PH in dimension bigger than one should vanish, capturing the intuition that in the absence of recombination, with a tree-like data structure, no loops should be observed (Emmett and Rabadan 2016). The presence of loops in genomic data indicates the presence of recombinant sequences. Intuitively, these loops can be interpreted as sets of taxa that would include a recombinant and its parents or its ancestors (fig. 1A; Chan et al. 2013).

Global viral data sets that are representative samples of their epidemics usually comprise hundreds to thousands of sequences, as in the most studied viruses such as influenza A or HIV (Lam et al. 2015; Patiño-Galindo and González-Candelas 2017) or the recently emerging SARS-CoV-2. Although PH has been shown to be able to detect recombination in viruses (Chan et al. 2013) and can be a fast alternative to LD methods to study such large populations, the inference of population recombination rates using this technique has only been applied in humans, drosophila, or simulated data (Cámara et al. 2016; Camara, Rosenbloom, et al. 2016; Humphreys et al. 2019). In this work, we have used standard approaches and PH to infer, and compare, the contribution of recombination along the genomes of 30 different viral data sets. This comprehensive analysis, that involves thousands of sequences, aims to understand the relevance of different biological viral features, such as genome architecture or ability to infect new hosts, on the occurrence of recombination. Finally, we have been able to identify those genomic regions that act as preferential targets for recombination breakpoints.

Results

Inference of Recombination Rates in Large Data Sets

To evaluate the recombination rates in viral data sets, we compared standard LD with topological data analysis methods. LD is the most widely used approach to infer recombination rates. However, in large data sets, it can be very slow or even computationally intractable (fig. 1D). Data sets representing the global diversity of human viruses are usually very large (in some cases, there are thousands of sequences available). For this reason, we developed as an alternative fast approach to infer and compare recombination rates from large data sets. This approach is based on a branch of algebraic topology, PH, that has been previously successful in determining the rate of reticulate events such as recombination (fig. 1A; Chan et al. 2013).

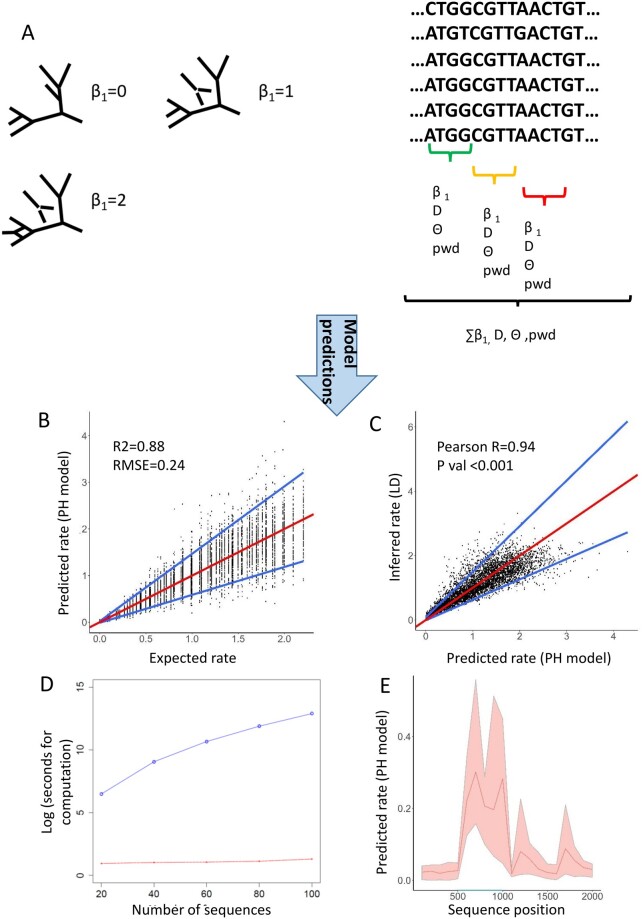
Fig. 1.

Overview of the PH-based model to infer recombination rates. (A) Our pipeline splits the sequence alignment into windows of a fixed length. Then, it infers different population genetic parameters and, by using PH, calculates the number of B1 events (loops) along the genome. PH is performed because of the correlation known to exist between number of loops and reticulate events in a population. Then, a regression model, based on the aforementioned variables, predicts the population recombination rate. In simulated data, the PH model has a strong predictive power. The red line represents the expected value, and the blue lines represent the quantile regression lines obtained from quantile regression at percentiles 5 and 95 (B). There is very high correlation between the predictions made by our pH model and the rates inferred using LD. Note that the red line represents the quantile regression line obtained from quantile regression using the median, and the blue lines represent the quantile regression lines for the percentiles 5 and 95 (C). (D) In simulated alignments of different number of sequences, the computational time of the PH-based model (red) is consistently lower than that required for LDhat (blue). Note that the analyses made with LDhat include the generation of the LK tables. (E) The PH model is able to detect changes in recombination rate (e.g., recombination hotspots) along a sequence. This plot represents the recombination rate inferred by our method (mean and minimum and maximum) in five sequence alignments 2,000 nts long with a recombination hotspot between positions 500 and 1,000 (highlighted in blue).

Specifically, we built an empirical square root regression model able to predict population recombination rates. It was trained, validated, and tested using sequence alignments that were simulated under different combinations of recombination rates and population scenarios (see Materials and Methods). We considered the following regression variables: The number of topological 1D bars (known as the first Betti number in topology or B1 here) inferred from PH, as well as the Watterson θ, Tajima’s D, the mean PWD among sequences, and the scalar ratio B1/θ (fig. 1A and table 1). Our rationale was to express recombination rate as a function of B1 and take into account population genetics characteristics such as population size and the degree of genetic differentiation. We opted for a linear model to fit the square root transformation of recombination rate. After performing 5-fold cross-validation (CV), the model that included all of these variables (sqrt(ρ) ∼ 0.1938 × B1 + 0.0367 × ϴ− 0.02846 × D − 0.0334 × PWD + 0.2150 × B1/θ + 0.3764) led to the lowest mean square error (MSE = 0.0127). The performance of this model was then assessed in a different test set. Its overall coefficient of determination was R² = 0.88, with a root mean square error (RMSE) of 0.24 (fig. 1B). In contrast, the coefficient of determination between the LD-inferred mean rate and the expected recombination rate was R² = 0.98, RMSE = 0.13. Overall, there was a significant, very high correlation between the mean ρ inferred from LD and the ρ inferred from PH (r = 0.94, P < 0.001) (fig. 1C). The model was generally applicable to a broad range of conditions, in terms of different scenarios of genetic variability and recombination rate ranges (supplementary fig. S1A, Supplementary Material online). As expected, PH was consistently much faster than LD: Whereas PH takes only a few seconds regardless of the number of sequences, LD can take several hours in sets that include a few tens of sequences or even days in sets that have hundreds of sequences (fig. 1D). In this way, LD is a more accurate approach than PH but at a relevant computational cost. Importantly, our PH-based method is also able to find changes in recombination rate along a sequence, such as recombination hotspots (fig. 1E).

Table 1.

Information of the PH-Based Regression Model to Infer ρ (definition of the variables and coefficient values in the model).

Variable	Definition	Coefficient Value
ρ	Population recombination rate to infer. In this regression, we model the square root of ρ, as a linear combination of the following variablesa	Response variable
B1	Number of 1D barsa from PH analysis	0.1938
ϴ	Watterson’s thetaa	0.0367
D	Tajima’s Da	−0.02846
PWD	Mean pairwise distancea	−0.0334
B1/θ	Number of 1D bars divided by Watterson’s thetaa	0.215
Ξ	Intercept	0.3764

^aCalculated per site.

In the same way as the aforementioned model, we also developed another regression model based on PH to directly predict the ratio of recombination versus mutational events (r/m). The best fitting model was sqrt(r/m ) ∼ 1.0758 × B1/ϴ + 0.1133 × D − 0.2673 × PWD + 1.1866 (table 2; MSE from the 5-fold CV = 0.174). The overall performance of this model was similar to that obtained by dividing the LDhat mean recombination rate and Watterson theta (coefficient of determination between the predictions and the expected r/m : R² = 0.89, RMSE = 2.36 and R² = 0.96, RMSE = 2.54 for PH and LD, respectively). This model was also generally applicable to a broad range of conditions in terms of different scenarios of genetic variability and r/m (supplementary fig. S1B, Supplementary Material online).

Table 2.

Information of the PH-Based Regression Model to Infer r/m (definition of the variables and coefficient values in the model).

Variable	Definition	Coefficient Value
r/m	Ratio of recombination versus mutational events. In this regression, we model the square root of ρ, as a linear combination of the following variablesa	Response variable
B1/θ	Number of 1D bars divided by Watterson’s thetaa	1.0758
D	Tajima’s Da	0.1133
PWD	Mean pairwise distancea	−0.2673
Ξ	Intercept	1.1866

^aCalculated per site.

In sum, we show that a simple regression model that incorporates population genetic and PH invariants can reproduce linkage-based methods with a significant scalability advantage in large viral data sets. The pipeline that uses the PH approach to infer ρ and r/m is publicly available in github: https://github.com/RabadanLab/PH_recombination_virus (last accessed February 8, 2021).

Recombination Rate Varies across Genome Type

To detect specific recombinant events, we used six different recombination tests implemented in RDP4 (RDP, Geneconv, Bootscan, Maxchi, Chimaera, and 3seq) (Martin et al. 2015). Among the potential events detected by any of the six methods, we consider only those affecting genomic regions with a good phylogenetic signal and that had a significantly different evolutionary history than the rest of the genome. Supplementary table 1, Supplementary Material online, provides a summary of the viral data sets and the results obtained from the analyses. The number of recombination events varied among viral species: from no reliable recombination signals in Zaire EbolaVirus (ZEBOV), Human Papillomavirus sp9 (HPV-9), Human parainfluenza virus (PHIV), and Marburg Virus (MARV) to 1.7 × 10⁻⁴ and 2 × 10⁻⁴ events/sequence/bp in Sarbecoviruses and Hepatitis Delta Virus (HDV), respectively.

The frequency of recombination in viral data sets was also assessed by inferring population recombination rates (LD and PH methods). Because of the computational limitations of generating likelihood (LK) tables in LDhat for data sets >100 sequences, for each original sample, a subsample of 100 sequences was analyzed using the LD method. The full data sets were used with the PH predictions, because this restriction does not exist in this approach. Significant correlations existed among the different measurements of recombination (direct confirmation with RDP, LD, and PH estimates). The Spearman correlations were: RDP4 versus LD: r = 0.67, P < 0.001; RDP4 versus PH: 0.56, P < 0.001; PH versus LD: r = 0.85, P < 0.001 (supplementary fig. S2, Supplementary Material online). Thus, strong monotonic associations were found across the different measurements of recombination.

HPV-9, ZEBOV, MARV, PHIV, Zika Virus (ZIKV), Mumps Virus (MuV), and Herpesvirus-3 (HHV-3) consistently displayed low levels of recombination in all three approaches (≤1 × 10⁻⁶ events/sequence/site, ρ from LD < 0.1, and ρ from PH < 0.10). On the other hand, high levels of recombination were supported by the three measurements in viruses such as Hepatitis B virus (HBV), Hepatitis E virus (HEV), Rhinovirus A (HRV-A), HIV-B, and HIV-C (>1 × 10⁻⁵ events/sequence/site, ρ from LD > 0.8, and ρ from PH > 0.4). Estimates using the (r/m) ratio showed similar results: in almost all aforementioned low-recombining viruses, we observed that LD–r/m < 0.1 and PH–r/m < 0.3, whereas in almost all high-recombining viruses: LD–r/m > 8 and PH–r/m > 2. Interestingly, eight viral sets presented an (r/m) ratio >1 using both LD and PH, suggesting a higher contribution of recombination than that of mutation (supplementary table 1, Supplementary Material online).

The most striking discrepancies between the number of recombination events detected and ρ (LD and PH) were observed for HDV and Sarbecoviruses: Although these viruses had the highest number of recombination events per sequence and bp, they displayed a low frequency of recombination inferred from LD (HDV: ρ = 0.069; Sarbecoviruses: ρ = 0.096) and a moderate one inferred from PH (HDV: ρ = 0.267; Sarbecoviruses: ρ = 0.13).

The biggest discrepancies between LD and PH were those regarding HIV-A, -B, -C, and Hepatitis C virus subtype 1a (HCV-1a). Although the occurrence of recombination in these viruses was inferred to be high in all different approaches, the mean ρ inferred from LD was one order of magnitude higher than the predicted ρ from our PH model.

Genome Length Is Inversely Associated with Recombination Rates

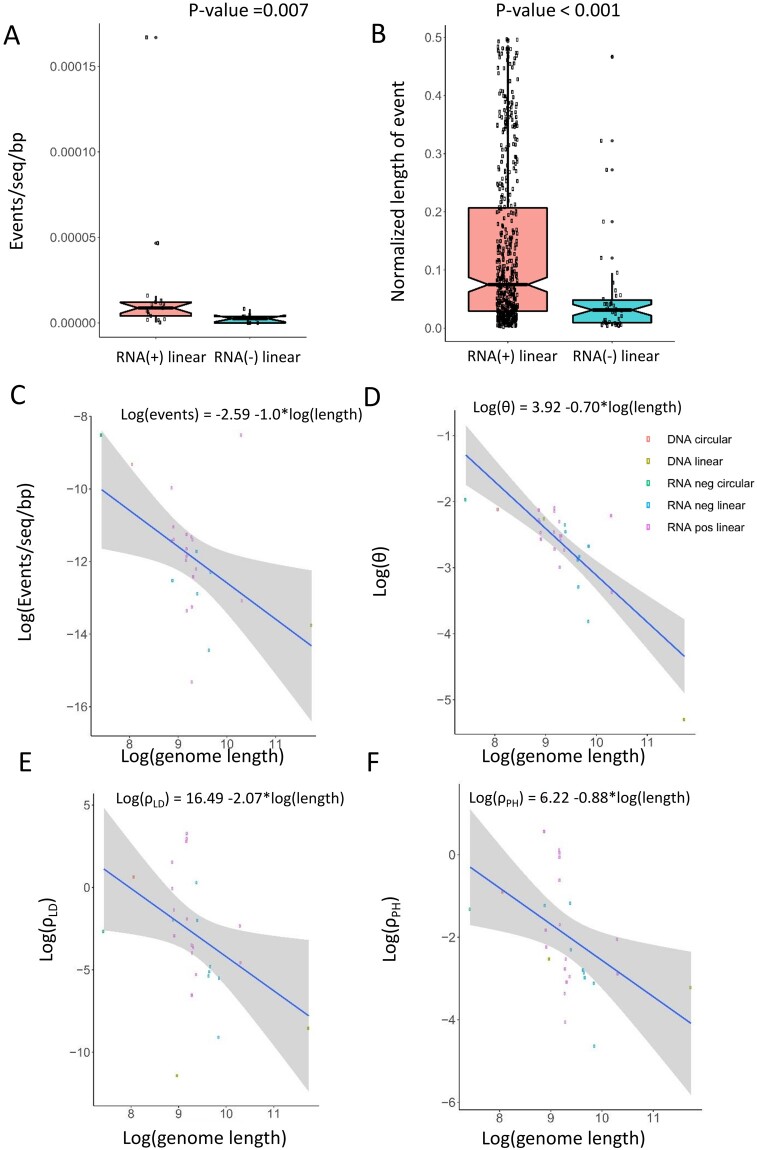
Next, we compared our different measures of recombination rate across viral groups. Linear ssRNA(+) viruses displayed a significantly higher frequency of recombination events than linear ssRNA(−) ones (Mann–Whitney test: P = 0.007; fig. 2A) and their recombinant segments affected a significantly longer fraction of the genome (Mann–Whitney test = P < 0.001; fig. 2B). Although the inferred ρ and r/m was also higher in ssRNA(+) both using LD and PH, such differences were not significant (P values ranged between 0.10 and 0.20 for LD and PH, respectively). No significant correlation was found between GC content and any of the recombination measures (Spearman correlation analyses: all r < 0.20, all P > 0.5).

Fig. 2.

The frequency of recombination differs across viral groups. (A) Recombination events (normalized by number of sequences and genome length) are significantly more frequent in viruses with linear ssRNA(+) genome than in those with ssRNA(−). (B) Recombination events also involve longer genome sections in ssRNA(+) than in ssRNA (−) viruses. (C–F) Decay with genome length of the frequency of recombination events, θ, ρLD, and ρPH. Gray bands represent standard errors.

A significant, inverse correlation between genome length and frequency of recombination events was found (Spearman correlation: r = −0.55, P = 0.005). Interestingly, this result was supported by all other measures of recombination (ρ and r/m, both from LD or PH: all r < −0.50, P values < 0.01 (fig. 2 B–F). A similar trend was also observed between genome length and theta (r = −0.66, P < 0.001), although at a different slope. We assessed whether this inverse association between length and recombination could be due to an unequal performance of LDhat and PH at different sequence lengths. After simulating sequence alignments of 1,000, 10,000, and 100,000 bp under a same recombination rate (ρ = 0.05), we observed that the recombination rates inferred by LD or PH at different sequence lengths were not statistically different (All P values in Mann–Whitney tests >0.1; supplementary fig. S3, Supplementary Material online).

Given that our viral sets differed notably in the number of sequences analyzed, we assessed any potential bias due to sample size. Thus, for each viral data set exceeding 100 sequences, we compared the original ρ inferences (based on LD and PH) with a distribution of ρ’s constructed from ten random subsamplings of size 100. As expected, in the vast majority of cases, the original estimate for ρ inferred from the entire data set fell within the corresponding subsampled ρ-distribution (supplementary fig. S4, Supplementary Material online). The above results hold true even if we replaced the original ρ’s with the medians of the corresponding subsampled ρ-distributions.

Profiles of Recombination across Viral Genomes

We used the frequency of recombination breakpoints along the genome of our viral data sets to find genomic regions associated with hotspots of recombination (i.e., regions more prone to be targets of recombination breakpoints) or coldspots (less prone to such breakpoints) and compared such trends with the results of LD and PH.

Overall, we found 28 hotspots of recombination along the genome of 18 different viral data sets (DENV, HCV-1a, HBV, HDV, HIV-A, HIV-B, HIV-C, Japanese Encephalitis Virus [JEV], MERS-CoV, Sarbecoviruses, HHV-3, HRV-A, CHIKV, HAV, LAS, MeV, MuV, and Tick-Borne Encephalitis Virus (TBEV); all P values < 0.05) and 11 coldspots in 7 sets (DENV, HBV, HDV, HIV-B, HIV-C, Sarbecovrisuses, and HRV-A). Thirty-one of these regions were in agreement with our PH or LD analyses: Hotspots were usually located within windows which, according to PH and/or LD, fell within the top quartile (percentile >75) in overall recombination rate among all windows along the corresponding genome. On the contrary, coldspots tended to be located in regions, where PH and/or LD inferred windows belonged to the bottom quartile (percentile <25) (fig. 3; supplementary fig. S5 and supplementary table 2, Supplementary Material online). Sixteen of these significant regions would be in agreement both by LD and by PH. Note that original breakpoint distribution plots and P-value distribution plots generated by RDP4 (supplementary fig. S6, Supplementary Material online) were highly in agreement with the breakpoint distribution plots that we used to detect such hotspots and coldspots, based only in those recombination events that met our inclusion criteria (see Materials and Methods).

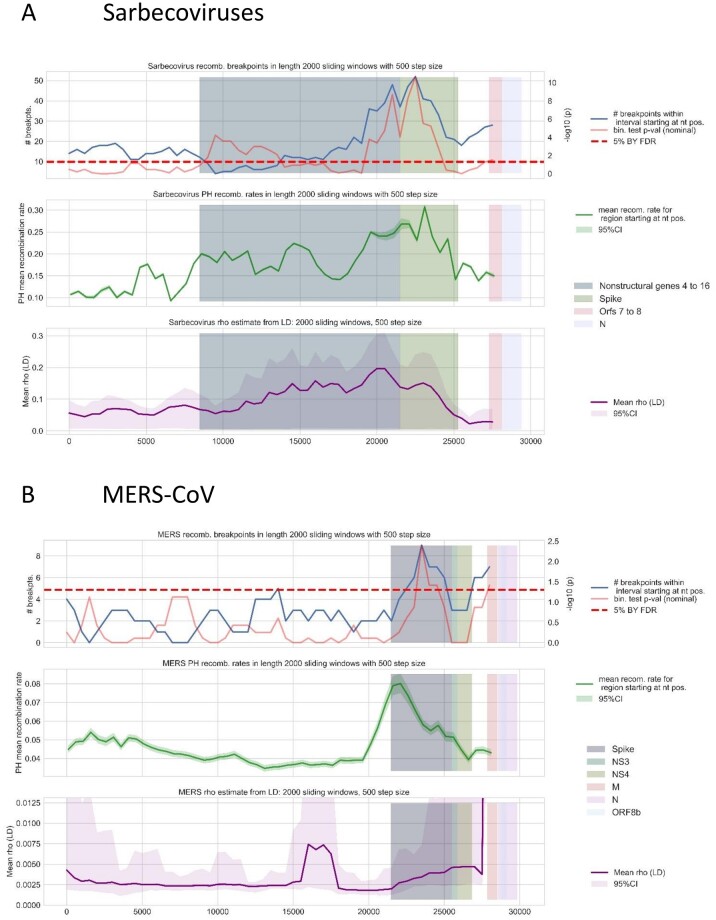
Fig. 3.

Conserved patterns of recombination of Sarbecoviruses (A) and MERS-CoV (B). Upper panel represents the mean number of recombination breakpoints detected at each window along the genome (blue) and the P-value obtained from the binomial tests (red). The dashed horizontal line represents the statistical significance threshold, set at 0.05. Middle panel (green line) represents the mean and 95% confidence interval for ρ (PH) inferred at each of these windows. Bottom panel (purple line) represents the mean and 95% posterior density interval for ρ (LD) inferred at each window. Highlighted genome regions represent coordinates of genes where binomial analyses detected significant windows.

In several viral groups, we observed a conservation of recombination patterns. This is the case of MERS-CoV and Sarbecoviruses. In these betacoronaviruses, there was a significant enrichment for recombination in the Spike. This result was in agreement with our PH inferences (percentile up to 89.5 in MERS and 98.2 in Sarbecoviruses) and LD analyses (percentile up to 87.8 in MERS and 98.2 in Sarbecoviruses). A second hotspot could be observed in a region that would include, in both sets, ORF8a and Nucleocapsid (N), which was supported only by LD in MERS (percentile 100) (fig. 3 and supplementary table 2, Supplementary Material online).

The general patterns of recombination were also conserved among HIV subtypes B and C. Binomial tests detected a recombination coldspot located in the pol gene (only supported by PH in HIV-C; percentile 13) and the presence of hotspots in the vpu and env genes (only supported by PH in both subtypes; percentiles up to 91.3 and 100 in HIV-B and HIV-C, respectively) (supplementary fig. S5 and supplementary table 2, Supplementary Material online).

Finally, we also observed partial conservation in the recombination patterns among those flaviviruses with moderate/high recombination signals (DENV, HCV, and JEV). Binomial tests detected a recombination hotspot in DENV and JEV that include their core (capsid) and M (membrane glycoprotein) genes, although PH and LD would only support the hotspot at JEV (percentile 76 and 84.6 for LD and PH, respectively). This hotspot at JEV includes part of the Envelope gene, which is also significant in HCV-1a (supported by PH: percentile 95.5) (supplementary fig. S5 and supplementary table 2, Supplementary Material online).

Discussion

In this work, we performed a comparative analysis of recombination among 30 different human-related virus data sets. Our alignments usually contained more than 100 genomes and were subjected to a common methodological framework. Recombination was measured using three different approaches: the direct detection of recombination events using an extensive battery of tests (RDP, Geneconv, Bootscan, Maxchi, Chimaera, and 3seq), and the inference of population recombination rates ρ (and r/m) using both an LD approach and our newly developed PH-based models.

In simulated data, our PH models have demonstrated to be generally applicable to a broad range of scenarios of genetic variability and frequency of recombination. As expected (and similar to LD), both PH models (aiming to infer ρ and r/m) tended to display a higher performance at populations with moderate or high levels of genetic variability.

Although LD tends to be more accurate than PH, our PH-based prediction usually takes a few seconds per data set. In this way, PH can be used as a fast and reliable method to quantify recombination. Although in this work, we present regression models, measures of recombination based on PH could be easily used as variables in other statistical frameworks. For instance, it could be used to speed up complex approximate Bayesian computation analyses, previously used for the joint estimation of recombination and other evolutionary parameters (Lopes et al. 2014).

In real data, PH also presented a significant correlation with the other measures of recombination. It is also noteworthy that most hot and coldspots detected through our enrichment analyses of recombination breakpoints (31 out of 39) were supported by the positional rate inferred either by LD or by PH. Sixteen of these 39 cases would be supported by both LD and PH. Consequently, these two methods to infer recombination rates based on different approaches (LD is based on the phenomenon of LD decay with genomic distance between loci; PH is based on topological data analyses that use genetic distances as input) can complement each other.

In viral sets such as HBV, HIV-B, HIV-C, HCV-1a, HEV, and HRV-A, we found not only a high number of recombination signals (>20) but also high estimates of ρ and r/m using both LD and PH. This suggests a major contribution of recombination in their evolution. Indeed, their r/m values >1 suggested an even higher contribution of recombination than that of mutation in their evolution. However, r/m should be interpreted with caution. On the one hand, the Watterson estimator, generally used to infer θ, is limited by its infinite sites assumption. On the other, our results with simulated data show that inferring r/m by dividing ρ (LD) and the Watterson estimator of θ can lead to spuriously high values in those cases with low θ (<0.01 per bp). Our PH model to predict r/m seems to correct this potential problem and display a similar performance when compared with the LD approach.

Most of our results were congruent with previous literatures. With a few exceptions, the highest recombination values were found in viruses known to undergo high levels of recombination. Some cases are HRV-A, the different subtypes of HIV-1, Enterovirus A, or HBV (Wu et al. 1999; Zhuang et al. 2002; Simmonds and Midgley 2005; Simmonds and Welch 2006; Huang et al. 2008; McIntyre et al. 2013). HEV, one of the sets with highest recombination values in our analyses, is less studied but there exist reports of 1zfrequent recombination events (Chen et al. 2012). There was also overall congruence with literatures in those viruses displaying the lowest recombination values. These are ZEBOV, MARV, HPV-9, HPIV, MuV, ZIKV, and Yellow Fever Virus (YFV) (Wittmann et al. 2007; Jiang et al. 2009; Han and Worobey 2011; McGee et al. 2011; Zhang and Liu 2011; Beck et al. 2012; Han et al. 2016).

There were a few yet noteworthy differences between our results and previous literatures. The two most relevant cases are Rabies Virus (RV) and HCV-1a. In our analyses, they were consistently associated with both high number of recombination events (at least 20 potential events) and r/m estimates (>1.0 in both cases). To our knowledge, the population recombination rate of RV has not been inferred previously, and the presence of recombination has been detected in this virus in different analyses (Chare et al. 2003; Geue et al. 2008). There is a recent article initially finding 23 recombination signals, but most of them were discarded through Simplot analyses (Deviatkin and Lukashev 2018). However, these confirmatory analyses were only performed with few selected sequences (4 or 5, based on an unspecified criterion). In addition, the authors did not specify any Simplot threshold used for confirmation of recombination.

The relevance of recombination on the evolution HCV is uncertain. It has been hypothesized that hepatocytes inhibit HCV coinfection, a phenomenon that has been observed in vitro (Tscherne et al. 2007). However, the prevalence of mixed infections has been estimated to be as high as 25% or 39% in some populations such as cohorts of prisoners (van de Laar et al. 2009; Pham et al. 2010). Although this does not necessarily imply cell coinfection, the detection of both intra- and intersubtype recombination events has been reported in many instances (e.g., Sentandreu et al. 2008; González-Candelas et al. 2011; Iles et al. 2015) as well as high levels of LD (Mes and van Doornum 2011). This contradicts the cellular exclusion hypothesis and suggests that recombination in HCV is probably underreported. One factor that may complicate the detection of recombination in HCV is that the sequencing typically performed for clinical (e.g., genotyping) analyses is usually based on short genome regions (usually, E1–E2 and NS5b genes), and thus, it misses relevant genomewide information.

In concordance with previous literatures (Chare et al. 2003; Han and Worobey 2011), a higher number of recombination events was found in ssRNA+ viruses than in ssRNA− viruses with linear genome. We also found that the recombining segments tended to affect longer proportions of the genome in the former than in the latter. In addition, there were similarities in the frequency of recombination among members of the same family (e.g., low recombination in Filoviridae and Paramyxoviridae and high recombination in Coronaviruses, Picornaviruses, or the different HIV subtypes). In the case of the Flaviviridae family, we found some degree of conservation in the recombination patterns of Dengue Virus, HCV-1a, and JEV. However, the signal of recombination was very low, even absent, in other Flaviviridae members (TBEV, YFV, and ZIKV).

Regarding such conserved patterns of recombination, the case of Coronaviruses is noteworthy. Indeed, both MERS-CoV and Sarbecoviruses (subgenera of Betacoronavirus that includes SARS-CoV and SARS-CoV-2) displayed a high frequency of recombination events and moderate population recombination rates inferred with PH along their genome. Our results do not only show that recombination occurs frequently in these viruses, but also that the distribution of recombination breakpoints would be conserved across these different Coronavirus subgroups. We found an enrichment for recombination in the Spike gene of MERS-CoV and Sarbecoviruses, a result that was supported by LD and our PH-based model. The role of this protein is to interact with host cell receptor. It is thus one of the key determinants of host tropism and, interestingly, the occurrence of recombination at Spike of Sarbecoviruses closely related to SARS-CoV-2 (RaTG13 strain) has previously been suggested (Hon et al. 2008; Li et al. 2020; Wang et al. 2020). We also found in these two viral sets, a second hotspot for recombination, affecting coding regions of proteins N and orf8. N protein is the capsid protein and it is required for genome encapsidation. Orf8 protein could be involved in mediating immune evasion in Sarbecoviruses such as SARS-CoV-2. It appears to bind directly to MHC-I, downregulating their surface expression (Zhang et al. 2020).

We also found similar patterns of recombination between HIV-B and -C, the most frequent HIV subtypes worldwide. In both subtypes, the 5′ side (specifically, pol gene) of the genome tended to have lower number of recombination breakpoints, and ρ (PH), than the 3′ side (particularly, gene env). These results are in agreement with previous experimental works that have found recombination hotspots all along the env gene (Galetto et al. 2004; Simon-Loriere et al. 2009; Song et al. 2018).

GC content has previously been found to be highly correlated with meiotic recombination in eukaryotes, such as yeasts (Gerton et al. 2000; Blat et al. 2002), but not in bacteria (González-Torres et al. 2019). In our analyses with viruses, we found no significant association. However, all our measures of recombination display a significant, negative correlation between recombination and genome length. This correlation, never assessed before in viruses, is known to occur among eukaryotes (from unicellular organisms to invertebrates, vertebrates, and plants) (Lynch 2006), even when analyzing single taxonomic groups, such as the clade of Angiosperms (Tiley et al. 2015). Interestingly, the rate at which recombination rate decays with increasing genome length (i.e., the slope) in eurkaryotes is −0.86 (log scale), a different slope than that inferred for viruses under the different approaches.

It is important to mention some limitations related to the comparisons of recombination across viral groups that we report. Viruses can display a very high level of genetic diversity. Viral subgroups, such as genotypes or subtypes, can have particularities in terms of selective pressures, transmission dynamics, etc., which can lead to notorious recombination rate differences among them. In this way, there have been reported relevant differences in viruses such as HBV (Castelhano et al. 2017) (see supplementary fig. S7A, Supplementary Material online). Other viruses, such as DENV, do not appear to show significant differences in recombination rates across genotypes (supplementary fig. S7B, Supplementary Material online). Thus, although our results related to differences in recombination frequency among viral groups (ssRNA+ vs. SSRNA−, genome length) could be in agreement with previous works, they should be considered with caution.

Finally, it is noteworthy that we assessed how the difference in data set sizes could affect our inferences and comparisons. For this, we obtained a distribution of ten ρ values (LD, PH) inferred from randomly taken subalignments. There were only a few exceptions where the original ρ fell outside such distribution (supplementary fig. S4, Supplementary Material online). The most notorious were the cases of HCV-1a, HIV-1B, and HIV-C: when inferring ρ with PH, the median ρ inferred from the subsampled data was around ∼0.50 (half of the original ones). This could be explained because the original ρ (PH) was obtained from whole alignments that included more than 400 sequences. Even in these cases, the subsampled data still showed some of the highest levels of recombination among all viruses. None of the reported results would change if we considered, for such viruses, the median of the ρ obtained from subsampling.

In summary, we have developed a faster approach based on Topological Data Analyses to measure the occurrence of recombination in large data sets. We demonstrated its utility by applying it in combination with other well-established approaches to study the recombination patterns of 30 different human-related viruses. Our results have revealed both common and lineage-specific patterns of recombination among viruses with potential relevance in viral adaptation.

Materials and Methods

PH Model to Infer Population Recombination Rates

Sequence alignments of 1,000 bp (n = 50, 100 sequences) were simulated using a forward simulation approach implemented in SFS_CODE (Hernandez 2008). Different combinations of initial effective population size (N_e = 100, 300, 600, and 1,200), population growth rate (g = −5, −2, −0.2, 0, 0.2, 2, and 5), initial population recombination rate (ρ ranging from 0 to 1), and θ (population mutation rate, θ = 0.02, 0.05, and 0.1) were generated. In total, ∼50,000 simulated alignments were generated. Note that in the forward simulation process, the basic recombination rate r (number of recombination events per site per generation) and mutation rate m (number of mutation events per site per generation) are static, but population recombination and mutation rates do change according to the population size.

Using nonoverlapping windows of 100 bp, different population genetics variables (Watterson estimator of θ, Tajima’s D, and mean and PWD) were inferred using the R packages ape and pegas (Paradis 2010; Paradis and Schliep 2019). The persistent analyses, used to count the number of “loops,” were performed with ripser software (Bauer U, unpublished data) (fig. 1A). The PWD matrixes used to calculate PWDs and to perform the PH analyses were obtained using the “raw” (i.e., no substitution model) number of nucleotide differences.

The simulated data were randomly split into training (80% of original number of alignments) and test sets (20%). Then, a square root regression model aiming to predict population recombination rates was built. Different models based on the combination of the variables “number of loops,” “θ,” “Tajima’s D,” and “mean PWD” were trained with the train set, then subjected to 5-fold CV to choose the model with lowest mean square error (fig. 1A).

The contribution of recombination to the genetic variability of a population is usually estimated from the basic recombination versus mutation rates ratio (r/m). Thus, r/m > 1 would indicate that recombination occurs more frequently than mutation. This is normally inferred by dividing the population recombination rate (ρ = 2N_e × r, in haploid organisms) and the Watterson estimator of theta (θ = 2N_e × m) (Guttman and Dykhuizen 1994; Vos and Didelot 2009). The Watterson estimator is easily calculated from the number of variable sites the number of sequences. However, since it assumes an infinite sites model (this means, a site can only be mutated once), it usually leads to underestimates of the true θ. This can hamper the r/m calculation. Similar to the model aiming to predict p, a linear regression model based on PH was built to predict the recombination versus mutation rates ratio, considering loop count/theta, Tajima’s D, and mean PWD.

Viral Data Sets and Alignments

Full-genome nucleotide sequences from different groups of human viruses were downloaded from GeneBank in October, 2017 (www.ncbi.nlm.nih.gov/genbank/). Alignments for each virus were generated using MAFFTv7 using the “align-G-ins-1” progressive method strategy (Katoh and Standley 2013). All sequence lengths, and coordinates, were fixed to the reference sequence of each viral species, as they appear in RefSeq (www.ncbi.nlm.nih.gov/refseq). Redundant (i.e., duplicated) sequences were removed as well as those regarded as outliers for the presence of indels and/or indeterminations. Lab-derived sequences were excluded, according to keywords “patent,” “mouse,” “mice,” “mus musculus,” “chimp,” “pan troglodytes,” “clone,” “construct,” “provirus,” “proviral,” “macaque,” “plasmid,” “chimera,” “chimeric,” “cell culture,” “replicon,” “vector,” “unverified.” Accession numbers of the sequences used are displayed in supplementary table 3, Supplementary Material online.

Recombination Detection and Inference of Population Recombination Rates

Sequence alignments were analyzed with six recombination detection methods implemented in the RDP4 software: RDP, Geneconv, Bootscan, Maxchi, Chimaera, and 3seq (Martin et al. 2015). Genomes were assumed to be circular for HDV and HBV. Recombination events in which at least one method suggested recombination with a P value <0.05 after Bonferroni correction were further validated. This validation was based on four criteria:

1. Events in regions with alignment problems were excluded.

2. The recombinant region should be phylogenetically informative. This was assessed with quartet analyses in Tree-Puzzle (Schmidt et al. 2002), and those regions leading to >30% unresolved quartets were no further considered.

3. The tree topology derived from the recombinant region should be significantly different to that obtained from the rest of the genome. This was tested also with Tree-Puzzle, by performing Expected Likelihood Weight (ELW) and Shimodaira-Hasegawa (SH) tests of maximum-likelihood phylogenetic trees obtained with PhyML (GTR + GAMMA 4 CAT substitution model, thus taking into account site-to-site rate variation) (Guindon et al. 2010). Only those cases where both tests were significant (P value <0.05) were considered.

4. The potential event was excluded if it was identified to occur among sequences sampled at the same time and laboratory and, in the recombinant region, the identified recombinant sequence was 100% identical to its supposedly parents. This was done to avoid potential laboratory-derived artifacts.

ρ were inferred with Interval, a commonly used LD approach implemented in LDhat (Auton and McVean 2007) that accounts for differences in recombination rate along the genome. As initial input, LK tables specific for each data set (regarding number of sequences and theta) were used. The generation of each of these tables is computationally costly, can take days (or more than 1 week), and can become intractable in larger sets. For this reason, those alignments with >100 sequences were randomly subsampled to n = 100 sequences before being analyzed with LDhat. Only biallelic sites where the minor allele displayed a frequency >3% and which frequency of indeterminations or gaps below 20% were considered. A block penalty of five was used. Markov chain Monte Carlo chains were run for at least 1 million states, sampling every tenth state. Convergence was tested by graphic visualization of the likelihood values along the chains.

As an alternative to LDhat, recombination rates of whole-genome sequence alignments were inferred using our model based on PH, following the same steps as in simulated data. The contribution of recombination to the genetic variability of the viral data sets was estimated from the recombination versus mutation rates ratio (r/m), obtained by dividing the mean ρ inferred from LD and the Waterson θ. Alternatively, we also predicted r/m directly with our PH model.

One factor that may hamper the comparison between viruses is the difference in alignment sizes (ranging between 28 sequences in Sarbecoviruses and 636 in HIV-C). In order to assess whether our comparisons could be biased, and make our data sets more easily comparable, we obtained ten subalignments of 100 randomly taken sequences from those viral sets with more than 100 sequences. We then inferred their ρ (from LD and PH) to assess how the original estimates differed from this distribution derived from downsampling.

Statistical Tests

The different measures of recombination obtained in this work were compared between viral sets. We compared the occurrence of recombination between RNA+ and RNA− viruses through Wilcoxon tests. We also performed Spearman correlation analyses between the inferred frequency of recombination and variables such as genome length or GC content.

We assessed differences in the frequency of recombination along the genome of each viral data set in order to detect coldspots and hotspots of recombination. Sliding window analyses identified genomic regions with a significantly different number of recombination breakpoints (as found with RDP software) than the rest of the genome. Windows of a fixed length (ranging from 400 to 3,000 nts, depending on viral genome length) were selected and binomial tests were performed for each window under the null hypothesis that recombination breakpoints are distributed uniformly along the genome. In summary, binomial tests are enrichment analyses aiming to assess whether a given window of the alignments tends to have a significantly different number of breakpoints than we would expect at random assuming a uniform distribution of breakpoints along the genome.

Finally, we assessed whether the significant results from binomial tests agreed with the positional ρ inferred from our PH model or LD. Given a significant region (e.g., enriched toward recombination or hotspot), we assessed whether there would be any overlapping genome window that would have an inferred ρ in the top quartile (for recombination coldspots, bottom quartile instead) among all windows considered along the genome.

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.