Abstract
High Angular Resolution Diffusion Imaging (HARDI) avoids the Gaussian diffusion assumption that is inherent in Diffusion Tensor Imaging (DTI), and is capable of characterizing complex white matter micro-structure with greater precision. However, HARDI methods such as Diffusion Spectrum Imaging (DSI) typically require significantly more signal measurements than DTI, resulting in prohibitively long scanning times. One of the goals in HARDI research is therefore to improve estimation of quantities such as the Ensemble Average Propagator (EAP) and the Orientation Distribution Function (ODF) with a limited number of diffusion-weighted measurements. A popular approach to this problem, Compressed Sensing (CS), affords highly accurate signal reconstruction using significantly fewer (sub-Nyquist) data points than required traditionally. Existing approaches to CS diffusion MRI (CS-dMRI) mainly focus on applying CS in the q-space of diffusion signal measurements and fail to take into consideration information redundancy in the k-space. In this paper, we propose a framework, called 6-Dimensional Compressed Sensing diffusion MRI (6D-CS-dMRI), for reconstruction of the diffusion signal and the EAP from data sub-sampled in both 3D k-space and 3D q-space. To our knowledge, 6D-CS-dMRI is the first work that applies compressed sensing in the full 6D k–q space and reconstructs the diffusion signal in the full continuous q-space and the EAP in continuous displacement space. Experimental results on synthetic and real data demonstrate that, compared with full DSI sampling in k–q space, 6D-CS-dMRI yields excellent diffusion signal and EAP reconstruction with low root-mean-square error (RMSE) using 11 times less samples (3-fold reduction in k-space and 3.7-fold reduction in q-space).
1. Introduction
Diffusion MRI (dMRI) is a unique non-invasive technique to investigate the white matter in brain. In dMRI, MR signal attenuation E(q) = S(q)/S(0) is a continuous function that depends on the diffusion weighting vector , where S(q) is a diffusion-weighted measurement at q, and S(0) is the measurement without diffusion weighting at q = 0. A central problem in dMRI is to reconstruct the MR signal attenuation E(q) from a limited number of noisy measurements in the q-space and to estimate some meaningful quantities such as the Ensemble Average Propagator (EAP) and the Orientation Distribution Function (ODF). The EAP P(R), which is the Fourier transform of E(q) under the narrow pulse assumption [1], fully describes the Probability Density Function (PDF) of water molecule displacements in a voxel. The radial integral of EAP results in the ODF [1], a PDF defined on S2. By assuming a Gaussian EAP, Diffusion Tensor Imaging (DTI) requires only a dozen of measurements for estimating the diffusion tensor for the EAP or the diffusion signal. However, it is well reported that DTI cannot fully characterize complex micro-structure such as crossing fibers [1]. On the other hand, Diffusion Spectrum Imaging (DSI) is a model-free technique for EAP estimation. However, DSI normally requires about 515 signal measurements in q-space, causing a scan time as long as an hour, thus limiting its clinical utility.
Compressed Sensing (CS) [2] is known for its effectiveness in signal reconstruction from a very limited number of samples by leveraging signal compressibility or sparsity. In general, the stronger the assumption is used in reconstruction, the less number of samples is needed. Note that the assumption in CS is always true if the dictionary is devised appropriately to sparsely represent signals. k-space CS techniques, such as Sparse MRI [3,4], have been proposed to reconstruct MR images from a sub-sampled k-space, where the sparsity dictionaries are the wavelet basis and the total variation operator. In dMRI, existing techniques mainly focus on applying CS to the q-space [5,6,7]. [8,5,6] represented diffusion signal and EAP discretely, which suffers from numerical errors in regridding and numerical integration. [9,10,7] represented diffusion signal and EAP continuously, which have closed form expressions of Fourier transform and ODF/EAP calculation. However, this line of work fails to harness information redundancy in the k-space. The correlation of the k-space and the q-space can be employed for even greater sub-sampling, thus further reducing scanning while retaining good reconstruction accuracy. To our knowledge, [11,12] are the only works on signal and ODF reconstruction in joint k–q space by using single-shell data (single b value), i.e., . However, reconstruction of continuous diffusion signal and EAP in whole q-space is much more challenging than single shell . In this paper, we propose a framework, called 6-Dimensional Compressed Sensing diffusion MRI (6D-CS-dMRI), for reconstruction of the diffusion signal and the EAP from data sub-sampled in both 3D k-space and 3D q-space. To our knowledge, 6D-CS-dMRI is the first work that applies compressed sensing in the full 6D k–q space and reconstructs the diffusion signal in the full continuous q-space and the EAP in full continuous displacement R-space. A preliminary abstract of this work was published in [13].
2. Compressed Sensing dMRI in Joint k–q Space
2.1. Sampling and Reconstruction in the 6D Joint k–q Space
Considering the diffusion-attenuated signal S(x, q) as a complex function in a 6-dimensional (6D) space, i.e. 3D voxel x-space and 3D diffusion q-space, for a fixed q value, the magnitude of S(x, q), denoted as |S(x, q)|, is a 3D diffusion weighted image volume. Then the k-space measurements and the EAP are related by [14]
| (1) |
where is the 3D Fourier transform of S(x, q) over x, and S(x, 0) is the image volume with q = 0. Two Fourier transforms are involved: the Fourier transform between in scanning k-space and S(x, q) in voxel x-space for any fixed q, and the Fourier transform between E(x, q) = |S(x, q)|/S(x, 0) in diffusion q-space and EAP P(x, R) in displacement R-space for a voxel x. Instead of dense sampling in k-space and q-space, sparse sampling in both spaces can significantly reduce the scanning time. Fig. 1 is an overview of the 6D space sampling and reconstruction framework that will be discussed in this paper. The goal is to reconstruct continuous functions E(x, q) and P(x, R) from a small number of samples of in the joint 6D k–q space.
Fig. 1.
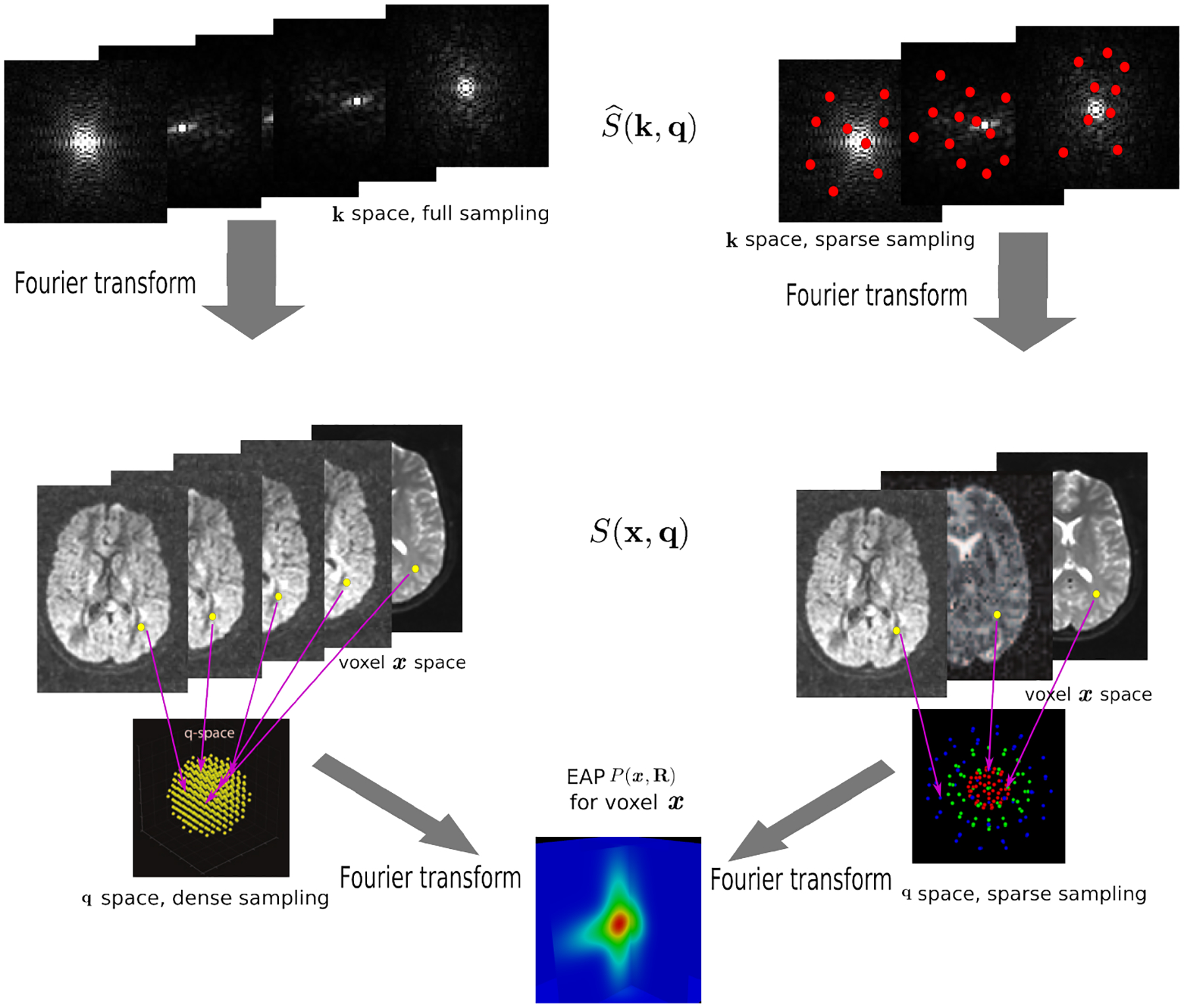
Overview of reconstruction in 6D k–q space. Dense sampling (left) and sparse sampling (right) in both k and q spaces.
A naive approach to 6D-CS-dMRI is to perform two CS reconstructions in association with the two Fourier transforms in Eq. (1). For a fixed q, Sparse MRI can be used to reconstruct the 3D diffusion weighted (DW) images S(x, q) from samples in k-space [3]. Then all these 3D DW images can be used in a CS-dMRI technique to reconstruct the EAP [6,7]. This approach separates the estimation into two independent steps. However, the first step fails to take into consideration the diffusion signal in the same voxel across different q values, and in the second step, information of different voxels in the same DW images is not used.
2.2. 6D-CS-dMRI Using Joint Optimization
We propose a novel reconstruction framework to jointly reconstruct the diffusion signal and EAP from the 6D space. For simplicity, we assume in the following that the baseline image S(x, 0) is known or pre-reconstructed by Sparse MRI [3]. The goal here is to estimate S(x, q) and P(x, R) from a number of samples of in Eq. (1).
We use to denote the partial Fourier sample vector of the v-th volume S(x, qv) and si to denote the vector of the diffusion weighted signals S(xi, q) at voxel i with different q values. We assume that the magnitude of the diffusion signal vector si can be sparsely represented by a real basis set M and coefficient vector ci, i.e. si = Mci⊙ψi, where ψi is the complex vector with unit magnitude that contains phase information, and ⊙ means element-wise multiplication. Then we estimate coefficients {ci} by solving
| (2) |
where Nq is the number of DW images, Ns is the number of spatial voxels, is the partial Fourier transform operator [3], TV(·) denotes the total variation operator, Φ is a chosen wavelet dictionary. Note that si is a complex vector because is complex, thus the signal representation Mci = |si| is only applied to the magnitude of si when M is a real basis set. The first three terms in Eq. (2) originate from Sparse MRI [3]. The sparsity term of {ci} and the equality constraint are from sparse representation in CS-dMRI [6,7]. Eq. (2) is essentially a non-convex optimization problem for variable ({ci}, {ψi}), because of the constraints Mci ⊙ ψi = si, ∀i.
We solve Eq. (2) using Alternating Direction Method of Multipliers (ADMM) [15]. ADMM is typically used for convex optimization, but it can also obtain a local minimum for some non-convex optimization problems [15]. The augmented Lagrangian cost function in ADMM is
| (3) |
where Ui is the complex Lagrangian variable U for voxel i, and ρ is the augmented Lagrangian parameter. Note that
| (4) |
where Uv denotes the complex Lagrangian variables for DW images {sv} with qv, and sv({ci, ψi}) means complex DW images calculated by {ci} and {ψi} based on the basis representation si = Mci ⊙ ψi, ∀i. Then the optimization can be separated into a sequence of three subproblems that can be solved iteratively:
| (5a) |
| (5b) |
| (5c) |
Note: 1) for complex vector f = (f1, f2, … , fn)T, . 2) If ∥f∥ ≥ ∥g∥, then ∥f − g∥2 ≥ ∥f∥ − ∥g∥, and the equality holds if and only if fm and gm have the same phase, ∀m. Thus c and ψ in Eq. (5a) can be solved separately by
| (6a) |
| (6b) |
where for a complex vector f, Ph(f) ≔ (f1/|f1|, … , fm/|fm|)T is the complex vector f divided by the magnitude values in each dimension, i.e., f = |f|⊙Ph(f).
Note that 1) The initialization of are set as the DW images {sv} estimated by Sparse MRI [3,16], and are set as zero. Thus the naïve 6D-CS-dMRI result is actually after the initialization and the subproblem Eq. (5a) when k = 1; 2) Eq. (6b) is performed for each tissue voxel using CS-dMRI technique [6,7], and Eq. (5b) is performed for each DW image volume using a variation, which considers the last term with , of the efficient method in [16]. Since Eq. (6a), Eq. (6b) and Eq. (5b) are iteratively updated, the information in voxel level and volume level are jointly used in each subproblem.

2.3. 6D-CS-dMRI Using Learned Continuous Dictionary in SPFI
6D-CS-dMRI in Eq. (2) requires a dictionary for sparsely representing the magnitude of the diffusion signal. We choose the dictionary via Dictionary Learning Spherical Polar Fourier Imaging (DL-SPFI) [7] which learns the DL-SPF dictionary from Gaussian signals, and allows a continuous closed form expression for the EAP and diffusion signal. In SPFI [17,18], the signal in each voxel is represented by SPF basis, and after estimating the SPF coefficients, the EAP is analytically represented by dual SPF basis, i.e.,
| (7) |
where {Bnlm(q|ζ)} are SPF basis functions with scale parameter ζ which form a continuous complete basis with Gaussian Laguerre polynomial in radial part and Spherical Harmonics in spherical part [17], are the Fourier transforms of SPF basis functions, and EAP and diffusion signal share the same coefficients [18]. For DL-SPFI [7], in voxel xi, the basis representation is
| (8) |
where is a diagonal scale matrix caused by the baseline image S(x, 0) with q = 0, B is the SPF basis matrix with SPF basis functions in its volumes, ai is the SPF coefficient vector, D is the learned parameterization matrix for the learned DL-SPF basis matrix BD, and ci is the coefficient vector for the learned DL-SPF basis. It is shown in [7] that the parameterization matrix D can be learned from single tensor model, and then adaptively applied to different voxels by adaptively setting the scale parameter ζ in B based on the mean diffusivity in voxels. The learned matrix D and the adaptive scale setting make ci under DL-SPF basis much sparser than ai under the original SPF basis. For 6D-CS-dMRI, we set in Eq. (2), and set adaptive scale ζ based on mean diffusivity in voxel xi as done in [7].
2.4. Implementation Issues
Following [7], we use SPF basis with N = 4, L = 8 in Eq. (5a) to learn 254 DL-SPF atoms. As shown in [7], there are two implementation details which can improve the result of CS-dMRI in Eq. (5a) using DL-SPFI. 1) The prior E(x, 0) = 1 can be incorporated in Eq. (5a) by removing isotropic parts from and B, and focusing the estimation on the independent coefficients. 2) Additional regularization can be devised as ∥Λc∥1 instead of λ3∥c∥ to give large regularization for the learned basis functions with small energy in the space of mixture of tensors. Please refer [7] for more details about these two issues.
There is a masking issue specifically for 6D-CS-dMRI. Note that the dictionary M used in Eq. (5a) and Eq. (8) was devised for the diffusion signal whose decay is known to be close to mono-/multi-exponential decay, while the noise signal in non-tissue voxels violates this property. Thus for non-tissue voxels, the representation Eq. (8) is not sparse, resulting in large representation error with the limited number of basis we used. Note that existing CS-dMRI works [5,6,7] in q-space normally perform estimation voxel by voxel or only considering information from neighborhood voxels, thus failed estimation in non-tissue voxels will not affect the estimation in tissue voxels. However if the non-tissue voxels are considered in Eq. (3), the representation error and total variation caused by these non-tissue voxels will dominate the minimization, such that the estimation of the signals in tissue voxels is problematic. Thus proper masking has to be used in 6D-CS-dMRI. We first extract the brain region using S(x, 0). Then Eq. (5a) is only performed on the tissue voxels. If xi is a non-tissue voxel, we set ci = 0 in Eq. (6b), and after Eq. (5b) we also set si = 0. Using this strategy, Ui, ψi, ci and si are always zero if xi is a non-tissue voxel. See Algorithm 1 for the 6D-CS-dMRI pipeline.
3. Experiments
3.1. Evaluation Strategy for CS Reconstruction of DWI/EAP/ODF
RMSE for Data Reconstruction.
Once the coefficient vectors {ci} are estimated, ODF, DWI and EAP fields all can be analytically obtained by SPF basis [7,18,19]. With a given set of samples of ODF/DWI/EAP, the Root-Mean-Square Error (RMSE) is defined as
| (9) |
where is the estimated value for the ground truth θi. The RMSE is calculated for each voxel, then the mean RMSE is calculated for an estimated field of DWI/EAP/ODF.
For DWI signal, we use two sets of samples, where one is the set of 321 uniform samples with b = 1200s/mm2, and the other one is the DSI sampling scheme in 3D q-space. These two sample sets determine two RMSEs, which can be used to evaluate the DWI signal reconstruction respectively in a single shell and the whole q-space.
For EAP, we use the 321 uniform orientations for EAP profile with radius 0.015μm as the samples in displacement space.
For ODF defined on , we use 321 uniform orientations from sphere tessellation as the samples.
Sampling Schemes in the Joint k–q Space.
Conventional DSI requires 514 diffusion-weighted images and one baseline image S(x, 0) [1]. Denoting the spatial size in k-space as Nx × Ny × Nz, the size of the fully sampled data is then Nx × Ny × Nz × 514. A 3-fold acceleration was considered in [6,7] by using only 170 samples with maximal b-value of 8000s/mm21. Considering E(x, q) = E(x, −q), we remove antipodal symmetric samples from these 170 samples to obtain finally 138 samples, resulting in a 3.7-fold q-space acceleration. In k-space, we follow the Sparse MRI approach to perform a 3-fold sub-sampling using a polynomial distribution [3]. Thus we have a sub-sampling scheme in k–q space with the total acceleration of approximately 11-fold compared with the full DSI scheme.
Evaluation Strategy.
6D-CS-dMRI was evaluated using synthetic and real data. For synthetic data with known ground truth, the RMSE can be calculated by comparing the estimated DWI/ODF/EAP using sub-sampled data and the ground truth. For real data without ground truth, the RMSE is calculated by comparing the results of DL-SPFI using the full DSI samples with the results of 6D-CS-dMRI and naive 6D-CS-dMRI using sub-sampled data.
3.2. Synthetic Data Experiments.
We generated a slice of synthetic data with size 20×20×1×514 using mixture of tensor model with eigenvalues [1.5, 0.3, 0.3] × 10−3 mm2/s, S(x, 0) = 1 for all voxels. The generated signal is real in the x–q space. By considering its imaginary part as zero, Fourier transform was performed to obtain the synthetic ground-truth Fourier samples in k–q space. Then we performed 6D-CS-dMRI and naive 6D-CS-dMRI to 11-fold sub-sampled data in k–q space. Note that although we generated data with ψi = 1, ∀i, 6D-CS-dMRI still estimates the unknown variables {ψi} in reconstruction. To evaluate the robustness to noise, we added some complex Gaussian noise in subsamples in k-space with SNR = 30 which is defined as S(x, 0)/σ [7], where σ is the variance of the complex Gaussian noise, then we performed 6D-CS-dMRI and naive 6D-CS-dMRI on the noisy samples in k–q space and re-calculated the RMSE. We tuned the parameters (λ1, λ2, λ3, ρ) in reconstruction to obtain the best results in terms of RMSE of DWI signal in 3D space. Fig. 2 shows the estimated EAP profiles with radius 15μm and the mean RMSE calculated respectively for the estimated DWI, ODF and EAP fields. It demonstrates that 1) Compared with the naive approach, which introduces some small spurious lobes, 6D-CS-dMRI is more robust and obtains sharper EAP profiles which are similar to the ground truth as indicated by the lower RMSE for all DWIs, ODFs, EAPs. 2) EAP is more difficult to reconstruct, giving larger RMSE than DWI and ODF. 3) Although EAP reconstruction RMSEs are larger, the fiber directions shown in EAP profiles are close to the ground truth fiber directions. 4) DWI signal in single shell has the lowest RMSE, and it is normally easier to be estimated than DWI signal in whole 3D space.
Fig. 2. Synthetic Data Experiment.
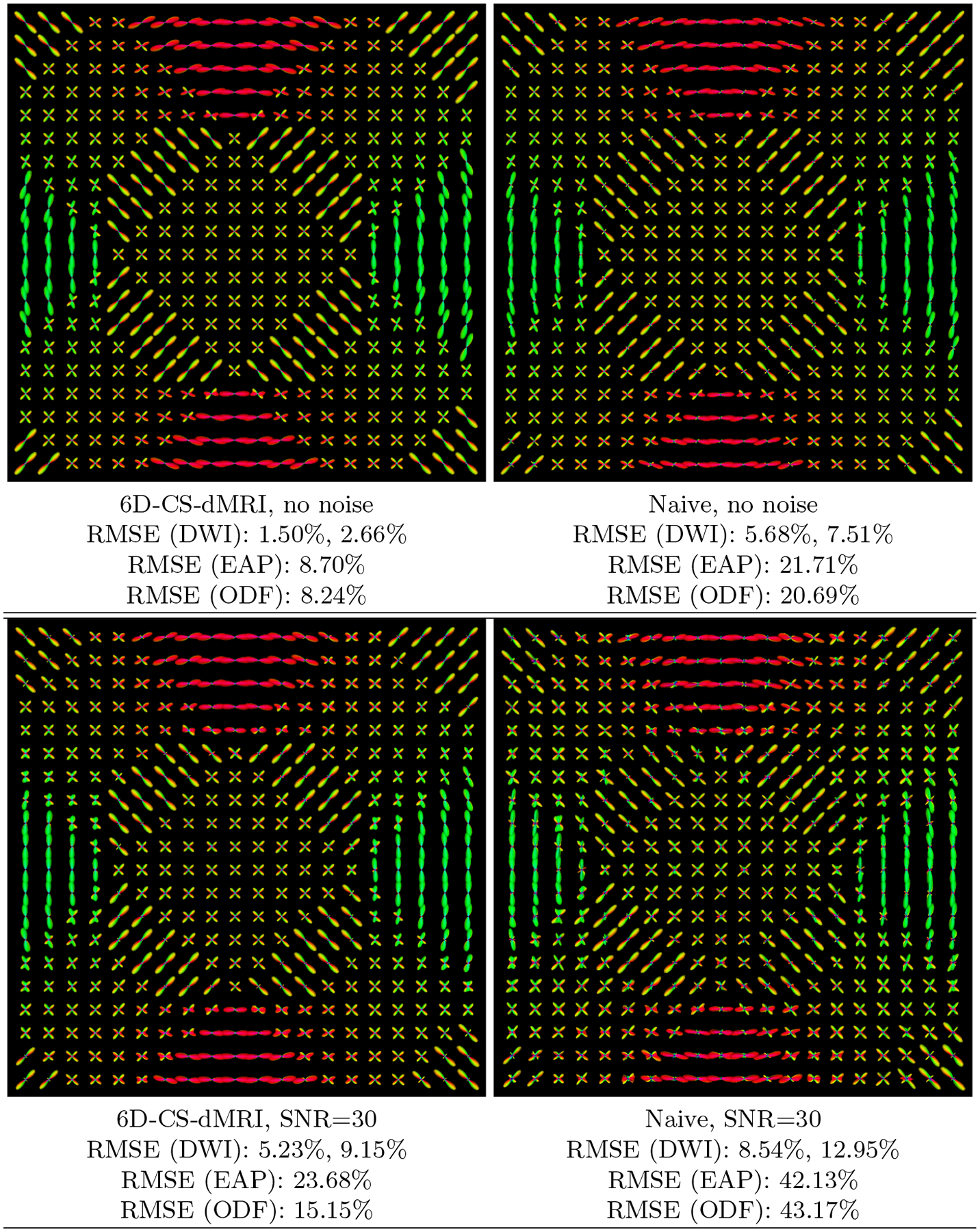
Visualization of the estimated EAP profiles with 15μm by 6D-CS-dMRI and naive 6D-CS-dMRI using 11-fold sub-sampling of the raw data, without and with complex Gaussian noise. Also shown are the RMSEs for ODFs and EAPs, and two RMSEs for DWI signal, where the first one is calculated for a single shell and the second one for the 3D space.
3.3. Real Data Experiments.
We evaluated 6D-CS-dMRI using the real DSI data used in [7,6]1. There is no ground truth for real data, thus direct comparison between the estimated DW images and the raw DWI data is not appropriate due to noise. Following [7], the coefficients {ci} were first estimated by DL-SPFI from full samples in k–q space, and DWIs, ODFs, and EAP profiles were generated from these estimated coefficients as golden standards. Then we estimated the coefficients by 6D-CS-dMRI and naive 6D-CS-dMRI using 11-fold sub-sampling, and calculated RMSE by comparing the estimated DWIs/ODFs/EAPs with the golden standards reconstructed from full sampled data. Mean RMSEs for DWIs, ODFs and EAPs shown in Fig. 3 are consistent with the observations in synthetic data experiments, i.e., DWI signal in a single shell is the easiest quantity to be reconstructed, while EAP profile is the most difficult quantity. From Fig. 3, the small RMSE (3.99% for DWIs, 13.44% for EAPs) given by 6D-CS-dMRI using 11-fold sub-sampled data indicates that reconstruction using sub-sampled data gives results similar to reconstruction using the full samples. Since acquiring the full DSI samples requires nearly one hour, the 11-fold subsampled data only need less than 6 minutes. Similar to the synthetic data experiments, we also added complex Gaussian noise with SNR=30 to the sub-sampled k-space data. After adding , where is the golden standard DWI samples in k–q space. We then performed 6D-CS-dMRI and naive 6D-CSdMRI on the noisy samples in k–q space and re-calculated the RMSEs. It can be seen from Fig. 3 that, compared with naive 6D-CS-dMRI, 6D-CS-dMRI is more robust to noise.
Fig. 3. Real Data Experiment.
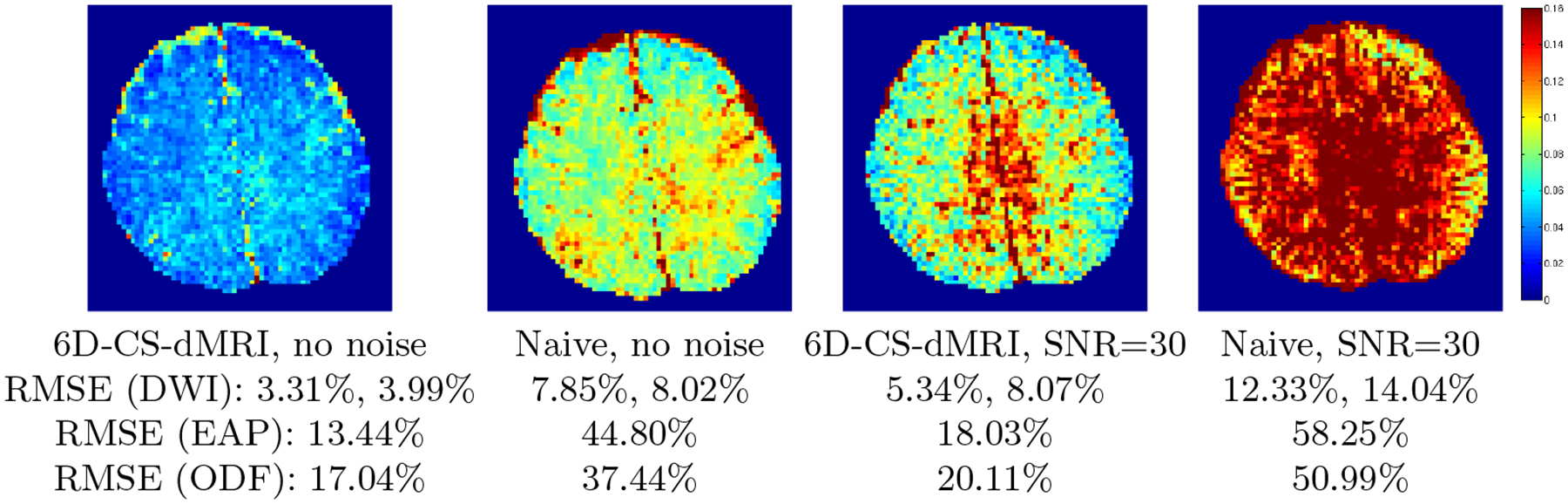
RMSE images (defined by DWI signal in 3D space) for 6D-CS-dMRI and naive 6D-CS-dMRI using 11-fold sub-sampling of the raw data, without or with complex Gaussian noise. Also shown are the mean RMSEs for DWIs, EAPs and ODFs. The first RMSE of DWI is calculated for a single shell and the second RMSE of DWI is for 3D space.
4. Conclusion
In this paper, we have proposed a novel compressed sensing framework, called 6D-CS-dMRI, for reconstruction of the continuous diffusion signal and EAP in the joint 6D k–q space. To our knowledge, 6D-CS-dMRI is the first work that applies compressed sensing in the full 6D k–q space and reconstructs simultaneously the diffusion signal in the full continuous q-space and the EAP in full continuous displacement R-space. The experiments on synthetic data and real data demonstrate that 1) compared with the reconstruction using full DSI sampling in k–q space, 6D-CS-dMRI using 11-fold sub-sampling data obtains similar results with low RMSE (less than 5% for DWI signal in synthetic data and real data), indicating that the scanning time can be reduced from nearly 1 hour to less than 6 minutes; 2) compared with naive 6D-CS-dMRI, which performs two CS reconstruction respectively in the k space and the q space, 6D-CS-dMRI generally obtains lower RMSE and is more robust to noise. Our future work is to incorporate the proposed 6D-CS-dMRI method with existing imaging techniques in k space, such that 6D-CS-dMRI can be used in clinical scanners.
Acknowledgement:
This work was performed at UNC with support in part by a UNC BRIC-Radiology start-up fund and NIH grants (EB006733, EB009634, AG041721, MH100217, and 1UL1TR001111).
Footnotes
References
- 1.Wedeen VJ, Hagmann P, Tseng WYI, Reese TG, Weisskoff RM: Mapping Complex Tissue Architecture With Diffusion Spectrum Magnetic Resonance Imaging. Magnetic Resonance In Medicine 54 (2005) 1377–1386 [DOI] [PubMed] [Google Scholar]
- 2.Donoho DL: Compressed sensing. Information Theory, IEEE Transactions on 52(4) (2006) 1289–1306 [Google Scholar]
- 3.Lustig M, Donoho D, Pauly J: Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic Resonance in Medicine 58(6) (2007) 1182–1195 [DOI] [PubMed] [Google Scholar]
- 4.Yang J, Zhang Y, Yin W: A Fast Alternating Direction Method for TVL1-L2 Signal Reconstruction From Partial Fourier Data. Selected Topics in Signal Processing, IEEE Journal of 4(2) (2010) 288–297 [Google Scholar]
- 5.Menzel MI, Tan ET, Khare K, Sperl JI, King KF, Tao X, Hardy CJ, Marinelli L: Accelerated diffusion spectrum imaging in the human brain using compressed sensing. Magnetic Resonance in Medicine 66(5) (2011) 1226–1233 [DOI] [PubMed] [Google Scholar]
- 6.Bilgic B, Setsompop K, Cohen-Adad J, Yendiki A, Wald LL, Adalsteinsson E: Accelerated diffusion spectrum imaging with compressed sensing using adaptive dictionaries. Magnetic Resonance in Medicine (2012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cheng J, Jiang T, Deriche R, Shen D, Yap PT: Regularized Spherical Polar Fourier Diffusion MRI with Optimal Dictionary Learning. In: MICCAI; (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Merlet S, Deriche R: Compressed Sensing for Accelerated EAP Recovery in Diffusion MRI. In: Computational Diffusion MRI - MICCAI Workshop. (2010) [Google Scholar]
- 9.Cheng J, Merlet S, Caruyer E, Ghosh A, Jiang T, Deriche R, et al. : Compressive Sensing Ensemble Average Propagator Estimation via L1 Spherical Polar Fourier Imaging. In: Computational Diffusion MRI - MICCAI Workshop. (2011) [Google Scholar]
- 10.Merlet S, Cheng J, Ghosh A, Deriche R: Spherical Polar Fourier EAP and ODF Reconstruction via Compressed Sensing in Diffusion MRI. In: ISBI. (2011) [Google Scholar]
- 11.Mani M, Jacob M, Guidon A, Liu C, Song A, Magnotta V, Zhong J: Acceleration of high angular and spatial resolution diffusion imaging using compressed sensing. In: Biomedical Imaging (ISBI), 2012 9th IEEE International Symposium on, IEEE (2012) 326–329 [Google Scholar]
- 12.Awate SP, DiBella EV: Compressed sensing HARDI via rotation-invariant concise dictionaries, flexible K-space undersampling, and multiscale spatial regularity. In: Biomedical Imaging (ISBI), 2013 IEEE 10th International Symposium on, IEEE (2013) 9–12 [Google Scholar]
- 13.Cheng J, Shen D, Yap PT: Joint kq space compressed sensing for accelerated multi-shell acquisition and reconstruction of the diffusion signal and ensemble average propagator. In: ISMRM. (2014) 664 [Google Scholar]
- 14.Callaghan PT: Principles of nuclear magnetic resonance microscopy. Oxford University Press; (1991) [Google Scholar]
- 15.Boyd S, Parikh N, Chu E, Peleato B, Eckstein J: Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends in Machine Learning 3(1) (2011) 1–122 [Google Scholar]
- 16.Yang J, Zhang Y: Alternating direction algorithms for ell 1-problems in compressive sensing. SIAM journal on scientific computing 33(1) (2011) 250–278 [Google Scholar]
- 17.Assemlal HE, Tschumperlé D, Brun L: Efficient and robust computation of PDF features from diffusion MR signal. Medical Image Analysis 13 (2009) 715–729 [DOI] [PubMed] [Google Scholar]
- 18.Cheng J, Ghosh A, Jiang T, Deriche R: Model-free and Analytical EAP Reconstruction via Spherical Polar Fourier Diffusion MRI. In: Medical Image Computing and Computer-Assisted Intervention - MICCAI. Volume 6361. (sep 2010) 590–597 [DOI] [PubMed] [Google Scholar]
- 19.Cheng J, Ghosh A, Deriche R, Jiang T: Model-Free, Regularized, Fast, and Robust Analytical Orientation Distribution Function Estimation. In: Medical Image Computing and Computer-Assisted Intervention - MICCAI. Volume 6361. (sep 2010) 648–656 [DOI] [PubMed] [Google Scholar]


