Abstract
A good clinical prediction score can help in the risk stratification of patients with colorectal cancer (CRC) undergoing colonoscopy screening. The aim of our study was to compare model performance of binary logistic regression (BLR), polytomous logistic regression (PLR), and classification and regression tree (CART) between the clinical prediction scores of advanced colorectal neoplasia (ACN) in asymptomatic Thai patients.
We conducted a cross-sectional study of 1311 asymptomatic Thai patients to develop a clinical prediction model. The possible predictive variables included sex, age, body mass index, family history of CRC in first-degree relatives, smoking, diabetes mellitus, and the fecal immunochemical test in the univariate analysis. Variables with a P value of .1 were included in the multivariable analysis, using the BLR, CART, and PLR models. Model performance, including the area under the receiver operator characteristic curve (AUROC), was compared between the model types.
ACN was diagnosed in 53 patients (4.04%). The AUROCs were not significantly different between the BLR and CART models for ACN prediction with an AUROC of 0.774 (95% confidence interval [95% CI]: 0.706–0.842) and 0.765 (95% CI: 0.698–0.832), respectively (P = .712). A significant difference was observed between the PLR and CART models in predicting average to moderate ACN risk with an AUROC of 0.767 (95% CI: 0.695–0.839 vs AUROC 0.675 [95% CI: 0.599–0.751], respectively; P = .009).
The BLR and CART models yielded similar accuracies for the prediction of ACN in Thai patients. The PLR model provided higher accuracy for ACN prediction than the CART model.
Keywords: advanced colorectal neoplasia, area under receiver operator characteristic curve, classification and regression tree, logistic regression, prediction score, screening
1. Introduction
Cancer is the second leading cause of death worldwide, with 9.6 million deaths in 2018, including colorectal cancer (CRC).[1] In Thailand, CRC was found in 12.64% of newly diagnosed cancer patients and ranked third in both men and women, according to the National Cancer Institute's statistics in 2017. Specifically, patients with CRC were found to be in the following stages: stage I (0.46%), stage II (2.18%), stage III (3.95%), stage IV (5%), and unknown (1.05%)[2]; the majority of patients were found to be in an advanced stage.
Colorectal screening is a process of detecting precancerous and early stage CRC in asymptomatic individuals.[3] In general, the detection and removal of precancerous lesions can reduce the incidence and mortality of CRC. Several randomized controlled trials have shown that the 5-year survival rate increased up to 73% in patients undergoing surveillance for CRC compared to non-surveillance groups.[4] Colonoscopy is considered the gold standard for the detection of CRC despite its invasive[5] and costly nature.[6] However, in Thailand, the cost of colonoscopy for detecting CRC is approximately 1 million baht, which is very high compared to the cost-effectiveness ratio in Thailand.[7] Some people also refuse to undergo surveillance colonoscopy because of concerns regarding the complications of the procedure.[8] A good clinical prediction score can help stratify CRC risks and alleviate these problems, particularly among those indicated for colonoscopy screening.
Advanced colorectal neoplasia (ACN) is defined as colorectal cancer and adenomas or serrated polyps with a size ≥1.0 cm, villous histology, or high-grade dysplasia.[6] There are many clinical prediction models for ACN in asymptomatic patients. The variables we included for those models were sex, age, body mass index (BMI), alcohol use, smoking history, diabetes mellitus, a family history of CRC in first-degree relatives, and fecal immunochemical test (FIT) results.[6,9–17] Although many models for the prediction of ACN have been developed, there are still limitations in the non-recorded risk factors, resulting in a lack of important data for predicting ACN.[18]
In general, the most commonly applied statistical method for developing a prediction model is logistic regression, for it easily identifies the relationship between variables with an odds ratio and determines variable scores.[19] The analysis of a regression model with a small sample size may cause overfitting, resulting in high accuracy in the developing phase, but lower accuracy when applied to the another data.[20] The classification and regression tree (CART) was analyzed as non-parametric without preliminary agreement on data analysis and no restrictions on missing values. A tree model that is easy to understand may overcome the overfitting problem in the regression analysis.[21] However, the CART analysis may cause a problem in choosing variables for the model, in particular the epidemiological analysis, which requires control variables that are expected to be dependent variables.[22]
Hence, in the present study, we aimed to compare statistical models to determine the clinical prediction scores for ACN in asymptomatic Thai patients. For ACN/non-ACN, we compared the following: binary logistic regression (BLR), polytomous logistic regression (PLR), and CART. For moderate and high-risk ACN, we compared PLR and CART.
2. Materials and methods
2.1. Eligible patients and outcome classification
This retrospective study was conducted between July 2009 and June 2010 and included individuals aged 50 to 65 years, presenting with no symptoms (i.e., bowel habit changes, lower gastrointestinal bleeding, decreased stool caliber, or anemia). Patients with a history of colorectal cancer or colonoscopy within 10 years were excluded from the study. All patients completed the standard questionnaires designed to elucidate the prediction scores of the ACN, FIT, and colonoscopic data.
Patients were categorized into 2 groups based on colonoscopic findings and pathological reports. The first group was ACN with malignant, villous, or tubulovillious histologic characteristics, high-grade dysplasia, or adenomatous lesions ≥ 10 mm in diameter. The second group included other polyps with pathological reports: adenoma size <1 cm, hyperplastic polyps, inflammatory polyps, colitis, lipoma, and no colorectal tumor. Another, the patients were categorized into 3 groups based on colonoscopy findings and pathological reports. The first group comprised those with ACN with malignant, villous, or tubulovillious histologic characteristics, high-grade dysplasia, or adenomatous lesions ≥10 mm in diameter. The second group (moderate group) comprised those who had other polyps with pathological reports of adenoma size <1 cm and hyperplastic polyps ≥1 cm. The third group (average group) comprised those who had hyperplastic polyps <1 cm in size, inflammatory polyps, colitis, lipoma, and no colorectal tumors.
2.2. Study variables
The variables developed for the clinical prediction scores of ACN were sex, age, BMI, family history of CRC in first-degree relatives, alcohol use, smoking history, diabetes mellitus, and FIT results.
2.3. Data analysis
2.3.1. Derivation of clinical scoring
2.3.1.1. Binary logistic regression model
Multivariate analysis was performed on the derivation set using non-ACN (adenoma size <1 cm, other polyps, and no colorectal tumor) as the base outcome to examine the association between clinical risk factors and ACN. For logistic regression, we used multiple logistic functions using the following equation:
Where Y = (non-ACN(0), ACN(1)) = binary variable, X = (X1,…, Xn) for “n” clinical risk factors, and β = (β0,…, βn) for the estimated regression coefficients based on the data.[23]
The variables related to ACN in the univariate analysis (P value <.10) and the area under the receiver operating characteristic (AUROC) curve close to 1 were included in the forward stepwise BLR. The significant risk factors in the forward stepwise BLR were incorporated into the clinical risk scores. The discriminative performance of the model was calculated using AUROC. The regression coefficients for each level of clinical predictors were divided by the smallest coefficient of the model and rounded to the nearest half (.5) as the item risk scores. The scores for each clinical predictor were summed to obtain the total risk score.
2.3.1.2. Polytomous logistic regression model
Multivariate analysis was performed on the derivation set using the average group as the base outcome to examine the association between clinical risk factors and the ACN or moderate group. The PLR model was applied using the following formula:
Where log (ACN or moderate group) is the natural logarithm of class versus (ACN or moderate group) reference class average group, X is a set of explanatory variables (X1, X2, …, Xk), Α (ACN or moderate group) = intercept term for class (ACN or moderate group) vs reference class, and B = slopes for the classes (the coefficient vector).[24]
The variables associated with ACN in the univariate analysis (P < .10) were entered into a forward stepwise PLR. Item scores for ACN and the moderate groups were derivedFta from the polytomous logistic coefficient of the corresponding diagnosis. The scores for each clinical predictor were summed to obtain the total risk score. We compared the sum of the item scores in each diagnosis to represent the diagnostic possibilities with a designed algorithm for the prediction of diagnosis using the scoring systems.
2.3.1.3. Classification and regression tree
They were divided into 2 groups:
-
1.
dependent variables of ACN and non-ACN, and
-
2.
dependent variables of ACN, moderate risk, and average risk.
Univariate analysis was performed using an exact probability test. A P value <.05 was used to create a decision model.
2.3.2. Testing for score performance
2.3.2.1. Binary logistic regression model
Discrimination of scores was conducted using AUROC. The predictive scores were calibrated using Hosmer-Lemeshow goodness-of-fit statistics. The predictive and observed risk scores were compared and presented in graphs. Internal validation of the scores was performed using the bootstrap method with 1000 replications.
2.3.2.2. Polytomous logistic regression model
Discrimination of the scores was performed using AUROC for group-specific logistic models. The distributions of the scores on average risk and moderate risk were compared and are presented in graphs. The comparison of the suggestive (predicted) and final (true) diagnoses with the diagnostic indices was calculated. Internal validation of the scores was performed using the bootstrap method with 1000 replications.
2.3.2.3. Classification and regression tree
Discrimination of scores was conducted using AUROC. A sample size of 100% was used for the model development process. A randomized sample size of 5% was used for the validation process.
2.3.3. Comparison of predictive scores
Comparison of the predictive scores for ACN was performed using AUROC. The BLR model and the CART were applied to the 2 groups. The PLR model and the CART were employed for the 3 groups. The Chi-Squared test was used to compare the AUROC scores.
2.4. Statistical analysis
STATA/SE version 12 software (StataCorp LP, College Station, TX) was used for the statistical analysis. Statistical significance was set at P < .05.
2.5. Ethics approval
This study was approved by the Ethics Committee of Human Research, Chulabhorn Research Institute (Project code: 01/2561) and the Ethics Subcommittee of Human Research, Thammasat University, 1st set (Project code: 007/2561).
3. Results
3.1. Patient characteristics
As shown in Figure 1, 1404 participants who underwent colonoscopy screening were initially eligible. Of these, 93 were excluded due to CRC-presenting symptoms (n = 55), incomplete colonoscopy (n = 10), non-retrieved polyps (n = 9), and undone FITs (n = 15). Thus, 1311 participants were analyzed in this study. The mean age was 56.69 ± 4.20 years, and the mean BMI was 25.05 ± 4.01 kg/m2. The majority of the participants (69.8%) were women.
Figure 1.
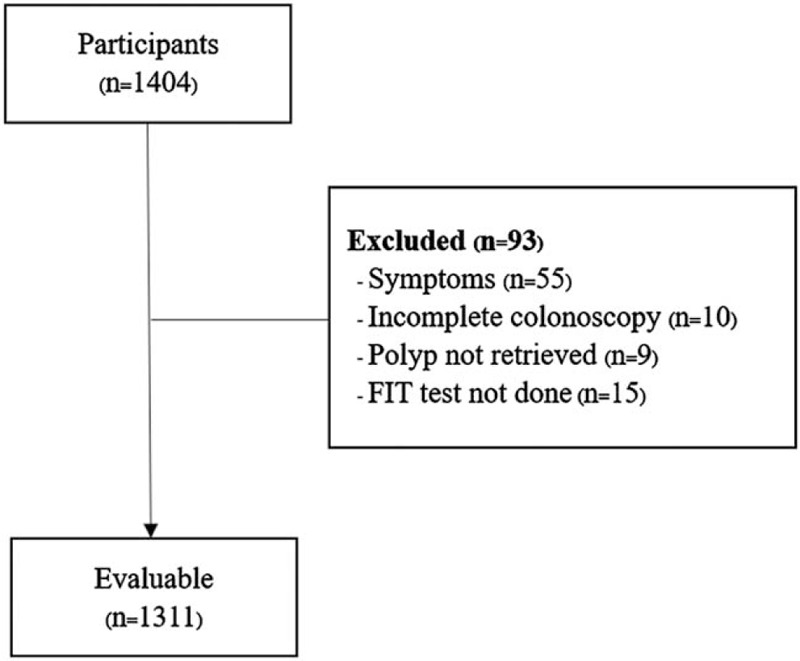
Study flow diagram.
3.2. Derivation and validation
3.2.1. Binary logistic regression model
There were 53 patients with ACN and 1258 non-ACN cases, with statistically significant differences (P < .10) in gender(male 58.5% vs female 29%, P < .001), age ≥60 years (41.5% vs 27.3%, P = .027), BMI ≥30 kg/m2 (20.8% vs 10.1%, P = .013), current and past drinking (60.4% vs 35.9%, P < .001), current and past smoking (34% vs 10.7%, P < .001), FIT positivity (20.8% vs 3.3%, P < .001), and diabetes mellitus (15.1% vs 8.2%, P = .082). The predictive value of clinical presentation as measured by AUROC was the highest for gender (Table 1).
Table 1.
Patient characteristics with and without advanced colorectal neoplasia, other polyp, normal colonoscopy area under receiver operating curve (AUROC) and 95% confidence interval (CI).
| Logistic Regression | Polytomous Logistic regression | |||||||||
| Patient Characteristics | Total | ACN (n = 53) | Non-ACN (n = 1258) | Pvalue | AUROC (95% CI) | ACN (n = 53) | Moderate risk (n = 196) | Average risk (n = 1062) | P value (ACN) | P value (Moderate) |
| Sex | ||||||||||
| Male | 369 (30.2) | 31 (58.5) | 365 (29) | <.001 | 0.65 (0.58–0.72) | 31 (58.5) | 81 (41.3) | 284 (26.7) | <.001 | <.001 |
| Female | 915 (69.8) | 22 (41.5) | 893 (71) | 22 (41.5) | 115 (58.7) | 778 (73.3) | ||||
| Age (yr) | ||||||||||
| ≥60 | 366 (27.9) | 22 (41.5) | 344 (27.3) | .027 | 0.57 (0.50–0.64) | 22 (41.5) | 61 (31.1) | 283 (26.7) | .020 | .197 |
| <60 | 945 (72.1) | 31 (58.5) | 914 (72.7) | 31 (58.5) | 135 (68.9) | 779 (73.3) | ||||
| BMI (kg/m2) | ||||||||||
| < 25 | 706 (53.9) | 23 (43.4) | 683 (54.3) | 23 (43.4) | 90 (45.9) | 593 (55.84) | ||||
| 25–30 | 467 (35.6) | 19 (35.9) | 448 (35.6) | .465 | 0.57 (0.50–0.65) | 11 (20.8) | 22 (11.2) | 105 (9.9) | .009 | .215 |
| ≥30 | 138 (10.5) | 11 (20.8) | 127 (10.1) | .013 | 19 (35.9) | 84 (42.9) | 364 (34.3) | .349 | .011 | |
| Family history of CRC in first-degree relatives | ||||||||||
| Present | 115 (8.8) | 8 (15.1) | 107 (8.5) | .102 | 0.53 (0.48–0.58) | 8 (15.1) | 16 (8.2) | 91 (8.6) | .109 | .852 |
| Absent | 1196 (91.2) | 45 (84.9) | 1151 (91.5) | 45 (84.9) | 180 (91.8) | 971 (91.4) | ||||
| Alcohol consumption | ||||||||||
| Current or past drinking | 483 (36.8) | 32 (60.4) | 451 (35.9) | <.001 | 0.62 (0.55–0.69) | 32 (60.4) | 92 (26.9) | 359 (33.8) | <.001 | <.001 |
| Never | 828 (63.2) | 21 (39.6) | 807 (64.1) | 21 (39.6) | 104 (53.1) | 703 (66.2) | ||||
| Smoking history | ||||||||||
| Current or past smoker | 153 (11.7) | 18 (34.0) | 135 (10.7) | <.001 | 0.61 (0.55–0.68) | 18 (34.0) | 36 (18.4) | 99 (9.3) | <.001 | <.001 |
| Never | 1158 (88.3) | 35 (66.0) | 1123 (89.3) | 35 (66.0) | 160 (81.6) | 963 (90.7) | ||||
| Diabetes mellitus | ||||||||||
| Yes | 111 (8.5) | 8 (15.1) | 103 (8.2) | .082 | 0.53 (0.49–0.58) | 8 (15.1) | 16 (8.2) | 87 (8.2) | .085 | .989 |
| No | 1200 (91.5) | 45 (84.9) | 1155 (91.8) | 45 (84.9) | 180 (91.8) | 975 (91.8) | ||||
| Fecal immunochemical test (FIT) | ||||||||||
| Positive | 52 (4.0) | 11 (20.8) | 41 (3.3) | <.001 | 0.59 (0.53–0.64) | 11 (20.8) | 4 (2.0) | 37 (3.5) | <.001 | .302 |
| Negative | 1259 (96.0) | 42 (79.2) | 1217 (96.7) | 42 (79.2) | 192 (98.0) | 1025 (96.5) | ||||
The significant variables in the multivariable model for ACN were age, BMI, alcohol consumption, smoking, and FIT. An item score was assigned to each level of the significant variables by dividing the logistic regression coefficient by the smallest coefficient (Table 2). A summary of the individual risk scores was obtained by adding the item scores of each individual.
Table 2.
Significant predictors of advanced colorectal neoplasia other polyp and assigned item score.
| Logistic regression | Polytomous logistic regression | |||||||||
| Predictors | OR (95% CI) | P value | β | Score | ACN (95% CI) | P value | Moderate risk (95% CI) | P value | ACN Score | Moderate risk Score |
| Sex | ||||||||||
| Male | - | - | - | - | 0.89 (0.20–1.58) | .012 | 0.46 (0.09–0.83) | .014 | 0.9 | 0.5 |
| Female | - | - | - | - | Ref. | Ref. | 0 | 0 | ||
| Age (yr) | ||||||||||
| ≥60 | 1.98 (1.10–3.56) | .023 | 0.68 | 3.5 | 0.69 (0.17–1.36) | .023 | 0.19 (−0.15–0.53) | .268 | 0.7 | 0 |
| <60 | Ref. | 0 | Ref. | Ref. | 0 | 0 | ||||
| BMI (kg/m2) | ||||||||||
| <25 | Ref. | 0 | Ref. | Ref. | 0 | 0 | ||||
| 25–30 | 1.23 (0.65–2.33) | .524 | 0.21 | 1 | 0.25 (−0.39–8.90) | .441 | 0.38 (0.05–0.71) | .022 | 0 | 0.4 |
| ≥30 | 2.70 (1.22–5.96) | .014 | 0.99 | 5 | 1.02 (0.22–1.81) | .012 | 0.29 (0.09–0.83) | .263 | 1.0 | 0 |
| Alcohol consumption | ||||||||||
| Current or past drinking | 2.08 (1.11–3.89) | .022 | 0.73 | 3.5 | 0.25 (−0.39–8.90) | .441 | 0.38 (0.05–0.71) | .022 | 0 | 0.4 |
| Never | Ref. | 0 | Ref. | Ref. | 0 | 0 | ||||
| Smoking | ||||||||||
| Current or past smoker | 2.89 (1.48–5.65) | .002 | 1.06 | 5 | 0.95 (0.19–1.70) | .014 | 0.46 (−0.02–0.95) | .062 | 1.0 | 0 |
| Never | Ref. | 0 | ||||||||
| Fecal immunochemical test | ||||||||||
| Positive | 8.05 (3.65–17.72) | <.001 | 2.09 | 10 | 1.98 (1.18–2.78) | <.001 | −0.55 (−1.60–0.50) | .303 | 2.0 | 0 |
| Negative | Ref. | 0 | Ref. | Ref. | 0 | 0 | ||||
| Constant | - | - | - | - | −4.22 (−4.83-(−3.62)) | <.001 | −2.13 (−2.40−(−1.86)) | <.001 | −4.2 | −2.1 |
Discrimination of the derived clinical risk score ranging from 0 to 27 was directly observed by the different percentage distributions between ACN and non-ACN (Fig. 2A). The clinical risk score predicted ACN with an AUROC of 77.4% (95% CI: 70.6%–84.2%), and the P value for the Hosmer-Lemeshow goodness-of-fit test was .800. Internal validation by the bootstrapping model method reduced the AUROC to 72.2% (95% CI: 77%–77.4%), with a bias of 0.002 (95% CI: 0.000–0.003). Regarding translation into absolute risks, the score for the predictive risk of ACN was higher with increasing risk scores (Fig. 2.B).
Figure 2.
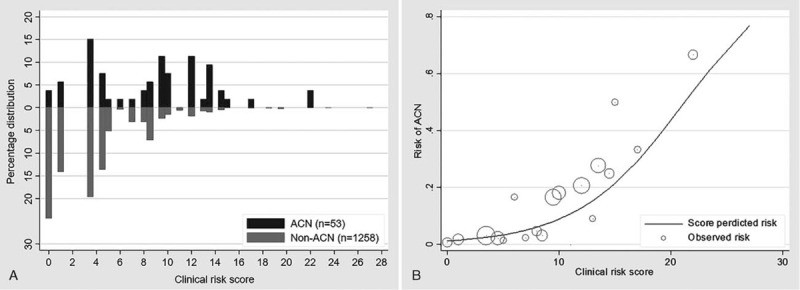
(A): Percentage distribution of clinical risk score of ACN (n = 53) vs Non-ACN (n = 1258). (B): Observed risk (circle) vs score predicted risk (solid) of ACN, size of circle represent frequency of participants in each score.
3.2.2. Classification and regression tree (ACN/Non-ACN)
Based on the CART model analysis, the variables for predicting ACN were gender, age, BMI, history of alcohol consumption, smoking history, family history of CRC in first-degree relatives, diabetes mellitus, and FIT. According to the data of 1311 patients (100%) for model prediction, we found that the factors associated with ACN (as shown in Fig. 3) yielded an AUROC of 76.5% (95% CI: 69.8–83.2%). Model testing in 656 cases (50%) from the data set analysis showed an AUROC of 78.2% (95% CI: 68.8–87.5%).
Figure 3.
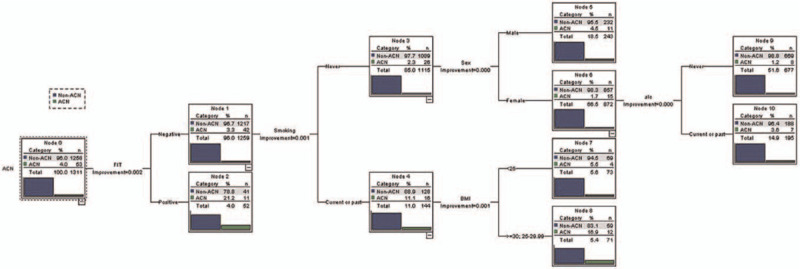
Classification and regression tree model for ACN.
3.2.3. Polynomial logistic regression model
There were 53 cases of ACN, followed by moderate risk (196 cases), and average risk (1062 cases). Significant differences (P < .10) between the ACN, moderate risk, and average risk groups with the baseline group were noted in male gender (58.5% vs 26.7%, P < .001 and 41.3% vs 26.7%, P < .001), age ≥60 years (41.5% vs 26.7%, P = .020 and 31.1% vs 26.7%, P = .197), BMI ≥30 kg/m2 (20.8% vs 9.9%, P = .009 and 11.2% vs 9.9%, P = .215), BMI 25 to 29.9 kg/m2 (35.9% vs 34.3%, P = .349 and 42.9% vs 34.3%, P = .011), current and past drinking (60.4% vs 33.8%, P < .001 and 26.9% vs 33.8%, P < .001), current and past smoking (34% vs 9.3%, P < .001 and 18.4% vs 9.3%, P < .001), FIT positivity (20.8% vs 3.5%, P < .001 and 2.0% vs 3.5%, P = .302), and diabetes mellitus (15.1% vs 8.2%, P = 0.085 and 8.2% vs 8.2%, P = .989) (Table 1).
The best multivariable clinical predictions for ACN were sex, age, BMI, smoking history, and FIT. The item scores were assigned to each level of the 5 clinical characteristics by a simple transformation of the PLR coefficients. The multivariable clinical predictions for moderate risk were gender, BMI, and alcohol consumption (Table 2). A summary risk score was obtained by summing the item scores.
The median (p25 and p75) of the ACN score was −3.5 (−4.2, −3.2) for the diagnosis of average risk, −3.4 (−4.2, −2.6) for moderate risk and −2.3 (−3.3, −1.6) for ACN. The median (p25 and p75) score of moderate risk was −1.7 (−2.1, −1.6) for the diagnosis of average risk, followed by −1.7 (−2.1, −1.6) for moderate risk and −1.6 (−2.1, −1.2) for ACN (Fig. 4). The AUROC of the ACN and non-ACN scores was 76.7% (95% CI: 69.5–83.9%). Internal validation by the bootstrapping model method reduced the AUROC to 76.6% (95% CI: 76.4–76.8%) for ACN versus non-ACN patients.
Figure 4.
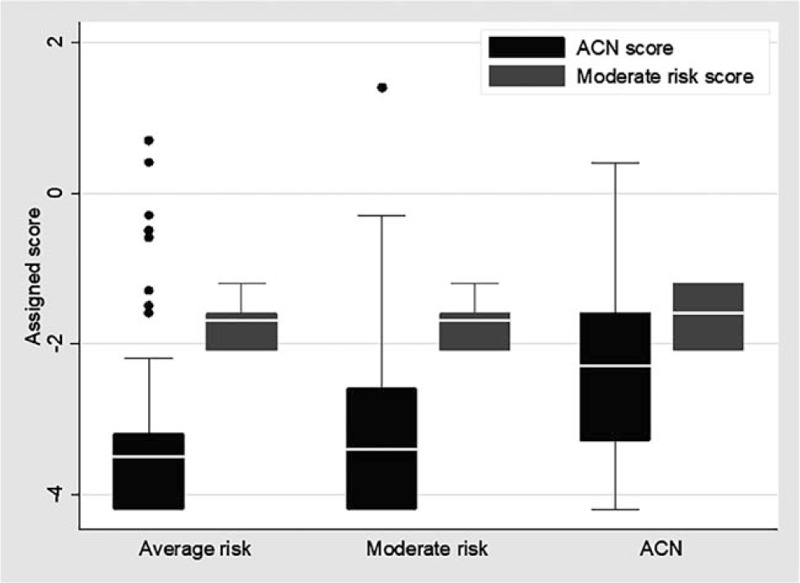
Distribution (box plot) of ACN score and moderate risk score in average risk, moderate risk and ACN.
Regarding the concept of relative probabilities, an algorithm for diagnosis from the scoring system was created (Table 3).
Table 3.
Criteria for diagnostic preferences in polytomous logistic regression model.
| Diagnostic preferences | Criteria |
| Advanced colorectal neoplasia | ACN score > Other polyps score orACN score < Otherscore and ACNscore > −2 |
| Other polyps | ACN score < Other polyps score and−3 < ACN score ≤ −1 |
| No Colorectal tumor | ACN score < Other polyps score andACN score ≤ −1 |
3.2.4. Classification and regression tree (ACN, moderate risk, and average risk)
Based on the CART model analysis, the variables for predicting ACN, moderate risk, and average risk were gender, age, BMI, history of alcohol consumption, smoking history, family history of CRC in first-degree relatives, diabetes mellitus, and FIT. According to the data of 1311 patients (100%) for model prediction, we found that the factors associated with ACN (as shown in Fig. 5) yielded an AUROC of 67.5%. Model testing in 656 cases (50%) from the data set analysis showed an AUROC of 64.5%.
Figure 5.
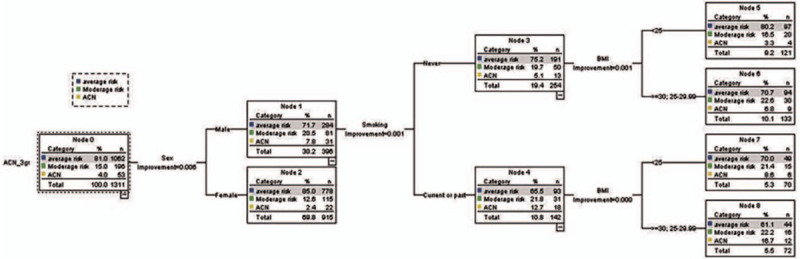
Classification and regression tree model for ACN, moderate risk and average risk.
3.2.5. Comparison of binary logistic regression, classification and regression tree, and polynomial logistic regression models
When comparing the BLR model and the CART for their capability to discriminate ACN, the AUROCs of the BLR model and the CART were 0.774 (95% CI: 0.774–0.842) and 0.765 (95% CI: 0.698–0.832), respectively. The AUROC scores of both models were not significantly different at a p-value of 0.712 (Fig. 6.A).
Figure 6.
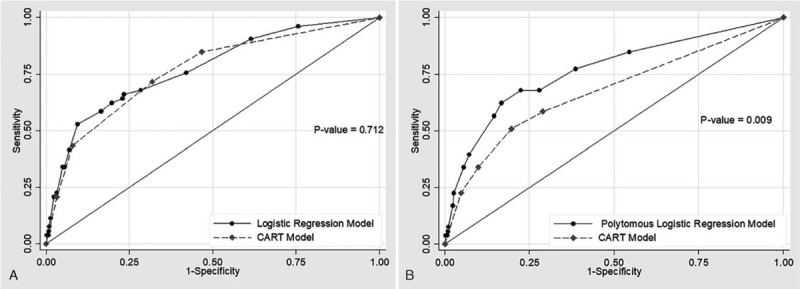
(A): Receiver operating characteristic (ROC) curves of logistic regression model (solid line) and classification and regression tree (dash line) for diagnosis of ACN. (B): Receiver operating characteristic (ROC) curves of polynomial logistic regression model (solid line) and classification and regression tree (dash line) for diagnosis of ACN.
However, a comparison of the PLR model and the CART for their capabilities to discriminate yielded AUROCs of 0.767 (95% CI: 0.695–0.839) and 0.675 (95% CI: 0.599–0.751), respectively. The AUROC of the polynomial logistic regression model was higher than that of the CART, with statistical significance (P = .009) (Fig. 6.B).
4. Discussion
In this study, we developed a clinical risk score for the prediction of ACN in asymptomatic subjects based on demographic data (age, sex, BMI, family history of CRC in first-degree relatives, drinking, smoking, diabetes mellitus), and the FIT. The BLR, CART, and PLR models were compared after modifying the clinical risk score in participants who underwent colonoscopic screening. Screening could diagnose colorectal cancer cases in the early stage, leading to lower mortality and potential prevention.[25,26] The accuracy and reliability of estimating and stratifying the risks for ACN may be helpful as an alternative to several available testing options for patients and care providers.
The BLR model yielded high discriminatory power measured by AUROC and could be applied for the identification of individuals at high risk of ACN. In the univariable and multivariable analyses, the predictive values of the 5 clinical risk factors chosen by the model were previously reported to be age,[6,9–17] BMI,[6,9,11,13,15] alcohol drinking,[12,14] smoking,[6,9–17] and FIT.[27,28]
The PLR model demonstrated good discriminatory power measured by AUROC and could be applied to identify the ACN. In the univariate and multivariate analyses, the predictive values of the 5 clinical risk factors chosen by the model were previously reported to be sex,[6,9–11,13–17] age,[6,9–17] BMI,[6,9,11,13,15] smoking,[6,9–17] and FIT.[27,28]
The CART provided a good discriminatory power measured by AUROC and could be applied to identify the ACN (ACN/non-ACN). There was fair discriminatory power measured by AUROC, which could be applied to identify the ACN (ACN, moderate risk, average risk). The predictive values of the 6 clinical risk factors chosen by the model were previously reported to be sex,[6,9–11,13–17] age,[6,9–17] BMI,[6,9,11,13,15] drinking,[12,14] smoking,[6,9–17] and FIT.[27,28]
Following the BLR model, CART, and the PLR model, a positive family history of CRC in first-degree relatives was not identified as an important component of the risk score among asymptomatic populations in this study.[6,11,12,15,17] Recall bias in subjects may have influenced the observation, as the study in the population group was aged 50 to 60 years.[29]
We evaluated the accuracy of the screening risk score for the prediction of ACN using the BLR model (AUROC = 0.774) and CART (AUROC = 0.765). No significant difference was noted between the BLR model and the CART for ACN prediction.[30] The analysis of the logistic regression and CART models yielded similar dependent variables for prediction.[31]
A comparison of AUROC for predicting ACN, moderate risk, and average risk showed that the PLR had a higher AUROC than the CART, with statistical significance. This may be due to the inadequate sample size in each group of ACN, moderate risk, and average risk for the CART, which required a large sample size.[32]
There were some limitations to this study. The data were only secondary data from the Royal Charity Project of Colorectal Cancer Screening. Additional details of clinical information or clinical risks, such as waist circumference,[10] may increase the accuracy of this risk score. Many clinical characteristics have been recorded and are readily accessible in routine practice. The validation of the study results should be evaluated using well-planned prospective data collection with calibrated instruments.
5. Conclusions
The BLR model and the CART yielded similar accuracy for the prediction of ACN in Thai patients, and the CART was easily interpreted. However, the PLR model yielded higher accuracy for the prediction of ACN (ACN, moderate risk, and high risk) than the CART. A simple clinical risk score may be helpful in selecting participants for colonoscopic screening. Future studies are needed to externally validate the scoring performance of diverse populations for cost-effectiveness.
Acknowledgments
We would like to convey our sincere thanks to the team of the Royal Charity Project 2009, Colorectal Cancer Screening, Clinical Epidemiology Unit, Faculty of Medicine, Thammasat University, for valuable advice and suggestions for this study.
Author contributions
Conceptualization: Kamonwan Soonklang, Boonying Siribumrungwong, Bunchorn Siripongpreeda, Chirayu Auewarakul.
Data curation: Kamonwan Soonklang, Bunchorn Siripongpreeda.
Formal analysis: Kamonwan Soonklang, Boonying Siribumrungwong.
Methodology: Kamonwan Soonklang, Boonying Siribumrungwong, Bunchorn Siripongpreeda.
Writing – original draft: Kamonwan Soonklang.
Writing – review & editing: Kamonwan Soonklang, Boonying Siribumrungwong.
Footnotes
Abbreviations: ACN = advanced colorectal neoplasia, AUROC = area under the receiver operator characteristic curve, BLR = binary logistic regression, BMI = body mass index, CART = classification and regression tree, CRC = colorectal cancer, FIT = fecal immunochemical test, PLR = polytomous logistic regression.
How to cite this article: Soonklang K, Siribumrungwong B, Siripongpreeda B, Auewarakul C. Comparison of multiple statistical models for the development of clinical prediction scores to detect advanced colorectal neoplasms in asymptomatic Thai patients. Medicine. 2021;100:20(e26065).
The authors have no conflicts of interest to disclose.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
References
- [1].World Health Organization. Cancer. 2018. [cited Jan 28, 2019]. Available from: https://www.who.int/news-room/fact-sheets/detail/cancer [Google Scholar]
- [2]. Nation Cancer Institute. Hospital-based cancer registry [Internet]; 2017. [cited Jan 28, 2019]. Available from: http://www.nci.go.th/th/File_download/Nci%20Cancer%20Registry/HOSPITAL-BASED%202016%20Revise%204%20Final.pdf. [Google Scholar]
- [3].Virk GS, Jafri M, Mehdi S, Ashley C. Staging and survival of colorectal cancer (CRC) in octogenarians: nationwide study of US Veterans. J Gastrointest Oncol 2019;10:12–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Maida M, Macaluso FS, Ianiro G, et al. Screening of colorectal cancer: present and future. Expert Rev Anticancer Ther 2017;17:1131–46. [DOI] [PubMed] [Google Scholar]
- [5].Schreuders EH, Ruco A, Rabeneck L, et al. Colorectal cancer screening: a global overview of existing programmes. Gut 2015;64:1637–49. [DOI] [PubMed] [Google Scholar]
- [6].Sung JJY, Wong MCS, Lam TYT, Tsoi KKF, Chan VCW. A modified colorectal screening score for prediction of advanced neoplasia: a prospective study of 5744 subjects. J Gastroenterol Hepatol 2018;33:187–94. [DOI] [PubMed] [Google Scholar]
- [7].Joob B, Wiwanitkit V. Colonoscopy colorectal cancer screening: cost-effectiveness in Thailand. S Asian J Cancer 2016;5:19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Saengow U, Chongsuwiwatvong V, Geater A, Birch S. Preferences and acceptance of colorectal cancer screening in Thailand. Asian Pac J Cancer Prev 2015;16:2269–76. [DOI] [PubMed] [Google Scholar]
- [9].Sekiguchi M, Kakugawa Y, Matsumoto M, Matsuda T. A scoring model for predicting advanced colorectal neoplasia in a screened population of asymptomatic Japanese individuals. J Gastroenterol 2018;53:1109–19. [DOI] [PubMed] [Google Scholar]
- [10].Imperiale TF, Monahan PO, Stump TE, Glowinski EA, Ransohoff DF. Derivation and validation of a scoring system to stratify risk for advanced colorectal neoplasia in asymptomatic adults: a cross-sectional study. Ann Intern Med 2015;163:339–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Kim DH, Cha JM, Shin HP, et al. Development and validation of a risk stratification-based screening model for predicting colorectal advanced neoplasia in Korea. J Clin Gastroenterol 2015;49:41–9. [DOI] [PubMed] [Google Scholar]
- [12].Schroy PC, 3rd, Wong JB, O’Brien MJ, Chen CA, Griffith JL. A risk prediction index for advanced colorectal neoplasia at screening colonoscopy. Am J Gastroenterol 2015;110:1062–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Wong MC, Lam TY, Tsoi KK, et al. A validated tool to predict colorectal neoplasia and inform screening choice for asymptomatic subjects. Gut 2014;63:1130–6. [DOI] [PubMed] [Google Scholar]
- [14].Tao S, Hoffmeister M, Brenner H. Development and validation of a scoring system to identify individuals at high risk for advanced colorectal neoplasms who should undergo colonoscopy screening. Clin Gastroenterol Hepatol 2014;12:478–85. [DOI] [PubMed] [Google Scholar]
- [15].Kaminski MF, Polkowski M, Kraszewska E, Rupinski M, Butruk E, Regula J. A score to estimate the likelihood of detecting advanced colorectal neoplasia at colonoscopy. Gut 2014;63:1112–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Cai QC, Yu ED, Xiao Y, et al. Derivation and validation of a prediction rule for estimating advanced colorectal neoplasm risk in average-risk Chinese. Am J Epidemiol 2012;175:584–93. [DOI] [PubMed] [Google Scholar]
- [17].Yeoh KG, Ho KY, Chiu HM, et al. The Asia-Pacific Colorectal Screening score: a validated tool that stratifies risk for colorectal advanced neoplasia in asymptomatic Asian subjects. Gut 2011;60:1236–41. [DOI] [PubMed] [Google Scholar]
- [18].Hong SN, Son HJ, Choi SK, et al. A prediction model for advanced colorectal neoplasia in an asymptomatic screening population. PLOS ONE 2017;12:e0181040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Adams ST, Leveson SH. Clinical prediction rules. BMJ 2012;344:d8312. [DOI] [PubMed] [Google Scholar]
- [20].Lee YH, Bang H, Kim DJ. How to establish clinical prediction models. Endocrinol Metab (Seoul) 2016;31:38–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Speybroeck N. Classification and regression trees. Int J Public Health 2012;57:243–6. [DOI] [PubMed] [Google Scholar]
- [22].Gordon L. Using Classification and Regression Trees (CART) in SAS( Enterprise MinerTM For Applications in Public Health. [Internet]; 2013. [cited Jan 28, 2019]. Available from: http://support.sas.com/resources/papers/proceedings13/089-2013.pdf. [Google Scholar]
- [23].Stoltzfus JC. Logistic regression: a brief primer. Acad Emerg Med 2011;18:1099–104. [DOI] [PubMed] [Google Scholar]
- [24].Mustafa A, Heppenstall A, Omrani H, Saadi I, Cools M, Teller J. Modelling built-up expansion and densification with multinomial logistic regression, cellular automata and genetic algorithm. Comput Environ Urban Syst 2018;67:147–56. [Google Scholar]
- [25].Zauber AG, Winawer SJ, O’Brien MJ. Colonoscopic polypectomy and long-term prevention of colorectal-cancer deaths. N Engl J Med 2012;366:687–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Winawer SJ. The history of colorectal cancer screening: a personal perspective. Dig Dis Sci 2015;60:596–608. [DOI] [PubMed] [Google Scholar]
- [27].Aniwan S, Rerknimitr R, Kongkam P, et al. A combination of clinical risk stratification and fecal immunochemical test results to prioritize colonoscopy screening in asymptomatic participants. Gastrointest Endosc 2015;81:719–27. [DOI] [PubMed] [Google Scholar]
- [28].Jung YS, Park CH, Kim NH, Park JH, Park DI, Sohn CI. A combination of clinical risk stratification and fecal immunochemical test is useful for identifying persons with high priority of early colonoscopy. Dig Liver Dis 2018;50:254–9. [DOI] [PubMed] [Google Scholar]
- [29].Althubaiti A. Information bias in health research: definition, pitfalls, and adjustment methods. J Multidiscip Healthc 2016;9:211–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Colombet I, Ruelland A, Chatellier G, Gueyffier F, Degoulet P, Jaulent MC. Models to predict cardiovascular risk: comparison of CART, multilayer perceptron and logistic regression. Proc AMIA Symp 2000;156–60. [PMC free article] [PubMed] [Google Scholar]
- [31].Muller R, Möckel M. Logistic regression and CART in the analysis of multimarker studies. Clin Chim Acta 2008;394:01–6. [DOI] [PubMed] [Google Scholar]
- [32].Song YY, Lu Y. Decision tree methods: applications for classification and prediction. Shanghai Arch Psychiatry 2015;27:130–5. [DOI] [PMC free article] [PubMed] [Google Scholar]


