The human preference for symmetric walking often disappears when one leg is constrained

Abstract

The bilateral symmetry inherent in healthy human walking is often disrupted in clinical conditions that primarily affect one leg (e.g. stroke). This seems intuitive: with one leg constrained, gait becomes asymmetric. However, the emergence of asymmetry is not inevitable. Consider that symmetric walking could be preserved by matching the movement of the unconstrained leg to that of the constrained leg. While this is theoretically possible, it is rarely observed in clinical populations. Here, we hypothesized that minimization of metabolic power could drive people to walk asymmetrically when one leg is constrained, even when symmetric walking remains possible. We tested this hypothesis by performing two experiments in healthy adults. In Experiment 1, we constrained one step to be markedly shorter or longer than preferred. We observed that participants could significantly reduce metabolic power by adopting an asymmetric gait (one short/long step, one preferred step) rather than maintaining a symmetric gait (bilateral short/long steps). Indeed, when allowed to walk freely in this situation, participants naturally adopted a less effortful asymmetric gait. In Experiment 2, we applied a milder constraint that more closely approximated magnitudes of step length asymmetry that are observed in clinical populations. Responses in this experiment were more heterogeneous, though most participants adopted an asymmetric gait. These findings support two central conclusions: (1) symmetry is not necessarily energetically optimal in constrained human walking, and (2) people may prefer to walk asymmetrically to minimize metabolic power when one leg is constrained during fixed-speed treadmill walking, especially when the constraint is large.

Introduction

Healthy human walking is largely symmetric (Ankarali et al., 2015; Forczek and Staszkiewicz, 2012; Gundersen et al., 1989; Hamill et al., 1984; Hannah et al., 1984) with relatively small differences between the kinematics and kinetics of the two legs (Herzog et al., 1989; Sadeghi et al., 2000). Symmetric gait is thought to be preferable to asymmetric gait for several reasons: symmetric walking is less metabolically costly (Ellis et al., 2013; Finley et al., 2013), more stable (Lewek et al., 2014), and less likely to result in orthopaedic injury (Jorgensen et al., 2000). In sum, symmetric gait allows us to walk from one location to another in the most stable, economical manner.

But this may only be true of a healthy, unconstrained gait. Many conditions that cause asymmetric damage to the nervous or musculoskeletal systems (e.g. stroke, Parkinson’s disease, cerebral palsy, lower limb amputation, osteoarthritis) result in gait asymmetry (Cichy and Wilk, 2006; Gillette, 1966; Knutsson, 1981, 1972; Olney and Richards, 1996; Seligman, 1952). These conditions induce unilateral neuromuscular or mechanical constraints that disproportionately impair the function of one leg. The emergence of gait asymmetry is often considered inevitable: if the function of one leg is constrained, it is intuitive that walking should become asymmetric. However, asymmetric gait is not obligatory when one leg is constrained. Consider that a symmetric gait could be maintained simply by matching the movement of the unconstrained leg to that of the constrained leg. While this is possible in theory, it is rarely observed in the clinical populations mentioned above. So why might people prefer to walk asymmetrically even when symmetric walking (or, at least, more symmetric walking) remains possible?

One possibility is that people adopt asymmetric gait patterns when asymmetric walking becomes less effortful than symmetric walking. Minimization of the metabolic cost of transport (i.e. energy expended per unit distance walked) is thought to be an important objective of human locomotor control (Alexander, 1989; Bertram, 2005; Bertram and Ruina, 2001; Donelan et al., 2001; Ralston, 1958; Zarrugh et al., 1974), as our preferred walking speed (Ralston, 1958), step length (Zarrugh et al., 1974) and step width (Donelan et al., 2001) all appear tuned to minimize metabolic cost. Certainly, objectives beyond minimization of metabolic cost – e.g. maintaining stability, minimizing pain – also play prominent roles. However, recent work has shown convincingly that healthy adults change their preferred walking patterns when a new pattern becomes less effortful (Selinger et al., 2015), underscoring minimization of metabolic cost as a salient objective that drives people to adjust their gait when they encounter new environments with different cost landscapes.

Recent studies of healthy young adults and persons post-stroke support the hypothesis that one’s preferred gait symmetry (or asymmetry) is also influenced by the metabolic cost of walking (Finley et al., 2013; Roemmich et al., 2019; Sanchez and Finley, 2018). For example, we created a treadmill-based environment where participants could control the speed of the treadmill by walking with various patterns of symmetric or asymmetric step lengths. When walking in this environment, we observed that both healthy adults and persons post-stroke tended to adjust their gait symmetry to walk at a speed that minimized metabolic cost (Roemmich et al., 2019). Similarly, healthy adults adopt an asymmetric gait when walking on a split-belt treadmill (where two treadmill belts – one under each foot – move at different speeds simultaneously) and achieve a less costly walking pattern (Sanchez et al., 2019). These findings suggest that minimization of metabolic cost plays a role in shaping human gait symmetry. However, previous studies have relied on robotic exoskeletons or specialized treadmills to reshape the metabolic cost landscape in ways not encountered in the real world.

In this study, we posed two questions: (1) how do people prefer to walk when one leg is constrained to take a short step (as commonly occurs after unilateral neurologic or musculoskeletal impairment), and (2) why do people prefer to walk in this way? While less clinically relevant, we also asked the same questions when one leg is constrained to take a longer step. When one leg is forced to step shorter or longer than preferred, consideration of the costs associated with swinging the legs (Doke et al., 2005; Doke and Kuo, 2007) and redirecting the centre of mass (COM) (Donelan et al., 2002) lead to the hypothesis that an asymmetric gait – where the unconstrained leg maintains the preferred step length – will result in a lower metabolic cost than a symmetric gait where both steps are shortened or lengthened similarly. Previous work that measured the effects of step time and step time asymmetry on the metabolic cost of walking supports this hypothesis (Ellis et al., 2013). Therefore, when one leg is constrained to take a short or long step, we hypothesized that (1) people will prefer to walk asymmetrically, and (2) this can be explained by a preference to minimize the metabolic cost of walking. We suggest that the findings of this study could inform our basic understanding of human locomotor control and the design of rehabilitation approaches that aim to restore gait symmetry in clinical populations.

Methods

General methods

Ethical approval.

Twenty-eight healthy adults participated in this study (n = 14 in each experiment). All participants provided written, informed consent in accordance with the Johns Hopkins Medicine Institutional Review Board before participation. The studies performed conformed to the standards set by the Declaration of Helsinki though were not registered in a research database. Participants were paid for participation and participated in only one of the two experiments. All participants were screened for neurological, musculoskeletal or cardiovascular conditions prior to enrolment.

Data collection.

All walking trials were performed on an instrumented split-belt treadmill with both belts moving at 1.25 m/s (Motek Medical, Amsterdam, Netherlands). Participants wore a safety harness, did not hold onto the treadmill handrails, and were instructed to keep one foot on each belt. Kinematic data were recorded using a 10-camera three-dimensional motion capture system (Vicon Motion Systems, Centennial, CO; 100 Hz). Passive, reflective markers were placed bilaterally over the second and fifth metatarsal heads, calcaneus, lateral malleolus, lateral shank, lateral femoral epicondyle, lateral thigh, greater trochanter, anterior superior iliac spine, posterior superior iliac spine and iliac crest. All participants wore their typical, comfortable walking shoes and form-fitting clothing. Three-dimensional ground reaction forces (GRFs) were collected at 1000 Hz using the force plates under each treadmill belt.

We collected metabolic data using a TrueOne 2400 system (Parvomedics, Sandy, UT). After warming the system for at least 30 min prior to collection and manufacturer-recommended calibration, we sampled oxygen consumption and carbon dioxide production breath-by-breath. We measured baseline metabolic rate during a 2 min period of quiet standing and then subtracted this baseline value from all subsequent walking trials to calculate net metabolic power using a traditional equation (Brockway, 1987); we also normalized to body mass. We analysed the final 2 min of each 5 min walking trial to ensure that measurements had reached steady state. Our experimental setup is shown in Fig. 1A.

Figure 1. Experimental setup and protocols.

A, experimental setup demonstrating a split-belt treadmill operating at 1.25 m/s while participants donned retroreflective markers for three-dimensional motion capture, wore a mask capturing expired gas, and viewed a screen providing step length feedback. B, example of step length feedback with red and blue circles appearing at each heel-strike representing each leg’s step length. Each target 1–20 equated to 0.05 m of step length and participants were instructed which number to achieve with each foot. C and D, Experiment 1 and 2 protocols defining, in randomized order, left and right step length pairings for each trial and each experiment.

Data analysis.

Custom MATLAB (Mathworks, Natick, MA, USA) software was used for all data analysis. Marker and GRF data were filtered using fourth order low-pass Butterworth filters with cut-off frequencies of 6 and 28 Hz, respectively. Heel-strikes were detected using a 40 N vertical GRF threshold, and crossover steps (when one foot stepped onto both belts) were omitted prior to further analysis. Step lengths were calculated as the absolute value of the anteroposterior distance between left and right lateral malleolus markers at each heel-strike. Step time was calculated as the time interval between consecutive heel-strikes; this was used to calculate cadence. GRFs were used to estimate the COM velocity, and the power and average work rate performed on the COM in each stride were calculated using the individual limbs method (Donelan et al., 2002) then averaged across all strides (after removal of crossover steps) for each participant.

Visual display.

Our visual feedback display was created in D-Flow (Motek Medical, Amsterdam, Netherlands) and showed 20 vertically arranged virtual targets on a screen placed in front of the treadmill (Fig. 1B). Each target represented a bin of 0.05 m, and targets were numbered 1–20 (e.g. target 1 corresponded to zero step length, target 2 corresponded to 0.05 m step length, etc.). Red and blue circles appeared at each heel-strike for left and right legs, respectively, to visualize step lengths. When participants stepped within a target, the number within that target changed to the corresponding foot’s colour (i.e. left = red and right = blue) to indicate which target had been stepped in.

Experiment 1

In Experiment 1, our goals were to (1) map the metabolic power landscape of walking with symmetric or asymmetric step lengths where one or both step lengths become shorter or longer than preferred and (2) determine how people prefer to walk when one leg is constrained to step shorter or longer than preferred but the contralateral leg is unconstrained. Fourteen healthy adults participated in Experiment 1 (six female, age (mean ± standard deviation): 23.6 ± 3.7 years, body mass: 70.0 ± 19.0 kg).

The Experiment 1 protocol is shown in Fig. 1C. All participants first walked at 1.25 m/s for 1 min with the display off while the experimenter measured their preferred step lengths on a separate monitor. We then turned on the display with the treadmill stationary and asked participants to step forward with their left or right foot to demonstrate the functionality of the feedback. The experimenter informed the participant that they would be asked to step to specific left and right targets that corresponded with either their preferred step lengths, short step lengths (50% of preferred) or long step lengths (150% of preferred). For example, if a participant naturally walked with step lengths of 0.50 m, they would be asked to step to target 10 to execute a preferred step, target 5 to execute a short step, and target 15 to execute a long step. All participants then walked at 1.25 m/s for 5 min each in six different mapping trials (order randomized) that consisted of different pairings of left (L) and right (R) step lengths: Pref (no display, preferred step length), L Short/R Short, L Long/R Long, L Pref/R Short, L Pref/R Long and L Short/R Long.

After mapping the metabolic power landscape, we tested how participants preferred to walk when one leg was constrained. Participants performed two choice trials (order randomized) where we removed visual feedback for the left leg such that participants only received feedback about the right step length. We instructed participants to walk with their right step length either short (L Choice/R Short) or long (L Choice/R Long) while the left step length (without feedback) was unconstrained. This meant that the participants could walk however they preferred with the left leg while the right leg took a shortened or lengthened step. Participants rested after each trial such that their breathing returned to baseline.

Experiment 2

In Experiment 2, we tested the effects of more subtle step length constraints. Fourteen healthy adults participated in Experiment 2 (seven female, age: 23.7 ± 3.6 years, body mass: 71.6 ± 14.0 kg). The Experiment 2 protocol is shown in Fig. 1D. We repeated the Experiment 1 protocol with the following exceptions: step length was constrained to be 25% longer (Long) or shorter (Short) than preferred (rather than 50% as in Experiment 1) and the choice period consisted of only a L Choice/R Short condition (since this is the more clinically relevant of the two: clinical conditions typically do not lengthen one of the steps). Lastly, the ‘Preferred’ condition in Experiment 2 was done with the display on to examine any potential effect of the visual feedback on metabolic power during walking.

Statistical analysis

To simplify the comparisons made in each experiment, we performed separate one-way repeated measures analyses of variance (rmANOVAs) to test for main effects of trial when the step lengths of the right leg were constrained to be either short or long for each experiment. Within each rmANOVA, we tested for main effects of trial on right step length, left step length, cadence, metabolic power, negative and positive work rate across a stride, peak braking and propulsive force extracted from the anteroposterior GRF (AP GRF), first and second peaks of the vertical GRF, as well as maximum and minimum COM velocities in the AP and vertical directions when each foot was in contact with the ground. This meant that, for Experiment 1, the first rmANOVA compared these outcome measures among the following trials that included a shortened right step: L Short/R Short, L Pref/R Short and L Choice/R Short. The second rmANOVA compared the same outcome measures among trials that included a lengthened right step: L Long/R Long, L Pref/R Long, L Short/R Long and L Choice/R Long. Data from the Preferred trial (i.e. both step lengths preferred) are shown in all relevant Figures as reference data. Similarly, for Experiment 2, we performed an rmANOVA to test for differences in the same outcome measures between L Short/R Short, L Pref/R Short and L Choice/R Short. When a significant main effect was observed, post hoc tests using Bonferroni correction for multiple comparisons (P value = 0.017 for right short step length comparisons and P value = 0.013 for long step length comparisons) were used to detect differences among trials.

We were also interested in understanding what variables were significant predictors of changes in metabolic power across trials. We performed two linear regressions with change in metabolic power relative to Preferred as the dependent variable and change relative to Preferred in cadence, left leg positive work rate, right leg positive work rate and trial as independent variables. The first model included data from the trials where the right step was constrained to be short (L Short/R Short and L Pref/R Short) from both Experiments 1 and 2 while the second model included data from the trials where the right step was constrained to be long (L Long/R Long and L Pref/R Long) from both Experiments 1 and 2. As a final post hoc analysis, we performed a quadratic fit on all individual subject absolute step length asymmetry and metabolic power data from Experiment 1 (we used the data from Experiment 1 here due to the large dynamic range provided by the more pronounced differences in step lengths among trials). Absolute step length asymmetry was defined as the absolute value of the difference between left and right step lengths normalized to their mean and, in this analysis, we calculated a change score for metabolic power by subtracting each participant’s metabolic power measured during the preferred walking trial. All analyses were performed with α ≤ 0.05 (prior to any correction for multiple comparisons).

Results

Experiments 1 and 2 were designed to (1) map the metabolic power landscape associated with different symmetric and asymmetric step lengths (mapping trials), and (2) examine how people prefer to walk when the step length of one leg is constrained in different ways (choice trials). Based on previous work investigating the energetics associated with redirecting the COM (Donelan et al., 2002), swinging the legs (Doke et al., 2005; Doke and Kuo, 2007), and walking with asymmetric step times (Ellis et al., 2013), we developed hypotheses for the metabolic power associated with each of the mapping trials (Fig. 2). Specifically, we expected that walking with two preferred step lengths (Preferred trial) would show the lowest metabolic power of the six trials. However, we also expected that an asymmetric gait where one leg steps at the preferred length while the other steps shorter or longer than preferred (i.e. the L Pref/R Short and L Pref/R Long trials) would be less costly than (1) symmetric walking patterns where both steps were shorter or longer than preferred (i.e. the L Short/R Short and L Long/R Long trials), and (2) an asymmetric gait where preferred stride length and cadence are maintained but one step is shorter than preferred and the other is longer than preferred (i.e. the L Short/R Long trial). We then hypothesized that, during the choice trials when one leg was constrained to walk with a shorter/longer step than preferred while the contralateral leg was unconstrained, people would naturally adopt the less costly asymmetric walking patterns.

Figure 2. Hypotheses for changes in metabolic power across different symmetric and asymmetric stepping conditions.

Hypotheses suggesting the mechanisms underlying expected changes in metabolic power among different walking patterns with symmetric or asymmetric step lengths. Arrow thickness suggests expected cost due to centre of mass (COM) redirection or leg swing (thicker = more costly). Here, we hypothesize that the cost of each step is cumulative such that two symmetric short steps result in elevated cost due to the high cost of swinging each leg with a high cadence, while two symmetric long steps result in elevated cost due to the increased need to redirect the COM with each leg. With asymmetric steps, we suggest that a short step paired with a long step would similarly elevate cost due to high leg swing cost during one step and high COM redirection cost during the following step. Instead, pairing a short or long step with a preferred step will result in only incurring the elevated cost due to one leg with high swing costs or COM redirection costs, respectively.

Experiment 1: right step length constrained to be much shorter than preferred

Asymmetric walking patterns emerge when one leg is constrained to take a very short step.

Participants successfully executed the desired walking patterns when the right step was constrained to be shorter than preferred. We observed a significant main effect of trial on left step length (F(2,26) = 45.02, P < 0.001) when comparing the L Short/R Short, L Pref/R Short and L Choice/R Short trials. Post hoc analyses revealed that participants walked with significantly shorter left step lengths during the L Short/R Short trial as compared with the L Pref/R Short and L Choice/R Short trials (P < 0.001; Fig. 3A). There was no significant difference between the left step lengths during the L Pref/R Short and L Choice/R Short trials (P = 0.844, Fig. 3A). This revealed that, during the choice trial, most participants walked with asymmetric step lengths where the left step length remained similar to preferred despite the shortened right step length (Fig. 3B). We also observed a significant main effect of trial on right leg step length (F(2,26) = 5.15, P = 0.013) though pairwise comparisons only revealed a modestly longer right step length (~2 cm) in L Short/R Short compared with L Pref/R Short (P = 0.015).

Figure 3. Spatiotemporal, metabolic, and center of mass mechanics results from Experiment 1 trials where the right step was constrained to be short.

A, mean ± standard error left and right step lengths when at least one step was constrained to be short in Experiment 1. Grey open circles represent individual subject left step lengths during L Choice/R Short. B, between-subject mean ± standard error left and right step lengths across entire 5 min L Choice/R Short trial to demonstrate subtle decrease in the left step length toward preferred over time. The preferred step length – averaged between legs and across participants – is represented by the grey dashed line for reference. C, mean ± standard error metabolic power. The preferred metabolic power (averaged across participants) is represented by the grey dashed line for reference. D, mean ± standard error cadence. E, mean ± standard error left and right power performed on the centre of mass (COM) from left heel-strike to left heel-strike over time. F, mean ± standard error left and right, positive and negative work rates. Red and blue represent left and right leg values throughout, respectively. Letters (a–c) denote significant pairwise differences (P < 0.017) between trials after a significant main effect of trial in our rmANOVA (n = 14) was found. Here and in successive Figures, we only place letters over one of the two columns in each pairwise comparison to minimize clutter.

Asymmetric walking costs less energy than symmetric walking when one leg is constrained to take a very short step.

We also observed a significant main effect of trial on metabolic power (F(2,26) = 25.82, P < 0.001). Post hoc analyses revealed that metabolic power was significantly higher during the L Short/R Short trial as compared with the L Pref/R Short and L Choice/R Short trials (both P < 0.001; Fig. 3C). There was no significant difference in metabolic power between the L Pref/R Short and L Choice/R Short trials (P = 0.602; Fig. 3C). This demonstrated that the asymmetric walking pattern adopted by the participants in the choice trial cost significantly less energy than a symmetric walking pattern where both step lengths were shortened similarly.

Differences in cadence – not COM work rate – parallel differences in metabolic power among trials when one leg is constrained to take a very short step.

We observed a significant main effect of trial on cadence (F(2,26) = 42.66, P < 0.001; Fig. 3D). Post hoc analyses revealed that cadence was significantly higher during the L Short/R Short trial as compared with the L Pref/R Short and L Choice/R Short trials (P < 0.001). There was no significant difference in cadence between the L Pref/R Short and L Choice/R Short trials (P = 0.879). We also observed significant main effects of trial on right leg positive work rate and left leg negative work rate (F(2,26) = 5.40, P = 0.011 and F(2,26) = 4.38, P = 0.023, respectively; COM power traces shown in Fig. 3E, work rates shown in Fig. 3F). Post hoc analyses revealed that participants walked with significantly greater right leg positive work rate during L Choice/R Short than L Pref/R Short (P = 0.011) and L Short/R Short (P = 0.002). Participants also walked with significantly greater left leg negative work rate during L Choice/R Short compared with L Short/R Short (P = 0.007).

To explain these changes in COM work rate, we examined the COM velocities and GRFs. We focused on the AP and vertical components of these parameters since these are relevant to movement in the sagittal plane. We observed significant main effects of trial on the maximum AP, minimum AP, and maximum vertical COM velocities during left leg stance (F(2,26) = 43.17, P < 0.001; F(2,26) = 23.67, P < 0.001; F(2,26) = 28.43, P < 0.001, respectively) along with maximum AP, minimum AP, and minimum vertical COM velocities (F(2,26) = 24.23, P < 0.001; F(2,26) = 4.39, P = 0.023; F(2,26) = 27.45, P < 0.001, respectively) during right leg stance. Furthermore, we observed a significant main effect of trial on left peak braking (F(2,26) = 38.33, P < 0.001), left and right peak propulsive (F(2,26) = 7.22, P = 0.003; F(2,26) = 52.80, P < 0.001, respectively), right first peak of vertical (F(2,26) = 3.44, P = 0.047), and both left and right second peaks of vertical GRFs (F(2,26) = 16.22, P < 0.001; F(2,26) = 11.52, P < 0.001, respectively). Post hoc pairwise comparisons are omitted here for brevity but are shown in Fig. 4.

Figure 4. Ground reaction force and center of mass velocity results from Experiment 1 trials where the right step was constrained to be short.

A, mean ± standard error left and right anterior component of the ground reaction force (GRF) from left heel-strike to left heel-strike over time when at least one step was constrained to be short in Experiment 1. Bar graph represents mean ± standard error peak propulsive (dark red/blue) and peak braking (light red/blue) GRF. B, mean ± standard error left and right vertical component of the GRF from left heel-strike to left heel-strike over time. Bar graph represents mean ± standard error first (dark red/blue) and second peak (light red/blue) of the vertical GRF. The L Short/R Short trial resulted in attenuation of the second vertical peak in many subjects such that a subtle peak appears in the between-subject time series data though the mean peak is substantially lower. C, mean ± standard error left and right anterior centre of mass (COM) velocity from left heel-strike to left heel-strike over time. Bar graph represents mean ± standard error maximum anterior velocity (dark red/blue) and minimum anterior velocity (light red/blue) during left and right stance. D, mean ± standard error left and right vertical COM velocity from left heel-strike to left heel-strike over time. Bar graph represents mean ± standard error maximum vertical velocity (dark red/blue) and minimum vertical velocity (light red/blue) during left and right stance. Red and blue represent left and right leg values throughout, respectively. Letters (a–c) denote significant pairwise differences (P < 0.017) between trials after a significant main effect in our rmANOVA (n = 14) was found.

Experiment 1: right step length constrained to be much longer than preferred

Asymmetric walking patterns emerge when one leg is constrained to take a very long step.

Participants also successfully executed the desired walking patterns when the right step was constrained to be longer than preferred. We observed a significant main effect of trial on left step length (F(3,39) = 123.23, P < 0.001) when comparing the L Long/R Long, L Pref/R Long, L Short/R Long and L Choice/R Long trials. Post hoc analyses revealed that participants walked with significantly longer left step lengths during the L Long/R Long trial as compared with the L Pref/R Long, L Short/R Long and L Choice/R Long trials (P < 0.001; Fig. 5A). There was no significant difference between the left step lengths during the L Pref/R Long and L Choice/R Long trials (P = 0.838, Fig. 5A). Participants walked with significantly shorter left step lengths during the L Short/R Long trial than during all other trials (P < 0.001; Fig. 5A). This revealed that, during the choice trial, participants generally walked with asymmetric walking patterns where the left step length remained similar to preferred despite the lengthened right step length (Fig. 5B).

Figure 5. Spatiotemporal, metabolic, and center of mass mechanics results from Experiment 1 trials where the right step was constrained to be long.

A, mean ± standard error left and right step lengths when at least one step was constrained to be long in Experiment 1. Grey open circles represent individual subject left step lengths during L Choice/R Long. B, between-subject mean ± standard error left and right step lengths across entire 5 min L Choice/R Long trial to demonstrate subtle increase of the left step length toward preferred overtime. The preferred step length, averaged between legs and across participants is represented by the grey dashed line for reference. C, mean ± standard error metabolic power. The preferred metabolic power, averaged across participants is represented by the grey dashed line for reference. D, mean ± standard error cadence. E, mean ± standard error left and right power performed on the centre of mass (COM) from left heel-strike to left heel-strike over time. F, mean ± standard error left and right, positive and negative work rates. Red and blue represent left and right leg values throughout, respectively. Letters (d–g) denote significant pairwise differences (P < 0.012) between trials after a significant main effect in our rmANOVA (n = 14) was found.

Moderately asymmetric walking costs less energy than symmetric walking when one leg is constrained to take a very long step.

We again observed a significant main effect of trial on metabolic power (F(3,39) = 10.88, P < 0.001). Post hoc analyses revealed that metabolic power was significantly higher during the L Long/R Long trial than during the L Pref/R Long and L Choice/R Long trials (P < 0.001; Fig. 5C). There was no significant difference in metabolic power between the L Pref/R Long and L Choice/R Long trials (P = 0.883) nor between L Long/R Long and L Short/R Long (P = 0.567; Fig. 5C). This demonstrated that the moderately asymmetric walking pattern adopted by the participants in the choice trial cost significantly less energy than a symmetric walking pattern where both step lengths were lengthened similarly, though extremely asymmetric walking patterns appear to be particularly costly.

Differences in COM work rate – not cadence – parallel differences in metabolic power among trials when one leg is constrained to take a very long step.

We observed a significant main effect of trial on cadence (F(3,39) = 97.47, P < 0.001; Fig. 5D). Post hoc analyses revealed that cadence was significantly lower during the L Long/R Long trial than during the L Pref/R Long, L Short/R Long and L Choice/R Long trials (P < 0.001). There was no significant difference in cadence between the L Pref/R Long and L Choice/R Long trials (P = 0.975). Participants walked with significantly higher cadence during the L Short/R Long trial than during all other trials (P < 0.001; Fig. 5D).

We also observed significant main effects of trial on right leg positive work rate and left and right leg negative work rate (F(3,39) = 25.57, P < 0.001, F(3,39) = 61.37, P < 0.001, and F(3,39) = 11.86, P < 0.001, respectively; COM power curves are shown in Fig. 5E, COM work rates in Fig. 5F). Post hoc analyses revealed that participants walked with significantly greater right leg positive work rate during L Long/R Long than L Pref/R Long (P < 0.001), L Short/R Long (P < 0.001), and L Choice/R Long (P < 0.001). Participants also walked with significantly greater left leg negative work rate during L Long/R Long than L Pref/R Long (P < 0.001), L Short/R Long (P < 0.001), and L Choice/R Long (P < 0.001) but significantly less right leg negative work rate during L Long/R Long than L Pref/R Long (P = 0.005), L Short/R Long (P < 0.001) and L Choice/R Long (P = 0.009). Lastly, participants also walked with significantly greater right leg negative work rate during L Short/R Long than L Pref/R Long (P = 0.007) though did not reach a significant difference with L Choice/R Long (P = 0.019).

To explain the differences in COM work rate observed across trials, we examined the contributing COM velocities and GRFs. We observed significant main effects of trial on the maximum AP, minimum AP, maximum vertical, and minimum vertical COM velocities during left leg stance (F(3,39) = 118.36, P < 0.001; F(3,39) = 31.12, P < 0.001; F(3,39) = 43.39, P < 0.001; F(3,39) = 3.13, P = 0.036, respectively) along with maximum AP, maximum vertical, and minimum vertical COM velocities (F(3,39) = 17.43, P < 0.001; F(3,39) = 6.90, P = 0.001; F(3,39) = 44.81, P < 0.001, respectively) during right leg stance. Furthermore, we observed a significant main effect of trial on left and right peak braking (F(3,39) = 102.91, P < 0.001; F(3,39) = 14.29, P < 0.001, respectively), right peak propulsive (F(3,39) = 89.91, P < 0.001), left and right first peak of vertical (F(3,39) = 7.35, P = 0.001; F(3,39) = 6.53, P = 0.001, respectively), and both left and right second peaks of vertical GRFs (F(3,39) = 5.19, P = 0.004; F(3,39) = 73.71, P < 0.001, respectively). Post hoc pairwise comparisons are omitted here for brevity but shown in Fig. 6.

Figure 6. Ground reaction force and center of mass velocity results from Experiment 1 trials where the right step was constrained to be long.

A, mean ± standard error left and right anterior component of the ground reaction force (GRF) from left heel-strike to left heel-strike over time when at least one step was constrained to be long in Experiment 1. Bar graph represents mean ± standard error peak propulsive (dark red/blue) and peak braking (light red/blue) GRF. B, mean ± standard error left and right vertical component of the GRF from left heel-strike to left heel-strike over time. Bar graph represents mean ± standard error first (dark red/blue) and second peak (light red/blue) of the vertical GRF. C, mean ± standard error left and right anterior centre of mass (COM) velocity from left heel-strike to left heel-strike over time. Bar graph represents mean ± standard error maximum anterior velocity (dark red/blue) and minimum anterior velocity (light red/blue) during left and right stance. D, mean ± standard error left and right vertical COM velocity from left heel-strike to left heel-strike over time. Bar graph represents mean ± standard error maximum vertical velocity (dark red/blue) and minimum vertical velocity (light red/blue) during left and right stance. Red and blue represent left and right leg values throughout, respectively. Letters (d–g) denote significant pairwise differences (P < 0.012) between trials after a significant main effect in our rmANOVA (n = 14) was found.

Experiment 2: right step length constrained to be mildly shorter than preferred

Some people prefer asymmetric walking patterns when one leg is constrained to take a mildly short step.

In Experiment 2, we enforced a smaller constraint that more closely approximated magnitudes of step length asymmetry that are commonly observed in clinical populations. Participants again successfully executed the desired walking patterns when the right step was constrained to be shorter than preferred. We observed a significant main effect of trial on left step length (F(2,26) = 40.14, P < 0.001) when comparing the L Short/R Short, L Pref/R Short and L Choice/R Short trials. Post hoc analyses revealed that participants walked with significantly shorter left step lengths during the L Short/R Short trial as compared with the L Pref/R Short and L Choice/R Short trials (P ≤ 0.001; Fig. 7A) but also significantly shorter steps during L Choice/R Short as compared with L Pref/R Short (P = 0.003; Fig. 7A). This revealed that, during the choice trial with more mild constraints, many participants again walked with asymmetric walking patterns, though some participants shortened both step lengths to maintain a relatively symmetric gait (Fig. 7B). We also observed a significant main effect of trial on right leg step length (F(2,26) = 3.51, P = 0.45) though no significant pairwise differences between trials. Due to this heterogeneity in response during the choice trial and the more mild step length constraints, we did not observe a significant main effect of trial on metabolic power (P = 0.104; Fig. 7C). We did also observe a significant main effect of trial on right leg step length (F(2,26) = 3.89, P = 0.033) though pairwise comparisons did not reveal significant differences between conditions.

Figure 7. Spatiotemporal, metabolic, and center of mass mechanics results from Experiment 2 trials where the right step was constrained to be short.

A, mean ± standard error left and right step lengths when at least one step was constrained to be short in Experiment 2. Grey open circles represent individual subject left step lengths during L Choice/R Short. B, between-subject mean ± standard error left and right step lengths across entire 5 min L Choice/R Short trial. The preferred step length, averaged between legs and across participants is represented by the grey dashed line for reference. C, mean ± standard error metabolic power. The preferred metabolic power, averaged across participants is represented by the grey dashed line for reference. D, mean ± standard error cadence. E, mean ± standard error left and right power performed on the centre of mass (COM) from left heel-strike to left heel-strike over time. F, mean ± standard error left and right, positive and negative work rates. Red and blue represent left and right leg values throughout, respectively. Letters (h–j) denote significant pairwise differences (P < 0.017) between trials after a significant main effect in our rmANOVA (n = 14) was found.

Similar to Experiment 1, we observed a significant main effect of trial on cadence (F(2,26) = 26.46, P < 0.001; Fig. 7D). Post hoc analyses revealed that cadence was significantly higher during the L Short/R Short trial than during the L Pref/R Short and L Choice/R Short trials (P ≤ 0.003); however, cadence was also significantly higher during L Choice/R Short than L Pref/R Short (P = 0.001).

Also similar to Experiment 1, we observed significant main effects of trial on right leg positive work rate and left leg negative work rate (F(2,26) = 7.02, P = 0.004 and F(2,26) = 9.10, P = 0.001, respectively; COM power curves shown in Fig. 7E and COM work rates in Fig. 7F). Post hoc analyses revealed that participants walked with significantly less right leg positive work rate during L Short/R Short than L Pref/R Short (P = 0.002) and L Choice/R Short (P = 0.004). Participants also walked with significantly less left leg negative work rate during L Short/R Short compared with L Pref/R Short (P < 0.001) and L Choice/R Short (P = 0.008). There was no significant difference between L Pref/R Short and L Choice/R Short in either right positive or left negative work rates (P = 0.612 and P = 0.468, respectively).

We also observed significant main effects of trial on the maximum AP, minimum AP, and maximum vertical COM velocities during left leg stance (F(2,26) = 44.27, P < 0.001; F(2,26) = 11.81, P < 0.001; F(2,26) = 14.65, P < 0.001, respectively) along with maximum AP and minimum vertical COM velocities (F(2,26) = 6.43, P = 0.005; F(2,26) = 17.73, P < 0.001, respectively) during right leg stance. Furthermore, we observed a significant main effect of trial on left peak braking and right peak propulsive GRFs (F(2,26) = 31.17, P < 0.001; F(2,26) = 27.80, P < 0.001, respectively). Post hoc pairwise comparisons are shown in Fig. 8.

Figure 8. Ground reaction force and center of mass velocity results from Experiment 2 trials where the right step was constrained to be short.

A, mean ± standard error left and right anterior component of the ground reaction force (GRF) from left heel-strike to left heel-strike overtime when at least one step was constrained to be short in Experiment 1. Bar graph represents mean ± standard error peak propulsive (dark red/blue) and peak braking (light red/blue) GRF. B, mean ± standard error left and right vertical component of the GRF from left heel-strike to left heel-strike over time. Bar graph represents mean ± standard error first (dark red/blue) and second peak (light red/blue) of the vertical GRF. C, mean ± standard error left and right anterior centre of mass (COM) velocity from left heel-strike to left heel-strike over time. Bar graph represents mean ± standard error maximum anterior velocity (dark red/blue) and minimum anterior velocity (light red/blue) during left and right stance. D, mean ± standard error left and right vertical COM velocity from left heel-strike to left heel-strike over time. Bar graph represents mean ± standard error maximum vertical velocity (dark red/blue) and minimum vertical velocity (light red/blue) during left and right stance. Red and blue represent left and right leg values throughout, respectively. Letters (h–j) denote significant pairwise differences (P < 0.017) between trials after a significant main effect in our rmANOVA (n = 14) was found.

Experiments 1 and 2: linear regressions to predict changes in metabolic power across trials

We were additionally interested in understanding the contributions of leg swing and the redirection of the COM to changes in metabolic power across trials. Our two separate linear regression models combined data from Experiments 1 and 2 to assess whether cadence and COM work rate were significant predictors of changes in metabolic power associated with different step lengths/step length asymmetries.

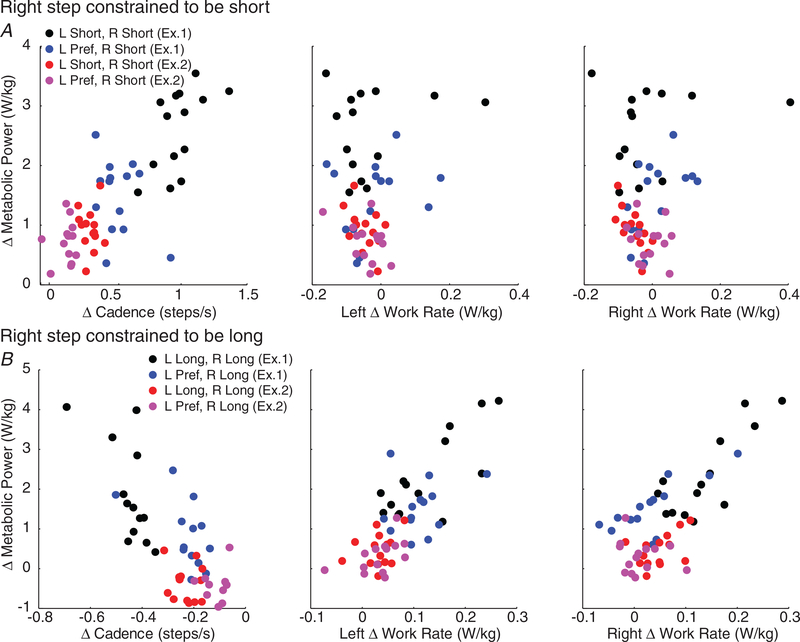
The first linear regression focused on shorter step lengths and included data from the L Short/R Short and L Pref/R Short trials from both Experiments 1 and 2. Here, we found that only the change in cadence (relative to Preferred) was a significant predictor of change in metabolic power relative to Preferred (Fig. 9A; β = 0.795, P < 0.001).

Figure 9. Relationships between changes (relative to walking with preferred step lengths) in metabolic power and changes in cadence, left leg work rate, and right leg work rate in Experiments 1 and 2.

The difference in cadence, left and right work rate from preferred plotted against the difference in metabolic power from preferred for when at least one step was constrained to be short in Experiment 1 and 2 (A) and at least one step was constrained to be long in Experiment 1 and 2 (B). We did not include L Short/R Long to maintain parallel models between short and long step length constraints. Two separate linear regression models demonstrated that changes in cadence (used here as a surrogate for leg swing) was primarily responsible for elevated metabolic power when one leg was constrained to be short while left and right work rate (COM redirection) were primarily responsible for elevated metabolic power when one leg was constrained to be long.

The second linear regression focused on longer step lengths and included data from the L Long/R Long and L Pref/R Long trials from both Experiments 1 and 2. Here, we found that the changes in positive left leg work rate and positive right leg work rate (relative to Preferred) as well as L Pref/R Long trial from Experiment 1 (dummy variable) were significant predictors of changes in metabolic power relative to Preferred (β = 0.466, P < 0.001; β = 0.549, P < 0.001; β = 0.167, P = 0.021, respectively).

Experiment 1: a quadratic fit to estimate a metabolic optimum with asymmetric steps

As a final post hoc analysis, we report a significant quadratic fit relating step length asymmetry to changes in metabolic power across all trials in Experiment 1 (Fig. 10; P < 0.001, R² = 0.342). Interestingly, the absolute step length asymmetry value predicting optimal metabolic power using this model fit is approximately 0.22 which appears to be a reasonable approximation of the average asymmetries during L Choice/R Short and L Choice/R Long (0.25 and 0.18, respectively). These data further suggest that, when one leg is constrained to take either short or long steps, an asymmetric gait is energetically optimal.

Figure 10. Relationship between change in metabolic power (relative to walking with preferred step lengths) and step length asymmetry.

The absolute value of step length asymmetry plotted against the difference in metabolic power from preferred when at least one leg is constrained to be either short or long in Experiment 1. A quadratic fit predicts an absolute asymmetry value of approximately 0.22 as the most economical when one leg is constrained to be short or long. Values for the choice trials are made larger to highlight the patterns that participants adopted when one leg was allowed to move freely while the other was constrained.

Discussion

In this study, we showed that healthy adults often adopt asymmetric walking patterns when one leg is constrained, despite the preserved ability to walk symmetrically. In Experiment 1, we observed that some asymmetric walking patterns cost less energy than symmetric walking patterns when one leg was constrained to take a substantially shorter or longer step than preferred. Participants then tended to naturally adopt these more economical asymmetric patterns when allowed to step freely with the contralateral limb. We observed similar results in Experiment 2 where the step length constraints were more subtle, although some participants showed preferences for symmetric steps. These findings underscore the flexible nature of human gait symmetry and show that the seemingly inherent preference for symmetric gait often does not persist when one leg is constrained.

Energy optimization is thought to play an important role in shaping human walking patterns (Alexander, 1989; Donelan et al., 2001; Ralston, 1958; Selinger et al., 2015; Zarrugh et al., 1974). Our findings and others suggest that the symmetry of our walking patterns is also probably influenced by energy optimization. Earlier work has shown that symmetry is energetically optimal in unconstrained, natural human gait (Ellis et al., 2013) but not in other more unusual situations (Roemmich et al., 2019; Sanchez et al., 2019). Here, our findings suggest that energy optimization may play an important role in shifting the preference from a symmetric gait to an asymmetric gait when one leg is constrained (as often occurs after unilateral damage to the nervous or musculoskeletal systems), especially when this constraint is dramatic.

In Experiment 1, we first mapped the cost landscapes (i.e. metabolic power associated with different walking patterns) when one leg was constrained to take a markedly shorter or longer step than preferred. Previous studies have demonstrated a U-shaped relationship between symmetric stride frequency and metabolic cost such that humans’ preferred stride frequency minimizes metabolic cost while slower or faster frequencies increase cost (Minetti et al., 1995). Our data largely agree with this such that symmetric short or long steps (i.e. largest deviation from preferred stride frequency) resulted in the highest metabolic cost while asymmetric step lengths with one step length remaining preferred (i.e. less deviation from preferred stride frequency) resulted in a less elevated metabolic cost.

However, the L Short/R Long condition constrained participants to extreme asymmetry but also preferred stride frequency/cadence while ultimately resulting in a similarly high metabolic cost to symmetric short or long steps. We found that maintaining one’s preferred step length with the contralateral leg (i.e. adopting an asymmetric gait where one leg took a preferred step and the other took a shortened/lengthened step) cost significantly less energy than preserving a symmetric gait where both steps were either shorter or longer than preferred or when walking with an excessive asymmetry. This is because walking with shortened steps causes an elevated cost of swinging the legs due to the increased cadence (Doke et al., 2005; Minetti et al., 1995). Leg swing at a high cadence is particularly costly as it requires a large amount of internal work performed by muscles to rapidly accelerate the limbs with respect to the COM while overcoming limb friction (Cavagna and Kaneko, 1977; Minetti et al., 2020). Walking with lengthened steps causes an elevated cost associated with redirecting the body’s COM (Adamczyk and Kuo, 2009; Cavagna and Franzetti, 1986; Donelan et al., 2002; Kuo et al., 2005). In sum, it is more economical to walk asymmetrically with one natural step and one unnatural step than symmetrically with two unnatural steps. In this way, energy can be conserved by minimizing internal work while still allowing potential energy to be converted in to positive work applied to the COM during push-off (Cavagna et al., 2002). We observed similar findings in Experiment 2 where the unilateral constraint was less dramatic, although the differences in metabolic power between the conditions were unsurprisingly not as stark as in Experiment 1.

In both Experiments 1 and 2, we concluded the testing sessions with choice trials where we constrained the step length of one leg to be shorter or longer than preferred and allowed the participants to step freely with the unconstrained contralateral leg. In Experiment 1 – where the step length constraint was more severe – we found that participants nearly unanimously adopted an asymmetric gait pattern. However, the Experiment 2 findings were more mixed: some participants adopted an asymmetric gait where one leg maintained a preferred step length while others shortened the unconstrained leg to preserve a symmetric gait. The differences observed in the choice trials between Experiments 1 and 2 suggest that energy optimization may have a stronger influence on shifting the preference toward an asymmetric gait pattern when one leg is markedly constrained and the energy savings obtained by walking asymmetrically are larger. This may be explained in part by previous findings demonstrating little effect of small velocity fluctuations (in our case to the COM) on the cost of walking, likely due to the human propensity to frequently change speed over ground (Minetti et al., 2013, 2001).

It is important to clarify that we cannot confirm that a preferred step length paired with a short or long step length elicits the absolute minimum metabolic power, as we did not assess walking patterns with intermediate step lengths. Consider that Figs 3B and 5B demonstrate a subtle change in the unconstrained step length across the 5 min trial, with both choice trials revealing that the unconstrained limb gradually drifts toward a more symmetric gait. While it appears that the participants tended to plateau at their preferred step length over the final 2 min of the choice trials, a longer trial may reveal a shift toward a smaller asymmetry. To further investigate this issue, we performed a quadratic regression comparing absolute step length asymmetry to metabolic power across all conditions in Experiment 1 (where participants walked with a large range of step length asymmetries). This analysis revealed that, if one step is constrained to be short or long, an asymmetry that corresponds to keeping the unconstrained step at the preferred length is approximately associated with the minimum metabolic power. Therefore, our data suggest that maintaining a preferred step length when the contralateral leg is constrained may indeed minimize energy expenditure. This is further supported by prior work that measured energy expenditure across a variety of walking patterns with symmetric and asymmetric step times (Ellis et al., 2013).

Many clinical conditions – including stroke, Parkinson’s disease, cerebral palsy and lower limb amputation – result in asymmetric walking patterns (Fabrica et al., 2019; Gillette, 1966; Knutsson, 1981, 1972; Lloyd et al., 2010; Olney and Richards, 1996). We did not study clinical populations in this experiment but suggest that our findings may have relevance for determining how people develop preferences for asymmetric walking patterns after damage to the nervous or musculoskeletal systems. For example, we have previously shown that persons post-stroke walk with more symmetric step lengths when doing so costs less energy than walking with asymmetric step lengths (Roemmich et al., 2019). However, it is also clear that energy optimization is not the sole factor that shapes gait preferences after stroke (Sanchez and Finley, 2018). It is likely that other objectives (e.g. improving stability, avoiding pain) play important roles in locomotor control in stroke and other clinical populations. This is also supported by our Experiment 2 findings, as not all participants naturally adopted an economical asymmetric walking pattern during the choice trial. Understanding the factors that drive individual patients to walk in particular ways will likely be crucial to developing improved, patient-specific rehabilitation approaches that align training goals with objectives of the locomotor system.

We recognize several limitations of this current study. First, in Experiment 1, we constrained step lengths to 50% shorter or longer than preferred while maintaining a constant walking speed of 1.25 m/s. Frequently, asymmetries observed in clinical populations occur with smaller magnitudes and at slower walking speeds. We designed Experiment 1 to ensure large differences among trials and allow clear trends which we might find at this speed and with these asymmetries. We designed Experiment 2 to more closely approximate magnitudes of asymmetry that are observed in patient populations, though even these asymmetry magnitudes are rather large. This study was designed to tease out symmetry preferences when one leg is constrained at a fixed speed, such that these results may not be entirely generalizable to over-ground walking. Without a constant treadmill-imposed speed constraint such as we used, humans may prefer to change speeds to maintain symmetric step lengths in the presence of a unilateral step length constraint. We also designed these experiments to explore only step length asymmetry because we have previously found this parameter to be easy to control with visual feedback and useful for studying human gait preferences (Roemmich et al., 2019); studies of other kinematic or kinetic gait parameters may show different results. We note that all conditions with modified step lengths, whether symmetric or asymmetric, were more metabolically costly than preferred for our participants. This may be, at least in part, because this study only included healthy adults. The heterogeneous motor deficits that lead to gait asymmetry in clinical populations likely have different effects on metabolic cost, underscoring the need to study the objectives of locomotor control on an individual patient basis.

Conclusions

The human preference for a symmetric walking pattern often disappears when one leg is constrained during fixed-speed treadmill walking. Here, we showed that many healthy adults adopted asymmetric walking patterns when one leg was constrained rather than preserving a symmetric walking pattern by matching the movement of the unconstrained leg to that of the constrained leg. While all walking patterns were more costly than symmetric walking with bilateral preferred step lengths, we observed that asymmetric walking patterns cost less energy than symmetric walking patterns when one leg was constrained, and this coincided with the shift in preference from a symmetric gait to asymmetric gait, especially when the constraint was severe. These findings show that the preference for symmetric gait often does not persist when one leg is constrained and may provide insight into why some people develop preferences for asymmetric walking patterns after experiencing damage to the nervous or musculoskeletal systems.

Key points.

• We hypothesized that minimization of metabolic power could drive people to walk asymmetrically when one leg is constrained

• We studied healthy young adults and independently constrained one or both step lengths to be markedly shorter or longer than preferred using visual feedback

• When one leg was constrained to take a shorter or longer step than preferred, asymmetric walking patterns were less metabolically costly than symmetric walking patterns

• When one leg was constrained to take a shorter or longer step than preferred and the other leg was allowed to move freely, most participants naturally adopted an asymmetric gait

• People may prefer to walk asymmetrically to minimize metabolic power when the function of one leg is constrained during fixed-speed treadmill walking

Biography

Michael G. Browne has his MS and PhD from the Joint Department of Biomedical Engineering at UNC Chapel Hill and NC State University. During that training Michael designed biofeedback systems to promote ‘improved’ walking mechanics for our ageing population while striving to understand how changes were attained from whole-body, joint and muscle perspectives. In transitioning to his current postdoctoral position, Michael aims to better understand how higher-level objectives (e.g. energetic cost, balance control, external tasks) govern how people choose to walk. Ultimately, he hopes to develop devices and techniques for walking rehabilitation which leverage motor learning principles to aid in optimizing these objectives.