Discrepancies in metabolomic biomarker identification from patient-derived lung cancer revealed by combined variation in data pre-treatment and imputation methods

Abstract

Introduction:

The identification of metabolomic biomarkers predictive of cancer patient response to therapy and of disease stage has been pursued as a “holy grail” of modern oncology, relying on the metabolic dysfunction that characterizes cancer progression. In spite of the evaluation of many candidate biomarkers, however, determination of a consistent set with practical clinical utility has proven elusive.

Objective:

In this study, we systematically examine the combined role of data pre-treatment and imputation methods on the performance of multivariate data analysis methods and their identification of potential biomarkers.

Methods:

Uniquely, we are able to systematically evaluate both unsupervised and supervised methods with a metabolomic data set obtained from patient-derived lung cancer core biopsies with true missing values. Eight pre-treatment methods, ten imputation methods, and two data analysis methods were applied in combination.

Results:

The combined choice of pre-treatment and imputation methods is critical in the definition of candidate biomarkers, with deficient or inappropriate selection of these methods leading to inconsistent results, and with important biomarkers either being overlooked or reported as a false positive. The log transformation appeared to normalize the original tumor data most effectively, but the performance of the imputation applied after the transformation was highly dependent on the characteristics of the data set.

Conclusion:

The combined choice of pre-treatment and imputation methods may need careful evaluation prior to metabolomic data analysis of human tumors, in order to enable consistent identification of potential biomarkers predictive of response to therapy and of disease stage.

1. INTRODUCTION

Metabolomics has emerged as an important technique of biomarker discovery (Patel, Ahmed 2015), giving insight into the rate of chemical reactions occurring within cells and providing a closer representation of phenotype compared to other omics technologies (Holmes, Wilson, Nicholson 2008). Yet the identification of viable cancer metabolomic-derived biomarkers has proven frustratingly elusive, and especially so in regards to lung cancer. Multiple studies have evaluated biomarker candidates obtained from patient samples, including plasma, sputum, and urine, with results struggling to provide a consistent set of potential clinical utility (Bamji-Stocke, van Berkel, Miller, Frieboes 2018). Even when accounting for differences expected due to tissue origins, biomarker candidates often do not match across different studies.

Nuanced data analysis is a critical component of interpreting omics data (Considine, Thomas, Boulesteix, Khashan, Kenny 2017). Omics data sets are complex and specific, warranting the investigation of the most appropriate method of analysis for particular experiments. Currently, there is no ‘gold standard’ analytical pipeline for most omics fields (Hasin, Seldin, Lusis 2017). This reduces the reproducibility of omics studies, especially when studying disease states in human patients due to the large number of confounding variables. In particular, data pre-treatment is a necessary step to normalize data before statistical analysis is performed (Brereton 2006), and is often under-emphasized in metabolomics studies. Sample volume differences, different feature abundances and heteroscedasticity can cause misinterpretations of biological data if an inadequate pre-treatment method is selected (Jan Walach 2018). Consequently, metabolomics studies with human patients often reach different conclusions, limiting their clinical insight. Possibly even worse, improperly planned experiments or statistical analyses can result in false positives which can yield misleading conclusions. This is partially due to the lack of comprehensive data analysis protocols, with many studies using different techniques.

Although metabolomics approaches are not as high-throughput as other omics technologies such as genomics, metabolomics can generate large data sets that are difficult or impossible to interpret without proper data analysis. As part of the metabolomics standards initiative (MSI) (Members, Sansone, Fan, Goodacre, Griffin, Hardy, Kaddurah-Daouk et al. 2007), the minimum reporting standards for data analysis in metabolomics was proposed in 2007 (Goodacre, Broadhurst, Smilde, Kristal, Baker, Beger, Bessant et al. 2007). However, in 2017 a call for a revision to the MSI was published, mentioning that the minimum reporting standards are often not followed (Spicer, Salek, Steinbeck 2017). In a critical review of the reporting of metabolomics data analysis, Considine et al. (Considine, Thomas, Boulesteix, Khashan, Kenny 2017) found that the pretreatment phase was consistently the most underreported step of the analytical pipeline in studies related to disease prediction from serum metabolomics. For example, 89% of studies failed to mention missing values or how they were handled (Considine, Thomas, Boulesteix, Khashan, Kenny 2017). Missing data reveals a potential for bias, depending on the mechanism causing the missing data and the analytical methods applied (Sterne, White, Carlin, Spratt, Royston, Kenward, Wood et al. 2009). Failure to carefully plan missing value substitutions may cause large discrepancies during both supervised and unsupervised analysis methods (Gromski, Xu, Kotze, Correa, Ellis, Armitage, Turner et al. 2014). van den Berg et al. found that different data pre-treatment methods (scaling, centering and transformations) greatly affected the outcome of principal component analysis (PCA) in terms of score plot clustering and metabolite rankings based on loadings (van den Berg, Hoefsloot, Westerhuis, Smilde, van der Werf 2006). Gromski et al. (Gromski, Xu, Kotze, Correa, Ellis, Armitage, Turner et al. 2014) reported that different methods of handling missing data had a significant impact on group clustering in supervised and unsupervised analysis methods. The random forest (RF) imputation technique and k-nearest neighbor (kNN) performed best in supervised methods of principal component linear discriminant analysis (PC-LDA) and partial least squares-discriminant analysis (PLS-DA), while mean and zero substitutions generally performed the worst (Gromski, Xu, Kotze, Correa, Ellis, Armitage, Turner et al. 2014). Different methods of scaling or transformations were not considered, as only autoscaling was used. Sim et al. (Sim, Lee, Kwon 2015) found that the performance of different imputation methods changed depending on the type of data set, which infers that studies on imputation methods are only applicable to specific types of data sets. Additionally, they found that different missing value characteristics affected imputation methods to different degrees. For example, the ‘hot deck’ method was more accurate than ‘group mean imputation’ between 16% and 24% missing values but became less accurate in a non-linear fashion as the percentage of missing values increased.

Here, we evaluate discrepancies in metabolomic biomarker identification from patient-derived lung cancer core biopsies. Patient response to chemotherapy categorized based on the RECIST guideline (Eisenhauer, Therasse, Bogaerts, Schwartz, Sargent, Ford, Dancey et al. 2009) as well as disease stage were evaluated. Due to the nature of human patient tissue collection and analysis, biological replicates are sometimes not possible and sample volume cannot be controlled. Further, mass spectrometry (MS) data sets typically contain approximately 10-20% missing values (Considine, Thomas, Boulesteix, Khashan, Kenny 2017; Gromski, Xu, Kotze, Correa, Ellis, Armitage, Turner et al. 2014) for various technical or biological reasons. This is an issue because statistical analysis techniques, including PCA and PLS-DA, typically require complete data sets (Tang, Ishwaran 2017). Unlike other studies exclusively focused on either data pre-treatment methods or missing value substitutions (Godzien, Ciborowski, Angulo, Barbas 2013; Gromski, Xu, Kotze, Correa, Ellis, Armitage, Turner et al. 2014; Sim, Lee, Kwon 2015; van den Berg, Hoefsloot, Westerhuis, Smilde, van der Werf 2006), the unique data set in this study enables testing pre-treatment methods on a novel source of metabolomics data with true missing values, obtained from patient-derived tumor samples. We are therefore able to systematically investigate how the combination of different data pre-treatment and imputation methods changes the outcomes and biomarker selection from both unsupervised (PCA) and supervised (PLS-DA) multivariate data analysis.

2. MATERIAL AND METHODS

2.1. Raw Data Processing

De-identified metabolomic data were previously obtained as part of a separate lung cancer patient study (Miller, Yin, Lynch, Bockhorst, Smith, Hu, Zhang et al. 2021). In that study, after tissue homogenization and metabolite extraction from patient tumor core biopsies, samples were randomly analyzed on a Thermo Q Exactive HF Hybrid Quadrupole-Orbitrap Mass Spectrometer coupled with a Thermo DIONEX UltiMate 3000 HPLC system (Thermo Fisher Scientific, Waltham, MA, USA) equipped with a hydrophilic interaction chromatography (HILIC) column and a reversed phase chromatography (RPC) column configured to create a parallel 2DLC-MS system.(Klavins, Drexler, Hann, Koellensperger 2014). For metabolite identification, one unlabeled sample in each group was analyzed by 2DLC-MS/MS in positive mode (+) and negative mode (−) to acquire MS/MS spectra at three collision energies (20, 40 and 60 eV). For 2DLC-MS data analysis, XCMS software was used for spectrum deconvolution (Tautenhahn, Patti, Rinehart, Siuzdak 2012) and MetSign software was used for metabolite identification, cross-sample peak list alignment, normalization, and statistical analysis (Wei, Shi, Kim, S, Patrick, Binkley, Kong et al. 2014; Wei, Shi, Kim, Zhang, Patrick, Binkley, McClain et al. 2012; Wei, Sun, Shi, Koo, Wang, Zhang, Yin et al. 2011). 2DLC-MS/MS data of unlabeled samples were first matched to our in-house database that has parent ion m/z, MS/MS spectra, and retention time of authentic standards (MSI Level 1 identification). Data without a match were analyzed (MSI Level 2 identification) using Compound Discoverer software v2.0 (Thermo Fisher Scientific, Inc., Germany).

2.2. Common metabolites

A common set of metabolites was chosen among the 36 samples. If a metabolite was detected in at least 31 samples, it was considered a “common” metabolite. A threshold of 31 was chosen because with a higher threshold, some metabolites would not have sufficiently detected occurrences to be imputed, while a lower threshold would exclude some metabolites that could be imputed. This resulted in a set of 36 common metabolites. MS data from positive and negative alignment tables were combined into a single data set by choosing the data set (positive or negative) that contained the greater number of occurrences among the 36 samples.

2.3. Software Packages

Data analysis methods were conducted in R version 4.0.2, while PCAtoTree software (Worley, Halouska, Powers 2013) was used to quantify score plots. Following R packages were employed for statistical analysis and data visualization: mice package version 3.9.0 for CART, RF, and PMM imputation (Zhang 2016); stats package in base R for PCA, using the prcomp function; VIM version 6.1.0 package for kNN imputation; pcaMethods version 1.80.0 package for BPCA and PPCA imputation; PLS-DA with mdatools version 0.11.2 package (Kucheryavskiy 2020).

2.4. Pre-Treatment Methods for Data Normalization

A data frame was created to contain the raw data with the 36 samples as rows and the 36 metabolite MS peak areas (intensities) as columns. Three general types of pre-treatment methods were applied, with representative methods chosen from each type. Details on the formulations of these methods along with their characteristics can be found in van den Berg et al. (van den Berg, Hoefsloot, Westerhuis, Smilde, van der Werf 2006). Briefly, centering methods transform values to fluctuations centered at zero instead of the mean of the values, adjusting for variation in the offset between low and high values (Bro, Smilde 2003,), Scaling methods divide each variable by a unique scaling factor, adjusting for variation in fold differences between values by converting the data into differences relative to this factor. One type of scaling methods uses a size measure, e.g., the mean, as a factor (including level scaling (van den Berg, Hoefsloot, Westerhuis, Smilde, van der Werf 2006)), while another type uses a measure of the data dispersion, e.g., standard deviation (including range scaling (Smilde, van der Werf, Bijlsma, van der Werff-van der Vat, Jellema 2005), vast scaling (Keun, Ebbels, Antti, Bollard, Beckonert, Holmes, Lindon et al. 2003,), autoscaling (Jackson 1991.), and pareto scaling (Eriksson, Johansson, Kettaneh-Wold, Wold 1999)). Lastly, transformations are nonlinear conversions of the data that convert multiplicative relations into additive relations and correct for heteroscedasticity (Kvalheim, Brakstad, Liang 1994). Transformations typically used with biological data include the log transform and the power transform (such as a square root or arcsine transform). Tukey’s Ladder of Powers provides a means to systematically scan across various power transformations (Tukey 1977), as does the slightly more complex Box-Cox transform (Box 1964).

2.5. Imputation Methods to Handle Missing Values

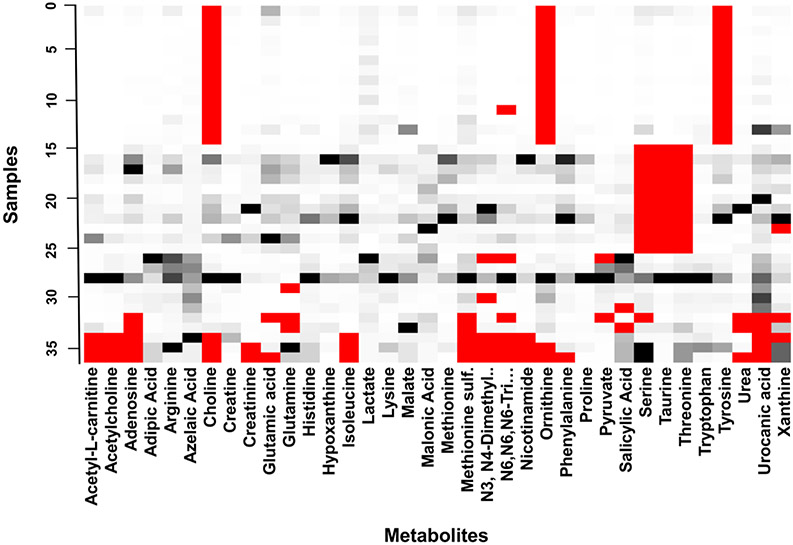
The data set analyzed in this study contains a complex mixture of different types of missing data. Based on Figure 1, some data appears to be missing not at random (MNAR) while some is missing at random (MAR). It is clear that certain metabolites were not detected in the control sample when certain batches of samples were analyzed, but there are other instances of seemingly random missing values. Therefore, we could not operate under the assumption that all missing values are either MNAR, MAR, or MCAR (missing completely at random). However, the data set is likely representative of other metabolomics data sets derived from human patient specimens, and thus provides a real-world example of how different pre-treatment and imputation methods applied in this study may affect the results of a statistical analysis.

Figure 1. Original patient tumor core biopsy metabolomic data.

MS peak areas (intensities, black to white) of 36 analyzed samples of human lung cancer tissue. Red cells indicate missing values. The data set contains approximately 10% missing values, which is typical for MS data sets (Considine, Thomas, Boulesteix, Khashan, Kenny 2017; Gromski, Xu, Kotze, Correa, Ellis, Armitage, Turner et al. 2014). Color figure online.

Ten different methods of handling missing values were evaluated, as summarized in Supplemental Table 1. The imputation methods were chosen to be compatible with the data analysis methods (described further below). Since MS peak areas are represented by continuous values, only methods appropriate for imputing continuous data were evaluated. Perhaps the simplest method of dealing with missing data (besides ignoring features with missing values) is to replace them with constants (Somasundaram 2011). Here, we focus on the zero, mean, median, and ½ minimum (half-min) constant substitution methods, which simply replace all missing values with zero, the mean, the median, or half the minimum value of each feature, respectively. We also considered more sophisticated methods of imputation (described in Supplement) such as multiple imputation by chained equations (MICE), including: predictive mean matching (PMM), random forest (RF) and classification and regression trees (CART). These multiple imputation methods were performed with the R package mice and seeded with a value of ‘1234’ to allow for reproducibility. k nearest neighbor (kNN) imputation was performed with the VIM package with number of nearest neighbors set to 10 and the weights for the variables for the distance calculation based on variable importance from random forest regression. Bayesian principal component analysis imputation (BPCA) and probabilistic principal component analysis (PPCA) were performed with the pcaMethods package seeded with a value of ‘1234’ to allow for reproducibility. “maxSteps” was set to 10 for BPCA and “maxIterations” was set to 1000 for PPCA.

2.6. Data Analysis Methods

Two commonly used multivariate statistical analysis methods were chosen to quantitatively evaluate the variation in the pretreatment and imputation methods.

2.6.1. Principal Component Analysis

PCA is useful for visualization and feature extraction and is commonly used as a first step in the analytical pipeline to check for clustering, separation, and outliers among groups of samples (Giuliani 2017). Although a variety of unsupervised analysis techniques exist, we chose PCA due to its ability to reduce the dimensionality of the feature space with minimal information loss. This is convenient considering that metabolomics data sets often involve a large number of predictor variables. PCA relies on an eigenvector decomposition of the covariance matrix of X,cov(X) = X^TX/n – 1, where X (nxN) is the data matrix containing samples and features. If only the first A (A < N) dimension of scores is needed, PCA decomposes X into the sum of the outer products of score vectors t_i and loadings vectors p_i plus a residual matrix E (Cho, Kim, Jeong, Park, Miller, Ziegler, Jones 2008):

$$\mathbf{X}={\mathbf{t}}_1{\mathbf{p}}_1^T+{\mathbf{t}}_2{\mathbf{p}}_2^T+\cdots +{\mathbf{t}}_A{\mathbf{p}}_A^T+\mathbf{E}={\mathbf{TP}}^T+\mathbf{E}$$ Equation [1]

The contribution of individual features in each principal component dimension is accounted for by the loading vectors p_i obtained from the eigenvectors of the covariance of X (Qin 2003).

2.6.2. Partial Least-Squares Discriminant Analysis

Partial least squares-discriminant analysis (PLS-DA) was used to generate predictive models and rank the metabolites by the variable importance in the projection (VIP score). The major advantage of a supervised method such as PLS-DA over PCA is that the dependent ‘response’ variable is taken into consideration along with the independent ‘predictor’ variables during the matrix decomposition. PLS seeks to find a set of latent features that maximizes the covariance between X (n x N) and Y (n x M), where X and Y are the independent variables and dependent variables, respectively (Cho, Kim, Jeong, Park, Miller, Ziegler, Jones 2008). Similar to PCA, it is used to produce a low-dimensional representation of a data set. It is able to handle situations where multicollinearity is present and when the number of predictor variables is larger than the number of observations (Perez-Enciso, Tenenhaus 2003).

2.7. Model validation and performance

A bootstrapping procedure was performed on PCA to obtain stable metabolite loadings which were used to rank metabolites. Briefly, bootstrapping involves resampling a data set with replacement n number of times and calculating the desired statistic on the resampled data sets. This allows for the calculation of confidence intervals and statistics of interest can be averaged across all resampled data sets to simulate having a larger data set (Fisher, Caffo, Schwartz, Zipunnikov 2016). 10,000 iterations of bootstrapping were applied to every working data set, after which the loadings of every metabolite were averaged.

For PLS-DA, internal model validation was achieved with 5-fold cross-validation, performed with 100 iterations of random subsampling. Although bootstrapping is often touted as a superior method to cross validation (Mendez, Broadhurst, Reinke 2020; Rodriguez-Perez, Fernandez, Marco 2018), the small sample size in this study (n = 23 with chemotherapy response data) does not warrant the use of bootstrapping for PLS-DA. Small sample sizes may result in large differences between results after multiple bootstrap resampling, depending on how the samples are split into training and test sets.

2.8. Quantifying group separation in PCA and PLS-DA score plots

Score plots generated from PCA and PLS-DA are useful visual tools for inspecting separation between sample classifications. However, quantitatively interpreting subtle differences between score plots is often difficult. We chose to quantify the score plots with the J₂ criterion (Anderson 2008) and by finding p-values of the overlap between groups by using the PCAtoTree software developed by Worley et. al. (Worley, Halouska, Powers 2013). The J₂ criterion is used to measure how tightly clustered groups of samples are, and is defined as follows (Anderson 2008):

$$J_2=\frac{\mid S_w+S_b\mid }{\mid S_w\mid }$$ Equation [2]

where S_w is the within-class scatter and S_b is the between-class scatter. Briefly, p-values are determined by the Mahalanobis distance metric, Hotelling’s T² statistic and an F distribution (Anderson 2008), with the null hypothesis: points in groups i and j are drawn from the same multivariate normal distribution. Text files of the scores on the first two principal components for all pre-treatment and imputation methods for both PCA and PLS-DA were used as inputs for the PCAtoTree software.

2.9. Patient sample categorizations

To evaluate the results in terms of potential biomarkers predictive of response to therapy and of disease stage, three patient sample categorizations were analyzed: disease control (DC) vs. progressive disease (PD); complete response (CR) and partial response (PR) vs. stable disease (SD) and PD; cancer stage I/II/III vs. stage IV.

3. RESULTS

3.1. Experimental workflow

The workflow diagram is outlined in Supplemental Figure 1. Data pre-treatment methods were applied to the MS peak areas, and then imputation methods were applied to handle missing values. These pre-treated and imputed data sets represent the working data. The working data sets were then analyzed by unsupervised (PCA) and supervised (PLS-DA) analyses. Model validation was achieved by bootstrapping PCA with 10,000 iterations for finding PCA loadings, and a 5-fold cross validation with 100 permutations with PLS-DA. Results of the analyses were found by quantification of score plots and identification of key metabolites for every working data set.

3.2. Effect of pre-treatment on data

The effects of pre-treatment methods on the original data set are evident in Figure 2, where the average peak areas among all samples for each metabolite in the data set are shown for a representative case for which zero imputation was applied to the data. In the raw data (Figure 2A), some metabolites stand out with large values and dwarf most of the other peaks. Scaling methods, such as autoscaling (Figure 2C) and the log transformation (Figure 2H) clearly reduce the spread between the largest and smallest magnitudes of metabolite peak areas. Additionally, the data patterns change with different methods. For example, autoscaling, pareto scaling and range scaling (Figure 2C,2D,2E) leave several large peaks while the log transformation (Figure 2H) reduces these large peaks to a scale more similar to the other peaks. Altogether, these results highlight the potential effects that data pre-treatment methods may have on results further down the analytical pipeline.

Figure 2. Effect of pre-treatment methods and zero imputation on original data set.

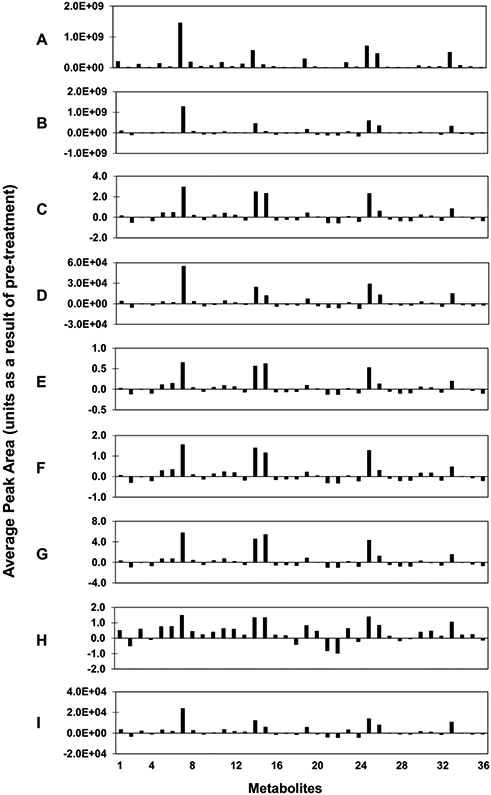
Peak areas were averaged among all 36 samples for each metabolite (x-axis). The following pre-treatment methods were applied: (A) Raw data, (B) Centering, (C) Autoscaling, (D) Pareto scaling, (E) Range scaling, (F) Vast scaling, (G) Level scaling, (H) Log transform, (I) Square root transform.

3.3. Effect of combined pre-treatment and imputation on PCA scores

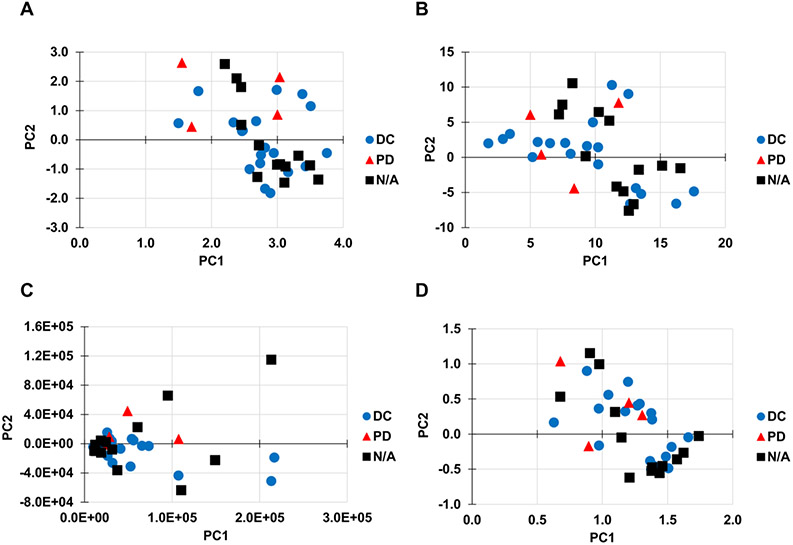
The performance of different pre-treatment and imputation methods was first evaluated by clustering and separation of samples in the respective score plots, where samples are expected to be clustered within their respective groups and each group separated from one another. Representative PCA score plots are shown in Figure 3. In all score plots, the first two components were used as the x and y-axes. The pre-treatment and imputation combinations of vast scaling/CART (Figure 3A) and pareto scaling/RF (Figure 3C) achieved a statistically significant separation between the DC and PD groups, while level scaling/CART(Figure 3B) and range scaling/RF (Figure 3D) did not. These results highlight the fact that different scaling methods may offer varying performance for group separation in PCA score plots when paired with certain imputation methods. Quantification of the plots for the top 20 performing pre-treatment and imputation methods is shown in Supplemental Table 2A. Pareto scaled data with zero substitution performed best at separating the two groups (p = 0.028). The zero, half-min, and BPCA imputations occurred more often in the top 20 performing methods.

Figure 3. Effect of pre-treatment and imputation methods on PCA scores.

Representative PCA score plots of all 36 samples in the data set. The following pre-treatment methods and imputation methods were applied: (A) Vast scaling and CART imputation, (B) Level scaling and CART imputation, (C) Pareto scaling and RF imputation, (D) Range scaling and RF imputation. Panels A and C achieved a statistically significant separation between the disease control (DC) and progressive disease (PD) groups (p ≤ 0.05), while panels B and D did not reach significance. N/A: not applicable (sample was not used for patient categorization in our dataset).

Effect of pre-treatment and imputation for the other sample categorizations (CR/PR vs. SD/PD and stage I/II/III vs. IV) are in Supplement. Note that the score plots do not change with different sample categorizations, since the dependent response variable is not taken into consideration during PCA. However, overlap p-values and J₂ values are expected to be different.

3.4. Effect of combined pre-treatment and imputation on PCA loadings

Representative PCA loadings are shown for half-min substitution and PPCA imputation in Figure 4A,4C). The log transformation clearly reduced the variance between metabolite loadings compared to vast scaling. The rankings of metabolites based on PCA loadings (Figure 4B,4D)) changed considerably between the two pre-treatment methods and between the two imputation methods. Vast scaling resulted in isoleucine being ranked as the top metabolite with both half-min substitution and PPCA imputation, while the log transformation ranked phenylalanine highest with half-min substitution and choline highest with PPCA imputation. On the other hand, N3,N4-dimethyl-L-arginine was ranked consistently as the 7^th most important metabolite by the log transformation but with vast scaling was ranked 10^th with half-min substitution and 14^th with PPCA imputation. Additionally, lactate consistently ranked 3^rd with both pre-treatment methods and both imputation methods. Since the dependent response variable is not taken into consideration during PCA, the PCA loadings will not change with the other sample categorizations (CR/PR vs. SD/PD or stage I/II/III vs. stage IV).

Figure 4. Effect of pre-treatment and imputation methods on PCA loadings and metabolite ranks.

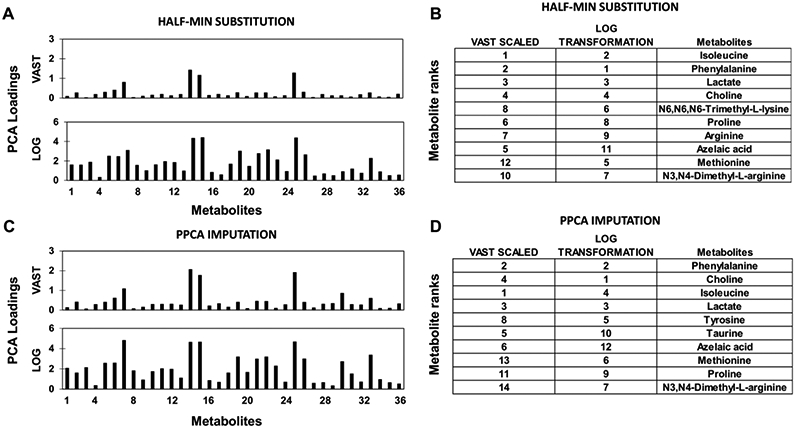
(A,B) Half-min substitution and (C,D) PPCA imputation of missing values was applied after pre-treatment (vast scaled or log transformation).

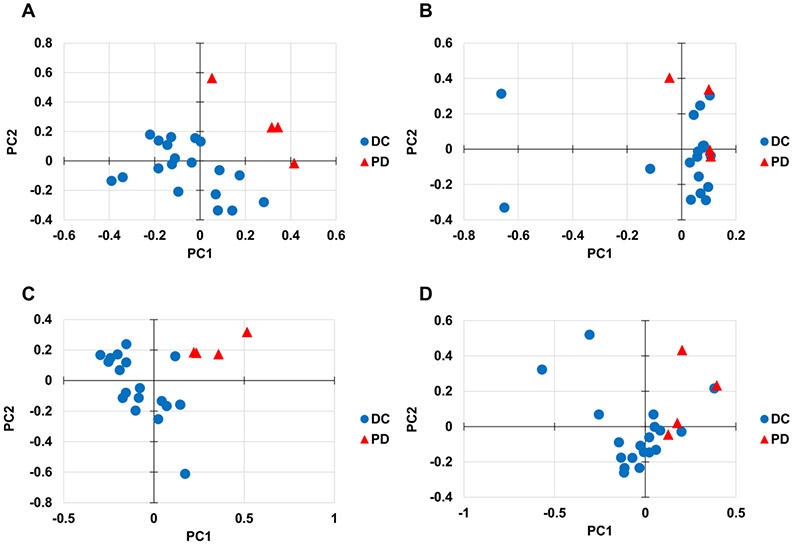
3.5. Effect of combined pre-treatment and imputation on PLS-DA score plots

The performance of different pre-treatment and imputation methods was further investigated by clustering and separation of samples in PLS-DA score plots. In all score plots, the first two components were used as the x and y-axes. Representative PLS-DA score plots for DC vs. PD patient categorization are shown in Figure 5. The pre-treatment and imputation combinations of log transformation/RF (Figure 5A) and vast scaling/PMM (Figure 5C) achieved a statistically significant separation between the DC and PD groups, while level scaling/RF imputation (Figure 5B) and pareto scaling/PMM (Figure 5D) did not. Quantification of PLS-DA score plots for the top 20 performing pre-treatment and imputation methods is shown in Supplemental Table 2B. Log transformed data with median substitution performed best at separating the two groups (p = 0.0000). Overall, the pre-treatment methods of log transformation and vast scaling and the substitution methods of median and mean outperformed most other methods for separating groups in score plots. The log transformed data in general had higher J₂ values for the PD group compared to other pre-treatment methods, meaning that the PD groups were clustered more tightly.

Figure 5. Effect of pre-treatment and imputation methods on PLS-DA scores.

Representative PLS-DA score plots of 23 samples with chemotherapy response data categorized as disease control (DC) vs. progressive disease (PD). The following pre-treatment methods and imputation methods were applied: (A) Log transformation and RF imputation, (B) Level scaling and RF imputation, (C) Vast scaling and PMM imputation, (D) Pareto scaling and PMM imputation. Panels A and C achieved a statistically significant separation between the DC and PD groups (p ≤ 0.05), while panels B and D did not reach significance.

3.6. Effect of combined pre-treatment and imputation on PLS-DA accuracy and variable importance measures

PLS-DA misclassification rates for the top 20 performing pre-treatment and imputation methods are shown in Supplementary Table 5, where the best misclassification rate was 13% across five different combinations of methods. The log transformation performed well regarding classification accuracy. When paired with the imputation methods of PMM, mean, median, and zero, the log transformation achieved a misclassification rate of 17.4%, the second-best possible misclassification rate for this particular data set (data not shown). There was little consistency in which imputation methods resulted in the best misclassification rates, but generally the square root transform outperformed other pre-treatment methods.

Representative PLS-DA VIP scores are shown for kNN and BPCA imputation in Figure 6A,6C. A pronounced difference between the VIP score pattern for level scaling after kNN or BPCA imputation is evident, while the log transform seemed to maintain the relative patterns after the imputation. Metabolite rankings based on VIP scores show clear differences between both the pre-treatment methods and imputation methods (Figure 6B,6D). A pronounced difference between the two imputation methods is the presence of choline in the top ten most important metabolites with BPCA but not with kNN. This indicates that BPCA is likely replacing missing values for choline in a manner that increases the variance between samples. In contrast, metabolites such as glutamic acid and phenylalanine were ranked the same between the imputation methods with level scaling but changed rank with log transformation.

Figure 6. Effect of pre-treatment and imputation methods on PLS-DA VIP scores and metabolite ranks.

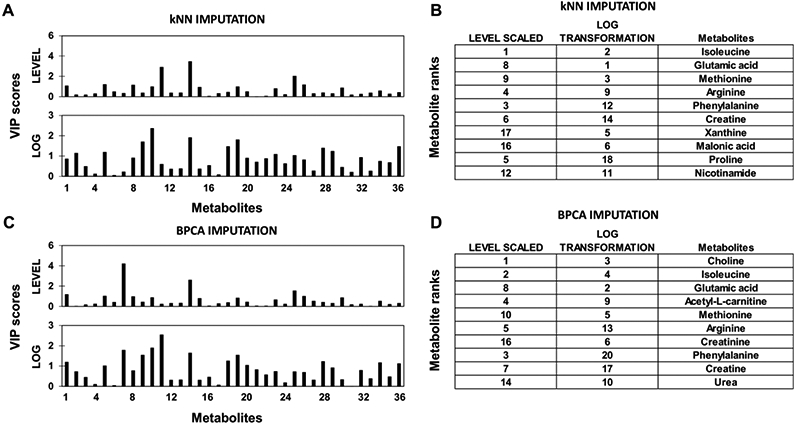
(A,B) kNN imputation and (C,D) BPCA imputation of missing values applied after pre-treatment (level scaling or log transformation) using samples with chemotherapy response data categorized as disease control (DC) vs. progressive disease (PD).

Analyses of PLS-DA with respect to CR/PR vs. SD/PD and stage I/II/III vs. IV sample categorizations are in the Supplement.

4. DISCUSSION

This study evaluated variations in potential metabolomic biomarkers caused by the combined choice of data pre-treatment and imputation methods applied to metabolomics data. We used a metabolomics data set generated from human derived lung cancer tissue specimens that contained a complex mixture of true missing values to capture errors commonly seen in applied metabolomics. The results demonstrate that changes made to a metabolomics data set by pre-treatment and imputation methods can have downstream effects on the data analysis. These effects can potentially lead to misinterpretations of results and difficulty with replicating metabolomics studies in general.

According to Rubin et al., there are three ways to classify missing data (Rubin 1976): MCAR MAR, and MNAR. Specifically for MS data, there are various potential causes of missing data, including biological and technical origins, such as: sample heterogeneity resulting in metabolites being below the MS detection limit, an inability of the deconvolution software to separate peaks, or a temporary reduction in performance in electrospray due to particulate material in the spray nozzle (Hrydziuszko 2012; Payne 2009). According to Jakobsen et al. (Jakobsen, Gluud, Wetterslev, Winkel 2017), multiple imputation is appropriate when missing values represent between 5% and 40% of the data set and the MCAR or MNAR assumptions are plausible. In our data set, we can safely assume that both of these types of missing data are present based on the distribution of missing values seen in the original data set (Figure 1). For example, missing values for taurine in samples 15-25 (Figure 1) were most likely caused by taurine not being detected in the quality control sample for that particular analytical batch, making missing values for taurine MNAR. Additionally, since taurine is known to be one of the most abundant free amino acids in mammalian tissues (Ripps, Shen 2012), it is unlikely that the missing values were MAR or MCAR. Missing values for pyruvate, on the other hand, are most likely MAR or MCAR since there is no apparent pattern to the distribution of missing values. There are a number of metabolomics data analysis tools which include methods to deal with missing values such as: XCMS (Tautenhahn, Patti, Rinehart, Siuzdak 2012), MeltDB (Kessler, Neuweger, Bonte, Langenkamper, Niehaus, Nattkemper, Goesmann 2013) and MetaboAnalyst (Chong, Soufan, Li, Caraus, Li, Bourque, Wishart et al. 2018). For example, the web tool MetaboAnalyst provides a total of 12 modules for exploratory statistical analysis, functional enrichment analysis, data integration and system biology, and data processing utility functions tools designed for metabolomics data. However, since it has limited options for data pre-treatment and missing value imputation, it may lead to choosing sub-optimal methods. The default method of handling missing data in MetaboAnalyst version 4.0 is the half-min substitution method, which studies have shown to be an inferior method (Wei, Wang, Su, Jia, Chen, Chen, Ni 2018), especially when missing values are not necessarily caused by low abundance metabolites.

The effects of data pre-treatment on the original data are shown in Figure 2. Peak patterns across all metabolites have the potential to change dramatically with different pre-treatment types, indicating that the results of any imputation or analysis method applied further down the pipeline could be influenced by the choice of pre-treatment method. We utilized PCA and PLS-DA as representative examples of unsupervised and supervised analyses, respectively, after applying various pre-treatment and imputation methods to the original data. Vast, level, pareto and range scaling produced different distributions of samples in the PCA score plots (Figure 3). For example, although CART imputation achieved significance for separating the DC and PD groups after vast scaling, CART failed to achieve significant separation after level scaling. A similar trend can be observed with PLS-DA in Figure 5, where RF imputation achieved a significant separation after log transformation, but failed after level scaling, while PMM imputation achieved a significant separation after vast scaling but failed after pareto scaling. These results indicate that the performance of an imputation method may change depending on the pre-treatment method used. We also investigated how changing the binary response categorization of the samples could affect the results of the PCA and PLS-DA analyses. There is little consistency for which imputation methods performed best for separating groups between the different response categorizations (Supplemental Tables 2, 3, 4). However, certain pre-treatment methods such as log transformation and vast scaling generally performed better than other methods at separating groups in PLS-DA (Supplemental Tables 2B, 3B, 4B). An important aspect of metabolomics studies is the identification of small molecule biomarkers for disease diagnosis and prognosis. Here, we show that ranking metabolites based on importance with either PCA loadings or PLS-DA VIP scores can vary considerably depending on the pre-treatment and imputation methods applied (Figure 4B,4D, Figure 6B,6D, Supplementary Figure 3B,2D, Supplementary Figure 5B,4D). From these results it is apparent that extemporaneous data pre-treatment and imputation could result in important biomarkers either being overlooked or reported as a false positive.

To our knowledge, this is the first study that has evaluated the effects of both pre-treatment and imputation methods on the interpretation of unsupervised and supervised analyses of human metabolomics data. One limitation is that conclusive performance metrics of pre-treatment and imputation methods cannot be obtained from using a data set with true missing values. However, we were able to show that there is a complex relationship between pre-treatment methods, imputation methods, and sample categorizations depending on the methods used. A potential pitfall of applying a “shotgun” approach with pre-treatment and imputation methods is the tendency to choose biased results based on score plot group separation and misclassification rate (i.e., AUROC) of the supervised learning method. It is important to note that better group separations and misclassification rates do not necessarily reflect that the data is being represented more accurately. It is possible that inaccurate imputation methods could result in better group separation, which the results here demonstrate. For instance, the substitution methods of zero, mean and median imputation have previously been shown to have poor performance for estimating missing values (Wei, Wang, Su, Jia, Chen, Chen, Ni 2018). However, these substitution methods along with the half-min substitution were shown to outperform other methods such as RF, kNN and PPCA for separating groups and achieving higher classification accuracy within the same pre-treatment method. Therefore, it would be valuable to perform internal testing by using subsets of original data that only contain complete cases and introducing simulated missing values to evaluate the accuracy of imputation methods before performing statistical analyses on the working data set, as has been previously suggested (Sim, Lee, Kwon 2015; Wei, Wang, Su, Jia, Chen, Chen, Ni 2018).

Additionally, the accuracy of imputation methods will likely be affected by data pre-treatment. Previously, both Gromski et al. and Kokla et al. have shown that the RF method of imputation produced the most accurate results when imputing metabolomics data (Gromski, Xu, Kotze, Correa, Ellis, Armitage, Turner et al. 2014; Kokla, Virtanen, Kolehmainen, Paananen, Hanhineva 2019). The RF method achieved the best classification rates using principal component-linear discriminant analysis (PC-LDA) and PLS-DA using cell culture data with groups based on incubator oxygen concentration (Gromski, Xu, Kotze, Correa, Ellis, Armitage, Turner et al. 2014). The RF method performed best at replacing missing values in complete data sets that had values removed to simulate missing data (Kokla, Virtanen, Kolehmainen, Paananen, Hanhineva 2019). Vast scaling and autoscaling were shown to be stable pre-treatment methods in a study using four different classification models on representative GC-TOF MS and NMR metabolomics data sets (Gromski 2015). However, (Gromski 2015) used complete data sets and classification accuracy was the sole performance metric. The average classification accuracy of the GC-TOF MS Arabidopsis Thaliana data using a log transformation did not differ considerably compared to the other methods but resulted in smaller confidence intervals during resampling for all four methods tested. Overall, in our study the log transformation appeared to normalize the original data most effectively and resulted in the highest classification accuracies in the stage I/II/III vs. stage IV classification, while the square root transformation also consistently performed well and represented three of the top five performing models in the DC vs. PD classification. However, the performance of the imputation methods applied after the transformation was highly dependent on the characteristics of the data set. The results indicate that log transformation and square root transformation could be recommended as starting points for analyzing human metabolomics data. Based on (Gromski 2015), vast scaling and autoscaling could be further options if a log transformation or square root transformation proves unsatisfactory. The combined choice of pre-treatment and imputation methods, therefore, needs to be carefully evaluated prior to metabolomic data analysis from human tumors. This approach would enable a more consistent identification of potential biomarkers predictive of response to therapy and of disease stage, and thus advance the clinical utility of biomarker discovery, especially in regards to lung cancer.

ABBREVIATIONS

BPCA

Bayesian principal component analysis

CART

Classification and regression trees

CR

Complete response

DC

Disease control

kNN

k-Nearest neighbor

MICE

Multiple imputation by chained equations

MAR

Missing-at-random

MCAR

Missing-completely-at-random

MNAR

Missing-not-at-random

MS

Mass Spectrometry

MSI

Metabolomics standards initiative

PCA

Principal component analysis

PD

Progressive disease

PLS-DA

Partial least squares discriminant analysis

PMM

Predictive mean matching

PPCA

Probabilistic principal component analysis

PR

Partial response

RF

Random forest

SD

Stable disease