DNF: A differential network flow method to identify rewiring drivers for gene regulatory networks

Abstract

Differential network analysis has become an important approach in identifying driver genes in development and disease. However, most studies capture only local features of the underlying gene-regulatory network topology. These approaches are vulnerable to noise and other changes which mask driver-gene activity. Therefore, methods are urgently needed which can separate the impact of true regulatory elements from stochastic changes and downstream effects. We propose the differential network flow (DNF) method to identify key regulators of progression in development or disease. Given the network representation of consecutive biological states, DNF quantifies the essentiality of each node by differences in the distribution of network flow, which are capable of capturing comprehensive topological differences from local to global feature domains. DNF achieves more accurate driver-gene identification than other state-of-the-art methods when applied to four human datasets from The Cancer Genome Atlas and three single-cell RNA-seq datasets of murine neural and hematopoietic differentiation. Furthermore, we predict key regulators of crosstalk between separate networks underlying both neuronal differentiation and the progression of neurodegenerative disease, among which APP is predicted as a driver gene of neural stem cell differentiation. Our method is a new approach for quantifying the essentiality of genes across networks of different biological states.

1. Introduction

Identifying significantly changed genes in development and progression of diseases is of great benefit to uncover new biomarkers and prognostic signatures [1]. Differential expression analysis is capable of narrowing the whole genome down to a short list of candidate driver genes [2]. However, the quantification of significance among identified genes remains an open and challenging question [3]. Furthermore, the reductive identification of differentially expressed genes by multiple-hypothesis testing fails to highlight the complex interactions occurring in real biological systems.

To explicitly address this multiscale structure, state-dependent molecular interactions can be abstracted as a network whose nodes represent molecules and whose edges represent the existence and strength of their respective interactions [4, 5]. Because networks have both global and local properties, this approach epitomizes the ‘Systems Biology’ perspective. Differential network analysis aims to identify the differences between networks under different conditions [6]. Therefore, differential network analysis becomes an essential approach to assess the importance of biological entities (such as genes) in biological systems which undergo change, or which utilize feedback to maintain homeostasis [7–9].

In the past ten years, many differential network analysis methods have been proposed to assess the essentiality of genes between two biological conditions. The existing differential network analysis methods mainly fall into two categories. The first category is focused on capturing linear or nonlinear correlation differences in gene expression between two gene regulatory networks (GRNs). For instance, DDN [10] is the first algorithm to detect topological differences by lasso regression in network inference. DISCERN [11] computes a novel perturbation score to capture how likely a given gene has a distinct set of regulators between different conditions, which is shown to be robust to errors in network structure estimation. pDNA [12] incorporates prior information into differential network analysis using non-paranormal graphical models, which relaxes the assumption of normality of omics data to find more cancer-related genes.

The second category is focused on topological differences between constructed GRNs. For instance, DEC captures the global differential eigenvector connectivity to prioritize nodes in networks [7]. DiffRank [13] computes the linear combination of differential connectivity and differential betweenness centrality to order genes. DCloc [14] computes the average proportion of changes of each node’s neighborhood as a significance score by iteratively removing edges with different thresholds. DiffNet [15] evaluates topological differences between two networks based on generalized hamming distance and its statistical significance. KDS [8] measures the importance of genes by calculating the graphlet vector distance.

Two issues remain which the above methods fail to address. First, all the above methods utilize networks which assume the existence of edges based on co-expression. While global network features (such as eigenvector connectivity) may be taken into account during differential network analysis, co-expression is an unreliable starting point based on long-standing biological results. In particular, measured gene expression is inherently noisy due to intrinsic (transcriptional) and extrinsic (measurement) sources of variation [16], contributing to a high false positive rate in network construction. Therefore, the existence of edges in a reconstructed network must reflect the uncertainty of these observations [17].

The second issue is more subtle. While techniques such as spectral analysis provide a global perspective on connectivity, these approaches fail to encapsulate the flow of information inherent in all biological networks. Network flow has been investigated extensively in connection with commerce and telecommunication [18]. The notion of optimality with regard to information flow, originally designed around these manufactured networks, takes into account the nonlinear contribution of all nodes, and thus is not reductive in the sense of spectral analysis, whose rank-based metrics reflect only linear contributions. Despite wide adoption of these methods in their original context, characterization of biological networks (including gene-regulatory networks) by optimal flow has not been widely explored. Although the statistical properties of dynamic networks have recently been studied in the context of epidemiology and biochemistry [19], methods that can overcome the uncertainty of networks and capture comprehensive topological differences are urgently needed to quantify the essentiality of genes from a systems view.

In this paper, we propose the differential network flow (DNF) method to identify key regulators between two networks under different biological conditions. This algorithm is built upon the idea of network flow and information theory. Rewiring of a GRN can be characterized as a dynamic pattern of network flow [19], such a flow-based model captures multiple (from local to global) features of network structure. Information theory is able to quantify the uncertainty in networks, making networks built upon information-theoretic measurements a more acceptable representation of biological systems at the molecular scale [20]. Therefore, DNF is capable of capturing comprehensive topological differences by quantifying the flow in a network. Its identification accuracy is compared with several state-of-the-art methods, first to simulated datasets and second to clinical and experimental datasets. In addition, DNF is applied to predict driver genes of neural stem cell differentiation in single-cell RNA-seq datasets.

2. Materials and methods

2.1. Gene regulatory network construction by using both transcriptomics and proteomics datasets

Network analysis requires a robust network skeleton, and the choice of network skeleton is important, allowing network-based approaches to achieve higher precision [21]. Constructing network skeletons that integrate single-cell transcriptomics data and other omics data provides attractive opportunities to mechanistically understand this heterogeneity under different cell states [22].

To improve the performance of driver-gene prediction, we employ a three-step process to integrate both transcriptomics and proteomics datasets in GRN-construction. First, a network skeleton is built by differential expression analysis using the transcriptomics dataset. Specifically, the skeleton gene sets are selected based on a given criterion, such as | log₂ Fold Change |>u, p-value<v, where u represents the fold change of gene expression and v represents the statistical significance of differential expression. Second, the known corresponding protein-protein interactions in the STRING database (http://string-db.org) are used to establish the gene-gene network for the selected genes. For example, suppose p skeleton genes are selected in the first step, then a network skeleton with p nodes is described by an adjacency matrix A_i,j, such that A_i,j > 0, i, j=1, …, p, if protein i and protein j are functionally associated. Finally, the absolute value of the spearman correlation coefficient (scc) of expression is adopted to estimate the strength of connections between adjacent genes, and edges A_i,j, for which scc(i, j) < 0.1 are discarded (see Supplementary Text 1 and Supplementary Figure 1 for more explanation of parameter selection). Following this procedure, we construct a pair of GRNs based on a specific transcriptomics dataset (e.g. cancer and control samples) and a generic proteomics dataset, described as $A_{i,j}^1,i,j=1,\dots ,l,A_{i,j}^2,i,j=1,\dots ,r$, in which l ≠ r and l, r ≤ p.

To effectively study the new differential network method in this study, we use both previously existing networks for bulk RNA-seq datasets and the networks specifically constructed for single-cell RNA-seq datasets.

2.2. Estimating differential network flow to prioritize genes

DNF is built upon the ideas of network flow and information theory. The novelty of DNF lies in quantifying node-to-node information entropy according to the network flow in a gene regulatory network, and in characterizing each node as a distribution of network flow, which is equal to the distribution of information entropy. The distribution differences of one gene in different networks represents its essentiality in the biological process responsible for the network’s evolution. Genes are ordered by the magnitude of this difference to establish a ranking. Given two networks constructed as described in 2.1. DNF produces this ranking in four steps:

2.2.1. Calculate signal matrix using gene-gene interaction strengths

We consider two weighted networks as two biological states, abstracted as $A_{i,j}^1$. d $A_{i,j}^2$, and we suppose that there are k common genes between the two matrices.

Since scc(i, j) is a random variable, we can probabilistically estimate the strength of a bi-directional signal $z_{i,j}$ from gene i to gene j as the product of scc(i, j) and its information content [20]. Through the transformation from edge weight to the expectation of information, z_i,j is described as the sub-item of entropy. The network labels are suppressed in the following equations for notational convenience,

$$z_{i,j}=A_{i,j}log\frac{1}{A_{i,j}}$$ (1)

We assume that changes in the biological state of the system can only change the weight of the edges (as calculated in 2.1) of a given network skeleton. Thus, by assigning a cost, capacity and normalized flow to each edge, we can probabilistically measure the global and local change between network flow solutions for any treatment applied to the underlying system.

2.2.2. Quantify gene-to-gene entropy according to the network flow

Rank-based metrics like degree centrality usually only reflects linear contributions of all nodes. The optimal flow, however, takes into account potentially nonlinear contributions, allowing more sensitive detection of changes in network structures, such as the strongest and most stable connections among a group of nodes (even if they are not neighbors) in a gene regulatory network. In this approach, the maximum flow describes the strongest regulatory relationship between nodes, and the minimum cost is similar to the concept of entropy that describes the most stable regulatory relationship between nodes.

The optimal flow model is based on the theory of the shortest path between any two nodes. In the flow model, each edge is given the capacity c_i,j that represents the bandwidth of that edge, the flow f_i,j through the edge, and the fixed signal z_i,j of flow through the edge. Suppose any two nodes in a network, source node s and sink node t, s ≠ t, the network flow F_s,t from s to t can be measured as follows,

$$\begin{gathered} F_{s,t}=Min\left\{{\displaystyle {\sum }_{i,j}{f}_{i,j}}{Z}_{i,j}\right\} \\ \text{s.t.}Max\left\{{{\displaystyle {\sum }_{i,j}f}}_{i,j}\right\}, \\ {f}_{i,j}\le c_{i,j}, \\ \sum _w{f}_{s,w}=\sum _w{f}_{w,t},w\text{is any node} \end{gathered}$$ (2)

Where the network flow from s to t meet the requirements of minimum signal in multiple maximum flow strategies. The first restriction means that the optimal flow must meet the requirement of maximum flow; The second restriction means that the amount of flow through any edge of network cannot exceed its capacity; The third restriction means that the flow flows only from the node s to the node t. Since the network is undirected, F_s,t = F_t,s.

In DNF, the capacity of each edge is set as c_i,j = 1, and we obey the rule that the flow f_i,j on each edge of each shortest path is computed only once, in other words, there is a unique sequence of nodes between the source and the sink. Because the sum z_i,j, for all A_i,j > 0, is the Shannon entropy of scc(i, j), the information flow F_s,t is like the concept of entropy that is weighted by the signal of flow. In particular, the information flow F_s,t is equivalent to entropy when it is calculated in a two-node network. The optimal flow solution therefore defines a globally unique path as well as a unique set of local edge signals for every pair-wise gene interaction.

2.2.3. Characterize each node as a distribution of network flow

DNF assumes that each gene’s potency of signal propagation is relatively stable, while the strength of signals propagating to different genes is variable in different conditions, contributing to changes in the correlation between gene expression levels. Thus, the signal propagation of a gene under a specific state can be abstracted as a distribution. DNF aims to track the distribution-level differences of each gene under two biological states.

To facilitate the probabilistic notion of network difference, we require that ∑_tF_s,t = 1. This is enforced by normalizing F_s,t as,

$$F_{s,t}=\frac{F_{s,t}}{{\sum }_t{F}_{s,t}}$$ (3)

Therefore, the flow from any node i to the other nodes in the network can be characterized as a probability distribution ${\mathcal{F}}_i$,

$${\mathcal{F}}_i=\left\{F_{i,1},\dots \dots ,F_{i,k}\right\}$$ (4)

because we measure network difference via a symmetric divergence score, we also require that the support of i be equal for the two networks of interest. Therefore, only the k common nodes between two networks are considered.

2.2.4. Measure distribution differences of network flow for each gene in two networks

In order to quantify the difference of distribution-level of signal propagation between two biological states, we adopt the sum of the reciprocal Kullback-Leibler divergence (KLD) to estimate the distance between two node-wise flow distributions ${\mathcal{F}}_i^m$, m in{1, 2}. Therefore, the differential score D_i, corresponding to the distance of common node i between two networks, is characterized as follows,

$$D_i=\sum \left({\mathcal{F}}_i^{1}log\frac{{\mathcal{F}}_i^1}{{\mathcal{F}}_i^2}+{\mathcal{F}}_i^{2}log\frac{{\mathcal{F}}_i^2}{{\mathcal{F}}_i^1}\right)=\sum _{j=1}^k\left(F_{i,j}^{1}log\frac{F_{i,j}^1}{F_{i,j}^2}+F_{i,j}^{2}log\frac{F_{i,j}^2}{F_{i,j}^1}\right)$$ (5)

where ${\mathcal{F}}_i^1$, ${\mathcal{F}}_i^2$ represents distribution-level information flow of common node i in two biological conditions.

3. Datasets

3.1. Simulation datasets

To compare the accuracy of our methods and other state-of-the-art methods without bias in identifying the significant rewiring nodes between two networks, we generate simulated dynamic networks as previously described [12]. In our simulated data, 100 pairs of networks, each containing 100 nodes whose degree distribution follows a power-law distribution were generated. For each pair of networks, a random selection of 10 nodes was disturbed, reflecting critical regulation of the network from one state to another. The edges of each disturbed node were perturbed with fixed percentage λ=0.1, and the perturbed edges were randomly selected based on a previously published method [12].

3.2. Four TCGA datasets

To compare the performance of DNF against other state-of-the-art methods in identifying rewired driver genes in cancer networks for bulk RNA-seq datasets, four kinds of cancer RNA-seq datasets were used in this study, which were downloaded through TCGAbiolinks [23]: breast invasive carcinoma (BRCA), prostate adeno-carcinoma (PRAD), liver hepatocellular carcinoma (LIHC) and lung adenocarcinoma (LUAD). The downloaded TCGA datasets were in read-count format, and were quality controlled and normalized by the ‘DEseq’ package [24]. For each method, network construction of above four datasets was done as previously reported in [7].

3.3. Three single-cell RNA-seq datasets

Three single-cell RNA-seq datasets of mice are analyzed in this study, including neural stem cell differentiation (PRJNA324289) [25], neural progenitor cell differentiation (GSE76381) [26] and hematopoietic stem cell differentiation (GSE59114) [27]. Notably, network construction of three single-cell RNA-seq datasets followed the protocol introduced in section 2.1, rather than the protocol used for the bulk-sequencing datasets [7]. The datasets were downloaded in raw read counts format, their differential gene expression analyzed by ‘edgeR’ package [28], and subsequently transformed into counts-per-million (CPM) format by ‘DEseq’ package. Network construction was based on the transformed transcriptomics datasets and generic proteomics datasets.

4. Results

4.1. Comparison with four existing methods using simulation datasets

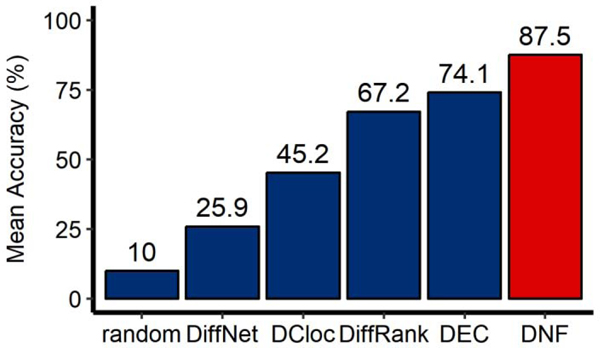
DNF is compared against four state-of-the-art differential network analysis methods on each simulated network pair. For the comparison, we include results from DiffRank [13], DEC [7], DCloc [14] and DiffNet [15]. In addition, a random selection method is also compared with these differential network analysis methods. The accuracy of each method is evaluated through the average hit number of the top 10 scored nodes intersecting with the 10 disturbed nodes.

As shown in Figure 1, methods that rely on capturing local topological features (DiffNet and DCloc) do not perform as well as methods that rely on capturing global topological features (DEC) and mixed topological features (DiffRank). This is because all perturbed nodes present subtle topological differences (local or global, linear or non-linear). DNF has the potential of capturing comprehensive topological differences from local to global feature domains. Therefore, DNF outperforms the other four state-of-the-art methods in mean accuracy of identifying perturbed nodes between different networks. Furthermore, all differential network analysis methods outperform the random selection method, underscoring the necessity of differential network analysis.

Figure 1.

Comparison of different methods in detecting perturbed nodes using simulated datasets. DNF (the red bar) is compared with 5 methods (the blue bars), including 4 state-of-the-art differential network analysis methods and the random selection method. Results are averaged by 100 pairs of simulation networks.

4.2. DNF reveals rewiring driver genes in cancer networks more consistent with the known cancer gene list for four different TCGA datasets

4.2.1. Assessment criteria

In order to assess ranking and identification accuracy in the TCGA data, 138 known cancer genes [29] and 723 genes from the Cancer Gene Census (CGC) [30] were adopted as two reference sets. For each method, the overlap between the top 20 ranked markers and the reference defines the score for the method (see Supplementary Text 2 and Supplementary Figure 2 for more explanation of parameter selection).

In addition, we tested whether dosage of each method’s top 20 genes can predict the treatment outcome of TCGA patients at various endpoints. Survival analysis aims to identify the candidate cancer biomarker genes and prognosis genes by applying a log-rank test to the end-point event for high and low dose populations which we established by standard univariate clustering based on expression of each predicted marker. TCGA survival analysis was conducted through RTCGA [31], the number of significantly (p-value < 0.05) survival-related genes was regarded as another evaluation criteria of performance of each differential network method.

4.2.2. Comparison with other methods in four TCGA datasets

DNF was compared with other methods on four TCGA datasets (BRCA, PRAD, LIHC and LUAD) to compare the effectiveness of each method in detecting known cancer genes. In our study of detecting 138 known cancer genes (Supplementary Table 1), the set of differential nodes identified by DNF reflects more known cancer genes in BRCA, PRAD and LIHC. In LUAD, the graphical hamming distance-based method, DiffNet, outperforms any other methods. While systematically analyzing these detected genes by each method (Supplementary Table 2), we found that DNF has the largest number of uniquely detected genes, and that the average number of genes detected by both DNF and one of the four other methods is also the largest. This is because the optimal flow considers both linear and nonlinear contributions of all nodes, allowing more sensitive detection of changes in network structure. Suggesting that DNF is potentially a more sensitive method of identifying topological differences between gene regulatory networks. In our study of detecting 723 genes in the CGC (Table 1), DNF shows similar performance compared to the analysis using 138 known cancer genes. In addition, the methods that rely on a single topological feature (DCloc, DEC and DiffNet) do not perform as well as the methods that are capable of capturing mixed topological features (DiffRank and DNF). Overall, DNF is more sensitive than other tested methods in detecting known driver genes of these four cancers.

Table 1.

Comparison of different methods in detecting known rewiring driver genes (723 genes in the Cancer Gene Census) in cancer networks for four TCGA datasets (numbers in table corresponding to the number of cancer driver genes in top 20 genes detected by different methods in each dataset)

	BRCA	PRAD	LIHC	LUAD	Total
DEC	6	6	10	7	29
DCloc	5	7	9	7	28
DiffRank	8	10	9	9	36
DiffNet	8	6	8	8	30
DNF	7	11	9	10	37

From another perspective, the differential genes between cancer and control samples may include many survival-related genes, whose expression level may significantly impact survival time of patients. Additional experiments were performed on the top 20 scored genes by each method. For each gene, each sample was divided into high and low expression groups by its median expression. Then, the log-rank test was performed between gene expression and survival time of the two groups. The genes whose median expression divided the patient samples into two groups for which the log-rank test rejected the null hypothesis of “no difference” with p-value < 0.05 were regarded as survival-related genes in each cancer. As shown in Figure 2, many of the top 20 scored genes by different methods are statistically related to survival in each of the four cancer datasets.

Figure 2.

Comparison of different methods in uncovering statistically survival-related genes for four TCGA datasets. The height of bars corresponds to the number of statistically (p-value<0.05) survival-related genes uncovered by each method (top ranked 20 genes) for each TCGA dataset.

Overall, DNF outperforms other state-of-the-art methods, being tied with DiffRank and DCloc for PRAD and BRCA, respectively, and recovering more survival-related genes than other methods for LUAD. In addition, DNF is able to uncover some survival-related genes that other methods fail to detect. Several notable genes were detected only by DNF (see Supplementary Figure 3), including APEX1 in BRCA, FOXP3 in BRCA, FOSL1 in LUAD and GATA1 in PRAD. In particular, APEX1 [32] and FOSL1 [33] are newly identified targets in cancer treatment, and GATA1 is one of 138 known cancer-related genes mentioned above. Hence, DNF shows promise in the detection of new and established cancer driver-genes and survival-related genes.

4.3. DNF identifies differentiation regulators for three single-cell RNA-seq datasets

4.3.1. Assessment criteria

The Gene Ontology is a curated database of annotated markers which has successfully guided exploratory analysis in many previous studies [34]. In order to rank predictions of the tested methods, we utilize the GO0045595 (regulation of cell differentiation) gene list as a reference list for differentiation processes. The GO0045595 gene list contains 1888 genes that are related to the process in which relatively unspecialized cells (stem cells) acquire specialized structural and functional features. The full list of these genes can be found in the Gene Ontology Resource [35]. The performance of each method in this study was evaluated by the number of intersections of top 20 ranked genes by each method and the gene list of GO0045595.

4.3.2. Comparison with other methods

DNF was applied to three single-cell RNA-seq datasets, which cover three differentiation processes: neural stem cells to neural progenitor cells (PRJNA324289), neural progenitor cells to radial glial cells (GSE76381), and hematopoietic stem cells to hematopoietic progenitor cells (GSE59114). For the network construction of each dataset, the network skeleton was established through the online database of protein-protein intersection (https://string-db.org/). Because the online database does not support input of more than 2000 proteins, the skeleton genes were limited to 2000 to ensure compatibility with the online database. For PRJNA324289, | log₂ Fold Change |>0.5, p-value<0.05 was used, giving 1039 skeleton genes. For GSE76381 and GSE59114, | log₂ Fold Change >1, p-value<0.05 was used, giving 452 skeleton genes and 647 skeleton genes respectively.

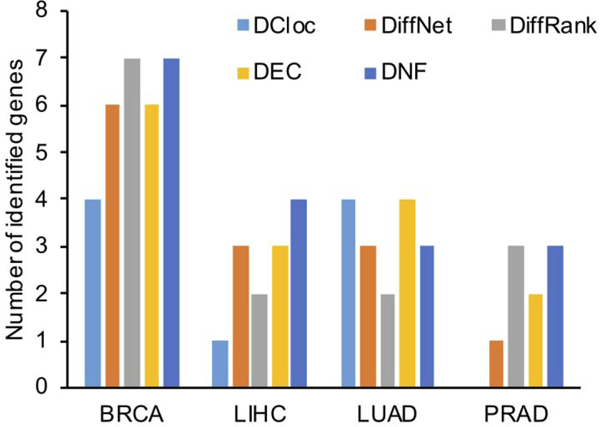
DNF was compared to the other four state-of-the-art methods regarding the number of detected differentiation-related genes. As shown in Table 2, DNF finds the most cell-differentiation related genes in total and presents consistently higher detection rates in each dataset. In addition, the performance of DNF in detecting network rewiring genes is robust to different network skeletons, while other methods are more sensitive to prior network structure. These results, in combination with the results of section 4.2, suggest that DNF is more reliable in detecting and predicting driver genes in both cancer and development across bulk RNA-seq and single-cell RNA-seq datasets.

Table 2.

Comparison of different methods in detecting differentiation-related genes in three single-cell RNA-seq datasets. (numbers in table corresponding to the number of cancer driver genes in top 20 genes detected by different methods in each dataset)

	GSE59114	GSE76381	PRJNA324289	Total
DEC	3	6	1	10
DCloc	2	7	1	10
DiffNet	7	7	2	14
DiffRank	5	5	7	17
DNF	6	8	7	21

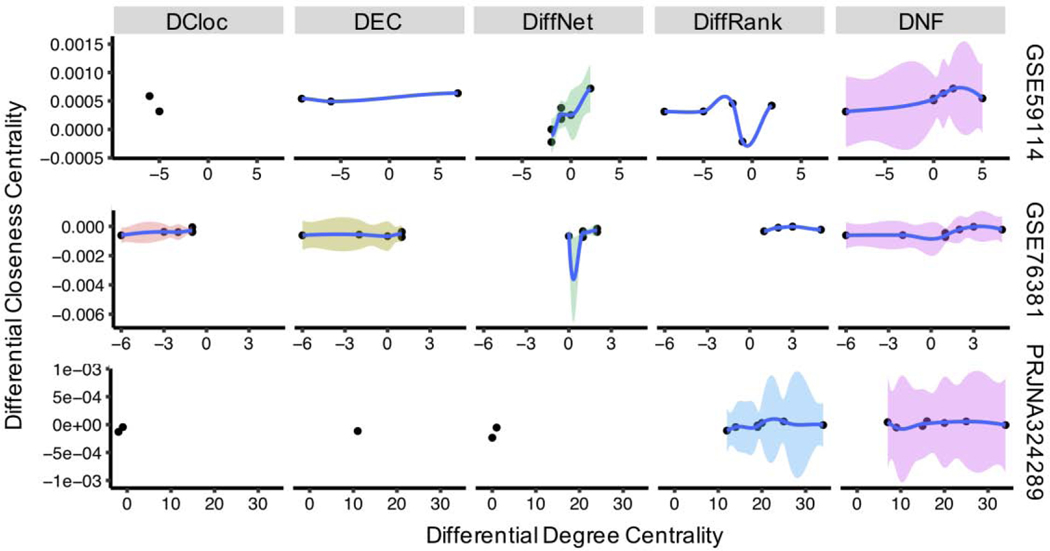
We also focused on the topological features of identified genes by each method. Two basic metrics that measure the importance of nodes in networks were adopted. The first metric is degree centrality, a local topology feature, which captures the important nodes by higher numbers of connections between nodes. The second is closeness centrality, a global topology feature, which captures the important nodes in network by higher average distance among other nodes. Therefore, the differential degree and closeness centrality between two networks capture the local and global topology differences of nodes. To explore the changing tendency and associated confidence intervals of the local and global topology, we used loess regression to connect the nodes detected by each method. As shown in Figure 3, the topological features of identified genes by each method vary a lot. Importantly, the DNF approach presents the greatest change of degree and highest confidence (the area covered by color), which implies that DNF is able to capture both local and global network topological differences.

Figure 3.

The fitted scatter plot of the local (degree centrality) and global (closeness centrality) differential network topology of detected nodes by different methods for three single-cell RNA-seq datasets. Nodes in the plot are fitted by the local polynomial regression, and the color of area represents the confidence area of 95%, this confidence area describes the statistical confidence of tendency in topological differences

4.4. Predict driver genes for neural stem cell differentiation using temporal single-cell RNA-seq datasets

Stem cells are multipotent, having the ability to replenish differentiated cell populations. Identifying the driver genes of differentiation will shed light on new biological questions [36]. However, the molecular mechanisms of stem cell differentiation are still poorly understood [37]. Differentiation is thought to require one or more discrete transitions from one intermediate state to another, each of which is determined by a set of genes that interact in a complex network, instead of a single perturbed gene [38]. Therefore, we combined changing network topology and functional relevance of gene sets to identify the underlying molecular mechanisms.

4.4.1. A temporal single-cell RNA-seq dataset

A temporal single-cell RNA-seq dataset of neural stem cell differentiation (PRJNA324289) [25] partially used in section 4.3 was further analyzed in this section. It contains two continuous differentiation processes, the one is from neural stem cells (NSC) to neural progenitor cells (NPC), the another is from neural progenitor cells to astrocytes (Ast). The functional relevance of selected genes in each processes was confirmed by gene-set-enrichment using the GO web-based tool (the Gene Ontology Consortium [39]).

4.4.2. Prediction of driver genes

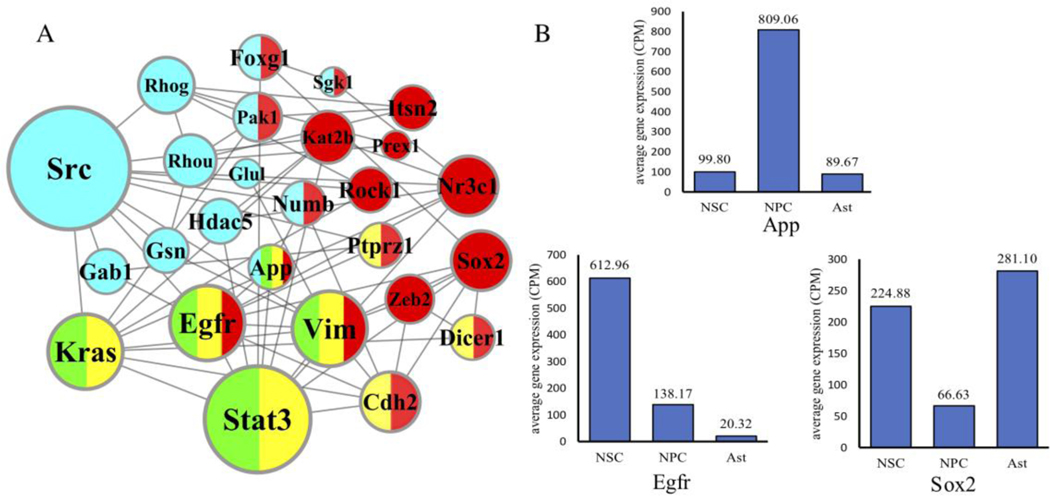
DNF was applied to order the essentiality of genes in both the process of NSC_NPC and NPC_Ast, and the top 100 scored genes (Formula 5) in each process were analyzed by gene ontology enrichment analysis. The enrichment analysis (see Supplementary figure 4) shows that NSC_NPC is significantly enriched in terms relating to cell differentiation and regulation (e.g. glial cell differentiation (GO:0010001) with p-value=9.85e-3, regulation of neuron differentiation (GO:0045664) with p-value=2.56e-3, central nervous system development (GO:0007417) with p-value=4.53e-6), while NPC_Ast is significantly enriched in the enrichment terms relating to cellular and metabolic process (e.g. cellular component biogenesis (GO:0044085) with p-value=2.1e-6, cellular process (GO:0009987) with p-value=1.01e-6, metabolic process (GO:0008152) with p-value=3.03e-4). This implies that the driver genes regulating the continuous differentiation processes mainly occur in NSC_NPC differentiation. Therefore, genes significantly related to enrichment terms of differentiation in NSC_NPC are considered candidate genes, among which three enrichment terms are highlighted, including glial cell differentiation (GO:0010001), astrocyte differentiation (GO:0048708) and regulation of neuron differentiation (GO:0045664). We then examined the first order neighbors of these genes among the top 20 genes identified by DNF. We observed that the network topology of NSC is almost unconnected, while the network topology of NPC is densely connected (see Supplementary Figure 5). After combining above three networks in NPC (Figure 4A), we found that the shortest path between any two nodes in the combined network is lower than six, which makes it a small-world network. Among these genes, Sox2 [40] and Egfr [41] are driver genes of neural stem/progenitor cell differentiation, Src and Cdh2 play important roles in cell development and growth [42], and Hdac5 [43] and Stat3 [44] are essential for axon regeneration. Each of these genes is depicted in a color-coded plot (Fig 4A) where red, green and yellow represent inclusion in one of the three separate GO terms, while blue represents inclusion in the DNF top 20 genes. App is the only gene which is present in all three GO lists in addition to the DNF top 20, and has long been considered a key driver of neurodegenerative disease [45]. Interestingly, App has never been implicated in neuronal differentiation. App and the other two driver genes (Sox2 and Egfr) are all differentially expressed consistently (Figure 4B). Therefore, App could be another potential driver gene regulating the neural stem cell differentiation.

Figure 4.

Network topology and gene expression analysis to identify driver genes in neural stem cell differentiation. (A) The combined network topology of three gene ontology enrichment terms and their first-order neighbors in the top 20 nodes scored by DNF. The size of nodes represents the degree of genes in the network. The red represents the term of GO:0045664, the yellow represents the term of GO:0010001, the green represents the term of GO:0048708, and the blue represents the top 20 nodes score by DNF. (B) The average gene expression of temporal single-cell RNA-seq datasets. The gene expression of three cell types is standardized into read-counts-per-million (CPM) format.

5. Discussion

To assess the performance of DNF in identification and prediction of drivers, we compared its performance with that of four other state-of-the-art methods in simulated, clinical, and experimental datasets. In the simulation study, DNF shows almost best performance in detecting perturbated nodes between two networks. Among bulk RNA-seq datasets from human cancer patients, DNF detects more known cancer genes and survival-related genes, demonstrating superior prediction of cancer biomarkers and prognosis genes. For the murine single-cell RNA-seq datasets, DNF detects more differentiation-related genes than other methods. The topological features of these genes’ network representation shows that DNF is able to capture multiple features of network topology from both local and global domains.

By integrating DNF and biological function enrichment analysis, App is predicted as a driver gene of neural stem cell differentiation. This finding provides compelling motivation for future therapeutic research. The underlying cause of many neurodegenerative diseases is not well understood [46]. It is possible that de-regulation of App and other differentiation factors could lead to the depletion of multipotent neuronal stem cells through unchecked differentiation. Next-generation treatments for neurodegenerative disease may be able to utilize somatic cell reprogramming to activate multipotency among a population of differentiated cells [47]. It is possible that targeting genes such as App (whose function may be reversable) to facilitate reprogramming, may have the added benefit of counteracting the pathological deregulation of these genes.

Differential network methods provide novel insights into the complex mechanisms of life processes, and contribute to the identification of rewiring drivers for gene regulatory networks. We have developed a new differential network analysis approach based on information flow to identify key regulators between two networks under different biological conditions. The novelty of DNF lies in its potential to capture comprehensive topological differences from local to global feature domains, by quantifying the node-to-node information flow in a network. Each node in the network is a distribution-level representation of information flow, while differences between the distribution of nodes in different biological conditions imply the change of multiple features of network structure. Thus, the key driving genes that are not necessarily identifiable as single-scale features or linear combinations of other features are detected by DNF. In summary, DNF is a stable and general method for quantifying the essentiality of genes across different networks. To compare networks of limited overlapping nodes, one can potentially first use a network alignment method (e.g. HGA method [48]) to construct the most similar mapping between the two networks, and then directly apply DNF based on this mapping. Although DNF in this study was applied to undirected networks, it could, in principle be applied to directed networks, with modification to the edge potentials of the underlying network skeleton.

Biography

Jiang Xie: Formal analysis, Writing - Review & Editing; Supervision Fuzhang Yang: Conceptualization, Methodology; Software, Writing - Original Draft, Writing - Review & Editing, Visualization, Formal analysis Jiao Wang: Formal analysis Mathew Karikomi: Formal analysis, Writing - Review & Editing Yiting Yin: Resources, Visualization Jiamin Sun: Investigation Tieqiao Wen: Formal analysis, Writing - Review & Editing Qing Nie: Formal analysis, Writing - Review & Editing Jiang Xie obtained a Ph.D. in Computer Application Technology at Shanghai University in 2008. From September 2011 to December 2012, she was a visiting associate researcher in the Department of Mathematics at the University of California, Irvine, USA. She is an associate professor at the School of Computer Engineering and Science at Shanghai University. She has been working in the research area of Computational Biology and Bioinformatics, high-performance computing and applications since 2004, supported by the Specialized Research Fund for the Doctoral Program of

Higher Education, partly supported by NSFC and the Key Project of Science and Technology Commission of Shanghai Municipality. She is currently a senior member of the Chinese Computer

Federation (CCF) and a member of the Technical Committee of Open System and Parallel Computing under the CCF.

Fuzhang Yang is a postgraduate student at the school of computer science and engineering, Shanghai University. His interests include bioinformatics and system biology.

Jiao Wang obtained a Ph.D. in Neurobiology at Shanghai University in 2012. From October 2012 to October 2013, she conducts postdoctoral research at the University of British Columbia in Canada. From April 2014 to March 2018, she was a assistant professor at the school of life sciences, Shanghai University. She has been working in the research area of Molecular Neurobiology, Biochemistry and molecular biology since 2004, supported by the Specialized Research Fund for the Doctoral Program of Higher Education, partly supported by NSFC and the Key Project of Science and Technology Commission of Shanghai Municipality. She is currently an associate professor at the school of life sciences, Shanghai University

Mathew Karikomi recieved a B.S. in Mathematics from Ohio State in 2017 and is currently a Ph.D. student in Mathematical, Computational, and Systems Biology at U.C. Irvine. His research interests include probabilistic networks and cell-signaling dynamics.

Yiting Yin is a postgraduate student at the school of computer science and engineering, Shanghai University. His interests include bioinformatics and system biology.

Jiamin Sun is a postgraduate student at the school of computer science and engineering, Shanghai University. His interests include bioinformatics and system biology.

Tieqiao Wen obtained a Ph.D. in Microbiology at Huazhong Agricultural University in 1997. From September 1997 to July 1999, he works as a postdoc at the Institute of Genetics, Fudan University. From August 2001 to September 2002, he works as a postdoc in Neurobiology, University of Georgia. He is a professor at the College of Life Science at Shanghai University. He has been working in the research area of Neurobiology since 2002, supported by the National Natural Science Foundation of China, National Key Basic Research and Development Plan of the Ministry of Science and Technology (973 Plan), Science and Technology Commission of Shanghai and the Key Innovation Project of Shanghai Municipal Education Commission. He is a member of the International Human Genome Organization, Chinese Neuroscience Society and American Genetics Society.

Qing Nie is the Chancellor’s Professor of Mathematics and Developmental & Cell Biology, affiliated with the Department of Biomedical Engineering, at the University of California, Irvine. He is the director of The NSF-Simons Center for Multiscale Cell Fate Research. He works on computational systems biology, cell fates, multiscale biology, and tools for analyzing single-cell RNA-seq data, scientific computing, and computational mathematics.