Abstract
The purpose of this study was threefold: i) to analyse the load-velocity relationship of the shoulder press (SP) exercise, ii) to investigate the stability (intra-individual variability) of this load-velocity relationship for athletes with different relative strength levels, and after a 10-week velocity-based resistance training (VBT), and iii) to describe the velocity-time pattern of the SP: first peak velocity [Vmax1], minimum velocity [Vmin], and second peak velocity [Vmax2]. This study involves a cross-sectional (T1, n = 48 subjects with low, medium and high strength levels) and longitudinal (T2, n = 24 subjects randomly selected from T1 sample) design. In T1, subjects completed a progressive loading test up to the 1RM in the SP exercise. The barbell mean, peak and mean propulsive velocities (MV, PV and MPV) were monitored. In T2, subjects repeated the loading test after 10 weeks of VBT. There were very close relationships between the %1RM and velocity attained in the three velocity outcomes (T1, R2: MV = 0.970; MPV = 0.969; PV = 0.954), being even stronger at the individual level (T1, R2 = 0.973–0.997). The MPV attained at the 1RM (~0.19 m·s-1) was consistent among different strength levels. Despite the fact that 1RM increased ~17.5% after the VBT programme, average MPV along the load-velocity relationship remained unaltered between T1 and T2 (0.69 ± 0.06 vs. 0.70 ± 0.06 m·s-1). Lastly, the three key parameters of the velocity-time curve were detected from loads > 74.9% 1RM at 14.3% (Vmax1), 46.1% (Vmin), and 88.7% (Vmax2) of the concentric phase. These results may serve as a practical guideline to effectively implement the velocity-based method in the SP exercise.
Keywords: Velocity-based method, Barbell velocity, Strength, Upper-limb training, Kinematics
INTRODUCTION
The velocity-based training (VBT) approach has been suggested as a more practical alternative to traditional methods to make objective load adjustments within and between sessions and reducing training stress by the use of real-time velocity data [1]. To be effectively implemented, VBT requires the athlete to lift the load at maximal intended velocity in order to describe the load-velocity relationship (i.e., the velocity attained along a spectrum of loads) for a given exercise [2, 3]. Then, practitioners can determine the load-velocity relationship for a given exercise by regression analysis equations (i.e., load-velocity curve) and precisely estimate the relative intensity (%1RM) associated with the resulting velocity [4–7]. This information has relevant practical implications, mainly individualizing training prescription and load monitoring on a day-to-day basis using velocity monitoring systems [5, 8, 9].
Because the load-velocity relationship varies among exercises, the knowledge of particular equations is indispensable to effectively implement the VBT method. Whereas the load-velocity relationship of exercises such as the bench press [5, 10–12], squat [4, 6, 12] or the deadlift [7, 13] has been well established, there is some controversy over the shoulder press (SP) exercise. From the three available studies [14–16], only two of them provided the velocities attained at a given %1RM [14, 16] but with a very large disagreement, especially between 30 and 80% 1RM (from 0.05 to 0.31 m·s-1). Additionally, these studies only present data from the mean velocity (MV). While MV is probably the most common variable used for VBT, there are other measures of interest provided by most of the current barbell velocity monitoring devices, such as the peak velocity (PV) or the mean propulsive velocity (MPV, average bar velocity values of the propulsive phase, the portion of the concentric phase during which bar acceleration is greater than acceleration due to gravity) [17]. However, there are no reports showing MPV and PV data during the SP exercise.
The stability of the load-velocity relationship after a resistance training programme is another aspect on which there is no consensus. While some studies did not find significant changes in the load-velocity relationship when the 1RM increased after a strength training intervention [5, 18], other authors reported modifications of this relationship after a period of training [15]. Moreover, it has been suggested that the velocity value attained at each %1RM (i.e., load-velocity curve) does not present significant differences between subjects with different strength levels, for instance, between athletes with high and low relative strength ratio (RSR = 1RM weight lifted/body mass) [5–7, 18]. Therefore, extending the knowledge about the influence of a resistance training period or the strength level on the stability of the SP load-velocity relationship is deemed necessary.
A main biomechanical aspect that coaches and practitioners dealing with resistance training should consider is the identification of the so-called sticking region [19–21]. During a lift at near maximal loads (~80% 1RM) there is a zone where the upward barbell movement decelerates or even stops completely for a short time (sticking region). At that point, the athlete experiences a disproportionately large increase in the difficulty to continue the lift, which may lead to muscle failure and eventually cause an injury [19]. The sticking region can be identified from the velocity-time curve [4, 11] by three key parameters: the first peak velocity attained during the lift (Vmax1), the minimum velocity that occurs due to the sticking (Vmin) and the second peak barbell velocity indicating that the athletes overcome the critical zone (Vmax2). The identification of the position of these three parameters within the concentric phase of the lift would provide great practical implications for athletes and coaches, for instance, to incorporate strategies such as technical execution modifications (e.g., reduction in the range of motion) or the use of external objects (e.g., elastic bands) to more easily solve this region [19, 20]. Nonetheless, information about the sticking region of the SP is lacking.
The purpose of this study was threefold: i) to analyse the loadvelocity relationship of the shoulder press (SP) exercise, ii) to investigate the stability (intra-individual variability) of this load-velocity relationship for athletes with different relative strength levels, and after a 10-week velocity-based resistance training (VBT), and iii) to describe the velocity-time pattern of the SP: first peak velocity [Vmax1], minimum velocity [Vmin], and second peak velocity [Vmax2].
MATERIALS AND METHODS
Design
This study involves a cross-sectional design (T1) and a pre-post intervention with no control group (T2). In T1, all 48 subjects performed a strength test with increasing loads up to the 1RM to determine the full individual load-velocity relationship of the SP exercise and identify the sticking region key parameters of this exercise. In T2, a random subset of the total sample (24 subjects) completed a 10-week VBT programme (SP exercise, 2 sessions/week, 3 sets, 65–90% 1RM, 4 min inter-set rest) and repeated the same progressive loading test on a second occasion (T2) to examine the stability of the load-velocity relationship.
Subjects
Forty-eight men (age 22.1 ± 3.5 years, body mass 76.3 ± 8.8 kg, height 175.8 ± 5.9 cm) volunteered to take part in this study. Inclusion criteria were: i) having a relative strength ratio (RSR = 1RM weight lifted/body mass) higher than 0.60 in the SP exercise and ii) no health problems, physical limitations or musculoskeletal injuries that could affect the technical executions. Participants had at least 4 years of strength-training experience. In order to study whether the velocity attained with each %1RM was dependent upon individual strength levels, participants were ranked according to their RSR and divided into three equal size groups: G1 (n = 16, RSR < 1/3 of the sample), G2 (n = 16, RSR between 1/3 and 3/3 of the sample) and G3 (n = 16, RSR > 3/3 of the sample). The study, which was conducted according to the Declaration of Helsinki, was approved by the Ethics Commission of the University of Murcia (ID: 2504/2019). All participants signed a written consent form after being informed of the purpose and experimental procedures.
Testing procedures
The week before T1, subjects underwent two familiarization sessions. The individual load-velocity relationship and 1RM were determined in a third session through an incremental loading test as explained below.
One-repetition maximum test (1RM): After at least three full rest days following the familiarization sessions (T1) and the end of the resistance training programme (T2), the individual load-velocity relationship was determined by means of a progressive loading test up to the 1RM in the SP exercise [10, 22]. The initial load was set at 20 kg for all subjects and was progressively increased by 10 kg until the MPV was lower than 0.5 m·s-1. Thereafter, load was individually adjusted with smaller increments (5 down to 2.5 kg) so that the 1RM strength could be precisely determined. The heaviest load that each subject could properly lift, while completing the full range of motion and without any external help, was considered to be his 1RM. Three attempts were executed for light (< 50% 1RM), two for medium (50–80% 1RM), and only one for the heaviest (> 80% 1RM) loads. Inter-set rest intervals were 3 min for the light and medium loads (< 50–80% 1RM) and 5 min for the heaviest loads (> 80% 1RM). Only the best repetition (fastest and executed correctly) at each load was considered for subsequent analysis. Subjects performed a total of 6.1 ± 0.9 increasing loads.
Participants completed a front SP with full range of motion, seated on an inclined bench, with the back of the bench 10º leaning backwards, where they rested their head, back and gluteus [22]. Feet rested flat on the floor, and pronated hands were placed on the barbell slightly wider (5–7 cm) than shoulder width. Participants were not allowed to raise the gluteus or back off the bench. The barbell was lowered in a continuous motion until it contacted the upper chest, and it was then immediately lifted back until the elbows were fully extended. Arms were moved mostly parallel in the frontal plane. The eccentric phase was performed at a controlled MPV (~0.50–0.70 m·s-1). The concentric phase of each repetition was always performed at maximal intended velocity (i.e., as fast as possible). In addition, T1 and T2 were conducted i) at the same time of day (11:00–13:00 h) to control the circadian rhythms effects [23], ii) under similar environmental conditions (21–22 ºC and 53–62% humidity) and iii) after an identical warm up [24].
Resistance training programme: Following the initial evaluation (T1), half of the participants (n = 24) were randomly selected to undergo a 10-week VBT programme of the SP exercise. This selection was made to ensure the quality of the intervention according to the human and technical resources available. During the intervention, subjects did not perform different training activities other than those scheduled for the study. All training variables, including relative intensity (65–90% 1RM), number of sets (three), between-sets (4 min) and between-sessions (72 hours) recovery, frequency (2 sessions per week) and the number of times each %1RM was used, were identical for all participants (Table 1). Participants performed the same technique as during the progressive loading test: full range of motion, controlled eccentric phase and concentric phase at maximal intended velocity [25]. Since the resistance training programme was based on the velocity-based approach, a target MPV to be attained in the first (usually the fastest) repetition of the SP exercise during the first set of each training session was used as an estimation of %1RM. Consequently, before starting the first set in each training session, adjustments in the proposed load (kg) were made when needed so that the MPV of the first repetition matched that programmed velocity (± 0.03 m·s-1). Once the load (kg) was adjusted, it was maintained for the 3 training sets.
TABLE 1.
Descriptive characteristics of the velocity-based resistance training (VBT) program performed.
| Scheduled | Wk 1 | Wk 2 | Wk 3 | Wk 4 | Wk 5 | Wk 6 | Wk 7 | Wk 8 | Wk 9 | Wk 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| %1RM | ~65% | ~70% | ~70% | ~75% | ~75% | ~80% | ~80% | ~85% | ~85% | ~90% |
| Sets x Reps | 3 x 8 | 3 x 6 | 3 x 6 | 3 x 5 | 3 x 5 | 3 x 4 | 3 x 4 | 3 x 3 | 3 x 3 | 3 x 2 |
| Target MPV (m·s-1) | 0.78 | 0.69 | 0.69 | 0.61 | 0.61 | 0.51 | 0.51 | 0.43 | 0.43 | 0.35 |
1RM: one-repetition maximum; Wk.: week; Reference rep: maximal intended velocity repetition performed at the end of each session’s warm-up to ensure that the load (kg) to be used matched the velocity associated with the intended %1RM.
Measurement equipment and variables analysed
A Smith machine (Multipower Fitness Line, Peroga, Murcia, Spain) was used for all sessions. The weight of the barbell, including the guidance system, totalled 20 kg. Extra load was added by sliding calibrated weight discs (Eleiko, Sport AB, Halmstad, Sweden) onto both ends of the barbell. Each lift performed during testing (T1, T2) and training sessions was recorded using a linear velocity transducer with a sampling frequency of 1,000 Hz (T-Force System, Ergotech, Murcia, Spain). This technology has been tested for barbell velocity measurement with excellent results of reproducibility and repeatability, as detailed elsewhere [26, 27]. Four velocity outcome variables were included in the analysis of the L-V relationship [5, 6, 11]:
Mean velocity (MV): average of the barbell velocity values for the total concentric phase of each repetition.
Mean propulsive velocity (MPV): average of the barbell velocity values of the propulsive phase, so removing the braking phase. The propulsive phase was defined as that portion of the concentric phase during which bar acceleration is greater than acceleration due to gravity (≥ -9.81 m·s-2), while the braking phase was the part of the concentric action during which acceleration is lower than gravity, i.e., a deceleration [17]. Moreover, the contribution (%) of both phases for each lift was registered.
Peak velocity (PV): the maximum at a specific instant barbell velocity value recorded at a specific instant (1 ms) during the concentric phase.
Mean test velocity (MPVAve): the mean of the MPV values, calculated each 5% from 30 to 100% 1RM, and derived from secondorder polynomial fits to load-velocity data for each subject’s incremental loading test.
1RM velocity (MPV1RM): MPV value attained with the 1RM load.
Each subject’s velocity-time curve corresponding to the 1RM load was examined to identify, both in absolute (m·s-1 and cm) and relative (%) terms, the three key parameters related to the sticking region [4, 11, 28, 29]: the first peak velocity (Vmax1), the minimum velocity (Vmin) and the second peak velocity (Vmax2).
Statistical analysis
Standard statistical methods were used for the calculation of means, standard deviation (SD), coefficient of determination (R2), standard error of the estimate (SEE), Pearson correlation coefficients (r), intraclass correlation coefficient (ICC) and 95% confidence intervals (95% CI). Relationships between load (% 1RM) and velocity variables were studied by fitting second-order polynomials to data. Normality of the data was verified using the Shapiro-Wilk test. Cross-sectional differences between subjects with different strength levels (G1, G2 and G3) were examined through a one-way ANOVA with Scheffé’s post-hoc comparisons. Pre-post intervention (T1 vs. T2) velocity changes for each load (%1RM) were analysed by means of a relatedsample t-test. Effect size was estimated by partial eta squared (η2 p) for ANOVA comparisons and Cohen’s d (d) for the t-test [30]. Significance was accepted at p < 0.05. Analyses were performed using SPSS software version 20.0 (IBM Corp., Armonk, NY).
RESULTS
Relationship between relative load (%1RM) and velocity variables
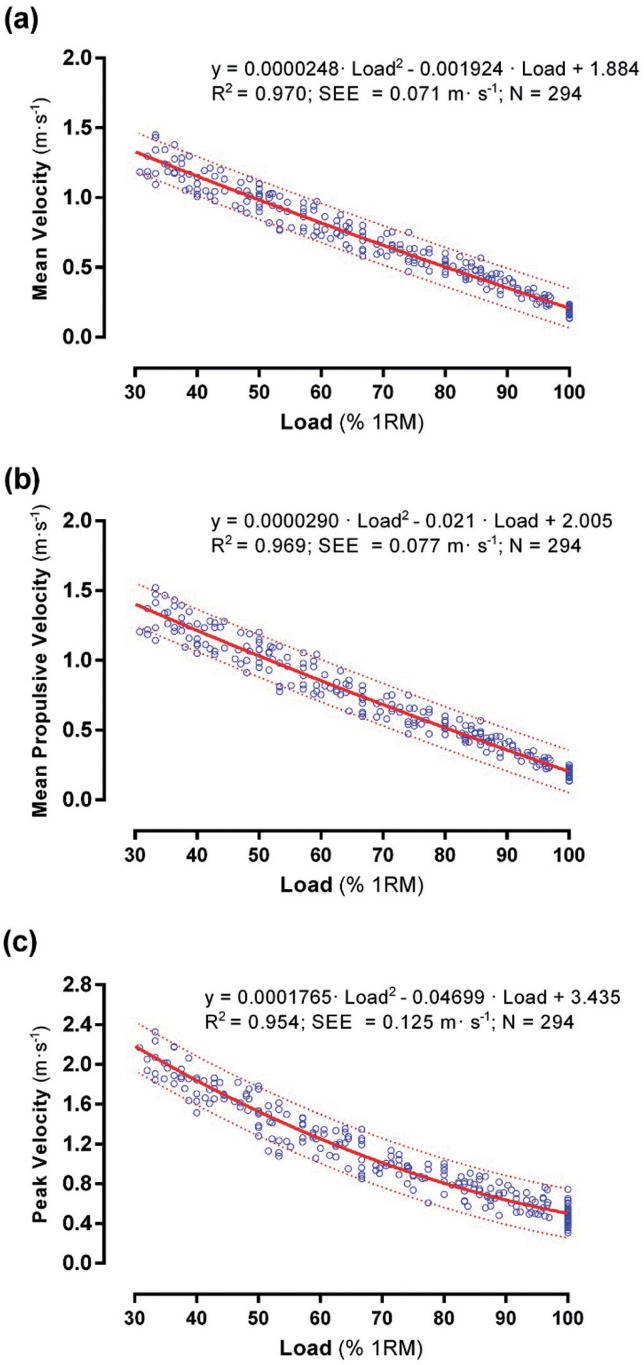
After plotting MV, MPV and PV against %1RM and fitting a second-order polynomial to all respective raw load-velocity data pairs, a very close relationship was found for the three velocity variables: MV (R2 = 0.970, SEE = 0.071 m·s-1, p < 0.001), MPV (R2 = 0.969, SEE = 0.077 m·s-1, p < 0.001) and PV (R2 = 0.954, SEE = 0.125 m·s-1, p < 0.001) (Figure 1). The analysis of the individual curves (i.e., fit of the individual load-velocity relationship) showed a closer fit for each variable: MV (R2 = 0.996 ± 0.003, R2 range: 0.989–1.000, p < 0.001), MPV (R2 = 0.997 ± 0.003, R2 range: 0.988–1.000, p < 0.001), and PV (R2 = 0.995 ± 0.005, R2 range: 0.973–1.000, p < 0.001). The MV, MPV and PV values attained with each %1RM were obtained from these polynomial fits, from 40% 1RM onwards, in 5% increments (Table 2). The MPV1RM was 0.19 ± 0.03 m·s-1, ranging from 0.10 m·s-1 to 0.24 m·s-1.
FIG. 1.
Relationships between relative load (%1RM) and barbell velocity: a) mean velocity (MV); b) mean propulsive velocity (MPV); and c) peak velocity (PV) for the shoulder press (SP) exercise. Note: Data obtained from raw load-velocity values derived from the progressive isoinertial loading tests performed in T1 and T2. Solid lines show the curve fitted to the data. Dotted lines indicate limits within which 95% of predictions will fall.
TABLE 2.
Mean velocity (MV), mean propulsive velocity (MPV), and peak velocity (PV) attained with each relative intensity (%1RM) and relative contribution of the propulsive and braking phases to the total concentric duration in the shoulder press (SP) exercise (n = 48).
| Load (% 1RM) | MV (m·s -1) | MV 95% Confidence Interval | MPV (m·s-1) | MPV 95% Confidence Interval | PV (m·s-1) | PV 95% Confidence Interval | Propulsive Phase (%) | Braking Phase (%) |
|---|---|---|---|---|---|---|---|---|
| 40 | 1.15 ± 0.08 | 1.13–1.18 | 1.22 ± 0.08 | 1.20–1.25 | 1.82 ± 0.14 | 1.78–1.87 | 84 | 16 |
| 45 | 1.07 ± 0.08 | 1.04–1.09 | 1.13 ± 0.08 | 1.11–1.15 | 1.67 ± 0.13 | 1.63–1.71 | 87 | 13 |
| 50 | 0.98 ± 0.08 | 0.96–1.00 | 1.04 ± 0.08 | 1.02–1.06 | 1.53 ± 0.13 | 1.49–1.57 | 89 | 11 |
| 55 | 0.90 ± 0.08 | 0.88–0.92 | 0.96 ± 0.07 | 0.94–0.98 | 1.39 ± 0.14 | 1.35–1.44 | 91 | 9 |
| 60 | 0.82 ± 0.07 | 0.80–0.84 | 0.87 ± 0.07 | 0.85–0.89 | 1.26 ± 0.14 | 1.22–1.31 | 93 | 7 |
| 65 | 0.74 ± 0.07 | 0.72–0.76 | 0.78 ± 0.07 | 0.76–0.80 | 1.14 ± 0.14 | 1.09–1.18 | 94 | 6 |
| 70 | 0.66 ± 0.07 | 0.64–0.68 | 0.69 ± 0.06 | 0.67–0.71 | 1.02 ± 0.14 | 0.97–1.07 | 96 | 4 |
| 75 | 0.58 ± 0.07 | 0.56–0.60 | 0.61 ± 0.06 | 0.59–0.62 | 0.91 ± 0.14 | 0.86–0.95 | 97 | 3 |
| 80 | 0.50 ± 0.06 | 0.49–0.52 | 0.51 ± 0.06 | 0.49–0.52 | 0.80 ± 0.15 | 0.76–0.85 | 98 | 2 |
| 85 | 0.43 ± 0.05 | 0.41–0.44 | 0.43 ± 0.05 | 0.41–0.44 | 0.71 ± 0.15 | 0.66–0.76 | 99 | 1 |
| 90 | 0.35 ± 0.05 | 0.33–0.36 | 0.35 ± 0.04 | 0.34–0.36 | 0.62 ± 0.16 | 0.56–0.67 | 100 | 0 |
| 95 | 0.27 ± 0.04 | 0.26–0.28 | 0.27 ± 0.04 | 0.26–0.28 | 0.53 ± 0.17 | 0.47–0.58 | 100 | 0 |
| 100 | 0.19 ± 0.03 | 0.18–0.20 | 0.19 ± 0.03 | 0.18–0.20 | 0.45 ± 0.19 | 0.39–0.51 | 100 | 0 |
Table 2 shows the contribution of the propulsive and braking phases to the total concentric duration from 40 to 100% 1RM. As can be observed, the propulsive phase accounted for ~84% of concentric duration at 40% 1RM, gradually increasing until reaching 100% at 90% of the 1RM load. Also, a very close association (R2 = 0.91, p < 0.001) was found between the %1RM and relative contribution of the propulsive phase (y): y = -0.0037x2 + 0.7985x + 58.166.
Predicting relative load (%1RM) from velocity data
Because estimating the %1RM from velocity measurements is one of the main advantages of the load-velocity relationship, the resulting prediction equations for estimating this parameter from the MPV, MV and PV are described below:
From MPV: %1RM = 10.428 MPV2 – 73.583 MPV + 114.46 (R² = 0.973, SEE = 4.13%, p < 0.001)
From MV: %1RM = 10.592 MV2 – 77.083 MV + 115.35 (R² = 0.973, SEE = 4.14%, p < 0.001)
From PV: %1RM = 9.6445 PV2 – 65.272 PV + 127.21 (R² = 0.961, SEE = 5.07%, p < 0.001)
Stability in the load-velocity relationship regardless of individual relative strength
A sub-analysis was conducted in order to study whether the velocity attained with each %1RM was dependent upon individual strength levels. Whereas three significantly (F-value = 79.771, p < 0.001, η2 p = 0.44) different strength levels were identified (G1: RSR = 0.77 ± 0.05, G2: RSR = 0.90 ± 0.05 and G3: RSR = 1.06 ± 0.08), no significant differences in the MPVAve (F-value = 1.269, p = 0.291, η2 p = 0.05) and MPV1RM (F-value = 0.851, p = 0.434, η2 p = 0.05) variables were found between them (Table 3).
TABLE 3.
Comparison of mean propulsive velocity (MPV) for the load-velocity spectrum (MPVAve) and attained with the 1RM (MPV1RM) between subgroups of different strength level.
| Subgroup | RSR | MPV Ave (m·s-1) | MPV1RM (m·s-1) |
|---|---|---|---|
| G1 (n = 16) | 0.77 ± 0.05* | 0.78 ± 0.06 | 0.19 ± 0.02 |
| G2 (n = 16) | 0.90 ± 0.05* | 0.80 ± 0.05 | 0.20 ± 0.02 |
| G3 (n = 16) | 1.06 ± 0.08* | 0.77 ± 0.06 | 0.20 ± 0.03 |
Note: RSR: Relative strength ratio, defined as 1RM value divided by body mass.
All groups were significantly different from each other (p < 0.05).
Stability in the load-velocity relationship after a resistance training programme
Table 4 shows the differences in MPV attained with each %1RM for the 24 subjects who performed the incremental loading test twice (T1 and T2) following 10 weeks of VBT. Compliance with the RT programme was 100% of all sessions scheduled. The agreement (T1 vs. T2) of the individual load-velocity relationship was very high among the 24 subjects (ICC = 0.998; 95% CI: 0.996–0.999). From T1 to T2, the mean 1RM value increased by 17.5 ± 9.8% (changing from 57.6 ± 10.2 kg to 67.7 ± 12.1 kg). Despite this fact, the difference in MPVAve was only 0.01 ± 0.03 m·s−1 (p = 0.582, d = 0.17), changing from 0.69 ± 0.06 m·s−1 to 0.70 ± 0.06 m·s−1.
TABLE 4.
Changes (m·s-1) in the mean propulsive velocity (MPV) attained with each relative load (%1RM), from initial test (T1) to retest (T2), after 10 weeks of velocity-based resistance training (VBT), in the shoulder press (SP) exercise. Values are mean ± SD (N = 24).
| Load (% 1RM) | T1 | T2 | Difference (T1–T 2) | ES | p-value |
|---|---|---|---|---|---|
| 40 | 1.21 ± 0.09 | 1.23 ± 0.09 | -0.02 | 0.22 | 0.621 |
| 45 | 1.12 ± 0.09 | 1.14 ± 0.08 | -0.01 | 0.23 | 0.362 |
| 50 | 1.03 ± 0.08 | 1.04 ± 0.08 | -0.01 | 0.13 | 0.652 |
| 55 | 0.95 ± 0.08 | 0.96 ± 0.07 | -0.01 | 0.13 | 0.540 |
| 60 | 0.86 ± 0.07 | 0.87 ± 0.07 | -0.01 | 0.14 | 0.461 |
| 65 | 0.78 ± 0.07 | 0.78 ± 0.07 | 0.00 | < .01 | 0.393 |
| 70 | 0.69 ± 0.07 | 0.69 ± 0.06 | 0.00 | < .01 | 0.732 |
| 75 | 0.61 ± 0.06 | 0.61 ± 0.06 | 0.00 | < .01 | 0.938 |
| 80 | 0.51 ± 0.06 | 0.51 ± 0.06 | 0.00 | < .01 | 0.917 |
| 85 | 0.43 ± 0.06 | 0.43 ± 0.05 | 0.00 | < .01 | 0.740 |
| 90 | 0.35 ± 0.05 | 0.35 ± 0.04 | 0.00 | < .01 | 0.921 |
| 95 | 0.27 ± 0.04 | 0.27 ± 0.04 | 0.00 | < .01 | 0.416 |
| 100 | 0.19 ± 0.04 | 0.18 ± 0.03 | 0.01 | 0.28 | 0.584 |
| Mean | 0.69 ± 0.06 | 0.70 ± 0.06 | 0.00 | 0.17 | 0.582 |
Note: ES: Effect size (Cohen’s d).
Analyses of the sticking region in the shoulder press exercise
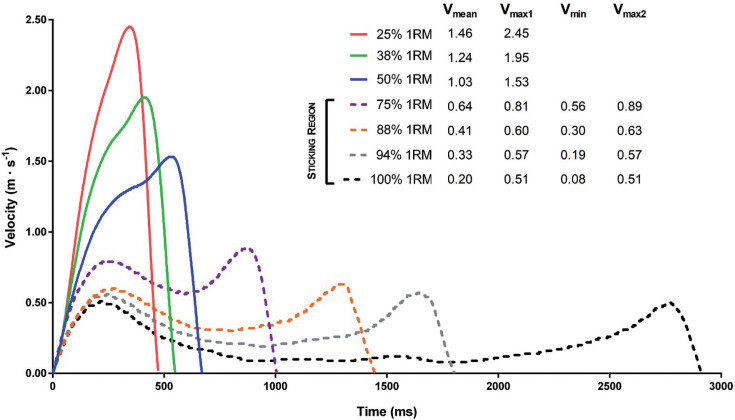
As shown in Table 5, the mean concentric displacement of the barbell was 53.4 ± 6.5 cm. The representative parameters of the sticking region (Vmax1, Vmin, and Vmax2) were only detected at loads higher than 74.9% ± 12.7% 1RM. The position in which these parameters appeared during the concentric phase of the 1RM load, in absolute (cm) and relative terms (%), was: Vmax1 (7.5 ± 1.8 cm and 14.3 ± 4.18%), Vmin (24.6 ± 4.7cm and 46.1 ± 6.48%), and Vmax2 (47.4 ± 6.5 cm and 88.7 ± 3.62%) (Table 5). An example of the actual velocity-time curve for a representative subject when lifting each load of the progressive loading test is provided in Figure 2.
TABLE 5.
One-repetition maximum absolute (1RM) and relative to body weight (RSR), mean propulsive velocity (MPV) attained with the 1RM load (MPV1RM), concentric displacement, lowest load in which the three parameters of the sticking region were identified and sticking region’s key parameters at 1RM load (n = 48).
| Mean SD | ||
|---|---|---|
| 1RM (kg) | 69.1 ± 10.6 | |
| RSR | 0.91 ± 0.13 | |
| MPV1RM (m·s-1) | 0.19 ± 0.03 | |
| Concentric displacement (cm) | 53.4 ± 6.5 | |
| Lowest relative load with sticking region (%1RM) | 74.9 % ± 12.7% | |
| First peak velocity (Vmax1) | MPV (m·s-1) | 0.39 ± 0.10 |
| Position (cm) | 7.5 ± 1.8 | |
| Position (%) | 14.3 ± 4.18 | |
| Minimum velocity (Vmin) | MPV (m·s-1) | 0.11 ± 0.08 |
| Position (cm) | 24.6 ± 4.7 | |
| Position (%) | 46.1 ± 6.48 | |
| Second peak velocity (Vmax2) | MPV (m·s-1) | 0.46 ± 0.09 |
| Position (cm) | 47.4 ± 6.5 | |
| Position (%) | 88.7 ± 3.62 | |
FIG. 2.
Example of the actual velocity-time curve for a representative subject when lifting each load of the progressive loading test. Note: Solid lines represent loads (~ < 75%) in which the three sticking region parameters were not detected, whereas dotted lines show loads in which the first peak barbell velocity (Vmax1), minimum velocity (Vmin), and second peak barbell velocity (Vmax2) were identified.
DISCUSSION
This study aimed to examine the SP exercise using the velocity-based method in order to: i) analyse the load-velocity relationship, ii) investigate the stability (intra-individual variability) of this load-velocity relationship for athletes with different relative strength levels, and after a 10-week VBT, and iii) describe the velocity-time pattern of this exercise. Taking into account these objectives, the main findings of the current investigation were: i) a very close relationship (R2 ≥ 0.961) between the three velocity variables (MV, MPV, and PV) and the relative load (% 1RM), ii) no differences in the loadvelocity relationship between subjects with different relative strength levels, and iii) high stability of this load-velocity relationship despite the notable increase in the 1RM strength. Furthermore, to the best of our knowledge, iv) this is the first study describing the sticking region’s key parameters during the SP exercise.
Second-order polynomials revealed a very close association between the %1RM and the three velocity variables, especially for MV (R2 = 0.970) and MPV (R2 = 0.969) (Figure 1). These relationships agree with previous studies examining the SP exercise (R2 ≥ 0.963) [14, 16]. Nevertheless, due to the fact that this is the first study providing the SP load-velocity relationship for MPV and PV, no comparisons can be made with other investigations concerning these variables. On the other hand, similar to preceding investigations [4, 6, 10, 11, 15, 18], closer relationships were found when the individual load-velocity was explored (R2 = 0.973–0.996). Overall, these extremely close associations, both general and individual, allow practitioners to determine with high accuracy which %1RM is being used in the SP exercise as soon as the first repetition of a set is performed with maximal voluntary velocity [1, 5].
As observed in Table 2, differences in MV and MPV in each %1RM increment (from 40 to 100% 1RM) varied between 0.07 and 0.10 m·s-1 (mean = 0.08 m·s-1). Therefore, an improvement (or reduction) by 5% in the 1RM could be considered if a subject increases (or decreases) by 0.07–0.10 m·s-1 his MV or MPV against an absolute load (kg), after a resistance training programme or detraining period [5, 6]. Taking into account the whole spectrum of %1RM and strength levels, the average test velocity of the SP was 0.72 m·s-1 and 0.75 m·s-1 for the MV and MPV, respectively. Whereas no previous investigations have examined the average velocity of the SP load-velocity spectrum using the MPV, average test velocity for the MV obtained in the current study is in agreement with that reported by García-Ramos et al. [14] (0.75 m·s-1) and slightly higher than that reported by Garnacho-Castaño et al. [16] (0.64 m·s-1). However, the velocity attained with the 1RM load recorded in our study matched the values obtained in both cited studies (0.19 m·s-1) [14, 16]. This comparison can be made because the 1RM velocity is identical for MPV and MV variables, since there is no braking phase from 90% 1RM (Table 2). Moreover, this MPV1RM has been found very similar to that described in other upper-limb exercises, both pulling (e.g., bench press = 0.18 m·s-1) [5, 10] and pushing (e.g., pull-up = 0.20 m·s-1) [18].
New data about the contribution of the propulsive and braking phases during the SP exercise are described in Table 2. Despite the lack of previous data, the results obtained in the current study (from ~84% at 40% 1RM to 100% at 90% 1RM) were quite similar to those reported in the bench press exercise (from ~81% at 40% 1RM to 100% at 85% 1RM) [10]. Moreover, similar to preceding analyses on the bench press (R2 = 0.92) and prone bench pull (R2 = 0.91) [10], a strong association was found between the %1RM and relative contribution of the propulsive phase in the SP (R2 = 0.91). This fact will enable coaches and athletes to precisely determine how much contribution the propulsive phase will have in each %1RM programmed for the training session.
The SP load-velocity relationship was found independent of the relative strength as well as the notable increase in the 1RM strength generated after a VBT. Relative to the first aspect, whereas the subanalysis revealed three significantly different groups in the RSR, no significant differences in the MPVAve and MPV1RM were found between the different strength levels (Table 3). This independence of the loadvelocity relationship upon the RSR was also previously found in exercises such as the bench press [5], squat [6], and pull-up [18]. Other authors have suggested an effect of participant characteristics, such as gender [14, 15], or age [31], on the load-velocity relationship. Therefore, future research should extend the knowledge about this aspect. On the other hand, in agreement with previous test-retests examining the stability of the load-velocity relationship after a training intervention [5, 18], no significant changes were identified either in the MPVAve (T1 = 0.69 m·s-1 vs. T2 = 0.70 m·s-1) or each specific %1RM (differences ≤ 0.02 m·s-1, p = 0.582) after a notable increase in the 1RM strength (∼17.5%). Therefore, these results support the usability of the load-velocity relationship to determine or adjust the %1RM despite the different relative strength or 1RM changes.
To the best of our knowledge, this is the first study examining the sticking region key parameters in the SP exercise. In the current research, the sticking region parameters Vmax1, Vmin, and Vmax2 were only detected at loads higher than 74.9% 1RM (an example is illustrated in Figure 2). These results agree with previous investigations demonstrating, by using the bench press exercise, that the sticking region occurs not only against the maximal load (i.e., 100% 1RM), but against sub-maximal %1RM (> 70 %1RM) [32, 33]. Identifying the intensity from which the sticking region appears allows the load magnitude to be adapted according to the main objective or status of the athlete. For instance, overcoming the sticking region during resistance training with intensities ≥ 75% 1RM would likely maximize the long-term neuromuscular and functional adaptations, as previously observed in other exercises such as the squat [34] and bench press [35]. Conversely, avoiding this zone of biomechanical disadvantage by using loads < 75% 1RM could be an interesting strategy to reduce the muscle tension and fatigue in post-injury athletes or during specific periods (e.g., tapering). On the other hand, the position (%) and MPV (m·s-1) in which these parameters occur was found to be different to those found in the bench press following the same methodology [11]. Briefly, the Vmin but especially the Vmax1 were higher in SP exercise (Vmin = 0.11 m·s-1, Vmax1 = 0.39 m·s-1) in comparison with the bench press (Vmin = 0.08 m·s-1, Vmax1 = 0.20 m·s-1), whereas the Vmax2 was the same (0.46 m·s-1). Regarding the position, the moments in which the Vmax1 (∼12–14%) and Vmax2 (∼88–89%) appeared were similar between both exercises, whereas they differed in the Vmin position (SP = 46.1%, bench press = 35.5%) [11].
It is important to acknowledge that the lack of a control group is the main limitation of the present study, given that we cannot determine whether training cessation or performing another type of training could have affected, in a different way, the stability of the loadvelocity relationship. Future research is needed to confirm the current results. Furthermore, no women were included in the current investigation, so we encourage these analyses to be replicated in the female population. Lastly, although the load-power relationship would provide fewer practical applications than the load-velocity relationship [10], it would be interesting to analyse it, as it has been conducted previously in the bench press [17] and back squat [4] exercises.
CONCLUSIONS
The main findings of the current investigation may serve as a practical guideline to effectively implement the velocity-based method in the SP exercise. Specifically:
The extremely close relationships (R2 ≥ 0.961) between barbell velocity and %1RM enable coaches to determine the load (%1RM) being used by an athlete “on the go”, as soon as the first repetition with any given absolute load is performed with maximal voluntary effort.
Changes in SP performance after a resistance training intervention could be accurately assessed without the need to perform a maximal test or repetitions to failure test. Regarding this matter, an increase of ~0.08 m·s-1 in MPV or MV against the same absolute load (kg) lifted before and after a training programme would mean an enhancement of ~5% in the 1RM.
Practitioners can determine with great accuracy how much contribution the propulsive phase will have in the %1RM programmed for the SP training session by using the following equation: % propulsive phase = -0.00372 + 0.7985x + 58.166.
Due to the high stability of the L-V relationship, coaches could benefit from the different equations provided for training prescription and load monitoring in the SP exercise, both with subjects of different strength levels and with the same subject at different time points of the season.
Information about the position of the sticking region key parameters allows practitioners to incorporate strategies to increase neuromuscular adaptations in this exercise. For example, against high loads (> 75% 1RM), athletes could use elastic bands at ~50% of the concentric phase (Vmin) or avoid this critical point through partial repetitions starting above the middle of the displacement.
Acknowledgments
The authors wish to thank the participants for their invaluable contribution to the study.
Conflict of interest declaration
No funding was received for this study and the authors report no conflict of interest.
REFERENCES
- 1.González Badillo JJ, Sánchez-Medina L, Pareja-Blanco F, Rodriguez-Rosell D. Fundamentals of velocity-based resistance training. Ergottech; 2017. [Google Scholar]
- 2.González-Badillo JJ, Rodríguez-Rosell D, Sánchez-Medina L, Gorostiaga EM, Pareja-Blanco F. Maximal intended velocity training induces greater gains in bench press performance than deliberately slower half-velocity training. Eur J Sport Sci. 2014;14(8):772–781. doi: 10.1080/17461391.2014.905987. [DOI] [PubMed] [Google Scholar]
- 3.Pareja-Blanco F, Rodríguez-Rosell D, Sánchez-Medina L, Gorostiaga EM, González-Badillo JJ. Effect of movement velocity during resistance training on neuromuscular performance. Int J Sports Med. 2014;35(11):916–924. doi: 10.1055/s-0033-1363985. [DOI] [PubMed] [Google Scholar]
- 4.Martínez-Cava A, Morán-Navarro R, Sánchez-Medina L, González-Badillo JJ, Pallarés JG. Velocity- and power-load relationships in the half, parallel and full back squat. J Sports Sci. 2019;37(10):1088–1096. doi: 10.1080/02640414.2018.1544187. [DOI] [PubMed] [Google Scholar]
- 5.González-Badillo JJ, Sánchez-Medina L. Movement velocity as a measure of loading intensity in resistance training. Int J Sports Med. 2010;31(5):347–352. doi: 10.1055/s-0030-1248333. [DOI] [PubMed] [Google Scholar]
- 6.Sánchez-Medina L, Pallarés J, Pérez C, Morán-Navarro R, González-Badillo J. Estimation of relative load from bar velocity in the full back squat exercise. Sport Med Int Open. 2017;1(2):E80–E88. doi: 10.1055/s-0043-102933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Morán-Navarro R, Martínez-Cava A, Escribano-Peñas P, Courel-Ibáñez J. Load-velocity relationship of the deadlift exercise. Eur J Sport Sci. 2020:1–19. doi: 10.1080/17461391.2020.1785017. [DOI] [PubMed] [Google Scholar]
- 8.Weakley J, Mann B, Banyard H, Mclaren S, Scott T, Garcia-Ramos A. Velocity-based training: From theory to application. Strength Cond J. 2020 [Google Scholar]
- 9.Jovanović M, Flanagan EP. Researched applications of velocity based strength training. J Aust Strength Cond. 2014;22(2):58–69. [Google Scholar]
- 10.Sánchez-Medina L, González-Badillo JJ, Pérez CE, Pallarés JG. Velocity- and power-load relationships of the bench pull vs bench press exercises. Int J Sports Med. 2014;35(3):209–216. doi: 10.1055/s-0033-1351252. [DOI] [PubMed] [Google Scholar]
- 11.Martínez-Cava A, Morán-Navarro R, Hernández-Belmonte A, Courel-Ibáñez J, Conesa-Ros E, González-Badillo JJ, Pallarés JG. Range of motion and sticking region effects on the bench press load-velocity relationship. J Sport Sci Med. 2019;18(4):645–652. [PMC free article] [PubMed] [Google Scholar]
- 12.Pallarés JG, Sánchez-Medina L, Pérez CE, De La Cruz-Sánchez E, Mora-Rodriguez R. Imposing a pause between the eccentric and concentric phases increases the reliability of isoinertial strength assessments. J Sports Sci. 2014;32(12):1165–1175. doi: 10.1080/02640414.2014.889844. [DOI] [PubMed] [Google Scholar]
- 13.Benavides-Ubric A, Díez-Fernández DM, Rodríguez-Pérez MA, Ortega-Becerra M, Pareja-Blanco F. Analysis of the load-velocity relationship in deadlift exercise. J Sport Sci Med. 2020;19(3):452–459. [PMC free article] [PubMed] [Google Scholar]
- 14.García-Ramos A, Suzovic D, Pérez-Castilla A. The load-velocity profiles of three upper-body pushing exercises in men and women. Sport Biomech. 2019;1:13. doi: 10.1080/14763141.2019.1597155. [DOI] [PubMed] [Google Scholar]
- 15.Balsalobre-Fernández C, García-Ramos A, Jiménez-Reyes P. Load–velocity profiling in the military press exercise: Effects of gender and training. Int J Sport Sci Coach. 2018;13(5):743–750. [Google Scholar]
- 16.Garnacho-Castaño MV, Muñoz- González A, Garnacho-Castaño MA, Maté-Muñoz JL. Power– and velocity– load relationships to improve resistance exercise performance. Proc Inst Mech Eng Part P J Sport Eng Technol. 2018;232(4):349–359. [Google Scholar]
- 17.Sanchez-Medina L, Perez CE, Gonzalez-Badillo JJ. Importance of the propulsive phase in strength assessment. Int J Sports Med. 2010;31(2):123–129. doi: 10.1055/s-0029-1242815. [DOI] [PubMed] [Google Scholar]
- 18.Sánchez-Moreno M, Rodríguez-Rosell D, Pareja-Blanco F, Mora-Custodio R, González-Badillo JJ. Movement velocity as indicator of relative intensity and level of effort attained during the set in pull-up exercise. Int J Sports Physiol Perform. 2017;12(10):1378–1384. doi: 10.1123/ijspp.2016-0791. [DOI] [PubMed] [Google Scholar]
- 19.Kompf J, Arandjelović O. Understanding and Overcoming the Sticking Point in Resistance Exercise. Sports Medicine. 2016;46(6):751–762. doi: 10.1007/s40279-015-0460-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kompf J, Arandjelović O. The sticking point in the bench press, the squat, and the deadlift: similarities and differences, and their significance for research and practice. Sport Med. 2017;47(4):631–640. doi: 10.1007/s40279-016-0615-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Van den Tillaar R, Ettema G. The “sticking period” in a maximum bench press. J Sports Sci. 2010;28(5):529–535. doi: 10.1080/02640411003628022. [DOI] [PubMed] [Google Scholar]
- 22.Morán-Navarro R, Martínez-Cava A, Sánchez-Medina L, Mora-Rodríguez R, González-Badillo JJ, Pallarés JG. Movement velocity as a measure of level of effort during resistance exercise. 2017;33(6):1496–1504. doi: 10.1519/JSC.0000000000002017. [DOI] [PubMed] [Google Scholar]
- 23.Pallarés J, López-Samanes A, Fernández-Elías VE, Aguado-Jiménez R, Ortega JF, Gómez C, et al. Pseudoephedrine and circadian rhythm interaction on neuromuscular performance. Scand J Med Sci Sport. 2015;25(6):e603–12. doi: 10.1111/sms.12385. [DOI] [PubMed] [Google Scholar]
- 24.Sánchez-Medina L, González-Badillo JJ. Velocity loss as an indicator of neuromuscular fatigue during resistance training. Med Sci Sport Exerc. 2011;43(9):1725–1734. doi: 10.1249/MSS.0b013e318213f880. [DOI] [PubMed] [Google Scholar]
- 25.Coratella G, Longo S, Cè E, Esposito F. Commentaries on viewpoint: Distinct modalities of eccentric exercise: Different recipes, not the same dish/ commentary on viewpoint: Distinct modalities of eccentric exercise: Different recipes, not the same dish. J Appl Physiol. 2019;127(3):884–891. doi: 10.1152/japplphysiol.00496.2019. [DOI] [PubMed] [Google Scholar]
- 26.Martínez-Cava A, Hernández- Belmonte A, Courel-Ibáñez J, Morán-Navarro R, González-Badillo JJ, Pallarés JG. Reliability of technologies to measure the barbell velocity: Implications for monitoring resistance training. PLoS One. 2020;15(6):e0232465. doi: 10.1371/journal.pone.0232465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Courel-Ibáñez J, Martínez-Cava A, Morán-Navarro R, Escribano-Peñas P, Chavarren-Cabrero J, González-Badillo JJ, Pallarés JG. Reproducibility and repeatability of five different technologies for bar velocity measurement in resistance training. Ann Biomed Eng. 2019;47(7):1523–1538. doi: 10.1007/s10439-019-02265-6. [DOI] [PubMed] [Google Scholar]
- 28.Van den Tillaar R, Saeterbakken AH, Ettema G. Is the occurrence of the sticking region the result of diminishing potentiation in bench press? J Sports Sci. 2012;30(6):591–599. doi: 10.1080/02640414.2012.658844. [DOI] [PubMed] [Google Scholar]
- 29.Gomo O, Van Den Tillaar R. The effects of grip width on sticking region in bench press. J Sports Sci. 2016;34(3):232–238. doi: 10.1080/02640414.2015.1046395. [DOI] [PubMed] [Google Scholar]
- 30.Lakens D. Calculating and reporting effect sizes to facilitate cumulative science: A practical primer for t-tests and ANOVAs. Front Psycho. 2013;4:863. doi: 10.3389/fpsyg.2013.00863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Fernandes JFT, Lamb KL, Twist C. A comparison of load-velocity and load-power relationships between well-trained young and middle-aged males during three popular resistance exercises. J Strength Cond Res. 2018;32(5):1440–1447. doi: 10.1519/JSC.0000000000001986. [DOI] [PubMed] [Google Scholar]
- 32.Elliott BC, Wilson GJ, Kerr GK. A biomechanical analysis of the sticking region in the bench press. Med Sci Sports Exerc. 1989;21(4):450–462. [PubMed] [Google Scholar]
- 33.Król H, Golas A, Sobota G. Complex analysis of movement in evaluation of flat bench press performance. Acta Bioeng Biomech. 2010;12(2):93–98. [PubMed] [Google Scholar]
- 34.Pallarés JG, Cava AM, Courel-Ibáñez J, González-Badillo JJ, Morán-Navarro R. Full squat produces greater neuromuscular and functional adaptations and lower pain than partial squats after prolonged resistance training. Eur J Sport Sci. 2020;20(1):115–124. doi: 10.1080/17461391.2019.1612952. [DOI] [PubMed] [Google Scholar]
- 35.Martínez-Cava A, Hernández- Belmonte A, Courel-Ibáñez J, Morán-Navarro R, González-Badillo JJ, Pallarés JG. Bench press at full range of motion produces greater neuromuscular adaptations than partial executions after prolonged resistance training. J Strength Cond Res. 2019:1. doi: 10.1519/JSC.0000000000003391. [DOI] [PubMed] [Google Scholar]