Abstract
Timely monitoring of incidence risks of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) and associated deaths at small-area level is essential to inform containment strategies. We analysed the spatiotemporal epidemiology of the SARSCoV- 2 pandemic at district level in Germany to develop a tool for disease monitoring. We used a Bayesian spatiotemporal model to estimate the district-specific risk ratios (RR) of SARS-CoV-2 incidence and the posterior probability (PP) for exceedance of RR thresholds 1, 2 or 3. Of 220 districts (55% of 401 districts) showing a RR > 1, 188 (47%) exceed the RR threshold with sufficient certainty (PP ≥ 80%) to be considered at high risk. 47 districts show very high (RR > 2, PP ≥ 80%) and 15 extremely high (RR > 3, PP ≥ 80%) risks. The spatial approach for monitoring the risk of SARS-CoV-2 provides an informative basis for local policy planning.
Keywords: Covid-19, SARS-CoV-2, Infectious disease monitoring, Bayesian spatial analysis, Infectious disease modelling
1. Introduction
The pandemic of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) has caused yet more than 67,500,000 notified cases and about 1540,000 deaths worldwide, which are still progressively increasing (World Health Organization 2020). Since the first notified case in Germany (January 2th, 2020), a total of 1218,524 cases and 19,932 associated deaths have been registered until 8th December 2020 (Robert-Koch Institute 2020).
Measures proposed by the WHO to contain the outbreak and protect the population are adopted on governmental and societal levels within the countries. These measures include a wide range of non-pharmaceutical interventions (NPI) on national and subnational level considering restrictions for public events, institutions, spaces and transport as well as travelling, strengthening healthcare systems, protecting vulnerable populations, and testing policies (World Health Organization. Covid-19 Strategy Update Geneva: WHO 2020) . Ongoing monitoring and epidemiological risk assessments of SARS-CoV-2 incidence and mortality on a local level are essential to identify high-risk areas and to inform policy decision-making and planning for implementation, withdrawal, or re-implementation of control and mitigation strategies (World Health Organization 2020). The use of spatial epidemiological methods as a tool to assess the pandemic course and spatial distribution of SARS-CoV-2 is an essential approach for evaluating the outbreak in terms of different regional characteristics and for informing local decision-makers on containing the epidemiological spread of SARS-CoV-2. However, only few studies focus on analysis and monitoring SARS-CoV-2 incidence or associated deaths on a small-area level using real-time data (Guliyev 2020; Huang et al., 2020; Lakhani 2020; Mollalo et al., 2020). The majority of geographical information system dashboards or tools predominantly reflect crude cumulative counts and rates of cases and deaths (Kamel Boulos and Geraghty 2020) neglecting spatial dependencies. However, unbiased risk measures on a regional level are needed to inform local containment strategies.
After an initial phase of concerted policy measures and NPI aimed at flattening the epidemiological curve in Germany, questions of regional differentiation and risk-adapted mitigation strategies have emerged and are subject to ongoing intensive policy debates of how to conceptualise risk (Abele-Brehm et al., 2020). In an attempt for practical solutions, an arbitrary incidence threshold of 50 per 100,000 population per week has been set by the German Government to determine high-risk districts.
We sought to develop an approach for continuous and reliable monitoring of regional risks of SARS-CoV-2 incidence at small-area level, based on measures that go beyond arbitrary absolute values, crude cases and cumulative incidence rates per population. Using the example of Germany, the aim of our study was to (i) analyse the spatiotemporal epidemiology of SARS-CoV-2 incidence and associated deaths at district level from the beginning of the pandemic in Germany on January 2th 2020 until December 8th 2020 on a daily basis, and to (ii) implement the approach into a tool for ongoing monitoring of standardised incidence and mortality ratios as well as district-specific risks.
2. Data and methods
2.1. Study design
We conducted a longitudinal small-area analysis in Germany at level of 401 districts (Nomenclature of Territorial Units for Statistics, NUTS 3) to assess the distribution of SARS-CoV-2 incidence and associated deaths using standardised incidence (SIR) and mortality ratios (SMR). We further estimate the district-specific risks and probabilities of exceeding risk thresholds for disease incidences using a Bayesian spatiotemporal model. The analysis based on daily-notified cases of SARS-CoV-2 from 2th January 2020 to 8th December 2020.
2.2. Data sources
We linked three different nationally representative data sources, including district data on SARS-CoV-2 incidence and deaths, population statistics, and cartographical data. Daily data on SARS-CoV-2 incidence and associated deaths (02/01/2020 to 08/12/2020) was obtained from the Robert-Koch Institute, which provides the national surveillance system of infectious diseases in Germany, stratified by sex and age groups (0–4, 5–14, 15–34, 35–59, 60–79, 80+) (Robert-Koch Institute 2020b) . We used most recent district-level population statistics (2019) from a database of the system of social reporting in official statistics to calculate expected incidences and deaths (Statistische Ämter des Bundes und der Länder 2019). Cartographical data were taken from the Federal Agency of Cartography and Geodesy (Bundesinstitut für Kartographie und Geodäsie 2018).
2.3. Statistical analysis
We first assessed the distribution of SARS-CoV-2 incidence and associated deaths by calculating weekly standardised incidence (SIR) and mortality ratios (SMR) at district level stratified for sex and age groups (0–4, 5–14, 15–34, 35–59, 60–79, 80+) and on federal states level. For the calculation of SIR and SMR, and corresponding Poisson 95% confidence intervals (95%-CI), the ratio of observed versus expected counts was calculated (Bivand et al., 2008; Blangiardo and Cameletti 2015).
We then used a Bayesian spatiotemporal model, fitted by the integrated nested Laplace approximation (INLA) approach(Martins et al., 2013, Rue et al., 2009), to assess the spatial risk of SARS-CoV-2 incidence. For this analysis, we used daily notifications from 02/01/2020 to 08/12/2020. In order to select the likelihood distribution for the model that fit the count data best (e. g. Poisson, zero-inflated Poisson, negative binomial or zero-inflated negative binomial), four intercept-only models were specified at first. Using the Watanabe-Akaike information criterion (WAIC), the likelihood of the intercept-only model with lowest WAIC was selected for fitting two spatiotemporal models, which included a parametric and a non-parametric time trend, respectively. Based on lowest WAIC, we then selected the model that fit the data best for further calculation (see supplementary material 1 for additional data on model selection) (Blangiardo and Cameletti 2015).
A negative binomial spatiotemporal model fit the data best. The model included a Besag-York-Mollié (BYM) model and a non-parametric dynamic time trend. For districts and notification days the rate of observed SARS-CoV-2 incidence and expected number of cases integrated as offset was modelled on a logarithmic scale:
Where is the intercept, is the BYM-model with as spatially structured random effect modelled using intrinsic conditional auto-regression (neighbouring structure of districts) and as spatially unstructured effect modelled exchangeable among the districts (independent and identically distributed, iid). The dynamic temporal trend incorporates a temporal structured random effect modelled dynamically using a random-walk model of order two, and an unstructured temporal effect modelled using the iid (Blangiardo and Cameletti 2015; Knorr-Held 2000).
The district-specific risk ratios (RR) and corresponding 95% credibility intervals (95%-CrI) are calculated by combining the spatial structured and unstructured random effects, e. g. (Knorr-Held 2000). For assessing the uncertainty associated with the , we compute the posterior probability (PP) of exceeding an threshold greater than 1, 2 and 3, respectively. Following the Richardson criterion, an exceedance probability of greater than or equal to 80-% determines a high certainty of exceeding one of the mentioned thresholds in the respective district (Richardson et al., 2004). We further assess the posterior temporal mean trend at national level to provide an estimate for the time-dependent change in the risks of SARS-CoV-2 incidences in Germany. Therefore, we combined the temporal effects trough a linear combination and calculated time-specific risk ratios () and 95%-CrI (Blangiardo and Cameletti 2015).
The analysis was conducted using the R-programming language for statistical computing (V. 3.6.3). The R-INLA package (Rue et al., 2009) was used to fit the Bayesian models, the tmap (Tennekes 2018) and the leaflet (Graul 2016) packages were used for generating the maps.
2.4. Calculation of expected values
The expected SARS-CoV-2 incidence for district and notification day used for the Bayesian spatiotemporal models were calculated on the basis of the cumulative incidence rate of SARS-CoV-2 (with observed incidence ) until the current notification day weighted by the respective district population size (formula 1) (Blangiardo and Cameletti 2015; Knorr-Held 2000):
| (1) |
The calculation of the weekly expected incidence and deaths used for estimating SIR and SMR is based on formula 1. The cumulative incidence rate for the most recent notification week with was calculated on the basis of the respective preceding notification weeks (formula 2):
| (2) |
The same calculation procedure was applied for estimating stratified SIR and SMR for age groups (0–4, 5–14, 15–34, 35–59, 60–79, 80+) and sex, and for the 16 federal states in Germany.
2.5. Approach for ongoing monitoring
In order to ensure an ongoing daily monitoring, we implement the statistical approach explained above in an automatic process and generate interactive maps for SIR, SMR and district specific risk estimates for SARS-CoV-2 incidence and mortality on a daily basis. The data management and data analysis is carried out with the R programming language, and is automatically started when the database of the Robert-Koch Institute is updated for the previous notification day at 00:00. The output of the analysis contains maps grouped by calendar weeks for daily and weekly SIR and SMR estimates (including age group and sex stratified estimates and counts for SARS-CoV-2 morbidity and mortality), as well as a daily updated map for district specific risk ratios based on the model configuration and selection process explained above. The daily updated interactive maps are then automatically integrated in an interactive web surface, the “Covid-19 Small Area Monitor” (CoV-19 SAM) (Rohleder 2020), which is programmed using JavaScript and the JavaScript library jQuery.
3. Results
We analysed a total of 1218,524 incident SARS-CoV-2 cases (51% female) and 19,932 associated deaths (46% female) between 02/01/2020 and 08/12/2020. See descriptive statistics in supplementary material 2.
3.1. Standardised incidence and mortality ratios
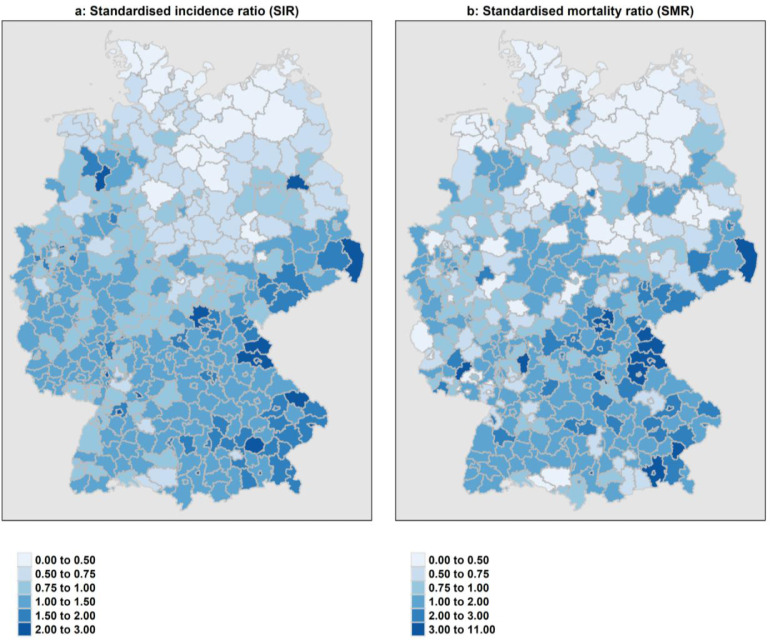
Fig. 1 shows the maps of SIR (a) and SMR (b) estimates on district-level. Elevated estimates were observed especially in Southern and Western Germany ranging from 0.28 to 2.54 (SIR) and from 0.06 to 10.35 (SMR) times the observed incident cases or associated deaths than expected. The median SIR and SMR were 1.08 (1.03–1.12) and 1.02 (0.68–1.48) across all districts in Germany. The number of districts with elevated SIR (greater than 1) was 151 in week 10, peaked in week 12 to a total of 382 districts and declined to a total of 17 districts until week 28. As of week 33, the number of districts with SIR greater 1 sharply increased to 138 districts, peaked with a total of 401 districts in week 44 and declined to 349 districts until the most recent week covered by the analysis (week 50). The SMR distribution across Germany follows a similar pattern, where elevated estimates were observed particularly in southern and western districts of Germany. From week 10 to week 14, the number of districts with SMR greater than 1 increased from 9 to 279. As of week 17, the number of districts with elevated SMR declined until week 38. From this time, the number of districts with elevated SMR increased and peaked to a total of 274 districts in week 47 and declined to 52 districts until week 50. See supplementary material 3 for SIR and SMR maps by notification week. Highest estimates across Germany were found following an outbreak in the district Rosenheim (southwestern Germany in the federal state Bavaria) with SIR of 2.54 (95%-CI: 2.43–2.66). Lowest SIR were found in the rural district Rostock with SIR of 0.28 (0.26 to 0.3). On weekly basis, highest SIR were found in the district Oberhausen (western Germany in the Ruhr metropole) with SIR of 393.78 (356.05–433.84) in week 2. However, estimates with such high values greater than 100 are comparable rare. Only small variations in SIR values were found for females and males with median weekly SIR of 0.61 (0–774.31) and 0.67 (range 0–797.41), respectively. For female, highest SMR were observed on week 10 in district Heilbronn (southern Germany) with 315.5 (282.12–351.78). For male, highest SMR was found on week 11 in district Weilheim-Schongau (southern Germany) with 428.28 (389.36–470.53). Median weekly SMR for female and male over the considered calendar weeks were 0 (range 0–315.5) and 0 (range 0–428.28). See maps on sex stratified SIR and SMR estimates in the supplementary material 4. Age-specific SIR cluster were especially dense for 15–34, 35–59 and 60–79 years old in western and southern parts of Germany. SMR estimates were highest for 60–79 and 80+ aged people. See maps on age-specific SIR and SMR estimates in supplementary material 4.
Fig. 1.
Standardised incidence (SIR) and mortality ratios (SMR) on district level in Germany.
A SIR greater than 1 means that the observed number of SARS-CoV-2 cases (O) is higher than expected (E).
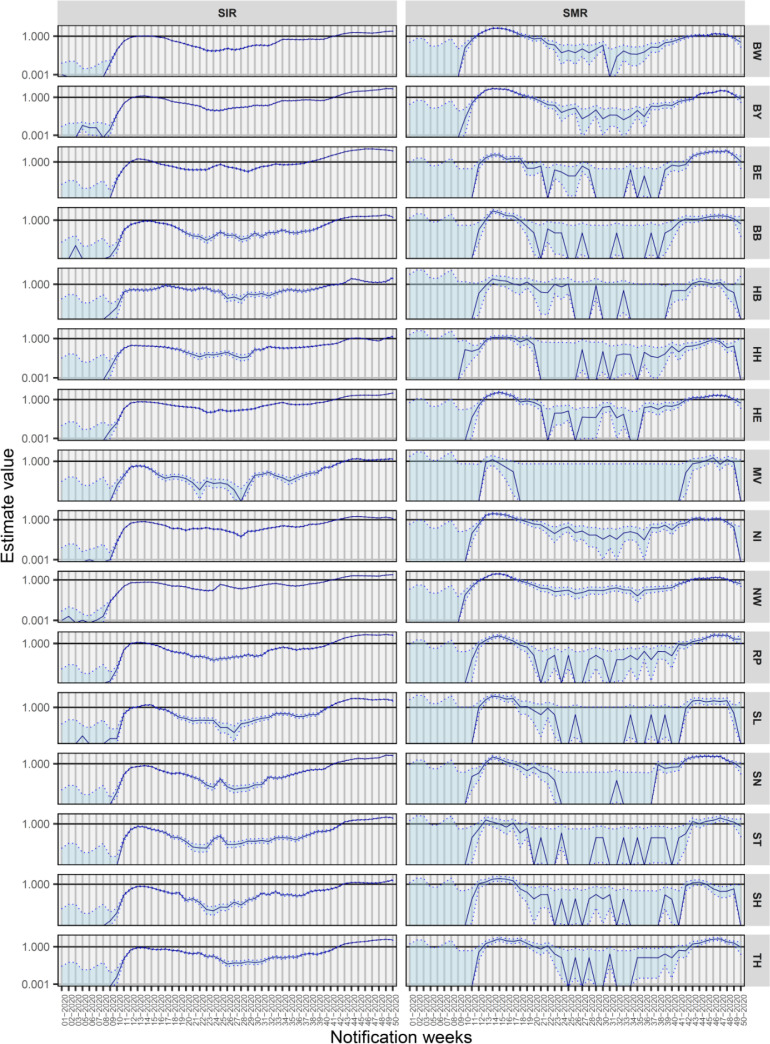
On federal states level (Fig. 2 ), the epidemiological curve of SARS-CoV-2 cases and deaths fluctuated in every state with highest peaks between the weeks 13 and 16, and 43 to 50 respectively. The states Bavaria, Baden-Württemberg, Northrhine-Westphalia, Hamburg, Berlin and also Saarland showed highest SIR and SMR trends over time. On week 46, the highest SIR and SMR were observed in Berlin with 10.86 (10.63–11.10) and 7.68 (6.24–9.36). SIR and SMR estimates on federal states level are provided in supplementary material 5.
Fig. 2.
Standardised incidence (SIR) and mortality ratios (SMR) of federal states in Germany by notification week.
A SIR or SMR greater than 1 means that the observed number of SARS-CoV-2 cases (O) is higher than expected (E). Estimates illustrated on a log-scale. BW: Baden-Wuerttemberg, BY: Bavaria, BE: Berlin, BB: Brandenburg, HB: Bremen, MV: Mecklenburg Pomerania, NI: Lower Saxony, NW: Northrhine-Westphalia, RP: Rhineland Palatinate, SL: Saarland, SN: Saxony, ST: Saxony-Anhalt, SH: Schleswig Holstein, TH: Thuringia.
3.2. District-specific risks and exceedance probability
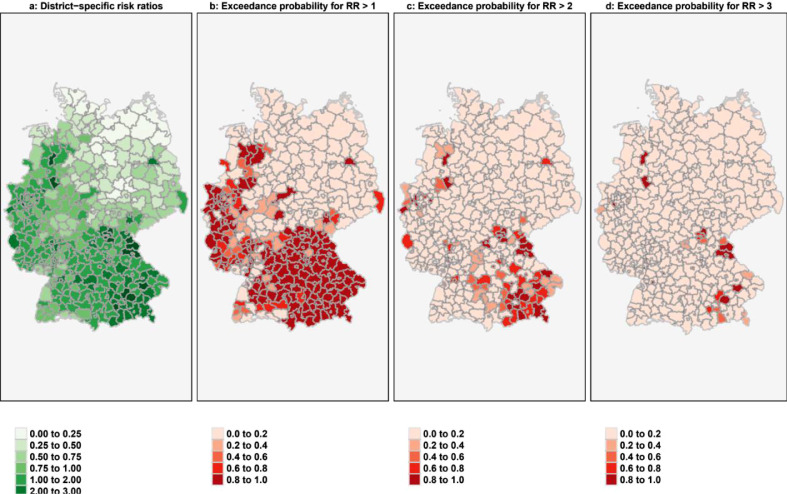
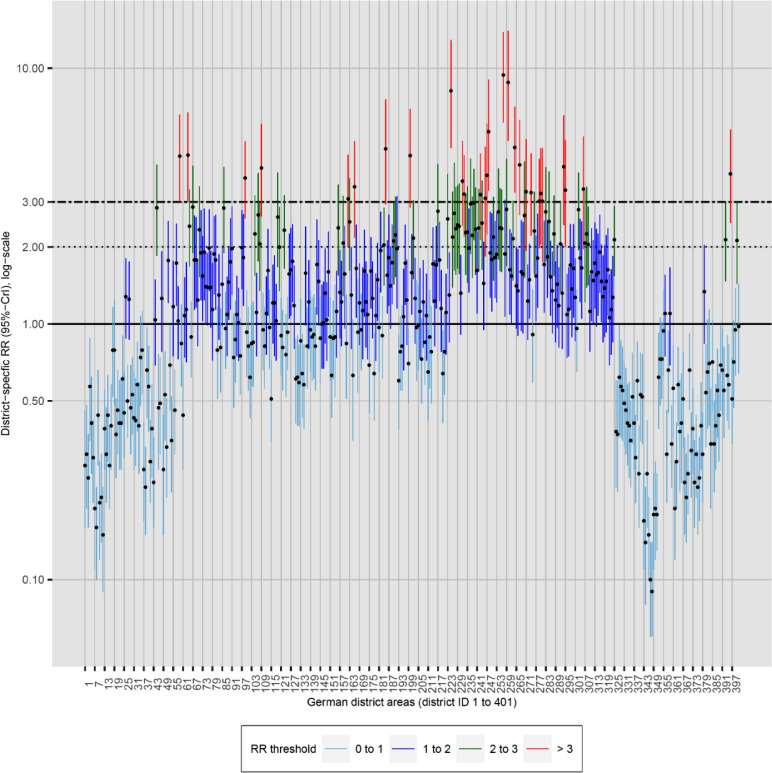
The district-specific RR and the posterior probability (PP) of exceeding an RR threshold at level of 401 districts are illustrated in Fig. 3 . RR and corresponding 95%-CrI grouped by RR thresholds are shown in Fig. 4 . Median RR over all districts was 1.11 (95%-CrI: 0.75–1.61), ranging from 0.09 to 9.42. Elevated RR for SARS-CoV-2 incidence are predominantly clustered in southern and western districts of Germany with highest RR in the districts Dingolfing-Landau (RR = 9.42, 95%-CrI: 6.16–13.79) and Weiden (8.82, 5.21–13.99). In addition, Düsseldorf (4.58; 3.00–6.70) and Berlin (12.14, 1.54–2.89) and its periphery districts in Eastern Germany are at higher risk for SARS-CoV-2 incidence. In total, 220 of 401 districts have a RR greater than 1, and the threshold was exceeded by 188 regions (RR > 1, PP ≥ 80-%). A total of 79 and 28 districts have a RR greater than 2 and 3, respectively, of which 47 and 15 districts exceeded the threshold with a posterior probability of greater or equal to 80%, respectively. District-specific risks estimates and exceedance probabilities for given threshold are provided in supplementary material 6.
Fig. 3.
District-specific risk ratios (RR) and exceedance thresholds.
Fig. 4.
District-specific risk ratios (RR) and corresponding 95% credibility intervals (95%-CrI).
A RR above 1 means that the posterior mean of district-specific risks is higher than the average incidence risk across Germany. An exceedance probability above or equal to 80% determines a high certainty of exceeding one of the RR thresholds.
A RR above 1 means that the posterior mean of district-specific risks is higher than the average incidence risk across Germany. An exceedance probability above or equal to 80-% determines a high certainty of exceeding one of the RR thresholds.
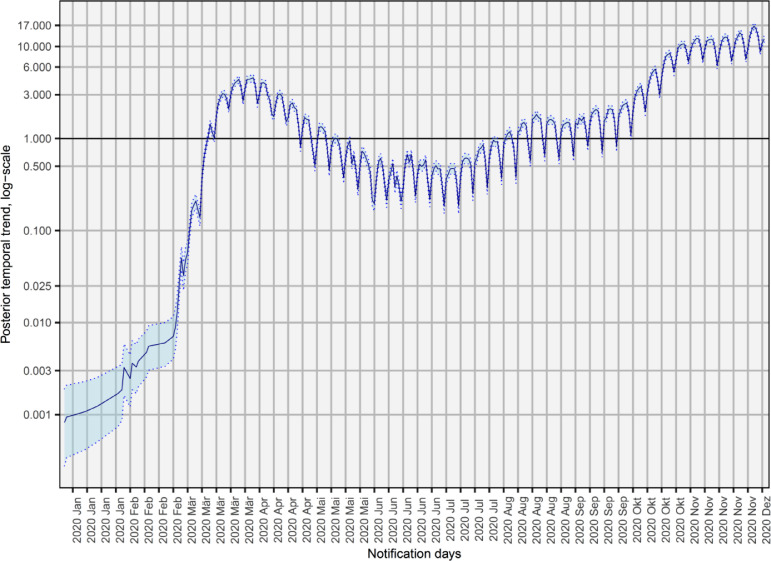
Fig. 5 shows the temporal trend of relative risks (TRR) of SARS-CoV-2 incidence in Germany. Since the beginning of the pandemic in Germany, the TRR has increased daily with a peak on 04/03/2020 (TRR = 4.58; 4.20–4.50), after which the incidence risk tended to decrease and showed fluctuations below TRR of 1 in the months May to mid-July. However, as of the end of June, the TRR sharply increased over time and peaked on 30/12/2020 at its maximum with an estimate of 16.75 (15.41–18.16).
Fig. 5.
Posterior temporal mean trend for SARS-CoV-2 incidences in Germany.
Temporal risk ratio (TRR) and corresponding 95% credibility intervals (95%-CrI) of SARS-CoV-2 incidence by notification day on a log-scale.
4. Discussion
Our analysis showed that the spatiotemporal risk for SARS-CoV-2 incidence was highest in 220 districts, predominantly across southern and western parts of Germany, of which 188 exceeded the risk threshold of 1 with high certainty (posterior probability) and are hence associated with a high risk of disease. Of those 188 districts, 47 and 15 areas further exceeded the risk thresholds greater than 2 and 3 with high certainty, respectively. Those districts are indicated to be at very high and extremely high risk for SARS-CoV-2 infections, respectively. The temporal trend for the risks of SARS-CoV-2 incidence showed two peaks in the beginning of the pandemic in spring and winter season across Germany. Also the SIR and SMR estimates showed visible dynamics of observed to expected incidence and associated deaths, especially in high, very high and extremely high risk areas identified through the modelling approach.
As situations may change dynamically, the ongoing and continuous re-calculation and provision of small-area risk estimates by means of the presented methods will form a relevant and solid basis for local and regional decision-making. Beside the district-specific risk estimates, the calculation of SIR and SMR based on population-weighted observed vs. expected numbers of confirmed SARS-CoV-2 cases and associated deaths detects "at-risk" districts that deviate from the mean national incidence or death rate without introducing a fix (arbitrary) threshold. Such a relative measure for risk may be more appropriate for early detection of local transmission dynamics, especially in times with lower absolute number of incident cases.
The analysis generates a robust basis for local decision-making and makes best use of best-available data by considering daily updated risks relative to a national reference, and by considering temporal dynamics and spatial dependencies. Implications of the estimates could be that mitigation measures are partially ceased, or withdrawn in districts with estimated lower risk of infections and low probability of exceeding an RR threshold with high certainty.
As the presented analysis is re-run on a daily basis in our web-platform “Covid-19 Small Area Monitor” (CoV19-SAM) (Rohleder et al., 2020), a re-introduction or intensification of mitigation strategies is also possible if districts change their risk profile from low to higher risks with high probabilities of exceeding RR thresholds. In comparison to other suggested measures (such as a fix incidence threshold of 50 per 100,000) (Robert-Koch Institute 2020), the focus on relative risks may be both more sensitive and flexible by considering local and age-sex-specific disease incidence relative to the overall course of the epidemic in the country.
While we provide a tool that deliver timely information on district-specific risk to guide political decisions, limitations of the underlying notification data cannot be resolved by our analysis. For example, as notified cases are also a function of testing strategies, local variations and adaptations of the national testing guideline may affect incidence variations. Local planners and public health officers should be aware of such potential sources of variation and consider these carefully when interpreting the estimates. As the analysed outcomes can be considered as rare, daily analysis of SIR and SMR leads to strong variations over time. These are, however, levelled by analysis of weekly periods. Overall and stratified SIR and SMR in a few districts, which were particularly affected by the pandemic, showed extremely high values (SIR or SMR >100) temporarily as the national references are comparably low. These extreme values (outliers) are exceptional and need to be interpreted very carefully. The age and sex stratified SIR and SMR are useful for comparative purposes between districts and also take into account the underlying age and sex distribution as well as temporal changes in morbidity and mortality profile within districts. However, it is important to consider that the SIR and SMR are epidemiological measures for comparison purposes only and not measures for the absolute magnitude of infection or death events in a population, for which crude event rates are commonly used. However, crude event rates make no reference to population structure within districts and do not include changes over time. Thus, with regard to potential tailored age and sex targeted public health interventions, an approach is needed which considers both the absolute magnitude for age and sex groups within each district and information on the standardised rates. Further research into measures that represent absolute and standardised rates in composite indices could be useful for such purposes.
The approach allows in the course of the pandemic to considering health system resources, mobility measures or time-projections in estimation of risk, as well as socio-economic and other potential determinants of SARS-CoV-2 incidence at small-area level. The approach may also serve as blueprint for monitoring approaches elsewhere.
5. Conclusions
A spatial epidemiology approach for monitoring the risk of SARS-CoV-2 incidence and associated deaths provides an informative and timely basis for local policy planning and decision-making. Areas at high (RR > 1), very high (RR > 2) and extremely high risk (RR > 3) can be detected with high certainty (exceedance probability ≥ 80%) while considering both the spatial and temporal dynamics of disease incidence. The approach may not replace, but complement the monitoring of crude cases and population-weighted cumulative incidence rates. Based on the presented approach, the small-area risk of disease incidence can be routinely quantified to inform local SARS-CoV-2 containment strategies.
CRediT authorship contribution statement
Sven Rohleder: Methodology, Software, Formal analysis, Investigation, Resources, Data curation, Writing – original draft, Visualization. Kayvan Bozorgmehr: Conceptualization, Methodology, Validation, Writing – review & editing, Supervision.
Declaration of Competing Interest
None.
Acknowledgements
We acknowledge the contributions of Markus Qreini (Heidelberg University hospital) for technical support in data management and joint development of the monitoring tool.
Footnotes
Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.sste.2021.100433.
Appendix. Supplementary materials
References
- Abele-Brehm A., Dreier H., Fuest C., Grimm V., Kräusslich H., Krause G., et al. Die Bekämpfung der Coronavirus-Pandemie tragfähig gestalten. Empfehlungen für eine flexible, risikoadaptierte Strategie. 2020 [Google Scholar]
- Bivand R., Pebesma E., Gómez-Rubio V. Springer Science+Business Media; New York: 2008. Applied Spatial Data Analysis with R. [Google Scholar]
- Blangiardo M., Cameletti M. John Wiley & Sons, Ltd; New Jersy: 2015. Spatial and Spatio-temporal bayesian Models with R-INLA. [Google Scholar]
- Bundesinstitut für Kartographie und Geodäsie. Verwaltungsgebiete 1:1.000 000 Frankfurt am Main: BKG. 2018. http://www.geodatenzentrum.de/geodaten/gdz_rahmen.gdz_div?gdz_spr=deu&gdz_akt_zeile=5&gdz_anz_zeile=1&gdz_unt_zeile=16&gdz_user_id=0 . Accessed 30 Apr 2018.
- Graul C. leafletR: Interactive Web-Maps Based on the Leaflet JavaScript Library. R package version 0.4-0. 2016.
- Guliyev H. Determining the spatial effects of COVID-19 using the spatial panel data model. Spat. Stat. 2020 doi: 10.1016/j.spasta.2020.100443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang R., Liu M., Ding Y. Spatial-temporal distribution of COVID-19 in China and its prediction: a data-driven modeling analysis. J. Infect. Dev. Ctries. 2020;14(3):246–253. doi: 10.3855/jidc.12585. [DOI] [PubMed] [Google Scholar]
- Kamel Boulos M.N., Geraghty E.M. Geographical tracking and mapping of coronavirus disease COVID-19/severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) epidemic and associated events around the world: how 21st century GIS technologies are supporting the global fight against outbreaks and epidemics. Int. J. Health Geogr. 2020;19(1):8. doi: 10.1186/s12942-020-00202-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knorr-Held L. Bayesian modelling of inseparable space-time variation in disease risk. Stat. Med. 2000;19:2555–2567. doi: 10.1002/1097-0258(20000915/30)19:17/18<2555::aid-sim587>3.0.co;2-#. [DOI] [PubMed] [Google Scholar]
- Lakhani A. Introducing the percent, number, availability, and capacity [PNAC] Spatial approach to identify priority rural areas requiring targeted health support in light of COVID-19: a commentary and application. J. Rural Health. 2020 doi: 10.1111/jrh.12436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martins T., Simpson D., Lindgren F., Rue H. Bayesian computing with INLA: new features. Comput. Stat. Data Anal. 2013;67:68–83. [Google Scholar]
- Mollalo A., Vahedi B., Rivera K.M. GIS-based spatial modeling of COVID-19 incidence rate in the continental United States. Sci. Total Environ. 2020;728 doi: 10.1016/j.scitotenv.2020.138884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richardson S., Thomson A., Best N., Elliott P. Interpreting posterior relative risk estimates in disease-mapping studies. Environ. Health Perspect. 2004;112(9):1016–1025. doi: 10.1289/ehp.6740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robert-Koch Institute. Coronavirus Disease 2019 (COVID-19) Daily Situation Report of the Robert Koch Institute. 09/12/2020 - Updated status for Germany: RKI. 2020. https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Situationsberichte/Dez_2020/2020-12-08-en.pdf?__blob=publicationFile . Accessed 9 Dec 2020.
- Robert-Koch Institute. COVID-19 Dashboard: RKI. 2020. https://corona.rki.de. Accessed 9 Dec 2020.
- Rohleder S., Qreini M., Bozorgmehr K. Covid-19 Small Area Monitor (Cov-19 SAM): university of Bielefeld. 2020. https://covidmonitor.de/ . Accessed 9 Dec 2020.
- Rue H., Martino S., Chopin N. Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximation. JR Stat. Soc. B. 2009;71:319–392. [Google Scholar]
- Statistische Ämter des Bundes und der Länder. Regionaldatenbank Deutschland Düsseldorf: information und Technik Nordrhein-Westfalen (IT.NRW). 2019. https://www.regionalstatistik.de/genesis/online/logon . Accessed 1 May 2020.
- Tennekes M. tmap: thematic Maps in R. J. Stat. Softw. 2018;84(6):1–39. [Google Scholar]
- World Health Organization. Coronavirus disease (COVID-19) Pandemic: WHO. 2020. https://www.who.int/emergencies/diseases/novel-coronavirus-2019. Accessed 9 Dec 2020.
- World Health Organization. Covid-19 Strategy Update Geneva: WHO. 2020. https://www.who.int/docs/default-source/coronaviruse/covid-strategy-update-14april2020.pdf?sfvrsn=29da3ba0_19 . Accessed 18 May 2020.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.