Electrocardiogram machine learning for detection of cardiovascular disease in African Americans: the Jackson Heart Study

Abstract

Aims

Almost half of African American (AA) men and women have cardiovascular disease (CVD). Detection of prevalent CVD in community settings would facilitate secondary prevention of CVD. We sought to develop a tool for automated CVD detection.

Methods and results

Participants from the Jackson Heart Study (JHS) with analysable electrocardiograms (ECGs) (n = 3679; age, 62 ± 12 years; 36% men) were included. Vectorcardiographic (VCG) metrics QRS, T, and spatial ventricular gradient vectors’ magnitude and direction, and traditional ECG metrics were measured on 12-lead ECG. Random forests, convolutional neural network (CNN), lasso, adaptive lasso, plugin lasso, elastic net, ridge, and logistic regression models were developed in 80% and validated in 20% samples. We compared models with demographic, clinical, and VCG input (43 predictors) and those after the addition of ECG metrics (695 predictors). Prevalent CVD was diagnosed in 411 out of 3679 participants (11.2%). Machine learning models detected CVD with the area under the receiver operator curve (ROC AUC) 0.69–0.74. There was no difference in CVD detection accuracy between models with VCG and VCG + ECG input. Models with VCG input were better calibrated than models with ECG input. Plugin-based lasso model consisting of only two predictors (age and peak QRS-T angle) detected CVD with AUC 0.687 [95% confidence interval (CI) 0.625–0.749], which was similar (P = 0.394) to the CNN (0.660; 95% CI 0.597–0.722) and better (P < 0.0001) than random forests (0.512; 95% CI 0.493–0.530).

Conclusions

Simple model (age and QRS-T angle) can be used for prevalent CVD detection in limited-resources community settings, which opens an avenue for secondary prevention of CVD in underserved communities.

Introduction

Many African American (AA) men and women have some form of cardiovascular disease (CVD).¹ Notable racial disparities in CVD prevalence, management, and outcomes have persisted for decades.² Both daily and lifetime racial discrimination experienced by AAs is associated with mistrust of and decreased satisfaction with healthcare providers, potentially negatively impacting continuity of care and treatment adherence.³ In AA communities, health outreach to barbershops is common.⁴ A recent randomized controlled trial showed that pharmacist-led treatment of hypertension in barbershops produces larger blood pressure (BP) reduction, when compared with standard BP management provided by primary care practices.⁵ Sustained effect of community-based intervention⁶ generated further ideas for pharmacist-led CVD management.⁷

Up to one-half of acute myocardial infarctions (MIs) are missed or unrecognized at the time of the event but ultimately cause heart failure⁸ or sudden cardiac death (SCD).⁹ An electrocardiogram (ECG) is one of the simplest, cheapest, and most widely available methods used to evaluate the heart. While ECG diagnosis of MI requires a physician’s interpretation, there is a growing number of automated algorithms analysing ECG in smartphones and mobile devices. Detection of prevalent CVD in community settings (e.g. barbershops) can potentially open an opportunity for secondary prevention of CVD¹⁰ in patients who have limited access to medical care. Still, it is unclear how accurately ECG can detect prevalent CVD.

Global electrical heterogeneity (GEH)¹¹ is a novel vectorcardiographic (VCG) phenotype providing additional predictive value beyond traditional ECG metrics.¹² Global electrical heterogeneity is associated with SCD,¹³ cardiovascular mortality,¹⁴ and left ventricular dysfunction¹⁵ after adjustment for cardiovascular risk factors. However, the predictive value of GEH for CVD detection is unknown. We conducted a cross-sectional study of GEH in AA participants of the Jackson Heart Study (JHS) using machine learning (ML) to find patterns in the data with the goal to develop and validate a simple tool for detection of prevalent CVD on 12-lead ECG. We hypothesized that automated 12-lead ECG analysis could be used to detect prevalent CVD.

Methods

The JHS data are available through the National Heart, Lung, and Blood Institute’s Biological Specimen and Data Repository Information Coordinating Center and the National Center of Biotechnology Information’s database of Genotypes and Phenotypes. All study participants provided written informed consent before entering the JHS study. This study was approved by the Oregon Health & Science University (OHSU) Institutional Review Board.

Study population

The JHS was designed as a prospective cohort study of CVD in AAs,^16,17 and enrolled 5306 participants from the Jackson, Mississippi metropolitan area in 2000–2004. Eligible participants were 21–84 years of age.

In this cross-sectional study, we included JHS participants with analysable resting 12-lead ECG recorded during the third clinical examination in 2009–2013 (n = 3717). We excluded participants with missing major risk factors (hypertension and smoking history) and anthropometric data (n = 38). The study population included 3679 participants (Figure 1).

Figure 1.

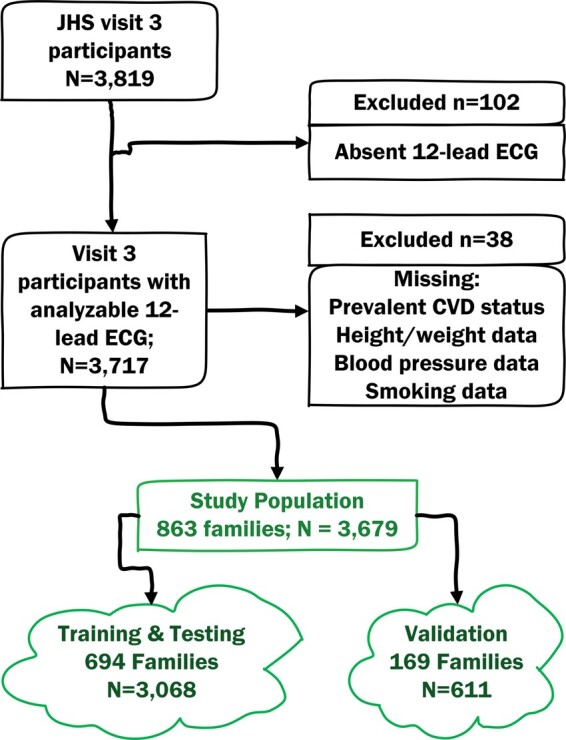
Study flowchart.

Families structure

The JHS enrolled the secondary family members and comprised a Family Cohort with nearly 300 pedigrees.¹⁸ In this study, we comprised family units of participants with the same four-symbols code indicating similar family name.

Electrocardiogram and vectorcardiographic analysis: candidate predictor variables measurement

Raw digital ECG signal was analysed in the Tereshchenko laboratory at OHSU.^12,13,19,20 Each cardiac beat was manually labelled by at least two physician investigators (K.J.L., K.A.P., L.G.T.). Kors matrix²¹ was used to transform 12-lead ECG into XYZ ECG. Using only one (dominant) type of beat, the time-coherent global median beat was constructed, and the origin of the heart vector was identified.²⁰ The following categories of median beats were included in this study. Normal (N) category included normal sinus, atrial paced, junctional, and ectopic atrial median beats. The ventricular pacing category included ventricular paced median beats. The supraventricular (S) category included atrial fibrillation or atrial flutter with consistently one type of ventricular conduction.

The direction (azimuth and elevation) and magnitudes of the spatial peak and area QRS, T, and spatial ventricular gradient (SVG) vectors were measured.^12,19,20 Scalar values of SVG were measured by sum absolute QRST integral (SAIQRST)^22–24 and by QT integral on vector magnitude (VMQTi) signal (Figure 2).¹⁹ The area and peak QRS-T angles were measured.^12,19,20 Study investigators (K.T.H., N.M.R.) reviewed automated VCG analysis quality using visual display aid. The open-source MATLAB (MathWorks, Natick, MA, USA) code is provided at https://physionet.org/physiotools/geh and https://github.com/Tereshchenkolab/Origin.

Figure 2.

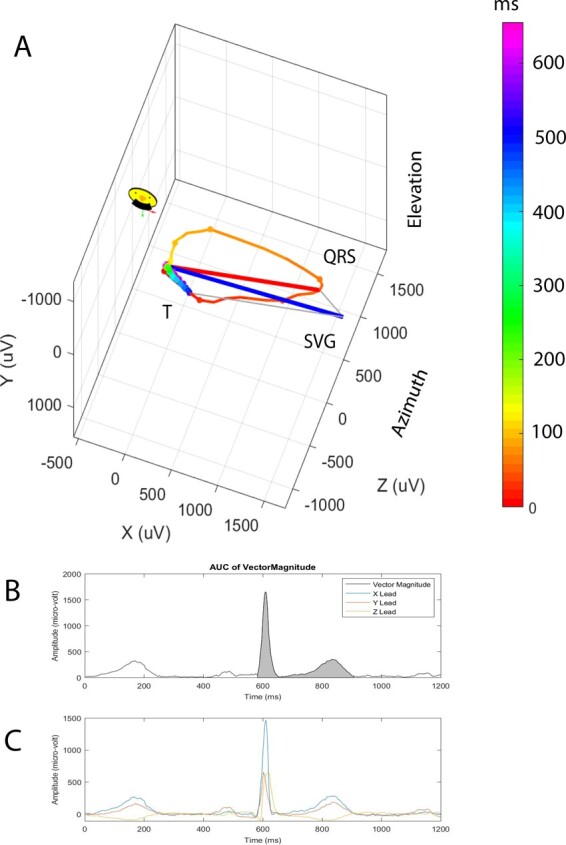
Representative vectorcardiogram. (A) Colour-coded (from red to purple) propagation of cardiac activation (red-yellow QRS loop) and repolarization (green-blue T loop). Peak QRS (red), T (green), and spatial ventricular gradient (blue) vectors. (B) Vector magnitude signal of a normal sinus median beat. Gray area indicates QT integral (scalar spatial ventricular gradient measure). (C) Corresponding orthogonal X, Y, Z ECG signal.

Traditional ECG measurements were performed by the 12SL algorithm as implemented in Magellan ECG Research Workstation V2 (GE Marquette Electronics, Milwaukee, WI, USA) and included median beat measurements (PR, QRS, QT intervals, and frontal P, QRS, and T axes), as well as durations, amplitudes, and areas of all identified by the algorithm waves and segments on all 12 leads. We used the results of automated 12-lead ECG measurements as reported by the 12SL algorithm, without further quality control procedures.

Ventricular conduction abnormalities were diagnosed by the EPICARE (Wake Forest University, NC) using Minnesota code,²⁵ and included code 7-1-1 (left bundle branch block), 7-4 (intraventricular block), 6-8 (pacemaker), and 6-6 (intermittent aberrant ventricular conduction). QT interval was corrected for heart rate by Bazett, Fridericia, Hodge, and Framingham approaches, as provided by the JHS Coordinating Center. Cornell voltage was calculated as the sum of the R_aVL and the S_V3 amplitudes. Frontal QRS-T angle was calculated as previously described.²⁶

Cardiovascular risk factors candidate predictor variables

The 3rd clinical examination included BP measurement, anthropometry, a review of medical history, and cardiovascular risk factors. Height and weight were measured, and body mass index (BMI) and body surface area (BSA) were calculated. BMI categories included under- or normal weight (<25.0 kg/m²), overweight (25.0 to <30.0 kg/m²), or obese (≥30.0 kg/m²). Smoking status was defined as current, former, and never smoker. Hypertension was defined as BP ≥140/90 mmHg or use of antihypertensive therapy.

Outcome: prevalent cardiovascular disease

Prevalent CVD was defined at the 3rd clinical examination if the study participant had either (i) history of coronary heart disease defined as either self-reported prior MI (diagnosed by a doctor or health professional, or hospitalization for MI), or ECG diagnosis of MI, or (ii) history of cardiac procedure defined as either prior coronary revascularization (coronary artery bypass grafting or percutaneous coronary intervention) or peripheral arterial revascularization, or (iii) prior carotid angioplasty or carotid endarterectomy, or (iv) self-reported stroke history (diagnosed by a doctor or health professional). Stable angina was not included in the definition of prevalent CVD.

Statistical machine learning and analysis

Machine learning approach for detection of prevalent cardiovascular disease

We randomly split the ML study population into two non-overlapping samples in such a way that each family cluster was contained entirely within one set: training and testing (80%; 694 families; n = 3068), and validation (20%; 169 families; n = 611). Considering the future implementation of our CVD detection tool in underserved communities, we included predictor variables that can be easily obtained in community settings: age, sex, anthropometric characteristics (height, weight, BMI, BMI categories, BSA), history of hypertension, systolic and diastolic BP, smoking history, and automatically measured ECG and VCG metrics (43 variables).

We fitted eight different models [random forests,²⁷ convolutional neural network (CNN),²⁸ lasso, adaptive lasso, plugin-based lasso, elastic net, ridge with penalized and post-selection coefficients, and logistic regression].

Random forests model uses bagging, or bootstrap aggregation, which is a technique for reducing the variance of an estimated prediction function. Random forests model builds a large collection of de-correlated trees and then averages them. To train the random forests algorithm, we arranged the data in a randomly sorted order and tuned the number of subtrees and number of variables to randomly investigate at each split. We used both out-of-bag error (tested against training data subsets that are not included in subtree construction) and a validation error (tested against the validation data) to find the model with the highest testing accuracy.

Convolutional neural network is a nonlinear statistical model. The central idea is to identify optimal linear combinations of the input variables and then model the outcome as a nonlinear function of these covariates (features). We trained the CNN with 20 hidden layers, using 500 iterations with a training factor 2, and 4 normalization parameters. For the model with VCG input (43 variables), the network was comprised of 3 layers, 64 neurons per layer, and 901 synapse weights. For the model with ECG input (153 variables), the network was comprised of 3 layers, 174 neurons per layer, and 3101 synapse weights.

The least absolute shrinkage and selection operator (lasso) family of models utilized 10-fold cross-validation in the training (training and testing) sample. The lasso family of models is widely used to identify key variables needed in the predictive model and remove those that do not belong in the model. In the lasso model, cross-validation selected the tuning parameter λ that minimized the out-of-sample deviance (a goodness-of-fit statistic). The tuning parameter λ is the lasso penalty parameter. As λ increases, the number of coefficient estimates that are zero at the solution increases. Covariates with estimated coefficients of zero are excluded, and covariates with estimated coefficients that are not zero are included. Cross-validation selects the λ value that minimizes the out-of-sample mean squared error of the predictions.

Cross-validation tends to include many covariates whose coefficients are close to zero. The adaptive lasso is a multistep version of cross-validation. The adaptive lasso performs multistep cross-validation, performing the second cross-validation step among the covariates selected in the first cross-validation step. In the second step, the penalty loadings are set to the inverse of the first-step estimates coefficients. The adaptive lasso usually selects fewer coefficients than the regular lasso.

The plugin-based lasso uses partialing-out estimators to determine which covariates belong in the model, achieving an optimal bound on the number of covariates it included.²⁹ Plugin estimators find the value of λ that is large enough to dominate the estimation noise; it normalizes the scores for each parameter. The plugin-based lasso is very good at excluding covariates that do not belong in the model.

The elastic net is an extension of the lasso that permits the retention of correlated covariates.³⁰ The elastic net was originally motivated as a method that would produce better predictions when the covariates are highly correlated. When two variables are correlated, the lasso tends to include one and exclude the other, but the elastic net permits the retention of correlated covariates if they improve prediction.

In the ridge model, the penalty parameter uses squared terms and keep all predictors in the model. The ridge model was designed as a model that has highly correlated variables, even more so than the elastic net.

We compared the predictive accuracy of the models by comparing the area under the receiver operator curve (ROC AUC). As the goal of screening is to identify all individuals with prevalent CVD, we strived to maximize the test's sensitivity, and we selected a 100% sensitivity threshold. We validated the CVD detection tool in the validation sample by measuring ROC AUC and assessing the sensitivity and specificity of the selected at the previous step threshold. To assess calibration, we evaluated the goodness of fit in the validation sample, using several approaches. We compared the observed and predicted proportions within the groups formed by the Hosmer–Lemeshow test.³¹ We also used the calibration belt³² to examine the relationship between estimated probabilities and observed CVD rates. For the lasso family of models, we also calculated the out-of-sample deviance and deviance ratio.

Comparison of machine learning models using the input of 12SL algorithm electrocardiogram features

To compare the composition and predictive accuracy of the ML models using ECG features measured on 12-lead ECG by the 12SL algorithm (GE Marquette Electronics, Milwaukee, WI, USA), we repeated the described above ML steps with the input of the additional 652 variables, which included frontal QRS-T angle and fine 12-lead ECG features (amplitudes, durations, and areas of all ECG waves). We compared random forests, CNN, lasso, adaptive lasso, plugin-based lasso, and elastic net with penalized and post-selection coefficients. Due to a large number of input variables (n = 695), we did not test the performance of logistic regression and ridge models, as nearly all the predictors were kept in the model. For an adequate comparison of CNN with VCG and ECG input, a model with ECG input did not include VCG variables and included only measurements of main ECG waves, without ‘prime’ ECG waveforms (153 variables).

Statistical ML analysis was performed using STATA MP 16.1 (StataCorp LP, College Station, TX, USA). P-value <0.05 was considered statistically significant. STATA code is provided at https://github.com/Tereshchenkolab/statistics.

Results

Study population

The study participants were on agerge 62 years of age; more than half were female (Table 1). Nearly three-quarters of participants had hypertension, and one-third were current or former smokers. Prevalent CVD was diagnosed in 411 out of 3679 participants (11.2%).

Table 1.

Comparison of training and testing, and validation groups

Characteristics	All (n = 3679)	Training and testing (n = 3068)	Validation (n = 611)
Age (SD), years	61.6 (11.9)	61.4 (11.9)	62.6 (11.6)
Male, n (%)	1332 (36.2)	1109 (36.2)	223 (36.5)
Weight (SD), kg	91.2 (21.5)	91.2 (21.6)	91.3 (21.5)
Height (SD), cm	168.5 (9.4)	168.5 (9.4)	168.6 (9.3)
BMI (SD), kg/m2	32.1 (7.2)	32.1 (7.2)	32.1 (7.4)
Obese BMI group, n (%)	2084 (56.7)	1738 (56.6)	346 (56.6)
BSA (SD), m2	2.00 (0.25)	2.00 (0.24)	2.00 (0.23)
Ever tobacco smoker, n (%)	1097 (29.8)	908 (29.6)	189 (30.9)
Hypertension, n (%)	2703 (73.5)	2242 (73.1)	461 (75.5)
Systolic blood pressure (SD), mmHg	127.6 (18.7)	127.6 (18.6)	127.9 (19.0)
Diastolic blood pressure (SD), mmHg	75.0 (10.9)	75.1 (11.0)	74.6 (10.3)
Heart rate (SD), b.p.m.	64.0 (10.7)	64.0 (10.7)	63.8 (10.6)
QRS duration (SD), ms	89.0 (15.6)	89.0 (15.7)	89.1 (15.3)
Ventricular conduction defect, n (%)	27 (0.73)	17 (0.55)	10 (1.64)
QT interval (SD), ms	416.5 (30.6)	416.3 (31.5)	417.6 (32.9)
Bazett corrected QT (SD), ms	426.7 (25.8)	426.6 (25.7)	427.2 (26.3)
Framingham corrected QT (SD), ms	422.2 (22.7)	422.0 (22.5)	422.9 (23.5)
Hodge corrected QT (SD), ms	423.5 (23.0)	423.3 (22.7)	424.2 (24.4)
Fridericia corrected QT (SD), ms	423.0 (22.1)	422.9 (22.6)	423.7 (23.6)
Cornell voltage(SD), µV	1514 (597)	1507 (593)	1547 (618)
Median beat: normal sinus, n (%)	3629 (99)	3026 (98.6)	603 (98.7)
Median beat: atrial fibrillation, n (%)	36 (1.0)	13 (0.4)	1 (0.2)
Median beat: ventricular pacing, n (%)	14 (0.4)	29 (1.0)	7 (1.2)
QRS area (SD), mV*ms	38.4 (18.3)	38.4 (18.3)	38.7 (18.3)
Peak QRS magnitude (SD), mV	1.59 (0.44)	1.59 (0.44)	1.60 (0.45)
Area QRS azimuth (95% CI)	20.9 (20.1–21.6)	20.7 (19.9–21.6)	21.5 (19.5–23.4)
Peak QRS azimuth (95% CI)	9.7 (8.9–10.4)	9.6 (8.8 = 10.4)	9.8 (8.0–11.7)
Area QRS elevation (95% CI)	73.3 (72.8–73.9)	73.1 (72.5–73.7)	74.4 (72.9–75.8)
Peak QRS elevation(95%CI)	72.3 (71.8–72.7)	72.2 (71.7–72.7)	72.9 (71.8–74.0)
T area (SD), mV*ms	48.5 (23.1)	48.5 (22.9)	48.3 (24.0)
Peak T magnitude (SD), mV	0.36 (0.16)	0.36 (0.16)	0.35 (0.16)
Area T azimuth (95% CI)	−45.1 (−46.1 to −44.1)	−45.2 (−46.3 to −44.2)	−44.5 (046.8 to −42.2)
Peak T azimuth (95% CI)	−36.2 (−37.2 to −35.1)	−36.3 (−37.4 to −35.2)	−35.4 (−37.9 to −33.0)
Area T elevation (95% CI)	75.6 (75.1–76.1)	75.6 (75.0–76.1)	76.0 (74.8–77.2)
Peak T elevation (95% CI)	69.9 (69.4–70.4)	69.9 (69.4–70.4)	69.8 (68.7–71.0)
Area SVG (SD), mV*ms	69.3 (28.2)	69.4 (28.2)	68.7 (28.3)
Peak SVG magnitude (SD), mV	1.81 (0.50)	1.81 (0.50)	1.81 (0.50)
Area SVG azimuth (95% CI)	−14.0 (−14.7 to −13.3)	−14.1 (−14.9 to −13.3)	−13.3 (−15.1 to −11.5)
Peak SVG azimuth (95% CI)	3.7 (3.0–4.4)	3.6 (2.9–4.4)	3.9 (2.2–5.7)
Area SVG elevation (95% CI)	71.5 (71.1–72.0)	71.3 (70.8–71.9)	72.6 (71.4–73.9)
Peak SVG elevation (95% CI)	70.8 (70.4–71.2)	70.7 (70.2–71.1)	71.4 (70.3–72.5)
SAIQRST (SD), mV*ms	153.9 (51.4)	153.7 (51.2)	154.9 (52.6)
VM QT integral (SD), mV*ms	102.9 (34.3)	102.8 (34.1)	103.5 (35.4)
Area QRS-T angle (95% CI)	67.1 (66.0–68.3)	67.1 (65.9–68.3)	67.2 (64.3–70.0)
Peak QRS-T angle (95% CI)	48.3 (47.2–49.4)	48.4 (47.2–49.6)	48.0 (45.2–50.7)

There were 863 family units in our study. More than half of them consisted of a single person (579 units; 67%), and 25% (212 units) consisted of two participants. There were 17 large family units (2%) with 20–79 family members per unit, accounting for 24% of the study population (n = 734). Overall, prevalent CVD was slightly less frequent in large (n = 67; 9.1%) than in small (n = 344; 11.7%) families (P = 0.049).

Development and validation of prevalent cardiovascular disease detection tool

Training and testing and validation subsamples were balanced, without major differences in clinical and ECG characteristics between subsamples (Table 1).

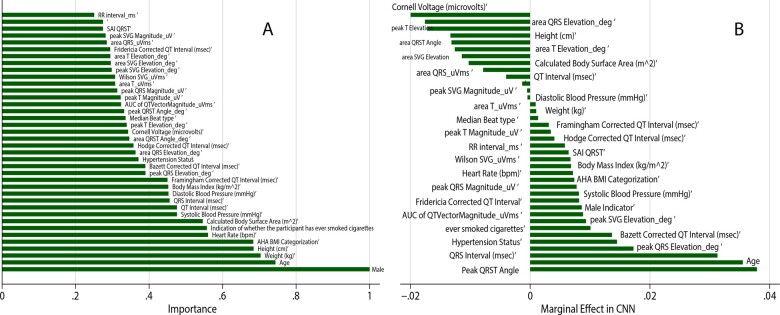
In tuning the random forests algorithm, we observed that both out-of-bag error and validation error stabilized after 200 iterations at 11–12% (Supplementary material online, Figure S1), and we conservatively chose 500 subtrees. The minimum validation error (12%) was observed for 23 variables. Thus, we chose 23 variables to investigate at each split randomly. The final random forests model reported a small error in the validation sample (12.2% or 75 out of 611 individuals), indicating good prediction. However, while the random forests model accurately predicted freedom from CVD in 534 out of 536 participants (specificity 99.6%), it correctly predicted CVD in only 2 out of 75 individuals (sensitivity 2.7%), indicating no clinical usefulness (if used alone). Validation ROC AUC was non-significant (0.512; 95% confidence interval 0.493–0.530). The single most important predictor was sex (Figure 3A), which, together with well-known clinical CVD risk factors (age, weight, height, BMI category), comprised the five most important predictors. ECG characteristics had very little impact on the random forests decision tree.

Figure 3.

(A) Importance scores of predictor variables in a random forests model with vectorcardiographic input. (B) Comparison of the marginal effect size in a convolutional neural network with vectorcardiographic input.

A comparison of the prediction models’ performance is shown in Table 2. The CNN demonstrated the highest predictive accuracy in the training and testing sample across all models, with a final error of only 8%. However, the CNN model's calibration was unsatisfactory (Hosmer–Lemeshow test P < 0.0001; Table 3). Peak QRS-T angle and age demonstrated the largest marginal effect in the CNN with VCG input (Figure 3B).

Table 2.

Comparison of models for prevalent CVD detection

		Training and testing sample					Validation sample
Input	Model (coefficients)	Deviance	Deviance ratio	Number of predictors	ROC AUC (95% CI)	P-value	Deviance	Deviance ratio	ROC AUC (95% CI)	P-value
Clinical + VCG	Adaptive lasso, penalized	0.616	0.108	17	0.737 (0.709–0.765)	0.267	0.669	0.101	0.740 (0.683–0.796)	0.928/0.014a
	Lasso, penalized	0.618	0.106	22	0.737 (0.709–0.764)		0.669	0.102	0.740 (0.683–0.796)
	Elastic net, penalized	0.618	0.106	23	0.737 (0.710–0.765)		0.670	0.103	0.741 (0.684–0.798)
	Ridge, penalized	0.617	0.107	43	0.739 (0.712–0.767)		0.668	0.104	0.743 (0.686–0.800)
	Logistic regression	0.608	0.120	42	0.748 (0.721–0.776)		0.670	0.100	0.737 (0.681–0.792)
	Plugin lasso, postselection	0.640	0.073	2	0.707 (0.678–0.737)	0.0008	0.696	0.065	0.687 (0.625–0.749)	0.394
	CNN	—	—	—	0.778 (0.746–0.809)	0.008	—	—	0.660 (0.597–0.722)
	Random Forests	—	—	—	—	—	—	—	0.512 (0–493–0.530)	<0.0001
Clinical + VCG + ECG	Adaptive lasso, penalized	0.555	0.197	47	0.800 (0.775–0.825)	<0.0001b	0.670	0.100	0.732 (0.671–0.792)	0.732b
	Lasso, penalized	0.578	0.163	54	0.786 (0.760–0.812)	<0.0001b	0.665	0.107	0.736 (0.676–0.795)	0.821b
	Elastic net, penalized	0.576	0.167	79	0.792 (0.767–0.818)	<0.0001b	0.664	0.108	0.742 (0.683–0.800)	0.959b
	Plugin lasso, postselection	0.618	0.106	5	0.733 (0.705–0.761)	0.0002b	0.695	0.067	0.676 (0.613–0.738)	0.440b
	CNN	—	—	—	0.664 (0.631–0.697)	<0.0001b	—	—	0.549 (0.478–0.620)	0.020b

^aIn comparison to the convolutional neural network (CNN) and plugin-based lasso models.

^bIn comparison to corresponding VCG model.

Table 3.

CNN—predicted and observed CVD in deciles of predicted CVD risk

CVD risk group	N	Observed (%)	Predicted (%)	Min%	Max%	HL χ2
1	3456	241 (7.0)	28.1 (0.8)	0	9.9	1616.05
2	32	17 (53.1)	4.4 (13.8)	10.2	19.2	3.25
3	22	9 (40.9)	5.4 (24.4)	20.5	28.8	4.03
4	17	10 (58.8)	6.0 (35.5)	30.9	39.8	2.51
5	10	7 (70.0)	4.5 (45.1)	41.2	47.3	4.72
6	14	12 (85.7)	8.0 (57.0)	50.2	60.0	1.40
7	26	20 (76.9)	17.1 (65.9)	60.9	70.0	0.38
8	27	21 (77.8)	19.6 (72.5)	70.6	79.9	0.87
9	5	5 (100)	4.3 (85.2)	82.7	89.5	0
10	69	68 (98.6)	68.0 (98.5)	91.2	100.0	1674.92
Total	3679	411 (11.2)	166.5 (4.5)	0	100	1674.9

CNN, convolutional neural network; HL, Hosmer–Lemeshow χ².

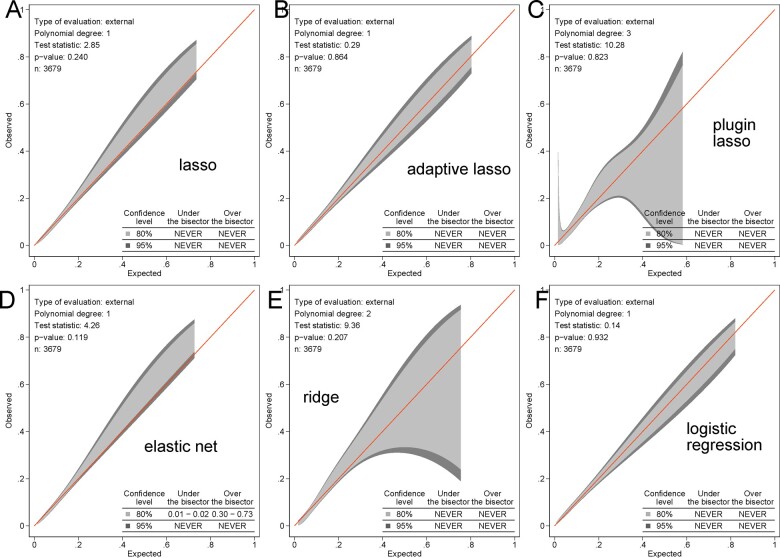
Several models (lasso, adaptive lasso, elastic net, ridge, and logistic regression) demonstrated an intermediate accuracy, similar fit, and no differences in ROC AUC. Supplementary material online, Figure S2 shows the cross-validation function and selected λ for each model. Selected predictors and their coefficients for all models are reported in Table 4. Remarkably, the plugin-based lasso model selected only two predictors: age and spatial peak QRS-T angle (Supplementary material online, Figure S3), while demonstrating only slightly smaller ROC AUC. The threshold of predictive function ≥0.026 identified all participants with prevalent CVD in the testing sample (100% sensitivity). Calibration of logistic regression, lasso, adaptive lasso, plugin-based lasso, elastic net, and ridge models was satisfactory (Figure 4 and Supplementary material online, Figure S4).

Table 4.

Beta-coefficients for selected variables in VCG-based prediction models

Input variable	OLS	Ridge	Elastic net	Lasso	Adaptive	Plugin
Age, years	0.026	0.268	0.304	0.332	0.341	0.042
Male	0.072	0.026	—	—	—	—
Weight, kg	−0.028	0.004	—	—	—	—
Height, cm	0.097	−0.002	—	—	—	—
BMI, kg/m2	0.169	0.055	0.051	0.053	0.094	—
BMI three categories	−0.230	−0.042	−0.028	−0.024	—	—
BSA, m2	−3.49	−0.002	—	—	—	—
Ever tobacco smoker	0.426	0.166	0.172	0.176	0.202	—
Hypertension	0.756	0.239	0.258	0.289	0.331	—
Systolic blood pressure, mmHg	0.010	0.115	0.088	0.075	0.105	—
Diastolic blood pressure, mmHg	−0.024	−0.176	−0.151	−0.138	−0.177	—
Heart rate, b.p.m.	−0.113	0.032	0.039	0.040	0.092	—
QRS duration, ms	0.003	0.087	0.088	0.091	0.096	—
QT interval, ms	−0.018	−0.030	—	—	—	—
Bazett corrected QT, ms	0.246	0.045	0.024	0.016	—	—
Framingham corrected QT, ms	0.086	0.005	—	—	—	—
Hodge corrected QT, ms	—	−0.015	—	—	—	—
Fridericia corrected QT, ms	−0.316	0.021	—	—	—	—
Cornell voltage, µV	−0.0005	−0.118	−0.100	−0.093	−0.134	—
Median beat type (three categories)	0.172	0.026	0.015	0.011	—	—
Mean RR’ interval, ms	0.026	−0.027	−0.035	−0.034	−0.002	—
QRS area, µV*ms	−0.00002	−0.029	—	—	—	—
Peak QRS magnitude, µV	0.0003	0.081	0.073	0.063	0.097	—
Area QRS azimuth	0.001	−0.009	—	—	—	—
Peak QRS azimuth	0.0008	0.004	—	—	—	—
Area QRS elevation	−0.005	−0.022	—	—	—	—
Peak QRS elevation	0.015	0.096	0.102	0.087	0.124	—
T area, µV*ms	−0.00003	−0.065	−0.030	−0.028	−0.019	—
Peak T magnitude, µV	0.0007	−0.003	—	—	—	—
Area T azimuth	0.002	0.113	0.125	0.131	0.162	—
Peak T azimuth	0.0008	0.001	—	—	—	—
Area T elevation	0.002	−0.003	—	—	—	—
Peak T elevation	−0.006	−0.038	−0.033	−0.040	−0.047	—
Area SVG, µV*ms	0.000001	0.010	—	—	—	—
Peak SVG magnitude, µV	−0.0001	0.020	—	—	—	—
Area SVG azimuth	0.001	0.041	0.014	0.007	—	—
Peak SVG azimuth	−0.002	−0.012	—	—	—	—
Area SVG elevation	−0.008	−0.078	−0.056	−0.045	−0.072	—
Peak SVG elevation	0.003	0.061	0.004	—	—	—
SAIQRST, µV*ms	−0.00001	0.009	—	—	—	—
VM QT integral, µV*ms	0.00004	0.035	—	—	—	—
Area QRS-T angle	0.004	0.140	0.083	0.020	—	—
Peak QRS-T angle	0.019	0.270	0.320	0.389	0.444	0.010
Constant	−24.73	−2.312	−2.323	−2.336	−2.377	−5.442

Figure 4.

Calibration of vectorcardiographic models. The calibration belt with 80% and 95% confidence intervals on the external sample shows the observed and predicted cardiovascular disease proportions in (A) lasso, (B) adaptive lasso, (C) plugin lasso, (D) elastic net, (E) ridge, (F) logistic regression models with vectorcardiographic input (43 predictors).

In the validation out-of-sample population (Table 2), several models (logistic regression, lasso, adaptive lasso, elastic net, and ridge) had similarly high predictive accuracy, whereas CNN and plugin-based lasso demonstrated slightly, but statistically significantly lower accuracy. A pre-selected threshold of plugin-based lasso predictive function was 100% sensitive and identified all participants with prevalent CVD in the validation sample. Random forests model performance was unsatisfactory.

Comparison of machine learning models with the input of vectorcardiographic and 12-lead electrocardiogram features

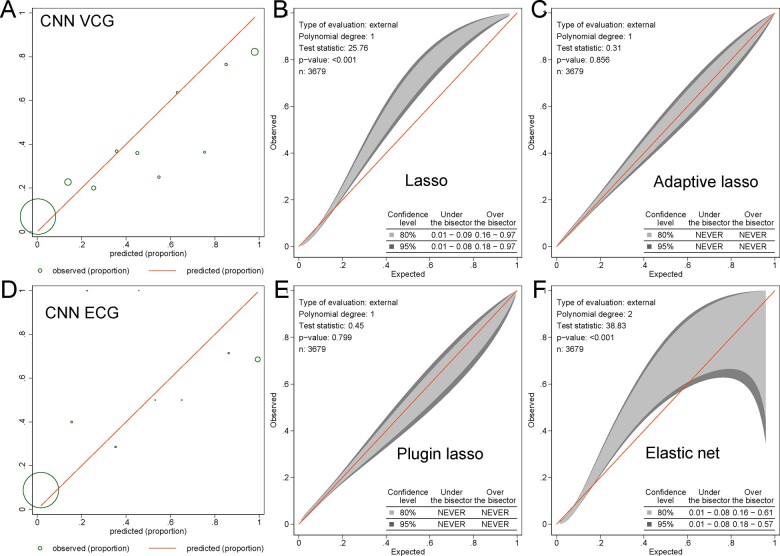
Selected predictor variables and beta-coefficients are reported in Table 5. Lasso family models selected 5-79 predictors, which included finicky features of ECG (P-prime, Q, and R-prime measurements). In a training and testing sample, all models that included both VCG and ECG predictors showed higher accuracy than VCG-only models (Table 2). However, there was no difference in ROC AUC between the respective models in the validation sample. Furthermore, only plugin-based lasso and adaptive lasso models showed satisfactory calibration, whereas elastic net and lasso models’ calibration became unsatisfactory (Figure 5 and Supplementary material online, Figure S5).

Table 5.

Beta-coefficients for selected variables in VCG + ECG-based models

Input variable	Elastic net	Lasso	Adaptive	Plugin
Age, years	0.220	0.287	0.321	0.037
Ever tobacco smoker (yes-no)	0.075	0.079	0.150
Hypertension (yes-no)	0.162	0.186	0.323
Diastolic blood pressure, mmHg	−0.037	−0.010	−0.032
Peak QRS-T angle	0.102	0.154	0.192	0.005
Peak QRS elevation	0.019	—	—
Area SVG azimuth	0.018	0.001	—
Area T azimuth	0.081	0.100	0.214
P V1 amplitude, µV	0.017	—	—
P aVL duration, ms	0.004	—	—
P aVL intrinsicoid, ms	0.015	0.015	0.104
P V4 intrinsicoid, ms	−0.011	—	—
Pprime III duration, ms	0.024	0.015	0.040
Pprime V4 duration, ms	0.027	0.027	0.048
Pprime aVF duration, ms	0.025	0.015	0.028
Pprime V6 area, µV*ms	−0.008	—	—
Q V3 amplitude, µV	0.077	0.043	0.101
Q III amplitude, µV	0.066	0.076	0.144
Q aVF amplitude, µV	0.003	—	—
Q II duration, ms	0.039	0.037	0.102
Q V3 duration, ms	0.159	0.211	0.252	0.056
Q aVF duration, ms	0.042	0.030	0.018
Q I intrinsicoid, ms	—	0.022	0.066
Q aVF intrinsicoid, ms	0.043	0.054	0.015
Q V1 intrinsicoid, ms	0.029	—	—
Q aVL area, µV*ms	0.006	—	—
R V4 duration, ms	0.017	0.011	0.076
R aVL duration, ms	0.026	0.005	—
R V1 area, µV*ms	0.022	0.010	—
R V2 area, µV*ms	0.045	0.045	0.082
R V6 area, µV*ms	0.003
R III intrinsicoid, ms	0.044	0.042	0.056
R aVL intrinsicoid, ms	0.034	0.031	0.084
R aVF intrinsicoid, ms	0.051	0.047	0.153
R V6 intrinsicoid, ms	0.036	0.025	0.056
S V1 duration, ms	−0.026	−0.018	−0.016
Rprime V4 amplitude, µV	0.055	0.066	0.115
Rprime I area, µV*ms	0.064	0.060	0.102
Rprime aVR area, µV*ms	0.046	0.037	0.073
Sprime V4 amplitude, µV	0.030	0.012	0.039
S prime V6 duration, ms	−0.0005	—	—
Sprime V1 area, µV*ms	0.033	0.033	0.089
Sprime V6 area, µV*ms	−0.005	—	—
Sprime V2 intrinsicoid, ms	−0.038	−0.040	−0.193
J-point amplitude in lead I, µV	−0.038	—	—
ST segment middle amplitude in aVR, µV	0.031	—	—
Maximum of ST amplitude in aVR, µV	0.024	0.012	—
Minimum of STJ and STM amplitudes in lead I, µV	−0.074	—	—	−0.007
Minimum of ST amplitudes in lead I, µV	—	−0.153	−0.241
Minimum of either T amplitude or T-ST aVL, µV	−0.057	−0.081	−0.179
Peak-to-peak QRS complex amplitude II, µV	−0.045	−0.033	−0.168
T aVL amplitude, µV	−0.005	—	—
T area in lead I, µV*ms	−0.026	—	—
T area in aVL, µV*ms	−0.009	—	—
T V1 intrinsicoid, ms	0.028	0.025	0.079
T V2 intrinsicoid, ms	0.029	0.014	0.064
Tprime aVL amplitude, µV	−0.008	—	—
Tprime aVF amplitude, µV	0.037	0.040	0.104
Tprime V1 area, µV*ms	0.031	0.027	0.097
Tprime V4 area, µV*ms	−0.007	—	—
Tprime III area, µV*ms	0.022	0.014	0.061
Tprime aVL area, µV*ms	−0.016	−0.014	−0.054
Tprime V2 intrinsicoid, ms	0.006	—	—
T and Tprime area in lead I, µV*ms	−0.020	—	—
T and Tprime area in aVL, µV*ms	−0.024	—	—
Peak of T > ST in aVL (yes-no)	—	−0.004	—
ST depression V2 (yes-no)	0.001	—	—
ST depression V3 (yes-no)	0.034	0.033	0.033
ST depression V4 (yes-no)	0.020	0.007	—
ST elevation in lead I (yes-no)	−0.004	—	—
ST elevation in lead V1 (yes-no)	0.004	—	—
ST elevation in lead V2 (yes-no)	0.038	0.031	0.088
ST elevation in lead V4 (yes-no)	0.0008	—	—
ST elevation in lead V6 (yes-no)	−0.009	—	—
J point elevated by 100 μV in lead V1 (yes-no)	−0.064	−0.065	−0.167
J point elevated by 100 μV in lead III (yes-no)	−0.019	—	−0.115
J point elevated by 100 μV in lead aVF (yes-no)	—	−0.019	—
Delta-wave was detected in lead III (yes-no)	−0.022	−0.021	−0.058
Delta-wave was detected in aVL (yes-no)	−0.040	−0.034	−0.157
ST J-point elevated in V1 (yes-no)	−0.012	−0.003	—
ST J-point elevated in V2 (yes-no)	−0.011	−0.011	−0.055
Frontal QRS-T angle, degrees	0.069	0.069	0.040	0.003
Constant	−2.30	−2.31	−2.51	−4.92

STJ, end of QRS point amplitude; STM, middle of ST segment amplitude.

Figure 5.

Calibration of electrocardiogram and vectorcardiographic models. The calibration plot shows the observed and predicted cardiovascular disease proportions in the (A) convolutional neural network model with vectorcardiographic input (43 variables) and (D) electrocardiogram input (153 variables). The size of the circles is proportional to the amount of data. The calibration belt with 80% and 95% confidence intervals on the external sample shows the observed and predicted cardiovascular disease proportions in (B) lasso, (C) adaptive lasso, (E) plugin lasso, (F) elastic net models with electrocardiogram and vectorcardiographic input (695 predictors).

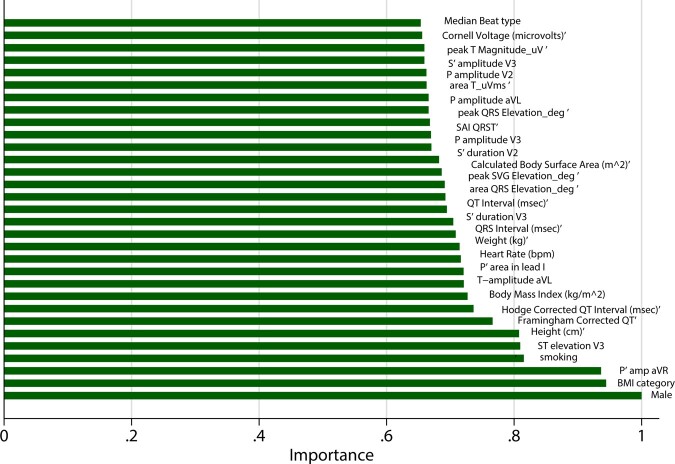
Random forests model with 695 input variables that included both ECG and VCG predictors was tuned (Supplementary material online, Figure S1) and included 500 subtrees and 26 variables to randomly investigate at each split. The final VCG + ECG random forest model reported smaller error (10%) than the VCG-based model in the validation sample. The model correctly detected CVD in only 14 out of 75 individuals (sensitivity 19%), while it accurately identified all 536 CVD-free participants (specificity 100%). The most influential predictors are shown in Figure 6.

Figure 6.

Importance scores of the most important predictor variables in a random forest model with both vectorcardiographic and electrocardiogram input (695 predictors).

The CNN with the input of 153 ECG predictor variables demonstrated moderate predictive accuracy, which was significantly worse when compared to the CNN model with VCG input (Table 2) and had poor calibration (Figure 5D).

Discussion

In this large community-based cross-sectional study of nearly 4000 African American men and women with the nested family cohort, we used ML to detect prevalent CVD. We developed and validated a simple model for the detection of prevalent CVD, which included age and spatial QRS-T angle. In the future, automated ECG measurements could be implemented in community settings (barbershops, community centres, churches). Our findings open an avenue for a randomized controlled trial of pharmacist-led interventions for secondary prevention of CVD (e.g. statins, aspirin, BP-lowering drugs) in barbershops and other community centres, which may ultimately reduce cardiovascular morbidity and mortality in underserved and resource-limited communities.

Overwhelming data have proved that statins, aspirin, and BP-lowering medications for secondary prevention of CVD reduce mortality. However, in the USA, only 45% of CVD patients receive aspirin, 88% receive antihypertensive medication, and 65% receive statins.³³ Furthermore, adherence to statin use is low, especially in AA adults.³⁴ Among AAs, CVD is underdiagnosed and undertreated,² which reflects underdiagnosed and undertreated CVD in underserved communities across the globe. Screening for prevalent CVD in community centres with subsequent pharmacist-led interventions can save thousands of lives in resource-limited communities. Randomized clinical trials are warranted to test the proposed strategy in different countries, where community centres’ names and settings can vary considerably.

In this study, the ML approach selected the QRS-T angle as the most important predictor, which, together with age, is necessary and sufficient to detect prevalent CVD. Spatial QRS-T angle is a well-known cardiovascular risk marker.^26,35 Remarkably, the QRS-T angle outperformed other well-known CVD risk markers, including hypertension, smoking, and BMI, which highlights the importance of information carried by VCG. Equally notably, the QRS-T angle was selected and ranked highly by all ML algorithms, regardless of the initial input set of predictor variables, specific ML model approach to the features selection, importance ranking, and handling correlated variables. This is the strong evidence that both spatial QRS-T angle and age truly belong to the model of prevalent CVD outcome, regardless of all other risk factors and ECG features. Interestingly, Jensen et al.³⁶ showed that the spatial QRS-T angle was the only GEH parameter that interacted with race in the association with SCD.³⁶ This finding is consistent with our results, showing the strongest association of spatial QRS-T angle with prevalent CVD in AA men and women.

It is important to note the differences between spatial area and peak QRS-T angles. By measuring peak QRS and T vectors, we assess the moment when most of the heart is depolarized (QRS) or repolarized (T).^37,38 By measuring QRS and T areas, we aim to assess the entire depolarization (QRS) and repolarization (T) phase, which can be done in healthy hearts. However, diseased hearts are characterized by the heterogeneity of activation and repolarization.³⁹ A single-diploe ECG approximation carries inherent limitation in modelling multipolar electrical activity,³⁹ reflected by inaccuracies in the onset and offset of QRS and T waves definitions. Notably, in this study, peak-based QRS-T angle was preferentially selected by all ML models, whereas some models (lasso, elastic net) selected both peak-based and area-based angles, or both peak-based and frontal (two-dimensional) angles, suggesting their complementary value.

The Personalized Risk Identification and Management for Arrhythmias and Heart Failure by ECG and CMR (PRIMERI) study⁴⁰ prospectively enrolled participants (40% AAs) with spatial QRS-T angle ≥105°or Selvester score ≥5 and showed that more than half of them had a myocardial scar.⁴¹ It is known that silent MI is frequent in the community and is associated with worse clinical outcomes.⁸ Furthermore, it was previously shown that the QRS-T angle is associated with future silent MI.⁴² The awareness of common heart attack symptoms is low in AAs (43.1%).¹ Only 11.8% of AA adults (≥20 years of age) meet ideal cardiovascular health criteria.¹ Socioeconomic factors (absence of medical insurance and lack of access to specialized cardiovascular care) increase the number of individuals with prevalent but undiagnosed CVD in underserved communities, highlighting our study findings’ importance.

Importantly, our study compared the performance of models selected by supervised ML with two sets of input variables. We found that the models using the input of nearly 700 ECG features selected finicky, rarely observed ECG features (e.g. P-prime in V2-V5, R-prime in lead I and aVR), and did not improve final VCG-based models, which selected global VCG features that describe the directions of QRS, T, and SVG vectors. For all models, the set of input variables determined the final selection of variables. The performance of VCG + ECG models was slightly worse in the validation sample than in training and testing sample, whereas the performance of VCG models in the validation sample was slightly better than in training and testing sample. Besides a random chance (a random seed selection by ML machinery), one possible reason for that is a type of input variables. ECG input variables included tiny, particular, infrequently observed ECG features, which more easily lead to over-fitting ML models in a training and testing sample, but, as expected, to lower performance in the validation sample. In contrast, VCG features provided a robust and reproducible out-of-sample validation. Further studies are needed to compare the performance of ML models using the raw ECG signal input as compared to the derived ECG/VCG metrics input.

While the ML approach is gaining strengths in cardiology, only one previous study used ML to detect prevalent CVD. Dinh et al.⁴³ used an input of 131 clinical characteristics in the National Health and Nutrition Examination Survey (NHANES) data and reported a ROC AUC of ∼0.8. Unfortunately, Dinh et al.⁴³ did not report β-coefficients for the selected final 24 features, which made external validation of their findings impossible. Also, many of the selected NHANES features are prone to recall bias (e.g. dietary habits: carbohydrate, calcium, fibre, caffeine, sodium intake) and are burdensome for participants.

The selection of the ‘best’ ML model deserves discussion. Our goal was to select the most accurate, well-calibrated, and well-validated parsimonious model. Adaptive lasso model with clinical + VCG (43 variables) input and selected 17 predictor variables met these criteria as ‘the best’ model. The plugin-based lasso model with only two predictor variables (age and spatial QRS-T angle) was the second best. The attraction of a simple model that contains only age and QRS-T angle is that it can be readily implemented in underserved communities, as it does not require complex ECG signal processing or computing. On the other hand, we can foresee that this study results can also be used more broadly. In a resource-rich environment, ECG-based CVD detection can be potentially used as a first screening step to prompt further diagnostic evaluation and precise CVD diagnostics, where the adaptive lasso model would be preferable. Such a strategy should be tested in prospective clinical trials. We reported all coefficients (Tables 4 and 5) and CVD equation (Supplementary material online, Figure S3), allowing future validation and comparison of all reported models. Further studies are needed to assess benefits, harms (for false-positives), and cost-effectiveness of ECG screening for prevalent CVD.

Strengths and limitations

The study’s strengths include its design of a large community study of AA adults with the nested family cohort and well-validated definitions of prevalent CVD and traditional cardiovascular risk factors. The JHS definition of prevalent CVD used strict criteria and did not consider stable angina, which excluded the possibility of false-positive CVD cases.⁴⁴ However, the study limitations have to be acknowledged. The strict CVD definition did not consider stable angina and thus permitted false-negative CVD cases. While we employed out-of-sample validation of our models, validation of the study findings in a larger population of unrelated persons is warranted. Measurement of all 12-lead ECG waves’ durations, amplitudes, and areas was fully automated and may carry measurement error. It is possible that reducing the measurement error of ECG features can improve ML algorithms’ predictive accuracy, which should be studied further.

Conclusion

A simple model for CVD detection, comprised of age and QRS-T angle, has a 70% chance to distinguish between CVD presence or absence. A cut-off that corresponds to 100% sensitivity (≥0.026) makes it useful for prevalent CVD screening in limited-resource settings. In the future, inexpensive automated (utilizing ECG recording) CVD screening can be employed in barbershops, churches, and other community centres. A strategy of automated CVD detection in underserved communities with subsequent interventions for secondary prevention of CVD should be tested in future clinical trials.

Supplementary material

Supplementary material is available at European Heart Journal is available at online.