Entropy analysis of human death uncertainty

Abstract

Uncertainty about the time of death is part of one’s life, and plays an important role in demographic and actuarial sciences. Entropy is a measure useful for characterizing complex systems. This paper analyses death uncertainty through the concept of entropy. For that purpose, the Shannon and the cumulative residual entropies are adopted. The first may be interpreted as an average information. The second was proposed more recently and is related to reliability measures such as the mean residual lifetime. Data collected from the Human Mortality Database and describing the evolution of 40 countries during several decades are studied using entropy measures. The emerging country and inter-country entropy patterns are used to characterize the dynamics of mortality. The locus of the two entropies gives a deeper insight into the dynamical evolution of the human mortality data series.

Introduction

The age at death is uncertain in nature. With this regard we can quote Thomas Paine “Nothing, they say is more certain than death, and nothing more uncertain than the time of dying”. Nevertheless, it is well-known that the risk of death depends on several factors, such as age, sex, genetics, lifestyle, and others. This knowledge comes from the analysis of specific groups of people, often organized per sex and in a country basis. The information is gathered in lifetables, which provide a complete description of mortality in a given population [17, 38, 47].

Mortality is determinant to the population dynamics and the uncertainty associated either with the time of death, or the risk regarding the duration of life, is crucial in many fields of human activity, such as economy, demography and social sciences [26, 31]. In recent years, the topic has received increasing attention, especially due to the trend in population aging in developed countries, showing that people aged 65 or older is increasing faster than all other age groups. Life expectancy statistics give insight about the expected duration of life conditionally on age-specific mortality rates. However, individuals in a population usually do not have idea about the risk relative to their age at death, as well as about the speed at which that risk is resolved as they become older [34]. To tackle these questions, the modeling and forecasting of mortality and the uncertainty in mortality rates have been widely investigated [29, 43, 49, 61].

A lifetable is a 2-dimensional array that summarizes the mortality experience of a population and highlights information about longevity [38]. The array lines correspond to age intervals, typically of 1-year width, starting at age 0 and ending at ages greater than 100 years. The array columns stand for several variables computed from population data. The basic information is the probability of death at a given age, which means the probability of a person living until that age to die before his/her next birthday. However, a number of distinct variables and statistics can be derived and included in standard lifetables.

The complementary cumulative distribution function is used in a broad range of applications, including engineering and demography, where it is often denoted by reliability function and survival function, respectively. This mathematical description gives the probability that an “item”, or individual, works, or survives, beyond any specified time, or age [27, 63]. The survival function can be derived from the lifetable and, in the case of human survival, the shape of the curve conveys important information about the population. For example, a more rectangular-like shape means a lower degree of uncertainty about the age at death and, in the limit, a pure rectangular form would correspond to the hypothetical case where all individuals in a population would survive until a specific age and, then, all would die at that same age [34, 60]. Different measures to quantify death uncertainty have been proposed based on the survival functions. We can mention the Kannisto’s coefficient [22], the standard deviation of the age at death [15, 28], the Gini index of the length of life [53] and the lifetime entropy [35].

The entropy was developed by Clausius [10] and Boltzmann [8], and later by Shannon [50] and Jaynes [20], in the scope of thermodynamics and information theory, respectively. The entropy has been adopted to characterize complex dynamical systems and used as a measure to quantify uncertainty, diversity and randomness. In the last decades, the original formulation of entropy has been extended by several authors to better adapt to certain systems’ characteristics [30].

In demographic sciences, the entropy has been used to quantify the influence of the mortality rate on the expected lifetime [3, 18, 19, 25]. A higher entropy means that the expected lifetime is more sensitive to changes in the mortality rate, and vice-versa. The entropy is also regarded as a measure of the “rectangularization” of the survival function. Rectangular-like shapes characterize populations where most people die at older ages and, thus, the volatility of the age at death is small. A full rectangular survival function would translate into zero entropy [37].

The Keyfitz’s entropy [25] was proposed to measure the variation of the lifespan. This formulation is a normalized version of the Shannon’s expression, and can be interpreted as the “elasticity” of the life expectancy to a change in the mortality. The concept was further explored by Goldman and Lord [19], Vaupel [57], and Vaupel and Canudas Romo [58].

Zhang and Vaupel [62] studied the entropy of the lifetable and showed that there is an age for which averting deaths before (after) that value reduces (increases) life disparity. Therefore, such threshold age separates early and late deaths. If the entropy is less than one, then we have a threshold age that separates early and late deaths. Otherwise, if the entropy is greater than one, then averting deaths at any age increases the disparity. If the entropy has the value one, then preventing deaths at age zero has no effect, but avoiding a death at any age after zero increases the disparity. Aburto et al. [3] derived a formal proof of the threshold age at which age-specific mortality improvements translate into either a reduction or an increase in the lifespan inequality. More recently, Aburto et al. [4] studied the life expectancy and lifespan equality over time. The results demonstrated that the link between both indicators is particularly strong for a life expectancy less than 70 years, and that saving lives at ages below life expectancy is the key to increase the life expectancy and lifespan equality. In this regard, van Raalte and Caswellere [56] studied the response of seven lifespan variation indices with relation to variations in the mortality schedule. The Theil’s index and the mean logarithmic deviation [52] are obtained from the entropy of the distribution of the age at death. All indices were derived within the framework of absorbing Markov chains and used to obtain the sensitivity and the elasticity of lifetables with regard to changes in age-specific mortality. Meyer and Ponthiere [34] addressed the quantification of risk regarding the duration of life in the viewpoint of the Shannon’s entropy using the logarithm of base 2. The entropy was interpreted as the expectation of the amount of information (expressed in bits) exhibited by the event of a life of a particular length or, alternatively, of the information disclosed by a death at a given age. Consequently, the lifetime entropy is the informational analogous of the life expectancy. In another study, Meyer and Ponthiere [35] investigated the uncertainty about the duration of life, quantified by the Shannon’s entropy (measured in bits), due to variations in the age-specific probability of death. They found two threshold ages, namely: (i) a low value, below (above) which a rise in the mortality risk decreases (increases) the lifetime entropy, and (ii) a high value, above which a raise in mortality risk reduces the lifetime entropy.

Reliability engineering addresses the ability of a system, or component, to function under expected conditions for a given period of time. This field deals with the concepts of lifetime uncertainty and risk of failure, among others [13, 16]. In demography, the counterparts of these concepts are the human lifetime uncertainty and the risk of death, while the systems subjected to failure are people. Therefore, many tools adopted in the area of reliability engineering are identical to those used in the study of human lifetime. The entropy has been widely adopted, specifically the classical formulations and their most common generalizations. Moreover, we can mention the Rényi [42], Tsallis [9], residual [14], cumulative [12] and past [36] entropies, as well as extropies [2], and other closely related indices [21, 55].

This paper studies the time at death uncertainty under the perspective of the entropy concept. Data series obtained at the Human Mortality Database for a set of 40 countries are processed by means of several entropy measures. The results unveil patterns that are used to characterize the dynamics of mortality.

The paper includes six sections. Section 2 introduces the concept of entropy and several entropy formulations. Section 3 describes the dataset used in the work. Section 4 analyses the mortality of 40 countries by means of entropy measures. Section 5 compares the different countries using the locus of cumulative residual entropy versus entropy. Finally, Sect. 6 outlines the conclusions.

The concept of entropy

Let X be a finite discrete random variable with possible values $\{x_1,x_2,\cdots ,x_N\}$ and probability mass function $P=\{p_1,p_2,\cdots ,p_N\}$, where $p_i=P(X=x_i)$, $i=1\cdots ,N$, ${\sum }_i{p}_i=1$ and $p_i\ge 0$. The Shannon entropy, H, of the random variable X is defined as:

$$\begin{array}{c}\hfill H=\sum _i{p}_{i}I(p_i)=-\sum _i{p}_{i}ln{p}_i.\end{array}$$ 1

Expression (1) is the expected value of the information of the event $X=x_i$ given by $I(p_i)=-ln{p}_i$. For the uniform distribution $p_i=N^{-1}$, $N\in \mathbb{N}$, and the Shannon entropy reaches the maximum $H=lnN$.

The expression (1) can be extended to the continuous case, at the cost of loosing some properties of the discrete formulation [46].

Let us consider a continuous nonnegative random variable X with probability density function f(x). The Shannon differential entropy, H, of X is defined as [51]:

$$\begin{array}{c}\hfill H=-{\int }_0^{\infty }f(x)lnf(x)\text{d}x,\end{array}$$ 2

and represents a measure of uncertainty for X.

The entropy, viewed as a measure of uncertainty in lifetime, attracted attention of several researchers during the last years [11, 23, 24, 34]. Let X describe the random lifetime of an “item”, and let us denote by F(x) and $\overline{F}(x)$ the cumulative distribution and survival functions of X:

$$\begin{array}{c}\hfill F(x)={\int }_0^{x}f(x)\text{d}x,\end{array}$$ 3a

$$\begin{array}{c}\hfill \overline{F}(x)=1-F(x).\end{array}$$ 3b

Suppose that the “item” survived up to age $t>0$. We define the Shannon residual entropy of X at time t, H(t), as the entropy of $[X|X>t]$, where [X|A] stands for probability distribution identical to the one of X conditional on A. Therefore, we have [11]:

$$\begin{array}{cc}\hfill H(t)& =-{\int }_t^{\infty }\frac{f(x)}{\overline{F}(t)}ln\frac{f(x)}{\overline{F}(t)}\text{d}x\hfill \\ \hfill & =1-\frac{1}{\overline{F}(t)}{\int }_t^{\infty }f(x)ln\lambda (x)\text{d}x,\hfill \end{array}$$ 4

where $\lambda (t)=f(t)/\overline{F}(t)$ is the hazard function, or failure rate, of X. By other words, given that the “item” has survived up to time t, the residual entropy of X, H(t), reflects the uncertainty about its continuing lifetime.

In certain cases, it is reasonable to presume that uncertainty is not only associated with the future, but is also interconnected to the past. For instance, if the state of an “item” is observed only at certain preassigned time instants and, at the instant t, it is found to be not working, or dead, then the uncertainty relies on the past. Therefore, the Shannon past entropy of X at time t, $\overline{H}(t)$, is the differential entropy of the distribution $[X|X\le t]$. The past entropy $\overline{H}(t)$ represents an uncertainty that is the dual of H(t), in the sense that it focuses on the past, and is defined as:

$$\begin{array}{c}\hfill \overline{H}(t)=-{\int }_0^t\frac{f(x)}{F(t)}ln\frac{f(x)}{F(t)}\text{d}x.\end{array}$$ 5

We must note that $\overline{H}(t)\in \mathbb{R}$ and that, for $t=0$, expression (4) yields the Shannon differential entropy (2), while expression (5) has no meaning.

Both the residual and past entropies have application in different branches of sciences, namely in reliability engineering [46], computer vision [5], survival analysis [1], image processing [59] and actuarial sciences [48].

A more general measure of uncertainty was proposed by Rao et al. [46], being denoted by Shannon cumulative residual entropy, $\mathcal{E}$, which is obtained when replacing f(x) by $\overline{F}(x)$ in (2), yielding:

$$\begin{array}{c}\hfill \mathcal{E}=-{\int }_0^{\infty }\overline{F}(x)ln\overline{F}(x)\text{d}x={\int }_0^{\infty }\overline{F}(x)\Lambda (x)\text{d}x,\end{array}$$ 6

where $\Lambda (x)=-ln\overline{F}(x)={\int }_0^x\lambda (t)\text{d}t$ is the so-called cumulative hazard function. The cumulative residual entropy addresses the information content of the distribution of a random variable and thereby is also a measure of uncertainty. This measure is valid in the continuous and discrete domains and can be easily computed from sample data.

Identically, the Shannon cumulative entropy is given by:

$$\begin{array}{c}\hfill \mathcal{CE}=-{\int }_0^{\infty }F(x)lnF(x)\text{d}x.\end{array}$$ 7

The dynamic cumulative residual and dynamic cumulative entropies are, in turn, given by [11]:

$$\begin{array}{cc}\hfill \mathcal{E}(t)& =-{\int }_t^{\infty }\frac{\overline{F}(x)}{\overline{F}(t)}ln\frac{\overline{F}(x)}{\overline{F}(t)}\text{d}x\hfill \\ \hfill & ={\int }_t^{\infty }\frac{\overline{F}(x)}{\overline{F}(t)}[\Lambda (x)-\Lambda (t)]\text{d}x\hfill \end{array}$$ 8

and

$$\begin{array}{c}\hfill \mathcal{CE}(t)=-{\int }_0^t\frac{F(x)}{F(t)}ln\frac{F(x)}{F(t)}\text{d}x.\end{array}$$ 9

Several generalizations of expressions (6)-(9), for $n\in \mathbb{N}$, were proposed, such as [55]:

$$\begin{array}{cc}& {\mathcal{E}}_n=\frac{1}{n!}{\int }_0^{\infty }\overline{F}(x){[-ln\overline{F}(x)]}^n\text{d}x,\hfill \end{array}$$ 10

$$\begin{array}{cc}& {\mathcal{CE}}_n=\frac{1}{n!}{\int }_0^{\infty }F(x){[-lnF(x)]}^n\text{d}x,\hfill \end{array}$$ 11

$$\begin{array}{cc}& {\mathcal{E}}_n(t)=\frac{1}{n!}{\int }_t^{\infty }\frac{\overline{F}(x)}{\overline{F}(t)}{\left[-,ln,\frac{\overline{F}(x)}{\overline{F}(t)}\right]}^n\text{d}x,\hfill \end{array}$$ 12

$$\begin{array}{cc}& {\mathcal{CE}}_n(t)={\int }_0^t\frac{F(x)}{F(t)}{\left[-,ln,\frac{F(x)}{F(t)}\right]}^n\text{d}x.\hfill \end{array}$$ 13

Some properties of $\mathcal{E}$ and $\mathcal{E}(t)$, given by (6) and (8), were discussed by Asadi and Zohrevand [6] and Navarro et al. [39], while the properties of ${\mathcal{E}}_n$ and ${\mathcal{E}}_n(t)$, expressed by (10) and (12), were explored by Navarro and Psarrakos [40], Psarrakos and Navarro [44] and Psarrakos and Toomaj [45].

The generalization of differentiation and entropy has received considerable attention in the last decades. New formulations extended the application of these concepts to highlight characteristics of complex systems [32, 41, 54]. For a recent review on both topics, interested readers can see [30].

Different entropy formulations can have particular interpretations in the scope of a given application [7]. In the present case, we shall adopt a more abstract point of view and consider them as alternative information measures for capturing distinct properties of the system under study. Indeed, an eclectic assessment of the dataset seems a better strategy to avoid a priori assumptions that may overlook relevant information embedded in the dataset.

Brief description of the dataset

Data for 40 countries (Table 1 in the Appendix) were collected at the Human Mortality Database website on February 2, 2021 (https://www.mortality.org/). The Human Mortality Database, held by the University of California, Berkeley, and Max Planck Institute for Demographic Research, contains original information of death rates and lifetables for national populations. The lifetables are available for men, women and both genders, in an annual basis. The age intervals have 1-year width, starting at the age $t=0$ (i.e., birth) and ending at age $t=110$, meaning that the last interval includes ages $t>110$. The probabilities of death, q(t), and other indicators of mortality and longevity are given at each age t. The data covers different periods of time for each country. The longest and shortest records are those collected for Sweden and the Republic of Korea comprising 269 and 16 years, respectively.

From the lifetables we derive the survival function, $\overline{F}(t)$, as:

$$\begin{array}{c}\hfill \overline{F}(t+1)=[1-q(t)]·\overline{F}(t),t=1,2,\cdots ,109,\\ \hfill \end{array}$$ 14

with $\overline{F}(0)=1$.

The probability density function, f(t), is computed by:

$$\begin{array}{c}\hfill f(t)=\frac{\text{d}}{\text{d}t}F(t).\end{array}$$ 15

Figure 1 depicts the functions f and $\overline{F}$ versus calendar time and age, $\tau$ and t (expressed in years), for the whole population (male plus female) lifetables of France and Norway.

Fig. 1.

The probability density and survival functions, f and $\overline{F}$, versus calendar time and age, $\tau$ and t (expressed in years), for the whole population (male plus female) lifetables of France and Norway: a f for France; b $\overline{F}$ for France; c f for Norway; (d) $\overline{F}$ for Norway. The probability density function, f, is in log units. The colorbar represents $f(\tau ,t)$ in a logarithmic scale

We verify that the probability of death is high for newborn and for $t\in [65,90]$ years old people. Above the age $t\approx 90$ years the probability of death drops very fast towards zero. Moreover, we observe that for children the mortality has been decreasing in calendar time, while for the group $t\in [65,90]$ years the age of maximum probability of death has been increasing. The effect of certain extreme events, as the two World Wars (WWI and WWII) are well visible in the plots. The other countries have f and $\overline{F}$ patterns of the same type.

Human lifetime entropy

This section analyses the lifetime entropy along calendar time and age, $\tau$ and t, using data of period lifetables. For a given year, $\tau$, the lifetime entropy quantifies the amount of risk, or uncertainty, about the age at death that is unresolved at age t. Therefore, for the particular case of $t=0$, we obtain the lifetime entropy at birth, which represents the risk of a complete lifetime.

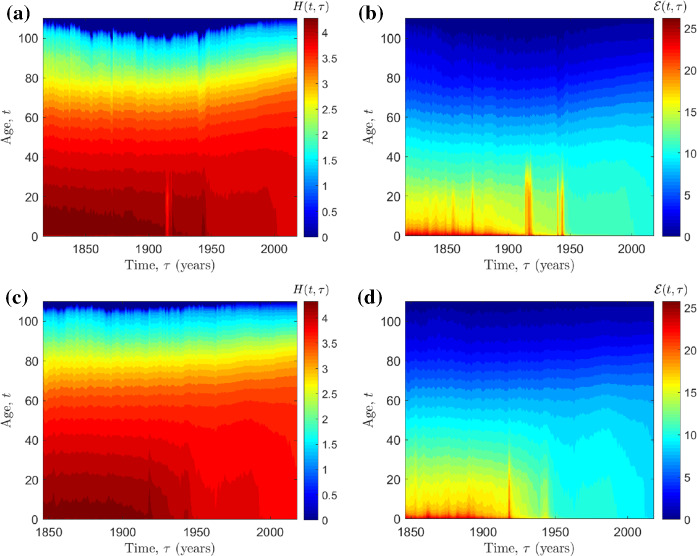
Figure 2 depicts the Shannon and cumulative residual entropies versus time and age, $H(\tau ,t)$ and $\mathcal{E}(\tau ,t)$, for the France and Norway complete populations (i.e., males plus females). By other words, for each year, $\tau$, the entropies are calculated for the variable t (i.e., the age) by means of expressions (4) and (8). We verify that the lifetime entropy is higher at younger ages and reduces progressively as age increases. This means that the duration of life is progressively resolved when individuals become older. In fact, at younger ages numerous factors can affect the duration of life and make it more unpredictable, which translates into larger entropy. On the contrary, at older ages, the number of possible scenarios that determine the duration of life becomes more limited, and the lifetime entropy is reduced. In this perspective, the lifetime entropy at successive ages pictures how the amount of risk regarding the duration of life varies with age and how it evolves when individuals become older [35]. For other countries the results are of the same type.

Fig. 2.

The values of Shannon and dynamic cumulative residual entropies, $H(\tau ,t)$ and $\mathcal{E}(\tau ,t)$, versus calendar time and age, $\tau$ and t, for the populations of: a France; b Norway

Comparing these plots with those depicted in Fig. 1, we note that we reduce slightly the visibility of the WWI and WWII periods, but, on the other hand, we obtain a more uniform variation with the age t.

It should also be mentioned that other entropy formulations were experimented and led to results of the same type as those presented. Naturally, the analysis can also be performed for groups, namely organized by gender or by age, instead for the whole country population.

Residual lifetime entropy

We compare countries based on the uncertainty about remaining lifetimes. We consider $H(\tau ,t)$ and $\mathcal{E}(\tau ,t)$ for the years $\tau =\{$1958, 1978, 1998, 2018$\}$ and ages $t=\{0,\cdots ,110\}$. The set covers a wide period of time. We must note that lifetables are not available for some countries during all years and, therefore, the lines exhibit different starting and ending dates.

Figures 3 and 4 depict the Shannon and dynamic cumulative residual entropies, $H(\tau ,t)$ and $\mathcal{E}(\tau ,t)$, and reveal that the countries exhibit identical entropy patterns. Two notable points emerge, where the slope of the curves changes considerable and, simultaneously, the entropy values approach to each other. The first point corresponds approximately to age threshold value $t_{h1}=52$ years in year $\tau =1958$ and increases until $t_{h1}=65$ in $\tau =2018$. The second point corresponds to age $t_{h2}=105$ years and practically does not change in time.

Fig. 3.

The Shannon entropy $H(\tau ,t)$ of various countries for 4 years and all ages $t=\{0,\cdots ,110$}: a $\tau =1958$; b $\tau =1978$; c $\tau =1998$; d $\tau =2018$

Fig. 4.

The dynamic cumulative residual entropy $\mathcal{E}(\tau ,t)$ of various countries for 4 years and all ages $t=\{0,\cdots ,110$}: a $\tau =1958$; b $\tau =1978$; c $\tau =1998$; d $\tau =2018$

The variation of the threshold values $t_{h1}$ and $t_{h2}$ is also noticeable when analyzing a given country. For instance, Fig. 5 represents $t_{h1}$ and $t_{h2}$ for France and Norway. We verify that, for France, $t_{h1}$ increases slowly from $t=62$ at $\tau =1816$ up to $t=67$ at $\tau =1960$. Then, $t_{h1}$ increases faster, reaching approximately $t=75$ at $\tau =2018$. The threshold $t_{h2}$ is almost constant. For Norway, $t_{h1}$ increases from $t=52$ at $\tau =1816$ up to $t=60$ at $\tau =1890$. For $\tau \in [1890,1975]$, $t_{h1}$ increases, reaching approximately the value $t=65$ at $\tau =2017$. The threshold $t_{h2}$ is somewhat noisy, but maintains its constant trend over time. We can conjecture that $t_{h1}$ reflects public health policies that led to an higher expectancy of life, while $t_{h2}$ points to some intrinsic biological limit, but we must highlight that this is merely an interpretation based on the numbers.

Fig. 5.

The variation of the threshold values $t_{h1}$ and $t_{h2}$ for: a France; b Norway

Period lifetime entropy

We now compare all countries based on the evolution of their lifetime entropy versus time $\tau$. As such, we compute $H(\tau ,t)$ and $\mathcal{E}(\tau ,t)$, for all years, $\tau$, and a set of six ages $t=\{0,25,45,60,75,85\}$.

Figures 6 and 7 depict the entropies $H(\tau ,t)$ and $\mathcal{E}(\tau ,t)$, respectively, for the 40 countries listed in Table 1 when considering the whole country populations.

Fig. 6.

The Shannon entropy $H(\tau ,t)$ of various countries for $t\in [1751,2019]$ and the ages: a $t=0$; b $t=25$; c $t=45$; d $t=60$; e $t=75$; f $t=85$

Fig. 7.

The dynamic cumulative residual entropy $\mathcal{E}(\tau ,t)$ of various countries for $t\in [1751,2019]$ and the ages: a $t=0$; b $t=25$; c $t=45$; d $t=60$; e $t=75$; f $t=85$

Table 1.

List of countries with dataset time ranges

Number	Name	Acronym	Start year	End year	Number	Name	Acronym	Start year	End year
1	Australia	AUS	1921	2018	21	Japan	JPN	1947	2019
2	Austria	AUT	1947	2017	22	Latvia	LVA	1959	2017
3	Belarus	BLR	1959	2018	23	Lithuania	LTU	1959	2019
4	Bulgaria	BGR	1947	2017	24	Luxembourg	LUX	1960	2019
5	Canada	CAN	1921	2016	25	Netherlands	NLD	1850	2018
6	Chile	CHL	1992	2017	26	New Zealand	NZL	1948	2013
7	Croatia	HRV	2001	2018	27	Norway	NOR	1846	2018
8	Czechia	CZE	1950	2018	28	Poland	POL	1958	2018
9	Denmark	DNK	1835	2019	29	Portugal	PRT	1940	2018
10	Estonia	EST	1959	2017	30	Republic of Korea	KOR	2003	2018
11	Finland	FIN	1878	2019	31	Russia	RUS	1959	2014
12	France	FRA	1816	2018	32	Slovakia	SVK	1950	2017
13	Germany	DEU	1990	2017	33	Slovenia	SVN	1983	2017
14	Greece	GRC	1981	2017	34	Spain	ESP	1908	2018
15	Hong Kong	HKG	1986	2017	35	Sweden	SWE	1751	2019
16	Hungary	HUN	1950	2017	36	Switzerland	CHE	1876	2018
17	Iceland	ISL	1838	2018	37	Taiwan	TWN	1970	2014
18	Ireland	IRL	1950	2017	38	U.K.	GBR	1922	2018
19	Israel	ISR	1983	2016	39	U.S.A.	USA	1933	2018
20	Italy	ITA	1872	2017	40	Ukraine	UKR	1959	2013

We verify that H is quite noisy until around year $\tau =1880$, probably because the information had to be tackled manually, with strong limitations in collecting and communicating data, and no computational resources available to construct and maintain accurate datasets. For $t=0$, we can see that H increases in time until approximately year $\tau =1914$, corresponding to the beginning of WWI, while we observe a convergence of its values for all countries. The effect of the WWI (1914 – 1918) is clear, translating into a perturbation characterized by a local maximum at year $\tau =1918$, for most countries, and a minimum for France, Italy and Spain. Between the two World Wars, the entropy decreases slowly, while the convergence between its behavior for all countries continues. During the WWII (1939 – 1945) the entropy increases in time. In the decade post WWII, the values fall down quickly and the country entropies reveal maximum convergence. For most countries, this effect is followed by a relative stable period that goes from year $\tau =1957$, the beginning of the “Asian flu” pandemic, until year $\tau =1988$, the beginning of the collapse of the Soviet Union. Then, from $\tau =1994$ onward, the entropy diminishes moderately in time. Simultaneously, for a group of Eastern Europe countries, the entropy firstly increases slowly, has clear local minimum and maximum around years $\tau =1988$ and $\tau =1994$, respectively, and diminishes moderately from $\tau =1994$ onward. Starting around year $\tau =1957$ and becoming more evident from year $\tau =1988$ onward, the 40 countries separate in three clusters: ${\mathcal{C}}_1=\{$BLR, EST, LTU, LVA, RUS, UKR$\}$, ${\mathcal{C}}_2=\{$BGR, CHL, HUN, POL, SVK, TWN, USA$\}$ and ${\mathcal{C}}_3=\{$AUS, AUT, CAN, CHE, CZE, DEU, DNK, ESP, FIN, FRA, GBR, GRC, HKG, HRV, IRL, ISL, ISR, ITA, JPN, KOR, LUX, NLD, NOR, NZL, PRT, SVN, SWE$\}$. The effect of other extreme events in the behavior of H is not visible.

For age $t=25$ the entropy increases until approximately year $\tau =2007$ and then it inverts the tendency. There is a trend to convergence between values for all countries. This behavior is even more evident at age $t=45$ years. For age $t=60$ the general entropy pattern changes and, for $t=75$ and $t=85$, the clusters identified at $t=0$ show up again.

In what concerns the plot of the dynamic cumulative residual entropy $\mathcal{E}$ versus time (Fig. 7), we verify the existence of three main periods for the ages $t=\{0,25,45\}$. The first period lasts until approximately year $\tau =1880$, where $\mathcal{E}$ is roughly constant, the second period is $\tau \in [1880,1957]$ with $\mathcal{E}$ diminishing considerably, and the third goes from $\tau =1957$ onward, characterized by moderate decreasing values of $\mathcal{E}$. Moreover, it can be seen that (i) $\mathcal{E}$ is less noisy that H, (ii) the period $\tau \in [1880,1957]$ exhibits large differences among countries, with the effect of the two World Wars clearly visible through the peak values, and (iii) in the period from $\tau =1957$ onward the clusters identified for H are also present. For the age $t=60$ the pattern changes and, for $t=75$ and $t=85$, the entropy increases over time. Therefore, $\mathcal{E}$ characterizes long-period trends better than H, while signaling also the local behavior of lifetime. We observe also that H and $\mathcal{E}$ exhibit some correlation, but they highlight different characteristics of the lifetime.

The locus of dynamic cumulative residual entropy versus Shannon entropy

We consider here that $H(\tau )$ and $\mathcal{E}(\tau )$, are the state variables of a dynamical system describing human lifetime.

Figure 8 shows the locus of $\mathcal{E}(\tau )$ versus $H(\tau )$ for the 40 countries at ages $t=\{0,25,45,60,75,85\}$. We have a similar behavior for all countries and ages. However, we verify that there is a change in the patterns over time, as already noticed in Figs. 6 and 7. In fact, we note a modification of the shape of the locus for ages between $t=60$ and $t=75$, which is consistent with the previous observations for $t_{h1}$. In what concerns viewing the influence of $t_{h2}$, we have difficulties due to the lack of data. In fact, the loci for high values of the age are simply a collection of points with a limited scatter along a simple straight line. This means, somehow, that at such ages and at present state of public health, we have presently an evolution with almost a deterministic nature.

Fig. 8.

The locus of $\mathcal{E}(\tau )$ versus $H(\tau )$ for the set of 40 countries and the ages: a $t=0$; b $t=25$; c $t=45$; d $t=60$; e $t=75$; f $t=85$. Each point corresponds to one year and the arrow of time flows from left to right

Loosely speaking, we can say that with regard with the topic of this paper each country has it own, and distinct, calendar time. Nonetheless, the differences between countries have reduced significantly along years. Therefore, we can say that some close “synchronization” between countries will occur in the years to come. At the time of writing this paper we have the COVID-19 pandemic [33], but no data is yet available. It will be an interesting future study to assess its effect upon the results discussed here.

Conclusion

This paper analyzed death uncertainty through the concept of entropy. A set of 40 countries was studied based on different entropy measures. The entropy patterns were used to characterize the dynamics of mortality. Contrary to some results reported in the literature, in the last decades country lifetime entropy is not converging to a single point. The convergence to several distinct values started approximately in 1957. Since then, three clusters emerged, their relative differences firstly increased and, then, stabilized. The evolution of the entropy in time and the locus of the dynamic cumulative residual entropy versus Shannon entropy led to relevant results. The locus, in particular, is more advantageous since brings into evidence long range patterns embedded in the data.

Declarations

Conflict of interest

The authors declare that they have no conflict of interest