Computational Fluid Dynamics Modeling of Intracranial Aneurysms: Effects of Parent Artery Segmentation on Intra-Aneurysmal Hemodynamics

Abstract

PURPOSE: The purpose of this study is to show the influence of the upstream parent artery geometry on intraaneurysmal hemodynamics of cerebral aneurysms.

METHODS: Patient-specific models of 4 cerebral aneurysms (1 posterior communicating artery [PcomA], 2 middle cerebral artery [MCA], and 1 anterior communicating artery [AcomA]) were constructed from 3D rotational angiography images. Two geometric models were constructed for each aneurysm. One model had the native parent vessel geometry; the second model was truncated approximately 1 cm upstream from the aneurysm, and the parent artery replaced with a straight cylinder. Corresponding finite element grids were generated and computational fluid dynamics simulations were carried out under pulsatile flow conditions. The intra-aneurysmal flow patterns and wall shear stress (WSS) distributions were visualized and compared.

RESULTS: Models using the truncated parent vessel underestimated the WSS in the aneurysms in all cases and shifted the impaction zone to the neck compared with the native geometry. These effects were more pronounced in the PcomA and AcomA aneurysms where upstream curvature was substantial. The MCA aneurysm with a long M1 segment was the least effected. The more laminar flow pattern within the parent vessel in truncated models resulted in a less complex intra-aneurysmal flow patterns with fewer vortices and less velocity at the dome.

CONCLUSIONS: Failure to properly model the inflow stream contributed by the upstream parent artery can significantly influence the results of intra-aneurysmal hemodynamic models. The upstream portion of the parent vessel of cerebral aneurysms should be included to accurately represent the intra-aneurysmal hemodynamics.

The concept that flow dynamics plays an important role in the initiation, growth, and rupture of cerebral aneurysms has been widely accepted, largely as a result of data from numerous experimental models and clinical studies.^1–8 These works have characterized the complexity of intra-aneurysmal hemodynamics in experimental and computational models but, because of technical factors, have largely focused on idealized aneurysm geometry or surgically created aneurysms in animals. In vitro studies have allowed very detailed measurement of hemodynamic variables but are of limited value in understanding the hemodynamic forces in an individual clinical case. Current technology cannot provide analogous information in vivo through either invasive or noninvasive measurements; therefore, researchers have turned to computational fluid dynamic simulations to gain a better understanding of the intra-aneurysmal hemodynamics.

Computational based models provide an attractive method of investigating intra-aneurysmal flow dynamics by providing the ability to theoretically model and study any possible geometries.^9–12 Until recently computational studies have been only performed on idealized aneurysm geometries or approximations of a specific patient geometry. These experiments have greatly influenced thinking about the mechanisms of aneurysm development because researchers have attempted to make generalized statements about aneurysmal hemodynamics from these simplified models. As computational methods and modeling have improved, more refined models have been constructed, leading to a transition from idealized geometries to “realistic” models based on typical patient anatomies. Most recently, studies have tried to replicate the exact anatomy of specific patients to connect specific hemodynamic factors to clinical events allowing statistical analysis in a patient population.^13,14

In the absence of in vivo measurements, complete validation of these methods has not been possible. However, comparisons with simplified experimental systems have shown good correlation with computational models.^15–20 In addition to direct validation, sensitivity analysis can be performed to obtain an understanding of the influence of a variable within a physiologic range on the results of a specific model.^21,22 These analyses have been done on a variety of assumptions used in modeling including flow rates, flow asymmetries, Newtonian properties of fluids, reconstruction/grid generation techniques, and small branch segmentation.²¹ Even without knowing the exact value of the input variable, this analysis can measure the influence changes (or errors) in the variable would have on the results of a simulation. Previous work has shown that inaccuracies in geometry have the largest potential for adversely influencing intra-aneurysmal hemodynamics.²¹

Implicit in computational modeling has been the study of the aneurysmal system in effect disconnected from the systemic circulation. A portion of the vascular tree, including the aneurysm, is reconstructed, and inflows and outflow are assigned based on a variety of assumptions. Early “idealized” models used a short straight tube as the parent artery and therefore largely neglected the potential effects of parent artery geometry. More recently, “realistic” approximations of patient anatomies and patient-specific anatomic models are being used. There is wide variation among the models used in these studies in the amount of parent artery used. Considering that the cerebral arteries like aneurysms have a great deal of variation between patients, the effects of the segmentation of the parent artery upstream to an aneurysm could be significant on the intra-aneurysmal hemodynamics. The purpose of this study is to extend previously reported sensitivity analysis of our computational modeling to better understand the influence of the geometry of the upstream parent on the intra-aneurysmal hemodynamics. Our hypothesis is that curvatures in the parent artery upstream to the aneurysm neck will significantly influence the direction of the inflow jet so that failure to include these segments in a vascular model may lead to misrepresenting the impaction zone of the inflow jet, a feature that has been shown to correlate with a history of aneurysm rupture.

Methods

Patients and Images

Four patients with cerebral aneurysms were selected from our data base to study the effects on the intra-aneurysmal hemodynamics of truncating the parent vessel at different distances upstream from the neck. Characteristics of these aneurysms are summarized in Table 1. Three common locations of aneurysms in the anterior circulation were chosen that have significant curvatures in the upstream (afferent) parent artery. Two middle cerebral artery (MCA) bifurcation aneurysms were chosen to represent aneurysms with short and long M1 segments. In all the cases, during conventional cerebral angiography, rotational acquisitions were obtained in the internal carotid artery using a Phillips Integris system (Philips Medical Systems, Best, The Netherlands). Images were obtained using a 5-inch image intensifier and the smallest focal spot. In the case of patient 4, bilateral rotational scans were obtained to visualize both avenues of flow into the anterior communicating artery (AcomA) aneurysm. These images were obtained during a 180° rotation and imaging at 15 frames per second for a total of 8 seconds. The corresponding 120 projection images were reconstructed into a 3D dataset of 128 × 128 × 128 voxels covering a field of view of 54.02 mm on a dedicated Philips Integris workstation. The voxel resolution was therefore 0.422 mm. These data were exported into a PC for mathematic vascular modeling using a recently developed method.^21,23,24

Table 1:

Cases selected for study

Patient No.	Location	Size (mm)	Parent Artery	Ruptured
1	Left ICA	9	ICA siphon	No
2	Left MCA	8	Short M1	No
3	Right MCA	6	Long M1	Yes
4	AcomA	10	Symmetrical A1s	No

Note:—ICA indicates internal carotid artery; MCA, middle cerebral artery; AcomA, anterior communicating artery.

Vascular Models

Vascular models were constructed from the 3D rotational angiography (3DRA) images by using geometric deformable models.²⁵ For patient 4, the left and right portions of the anterior vascular network were independently reconstructed from the corresponding 3DRA images and subsequently fused together using a surface-merging algorithm²⁶ and rigid manual registration.^23,24 High-quality volumetric finite element grids composed of tetrahedral elements were then generated with the use of an advancing front technique to fill the space inside these geometric models.^27–29 The mesh minimum resolution was approximately 0.16 mm. The meshes contained roughly 2, 1.8, 3, and 1.3 × 10⁶ elements for patients 1–4, respectively. In all these models, the entire proximal portions of the parent arteries visible in the 3DRA images were reconstructed. A second model was constructed for each patient by cutting the parent vessel in the original models at a proximal location close to the aneurysm neck. The proximal artery was replaced by a straight tube extruded from the site of the “cut.” New computational meshes were generated for the truncated models by using the same spatial resolution (ie, same element size distribution). The new meshes contained approximately 800, 500, 650, and 760 × 10³ elements, respectively. Differences in the number of elements of the models are accounted for by the differences in volumes of the various models as the resolution of the meshes was held constant. In what follows, we denote as model 1 the original model, and as model 2 the truncated model for each patient. The 3DRA images and the vascular models for each patient are shown in Fig 1. From left to right, this figure shows volume renderings of the 3DRA images, the original reconstructed model (model 1), and the truncated model (model 2) for each patient. In the case of patient 4 (bottom row), this figure shows, from left to right, the 3DRA images obtained by contrast injection in the right and left internal carotid arteries, the coregistered 3DRA images, the original reconstructed vascular model, and the truncated vascular model.

Fig 1.

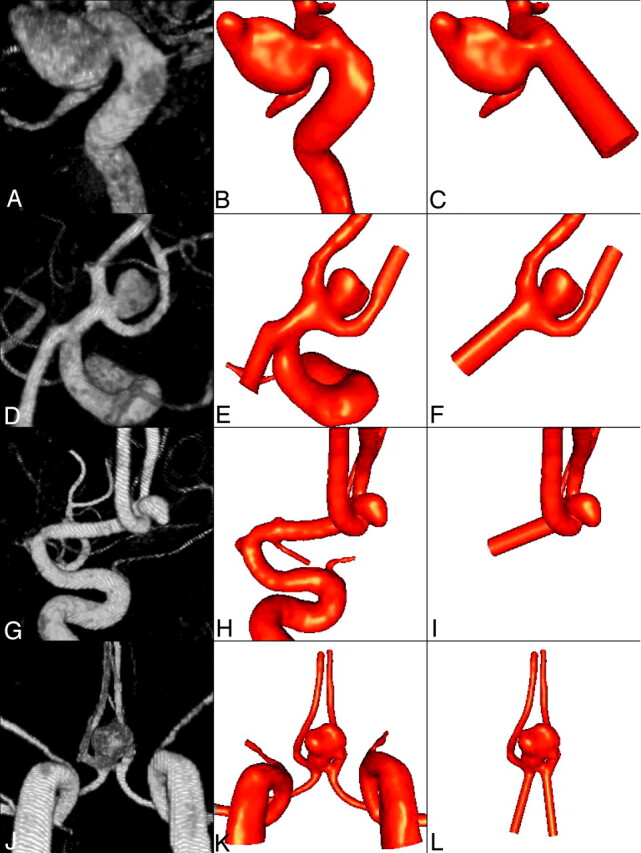
Vascular models of 4 cerebral aneurysms reconstructed from 3D rotational angiography images.

Blood Flow Models

Blood flow was modeled as an incompressible Newtonian fluid described by the unsteady Navier-Stokes equations in 3D.³⁰ The blood attenuation was ρ = 1.0 g/cm³ and the viscosity was μ = 0.04 (dyne s/cm²). Vessel walls were assumed rigid, and no slip boundary conditions were applied at the walls. Assuming that all the distal vascular beds have similar total resistance to flow, traction-free boundary conditions with the same pressure level were applied to all the model outlets. At the inflows, pulsatile velocity profiles were prescribed using the Womersley solution for the fully developed pulsatile flow in a rigid straight pipe.³¹ These velocity profiles were computed from the Fourier decomposition of the prescribed flow rate curves.³² Flow measurements were not available for these patients; therefore, the flow conditions were derived from phase-contrast MR measurements performed on normal subjects in the same arteries.³³ Numeric solutions of the Navier-Stokes equations were obtained with the use of a fully implicit finite element formulation that allows arbitrary time-step sizes.²¹ Two cardiac cycles were computed using 100 time-steps per cycle, and all the results presented correspond to the second cardiac cycle. Each of these simulations takes approximately 12 hours on the 16 Itanium2 processors (1.3 GHz) of an SGI Altix (SGI, Mountain View, Calif) running in parallel shared-memory mode. The flow conditions for the truncated models were derived from the results obtained with the original models by subtracting the flow rates through proximal branches that were not present in the truncated model. For instance, the flow rates in the A1 segments of the truncated AcomA aneurysm model (patient 4, model 2) were obtained by subtracting the flow rates in the ipsilateral ICA and MCA. This ensures that the same flow conditions are imposed in the feeding vessels of both models of each patient; therefore, any differences found in the intra-aneurysmal hemodynamics are due to the geometry of the parent vessel and not to different flow rates.

Postprocessing and Visualization

Animations or cine loops of the wall shear stress (WSS) magnitude and flow velocity were produced for both models of each patient. Instantaneous streamlines at peak systole were calculated for each model. The origins of the streamlines were interactively placed in the neck of the original models of each patient. The streamlines were then computed from these origins in both directions (upstream and downstream). The same origins were used for the corresponding truncated models to ensure that differences in the flow visualizations were not due to different placement of the origins of the streamlines.

Results

Internal Carotid Artery Aneurysm

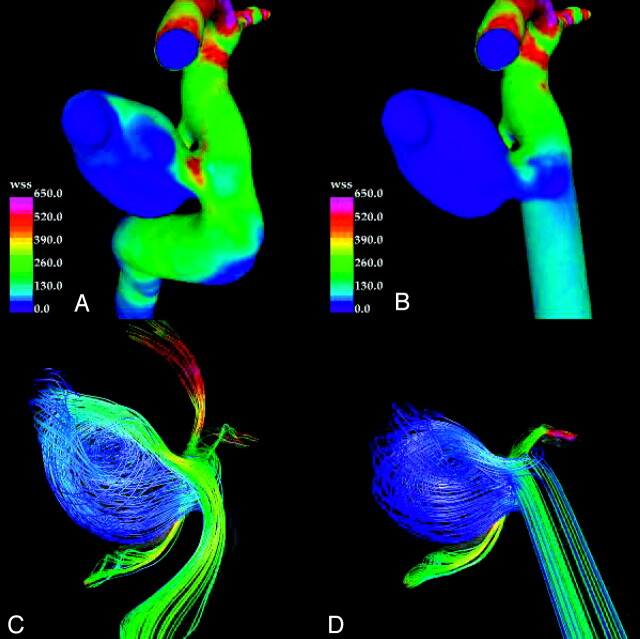
The results for patient 1 are presented in Fig 2. This figure shows the distributions of WSS magnitude and instantaneous streamlines at peak systole for the original and truncated models. For the truncated model, the WSS is high only at the neck of the aneurysm (Fig 2B) (ie, at the zone of the inflow impingement on the downstream wall). The dome has lower WSS than either the upstream or downstream parent artery. The streamlines show a simple univortex pattern that does not appreciably affect the tip of the dome or daughter lobulation. The upstream parent artery flows are laminar and meet the neck of the aneurysm nearly tangentially accounting for the “quietness” of the intra-aneurysmal flows. In contrast, the original model has more activity within the aneurysm (Fig 2A). The flow stream in the parent artery is more directed into the aneurysm. Although the peak WSS remains near the neck, elevations of WSS compared with the parent artery extend well into the body and to the dome on the downstream wall. Peak WSS at the neck exceeds the WSS in the adjacent parent artery. Streamlines show a more complex flow pattern within the aneurysm with at least 2 zones of recirculation and extension of flow into the tip of the dome.

Fig 2.

Visualizations of the hemodynamics of internal carotid artery aneurysm (patient 1) at peak systole: wall shear stress distribution in the original model (A), wall shear stress distribution in the truncated model (B), streamlines in the original model (C), and streamlines in the truncated model (D). Streamlines are colored according to velocity magnitude.

MCA Aneurysms

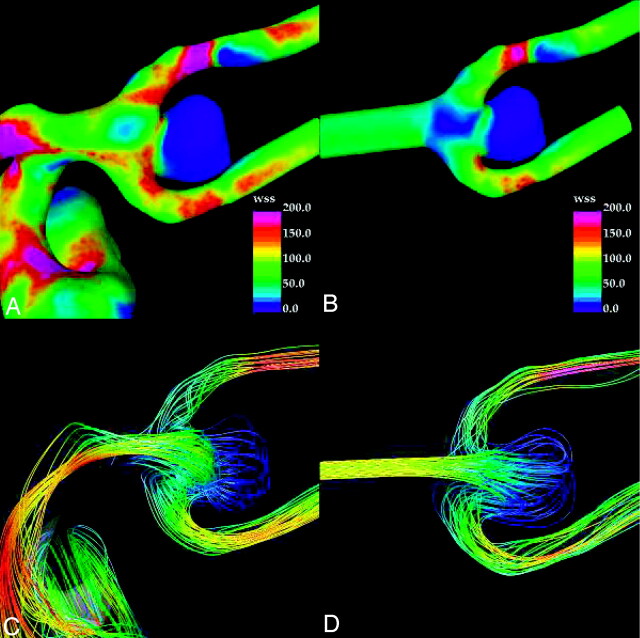
Visualizations of the distribution of WSS magnitude and streamlines at peak systole for patients 2 and 3 are presented in Figs 3 and 4, respectively. For patient 2, the WSS distribution obtained with the truncated model (Fig 3B) and the original model (Fig 3A) are similar, with low WSS within the dome of the aneurysm compared with the parent artery. In both simulations, high WSS is located at the neck, but the original model predicts higher values of shear stress compared with the truncated model. In both simulations, the streamlines show modest flows into the aneurysm dome but a marked difference can be seen in the flow patterns (Fig 3C, -D). The truncated model predicts a characteristic flow pattern commonly seen in idealized models of terminal aneurysms exhibiting 2 main vortices (Fig 3D). In contrast, the flow pattern with the original model (Fig 3C) has a completely different and more complex vortex structure. Strong secondary flows can also be seen near the neck of the original model, whereas in the truncated model, less mixing and swirling flows can be observed at these locations. These differences are also evident in the flows of the upstream parent artery.

Fig 3.

Visualizations of the hemodynamics of middle cerebral artery aneurysm (patient 2) at peak systole: wall shear stress distribution in the original model (A), wall shear stress distribution in the truncated model (B), streamlines in the original model (C), and streamlines in the truncated model (D). Streamlines are colored according to velocity magnitude.

Fig 4.

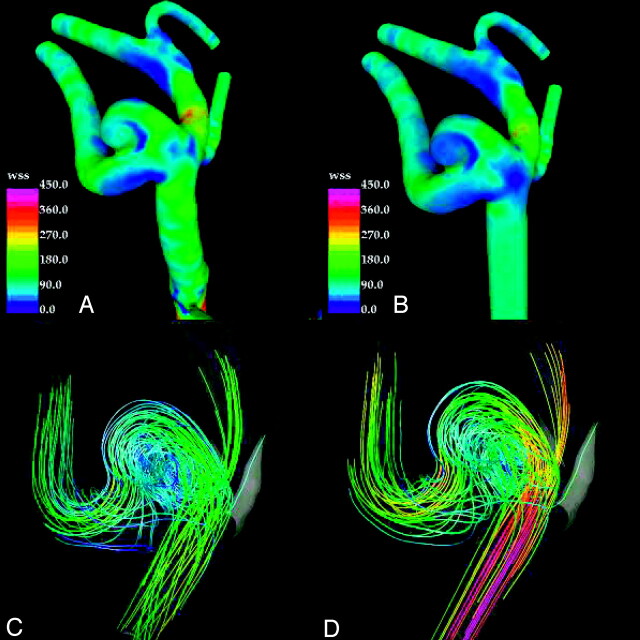
Visualizations of the hemodynamics of middle cerebral artery aneurysm (patient 3) at peak systole: wall shear stress distribution in the original model (A), wall shear stress distribution in the truncated model (B), streamlines in the original model (C), and streamlines in the truncated model (D). Streamlines are colored according to velocity magnitude.

In the case of patient 3, the results obtained with the original and truncated models are in better agreement (Fig 4), because in this case, the M1 segment where the model was truncated is quite long and straight, resulting in the original model having near laminar flow pattern. However, some differences are present. In both models streamlines indicate impaction in the downstream wall at the neck and the body of the aneurysm. Elevation of the high WSS extends into the body and dome of the aneurysm. The truncated model predicts less extensive WSS distribution compared with the original model. The streamlines within the aneurysm of the truncated model and original model are quite complex with secondary flows in a similar distribution (Fig 4).

AcomA Aneurysms

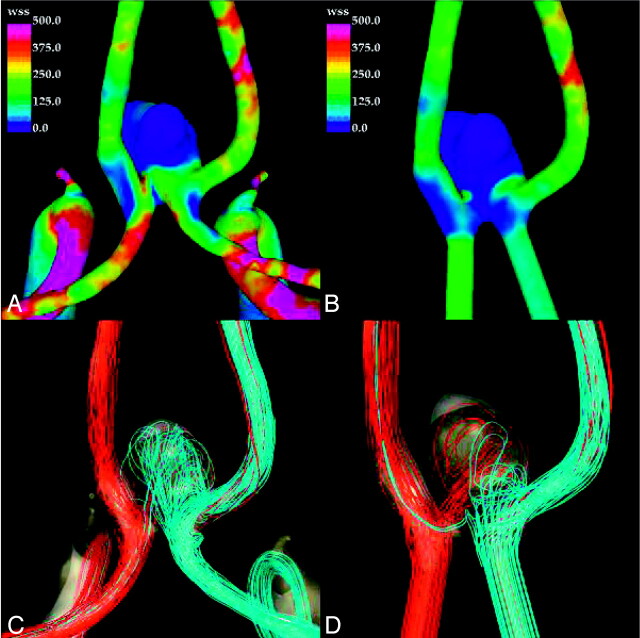
The results obtained for patient 4 are presented in Fig 5. As in the previous cases, the truncated model (Fig 5B) tends to yield lower values of the WSS forces on the aneurysm sac. In particular, a region of relatively elevated WSS that is not present in the truncated model can be observed at the dome of the original model (Fig 5A). The streamlined visualizations show quite different intra-aneurysmal flow patterns between the original (Fig 5C) and truncated models (Fig 5D). In the original model, the inflow jets from the left and right A1 segments merge and penetrate toward the dome of the aneurysm, but with the left A1 flows dominating the intra-aneurysmal flow pattern. In contrast, in the truncated model, the inflow jets collide closer to the neck of the aneurysm, resulting in a more symmetric intra-aneurysmal flow pattern with a more significant contribution from the right A1. This results in a state of low flow near the dome.

Fig 5.

Visualizations of the hemodynamics of anterior communicating artery aneurysm (patient 4) at peak systole: wall shear stress distribution in the original model (A), wall shear stress distribution in the truncated model (B), streamlines in the original model (C), and streamlines in the truncated model (D). Streamlines are colored according to velocity magnitude.

Discussion

Computational fluid dynamic modeling can be a powerful tool in studying physical systems such as aneurysms, but extrapolating from idealized experimental systems to the in vivo state must be done carefully. All computational methods require the use of assumptions that are essentially shortcuts to predicting the more complicated natural state. Ill-considered assumptions could affect the results of a computational fluid dynamic model and thereby adversely affect one’s understanding of a particular system.

Previous works have studied the effects of commonly used assumption in computational fluid dynamics (CFD) modeling of aneurysms. Our current work has extended this effort to the effects caused by the truncation of the parent artery used for the CFD simulations. We have found that the geometry of the parent artery upstream to the aneurysm neck can influence the intra-aneurysmal hemodynamics. For the 4 cases we studied, the use of a truncated upstream parent artery tends to result in lower WSS states for the aneurysmal wall with a shift of the flow impingement from the aneurysm dome toward its neck. In addition, the intra-aneurysmal flows demonstrated by the streamline graphics were quieter with a more simplified vortical pattern. These changes are more pronounced in cases with high degrees of upstream curvature (eg, patients 1 and 4) compared with situations with less upstream curvature (patient 2 and 3).

The cause of these differences seems to be related to the geometry and complexity of the flow stream delivered by the upstream parent artery. For the truncated models, the flow stream entering the aneurysm neck is parallel to the walls of the parent artery and therefore more tangential to the aneurysm neck in sidewall aneurysms. Curvature of the upstream artery can influence this angle of entry into the aneurysm as seen in patient 1, causing the impingement region to be shifted into the body and dome of the aneurysm. This effect greatly changed the relative contribution of flows in patient 4, resulting in the greater influence on intra-aneurysmal hemodynamics by the left A1 flow stream and a region of elevated WSS in the dome. The complexity of the flow stream in the upstream parent artery also plays a role. In the truncated models, near laminar flow is found in the parent artery compared with more complex flows with secondary motions related to the curvature and changes in shape in the native parent artery. These nonlaminar elements to the flow pattern may be responsible for the more complex intra-aneurysmal flow patterns we found in the original models in all 4 cases. These effects were less pronounced when the proximal segment of the parent vessel was long and straight (as in our patient 3).

The implications of our findings are that failure to include upstream anatomy results in nonphysiologic near-laminar inflow into the modeled aneurysm compared with the in vivo state. This can alter the angle of entry of the inflow jet and reduce the complexity of streamline flow into the aneurysm resulting in simplified intra-aneurysmal flows and underestimation of the WSS in the aneurysm body and dome. Therefore, CFD models need to include/account for the nonlaminar inflow by including upstream arterial anatomy if the goal is to reproduce patient specific flow information.

The observations made in this study are important not only from the modeling point of view but also because they carry implications to the way we think about the processes of aneurysm growth and rupture. Currently, there are 2 opposing schools of thought about these processes. On the one hand, low flow theories claim that the dome of aneurysms are under low WSS states that trigger mechanobiologic processes that weaken the arterial wall, which in turn results in growth or rupture of the aneurysm.^34–37 These theories are based on observations of low WSS in the dome made on idealized experimental and computational models and clinical observations. On the other hand, high-flow theories claim that a different set of mechanobiologic processes are triggered by unusually large WSS at the aneurysm wall (in particular at the flow impaction zone) that weaken the vessel structure and result in growth or rupture.^1,38–41 The current study indicates that in vivo hemodynamic patterns exhibit regions of elevated WSS in the aneurysm sac. Previous works from modeling of idealized aneurysm geometries probably underestimate the complexity of intra-aneurysmal flows, location of the inflow impingement zone, and WSS within an aneurysm dome. Although the magnitudes of these differences are not known, generalizing from idealized models may be misleading. In particular, theories of aneurysm rupture mechanisms should take into account the possible errors. Low flow theories relying on prior “low WSS states” in the dome need to be reexamined. Further hemodynamic studies using “realistic” (ie, including the correct geometry of the proximal segment of the parent vessel) patient-specific vascular models are needed to discriminate between the mechanisms that are actually driving the processes of growth and rupture.

Although we have found changes in intra-aneurysmal flow patterns and WSS in our study, there are limitations to our study that may influence our results. As in all modeling, the CFD analysis relies on several assumptions that are an approximation of the in vivo state, including Newtonian flow, rigid walls, assumed outflow conditions, input flow conditions measured from normal volunteers, and elimination of small low flow vessel branches (ie, perforators or posterior communicating arteries). How these assumptions would interact with the truncation of the upstream parent artery has not been directly studied. Based on prior sensitivity analysis, we believe any effect would be small.²¹ Our sample size is small and biased by our intention to show an effect. A larger and more representative sample would be needed to better understand the magnitude of the effect for the wide range of aneurysm locations and morphologies. Without these studies it could not be determined if there are situations where truncation elevates intra-aneurysmal complexity or aneurysmal WSS. The location of the truncation was arbitrary and may not be representative of idealized geometries from prior works. Each of these simulations would need to be individually re-examined to determine whether the truncation effect applies.

Our work does not define how much of the parent artery needs to be included to accurately model the upstream flow pattern. Although the natural conclusion is that inclusion of more upstream artery would result in better simulations of the in vivo state, what is the minimum required to achieve an acceptable result? The current CFD theories do not provide a straightforward answer to this question because works on curved flow systems, much less the complex geometries found in the arterial vascular structures, are limited. However, some guidance may be provided by applying the concept of the developing distance. Developing distance is the length of a straight pipe required to fully form the stable flow profile from an entry point such as a reservoir. Travel through the pipe affects the flow profile incrementally until a stable pattern characteristic of the pipe geometry is achieved. This distance for a circular pipe is related to the Reynolds number (Re = D × u/ν where D = diameter, u = mean velocity, ν = kinematic viscosity = 0.04) and the diameter of the flow in a manner that differs for the flow types. For laminar flow, the equation is Le = 0.06 × Re × D, and for turbulent flows, the equation is Le = 4.4 × Re^1/4 × D.³⁰ So, for an average-size internal carotid artery with a D = 0.5 cm and a peak velocity of 100 cm/s, we have a Reynolds number of 1250. The distances required to reach a fully developed flow in laminar and turbulent systems would be 37 and 7 cm, respectively. Given the complexity of anatomy and the typically nonlaminar state of flow in vivo, the calculation for the turbulent condition may be the most appropriate. This being said, the diameters of arteries are not constant and not circular. Non-Newtonian effects and wall compliance are expected to add to the complexity of flows and may shorten the distance that a particular geometric induced perturbation of the flow pattern will be propagated. Arriving at a theoretic answer to this question for complex vascular systems using our current knowledge and techniques is not possible. In effect, each patient-specific anatomy has its unique solution. It is our belief that individual sensitivity analyses will be necessary for each of the typical aneurysm locations so that an estimation of length of upstream parent artery needed for an appropriate computational simulation can be determined to be used as a rule of thumb for each aneurysm location. These studies are currently in progress by our group.

Conclusions

Failure to accurately to account for the geometry of the upstream parent artery can cause important changes on intra-aneurysmal hemodynamics in CFD models. Generalizing from models that do not include upstream artery geometry may lead to an underestimation of aneurysmal WSS in the dome and body, and oversimplified intra-aneurysmal flow pattern.