Abstract
In their 2007(a) Psychological Review paper, Xu and Tenenbaum found that early word learning follows the classic logic of the “suspicious coincidence effect:” when presented with a novel name (‘fep’) and three identical exemplars (three Labradors), word learners generalized novel names more narrowly than when presented with a single exemplar (one Labrador). Xu and Tenenbaum predicted the suspicious coincidence effect based on a Bayesian model of word learning and demonstrated that no other theory captured this effect. Recent empirical studies have revealed, however, that the effect is influenced by factors seemingly outside the purview of the Bayesian account. A process-based perspective correctly predicted that when exemplars are shown sequentially, the effect is eliminated or reversed (Spencer, Perone, Smith, & Samuelson, 2011). Here, we present a new, formal account of the suspicious coincidence effect using a generalization of a Dynamic Neural Field (DNF) model of word learning. The DNF model captures both the original finding and its reversal with sequential presentation. We compare the DNF model’s performance with that of a more flexible version of the Bayesian model that allows both strong and weak sampling assumptions. Model comparison results show that the dynamic field account provides a better fit to the empirical data. We discuss the implications of the DNF model with respect to broader contrasts between Bayesian and process-level models.
Keywords: Bayesian model, dynamic field model, word learning, category hierarchy, comparison
Bayesian models of cognition have entered the mainstream of cognitive science in the last two decades. Bayesian models investigate cognition from the perspective of optimal rational inference and have been applied to a range of cognitive phenomena from visual perception (de Lange et al., 2018; Yuille & Kersten, 2006), to everyday statistical intuition (Griffiths & Tenenbaum, 2006), to social learning (Krafft et al., in press). Bayesian models have also been used to capture word learning (Xu & Tenenbaum, 2007a, 2007b). Reasoning from Bayesian principles, Xu and Tenenbaum (2007b) predicted and demonstrated a novel word learning behavior they referred to as the “suspicious coincidence” effect (SCE): both adults and children generalize novel words more narrowly when multiple identical exemplars (such as three Labradors) are provided by a teacher than when a single exemplar is provided (one Labrador). Xu and Tenenbaum explained this behavior as a result of optimal inductive inferences about the higher probabilities of narrower hypotheses for word meanings given the size of an exemplar set1.
Bayesian models can be contrasted with process-based models of cognition. Rather than focusing on abstract principles like inductive inference, process models aim to capture lower-level details of cognitive processes including the second-to-second or step-by-step cognitive operations that underlie behavioral phenomena. Process models are—more often than Bayesian models—concerned with the influence of task details, such as the timing or intensity of specific events. This distinction is most notable when these types of details are not obviously relevant to the optimal rational solution to a problem as is the case for the SCE. Reasoning from a process-based perspective, Spencer, Perone, Smith, and Samuelson (2011) predicted that the suspicious coincidence effect would be sensitive to the timing and spacing of word learning exemplars. In particular, Spencer and colleagues predicted that sequential versus simultaneous presentation of exemplars would eliminate or reverse the SCE. This was the case across multiple experiments. Although these researchers explained the effect in terms of well-studied processes of feature comparison (e.g., Garner, 1974; Gentner & Namy, 2006), they did not provide a formal model of the SCE or its reversal.
Here, we generalize a process-based model of word-referent binding by Samuelson, Smith, Perry, and Spencer (2011) to both the original SCE and its reversal. The model uses dynamic neural fields (DNFs) to simulate both effects at the level of neural population dynamics. The dynamic field approach is a neurally-grounded process model that has, like Bayesian models, entered broadly into the mainstream cognitive literature in the last two decades (Erlhagen & Schöner, 2002; Erlhagen & Bicho, 2006; Faubel & Schöner, 2008; Johnson et al., 2009; Johnson et al., 2014; Lipinski et al., 2012). Our model explains the SCE as a result of local neural interactions that occur between representations of objects that are close in space, time, and feature values under simultaneous conditions – interactions that differ when items are presented sequentially.
At a broader level, the DNF account opens the door to compare a Bayesian model with a process-based model head-to-head. There have been several efforts to evaluate the broad, relative merits of Bayesian and process-based approaches (Brighton & Gigerenzer, 2008; Chater, 2009; Jones & Love, 2011; Sakamoto et al., 2008), and Bayesian and process theories have addressed similar phenomena in the past (McClelland, 2013; Xu & Tenenbaum, 2007b; A. J. Yu & Cohen, 2009). Rarely are head-to-head, fully implemented model comparisons performed, however, despite the scientific importance of such comparisons. This is, in part, because significant obstacles exist to performing quantitative comparisons. For instance, the language of Bayesian theory—likelihoods and posterior probabilities—is difficult or impossible to apply to many process models (Jones & Love, 2011). Conversely, the Bayesian approach has rarely interfaced with the low-level cognitive details that are central to many process-level models (Chater et al., 2003; Griffiths & Tenenbaum, 2006). Indeed, the feasibility of low-level implementation of Bayesian models is hotly debated (Baddeley et al., 1997; Brighton & Gigerenzer, 2008; Deneve, 2008; Feldman, 2010; Knill & Pouget, 2004; Kover & Bao, 2010).
One model comparison option is to qualitatively compare models by comparing each model’s ability to capture patterns of effects. Another option is to use quantitative measures of data fit such as the Akaike Information Criterion (AIC) or Bayesian Information Criterion (BIC). These measures are useful in that they penalize complex models which often have more ‘free’ parameters. A third option is to fit the models to one data set and then generalize them to another while holding model parameters constant. Here, we adopt all three of these approaches. We proceed as follows. In the next section, we explain the behavioral data to be modeled: two variants of the “suspicious coincidence” effect in the domain of hierarchical word learning. We next discuss the details of the Bayesian model and its account of the behavioral data. We introduce a more flexible version of Xu and Tenenbaum’s model (2007b) that includes the same capabilities as the 2007(a) version but adds a new parameter that makes it theoretically better suited to account for the distinction between simultaneous and sequential presentation. We then provide an overview of the DNF model and how it captures the SCE. Next, we use both models to simulate data from three experiments from Spencer et al. (2011): a replication of Xu and Tenenbaum’s (2007a) original findings with simultaneous exemplar presentation, the reversal of this effect with sequential presentation, and a generalization dataset with sequential presentation but changes in spacing and number of exemplars designed for concessions to the Bayesian theory. We compare the model simulations head-to-head qualitatively and using quantitative metrics (AIC/BIC). This serves as the basis for our more general evaluation of Bayesian and DNF models in the General Discussion.
1.1. The Suspicious Coincidence Effect
An important question in the word learning literature is how people are able to learn overlapping or hierarchical categories without explicit definitions. A single object, for example a dog, can often belong to a number of different categories at once (“animal,” “mammal”, “dog,” “Labrador”, “Rover”). When a learner hears a novel word applied to an object, how can the learner determine which of these possible categories is the correct referent for that novel word? Process of elimination is one commonly cited strategy for dealing with word learning ambiguity (Golinkoff et al., 1992; E. M. Markman, 1991). For example, if a cluttered scene has many objects with known labels and one unfamiliar one, then a novel label is more likely to apply to the unknown object. This does not help with hierarchical categories, however, because knowing something is a “dog” does not rule out also having a label at a different hierarchical level, like “Labrador.” Another possibility is that word learners have a bias to assume that most novel words refer to basic-level categories ( like “dog,” as opposed to “Labrador” or “mammal”; Markman, 1991; Rosch & Mervis, 1975). This bias does not help in hierarchical situations either, because by definition, hierarchies involve categorization at more than just the basic level.
Xu and Tenenbaum (2007a) suggested that rational Bayesian inference could offer a solution. After seeing novel labels applied to some number of objects, a learner can calculate the relative probabilities of every possible meaning and use these to infer the correct meaning. For example, when a single Labrador is labeled “fep,” the evidence is consistent with any of the possible meanings for “fep” that includes Labradors (Rover, Labrador, dog, mammal, animal, etc.). However, certain categories are more or less likely. The chance of seeing a Labrador from the category of Labradors is 100%, whereas the chance of seeing a Labrador from all species and breeds of animals is lower. Xu and Tenenbaum claim that children (3.5–5-year-olds) and adults follow Bayesian principals, are sensitive to these probabilities, and that they use this information to make inferences about word meanings.
One prediction of Xu and Tenenbaum’s theory is particularly important, because it was initially a unique prediction relative to other theories of word learning: if three exemplars of Labradors in a row are labeled “fep”, then it would seem more likely for “fep” to refer to “Labrador” than to all dogs relative to a case when just one exemplar is labeled. According to Xu and Tenenbaum, this is because as more Labradors are seen and labeled with the same word, the hypothesis that the word refers to Labradors is no less reasonable, but the hypothesis that the word refers to dogs becomes less and less plausible. In other words, it would be an increasingly “suspicious coincidence” as two, three, or more Labradors in a row were drawn randomly from the set of all dogs, whereas the first Labrador is not more or less likely than any other breed. Xu and Tenenbaum tested this prediction of the Bayesian approach empirically and confirmed the suspicious coincidence effect: both children (3.5- to 5-year-olds) and adults generalized three identical exemplars more narrowly than one exemplar of a novel label. Xu and Tenenbaum captured these results in their Bayesian model and demonstrated that several other models of word learning do not show this pattern (see Xu & Tenenbaum, 2007b).
Spencer, Perone, Smith, and Samuelson (2011) later provided an alternative non-rational explanation of the suspicious coincidence effect based on low-level cognitive processes. Process-based models have a long history of explaining behavioral consequences of proximity of objects in time and space. When similar items are near each other in time and space, they are easier to align and compare, and their relationships are easier to remember (Gentner & Namy, 2006; Hahn et al., 2005; Samuelson et al., 2009). Narrower generalization may therefore be a result of fine-grained attention or more robust memory for fine-grained features created because the simultaneous comparison in Xu and Tenenbaum’s task make the stimuli highly alignable. Spencer and colleagues hypothesized that the inverse might also be true: exemplars separated in time or space might yield broader category extensions, because the experiences are harder to directly compare.
Spencer and colleagues replicated Xu and Tenenbaum’s (2007b) methodology and results in an initial experiment. In two subsequent experiments, however, participants showed a reverse-suspicious coincidence effect when stimuli were presented sequentially. That is, participants generalized novel names more broadly when shown three exemplars sequentially than when shown a single Labrador.
In the present report, we focus on the empirical data from Spencer et al. (2011) (including the replication experiment), because they offer a broad empirical range of effects for this theoretically important phenomenon. We consider whether a more flexible version of the Bayesian model (Xu & Tenenbaum, 2007a) can explain the new empirical findings. We also present a new account of the SCE by generalizing a DNF model of early word learning (Samuelson, Smith, Perry, & Spencer, 2011) to this task. We then ask whether this model offers novel insights into why the SCE is modulated by seemingly low-level task details (i.e., simultaneous versus sequential stimulus presentation). Our central goal is to compare these models head-to-head in an effort to understand the SCE and to clarify the strengths and weakness of Bayesian and process-based models. We proceed by describing the details of each model in turn.
1.2. Xu and Tenenbaum’s Bayesian Model
We used Xu and Tenenbaum’s 2007(a) model for fitting data in the present report. This model is identical to the 2007(b) version except with an extra parameter described below that allowed it to distinguish between simultaneous and sequential exemplar presentation.
The Bayesian model combines three main ingredients to arrive at a prediction about how a word learner will generalize a novel word: the set of hypotheses the learner will consider for that word’s extension, the likelihood of each hypothesis, and the prior probability of each hypothesis. Together, these lead to a set of posterior probabilities:
Here, h = a given hypothesis about a word’s extension, h’ = each of the individual hypotheses that the learner is considering in turn within the sum, X = the set of exemplars that have been labeled with the novel word being learned, and H = the space of all considered hypotheses.
1.2.1. Hypotheses
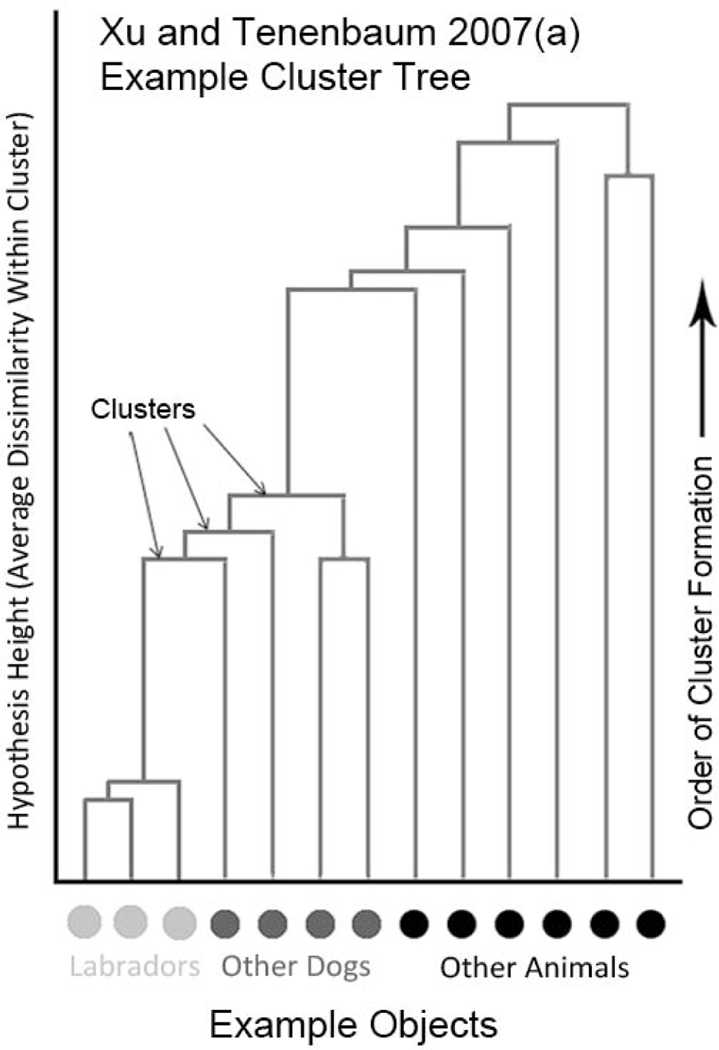
A hypothesis in the Bayesian model is a set of one or more categories that represent one guess about the extension of the novel word. For example, [Labrador, penguin, Terrier] is a hypothesis representing the possibility that a novel word refers to the set of animals covered by any of the English categories “Labrador,” “penguin” and “Terrier.” Hypotheses that may be considered for a novel label are chosen before the model sees any labeled exemplars. In Xu and Tenenbaum’s model, the choice of hypotheses is based on pairwise similarity ratings collected in a separate task. They are expressed in the form of a hierarchical cluster tree, where each cluster is a hypothesis (Figure 1). After gathering similarity data for a set of objects, an experimenter makes a cluster tree by first joining the two most similarly rated objects into a cluster. Then, the experimenter forms another cluster with the next highest possible internal similarity, either by pairing off two unassigned objects, pairing an unassigned object onto a cluster, or pairing two clusters. This process is repeated until all objects are included in at least one cluster. The final cluster tree shows the order that linkages were formed. In addition, the height of each cluster represents the average dissimilarity between objects within that cluster. An example for animal stimuli from Xu and Tenenbaum’s study is shown in Figure 1.
Figure 1.
A representation of Xu and Tenenbaum’s (2007a) hierarchical cluster tree. Objects (bottom dots) are grouped together in clusters. The algorithm begins with the most similar (lowest connecting horizontal bars) and progresses by joining the next most similar object or other cluster in order until all objects are a member of at least one cluster. Each cluster corresponds to a hypothesis in Xu and Tenenbaum’s Bayesian model.
1.2.3. Likelihood
Another input to the Bayesian model is the set of one or more exemplars of the novel word it is trying to learn. Likelihood, p(X | h), is the probability of having received these particular exemplars, given a hypothesis h. For example, a Labrador might be given as an example of “fep.” The likelihood of this exemplar for broad hypotheses like “all animals” would be lower than for narrower hypotheses like “all dogs,” because a Labrador exemplar from amongst the set of dogs is more likely than a Labrador exemplar from amongst the set of animals. In the case of three Labrador exemplars, the likelihood depends on whether the additional Labradors are new individuals or not. In Xu and Tenenbaum’s earlier model (2007b), both likelihoods of “all animals” and “all dogs” always become exponentially lower with more exemplars. Mathematically, this was due to the following likelihood equation:
n is the number of exemplars seen, and the size of the hypothesis’ extension is approximated by cluster height plus a small constant to avoid division by zero. Hypotheses that are missing any exemplars automatically receive a likelihood of 0. Xu and Tenenbaum call this likelihood function the “size principle.”
In their 2007(a) model, Xu and Tenenbaum specify that the size principle applies only in “strong sampling” conditions, where additional exemplars are assumed to be unique objects drawn representatively from the category. The size principle does not apply in “weak sampling” conditions, where the exemplars are repeats or not necessarily representative. The weak sampling version of the likelihood in the Bayesian model is as follows:
This equation holds regardless of the number of exemplars.
The distinction between strong and weak sampling lends itself to a possible interpretation of data from Spencer et al. (2011). If the learner interprets multiple “exemplars” in the sequential presentation task as simply different views of the same object, this might lead to weak sampling assumptions. Thus, in simulations below, we included a free parameter that would turn strong vs. weak sampling on or off across conditions. In practice, this was equivalent to fitting both likelihoods to all data and choosing the best-fitting version per experiment to account for ambiguity in whether participants saw exemplars as unique instances or not (i.e., strong sampling vs. weak sampling).
1.2.4. Prior Probability
The prior, p(h), is a learner’s pre-existing bias to favor a given hypothesis prior to seeing any exemplars labeled. Xu and Tenenbaum’s priors were based on the same data as their hypothesis set—pairwise similarity ratings. In the cluster tree defined by these ratings (Figure 1), the prior probability of each is proportional to that hypothesis’ cluster height subtracted from the height of the next highest (parent) cluster:
The larger the difference between cluster height and parent cluster height, the more informational content is held by that hypothesis (in the sense of Rosch, 1978; Rosch & Mervis, 1975), and the more likely it is to be the most appropriate hypothesis for any new object, a priori.
1.2.5. Basic Level Bias
Basic level bias is an important sub-component of calculating the final priors. Xu and Tenenbaum included this term because earlier work suggests early word learners have a bias towards the basic level (Golinkoff et al., 1994; Markman, 1989).2 The basic level bias is a scalar, which multiplies the prior probability for basic level hypotheses only. A “basic level hypothesis” is one that aligns with adult English basic-level categories—for example, a hypothesis that includes all dogs and nothing else. Basic level bias is a free parameter, set to best match simulated and behavioral data.
1.2.6. Output
The model outputs a posterior probability for each of the hypotheses given in the input tree, as discussed above. These posterior probabilities are then converted to generalization probabilities by averaging the predictions of all hypotheses weighted by their posterior probabilities:
Note that p(y ∈ C|h) is 1 if y ∈ h, and 0 otherwise, and p(h|X) = 0 unless the examples X are all contained with h. Thus, the generalization probability can be written as:
In this equation, the probability that the novel word C will be generalized to the test object y, given the exemplar(s) shown, is equal to the sum of the posterior probabilities of all hypotheses that include both the exemplar(s) and the test object. These probabilities can then be compared to the proportion of time participants generalized a novel name for a labeled exemplar (or set of exemplars) to a generalization set.
1.3. A Dynamic Neural Field Model of Early Word Learning
The process-based model we used is a generalization of a DNF model proposed by Samuelson, Smith, Perry, and Spencer (2011). The original model captured the roles of space and time in binding novel labels to referents and has been used to capture data from a variety of word learning tasks (Samuelson, Jenkins & Spencer, 2013). Thus, this model is appropriate for simulating the word learning behaviors captured by Xu and Tenenbaum’s (2007b) model. Moreover, because the model captures how children bind labels and referents even when they are separated in time, we thought the DNF model might shed light on why the sequential stimulus presentation condition in Spencer et al. (2011) reversed the suspicious coincidence effect. In the sections below, we describe the architecture of the model and how we adapted it to capture performance in the suspicious coincidence task.
1.3.1. Architecture of the DNF Model
Figure 2 shows the DNF model (note: for a full mathematical description of the model, see the appendix, full model code and all reported results are available at https://github.com/developmentaldynamicslab/Jenkins_Samuelson_Learning_Words, see Supplemental Materials). The model consists of two 2-dimensional dynamic neural fields—a space-feature field and a label-feature field (Figure 2, A and B). Each field consists of a set of neural units whose activation is depicted by the color scheme in Figure 2 (warmer colors = higher activation). Each unit is receptive to stimulation along two metrically-organized dimensions, and the graphical location of a unit represents the values it is maximally receptive to along each dimension. Space is in the frame of the task with the linear position of exemplars along a horizontal axis, as they would be shown to participants along the bottom of a computer monitor. Label is a dimension of lexical entries where positions along the dimension represent different words. In Samuelson et al. (2011), the other dimension in each field mapped to specific features, color and shape. In the current model, the other dimension (the vertical in Figure 2) still represents object features, but with naturalistic stimuli, exact feature dimensions are unknown. Instead, the feature dimension is derived from a multidimensional scaling (MDS) solution of the data from Xu and Tenenbaum’s (2007b) hierarchical cluster trees (Figure 1) fit to a single dimension. We will refer to the fields in our model specifically as space-MDS and label-MDS fields.
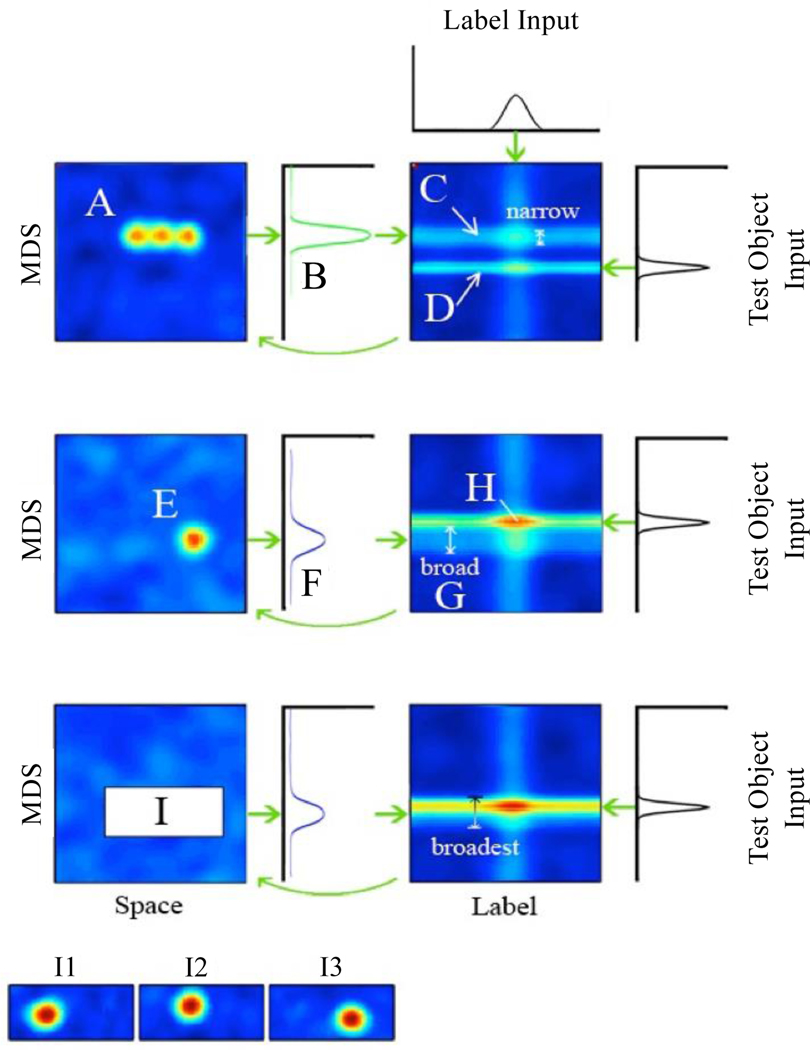
Figure 2.
The DNF model’s architecture. The model has two fields, one (A) organized by space and a dimension formed from an MDS solution of Xu and Tenenbaum’s (2007a) cluster trees, the other (B) by label and the same MDS dimension. Each unit (e.g., C) is tuned most strongly to a particular value along its fields’ two dimensions. Objects are represented by peaks of activation (D) in the space-MDS field, that after being weighted by a Gaussian kernel (result E) project ridges (F) in the label-MDS field. External inputs to the model are Gaussian patterns representing labels (G) that project vertical ridges of their own into the label-MDS field, two dimensional Gaussian patterns representing exemplars (H) that drive the formation of the peaks in the space-MDS field (D), and Gaussian patterns representing test objects for generalization (I) that project additional horizontal ridges (J) into the label-MDS field. Following the model through a test trial to Row 2 after 40 time steps, the exemplar peaks have strengthened, projecting activation (K) into a stronger ridge (L), which is almost forming a peak with the overlap of the test object ridge. 40 time steps later in Row 3, the model has built a generalization peak (M). In an alternative trial with a different test item (Row 4), the test item is in between the features of the exemplars, and does not overlap enough to raise a generalization peak.
1.3.2. MDS Dimension Algorithm
The MDS dimension in the DNF model was derived from the tree plot similarity data of Xu and Tenenbaum (2007b) seen in Figure 1, fit to a single dimension. The algorithm first chooses a subordinate level object and places it at an arbitrary zero point along a dimension. As an example, it might start with the leftmost Labrador in Figure 1. The algorithm then searches up the tree plot to the next node of the tree. Each additional object is placed on the one-dimensional solution such that the distance between it and the average of already-placed objects is proportional to the height of the node that connects the new object to the previous ones. The left/right relationship between previously and newly placed objects is determined randomly.
If a node connects several units at once, like the last two clustered items on the right in Figure 1, it recursively solves this sub cluster as if it were a tree of its own. The recursive solution is then added to the main solution as if it were one object at the average position of the new objects in the recursive solution. The total solution is then scaled to fit into the DNF model’s field size. The result of the algorithm is one of many possible fits of hierarchical tree data to a single dimension that meets the constraints on data implied by the tree. The algorithm was run once per simulated participant in our modeling experiments. Thus, each simulation had a different pattern of inputs, ensuring that the performance of the model reflects the general constraints of the similarity data and not the details of one particular instantiation of the MDS algorithm.
1.3.3. Model Dynamics
Neural sites within each field interact according to a local excitation/lateral inhibition function (Spencer et al., 2012), a common form of interaction in neural models of cortical function (Durstewitz et al., 2000) where units excite their nearest neighbors strongly, and inhibit a broader range of neighbors more weakly. In our implementation of the Samuelson et al. model, this form of interaction was implemented across two layers—a layer of excitatory neurons and a layer of inhibitory interneurons (see appendix). Only neural sites that are sufficiently activated participate in interactions. This is implemented using a sigmoidal function (a type of step function) with the activation threshold set to zero activation. This type of neural interaction allows stable “peaks” of activation to form within the excitatory layer shown in Figure 2D—stable patterns of above-threshold activation that maintain themselves through local excitation and avoid expanding uncontrollably due to lateral inhibition. For instance, when presented with a red color at a leftward location, the space-MDS field would build a peak representing that this hue value is present on the left.
The fields shown in Figure 2 also pass activation between one another along the shared MDS dimension. In particular, at each time step, above-threshold activation within the space-MDS field is summed along the spatial dimension. The resulting sum is then weighted with a Gaussian kernel (Fig 2E) and projected into the label-MDS field, sending a “ridge” of activation horizontally across the label dimension (Fig 2F). The label-MDS field also projects above-threshold activation back to the space-MDS field in the same manner (see green arrow in Fig 2).
1.3.4. Simulating Behavior in the Suspicious Coincidence Task
To perform the suspicious coincident task, the model receives three external inputs: (1) labels, (2) exemplar objects, and (3) test objects. Labels (such as a “fep”) are specified as a Gaussian input pattern (Fig 2G) that are projected as vertical ridges into the label-MDS field. Exemplars are defined as 2-dimensional Gaussian input patterns, specifying both the position and MDS values of each exemplar object (Fig 2H). This input feeds into the space-MDS field in a 1:1 pattern, representing visual input from hypothesized lower-level visual fields. Note that the three green circles seen at Figure 2D reflect the same pattern shown in Figure 2H but viewed from above such that ‘hot spots’ of activation take on a greener and then redder color. The final input—the test objects—are defined by their MDS values only (see Fig 2I). These are projected into the label-MDS field as horizontal ridges (Fig 2J). Conceptually, the lack of spatial localization of the test inputs reflects the nature of the task: each test input is considered individually and appears in its own unique (retinal) space separate from other test items and from the exemplars. A more complete model would specify how the test input is mapped from a retinal space into the task space depicted in Figure 2. We have proposed such a model (see Schneegans et al., 2016). In this model, features are mapped from a retinal space into a task space using an attentional layer that projects a horizontal ridge into a feature-space field like the one shown in Figure 2. To save computation time in the current simulations, we did not include this spatial mapping process.
The first three rows in Figure 2 show the sequence of events that unfold in a single trial of the suspicious coincidence task. Row 1 shows the model just a few time steps after initialization. Noise is relatively strong, and input has not yet raised stable peaks in either field (activation patterns have no yellow red in them). Rather, weak influences are evident from all three sources of input: the exemplars can be seen in field A, vertical label ridge in field B (e.g., ‘fep’), and the horizontal test object ridge in field B. Row 2 shows the model after 40 time steps. The input-driven peaks and ridges have begun to stabilize. More activation is flowing between fields as well. The two-humped activation profile shown in Fig 2K projects two ridges (Fig 2L) to the label-MDS field: the upper ridge at K is stronger, because there are two objects with the same MDS values in the visual field, while the faint lower ridge reflects the third exemplar. In Row 3, activation has grown, creating a peak in the label-MDS field (Fig 2M) at the interaction of the label ridge, the test object ridge, and the projection from the space-MDS field. This above-threshold peak (i.e., above zero activation) indicates that the model has generalized the test object to the novel label (‘yes, this is a fep’). The bottom of panel of Fig 2 (see Row 4) shows a simulation of an alternate test object. This test object is less similar to the exemplars (i.e., there is a bigger difference along the MDS dimension). Even at the same point late in the simulation, the model has not formed a peak in the label-MDS field—it does not think the test object is a “fep.”
The DNF model captures the suspicious coincidence effect due to a narrowing of neural activation patterns when three simultaneous, virtually identical exemplars are presented. Figure 3 shows an example. Three simultaneously presented subordinate-level exemplars (i.e., three Labradors) are shown in the top row in the space-MDS field (Fig 3A). In this three-subordinate-exemplars condition, the peaks are close together in MDS space, so the broad ring of inhibition from each peak overlaps with the neighboring peaks. This mutually shared inhibition narrows and sharpens all three peaks. A Gaussian kernel is applied (result in Fig 3B) which projects a narrow ridge (Fig 3C) to the label-MDS field. The ridge is too narrow to overlap with the ridge from the test object (Fig 3D), so activity does not interact strongly enough to form a peak, and the model does not generalize the novel label to the test object. When a single item is presented (i.e., one dog; middle row of Figure 3), the peak in the space-MDS field (Fig 3E) is sharing no inhibition and is thus broader than in the three-subordinate-exemplars condition, as is the activation pattern (Fig 3F) that projects a ridge (Fig 3G) to the label-MDS field. Consequently, a peak forms (Fig 3H), and the model generalizes the novel label to the test object. Thus, the DNF model shows the suspicious coincidence effect: three nearly identical exemplars result in narrower generalization than a single exemplar.
Figure 3.
In the top row, three, subordinate, simultaneous exemplars interact (A) to cause mutual narrowing and project activation (B) as a narrow ridge (C) into the label-MDS field, becoming less likely to overlap with test object ridges (D). In the middle row, a single exemplar (E) does not experience mutual narrowing, so its activation is projected (F) as a broader ridge (G), which is more likely to overlap with test item ridges to form peaks (H). This leads to more broad generalization decisions than in the three simultaneous exemplars (overall, this is the suspicious coincidence effect). In the bottom row, sequentially presented exemplars appear at location I at different time points (I1, I2, and I3), thus each behaving as if it were a single exemplar. Each therefore sends a broad ridge. Since, over time, the sequential exemplars vary slightly along the MDS dimension (vertical), the overall chance of overlapping test item ridges and generalizing is slightly broader than for a single exemplar. This relationship represents a reverse suspicious coincidence effect.
The bottom row of Figure 3 demonstrates the reversal of the suspicious coincidence effect with sequential presentation. Each of the insets I1, I2, and I3 show the contents of the empty spot in the space-MDS field (Fig 3I) over sequential time. As can be seen in the figure, sequential presentation is analogous to presenting a single exemplar: since the three objects are never seen at the same time, no mutual narrowing occurs within the space-MDS field, and generalization is broad. In fact, because the three exemplars are not perfectly identical (slight vertical differences between peaks in panels I1, I2, and I3 of Figure 3), the model generalizes even more broadly than with a single exemplar, because any of the three slightly different exemplars can overlap with the test object and lead to a generalization.
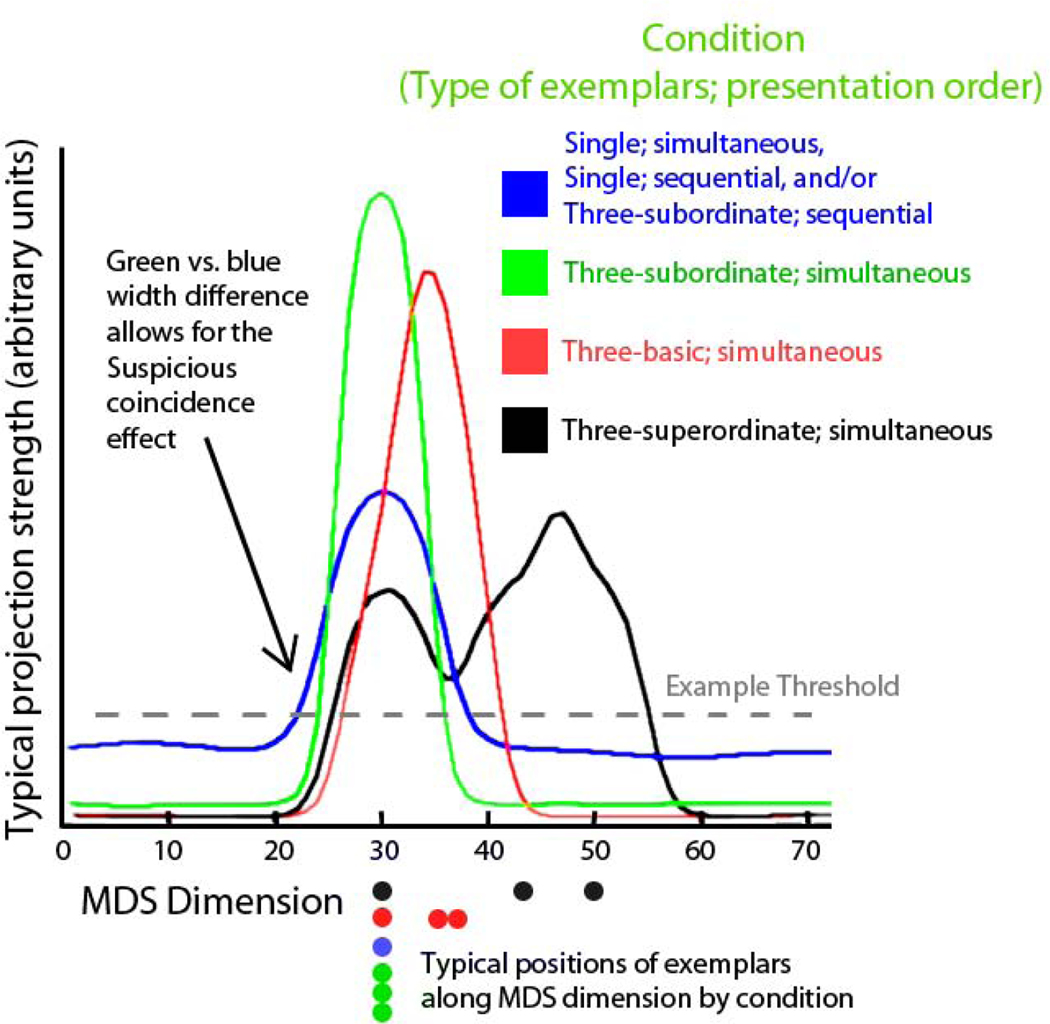
To highlight the origin of the suspicious coincidence effect in the DNF model, Figure 4 shows typical projections from the space-MDS field to the label-MDS field superimposed across all conditions. In the three-subordinate-exemplars simultaneous condition, three nearly identical exemplars were presented at position 30 along the x-axis (i.e., along the MDS dimension), yielding the narrow, green projection (curves are color-coded the same way in Figures 2 and 3). In the single-exemplar condition and in the three-subordinate-exemplars sequential condition, the exemplars were once again placed at position 30, but now the projection was broader, yielding the blue projection. In the three-basic-exemplars condition (simultaneous and sequential versions act similarly from here on), the three examples were separated along the x-axis (see red dots), yielding the broad red projection. Finally, in the superordinate condition, the three examples were very spread apart along the x-axis (see black dots), yielding the very broad, two-humped black projection. If the activation threshold for a field were set at the dotted line, then the coverage of each curve at that line would be a good approximation of breadth of generalization in the suspicious coincidence task.
Figure 4.
A side view of activation ridges in the DNF model, as they are projected from the space-MDS field to the label-MDS field (fields not shown) in different experimental conditions. Single exemplars project short, broad ridges, as do multiple exemplars presented simultaneously (both blue). Multiple sequential exemplars can achieve broader generalization, but only over time. The three-subordinate-exemplars trials create peaks that interact with one another in the space-MDS field, creating a narrower ridge (green) at the dotted threshold and thus narrower generalization. The difference between green and blue ridges represents the suspicious coincidence effect. Groups of exemplars matching at the basic (red) or superordinate (black) levels show shifted and/or broader ridges and generalizations. Colored dots depict positions along the MDS dimension of exemplars that would project these ridges.
Below, we examine whether the DNF model can capture the full array of behaviors observed in the suspicious coincidence task, and we compare this model head-to-head with Xu and Tenenbaum’s Bayesian model. Before moving to this head-to-head comparison, however, we acknowledge that some readers might see similarities between the DNF model and the Bayesian account because they both use Gaussian functions. We contend this is a surface similarity, rather than a deep similarity. There is a long history using Gaussian receptive fields in neurophysiology. Gaussians have been used to fit receptive field profiles (radial basis functions, which are built from Gaussians). Similarly, wavelets are often used which are built from Gaussians and sinusoidal functions. In this context, Gaussians are convenient approximate descriptions of connectivity patterns. The exact pattern of connectivity, however, does not matter too much in DNF models. The logic here is really one of “topological” equivalence, that is, even a distorted Gaussian would have the same qualitative properties as the original Gaussian. Thus, the use of Gaussians in our theory is convenient in that they produce the key qualitative features we desire including the stability properties central to DFT (i.e., the non-linear transitions from the resting state to the ‘peak’ state and the resistance of each state to, for instance, neural noise). But Gaussians do not play a central theoretical role in DFT as they do in the Bayesian approach.
2.0. Modeling Experiment 1
We compared the Bayesian and DNF models by asking whether both models could capture the suite of effects reported in Experiments 1 and 2 of Spencer et al. (2011) from both simultaneous and sequential exemplar presentation conditions. This served as an initial head-to-head comparison of the models. It also allowed us to fix parameters of both models for the second modelling experiment where we probed the ability of each model to generalize to a third experiment.
2.1. Methods
2.1.2. Bayesian methods.
The Bayesian model is deterministic and has two free parameters: basic level bias and the distinction between weak and strong sampling. Xu and Tenenbaum’s cluster trees were used as input to the model. The model was run several times, once each for weak vs. strong sampling and at each of a variety of basic level bias values from 1 to 100. The posterior probabilities of different hypotheses were taken to be proportional to the percent of trials where participants would generalize a novel label to a test item (see Xu and Tenenbaum, 2007b). Thus, posterior probabilities were compared to behavioral data and the best fit recorded.
To determine “best fit,” we used root mean square error (RMSE) compared to results from Experiments 1 and 2 from Spencer et al. (2011), across test trial types. Specifically, there were twelve test trial types for RMSE analysis: exemplars were single (such as one Labrador), three subordinate (three Labradors), basic (three different dog breeds), or superordinate (three different animals). Test items were divided into groups based on their closest match to any exemplar being identical (subordinate), basic-level, or superordinate-level. These were the same twelve test trial types reported by both Xu and Tenenbaum (2007b) and Spencer et al. (2011) for all results. Although the Bayesian model was allowed to vary in free parameters across experiments, parameters were not allowed to change between the test conditions or trial types. That is, if the best fit assumed strong sampling for the sequential condition, we fixed this choice even though weak sampling might fit an individual test trial type better.
Xu and Tenenbaum’s Bayesian model mathematically must show a SCE when operating under strong sampling assumptions, but not under weak sampling assumptions. The size principle under strong sampling requires that the likelihood of the model be lower for basic level hypotheses when multiple identical exemplars are observed than one exemplar, since all hypotheses have nonzero “size”, and the subordinate exemplars (one or three) are always consistent with basic-level hypotheses. Under weak sampling, however, the size principle does not hold, so increasing the number of exemplars leads to no suspicious coincidence effect.
2.1.3. DNF methods.
Simulations with the DNF model matched the timing, spacing, and MDS values of the two experimental conditions. In Spencer et al.’s (2011) tasks, stimuli stayed visible for the entire trial while participants chose category matches from an array of generalization choices on the screen, and sequential exemplars cycled continuously at a rate of one per second. In the model, we simulated participants’ passive viewing of a full presentation of stimuli before making any choices, and then their consideration of each test item for 1 second each (125 time steps). For example, in the three-subordinate-exemplars sequential condition, the DNF model was presented with two full sequences of stimuli across 6 seconds (750 time steps). Then, the model considered one test item per second, while the exemplars changed at the same rate. Simultaneous versus sequential presentation conditions were simulated with the same parameter values, except for changes to the timing of the specific events necessary to simulate these two conditions.
For maximum consistency with the Bayesian model, we used Xu and Tenenbaum’s cluster trees to determine the featural details of the exemplar and test inputs. Recall that Xu and Tenenbaum showed participants pairs of items and asked them to rate the item similarity on a 1–9 scale. These data were then used to construct a hierarchical cluster tree where clusters were, on average, more similar to each other than other nearby objects, and the height of each branch reflected the average similarity. Thus, these data were not in any way intrinsic to the Bayesian account a priori. As such, we don’t see any conflict in using data from this separate task as the base “input” to the DNF model (and the Bayesian model).
We applied the 1D MDS algorithm described above to map the cluster tree data onto the MDS dimension in the model. The position of the three labels was randomly determined. Since labels do not interact on any one trial in the suspicious coincidence task, exact positions along the label dimension are not important. We conducted 60 simulation runs of the full behavioral task. Each run included the same number and type of trials used in the experiment (see Spencer et al., 2011), but a different mapping to the 1D MDS dimension.
Generalization to a particular test object was determined based on whether the model formed a peak at the location of the test object in the label-MDS field (see Fig 2). A peak was defined as any activation above threshold (i.e., above zero) in the label-MDS field at any point during a trial. If a peak was formed while the test object was presented, the model generalized the label to this item. If no peak formed during presentation of a given test item (which lasted for about a second), the model did not generalize the label to this item. We report average model responses below. Note that it took approximately 12 hours of simulation time to complete a full batch of simulations (60 simulation runs x 2 experiments).
2.1.4. DNF Parameter Tuning.
The DNF model has many parameters. Each layer has a strength parameter and a width parameter that determines how quickly neural interactions fall off between neighboring units for self-excitation and lateral-inhibition. There is also a global inhibition strength, a beta parameter (how sharp the sigmoidal function is), and a resting level for each layer. Moreover, the connections between fields in each direction have a beta, strength, and width parameter. Each input to the model (exemplars, test items, and labels) has a strength and a width parameter. There are also global parameters for noise and granularity of simulation steps (the mapping from time steps in the model to milliseconds in the experiment).
Although all of these parameters are free to vary in principle, in practice the model is not fit to data through a comprehensive search of the parameter space. There are two reasons. The first is theoretical: parameters must systematically co-vary with one another to maintain plausible neural dynamics and these constraints are difficult to specify formally. For instance, excitatory and inhibitory parameters must remain in balance, otherwise activation peaks will not arise, or the entire field will become active, essentially simulating a seizure. The second reason is practical: the parameter space cannot be searched broadly due to constraints on computation time. For instance, sampling just two values for each of 19 parameters (the number we tuned in our model) would take immense computation time (12 hours per batch of simulations x 219 parameter combinations = 6,291,456 hours of simulation time). An alternative to such a ‘grid’ search is to use an optimization procedure. For instance, Markov Chain Monte Carlo methods ( MCMC; see Valderrama-Bahamóndez & Fröhlich, 2019) have been successfully used to optimize the parameters of some classes of dynamical models. Unfortunately, it is unclear whether such approaches can be used with the family of integro-differential equations that contain DNF models.
Given this, tuning a DNF model is instead done ‘by hand’. Overall, 19 parameters were re-tuned from the initial Samuelson et al. (2011) model of word-object binding from which our model was derived. These are listed in Table 1. Note that the same values were used for simulating both simultaneous and sequential data.
Table 1.
DNF model paramters re-tuned from the initial Samuelson et al. (2011) model of word-object binding.
| Parameter | Original Value | Our Value | Description | In Appendix (L=Line) |
|---|---|---|---|---|
| Space-MDS Field | ||||
| Local excitation strength | .08 | 6 | How strongly neighbors are locally excited. | ce and σe, in G() of L2, smf |
| Lateral inhibition strength / width | .03/18 | 40/15 | How strongly closely neighbors are laterally inhibited. | ci and σi, in G() of L3, smf |
| Global inhibition | 0.18 | 0.06 | Strength of global inhibition. | kix, L3, smf |
| Resting level | −6.35 | −4 | Baseline level of activation. | hlmfu, L1, smf |
| Label-MDS Field | ||||
| Local excitation strength | 1.6 | 4 | same as above | as above, but in lmf |
| Lateral inhibition strength | 3 | 22.5 | ||
| Global inhibition | 0.35 | 0.004 | ||
| Inputs | ||||
| Noise width | 1 | 4 | Spatially-correlated noise added to fields. | q in L5 |
| Label ridge strength | 0.4 | 8 | The strength of the ridge projected into the label-MDS field from a label. | St(), L1, lmf |
| Label ridge width | 1 | 5 | The width of the label ridge. | St(), L1, lmf |
| Test object ridge strength | 0.162 | 16 | The strength of the MDS ridge for the test object. | St(), L1, lmf |
| Exemplar object peak strength | 0.162 | 11.1 | The strength of the exemplar inputs. | St(), L1, smf |
| Exemplar object peak width | 3 | 3.25 | The width of the exemplar inputs. | St(), L1, smf |
| Spread of exemplars in space | N/A | 10 to either side | How far apart the three exemplar positions were in the model. | St(), L1, smf |
| Field interactions | ||||
| Beta space-MDS to label-MDS | 1 | .8 | Beta is the sharpness of a sigmoid function for gating activation. | β in Λ() of L4, lmf |
| Strength space-MDS to label-MDS | 0.06 or 0.2 | 0.6 | The weighting of the projection from the space-MDS field to the label- MDS field. | Ce in G() of L4, lmf |
| Width space-MDS to label-MDS | 10 or 3 | 1 | The spread of the projection along the share MDS dimension. | βe in G() of L4, lmf |
| Strength label-MDS to space-MDS | 0.06 or 0.2 | 0.01 | (same as above) | Ce in G() of L4, smf |
The first goal in the re-tuning process was to get the model to simulate the appropriate task details like stimulus timing and to roughly match the behaviors of interest. We created a simulator and mimicked the stimulus presentation and timing details from the Spencer et al. (2011) experiments. Next, we adjusted global details of the model to approximate the types of behaviors we thought might conceptually underlie performance in the SCE task. We walk through these changes below.
The hypothesis made by Spencer et al. (2011) that led to testing sequential exemplar presentation in the SCE task centered on simultaneous memory representations of nearby, similar objects interacting with one another neurally. The Samuelson et al. model simulated data from experiments where a single item was presented on each familiarization trial, and it was not tuned to investigate the details of simultaneous interactions. The global inhibition parameter in the space-MDS field was thus too strong, enforcing a single clear peak as appropriate to the Samuelson et al. task. We began by reducing this global inhibition to allow multiple peaks to form and interact (see Table 1 for a list of all changes). At the same time, we increased local inhibition to allow ‘close’ peaks to sharpen one another through shared inhibition. Self-excitation and a more excitable resting level for the field also balanced stronger local inhibition.
Similar adjustments were made to the label-MDS field (see Table 1). In this field, local neural interactions were again more important than global interactions for the task, since test items were compared to multiple ridges at once in simultaneous exemplar conditions. Increased excitation, a higher resting level, and weaker global inhibition balanced the increase in local inhibition strength as in the space-MDS field. Additionally, the higher overall inhibition and excitation from the space-MDS field must be generally matched by the label-MDS field; otherwise, activation in one field will overwhelm the other. We also discovered that the width of lateral inhibition in the Samuelson et al. model was too broad. Unlike in the Samuelson et al. model, we wanted this model to consider generalizing a label to multiple exemplars or sets of exemplars during a trial, and this requires narrower inhibitory interactions. Thus, we decreased the width from a value of 60 (very broad) to a value of 6. Finally, inputs used in the Samuelson et al. model were generally too weak. Thus, we increased the strengths of all inputs, including the input from the space-MDS field to the label-MDS field.
With these changes in place, the revised version of the Samuelson et al. model started to show the right qualitative behaviors. It built peaks when exemplars and test items were near enough in similarity, allowing for basic competence in the SCE task, and allowing for nearby peaks (in space and features) to locally interact and sharpen one another via shared inhibition. The remaining initial parameter tuning focused largely on the width parameters in the model, especially the widths of inputs and the widths of the projections between the space-MDS and label-MDS fields. Widths in the model correspond to breadth of generalization in the SCE task—wider peaks overlap more easily even when objects are less similar and lead to broader parameters. The scale of the spatial dimension in the model is abstract, so spacing of inputs covaries with other width parameters. The only consideration here was to choose a spacing that allowed sufficient resolution between peaks (i.e., the peaks were distinct when visualized).
Once we arrived at a set of parameters that generally showed the right qualitative pattern across test trial types, we entered a final round of parameter tuning where we fine-tuned the model in an effort to maximize fit. This process cannot be exhaustive since there are too many possible parameters to probe. Thus, we targeted a few candidate parameters that were known to be most influential and that therefore merited detailed exploration based on our experience working with the model. Specifically, we focused on the space-MDS width parameters for exact generalization breadth and the resting level of this field to modulate the overall level of excitability. These parameters were adjusted across batches of many simulations, and we picked the parameter value that yielded the best match to the empirical data (lowest RMSE).
We note that hand tuning a model is unlikely to result in optimal model performance; the goal is to identify parameters that provide a fit to the data that is ‘good enough’ given the time constraints, while also performing the task in a manner that is consistent with the theory (e.g., forming a peak to select an item at test). In addition, it is important to evaluate whether the model’s performance is robust to parameter changes, that is, to check whether the modeler has found a local minimum where the model does well, but only with a narrow set of parameter values. This was not the case with our final parameters. Despite the fact that the final round of parameter tuning took between one and two months to complete, the model was already performing the different tasks in qualitatively the right way before we entered the final adjustment phase. Concretely, just before the final fine-tuning phase, the RMSE fit of the DNF model to data from the simultaneous presentation experiment was 0.23, and the RMSE fit to data from the sequential presentation experiment was 0.21. Table 2 shows that these pre-fine-tuning values were comparable to the Bayesian model’s final performance.
Table 2.
RMSE fits of the Bayesian and DNF models for modeling experiments 1 and 2.
| RMSE (basic bias) | Bayesian Model | DNF Model | |
|---|---|---|---|
| Sampling Assumption | |||
| Exp. Fitted | Strong | Weak | |
| Simultaneous | 0.17 (6) | 0.24 (4) | |
| Sequential | 0.22 (71) | 0.24 (11) | |
| Both | 0.21 (19) | 0.24 (7) | 0.17 |
| Generalization | 0.21(19) | 0.14 | |
Lower AIC/BIC values indicate a better quantitative fit
2.1.5. Model comparison metrics.
To compare the quantitative fit of the models, we calculated AIC and BIC values. AIC and BIC are commonly used in the cognitive literature and provide an indication of the accuracy of the model fit while penalizing models that are more complex.
The log-likelihood, L(i), of subject i’s data under a binary/Bernoulli response model is given by
where s=1..S indexes the broad stimulus category (S=3: vegetables, vehicles, other), j=1..J indexes the stimulus test type (J=4: single cue, three subordinate cues, three basic cues, three superordinate cues), k=1..K indexes the hierarchical level (K=3: subordinate, basic, superordinate), n=1..Nk indexes the valid items that could be selected (N1=2, N2=2, N3=4), yisjkn is subject i’s binary response (i.e. the behavioural data; 1 if item was selected, 0 if not), and pjk is the probability of item selection under a given model (e.g. DNF or Bayesian model).
The above equation can be rewritten as follows
where Tk is the total number of trials at level k (i.e., summing over s and n to give T1=6, T2=6, T3=12) and qijk is subject i’s response probability (percent generalization from Figures 5 and 6 divided by 100). This equation is in a more convenient form as data from Figures 5 and 6 can be entered directly.
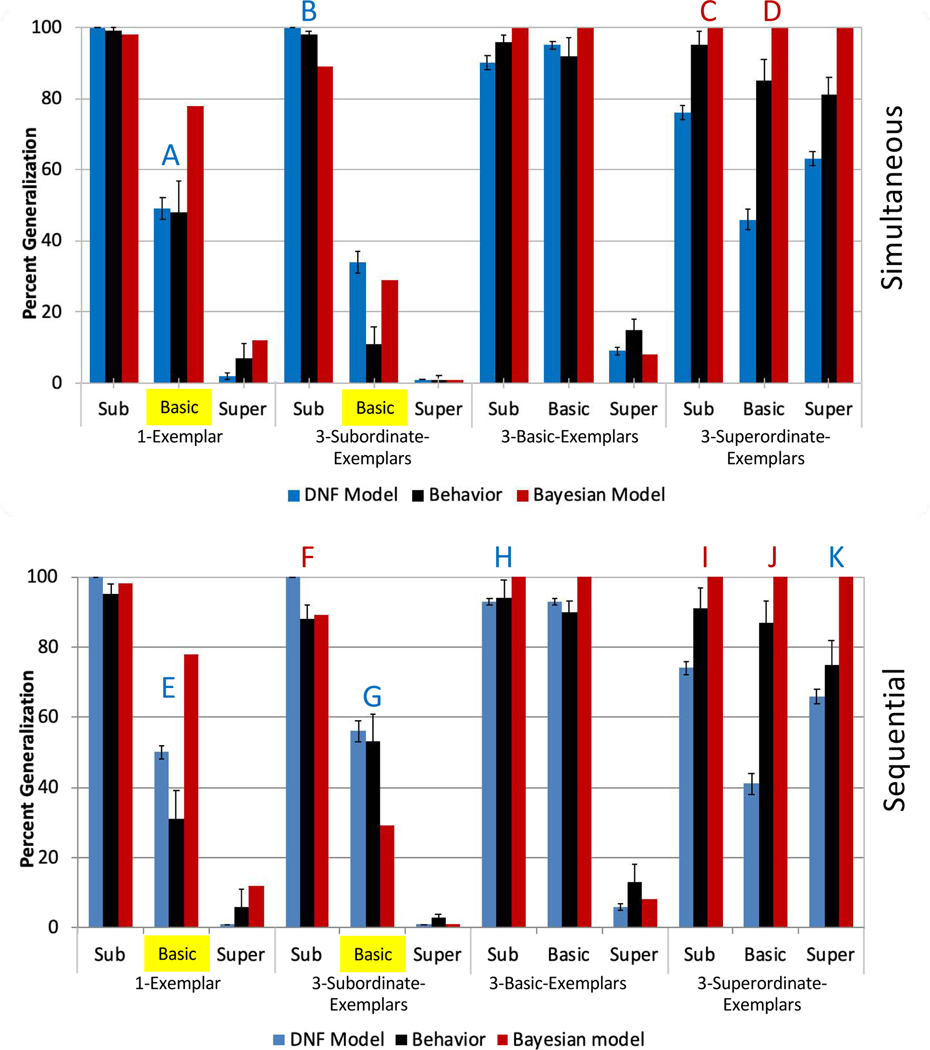
Figure 5.
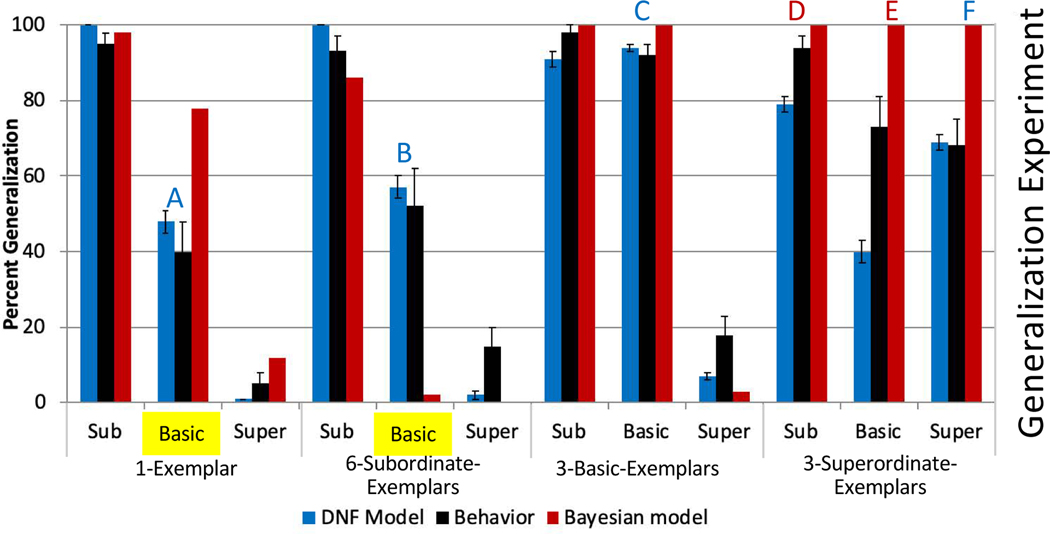
The top panel shows experimental data from Spencer et al.’s (2011) simultaneous exemplars experiment in black. DNF model and Bayesian model fits are shown in blue and red, respectively. The larger denominations along the x-axis refer to experimental conditions, and the smaller denominations refer to test trial types. The two sets of bars relevant to the suspicious coincidence effect are highlighted in yellow, with a decrease from left to right between these bars corresponding to a positive suspicious coincidence effect. The bottom panel shows behavior and fits for Spencer et al.’s (2011) sequential three-exemplars experiment. Letter labels indicate those test trial types where one model fit more than five generalization percentage points (y axis units) better to behavior than the other model. Blue letters (A,B,C,F,G,H,I) indicate the DNF model fits at least this much better, and red letters (D,E,J,K) indicate the Bayesian model fits better.
Figure 6.
Behavioral data and model fits for Spencer, et al.’s (2011) six-exemplars sequential presentation experiment. The format of this figure follows that of Figure 5.
The model selection criteria can then be computed as
where L is total log likelihood, b is the number of model parameters, and N is the total number of binary responses (number of data points). In Table 3 below, b = 19 for the DNF model and 2 for the Bayesian model. We also fit a uniform model for comparison (all response values for this model = 50%) with b = 0 (i.e., zero free parameters). This gave us baseline AIC and BIC values from a neutral, theory-free model.
Table 3.
Quantitative metrics compairing the model fits for modeling experiments 1 and 2. Metrics for a uniform model that had all response values set to 50% are provided as a baseline.
| AIC (BIC) | Best-fitting Bayesian Model | DNF Model | Uniform Model |
|---|---|---|---|
| Simultaneous | 1379.49(1390.51) | 1238.20 (1342.87) | 2456.36 (2456.36) |
| Sequential | 1784.64 (1795.66) | 1489.10 (1593.76) | 2456.36 (2456.36) |
| Generalization | 2518.94 (2529.96) | 1639.46 (1744.13) | 2456.36 (2456.36) |
2.2. Results
We explored the free parameter space of the Bayesian model and chose the parameterization that minimized RMSE when fitting all data from Experiments 1 and 2 from Spencer et al. (2011). The DNF model was tuned ‘by hand’ as described above. Once the DNF model qualitatively reproduced the basic patterns, RMSEs to all data were used to arrive at the final parameters. Table 2 shows RMSEs for final model fits across all 24 test trial types (12 each between two experiments). The DNF model was only tuned once for both experiments and thus has only one value. This value was low, generally outperforming the RMSE values from the Bayesian model. The RMSEs for the Bayesian model are shown for the best fitting basic level bias value in each cell (1–100 tested) across strong and weak sampling assumptions, for the simultaneous and sequential experiments, as well as both sets of experimental data combined. The strong sampling assumption for the Bayesian model fit the data more closely for each individual experiment and when both are combined. Thus, we focus on simulation results from the strong sampling model fit to both conditions since this minimized RMSE. The best-fitting basic level bias parameter in this case was 19.
The best fits of the Bayesian and DNF models are shown in Figure 5. The blue bars show best-fitting data from the DNF model; the red bars show best-fitting data from the Bayesian model. The black bars show the empirical data, that is, the proportion of trials on which participants generalized the novel name to test objects at the subordinate, basic, or superordinate level in the single-exemplar condition (far left), three-subordinate-exemplars condition (middle left), three-basic-exemplars condition (middle right), and three-superordinate-exemplars condition (far right). Data from the simultaneous experiment are in the top panel, and data from the sequential experiment are in the bottom panel.
We have highlighted the bars relevant to the SCE in yellow. These bars were not the sole basis of fit, and either model could fit them more closely than seen here if not considering the full set of data. As can be seen in the top panel, participants generalized the novel label (“Fep”) to other basic level test items (i.e., other dogs) when a single item (Labrador) was shown, but not when three subordinate-level exemplars (three Labradors) were shown. As can be seen in the figure, both models capture this effect. The DNF model fits the magnitude of the difference across exemplar conditions better in the 1-Exemplar condition of the simultaneous experiment. In the sequential condition, the DNF model fits the direction of the reverse suspicious coincidence effect and most closely approximates the data, while the Bayesian model shows a strong positive SCE and fits the individual bars more poorly.
More generally, the qualitative fit of the DNF model to the whole pattern of data is better than that of the Bayesian model. In Figure 5, test trial types where one model’s fit was 5% closer to the data than the other model are marked with letters. In the simultaneous condition, the DNF model fits the data more closely on two test trial types (A, B), and the Bayesian model fits the data more closely on two (C, D). In the sequential condition, the DNF model fits the behavioral data more closely on four test trial types (E, G, H, K), while the Bayesian model fits the data more closely on three test trial types (F, I, J). Note that the DNF model is generally under-performing on the 3-Superordinate-Exemplars condition. Given the good fits to the data pattern otherwise, we did not attempt to optimize this aspect of the model further.
Table 3 reports the quantitative metrics comparing the model fits. The DNF model has the lowest AIC/BIC values for both the Simultaneous and Sequential experiments (recall that lower AIC/BIC values indicate better performance). Note that the DNF model outperforms the Bayesian model, even with the penalty for having more ‘free’ parameters.
2.3. Discussion
Results indicate that the DNF model captures hierarchical word learning across conditions more effectively than the Bayesian model: the DNF model fares better both qualitatively and in terms of quantitative measures of fit. Most critically, the model explains the presence—and reversal—of the SCE across the conditions reported by Spencer et al. (2011). In particular, simultaneous presentation yields sharper neural activation peaks due to shared inhibition between object representations and, consequently, narrower generalization. By contrast, sequential presentation yields broader neural activation peaks and broader generalization as peaks spread out in space and time.
The Bayesian model did not account for these differences across conditions. We thought that the distinction between weak versus strong sampling might effectively modulate the strength of the SCE and capture differences between simultaneous and sequential presentation. In particular, we reasoned that participants might interpret exemplars as one object in the sequential condition and, thus, as not instructive evidence for a category. However, when we fit the weak sampling model to the data, this model did not provide better fits to the data in any condition. Rather, the Bayesian model showed the best overall fits with strong sampling assumptions.
Note that we did not modify either model’s architecture from previous models. The Bayesian equations were from Xu and Tenenbaum (2007b; strong sampling) and Xu and Tenenbaum (2007a; strong and weak sampling). The DNF architecture was adapted from Samuelson et al.’s (2011) word learning model. Nevertheless, the DNF model has more parameters and, therefore, potentially greater flexibility, leaving open the possibility that we over-fit data from these two experiments during the parameter tuning process. Although hand tuning likely yielded a non-optimal fit of the DNF model, it is useful to examine this issue directly in Modeling Experiment 2 by asking whether the best-fitting models generalize to capture data from a third experiment reported by Spencer et al. without re-fitting.
3.0. Modeling Experiment 2
We selected the best-fitting models from Modeling Experiment 1 and asked whether these models captured data from a third experiment from Spencer et al. (2011). In Spencer and colleagues Experiment 3, exemplars were presented sequentially, but in the multiple-exemplars trials, six exemplars were shown instead of three, and their positions were superimposed at a single location to highlight differences between the objects. This manipulation was explicitly designed to reduce the likelihood that a Bayesian weak sampling assumption would apply. Spencer and colleagues found a behavioral trend toward a reverse SCE. Unlike with three sequentially presented exemplars, there was no statistically significant difference between a single exemplar trial versus a six subordinate-level exemplars trial in the behavioral data, and the reversal effect was one half the magnitude with six exemplars.
3.1. Methods
All parameters were fixed relative to Modeling Experiment 1. The only changes in the simulations reflected the difference in the stimulus inputs. The Bayesian model was able to simulate this new experiment by changing n to 6 instead of 3 in its likelihood equation, reflecting the increased number of exemplars. The DNF model was presented with six exemplar inputs, one second for each presentation, all at the same spatial position. There was no guarantee that either model would capture data from this third experiment as both models were sensitive to the experimental change in procedure.
3.2. Results and Discussion
The RMSE fits of the two models are listed in Table 2 and the simulated data are shown in Figure 6. Similar to the first two conditions, the DNF model outperformed the Bayesian model with a lower RMSE. Note that the RMSE value was lower for the DNF model in the present experiment, even though the model was not tuned to this particular set of data. This shows impressive generalization given that the stimulus presentation details—something that the DNF model is quite sensitive to—differed considerably. Qualitative comparison of bars in Figure 6 shows four test trial types where the DNF model fits are more than 5% closer to the behavioral data than the Bayesian model (points A, B, C, and F) and the same two where the Bayesian model fits more than 5% closer than the DNF model (D, E). The SCE is reversed in the behavioral data, but only weakly. The DNF model accurately captures these data. The Bayesian model, by contrast, shows a very large SCE because there were 6 exemplars which magnifies the effect of the size principle.
Quantitative comparison of the models for the Generalization experiment is shown in Table 3. As in the previous simulation experiment, the DNF model showed the lowest AIC/BIC values. The Bayesian model performed poorly in this experiment, with AIC/BIC values higher than the uniform ‘baseline’ model. This was driven primarily by low log likelihoods in the two conditions central to the suspicious coincidence. In particular, the log likelihood at the basic level for the 1-Exemplar condition was −0.98, while the log likelihood at the basic level for the 3-Subordinate Exemplars condition was −1.83. By contrast, the log likelihood for all conditions for the uniform model was −0.67.
4.0. General Discussion
The DNF model presented here is the first process-oriented account of the suspicious coincidence effect, previously captured only by Xu and Tenenbaum’s (2007b) Bayesian model. The work presented here contributes to both our understanding of word learning by elucidating the processes by which people learn multiple hierarchical labels for categories and by providing a direct comparison between rational and process-oriented cognitive accounts on common ground with same phenomenon. Both of the models we tested received the same inputs—hierarchical cluster trees from Xu and Tenenbaum’s (2007b) data. Both models were also compared to behavioral data from the same three experiments from Spencer et al. (2011), including a replication of Xu and Tenenbaum’s (2007b) original effect. Both models had means by which to theoretically distinguish between all three experiments we simulated. In particular, differences between simultaneous versus sequential exemplar presentation can be explained by neural interactions in the DNF model or by strong versus weak sampling assumptions in the Bayesian framework (Xu & Tenenbaum, 2007a). The difference in performance found in the generalization experiment can be captured by the timing and spacing of representations in the DNF model or by the exemplar repetition parameter in the Bayesian model’s “size principle” likelihood equation.
Critically, the DNF model captured a meaningful qualitative effect that the Bayesian model does not: a reversal of the suspicious coincidence effect with sequential presentation. The use of a weak sampling assumption in the Bayesian framework can reduce the strength of the suspicious coincidence effect and could potentially have allowed quantitatively closer fits across conditions compared to the DNF3. A fully reversed effect, however, is a qualitative achievement that holds meaning beyond its contribution to an overall quantitative fit. This is because the reverse suspicious coincidence effect calls into question the theoretical foundation of the Bayesian model. This has implications for the concepts used by each theoretical approach.
A separate qualitative question in model evaluation is whether models generate novel, testable predictions. On this front, the Bayesian model fares well. Recall that Xu and Tenenbaum (2007b) initially predicted the suspicious coincidence effect based on a rational analysis of hierarchical word learning. Although the DNF model reported here captures the suspicious coincidence effect, it is important to note that these were post-hoc model fits to the replication condition. That said, Spencer and colleagues were inspired by DNF-style thinking when they initially tried to “break” the suspicious coincidence effect by manipulating the nature of stimulus presentation (see Spencer et al., 2011). Spencer et al.’s (2011) experiments were based on the fact that in the DNF framework peaks can be sharpened with interaction such as when similar items are presented together in space and time, similar to phenomena we had observed in studies of visual working memory (Johnson, Spencer, Luck, & Schöner, 2009; Johnson, Spencer, & Schöner, 2009). Thus, the DNF model also led to a confirmed novel prediction and an empirical discovery.
Yet another metric for comparing models is generality. Models can be general in at least two senses: the model can be considered one example of a more general modeling framework, and the specific model can capture multiple phenomena without substantial modification. In the former sense, the Bayesian model fares well. There has been an explosion of Bayesian accounts of different phenomena in the literature, ranging from the Bayesian account of word learning highlighted here, to Bayesian accounts of visual perception (de Lange et al., 2018; Yuille & Kersten, 2006), syllogistic reasoning (Oaksford & Chater, 2001), or people’s estimates of duration and extent (Griffiths & Tenenbaum, 2006). Clearly, the Bayesian framework is a powerful general modeling approach within the cognitive sciences.
In the sense of capturing a variety of phenomena, evaluating generality is trickier. Bayesian models have been used to capture several novel findings in word learning, including how children generalize novel names depending on the pedagogical context (Xu & Tenenbaum, 2007a,b) and children’s bias to extend novel names to objects based on shape similarity (Kemp et al., 2007). Although these different phenomena have been modeled using a Bayesian framework, it is not clear whether this is a case of the same model being generalized across conditions. Rather, we contend that the strongest theoretical claims from Xu and Tenenbaum (2007a) are specified not in the model simulations, but by the modeler. For example, the modeler chooses strong versus weak sampling assumptions in Xu and Tenenbaum’s 2007 (a and b) models prior to the start of simulations. There is a claim that some psychological process—which is not specified—causes children to treat information differently in the teacher and learner conditions and which justifies the equation change.
What about with the DNF model? Does this model generalize at the levels of the modeling framework and the specific model? At the framework level, dynamic field theory (DFT) has been used to capture a host of phenomena ranging from neural population dynamics in visual cortex (Jancke et al., 1999; Markounikau et al., 2010), to visual looking and learning in infancy (Perone & Spencer, 2012, 2013; Perone et al., 2011), to aspects of spatial cognition (Schutte & Spencer, 2009, 2010), to visual working memory (Johnson, Spencer, Luck, & Schöner, 2009; Simmering & Spencer, 2008), and into higher-level cognition including dual-task performance (Buss et al., 2013) and autonomous behavioral organization in robots (Sandamirskaya et al., 2013; Steinhage & Schöner, 1997). Our sense is that this level of generality is comparable to the generality evident within the broader Bayesian framework.
At the level of the specific model architecture examined here, the model also generalizes, at least to the degree of the Bayesian model. The DNF architecture presented here has been used to simulate how children use space to bind words to objects (Samuelson et al., 2011), as well as developmental changes in children’s bias to generalize novel names based on shape similarity (Perone et al., 2020). At the level of task-specific details, there are differences across studies: for example, we used a single MDS dimension to accommodate the unknown features in our naturalistic stimuli versus the controlled color and shape features in Samuelson et al. (2011). Although this is the case, the architecture of the DNF models are comparable (see Appendix; Samuelson et al., 2011). Additionally, Samuelson, Spencer, and Jenkins (2013) showed a version of our present model was able to capture a suite of different effects in early word learning including differences in comprehension, production, novel noun generalization with both yes/no and forced choice response modes, and referent selection.
To summarize, both the Bayesian model and the DNF model fare relatively well on different model evaluation metrics. Both have generated novel predictions, and both capture some sense of generality, although there are differences on this front. The fact that both models fare well on these metrics, however, makes the head-to-head comparison reported here all the more important. It shows that at least one set of results clearly favored one model over another in specific qualitative and quantitative ways, where other forms of analysis have not drawn such sharp distinctions. This sort of substantial, concrete evaluation between models is relatively rare, but in this case, it proves to be quite informative.
4.1. Rational and Process Accounts
Head-to-head comparison of the Bayesian and DNF models provides insight into theoretical issues regarding rational and process accounts in general. Here, we see two key points of contrast. First, DFT – the general framework of which the DNF model reported here is a member – embraces neural grounding and assumes that neural details are important for understanding behavior; the Bayesian approach espoused by Xu and Tenenbaum does not explore this level of processing and, instead, commits to a computational level description. Second, these approaches appear to have different end goals which we characterize as deep (DFT) versus broad (Bayesian) integration. We discuss each of these points of contrast below.
DFT uses simulated real-time neural population dynamics within artificial cortical fields to capture the processes hypothesized to underlie behavioral decisions in-the-moment, as well as how neural processes change over learning and development (for reviews, see Schöner, 2009; Spencer, Perone, & Johnson, 2009). For instance, Schöner, Erlhagen and colleagues developed an approach to directly link simulated activation dynamics in neural field models to single- and multi-unit neurophysiology (Bastian et al., 1998; Erlhagen et al., 1999; Jancke et al., 1999), enabling researchers to test a theory of response preparation both behaviorally and neurally with non-human primates (A Bastian et al., 1998; Annette Bastian et al., 2003). This approach has also been extended to studies of visual cortical processing using voltage-sensitive dye imaging (Markounikau et al., 2010). Several studies have probed the link between DFT and ERP measures with humans, testing dynamic neural field accounts of motor planning (McDowell et al., 2002) and multi-object tracking (Spencer et al., 2012). Finally, recent efforts have used a local-field potential measure from dynamic neural field models to simulate changes in the hemodynamic response over learning from an fMRI study of dual-task performance (Buss et al., in press).
Xu and Tenenbaum (2007b), by comparison, explicitly disavow any strong assumptions about the neural realism of the Bayesian model:
We make no claim that Bayesian computations are implemented exactly in the mind or brain, with explicitly represented probabilities. On the contrary, it is more likely that the details of mental or neural processing correspond to some efficient approximation to the Bayesian computations we propose here (p. 270).
Explanations of Bayesian computations at a neural level are being actively pursued (Deneve, 2008; Friston et al., 2017; Kover & Bao, 2010), although the efficiency and plausibility of Bayesian neural mechanisms have been questioned (Baddeley, et al., 1997; Brighton & Gigerenzer, 2008; Feldman, 2010).
Clearly, DFT makes strong claims about neural realism, while Xu and Tennenbaum’s Bayesian approach does not. Is this an important distinction? In our view, neural grounding is a useful evaluation metric. First, neurally-grounded models are open to more empirical constraints—they can, in theory, capture both behavioral and neural data (conversely, they can also fail to capture data in multiple ways). Second, neural grounding forces the modeler to be fully attentive to the multiple timescales at work in any given task: the real-time dynamics that underlie changes in neural activation patterns from second-to-second, and the changes that occur in these neural dynamics over learning in a task. In short, neural models force attention to task-specific details. In the context of the present report, this detail-oriented mindset led to our discovery that simultaneous versus sequential presentation matters (Spencer et al., 2011).
Our sense is that task-specific details are less emphasized within the Bayesian perspective. Rather, experiments are a means to a more general end—to demonstrate the rational principles that underlie and organize human cognition. This is explicit in the computational perspective offered by Xu and Tenenbaum (2007b):
Our analysis of word learning focuses on what Marr (1982) called the level of computational theory. We have tried to elucidate the logic behind word learners’ inductive inferences, without specifying how that logic is implemented algorithmically in the mind or physiologically in neural hardware (p. 270).
Clearly, then, the goals of these theoretical perspectives differ. The question is: does this difference matter? In our view, these different perspectives create challenges that both perspectives must overcome. Ultimately, to explain human thinking, theories will have to bridge levels of analysis to explain how the brain gives rise to behavior (see Samuelson et al., 2015). Similarly, theories must be sufficiently general to extrapolate away from the details of behavior-in-context to identify the more abstract principles around which behavior is organized.
Although both perspectives are important, we contend that there is a deep challenge in trying to infer a computational-level theory from an inherently non-linear, complex, and emergent system (Samuelson, Jenkins, & Spencer, 2015). Emergence—the idea that behavior arises through the interaction of many self-organizing components over time—plays a central role in learning and development (e.g., Elman et al., 1996; Thelen & Smith, 1994). The challenge with emergence is that there are often non-obvious causes of behavior that elude rational analysis. One of our favorite examples comes from the domain of early word learning. For decades, researchers approached the challenge of figuring out the referents of words from a largely philosophical perspective, debating questions such as innateness of grammar or other hardwired constraints (Chompsky, 1965; Quine, 1960; Wittgenstein, 1967). Researchers focused on early word learning, however, have recently gained greater appreciation for the child’s perspective and the multiple dynamic supports provided to reduce referential ambiguity. For example, Yu and Smith (2012) discovered that at the moment when a parent says a novel word, it is often the case that children have one object in view. Why? Because children have short arms: when they hold objects, the objects are close. Conveniently, parents also tend to name objects that children hold. Thus, the problem of determining the referent of a novel word is not solved entirely by constraints in the head. The solution is leveraged at least in part by dynamics of the typical naming situations presented to children (for discussion, see Spencer, Blumberg, McMurray, Robinson, Samuelson & Tomblin, 2009; Kucker, McMurray & Samuelson, 2015). Is there an inner logic here that might resonate with a Bayesian analysis? Certainly, there is. But we think it is telling that this aspect of word learning was discovered by attention to in-the-moment details and eluded a rational analysis of behavior for decades.
This leads to the final contrast between the rational and process-based perspectives—the end game. Our sense is that the Bayesian approach has broad integration as the goal—to bring together many phenomena under the same theoretical umbrella. The upside of this approach is that one can see connections between phenomena that were previously thought to be completely unrelated. This is certainly part of the reason why the Bayesian perspective has been embraced so enthusiastically (Baker et al., 2009; Chater et al., 2006; Körding & Wolpert, 2006; Norris, 2006; Rao, 2005). The downside is that sometimes details come along that don’t quite fit a rational explanation—such as our data showing that simultaneous versus sequential presentation of stimuli can reverse the suspicious coincidence effect (Spencer et al., 2011), that less knowledgeable children show stronger suspicious coincidence effects than more knowledgeable ones (Jenkins et al., 2015), or other work addressing when and why humans behave irrationally or suboptimally in general (Derks & Paclisanu, 1967; Gainsbury et al., 2014; Kahneman & Tversky, 1979; Tversky, 1977). It is critical that these exceptions-to-the-rule be treated seriously, because they place limits on how broadly the theoretical framework generalizes.
By contrast, process-based approaches tend to seek deep integration—to weave together the details of how processes come together in different tasks and across different contexts to create behavior. The upside of this approach is that deep integration can be quite robust when successful—if the processes are well described, they can explain behavior in detail across many different situations. The downside is that process-level theories can get mired in the weeds, so focused on the details of particular paradigms that the theory loses contact with how behavior is organized in the real world.
Where do these points of contrast leave our evaluation of the Bayesian and DNF models of hierarchical world learning? In the context of the suspicious coincidence effect, the DNF model gets more of the local details correct, and it does so while retaining neural-grounding and generalizing to other phenomena in early word learning. Future efforts will be needed to more fully explore the range of behaviors that each model can explain and predict. Such efforts are important given the healthy debate taking place between the rational and process-based perspectives in cognitive science (Brighton & Gigerenzer, 2008; Chater, 2009; Jones & Love, 2011). In the end, such debates will undoubtedly sharpen our understanding of the contrasts that exist between these very different approaches to the study of cognition.
Acknowledgments
Author Note
The authors would like to acknowledge Bob McMurray for his contributions to an earlier version of this manuscript. We also thank Gregor Schöner for discussions of the theoretical ideas and Samuel Forbes for help with the model repository. This research was supported in part by the Department of Defense (DoD) through the National Defense Science & Engineering Graduate Fellowship (NDSEG) Program award to GWJ and by the Eunice Kennedy Shriver National Institute of Child Health & Human Development award number R01HD045713 to LKS. The content is solely the responsibility of the authors and does not necessarily represent the official views of the Eunice Kennedy Shriver Institute of Child Health & Human Development or the National Institutes of Health.
Appendix
Model and Simulation Details
Below we define the equations for the two dynamic neural fields in the model used to capture the suspicious coincidence effect: the label-MDS field (lmf) and the space-MDS field (smf). Each field consists of reciprocally coupled excitatory, u, and inhibitory, v, layers. Field equations specify the rate of change of neural activation, or , over two field dimensions. We adopt the following convention for the dimensions: x refers to the label dimension, y refers to the MDS dimension, and z refers to the space dimension.
Activation in the excitatory layer of the label-MDS field, ulmf, is governed by the following equation:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
where is the rate of change of the activation level across the label dimension, x, and the MDS dimension, y, as a function of time, t. The constant τ excite sets the time scale of the dynamics. The current activation in the field is given by ulmf (x, y). This component is negative so that activation changes in the direction of the neuronal resting level, hlmfu. The term in line (1), St(x,y), signifies task-specific contributions, specifically the label ridge and test item ridges. Note that inputs to the field took the form of localized, two-dimensional Gaussian distributions (see (6) below) for exemplars in the space-MDS field, and one-dimensional Gaussian distributions for label and test item ridges in the label-MDS field.
The next term in the equation (line 2) specifies locally-excitatory interactions within the label-MDS field. These excitatory interactions are given by the convolution of a two-dimensional Gaussian kernel with a sigmoidal threshold function.The Gaussian kernel in equation (2), for example, was specified by:
| (6) |
with excitatory strengths, ce, and excitatory widths, σe. The level of activation required to enter into the interaction was determined by the following generic sigmoidal function:
| (7) |
where β is the slope of the sigmoid. The slope determines whether neurons close to threshold (i.e., 0) contribute to the activation dynamics with lower slope values permitting graded activation near threshold to influence performance, and higher slope values ensuring that only above-threshold activation contributes to the activation dynamics.
Line 3 specifies contributions from the inhibitory layer of the field, vlmf, to the excitatory layer, ulmf, leading to lateral or surround inhibition in the field. This component is specified by the convolution of a Gaussian kernel with a sigmoidal function, where the sigmoid operates on the activation level of the inhibitory layer. That is, inhibition is only passed from units in the inhibitory layer that are active above threshold. The widths of the inhibitory interactions in the Gaussian kernel, σi, are larger than corresponding excitatory widths, σe (Table 1). In addition to inhibition from the sigmoided inhibitory layer, the excitatory layer is also globally inhibited based on the overall summed activation in the inhibitory layer, shown as the second term on line 3. Global inhibition is scaled by a strength parameter, kix.
The fourth term in the excitatory field equation specifies the contribution of above-threshold activation in the space-MDS field (smf) to the label-MDS field (lmf). All above-threshold activation in the space-MDS field is integrated across the MDS feature dimension, y, and projected uniformly across the label dimension in the label-MDS field. This interaction occurs between excitatory layers of the two fields. Note that this projection is via the convolution of a Gaussian kernel with the integrated activity. This enables perceived exemplar features to pass to the label-MDS field to be compared to test items for a generalization match.
The fifth contribution to the field dynamics on line 5 is spatially correlated noise. This is the convolution of a Gaussian kernel with a field of white noise sources scaled by the noise strength parameter, q.
The inhibitory layer of the label-MDS field, vlmf, is governed by the following equation:
| (8) |
| (9) |
| (10) |
This equation specified the rate of change of activation of the layer of inhibitory interneurons over the time scale specified by τ inhib. The rate of change is influenced by the negative of the current state to ensure that the system has an attractor at the resting level, h (line 8). The inhibitory layer receives positive input from the excitatory layer, via the convlution of a Gaussian kernel and a sigmoid function over activation in the excitatory layer (line 9). Thus, the inhibitory layer only receives input around sites that are active in the excitatory layer. Finally, line (10) specifies a contribution from spatially correlated noise.
The equations for the excitatory and inhibitory layers of the space-MDS field, usmf and vsmf, are identical to the equations for the label-MDS field except that the x dimension is swapped with the z dimension, and the task-specific inputs St(x,y) refer to exemplar inputs instead of label and test object ridges.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
For an earlier discussion of ‘suspicious coincidences’, see Barlow (1985).
Xu and Tenenbaum (2007b) investigated both adult and child word learners, and modeling the distinction was their motivation for the basic level bias parameter. Xu and Tenenbaum ultimately found that the basic level bias was most useful for fitting adult behavior, however, and we therefore still consider the parameter here.
The Bayesian model cannot show a reverse SCE. However, a positive to zero SCE change due to sampling assumptions could still potentially fit the data better than the DNF model. Even a DNF model that can show a reverse SCE can overshoot its reversal, only show reversal in all conditions at once, be generally noisier, etc.
References
- Baddeley R, Abbot LF, Booth MCA, Sengpiel F, Freeman T, Wakeman EA, & Rolls E (1997). Responses of neurons in primary and inferior temporal visual cortices to natural scenes. Proceedings of the Royal Society of London: Biological Sciences, 264, 1775–1783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker CL, Saxe R, & Tenenbaum JB (2009). Action understanding as inverse planning. Cognition, 113(3), 329–349. [DOI] [PubMed] [Google Scholar]
- Barlow HB (1985). Cerebral cortex as model builder. In Rose D and Dobson VG, editors, Models of the visual cortex, p. 37–46. Wiley, New York. [Google Scholar]
- Baddeley R, Abbot LF, Booth MCA, Sengpiel F, Freeman T, Wakeman EA, & Rolls E (1997). Responses of neurons in primary and inferior temporal visual cortices to natural scenes. Proceedings of the Royal Society of London: Biological Sciences, 264, 1775–1783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker CL, Saxe R, & Tenenbaum JB (2009). Action understanding as inverse planning. Cognition, 113(3), 329–349. 10.1016/j.cognition.2009.07.005 [DOI] [PubMed] [Google Scholar]
- Bastian A, Riehle A, Erlhagen W, & Schöner G (1998). Prior information preshapes the population representation of movement direction in motor cortex. NeuroReport, 9, 315–319. [DOI] [PubMed] [Google Scholar]
- Bastian Annette, Schöner G, & Riehle A (2003). Preshaping and continuous evolution of motor cortical representations during movement preparation. European Journal of Neuroscience, 18(7), 2047–2058. 10.1046/j.1460-9568.2003.02906.x [DOI] [PubMed] [Google Scholar]
- Brighton H, & Gigerenzer G (2008). Bayesian brains and ognitive mehanisms: Harmony or dissonance? In Chater N & Oaksford M (Eds.), The Probabilistic Mind: Prospects for Bayesian Cognitive Science (pp. 189–208). Oxford University Press. [Google Scholar]
- Buss AT, Wifall T, Hazeltine E, & Spencer JP (2013). Integrating the behavioral and neural dynamics of response selection in a dual-task paradigm: A dynamic neural field model of Dux et al. (2009). Journal of Cognitive Neuroscience, 26, 334–351. [DOI] [PubMed] [Google Scholar]
- Chater N (2009). Rational and mechanistic perspectives on reinforcement learning. Cognition, 113(3), 350–364. 10.1016/j.cognition.2008.06.014 [DOI] [PubMed] [Google Scholar]
- Chater N, Oaksford M, Nakisa R, & Redington M (2003). Fast, frugal, and rational: How rational norms explain behavior. Organizational Behavior and Human Decision Processes, 90(1), 63–86. 10.1016/S0749-5978(02)00508-3 [DOI] [Google Scholar]
- Chater N, Tenenbaum JB, & Yuille A (2006). Probabilistic models of cognition: Conceptual foundations. Trends in Cognitive Sciences, 10(7), 287–291. 10.1016/j.tics.2006.05.007 [DOI] [PubMed] [Google Scholar]
- Chompsky N (1965). Aspects of the theory of syntax. MIT Press. [Google Scholar]
- de Lange FP, Heilbron M, & Kok P (2018). How Do Expectations Shape Perception? Trends in Cognitive Sciences, 22(9), 764–779. 10.1016/j.tics.2018.06.002 [DOI] [PubMed] [Google Scholar]
- Deneve S (2008). Bayesian spiking neurons I: Inference. Neural Computation, 20, 91–117. [DOI] [PubMed] [Google Scholar]
- Derks P, & Paclisanu MI (1967). Simple Strategies in Binary Prediction By Children and Adults. Journal of Experimental Psychology, 73(2), 278–285. 10.1037/h0024137 [DOI] [Google Scholar]
- Durstewitz D, Seamans JK, & Sejnowski TJ (2000). Neurocomputational models of working memory. Nature Neuroscience, 3, 1184–1191. 10.1038/81460 [DOI] [PubMed] [Google Scholar]
- Elman JL, Bates EA, Johnson MH, Karmiloff-Smith A, Parisi D, & Plunkett K (1996). Rethinking innateness: A connectionist perspective on development. MIT Press. [Google Scholar]
- Erlhagen W, Bastian A, Jancke D, Riehle A, & Schoner G (1999). The distribution of neuronal population activation (DPA) as a tool to study interaction and integration in cortical representations. Journal of Neuroscience Methods, 94(1), 53–66. 10.1016/S0165-0270(99)00125-9 [DOI] [PubMed] [Google Scholar]
- Erlhagen W, & Schöner G (2002). Dynamic field theory of movement preparation. Psychological Review, 109(3), 545–572. 10.1037/0033-295X.109.3.545 [DOI] [PubMed] [Google Scholar]
- Erlhagen Wolfram, & Bicho E (2006). The dynamic neural field approach to cognitive robotics. Journal of Neural Engineering, 3(3). 10.1088/1741-2560/3/3/R02 [DOI] [PubMed] [Google Scholar]
- Faubel C, & Schöner G (2008). Learning to recognize objects on the fly: a neurally based dynamic field approach. Neural Networks : The Official Journal of the International Neural Network Society, 21(4), 562–576. 10.1016/j.neunet.2008.03.007 [DOI] [PubMed] [Google Scholar]
- Feldman J (2010). Ecological expected utility and the mythical neural code. Cognitive Neurodynamics, 4(1), 25–35. 10.1007/s11571-009-9090-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K, FitzGerald T, Rigoli F, Schwartenbeck P, & Pezzulo G (2017). Active Inference: A Process Theory. Neural Computation, 29, 1–49. 10.1162/NECO [DOI] [PubMed] [Google Scholar]
- Gainsbury SM, Suhonen N, & Saastamoinen J (2014). Chasing losses in online poker and casino games: Characteristics and game play of Internet gamblers at risk of disordered gambling. Psychiatry Research, 217(3), 220–225. 10.1016/j.psychres.2014.03.033 [DOI] [PubMed] [Google Scholar]
- Garner WR (1974). The processing of information and structure. Erlbaum. [Google Scholar]
- Gentner D, & Namy LL (2006). Analogical processes in learning. Current Directions in Psychological Science, 15(6), 335–361. 10.1111/j.1467-8721.2006.00456.x [DOI] [Google Scholar]
- Golinkoff RM, Hirsh-Pasek K, Bailey LM, & Wenger NR (1992). Young children and adults use lexical principles to learn new nouns. Developmental Psychology, 28(1), 99–108. 10.1037//0012-1649.28.1.99 [DOI] [Google Scholar]
- Golinkoff RM, Mervis CB, & Hirsh-Pasek K (1994). Early object labels: the case for a developmental lexical principles framework. Journal of Child Language, 21(01), 125–155. 10.1017/S0305000900008692 [DOI] [PubMed] [Google Scholar]
- Griffiths TL, & Tenenbaum JB (2006). Optimal predictions in everyday cognition. Psychological Science, 17(9), 767–773. 10.1111/j.1467-9280.2006.01780.x [DOI] [PubMed] [Google Scholar]
- Hahn U, Bailey TM, & Elvin LBC (2005). Effects of category diversity on learning, memory, and generalization. Memory and Cognition, 33(2), 289–302. 10.3758/BF03195318 [DOI] [PubMed] [Google Scholar]
- Jancke D, Erlhagen W, Dinse HR, Akhavan AC, Giese M, Steinhage A, & Schoner G (1999). Parametric population representation of retinal location: Neuronal interaction dynamics in cat primary visual cortex. Journal of Neuroscience, 19(20), 9016–9028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkins GW, Samuelson LK, Smith JR, & Spencer JP (2015). Non-Bayesian noun generalization in 3–5-year-old children: Probing the role of prior knowledge in the suspicious coincidence effect. Cognitive Science, 39(2). 10.1111/cogs.12135 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson JS, Spencer JP, Luck SJ, & Schöner G (2009). A dynamic neural field model of visual working memory and change detection. Psychological Science, 20, 568–577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson Jeffrey. Simmering VR, & Buss AT (2014). Beyond slots and resources: Grounding cognitive concepts in neural dynamics. Attention, Perception, and Psychophysics, 76(6), 1630–1654. 10.3758/s13414-013-0596-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson Jeffrey S, Spencer JP, & Schöner G (2009). A layered neural architecture for the consolidation, maintenance, and updating of representations in visual working memory. Brain Research, 1299, 17–32. 10.1016/j.brainres.2009.07.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones M, & Love BC (2011). Bayesian Fundamentalism or Enlightenment ? On the Explanatory Status and Theoretical Contributions of Bayesian Models of Cognition. Behavioral and Brain Sciences, 34(2011), 169–231. [DOI] [PubMed] [Google Scholar]
- Kahneman D, & Tversky A (1979). Prospect theory:An analysis of decision under risk. Econometrica, 47(2), 263–292. [Google Scholar]
- Kemp C, Perfors A, & Tenenbaum JB (2007). Learning overhypotheses with hierarchical Bayesian models. Developmental Science, 10(3), 307–321. 10.1111/j.1467-7687.2007.00585.x [DOI] [PubMed] [Google Scholar]
- Knill DC, & Pouget A (2004). The Bayesian brain: The role of uncertainty in neural coding and computation. Trends in Neurosciences, 27(12), 712–719. 10.1016/j.tins.2004.10.007 [DOI] [PubMed] [Google Scholar]
- Körding KP, & Wolpert DM (2006). Bayesian decision theory in sensorimotor control. Trends in Cognitive Sciences, 10(7), 319–326. 10.1016/j.tics.2006.05.003 [DOI] [PubMed] [Google Scholar]
- Kover H, & Bao S (2010). Cortical plasticity as a mechanism for storing bayesian priors in sensory perception. PloS One, 5(5), e10497. 10.1371/Citation [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krafft PM, Shmueli E, Griffiths TL, Tenenbaum JB, Sandy A “, & Pentland, “. (2020). Bayesian Collective Learning Emerges from Heuristic Social Learning. Cognition. [DOI] [PubMed] [Google Scholar]
- Lipinski J, Schneegans S, Sandamirskaya Y, Spencer JP, & Schöner G (2012). A neurobehavioral model of flexible spatial language behaviors. Journal of Experimental Psychology. Learning, Memory, and Cognition, 38, 1490–1511. 10.1037/a0022643 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markman E (1989). Categorization and naming in children: Problems of induction. MIT Press. [Google Scholar]
- Markman EM (1991). The whole-object, taxonomic, and mutual exclusivity assumptions as initial constraints on word meanings. In Gelman SA& Byrnes JP(Eds.), Perspectives on language and thought: Interrelations in development (pp. 72–106). Cambridge University Press. [Google Scholar]
- Markounikau V, Igel C, Grinvald A, & Jancke D (2010). A Dynamic Neural Field Model of Mesoscopic Cortical Activity Captured with Voltage-Sensitive Dye Imaging. Plos Computational Biology, 6(9), e1000919–e1000919. 10.1371/journal.pcbi.1000919 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClelland JL (2013). Integrating probabilistic models of perception and interactive neural networks: A historical and tutorial review. Frontiers in Psychology, 4(August), 1–25. 10.3389/fpsyg.2013.00503 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDowell K, Jeka JJ, Schöner G, & Hatfield BD (2002). Behavioral and electrocortical evidence of an interaction between probability and task metrics in movement preparation. Experimental Brain Research, 144(3), 303–313. 10.1007/s00221-002-1046-4 [DOI] [PubMed] [Google Scholar]
- Norris D (2006). The Bayesian reader: Explaining word recognition as an optimal Bayesian decision process. Psychological Review, 113(2), 321–357. [DOI] [PubMed] [Google Scholar]
- Oaksford M, & Chater N (2001). The probabilistic approach to human reasoning. Trends in Cognitive Sciences, 5(8), 349–357. 10.1016/S1364-6613(00)01699-5 [DOI] [PubMed] [Google Scholar]
- Perone S, & Spencer JP (2012). Autonomy in action: Linking the act of looking to memory formation in infancy in infancy via dynamic neural fields. Cognitive Science, 1–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perone S, & Spencer JP (2013). Autonomous visual exploration creates developmental change in familiarity and novelty seeking behaviors. Frontiers in Psychology, 4(September), 648. 10.3389/fpsyg.2013.00648 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perone Sammy, Simmering VR, & Spencer JP (2011). Stronger neural dynamics capture changes in infants’ visual working memory capacity over development. Developmental Science, 14(6), 1379–1392. 10.1111/j.1467-7687.2011.01083.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perone Sammy, Spencer JP, & Samuelson LK (2020). A dynamic neural field model of the shape bias and its development. Manuscript in Preparation. [Google Scholar]
- Quine WVO (1960). Word and object. MIT PRess. [Google Scholar]
- Rao RPN (2005). Bayesian inference and attentional modulation in the visual cortex. Cognitive Neuroscience and Neuropsychology, 16(16), 1843–1848. [DOI] [PubMed] [Google Scholar]
- Rosch E (1978). Principles of categorization. In Rosch E& Lloyd BB(Eds.), Cognition and Categorization (pp. 27–48). Erlbaum. [Google Scholar]
- Rosch E, & Mervis CB (1975). Family resemblances: Studies in the internal structure of categories. Cognitive Psychology, 7(4), 573–605. 10.1016/0010-0285(75)90024-9 [DOI] [Google Scholar]
- Sakamoto Y, Jones M, & Love BC (2008). Putting the psychology back into psychological models: Mechanistic versus rational approaches. Memory and Cognition, 36(6), 1057–1065. 10.3758/MC.36.6.1057 [DOI] [PubMed] [Google Scholar]
- Samuelson LK, Jenkins GW, & Spencer JP (2015). Grounding Cognitive-level processes in behavior: The view from dynamic systems theory. Topics in Cognitive Science, 7(2). 10.1111/tops.12129 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samuelson LK, Schutte AR, & Horst JS (2009). The dynamic nature of knowledge: insights from a dynamic field model of children’s novel noun generalization. Cognition, 110(3), 322–345. 10.1016/j.cognition.2008.10.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samuelson LK, Smith LB, Perry LK, & Spencer JP (2011). Grounding word learning in space. PLoS ONE, 6(12), e28095. 10.1371/journal.pone.0028095 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samuelson LK, Spencer JP, & Jenkins GW (2013). A Dynamic Neural Field Model of Word Learning. In Theoretical and Computational Models of Word Learning: Trends in Psychology and Artificial Intelligence (pp. 1–27). IGI Global. 10.4018/978-1-4666-2973-8.ch001 [DOI] [Google Scholar]
- Sandamirskaya Y, Zibner SKUU, Schneegans S, & Schöner G (2013). Using Dynamic Field Theory to extend the embodiment stance toward higher cognition. New Ideas in Psychology, 31(3), 322–339. 10.1016/j.newideapsych.2013.01.002 [DOI] [Google Scholar]
- Schneegans S, Spencer JP, & Schoner G (2016). Integrating “ what” and “ where ”: Visual working memory for objects in a scene. In Dynamic Thinking-A Primer on Dynamic Field Theory. (pp. 197–226). Oxford University Press. [Google Scholar]
- Schöner G (2009). Development as Change of System Dynamics: Stability, Instability, and Emergence. Toward a New Grand Theory of Development? Connectionism and Dynamic Systems Theory Reconsidered, 25–49. 10.10.1093/acprof:oso/9780195300598.003.0002 [DOI] [Google Scholar]
- Schutte AR, & Spencer JP (2009). Tests of the dynamic field theory and the spatial precision hypothesis: capturing a qualitative developmental transition in spatial working memory. Journal of Experimental Psychology: Human Perception & Performance, 35(6), 1698–1725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schutte AR, & Spencer JP (2010). Filling the Gap on Developmental Change : Tests of a Dynamic Field Theory of Spatial Cognition. Journal of Cognition and Development, 11(3), 328–355. [Google Scholar]
- Simmering VR, & Spencer JP (2008). Generality with specificity: The dynamic field theory generalizes across tasks and time scales. Developmental Science, 11(4), 541–555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simmering Vanessa R. (2012). The development of visual working memory capacity during early childhood. Journal of Experimental Child Psychology, 111(4), 695–707. 10.1016/j.jecp.2011.10.007 [DOI] [PubMed] [Google Scholar]
- Spencer JP, Blumberg MS, Mcmurray B, Robinson SR, Samuelson LK, & Tomblin JB (2009). Short arms and talking eggs: Why we should no longer abide the nativiste-mpiricist debate. Child Development Perspectives, 3(2). 10.1111/j.1750-8606.2009.00081.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer JP, Barich K, Goldberg J, & Perone S (2012). Behavioral dynamics and neural grounding of a dynamic field theory of multi-object tracking. Journal of Integrative Neuroscience, 11(3), 339–362. 10.1142/S0219635212500227 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer JP, Perone S, & Johnson JS (2009). The Dynamic Field Theory and Embodied Cognitive Dynamics. In Spencer John P, Thomas MS, & McClelland JL(Eds.), Toward a Unified Theory of Development: Connectionism and Dynamic Systems Theory Re-Considered (pp. 86–118). Oxford University Press. [Google Scholar]
- Spencer John. Perone S, Smith LB, & Samuelson LK (2011). Learning words in space and time: Probing the mechanisms behind the suspicious-coincidence effect. Psychological Science, 22(8), 1049–1057. 10.1177/0956797611413934 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer John P, Austin A, & Schutte AR (2012). Contributions of dynamic systems theory to cognitive development. Cognitive Development, 27(4), 401–418. 10.1016/j.cogdev.2012.07.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinhage A, & Schöner G (1997). Self-calibration based on invariant view recognition: Dynamic approach to navigation. Robotics and Autonomous Systems, 20, 133–156. [Google Scholar]
- Thelen E, & Smith LB (1994). A dynamic systems approach to the development of cognition and action. The MIT Press. [Google Scholar]
- Tversky A (1977). Features of similarity. Psychological Review, 84(4), 327–352. 10.1037//0033-295x.84.4.327 [DOI] [Google Scholar]
- Valderrama-Bahamóndez GI, & Fröhlich H (2019). MCMC Techniques for Parameter Estimation of ODE Based Models in Systems Biology. Frontiers in Applied Mathematics and Statistics, 5(November), 1–10. 10.3389/fams.2019.00055 [DOI] [Google Scholar]
- Wittgenstein L (1967). Philosophical Investigations. Basil Blackwell. [Google Scholar]
- Xu F, & Tenenbaum JB (2007a). Sensitivity to sampling in Bayesian word learning. Developmental Science, 10(3), 288–297. 10.1111/j.1467-7687.2007.00590.x [DOI] [PubMed] [Google Scholar]
- Xu F, & Tenenbaum JB (2007b). Word learning as Bayesian inference. Psychological Review, 114(2), 245–272. 10.1037/0033-295X.114.2.245 [DOI] [PubMed] [Google Scholar]
- Yu AJ, & Cohen JD (2009). Sequential effects: Superstition or rational behavior? Advances in Neural Information Processing Systems 21 - Proceedings of the 2008 Conference, 1873–1880. [PMC free article] [PubMed] [Google Scholar]
- Yu C, & Smith LB (2012). Embodied attention and word learning by toddlers. Cognition, 125(2), 244–262. 10.1016/j.cognition.2012.06.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuille A, & Kersten D (2006). Vision as Bayesian inference: analysis by synthesis? Trends in Cognitive Sciences, 10(7), 301–308. 10.1016/j.tics.2006.05.002 [DOI] [PubMed] [Google Scholar]