Abstract
Purpose:
Single photon emission computed tomography (SPECT) scanners using cadmium zinc telluride (CZT) offer compact, lightweight, and improved imaging capability over conventional NaI(Tl)-based SPECT scanners. The main purpose in this study is to propose a full-ring SPECT system design with eight large-area CZT detectors that can be used for a broad spectrum of SPECT radiopharmaceuticals and demonstrate the performance of our system in comparison to the reference conventional NaI(Tl)-based two-head Anger cameras.
Methods:
A newly-designed full-ring SPECT system is composed of 8 large-area CZT cameras (128 mm × 179.2 mm effective area) that can be independently swiveled around their own axes of rotation independently and can have radial motion for varying aperture sizes that can be adapted to different sizes of imaging volume. Extended projection data were generated by conjoining projections of two adjacent detectors to overcome the limited field-of-view (FOV) by each CZT camera. Using Monte Carlo simulations, we evaluated this new system design with digital phantoms including a Derenzo hot-rod phantom and a Zubal brain phantom. Comparison of performance metrics such as spatial resolution, sensitivity, contrast-to-noise ratio (CNR), and contrast-recovery ratio was made between our design and conventional SPECT scanners having different pixel sizes and radii of rotation (one clinically well-known type and two arbitrary types matched to our proposed CZT-SPECT geometries).
Results:
The proposed scanner could result in up to about 3 times faster in acquisition time over conventional scan time at same acquisition time per step. The spatial resolution improvement, or deterioration, of our proposed scanner compared to the clinical type scanner was dependent upon the location of the point source. However, there was overall performance improvements over the three different setups of the conventional scanner particularly in volume sensitivity (approximately up to 1.7 times). Overall, we successfully reconstructed the phantom image for both 99mTc-based perfusion and 123I-based dopamine transporter (DaT) brain studies simulated for our new design. In particular, the striatal/background contrast-recovery ratio in 3-to-1 reference ratio was over the 0.8 for the 123I-based DaT study.
Conclusions:
We proposed a variable-aperture full-ring SPECT system using combined pixelated CZT and energy-optimized parallel-hole collimator modules and evaluated the performance of this scanner using relevant digital phantoms and MC simulations. Our studies demonstrated the potential of our new full-ring CZT-SPECT design, showing reduced acquisition time and improved sensitivity with acceptable CNR and spatial resolution.
Keywords: SPECT, CZT detector, Full ring, Brain SPECT, Monte Carlo simulation
1. INTRODUCTION
Single photon emission computed tomography (SPECT) is one of the most important biomedical imaging modalities, used for the management of many human diseases.1–3 The SPECT scanner is typically performed by rotating dual-head (or triple-head) gamma cameras that were originally introduced by Hal Anger in 1958,4 around an imaging object for 180 or 360 degrees. The gamma cameras consist of a radionuclide collimator to reject off-directional and scattered photons, scintillation crystals such as NaI (Tl), and a set of photodetectors like photomultiplier tubes (PMTs).5 Due to the physical and mechanical characteristics, the conventional SPECT scanner has relatively poor spatial resolution and low photon-detection sensitivity.
In recent years, SPECT scanners using solid-state direct-conversion detectors, particularly cadmium zinc telluride (CZT), have been introduced. CZT-SPECT offers improved quantitative imaging capability over conventional NaI (Tl)-based SPECT scanners by offering improved energy resolution.6,7 Based on the promising CZT performance, the use of parallel-slit collimator and small pixels for high spatial resolution applications or the use of large collimator hole matched with four pixels for high sensitivity applications were previously proposed.8,9 Furthermore, in order to overcome the trade-off between the sensitivity and spatial resolution, a stack-up method of two large-hole parallel-hole collimators for preclinical study,10 or virtual sub-pixels using 3D positioning algorithm11 were proposed.
Instead of these previous methods of manipulating collimator geometries, we proposed a more straightforward pixel-matching collimator design that takes advantage of placing collimator septa directly on inactive areas of detector pixels (i.e., spacings between adjacent pixels). This design with a careful choice of collimator material (i.e., tungsten alloy) and septal thickness allows an energy-optimized collimator geometry when coupled with CZT detectors, implying the potential of using a single collimator for a broad energy range of SPECT radionuclides (up to 250 keV).12
The lightweight, one of the important characteristics of the CZT detectors, enables easy mechanical motion, and nonstandard SPECT geometry is readily possible so that it could reduce the scan time or improve the sensitivity. For example, a recently introduced CZT-based SPECT system, D-SPECT (Spectrum Dynamics) heavily relies on swiveling (i.e., multi-step acquisitions) small rectangular pixelated CZT detector modules and high aspect-ratio parallel-hole collimators13 for cardiac applications, providing high sensitivity. The D-SPECT system was also studied for quantitative assessment of centrally located brain regions14 to take advantage of its high sensitivity for other applications than the heart and the similar technology was extended for general purpose applications.15,16
In this study, on top of the previously developed energy-optimized collimator design, we further evaluated a full-ring SPECT system design with eight large-area CZT detectors that can be used for a broad spectrum of single-photon emitting radiopharmaceuticals. Our design feature includes a variable-aperture full-ring geometry to overcome the limited field of view and independently swiveling detectors to minimize the interference between each detector. In order to evaluate the imaging performance of our proposed CZT-SPECT system, we employed analytical digital phantoms and realistic digital brain phantoms for conventional NaI(Tl)-SPECT systems with comparable pixel sizes and radii of rotation.
2. METHODS
2.1. Proposed scanner geometry and image acquisition design
The proposed CZT-SPECT scanner technology uses eight large-area detector heads coupled with energy-optimized tungsten-alloy collimators arranged in a full-ring configuration for general-purpose studies, including brain SPECT. Adjacent detector heads need small gaps between them to rotate around the common axes of rotation (i.e., swivel) individually without interference. Each detector head consists of 80 × 112 individual CZT pixels (1.6 mm × 1.6 mm × 5 mm) paired with the energy-optimized tungsten-alloy parallel hole collimator previously designed by our group,12 resulting in a total detector surface of 128 mm × 179.2 mm. Each square collimator hole matches each pixel of the CZT detector pixel. There are two image acquisition types we simulated for our proposed system, Angular Step 3° (AS-3) and Angular Step 5° (AS-5). Each detector head in AS-3 and AS-5 is swiveled around the center of the head from −42° to 42° or from −42.5° to 42.5° with 29 steps or 18 steps, respectively (Figure 1). However, there is no rotation of all detectors around the common axis of rotation. In order to overcome the limited field-of-view (FOV) of an individual detector head, an extended projection by conjoining projections of two adjacent detectors was generated so that the number of angular projections of AS-3 and AS-5 are 120 and 72, respectively. After all, AS-3 has a similar number of projections as a typical number of projections for a brain SPECT study and AS-5 has a reduced number of projections in order to compare with a typical one. The details are described in the next section.
Figure 1.

Example diagrams for Angular Step 3° (AS-3, top) and Angular Step 5° (AS-5, bottom) image acquisition mode for our proposed SPECT scanner. Each detector head is swiveled from −42° to 42° for AS-3 or −42.5° to 42.5° for AS-5 within the rotation angular range. Each detector head has a collimator (blue) and a detector (black).
In order to compare imaging performances between our proposed full-ring CZT-SPECT and one of the conventional two-headed SPECT systems, we simulated three different NaI (Tl)-based SPECT systems from a GE Infinia Hawkeye 4 SPECT/CT system. The Clinical_3.18 scanner was modeled to have a 3.18 mm × 3.18 mm bin size using a zoom of 1.38 with 150 mm radius of rotation17–19 and Arb_1.6RR150 and Arb_1.6RR185 scanners were modeled to have the 1.6 mm × 1.6 mm bin size same as that of our proposed scanner, with 150- (Arb_1.6RR150) or 185- (Arb_1.6RR185) mm radius of rotation in order to match those of the Clincal_3.18 scanner and our proposed scanner, respectively. For our proposed scanner, to avoid interference between adjacent detector heads, the radius of rotation was set at 185 mm larger than 150 mm that is a typical radius of rotation for a conventional 2-headed NaI(Tl)-based SPECT system for brain studies.20 Table 1 summarizes the specifications of our proposed (AS-3 and AS-5) and the conventional NaI(Tl)-based SPECT scanners modeled in our simulations.
Table 1.
Specifications of the proposed (AS-3 and AS-5) and NaI(Tl)-based SPECT scanners simulated in this work
| Parameter | NaI(Tl)-based Conventional | Proposed | |||
|---|---|---|---|---|---|
| Clinical_3.18 | Arb_1.6RR150 | Arb_1.6RR185 | AS-3 | AS-5 | |
| Detector head | 2 | 8 | |||
| Detector type | NaI(Tl)-PMT | CZT | |||
| Detector size (mm3) | 563.2 × 563.2 × 9.5 | 128 × 179.2 × 5.0 | |||
| Pixel (binning) size (mm2) | 3.18 × 3.18 | 1.6 × 1.6 | 1.6 × 1.6 | ||
| Hole Shape | Hexagonal | Rectangular | |||
| Material | Lead | Tungsten-Alloy | |||
| Hole length (mm) | 35 | 23 | |||
| Septal thickness (mm) | 0.2 | 0.32 | |||
| Hole diameter (mm) | 1.5 | 1.28 | |||
| Radius of Rotation (mm) | 150 | 185 | 185 | ||
| Rotation Angle Range | - | −42° ~ 42° | −42.5° ~ 42.5° | ||
| # of Total Angles | 120 | 120 | 72 | ||
| Step Angle | 3° | 3° | 5° | ||
| # of Steps | 60 | 29 | 18 | ||
2.2. Generation of extended projection
As mentioned earlier, we generated an extended projection by conjoining projections of two adjacent detector heads to extend the limited transaxial view. However, this method creates a gap between conjoined projections and different radial positions between two detector heads (Figure 2a). The center of all extended projections is also shifted corresponding to a specific swiveled angle of the projection. In order to solve these problems, we calculated the gap between two detector heads and shifted the center position of the extended projection using the geometrical information. The shifted center position was simply calculated as
| (1) |
where r is the distance from the origin to center of the detector head and θstep is the rotation step angle of the detector head. In Figure 2a, the shifted center position for the extended projection between Detector Head (DH) #0 and DH#1 is moved from DH#0 to DH#1 according to the above equation. The gap between two detector heads was calculated by subtracting the fixed width between two detector heads and from the end-to-end length of the DHs as
| (2) |
| (3) |
| (4) |
where d is the length between two DHs (#0 and #1) at a specific angle and a, b, and c are coefficients for the line equation. The coefficients, a, b, and c, were calculated as
| (5) |
| (6) |
| (7) |
where the parameters in the above equations were described in Figure 2a.
Figure 2.

Example diagrams for the gap and shifted center corrections (a) and truncated edge (b). The gap correction and edge correction were needed when an extended projection was generated by combining projections of DH #1 at 23rd step and DH #0 at 8th step, and projections of DH #1 at 29th step and DH #0 at 14th step, respectively. These examples are based on the AS-3 scanning geometry.
Some extended projections also suffer truncation, as an extended projection that combines projections of DH #0 at the 14th step and DH #1 at the 29th step in Figure 2b. To generate a corrected extended projection, we calculated the gap and edge values using a linear interpolation method. Finally, in order to correct the overlapping projections and different transaxial positions of independently swiveling detectors, we normalized each extended projection using the uniform phantom (a cylinder with a radius of 110 mm and an axial length of 120 mm) data simulated for a typical two head SPECT system having the same detector specification and the radius of rotation.
2.3. Monte Carlo simulation model
The proposed and conventional scanners were modeled by Geant4 Application for Tomographic Emission (GATE), a Monte Carlo (MC) simulation framework.21 A standard physics process model was used, which includes physical processes of photoelectric effect, Compton scattering, Rayleigh scattering, bremsstrahlung, and ionization. Each projection was simulated assuming an 8.5% energy resolution with ±8.5% energy window for the CZT-SPECT scanner22 or a 10% energy resolution with ±10% energy window for the conventional NaI (Tl)-SPECT scanners at Tc-99m or I-123. We modeled that each detector head consisted of seven rows and five columns pixelated CZT crystal (density = 5.78 g/cm3) of 25.6 mm in width and length and 5 mm thickness. Each crystal was divided into 16 by 16 pixels with a pitch of 1.6 mm. For CZT crystal modeling, neither charge sharing, nor electronic noise was introduced; However, we decreased the photopeak counts acquired from the CZT simulation to 65% of that of the NaI detector incorporating the reduction in sensitivity due to the low-energy tailing effect.23,24 For the NaI(Tl)-SPECT scanner model, a back compartment (Glass, density: 2.5 g/cm3) was simplified to represent photomultipliers and associated electronics, and overall intrinsic spatial blurring of 2.5 mm FWHM was implemented corresponding to effects of crystal and the back compartment. This simplified model was previously validated with medium-energy isotopes (under 300 keV).25–27 We set the CZT and NaI(Tl) detectors as a sensitive detector in the GATE simulation and then each SD detector was used to store energy deposition, positions of interaction, origin of the particle and types of interaction regarding interactions taking place inside the detector. And the SD detectors were able to track and store all information inside the detectors and convert the signals without any dead time for the detectors. Lead shielding on all four sides of each detector head for both scanner configurations was added to the detector model to avoid unexpected scatter events coming from the side. All simulation jobs ran in parallel with GATE (version 8.2) in three high performance computing clusters, having Xeon (Intel) series CPUs. The output format from the simulation was configured to be projection data for each angle which were then used for iterative image reconstruction. The details for phantoms and activities are described in section 2.5 below.
2.4. Iterative image reconstruction
The extended projections acquired in our proposed scanner using the two acquisition types (AS-3 and AS-5) were in a 160 × 112 matrix with a 1.6 mm × 1.6 mm pixel size; while the acquired projections were in a 128 × 128 matrix size with a 3.18 mm × 3.18 mm pixel size for the Clincal_3.18 scanner, and in a 350 × 350 matrix size with a 1.6 mm × 1.6 mm pixel size for both Arb_1.6RR150 and Arb_1.6RR180 scanners. The Software for Tomographic Image Reconstruction (STIR) package,28 with an open source objected-oriented library implemented in C++, for a maximum-likelihood expectation maximization (MLEM) reconstruction algorithm was used to reconstruct the simulated projection data. The version 4.0.1 of STIR allows modeling 3D SPECT along with both attenuation and Collimator and Detector Response (CDR) corrections,29 and both corrections were applied in our image reconstructions. To obtain CDR function of the proposed SPECT scanner and conventional SPECT scanner, we used previously simulated spatial resolution data as a function of distance from a point source to collimator12 and we simulated it previously to our study using the GATE tool, respectively. The CDR of the proposed scanner at other distances was linearly interpolated. The distance dependent resolutions were described as
| (8) |
where σ is the standard deviation of the Gaussian-modeled CDR, d is the source-to-collimator distance (mm), b is the intercept (mm), and a is the slope (mm/mm). The standard deviation is its full width at half maximum (FWHM) divided by 2.355. We applied the collimator-detector response (CDR) function with a slope of 0.028 and an intercept of 0.7821 (R2=0.9880) and a slope of 0.018 and an intercept of 1.2877 (R2=0.9836), for the proposed scanner and the modeled conventional scanners, respectively. Attenuation correction was applied to all reconstructed images; however, CDR correction was only applied to reconstructed images of brain SPECT examples. The penetration, scatter, and partial volume corrections were not incorporated. The matrix and the pixel size of the reconstructed images were 160 × 160 × 112 with 1.6 mm × 1.6 mm × 1.6 mm for the proposed scanner, 128 × 128 × 128 with 3.18 mm × 3.18 mm × 3.18 mm for the Clinical_3.18 scanner, and 350 × 350 × 350 with 1.6 mm × 1.6 mm × 1.6 mm for both the Arb_1.6RR150 and Arb_1.6RR185 scanners. We set each number of iterations for the reconstructions based on the contrast-to-noise ratio (CNR) or the contrast recovery ratio.
2.5. Performance evaluations using digital phantoms
At first, we simulated all projection data in acquisition times shown in Table 2. In comparison to the conventional acquisition time for all phantom studies, the acquisition times for our proposed scanner were reduced by about 52% and 70% for two types of acquisition modes when the acquisition time per step is kept the same. The acquisition time of the brain perfusion study was the same as that of the hot-rod phantom study; however, the acquisition time of the DaT imaging was increased to meet the minimum total counts in the practice guideline of DaT SPECT imaging.30 All acquisitions were based on a step and shoot mode, and the transition time between steps was not considered.
Table 2.
Comparison of acquisition times between the NaI(Tl)-based conventional scanners and two types of acquisition modes for the proposed CZT-SPECT scanner for brain perfusion and dopamine receptor imaging studies (s = seconds).
| Phantom Study | NaI(Tl)-based Conventional Scanners (60 steps) | AS-3 (29 steps) | AS-5 (18 steps) | |||
|---|---|---|---|---|---|---|
| per step | total | per step | total | per step | total | |
| Line, Cylindrical and Hot-rod phantoms | 10 s | 600 s | 10 s | 290 s | 10 s | 180 s |
| Brain Perfusion phantom | 10 s | 600 s | 10 s | 290 s | 10 s | 180 s |
| Brain DaT phantom | 15 s | 900 s | 15 s | 435 s | 25 s | 450 s |
For tomographic spatial resolution, two line-sources (1 mm diameter and 10 cm length) were located in the FOV; one at the center of the FOV and the other one placed 100 mm away from the center. The projection data were reconstructed using the filtered back-projection algorithm implemented in STIR without attenuation correction. A uniform cylindrical water phantom (200 mm in diameter × 200 mm) was simulated for the tomographic volume sensitivity assessment. The volume sensitivity was calculated as follows:
| (9) |
where C is the deposited total counts in all projections, t the acquisition time, A the decay corrected activity, and L the axial length of the cylindrical phantom.31,32 All of these sources had an activity of 37 MBq of Tc-99m.
Then, the proposed scanner was compared with the conventional SPECT scanners using a Derenzo hot-rod phantom in terms of CNR and profile amplitudes. Tc-99m aqueous solution-filled phantom was generated in a cylinder with 216 mm diameter and 150 mm height and was modeled based on the geometry of the Flanged Deluxe Jaszczak ECT Phantom,33 as shown in Figure 3a. The hot-rod Derenzo phantom consisted of acrylic (attenuation coefficient: 0.147 cm−1 at 140 keV) and six sectors of hot rods with different diameters, 12.7, 11.1, 9.5, 7.9, 6.4, and 4.8 mm with 88-mm height for hot rods. The activity concentration of the Tc-99m in the six sectors of hot rods was 300 Bq/mm3 (total activity: ~170 MBq) and the background activity in the center of the phantom was zero.
Figure 3.

Derenzo hot-rod phantom (a) has acryl material for the background. The yellow dashed line in the hot-rod region indicates the location of profiles of the hot-rods and the yellow dashed circle and blue circle indicates the ROI and background for CNR, respectively. Original Zubal phantom (b) and activity maps for brain perfusion imaging with Tc-99m (c) and DaT imaging with I-123 (d) and attenuation map (e) for both brain phantom studies. The yellow circles indicate the grey matter and striatal ROIs and the blue circles indicate the background.
To evaluate the CNR in reconstructed images of the hot-rods as a figure of merit, we calculated the average value of the regions of interest (ROI) of two rods with 12.7- and 9.5-mm diameter and obtained the profiles through the rods (yellow dashed circle) and background (blue circle) as shown in Figure 3a. The CNR is defined as
| (10) |
where MROI is the average value in each of the ROI, MBG is the average value in the background ROI and sigma values are the standard deviation of each ROI.
Finally, we validated our proposed scanning geometries (AS-3 and AS-5) using the computational brain model in terms of amplitudes of line profiles, CNR, and contrast-recovery ratio compared to the conventional scanners. The brain anatomy model was simplified from the real human data proposed by Zubal.34 (Figure 3b). The simplified Zubal phantom has 10 materials consisting of air, blood, skull, grey matter, white matter, caudate, putamen, cartilage, muscle, and adipose tissue. The matrix and voxel size of the Zubal phantom were also modified from 256 × 256 × 128 matrix, 1.1 mm × 1.1 mm × 1.4 mm to 200 × 260 × 168 matrix, 0.8 mm × 0.8 mm × 0.8 mm. We modeled two kinds of brain SPECT studies: perfusion imaging with 99mTc-exametazime and dopamine transporter (DaT) imaging with 123I-ioflupane. In order to create a range of realistic Tc-99m and I-123 uptake ratios, total activity was defined around 10% of the recommended dosage of radiopharmaceutical for each brain study, ~ 112 MBq and ~18.5 MBq, respectively.30,35 For the brain perfusion study, grey matter, white matter, soft tissues, and others that are bone or air were defined and the uptake ratios were 100, 25, 4, and 0, respectively (Figure 3c).36 On the other hand, the striatal volume that contains caudate and putamen, and others as a background that is neither bone nor brain were defined, and different intensities of I-123 solution with different striatal-to-background uptake ratios, ranging from 3:1 to 10:1 were set for the DaT imaging (Figure 3d). Each nonuniform attenuation map was obtained by setting the attenuation coefficients to 0.143 cm−1 for brain tissues and 0.304 cm−1 for bone when Tc-99m was simulated and 0.138 cm−1 for brain tissues and 0.289 cm−1 for bone when I-123 was considered (Figure 3e).37
We obtained the profiles of brain perfusion images and calculated the average value of six grey matter Regions of Interest (ROIs) and two white matter ROIs for CNR evaluation. Average values in caudate and putamen ROIs and background ROI were calculated from DaT images with different uptake ratios for contrast-recovery ratio evaluation. The values of contrast-recovery ratio were calculated as follows:
| (11) |
where MSTRLATAL is the Measured average value in the caudate or putamen region and MBG is the Measured average value in the background ROI and RSTRLATAL is the Reference activity value in the caudate or putamen region and RBG is the Reference activity value in the background ROI. All ROIs for brain phantom studies were defined by anatomical information based on the segmented Zubal model.
The CNR and contrast-recovery ratio in the reconstructed images of the sphere and brain phantoms were calculated as a function of iteration number in order to define the stopping iteration number.
3. RESULTS
3.1. Spatial resolution and sensitivity
Table 3 includes the planar spatial resolution and sensitivity results calculated in our previous report for the energy-optimized collimator12 and other studies.38 Compared to the planar spatial resolution and sensitivity at 10 cm, the proposed scanner had comparable sensitivity but better planar spatial resolution. For the tomographic spatial resolution, compared to the conventional NaI(Tl) scanner with a zoom of 1.0 and 4.4 mm pixel size,38 our proposed systems had relatively similar resolution (approximately 1.0 mm FWHM difference) when the line source was positioned at the center of the FOV and even the radius of rotation was larger. At the center of FOV, however, the tomographic spatial resolution for our proposed scanner was poorer compared to those of the Clinical_3.18, Arb_1.6RR150, and Arb_1.6RR185 scanners that were modeled in our simulation. On the other hand, the tomographic spatial resolution for our proposed system was greatly improved when the source was moved to a peripheral position so that it had similar or better resolution to those of the three NaI(Tl)-based scanners we modeled (Clinical_3.18, Arb_1.6RR150, and Arb_1.6RR185). Moreover, the tomographic volume sensitivities of our proposed scanning geometries (AS-3 and AS-5) are much higher than those of the three conventional scanners modeled (approximately up to 1.7 times).
Table 3.
Spatial resolution and sensitivity values for the NaI(Tl)-based conventional scanners with three different configurations (Clinical_3.18, Arb_1.6RR150, and Arb_1.6RR185) and our proposed CZT-based scanner with two different geometries (AS-3 and AS-5) in this simulation study.
| NaI(Tl)-based Conventional | Proposed | |||||
|---|---|---|---|---|---|---|
| Clincal_3.18 | Arb_1.6RR150 | Arb_1.6RR185 | AS-3 | AS-5 | ||
| Spatial resolution | Planar @10 cm (mm FWHM) | 7.4* | 6.91** | |||
| Tomographic @ 0 cm from center of FOV (mm FWHM) | 8.74 (≤9.9*) | 8.08 | 8.73 | 11.10 | 11.55 | |
| Tomographic @ 10 cm from radial of FOV (mm FWHM) | 8.65 (≤9.9*) | 7.10 | 7.72 | 7.53 | 7.68 | |
| Tomographic @ 10 cm from tangential of FOV (mm FWHM) | 7.36 (≤7.5*) | 5.58 | 6.16 | 4.85 | 4.69 | |
| Sensitivity | Planar @10 cm (cpm/mCi) | 202* | 261** | |||
| Tomographic Volume (kcps/(MBq/ml)/cm) | 29.87 | 29.79 | 23.59 | 38.82 | 37.96 | |
3.2. Hot-rod phantom study
Figure 4 shows that the reconstructed images from the Derenzo hot-rod phantom for three different configurations of the conventional scanner and the two scan geometries of the proposed scanner. Although some rods of the Derenzo phantom were outside of the FOV of several detectors of our proposed scan geometries, there were no truncation artifacts in the reconstructed images. The peripheral rods of the smallest-rod segment (4.8 mm in diameter) in AS-3 and AS-5 scan geometries were better resolved than those in the images from the Clinical_3.18 scanner, and they are similarly resolved by the Arb_1.6RR150 and the Arb_1.6RR185 scanners. These results correspond to the line profiles of the Derenzo phantom as shown in Figure 5 and the tomographic spatial resolution results in Table 3. The peak values of the rods for the proposed scanners (AS-3 and AS-5) and two scanners having arbitrary 1.6 mm pixels (Arb_1.6RR150 and Arb_1.6RR185) were decreased slightly toward the center. Even the peak-to-valley ratios were higher for the peripheral rods in AS-3 and AS-5 scan geometries, while the image for the Clinical_3.18 scanner did not show this behavior.
Figure 4.

Reconstructed images of the Derenzo hot-rod phantom from three different setups for conventional scanners (Clinical_3.18, Arb_1.6RR150 and Arb_1.6RR185) and our proposed system with two acquisition modes (AS-3 and AS-5). All images were reconstructed with 50 iterations and with a post-processed 3D Gaussian filter with sigma equal to 1 pixel. The phantom images were summed axially (28 slices for the Clinical_3.18 configuration and 55 slices for the others).
Figure 5.

The line profiles of reconstructed images for the Derenzo hot-rod phantom from line profile A (11.1 to 7.9 mm diameter, middle) and line profile B (4.8 mm diameter third row, bottom) as shown in Figure 3a. All values were normalized by the maximum value in the reconstructed images.
CNR values with 50 and 100 iterations were plotted for two different rods of the reconstructions of the Derenzo phantom obtained from the three conventional scanner configurations and our proposed scanner with AS-3 and AS-5 acquisition modes (Figure 6). The CNR values of the 12.7-mm diameter and 9.5-mm rods in the Derenzo phantom for our proposed scanner were slightly improved than those of the conventional scanner; however, the difference of CNR values was below 1. It was determined that, based on the data shown in Figure 6, reconstructions with 50 iterations are sufficient for image reconstruction since the improvement after 50 iterations was almost negligible.
Figure 6.

CNRs for two different rods of the Derenzo hot-rod phantom corresponding to 50 and 100 iterations.
3.4. Brain phantom studies
Figures 7 and 8 show reconstructed images with CDR correction, line profiles, and CNRs for a brain perfusion study with Tc-99m obtained by two acquisition types of our proposed scanner and the three types of the conventional scanner. In comparison to three configurations of the conventional scanner (Clinical_3.18, Arb_1.6RR150, and Arb_1.6RR185), our proposed scanner in both acquisition modes (AS-3 and AS-5) has a similar contrast between gray matter and white matter, and also has a similar spatial resolution. The line profile and CNR as a function of the number of iterations show the performance similarity. The CNR of the Clinical_3.18 scanner was slightly lower than those of the others; however, the difference of the CNR was also below 1. The images for both acquisition modes show no artifacts and reasonable image quality in the peripheral part of the brain images and there was no notable difference in line profiles and CNRs between the two acquisition modes. In the central part of each image for the AS-3 and AS-5 acquisition modes, the structures of the striatum and the thalamus were not much distorted so that putamen and the caudate could be distinguishable. It was determined that, based on the CNR data as a function of the number of iterations in Figure 8, reconstructions with 100 iterations were sufficient since the improvement after 100 iterations was almost negligible.
Figure 7.

The 3D activity map (left) and the 3D reconstructed images for the brain perfusion study using the three configurations of the conventional scanner and our proposed scanner in AS-3 and AS-5 acquisition modes with 100 iterations and post-processed using a 3D Gaussian filter with a sigma of 1 pixel.
Figure 8.

Left: Brain perfusion image from AS-3 with ground-truth activity map (yellow for location of the line profiles). Center: line profiles for the reference activity phantom (orange, dotted line) compared to the reconstructed brain perfusion images for the Clincal_3.18 (green, dash line), Arb_1.6RR150 (gray, dash line), Arb_1.6RR185 (black, dash line), AS-3 (blue line) and AS-5 (red line) configurations. Right: CNRs as a function of the number of iterations.
Figure 9 shows the reconstructed images with CDR correction for I-123 DaT imaging. Images in the first to third columns are from the three configurations of the conventional scanner while the fourth and fifth columns are from the AS-3 and AS-5 acquisition modes of our proposed scanner, respectively. Images in each row correspond to different simulated reference striatal/background ratios ranging from 3:1 to 10:1. As expected in all evaluated scanners, the putamen and the caudate were more clearly separated and the striatal shape was more characterized by two symmetric comma- or crescent-shaped focal regions when the simulated striatal/background ratio was higher. A quantitative and detailed assessment of contrast recovery for uptake ratios from the two proposed acquisition modes of our proposed scanner is shown in Table 4.
Figure 9.

Reconstructed images with 150 iterations and CDR correction for I-123 brain DaT imaging from the three configurations of the conventional scanner and our proposed scanner in AS-3 and AS-5 acquisition modes as a function of striatal-to-background activity ratio. All images in each row were normalized by the maximum value in the images for 10 to 1 striatal/background ratio and postprocessed using a 3D Gaussian filter with a sigma of 1 pixel.
Table 4.
Contrast recovery values obtained from the three configurations of the conventional scanner and our proposed scanner in AS-3 and AS-5 acquisition modes for striatal to background uptake ratios of 3:1, 5:1, 8:1 and 10:1.
| Organ | Type | Activity Ratio | |||
|---|---|---|---|---|---|
| 3 to 1 | 5 to 1 | 8 to 1 | 10 to 1 | ||
| Caudate | Clinical_3.18 | 0.75±0.08 | 0.73±0.02 | 0.68±0.05 | 0.63±0.01 |
| Arb_1.6RR150 | 0.82±0.03 | 0.72±0.01 | 0.72±0.04 | 0.70±0.03 | |
| Arb_1.6RR185 | 0.81±0.02 | 0.72±0.04 | 0.73±0.09 | 0.65±0.05 | |
| AS-3 | 0.80±0.04 | 0.74±0.01 | 0.70±0.02 | 0.65±0.02 | |
| AS-5 | 0.82±0.09 | 0.75±0.04 | 0.72±0.03 | 0.69±0.02 | |
| Putamen | Clinical_3.18 | 0.77±0.03 | 0.77±0.02 | 0.69±0.00 | 0.67±0.01 |
| Arb_1.6RR150 | 0.82±0.08 | 0.75±0.03 | 0.73±0.01 | 0.71±0.02 | |
| Arb_1.6RR185 | 0.81±0.03 | 0.77±0.04 | 0.72±0.06 | 0.70±0.05 | |
| AS-3 | 0.81±0.10 | 0.74±0.01 | 0.70±0.05 | 0.72±0.02 | |
| AS-5 | 0.83±0.03 | 0.76±0.05 | 0.71 ±0.04 | 0.69±0.02 | |
Figures 10 shows a brain DaT image from AS-3 superimposed on the ground-truth activity map, line profiles and contrast recovery ratios from the brain image for 10 to 1 uptake ratio. The structures of the striatum and the thalamus were also only somewhat distorted so that putamen and the caudate could be distinguishable in the central part of each image. The line profiles for our proposed scanner in the two acquisition modes were very similar to those of the Clinical_3.18 and Arb_1.6RR185 scanner. The Arb_1.6RR150 scanner showed the best line profile in terms of the peak-to-valley ratio even when the peak values of the scanner were lower than the others. To assess the improvement in reconstruction from a quantitative point of view, contrast recovery was estimated as a function of the number of iterations for the putamen and the caudate. The figure displays the results of the striatal to background uptake ratio of 10:1. The plots correspond to the mean values after averaging right and left ROI values as shown in Figure 2d. These results were similar to the other previous study.37
Figure 10.
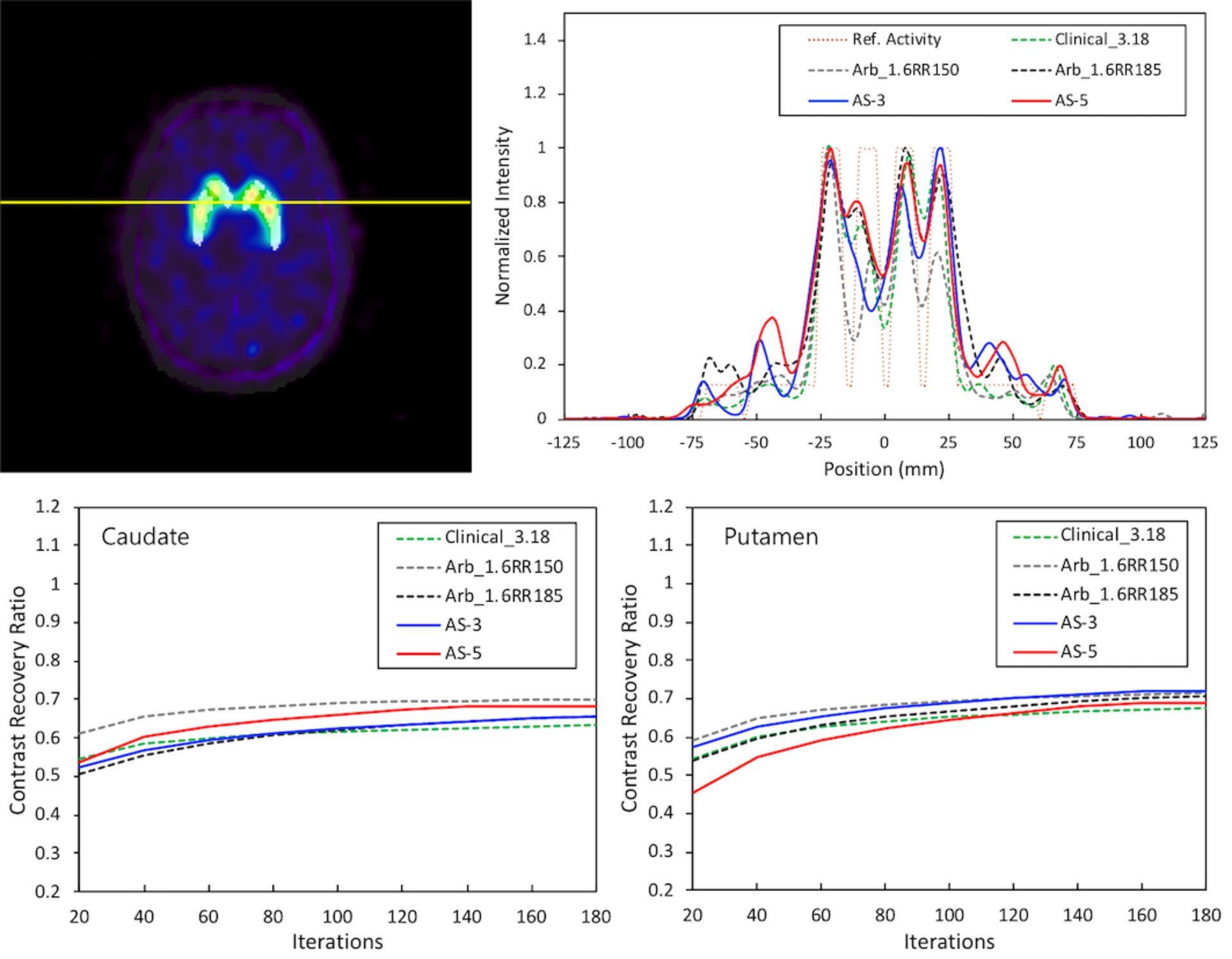
Upper Left: Brain DaT image from AS-3 with the ground-truth activity map (yellow for the location of the line profiles). Upper Right: Line profiles of the reconstructed brain DaT images compared to the reference activity (orange, dotted line). Caudate (lower left) and putamen (lower right) contrast recovery as a function of the number of iterations for the striatal to background uptake ratio of 10:1. The plots correspond to contrast recovery values when reconstruction was performed based on the attenuation correction with CDR correction.
4. DISCUSSION
In this study, our proposed full-ring SPECT scanner using pixelated CZT and energy-optimized parallel-hole collimator with two acquisition modes were evaluated using analytical digital phantoms including Derenzo hot rod phantom as well as simulated digital brain phantoms replicating perfusion and dopamine transporter imaging. In our nonstandard system geometry, eight large-area CZT detectors were enough to cover the brain fully, and they can acquire extended projections using independent swivel movements without a need to rotate the entire gantry. Because of the simple and efficient scanning geometry, our proposed scanner can decrease the acquisition time as much as 2–3 times as shown in this report, particularly using the AS-5 acquisition mode as described above, compared to the acquisition time conventionally performed at the same acquisition time per step. The compactness of CZT detector modules allows the simple and efficient implementation of a scanning geometry, which is an advantage over a bulkier construction of a gamma camera using NaI(Tl) crystals with photomultiplier tubes. Furthermore, each square parallel hole matches each pixel of the CZT detector in our design, so that this design gives high detection efficiency and sensitivity because the dead space from collimator septa that are placed over the gaps between pixels is minimized. The values of the septa thickness, length, and diameter were chosen considering scatter/penetration ratios, resolution and sensitivity over a broad range of gamma emission energies. Therefore, the efficient scanning geometry was able to make the swiveled detectors be close to the object, compared to the standard geometry, and the proposed parallel-hole collimator was also well adapted to the pixelated CZT detector module, showing volume sensitivity improvements in this study.
However, our proposed scanning geometries had wide swiveling angle ranges to compare with a typical SPECT brain study acquisition having 120 projections and 3-angular steps as mentioned earlier. Those wide rotation angles could have limited object sizes within the FOV in order to avoid interferences with the rotation of detectors, especially at the edge of the detector. Each detector with the first or last angular step was overly rotated compared to the object size, and each detector’s view was half blocked by its adjacent detector as shown Fig. 2.b. Our proposed scanning geometries also had a fixed radius of rotation in order to avoid the interference between adjacent detectors, so that they had about 2 mm FWHM difference in tomographic spatial resolution in the center of the FOV compared to the resolution using a zoom of 1.38 with a conventional scanner geometry. The difference showed suboptimal resolution in the center of the hot-rod phantom image, especially in the sector of the smallest rods in Figure 4. The large differences between resolutions in the radial and tangential directions caused by a smaller diameter but shorter hole length of the proposed collimator also showed that each rod of the phantom was slightly distorted. This asymmetric resolution could potentially underestimate the volume at the edge in the cortex region in a brain perfusion study. Novel approaches that will optimize rotation angle for large FOVs and minimize geometric resolution differences will be pursued as a future study.
We simulated a clinically well-known NaI(Tl)-based two-headed SPECT scanner with conventional binning and two arbitrary types of binning in order to compare with our proposed scanners. The simulation results between the three types showed that the spatial resolution and sensitivity correlated with bin size and radius of rotation. Firstly, comparing Clinical_3.18 and Arb_1.6RR150 (same radius of rotation), the smaller bin size provided the better spatial resolution. Comparing Arb_1.6RR150 and Arb_1.6RR185 (same binning size), the longer radius of rotation resulted in poorer spatial resolution and sensitivity.
Our proposed detector head consisted of a pixelated CZT detector and pixel matching parallel hole collimator has a limited FOV although the combination has good sensitivity and spatial resolution in general. In order to minimize a truncation problem, the detector size should be as large as possible or the detector should have a motion which can cover the whole geometry of the imaging object. However, these approaches could be associated with a high cost or mechanical complexity, and trade-offs need to be considered. Our proposed geometry reduced the number of detectors as well as the detector size and minimized the detector movements, compared to the dual-head CZT-SPECT scanner (e.g., GE Discovery NM series) or multi-head CZT-SPECT scanner (e.g., VERITON). In addition, even when NaI detectors were used in place of the CZT detectors in our proposed scanner, scan time could be reduced in our two types of acquisition modes. However, the NaI-based scanner still faces the issues related to the gaps and edges.
Our proposed geometry appears to be quite similar to the commercial VERITON system due to multiple detectors using CZT material and tungsten parallel-hole collimator and data acquisition strategy with swiveling detectors. However, our detector size is larger than that of the VERITON and it can reduce the number of overlap or gap portions between adjacent detectors with minimum detector combinations when projection data required for reconstruction are generated. And our collimator design is also optimized for a broad energy range of SPECT radionuclides (up to 250 keV), compared to that of the VERITON optimized for only Tc-99m39. Despite these performance benefits for our system, the proposed detector design has a limitation that the absence of a common axis of rotation and the wide width of detectors do not allow very close patient proximity, compared to the narrow width of the VERITON detector.
In order to extend the FOV, the simple linear interpolation was applied corresponding to rotation step angles with 3-degree or 5-degee; however, some rods in the center were still distorted (Figure 4) and the quantitative performance differences of the reconstructed images between AS-3 and AS-5 acquisition modes were similar even though the number of angular samples for an AS-3 acquisition was 120, which was 1.6 times that of an AS-5 acquisition. We found that an AS-3 acquisition needed many more pixels for the corrections compared to an AS-5 acquisition when we investigated pixel by pixel the raw data of each projection before any correction. Further correction may be needed using novel techniques such as deep learning-based correction methods,40–42 which is beyond the scope of this current study.
The well-established open-source Monte Carlo simulation and reconstruction tool, including physical processes of attenuation and collimator-to-detector response correction, were used in this study; however, there are some limitations for the simulation setup between the conventional system and the proposed system each other. At first, we did not implement a full hardware part and positioning algorithm such as Anger Logic with multiple circular PMTs into the detector part for the conventional SPECT simulation. The position information for detected gamma events in a NaI crystal was sampled with a pixel size considering the specification of a conventional SPECT (e.g., 3.18 mm pixel size for GE Infinia Hawkeye with a zoom of 1.38). And, we did not include the realistic charge-transport effect for CZT material in relation to crystal size and incomplete charge collection in the simulation as mentioned above even though the photopeak counts were decreased to 65% that of NaI(Tl). At first, In order to improve the energy resolution, a 10 mm thickness for 1.6 mm pixel size would be better than a 5 mm thickness based on a charge sharing simulation previously reported.43 However, the performance difference for the SPECT application was not significant and the cost and performance trade-off should be considered. And, charge sharing events can produce a large amount of tailing in the photopeak leading to an increased FWHM or sensitivity44 and can affect count statistics during dual-isotope acquisition, for example, count statistics error within the Tc-99m photopeak during I-123/Tc-99m acquisition.45,46 The approximated the low-energy tailing effect in this study may induce errors and further investigation will be needed. Furthermore, we did not apply additional correction methods such as scatter correction for the CZT detector. It has been reported that adding the scatter correction to the image reconstruction for DaT imaging could improve the contrast recovery ratios over 0.9.37 Including these effects would make our future work more realistic and reliable.
Finally, as we mentioned earlier, our proposed system has approximately 2–3.3 times reduction in scan time, up to 1.7 times improved volume sensitivity and reasonable spatial resolution for a brain study when compared to the conventional dual-head scanner. However, if we compare our proposed scanner with an experimental dedicated multi-pinhole brain SPECT system,47,48 the dedicated system has good spatial resolution (~4.8 mm FWHM in the center of the cylindrical volume of interest) and the caudate and putamen in the brain phantom are well differentiated due to the magnification of the pinhole collimator for a small spherical volume having a 21 cm-diameter. In addition, the investigational multi-pinhole dedicated brain SPECT (e.g., G-SPECT) having a high spatial resolution (below 3 mm) and a high sensitivity of 415 cps/MBq takes only 30s for a total brain perfusion scan with optimized bed position sequences.49,50 However, these dedicated brain designs using multi-pinhole collimators have a significant limitation as for general-purpose imaging scenarios (e.g., bone SPECT) due to a small cylindrical volume of interest.48 On the other hand, our proposed detector head geometry could be radially extended and still could have shorter scan time by swiveling individual detectors, which will be further investigated to optimize the acquisition mode with a slightly common axis of rotation if needed.
5. CONCLUSIONS
In this study, we proposed a variable-aperture full-ring SPECT system using combined pixelated CZT and energy-optimized parallel-hole collimator modules and evaluated the performance of this scanner using relevant digital phantoms and MC simulations. Our simulation studies showed that the proposed CZT-SPECT design could result in reduced acquisition time and improved sensitivity with acceptable contrast-to-noise ratio spatial resolution. This encouraging result warrants further studies to realize the full potential of our new system design for general-purpose studies such as fully 3D bone SPECT with acquisition strategy optimization of radial positions using large-area CZT cameras.
ACKNOWLEDGMENTS
This work was supported in part by National Institute of Biomedical Imaging and Bioengineering grants R01EB026331 and R01EB012965, and National Heart, Lung, and Blood Institute grant R01HL135490.
Footnotes
CONFLICT OF INTEREST
The authors have no conflict to disclose.
References
- 1.Chowdhury FU, Scarsbrook AF. The role of hybrid SPECT-CT in oncology: current and emerging clinical applications. Clin Radiol. 2008;63(3):241–251. [DOI] [PubMed] [Google Scholar]
- 2.Wu J, Liu C. Recent advances in cardiac SPECT instrumentation and imaging methods. Phys Med Biol. 2019;64(6):06TR01. [DOI] [PubMed] [Google Scholar]
- 3.Zhang L, Villalobos A. Recent advances in the development of PET and SPECT tracers for brain imaging. In: Annual Reports in Medicinal Chemistry. Vol 47. Elsevier; 2012:105–119. [Google Scholar]
- 4.Anger H. A new instrument for mapping gamma-ray emitters. Biology and Medicine Quarterly Report UCRL. 1957;3653:38. [Google Scholar]
- 5.Anger HO. Scintillation camera with multichannel collimators. Journal of Nuclear Medicine. 1964;5(7):515–531. [PubMed] [Google Scholar]
- 6.Lee JS, Kovalski G, Sharir T, Lee DS. Advances in imaging instrumentation for nuclear cardiology. J Nucl Cardiol. 2019;26(2):543–556. [DOI] [PubMed] [Google Scholar]
- 7.Singh M, Mumcuoglu E. Design of a CZT based breast SPECT system. Ieee T Nucl Sci. 1998;45(3):1158–1165. [Google Scholar]
- 8.Zeng GL, Gagnon D. Image reconstruction algorithm for a spinning strip CZT SPECT camera with a parallel slat collimator and small pixels: CZT SPECT camera using small pixels. Medical physics. 2004;31(12):3461–3473. [DOI] [PubMed] [Google Scholar]
- 9.Suzuki A, Takeuchi W, Ishitsu T, Tsuchiya K, Ueno Y, Kobashi K. A four-pixel matched collimator for high-sensitivity SPECT imaging. Phys Med Biol. 2013;58(7):2199–2217. [DOI] [PubMed] [Google Scholar]
- 10.Lee YJ, Kim HJ. Comparison of a newly-designed stack-up collimator with conventional parallel-hole collimators in pre-clinical CZT gamma camera systems: a Monte Carlo simulation study. J Korean Phys Soc. 2014;65(7):1149–1158. [Google Scholar]
- 11.Robert C, Montemont G, Rebuffel V, Buvat I, Guerin L, Verger L. Simulation-based evaluation and optimization of a new CdZnTe gamma-camera architecture (HiSens). Phys Med Biol. 2010;55(9):2709–2726. [DOI] [PubMed] [Google Scholar]
- 12.Weng F, Bagchi S, Zan Y, Huang Q, Seo Y. An energy-optimized collimator design for a CZT-based SPECT camera. Nucl Instrum Methods Phys Res A. 2016;806:330–339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Erlandsson K, Kacperski K, van Gramberg D, Hutton BF. Performance evaluation of D-SPECT: a novel SPECT system for nuclear cardiology. Phys Med Biol. 2009;54(9):2635–2649. [DOI] [PubMed] [Google Scholar]
- 14.Park MA, Moore SC, Muller SP, McQuaid SJ, Kijewski MF. Performance of a high-sensitivity dedicated cardiac SPECT scanner for striatal uptake quantification in the brain based on analysis of projection data. Med Phys. 2013;40(4):042504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Goshen E, Beilin L, Stern E, Kenig T, Goldkorn R, Ben-Haim S. Feasibility study of a novel general purpose CZT-based digital SPECT camera: initial clinical results. EJNMMI Phys. 2018;5(1):6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Imbert L, Chevalier E, Claudin M, et al. A one-shot whole-body bone SPECT may be recorded in less than 20 minutes with the high-sensitivity Veriton® CZT-camera. Journal of Nuclear Medicine. 2019;60(supplement 1):1288–1288. [Google Scholar]
- 17.Varrone A, Dickson JC, Tossici-Bolt L, et al. European multicentre database of healthy controls for [123 I] FP-CIT SPECT (ENC-DAT): age-related effects, gender differences and evaluation of different methods of analysis. Eur J Nucl Med Mol I. 2013;40(2):213–227. [DOI] [PubMed] [Google Scholar]
- 18.Matsuda H, Murata M, Mukai Y, et al. Japanese multicenter database of healthy controls for [123 I] FP-CIT SPECT. Eur J Nucl Med Mol I. 2018;45(8):1405–1416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Taylor JC, Vennart N, Negus I, et al. The subresolution DaTSCAN phantom: a cost-effective, flexible alternative to traditional phantom technology. Nuclear medicine communications. 2018;39(3):268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Djang DS, Janssen MJ, Bohnen N, et al. SNM practice guideline for dopamine transporter imaging with 123I-ioflupane SPECT 1.0. J Nucl Med. 2012;53(1):154–163. [DOI] [PubMed] [Google Scholar]
- 21.Jan S, Benoit D, Becheva E, et al. GATE V6: a major enhancement of the GATE simulation platform enabling modelling of CT and radiotherapy. Phys Med Biol. 2011;56(4):881–901. [DOI] [PubMed] [Google Scholar]
- 22.Technologies R. M1085 CZT Detector Assembly https://redlen.com/. Published 2014. Accessed.
- 23.Hutton BF, Erlandsson K, Thielemans K. Advances in clinical molecular imaging instrumentation. Clin Transl Imaging. 2018;6(1):31–45. [Google Scholar]
- 24.Chen H, Awadalla S, Marthandam P, Iniewski K, Lu P, Bindley G. CZT device with improved sensitivity for medical imaging and homeland security applications. Paper presented at: Hard X-Ray, Gamma-Ray, and Neutron Detector Physics XI2009. [Google Scholar]
- 25.Assié K, Gardin I, Vera P, Buvat I. Validation of the Monte Carlo simulator GATE for indium-111 imaging. Physics in Medicine & Biology. 2005;50(13):3113. [DOI] [PubMed] [Google Scholar]
- 26.Rault E, Staelens S, Van Holen R, De Beenhouwer J, Vandenberghe S. Accurate Monte Carlo modelling of the back compartments of SPECT cameras. Physics in Medicine & Biology. 2010;56(1):87. [DOI] [PubMed] [Google Scholar]
- 27.Garcia MP, Villoing D, McKay E, et al. TestDose: A nuclear medicine software based on Monte Carlo modeling for generating gamma camera acquisitions and dosimetry. Medical Physics. 2015;42(12):6885–6894. [DOI] [PubMed] [Google Scholar]
- 28.Thielemans K, Tsoumpas C, Mustafovic S, et al. STIR: software for tomographic image reconstruction release 2. Phys Med Biol. 2012;57(4):867–883. [DOI] [PubMed] [Google Scholar]
- 29.Fuster BM, Falcon C, Tsoumpas C, et al. Integration of advanced 3D SPECT modeling into the open-source STIR framework. Medical physics. 2013;40(9):092502. [DOI] [PubMed] [Google Scholar]
- 30.Subramaniam RM, Frey KA, Hunt CH, et al. ACR-ACNM Practice Parameter for the Performance of Dopamine Transporter (DaT) Single Photon Emission Computed Tomography (SPECT) Imaging for Movement Disorders. Clin Nucl Med. 2017;42(11):847–852. [DOI] [PubMed] [Google Scholar]
- 31.Kouris K, Clarke GA, Jarritt PH, Townsend CE, Thomas SN. Physical performance evaluation of the Toshiba GCA-9300A triple-headed system. Journal of Nuclear Medicine. 1993;34(10):1778–1789. [PubMed] [Google Scholar]
- 32.Rahman T, Tahtali M, Pickering MR. Performance evaluation of a novel high performance pinhole array detector module using NEMA NU-4 image quality phantom for four head SPECT Imaging. Paper presented at: Medical Imaging 2015: Physics of Medical Imaging2015. [Google Scholar]
- 33.Islamian JP, Bahreyni Toossi MT, Momennezhad M, Naseri S, Ljungberg M. Simulation of a quality control Jaszczak phantom with SIMIND Monte Carlo and adding the phantom as an accessory to the program. Iranian Journal of Medical Physics. 2012;9(2):135–140. [Google Scholar]
- 34.Zubal IG, Harrell CR, Smith EO, Rattner Z, Gindi G, Hoffer PB. Computerized three-dimensional segmented human anatomy. Med Phys. 1994;21(2):299–302. [DOI] [PubMed] [Google Scholar]
- 35.Committee AGaS. ACR Guidelines and Standards Committee. ACR-SPR Practice Guideline for the Performance of Single Photon Emission Computed Tomography (SPECT) Brain Perfusion and for Brain Death Examinations. Practice Guideline Revised. 2012:1–11. Resolution 25. 2016. [Google Scholar]
- 36.Marti-Fuster B, Esteban O, Thielemans K, et al. Including anatomical and functional information in MC simulation of PET and SPECT brain studies. Brain-VISET: a voxel-based iterative method. IEEE Trans Med Imaging. 2014;33(10):1931–1938. [DOI] [PubMed] [Google Scholar]
- 37.Pareto D, Cot A, Pavia J, et al. Iterative reconstruction with correction of the spatially variant fan-beam collimator response in neurotransmission SPET imaging. Eur J Nucl Med Mol Imaging. 2003;30(10):1322–1329. [DOI] [PubMed] [Google Scholar]
- 38.Seret A, Nguyen D, Bernard C. Quantitative capabilities of four state-of-the-art SPECT-CT cameras. EJNMMI Res. 2012;2(1):45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Wacholz C, Hruska C, OConnor M. Veriton Multi-CZT Detector SPECT/CT System Acceptance Testing. Journal of Nuclear Medicine. 2020;61(supplement 1):3003–3003. [Google Scholar]
- 40.Whiteley WJ, Gregor J. CNN-based PET sinogram repair to mitigate defective block detectors. Phys Med Biol. 2019. [DOI] [PubMed] [Google Scholar]
- 41.Yu J, Lin Z, Yang J, Shen X, Lu X, Huang TS. Generative image inpainting with contextual attention. Paper presented at: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition2018. [Google Scholar]
- 42.Wang G, Ye JC, Mueller K, Fessler JA. Image Reconstruction Is a New Frontier of Machine Learning. Ieee T Med Imaging. 2018;37(6):1289–1296. [DOI] [PubMed] [Google Scholar]
- 43.Myronakis ME, Darambara DG. Monte Carlo investigation of charge-transport effects on energy resolution and detection efficiency of pixelated CZT detectors for SPECT/PET applications. Med Phys. 2011;38(1):455–467. [DOI] [PubMed] [Google Scholar]
- 44.Pretorius PH, Liu C, Fan P, Peterson M, Ljungberg M. Monte Carlo simulations of the GE discovery alcyone CZT SPECT systems. Ieee T Nucl Sci. 2015;62(3):832–839. [Google Scholar]
- 45.Suzuki A, Takeuchi W, Ueno Y, et al. Monte Carlo-based scatter correction considering the tailing effect of a CdTe detector for dual-isotope brain SPECT imaging. Biomed Phys Eng Expr. 2016;2(4):045010. [Google Scholar]
- 46.Blaire T, Bailliez A, Bouallegue FB, Bellevre D, Agostini D, Manrique A. First assessment of simultaneous dual isotope (123 I/99m Tc) cardiac SPECT on two different CZT cameras: A phantom study. Journal of Nuclear Cardiology. 2018;25(5):1692–1704. [DOI] [PubMed] [Google Scholar]
- 47.Zeraatkar N, Kalluri KS, Könik A, et al. Preliminary investigation of axial and angular sampling in multi-pinhole AdaptiSPECT-C with XCAT phantoms. Paper presented at: 2017 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC)2017. [Google Scholar]
- 48.Könik A, De Beenhouwer J, Mukherjee JM, et al. Simulations of a Multipinhole SPECT Collimator for Clinical Dopamine Transporter (DAT) Imaging. IEEE transactions on radiation and plasma medical sciences. 2018;2(5):444–451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Beekman FvdH FJ, Goorden MC, Vaissier PEB, van Roosmalen J, During H, Vastenhouw B. G -SPECT-I: a full ring high sensitivity and ultra-fast clinical molecular imaging system with < 3mm resolution. European Journal of Nuclear Medicine and Molecular Imaging. 2015;42(1). [Google Scholar]
- 50.Chen Y, Goorden MC, Vastenhouw B, Beekman FJ. Optimized sampling for high resolution multi-pinhole brain SPECT with stationary detectors. Physics in Medicine & Biology. 2020;65(1):015002. [DOI] [PubMed] [Google Scholar]


