Abstract
We redevelop the variational free energy profile (vFEP) method using a cardinal B-spline basis to extend the method for analyzing free energy surfaces (FESs) involving 3-or-more reaction coordinates. We also implemented software for evaluating high-dimensional profiles based on the multistate Bennett acceptance ratio (MBAR) method which constructs an unbiased probability density from global reweighting of the observed samples. The MBAR method takes advantage of a fast algorithm for solving the unbinned weighted histogram (UWHAM)/MBAR equations which replaces the solution of simultaneous equations with a nonlinear optimization of a convex function. We make use of cardinal B-splines and multiquadric radial basis functions to obtain smooth, differentiable MBAR profiles in arbitrary high dimensions. The cardinal B-spline vFEP and MBAR methods are compared using three example systems that examine 1-, 2-, and 3-dimensional profiles. Both methods are found to be useful and produce nearly indistinguishable results. The vFEP method is found to be 150 times faster than MBAR when applied to periodic 2-dimensional profiles, but the MBAR method is 4.5 times faster than vFEP when evaluating unbounded 3-dimensional profiles. In agreement with previous comparisons, we find the vFEP method produces superior FESs when the overlap between umbrella window simulations decreases. Finally, the associative reaction mechanism of hammerhead ribozyme is characterized using 3-, 4-, and 6-dimensional profiles, and the higher-dimensional profiles are found to have smaller reaction barriers by as much as 1.5 kcal/mol. The methods presented here have been implemented into the FE-ToolKit software package along with new methods for network-wide free energy analysis in drug discovery.
Keywords: Free energy calculations, graphics processing unit, thermodynamic integration
Graphical Abstract
Introduction
Chemical processes are driven by changes in free energy and can be studied using molecular simulations that can predict these changes and provide a molecular-level understanding to help guide design.1–4 There are several types of free energy calculations encountered in the field of computational chemistry. Among the most common are so-called alchemical free energy methods2,4 that utilize the state property of the free energy to determine thermodynamic changes between two states using a non-physical (i.e., “alchemical”) pathway. For many other applications, the desired goal is to determine the mechanism of a chemical process; that is, the likely pathway (or set of pathways) that physically connect the states, including the location of key transition states and intermediates, and determining factors that regulate the rates and outcomes of the process. Examples include transitions between conformational states,5–12 association/binding events,13–21 traversal of ions through channels and membranes,22–25 and enzymatic and non-enzymatic chemical reactions in the condensed phase.26–32 One way of characterizing such mechanisms is through the construction of a free energy surface (FES) or related potential of mean force (PMF), in a reduced coordinate space (henceforth referred to as “reaction coordinates”) that provides a practical basis for interpretation.15,33–35 Free energy surfaces are also referred to as free energy profiles, and these terms are used interchangeably. We will henceforth use FES as an acronym to refer to free energy surface/profile rather than “FEP” so as to avoid confusion with the acronym “vFEP” which refers to one of the main methods being developed.
Free energy profiles are derived from the analysis of sets of enhanced sampling simulations. A common enhanced sampling strategy is to introduce biasing potentials that facilitate transitions over barriers that would otherwise be prohibited or only very sparsely sampled. In this way, the methods help to establish more uniform coverage of the relevant configurational space. The most common approach is to use sets of “umbrella sampling” simulations,36,37 where the biasing potential is a harmonic (quadratic) penalty function in the space of reaction coordinates that is used to localize sampling near to the harmonic (or “umbrella”) centers. Typically these simulations are performed by having multiple umbrella potentials (umbrella centers and/or force constants) distributed so as to collectively provide statistical sampling of the important regions of the FES. Sometimes these umbrella potentials are further enhanced by additional biasing potentials that help to “flatten out” the FES so as to facilitate more uniform sampling.38 Adaptive umbrella sampling is another method designed to improve the uniformity of the sampling39–42 which has been found to be a cost-effective approach for characterizing high-dimensional FESs.43
The relevant reaction coordinates are collected from the biased simulations. This data must be analyzed to remove the bias, and represented in the form of a free energy profile. In order to convert the biased sampled fluctuation data into unbiased data, one must first locally unbias (reweight) the frames within each simulation using the appropriate inverse Boltzmann weight from the biasing potential. Next, the different simulation ensembles need to be globally reweighted using statistical methods34,44–54 that estimate the relative free energy of each umbrella simulation. The unbiased data can then be used to construct a numerical or analytical model representation of the free energy profile in the space of the reaction coordinates. These profiles can be used to identify catalytic pathways and characterize rate-controlling transition state ensembles. Recently, free energy profiles for the twister55 and Varkud satellite56 ribozymes from ab initio combined quantum mechanical/molecular mechanical (QM/MM) simulations have been used within a computational enzymology approach55–59 to study RNA-cleavage reactions60 and gain insight into nucleic acid enzyme design.61
There is a number of methods that have been developed to compute free energy profiles from analysis of molecular dynamics simulations, including the weighted histogram analysis method34,44,45,62 (WHAM) and unbinned variations (UWHAM),46 umbrella integration (UI),47–49 multistate Bennett acceptance ratio method (MBAR),50,51 and the variational free energy profile (vFEP) method.52–54 The latter affords some distinct advantages with respect to the ability to provide a robust, analytic representation (including derivatives with respect to reaction coordinates) of the free energy profile with minimal sampling.52 Such an analytic representation is important for applications in that: (1) it enables one to efficiently search for minimum free energy pathways that connect the relevant chemical or conformational states and characterize the mechanism,55,56 (2) it can be used in automated iterative refinement procedures to identify regions where further sampling is required,54 (3) it can be exploited by enhanced sampling methods as an inverse biasing potential to facilitate uniform sampling on the free energy surface,40–42 and (4) it can serve as a correction potential to improve the accuracy of force fields.63–65
The vFEP approach has been implemented and demonstrated to be useful using a cubic spline representation for 1D52 and 2D53 free energy profiles. However, extension to general higher dimensions has been challenging, despite the need for such an approach for many applications, particularly path methods such as the finite temperature string66 and nudged elastic band67,68 methods that consider more reaction coordinates. The vFEP method tackles the problems of reweighting and analytic representation of the data simultaneously. Other methods such as MBAR formally only address the data reweighting step, and the representation of the data in terms of a robust analytic surface requires some form of fitting or interpolation in a second step. No general methods exist for determining robust analytic representations of free energy profile data in arbitrarily high dimensions, particularly when non-uniform sampling is performed. Herein we address these challenges by introducing new methods and novel computational tools, implemented in the FE-ToolKit software package69 and made freely available to the community for calculating free energy profiles using both MBAR and vFEP in high dimensions.
In this work, we present an extension of the vFEP method to arbitrary high dimensions using cardinal B-splines.70 We further describe an efficient, scalable software implementation of an MBAR approach for calculating free energy profiles51,71 that incorporates a fast solution for the MBAR/UWHAM equations to nonlinearly optimize a convex function.46 Finally, we present a novel method for robust analytic representation of the data using multiquadric radial basis functions to obtain smooth, differentiable free energy profiles in arbitrary high dimensions from non-uniformly sampled data and fast MBAR analysis. These tools have been integrated into the ndfes program within the FE-ToolKit software package, which is freely available.69
We compare the MBAR and vFEP methods using several examples: (1) The 1-dimensional FES of a phosphoryl transfer reaction of a model compound with an ethoxide leaving group computed from ab initio QM/MM simulations. (2) Periodic 2-dimensional Ramachandran FESs of alanine, glycine, and valine dipeptide computed from MM simulations. (3) A 3-dimensional FES of the associative transphosphorylation reaction mechanism catalyzed by the hammerhead ribozyme (HHr) from semiempirical QM/MM simulations. We further explore how the HHr minimum free energy pathway is effected by increasing the dimensionality of the FES to 4 and 6 reaction coordinates.
Methods
The variational free energy profile method (vFEP), derived in Ref. 52, is a procedure for obtaining an unbiased FES from a series of biased umbrella window simulations. Given the umbrella biasing potentials and the time series of observed reaction coordinate values {xobs} for each simulation, the goal is to construct an analytic representation of the global unbiased FES. The vFEP approach for reconstructing the global FES is to assume a model form for the reduced FES, f(x; p), that depends on the parameters p. Reduced potential energy units of kBT are used throughout the manuscript, where kB is the Boltzmann constant and T is the absolute temperature, such that the inverse temperature β = (kBT)−1 does not explicitly appear. Here the argument x of the reduced FES model represents the N-dimensional (Ndim) set of reaction coordinate values that define the spanned free energy space. The model parameters that best reproduce the global FES, p*, are those that minimize the objective function shown in Eq. 2.
| (1) |
| (2) |
Nsim is the number of umbrella window simulations. Na is the number of observations drawn from simulation a. xobs,ai is the array of reaction coordinate values of sample i within simulation a. Za(p) is a configurational integral of simulation a.
| (3) |
wa(x) is the umbrella biasing (reduced) potential used in simulation a. The formulation presented in this manuscript does not presume a form for the umbrella biasing potential, but it is common for it to be a sum of Ndim uncoupled harmonic oscillators centered about x0,d with force constants kd, where Ndim is the number of reaction coordinates.
| (4) |
In some cases, an additional biasing potential is introduced to attempt to flatten out the free energy surface in the space of the reaction coordinates such that sampling within different umbrella windows is more uniform. In fact, such a biasing potential can be derived from a rough estimate of −f(x; p*) itself (e.g., from coarse-grained sampling).38
The gai quantity appearing in Eq. 2 is a minor generalization of the original vFEP method in the present work to reweight trajectories to remove the effect of additional restraint potentials (not directly involving the reaction coordinates) on the FES. Specifically, this term is the degeneracy of sample i drawn from simulation a. If the umbrella window simulations are unencumbered by additional restraints (and hence there is no additional restraint bias that requires reweighting), then the degeneracy of each frame is unity (gai = 1); however, if the additional bias introduced by a reduced restraint potential urest,ai needs to be removed, then the sample degeneracy is given by Eq. 5.
| (5) |
Formally, the value of umax has no effect; in practice, one chooses umax to be the maximum observed value of urest,ai to prevent overflow of the exponential function.
In the present work, we describe a vFEP implementation that can be solved for arbitrarily high dimensional FESs. The main approximations of our method are:
Space is divided into a uniform Ndim-dimensional grid consisting of bins (Ndim-dimensional grid “volumes”) and corners (grid line intersections). Every bin is the same shape and size, but each dimension of a bin may have a different fixed width.
The FES is assumed to be positive infinity throughout space except within those bins populated by at least one sample from any simulation (that is, the probability is zero for the unoccupied bins).
For those regions of space populated by at least one sample, the FES is modeled by cardinal B-spline functions.70 The values of the FES are defined by a weighted average of control parameters associated with the nearby corners, and the weights are the B-spline values evaluated at those corners.
The configurational integral of Eq. 3 is numerically evaluated from Gauss-Legendre quadrature72 of each bin.
Division of space into a uniform grid for non-periodic systems.
Given a target bin width for each dimension, Δxd, appropriate values for the grid minimum xmin,d and the number of bins Nbin,d in each direction are chosen such that the grid maximum is an integer multiple of the grid size xmax,d = Nbin,dΔxd + xmin,d and all observed points are enclosed within the range xmin and xmax. To do this, note the maximum and minimum coordinates from the observed samples, calculate the number of bins that can fit within that range, expand the range minimum by Δxd and increase the number of bins in direction d by two. This produces a range that is guaranteed to contain all samples while also being an integer multiple of the target bin width. The range must further be padded on either side by additional bins to fully define the B-splines evaluated near the grid edges (this will depend on the order n of the B-spline used). Although the free energy is assumed to positive infinity within this buffer region, the padded bin corners contribute control parameters accessible to the non-buffer region. Specifically, the ranges must be extended by an additional bins on both sides (where ⌊x⌋ denotes the floor function of x, i.e., the largest integer ≤ x), such that the bin counts increase by . For example, for a B-spline order of n = 5 or n = 6, . Application of this procedure to each dimension creates a grid consisting of bins and corners; however, many bins will be unoccupied by samples, so only a petite list of occupied bins need to be tracked.
Division of space into a uniform grid for periodic systems.
For periodic systems, one specifies a number of bins, Nbin, from which the target bin width is determined so as to obey the periodicity of the system. Hence, for a periodic interval of 2π, the bin width is Δxd = 2π/Nbin. Unlike the non-periodic case, there is no need to pad the grid, rather the B-spline weights are simply “wrapped” to the appropriate interval of periodic grid points.
The cardinal B-splines.
The model form of the reduced free energy is a weighted average of the B-spline control parameters pc associated with the grid corners, and the weights are the cardinal B-spline values evaluated at the corner positions, xc
| (6) |
where θn(x − xp) is a Ndim-dimensional cardinal B-spline of order n centered about the point xp
| (7) |
and Mn is given by Eq. 8.
| (8) |
Cardinal B-splines have compact support; that is, they are nonzero only within a well-defined range. Only the nearest Nnear,d = 2⌊(n + 1)/2⌋ corners in each dimension can have a nonzero value of Mn; therefore, only total corners need to be considered for any FES evaluation. For example, if n is even, then Mn will be nonzero for the n nearest corners. If n is odd, then the location of the n nearest corners will depend on whether the evaluation point is located before or after the bin midpoint. For notational purposes, let be an operator that accepts a point in space x and an integer in the range c ∈ [1, Nnear] and returns the global index of a nearby corner. Equation 6 can then be rewritten to emphasize the B-spline’s compact support, when appropriate.
| (9) |
Inserting Eq. 6 into Eq. 2 yields:
| (10) |
where hc arises from regrouping of parentheses.
| (11) |
The hc values can be precomputed and stored at the start of the nonlinear optimization procedure to eliminate B-spline evaluations for every observed data point in each optimization step.
Numerical Integration of Za.
Gauss-Legendre quadrature is an efficient numerical solution for integration in the range [−1, 1].72
| (12) |
The xq,i values are the roots of a Legendre polynomial of order Nq,d, , and the weights are . The range of integration is easily adjusted via u–substitution; an integral over the range [−Δx/2, Δx/2] merely requires scaling of wq,i and xq,i by 2/Δx. Integration in multiple dimensions leads to an analogous summation over a mesh of quadrature points xq, whose weights are an outer-product of appropriately-scaled, one-dimensional weights. The configurational integral, Za, evaluated over all-space can be replaced by the sum of Ndim-dimensional Gauss-Legendre quadratures, each integrating the volume of an occupied bin.
| (13) |
The quadrature weights and umbrella biasing potential exponential have been absorbed into a single term , xb,b is the center of bin b, and fib(p) is a shortened notation for Eq. 14.
| (14) |
In our notation, the mesh of quadrature points xq,i is the same for each bin (ranging from −Δx/2 to Δx/2); the only spatial difference between the local quadrature meshes are the location of their bin centers. Consequently, the B-spline evaluations can be precomputed as a matrix for a single, prototype bin centered at the origin, and the FES evaluation at the quadrature mesh points becomes matrix-vector product between the prototype B-spline weight matrix and the petite list of nearby corner parameters.
| (15) |
| (16) |
The values are the positions of the Nnear nearby corners about the prototype bin centered at the origin.
Within the context of the numerical optimization procedure, the computational scaling of the cardinal B-spline vFEP objective function is , where n is the B-spline order and Nq,d is the quadrature rule in each dimension. The scaling behavior is dominated by the calculation of the Za values. The component of the scaling is the evaluation of the reduced free energy at each quadrature point (Eq. 15) within one bin. The scaling is proportional to Nbin because each occupied bin contributes to the integration. The second term in the scaling expression corresponds to the double summation in Eq. 13 for each of the Nsim configuration integrals. In practice, the number of occupied bins that need to be integrated does not scale proportionally to the number of simulations, because there is often some overlap between the simulated distributions. Furthermore, distant bins – relative to the umbrella window center – do not significantly contribute to the configuration integral because the umbrella biasing potential becomes very large and thus the integrand becomes very small. One should therefore expect the scaling to be proportional to Nsim rather than in practice.
Parameter gradients.
Some nonlinear optimization methods require the derivative of the objective function with respect to the parameters. These gradients are given by Eqs. 17–19.
| (17) |
| (18) |
| (19) |
High-dimensional free energy profiles using the Multistate Bennett Acceptance Ratio method.
We have also implemented an algorithm for producing arbitrarily high dimensional FESs using the Multistate Bennett Acceptance Ratio (MBAR) formalism, described in Ref. 51. In this approach, the reduced free energy is computed for each bin from an unbiased probability density obtained from reweighting the observed samples. The expression for the reduced free energy at the bin center (Eq. 20) makes use the indicator function (Eq. 21), which acts to select the frames within the volume of the bin.
| (20) |
| (21) |
The fa values appearing in Eq. 20 are the reduced free energy of each biased simulation. Formally, the fa values can be obtained from self-consistent solution of the coupled MBAR equations (Eq. 22); however, our implementation solves the MBAR/UWHAM equations,46,50,71,73,74 (Eqs. 23 and 24), which were first derived in Ref. 46. The MBAR/UWHAM method benefits from leveraging existing nonlinear parameter optimization software to obtain a solution.
| (22) |
In the present context, the MBAR/UWHAM method minimizes the objective function shown in Eq. 23 with respect to the ba parameters. The fa values are then obtained from Eq. 24.
| (23) |
| (24) |
The quantity appearing in Eqs. 23 and 24 is the total number of observations drawn from all umbrella window simulations.
Within the context of the numerical optimization procedure, the computational scaling of the MBAR/UWHAM objective function is , where Na is the number of samples per simulation. The scaling is dominated by the calculation of the first term in Eq. 23.
The MBAR free energy values (Eq. 20) are obtained from histogram binning. To view the free energy as a surface, one could assume the value of the free energy is a constant within each bin; however, this would make it difficult to use the surface for obtaining minimum free energy paths. A better approach is to assume the computed values are the free energies at the histogram bin centers and then construct a continuous surface by interpolating between the bin centers. An appropriate choice for the interpolating function depends on factors such as whether the reaction coordinates are periodic, or if the available data forms a regular grid. For example, if the MBAR histogram bin centers form a complete uniform grid over a periodic range, then cardinal B-splines are good interpolation functions, because they offer compact support and the spline coefficients can be easily determined. The B-spline coefficients that reproduce the free energy values are the reverse Fourier transform of the ratio between the free energy’s Fourier coefficients and the B-spline function’s Fourier coefficients.63,75 If the histogram centers do not form a complete uniform grid, then the data is “scattered” and the cardinal B-spline representation is not well suited; however, a smooth, differentiable interpolation of scatter data can be constructed using multiquadric radial basis functions (RBFs).76,77 A radial basis function is any function that satisfies φ(x) = φ(‖x‖), where ‖·‖ returns the Euclidean distance of a vector. The multiquadric radial basis function is the particular form of φ(x) shown in Eq. 25.
| (25) |
The ϵ value is a “shape parameter”. The optimal choice of the shape parameter is a subject of active research77–79 which has led to a number of heuristics for choosing its value; however, it remains quite common to choose an acceptable value from trial and error.79 Our experience is that ϵ = 10 yields good interpolations for the free energy surfaces we have studied. Small values of ϵ may lead to interpolations that display unphysical oscillations. Radial basis functions are advantageous because few restrictions are placed on the data to be interpolated. The data does not need to be uniformly distributed and their locations can be of any dimensionality. The disadvantage of RBFs is they become expensive to evaluate as the amount of input scatter data increases. This expense is not a significant issue when applied to MBAR because the RBFs are not required in the nonlinear optimization of the MBAR/UWHAM equations (Eq. 23) nor the calculation of the free energy values at the histogram centers (Eq. 20); the RBFs are only used to interpolate the data to create an analytic representation. The expense associated with RBFs do not make them an ideal model for solving the vFEP equations, however, because the numerical integration of the configuration integral would require their re-evaluation within every step of the vFEP objective function optimization.
The interpolation of scattered MBAR free energies at an arbitrary position, x, is a weighted sum of multiquadric radial basis functions evaluated at the histogram centers, xb,b.
| (26) |
The weights are chosen by solving a set of linear equations that guarantee reproduction of the free energy values at each histogram center.
| (27) |
The solution for the weights are unique if the interpolation matrix (Eq. 28) is non-singular.
| (28) |
The multiquadric radial basis functions are positive-definite functions, making it unlikely to encounter a singular interpolation matrix, in practice.
In summary, the MBAR method addresses reweighting of the data to obtain free energy values within occupied bins. As a second step, the binned values must be represented using analytic functions to analyze the FES. The analysis of the FES often includes the determination of pathways and stationary points that provide insight into mechanism. The analytic model of the FES could potentially be exploited to enhance sampling or correct potential functions. We have described general procedures for creation of an analytic FES from MBAR data using either B-splines (for uniform grid data) or RBFs (for “scattered” data).
Computational Details.
We performed simulations of 3 sets of systems to generate data used to compare the vFEP and MBAR FES analysis methods. A description of the simulations is provided here. For 1-dimensional surfaces, umbrella window simulations were performed of a model phosphoryl transesterification reaction with an ethoxide leaving group (Fig. 1). The reaction coordinate, ξPT, is the difference in distances RP-O5’ − RP-O2’, which was sampled from −4 to 5 Å using 91 umbrella window QM/MM simulations. The solute was treated with the PBE0/6–31G* hybrid density functional method,80,81 and the solvent was modeled with 1510 TIP4P/Ew water molecules.82 The system density was equilibrated at a constant pressure of 1 atm, and the production simulations were performed at constant volume and temperature (298 K) using a Langevin thermostat. A 50 kcal mol−1 Å−2 umbrella potential force constant was used, and each simulation was performed for 25 ps using a 1-fs timestep. The reaction coordinate was saved every 25 frames. The Lennard-Jones potential was cutoff at 9 Å and a long-range tail correction was used to model the LJ interactions beyond the cutoff. Long-range electrostatics were treated with the ambient potential composite Ewald method.83
Figure 1:
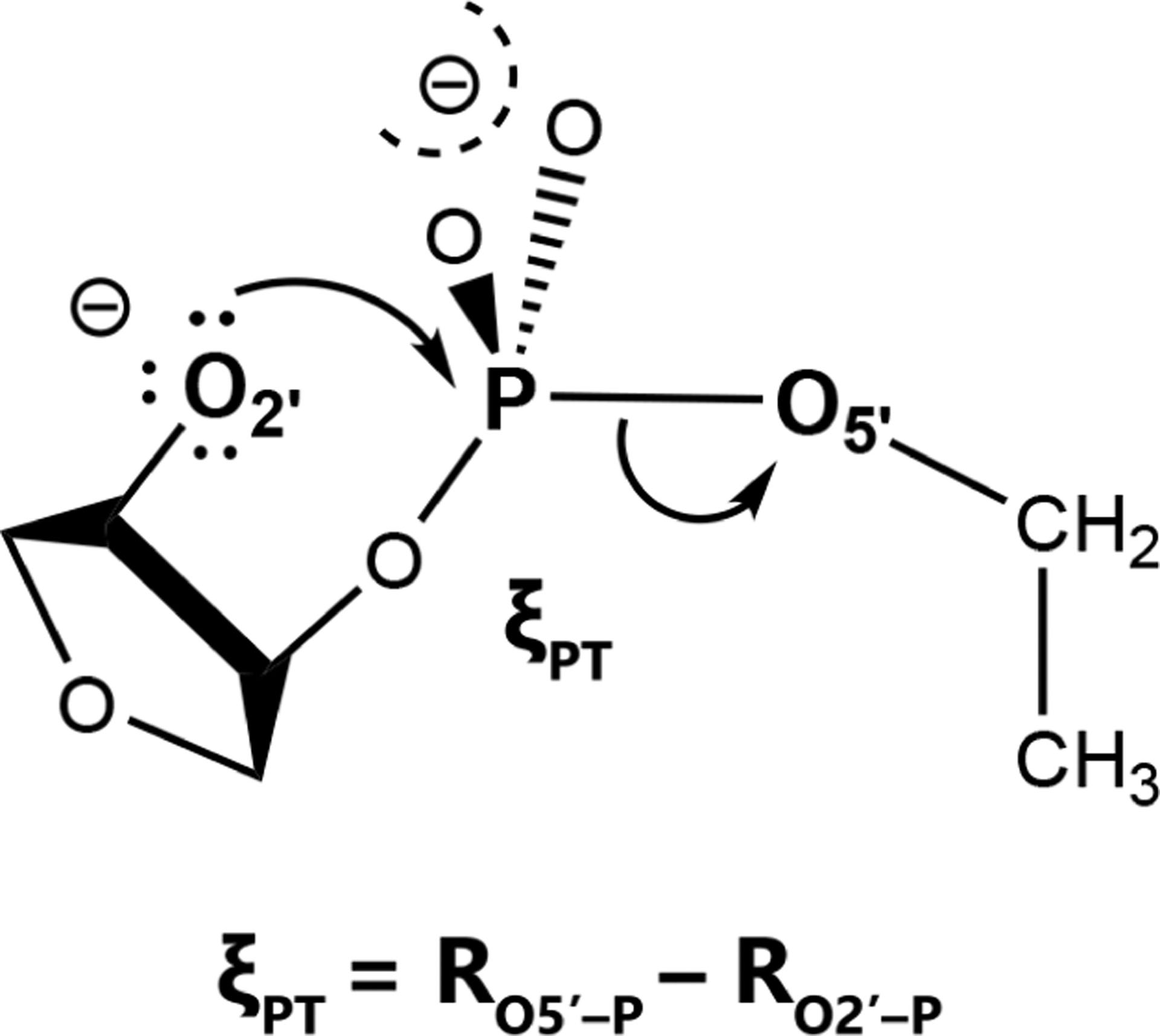
Model phosphoryl transfer reaction with an ethoxide leaving group and the reaction coordinate studied.
For 2-dimensional surfaces, we performed a series of umbrella window simulations that explore the glycine, alanine, and valine dipeptide FESs with respect to the ϕ and ψ peptide dihedral angles. The dipeptide solute was modeled with the Amber ff14SB force field84 solvated by 1398 (alanine), 1493 (valine), or 1335 (glycine) TIP4P/Ew waters.82 A 45-by-45 array of umbrella window simulations that sample the ϕ and ψ coordinates every 8 degrees (from 0 to 352 degrees) were performed using an umbrella force constant of 200 kcal mol−1 rad−2 for each coordinate. Each production simulation was run in the isothermal-isobaric ensemble using the Langevin thermostat and Berendsen barostat to maintain 298 K and 1 bar for 200 ps. The simulations were performed with a 2 fs timestep and hydrogen mass repartitioning to allow for a larger timestep. The reaction coordinates were recorded every 1000 steps. The Lennard-Jones potential was truncated at 8 Å and a long-range tail correction was used to model the LJ interactions beyond the cutoff. Long-range electrostatics were treated with the particle mesh Ewald (PME) method.85,86
For 3-, 4- and 6-dimensional surfaces, we performed simulations to characterize the associative transphosphorylation reaction mechanism catalyzed by the hammerhead ribozyme (HHr), where residues G8 and G12 act as the general acid and base, respectively. The mechanism is depicted in Fig. 2. The HHr system was built starting from the crystal structure87 (PDB ID: 2OEU). The Mn2+ ions were replaced with Mg2+. The GTP, OMC, and 5BU modified nucleobases were replaced with wild-type G, C, and U, respectively. The nucleophile (N-1:O2′) was deprotonated and connected to the scissile phosphate to create a transition state (TS) mimic. The system was then placed in a 85 Å truncated octahedron water box. Ions were added to balance the system charge and achieve a bulk ion concentration of 0.14 M NaCl. The solvated system was equilibrated (as described in Ref. 58), and simulated for 100 ns. During the simulation, the active site Mg2+ shifted from the crystallographic position at C-site to the B-site,88 where it coordinates N+1:pro-RP, A9:pro-RP, and G8:O2′. The MM simulations were carried out using AMBER18,89 employing ff99OL3 RNA force field,90,91 TIP4P/Ew water model82 and corresponding ions.92–95 Simulations were performed under periodic boundary conditions at 300 K using an 12 Å nonbond cutoff and PME electrostatics.85,86 The Langevin thermostat with γ=5 ps−1 and Berendsen isotropic barostat with τ=1 ps were used to maintain a constant pressure and temperature. A 1 fs was used along with the SHAKE algorithm to fix hydrogen bond lengths.96 The HHr umbrella window simulations were performed using the AM1/d-PhoT semiempirical Hamiltonian97 to model a QM region consisting of 89 atoms, including: the scissile phosphate and flanking sugars, the G12 nucleobase and sugar, the G8 sugar, the A9 phosphate, a Mg2+ ion, and 4 nearby waters (three of which are directly coordinating Mg2+). The remainder of the system was treated with the molecular mechanical force field, described above.
Figure 2:

Associative transphosphorylation mechanism catalyzed by the hammerhead ribozyme and the three reaction coordinates used to represent progression of the general base (ξGB), phosphoryl transfer (ξPT), and general acid (ξGA) steps. Atoms in QM and MM regions are shown as black and gray, respectively. Although not shown in the scheme to avoid crowding, the QM region additionally includes the sugar of G12, and four waters three of which coordinate the Mg2+.
The minimum free energy paths were determined by repeating finite temperature string umbrella sampling simulations using different sets of reaction coordinates in successively higher dimensions. For 3-dimensional surfaces, the mechanism was described by 3 bond length differences that track the progress of the general base (ξGB = RO2’-H − RG12:N1-H), phosphoryl transfer (ξPT = RO5’-P − RO2’-P), and general acid (ξGA = RG8:O2’-H − RO5’-H) steps (Fig. 2). For the 4D surface, a separate set of umbrella window simulations were performed to explicitly track the O2’-P and O5’-P bond distances rather than the combined coordinate ξPT used to monitor the phosphoryl transfer. In other words, the 4 reaction coordinates are ξGB, RO2’-P, RO5’-P, and ξGA. A 6-dimensional profile was similarly constructed by decomposing the combined ξGB and ξGA coordinates into their component distances as well. The umbrella window locations were iteratively refined to converge upon the minimum free energy path using the string method described in Ref. 98. This method combines the finite temperature string method66 with umbrella sampling simulations,37 and it has sometimes been referred to as the finite temperature string umbrella sampling method.99 In brief, an initial guess is made for a parametric curve that defines the reaction pathway. Umbrella window molecular dynamics simulations are performed along the parametric curve by uniformly discretizing the path. The parametric curve is then updated by fitting it to the observed average reaction coordinate values from each simulation. In the present work, the parametric curve is obtained by Akima spline discretized with 32 umbrella window simulations, and the iterative process is repeated 50 times. A 100 kcal/mol force constant was used for each reaction coordinate in all umbrella simulations. Each umbrella window simulation was run for 2 ps. The reported free energy pathway is the parametric curve generated by the last iteration, and the free energy values are obtained by analyzing the data from all 50 iterations.
Results and Discussion
We implemented a free energy analysis program, available for download on the internet,69 that enables the use of MBAR and vFEP for FESs of any dimension. The results discussed in this section include a comparison of these methods for 1-, 2-, and 3-dimensional FESs. We also compare the results obtained from a previously published vFEP method based cubic splines; however, that program is limited to 1- and 2-dimensional FESs only. Furthermore we explore the sensitivity of the FESs with respect to grid spacing, cardinal B-spline order, umbrella window spacing, and their computational cost. Finally, we examine how 1-dimensional projections of minimum free energy paths vary with respect to the dimensionality of the calculated FES.
1-dimensional example: non-enzymatic transphosphorylation reaction in solution
The purpose of this section is to concisely demonstrate that for a simple 1-dimensional example, there is consistency between vFEP methods using cubic spline and B-spline representations of the data, and these FESs are also consistent with MBAR results. The 1-dimensional FES of a model transphosphorylation reaction (1) simulated with an ab initio QM/MM method is shown in Fig. 3. The cardinal B-spline solution uses 5th order B-splines and a 0.15 Å node spacing. The MBAR histogram spacing is 0.15 Å, and the 1-dimensional FESs connects the MBAR histogram values using RBFs. The cubic spline vFEP method is described in Ref. 52. The MBAR, cardinal B-spline vFEP, and cubic spline vFEP methods are all nearly indistinguishable from each other. Furthermore, each method requires only a fraction of a second to compute the FES. The rate limiting barriers (kcal/mol) are: 19.65 (MBAR), 19.67 (B-spline vFEP), and 19.67 (cubic spline vFEP). Hence, for the 1-D example, all methods provide very consistent and affordable results.
Figure 3:
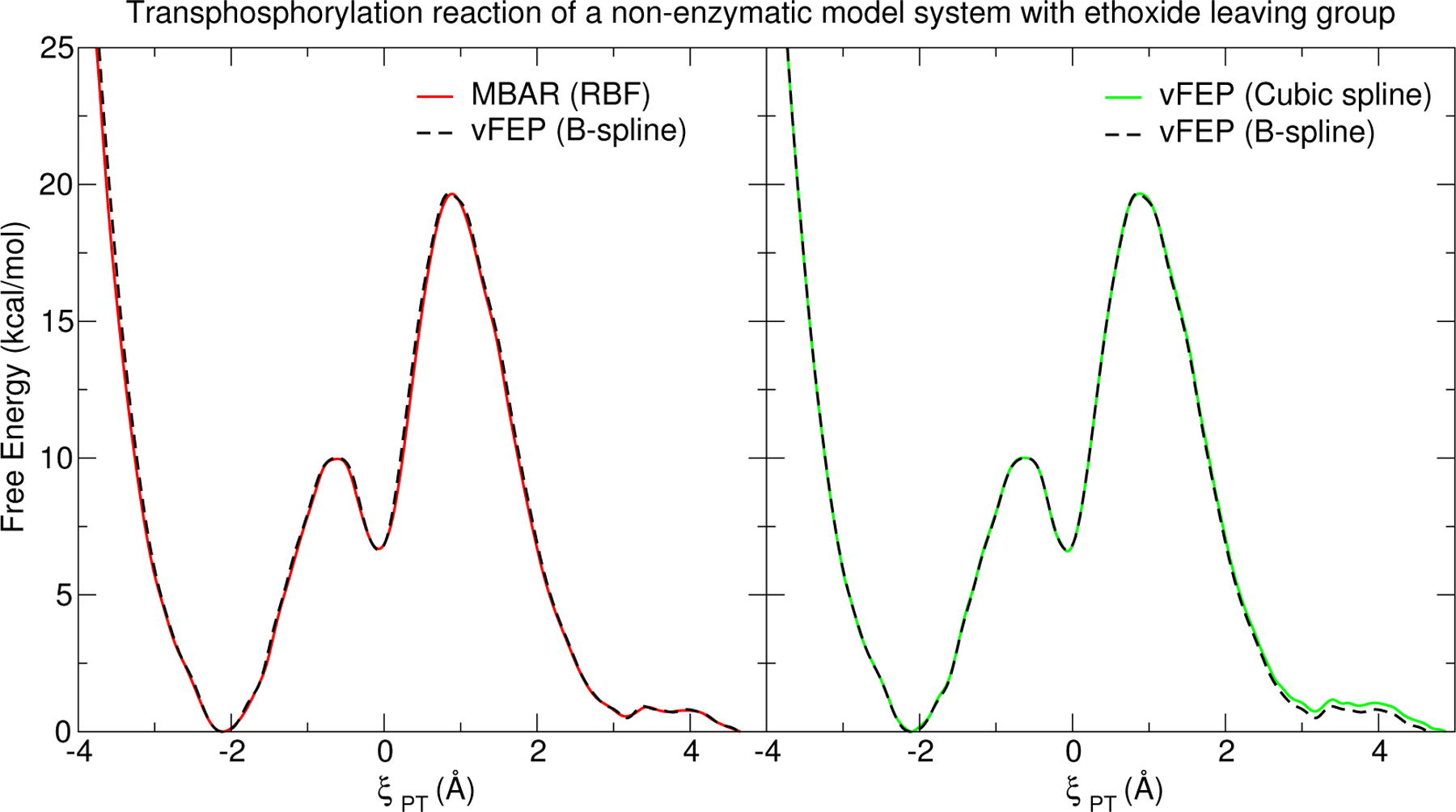
Free energy curve (1D) for the associative transphosphorylation reaction of a non-enzymatic model system with an ethoxide leaving group (illustrated in Fig. 1) simulated with PBE0/6–31G* QM/MM in explicit TIP4P/Ew water. Analysis with vFEP (B-spline) was performed using B-spline order 5 and 0.15 Å node spacing.
2-dimensional example: ϕ/ψ (Ramachandran) conformational maps for dipeptides in solution
The purpose of this section is to illustrate that the vFEP B-spline method is of equivalent or superior accuracy and computational efficiency for 2-D applications to the vFEP cubic spline implementation, and that both vFEP methods perform better than MBAR using a numerical histogram data representation. The 2-dimensional Ramachandran FESs of glycine, alanine, and valine dipeptide are shown in Fig. 4. The cardinal B-spline FESs use 5th order B-splines and a 10 degree node spacing. The MBAR histogram spacing is 10 degrees. The colored blocks in the MBAR FES are the histogram free energy values, whereas the stationary points and minimum energy path are determined from a B-spline representation of the histogram values. The free energy pathways were obtained from minimizations on the reduced dimensional FES rather than explicit dynamical simulation of the physical system. The procedure is analogous to our description of the finite temperature string umbrella sampling method; however, minimizations are performed on the umbrella-biased FES rather than performing umbrella simulations. In this sense, one can consider the procedure to be a zero temperature string umbrella minimization method. The peptide dihedral angles are periodic coordinates; therefore, the positions of the observed reaction coordinates are treated with a minimum image convention. The cardinal B-spline vFEP method does not require a buffer region to define the free energy within the periodic range. Instead, evaluation of the FES near the boundary make use of the B-spline node parameters that wrap to the other side of the periodic range. Similarly, the cubic spline vFEP method52 must vary the spline coefficients with consideration of the periodic boundary conditions.
Figure 4:
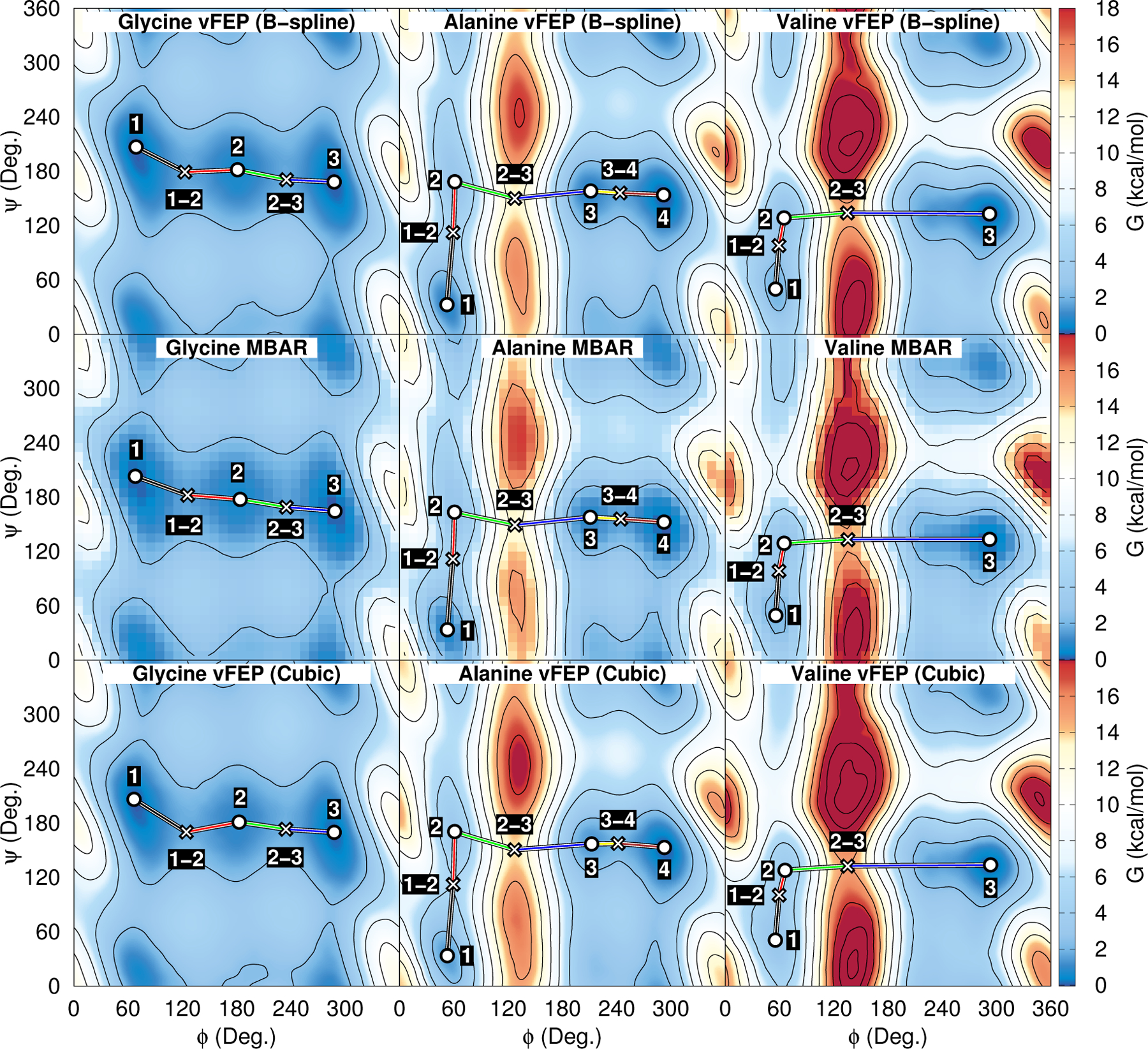
Glycine, alanine, and valine dipeptide FESs analyzed with vFEP and MBAR. The ϕ and ψ coordinates are the peptide dihedral angles. The umbrella window spacing is 8 degrees in each dimension. Analysis with vFEP (B-spline) was performed using B-spline order 5 and 10 degree node spacing.
We selected 3 or 4 minima from each system, connected them by a minimum energy path, and tabulate the stationary point positions and FES values in Table 1. In summary, the mean difference in the stationary point locations between B-spline vFEP and MBAR are 3.7, 1.5, and 0.7 degrees for glycine, alanine and valine, respectively. The larger differences in the glycine FES appear to be related to the broad, shallow minima. The root mean square deviation between the B-spline vFEP and MBAR stationary point FES values are less than 0.08 kcal/mol for each system. The cubic spline vFEP method does not compare as well to the MBAR results; the mean difference in locations are 5.8, 2.2, and 1.4 degrees for glycine, alanine and valine, respectively, and the root mean square deviation between the cubic spline vFEP and MBAR FES values are 0.16, 0.57, and 0.68 kcal/mol.
Table 1:
Selected stationary points from the glycine, alanine, and valine dipeptide free energy surfaces shown in Fig. 4.
| Label | vFEP (B-spline) | MBAR (B-spline) | vFEP (Cubic) | ||||||
|---|---|---|---|---|---|---|---|---|---|
|
Φ Deg. |
ψ Deg. |
ΔG kcal/mol |
Φ Deg. |
ψ Deg. |
ΔG kcal/mol |
Φ Deg. |
ψ Deg. |
ΔG kcal/mol |
|
| Glycine | |||||||||
| (1) | 68.9 | 206.8 | 0.03 | 67.9 | 203.1 | 0.05 | 66.6 | 206.3 | −0.05 |
| (1–2) | 122.7 | 179.1 | 1.65 | 125.8 | 182.2 | 1.58 | 124.3 | 170.2 | 1.44 |
| (2) | 181.0 | 181.7 | 0.60 | 183.8 | 177.6 | 0.54 | 182.7 | 181.1 | 0.80 |
| (2–3) | 235.1 | 170.7 | 1.69 | 235.0 | 169.0 | 1.64 | 234.5 | 173.3 | 1.83 |
| (3) | 287.8 | 168.2 | 0.00 | 288.7 | 164.6 | 0.00 | 287.8 | 169.8 | 0.00 |
| Alanine | |||||||||
| (1) | 52.4 | 32.7 | 0.81 | 52.9 | 33.6 | 0.73 | 52.8 | 33.6 | 1.42 |
| (1–2) | 59.2 | 112.3 | 4.45 | 58.9 | 111.6 | 4.37 | 59.2 | 112.3 | 5.08 |
| (2) | 61.0 | 168.4 | 2.76 | 60.7 | 163.5 | 2.75 | 60.9 | 170.8 | 3.37 |
| (2–3) | 127.4 | 150.0 | 13.20 | 127.5 | 149.3 | 13.06 | 127.1 | 150.6 | 13.69 |
| (3) | 211.3 | 158.3 | 0.88 | 210.8 | 157.9 | 0.81 | 212.3 | 157.0 | 1.40 |
| (3–4) | 243.7 | 156.1 | 1.63 | 244.5 | 155.9 | 1.57 | 241.5 | 157.6 | 1.95 |
| (4) | 291.9 | 154.0 | 0.00 | 292.3 | 152.6 | 0.00 | 292.7 | 153.2 | 0.00 |
| Valine | |||||||||
| (1) | 55.6 | 49.9 | 1.92 | 55.9 | 49.4 | 1.98 | 55.4 | 50.7 | 2.80 |
| (1–2) | 59.4 | 98.0 | 2.80 | 59.5 | 98.5 | 2.88 | 59.7 | 100.5 | 3.67 |
| (2) | 65.0 | 128.5 | 2.46 | 65.1 | 129.2 | 2.59 | 66.1 | 127.9 | 3.45 |
| (2–3) | 135.1 | 134.0 | 14.56 | 135.6 | 133.2 | 14.62 | 135.4 | 132.6 | 15.14 |
| (3) | 292.2 | 133.0 | 0.00 | 292.3 | 133.5 | 0.00 | 293.4 | 133.9 | 0.00 |
Figure 5 illustrates the sensitivity of the glycine minimum energy path with respect to grid spacing and cardinal B-spline order. The grid spacing does not effect the number of umbrella window simulations being analyzed, but it does effect the number of optimizable B-spline parameters. As the grid spacing decreases, the number of optimizable parameters increase and the B-splines are more capable of capturing the numerical noise in the data by introducing polynomic oscillations. The MBAR method suffers from a similar phenomenon whereby numerical noise becomes more pronounced when the histogram bin sizes are small. Figure 5 also shows the glycine minimum energy path is not sensitive to the cardinal B-spline order. Order 3 B-splines are the smallest order that produce smooth curves. Order 1 B-splines are discontinuous offset constants, and order 2 B-splines linearly interpolate between the nearest corners.
Figure 5:
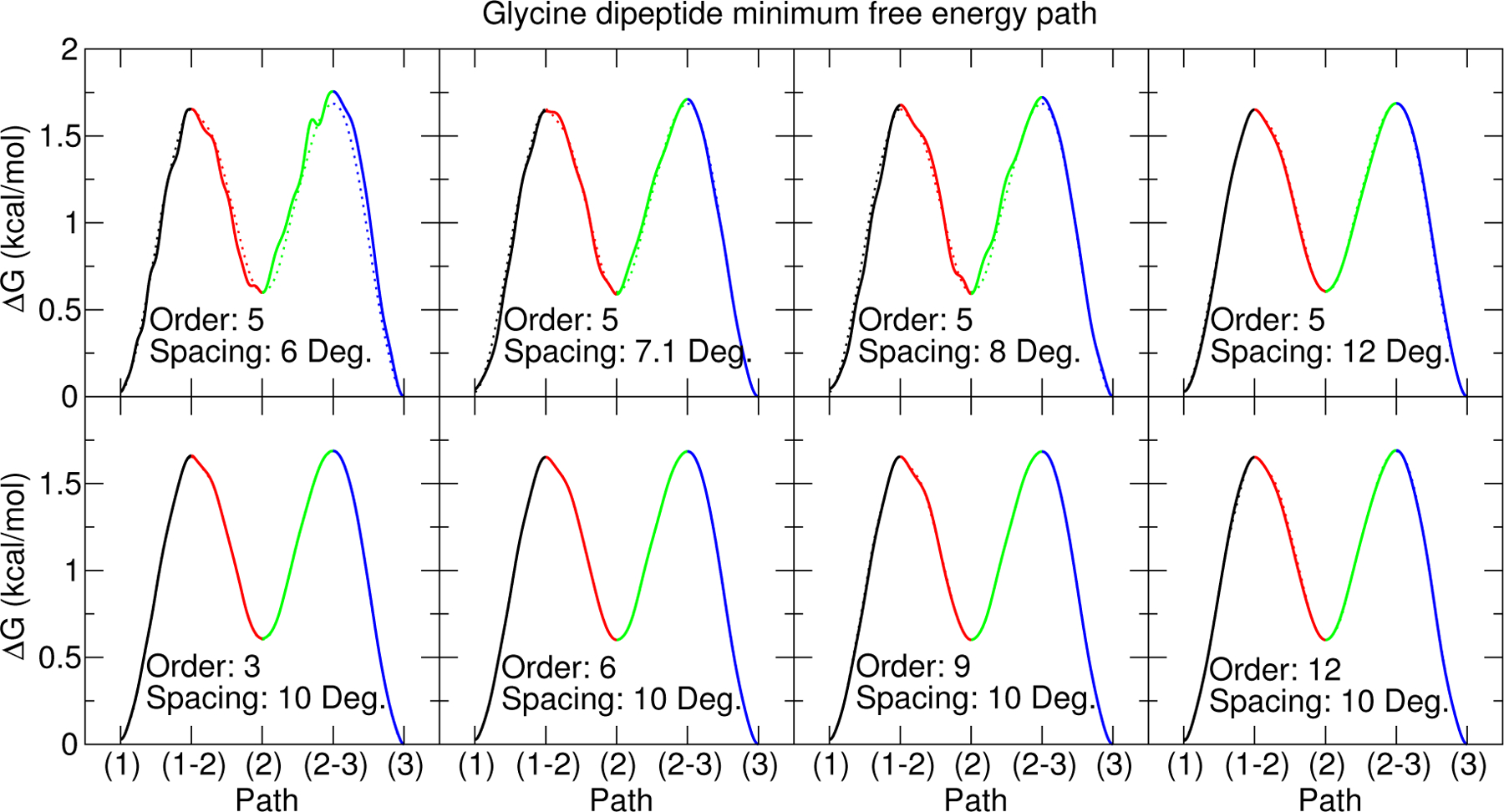
Comparison of vFEP glycine dipeptide minimum free energy paths as a function of cardinal B-spline order and node spacing. The stationary points labels correspond to those shown in Fig. 4. The dotted line in each pane is the vFEP result using 5th order B-splines and a 10 degree node spacing.
The non-enzymatic transphosphorylation reaction and Ramachandran profiles are expected to yield smooth FESs due to their simplicity; however, it may be difficult to distinguish between numerical noise and physically relevant features in FESs of highly diffusive processes such as those which might appear in protein conformational changes and protein folding. One approach explored in previous work to deal with numerical noise is to use Gaussian process regression to fit a smooth function to binned free energy values contaminated with numerical noise.51 The approach used in the present work is to choose a sufficiently large bin width to reduce the numerical noise and then interpolate between the observed values. In the context of MBAR, the histogram bins effectively average the free energy in a their respective regions of space, thus eliminating features within their interior. The free energy at the bin center is assumed to be the average value, and values near the histogram edges are approximated by interpolation. The strategy is to choose a small bin width to reduce the errors in these approximations, but large enough for each bin to contain a sufficient number of samples to adequately model the probability density. If the bins become too small, the FES will contain noise and possibly artificial minima. For example, Fig. 6(a) plots the number of minima on the non-enzymatic transphosphorylation reaction profile as a function of MBAR histogram bin width. The number of minima stabilizes for widths larger than 0.1 Å. That does not mean that the FESs using widths near 0.1 Å are free of numerical noise; it only only means that the magnitude of the noise is not large enough to produce additional minima. The addition of noise will also effect the activation energy (the difference between the lowest free energy near the reactant minimum and the highest free energy near the transition state), shown in Fig. 6(b). As the noise increases, the gap between these limits will also increase. Alternately, if the bin widths become large, the binning of data may result in an underestimation of the transition state free energies and overestimation of the free energies near the minima. Figure 6(c) plots the activation energy for bin widths between 0.1 Å (which is the smallest width that yields a stable number of minima) and 0.15 Å. In this range, the activation energy ranges from 19.6 to 19.7 kcal/mol. Ultimately, the inspection of Fig. 6(b) is not a very good approach for choosing bin widths because it compares two points on the surface to make a judgment on the entire surface. We find Fig. 6(a) to be a better means for distinguishing between noise and real features in simple surfaces. For complicated systems, a general mechanism for properly distinguishing numerical noise from real features may require multiple, independent umbrella window simulations.
Figure 6:
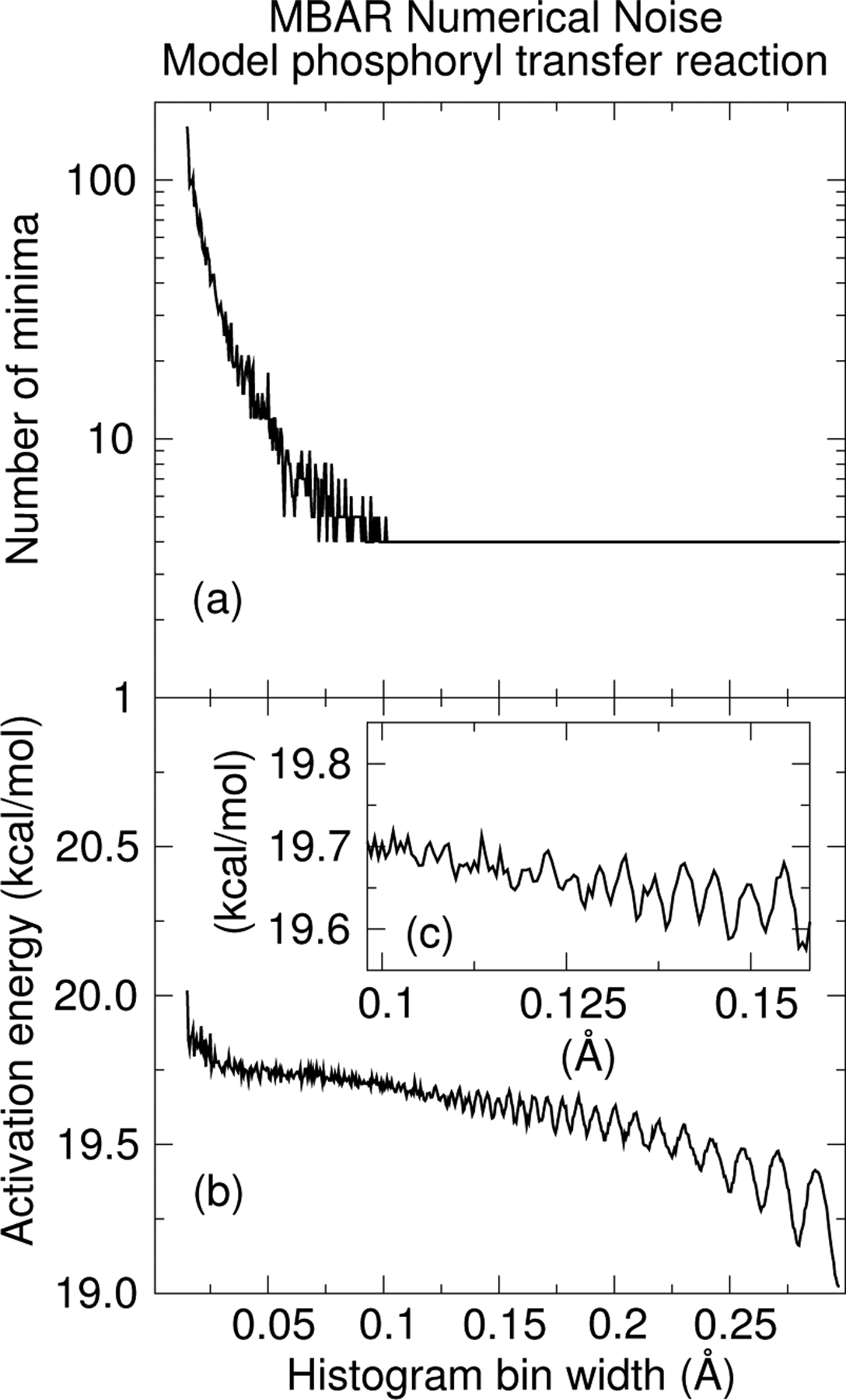
(a) The number of minima in the 1-dimensional non-enzymatic transphosphorylation reaction computed with MBAR and interpolated with RBFs. The image shows how the number of minima change as the histogram bin width is varied. (b) The activation free energy as a function of histogram bin width. The reactant and transition state free energies are the lowest and highest free energies found in the region of the reactant well and transition state region, respectively. (c) A zoomed version of (b) in the range 0.10 to 0.15 Å bin width.
Figure 7 compares the MBAR and vFEP wallclock times as a function of the number of windows included in the 2-dimensional analysis of the alanine dipeptide system. To make this plot, entire rows or columns from the 2-dimensional matrix of umbrella windows were uniformly deleted to create a sparse set of data to compare timings. For the vFEP methods, the timings include the nonlinear optimization of Eq. 2. The MBAR timings include the optimization of Eq. 23 and the evaluation of Eq. 20. The B-spline and cubic spline vFEP methods scale linearly with respect to the number of umbrella windows. The MBAR method scales quadratically. The quadratic character of the MBAR timings is more easily seen by comparing the ratio of timings between MBAR and B-spline vFEP, which scales linearly. The cardinal B-spline vFEP method is the fastest of the three. When the full set of data is analyzed, the B-spline vFEP method is 42 times faster than the cubic spline vFEP method and 166 times faster than MBAR. Optimization of the MBAR/UWHAM objective function using the full set of simulation data required 12 hours on a single Intel Xeon E5–2630 v3 (2.60 GHz) core, whereas the optimization of the vFEP B-spline parameters completed within 5 minutes.
Figure 7:
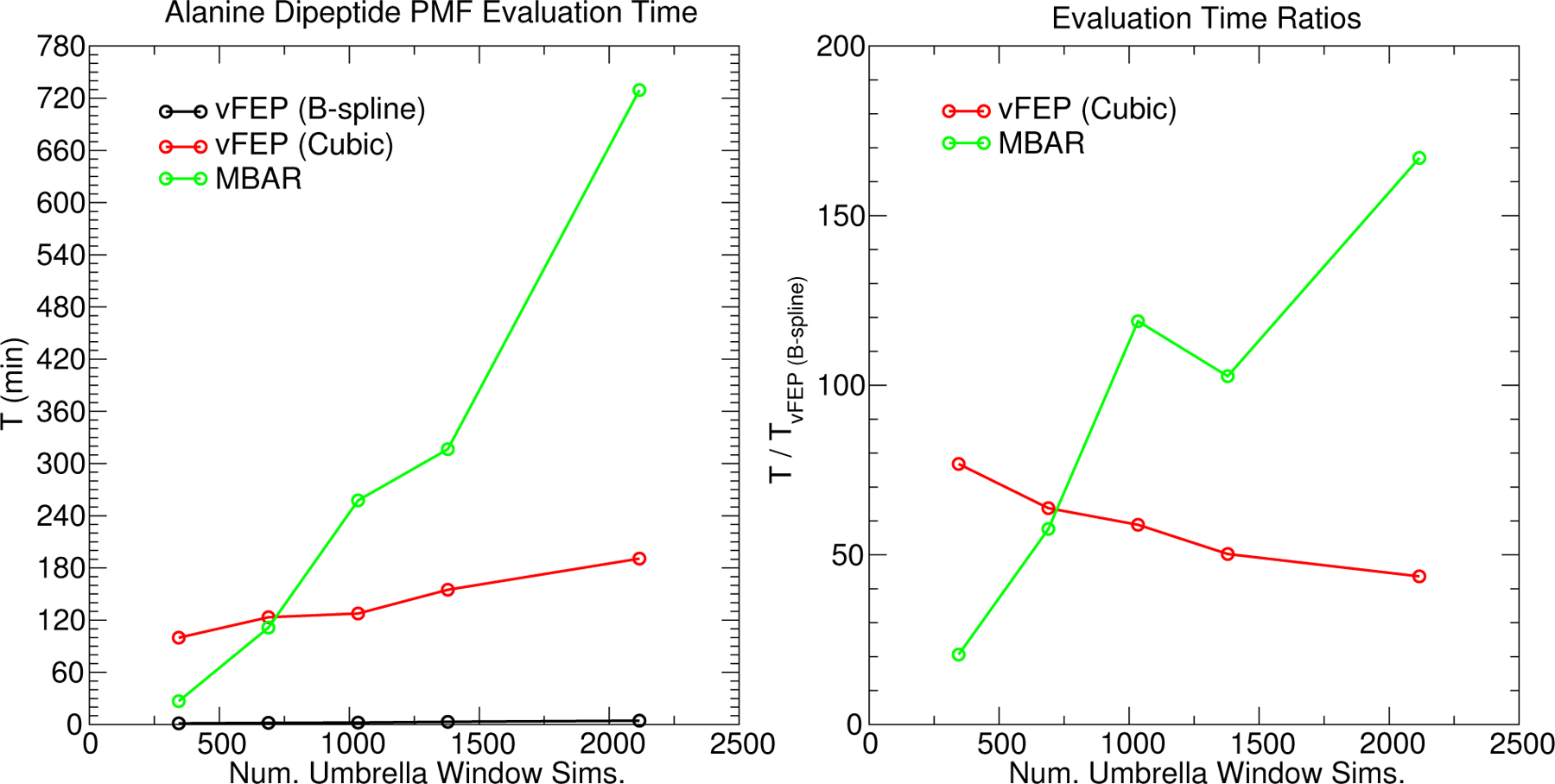
The wallclock time required to optimize the vFEP (Eq. 2) and MBAR/UWHAM (Eqs. 20 and 23) objective functions for the 2D alanine dipeptide FES as a function of the number of umbrella window simulations. Each simulation contributes 2000 data points.
Figure. 8 illustrates the behavior of the vFEP and MBAR FESs of alanine dipeptide as the number of umbrella window simulations included in the analysis becomes sparse. As the umbrella window spacing increases, fewer simulations are included in the analysis. The regular grid spacing of B-spline control points increases from 10 degrees to 24 and 40 degrees as the regular grid of umbrella windows increases from 8 to 24 and 40 degrees, respectively. The regular grid spacing of MBAR histogram bins and the cubic spline vFEP control points are similarly increased. By increasing the width of the histogram bins (or separation between control points), we avoid encountering spatial gaps in the observed samples when the number of simulations becomes sparse. The blocks of solid colors in the MBAR FESs are the histogram free energy values; however, the free energy pathway and stationary point locations are determined from B-spline interpolation through the histogram values. The cubic spline and cardinal B-spline vFEP methods produce nearly indistinguishable surfaces using 8 and 24 degree umbrella window spacing. When the spacing is increased to 40 degrees, the vFEP methods still appear to be qualitatively correct. In contrast, the quality of the MBAR surface degrades as the spacing is increased. At a 40 degree spacing, the MBAR method fails to predict one of the minima and associated transition state. The observation that vFEP yields good quality FESs with sparse umbrella window data is consistent with previous work.52,53
Figure 8:
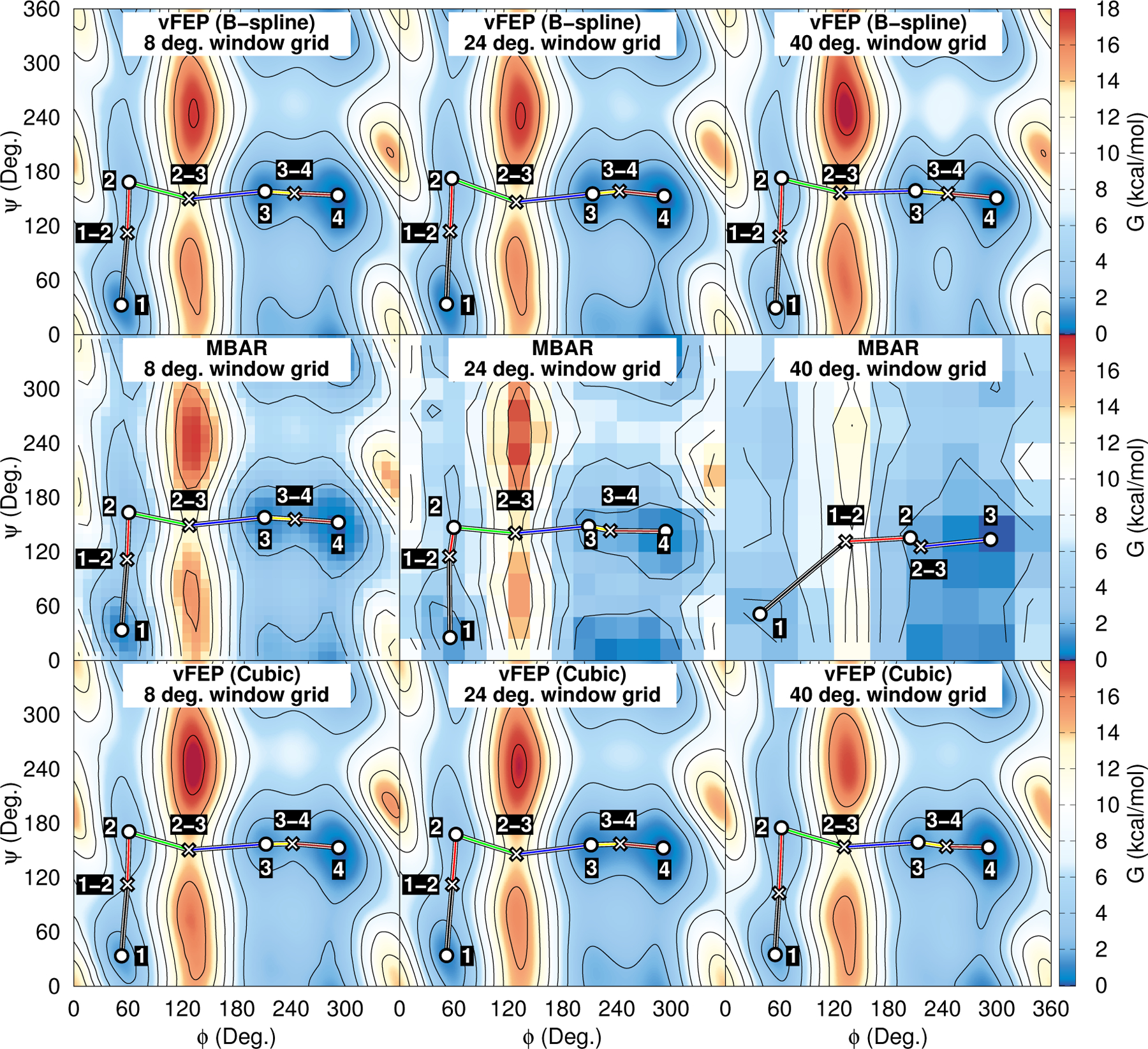
Alanine dipeptide FESs analyzed with vFEP and MBAR. The ϕ and ψ coordinates are the peptide dihedral angles. The umbrella window spacing are 8, 24, and 40 degrees in the left, center, and right columns, respectively.
3-, 4- and 6-dimensional examples: enzymatic transphosphorylation reaction catalyzed by the hammerhead ribozyme (HHr)
Previous formulations of vFEP could only be applied to 1- and 2-dimensional FESs;52,53 therefore, the purpose of this section is to apply the B-spline vFEP and MBAR methods to the calculation of a 3-dimensional FES. We have chosen a well studied archetype RNA enzyme, the hammerhead ribozyme (HHr) for the example.88,100–103 Study of HHr, along with other small self-cleaving ribozymes,104 has provided new insight into RNA enzyme design.61 The HHr catalyzes the self-cleavage of the RNA phosphodiester backbone using a general acid-base mechanism60 illustrated in Fig. 2. The reaction involves activation of a 2’OH nucleophile by a general base guanine residue (deprotonated at the N1 position). The resulting 2’O oxyanion then makes an inline attack to the adjacent scissile phosphate to form a pentavalent dianionic transition state (or high-energy intermediate), followed by departure of the O5’ leaving group with the assistance of a proton that is donated from a general acid. Hence, there are three fundamental reaction coordinates used to represent progression of the general base (ξGB = RO2’-H − RG12:N1-H), phosphoryl transfer (ξPT = RO5’-P − RO2’-P), and general acid (ξGA = RG8:O2’-H − RO5’-H) steps (Fig. 2).
Figure 9 illustrates the 3-dimensional FESs of the associative transphosphorylation reaction pathway catalyzed by the HHr computed using AM1/d-PhoT97 QM/MM. The MBAR and cardinal B-spline vFEP method yield near identical results. The B-spline vFEP reaction barrier is 35.24 kcal/mol, which closely agrees with the MBAR value of 35.20 kcal/mol. The comparison of analysis wall clock times is shown in Fig. 10. When all 50 string iterations are included in the analysis, the MBAR method is 4.5 times faster than the B-spline vFEP method. When fewer string iterations are included, the MBAR method is 10 to 20 times faster. The vFEP method becomes more competitive as the number of simulations increase because the B-spline vFEP and MBAR methods scale linearly and quadratically with respect to the number of simulations, respectively. Relative to the 2-dimensional timings, the performance of the MBAR and B-spline vFEP methods are far more comparable to each other for 3-dimensional analysis because the scaling of the MBAR method does not depend on dimensionality, whereas the numerical integration of the vFEP configuration integral quickly increases as the dimensionality increases. Based on the formal scaling of the algorithms and the observed timings of 2- and 3-dimensional analysis, we conclude that the MBAR approach is more practical for analyzing FESs involving 4-or-more reaction coordinates, and thus we use this approach in the 4- and 6-dimensional examples below.
Figure 9:
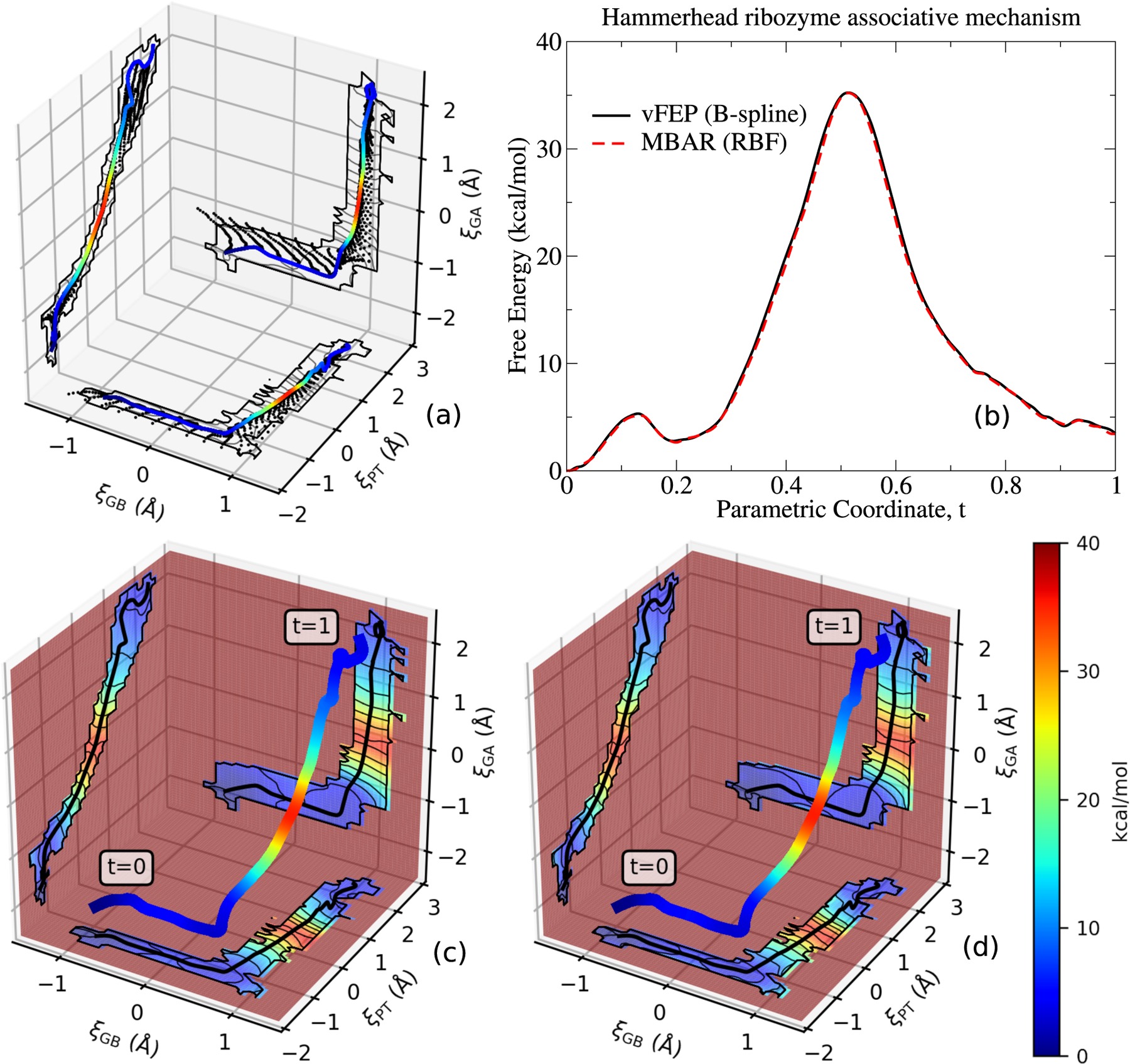
Free energy surface (3D) for the associative transphosphoylation reaction catalyzed by the HHr (illustrated in Fig. 2) computed from AM1/d-PhoT QM/MM. Subplot (a) shows the umbrella window locations encountered by the finite temperature string umbrella sampling method. The umbrella window locations are projected onto planes intersecting the final path, which is shown as the colored line. The RBF MBAR and B-spline vFEP free energy profile of the final path is shown in figure (b). Figures (c) and (d) display the RBF MBAR and B-spline vFEP free energy surfaces projected onto planes that intersect the final path.
Figure 10:
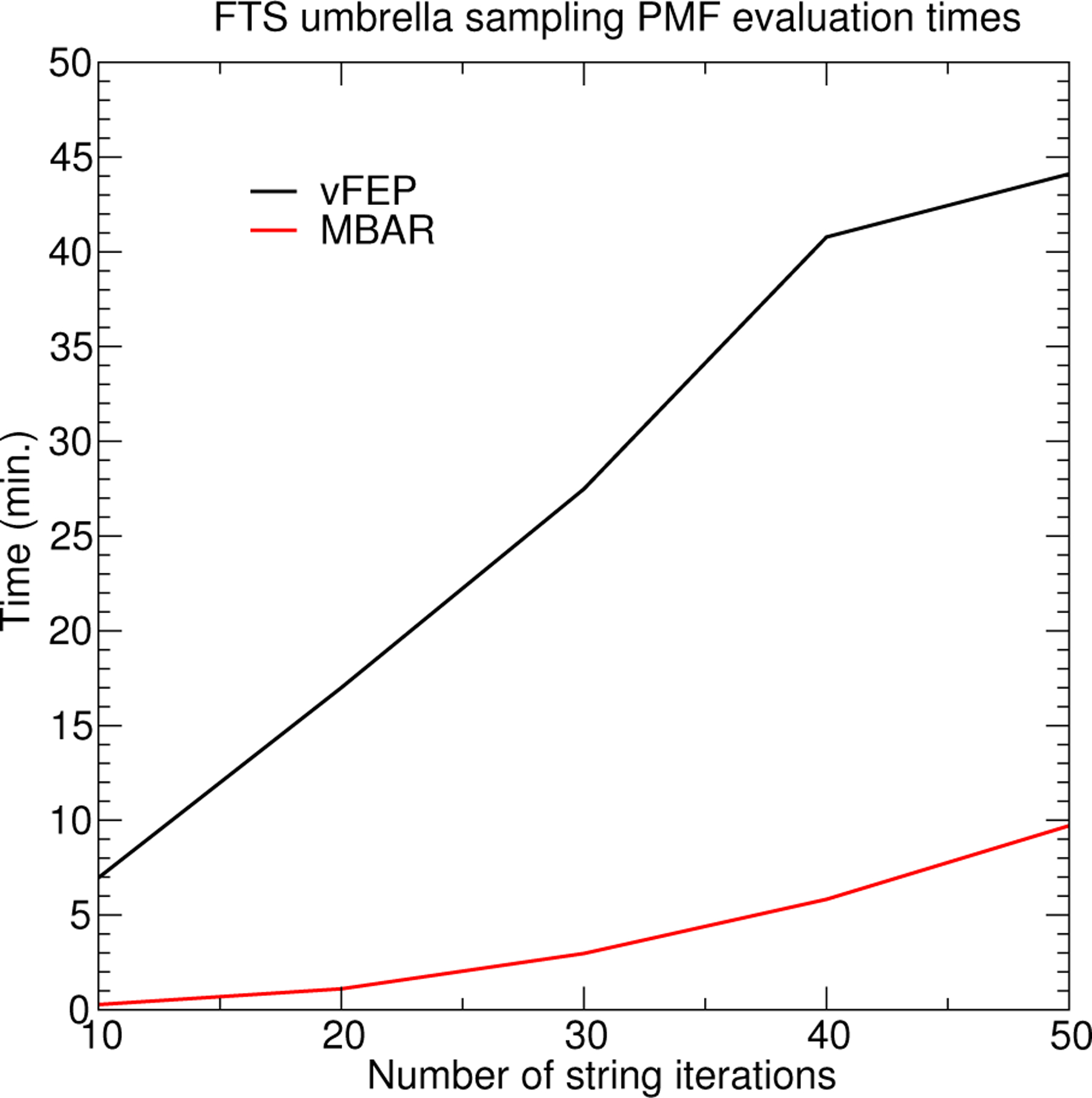
Comparison of evaluation times for generating the 3D Hammerhead ribozyme FES as a function of the number of finite temperature string umbrella sampling iterations. Each iteration contributes 32 umbrella window simulations, and each umbrella window simulation contributes 80 data points.
Calculated reaction pathways and barrier heights are effected by restricting the free energy profile to a reduced hypersurface of reaction coordinates. Performing the analysis with limited degrees of freedom effectively imposes constraints on the free energy. The remainder of this section illustrates application of the MBAR method for analyzing 3-, 4- and 6-dimensional FESs from the finite temperature string umbrella sampling method. Comparison of 3-, 4- and 6-dimensional FESs enable one to explore the degree to which the pathway and barriers are affected by choice of reaction coordinates. The 3-dimensional surface of the associative reaction consisted of ξGB, ξPT, and ξGA coordinates. Each of these coordinates are bond length differences between 3 atoms. We constructed a 4-dimensional profile by explicitly tracking the O2’-P and O5’-P bond distances, rather than the combined coordinate ξPT, to describe the phosphoryl transfer coordinate. In other words, the 4 reaction coordinates are ξGB, RO2’-P, RO5’-P, and ξGA. Exploration of these degrees of freedom separately can help to identify and distinguish associative pathways where nucleophilic attack occurs first, versus dissociative pathways where leaving group departure occurs first. A 6-dimensional profile was similarly constructed by decomposing the combined ξGB and ξGA coordinates into their component distances as well. The minimum free energy path was searched in the space of 3-, 4-, and 6-dimensional reaction coordinates, and the MBAR free energies along the converged pathways are shown in Fig. 11. The free energy barriers and average distances in the transition state ensemble are summarized in Table 2. The umbrella window simulations used to characterize the 3-, 4-, and 6-dimensional profiles were performed independently; that is, the 4- and 6-dimensional profiles are not a reanalysis of the umbrella window simulations generated for the 3-dimensional profile. Overall, the profiles are qualitatively similar (Fig. 11a); however, the 4- and 6-dimensional reaction barriers are 0.6 and 1.5 kcal/mol lower than the 3-dimensional barrier, respectively. This is consistent with the added degrees of freedom that enable identification of a slightly lower free energy pathway. Figure 11b shows that the 6-dimensional profile yields an “earlier” transition state (greater degree or O2’-P bond formation and lesser degree of O5’-P bond cleavage) than the 3- or 4-dimensional profiles. The comparison of transition state bond lengths suggests that the largest difference in the 6-dimensional profile is the O5’-P distance which undergoes a systematic contraction as the degrees of freedom increase. This contraction of the O5’-P distance is coupled with an increase in the O5’-H distance. This implies that cleavage of the O5’-P bond is less advanced, as is the degree of proton transfer (O5’-H bond formation) from the general acid. While this is a fairly subtle difference, it is nonetheless significant, and could be detected experimentally by measurement of linear free energy relations105,106 or kinetic isotope effects107,108 at primary and secondary oxygen positions, as have been performed recently for similar reactions in the Varkud satellite ribozyme56 and RNase A.109,110
Figure 11:
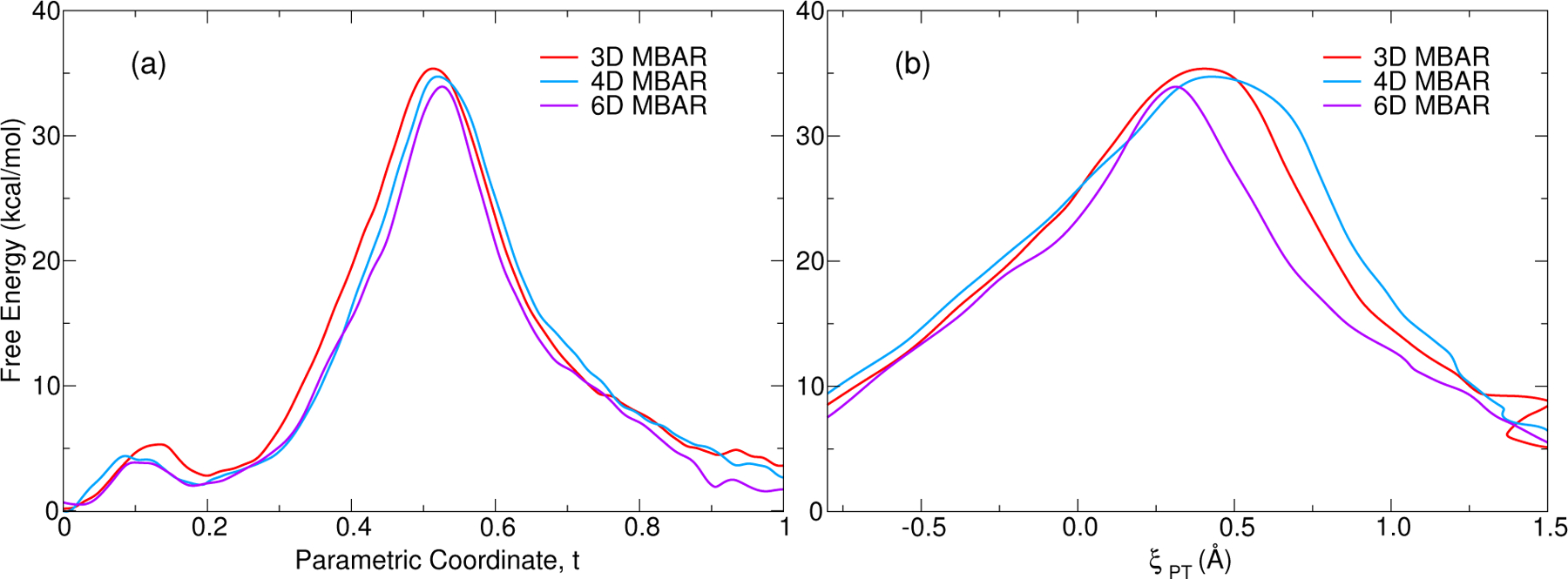
Comparison of minimum free energy paths from 3D, 4D and 6D representations of the associative transphosphoylation reaction catalyzed by the HHr. Left panel shows the RBF MBAR free energy with respect to progress along the path. Right panel shows the MBAR results with respect to the phosphoryl transfer coordinate ξPT.
Table 2:
Free energy barrier (kcal/mol) and average distances (Å) from the 3D, 4D and 6D minimum free energy pathways of the associative transphosphoylation reaction catalyzed by the HHr. Atom labels are defined in Fig. 2.
| ΔG‡ | G12:N1-H | O2’-H | O2’-P | O5’-P | O5’-H | G8:O2’-H | |
|---|---|---|---|---|---|---|---|
| 3D | 35.2 | 1.03 | 1.89 | 1.82 | 2.27 | 1.35 | 1.24 |
| 4D | 34.6 | 1.03 | 1.89 | 1.79 | 2.22 | 1.38 | 1.20 |
| 6D | 33.8 | 1.02 | 1.88 | 1.83 | 2.06 | 1.41 | 1.20 |
Hence, the ability to analyze and construct robust multidimensional free energy surfaces is important for mechanistic studies of protein and RNA enzymes. Frequently 2D or 3D surfaces are used with fairly dense sampling and coverage throughout the coordinate space in order to identify the main reaction pathways in a reduced coordinate space. These pathways can then undergo refinement to provide further resolution. The methods presented in the present work provide powerful analysis tools for construction of robust, analytic FESs for both of these scenarios. It is the hope that the use of these tools, which have been implemented in the FE-ToolKit software package,69 will enable new insights to be gained and facilitate discovery for a wide array of free energy applications.
Conclusions
We implemented two strategies for calculating high-dimensional FES profiles. We provided examples that utilized the methods to analyze 1-, 2-, 3-, 4-, and 6-dimensional FESs. The first strategy that we implemented is based on the vFEP method. Previous implementations of vFEP used a cubic spline function to parameterize the FES; however, the software was limited to 1- and 2-dimensional FES analysis. Our implementation uses cardinal B-spline functions to parameterize the FES. This functional form allowed us to extend the implementation to arbitrary dimensions and improve the efficiency of vFEP by exploiting the B-spline’s compact support. Our B-spline vFEP method was shown to be 50 times faster than a previous implementation of cubic spline vFEP when applied to the analysis of 2-dimensional Ramachandran profiles. The second strategy that we implemented used the MBAR method to generate an unbiased probability density from a global reweighting of the observed samples. The principles behind the MBAR approach are not new to this manuscript; however, (1) our implementation makes use of the fast MBAR/UWHAM method for generating FESs, rather than solving the coupled MBAR equations, (2) we made the use of MBAR FESs practical for high-dimensions, (3) we introduced the use of B-splines and multiquadric radial basis functions to interpolate between the histogram FES values. We demonstrated that the cardinal B-spline and MBAR FESs produce nearly identical 1-, 2-, and 3-dimensional FES profiles. We compared the performance between the vFEP and MBAR methods and found the B-spline vFEP method is 150 times faster than MBAR when applied to periodic 2-dimensional FESs, but the MBAR method is 4.5 times faster than vFEP when evaluating unbounded 3-dimensional profiles. In other words, both methods are useful, but they appear to offer different performance advantages depending on the situation. In addition to being much faster at computing 2-dimensional FESs, we also demonstrated that the vFEP method produced FESs of superior quality when the surface was only sparsely sampled. The associative mechanism of Hammerhead ribozyme was examined using 3-, 4-, and 6-dimensional profiles, and it was found that the 4- and 6-dimensional reaction barriers were 0.6 and 1.5 kcal/mol smaller than 3-dimensional profiles. This work has thus developed and demonstrated new B-spline vFEP and MBAR methods for creation and analysis of robust, analytic free energy surfaces in arbitrary dimensions, and provided the broad scientific community with new software tools in FE-ToolKit that will enable their application to important problems.
Acknowledgments
The authors are grateful for financial support provided by the National Institutes of Health (No. GM107485 and GM062248). Computational resources were provided by the National Institutes of Health under grant no. S10OD012346, the Office of Advanced Research Computing (OARC) at Rutgers, the State University of New Jersey, and by the Extreme Science and Engineering Discovery Environment (XSEDE),111 specifically resources COMET and COMET GPU, which is supported by National Science Foundation grant no. ACI-1548562 (allocation number TG-CHE190067). The authors also acknowledge the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing HPC resources, specifically the Frontera Super-computer, that have contributed to the research results reported within this paper. URL: http://www.tacc.utexas.edu
References
- (1).Jorgensen WL Free energy calculations: a breakthrough for modeling organic chemistry in solution. Acc. Chem. Res 1989, 22, 184–189. [Google Scholar]
- (2).Straatsma TP; McCammon JA Computational alchemy. Annu. Rev. Phys. Chem 1992, 43, 407–435. [Google Scholar]
- (3).Chipot C, Pohorille A, Eds. Free Energy Calculations: Theory and Applications in Chemistry and Biology; Springer Series in Chemical Physics; Springer: New York, 2007; Vol. 86. [Google Scholar]
- (4).Lee T-S; Allen BK; Giese TJ; Guo Z; Li P; Lin C; D. M. T Jr.; Pearlman DA; Radak BK; Tao Y et al. Alchemical Binding Free Energy Calculations in AMBER20: Advances and Best Practices for Drug Discovery. J. Chem. Inf. Model 2020, 60, 5595–5623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Elber R; Karplus M A method for determining reaction paths in large molecules: Apllication to myoglobin. Chem. Phys. Lett 1987, 139, 375–380. [Google Scholar]
- (6).Fischer S; Karplus M Conjugate Peak Refinement: An Algorithm For Finding Reaction Paths And Accurate Transition States In Systems With Many Degrees Of Freedom. Chem. Phys. Lett 1992, 194, 252–261. [Google Scholar]
- (7).Grubmüller H Predicting slow structural transitions in macromolecular systems: Conformational flooding. Phys. Rev. E 1995, 52, 2893–2906. [DOI] [PubMed] [Google Scholar]
- (8).Yang A-S; Honig B Free energy determinants of secondary structure formation: II. antiparallel β-sheets. J. Mol. Biol 1995, 252, 366–376. [DOI] [PubMed] [Google Scholar]
- (9).Simmerling C; Fox T; Kollman PA Use of Locally Enhanced Sampling in Free Energy Calculations: Testing and Application to the α → β Anomerization of Glucose. J. Am. Chem. Soc 1998, 120, 5771–5782. [Google Scholar]
- (10).Apostolakis J; Ferrara P; Caflisch A Calculation of conformational transitions and barriers in solvated systems: Application to the alanine dipeptide in water. J. Chem. Phys 1999, 110, 2099–2108. [Google Scholar]
- (11).Garate JA; Oostenbrink C Free-energy differences between states with different conformational ensembles. J. Comput. Chem 2013, 34, 1398–1408. [DOI] [PubMed] [Google Scholar]
- (12).Turupcu A; Oostenbrink C Modeling of Oligosaccharides within Glycoproteins from Free-Energy Landscapes. J. Chem. Inf. Model 2017, 57, 2222–2236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Bash PA; Singh UC; Brown FK; Langridge R; Kollman PA Calculation of the relative change in binding free energy of a protein-inhibitor complex. Science 1987, 235, 574–576. [DOI] [PubMed] [Google Scholar]
- (14).Hwang J-K; Warshel A Semiquantitative Calculations of Catalytic Free Energies in Genetically Modified Enzymes. Biochemistry 1987, 26, 2669–2673. [DOI] [PubMed] [Google Scholar]
- (15).Kottalam J; Case DA Dynamics of Ligand Escape from the Heme Pocket of Myoglobin. J. Am. Chem. Soc 1988, 110, 7690–7697. [Google Scholar]
- (16).He X; Liu S; Lee T-S; Ji B; Man VH; York DM; Wang J Fast, Accurate, and Reliable Protocols for Routine Calculations of Protein-Ligand Binding Affinities in Drug Design Projects Using AMBER GPU-TI with ff14SB/GAFF. ACS Omega 2020, 5, 4611–4619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Miao Y; Bhattarai A; Wang J Ligand Gaussian accelerated molecular dynamics (LiG-aMD): Characterization of ligand binding thermodynamics and kinetics. J. Chem. Theory Comput 2020, 16, 5526–5547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Cruz J; Wickstrom L; Yang D; Gallicchio E; Deng N Combining Alchemical Transformation with a Physical Pathway to Accelerate Absolute Binding Free Energy Calculations of Charged Ligands to Enclosed Binding Sites. J. Chem. Theory Comput 2020, 16, 2803–2813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Cui D; Zhang BW; Tan Z; Levy RM Ligand Binding Thermodynamic Cycles: Hysteresis, the Locally Weighted Histogram Analysis Method, and the Overlapping States Matrix. J. Chem. Theory Comput 2020, 16, 67–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Perthold JW; Petrov D; Oostenbrink C Toward Automated Free Energy Calculation with Accelerated Enveloping Distribution Sampling (A-EDS). J. Chem. Inf. Model 2020, 60, 5395–5406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Sakae Y; Zhang BW; Levy RM; Deng N Absolute Protein Binding Free Energy Simulations for Ligands with Multiple Poses, a Thermodynamic Path That Avoids Exhaustive Enumeration of the Poses. J. Comput. Chem 2020, 41, 56–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Homeyer N; Gohlke H Extension of the free energy work flow FEW towards implicit solvent/implicit membrane MM-PBSA calculations. Biochim. Biophys. Acta 2015, 1850, 972–982. [DOI] [PubMed] [Google Scholar]
- (23).Gumbart JC; Teo I; Roux B; Schulten K Reconciling the Roles of Kinetic and Thermodynamic Factors in Membrane Protein Insertion. J. Am. Chem. Soc 2013, 135, 2291–2297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Lindahl E; Sansom MSP Membrane proteins: molecular dynamics simulations. Curr Opin Struct Biol 2008, 18, 425–431. [DOI] [PubMed] [Google Scholar]
- (25).Roux B Statistical mechanical equilibrium theory of selective ion channels. Biophys. J 1999, 77, 139–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Acevedo O; Jorgensen WL Advances in quantum and molecular mechanical (QM/MM) simulations for organic and enzymatic reactions. Acc. Chem. Res 2010, 43, 142–151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).Hu H; Lu Z; Parks JM; Burger SK; Yang W Quantum mechanics/molecular mechanics minimum free-energy path for accurate reaction energetics in solution and enzymes: sequential sampling and optimization on the potential of mean force surface. J. Chem. Phys 2008, 128, 34105. [DOI] [PubMed] [Google Scholar]
- (28).Li W; Rudack T; Gerwert K; Gräter F; Schlitter J Exploring the Multidimensional Free Energy Surface of Phosphoester Hydrolysis with Constrained QM/MM Dynamics. J. Chem. Theory Comput 2012, 8, 3596–3604. [DOI] [PubMed] [Google Scholar]
- (29).Bentzien J; Muller RP; Florián J; Warshel A Hybrid ab Initio Quantum Mechanics/Molecular Mechanics Calculations of Free Energy Surfaces for Enzymatic Reactions: The Nucleophilic Attack in Subtilisin. J. Phys. Chem. B 1998, 102, 2293–2301. [Google Scholar]
- (30).Lennartz C; Schäfer A; Terstegen F; Thiel W Enzymatic reactions of triosephosphate isomerase: a theoretical calibration study. J. Phys. Chem. B 2002, 106, 1758–1767. [Google Scholar]
- (31).Nam K; Prat-Resina X; Garcia-Viloca M; Devi-Kesavan LS; Gao J Dynamics of an enzymatic substitution reaction in haloalkane dehylogenase. J. Am. Chem. Soc 2004, 126, 1369–1376. [DOI] [PubMed] [Google Scholar]
- (32).Klähn M; Braun-Sand S; Rosta E; Warshel A On Possible Pitfalls in ab Initio Quantum Mechanics/Molecular Mechanics Minimization Approaches for Studies of Enzymatic Reactions. J. Phys. Chem. B 2005, 109, 15645–15650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).Pettitt B; Karplus M Conformational Free Energy of Hydration for the Alanine Dipeptide: Thermodynamic Analysis. J. Phys. Chem 1988, 92, 3994–3997. [Google Scholar]
- (34).Roux B The calculation of the potential of mean force using computer simulations. Comput. Phys. Commun 1995, 91, 275–282. [Google Scholar]
- (35).Wereszczynski J; McCammon JA Statistical mechanics and molecular dynamics in evaluating thermodynamic properties of biomolecular recognition. Q. Rev. Biophys 2012, 45, 1–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (36).Torrie GM; Valleau JP Monte Carlo free energy estimates using non-Boltzmann sampling: Application to the sub-critical Lennard-Jones fluid. Chem. Phys. Lett 1974, 28, 578–581. [Google Scholar]
- (37).Torrie GM; Valleau JP Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys 1977, 23, 187–199. [Google Scholar]
- (38).Hansen HS; Hünenberger PH Using the local elevation method to construct optimized umbrella sampling potentials: calculation of the relative free energies and interconversion barriers of glucopyranose ring conformers in water. J. Comput. Chem 2010, 31, 1–23. [DOI] [PubMed] [Google Scholar]
- (39).Mezei M Adaptive umbrella sampling: Self-consistent determination of the non-Boltzmann bias. J. Comput. Phys 1987, 68, 237–248. [Google Scholar]
- (40).Bartels C; Karplus M Multidimensional adaptive umbrella sampling: applications to main chain and side chain peptide conformations. J. Comput. Chem 1997, 18, 1450–1462. [Google Scholar]
- (41).Bartels C; Karplus M Probability distributions for complex systems: adaptive umbrella sampling of the potential energy. J. Phys. Chem. B 1998, 102, 865–880. [Google Scholar]
- (42).Yang M; MacKerel AD Jr. Conformational sampling of oligosaccharides using Hamiltonian replica exchange with two-dimensional dihedral biasing potentials and the weighted histogram analysis method (WHAM). J. Chem. Theory Comput 2015, 11, 788–799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).Wojtas-Niziurski W; Meng Y; Roux B; Bernèche S Self-learning adaptive umbrella sampling method for the determination of free energy landscapes in multiple dimensions. J. Chem. Theory Comput 2013, 9, 1885–1895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (44).Kumar S; Bouzida D; Swendsen RH; Kollman PA; Rosenberg JM The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem 1992, 13, 1011–1021. [Google Scholar]
- (45).Boczko EM; Brooks III CL Constant-Temperature Free Energy Surfaces for Physical and Chemical Processes. J. Phys. Chem 1993, 97, 4509–4513. [Google Scholar]
- (46).Tan Z; Gallicchio E; Lapelosa M; Levy RM Theory of binless multi-state free energy estimation with applications to protein-ligand binding. J. Chem. Phys 2012, 136, 144102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Kästner J; Thiel W Bridging the gap between thermodynamic integration and umbrella sampling provides a novel analysis method: “Umbrella integration”. J. Chem. Phys 2005, 123, 144104. [DOI] [PubMed] [Google Scholar]
- (48).Kästner J; Thiel W Analysis of the statistical error in umbrella sampling simulations by umbrella integration. J. Chem. Phys 2006, 124, 234106. [DOI] [PubMed] [Google Scholar]
- (49).Kästner J Umbrella integration in two or more reaction coordinates. J. Chem. Phys 2009, 131, 034109. [DOI] [PubMed] [Google Scholar]
- (50).Shirts MR; Chodera JD Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys 2008, 129, 124105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Li P; Jia X; Pan X; Shao Y; Mei Y Accelerated Computation of Free Energy Profile at ab Initio Quantum Mechanical/Molecular Mechanics Accuracy via a Semi-Empirical Reference Potential. I. Weighted Thermodynamics Perturbation. J. Chem. Theory Comput 2018, 14, 5583–5596. [DOI] [PubMed] [Google Scholar]
- (52).Lee T-S; Radak BK; Pabis A; York DM A new maximum likelihood approach for free energy profile construction from molecular simulations. J. Chem. Theory Comput 2013, 9, 153–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (53).Lee T-S; Radak BK; Huang M; Wong K-Y; York DM Roadmaps through free energy landscapes calculated using the multidimensional vFEP approach. J. Chem. Theory Comput 2014, 10, 24–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (54).Schofield J Optimization and Automation of the Construction of Smooth Free Energy Profiles. J. Phys. Chem. B 2017, 121, 6847–6859. [DOI] [PubMed] [Google Scholar]
- (55).Gaines CS; Giese TJ; York DM Cleaning Up Mechanistic Debris Generated by Twister Ribozymes Using Computational RNA Enzymology. ACS Catal. 2019, 9, 5803–5815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (56).Ganguly A; Weissman BP; Giese TJ; Li N-S; Hoshika S; Saieesh R; Benner SA; Piccirilli JA; York DM Confluence of theory and experiment reveals the catalytic mechanism of the Varkud satellite ribozyme. Nat. Chem 2020, 12, 193–201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (57).Gaines CS; York DM Model for the Functional Active State of the TS Ribozyme from Molecular Simulation. Angew. Chem. Int. Ed 2017, 129, 13577–13580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (58).Ekesan Ş; York DM Dynamical ensemble of the active state and transition state mimic for the RNA-cleaving 8–17 DNAzyme in solution. Nucleic Acids Res. 2019, 47, 10282–10295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (59).Kostenbader K; York DM Molecular simulations of the pistol ribozyme: unifying the interpretation of experimental data and establishing functional links with the hammerhead ribozyme. RNA 2019, 25, 1439–1456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (60).Bevilacqua PC; Harris ME; Piccirilli JA; Gaines C; Ganguly A; Kostenbader K; Ekesan Ş; York DM An Ontology for Facilitating Discussion of Catalytic Strategies of RNA-Cleaving Enzymes. ACS Chem. Biol 2019, 14, 1068–1076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (61).Gaines CS; Picirilli JA; York DM The L-platform/L-scaffold framework: a blueprint for RNA-cleaving nucleic acid enzyme design. RNA 2020, 26, 111–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (62).Hub JS; de Groot BL; van der Spoel D g_wham – A Free Weighted Histogram Analysis Implementation Including Robust Error and Autocorrelation Estimates. J. Chem. Theory Comput 2010, 6, 3713–3720. [Google Scholar]
- (63).Huang M; Giese TJ; Lee T-S; York DM Improvement of DNA and RNA Sugar Pucker Profiles from Semiempirical Quantum Methods. J. Chem. Theory Comput 2014, 10, 1538–1545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (64).Huang M; Dissanayake T; Kuechler E; Radak BK; Lee T-S; Giese TJ; York DM A Multidimensional B-Spline Correction for Accurate Modeling Sugar Puckering in QM/MM Simulations. J. Chem. Theory Comput 2017, 13, 3975–3984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (65).Huang M; Giese TJ; York DM Nucleic acid reactivity: Challenges for next-generation semiempirical quantum models. J. Comput. Chem 2015, 36, 1370–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (66).E W; Ren W; Vanden-Eijnden E Finite temperature string method for the study of rare events. J. Phys. Chem. B 2005, 109, 6688–6693. [DOI] [PubMed] [Google Scholar]
- (67).Mills G; Jónsson H Quantum and thermal effects in H2 dissociative adsorption: Evaluation of free energy barriers in multidimensional quantum systems. Phys. Rev. Lett 1994, 72, 1124–1127. [DOI] [PubMed] [Google Scholar]
- (68).Mills G; Jónsson H; Schenter GK Reversible work transition state theory: application to dissociative adsorption of hydrogen. Surf. Sci 1995, 324, 305–337. [Google Scholar]
- (69).Giese TJ; York DM FE-ToolKit: The free energy analysis toolkit. https://gitlab.com/RutgersLBSR/fe-toolkit. [Google Scholar]
- (70).Milovanović GV; Udovičić Z Calculation of coefficients of a cardinal B-spline. Applied Mathematics Letters 2010, 23, 1346–1350. [Google Scholar]
- (71).Ding X; Vilseck JZ; Brooks CL III Fast Solver for Large Scale Multistate Bennett Acceptance Ratio Equations. J. Chem. Theory Comput 2019, 15, 799–802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (72).Press WH; Teukolsky SA; Vetterling WT; Flannery WP Numerical Recipes in Fortran, 2nd ed.; Cambridge University Press: Cambridge, 1992. [Google Scholar]
- (73).Ding X; Vilseck JZ; Hayes RL; Brooks CL Gibbs Sampler-Based λ-Dynamics and Rao-Blackwell Estimator for Alchemical Free Energy Calculation. J. Chem. Theory Comput 2017, 13, 2501–2510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (74).Zhang BW; Xia J; Tan Z; Levy RM A Stochastic Solution to the Unbinned WHAM Equations. J. Phys. Chem. Lett 2015, 6, 3834–3840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (75).Giese TJ; Panteva MT; Chen H; York DM Multipolar Ewald methods, 1: Theory, accuracy, and performance. J. Chem. Theory Comput 2015, 11, 436–450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (76).Hardy RL Multiquadric equations of topography and other irregular surfaces. J. Geophys. Res 1971, 76, 1905–1915. [Google Scholar]
- (77).Fornberg B; Wright G Stable compution of multiquadric interpolants for all values of the shape parameter. Comput. Math. with Appl 2004, 48, 853–867. [Google Scholar]
- (78).Acar E Optimizing the shape parameters of radial basis functions: An application to automobile crashworthiness. Proc. Inst. Mech. Eng. D 2010, 224, 1541–1553. [Google Scholar]
- (79).Fasshauer GE; Zhang JG On choosing “optimal” shape parameters for RBF approximation. Numer. Algorithms 2007, 45, 245–368. [Google Scholar]
- (80).Perdew JP; Ernzerhof M; Burke K Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys 1996, 105, 9982–9985. [Google Scholar]
- (81).Adamo C; Scuseria GE Accurate excitation energies from time-dependent density functional theory: Assessing the PBE0 model. J. Chem. Phys 1999, 111, 2889–2899. [Google Scholar]
- (82).Horn HW; Swope WC; Pitera JW; Madura JD; Dick TJ; Hura GL; Head-Gordon T Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. J. Chem. Phys 2004, 120, 9665–9678. [DOI] [PubMed] [Google Scholar]
- (83).Giese TJ; York DM Ambient-Potential Composite Ewald Method for ab Initio Quantum Mechanical/Molecular Mechanical Molecular Dynamics Simulation. J. Chem. Theory Comput 2016, 12, 2611–2632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (84).Maier JA; Martinez C; Kasavajhala K; Wickstrom L; Hauser KE; Simmerling C ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput 2015, 11, 3696–3713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (85).Darden T; York D; Pedersen L Particle mesh Ewald: An N log(N) method for Ewald sums in large systems. J. Chem. Phys 1993, 98, 10089–10092. [Google Scholar]
- (86).Essmann U; Perera L; Berkowitz ML; Darden T; Hsing L; Pedersen LG A smooth particle mesh Ewald method. J. Chem. Phys 1995, 103, 8577–8593. [Google Scholar]
- (87).Martick M; Lee T-S; York DM; Scott WG Solvent structure and hammerhead ribozyme catalysis. Chem. Biol 2008, 15, 332–342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (88).Chen H; Giese TJ; Golden BL; York DM Divalent Metal Ion Activation of a Guanine General Base in the Hammerhead Ribozyme: Insights from Molecular Simulations. Biochemistry 2017, 56, 2985–2994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (89).Case DA; Ben-Shalom IY; Brozell SR; Cerutti DS; Cheatham III TE; Cruzeiro VWD; Darden TA; Duke RE; Ghoreishi D; Gilson MK et al. AMBER 18. University of California, San Francisco: San Francisco, CA, 2018. [Google Scholar]
- (90).Pérez A; Marchán I; Svozil D; Sponer J; Cheatham III TE; Laughton CA; Orozco M Refinement of the AMBER force field for nucleic acids: Improving the description of α/γ conformers. Biophys. J 2007, 92, 3817–3829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (91).Zgarbová M; Otyepka M; Šponer J; Mládek A; Banáš P; Cheatham III TE; Jurečka P Refinement of the Cornell et al. nucleic acids force field based on reference quantum chemical calculations of glycosidic torsion profiles. J. Chem. Theory Comput 2011, 7, 2886–2902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (92).Joung IS; Cheatham III TE Determination of alkali and halide monovalent ion parameters for use in explicitly solvated biomolecular simulations. J. Phys. Chem. B 2008, 112, 9020–9041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (93).Li P; Roberts BP; Chakravorty DK; Merz KM Jr. Rational design of Particle Mesh Ewald compatible Lennard-Jones parameters for +2 metal cations in explicit solvent. J. Chem. Theory Comput 2013, 9, 2733–2748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (94).Panteva MT; Giambaşu GM; York DM Comparison of structural, thermodynamic, kinetic and mass transport properties of Mg2+ ion models commonly used in biomolecular simulations. J. Comput. Chem 2015, 36, 970–982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (95).Panteva MT; Giambasu GM; York DM Force Field for Mg2+, Mn2+, Zn2+, and Cd2+ Ions that have Balanced Interactions with Nucleic Acids. J. Phys. Chem. B 2015, 119, 15460–15470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (96).Ryckaert JP; Ciccotti G; Berendsen HJC Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of n-Alkanes. J. Comput. Phys 1977, 23, 327–341. [Google Scholar]
- (97).Nam K; Cui Q; Gao J; York DM Specific reaction parametrization of the AM1/d Hamiltonian for phosphoryl transfer reactions: H, O, and P atoms. J. Chem. Theory Comput 2007, 3, 486–504. [DOI] [PubMed] [Google Scholar]
- (98).Rosta E; Nowotny M; Yang W; Hummer G Catalytic mechanism of RNA backbone cleavage by ribonuclease h from quantum mechanics/molecular mechanics simulations. J. Am. Chem. Soc 2011, 133, 8934–8941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (99).Ganguly A; Thaplyal P; Rosta E; Bevilacqua PC; Hammes-Schiffer S Quantum Mechanical/Molecular Mechanical Free Energy Simulations of the Self-Cleavage Reaction in the Hepatitis Delta Virus Ribozyme. J. Am. Chem. Soc 2014, 136, 1483–1496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (100).Lee T-S; Silva Lopez C; Giambaşu GM; Martick M; Scott WG; York DM Role of Mg2+ in hammerhead ribozyme catalysis from molecular simulation. J. Am. Chem. Soc 2008, 130, 3053–3064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (101).Lee T-S; Giambaşu GM; Moser A; Nam K; Silva-Lopez C; Guerra F; Nieto-Faza O; Giese TJ; Gao J; York DM Unraveling the Mechanisms of Ribozyme Catalysis with Multiscale Simulations. In Multi-scale quantum models for biocatalysis; York DM, Lee T-S, Eds.; Challenges and advances in computational chemistry and physics; Springer: New York, 2009; Vol. 7; Chapter 14, pp 377–408. [Google Scholar]
- (102).Lee T-S; York DM Computational mutagenesis studies of hammerhead ribozyme catalysis. J. Am. Chem. Soc 2010, 132, 13505–13518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (103).Wong K-Y; Lee T-S; York DM Active participation of the Mg2+ ion in the reaction coordinate of RNA self-cleavage catalyzed by the hammerhead ribozyme. J. Chem. Theory Comput 2011, 7, 1–3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (104).Ganguly A; Weissman BP; Piccirilli JA; York DM Evidence for a Catalytic Strategy to Promote Nucleophile Activation in Metal-Dependent RNA-Cleaving Ribozymes and 8–17 DNAzyme. ACS Catal. 2019, 9, 10612–10617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (105).Huang M; York DM Linear free energy relationships in RNA transesterification: theoretical models to aid experimental interpretations. Phys. Chem. Chem. Phys 2014, 16, 15846–15855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (106).Chen H; Giese TJ; Huang M; Wong K-Y; Harris ME; York DM Mechanistic Insights into RNA Transphosphorylation from Kinetic Isotope Effects and Linear Free Energy Relationships of Model Reactions. Chem. Eur. J 2014, 20, 14336–14343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (107).Hengge AC Isotope effects in the study of phosphoryl and sulfuryl transfer reactions. Acc. Chem. Res 2002, 35, 105–112. [DOI] [PubMed] [Google Scholar]
- (108).Weissman BP; Li N-S; York DM; Harris M; Piccirilli JA Heavy atom labeled nucleotides for measurement of kinetic isotope effects. Biochim. Biophys. Acta 2015, 1854, 1737–1745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (109).Kellerman DL; York DM; Piccirilli JA; Harris ME Altered (transition) states: mechanisms of solution and enzyme catalyzed RNA 2′-O-transphosphorylation. Curr. Opin. Chem. Biol 2014, 21, 96–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (110).Harris ME; Piccirilli JA; York DM Integration of kinetic isotope effect analyses to elucidate ribonuclease mechanism. Biochim. Biophys. Acta 2015, 1854, 1801–1808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (111).Towns J; Cockerill T; Dahan M; Foster I; Gaither K; Grimshaw A; Hazlewood V; Lathrop S; Lifka D; Peterson GD et al. XSEDE: Accelerating Scientific Discovery. Comput. Sci. Eng 2014, 16, 62–74. [Google Scholar]


