Power and Sample Size for Observational Studies of Point Exposure Effects

Summary:

Inverse probability of treatment weights are commonly used to control for confounding when estimating causal effects of point exposures from observational data. When planning a study that will be analyzed with inverse probability of treatment weights, determining the required sample size for a given level of statistical power is challenging because of the effect of weighting on the variance of the estimated causal means. This paper considers the utility of the design effect to quantify the effect of weighting on the precision of causal estimates. The design effect is defined as the ratio of the variance of the causal mean estimator divided by the variance of a naïve estimator if, counter to fact, no confounding had been present and weights were not needed. A simple, closed-form approximation of the design effect is derived that is outcome invariant and can be estimated during the study design phase. Once the design effect is approximated for each treatment group, sample size calculations are conducted as for a randomized trial, but with variances inflated by the design effects to account for weighting. Simulations demonstrate the accuracy of the design effect approximation, and practical considerations are discussed.

1. Introduction

Researchers often aim to estimate causal effects rather than just associations between variables. In settings where experimental designs are implausible, inference relies on observational data from which measured associations can be confounded. Marginal structural models (MSMs) are a commonly used method to estimate causal effects in the presence of confounding variables (Hernán et al., 2000; Robins et al., 2000; Cole and Hernán, 2008; Brumback et al., 2004). These models can be fit using numerous methods, but are commonly fit via weighted estimating equations, where the weights are the inverse of each participant’s probability of the observed treatment (or exposure). For a binary point exposure, the estimand of interest is often the average causal effect, the difference in counterfactual means for the two treatment levels. With the assumptions of causal consistency, conditional exchangeability, and positivity, the inverse probability of treatment weight (IPTW) estimators are consistent for the MSM parameters for the causal means and the average causal effect (Lunceford and Davidian, 2004). Variance estimates are computed using standard estimating equation theory (Stefanski and Boos, 2002), with the empirical sandwich variance estimator providing a consistent estimator for the asymptotic variance of the estimated average causal effect.

While IPTW estimators provide researchers with an analytic tool for estimating causal effects in the presence of confounding variables, these estimators pose challenges during study design. The use of weights in the analysis affects the variance of the average causal effect estimator, making it challenging to determine the number of participants needed to achieve sufficient statistical power to detect a difference in causal means. Sample sizes cannot be calculated using standard methods that ignore weighting as in a randomized controlled trial (RCT) (e.g. as in Chow et al., 2017), as this will tend to be anti-conservative. Numerous papers have examined the properties of IPTWs and have developed guidelines and diagnostics for specifying weight models and adjusting estimated weights (Austin, 2009; Austin and Stuart, 2015; Cole and Hernán, 2008; Lee et al., 2011). However, currently no methods exist for power and sample size calculations for studies that will be analyzed using MSMs fit with IPTWs.

Weighted estimators are common in survey sampling, and methods have been developed to quantify the effect of weighting on the precision of estimates. Kish (1965, page 257) introduced the design effect under the randomization-based inferential paradigm for survey sampling. The design effect is the ratio of the variance of an estimator under a complex sample design to the variance of the estimator under a simple random sample. When participants are selected directly from the finite population rather than from clusters of correlated observations, the design effect for a population mean estimator simplifies to the design effect due to weighting (deff _w), or the unequal weighting effect (Kish, 1992). Let n be the sample size and w_i represent the sampling weight for the i^th participant, i.e., the inverse of participant i’s probability of selection. The design effect due to weighting is defined using either of the two equivalent forms:

$$def{f}_w=\frac{n{\sum }_{i=1}^n{w}_i^2}{{\left({\sum }_{i=1}^n{w}_i\right)}^2}=1+\frac{S^2(w)}{{\left(n^{-1}{\sum }_{i=1}^n{w}_i\right)}^2}$$ (1)

where S²(w) is the finite sample variance of the weights. The design effect is interpreted as an estimator’s increase in variance due to differential weights across participants. This metric is commonly applied to all types of complex sample designs in which individuals in the finite population have different probabilities of selection (Valliant et al., 2013, page 375). Gabler et al. (1999) provided a justification for how Kish’s design effect also applies to model-based estimators. In practice, the design effect is used to calculate the effective sample size, which is equal to the observed sample size divided by the design effect. The effective sample size can be interpreted as the sample size under simple random sampling that that would have produced the same variance as the sample selected under the complex design (Valliant et al., 2013, page 5).

Advantages of deff _w are that it is outcome invariant and allows the sample size under a complex design to be translated into a sample size under a simpler design with the same variance. The former implies that deff _w depends only on the participants’ weights and is constant across outcomes. The latter means that once deff _w is known or approximated, it can be used in power and sample size calculations along with the simpler assumptions needed to design a study without weights.

In this paper we consider design effects for planning observational studies to assess the effect of a treatment or exposure on an outcome of interest. In the analysis of observational data, McCaffrey et al. (2004, 2013) have used the effective sample size to quantify the loss of statistical precision following inference about causal effects using propensity score weighting. Here we describe the use of design effects for determining the sample size or power when designing an observational study to estimate point exposure effects. Section 2 introduces the design effect for causal inference and gives a large sample justification that the design effect can be approximated by Kish’s deff _w. Section 3 demonstrates how the design effect can be used to determine the sample size or power of an observational study that will be analyzed using IPTWs. Section 4 examines the accuracy of the design effect approximation for various exposure and outcome types via simulations, and Section 5 provides practical considerations regarding the use of design effects. Section 6 considers estimating the design effect in the setting where pilot data are available, and Section 7 concludes with a discussion of the results and implications. The supporting information includes proofs of the propositions appearing in the main text along with additional simulations and supplemental tables and figures.

2. The Design Effect

2.1. Preliminaries

Suppose an observational study is being planned where n independent and identically distributed copies of (A_i, L_i, Y_i) will be observed, where A_i is the binary treatment (exposure) status for participant i such that A_i = 1 if participant i received treatment and A_i = 0 otherwise, L_i is a vector of baseline covariates measured prior to A_i or unaffected by treatment A_i, and Y_i is the observed outcome for participant i. The outcome Y_i may be continuous or discrete.

The aim of the observational study will be to estimate the effect of treatment A on outcome Y. Specifically, let Y_1i denote the potential outcome if an individual i, possibly counter to fact, receives treatment. Similarly let Y_0i denote the potential outcome if individual i does not receive treatment, such that Y_i = A_iY_1i + (1 − A_i)Y_0i. Inference from the observational study will focus on parameters of the MSM E(Y_a) = β₀+β₁a, with particular interest in the parameter β₁ which equals the average causal effect ACE = E(Y₁)−E(Y₀) = μ₁ −μ₀. Note the MSM is saturated and thus does not impose any restrictions on the assumed structure of the data.

Under certain assumptions, the parameters of the MSM can be consistently estimated using IPTW. In particular, assume conditional exchangeability holds, i.e., Y_a ⊥ A | L for a ∈ {0, 1}. Also assume that positivity holds such that Pr(A = a | L = l) > 0 for all l such that dF_L(l) > 0 and a ∈ {0, 1}, where F_L is the cumulative distribution function of L. Estimating the average causal effect under the stated assumptions with the IPTW estimator first entails estimating the propensity score for each participant, defined as p_i = Pr(A_i = 1 | L_i) (Rosenbaum and Rubin, 1983). A model is fit to obtain ${\widehat{p}}_i$, each participant’s estimated probability of treatment conditional on observed covariates L_i. The estimated IPTW is then equal to ${\widehat{W}}_i=I\left(A_i=1\right){\widehat{p}}_i^{-1}+I\left(A_i=0\right){\left(1-{\widehat{p}}_i\right)}^{-1}$, where I(A_i = a) is a {0, 1} treatment indicator for participant i. The estimated average causal effect ${\widehat{\beta }}_1$ is obtained by regressing the observed outcome Y on treatment A with weights $\widehat{W}$ using weighted least squares. The resulting IPTW estimator is a difference in Hájek estimators for the two causal means (Hernán and Robins, 2020; Lunceford and Davidian, 2004):

$$\widehat{ACE}={\widehat{\mu }}_1-{\widehat{\mu }}_0=\frac{{\sum }_{i=1}^n{\widehat{W}}_i{Y}_{i}I\left(A_i=1\right)}{{\sum }_{i=1}^n{\widehat{W}}_{i}I\left(A_i=1\right)}-\frac{{\sum }_{i=1}^n{\widehat{W}}_i{Y}_{i}I\left(A_i=0\right)}{{\sum }_{i=1}^n{\widehat{W}}_{i}I\left(A_i=0\right)}$$ (2)

Augmented IPW estimators, which incorporate both outcome and treatment models, may be used instead of (2) to estimate the ACE. Such estimators are doubly robust and will be more efficient than (2) if both the treatment and outcome models are correctly specified (Robins et al., 1994; Lunceford and Davidian, 2004). Thus, the power and sample size calculations derived below, which are based on (2), will be conservative for studies analyzed with augmented IPW estimators when the outcome model is correctly specified.

2.2. The Design Effect for a Single Causal Mean

Define the design effect to equal the ratio of the (finite sample) variance of ${\widehat{\mu }}_a$ divided by the variance of a naïve causal mean estimator if, counter to fact, no confounding was present and weighting was not needed. That is,

$$def{f}_w^a=\frac{Var\left({\widehat{\mu }}_a\right)}{Var\left({\tilde{\mu }}_a\right)}$$

where ${\tilde{\mu }}_a=\left\{{\sum }_{i=1}^n{Y}_{i}I\left(A_i=a\right)\right\}/\left\{{\sum }_{i=1}^{n}I\left(A_i=a\right)\right\}$. The derivation of the design effect estimator relies on the following proposition. The proposition assumes that the weights are known and are denoted by W_a = P(A = a | L)⁻¹ for a ∈ {0, 1} with W = AW₁+(1−A)W₀. Let ${\sigma }_a^2=Var\left(Y_a\right)$ for a ∈ {0, 1}.

Proposition 1:

$$\sqrt{n}\left({\widehat{\mu }}_a-{\mu }_a\right)\stackrel{d}{\to }N\left(0,{\mathrm{\Sigma }}_a\right)$$

where

$${\mathrm{\Sigma }}_a={\sigma }_a^2\left(\frac{E\left\{W^{2}I(A=a)\right\}}{{[E\{WI(A=a)\}]}^2}\right)+R\left(L,Y_a\right)$$

and

$$R\left(L,Y_a\right)=E\left[\left\{W_a-E\left(W_a\right)\right\}{\left(Y_a-{\mu }_a\right)}^2\right]$$

with

$$\left|R\left(L,Y_a\right)\right|⩽\sqrt{Var\left(W_a\right)Var\left\{Y_a^2-2{\mu }_a{Y}_a\right\}}$$

for a ∈ {0, 1}

Proposition 1 implies that for large n the variance of ${\widehat{\mu }}_a$ can be approximated as:

$$Var\left({\widehat{\mu }}_a\right)\approx \frac{{\sigma }_a^2}{n}\left(\frac{E\left\{W^{2}I(A=a)\right\}}{{[E\{WI(A=a)\}]}^2}\right)+n^{-1}R\left(L,Y_a\right)$$

Because, for large n, $Var\left({\tilde{\mu }}_a\right)\approx {\sigma }_a^2/\{nP(A=a)\}$, it follows that

$$def{f}_w^a\approx \frac{P(A=a)E\left\{W^{2}I(A=a)\right\}}{{[E\{WI(A=a)\}]}^2}+E{r}_a$$ (3)

where $E{r}_a=\left\{P(A=a)/{\sigma }_a^2\right\}R\left(L,Y_a\right)$, which by Proposition 1 is bounded by:

$$\left|E{r}_a\right|⩽\left\{P(A=a)/{\sigma }_a^2\right\}\sqrt{\mathit{Var}\left(W_a\right)\mathit{Var}\left(Y_a^2-2{\mu }_a{Y}_a\right)}$$

An approximation of (3) that does not depend on the potential outcome Y_a omits the remainder term Er_a:

$${\widetilde{deff}}_w^a=\frac{P(A=a)E\left\{W^{2}I(A=a)\right\}}{{[E\{WI(A=a)\}]}^2}$$ (4)

When planning an observational study, prior or pilot study data may be available to estimate (4). In particular, suppose based on a pilot study n_p copies of (L_i, A_i) are observed. Then replacing P(A = a) with N_a/n_p where $N_a={\sum }_{i=1}^{n_p}I\left(A_i=a\right),E\left\{W^{2}I(A=a)\right\}$ with $n_p^{-1}{\sum }_{i=1}^{n_p}{\widehat{W}}_i^{2}I\left(A_i=a\right)$, and E{WI(A = a)} with $n_p^{-1}{\sum }_{i=1}^{n_p}{\widehat{W}}_{i}I\left(A_i=a\right)$, a consistent estimator of (4) is:

$${\widehat{\mathit{deff}}}_w^a=\frac{N_a{\sum }_{i=1}^{n_p}{\widehat{W}}_i^{2}I\left(A_i=a\right)}{{\left\{{\sum }_{i=1}^{n_p}{\widehat{W}}_{i}I\left(A_i=a\right)\right\}}^2}$$ (5)

This estimator has the same form as Kish’s design effect (1), applied to treatment group A = a. When prior data are not available, the design effect can be approximated using (4) based on an assumed distribution for A | L and the marginal distribution of L. The bias of (4) or (5) as an approximation to (3) in a given application depends on the value of Er_a. Bias of (4) and (5) for varying outcome types and confounding structures is evaluated empirically in simulation studies presented in Section 4. A modified design effect estimator that accounts for the remainder is considered in Section 6.

3. Sample Size Calculations using the Design Effects

When ACE is the focus of inference for the observational study being planned, the large sample distribution of $\widehat{ACE}$ can be used for power or sample size calculations. As n → ∞, $\widehat{ACE}$ is consistent and asymptotically normal. In particular, from (A.1) in Web Appendix A and the delta method it follows that

$$\sqrt{n}(\widehat{ACE}-ACE)\stackrel{d}{\to }N\left(0,{\mathrm{\Sigma }}^{*}\right),$$ (6)

where Σ* = Σ₁ + Σ₀. Treating the weights as fixed or known leads to a larger asymptotic variance for $\widehat{ACE}$ compared to appropriately treating the weights as estimated, i.e., Σ* is at least as large as the true asymptotic variance of $\widehat{ACE}$ (Lunceford and Davidian, 2004). Therefore, sample size formulae derived based on Σ* would in general be expected to be conservative.

The results in Proposition 1 and (6) allow for sample size calculations for studies that will be analyzed using MSM with IPTW. Suppose the sample size for the observational study being planned is to be determined on the basis of the power to test H₀ : ACE = 0 versus H_a : ACE ≠ 0 or equivalently H₀ : β₁ = 0 versus H_a : β₁ ≠ 0. Define the test statistic $t=\widehat{ACE}{\left\{Va{r}_n(\widehat{ACE})\right\}}^{-1/2}$, where $Va{r}_n(\widehat{ACE})={\{nP(A=1)\}}^{-1}{\sigma }_{1,adj}^2+{\{nP(A=0)\}}^{-1}{\sigma }_{0,adj}^2$, with ${\sigma }_{a,adj}^2={\sigma }_a^{2}def{f}_w^a$ for a ∈ {0, 1}. For large n, under the null t is approximately standard normal, thus H₀ is rejected when |t| > z_1−α/2, where α is the type I error rate and z_q is the q^th quantile of the standard normal distribution.

Proposition 2:

The sample size required to achieve power 1−β for effect size ACE = δ and type I error rate α is approximately:

$$n_{deff}=\frac{(1+k){\left(z_{1-\alpha /2}+z_{1-\beta }\right)}^2({\sigma }_{1,adj}^2/k+{\sigma }_{0,adj}^2)}{{\delta }^2}$$ (7)

where k = P(A = 1)/P(A = 0) is the marginal odds of treatment in the population. Note n_deff is the total required sample size across the two treatments.

The sample size formula (7) is the standard sample size equation commonly used to design RCTs, but with ${\sigma }_a^2$ replaced by ${\sigma }_{a,adj}^2$ (Chow et al., 2017, page 48). Thus, Proposition 2 simplifies power and sample size calculations for observational studies by allowing researchers to design studies as if they were designing an RCT, but inflating the assumed variances by the approximated design effects. The researcher first assumes that no confounding is present, specifies the desired α and 1−β, and makes assumptions about ${\sigma }_0^2$, ${\sigma }_1^2$, δ and k. The design effect is then approximated. When data from a pilot or prior study are available, $def{f}_w^1$ and $def{f}_w^0$ can be approximated based on (5) for each treatment group. When no prior study data are available, the distribution of the anticipated weights can be estimated based on assumptions about the distribution of L and A | L and the design effect can be calculated based on (4). While these assumptions may not be easy to make, this approach notably requires no assumptions about the potential outcomes Y₀ and Y₁ and their associations with A and L. Further discussion about these practical considerations is included in Section 5. Once the design effects are approximated by ${\widetilde{deff}}_w^a$ or ${\widehat{deff}}_w^a$, adjusted variances ${\sigma }_{a,adj}^2$ can be estimated by ${\tilde{\sigma }}_{a,adj}^2={\sigma }_a^2{\widetilde{deff}}_w^a$ or ${\widehat{\sigma }}_{a,adj}^2={\sigma }_a^2{\widehat{deff}}_w^a$, respectively, for a ∈ {0, 1}.

4. Simulation Study

4.1. Simulation Scenarios

Simulation studies were conducted to demonstrate use of the design effect in study design under a variety of confounding structures and outcome types. Data were simulated according to Scenarios 1–4 shown in Table 1 and also Scenario 5 described below. For all scenarios, α = 0.05 and 1 − β = 80% were chosen.

Table 1:

Simulation scenarios where no prior study data are available. B(p) indicates Bernoulli distribution with mean p, and N(m, v) indicates Normal distribution with mean m and variance v.

	Scenario	Confounders (L)	Exposure (A | L = l)	Potential Outcomes (Ya| L = l)	δ
1	binary Y, small $def{f}_w^a$	B(0.6)	B(0.5 + 0.25l)	B(0.85 – 0.2l + δa)	(a) −0.10 (b) −0.15 (c) −0.20
2	binary Y, large $def{f}_w^a$	B(0.5)	B(0.1 + 0.8l)	B(0.85 – 0.2l + δa)	(a) −0.10 (b) −0.15 (c) −0.20
3	continuous Y, small $def{f}_w^a$	B(0.6)	B(0.5 + 0.25l)	N(20 – 10l + δa, 144 + 112a)	(a) 2.5 (b) 5.0 (c) 7.5
4	continuous Y, large $def{f}_w^a$	B(0.5)	B(0.1 + 0.8l)	N(20 – 10l + δa, 144 + 112a)	(a) 2.5 (b) 5.0 (c) 7.5

4.2. Sample Size Calculation

Two general approaches can be used to design a study with the design effect approximation: when prior study data are not available, as in Scenarios 1–4, and when prior study data are available, as in Scenario 5. One example from each general approach is presented in detail.

4.2.1. Example 1: No prior study data (Scenario 1b).

Suppose no prior study data are available to design the study of interest. Then, the researcher must make the same assumptions and design choices as when designing an RCT, namely by specifying α, 1 – β, ${\sigma }_0^2$, ${\sigma }_1^2$, δ, and k. In general, ${\sigma }_1^2$ can be determined by deriving the marginal distribution of Y₁ based on the assumed distributions of Y₁ | L and L. For Scenario 1b, $P\left(Y_1=1\right)={\sum }_{l=0}^{1}P(Y_1=1\mid L=l)P(L=l)=0.58$, and thus ${\sigma }_1^2=0.2436$. Similarly, ${\sigma }_0^2=0.1971$. Here, the average causal effect is assumed to be δ = −0.15. The proportion of the population receiving treatment can be derived by integrating the distribution of A | L over L. For Scenario 1b, $P(A=1)={\sum }_{l=0}^{1}P(A=1\mid L=l)P(L=l)=0.65$, and thus k ≈ 1.857. When prior study data are not available, the distribution of the IPTWs must be assumed at the design phase. Based on the assumptions in Table 1, four possible values of W exist. These assumed values of W, along with the joint distribution of A and L, allow for the computation of the design effects using (4). This leads to ${\widetilde{deff}}_w^0=1.12$ and ${\widetilde{deff}}_w^1=1.04$, with approximated adjusted variances of ${\tilde{\sigma }}_{0,adj}^2=0.2208$ and ${\tilde{\sigma }}_{1,adj}^2=0.2533$.

Under the assumptions outlined in Table 1 for Scenario 1b, to achieve 80% power to detect an average causal effect of −0.15 at the α = 0.05 level, a sample size of approximately n_deff = 356 is required based on Proposition 2. The design effects and required sample sizes for Scenarios 1a, 1c, and Scenarios 2–4 can be determined similarly and are presented in Table 2. Note Scenarios 1 and 3 have the same design effects because in both instances the joint distribution of A and L is the same. Likewise, Scenarios 2 and 4 have the same design effects.

Table 2:

Variances, approximated design effects, approximated adjusted variances, and required sample sizes for simulation scenarios by treatment.

	Scenario	a	${\sigma }_a^2$	${\widetilde{deff}}_w^a$ or ${\widehat{deff}}_w^a$	${\tilde{\sigma }}_{a,adj}^2$ or ${\widehat{\sigma }}_{a,adj}^2$	ndeff	nrct
1	binary Y, small $def{f}_w^a$	0 1	0.1971 0.2436	1.12 1.04	0.2208 0.2533	(a) 801 (b) 356 (c) 201	(a) 736 (b) 327 (c) 184
2	binary Y, large $def{f}_w^a$	0 1	0.1875 0.2400	2.78 2.78	0.5208 0.6667	(a) 1862 (b) 828 (c) 466	(a) 671 (b) 298 (c) 168
3	continuous Y, small $def{f}_w^a$	0 1	168.0 280.0	1.12 1.04	188.2 291.2	(a) 1237 (b) 310 (c) 138	(a) 1143 (b) 286 (c) 127
4	continuous Y, large $def{f}_w^a$	0 1	169.0 281.0	2.78 2.78	469.4 780.6	(a) 3136 (b) 784 (c) 349	(a) 1129 (b) 283 (c) 126
5	prior study data, (NHEFS)	0 1	56.10 74.00	1.03 1.24	57.78 91.76	(a) 3409 (b) 853 (c) 379	(a) 2850 (b) 713 (c) 317

4.2.2. Example 2: Prior study data (Scenario 5).

Prior study or pilot data may allow for better informed assumptions about ${\sigma }_0^2$, ${\sigma }_1^2$, δ, and k. Because ${\sigma }_a^2=E\left(Y_a^2\right)-{\left\{E\left(Y_a\right)\right\}}^2$, ${\sigma }_a^2$ can be estimated by obtaining $\widehat{E}\left(Y_a^2\right)$ and $\widehat{E}\left(Y_a\right)$ from fitted MSMs based on the prior study data. The estimate $\widehat{ACE}$ and prevalence of the exposure or treatment in the prior study can inform assumptions about δ and k.

As an example, consider designing a new study based on the National Health and Nutrition Examination Survey Data I Epidemiologic Follow-up Study (NHEFS) example presented in Chapter 12 of Hernán and Robins (2020). Hernán and Robins use MSM with IPTWs to estimate the average causal effect of smoking cessation (A) on weight gain after approximately 10 years of follow-up (Y ) based on the NHEFS sample of smokers (n = 1566), assuming conditional exchangeability based on nine baseline confounders L: sex, age, race, education, smoking intensity, duration of smoking, physical activity, exercise, and weight.

Making the same assumptions as Hernán and Robins (2020), Scenario 5 considers the design of a new study to estimate the average causal effect of smoking cessation on 10-year weight gain. Based on the NHEFS data, assume that ${\sigma }_0^2=56.1$ and ${\sigma }_1^2=74.0$, obtained by fitting MSMs with IPTWs to estimate $E\left(Y_a^2\right)$ and E(Y_a). In the Hernán and Robins example, $\widehat{ACE}=3.441kg$. The new study will be designed to provide approximately 80% power to detect a difference in weight gain of δ ∈ {1.0, 2.0, 3.0}kg for Scenarios 5a-5c, respectively. From the NHEFS sample, assume k ≈ 0.346.

When prior study data are available, $def{f}_w^0$ and $def{f}_w^1$ can be estimated using (5). For the NHEFS data, ${\widehat{deff}}_w^0=1.03$ and ${\widehat{def{f}_w}}^1=1.24$. This leads to approximated adjusted variances of ${\widehat{\sigma }}_{0,adj}^2=57.78$ and ${\widehat{\sigma }}_{1,adj}^2=91.76$. Based on these assumptions, a sample size of n_deff = 853 is needed to achieve approximately 80% power to detect an average causal effect of 2.0kg at the α = 0.05 level using MSM with IPTWs.

4.2.3. Naïve Sample Size Calculations.

As a comparison, sample sizes n_rct were calculated naively under the assumptions of an RCT, ignoring the effect of weighting on the variances of the estimates. In other words, sample sizes were calculated as demonstrated above, except using ${\sigma }_a^2$ instead of ${\tilde{\sigma }}_{a,adj}^2$ or ${\widehat{\sigma }}_{a,adj}^2$ from Table 2. The sample size n_rct represents the total across the two treatments assuming that the marginal probability of treatment in the planned study is the same as in the population.

4.3. Evaluation

For Scenarios 1–4, empirical power based on samples of size n_deff was evaluated via simulation by following these steps:

1. Generate a superpopulation of size N = 1,000,000 based on distributions in Table 1.

2. Select a sample of size n_deff without replacement from the superpopulation, where n_deff is specified in Table 2.

3. Estimate ${\widehat{W}}_i$ for each member of the sample based on the predicted values from the logistic regression of A on L.

4. Fit the MSM E(Y_a) = β₀ + β₁a using weighted least squares, treating the weights as estimated by stacking the estimating equations from the weight model with the estimating equations for the causal means and difference in causal means using the geex package in R (Saul and Hudgens, 2020).

5. Test H₀ : β₁ = 0 versus H₁ : β₁ ≠ 0 using a Wald test, rejecting H₀ at the α = 0.05 significance level.

6. Repeat steps (ii)-(v) R = 2000 times and calculate empirical power as the proportion of simulated samples where H₀ was rejected.

For Scenario 5, empirical power based on a sample of size n_deff was evaluated via simulation by following these steps:

1. Estimate the propensity score for each of the 1566 NHEFS participants from a logistic regression model of A on L as ${\widehat{p}}_i=\widehat{\mathit{Pr}}\left(A_i=1\mid L_i=l_i\right)$. As in Hernán and Robins (2020), the logistic regression model includes main effects for each of the nine baseline confounders and quadratic terms for the four continuous covariates.

2. For each participant, calculate ${\widehat{Y}}_{ai}$, a ∈ {0, 1}, as the predicted value $\widehat{E}\left(Y_{ai}\mid L_i=l_i\right)$ from the following linear regression model, fit only on participants with A = a: E(Y_ai | L_i = l_i) = l_iβ, where l_i is a vector for participant i that includes an intercept term, the 9 previously defined covariates, and the four quadratic terms corresponding to continuous covariates. Also compute $\widehat{Var}\left(Y_{ai}\mid L_i=l_i\right)=MS{E}_a$, where MSE_a is the mean squared error from the model for E(Y_ai).

3. Add 3.441 − δ to ${\widehat{Y}}_{0i}$ for all participants, such that ACE = δ in the simulated population instead of 3.441 as in the NHEFS sample.

4. Select a sample of size n_deff with replacement from the NHEFS dataset, where n_deff is specified in Table 2.

5. Randomly sample A_i from $Bernoulli\left({\widehat{p}}_i\right)$.

6. Let $Y_{ai}={\widehat{Y}}_{ai}+{ϵ}_{ai}$, where ${ϵ}_{ai}\sim N(0,\widehat{Var}\left(Y_{ai}\mid L_i=l_i\right))$.

7. Follow steps (iii)-(v) from the above list for Scenarios 1–4.

8. Repeat steps (iv)-(vii) R = 2000 times and estimate empirical power as the proportion of simulated samples where H₀ was rejected.

The estimated propensity score distributions from simulated data sets for each of Scenarios 1–5 are displayed in Web Figure 5.

For each scenario, the steps above were repeated to calculate empirical power based on the naïve sample sizes, replacing n_deff with n_rct.

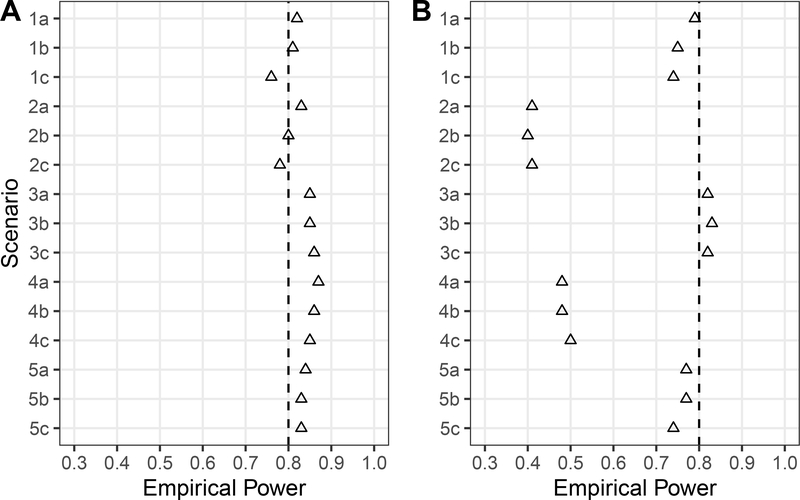
The results of the simulation study are presented in Figure 1. For all simulation scenarios, when the sample size was calculated using the design effect, empirical power was close to or exceeded the nominal 80% level. That is, use of the design effects to calculate required sample sizes led to close to the intended level of statistical power (Figure 1A). On the other hand, ignoring the effect of weighting and basing sample sizes on the naïve assumptions of an RCT led to empirical power that was lower than the nominal 80% level for all but Scenarios 3a-3c (Figure 1B). These results demonstrate that ignoring the weights in power and sample size calculations can lead to significantly underpowered studies, particularly when there are strong confounders that lead to high variability in the weights.

Figure 1.

Empirical power from the simulation study by scenario across R = 2000 samples based on sample sizes (A) n_deff and (B) n_rct from Table 2. Empirical power is the proportion of simulated samples in which the p-value for testing H₀ : β₁ = 0 versus H₁ : β₁ ≠ 0 was less than α = 0.05 for the MSM E(Y_a) = β₀ +β₁a. (Scenario 5c excludes 2 and 5 simulations for (A) and (B), respectively, in which the geex package failed to converge when estimating the standard error of $\widehat{ACE}$.)

4.4. Additional Simulations

The simulations summarized in Section 4.3 demonstrate the performance of the design effect approximation for Scenarios 1–4 when there is no pilot study data. Additional simulations were conducted to evaluate the design effect approximation in these scenarios when pilot study data are available to estimate k and ${\sigma }_{a,adj}^2$ for a ∈ {0, 1}. Results of these simulations are presented in Web Appendix B.1 and are similar to those presented in Section 4.3. Additional simulations were also conducted under the null hypothesis to empirically confirm type I error control; see Web Appendix B.2.

5. Practical Considerations

When prior study data are not available, specifying the design effects can be challenging. A few general guidelines are offered to help researchers determine reasonable assumptions to facilitate power and sample size calculations.

When only a few categorical covariates will be included in the weight model, researchers can use subject matter knowledge or prior study information to nonparametrically specify the joint distribution of A and L, or the marginal distribution of L and the conditional distribution of A | L (as in Example 1). Based on these assumptions, the anticipated weights can be calculated nonparametrically and the design effects for each treatment group can be approximated.

When specification of these distributions is not feasible, researchers can forgo approximating the values of the weights and instead consider more generally how much variation is expected in the weights. The lower bound for $def{f}_w^a$ is 1, which implies that the weights within both treatment groups are all equal and thus covariates are not predictive of the treatment. Design effects tend to increase when more covariates are added to the weight model. The presence of covariates that are strong predictors of treatment tends to increase the design effect. Care must be taken to identify the appropriate set of confounders to include in the weight model (Vansteelandt et al., 2012). Inclusion of instrumental variables, which are predictive of the exposure but which do not affect the outcome, inflate the variance of the ACE estimator without reducing bias (Rubin, 1997; Myers et al., 2011). The use of weight truncation will decrease the design effect.

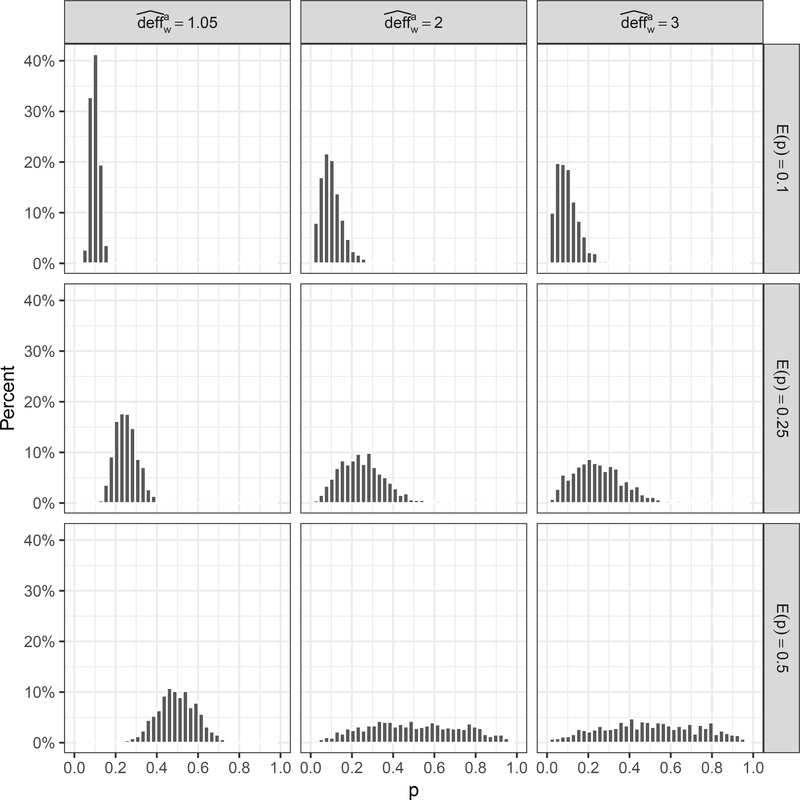
Figure 2 depicts propensity score distributions for various values of the design effect and mean propensity score E(p) to aid researchers in choosing a design effect consistent with the expected variation in the weights. The propensity score distributions were generated by N_a = 1000 random draws from beta distributions with shape parameters set to achieve the desired E(p) and design effect. The corresponding weight distributions are included in Web Figure 6. As variation in the propensity scores and thus the weights increases, so does the design effect approximation.

Figure 2.

Examples of propensity score distributions for various approximated design effects and mean propensity score E(p). Distributions were generated from N_a = 1000 random draws from beta distributions with shape parameters set to achieve the desired E(p) and design effect.

6. Estimating the Remainder with Pilot Study Data

The design effect estimators (4) and (5) omit the approximation error Er_a from (3). In this section estimators of the design effect are considered which include an estimate of Er_a. First we revisit the simulation study in Section 4 to examine the magnitude of the approximation errors for the data generating processes considered. Then we consider design effect estimators which incorporate an estimate of Er_a when pilot data are available.

Approximation errors Er_a were calculated for each of the scenarios included in the simulation study. For Scenarios 1–4, Er_a were calculated using the known distributions in Table 1 and are presented in Web Figure 4. For Scenario 5, Er_a were estimated empirically as approximately 0.03 for a = 0 and −0.03 for a = 1. Approximation errors were small for most scenarios and were in opposite directions for the two treatment groups, which tends to offset the effects of the errors (Web Figure 4). Scenario 2 had large approximation errors (Er₀ = 0.59 and Er₁ = −0.18 for Scenario 2b), but empirical power still equaled the nominal level when the design effect estimators (4) and (5) were used to calculate the sample size (Figure 1 and Web Figure 1). Note Scenario 2 is an extreme example, as it includes only a single and very strong confounding variable and only two possible and extreme values for W. For the binary outcome, this resulted in large approximation errors.

When pilot or prior data are available, Er_a can be estimated empirically rather than ignored, and a modified estimator of the design effect can be used for power or sample size calculations: ${\widehat{deff}}_{w,rem}^a={\widehat{deff}}_w^a+{\widehat{Er}}_a$, where

$${\widehat{Er}}_a=\left\{N_a/\left(n_p{\widehat{\sigma }}_a^2\right)\right\}\frac{{\sum }_{i=1}^{n_p}{\widehat{W}}_{i}I\left(A_i=a\right)\left\{{\widehat{W}}_i-\widehat{E}\left({\widehat{W}}_a\right)\right\}{\left(Y_i-{\widehat{\mu }}_a\right)}^2}{{\sum }_{i=1}^{n_p}{\widehat{W}}_{i}I\left(A_i=a\right)}$$

where $\widehat{E}\left({\widehat{W}}_a\right)$ is estimated empirically from the pilot sample and ${\widehat{\sigma }}_a^2$ is the estimator of ${\sigma }_a^2$ described in Section 4.2.2. Adjusted variances ${\sigma }_{a,adj}^2$ can then be estimated by ${\widehat{\sigma }}_{a,adj}^2={\widehat{\sigma }}_a^2{\widehat{deff}}_{w,rem}^a$ for a ∈ {0, 1}, and the sample size calculated using (7).

Additional simulations were conducted using ${\widehat{deff}}_{w,rem}^a$ to calculate required sample sizes. The simulations are described in Web Appendix B.3 with the results in Web Figure 3 and Web Figure 4. For Scenarios 1 and 3 (small design effect scenarios), estimates of Er_a were empirically unbiased, even for small pilot sample sizes (Web Figure 4). However, for Scenarios 2 and 4 (large design effect scenarios), estimates of Er_a demonstrate considerable empirical bias for small pilot samples, which was reduced as the pilot sample size increased. As shown in Web Figure 3, for all scenarios, empirical power was similar to the results in Figure 1. Thus, there may not be much benefit in using the modified design effect estimator ${\widehat{deff}}_{w,rem}^a$ instead of ${\widehat{deff}}_w^a$.

7. Discussion

The design effect approximation simplifies power and sample size calculations of observational studies. Using the design effect allows researchers to utilize standard power and sample size software (e.g., nQuery, SAS Proc Power) for randomized trials, but with variances inflated by the approximate design effects. An additional advantage of using the design effect approximation (4) that ignores the remainder term is that no assumptions are required about the relationship between the potential outcomes and either the treatment or the confounders. Empirical results demonstrate the design effect approximation can yield the nominal level of power over a range of confounding and outcome structures.

Approximating the design effect when planning an observational study may be challenging. In survey sampling, it is common practice to report estimated design effects in analytic reports for better understanding of the precision of the estimates and to assist other researchers who are designing similar studies (see, for example Center for Behavioral Health Statistics and Quality, 2019). Reporting the estimated design effects corresponding to treatment or exposure effect estimates in observational studies may assist researchers with future study designs. In time, as more studies analyzed with IPTW estimators start to report their design effects, rules of thumb and practical upper bounds for the design effects will likely emerge to aid in the design of future studies (see, for example, United Nations Statistical Division (2008, page 41), Daniel (2012, page 251), and Salganik (2006) from the survey sampling literature).

In the absence of knowledge of estimated design effects from prior studies, the design effect may be approximated either using (4) or, if pilot data are available, (5). In either case, the remainder in Proposition 1 is ignored, which in principle may introduce bias. The remainder may be large when individuals with extreme weight values tend to have potential outcomes that are also extreme relative to the mean. Nonetheless, simulation studies in Section 4 demonstrate empirically that using either (4) or (5) for sample size determination tends to yield the desired power. Of course, there may be other scenarios where this is not the case, and thus care should be exercised in generalizing beyond the simulation scenarios considered in this paper. When pilot data are available, the approximation error Er_a can be estimated as in Section 6. Empirical power when approximating Er_a tended to be similar to power when the remainder was ignored. Thus the simpler estimator that ignores the remainder may be preferred in practice.

In conclusion, the design effect approximation can be a useful tool for the design of studies to estimate point exposure effects with IPTW estimators, as currently no power and sample size methods exist in this context. The design effect can also be used in precision calculations using approaches analogous to those described in this paper, i.e., basing calculations on the adjusted variances ${\tilde{\sigma }}_{a,adj}^2$ or ${\widehat{\sigma }}_{a,adj}^2$ rather than ${\sigma }_a^2$.