Abstract
Background and Objective
Recently, the COVID-19 epidemic has become more and more serious around the world, how to improve the image resolution of COVID-CT is a very important task. The network based on progressive upsampling for COVID-CT super-resolution increases the reconstruction error. This paper proposes a progressive back-projection network (PBPN) for COVID-CT super-resolution to solve this problem.
Methods
In this paper, we propose a progressive back-projection network (PBPN) for COVID-CT super-resolution. PBPN is divided into two stages, and each stage consists of back-projection, deep feature extraction and upscaling. We design an up-projection and down-projection residual module to minimize the reconstruction error and construct a residual attention module to extract deep features. In each stage, firstly, PBPN performs back-projection to extract shallow features by two up-projection and down-projection residual modules; then, PBPN extracts deep features from the shallow features by two residual attention modules; finally, PBPN upsamples the deep features through sub-pixel convolution.
Results
The proposed method achieves the improvements of about 0.14~0.47 dB/0.0012~0.0060 for × 2 scale factor, 0.02~0.08 dB/0.0024~0.0059 for × 3 scale factor, and 0.08~0.41 dB/ 0.0040~0.0147 for × 4 scale factor than state-of-the-art methods (Bicubic, SRCNN, FSRCNN, VDSR, LapSRN, DRCN and DSRN) in terms of PSNR/SSIM on benchmark datasets.
Conclusions
The proposed mehtod obtains better performance for COVID-CT super-resolution and reconstructs high-quality high-resolution COVID-CT images that contain more details and edges.
Keywords: COVID-CT, Super-resolution, Progressive back-projection network, Residual attention module, Up-projection and down-projection residual module
1. Introduction
The COVID-19 [1, 2] is a highly contagious and harmful infectious disease. Seriously ill patients [3, 4] with COVID-19 will die if they are not treated in time. Image super-resolution reconstruction for COVID-CT is a hotspot issue at present. Improving the COVID-CT image reconstruction quality and resolution becomes a critically important task.
Recently, many deep neural networks for super-resolution (SR) have been studied [5], [6], [7], [8]. These networks can mainly be divided into three categories [9]: network based on predefined upsampling, network based on single upsampling, and network based on progressive upsampling.
Network based on predefined upsampling uses bicubic to generate high-resolution (HR) images before low-resolution (LR) images enter the network. SR reconstruction networks based on predefined upsampling include convolutional neural network for super-resolution (SRCNN), fusing multiple convolutional neural network for super-resolution (CNF) and deep convolutional network for super-resolution (VDSR). SRCNN [10] uses 3 convolutional layers to extract features and reconstruct high-resolution (HR) image, which achieves better performance than traditional methods. CNF [11] uses a context-wise network fusion scheme to fuse different individual networks based on SRCNN. VDSR [12] successfully constructs a 20-layer convolutional neural network by using residual learning. Although networks based on predefined upsampling can achieve better performance, they can produce new noise in the process of reconstruction.
Network based on single upsampling uses a deconvolution or sub-pixel convolution at the last layer of network to upsample the LR feature maps. Super-resolution reconstruction networks based on single upsampling include fast convolutional neural network for super-resolution (FSRCNN), efficient sub-pixel convolutional neural network for super-resolution (ESPCN), deeply-recursive convolutional network for super-resolution (DRCN), deep recursive residual network (DRRN) and enhanced deep residual network for super-resolution (EDSR). FSRCNN [13] directly inputs LR image into an 8-layer convolutional network with 3 × 3convolutional kernel, which firstly uses a deconvolutional layer to upsample in the last layer. ESPCN [14] directly extracts features from a low-resolution image and uses a sub-pixel convolution to upsample the extracted features, which not only reduces the computational complexity of reconstruction process but also improves the efficiency of reconstruction. DRCN [15] applies the recurrent neural network to reconstruct HR image to extend the receptive field, and uses residual learning to add the depth of network. DRRN [16] uses global and local residual learning and recursive learning to increase network depth, which improves the performance of SR reconstruction without weight parameters. EDSR [17] removes the batch normalization layers of ResNet to simplify the network architecture, which not only improves the performance but also improves the computational efficiency. Although these methods have achieved better reconstruction results, they cannot learn complex non-linear functions due to the limitation of network capacity.
Network based on progressive upsampling uses several upsampling modules to gradually reconstruct HR image. For example, deep laplacian pyramid super-resolution network (LapSRN) [18] gradually extracts feature maps by a cascade of convolutional layers and uses a deconvolution layer to upsample the extracted feature maps, which progressively predicts the residual and reconstructs the HR image with different scale factors ( × 2, × 4, × 8) by a coarse-to-fine fashion. LapSRN also uses a robust Charbonnier loss function to train the network.
However, super-resolution reconstruction network based on progressive upsampling increases the reconstruction error. To solve this problem, we propose a progressive back-projection network (PBPN) for COVID-CT super-resolution. In PBPN, we design up-projection and down-projection residual modules (UD) and construct residual attention modules (RA). PBPN is divided into two stages. Each stage is composed of three parts: back-projection, deep feature extraction and upscaling. In each stage, the operation of back-projection is implemented by UD modules, which consist of improved up-projection, improved down-projection and feature fusion layers; the operation of deep feature extraction is implemented by RA modules, which consist of residual attention blocks (RAB); the operation of upscaling is implemented by sub-pixel convolutional layer. In the process of several upsampling of LR image features, the proposed PBPN improves the performance of COVID-CT super-resolution reconstruction by back-projection and deep feature extraction.
2. Methods
In this paper, we propose a progressive back-projection network (PBPN). The architect of PBPN is shown in Fig. 1 . We can find that PBPN mainly consists of four up-projection and down-projection residual (UD) modules and four residual attention (RA) modules. The details of PBPN are as follows.
Fig. 1.
The architect of progressive back-projection network (PBPN). UD denotes the up-projection and down-projection residual module. RA denotes the residual attention module.
2.1. Improved up-projection block and improved down-projection block
Recently, Haris [19] proposed an up-projection block and a down-projection block, which reduce the reconstruction error by iterative error-correcting feedback mechanism. The structures of up-projection block and down-projection block are shown in Fig. 2 . From Fig. 2, we can find that the up-projection block consists of two deconvolutional layers and a convolutional layer by residual connection; the structure of down-projection is similar to up-projection. The up-projection block and down-projection block use 6 × 6kernel size. And the input channel and output channel of convolutional layer and deconvolutional layer are 64.
Fig. 2.
The structure of up-projection block and down-projection block.
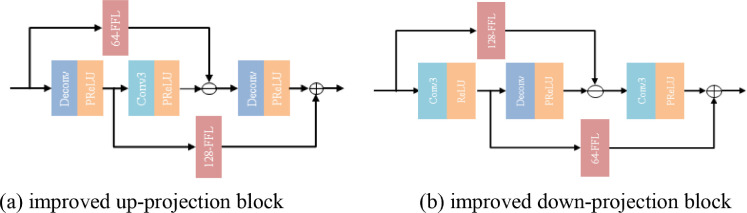
However, since the larger convolutional kernel has more parameters, the operation of up-projection block and down-projection block is complicated. The up-projection block and down-projection block don't fuse the features of adjacent convolutional layers. To solve this problem, we design an improved up-projection block and an improved down-projection block. The structures of improved up-projection block and improved down-projection block are shown in Fig. 3 . We add a 64-dimensional feature fusion layer (64-FFL) and a 128-dimensional feature fusion layer (128-FFL) in up-projection block and down-projection block. The improved up-projection block and improved down-projection block use4 × 4kernel size instead of 6 × 6kernel size. We set the input channel/output channel of convolutional layer and deconvolutional layer to 128/64 and 64/128, respectively. The 64-dimensional feature fusion layer and 128-dimensional feature fusion layer use 1 × 1kernel size. We set the input channel/output channel of 64-dimensional feature fusion layer and 128-dimensional feature fusion layer to 64/64 and 128/128, respectively.
Fig. 3.
The structure of improved up-projection block and improved down-projection block. 64-FFL denotes 64-dimensional feature fusion layer. 128-FFL denotes 128-dimensional feature fusion layer.
2.2. Up-projection and down-projection residual module
Up-projection and down-projection residual module (UD) consists of an improved up-projection block and an improved down-projection block by residual connection. Improved up-projection consists of feature upsampling, feature downsampling and residual upsampling. Improved down-projection is similar to the up-projection, which is composed of feature downsampling, feature upsampling, and residual downsampling. The up-projection and down-projection residual module is defined as follows:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
where*denotes the convolution operation. ↑sand ↓sdenote the upsampling operation and downsampling operation with scale factors, respectively. ptdenotes the upsampling deconvolutional layer of the t-th UD. gtdenotes the downsampling convolutional layer of the t-th UD. qtdenotes 128-dimensional feature fusion layer of the t-th UD. kt denotes 64-dimensional feature fusion layer of thet-th UD.
The structure of UD is composed of an improved up-projection block and an improved down-projection block, as shown in Fig. 4 . In the improved up-projection block, firstly, the input LR feature L t − 1 is mapped to HR feature by deconvolutional layerpt; secondly, is mapped back to LR feature by convolutional layergt, improved up-projection gets the residual between the reconstructed feature and the input LR feature L t − 1, which is calculated by 128-dimensional feature fusion layer qt; thirdly, the residual is mapped to HR feature by deconvolutional layerpt; finally, improved up-projection sums the HR feature and the HR feature , which is calculated by 64-dimensional feature fusion layer kt. The operation of improved down-projection is similar to improved up-projection. After the operation of improved up-projection and improved down-projection, the output of UD is . UD uses three times upsampling and three times downsampling by residual connection to extract shallow features by minimizing the reconstruction error.
Fig. 4.
The structure of up-projection and down-projection residual module (UD).
2.3. Residual attention module (RA)
The residual block has better performance in feature extraction [17]. The features extracted by the residual block contain a large amount of high- and low-frequency information. Low-frequency information is generally located in smooth areas, which is easier to reconstruct. However, high-frequency information is usually in the boundary, texture and other areas, which is difficult to reconstruct. In order to extract more deep high-frequency information of LR image, we propose the residual attention module (RA). The structure of RA is shown in Fig. 5 . The RA consists of three residual attention blocks (RAB) which are connected by residual connection. The RAB is composed of a residual block and a channel attention block. The operation of RAB can be described as:
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
where,*denotes convolution operation. ht, ut, and mt denote convolutional layers of the t-th RAB. ⊗ denotes element-wise multiplication. poolingmean( • )denotes the operation of mean-pooling.
Fig. 5.
The structure of residual attention module (RA).
2.4. Network architect
Fig. 1 shows the progressive back-projection network (PBPN). PBPN can be divided into two stages. Each stage performs the reconstruction with scale factor 2. Each stage consists of three parts: back-projection, deep feature extraction and upscaling. ILRandISRare set as the input image and the reconstructed image of PBPN. The input image ILR is extracted by an initial layer to get initial features Linitial. The operation of the initial layer is described as:
| (16) |
where Cinitial denotes the initial layer which is a convolutional layer.
In the first stage, firstly, PBPN performs the back projection for the initial features Linitial. The operation of back-projection is described as:
| (17) |
where fbp( • )denotes the operation of back-projection. Lbpdenotes the extracted shallow features by back-projection. The operation of back-projection is implemented by two UD modules. Secondly, PBPN uses two RA modules to extract deep features from the extracted shallow features. The operation of deep feature extraction is described as:
| (18) |
where fdeep( • )denotes the operation of deep feature extraction. Ldeep denotes the extracted features by deep feature extraction. Finally, PBPN upsamples the extracted features by sub-pixel convolutional layer. The operation of upscaling is described as:
| (19) |
where fup( • )denotes the operation of upscaling. Cmiddledenotes the middle layer which is a convolutional layer. Lupdenotes the upscaling features.
In the second stage, the PBPN operation is similar to the first stage. Finally, PBPN reconstructs HR image from the upsampling features. The operation of reconstruction is described as:
| (20) |
where Cresdenotes the reconstruction layer which is a convolutional layer. fGBPN( • )denotes the operation of PBPN. The network architect setting of PBPN is shown in Table 1 .
Table 1.
The network architect setting of PBPN. Including initial layer, UD module, RAB module, middle layer, upscale module, and reconstruction layer.
| Network part | Kernel size | Stride | padding | Input size | Output size | |
|---|---|---|---|---|---|---|
| Initial layer | 3 × 3 | 1 | 1 | H × W × 1 | H × W × 64 | |
| UD module | Deconv | 4 × 4 | 2 | 1 | H × W × 64 | H × W × 128 |
| 64-FFL | 1 × 1 | 1 | 0 | H × W × 64 | H × W × 64 | |
| 128-FFL | 1 × 1 | 1 | 0 | H × W × 128 | H × W × 128 | |
| Conv3 | 4 × 4 | 2 | 1 | H × W × 128 | H × W × 64 | |
| RAB module | Conv4 | 3 × 3 | 1 | 1 | H × W × 64 | H × W × 64 |
| Conv5 | 1 × 1 | 1 | 0 | H × W × 64 | H × W × 4 | |
| Conv6 | 1 × 1 | 1 | 0 | H × W × 4 | H × W × 64 | |
| Middle layer | 3 × 3 | 1 | 1 | H × W × 64 | H × W × 64 | |
| Upscale module | 3 × 3 | 1 | 1 | H × W × 64 | 2H×2W×64 | |
| Reconstruction layer | 3 × 3 | 1 | 1 | 2H×2W×64 | 2H×2W×1 | |
is set as the training set, which contains N low-resolution images and their high-resolution counterparts. We use L 1 loss function to optimize PBPN as follow:
| (21) |
whereθdenotes the parameters of PBPN. L 1loss function is minimized by Adam [20] algorithm. The overall process of PBPN is shown in Algorithm 1 .
Algorithm 1.
Progressive Back-Projection Network for COVID-CT super-resolution.
| Require: Learning ratel, batch sizem, and iteration epochE |
| Input: The training set |
| Output: super-resolution reconstruction imageISR |
| Ensure: Parameterθ |
| Initialization: θis initialized randomly |
| fore=1,…,Edo |
| n=1 |
| whilen ≤ N − mdo |
| The first stage |
| The second stage |
| θ = optimizer(L(θ),l), update parameter with Adam optimizer |
| n = n + m |
| end while |
| end for |
3. Experiment results
3.1. Implementation details
We use 200 HR images from the BSD500 dataset and 91 HR images from the T91 dataset [21, 22] to train PBPN. We also use Set5 [23], Set14 [24], BSD100 [25], and Urban100 [26] to test PBPN. And peak signal to noise ratio (PSNR) [27] and structural similarity (SSIM) [28] are used as evaluation metrics.
Matlab is used to process the dataset. Firstly, we augment the dataset by downscaling, rotation and flipping. Then, we crop 32 × 32patches from low-resolution images and 32s × 32spatches from high-resolution images, wheresis the scale factor. Finally, we generate LR-HR image pairs.
We use Adam optimizer withβ1 = 0.9,β2 = 0.999andε = 10−8 to minimize theL 1loss function. The learning rate is set to10−4 and the batch size is set to 16. We implement PBPN with Pytorch on NVIDIA GeForce 2080Ti GPU.
3.2. Comparison with state-of-the-art methods
To evaluate the performance of PBPN, we use Bicubic, SRCNN [10], FSRCNN [13], VDSR [12], LapSRN [18], DRCN [15], DSRN [29] as comparison methods.
The quantitative evaluation results are shown in Table 2 . From Table 2, compared with other SR methods for different scale factors on four datasets, we can find that PBPN obtains the improvement of PSNR/SSIM. Specifically, for × 4 scale factor, PBPN achieved the highest PSNR/SSIM on all four datasets. We also find that PBPN achieves the second-highest PSNR for × 3 scale factor on Set14 and for × 2 scale factor on BSD100. As for other testing datasets, PBPN outperforms other methods about 0.02~0.08 dB/0.0024~0.0059 for × 3 scale factor and 0.14~0.47 dB/0.0012~0.0060 for × 2 scale factor in terms of PSNR/SSIM.
Table 2.
Quantitative evaluation results of state-of-the-art SR methods: average PSNR and SSIM for scale factors (×2, ×3, ×4). Bold numbers indicate the best performance.
| Scale | Method | Set5 |
Set14 |
BSD100 |
Urban100 |
||||
|---|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | ||
| ×2 | Bicubic | 33.66 | 0.9299 | 30.24 | 0.8688 | 29.56 | 0.8431 | 26.88 | 0.8403 |
| SRCNN [10] | 36.66 | 0.9542 | 32.45 | 0.9067 | 31.36 | 0.8879 | 29.50 | 0.8946 | |
| FSRCNN [13] | 37.05 | 0.9560 | 32.66 | 0.9090 | 31.53 | 0.8920 | 29.88 | 0.9020 | |
| VDSR [12] | 37.53 | 0.9590 | 33.05 | 0.9130 | 31.90 | 0.8960 | 30.77 | 0.9140 | |
| LapSRN [18] | 37.52 | 0.9591 | 33.08 | 0.9130 | 31.08 | 0.8950 | 30.41 | 0.9101 | |
| DRCN [15] | 37.63 | 0.9588 | 33.06 | 0.9121 | 31.85 | 0.8942 | 30.76 | 0.9133 | |
| DSRN [29] | 37.66 | 0.9590 | 33.15 | 0.9130 | 32.10 | 0.8970 | 30.97 | 0.9160 | |
| PBPN | 37.80 | 0.9606 | 33.62 | 0.9190 | 31.90 | 0.8982 | 31.16 | 0.9194 | |
| ×3 | Bicubic | 30.39 | 0.8682 | 27.55 | 0.7742 | 27.21 | 0.7385 | 24.46 | 0.7349 |
| SRCNN [10] | 32.75 | 0.9090 | 29.30 | 0.8215 | 28.41 | 0.7863 | 26.24 | 0.7989 | |
| FSRCNN [13] | 33.18 | 0.9140 | 29.37 | 0.8240 | 28.53 | 0.7910 | 26.43 | 0.8080 | |
| VDSR [12] | 33.67 | 0.9210 | 29.78 | 0.8320 | 28.83 | 0.7990 | 27.14 | 0.8290 | |
| LapSRN [18] | 33.82 | 0.9227 | 29.87 | 0.8320 | 28.82 | 0.7980 | 27.07 | 0.8280 | |
| DRCN [15] | 33.82 | 0.9266 | 29.77 | 0.8314 | 28.80 | 0.7963 | 27.15 | 0.8277 | |
| DSRN [29] | 33.88 | 0.9220 | 30.26 | 0.8370 | 28.81 | 0.7970 | 27.16 | 0.8280 | |
| PBPN | 33.96 | 0.9244 | 30.24 | 0.8429 | 28.84 | 0.7998 | 27.26 | 0.8336 | |
| ×4 | Bicubic | 28.42 | 0.8104 | 26.00 | 0.7027 | 25.96 | 0.6675 | 23.14 | 0.6577 |
| SRCNN [10] | 30.48 | 0.8628 | 27.50 | 0.7513 | 26.90 | 0.7101 | 24.52 | 0.7221 | |
| FSRCNN [13] | 30.72 | 0.8660 | 27.61 | 0.7550 | 26.98 | 0.7150 | 24.62 | 0.7280 | |
| VDSR [12] | 31.35 | 0.8830 | 28.02 | 0.7680 | 27.29 | 0.7251 | 25.18 | 0.7540 | |
| LapSRN [18] | 31.54 | 0.8850 | 28.19 | 0.7720 | 27.32 | 0.7270 | 25.21 | 0.7560 | |
| DRCN[15] | 31.53 | 0.8854 | 28.03 | 0.7673 | 27.24 | 0.7233 | 25.14 | 0.7511 | |
| DSRN [29] | 31.40 | 0.8830 | 28.07 | 0.770 | 27.25 | 0.7240 | 25.08 | 0.7570 | |
| PBPN | 31.58 | 0.8872 | 28.48 | 0.7847 | 27.33 | 0.7293 | 25.29 | 0.7610 | |
We use COVID-CT [30] as the testing set to further verify the performance of PBPN. The visual comparison and PSNR/SSIM values comparison of PBPN with other methods for ×4 scale factor on COVID-CT are shown in Fig. 6 . From Fig. 6, we can find that PBPN achieves higher PSNR/SSIM values than other algorithms on COVID-CT. Specifically, PBPN achieves 32.81 dB/0.8520, 26.41 dB/0.7489, 25.71 dB/0.7481 on Fig. 6(a)–(c), respectively. We also find that PBPN can clearly reconstruct the details and edges of COVID-CT images when other SR methods produce blurry results. Compared with other SR methods, PBPN extracts more details and edges by up-projection and down-projection residual modules and residual attention modules to generate high-quality high-resolution COVID-CT images.
Fig. 6.
Visual comparison of PBPN and state-of-art methods for ×4 scale factor on COVID-CT.
4. Discussion
As super-resolution reconstruction network based on progressive upsampling increases the reconstruction error in the reconstruction process, the reconstructed COVID-CT image contains fewer details, which increases the diagnostic difficulty for a doctor. In order to obtain high-quality COVID-CT images, we propose a progressive back-projection network (PBPN) for COVID-CT super-resolution. The experimental results demonstrate the proposed PBPN outperforms networks based on predefined upsampling (SRCNN [10] and VDSR [12]), networks based on single upsampling (FSRCNN [13], DRCN [16], and DSRN [29]), and network based on progressive upsampling (LapSRN [18]) in terms of quantitative evaluation and visual evaluation. Specifically, from Table 2, we can find that the PNSR of PBPN achieves the improvements of 1.14 dB, 0.75 dB, 0.27 dB, 0.28 dB, 0.17 dB and 0.14 dB than SRCNN, FSRCNN, VDSR, LapSRN, DRCN and DSRN for ×2 scale factor on Set5, respectively.
The reasons for these results are as follows: SRCNN only has 3 convolutional layers and it cannot extract deep features of the low-resolution image, resulting in high-resolution image reconstructed by SRCNN with fewer details. Although VDSR uses residual learning to add the number of convolutional layers to 20, it is still difficult to extract deep features of the low-resolution image. SRCNN and VDSR belong to networks based on predefined upsampling, which upsample the low-resolution image to the desired spatial resolution before the low-resolution image enters the network. These methods increase unnecessary computational consumption and produce noise in the reconstruction process. FSRCNN only has 8 convolutional layers and uses a deconvolution layer to upsample the extracted features, so the ability of FSRCNN which extracts depth features is limited. Although DRCN uses a recursive convolutional network with 16 convolutional recursions and uses skip connections to reduce the difficulty of training, most of the features extracted by DRCN are shallow features, which contain less detailed information. DSRN uses a dual-state recurrent network to exchange recurrent signals between low-resolution to high-resolution and high-resolution to low-resolution. FSRCNN, DRCN and DSRN are networks based on single upsampling, which use a deconvolutional layer or a sub-pixel convolutional layer at the last layer of networks to upsample the extracted features. Due to the limitation of network capacity, these methods cannot learn the complex nonlinear functions between low-resolution images and high-resolution images. LapSRN progressively uses a cascade of convolutional layers to extract deep features of the low-resolution image and a deconvolutional layer to upsample the extracted features in a coarse-to-fine fashion. In other words, LapSRN can produce different scale factors high-resolution images by gradually extracting features and upsampling, it belongs to network based on progressive upsampling. However, LapSRN increases the reconstruction error in the reconstruction process, which cause that the reconstructed image cannot contain clear details and textures.
Compared with the above methods, the proposed PBPN firstly uses up-projection and down-projection residual module to gradually extract shallow features and reduce the reconstruction error, secondly, residual attention module is used to extract deep features, such as textures and edges, then residual learning is used to reduce the learning error between low-resolution image and high-resolution image, finally, sub-pixel convolutional layer is used to upsample the extracted shallow and deep features. As PBPN reduces the learning and reconstruction error in the reconstruction process and extracts more deep features (textures, edges, etc.), so PBPN can reconstruct high-quality high-resolution COVID-CT images. These COVID-CT images can be used to easily judge whether a patient is infected by COVID-19. If the patient is infected by COVID-19, these COVID-CT images can provide more details of patient lung and tissues to doctors. According to these details, doctors can identify the precise location of lesion and grasp the severity of lesion, so the diagnostic accuracy is improved.
5. Conclusion
To solve the problem of increasing reconstruction error in progressive upsampling network, we propose a progressive back-projection network (PBPN) for COVID-CT super-resolution. In PBPN, we design an up-projection and down-projection residual module (UD), which uses three times upsampling and three times downsampling by residual connection to minimize the reconstruction error; and we also construct a residual attention module to extract deep features. we progressively upsample the extracted deep features to reconstruct high-resolution images with different scale factors. Extensive experiments show that PBPN obtains higher values of PSNR/SSIM and gets more clear reconstruction image of COVID-CT. In future work, based on the idea of back projection, we will further optimize the network structure and design a better image super-resolution reconstruction network.
Ethical approval
No ethics approval is required.
Declaration of Competing Interest
The authors declare that they have no conflict of interests.
Acknowledgment
This work is supported by the National Natural Science Foundation of China (61763029), the Open Fund project of Key Laboratory of Gansu Advanced Control for Industrial Processes (2019KFJJ01, 2019KFJJ05), and the Industrial Support and Guidance Project of Colleges and Universities of Gansu Province (2019C-05), and the Natural Science Foundation of Gansu Province (20JR5RA459).
References
- 1.Team N C. The epidemiological characteristics of an outbreak of 2019 novel coronavirus diseases (COVID-19) in China. Chin. J. Epidemiol. 2020;41(2):145–151. [PMC free article] [PubMed] [Google Scholar]
- 2.Ouyang X., Huo J., Xia L., et al. Dual-sampling attention network for diagnosis of COVID-19 from community acquired pneumonia. IEEE Trans. Med. Imaging. 2020:2595–2605. doi: 10.1109/TMI.2020.2995508. [DOI] [PubMed] [Google Scholar]
- 3.Zhu N., Zhang D., Wang W., et al. A novel coronavirus from patients with pneumonia in China, 2019. N. Engl. J. Med. 2020;382(8):727–733. doi: 10.1056/NEJMoa2001017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Huang C., Wang Y., Li X., et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet. 2020;395(10223):497–506. doi: 10.1016/S0140-6736(20)30183-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Qiu D., Zhang S., Liu Y., et al. Super-resolution reconstruction of knee magnetic resonance imaging based on deep learning. Comput. Method. Program. Biomed. 2020;187 doi: 10.1016/j.cmpb.2019.105059. [DOI] [PubMed] [Google Scholar]
- 6.Fathi M.F., Perez-Raya I., Baghaie A., et al. Super-resolution and denoising of 4D-Flow MRI using physics-Informed deep neural nets. Comput. Method. Program. Biomed. 2020;197 doi: 10.1016/j.cmpb.2020.105729. [DOI] [PubMed] [Google Scholar]
- 7.Eun D., Woo I., Park B., et al. CT kernel conversions using convolutional neural net for super-resolution with simplified squeeze-and-excitation blocks and progressive learning among smooth and sharp kernels. Comput. Method. Program. Biomed. 2020;196 doi: 10.1016/j.cmpb.2020.105615. [DOI] [PubMed] [Google Scholar]
- 8.Lyu Q., Shan H., Wang G. MRI super-resolution with ensemble learning and complementary priors. IEEE Trans. Comput. Imaging. 2020;6:615–624. [Google Scholar]
- 9.Wang Z., Chen J., Hoi S.C.H. Deep learning for image super-resolution: a survey. IEEE Trans. Pattern. Anal. Mach. Intell. 2020:1–22. doi: 10.1109/TPAMI.2020.2982166. [DOI] [PubMed] [Google Scholar]
- 10.Dong C., Loy C.C., He K., et al. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016;38(2):295–307. doi: 10.1109/TPAMI.2015.2439281. [DOI] [PubMed] [Google Scholar]
- 11.Ren H., Elkhamy M., Lee J., et al. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. IEEE; 2017. Image super resolution based on fusing multiple convolution neural networks; pp. 1050–1057. [Google Scholar]
- 12.Kim J., Lee J.K., Lee K.M., et al. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. IEEE; 2016. Accurate image super-resolution using very deep convolutional networks; pp. 1646–1654. [Google Scholar]
- 13.Dong C., Loy C.C., Tang X., et al. European Conference on Computer Vision. Springer; 2016. Accelerating the super-resolution convolutional neural network; pp. 391–407. [Google Scholar]
- 14.Shi W., Caballero J., Huszar F., et al. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. IEEE; 2016. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network; pp. 1874–1883. [Google Scholar]
- 15.Kim J., Lee J.K., Lee K.M., et al. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. IEEE; 2016. Deeply-recursive convolutional network for image super-resolution; pp. 1637–1645. [Google Scholar]
- 16.Tai Y., Yang J., Liu X., et al. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. IEEE; 2017. Image super-resolution via deep recursive residual network; pp. 2790–2798. [Google Scholar]
- 17.Lim B., Son S., Kim H., et al. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. IEEE; 2017. Enhanced deep residual networks for single image super-resolution; pp. 1132–1140. [Google Scholar]
- 18.Lai W.S., Huang J.B., Ahuja N., et al. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. IEEE; 2017. Deep laplacian pyramid networks for fast and accurate super-resolution; pp. 5835–5843. [Google Scholar]
- 19.Haris M., Shakhnarovich G., Ukita N., et al. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. IEEE; 2018. Deep back-projection networks for super-resolution; pp. 1664–1673. [Google Scholar]
- 20.Kingma D.P., Ba J. Adam: A method for stochastic optimization. arXiv:14126980, 2014.
- 21.Yang J., Wright J., Huang T.S., et al. Image super-resolution via sparse representation. IEEE Trans. Image Process. 2010;19(11):2861–2873. doi: 10.1109/TIP.2010.2050625. [DOI] [PubMed] [Google Scholar]
- 22.Martin D., Fowlkes C.C., Tal D., et al. International Conference on Computer Vision. IEEE; 2001. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics; pp. 416–423. [Google Scholar]
- 23.Bevilacqua M., Roumy A., Guillemot C., et al. International Conference on Acoustics, Speech, and Signal Processing. IEEE; 2012. Neighbor embedding based single-image super-resolution using Semi-Nonnegative Matrix Factorization; pp. 1289–1292. [Google Scholar]
- 24.Zeyde R., Elad M., Protter M., et al. International Conference on Curves and Surfaces. Springer; 2010. On single image scale-up using sparse-representations; pp. 711–730. [Google Scholar]
- 25.Arbelaez P., Maire M., Fowlkes C.C., et al. Contour detection and hierarchical image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2011;33(5):898–916. doi: 10.1109/TPAMI.2010.161. [DOI] [PubMed] [Google Scholar]
- 26.Huang J., Singh A., Ahuja N., et al. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. IEEE; 2015. Single image super-resolution from transformed self-exemplars; pp. 5197–5206. [Google Scholar]
- 27.Huynh-Thu Q., Ghanbari M. Scope of validity of PSNR in image/video quality assessment. Electron. Lett. 2008;44(13):800–801. [Google Scholar]
- 28.Wang Z., Bovik A.C., Sheikh H.R., et al. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 2004;13(4):600–612. doi: 10.1109/tip.2003.819861. [DOI] [PubMed] [Google Scholar]
- 29.Han W., Chang S., Liu D., et al. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. IEEE; 2018. Image super-resolution via dual-state recurrent networks; pp. 1654–1663. [Google Scholar]
- 30.Yang X., He X., Zhao J., et al. COVID-CT-Dataset: a CT Scan Dataset about COVID-19. arXiv:2003.13865v3, 2020.