Abstract
Modern viral kinetic modeling and its application to therapeutics is a field that attracted the attention of the medical, pharmaceutical and modeling communities during the early days of the AIDS epidemic. Its successes lead to applications of modeling methods not only to HIV but a plethora of other viruses, such as hepatitis C virus (HCV), hepatitis B virus (HBV) and cytomegalovirus (CMV), which along with HIV cause chronic diseases, and viruses such as influenza, respiratory syncytial virus (RSV), West Nile virus (WNV), Zika virus, and SARS-CoV-2, which generally cause acute infections. Here we first review the historical development of mathematical models to understand HIV and HCV infections and the effects of treatment by fitting the models to clinical data. We then focus on recent efforts and contributions of applying these models towards understanding SARS-CoV-2 infection and highlight outstanding questions where modeling can provide crucial insights and help to optimize non-pharmaceutical and pharmaceutical interventions of the COVID-19 pandemic. The review is written from our personal perspective emphasizing the power of simple target cell limited models that provided important insights and then their evolution into more complex models that captured more of the virology and immunology. To quote Albert Einstein “Everything should be made as simple as possible, but not simpler”, and this idea underlies the modeling we describe below.
Keywords: Viral dynamics, viral kinetics, SARS-CoV-2, COVID-19, HIV, hepatitis C virus, influenza
Modeling HIV infection and treatment
Simple models1, 2, 3 of viral dynamics provided surprising insights into HIV infection. One critical element in modeling viral infections is keeping track of the change in viral load over time. For both HIV and HCV, which generate chronic infections, one usually finds that after the acute phase of infection, the virus and host come into accommodation, such that the viral load when measured over periods of days, weeks or months stays relatively constant. This constant level is called the viral set-point and to modelers, this means the viral-host system is at steady-state. To gain information about the underlying processes that generate and clear the virus, one can perturb the system from this steady state, for example by drug therapy. To understand the subsequent dynamics, what we now call the standard model of viral dynamics was introduced4. This model, as shown in Fig. 1, keeps track of cells susceptible to viral infection, which virologists call target cells, T, infected cells, I, and virus, V and their dynamics are given by the following system of ordinary differential equations (ODEs):
| (1a) |
| (1b) |
| (1c) |
where target cells are generated at rate s, die at rate dT per cell and become infected with rate constant β when virus, V, interacts with a target cell. Infected cells are generated at rate βVT and die at per capita rate δ. Lastly, virus, V, is produced by infected cells at rate p per cell and is cleared at rate c per virion. This system of equations (1) has been successfully used to model acute HIV infection if one assumes that initially all cells are uninfected and at time t=0 a small amount of virus is introduced into the body5. The model predicts that virus initially grows exponentially, reaches a peak, and then settles at a constant level, called the set-point (Fig. 2A).
Fig. 1. The basic model of viral infection.
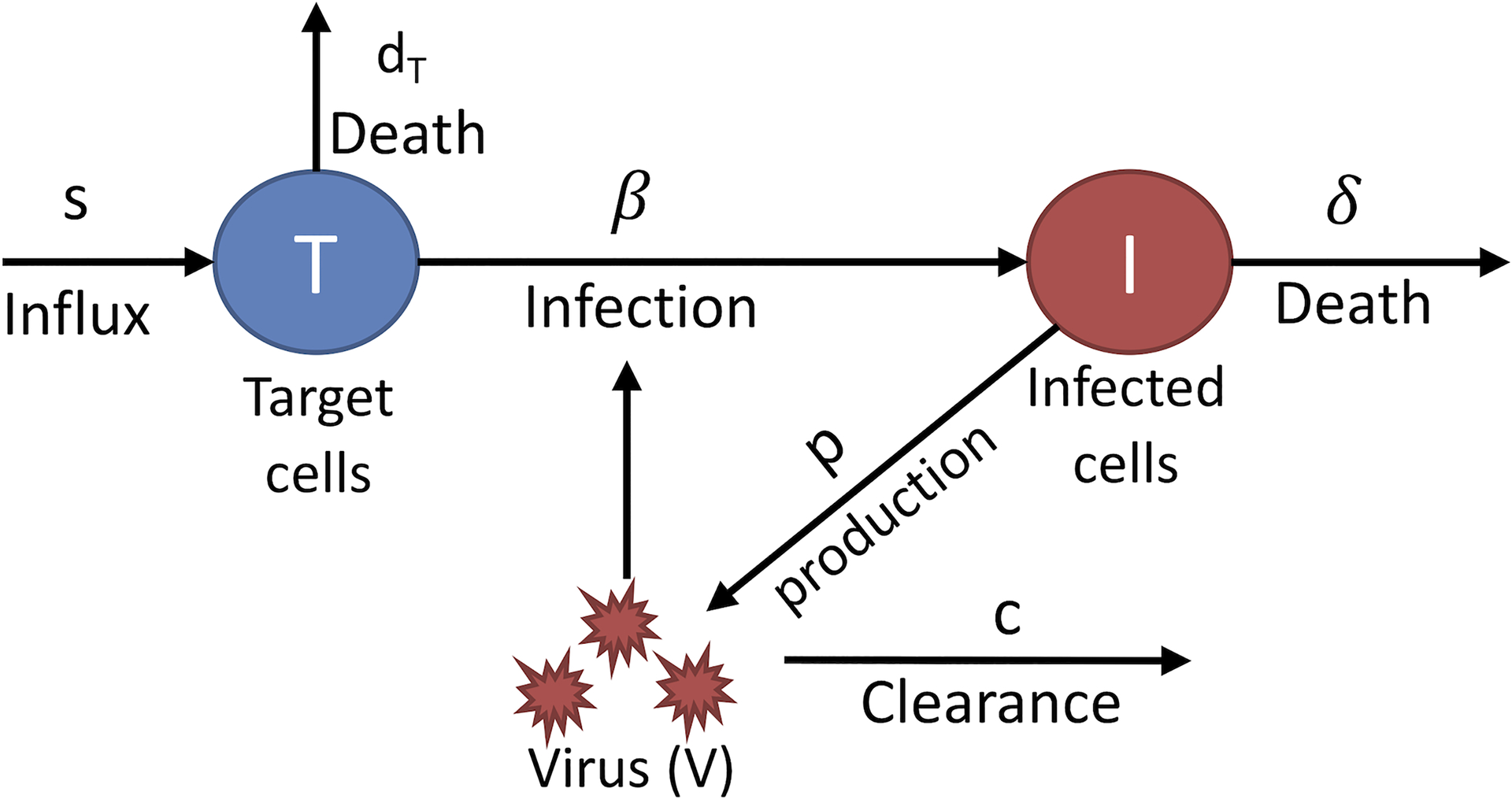
Target cells, T, which are cells susceptible to infection, are infected by virus, V, with rate constant β. Target cells are assumed to be made by a source at rate s and to die at per capita rate dT. Infected cells, I, produce virus as rate p per cell and die at rate δ per cell. Free virus particles, V, are cleared at per capita rate c.
Fig. 2. Modeling HIV infection and treatment.
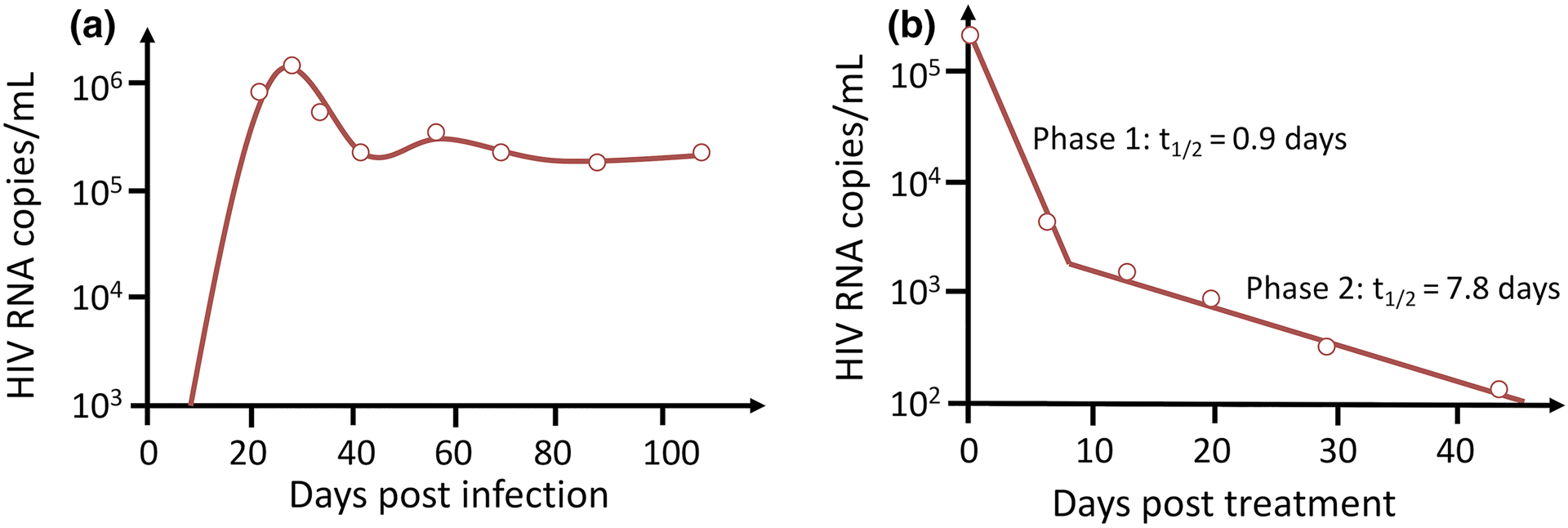
(A) The basic model can fit data (open circles) taken from individuals newly infected with HIV-1. The model solution (solid line) illustrates that virus initially grows exponentially, reaches a peak then falls and ultimately approaches a steady-state called the viral set-point. See Ref5 for details. (B) Biphasic decline of HIV-1 RNA after potent antiretroviral therapy is initiated. The basic model augmented with a population of long-lived infected cells (solid line) fits data taken from chronically infected HIV patients placed on combination antiretroviral therapy. The slopes of the first phase and second phase declines are mainly determined by the loss rate of short-lived and long-lived infected cells, respectively. See Ref11 for details.
The model has also been used to analyze the effects of antiretroviral therapy (ART) by incorporating into the model the effects of antiretroviral drugs. For example, reverse transcriptase (RT) inhibitors block the ability of HIV to productively infect a cell. HIV protease inhibitors (PI) cause infected cells to produce immature non-infectious viral particles, VNI. Thus, in the presence of these drugs, the model equations become3, 6
| (2) |
where εRT and εPI taken on values between 0 and 1, and represent the efficacies of RT and PI inhibitors (ε=1 being a 100% effective drug). Further, VI and VNI are the concentrations of “infectious” and noninfectious virus, respectively, and V= VI + VNI is the total virus concentration. An HIV entry inhibitor can be modeled in the same way as an RT inhibitor.
Equations (2) can be solved analytically if one assumes that during short-term therapy the number of target cells, T, remains at its baseline pre-therapy steady state value, T0=cδ/βp, and that therapy is with a 100% effective protease inhibitor (εPI=1, εRT=0). The solution is3, 6
| (3) |
where V0 is the set-point viral load before initiation of therapy. This solution only depends on three parameters, V0, c and δ. Allowing the target cell concentration, T, to vary necessitates using numerical methods to predict V(t) but does not substantially alter the outcome of the analysis.
Fitting either the analytical solution (3) or the numerical solution of V(t) to patient derived viral decline data allowed the first estimates of the rate of viral clearance, c, and the death rate of infected cells, δ, in vivo to be obtained3. These estimates were minimal because in reality protease inhibitors are not 100% effective (see Ref.3 for details). Later analysis using the same method but fitting to data obtained from patients treated with a four drug combination that is closer to being 100% effective yielded an estimate of δ = 1.0/day7. This implies that productively infected cells have an average lifespan, 1/δ, of about 1 day while producing virus and decay with a half-life t1/2 = ln 2/ δ = 0.7 days. The first estimate of c was 3/day, which corresponds to a half - life of virus in the circulation of t1/2 = 6 hrs. This estimate was not very accurate because drug does not act instantaneously after administration and later work showed the half-life to be closer to 45 min, i.e., c ~ 23/day8. Further, because c >> δ (i.e. ,23/day vs 1/day) one would expect from Eq (3) that the terms involving exp(−ct) would rapidly decay leaving the dominant decay to be proportional to exp(−δt).
One very important finding from this model was an estimate of how much virus was produced daily throughout the entire body. At the pre-therapy steady state, the total body wide rate of production of virus must equal the total viral clearance rate. The term cV0 gives the rate of clearance from 1 mL of blood plasma before therapy starts. The total extracellular body water in a 70 kg adult is approximately 15 liters. Thus, for an individual with an initial viral load of 105 HIV RNA copies/ml and c= 23/day, we can estimate that 3.5 × 1010 HIV RNAs are produced and cleared per day. This is a minimal estimate because some HIV is also in attached to cells in tissue. Because HIV mutates when it replicates one can compute that every possible single mutation and most double mutations are made every day9, 10. This observation suggested that combinations of three drugs should be used to treat HIV infections. When such combination therapy was given to chronically infected HIV individuals, the virus was observed to decline in two exponential phases, a fast first-phase followed by a slower second-phase (Fig. 2B). The second phase was attributed to the existence of a population of “long-lived infected cells”, with the slope of the second phase reflecting the death rate of these cells11.
One can analytically solve Eqs. (2) for any combination of protease inhibitor and reverse transcriptase inhibitor of any efficacy as long as one assumed that target cell level remained constant, as this made the system of equations (2) linear6. However, for HIV in vivo, drug efficacies were not known and analysis of the solutions to these linear equations showed that models still predicted exponential decays but now with eigenvalues that included the drug efficacy. Thus, simply fitting these models to data that exhibited exponential decays did not allow one to estimate the drug efficacy. Experiments done with combination therapy showed that the first-phase viral decay slope increased and when comparing different drug regimes, the ratio of such slopes was used as a measure of the relative efficacy of one regime versus another12. Also, later elaborations of the basic model used to describe the effects of therapy for HIV and HCV (discussed below) replaced the constant drug efficacies in this simple model by models in which the drug efficacy was allowed to change in time to mimic pharmacokinetic (PK) effects13 or by using full PK/pharmacodynamic models14, 15, 16, 17, 18.
After a cell is first infected by a virus it does not instantly start producing new progeny virions. Rather there is a period time called the eclipse phase during which no virus is produced by the cell. More biologically accurate models have been developed that include the eclipse phase. In the case of HIV this was first modeled by Herz et al.19 by a fixed time delay of length τ. Thus, in their model Eq. (1b) for productively infected cells was replaced by
| (4) |
where m is the mortality or death rate of a cell in the eclipse phase and the term exp(−mt) represents the fraction of initially infected cells that remain alive at time t. A more realistic model introduced by Mittler et al.20 assumed a distributed delay and replaced Eq. (4) by
| (5) |
where f(τ) is the probability distribution for the delay. If f(τ) is chosen as a Dirac delta function then Eq. (5) reduces to Eq. (4), so Eq. (5) is a rather general formulation. They then went on to study the case in which the delay distribution was given by a gamma function with an integer shape parameter, i.e. an Erlang distribution. They also showed that Eq. (5) could be converted to a set of n ordinary differential equation, where n is the integer shape parameter of the gamma distribution, which is sometimes convenient when fitting the model to data. Using such a model to fit patient viral decline data leads to slightly changed estimates of the basic parameters c and δ19, 21. Similar analyses were done for influenza and also showed that the choice of the delay distribution affects parameter estimates22. For in vivo modeling, there is generally not frequent enough sampling to accurately predict the additional parameters introduced by this approach. However, it has been useful to more precisely fit models to data from in vitro HIV/SHIV infection experiments23. In modeling other infections, such as influenza24 and Zika25, 26, cells in the eclipse phase were explicitly modeled as a separate population of infected cells. Thus, Eq. (1b) and (1c) were replaced by the equations
| (6a) |
| (6b) |
| (6c) |
where I1 represents cells in the eclipse phase and I2 represents productively infected cells, i.e. cells that produce virus. For these acute infections, one advantage of including the eclipse phase is that the models then generated more realistic estimates for the lifespan of an infected cell as it now includes the time spent in the eclipse phase plus the time in the productive phase of infection, i.e. 1/k + 1/δ24.
Another modeling approach that has been used to account for the delay between the time of infection and the start of viral production is to use and age-structured model where age, a, represents the time a cell has been infected. In this approach, Eqs. (1b) and (1c) of the basic model are replaced by
| (7a) |
| (7b) |
where the death rate of infected cells and the rate of viral production are now functions of how long a cell has been infected. Initially the viral production rate would be zero, i.e. p(0)=0 and then it could increase as a step-function, which would mimic having a fixed delay, or more realistically the viral production rate, after a delay, could increase gradually to a maximum level27.
Before HIV modeling was done there was no quantitative information about how HIV acted in vivo and it was mistakenly thought that the kinetics must be slow because it took on average 10 years for AIDS to develop into a full-blown disease. Thus, the major impact of this work was to show that at set-point the virus was not turning over slowly, but rather there was rapid production and clearance of both virus and infected cells. This led to the introduction of combination therapy and the hope that with potent enough drugs HIV could be cured. However, this was not to be. A population of latently infected cells that harbor the HIV genome, but which do not produce virus unless activated, were found to decay under potent therapy with a half-life of 44 months28. Based on estimates of the number of these cells in the body, it was calculated that it would take about 60 years of completely effective therapy to eliminate HIV28. Current efforts are being made to accelerate the elimination of the latent reservoir using pharmacological and immunological methods29.
Modeling HCV infection and treatment
HCV is a positive strand RNA virus that primarily infects human hepatocytes and like HIV can lead to chronic infection. About 180 million people are infected world-wide and there is no vaccine for it yet. The standard therapy for HCV for over a decade had been a combination of interferon-α (IFN), or pegylated interferon-α (PEG-IFN), and the nucleoside analog ribavirin (RBV). When given for 48 weeks, this combination was able to cure slightly less than 50% of patients with HCV genotype 1 infection, the most common form of infection in the US and Europe. In May 2011, the first direct acting antiviral (DAA) for the treatment of HCV, the HCV protease inhibitor telaprevir, was approved. Subsequently, many other DAAs have been approved. Unlike HIV, HCV does not have a DNA form and its RNA genome replicates in the cytoplasm of a cell. The replication can be stopped by drug therapy, and the HCV RNA within a cell can degrade. Probably because of this biology, combination therapy with two or three DAAs with different mechanisms of action has led to cure in almost all treated individuals.
Mathematical modeling played an important role in characterizing HCV kinetics, determining basic quantities such as the lifespan of infected cells and the clearance rate of HCV from the circulation as well as providing insight into the mechanism of action of DAAs. Work in this area began with the basic model, Eqs. (1a)–(1c), which when used to analyze the plasma viral declines in patients treated with IFN led to the realization that IFN acted to reduce the rate of viral production from infected cells, p. Interferon is a cytokine that binds IFN receptors and signals through these receptors, turning on hundreds of interferon-stimulated genes, whose gene products ultimately reduce viral production within an infected cell.
The viral declines were biphasic, like for HIV, but the first phase was considerably faster and only lasted 1–2 days and then was followed by a slower second phase decline (Fig. 3). Because IFN at doses of 10–15 MIU daily could reduce p by 95%, the first phase slope largely reflected the rate of viral clearance whereas the second phase slope largely reflected the rate of death of productively infected cells30. The following simple mathematical analysis led to a way to rapidly evaluate the in vivo effectiveness of IFN and later DAAs used to treat HCV. For a drug that affects viral production, the basic model equation (1c), should be modified such that the viral equation becomes
| (8) |
where 0 ≤ ε ≤ 1 is the effectiveness of therapy in blocking viral production. Note that, at the pre-therapy set-point, pI0=cV0, where the subscript 0 denotes the baseline value before therapy. If one assumes that over the first day of therapy the number of infected cells stays at I0, then Equation (7), with the initial condition V(0)=V0, can be solved to yield
| (9) |
where t0 is the pharmacological delay before IFN becomes effective. As c turns out to be about as large for HCV as for HIV31, V rapidly approaches V0 (1−ε). Note that this implies that, if a drug is 90% effective, i.e. if ε=0.9, then the viral load will rapidly decline by one log, whereas if it is 99% effective the decline will be two logs. Thus, from the magnitude of the first phase viral load decline one can get an estimate of the effectiveness of an HCV antiviral agent. This led to the estimation that the active tissue concentration of the HCV NS5A inhibitor, daclatasvir, is much lower than its plasma concentrations32. Moreover, this estimate can be made in a one- or two-day clinical trial. For this reason, the first HCV protease inhibitor to go into human trials, BILN-2061, was given for only two days33 and, using a viral kinetic model, the effectiveness, ε ,was estimated to be above 99.5% in patients with mild disease34.
Fig. 3. Dynamics of HCV RNA decline after therapy initiation.
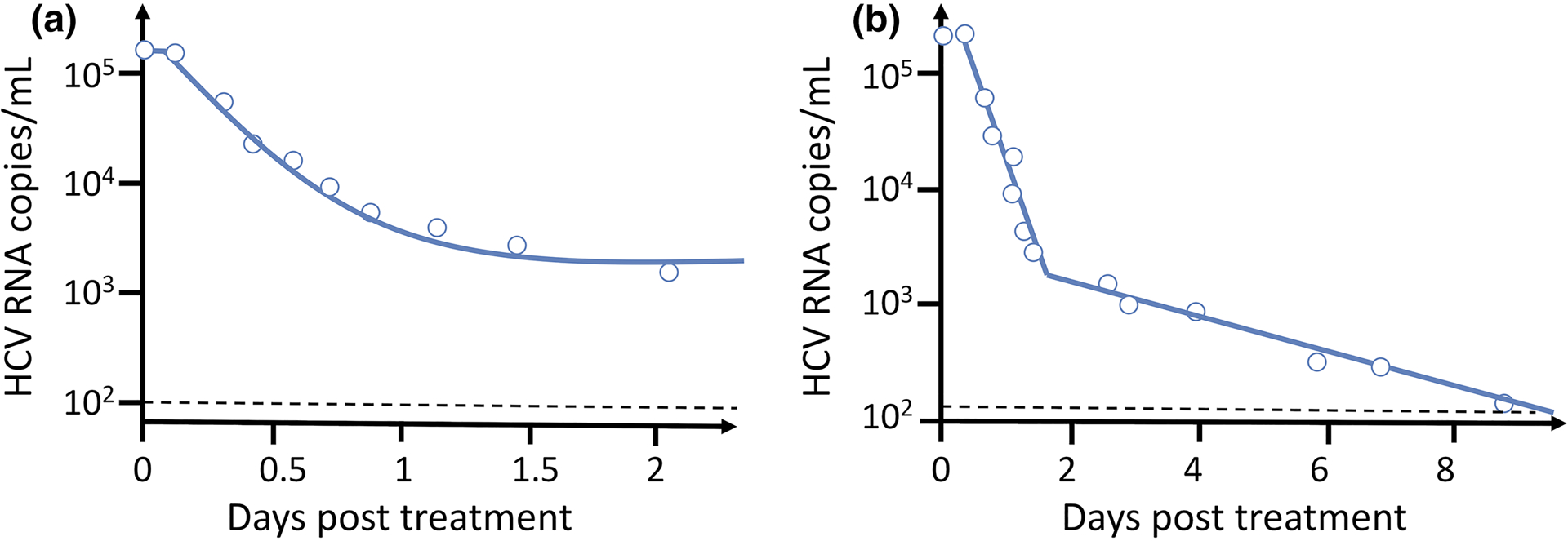
(A) Fit of Eq. (9) (solid line) to data from an HCV chronically infected patient treated with IFN given daily. After a very brief delay the viral load falls rapidly by about 1.5 log10 and appears to be approaching a steady state. (B) On a longer-time scale the viral load continues to fall. The solid line shows the best-fit solution of Eqs, (1a), (1b) and (8) to the data. As discussed in Ref30, the slope of the first phase decline mainly reflects the rate of viral clearance, c, whereas the slope of the second phase decline mainly reflects the rate of loss of infected cells, δ. The magnitude of the first phase decline determines the efficacy of the drug. When a more potent DAA, such as the NS5A inhibitor daclatasvir is used the first phase decline can be 3 logs, implying a drug effectiveness of 99.9%. See ref31 for details.
As the first phase is over after one or two days, data collected over the subsequent week or two allowed one to estimate the death rate of productively infected cells, δ. For IFN therapy, on average δ= 0.14/day30, 35. The same methodology was used to analyze the effects of DAA therapy. Interestingly, although two-phase viral declines were always seen, the estimates of c and δ varied with the drug under study. As these parameters should depend on the host’s ability to clear virus and infected cells, the application of the basic model was called into question and a multiscale model that tracked intracellular steps in the viral life cycle was developed. In particular, an equation was added to the basic model that followed the amount of intracellular positive strand HCV RNA, R, that was in a cell infected for time a. This generated the following age-structured model:
| (10) |
with boundary conditions I(0,t)=βVT, I(a,0)=I0(a), R(0,t) =1, R(a,0)=R0(a), where I0(a) and R0(a) are the pre-therapy steady state distributions and α is the rate of viral RNA (vRNA) synthesis, μ is the rate of vRNA degradation and ρ is the rate of vRNA loss due to incorporation into secreted virions. It was assumed that treatment begins at time t=0 and that cells when initially infected contain one vRNA. The treatment effects of an antiviral drug were assumed to be blocking vRNA synthesis with effectiveness εα, blocking viral assembly/secretion with effectiveness εs and increasing the rate of vRNA degradation by the factor κ. By integrating over the age-structure, Kitagawa et al.36 showed that these equations could be converted into a system of ordinary differential equations. Fitting this model to data from therapy with the HCV NS5A inhibitor daclatasvir and to data with the HCV protease inhibitor telaprevir, Guedj et al.31 predicted that both of these drugs had two modes of action, blocking vRNA synthesis and blocking viral assembly secretion, with efficacies of 99% or greater for daclatasvir. These predicted modes of action were then verified by in vitro experiments31, 37, 38. Multiscale model of hepatitis B virus (HBV) infection and treatment are now also being developed39 and should prove useful in analyzing the effects of new classes of HBV therapeutics currently in clinical development.
Modeling SARS-CoV-2 infection and treatment
Viral dynamic models for chronic infections above can be adapted to quantify dynamics of acute infections, such as influenza24, 40, West Nile virus41, RSV42, Zika26 and SARS-CoV-243, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53. In particular, extensive modeling efforts have been made towards understanding influenza infection and the immune response against it. These studies often serve as the basis for modeling other acute infections. See Refs.54, 55 for recent reviews of within-host influenza models. Because of the current interest in COVID-19, below we will focus on the models for SARS-CoV-2 infection, summarize key recent findings from these models and highlight outstanding questions relevant for non-pharmaceutical interventions as well as the development of therapeutics and vaccines.
SARS-CoV-2 is a single-stranded RNA virus that causes acute infection of the respiratory system. Viral loads are often measured in hospitalized patients (see Fig. 4 for a schematic) to understand the course of infection and clinical outcomes56, 57, and in non-human primate (NHP) infections to evaluate the efficacy of therapeutics, e.g. the antiviral remdesivir58. With the availability of clinical and experimental data, many mathematical models have been developed and calibrated with data43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53. Overall, these studies greatly advanced our quantitative understanding of SARS-CoV-2 infection in both humans and NHPs, the immune responses and the impact of therapeutics.
Fig. 4. Illustration of the dynamics of SARS-CoV-2 infection in the upper respiratory tract (URT; solid red line) and the lower respiratory tract (LRT; solid blue line).
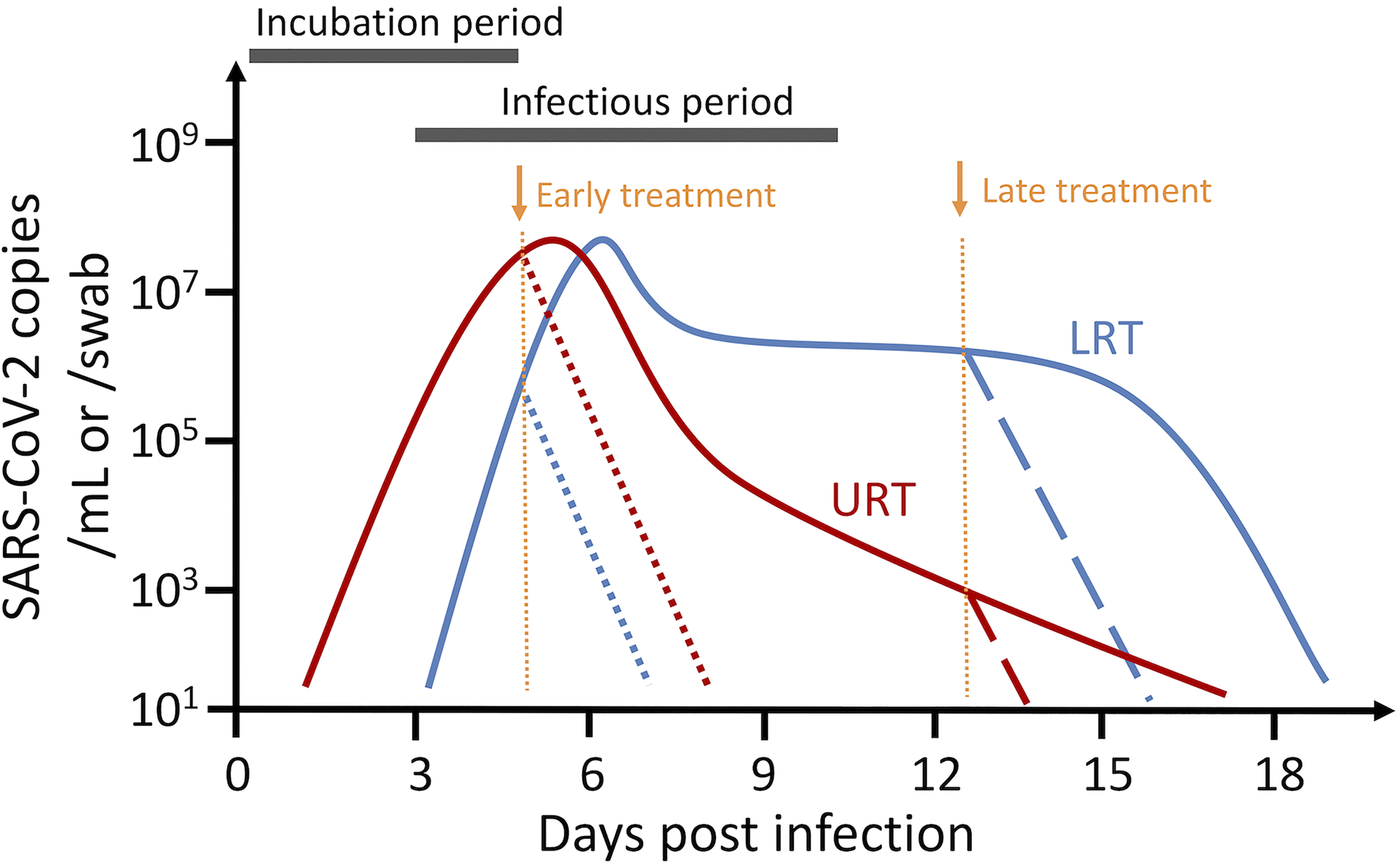
The incubation period lasts for approximately 4–6 days (5 day is shown in the figure). The virus population reaches peak viral load at or a couple of days post symptom onset. Individuals become infectious at or a few days before symptom onset. The viral load declines rapidly after peak viremia in the URT, whereas the viral load in the LRT is maintained at intermediate-to-high levels for several weeks. Dotted and dashed lines denote predicted viral load dynamics when individuals are treated with an effective antiviral (e.g. with 95% efficacy) at symptom onset (dotted lines), or 8 days post symptom onset (dashed lines). Viral load curves are drawn based on the data in Refs.57, 82 and parameter estimates in Ref.49.
Target cell limited model
The simplest form of acute infection model, that is often used as a starting point to understand SARS-CoV-2 infection dynamics in many studies43, 44, 47, 51, is derived from the basic viral dynamic model given by Eqs. (1). This model incorporates target cell replenishment and therefore allows the viral load to reach a steady state in which virus and infected cell production balances their clearance. In order to model acute infections where natural death and replenishment of target cells are negligible during the short period of infection, Eq. (1a) can be simplified to
| (11) |
This model is termed the target cell limited model, because the dynamics of this model are driven by the availability of target cells. During early infection, target cells are abundant, and thus the virus population grows exponentially until a viral peak is reached and most target cells are infected. Then, the viral load declines exponentially towards extinction because there are few target cells left in the system. The dynamics of the model are very similar to the often-used Susceptible-Infected-Recovered (SIR) model in epidemiology where epidemics spread through a population until the population runs out of susceptible individuals.
A simplification that one can make is to assume the time scales of virus production and clearance are much quicker than the dynamics of infected cells, and thus the dynamics of viruses are in quasi-equilibrium with infected cells: , and thus . This assumption simplifies the 3-ODE system to a 2-ODE system. A variation of this simplification has been used compare infection dynamics of SARS-CoV-1, SARS-CoV-2 and MERS50.
An extension of the basic model above is to add an eclipse phase for infected cells, because it usually take hours for infected cells to start to produce viral particles. The simplest form of an eclipse phase model given by Eqs, (6a–6c) has been used in SARS-CoV-2 modeling. This allows for more accurate estimation of parameter values in the model as well as composite parameters of interest, such as the within-host reproductive number R0.
Estimating key parameter values
One key challenge in modeling a novel viral infection, such as SARS-CoV-2 infection, is that key parameter values such as the number of target cells in the model are unknown. Efforts have been made to estimate these parameter values from data44, 48, 49, 50. For example, single cell gene expression data suggests that approximately 1% of cells in the respiratory tracts express the receptor and the coreceptor for SARS-CoV-2 entry, i.e., angiotensin-converting enzyme 2 (ACE2) and the type II transmembrane serine protease TMPRSS259, 60. Based on this finding, we estimated that there are approximately 4×106 and 4.8×108 target cells for SARS-CoV-2 in the URT and LRT respectively49. This represents a rough estimate, because whether a cell is a target of infection may also depend on other factors in addition to gene expression61. Another parameter that can be calculated directly from experimental data is the duration of the eclipse period, 1/k. In vitro experiments have shown that it usually takes 4–8 hours before an infected cell starts to produce SARS-CoV-2 particles61, 62. It is not known how quickly virus particles are cleared from the resiporatory tract. Initial guesses of this parameter are based on estimates from influenza infection24, 40.
Fitting the TCL model to viral load data, we and others have estimated that the death rate of infected cells ranges between 0.5 and 4 per day44, 48, 49, 50. The value of R0 is estimated to be between 5 and 3044, 49. The parameter p usually cannot be identified but only the product pT05. In a SARS-CoV-2 model fit to data where T0 was fixed and the viral load was measured per swab, only the product of p and the fraction of viruses sampled could be estimated49.
Overall, there still exists considerable levels of variation in estimated parameter values across studies. This partially reflects heterogeneities in the viral dynamics among individual patients and in different physiological compartments. They also likely arise from uncertainties in the dataset itself as we will discuss in the Outstanding questions section.
Innate immune model
The innate immune response represents the first line of defense against viral infections and thus may impact on the dynamics of SARS-CoV-2 infection kinetics. One important arm of the innate immune response is the antiviral response triggered by type I interferon (IFN)63. The production of IFN by infected cells and the subsequent autocrine and paracrine signaling can lead to an antiviral state in both infected cells and target cells. This in turn can lead to a reduction in virus production in infected cells and protection of target cells from infection. IFN also induces the recruitment of immune cells such as macrophages and natural killer cells to the site of infection63. This recruitment may lead to increased killing of infected cells.
To model the protection of target cells by IFN signaling in influenza infection, Pawelek et al. added a refractory cell compartment40. Similar formulations were used for SARS-CoV-2 infection44, 46, 49. The ODEs for the target cell population (T), the refractory cell population (R) and interferon (F) from Eqs. (1) are then modified to
| (12) |
where ϕ is the rate at which IFN causes a target cell to become refractory to infection, ρ is the rate at which the refractory state is lost, π is the rate of IFN production from an infected cell and w is the rate of IFN loss. Using this formulation, we recently found that adding the IFN response to the model does not significantly improve the fits to a set of data collected from 8 patients compared to the target cell limited model49. This could indicate that the IFN response is inhibited and does not play an important role in reducing viral load in these patients, consistent with experimental studies showing that the IFN signaling pathway is suppressed during SARS-CoV-2 infection64; or it is possible that the role of interferon cannot be statistically distinguished with this set of viral load data.
To model the recruitment of innate immune cells and thus increased killing of infected cells, Goyal et al.45 used a term −δIn (instead of −δI) in the infected cell equation to model the dependence of infected cell killing on the innate response. This formulation was originally developed to model the immune dependent killing of infected cells during HIV infection65, and also later used in influenza modeling66. The underlying assumption is that the immune cell mediated killing is determined by the size of the immune cell population, which in turn is dependent on the infected cell population. Goyal et al. found that this model was able to describe the rapid decrease in viral load observed immediately after the initial viral peak (Fig. 4) and predicts that the viral load decline rate decreases as viral load declines to a low level45.
Despite the majority of modeling work focusing on well-mixed models, an important aspect of acute respiratory infections is the spatial nature of the infection process in respiratory tract epithelium67. As discussed above, well-mixed models in general predict that the IFN response affects peak viral load and viral dynamics afterwards24, 40. In contrast, recent works of ours pointed out when target cells are spatially segregated, e.g., in epithelium, the combined impact of autocrine and paracrine signaling can strongly suppress viral spread during early infection before the viral peak68, 69. These types of models may be important in understanding how early IFN response or treatment determines long-term infection outcome as suggested recently by experimental studies of SARS-CoV-2 and MERS coronavirus64, 70, 71.
The quantitative impact of the IFN response on SARS-CoV-2 dynamics and which aspect of the response plays a more important role still need to be resolved. Also, the responses may vary from individual to individual. Simultaneously measuring the viral load and levels of interferon over time may help to resolve the question. In a study of Zika virus infection in nonhuman primates, IFN levels were measured along with viral load and including these IFN level in an immune response model did not improve the fit of the model to data over that using a target cell-limited model25. However, Zika like many other viruses including HCV and SARS-CoV-2 antagonizes the IFN response. Including the effect of antagonism in a modified innate immune response model to Zika virus then improved the model fit over that of the target cell-limited model72. To further elucidate the phenomenon of antagonism, Padmanabham et al.73 introduced a more detailed model of the intracellular IFN signaling network. They showed that HCV induces bistability in the network, causing the emergence of a new steady state where HCV persists73. Whether this is also the case for SARS-CoV-2 remains to be determined
Adaptive immune model
Adaptive immune responses to SARS-CoV-2 infection develop one to two weeks after infection56, 74. The most simplistic approach to model the impact of adaptive immune responses is to assume that the killing rate of infected cells increases after some time post-infection40. This increase in infected cell killing rate may arise from the development of antigen-specific effector cells, such as cytotoxic T cell responses74, 75. This approach involves adding only one or two extra parameters to an existing model, and thus is particularly well-suited for model calibration with data. Several studies have adopted this approach to understand SARS-CoV-2 infection dynamics beyond 2 weeks after infection45, 49, 51. In general, the increased killing explains the rapid viral load decreases that accompany viral clearance (see the solid blue line in Fig. 4). A more complex model that keeps track of the maturation of precursor cells into immune effector cells has been proposed45. This model effectively introduces a delay, as was done in modeling the eclipse phase with an Erlang distribution discussed earlier in the section on HIV infection models20. However, the parameters governing the immune effector response need to be calibrated and validated with experimental/clinical data measuring the kinetics of the T cell response and the expansion of the relevant immune cell populations. Another important consideration for models explicitly including T cell populations is individual heterogeneity in initial T cell populations, because some individuals due to prior infection with seasonal coronaviruses may have some pre-existing cross-reactive T cell immunity to SARS-CoV-275. Simple models of both the CD4+ and CD8+ T cell response to lymphocytic choriomeningitis virus (LCMV) infection in mice have been developed and model parameters estimated76. Also, a model of a dynamic motif underlying the interactions of antigens and CD8+ T cells was introduced in a rather general setting and then applied to LCMV and HCV infections77. Models of this type should be tried for SARS-CoV-2 infection.
In contrast to the approaches above, where the models focused only on key aspects of the immune response and their impact on viral dynamics, another approach is to incorporate much more detailed information about the innate and adaptive immune responses as well as comorbidities induced by the virus. This is being done using multiscale simulation-based models78, 79, 80. These models keep track of the complex molecular interactions involved in viral infection and virus replication within cells as well as spatial spread of the virus, the production of cytokines and chemokines, and the population dynamics of various types of immune cells, such as macrophages, neutrophils, CD4+ T cells, CD8+ T cells, etc. This modeling approach offers a unique opportunity to integrate existing knowledge about viral infection and the induced response of various immune molecules and cells. However, one important challenge of this approach is validating the plethora of details included in these models against data to make reliable predictions, because of the large number of parameters in these models and the high levels of uncertainty about their values in the context of SARS-CoV-2 infection.
URT/LRT model
SARS-CoV-2 causes distinct infection dynamics in different tissue compartments57 (Fig. 4). Infection in the upper respiratory tract (URT) exhibits typical acute infection dynamics57. After an initial viral peak, the viral load decreases rapidly to low or undetectable levels. In contrast, sputum samples, likely representing dynamics in the lower respiratory tract (LRT), taken from hospitalized patients with mild disease57, showed sustained intermediate-to-high viral loads for 3–4 weeks (Fig. 4). In some individuals, multiple viral load peaks were observed late in the infection. Motivated by these observations, we developed a two-compartment model to keep track of these distinct dynamics49. Models including a URT and an LRT have also been used to understand viral dynamics in non-human primates where viral load measurements were taken from both nasal swabs and BAL46, 49, 53. This type of model allows one to investigate the relationship between virus replication in different tissue compartments. For example, we have found that the rate of virus replication is positively correlated in the URT and the LRT49 in the patients studied in Wolfel et al.57. The rate of transport of virus from the URT to the LRT is probably low as mucocilliary clearance acts to bring particles out of the LRT. When virus does get into the LRT disease typically becomes more severe. Both the viral dynamics and some genetic sequencing information57 suggest there may be compartmentalization of virus populations.
Viral spread in the LRT and cell proliferation
Viral loads in the lower respiratory tract (LRT) are positively associated with disease outcomes81, 82. As mentioned above, viral loads in the LRT are maintained at intermediate-to-high levels for a prolonged period57, 82 (Fig. 4). Several mechanisms have been proposed to explain this pattern, including spatial spread of the virus and target cell proliferation46, 47, 49. We recently explored these hypotheses, and showed that spatial spread into new areas of the lungs could explain sustained viral shedding as well as multiple viral load peaks49. Type II alveolar cells, a major target cell population, proliferate in response to epithelial cell death and tissue damage83. Cell proliferation can be modeled by adding the term to Eqn. (1) for the target cell population, where T0 is the total number of target cells in the absence of infection49. This type of logistic term has been used for target cell proliferation in models of HIV, HCV and HBV infections84, 85, 86. We found that a proliferation model of this type can explain the long-term persistence of viral load better than the target cell limited model or models incorporating the IFN response49.
Overall, these model results suggest that new target cells for virus infection are needed to maintain the observed viral load. These can come from target cell proliferation or spatial spread of the virus to a new physiological compartment in the lungs. These insights may have important implications for therapeutic development to reduce disease severity. Other models were also proposed. For example, a model assumes that SARS-CoV-2 infects lymphocytes and predicts that the recruitment of lymphocytes to the infection site leads to sustained high viral loads51. However, the experimental evidence for lymphocytes being a major target for SARS-CoV-2 infection is not clear and the article cited in ref [51] as support for this hypothesis has been retracted.
Modeling therapy
As discussed earlier, mathematical models are widely used to estimate the efficacy of therapeutics in suppressing virus replication or infection1, 3, 4, 11, 24, 25, 30, 31. Studies have used terms of the form (1−ε), where ε varies between 0 and 1 to represent the drug efficacy, to understand the impact of potential therapeutics on SARS-CoV-2 infection dynamics43, 44, 45, 49, 50, 51. A converging conclusion emerges that therapeutics that block virus replication and spread have to be administered before or at the time of peak viral load; otherwise, the therapeutics will not be effective at reducing overall host exposure to viruses44 (Fig. 4). This is because most target cells are predicted to be infected by the time the peak viral load is reached and thus most viruses are produced during this period. Administration of therapeutics after peak viral load would only prevent a small fraction of total cell infections. For SARS-CoV-2, it has been estimated that peak viral load occurs at the time of or a couple of days after symptom onset44, 49, 87 and many infected individuals never show symptoms88. Thus, it is most effective to administer antivirals or other therapeutics that block virus infection as soon as one tests positive or shows symptoms rather than later in the infection when severe symptoms develop (Fig. 4). This may partially explain the conflicting results from remdesivir trials where the antiviral was administered several days after symptom onset89, 90. This also implies that we need antivirals that can be administered orally at home in addition to drugs such as remdesivir or the monoclonal antibodies now in clinical trials that need to be infused.
Drug efficacy can be modeled as a function of drug concentration by where C represents drug concentration and EC50 is the concentration of the drug that gives half-maximal response. More detailed approaches to model PK/PD of SARS-CoV-2 antivirals were done for lopinavir/ritonavir, hydroxychloroquine, interferon-β−1a44 and remdesivir and antibodies45. However, parameter values in these PK/PD models are in general estimated from in vitro studies, non-human primates, or plasma of humans. A challenge is to estimate/validate parameter values at the relevant tissue compartments in vivo. As estimated previously for HCV antivirals, the active concentration at relevant tissue can be very different from that in plasma32. With appropriate data, this type of model framework can be used to design and optimize therapeutics used singly or in combinations to better block virus infection.
Another way to use antiviral is to give them prophylactically, especially to individuals at high risk of exposure. To better understand the early events in the acute stage of HIV infection stochastic models were developed that follow the fate of individual infectious virions and infected cells91, 92. A similar approach has been adopted for SARS-CoV-2 by Czuppon et al.93 and used the model to predict what might occur when an individual taking antivirals prophylactically is exposed to different doses of infectious SARS-CoV-2. They studied the effects of four classes of antiviral: those that block viral entry or infection, those that block viral production from infected cells, e.g. remdesivir, those that enhance viral clearance such as a non-neutralizing antibody, and those such as an immunotoxin that can enhance infected cell death. Not surprisingly, they found that there is a critical drug efficacy needed to block establishment of infection that can depend on the drug’s mechanism of action. Below this crucial efficacy, prophylaxis can still sometimes prevent establishment of infection especially with drugs that block viral entry or enhance viral clearance and can also flatten the viral kinetic curve possibly leading to less severe symptoms.
Overall, current modeling studies estimated that the critical drug efficacy to suppress viral infection in the setting of prophylaxis or treatment is roughly in the range between 85% and 95%44, 49, 93. Repurposing antivirals such as lopinavir/ritonavir, hydroxychloroquine and remdesivir is unlikely to achieve such high efficacy in vivo44. Studies of human monoclonal antibodies, such as REGN-COV2 and bamlanivimab (LY-CoV555), showed that they are highly effective in suppressing viral replication, blocking infection and reducing viral load in both non-human primates and humans94, 95. They are likely to be highly efficacious in vivo, although formal model fitting to clinical data is needed for precise estimation of their antiviral efficacy. There are also mAbs in development that have Fc-effector functions and potentially could be used for treatment as these mAbs could in principle kill infected cells and mediate a vaccinal effect whereby presenting viral antigens to dendritic cells enhance T cell responses again the virus, e.g., Schafer et al.96.
Linking viral load kinetics to infectiousness
Viral load in the URT is often used as a surrogate measure of infectiousness of a person. However, how these two quantities relate to each other is not clear. For example, both viral load and the logarithm of viral load are used as a measure of infectiousness for influenza infection97. A quantitative framework to predict infectiousness of an individual from viral load measurements would be particular useful for optimizing non-pharmaceutical interventions, such as test and trace strategies, as well determining isolation duration after diagnosis. In a recent work, we addressed this question by comparing predictions from these two measures with epidemiological evidence. We found that the logarithm of the viral load better explains the observation that a large fraction of transmission occurs presymptomatically and that the serial interval is between 7–8 days without active intervention or self-isolation98, 99. We then constructed a physiological model keeping track of each step of virus transmission process. A key aspect of this model is the assumption that the number of infectious viral particles reaching the recipient host given a contact is a saturating function of the viral load in the donor. A similar relationship was previously used for influenza and HIV transmission100, 101, and was used by Goyal et al.102. This saturation effect explains why the logarithm of viral load is a better measure of infectiousness than the viral load49.
Superspreading events were often reported for SARS-CoV-2 transmission103. To understand these events, Goyal et al. generated an in silico population of infected individuals where their viral dynamics were simulated using parameters estimated from viral load data from hospitalized SARS-CoV-2 infected patients102. The transmission profiles for the individuals in the synthetic population were determined from their viral loads. Using their simulation, the authors show that variations in individual contact pattern (in addition to variations in individual viral load) play an important role in driving superspreading events102. It remains to be determined if other factors, such as heterogeneities in the level of infectious viruses57, and mode of transmission, i.e. aerosol vs. droplet104, also play important roles in driving these events.
Overall, these models serve as first steps towards predicting infectiousness from viral load data. Hopefully, as they develop, these models will prove useful in assessing the infectiousness of groups of infected individuals where viral load measurements are available and where epidemiological data are difficult to obtain or ascertain, such as asymptomatic individuals or children. Further improvement of the models, for example explicitly incorporating biological, physical and environmental factors during transmission104, 105, will be needed to make more accurate and individual-level predictions.
Outstanding questions
Within less than a year, we have obtained extensive understanding of SARS-CoV-2 infection kinetics. As we summarized above, many viral dynamic models have been developed to estimate key parameters governing viral kinetics and determine how infectiousness depends on viral load. Models have also considered the effects of the immune responses and the impact of therapeutics. However, even though knowledge about SARS-CoV-2 is rapidly evolving, there are still many unknowns and questions that need to be addressed to help design both pharmaceutical and non-pharmaceutical intervention strategies.
Rate of exponential growth and the within host reproductive number, R0
Despite many modeling efforts, there are still uncertainties in the rate of exponential expansion of the virus population during the early period of infection and thus in the within-host reproductive number R0. This prevents precise predictions of the drug efficacy needed to suppress the virus. The uncertainty arises from limitations in the data used for parameter estimation. First, for most of the datasets, the dates of initial infection are unknown. This makes estimation of the rate of exponential expansion unreliable. To address this issue, we recently used data from a study where infection dates were known through contact tracing49. This greatly reduces uncertainty in the parameter estimation, and we found that the viral growth rate is negatively correlated with the incubation period49. Second, in all datasets used for model inference so far, viral loads were measured after symptom onset, and the viral load during the presymptomatic period, i.e. the phase of viral exponential growth, is unknown. In a recent study, frequent testing of both uninfected and infected individuals was performed, and this enabled viral load measurements during the presymptomatic phase of infection87. This type of data will help to estimate the rate of exponential growth and the within-host reproductive number R0 more accurately.
The relationship between SARS-CoV-2 viral load kinetics and disease severity
An important question is how differences in viral load may lead to different disease outcomes. Several clinical studies found that a high viral load at diagnosis or during later stages of infection is associated with more severe disease outcomes81, 82, 106. This association is suggested to be a result of dysregulation of the immune responses64, 70, 107. In severe cases, the antiviral response mediated by IFN is suppressed, resulting in a higher viral load, which in turn can lead to an exacerbated inflammatory response108. Two recent studies highlighted the importance of the IFN response in preventing severe disease outcomes. One study shows that in 10% of severe COVID-19 cases, IFN was largely absent due to the presence of auto-antibodies targeting IFN109, whereas another study110 showed that 3.5% of patients with life-threatening COVID-19 had inborn errors in genes associated with the IFN response. Therefore, modeling that aims to better understand the role of IFN responses68, 69 and the responses to proinflammatory cytokines will be useful for designing and understanding the impact of therapeutics to mitigate severe disease.
Other outstanding questions include how the size of the infection inoculum affects the interaction of the virus population with the immune system and disease outcome. Because of the nonlinear interactions among the virus, the innate and the adaptive immune system, modeling approaches are particularly well suited for addressing these questions77.
Drug resistance
Mathematical models have been very successful and widely used to predict the risk of drug resistance in treating HIV, HCV and influenza infections9, 111, 112. Many of these predictions have led to a profound impact on clinical practice. Currently, the antiviral remdesivir89 is approved by the FDA, and many other antivirals and monoclonal antibodies94, 113, 114 may soon be approved for general use. Therefore, understanding and predicting drug resistance of SARS-CoV-2 will become important as we strive to identify the best strategies for treating patients.
One challenge to assessing the risk of resistance is to calculate the number of viruses produced during the course of infection112 as mutation occurs during the replication of the viral RNA. Nonetheless, given the high viral load in many patients and the duration of viremia particularly in the LRT it is likely that all one-point mutations and some two-point mutations can be generated in an infected person112. This suggests that resistant mutants can appear and rise to a high frequency quickly when an antiviral or an antibody with low genetic barrier to resistance (e.g. see ref.113) is administered alone. Combinations therapies are preferred treatment strategy95, 113. However, recent work suggests that a single amino-acid mutation can render the virus resistant to both antibodies in the REGN-COV2 cocktail115. Further clinical studies on drug resistant mutants and the cost of resistance are needed to precisely predict the risk of resistance and the genetic barriers needed to avoid selection of resistant mutants. These predictions can be further integrated into transmission models to evaluate how likely and how quickly drug resistance may spread in the population.
Conclusions
The interactions between viral and immune dynamics are highly complex and non-linear. The utility of mathematical models is to describe these non-linear interactions and allow for rigorous analysis and quantitative predictions. In this review we have strived to illustrate how this has worked for many viral infections and given us insights into viral pathogenesis and the effects of treatment. We believe these methods will also be beneficial in our attempts to tame the pandemic caused by SARS-CoV-2.
Acknowledgements
We thank Ruy M. Ribeiro for reading and commenting on the manuscript.
Funding:
Portions of this work were done under the auspices of the US Department of Energy under contract 89233218CNA000001 and supported by NIH grants R01-OD011095, R01-AI028433 (ASP), and R01-AI15270301 (RK); and DARPA grant HR0011047746 (RK), as well as the US National Science Foundation RAPID grant PHY-2031756 (ASP).
Footnotes
Conflict of interest: The authors declared no competing interests for this work.
References:
- 1.Ho DD, et al. Rapid turnover of plasma virions and CD4 lymphocytes in HIV-1 infection. Nature 373 123–126. (1995) [DOI] [PubMed] [Google Scholar]
- 2.Wei X, et al. Viral dynamics in human immunodeficiency virus type 1 infection. Nature 373 117–122. (1995) [DOI] [PubMed] [Google Scholar]
- 3.Perelson AS, Neumann AU, Markowitz M, Leonard JM, Ho DD. HIV-1 dynamics in vivo: virion clearance rate, infected cell life-span, and viral generation time. Science 271 1582–1586. (1996) [DOI] [PubMed] [Google Scholar]
- 4.Perelson AS. Modelling viral and immune system dynamics. Nat Rev Immunol 2 28–36. (2002) [DOI] [PubMed] [Google Scholar]
- 5.Stafford MA, et al. Modeling plasma virus concentration during primary HIV infection. J Theor Biol 203 285–301. (2000) [DOI] [PubMed] [Google Scholar]
- 6.Perelson AS, Nelson PW. Mathematical analysis of HIV-1 dynamics in vivo. SIAM Review 41 3–44. (1999) [Google Scholar]
- 7.Markowitz M, et al. A novel antiviral intervention results in more accurate assessment of human immunodeficiency virus type 1 replication dynamics and T-cell decay in vivo. J Virol 77 5037–5038. (2003) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ramratnam B, et al. Rapid production and clearance of HIV-1 and hepatitis C virus assessed by large volume plasma apheresis. Lancet 354 1782–1785. (1999) [DOI] [PubMed] [Google Scholar]
- 9.Perelson AS, Essunger P, Ho DD. Dynamics of HIV-1 and CD4+ lymphocytes in vivo. AIDS 11 Suppl A S17–24. (1997) [PubMed] [Google Scholar]
- 10.Perelson AS, Ribeiro RM. Modeling the within-host dynamics of HIV infection. BMC biology 11 96. (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Perelson AS, et al. Decay characteristics of HIV-1-infected compartments during combination therapy. Nature 387 188–191. (1997) [DOI] [PubMed] [Google Scholar]
- 12.Louie M, et al. Determining the relative efficacy of highly active antiretroviral therapy. J Infect Dis 187 896–900. (2003) [DOI] [PubMed] [Google Scholar]
- 13.Shudo E, Ribeiro RM, Talal AH, Perelson AS. A hepatitis C viral kinetic model that allows for time-varying drug effectiveness. Antivir Ther 13 919–926. (2008) [PubMed] [Google Scholar]
- 14.Wu H, et al. Pharmacodynamics of antiretroviral agents in HIV-1 infected patients: using viral dynamic models that incorporate drug susceptibility and adherence. J Pharmacokinet Pharmacodyn 33 399–419. (2006) [DOI] [PubMed] [Google Scholar]
- 15.Wu H, et al. Modeling long-term HIV dynamics and antiretroviral response: effects of drug potency, pharmacokinetics, adherence, and drug resistance. J Acquir Immune Defic Syndr 39 272–283. (2005) [DOI] [PubMed] [Google Scholar]
- 16.Talal AH, et al. Pharmacodynamics of PEG-IFN alpha differentiate HIV/HCV coinfected sustained virological responders from nonresponders. Hepatology 43 943–953. (2006) [DOI] [PubMed] [Google Scholar]
- 17.Guedj J, et al. Modeling viral kinetics and treatment outcome during alisporivir interferon-free treatment in hepatitis C virus genotype 2 and 3 patients. Hepatology 59 1706–1714. (2014) [DOI] [PubMed] [Google Scholar]
- 18.Canini L, et al. A pharmacokinetic/viral kinetic model to evaluate the treatment effectiveness of danoprevir against chronic HCV. Antivir Ther 20 469–477. (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Herz AV, Bonhoeffer S, Anderson RM, May RM, Nowak MA. Viral dynamics in vivo: limitations on estimates of intracellular delay and virus decay. Proc Natl Acad Sci U S A 93 7247–7251. (1996) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mittler JE, Sulzer B, Neumann AU, Perelson AS. Influence of delayed viral production on viral dynamics in HIV-1 infected patients. Math Biosci 152 143–163. (1998) [DOI] [PubMed] [Google Scholar]
- 21.Mittler JE, Markowitz M, Ho DD, Perelson AS. Improved estimates for HIV-1 clearance rate and intracellular delay. AIDS 13 1415–1417. (1999) [DOI] [PubMed] [Google Scholar]
- 22.Holder BP, Beauchemin CA. Exploring the effect of biological delays in kinetic models of influenza within a host or cell culture. BMC Public Health 11 Suppl 1 S10. (2011) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Beauchemin CA, Miura T, Iwami S. Duration of SHIV production by infected cells is not exponentially distributed: Implications for estimates of infection parameters and antiviral efficacy. Sci Rep 7 42765. (2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Baccam P, Beauchemin C, Macken CA, Hayden FG, Perelson AS. Kinetics of influenza A virus infection in humans. J Virol 80 7590–7599. (2006) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Best K, et al. Zika plasma viral dynamics in nonhuman primates provides insights into early infection and antiviral strategies. Proc Natl Acad Sci U S A 114 8847–8852. (2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Best K, Perelson AS. Mathematical modeling of within-host Zika virus dynamics. Immunol Rev 285 81–96. (2018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Nelson PW, Gilchrist MA, Coombs D, Hyman JM, Perelson AS. An age-structured model of hiv infection that allows for variations in the production rate of viral particles and the death rate of productively infected cells. Math Biosci Eng 1 267–288. (2004) [DOI] [PubMed] [Google Scholar]
- 28.Finzi D, et al. Latent infection of CD4+ T cells provides a mechanism for lifelong persistence of HIV-1, even in patients on effective combination therapy. Nat Med 5 512–517. (1999) [DOI] [PubMed] [Google Scholar]
- 29.Sengupta S, Siliciano RF. Targeting the Latent Reservoir for HIV-1. Immunity 48 872–895. (2018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Neumann AU, et al. Hepatitis C viral dynamics in vivo and the antiviral efficacy of interferon-alpha therapy. Science 282 103–107. (1998) [DOI] [PubMed] [Google Scholar]
- 31.Guedj J, et al. Modeling shows that the NS5A inhibitor daclatasvir has two modes of action and yields a shorter estimate of the hepatitis C virus half-life. Proc Natl Acad Sci U S A 110 3991–3996. (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ke R, et al. Modelling clinical data shows active tissue concentration of daclatasvir is 10-fold lower than its plasma concentration. J Antimicrob Chemother 69 724–727. (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hinrichsen H, et al. Short-term antiviral efficacy of BILN 2061, a hepatitis C virus serine protease inhibitor, in hepatitis C genotype 1 patients. Gastroenterology 127 1347–1355. (2004) [DOI] [PubMed] [Google Scholar]
- 34.Herrmann E, et al. Viral kinetics in patients with chronic hepatitis C treated with the serine protease inhibitor BILN 2061. Antivir Ther 11 371–376. (2006) [PubMed] [Google Scholar]
- 35.Snoeck E, et al. A comprehensive hepatitis C viral kinetic model explaining cure. Clin Pharmacol Ther 87 706–713. (2010) [DOI] [PubMed] [Google Scholar]
- 36.Kitagawa K, Nakaoka S, Asai Y, Watashi K, Iwami S. A PDE multiscale model of hepatitis C virus infection can be transformed to a system of ODEs. J Theor Biol 448 80–85. (2018) [DOI] [PubMed] [Google Scholar]
- 37.McGivern DR, et al. Protease Inhibitors Block Multiple Functions of the NS3/4A Protease-Helicase during the Hepatitis C Virus Life Cycle. J Virol 89 5362–5370. (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.McGivern DR, et al. Kinetic analyses reveal potent and early blockade of hepatitis C virus assembly by NS5A inhibitors. Gastroenterology 147 453–462 e457. (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Goncalves A, et al. What drives the dynamics of HBV RNA during treatment? J Viral Hepat 10.1111/jvh.13425. (2020) [DOI] [PubMed] [Google Scholar]
- 40.Pawelek KA, et al. Modeling within-host dynamics of influenza virus infection including immune responses. PLoS Comput Biol 8 e1002588. (2012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Banerjee S, Guedj J, Ribeiro RM, Moses M, Perelson AS. Estimating biologically relevant parameters under uncertainty for experimental within-host murine West Nile virus infection. J R Soc Interface 13. (2016) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wethington D, et al. Mathematical modelling identifies the role of adaptive immunity as a key controller of respiratory syncytial virus in cotton rats. J R Soc Interface 16 20190389. (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Dobrovolny HM. Quantifying the effect of remdesivir in rhesus macaques infected with SARS-CoV-2. Virology 550 61–69. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Gonçalves A, et al. Timing of antiviral treatment initiation is critical to reduce SARS-CoV-2 viral load. CPT: Pharmacometrics & Systems Pharmacology 9 509–514. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Goyal A, Cardozo-Ojeda EF, Schiffer JT. Potency and timing of antiviral therapy as determinants of duration of SARS-CoV-2 shedding and intensity of inflammatory response. Sci Adv 6 eabc7112. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Goyal A, Duke ER, Cardozo-Ojeda EF, Schiffer JT. Mathematical modeling explains differential SARS CoV-2 kinetics in lung and nasal passages in remdesivir treated rhesus macaques. bioRxiv 10.1101/2020.1106.1121.163550. (2020) [DOI] [Google Scholar]
- 47.Hernandez-Vargas EA, Velasco-Hernandez JX. In-host Mathematical Modelling of COVID-19 in Humans. Annu Rev Control 50 448–456. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Iwanami S, et al. Rethinking antiviral effects for COVID-19 in clinical studies: early initiation is key to successful treatment. medRxiv doi: 10.1101/2020.1105.1130.20118067. (2020) [DOI] [Google Scholar]
- 49.Ke R, Zitzmann C, Ribeiro RM, Perelson AS. Kinetics of SARS-CoV-2 infection in the human upper and lower respiratory tracts and their relationship with infectiousness. medRxiv 10.1101/2020.1109.1125.20201772. (2020) [DOI] [Google Scholar]
- 50.Kim KS, et al. Modelling SARS-CoV-2 Dynamics: Implications for Therapy. medRxiv 10.1101/2020.1103.1123.20040493. (2020) [DOI] [Google Scholar]
- 51.Wang S, et al. Modeling the viral dynamics of SARS-CoV-2 infection. Math Biosci 328 108438. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Tarek M, Savarino A. Pharmacokinetic Basis of the Hydroxychloroquine Response in COVID-19: Implications for Therapy and Prevention. Eur J Drug Metab Pharmacokinet 45 715–723. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Goncalves A, et al. Viral dynamic modeling of SARS-CoV-2 in non-human primates. PREPRINT (Version 1) available at Research Square [available at: https://wwwresearchsquarecom/article/rs-50301/v1]. (2020) [Google Scholar]
- 54.Smith AM, Perelson AS. Influenza A virus infection kinetics: quantitative data and models. Wiley Interdiscip Rev Syst Biol Med 3 429–445. (2011) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Smith AM, Ribeiro RM. Modeling the viral dynamics of influenza A virus infection. Crit Rev Immunol 30 291–298. (2010) [DOI] [PubMed] [Google Scholar]
- 56.To KK, et al. Temporal profiles of viral load in posterior oropharyngeal saliva samples and serum antibody responses during infection by SARS-CoV-2: an observational cohort study. Lancet Infect Dis 20 565–574. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Wolfel R, et al. Virological assessment of hospitalized patients with COVID-2019. Nature 581 465–469. (2020) [DOI] [PubMed] [Google Scholar]
- 58.Williamson BN, et al. Clinical benefit of remdesivir in rhesus macaques infected with SARS-CoV-2. Nature 585 273–276. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Muus C, et al. Integrated analyses of single-cell atlases reveal age, gender, and smoking status associations with cell type-specific expression of mediators of SARS-CoV-2 viral entry and highlights inflammatory programs in putative target cells. bioRxiv DOI: 10.1101/2020.1104.1119.049254. (2020) [DOI] [Google Scholar]
- 60.Sungnak W, et al. SARS-CoV-2 entry factors are highly expressed in nasal epithelial cells together with innate immune genes. Nat Med 26 681–687. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Hou YJ, et al. SARS-CoV-2 reverse genetics reveals a variable infection gradient in the respiratory tract. Cell 182 429–446 e414. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Ogando NS, et al. SARS-coronavirus-2 replication in Vero E6 cells: replication kinetics, rapid adaptation and cytopathology. J Gen Virol 101 925–940. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Tay MZ, Poh CM, Renia L, MacAry PA, Ng LFP. The trinity of COVID-19: immunity, inflammation and intervention. Nat Rev Immunol 20 363–374. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Blanco-Melo D, et al. Imbalanced host response to SARS-CoV-2 drives development of COVID-19. Cell 181 1036–1045 e1039. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Holte SE, Melvin AJ, Mullins JI, Tobin NH, Frenkel LM. Density-dependent decay in HIV-1 dynamics. J Acquir Immune Defic Syndr 41 266–276. (2006) [DOI] [PubMed] [Google Scholar]
- 66.Smith AP, Moquin DJ, Bernhauerova V, Smith AM. Influenza Virus Infection Model With Density Dependence Supports Biphasic Viral Decay. Front Microbiol 9 1554. (2018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Gallagher ME, Brooke CB, Ke R, Koelle K. Causes and Consequences of Spatial Within-Host Viral Spread. Viruses 10 627. (2018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Huang Y, Dai H, Ke R. Principles of Effective and Robust Innate Immune Response to Viral Infections: A Multiplex Network Analysis. Front Immunol 10 1736. (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Lavigne GM, Russell H, Sherry B, Ke R. Autocrine and paracrine interferon signaling as ‘ring vaccination’ and ‘contact tracing’ strategies to suppress virus infection in a host. medRxiv 10.1101/2020.1112.1109.20246777. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Lucas C, et al. Longitudinal analyses reveal immunological misfiring in severe COVID-19. Nature 584 463–469. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Channappanavar R, et al. IFN-I response timing relative to virus replication determines MERS coronavirus infection outcomes. J Clin Invest 129 3625–3639. (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Best K, Barouch DH, Gudej J, Ribeiro RM, Perelson AS. Zika virus dynamics: Effects of inoculum dose, the innate immune response and viral interference. PLoS Comput Biol. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Padmanabhan P, Garaigorta U, Dixit NM. Emergent properties of the interferon-signalling network may underlie the success of hepatitis C treatment. Nat Commun 5 3872. (2014) [DOI] [PubMed] [Google Scholar]
- 74.Weiskopf D, et al. Phenotype and kinetics of SARS-CoV-2-specific T cells in COVID-19 patients with acute respiratory distress syndrome. Sci Immunol 5 eabd2071. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Braun J, et al. SARS-CoV-2-reactive T cells in healthy donors and patients with COVID-19. Nature 587 270–274. (2020) [DOI] [PubMed] [Google Scholar]
- 76.De Boer RJ, Homann D, Perelson AS. Different dynamics of CD4+ and CD8+ T cell responses during and after acute lymphocytic choriomeningitis virus infection. J Immunol 171 3928–3935. (2003) [DOI] [PubMed] [Google Scholar]
- 77.Baral S, Antia R, Dixit NM. A dynamical motif comprising the interactions between antigens and CD8 T cells may underlie the outcomes of viral infections. Proc Natl Acad Sci U S A 116 17393–17398. (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Getz M, et al. Rapid community-driven development of a SARS-CoV-2 tissue simulator. bioRxiv 10.1101/2020.1104.1102.019075. (2020) [DOI] [Google Scholar]
- 79.Sego TJ, et al. A modular framework for multiscale, multicellular, spatiotemporal modeling of acute primary viral infection and immune response in epithelial tissues and its application to drug therapy timing and effectiveness. bioRxiv doi: 10.1101/2020.1104.1127.064139. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Voutouri C, et al. In silico dynamics of COVID-19 phenotypes for optimizing clinical management. Proc Natl Acad Sci USA 118 e2021642118 (2021) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Fajnzylber J, et al. SARS-CoV-2 viral load is associated with increased disease severity and mortality. Nat Commun 11 5493. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Zheng S, et al. Viral load dynamics and disease severity in patients infected with SARS-CoV-2 in Zhejiang province, China, January-March 2020: retrospective cohort study. BMJ 369 m1443. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Barkauskas CE, et al. Type 2 alveolar cells are stem cells in adult lung. J Clin Invest 123 3025–3036. (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Dahari H, Lo A, Ribeiro RM, Perelson AS. Modeling hepatitis C virus dynamics: liver regeneration and critical drug efficacy. J Theor Biol 247 371–381. (2007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Goyal A, Ribeiro RM, Perelson AS. The Role of Infected Cell Proliferation in the Clearance of Acute HBV Infection in Humans. Viruses 9 350. (2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Perelson AS, Kirschner DE, De Boer R. Dynamics of HIV infection of CD4+ T cells. Math Biosci 114 81–125. (1993) [DOI] [PubMed] [Google Scholar]
- 87.Kissler SM, et al. Viral dynamics of SARS-CoV-2 infection and the predictive value of repeat testing. medRxiv 10.1101/2020.1110.1121.20217042. (2020) [DOI] [Google Scholar]
- 88.Sakurai A, et al. Natural history of asymptomatic SARS-CoV-2 infection. N Engl J Med 383 885–886. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Beigel JH, et al. Remdesivir for the Treatment of Covid-19 - Final Report. N Engl J Med 383 1813–1826. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Wang Y, et al. Remdesivir in adults with severe COVID-19: a randomised, double-blind, placebo-controlled, multicentre trial. Lancet 395 1569–1578. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Pearson JE, Krapivsky P, Perelson AS. Stochastic theory of early viral infection: continuous versus burst production of virions. PLoS Comput Biol 7 e1001058. (2011) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Noecker C, et al. Simple mathematical models do not accurately predict early SIV dynamics. Viruses 7 1189–1217. (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Czuppon P, et al. Success of prophylactic antiviral therapy for SARS-CoV-2: predicted critical efficacies and impact of different drug-specific mechanisms of action. medRxiv 10.1101/2020.1105.1107.20092965. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Chen P, et al. SARS-CoV-2 Neutralizing Antibody LY-CoV555 in Outpatients with Covid-19. N Engl J Med DOI: 10.1056/NEJMoa2029849. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Baum A, et al. REGN-COV2 antibodies prevent and treat SARS-CoV-2 infection in rhesus macaques and hamsters. Science 370 1110–1115. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Schafer A, et al. Antibody potency, effector function, and combinations in protection and therapy for SARS-CoV-2 infection in vivo. J Exp Med 218 e20201993. (2021) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Handel A, Rohani P. Crossing the scale from within-host infection dynamics to between-host transmission fitness: a discussion of current assumptions and knowledge. Philos Trans R Soc Lond B Biol Sci 370 20140302. (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Ali ST, et al. Serial interval of SARS-CoV-2 was shortened over time by nonpharmaceutical interventions. Science 369 1106–1109. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.He X, et al. Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat Med 26 672–675. (2020) [DOI] [PubMed] [Google Scholar]
- 100.Fraser C, Hollingsworth TD, Chapman R, de Wolf F, Hanage WP. Variation in HIV-1 set-point viral load: epidemiological analysis and an evolutionary hypothesis. Proc Natl Acad Sci U S A 104 17441–17446. (2007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Handel A, Longini IM Jr., Antia R Neuraminidase inhibitor resistance in influenza: assessing the danger of its generation and spread. PLoS Comput Biol 3 e240. (2007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Goyal A, Reeves DB, Cardozo-Ojeda EF, Schiffer JT, Mayer BT. Wrong person, place and time: viral load and contact network structure predict SARS-CoV-2 transmission and super-spreading events. medRxiv 10.1101/2020.1108.1107.20169920. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Lau MSY, et al. Characterizing superspreading events and age-specific infectiousness of SARS-CoV-2 transmission in Georgia, USA. Proc Natl Acad Sci U S A 117 22430–22435. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Klompas M, Baker MA, Rhee C. Airborne Transmission of SARS-CoV-2: Theoretical Considerations and Available Evidence. JAMA 324 441–442. (2020) [DOI] [PubMed] [Google Scholar]
- 105.Morris DH, et al. The effect of temperature and humidity on the stability of SARS-CoV-2 and other enveloped viruses. bioRxiv 10.1101/2020.1110.1116.341883. (2020) [DOI] [Google Scholar]
- 106.Pujadas E, et al. SARS-CoV-2 viral load predicts COVID-19 mortality. Lancet Respir Med 8 e70. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Rydyznski Moderbacher C, et al. Antigen-specific adaptive immunity to SARS-CoV-2 in acute COVID-19 and associations with age and disease severity. Cell 183 1–17. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Hadjadj J, et al. Impaired type I interferon activity and exacerbated inflammatory responses in severe Covid-19 patients. Science 369 718–724. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Bastard P, et al. Autoantibodies against type I IFNs in patients with life-threatening COVID-19. Science 370 eabd4585. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Zhang Q, et al. Inborn errors of type I IFN immunity in patients with life-threatening COVID-19. Science 370 eabd4570. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Rong L, Dahari H, Ribeiro RM, Perelson AS. Rapid emergence of protease inhibitor resistance in hepatitis C virus. Sci Transl Med 2 30ra32. (2010) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Perelson AS, Rong L, Hayden FG. Combination antiviral therapy for influenza: predictions from modeling of human infections. J Infect Dis 205 1642–1645. (2012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Baum A, et al. Antibody cocktail to SARS-CoV-2 spike protein prevents rapid mutational escape seen with individual antibodies. Science 369 1014–1018. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Hansen J, et al. Studies in humanized mice and convalescent humans yield a SARS-CoV-2 antibody cocktail. Science 369 1010–1014. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Starr TN, et al. Prospective mapping of viral mutations that escape antibodies used to treat COVID-19. bioRxiv doi: 10.1101/2020.1111.1130.405472. (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]


