Veridical Causal Inference using Propensity Score Methods for Comparative Effectiveness Research with Medical Claims

Abstract

Medical insurance claims are becoming increasingly common data sources to answer a variety of questions in biomedical research. Although comprehensive in terms of longitudinal characterization of disease development and progression for a potentially large number of patients, population-based inference using these datasets require thoughtful modifications to sample selection and analytic strategies relative to other types of studies. Along with complex selection bias and missing data issues, claims-based studies are purely observational, which limits effective understanding and characterization of the treatment differences between groups being compared. All these issues contribute to a crisis in reproducibility and replication of comparative findings using medical claims. This paper offers practical guidance to the analytical process, demonstrates methods for estimating causal treatment effects with propensity score methods for several types of outcomes common to such studies, such as binary, count, time to event and longitudinally-varying measures, and also aims to increase transparency and reproducibility of reporting of results from these investigations. We provide an online version of the paper with readily implementable code for the entire analysis pipeline to serve as a guided tutorial for practitioners. The online version can be accessed at https://rydaro.github.io/. The analytic pipeline is illustrated using a sub-cohort of patients with advanced prostate cancer from the large Clinformatics TM Data Mart Database (OptumInsight, Eden Prairie, Minnesota), consisting of 73 million distinct private payer insurees from 2001-2016.

Introduction and Background

Health service billing data can be used to answer many clinical and epidemiological questions using a large number of patients and has the potential to capture patterns in health care practice that take place in the real world (Sherman et al. 2016; Izurieta et al. 2019; Noe et al. 2019; Nidey et al. 2020; O’Neal et al. 2018). Such large datasets allow investigators to conduct scientific queries which may be difficult, if not practically impossible, to answer via a randomized clinical trial. For example, comparing multiple medications that are produced by different drug companies and with varying guidelines for their use for a disease may only be feasible in a real healthcare database (Desai et al. 2019; Jackevicius et al. 2016). Although these large data sources offer a wealth of information, there are many challenges and drawbacks, such as measured and unmeasured confounding, selection bias, heterogeneity, missing values, duplicate records and misclassification of disease and exposures. As regulatory agencies and pharmaceutical companies increasingly consider studying the real world evidence present in such databases, the importance of proper methodology, reporting, and reproducibility of the analysis for a broad audience of researchers is of necessity (FDA 2011; Motheral et al. 2003; Birnbaum et al. 1999; Johnson et al. 2009; Berger et al. 2017; Dickstein and Gehring, 2014; FDA 2018). We emulate newly introduced principles from the predictability, computability, and stability (PCS) framework for veridical data science (Yu et al. 2020) to examine comparative effectiveness research questions that administrative claims data can be used to address. We provide documentation and code in R Markdown file available online at https://rydaro.github.io/.

Healthcare claims data have been extensively criticized for its use in epidemiological research (Grimes 2010; Tyree et al. 2006). These types of data are wrinkled with issues such as outcome and covariate misclassification, missing data, and selection bias. For example, International Classification of Disease (ICD) codes are entered into administrative records by the care provider, often only for the purpose of billing, and thus certain diagnoses may be missed or overrepresented or may differ across providers (Tyree et al. 2006). There is no agreed upon algorithm for identifying widely used outcomes like Emergency Room visits, and thus many definitions across analysts and institutions are used (Venkatesh et al. 2017). While not as accurate as gold standard clinical trial data, these datasets are still valuable and sometimes the only source of real-world data for a wide variety of questions regarding drug utilization, effectiveness, and monitoring of adverse events (Hoover et al. 2011; Wilson and Bock 2012). Claims data have the benefit of reflecting how medications are actually being prescribed, and thus may provide a more accurate depiction of treatment benefit in practice or real-life evidence. Further, these datasets capture a more comprehensive picture of a patient’s encounters with the healthcare system than standard electronic medical record (EHR) data alone (Schneeweiss et al. 2005), going beyond just visits by adding procedures, tests, and pharmacy fills. With proper study design and methodological considerations, many of the common issues and concerns with claims data can be addressed (FDA 2011; Motheral et al. 2003; Birnbaum et al. 1999; Johnson et al. 2009; Berger et al. 2017; Dickstein and Gehring, 2014; FDA 2018),and these large databases of longitudinal information can provide insight into many research questions and be used to complement/supplement/emulate a clinical trial (Hernan and Robins, 2018). While there are several approaches to handling confounding bias are available, propensity score-based methods are versatile in that they can be used for a variety of research questions and can be used for many different kinds of study designs and databases. Propensity score approaches also prevent p-hacking of a desired result in the outcome model (Braitman and Rosenbaum 2002). Thus, these methods have gained increasing popularity, especially for questions of comparative effectiveness in pharmacoepidemiologic and pharmacoeconomic research. With counterfactual thinking and causal inference gaining popularity in the statistical and epidemiological literature, principled use of propensity score based methods in observational databases have become more common.

A downside to this rise in popularity is that the assumptions and critical steps for the propensity score-based methods are often ignored or unreported. This lack of reporting hinders other researchers’ ability to replicate the findings. Many have noted common misuse or lack of reporting for propensity methods (Ali et al. 2015; Yao et al. 2017; Weitzen et al. 2004; Austin 2008; D’Ascenzo et al. 2012; Deb et al. 2016). Analysis questions arise, such as how the propensity score was calculated (logistic regression or otherwise), and even for many researchers who did describe such methods, sensitively analysis to the violation of assumptions or choice of the propensity score model were often not reported. Propensity score methods do not account for unmeasured confounding, and sensitivity analyses can provide the reader with crucial information on the robustness of the findings.

Some have offered valuable tutorials on propensity score estimation (Garrido et al. 2014; Austin 2011; Stuart et al. 2013; Brookhart et al. 2013). While these papers offer an elegant and lucid exposition of the underlying principles, and are extremely important contribution to the literature, these overviews do not provide the reader a complete practical guidance for every analysis step, or a detailed sensitivity analysis framework to understand the strength of evidence supporting the results when model assumptions change. Therefore, there is need for a usable, simple and comprehensive tutorial for all stages of analysis when characterizing a binary treatment effect on various outcome types using claims data, with accompanying annotated R software code for each step. This paper outlines the use of three primary propensity score-based methods: Spline Adjustment, Propensity Matching, and Inverse Probability of Treatment Weighting (IPTW) for comparing treatment effects with the goal of reducing bias due to confounding. The paper also details how to use each method to estimate average treatment effect for four common outcome types: 1) Binary, 2) Count, 3) Time to event, and 4) Longitudinally varying repeated measures. Finally, we conduct sensitivity analysis for two of the outcome types. To improve transparency for reproducibility and usage of the methods discussed, detailed R code is provided in an online version at https://rydaro.github.io/. The analytic pipeline is illustrated using a sub-cohort of patients with advanced prostate cancer from the large Clinformatics TM Data Mart Database (OptumInsight, Eden Prairie, Minnesota), consisting of 73 million distinct private payer insurees from 2001-2016.

Guideline for the Comparative Effectiveness Data Analysis Pipeline

Cohort Definition and Average Treatment Effect

The first stage of analysis, as shown in Figure 1, is cohort definition. The STROBE checklist for cohort studies provides guidelines for defining a cohort and research question for analysis (von Elm et al. 2007). Once a cohort is defined, comparative effectiveness research for that cohort relies on the potential-outcomes framework, which as described by Rubin (1975 and 2005), involves comparison of potential outcomes on the same (say i^th) individual for each treatment. Define Y_i(0) as the potential outcome under the control treatment, and Y_i(1) as the potential outcome under the active treatment of interest. We wish to know the treatment effect for each individual, typically defined as Y_i(1) − Y_i(0), which cannot be estimated directly from the observed data because for each individual we observe either Y_i(1) or Y_i(0), but never both. If subject i actually received the active treatment, denoted by T_i = 1, then Y_i(1) is observed and Y_i = Y_i(1); otherwise, T_i = 0, and we observe Y_i = Y_i(0), under the stable unit treatment value and consistency assumptions. We can define the average treatment effect (ATE) as E[Y_i(1) − Y_i(0)], which is the average treatment effect across the entire population (Imbens 2004). In a randomized trial, we can estimate ATE as E[Y_i(1) − Y_i(0)] = E[Y_i|T_i = 1] − E[Y_i|T_i = 0] as randomization ensures that the treatment groups are balanced and hence E[Y_i(a)] = E[Y_i(a)|T_i = a] = E[Y_i|T_i = a] for a = 0,1 (Austin 2011b; Lunceford and Davidian 2017) . ATE can be defined on different scales, such as a ratio $\frac{E\left[Y_i|T_i=1\right]}{E\left[Y_i|T_i=0\right]}$ or odds ratio for binary outcomes $\frac{E\left[Y_i|T_i=1\right]/\left(1-E\left[Y_i|T_i=1\right]\right)}{E\left[Y_i|T_i=0\right]/\left(1-E\left[Y_i|T_i=0\right]\right)}$. We can also define the average treatment effect on the treated (ATT) as E[Y_i(1) − Y_i(0)|T_i = 1] and the average treatment effect on the comparison group (ATC) as [Y_i(1) − Y_i(0)|T_i = 0] when a particular sub-population is of interest.

Figure 1:

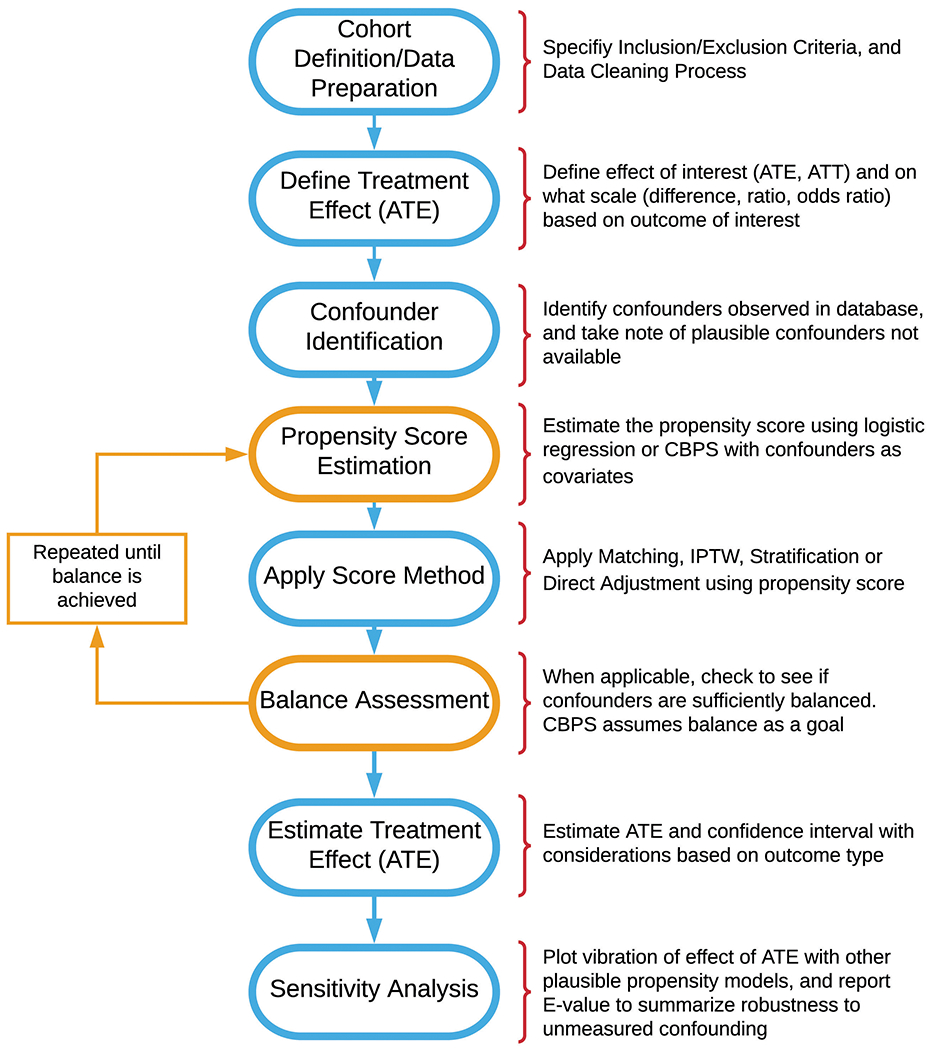
Comparative Effectiveness Data Analysis Pipeline Flow Diagram.

Gold pathway indicates steps done in iteration until acceptable balance is achieved.

The standard method of estimating treatment effect for data from a randomized trial, or from observational data that is sufficiently balanced, is a general linear model with the treatment variable as the sole predictor:

$$g\left({\mu }_i\right)={\beta }_0+{\beta }_1{T}_i$$

where μ_i = E[Y_i|T_i] and β₁ is the parameter of interest for treatment comparison. In the simple linear regression case where g(x) is the identity function, β₁ = E[Y_i|T_i = 1] − E[Y_i|T_i = 0]. When using claims data, the mechanism behind treatment assignment is not random, and thus the treatment populations may differ greatly. Therefore E[Y(1)|T = 1] ≠ E[Y(1)] and E[Y(0)|T = 0] ≠ E[Y(0)] in general (Austin 2011b). As a result, the estimate for β₁ will not equal the ATE because of confounding.

When confounders are present, a natural inclination would be to extend our outcome model to account for such confounders:

$$g\left({\mu }_i\right)={\beta }_0+{\beta }_1{T}_i+{\beta }_2{X}_{2i}+{\beta }_3{X}_{3i}+\dots +{\beta }_k{X}_{ki}$$

However, β₁ in the multivariate adjustment model generally does not estimate ATE even if we have the correct confounders and the model is correctly specified, particularly when g() is not a collapsible link function. One approach to estimate ATE is G-computation, which predicts the pair of potential outcomes for each individual (Robins 1986; Snowden et al. 2011). The accompanying standard error can be computed using sandwich estimation (Andersen 2019; Susanti et al. 2014). While a valid analytical approach, it may be difficult for the researcher to specify the outcome model, as there may be limited understanding of the relationship between the outcome and each covariate. The notion of the propensity score, a unidimensional construct, offers an alternative analytical approach that may be more suitable. The researcher may have more subject matter knowledge to construct a proper propensity score model, may want to avoid unconscious bias of demonstrating a desired causal effect in the outcome models by choosing confounders to adjust for, or use the propensity score simply as a dimension reduction technique.

Confounder Selection and Propensity Score Estimation

Proposed by Rosenbaum and Rubin (1983), the propensity score is defined as e_i = Pr(T_i = 1|X_i). The score can be interpreted as the probability a subject receives treatment, predicted from the confounding variables denoted as X_i. Rosenbaum and Rubin (1983) showed that conditional on the propensity score, an unbiased estimate of ATE can be obtained if the treatment is strongly ignorable. A treatment is strongly ignorable if two conditions are met: 1) The probability of treatment given the covariates is not exactly 0 or 1, and 2) each potential outcome is independent of treatment, conditional on the covariates. More formally, these two conditions are: 0 < P(T_i = 1|X_i) < 1 , 2) (Y_i(0), Y_i(1) ⊥ T_i|X_i (Rosenbaum and Rubin 1983). The second of these assumptions is the “no unmeasured confounders” assumption. Thus, a critical assumption for use of the propensity score is that all variables that affect the outcome and treatment assignment are measured. If all confounding variables are identified and included, and the model is correctly specified, this score achieves covariate balance between treatment and control groups. More formally, the correct e_i satisfies that T_i ⊥ X_i|e_i, removing the effect of the confounders from the treatment effect when we condition on e_i alone. While logistic regression is commonly used to estimate this propensity score, researchers have expanded their attention beyond parametric models. Many have used machine learning methods such as boosted logistic regression, random forests, and neural networks (Lee et al. 2010; Setoguchi et al. 2008; Westreich 2010). Another method we highlight in this paper is the covariate balancing propensity score (CBPS) proposed by Imai and Ratkovic (2014).

Covariate Balancing Propensity Score (CBPS) is a generalized method of moments estimate that captures two characteristics of the propensity score, namely, as a covariate balancing score and as the conditional probability of treatment assignment (Imai and Ratkovic 2014). This method is a more automated form of propensity score construction, in that it calculates the propensity score with the exact balancing goal in mind. Thus, CBPS provides a balancing score for each subject that ensures all covariates included in the CBPS construction are balanced. Therefore, CBPS is an efficient alternative to propensity score estimation by a parametric model. We do note that if using another estimation technique, the ultimate goal of the propensity model is not to predict treatment assignment, but to reduce bias by balancing covariates (Wyss et al. 2014).

Still, the treatment effect estimation methods are sensitive to misspecification of the propensity score model, and thus the variables and their functional forms used in this model can affect the estimation of average treatment effect. Many suggest including all variables at all associated with the outcome, while excluding those only associated with the treatment of interest, based on subject-matter knowledge (Brookhart et al. 2006; Rubin and Thomas 1996; Perkins et al. 2000; Wyss et al. 2013). Vanderweele (2019) provides a comprehensive general guide to confounder selection in observational studies. The sensitivity analysis can show how estimates can change under many plausible propensity score models.

Application of the Constructed Propensity Score

Once the propensity score is constructed, there are four basic ways to use the score in treatment effect estimation: 1) Stratification based on the propensity score, 2) Direct covariate adjustment using propensity score as a covariate in the outcome model, 3) Matching treatments and controls based on the propensity score (PM), and 4) Inverse probability treatment weighting on the propensity score (IPTW). Stratification ranks subjects by the estimated propensity score and splits them into mutually exclusive groups to obtain an overall treatment effect (Rosenbaum and Rubin 1984). We will not discuss stratification at length in the main paper as it is used less commonly (Austin et al. 2007; Austin 2009b), but the online materials provide further information. The rest of this paper will focus on the three routinely used methods: Spline Adjustment, Propensity Matching, and IPTW.

Spline Adjustment

The propensity score is the coarsest balancing score while the full list of confounders is the finest (Shi et al. 2020). This approach is similar to the G-computation approach above, except the confounders in the outcome model are replaced with a single covariate of the predicted propensity score. The ATE is calculated from the predicted potential outcomes for each individual, and estimate the standard error using sandwich estimation (Robins 1986; Snowden et al. 2011; Stefanski and Boos, 2002, Andersen 2019; Susanti et al. 2014). Typically, the propensity score is fit with a smoothing function, such as a polynomial spline function (Shi et al. 2020), allowing for a more flexible model that is also computationally fast and reliable.

Propensity Matching

Matching observations based on the propensity score to estimate ATT and is based on a measure of distance (Stuart et al. 2010; Rosenbaum and Rubin 1985a). Stuart et al. (2010) provide a comprehensive overview of the various matching methods available. In practice, it is common to do 1: k matching, where k is the specified number of controls. With a defined distance, called a caliper, all potential matches within the distance up to k will be matched. This allows for maximal efficiency of data while still reducing bias since all close matches are kept. There is little guidance on what caliper a researcher should specify; however, Austin (2011a) suggests a caliper of 0.2 standard deviations of the logit of the propensity score as a default choice that works well across scenarios. Matching typically estimates the ATT, though some packages and techniques can estimate ATE (Stuart et al. 2010).

Inverse Probability of Treatment Weighting (IPTW)

The next method we consider is the inverse probability of treatment weighting (IPTW) proposed by Rosenbaum (1987). We can calculate the weights v_i as

$$v_i=\frac{T_i}{{\widehat{e}}_i}+\frac{\left(1-T_i\right)}{\left(1-{\widehat{e}}_i\right)}$$

where ${\widehat{e}}_i$ is the estimated propensity score. These weights can be very unstable for extreme values of ${\widehat{e}}_i$, so trimming (sometimes called truncating) these values away from the extreme is often practiced (Rosenbaum 1987; Lee et al. 2011). The construction of weights used here estimates ATE, and different constructions can be used for ATT and other effect estimates of interest (Lee et al. 2011).

Balance Assessment

It is good practice to check if the chosen propensity method achieved its goal of balancing the covariates. Although there are several balance diagnostics, a common balance diagnostic originally proposed by Rosenbaum and Rubin (1985b) is the standardized difference (or standardized bias) for 1:1 matching, defined as

$$\frac{{\overline{x}}_t-{\overline{x}}_c}{s_p}$$

This is the difference in mean value of the covariate in the treatment group ${\overline{x}}_t$ vs. the control group ${\overline{x}}_c$, adjusting for variability s_p, where here we defined s_p as the pooled standard deviation of the two treatment groups, defined as $s_p=\sqrt{\frac{s_t^2+s_c^2}{2}}$ (Austin 2009a;Normand et al. 2001). This value is calculated for each covariate, with values closer to zero indicating better mean balance and potentially less bias. The measure can be calculated for both continuous and categorical indicator variables (Yao et al. 2017; Normand et al. 2001). A lack of balance indicates that the propensity model may be incorrect, or that a different method should be used. There is no generally accepted threshold, although some suggest that the standardized difference should not be greater than 0.1 (Austin 2008b; Austin 2009a; Normand et al. 2001). In practice, researchers may also report variable descriptive statistics before and after matching. We can modify this difference calculation for a different ration of matching, say 1: k, using weights (Joffe et all. 2004; Morgan and Todd 2008; Austin 2008b). The weighted mean is defined as ${\overline{x}}_w=\frac{\Sigma w_i{x}_i}{\Sigma w_i}$ and the weighted standard deviation is

$$s_w=\sqrt{\frac{\frac{\Sigma w_i{\left(x_i-{\overline{x}}_i\right)}^2}{\Sigma w_i}}{{\left(\Sigma w_i\right)}^2-\Sigma w_i{}^2}}$$

where w_i is the weight for subject i. For 1:1 matching, all observations have equal weight. If 1: k matching is used, observations in the control treatment group have 1/k weights and treated observations have weights 1. For IPTW, the calculated weights can be used, so v_i = w_i for each observation (Morgan and Todd 2008; Austin 2008b). If sufficient balance is not achieved, the process of propensity score construction and balance assessment is repeated, by changing the functional form of the propensity model. The researcher can repeat this process until balance is achieved to a desired level. Experimenting with the model specification at this stage is preferable to post-hoc modification of the outcome model with ATE as a desired target, especially in terms of reproducibility of results.

Treatment Effect Estimation and Sensitivity Analysis

Once sufficient balance has been achieved, one can estimate the average treatment effect using a general outcome model

$$g\left({\mu }_i\right)={\beta }_0+{\beta }_1{T}_i$$

This model can be used directly on the matched dataset if 1:1 matching is used. If 1: k matching or IPTW is used, the constructed weights need to be used as well. Weights can be incorporated in the same fashion as weights from a survey design, using robust standard error estimation to account for error in weight estimation (Lee et al. 2001; Morgan and Todd 2008). For the spline adjustment model, ATE is estimated by G-computation with direct variance calculation via M-estimation (Stefanski and Boos, 2002). Once an estimate is obtained, it is often useful to run a sensitivity analysis to see how the estimate may change under different model specifications and understand how sensitive the result is to some unmeasured confounder.

For the sensitivity analysis, we adapt a visualization tool of capturing vibration of effects from Patel et al. (2015) to a universe of potential propensity score models. This visualization tool allows the researcher to see the results of many possible models at once, providing an overall understanding of the treatment effect estimate’s robustness to changing model specifications with the observed set of measured confounders. To summarize sensitivity to an unobserved/unmeasured confounder, we calculate the estimate’s E-value (Van Der Weele and Ding 2017). The E-value captures the minimum value of the association parameter that an unobserved confounder must have with both the treatment and the outcome of interest to nullify the result regarding the treatment effect on the outcome. Put more simply, the E-value tells us how strong an unmeasured confounder must be to explain away a significant treatment effect.

Example: Comparing Oral Hormone Therapy vs. Immunotherapy for Advanced Prostate Cancer

Cohort Definition and Average Treatment Effect

The cohort was defined as men who received treatment for advanced prostate cancer at any time during January 2010 through June 2016, based on receiving one of four primary medications (abiraterone, enzalutamide, sipuleucel-T, docetaxel) known to have a survival benefit in men with advanced prostate cancer. Data were from the Clinformatics TM Data Mart Insurance Claims Database. The initial cohort included any patient over the age of 18 with a diagnosis of malignant neoplasm of the prostate, coded as “185” in ICD-9 and “C61” in ICD-10, and were continuously enrolled in the plan for at least 180 days before the first medication claim.

Treatments:

We are interested in comparing first-line therapies. First-line treatment was defined as the first medication given of the four focus medications. We then categorized oral therapies as abiraterone or enzalutamide. Thus, there are three final first-line treatment groups: 1) Immunotherapy, 2) Oral Therapy, and 3) Chemotherapy. We compared immunotherapy to oral therapy and compared immunotherapy to chemotherapy in two separate analyses. We chose immunotherapy as the reference group for both analyses. The remainder of this example will only discuss the oral therapy comparison, as all methods are directly translatable, and we report all results for both analyses in the tables.

Binary and Count Outcomes:

We defined the binary outcome to be whether the patient had any emergency room (ER) visit within 60 days of the first pharmacy claim of the focus medications. ER visits were identified using the provider definition, Current Procedural Technology (CPT) codes 99281-99285, and the facility definition, which is revenue center codes 0450-0459, 098 (Vankatesh et al. 2017; CMS 2020a, CMS 2020b). ATE is defined on the odds ratio scale. Using the previously defined ER visits, we counted the number of ER visits each patient had within 180 days from the first pharmacy claim as a count outcome. ATE is defined on the rate ratio scale.

Time to Event Outcome:

Time on treatment, the time to event outcome, was defined as the time from start of first medication to the last claim of any of the four focus medications, thus the event is stopping all focus treatment permanently. ATE is defined in terms of Restricted Mean Survival Time (RMST) (Royston et al. 2013; Andersen 2010) within a five year follow-up window. We can calculate RMST, denoted μ_τ, as the area under the curve of the survival function:

$${\mu }_{\tau }={\int }_0^{\tau }S\left(t\right)dt$$

where S(t) is the survival function, and τ is the parameter for restricted the follow-up time (five years). We can then define our ATE estimate as μ_τ1 − μ_τ0, or the difference in RMST between the treatment groups being compared.

Longitudinally Varying Outcome:

For the longitudinally varying outcome, we used opioid usage over time, calculated using prescription drug pharmacy claims. Common opioid drug types were identified and were converted into morphine milligram equivalents (MME) according to the Center for Disease Control conversion factors (CDC 2020). The average daily MME supply prescribed was calculated in 30-day periods, starting with the 30 days before the first-line of treatment, which was used as a baseline, and continuing at 30-day intervals for the duration of claims data available. ATE is defined as the mean difference in opioids prescribed at three specified time points: treatment start, 3 months after treatment start, and 6 months after treatment start. We can model the quantity of opioids prescribed in MME Y_ij at the j^th 30-day period t_j for each individual i as:

$$Y_{ij}={\beta }_0+b_{0i}+{\beta }_1{T}_i+S\left(t_j\right)+S\left(t_j\right)T_i+{\in }_{ij}$$

where j = 1,.., n_i, n_i ∈ {1,2,3,4,5,6,7}, b₀ ~ N(0, τ²) and ϵ_i ~ MVN_ni(0, σ²I_ni). Here, S(t_j) is specified as a penalized regression spline with 3 degrees of freedom, allowing more flexible smooths for modeling the prescribing trend over time. An important note when using IPTW and CBPS is that we are only weighting on the initial treatment, so at other time points the weights may bias the results. Any inferences using the full time period will be heavily biased by changing therapy or require advanced methods to handle switching treatments, such as marginal structure models (Cole and Hernan 2008).

Confounder Selection, Propensity Score Estimation and Balance Assessment

Confounders:

Potential confounders were identified using previous research to identify factors associated with both treatment and outcomes (Hoffman et al. 2011; Ward et al. 2004; Caram et al. 2019a; Barocas and Penson 2010; Caram et al. 2019b). These include age, race, sociodemographic variables and comorbid conditions from Elixhauser Comorbidity Index and Clinical Classification Software (CMS 2020a, CMS 2020b), all shown in Table 2. From the table, we can see differences across treatments groups, especially age, geographic region, and provider type. These variables may inform treatment assignment and as such should be considered as potential confounders.

Table 2.

Confounder Characteristics

	Immunotherapy (N = 504)		Chemotherapy (N = 2,214)		Oral Therapy (N = 2,747)
Variable	Count	(%)	Count	(%)	Count	(%)
Age
<55	14	(2.8)	93	(4.2)	62	(2.3)
55-64	87	(17.3)	329	(14.9)	341	(12.4)
65-74	194	(38.5)	915	(41.3)	769	(30.0)
≥75	209	(41.7)	876	(39.6)	1574	(57.3)
Race
White	369	(73.2)	1,582	(71.5)	1,863	(67.8)
Asian	7	(1.4)	33	(1.5)	68	(2.5)
Black	62	(12.3)	284	(12.8)	376	(13.7)
Hispanic	22	(4.4)	127	(5.7)	252	(9.2)
Unknown	24	(8.8)	188	(8.5)	188	(6.8)
Education level
No College	122	(24.2)	689	(31.1)	814	(29.6)
Some College or More	348	(69.0)	1400	(63.2)	1827	(66.5)
Unknown	34	(6.7)	124	(5.6)	105	(3.8)
Household income range
<50k	148	(29.4)	798	(36.0)	997	(36.3)
50k-99k	164	(32.4)	656	(29.6)	862	(31.4)
>99k	119	(23.6)	431	(19.5)	527	(19.2)
Unknown	73	(14.5)	329	(14.6)	361	(13.1)
Geographic Region1
New England	24	(4.8)	109	(5.0)	151	(5.5)
Middle Atlantic	37	(7.3)	134	(6.1)	257	(9.4)
South Atlantic	129	(25.6)	554	(25.0)	582	(21.2)
East North Central	76	(15.1)	305	(13.8)	403	(14.7)
East South Central	20	(4.0)	86	(3.9)	89	(3.2)
West North Central	63	(12.5)	386	(17.4)	137	(5.0)
West South Central	50	(9.9)	231	(10.4)	250	(9.1)
Mountain	75	(14.9)	221	(10.0)	302	(11.0)
Pacific	30	(6.0)	179	(8.1)	557	(20.3)
Unknown	0	(0.0)	9	(0.4)	19	(0.7)
Product
HMO	128	(25.4)	797	(36.0)	991	(36.1)
PPO	36	(7.1)	181	(8.2)	208	(7.6)
Other	340	(67.5)	1,236	(55.9)	1,548	(56.4)
Metastatic
Yes	474	(94.0)	2010	(90.8)	2,301	(83.8)
No	30	(6.0)	204	(9.2)	446	(16.2)
ASO
Yes	96	(19.0)	344	(15.7)	434	(15.8)
No	408	(81.0)	1,866	(84.3)	2,313	(84.2)
Provider
Urologist	167	(33.1)	4	(0.2)	318	(11.6)
Other/ Unknown	337	(66.9)	2209	(99.8)	2428	(88.4)
Comorbid Conditions
Diabetes	154	(30.6)	593	(26.8)	802	(29.2)
Hypertension	362	(71.8)	1,479	(66.8)	1,920	(69.9)
Arrhythmia	86	(17.1)	398	(18.0)	640	(23.3)
CHF	42	(8.3)	180	(8.1)	359	(13.1)
Osteoporosis	55	(11.0)	114	(5J)	204	(74)

Characteristics of patients by first of focus treatment given: immunotherapy (sipuleucel-T), chemotherapy (docetaxel), and oral therapy (enzalutamide or abiraterone)

HMO, health maintenance organization; PPO, preferred provider organization; ASO, administrative services only (self-funded health plan); CHF, Congestive Heart Failure

¹Geographic region:

• New England (NE): Connecticut (CT), Maine (ME), Massachusetts (MA), New Hampshire (NH), Rhode Island (RI), Vermont (VT)

• Middle Atlantic (MA): New Jersey (NJ), New York (NY), Pennsylvania (PA)

• East North Central (ENC): Illinois (IL), Indiana (IN), Michigan (MI), Ohio (OH), Wisconsin (WI)

• West North Central (WNC): Iowa (IA), Kansas (KS), Minnesota (MN), Missouri (MO), Nebraska (NE), North Dakota (ND), South Dakota (SD)

• South Atlantic (SA): Delaware (DE), Washington D.C. (DC), Florida (FL), Georgia (GA), Maryland (MD), North Carolina (NC), South Carolina (SC), Virginia (VA), West Virginia (WV)

• East South Central (ESC): Alabama (AL), Kentucky (KY), Mississippi (MS), Tennessee (TN)

• West South Central (WSC): Arkansas (AR), Louisiana (LA), Oklahoma (OK), and Texas (TX)

• Mountain (M): Arizona (AZ), Colorado (CO), Idaho (ID), Montana (MT), Nevada (NV), New Mexico (NM), Utah (UT), Wyoming (WY)

Pacific (PAC): Alaska (AK), California (CA), Hawaii (HI), Oregon (OR), Washington (WA)

All potential confounders listed in Table 2 were included. For chemotherapy estimation, the urologist variable was excluded as a confounder due to low cell counts. Thus, the model treatment assignment is T_i = 0 if immunotherapy was given and T_i = 1 if oral therapy was given using both logistic regression and the CBPS method. Propensity score constructed from the CBPS approach was implemented through the R package CBPS (Imai and Ratkovic 2013). To create a matched dataset, we used the R package Matchit (Hoe et al. 2007). We defined our distance with logistic regression using the “nearest neighbor” method select matches within a defined caliper distance of 0.2 standard deviations of the logit propensity score, with a variable matching ratio of 1:4 within the defined caliper, without replacement. Inverse weights were created, and propensity scores greater that 0.99 were trimmed to 0.99, and scores below 0.01 were trimmed to 0.01. Figure 2 shows a plot of the standardized difference of the covariates between the immunotherapy group, and oral therapy group for CBPS, IPTW and propensity matching methods. Here, we are assuming covariates have a linear relationship with the outcome, and thus checking means is sufficient. With covariate balance achieved to a desired level, we proceeded to treatment effect estimation.

Figure 2:

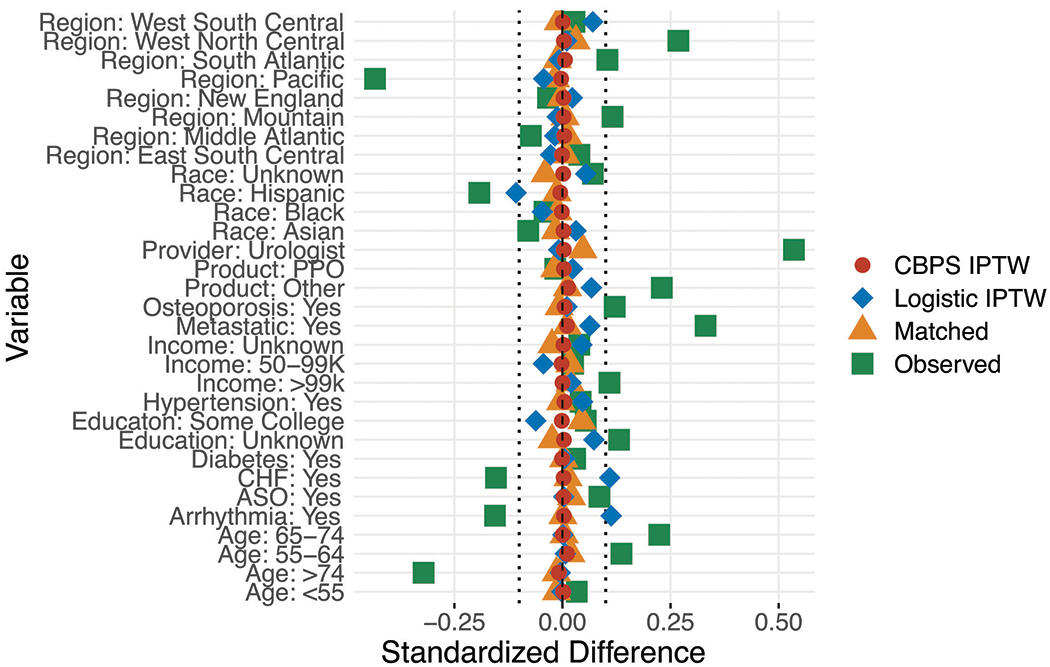
Balance Diagnostics Plot

Standardized differences shown for each confounder variable. Vertical dotted lines indicate the desired balance level. Differences shown for the observed data, after matching, and weighting with both calculated propensity scores (logistic regression and CBPS)

Treatment Effect Estimation and Sensitivity Analysis

Now we compute our estimates of ATT and ATE and report results in Table 3. Because covariate balance is achieved, we can run the marginal logistic regression model directly on our propensity matched dataset. The spline model was implemented spline function from the R package splines (Bates et al. 2020). Models using the IPTW weights form the propensity scores estimated from logistic regression and the CBPS used the R package survey (Lumley 2020). Finally, the ATE from multivariate adjustment model using G-computation is calculated with our own defined functions (shown in website).

Table 3:

Estimates of Causal Treatment Effects Across Methods of Oral Therapies or Chemotherapy Compared to Reference Immunotherapy

	Non-Causal	ATT	ATE
	Unadjusted Association	Matched	Spline of Propensity Score	IPTW using Propensity Score from Logistic Regression	IPTW using Propensity Score from CBPS	Multivariate Adjustment
Binary Outcome: Emergency Room visit in 60 days - Odds Ratio Scale
Oral Therapy	0.75 (0.46,1.23)	0.89 (0.53,1.50)	0.83 (0.50, 1.38)	0.56 (0.26,1.23)	0.59 (0.28,1.22)	0.80 (0.47, 1.37)
Chemotherapy	1.86 (1.16, 2.97)	1.74 (1.08, 2.80)	1.75 (1.09,2.82)	1.79 (1.09,2.93)	1.81 (1.11,2.95)	1.70 (1.03, 2.81)
Count Outcome: Number of Emergency Room visits in 180 Days - Rate Ratio Scale
Oral Therapy	0.92 (0.56,1.52)	1.00 (0.59,1.71)	0.99 (0.63,1.56)	0.87 (0.48,1.60)	0.88 (0.46,1.70)	0.96 (0.60, 1.53)
Chemotherapy	1.87 (1.36,2.58)	1.86 (1.15 3.00)	1.72 (1.13,2.61)	1.74 (1.29, 2.57)	2.75 (1.73, 4.38)	1.73 (1.15, 2.58)
Time to Event Outcome: Total Time on Treatment - Difference in Mean Days on Treatment from Immunotherapy (restricted to 5 years of follow-up)
Oral Therapy	−68 (−106, −30)	−52 (−92, −12)	−49 (−88, −9)	−27 (−45, −10)	−31 (−48, −13)	−57* (−95, −19)
Chemotherapy	−135 (−174, −96)	−164 (−213, −117)	−167 (−214, −120)	−164 (−184, −144)	−139 (−160, −119)	−135* (−174, −95)
Longitudinally Varying Outcome: Mean Daily Opioids Prescribed in Morphine Milligram Equivalents per 30-day period (mg/30 days) for Patients Prescribed
Difference in Mean mg/30 days, Oral Therapy from Immunotherapy
Treatment Start	−83 (−391,224)	−144 (−464, 177)	−104 (−420, 212)	−211 (−846, 423)	−44 (−311,221)	−106 (−419,208)
90 Days	−130 (−380, 121)	−169 (−431, 94)	−151 (−412, 110)	−342 (−738,52)	14 (−220, 249)	−130 (−388, 128)
180 Days	−178 (−497, 141)	−263 (−599, 73)	−199 (−526, 128)	−469 (−1114,177)	−63 (−343,216)	−181 (−506, 144)
Difference in Mean mg/30 days Chemotherapy from Immunotherapy
Treatment Start	187 (−155,530)	291 (−133, 716)	203 (−173, 578)	301 (−100, 702)	258 (−46, 563)	177 (191, 547)
90 Days	34 (−248,316)	97 (−252,447)	50 (−272, 373)	−64 (−415, 287)	44 (−229, 317)	25 (−290, 341)
180 Days	226 (−133, 586)	234 (−220,687)	242 (−150, 635)	112 (−298,521)	284 (−50, 619)	235 (−152, 622)

Table or estimates and confidence intervals for the treatment effect on each outcome. Immunotherapy is the reference group for each treatment comparison. Estimates reported are unadjusted association (before any adjustments are used, so estimate is non-causal observed association), using a propensity matched dataset, adjusting for propensity score in the outcome model, inverse propensity score weighting (IPTW) and covariate balance propensity score (CBPS), and estimate from predicted outcomes use full covariate adjustment. For binary and count outcomes, multivariate adjustment estimates come from G-computation. For time to event outcome, multivariate estimates are difference in mean time, restricted to 5 years of follow-up time. For time-varying, estimates are difference in mean opioid morphine milligram equivalents at the designated time points.

^*Adjustment covariates limited to age and race due to computational issues with full covariate set.

Binary and Count Outcomes:

For the binary outcome, we obtain an odds ratio of 0.83 (0.50,1.38) for oral therapy versus immunotherapy using the spline adjustment, and 0.56 (0.26,1.23) when using IPTW with the same propensity score. All models we fit for the binary outcome can be fit in a similar fashion to this count outcome, now considering the different link function and scale of ATE from above, also shown in Table 3. Here, we see a more consistent picture, with the spline adjustment rate ratio of 0.99 (0.63,1.56) and IPTW rate ratio of 0.87 (0.48,1.60).

Time to Event Outcome:

For time on treatment, the difference in RMST was estimated using the package survrm2 (Uno et al. 2014).⁸⁰ RMST was modified for covariate adjustment (Tian et al. 2014) and with weights calculated from the propensity score (Conner et al. 2019). In this case, the spline adjusted estimate for the difference in days on treatment within 5 years is −49 (−88,−9) days, suggesting immunotherapy patients stay on treatments longer than oral therapy. The IPTW estimate is −27 (−45, −10) days, now yielding a smaller interval than the spline adjusted for this outcome.

Longitudinally Varying Outcome:

For the longitudinally varying opioid usage outcome we use the R package mgcv (Simon et al. 2018). The spline adjusted estimate for the difference in mean daily opioid prescribed 90 days after treatment start is −151 (−412, 110) MME. This suggests that on average, of those given opioids, patients starting with immunotherapy may be prescribed less opioids than those starting with oral therapy 90 days after treatment start. The confidence interval is noticeably wide. The IPTW estimate at this same time point is even less certain with −342 (−738,52).

Sensitivity Analysis

Across all outcomes, patients given Immunotherapy as the first line therapy have better outcomes on average, though not all estimates are significant. To assess the robustness of those that are “noteworthy” in terms of significance, sensitivity analysis is performed. A sample sensitivity analysis for the binary outcome is shown for three selected methods in Figure 3. Age was included as a baseline predictor in all models. E-values are reported for the model that included the full covariate set. The figure tells us that when comparing patients starting on oral therapy vs. immunotherapy, none of the propensity models considered resulted in a significant difference. However, the difference between chemotherapy and immunotherapy was significant. The E-values for these models are 3.05 for the spline adjustment and 3.17 for the IPTW, indicating a unobserved confounder that has this risk ratio with both this treatment assignment and ER visit outcome can explain away the significant result.

Figure 3:

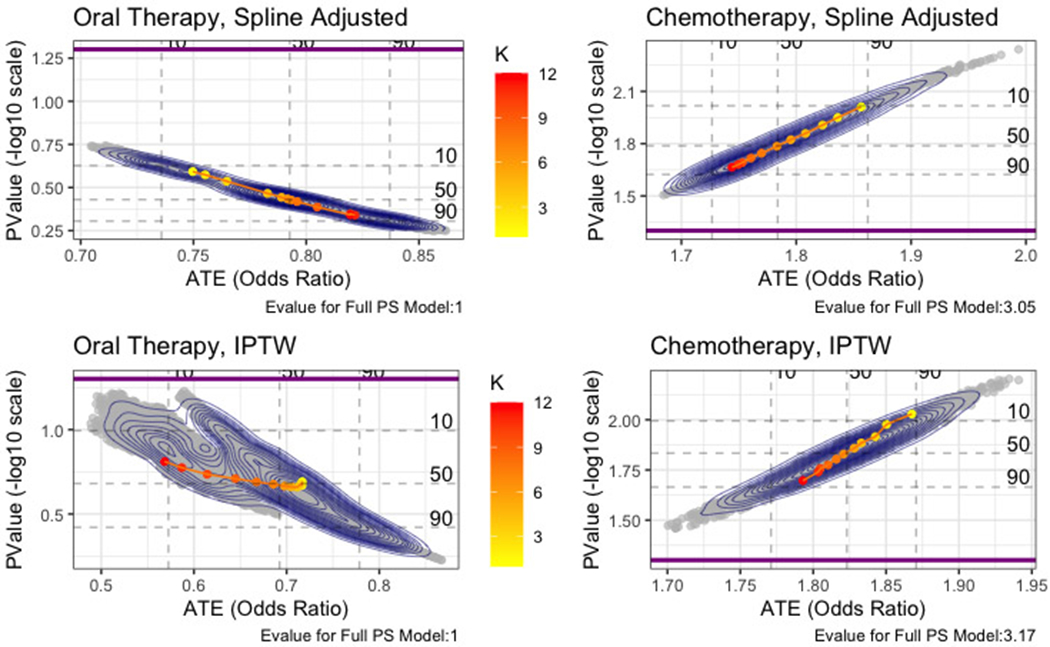
Visualized Sensitivity Analysis

Four sensitivity analyses for four ATE estimates are shown. Contours over scatterplot show the entire distribution of ATE and associated p-values for the set of plausible propensity score models. Dashed lines show denoted percentiles cutoffs for this distribution. K denotes number of covariates in shown model, and the dotted line plot shows median ATE and p-value for each set of K covariates from K=1 to K=12. Thick solid line indicates significance threshold of alpha=0.05. E-values for the full model (K=12) are listed in caption.

Discussion

We have presented propensity score methods for comparative effectiveness of a treatment on various types of health outcomes. We showed methods that can make the compared treatment groups more balanced on a large number of characteristics, and thus provide more accurate estimates of possible causal relationships. There are inherent limitations to these data, as the Clinformatics TM Data Mart Database is generated from information collected for billing purposes and not for research. Thus, the data is subject to misclassification of diagnosis codes and is missing socioeconomic values for many individuals. Although we could not identify if an individual was correctly classified as having prostate cancer, we only included those that also had a pharmacy claim of one of the focus medications which are primarily used for advanced prostate cancer. Those individuals with missing sociodemographic information were still included in the analysis and treated as a separate category. This method comes with assumptions about the missing data mechanism that, if violated, could bias ATE. There are more advanced methods for missing data analysis for a propensity score analysis that others discuss more extensively (D’Agostino et al. 2001; D’Agostino and Rubin, 2000).

There are also challenges and drawbacks to the methods used here. Propensity methods rely on correct specification of the propensity model. Here, we used a theoretical framework, pre-emptively specifying which variables are most associated with assignment of treatment, such as age, economic status, and pre-existing comorbid conditions. Yet, we assessed many plausible propensity score models in our sensitivity analysis to assess the robustness of our findings. We were unable to account for all known confounders from this data, and thus the propensity model may not have addressed all imbalance between groups. Our reporting of the E-value summarizes the sensitivity of our results to unobserved confounding. Another potential limitation to is that we used a logistic regression model to calculate the propensity scores. While this model allows for natural interpretation of the variables included (which may still be of interest), it may be poor at predicting propensity in comparison to machine learning models (Lee et al. 2010; Setoguchi et al. 2008; Westreich 2010). Furthermore, the uncertainty around the propensity estimates is not accounted for in many outcome models, especially when using propensity score matching, and thus lead to incorrect inference and confidence with the estimates (Stuart et al. 2013). Additionally, we effectively have three treatments of interest, yet we stratified the data to have two separate, independent analyses, of two treatment groups. This provided easier calculation and matching from propensity; however, segmenting may mis-specify the treatment allocation mechanisms, as in practice all options are available. Generalized propensity scores can be calculated for multiple categories, with the cost of considerably greater complexity (Hirano and Imbens 2005; Austin 2018). Nonetheless, the methods are very useful for two clear treatment groups to be compared, and when there are many confounding variables. There are also computational challenges when using R for these complex analyses on a large dataset, but the flexibility of custom code and available packages far outweigh this cost. Finally, our estimates for ATE varied across the methods demonstrated, and it is impossible to know which method performed best for each outcome when the true ATE and true propensity model are unknown. Our goal was to showcase the available options while recognizing each method comes with its own limitations. We recommend reporting the sensitivity analysis for transparency with researcher decision error surrounding ATE estimation.

Conclusion

In summary, the methods shown here outline a standard process for conducting comparative effectiveness research in claims databases. It is important to note that these tools cannot perfectly answer comparative effectiveness questions, even with the most extensive data. Careful consideration is required by the researchers as to what variables are confounding treatment and outcome, and what method and assumptions best fit the study. Adding sensitivity analysis to a study can add understanding to the robustness and generalizations of the results. We hope the extensive detail, documentation, and accompanying code aide researchers in their own studies and improve replication among these studies.

Table 1.

Outcome Characteristics

	Immunotherapy (N = 504)		Chemotherapy (N = 2,214)		Oral Therapy (N = 2,747)
Binary Outcome	Count	(%)	Count	(%)	Count	(%)
ER Visit in 60 Days	22	(4.4)	182	(8.2)	100	(3.6)
Count Outcome	Mean	(SD)	Mean	(SD)	Mean	(SD)
ER Visits in 180 Days	0.13	(0.44)	0.23	(0.79)	0.12	(0.50)
Time to Event Outcome (days)	Median	(Q1, Q3)	Median	(Q1, Q3)	Median	(Q1, Q3)
Time on Treatment1	227	(29,638)	110	(43,338)	224	(83,462)
Longitudinally Varying Outcome	Count	(%)	Count	(%)	Count	(%)
Enrolled at 90 days	438	(87.0)	1707	(77.1)	2235	(81.4)
Enrolled at 180 days	381	(75.6)	1353	(61.1)	1788	(65.1)
Any Opioids Prescribed at Any Time	166	(32.9)	936	(42.3)	1281	(46.6)
Opioids at Baseline2	73	(14.5)	653	(29.5)	825	(30.0)
Opioids at 90 Days	87	(19.9)	427	(25.0)	578	(25.9)
Opioids at 180 Days	65	(17.1)	359	(26.5)	515	(28.8)
Patients Prescribed (morphine milligram equivalents, 30-day supply)	Median	(Q1, Q3)	Median	(Q1, Q3)	Median	(Q1, Q3)
Opioids at Treatment Start	112	(39,435)	241	(75,1052)	184	(72,674)
Opioids 90 Days from Treatment Start	87	(73,871)	427	(87,1182)	578	(83,887)
Opioids 180 Days from Treatment Start	391	(97,895)	406	(89,1448)	191	(60,667)

Table 1 shows outcome characteristics across the three treatment groups: immunotherapy (sipuleucel-T), chemotherapy (docetaxel), and oral therapy (enzalutamide or abiraterone). ER is an abbreviation for emergency room. Q1 denotes first quartile of distribution, and Q3 denotes third quartile.

¹Total time on treatment was defined as when the last of any focus treatment was recorded.

²Opioids were identified from a list of generic brand names and converted into 30 day milligram morphine equivalents (MME) using the CDC compilation and conversion factors.