Abstract
Exquisite polarization control using optical metasurfaces has attracted considerable attention thanks to their ability to manipulate multichannel independent wavefronts with subwavelength resolution. Here we present a new class of metasurface polarization optics, which enables imposition of two arbitrary and independent amplitude profiles on any pair of orthogonal states of polarization. The implementation method involves a polarization-dependent interference mechanism achieved by constructing a metasurface composed of an array of nanoscale birefringent waveplates. Based on this principle, we experimentally demonstrate chiral grayscale metasurface and chiral shadow rendering of structured light. These results illustrate a general approach interlinking amplitude profiles and orthogonal states of polarization and expands the scope of metasurface polarization shaping optics.
An optical metasurface, composed of two-dimensional (2D) arrays of subwavelength meta-atoms, is a compact and planar nanophotonic platform being utilized for manipulating the various fundamental properties of an incoming electromagnetic wave [1-6]. Depending on the meta-atom design, metasurfaces are able to modify the phase profile, polarization ellipse, scattering angular, intensity distribution of incident light wave. One of the attractive features that distinguishes them from conventional optics is their ability to simultaneously perform multiple different optical operations since meta-atoms can be designed to respond differently to the wavelength [7-10], polarization [11-14], and/or the illumination angle of incident light [15]. For example, metasurface-based polarization optics has recently attracted much attention as a breakthrough concept for engineering multichannel independent wavefront encoding [16-27]. The implementation of this function requires the individual meta-atom to behave as a waveplate-like birefringent element. Typically, there are two wavefront regulation mechanisms in a polarization-dependent dielectric metasurface design—propagation phase and geometric (or Pancharatnam-Berry, PB) phase [28-29]. Recently, a strategy that combines both geometric phase and propagation phase is proposed to control independent phase profiles using a pair of orthogonal polarizations [21-27]. This exciting capability allows for a new class of polarization-dependent switchable photonic functionalities, such as chiral hologram [21], transformation of orbital angular momentum [22], manipulation of accelerating light beams [23], polarization imaging [24-26], and mode-selective waveguide couplers [27].
However, up until now, much of the effort in metasurface optics has primarily focused on establishing the relationship between polarization and phase profile. Usually it is expected that the amplitude profile of an incident polarized electromagnetic wave is maintained upon transmission through a metasurface. As a result, such metasurfaces exhibit high transmission efficiency, but they are limited to only manipulate the phase profile but not the amplitude profile of incident light [16, 18, 30-31]. Although the polarization conversion efficiency of individual meta-atom can be utilized to control the amplitude for a specific polarization state, these metasurfaces require additional free-space optical elements to fully perform the desired amplitude control [32, 33]. Furthermore, these devices exhibit the same amplitude response when the chirality of incident circularly polarized light is flipped, and cannot achieve the completely decoupled output amplitudes for two arbitrary, orthogonal incident polarization states [32-36]. To the best of our knowledge, the mapping from orthogonal polarization states to completely independent amplitudes has yet to be fully established in metasurface optics.
Here, we propose a new class of metasurface polarization optics where two arbitrary and independent amplitude profiles can be imposed on a pair of orthogonal polarization states (linear, circular, or elliptical) by a singlet metasurface, conceptually shown in Fig. 1(a). This is fundamentally different from previous works where the amplitude and phase control is only achieved for one specific incident polarization state [32-33]. Orthogonally polarized light incident on the metasurface experiences polarization-dependent constructive or destructive interference with contributions from both the propagation phase and the geometric phase. Here, the phase modulation act as an intermediary in associating the input polarization states with the output amplitudes of light. As the transmission amplitude control originates from the interference within each meta-molecule in our method, a single layer metasurface can perform the complete operation without requiring any additional optical elements, which is beneficial for their use in ultracompact integrated optical systems. To demonstrate the ability of this approach, we design and fabricate chiral grayscale metasurface and show nanoprinting with chiral shadow rendering of structured light. This method significantly expands the scope of metasurface polarization optics, paving the way towards engineering of novel polarization switchable meta-devices.
FIG. 1.
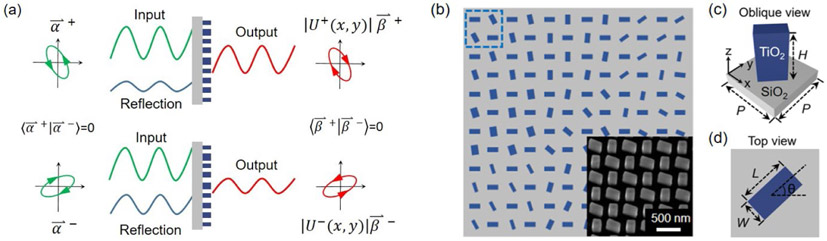
(a) Conceptual schematic diagram. Two independent amplitude profiles ∣U±(x,y)∣ can be imposed on a pair of orthogonal input polarization states through the metasurface, and makes the output polarization states flip handedness. The green, red, and blue wavy lines donate the input, output, and reflection of optical waves, respectively. (b) Schematic diagram of metasurface array. The amplitude controlled metasurface is formed by meta-molecules array. Each meta-molecule (blue dashed box) consists of multiplexed waveplate-like birefringent meta-atoms. The right bottom inset shows a scanning electron microscope image of the fabricated metasurface (Oblique view). (c-d) Perspective and top view of a meta-atom. The dimension (L, W) and orientation angle Θ of the meta-atom can be varied to respectively provide desired propagation phase and geometric phase.
Interference, as an important fundamental optical effect, corresponds to the coherent interaction of two or more optical waves yielding a resultant intensity distribution. In accordance with the principle of superposition, the complex electric field , at a point in space, arising from separate fields and of two contributing sources is given by . Dielectric elements can be considered as individual sources because the polarization ellipse and phase of the optical field transmitted through each element can be arbitrarily controlled by the element design. The implementation of the proposed concept requires at least two different meta-atoms to act as interference sources. In order to make the meta-molecule be with standard square shape which ensures the identical amplitude modulation capability in both the horizontal and vertical directions, here we employ a pair of staggered twin-meta-atoms to design a meta-molecule and form a sub-micron interference system, as shown in Fig. 1(b). The anisotropy of the meta-atoms ensures that the system has the capability of providing polarization-dependent complex amplitude modulation. For each meta-molecule (x,y), the two components of output electric fields in the scalar form can be expressed as:
| (1) |
| (2) |
where + and − denote a pair of orthogonal states of polarization. The interference occurs near the exit surface of the meta-atoms due to their subwavelength separation. Then the total complex amplitude of the interference system is given by U±(x, y) = P±(x, y) + Q±(x, y) and the resultant intensity is as:
| (3) |
where φ±(x, y) is the phase difference of the complex amplitudes between two pairs of meta-atoms and expressed as: φ±(x, y) = φp±(x, y) – (φq±(x, y). The resultant intensity ∣U±(x, y)∣2 therefore depends on the well-known interference term 2p(x, y)q(x, y)cos[φ±(x, y)]. Eq. (3) can be expressed as a composite function ∣U±(x, y)∣ = f[φ±(x, y)], and thus its inverse function has the form φ±(x, y) = f−1(∣U±(x, y)∣). If it is possible to generate arbitrary value of φ±(x, y), it would directly contribute to the modulation of resultant intensity in transmission space. Therefore, φ±(x, y) act as an intermediary in associating the input polarization states with output amplitudes of light field.
Supposing that a metasurface is designed to impose two independent amplitude profiles ∣U+(x, y)∣ and ∣U−(x, y)∣ on a pair of orthogonal polarization states {, }, as shown in Fig. 1. Concurrently, the metasurface is also required to consistently transform the input polarization states to output polarization states {, } as and during transmission. Considering each constituent meta-atom is a linearly birefringent waveplate, then the relationship between the input polarization and output polarization is , where * denotes complex conjugate [16, 23]. As mentioned above, using Eq. (3) one can convert the required amplitude profiles ∣U±(x, y)∣ into corresponding phase difference φ±(x, y). Hence, the metasurface can be described by a Jones matrix J(x, y) that simultaneously satisfies and . An arbitrary pair of orthogonal polarization states in the linear polarization basis has the form:
| (4) |
where χ and δ represent the azimuth and ellipticity of the polarization ellipse, respectively.
In this case, the required Jones matrix J(x, y) is:
| (5) |
This matrix provides a general mapping from orthogonal polarization states to independent amplitudes, which can be translated into the design of polarization-controlled amplitude meta-devices. The eigenvalues and eigenvectors of J(x, y) determine the birefringence phase shifts and fast-axis orientation angle of a meta-atom, respectively corresponding to propagation phase and geometric phase. Therefore, in principle, independent amplitude profiles can be imposed on any set of orthogonal polarization states by simultaneously modifying a meta-atom’s shape and angular orientation.
To demonstrate the amplitude control for any pair of orthogonal polarization states, including linear, circular, and elliptical polarization, we design and numerically simulate three kinds of meta-molecule arrays encoding normalized polarization-dependent amplitude values 0 and 1, as shown in Fig. 2. The meta-atoms in the designed meta-molecule are made of rectangular titanium dioxide (TiO2) nanopillars on a fused-silica substrate. The TiO2 nanopillars are designed to have identical heights of H=600 nm and organized in a square array with a lattice constant of P = 360 nm. Detailed information about these designs are described in the Supplemental Material, Sec. I. Based on Eq.(5), for linear polarization state, one can easily obtain the required phase shifts along fast and slow axes and rotation angles of meta-atom as φx(x, y) = f−1(∣U+(x, y)∣) , φy(x, y) = f−1(∣U−(x, y)∣), θ(x, y) = 0. It means that the constructed meta-molecules only need propagation phase design, which relies on the shape of the meta-atom. In contrast, for circular polarization state, one can find analytical solutions for the required phase shifts and rotation angle as a function of amplitude value given by (see Supplemental Material, Sec. II):
| (6) |
| (7) |
| (8) |
FIG. 2.
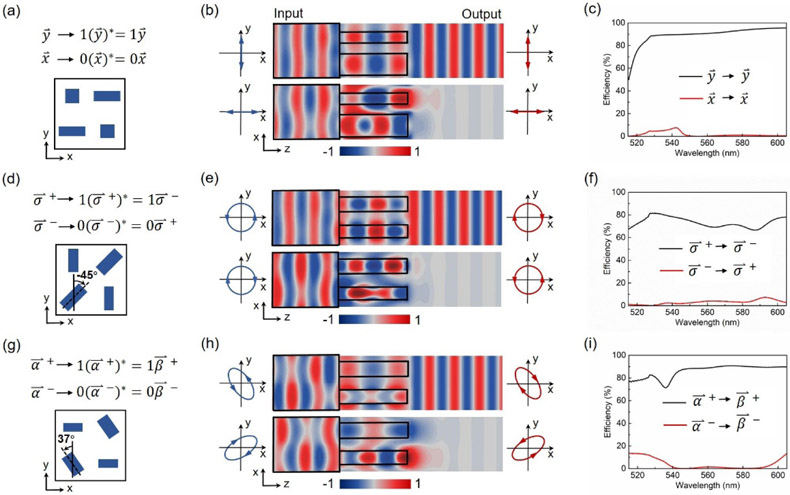
Dichroism of orthogonal polarization states in a meta-molecule system, including (a-c) linear (δ=π/2, χ=π/2), (d-f) circular (δ=π/2, χ=π/4), and (g-i) elliptical polarizations (δ=π/3, χ=π/6). (a, d, g) Schematic diagrams of the meta-molecule design. (, ), (), (, ) denote the linear, circular and elliptical polarization, respectively. Here, the symbol * denotes complex conjugate. (b, e, h) The distribution of electric field in each meta-molecule under the illumination of corresponding orthogonal polarized light at the wavelength of 550 nm from the substrate side, (c, f, i) Broadband transmission characteristics of three meta-molecules.
Different from linear polarization state, a unification of propagation phase and geometric phase is employed to achieve the polarization-dependent constructive or destructive interference. In the more general case of an elliptical polarization state, the analytical solutions do not yield simple and explicit expressions and thus need to be calculated for specific amplitude values and ellipticity of incident polarization states. The specific designs of meta-molecule for two orthogonal linear (δ = π/2 and χ = π/2), circular (δ = π/2 and χ = π/4) and elliptical (δ =π/3 and χ =π/6) polarizations are shown in Fig. 2(a), 2(d) and 2(g), respectively.
The finite-difference time-domain (FDTD) simulation results of three metasurfaces shown in Fig. 2(b, e, h) agree well with the theoretical design. One of the incident polarization states experiences constructive interference, while the other orthogonal state undergoes destructive interference, respectively leading to a complete transmission and a reflection back towards the source. In Fig. 2(c, f, i), the calculated transmittance spectra exhibit broadband characteristics and a strong dichroism, which implies that the designed amplitude modulation metasurfaces can be used as ultrathin and high-performance dichroic filters for arbitrary orthogonal polarization states.
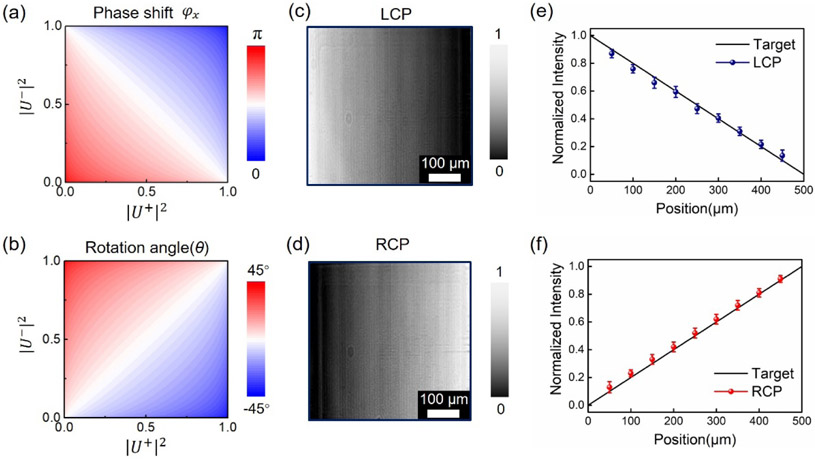
Relying on this ability to arbitrarily control amplitude using the designed meta-molecules, next we experimentally demonstrate a grayscale metasurface with gradient amplitude modulation. Since circular polarization has been widely investigated in metasurface polarization optics, here we choose two orthogonal circular polarization states for incident light for our proof-of-concept experimental demonstration. This demonstration can also be applied to orthogonal linear and elliptical polarizations as they have the similar physical mechanism for amplitude modulation. A metasurface encoding grayscale information but with opposite variation tendency for LCP and RCP light is designed. Fig. 3(a-b) show the calculated phase shifts, φx(φy = φx – π) and rotation angle, θ as a function of intensity ∣U±(x, y)∣2 for the designed metasurface, which intuitively shows the contribution of propagation phase and geometric phase. By using atomic layer deposition and electron beam lithography techniques (see Supplemental Material, Sec. III for details), the TiO2 grayscale metasurface is fabricated and the measurement results are shown in Fig. 3(c-f). As expected, for LCP and RCP light at the wavelength of 550 nm incident on the metasurface, the measured intensity distributions exhibit smooth grayscale variation from bright to dark and the variation tendency is opposite for the two orthogonal circular polarization states. Slight deviations between the design and measured results shown in Fig. 3(e-f) may originate from the fabrication imperfection of the nanostructures.
FIG. 3.
Grayscale metasurface and chiral transformation. (a, b) Required phase shifts, ψx (top) and rotation angle, Θ (bottom) as a function of the intensity ∣U±(x,y)∣2 of incident wave. (c, d) Experimentally measured intensity distributions for LCP and RCP light at the wavelength of 550 nm. (e, f) The corresponding quantitative results along the horizontal direction of the device. The uncertainties are standard deviation of light intensity for repeated experimental measurements (five in total).
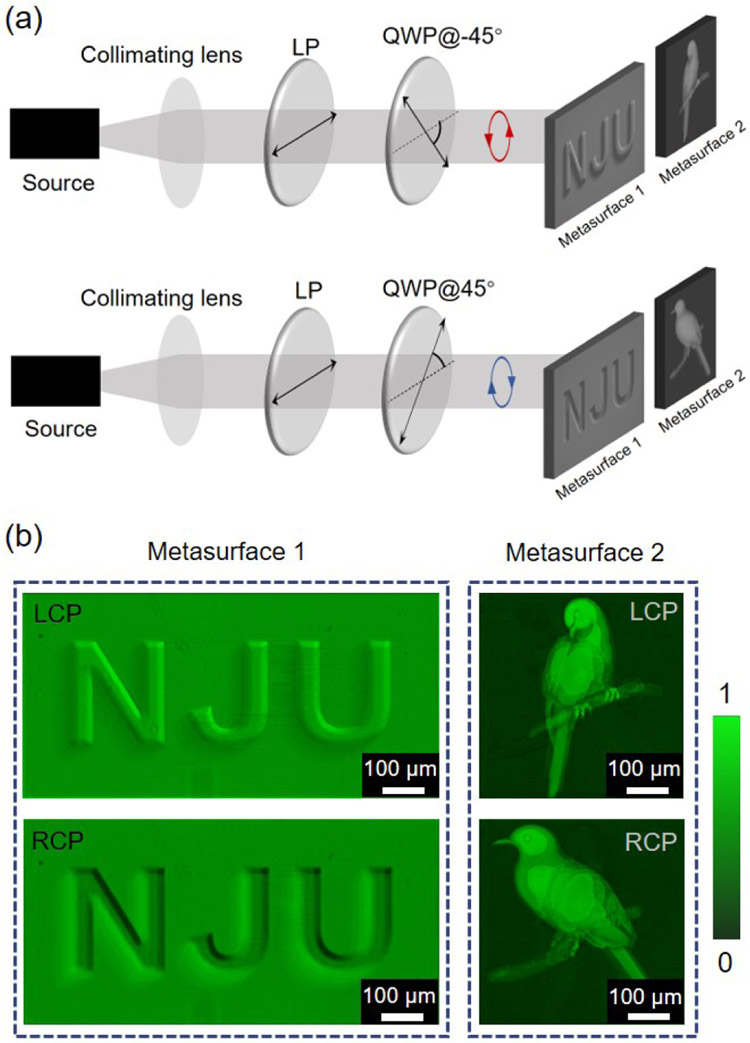
Besides the grayscale metasurface, we further demonstrate the amplitude modulation-induced chiral shadow rendering of structured light. Two metasurfaces (metasurface 1 and metasurface 2) are designed to respectively generate nanoprinting patterns of a character string ‘NJU’ and a bird perching on the twig. Different intensity profiles ∣U±(x, y)∣2 for two orthogonal circular polarization states are encoded on the metasurfaces. A collimated circularly polarized light at the wavelength of 550 nm is normally incident upon the fabricated metasurfaces and the schematic diagram of the measurement setup is shown in Fig. 4(a). As shown in Fig. 4(b), under the LCP light illumination, the ‘NJU’ characters on metasurface 1 present a stereoscopic convex effect, and the metasurface 2 exhibits a frontal portrait of the bird with a crooked head. When the incident light is switched from LCP to RCP, the pattern of ‘NJU’ characters on metasurface 1 present a totally different concave effect and the metasurface 2 shows a side portrait of bird. Further results illustrating polarization-controllable nanoprinting for orthogonal linear, circular and elliptical polarization states are described in the Supplemental Material, Sec. IV. These results clearly demonstrate that amplitude distributions imparted on two orthogonal polarization states can be completely decoupled by the metasurface, and thus it expands the degree of freedom of amplitude control in metasurface optics. This expansion of functionality enabled by the proposed metasurface has the potential to enable novel applications in the areas of optical data storage, information encryption and anti-counterfeiting.
FIG. 4.
Metasurface nanoprinting with chiral shadow rendering of structured light. (a) Experimental setup for measurement. A laser beam at the wavelength of 550 nm is collimated and incident on the metasurfaces though a linear polarizer (LP) and quarter wave plate (QWP). The images of metasurface nanoprinting can be captured by the standard microscope attached with a camera. (b) Experimentally captured optical images of the metasurface nanoprinting illuminated with LCP and RCP light.
In conclusion, we have proposed and demonstrated a new class of metasurface that imposes two arbitrary and independent amplitude profiles on a pair of orthogonal polarizations. The phase profile of metasurface acts as an intermediary in associating the input polarization state with output amplitude of light field. By combining the geometric phase and propagation phase, we provide a simple method for the design of polarization-dependent, amplitude-controlled meta-devices. This method significantly expands the scope of metasurface polarization optics and opens a new path towards achieving novel types of photonic functionalities in a compact platform.
Supplementary Material
Acknowledgement
Q. F, M. L., C. Z. and W. Z. contributed equally. The work is supported by the Key Research and Development Program from Ministry of Science and Technology of China (2017YFA0303700 and 2016YFA0202100) and National Natural Science Foundation of China (11774163). W. Z., L. C. and A. A. acknowledge support under the Cooperative Research Agreement between the University of Maryland and the National Institute of Standards and Technology, Award#70-NANB14H209, through the University of Maryland.
References
- [1].Yu N, Genevet P, Kats MA, Aieta F, Tetienne JP, Capasso F, and Gaburro Z, Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 334, 333 (2011). [DOI] [PubMed] [Google Scholar]
- [2].Qu C, Ma S, Hao J, Qiu M, Li X, Xiao S, Miao Z, Dai N, He Q, Sun S, and Zhou L, Tailor the Functionalities of Metasurfaces Based on a Complete Phase Diagram. Phys. Rev. Lett 115, 235503 (2015). [DOI] [PubMed] [Google Scholar]
- [3].Pu M, Li X, Ma X, Wang Y, Zhao Z, Wang C, Hu C, Gao P, Huang C, Ren H, Li X, Qin F, Yang J, Gu M, Hong M, and Luo X, Catenary optics for achromatic generation of perfect optical angular momentum. Sci. Adv 1, e1500396 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Zheng G, Mühlenbernd H, Kenney M, Li GX, Zentgraf T, and Zhang S, Metasurface hologram reaching 80% efficiency. Nat. Nanotechnol 10, 308 (2015). [DOI] [PubMed] [Google Scholar]
- [5].Decker M, Staude I, Falkner M, Dominguez J, Neshev DN, Brener I, Pertsch T, and Kivshar YS, High-efficiency dielectric huygens’ surfaces. Adv. Opt. Mater 3, 813 (2015). [Google Scholar]
- [6].Chang C, Zhao Z, Li D, Taylor A, Fan S, and Chen H, Broadband Linear-to-circular polarization conversion enabled by birefringent off-resonance reflective metasurfaces. Phys. Rev. Lett 123, 237401 (2019). [DOI] [PubMed] [Google Scholar]
- [7].Aieta F, Kats MA, Genevet P, and Capasso F, Multiwavelength achromatic metasurfaces by dispersive phase compensation. Science 347, 1342 (2015). [DOI] [PubMed] [Google Scholar]
- [8].Wang B, Dong F, Li QT, Yang D, Sun C, Chen J, Song Z, Xu L, Chu W, Xiao YF, Gong Q, and Li Y, Visible-Frequency Dielectric Metasurfaces for Multiwavelength Achromatic and Highly Dispersive Holograms. Nano Lett. 16, 5235 (2016). [DOI] [PubMed] [Google Scholar]
- [9].Arbabi E, Arbabi A, Kamali SM, Horie Y, and Faraon A, Multiwavelength polarization-insensitive lenses based on dielectric metasurfaces with meta-molecules. Optica 3, 628 (2016). [Google Scholar]
- [10].Wang S, Wu PC, Su VC, Lai YC, Chen MK, Kuo HY, Chen BH, Chen YH, Huang TT, Wang JH, Lin RM, Kuan CH, Li T, Wang ZL, Zhu SN, and Tsai DP, A broadband achromatic metalens in the visible. Nat. Nanotechnol 13, 227 (2018). [DOI] [PubMed] [Google Scholar]
- [11].Wen D, Yue F, Li G, Zheng G, Chan K, Chen S, Chen M, Li KF, Wong PWH, Cheah KW, Pun EYB, Zhang S, and Chen X, Helicity multiplexed broadband metasurface holograms. Nat. Commun 6, 8241 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Maguid E, Yulevich I, Veksler D, Kleiner V, Brongersma ML, and Hasman E, Photonic spin-controlled multifunctional shared-aperture antenna array. Science 352, 1202 (2016). [DOI] [PubMed] [Google Scholar]
- [13].Yue F, Wen D, Zhang C, Gerardot BD, Wang W, Zhang S, and Chen X, Multichannel Polarization-Controllable Superpositions of Orbital Angular Momentum States. Adv. Mater 29, 1603838 (2017). [DOI] [PubMed] [Google Scholar]
- [14].Dong F, and Chu W, Multichannel-Independent Information Encoding with Optical Metasurfaces. Adv. Mater 31, 1804921 (2019). [DOI] [PubMed] [Google Scholar]
- [15].Kamali SM, Arbabi E, Arbabi A, Horie Y, Faraji-Dana MS, and Faraon A, Angle-multiplexed metasurfaces: encoding independent wavefronts in a single metasurface under different illumination angles. Phys. Rev. X 7, 041056 (2017). [Google Scholar]
- [16].Arbabi A, Horie Y, Bagheri M, and Faraon A, Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nat. Nanotechnol 10, 937 (2015). [DOI] [PubMed] [Google Scholar]
- [17].Jha PK, Ni X, Wu C, Wang Y, and Zhang X, Metasurface-Enabled Remote Quantum Interference. Phys. Rev. Lett 115, 025501 (2015). [DOI] [PubMed] [Google Scholar]
- [18].Lin D, Fan P, Hasman E, and Brongersma ML, Dielectric gradient metasurface optical elements. Science 345, 298 (2014). [DOI] [PubMed] [Google Scholar]
- [19].Khorasaninejad M, and Crozier KB, Silicon nanofin grating as a miniature chirality-distinguishing beam-splitter. Nat. Commun 5, 5386 (2014). [DOI] [PubMed] [Google Scholar]
- [20].Tymchenko M, Gomez-Diaz JS, Lee J, Nookala N, Belkin MA, and Alù A, Gradient nonlinear Pancharatnam-Berry metasurfaces. Phys. Rev. Lett 115, 207403 (2015). [DOI] [PubMed] [Google Scholar]
- [21].Mueller JPB, Rubin NA, Devlin RC, Groever B, and Capasso F, Metasurface Polarization Optics: Independent Phase Control of Arbitrary Orthogonal States of Polarization. Phys. Rev. Lett 118, 113901 (2017). [DOI] [PubMed] [Google Scholar]
- [22].Devlin RC, Ambrosio A, Rubin NA, Mueller JPB, and Capasso F, Arbitrary spin-to–orbital angular momentum conversion of light. Science 358, 896 (2017). [DOI] [PubMed] [Google Scholar]
- [23].Fan Q, Zhu W, Liang Y, Huo P, Agrawal A, Huang K, Luo X, Lu Y, Qiu C, Lezec HJ, and Xu T. Broadband generation of photonic spin-controlled arbitrary accelerating light beams in the visible. Nano Lett. 19, 1158 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Arbabi E, Kamali SM, Arbabi A, and Faraon A, Full-Stokes Imaging Polarimetry Using Dielectric Metasurfaces. ACS Photonics 5, 3132 (2018). [Google Scholar]
- [25].Rubin NA, D’Aversa G, Chevalier P, Shi Z, Chen W, and Capasso F, Matrix Fourier optics enables a compact full-Stokes polarization camera. Science 365, eaax1839 (2019). [DOI] [PubMed] [Google Scholar]
- [26].Huo PC, Zhang C, Zhu WQ, Liu MZ, Zhang S, Zhang S, Chen L, Lezec HJ, Amit A, Lu YQ, and Xu T, Photonic spin-multiplexing metasurface for switchable spiral phase contrast imaging. Nano Lett. 20, 2791 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Meng Y, Liu ZT, Xie ZW, D Wang R, Qi TC, Hu FT, Kim H, Xiao QR, Fu X, Wu Q, Bae SH, Gong ML, and Yuan XC, Versatile on-chip light coupling and demultiplexing from arbitrary polarizations to controlled waveguide modes using an integrated dielectric metasurface. Photon. Res 8, 564 (2020). [Google Scholar]
- [28].Hasman E, Kleiner V, Biener G, and Niv A, Polarization dependent focusing lens by use of quantized Pancharatnam-Berry phase diffractive optics. Appl. Phys. Lett 82, 328 (2003). [Google Scholar]
- [29].Wu L, Tao J, and Zheng G, Controlling phase of arbitrary polarizations using both the geometric phase and the propagation phase. Phys. Rev. B, 97, 245426(2018). [Google Scholar]
- [30].Zhang C, Divitt S, Fan Q, Zhu W, Amit A, Lu Y, Xu T and Lezec HJ. Low-loss metasurface optics down to the deep ultraviolet region. Light Sci. Appl 9, 55 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Khorasaninejad M, Chen W, Devlin RC, Oh J, Zhu AY, and Capasso F, Metalenses at visible wavelengths: diffraction-limited focusing and subwavelength resolution imaging. Science 352, 1190 (2016). [DOI] [PubMed] [Google Scholar]
- [32].Overvig AC, Shrestha S, Malek SC, Lu M, Stein A, Zheng C, and Yu N, Dielectric metasurfaces for complete and independent control of the optical amplitude and phase. Light: Sci. Appl 8, 92 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Lee GY, Yoon G, Lee SY, Yun H, Cho J, Lee K, Kim H, Rho J, and Lee B, Complete amplitude and phase control of light using broadband holographic metasurfaces. Nanoscale 10(9), 4237–4245 (2018). [DOI] [PubMed] [Google Scholar]
- [34].Bao Y, Yu Y, Xu H, Guo C, Li J, Sun S, Zhou ZK, Qiu C, and Wang X, Full-colour nanoprint-hologram synchronous metasurface with arbitrary hue-saturation-brightness control. Light: Sci. Appl 8, 95 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Xu H, Hu G, Han L, Jiang M, Huang Y, Li Y, Yang X, Ling X, Chen L, Zhao J, and Qiu C, Chirality-Assisted High-Efficiency Metasurfaces with Independent Control of Phase, Amplitude, and Polarization. Adv. Opt. Mater 7, 1801479 (2019). [Google Scholar]
- [36].Zhang F, Pu M, Gao P, Jin J, Li X, Guo Y, Ma X, Luo J, Yu H, and Luo X, Simultaneous Full-Color Printing and Holography Enabled by Centimeter-Scale Plasmonic Metasurfaces. Adv. Sci 7, 1903156 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.