Effects of latency and age structure on the dynamics and containment of COVID-19

Graphical abstract

Abstract

In this paper we develop an SEIR-type model of COVID-19, with account for two particular aspects: non-exponential distribution of incubation and recovery periods, as well as age structure of the population. For the mean-field model, which does not distinguish between different age groups, we demonstrate that including a more realistic Gamma distribution of incubation and recovery periods may not have an effect on the total number of deaths and the overall size of an epidemic, but it has a major effect in terms of increasing the peak numbers of infected and critical care cases, as well as on changing the timescales of an epidemic, both in terms of time to reach the peak, and the overall duration of an outbreak. In order to obtain more accurate estimates of disease progression and investigate different strategies for introducing and lifting the lockdown, we have also considered an age-structured version of the model, which has allowed us to include more accurate data on age-specific rates of hospitalisation and COVID-19 related mortality. Applying this model to three comparable neighbouring regions in the UK has delivered some fascinating insights regarding the effect of lockdown in regions with different population structure. We have discovered that for a fixed lockdown duration, the timing of its start is very important in the sense that the second epidemic wave after lifting the lockdown can be significantly smaller or larger depending on the specific population structure. Also, the later the fixed-duration lockdown is introduced, the smaller is the resulting final number of deaths at the end of the outbreak. When the lockdown is introduced simultaneously for all regions, increasing lockdown duration postpones and slightly reduces the epidemic peak, though without noticeable differences in peak magnitude between different lockdown durations.

1. Introduction

As of 15th November 2020, there are $1,344,356$ confirmed cases of coronavirus disease (COVID-19) and $51,766$ COVID-19 associated deaths reported in the UK (coronavirus.data, 2021), with more than 54 M cases and over 1.3 M deaths globally (Worldometer coronavirus data, 2021). The virus is reported to first appeared in Wuhan, China in 2019 (Li et al., 2020), and has since silently and swiftly spread around the globe infecting populations in 212 countries and territories. When WHO declared it a global pandemic on the 11th of March 2020, there were $118,000$ cases in 100 countries. In order to contain and halt the spread of this deadly disease, countries around the world have taken extraordinary measures, introducing “lockdowns” and closing borders. The majority of cases of COVID-19 are spread via respiratory routes, especially among large gatherings of people in shopping malls, carnivals, celebrations etc., but a preliminary study has suggested that it can also spread via extra-respiratory routes, although the study was relatively small (Cai et al., 2020). Clinically, COVID-19 is characterised by high temperature, cough and loss of smell and taste in some people, with cases varying from mild to very severe with life-threatening implications. The disease can also present itself with no symptoms at all, whereby someone infected with COVID-19 experiences no symptoms but is able to spread it to other people. It is thought that the number of asymptomatic carriers varies from 15 to 75–80%. While testing of the Diamond Princess Cruise ship has estimated that there were 17.9% of asymptomatic carriers (Mizumoto et al., 2020), the population-wide testing of Vó Euganeo located 50 km west of Venice and closed off by authorities in February indicated that 50–75% of confirmed cases were symptomless (Day et al., 2020). This is one of the most challenging factors, which can have major implications in terms of managing and stopping the spread of the disease.

Another key epidemiological feature of COVID-19 is its relatively long incubation period, estimated to be about 5 days, where a person is exposed to the disease but the onset of symptoms appears some days later (Lauer et al., 2020). Since the exposed person can infect others while incubating the disease, this plays a major role in terms of epidemic control and management. The mortality rates from COVID-19 tend to be higher for older people, and children are thought to have either mild or no symptoms at all. CDC report of 6 April 2020 estimates that infection among people younger than 18 is 1.7%, 5.7% required hospitalisation compared to 10% for 18–64 age group (disease, 2020), while hospitalisation rates in adults ages 80+ are estimated to be around 30–70% (Verity et al., 2020).

At the moment, in order to ease the strain on healthcare and save lives, majority of countries around the globe are practicing physical distancing/self-isolation measures, which are aimed at slowing the disease progressing and its intensity. Mathematical models have been widely used to analyse various scenarios of COVID-19 disease development, and to predict the best possible outcomes depending on the severity and length of introduced physical distancing measures (Hellewell et al., 2020, Prem et al., 2020, Ferguson et al., 2020, Kissler et al., 2020). A number of these and other models (Yang et al., 2020, Peng, 2020, Fang et al., 2020) have used SIR- and SEIR-type epidemic models with an underlying assumption of exponential distributions of infection and recovery times.

In this paper we look into three specific aspects of COVID-19 dynamics and its containment. The first concerns an observation that the incubation period has a distinctly non-exponential distribution (Lauer et al., 2020), and the same applies to infectious period (Verity et al., 2020). We will include this feature in our model by means of a gamma distribution that much more accurately describes the behaviour of these major characteristics of disease dynamics. As we will show, this has a profound effect on disease dynamics in terms of its timescales (time to reach the peak and overall duration), as well as on the disease severity represented by the maximum number of infected individuals and the maximum number of critical care cases. The second aspect we will investigate concerns on observation that the infection, severity and mortality rates for COVID-19 are significantly different for disfferent age groups (Prem et al., 2020, Ferguson et al., 2020), thus it is essential to include the specific demographic structure of each particular region when modelling and assessing potential needs for healthcare facilities, and, in particular, the number of critical care beds at different stages of epidemic progression. The third and final aspect we are interested in is the analysis of the effects of timing and duration of lockdown on containment of COVID-19 progression for regions with different demographic age structure.

The outline of the paper is as follows. In the next section we derive and analyse a mean-field model of disease dynamics with account for non-exponential distributions of incubation and infectious periods. In Section 3 we develop an age-structured version of this model that takes into account age-specific values of parameters and a demographic structure. Interactions between different age groups are modelled using three different types of age-specific mixing matrices for the UK population (Mossong et al., 2008, Klepac et al., 2020, Jarvis et al., 2020), including one obtained very recently after the lockdown was introduced in the UK. To illustrate the effects of different mixing patterns and lockdown, in Section 4 we compare the results for three regions of the UK, focusing on the role of lockdown timing and duration. The paper concludes in Section 5 with a discussion of results and open questions.

2. Mean-field SEIR model

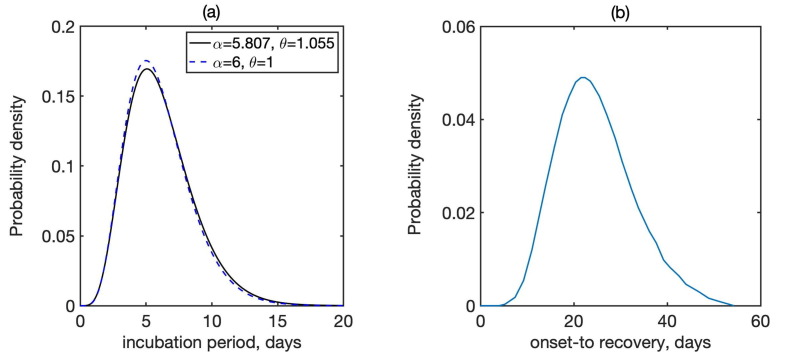
Before deriving a model for the dynamics of COVID-19, we note that one of the major assumptions behind SIR and SEIR-type models is an exponential distribution of incubation and recovery periods. Importantly, the actual distributions of these parameters as obtained from available epidemiological data rather obey a Gamma distribution (Lauer et al., 2020, McAloon et al., 2020, Byrne et al., 2020, Linton et al., 2020), as illustrated in Fig. 1 . To account for this fact in the model, we will represent Gamma distribution by means of models with multiple stages in the exposed and infected class, in a manner similar to Lloyd (2000). A very recent work by Boldog et al. (2020) considered an SEIR-type model of COVID-19 that explicitly includes two stages for exposed individuals and three stages for the infected class. However, the shape of distributions of incubation and recovery periods shown in Fig. 1 suggests that those numbers of stages may not be sufficient to properly represent the distributions of incubation and recovery periods; more specifically, with just two stages for exposed individuals, the distribution would be concave for smaller values of incubation period, while it should be convex according to the data from Lauer et al. (2020). With these observations in mind, we model disease dynamics using a modification of the very recent model in Kissler et al. (2020). Susceptibles (S) get exposed to the disease, and after acquiring infection at rate $\beta$ from infected individuals, they move to the Exposed (E) class. Similarly to the model of Kissler et al. (2020) and a number of other mathematical models of COVID-19 (Prem et al., 2020, Kucharski et al., 2020, Aguiar et al., 2020, Kyrychko et al., 2020), we assume that the incubation period, i.e. a period of time from acquiring the virus until developing symptoms, has the same duration as the latent period, which is the period from acquiring the virus until becoming infectious. While there is some evidence that individuals may also be infectious close to the end of pre-symptomatic period (Tindale et al., 2020, Nishiura et al., 2020), for simplicity we will assume that the incubation and latency periods coincide, in other words, the individuals become infectious around the same time as they start showing symptoms, for those of them who will eventually be symptomatic. In the model this is represented by individuals staying in the exposed class for an average incubation/latency period of $1/\nu$ before becoming infectious, either asymptomatically or symptomatically (See Fig. 2 ).

Fig. 1.

Distribution of (a) incubation period, where $\alpha$ is the shape, and $\theta$ is the scale of Gamma distribution, and (b) recovery periods (Lauer et al., 2020, Verity et al., 2020). In (a), solid line shows the best fit to data from Lauer et al. (2020), the dashed line is the closest fit to Gamma distribution with integer parameters.

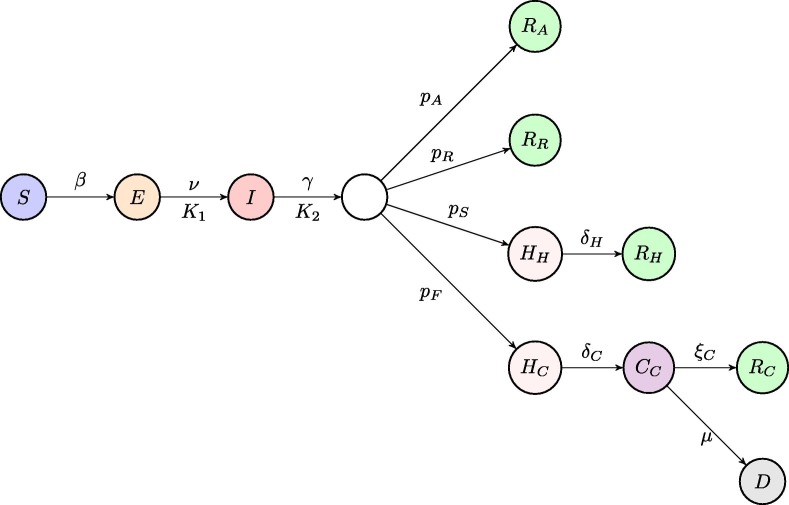
Fig. 2.

Schematic diagram of the disease transmission model. Each circle represents one of model compartments, arrows represent transitions between compartments, and letters above/below arrows represent the rates of those transitions. The pairs $(\nu ,K_1)$ and $(\gamma ,K_2)$ describe, respectively, incubation/latency period and infectious/recovery period, where the first element of each pair is the corresponding rate of transition, which is equal to the inverse of the average corresponding period, and the second element of each pair describes the number of stages in the gamma distribution of that time period.

In terms of virus transmission, an important question concerns the degree of contribution from truly asymptomatic (as opposed to pre-symptomatic) individuals, i.e. individuals who never develop symptoms. This aspect is extremely difficult to assess, because it relies on sufficient testing of large groups of people regardless of whether or not they ever exhibit symptoms, and then trying to track and trace the course of infections in order to identify their original source. Several studies have looked into this, and, in particular, they investigated the contribution of asymptomatic individuals to disease transmission by measuring their viral load, which was found to be generally the same in pre-symptomatic, asymptomatic and symptomatic patients (Liu et al., 2020, Furukawa et al., 2020, Savvides and Siegel, 2020, Walsh et al., 2020, Zou et al., 2020). This justifies including asymptomatic carriers into the force of infection with the same contribution as symptomatic carriers.

At the end of incubation/latency period, individuals become infectious, and they will remain infectious for an average period of time of $1/\gamma$, and after that they will progress into different routes. A proportion $p_A$ of them will simply recover and move to the Recovered class ($R_A$), and similarly a proportion $p_R$ of individuals with mild symptoms will move to their own Recovered class $R_R$. For this reason, we interpret the infectious period also as a recovery period. There are also people, who will require hospitalisation, and the model assumes that the time from the onset of symptoms to hospitalisation is roughly the same as infectious period (Linton et al., 2020, Davies et al., 2020). Hence, we assume that after the same period of time of $1/\gamma$, a proportion $p_H$ of individuals will move into a class of hospitalised individuals $H_H$, and from there they will then proceed to the Recovered class $R_H$ after an average period of $1/{\delta }_H$. Finally, there is a proportion $p_C$ of individuals who will require critical care, hence they will first move into the hospitalised class $H_C$, from which they proceed to a critical care class $C_C$ at rate ${\delta }_C$, and subsequently they either move into the recovered class $R_C$ at rate ${\xi }_C$, or die and move to the compartment D at rate $\mu$.

In terms of including the above-mentioned distributions of incubation and infectious periods in the model, we will assume that with the same mean incubation period $1/\mathit{nu}$, individuals in the exposed class go through $K_1$ sequential stages of equal duration, and in the infectious class with the average infectious period $1/\gamma$, they go through $K_2$ stages of the same duration. With these assumptions, the model equations now have the form

$$\begin{array}{c}\dot{S}=-\beta S{\displaystyle \sum _{k=1}^{K_2}}{I}_k/N,{\dot{E}}_1=\beta S{\displaystyle \sum _{k=1}^{K_2}}{I}_k/N-K_1\nu E_1,\hfill \\ {\dot{E}}_2=K_1\nu E_1-K_1\nu E_2,\dots ,{\dot{E}}_{K_1}=K_1\nu E_{K_1-1}-K_1\nu E_{K_1},\hfill \\ {\dot{I}}_1=K_1\nu E_{K_1}-K_2\gamma I_1,\dots ,{\dot{I}}_{K_2}=K_2\gamma I_{K_2-1}-K_2\gamma I_{K_2},\hfill \\ {\dot{H}}_H=p_H{K}_2\gamma I_{K_2}-{\delta }_H{H}_H,{\dot{H}}_C=p_C{K}_2\gamma I_{K_2}-{\delta }_C{H}_C,\hfill \\ {\dot{C}}_C={\delta }_C{H}_C-({\xi }_C+\mu )C_C,{\dot{R}}_A=p_A{K}_2\gamma I_{K_2},{\dot{R}}_R=p_R{K}_2\gamma I_{K_2},\hfill \\ {\dot{R}}_H={\delta }_H{H}_H,{\dot{R}}_C={\xi }_C{C}_C,\dot{D}=\mu C_C,\hfill \end{array}$$ (1)

where dot denotes the derivative with respect to time, and the parameters are

$$\begin{array}{cc}\hfill & p_H=\omega (1-p_A)(1-\sigma ),\hfill \\ \hfill & p_C=\sigma \omega (1-p_A),\hfill \\ \hfill & p_R=(1-p_A)(1-\omega ),\hfill \end{array}$$

where $\omega$ is the rate of hospitalisation, and $\sigma$ is the rate of critical care admission (Verity et al., 2020, Ferguson et al., 2020).

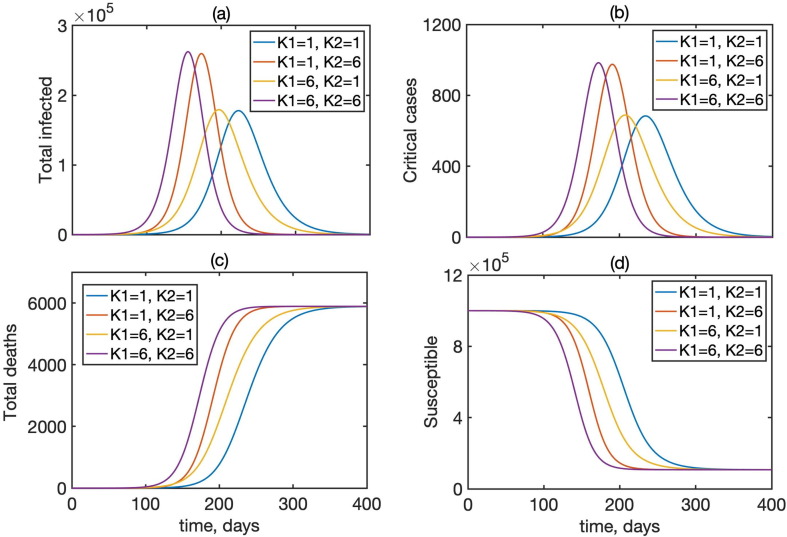
Fig. 3 shows a comparison of time dynamics of the epidemics with baseline values of parameters from Table 1 and different numbers of stages of incubation and recovery. This figure shows that the overall dynamics changes drastically when the numbers of stages are varied, and the situation for $K_1=K_2=1$, which corresponds to the standard SEIR model, is significantly different from the situation with $K_1=K_2=6$, which provides a much more realistic representation of incubation and recovery periods illustrated in Fig. 1. We observe that for the same mean incubation and recovery periods, increasing the number of stages in the incubation period results in slightly bringing forward the peak of the epidemic and its overall completion, while increasing the number of stages in the recovery period significantly increases the maximum total numbers of infected and the number of critical cases. (see Fig. 4 , Table 2 ).

Fig. 3.

Dynamics of the total infected I, critical cases $C_C$, total deaths D, and the susceptibles S in model (1) for different numbers of incubation and recovery stages, with $N=1,000,000$, and 5 individuals initially exposed to infection.

Table 1.

Parameter definitions and their baseline values from Kissler et al., 2020, except for $\gamma$ from Verity et al., 2020 and $\beta$ adjusted to have $R_0=2.5$.

Parameter	Value	Meaning
$\beta$	$0.15$	disease transmission/infection rate
K	$1-6$	number of exposed stages
$1/\nu$	5 days	incubation time
$1/\gamma$	$16.6$ days	infectious period/time to hospitalisation (both non-critical and critical care)
$p_A$	$0.5$ (assumed)	proportion of asymptomatic infections
$p_R$	$0.456$ (varies)	proportion of symptomatic infections without the hospital/critical care requirements
$p_H$	$0.0308$ (varies)	proportion of symptomatic infections requiring hospitalisation, but not critical care
$p_C$	$0.0132$ (varies)	proportion of symptomatic infections requiring critical care
$1/{\delta }_H$	8 days	recovery rate for non-critical hospital cases
$1/{\delta }_C$	8 days	average duration from hospital admission to requiring critical care
$1/{\xi }_C$	10 days	recovery rate for admissions requiring critical care
$\mu$	$0.1$ (varies)	death rate for admissions requiring critical care

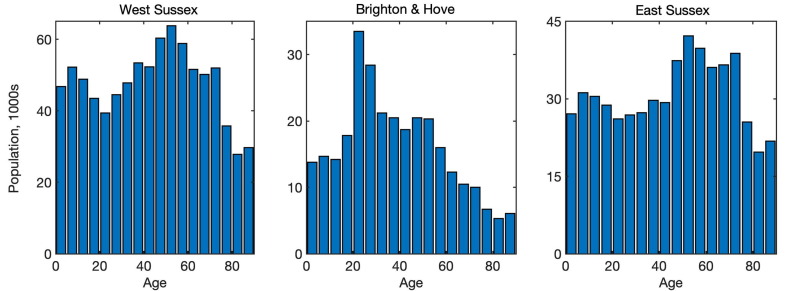
Fig. 4.

Age distribution in West Sussex, Brighton and Hove, and East Sussex (Office for National Statistics, 2019).

Table 2.

Variables of the model.

Variable	Meaning
S	Susceptibles
N	Total population size
$E_i,i=1,\dots ,K_1$	Exposed individuals in different stages after the exposure to the disease
$I_i,i=1,\dots ,K_2$	Infectious individuals in different stages
$H_H$	Hospitalised individuals not requiring critical care
$H_C$	Hospitalised individuals requiring critical care
$C_C$	Individuals in critical care
$R_A$	Recovered asymptomatic individuals
$R_R$	Recovered individuals without hospitalisation
$R_H$	Recovered individuals after hospital (without critical care) admission
$R_C$	Recovered individuals after critical care
D	Those who died in critical care

3. Age-structured model with latency and gamma distribution of incubation and recovery periods

Due to a significant variation in disease progression, and more specifically, in the probability of requiring hospitalisation, the proportions of severe/critical cases, and mortality, as well as a strongly inhomogeneous population structure, it is essential to include age distribution in the epidemic model. To achieve this, we subdivide each of the compartments in model (1) into 18 age classes representing age groups 0–4, 5–9, …, 85+, and then consider disease transmission through interactions between individuals in different age groups, as represented by a certain mixing matrix. An equivalent model has the form

$$\begin{array}{c}{\dot{S}}^i=-\beta S^i{\displaystyle \sum _{j=1}^{18}}{\displaystyle \sum _{k=1}^{K_2}}{C}_{\mathit{ij}}{I}_k^j/N^j,{\dot{E}}_1^i=\beta S^i{\displaystyle \sum _{j=1}^{18}}{\displaystyle \sum _{k=1}^{K_2}}{C}_{\mathit{ij}}{I}_k^j/N^j-K_1\nu E_1^i,\hfill \\ {\dot{E}}_2^i=K_1\nu E_1^i-K_1\nu E_2^i,\dots ,{\dot{E}}_{K_1}^i=K_1\nu E_{K_1-1}^i-K_1\nu E_{K_1}^i,\hfill \\ {\dot{I}}_1^i=K_1\nu E_{K_1}^i-K_2\gamma I_1^i,\dots ,{\dot{I}}_{K_2}^i=K_2\gamma I_{K_2-1}^i-K_2\gamma I_{K_2}^i,\hfill \\ {\dot{H}}_H^i=p_H^i{K}_2\gamma I_{K_2}^i-{\delta }_H{H}_H^i,{\dot{H}}_C^i=p_C^i{K}_2\gamma I_{K_2}^i-{\delta }_C{H}_C^i,{\dot{C}}_C^i={\delta }_C{H}_C^i-({\xi }_C+{\mu }^i)C_C^i,\hfill \\ \hfill \\ {\dot{R}}_A^i=p_A^i{K}_2\gamma I_{K_2}^i,{\dot{R}}_R^i=p_R^i{K}_2\gamma I_{K_2}^i,{\dot{R}}_C^i={\xi }_C{C}_C^i,{\dot{R}}_H^i={\delta }_H{H}_H^i,{\dot{D}}^i={\mu }^i{C}_C^i,\hfill \end{array}$$ (2)

where $i=1..18$ are different age groups, $K_1$ is the number of incubation stages and $K_2$ is the number of recovery stages, $C_{\mathit{ij}}$ is the mixing matrix. For simulations, it was assumed that a small proportion in each age group was initially exposed. Age-specific values of parameters $\omega ,\sigma$ and $\mu$ used for simulations are given in Table 3 and are based on Ferguson et al. (2020).

Table 3.

Age-specific parameter values from Ferguson et al. (2020).

Age-group	% symptomatic cases	% hospitalised cases	infection fatality
(years)	requiring hospitalisation, $\omega$	requiring critical care, $\sigma$	ratio, $\mu$
0–9	0.1%	5%	0.002%
10–19	0.3%	5%	0.006%
20–29	1.2%	5%	0.03%
30–39	3.2%	5%	0.08%
40–49	4.9%	6.3%	0.15%
50–59	10.2%	12.2%	0.6%
60–69	16.6%	27.4%	2.2%
70–79	24.3%	43.2%	5.1%
80+	27.3%	70.9%	9.3%

3.1. Mixing matrices

To model the effects of different levels of interaction between individuals in the population, we will consider three different mixing matrices. The first one, known as POLYMOD, comes from a major UK study in 2008 (Mossong et al., 2008) and has been subsequently used to model the infectious disease dynamics in a variety of contexts. The second mixing matrix was produced as a result of UK’s nationwide social experiment on online tracking of an influenza epidemic for a BBC programme “Contagion!” in 2018 (Klepac et al., 2020, Klepac et al., 2018). The BBC mixing matrices (all and physical only) were padded with POLYMOD data for the missing block describing interactions in the lowest age groups, which were scaled to ensure that the leading eigenvalue of the BBC matrices did not change. The resulting mixing matrices are largely similar to the POLYMOD matrices, with the only main difference being a change in the structure of interactions between teenagers and other age groups. This change was largely attributed to a significant level of using smartphones and other gadgets by teenagers, which resulted in the reduction of direct social interactions for this age group. The third matrix we will use comes from the so-called CoMix survey (Jarvis et al., 2020), an online survey conducted in March 2020 by Ipsos that looked into levels of social mixing in the UK following the introduction of a lockdown.

Since the POLYMOD and BBC matrices describe regular interactions between different age groups in the absence of any intervention, they were scaled with their respective leading eigenvalue to maintain the same basic reproduction number for the same transmission rate $\beta$. When analysing the effects of lockdown, we will use BBC-all mixing matrix as a baseline, with CoMix-all describing contacts during the lockdown, and for the same transmission rate, the CoMix matrix is rescaled by a leading eigenvalue of the BBC-all matrix to reflect a reduction in the number of contacts between these two matrices. As discussed in Jarvis et al. (2020), for a baseline value of the basic reproduction number of $R_0=2.6$, under CoMix mixing, this value was reduced to 0.62 for the case of all contacts, and to 0.37 for physical contacts only.

3.2. Age-specific regional information

To explore the dynamics of COVID-19 epidemics and its control using lockdown in regions with difference social structure, we will consider three neighbouring coastal UK regions, namely, West Sussex, Brighton and Hove, and East Sussex. These regions have respective total populations of 858,700, 290,500 and 554,800, median ages 41.1, 35.6 and 42.7 (Office for National Statistics, 2019), and their age distributions are illustrated in Fig. 5 .

Fig. 5.

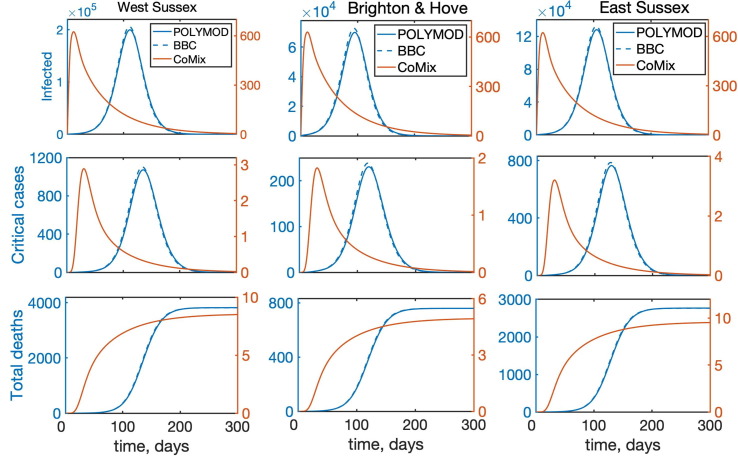
Temporal dynamics of the model (2) with all interactions between individuals for West Sussex, Brighton and Hove, and East Sussex. “Infected” denotes the total number of infected individuals, including asymptomatic, symptomatic, and all who require hospitalisation.

4. Results

For all numerical simulations in this section, we have used the values of parameters as given in Table 1, Table 3, with $K_1=K_2=6$, and the resulting model (2) was solved numerically using a Runge–Kutta-Fehlberg method. As an initial condition we took 100 people incubating the disease, distributed among age classes with proportions being the proportions in each age class, as determined by the actual age distribution for each specific region.

4.1. Effects of mixing matrices and age structure

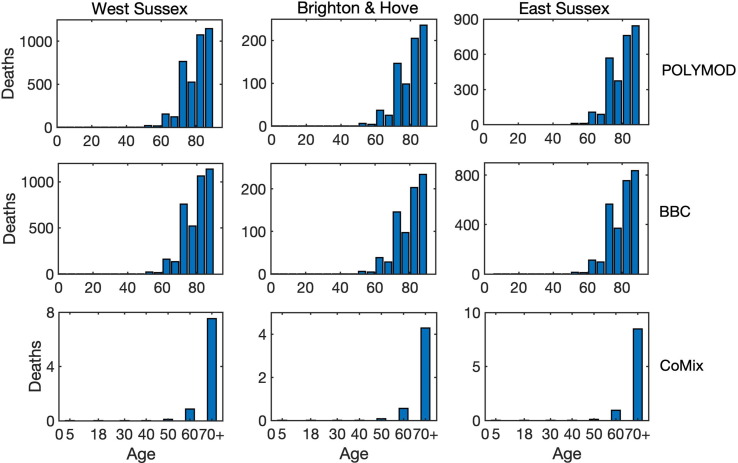
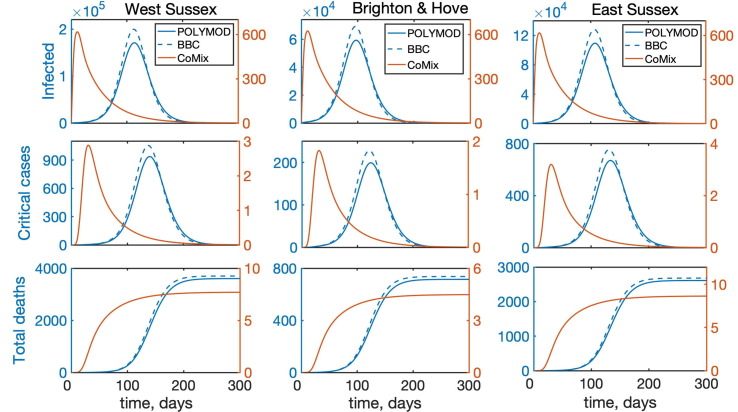
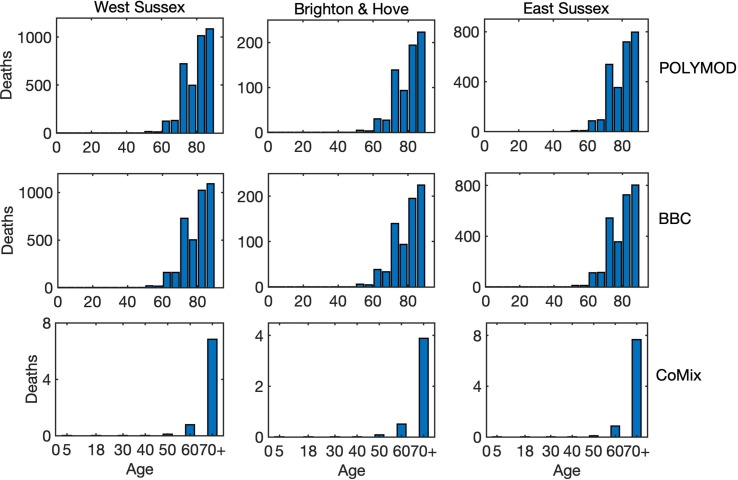
To investigate the role of interactions between different age groups in the dynamics of COVID-19, we have solved the model (2) numerically using each of the three mixing matrices, assuming that they characterise interactions between individuals from the very start of an epidemic until its end. Fig. 5 shows the results of such simulations for the cases, where all types of contacts were included, and the corresponding age distribution of deaths at the end of the epidemic is illustrated in Fig. 6 . We observe that for the more recently obtained BBC-all mixing matrix, the numbers of infected and critical cases are very slightly greater than for the POLYMOD mixing, though the differences are negligibly small. In contrast, for the CoMix mixing, all these numbers are two orders of magnitude smaller, supporting the underlying idea that the CoMix mixing matrix describes a substantially reduced level of interactions between individuals during a lockdown. When one looks only at physical interactions between individuals, as shown in Fig. 7 , the differences between POLYMOD-all and BBC-all mixing become more pronounced, with the numbers of infected and critical cases being higher for the BBC mixing compared to the POLYMOD mixing, though for the total deaths the differences are still very small. The age structure of deaths at the end of an epidemic is qualitatively the same for both all and physical contacts: the numbers of deaths are very small up until around 60 years of age, and after that they are growing, with the highest numbers of deaths observed in the eldest people, as consistent with current data. The underlying reason for this is that, as indicated in Table 3, the rates of hospitalisation, critical care, and fatality all increase with age and are highest for the age groups of 60+. We have explored how the dynamics would change if the initial conditions were to be modified, and the conclusion is that all results would remain effectively the same, with minor changes in terms of shifts in time and in magnitude (See Fig. 8 ).

Fig. 6.

Age distribution of death cases at the end of an epidemic with all interactions between individuals for West Sussex, Brighton and Hove, and East Sussex.

Fig. 7.

Temporal dynamics of the model (2) with account only for direct physical interactions between individuals for West Sussex, Brighton and Hove, and East Sussex. “Infected” denotes the total number of infected individuals, including asymptomatic, symptomatic, and all who require hospitalisation.

Fig. 8.

Age distribution of death cases at the end of an epidemic with only physical interactions between individuals for West Sussex, Brighton and Hove, and East Sussex.

4.2. Effects of timing and duration of lockdown

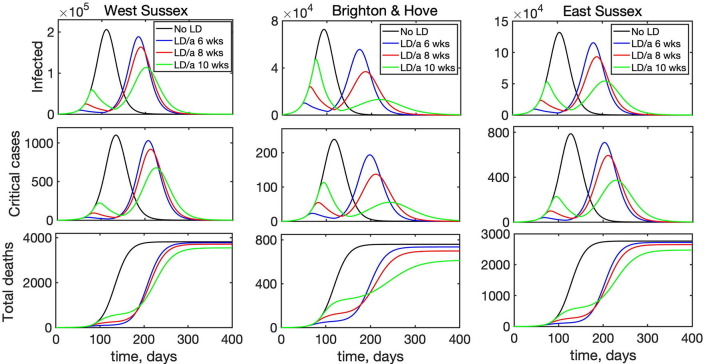
As a next step, we have looked into the effect of introducing lockdown on disease dynamics. Simulations shown in the previous section describe what would happen if the lockdown were introduced from the very beginning of the epidemic and stayed in force for the entire duration of the outbreak. In reality, however, lockdown is normally introduced some time after the start of an outbreak and lifted after a certain period of time, with the conflicting requirements of trying to minimise the number of critical cases and deaths, while also trying to minimise the duration of the lockdown. To model this scenario, we have chosen BBC-all as the underlying matrix describing interactions in the absence of lockdown, and CoMix describing interactions during lockdown. Fig. 9 shows how the disease dynamics changes depending on when the lockdown is introduced relative to the start of an epidemic outbreak, assuming that in all cases the lockdown remains in force for 8 weeks, after which point it is lifted. Although in each case there will be a second epidemic peak after the lockdown is lifted, interestingly and quite counter-intuitively, the later the lockdown is introduced, the smaller will be the maximum of the two peaks, and this reduction becomes quite substantial for lockdowns introduced at a later stage. One possible explanation of this is that if the lockdown is introduced very early on into the outbreak, the number of people who actually have the disease is still relatively small, and as the epidemic goes through its course, if the lockdown is lifted closer to the peak of the epidemic, there will be a large number of infected people in the population, and lifting the lockdown will release a pool of additional susceptibles who can get a disease. In contrast, if the lockdown is introduced later, so that it is lifted after the “natural” peak of the epidemic, the numbers of infected people will already be significantly reduced, so the second peak will be much smaller.

Fig. 9.

Effects of the time of introduction of lockdown on disease dynamics with BBC-all mixing matrix as baseline (black), and lockdown introduced for 8 weeks starting after 6 weeks (blue), 8 weeks (red), or 10 weeks (green).

Another interesting observation is that for the same lockdown duration, the timing may also be important in determining which of the two epidemic peaks will be larger, and this is different for different regions. The reason for the difference between regions is that since the main driving force behind any disease transmission is interactions between individuals, and even for the same mixing matrix these are very strongly determined by the underlying population structure. Fig. 9 indicates that for a fixed-duration lockdown introduced relatively early, i.e. 6 or 8 weeks after the start of an epidemic, in all three regions we have considered the first epidemic peak will be much smaller than the second peak. For a lockdown that is introduced after 10 weeks, the same conclusion still holds for West Sussex and East Sussex, which are both characterised by a significantly older population. In contrast, in Brighton and Hove the second peak is significantly smaller than the first, and this can be attributed to the fact that younger people have a chance to go through the cycle of disease earlier on in the epidemic, and since they are the biggest contributors to disease transmission due to a higher number of their contacts, when the lockdown is lifted, there will be fewer of them capable of transmitting the disease to the rest of the population. At the same time, a reduction in the total number of deaths by the end of en epidemic is much more strongly reduced for lockdowns that are introduced later: it is 7.1–19.5% for an 8-week lockdown introduced after 10 weeks, compared to only 1–3% for a lockdown introduced after 6 weeks). A major implication of this result is that the timing of optimal introduction of a fixed-duration lockdown should be adjusted for each individual region to make it most effective in terms of reducing the number of infections and critical care cases, and to avoid exacerbating the outbreak after the lockdown is lifted. Alternatively, lockdown duration should be sufficiently large, so that it would substantially exceed the time required to reach a natural peak of an epidemic, so that a subsequent lifting of the lockdown would not result in a major resurgence of infections and critical care cases.

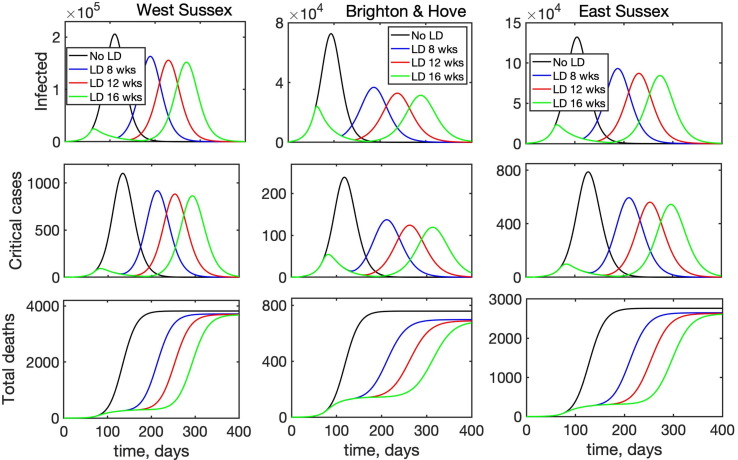
Another question of major research and practical importance is when is most appropriate time to lift lockdown restrictions and to allow people to resume their work and social contacts. To investigate this, we have considered the following scenario: an epidemic starts in a population, whose interactions are described by the BBC-all mixing matrix, then after 8 weeks a lockdown is introduced, which is modelled by the CoMix-all matrix, and the lockdown stays in force for 8, 12, or 16 weeks. At this point the lockdown is lifted, and the population mixing returns to its original state described by the BBC-all mixing matrix. Fig. 10 illustrates the resulting time dynamics of the epidemic, and it shows that in all cases when the lockdown is introduced, the curve is “flattened”, with the peak in the number of infected and deaths being smaller for longer lockdown duration. Since in all three simulated scenarios the lockdown is introduced relatively soon into the outbreak, the second epidemic peak is much higher than the first regardless of how long the lockdown lasts. Also, quite surprisingly, the reduction in the magnitude of the peak in the numbers of infected and critical care cases between an 8-week lockdown and a 16-week lockdown is quite small (5.4–7.4% for infected, and 5–8% for critical care cases), raising the question about practical justification of the longer lockdown. Another observation is that since the lockdown is introduced relatively early on, the difference between different regions becomes less pronounced, though similarly to the above analysis of the timing of the lockdown, we notice that a longer lockdown in Brighton and Hove makes the difference between two epidemic peaks much smaller, while both in West Sussex and East Sussex, the second peak remains significantly larger than the first for any lockdown duration. Interestingly, there are also almost no differences between the total numbers of deaths for different lockdown durations, though an overall reduction compared to a situation without lockdown is notably different for different regions: it is only 2.8–3.7% for West Sussex and 4.2–5.5% East Sussex, compared to 8–11% for Brighton and Hove.

Fig. 10.

Effects of the duration of lockdown on disease dynamics with BBC-all mixing matrix as baseline (black), and lockdown introduced after 8 weeks for 8 weeks (blue), 12 weeks (red), or 16 weeks (green).

5. Discussion

In this paper we have considered the effects of non-exponential distributions of incubation and recovery periods which are suggested by available data, as well as age structure, on dynamics of COVID-19 and its possible containment using lockdown. Numerical simulations of the mean-field model that does not include age-specific differences in disease parameters and contacts has shown that for the same mean incubation and recovery periods, increasing the number of stages of incubation period makes the epidemic reach its peak and die down faster, while increasing the number of stages in the recovery period leads to a significant increase in the maximum total numbers of infected and critical care cases.

Age structure has a major effects on how effective the lockdown is in “flattening the curve”, i.e. in reducing the number of hospitalised and critical care cases. In terms of optimal lockdown timing, if it is introduced for only 8 weeks, introducing it sooner will have a smaller effect on reducing the second peak of infection. In fact, it may even be possible that the second peak will be smaller than the first, but we only observed this for lockdowns that were introduced later in the epidemic. In terms of critical care cases, there is also a notable variation between different regions in terms of whether the second peak is smaller than the first, and by how much it is reduced compared to the case with no lockdown, depending on when a fixed-duration lockdown is introduced. Effectively, this suggests that if the lockdown is introduced for some fixed duration, the timing of its introduction should be adjusted for each particular region to achieve maximum effect, or it should be kept for a sufficiently long time. We have also investigated the potential impact of lockdown duration when it is introduced simultaneously in different regions 8 weeks after the start of an epidemic. The results suggest that changing the lockdown duration from 8 to 12 or 16 weeks does shift the timing of the second peak, but has very little effect on the magnitude of this second peak in terms of either the total number of infected, the number of critical care cases, or deaths. The biggest percentage reduction in these numbers was observed for Brighton and Hove, the region with the youngest population among the three regions we considered.

The model presented in this paper can be made more realistic by including some additional features of disease dynamics, and further details of its progression. One of these includes relaxing the assumption about equality of latency (time from infection to becoming infectious) and incubation (time from infection to displaying symptoms) periods and considering them as two independent parameters. This can be done by means of a more accurate splitting of exposed and infections compartments, clearly separating a latent stage, followed by the pre-asymptomatic infectious stage, followed by the infectious stage, in a manner similar to Davies et al., 2020, Giordano et al., 2020, Tsay et al., 2020. Some other relevant aspects that can be investigated are the inclusion of additional compartments, such as deaths outside hospitals, and analysis of some specific settings in which disease is transmitted, such as care homes, with their particular age-specific contacts. In the end of May/beginning of June 2020, the lockdown in the UK was partially lifted, with some schools being opened, and some groups of people returning to work, while trying to maintain social distance. With children returning to schools, and universities opening, the UK has subsequently experienced another substantial growth in cases of COVID-19, similarly to most other European countries. By November 2020 the numbers of daily confirmed cases have far exceeded numbers seen during the first epidemic wave in April-May 2020 (Worldometer Coronavirus Data, 2021), which necessitated the introduction of another lockdown from 5 November until 2 December 2020. Recent data suggest that by November 2020 only around 4.4% of the UK population have antibody positivity to SARS-CoV-2 (Ward et al., 2020), which means that once the lockdown is lifted in December 2020, there is a potential for another growth in the number of infections, though its magnitude is likely to differ in different parts of the country.

CRediT authorship contribution statement

K.B. Blyuss: Conceptualization, Methodology, Formal analysis, Investigation, Writing - original draft, Writing - review & editing. Y.N. Kyrychko: Conceptualization, Methodology, Formal analysis, Investigation, Writing - original draft, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.