Abstract
Combined quantum mechanical/molecular mechanical (QM/MM) models using semiempirical and ab initio methods have been extensively reported on over the past few decades. These methods have been shown to be capable of providing unique insights into a range of problems, but they are still limited to relatively short time scales, especially QM/MM models using ab initio methods. An intermediate approach between a QM based model and classical mechanics could help fill this time-scale gap and facilitate the study of a range of interesting problems. Reactive force fields represent the intermediate approach explored in this paper. A widely used reactive model is ReaxFF, which has largely been applied to materials science problems and is generally used as a stand-alone (i.e., the full system is modeled using ReaxFF). We report a hybrid ReaxFF/AMBER molecular dynamics (MD) tool, which introduces ReaxFF capabilities to capture bond breaking and formation within the AMBER MD software package. This tool enables us to study local reactive events in large systems at a fraction of the computational costs of QM/MM models. We describe the implementation of ReaxFF/AMBER, validate this implementation using a benzene molecule solvated in water, and compare its performance against a range of similar approaches. To illustrate the predictive capabilities of ReaxFF/AMBER, we carried out a Claisen rearrangement study in aqueous solution. In a first for ReaxFF, we were able to use AMBER’s potential of mean force (PMF) capabilities to perform a PMF study on this organic reaction. The ability to capture local reaction events in large systems using combined ReaxFF/AMBER opens up a range of problems that can be tackled using this model to address both chemical and biological processes.
Graphical Abstract
1. INTRODUCTION
Modeling accurate chemistry of relatively large and complex systems for sufficiently long simulation time scales is essential for computational atomistic modeling tools. Classical molecular mechanics (MM) simulations have proven to be useful for studying complex systems in which no bond breaking or formation is involved. In such methods, empirical force fields (EFF) that can describe the relationship between the geometry and energy of a system with a set of relatively simple potential functions has been used for describing many systems around their equilibrium configuration. However, EFF based methods are unable to simulate chemical reactions due to the rigid connectivity requirement of such methods. Quantum mechanics (QM) methods can mitigate the limitations of EFF based methods such as formation or breaking of bonds and charge fluctuations due to geometry changes. However, QM models are usually applied to fragments of the regions involved in, say an enzymatic reaction, limiting the ability to explore the influence of environmental effects. Although QM based methods can be very accurate in predicting chemical reaction events, they remain limited to small systems simulated over short time scales.
Hybrid quantum mechanics/molecular mechanics (QM/MM) methods were developed to combine the best features of EFF and QM models to tackle a range of chemical problems.1,2 In QM/MM methods, the total system is divided into two separate QM and MM zones. The QM zone is the chemically active region which is treated by a range of QM methods and the rest of the system is the MM zone which is treated using an EFF. Since the introduction of the QM/MM method, various approaches have been implemented, and this method has found extensive applications to deal with complex systems in realistic environments because of the significant reduction in the computational cost compared to pure QM methods.3–7 Different QM/MM simulation tools have long been supported in the AMBER MD package.8,9 Some QM methods including semiempirical neglect of diatomic overlap (NDDO)-type and density functional tight binding (DFTB) are built-in (i.e., internal) and are supported natively within AMBER.10,11 More advanced QM methods are supported via a file-based integration interface to external QM software packages.12,13
Despite highly innovative techniques, algorithmic improvements and fast implementations, the computational cost of the QM region still stands as the rate limiting factor in QM/MM simulations. The Reactive Force Field (ReaxFF) is a potential based on the bond length/bond order concept that bridges QM and MM methods in terms of functionality and computational costs. Importantly, ReaxFF provides a reasonable approximation of reactive phenomena at computational costs comparable to MM methods. In this paper, we report a hybrid ReaxFF/AMBER MD tool, which introduces ReaxFF capabilities to capture bond breaking and formation within the AMBER MD software package. This tool enables us to study local reactive events in large systems at a fraction of the computational costs of QM/MM models.
Another major challenge with atomistic simulations is that chemical reactions through transition states can take place on a time scale that cannot be reached by regular molecular dynamics simulations. Therefore, approaches based on enhanced sampling methods are used to locate the transition state for a chemical reaction using QM/MM methods. Umbrella sampling14 is one of the most well-known enhanced sampling methods and can readily be used in the new ReaxFF/AMBER tool. We use it herein to map out the reaction profile of the Claisen rearrangement as a validation study.
2. BACKGROUND ON REAXFF
ReaxFF is a classical MM model in spirit, which explicitly models chemical reactions based on the bond-length/bond-order concept and dynamic distribution of charges. Similar to nonreactive MM models, ReaxFF consists of two sets of terms: the bonded and nonbonded terms (van der Waals and electrostatic interactions). However, ReaxFF allows bond formation and dissociation, and hence has significantly different bonded terms than classical potentials.
To illustrate the philosophy of the method, we describe the determination of the bond energy using bond orders for carbon and hydrogen (other elements are similarly dependent based on their specific properties), while the structure and definition of the remaining terms can be found in the original description of ReaxFF.15 A single atom type in ReaxFF defines each element, for example, there are no sp, sp2, or sp3 hybridized carbon atoms, but only one carbon atom type. The bond energy (Ebond, eq 1) is described as a function of the sigma , first π and second π bond orders, as well as the corresponding De, pbe1 and pbc2 parameters. The different bond orders themselves are calculated using the pairwise distance (rij) between atoms i–j, the ideal bond distances for atom types of i and j, and the force field specific parameters pbo[1–6] as shown in eq 2. All three terms in eq 2 are considered for a bond between two carbon atoms, while only the first term is used for the σ bond that forms between a carbon atom and a hydrogen atom. However, a pairwise distance-based representation will yield small bond orders between 1 and 3 atoms causing a bond order overestimation between the relevant atoms. A bond order correction (BOij in eq 3) is applied to minimize the long-range bond orders for such situations, where (eq 4) is the deviation of the uncorrected bond order summation from the valence state of an atom (e.g., carbon and hydrogen have valences of four and one, respectively).
| (1) |
| (2) |
| (3) |
| (4) |
During an MD simulation, bond orders are evaluated at each time-step and are used to determine the atomic connectivity within a predefined distance cutoff (typically 5 Å). A time step of 0.25 fs can be used for most simulations, while a smaller time-step is needed for higher temperature studies (>1500K). The energy curves are continuous throughout the simulation process, even at regions involving bond formation/breaking where favorable reactions can automatically occur without any restraints. This is ensured by the inclusion of other bond order related terms (see eq 5). Bond angles (Eval) and torsions (Etor) are evaluated using similar bond order considerations. In a bond order potential, atoms often do not achieve their optimal coordination numbers. Therefore, ReaxFF requires additional abstractions such as lone pair (Elp), over/under-coordination correction (Eover and Eunder), 3-body penalty (Epen) for systems with two double bonds sharing an atom, three-body conjugation term (Ecoa), correction for C2 (EC2), triple bond energy correction (Etriple), and 4-body conjugation (Econj) terms. The potential is summarized below. The detailed expressions for each term can be found in the literature.15
| (5) |
To prevent energy jumps during bond formation/dissociation, there are nonbonded interactions between each atom pair (even for 1–2, 1–3, interactions) in ReaxFF. Electrostatic interactions are represented by a shielded Coulombic term and the van der Waals interaction uses a shielded Morse potential to prevent unrealistic values at very short distances. An important and computationally expensive precursor to the electrostatic interactions is the need to dynamically determine partial charges at every MD step, which is accomplished through charge models (such as QEq16 and EEM17) that require the solution of a linear system of equations. The resulting formulation is complex, but highly flexible and transferable. This allowed ReaxFF to be broadly applicable to a wide range of challenging problems. Developed originally for hydrocarbons;15 the ReaxFF method has been extensively used to investigate complex systems in a wide range of applications including biological systems,18–22 materials,23–29 catalysts,30,31 combustion and batteries.32
In addition to the original Fortran based ReaxFF program,15 ReaxFF is also available in the open-source Purdue Reactive Molecular Dynamics (PuReMD)33,34 package and has been integrated into the open-source large-scale atomic/molecular massively parallel simulator (LAMMPS).35 The ReaxFF method is also available in other important simulation environments, including the Amsterdam Density Functional (ADF)36 program and Materials Studio released under license by Biovia (https://www.3dsbiovia.com), as well as Nanohub (http://www.nanohub.org).
3. THE REAXFF/AMBER INTEGRATION
Similar to QM/MM methods, atoms are split into three categories in the ReaxFF/AMBER method: (i) ReaxFF atoms, which include all atoms in the chemically reactive region and are handled by a ReaxFF implementation, (ii) the ReaxFF/MM transition atoms, which include all atoms within a certain cutoff of the ReaxFF region and is handled by ReaxFF and AMBER collaboratively, and (iii) the MM atoms, which include all remaining atoms and is handled exclusively by AMBER. These categories are illustrated in Figure 1 with sphere-like shapes, but these regions can obviously be of any shape. In what follows, we describe the implementation of the ReaxFF/AMBER method.
Figure 1.
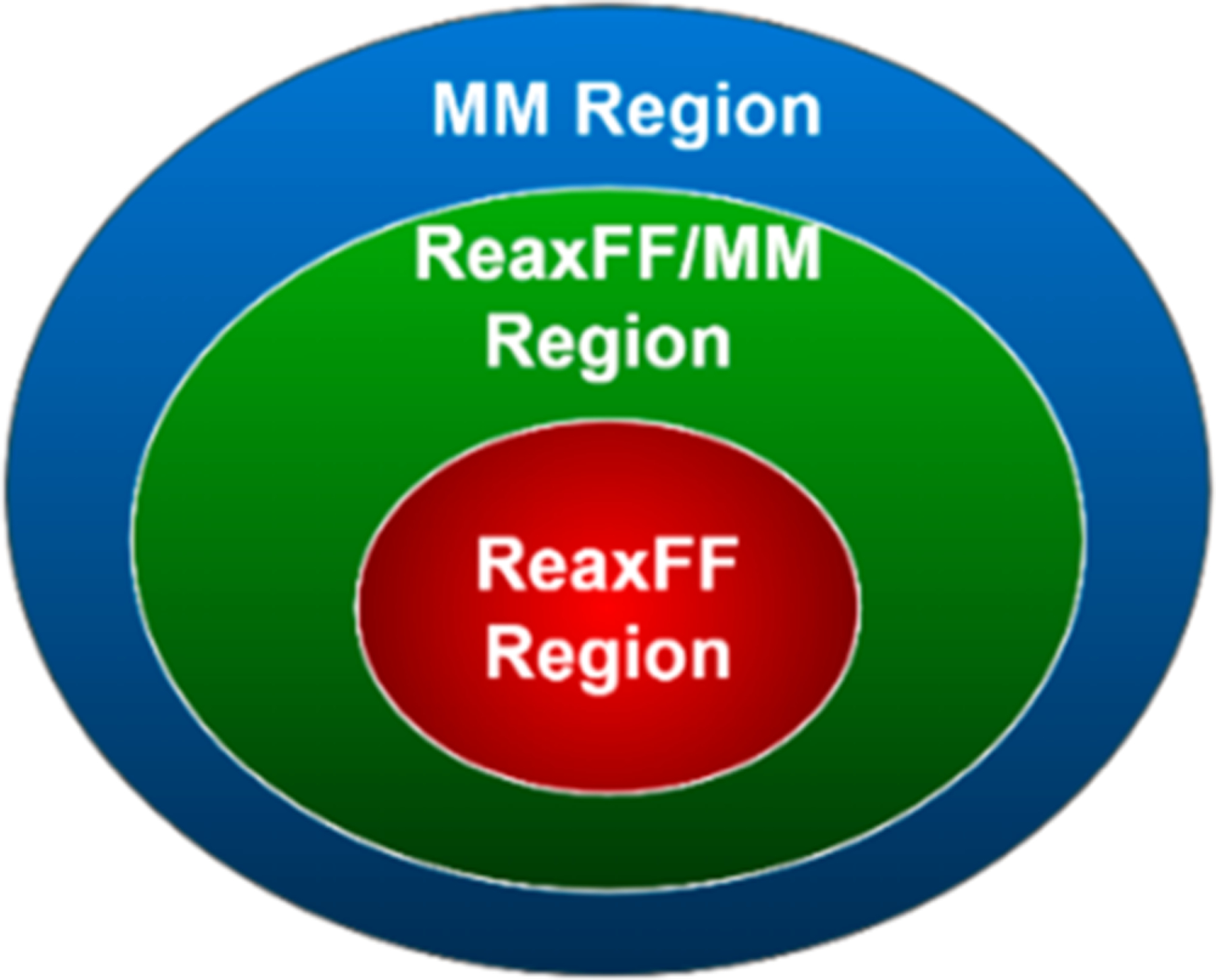
ReaxFF/AMBER regions in the integration implementation.
3.1. Implementation.
AMBER is the simulation driver in the ReaxFF/AMBER MD integration. After AMBER categorizes atoms into their respective groups, it sends all relevant information for ReaxFF and ReaxFF/MM atoms to the ReaxFF program. The ReaxFF/AMBER tool currently uses the external model interface; that is, the necessary data transfers between ReaxFF and AMBER are performed using file-based data exchange. Therefore, after AMBER completes writing the data exchange files, it launches the ReaxFF program as an external binary and waits for its output files. The ReaxFF program then runs a zero-step nonperiodic simulation to calculate the dynamic charges, energies, and forces on the ReaxFF and ReaxFF/MM atoms. Upon completion, it writes this information back into another file which is finally read by AMBER to complete the energy and force computations for the ReaxFF/MM and MM regions.
In implementing the interface between the ReaxFF and AMBER programs, we have adopted the following procedure for a successful hybrid model:
Dynamic charges on ReaxFF atoms are calculated under the influence of ReaxFF/MM atoms with static charges.
All ReaxFF interactions (as given in eq 5 above) between ReaxFF–ReaxFF pairs are calculated without any modifications.
Electrostatic interactions between ReaxFF (w/dynamic charge)-ReaxFF/MM (w/static charge) atom pairs are calculated by ReaxFF.
van der Waals interactions between ReaxFF–ReaxFF/MM atom pairs are handled by AMBER (e.g., using a Lennard-Jones potential).
Interactions between MM-ReaxFF/MM and MM-MM pairs are handled by AMBER as usual.
We should note that there are some limitations of the current ReaxFF/AMBER tool. Now, only systems with noncovalent bonds between ReaxFF and ReaxFF/MM regions can be studied. Also, only shared memory parallelism can be leveraged for the time-being. Nevertheless, as we demonstrate below, the current implementation serves as a proof-of-concept on the feasibility and advantages of this approach.
3.2. Dynamic Charges with the Modified Electronegativity Equalization Method (mEEM).
Since we allow the statically charged MM and transition region atoms to polarize the ReaxFF atoms, the dynamic charge model used by ReaxFF needs to be modified. As mentioned previously, ReaxFF can use the charge equilibration (QEq) or electronegativity equalization method (EEM) to determine the charges. Our current implementation is based on EEM. Before describing the necessary modifications, we briefly discuss the EEM charge model that is currently used by ReaxFF/AMBER.
The EEM charge model29 relies on the principle that charges should be distributed on atoms to satisfy constraints for both the net system charge and the equalized atom electronegativities. Let atomic charges be q = (q1, q2, …, qn) and the positions be R = (r1, r2, …, rn), where qi ∈ R and ri ∈ R3. On the basis of Sanderson’s Electronegativity Equalization Principle,37 the electronegativity of all atoms needs to be equalized
where ϵi is the electronegativity of atom i and is the average molecular electronegativity. The other constraint forces the sum of the atomic charges to be equal to the given net system charge
The constraints and the parametrized interatomic interactions can be merged into the following linear equation where the charges q are the solution of:
Here, χ is an n by 1 vector of atomic electronegativities, and the Hij values, that is, individual elements of the n by n H matrix, are defined as δijηi + (1 – δij)Fij, where δij is the Kronecker delta operator, ηi is the idempotential, and Fij is defined as
In the equations above, is the distance between atoms i and j, rnonb is the cutoff radius, is a pairwise shielding term tuned for element types of atoms i and j to avoid unbounded electrostatic energy at short distances, and is the dielectric constant of the medium. It has been demonstrated that the EEM model reproduces QM calculated Mulliken charges.38
To account for the polarization effect of the transition region atoms on the core ReaxFF region, we introduce the ReaxFF/AMBER atoms as particles with fixed charges to the EEM solver. This is done by modifying the system of equations as follows. Assuming that there are c ReaxFF atoms and t transition region atoms, then Hcore ∈ Rc×c captures the interactions within the core ReaxFF region and Hcore-trans ∈ Rc×t captures the impact of the transition region atoms on the ReaxFF atoms.
Since a direct solution of the above linear system scales cubically with the number of total atoms, typically iterative solvers are used to obtain approximations to the optimized dynamic charges. In such an iterative scheme, we only evolve the charges on the core atoms as qtrans are fixed values given in the MM force field. As such, the rows corresponding to the transition region atoms can be ignored in the above linear system, and we obtain
Since qtrans is fixed, it can be rearranged as
These modifications ensure that the existence of the fixed charges does not slow down the charge equilibration step since the fixed charges and dynamic charges are separated. See Supporting Information (S1) for an example.
The modifications above are sufficient to run nonperiodic ReaxFF/MM simulations, as well as periodic boundary simulations without long-range electrostatic interactions. When running periodic boundary simulations with long-range electrostatic interactions AMBER uses the particle mesh Ewald (PME) approach which calculates interactions within a certain cutoff distance directly and approximates the rest over a mesh.39 To be able to account for the long-range interactions in EEM, we have incorporated the impact of the mesh points on ReaxFF atoms by further extending the EEM matrix, that is, by adding a column and row containing the effects of the mesh points. This scheme does not conserve the energy in NVE simulations with periodic boundaries because ReaxFF uses tapered electrostatic interactions40 that force the Coulomb effects to slowly decay to 0 at the interaction cutoff radius which is typically set to 10–12 Å (see SI, Figure S1). Tapering of the Coulomb interactions is a built-in feature of the ReaxFF formulation, and existing ReaxFF parameter sets have been trained with this design principle in mind. We believe that by retraining ReaxFF parameters without tapered Coulomb kernels, periodic boundary simulations with PME can successfully be enabled, but doing so goes beyond the scope of this paper, so we leave it as a topic for further exploration.
3.3. Validation.
For validation of the resulting ReaxFF/AMBER combination, we performed experiments using benzene-in-water systems, one with periodic boundary conditions, and one without (Figure 2). Benzene is not reactive in water, but the goal of these computational experiments was to validate that the ReaxFF/MM method can achieve energy conservation and produce reasonable dynamic charges.
Figure 2.
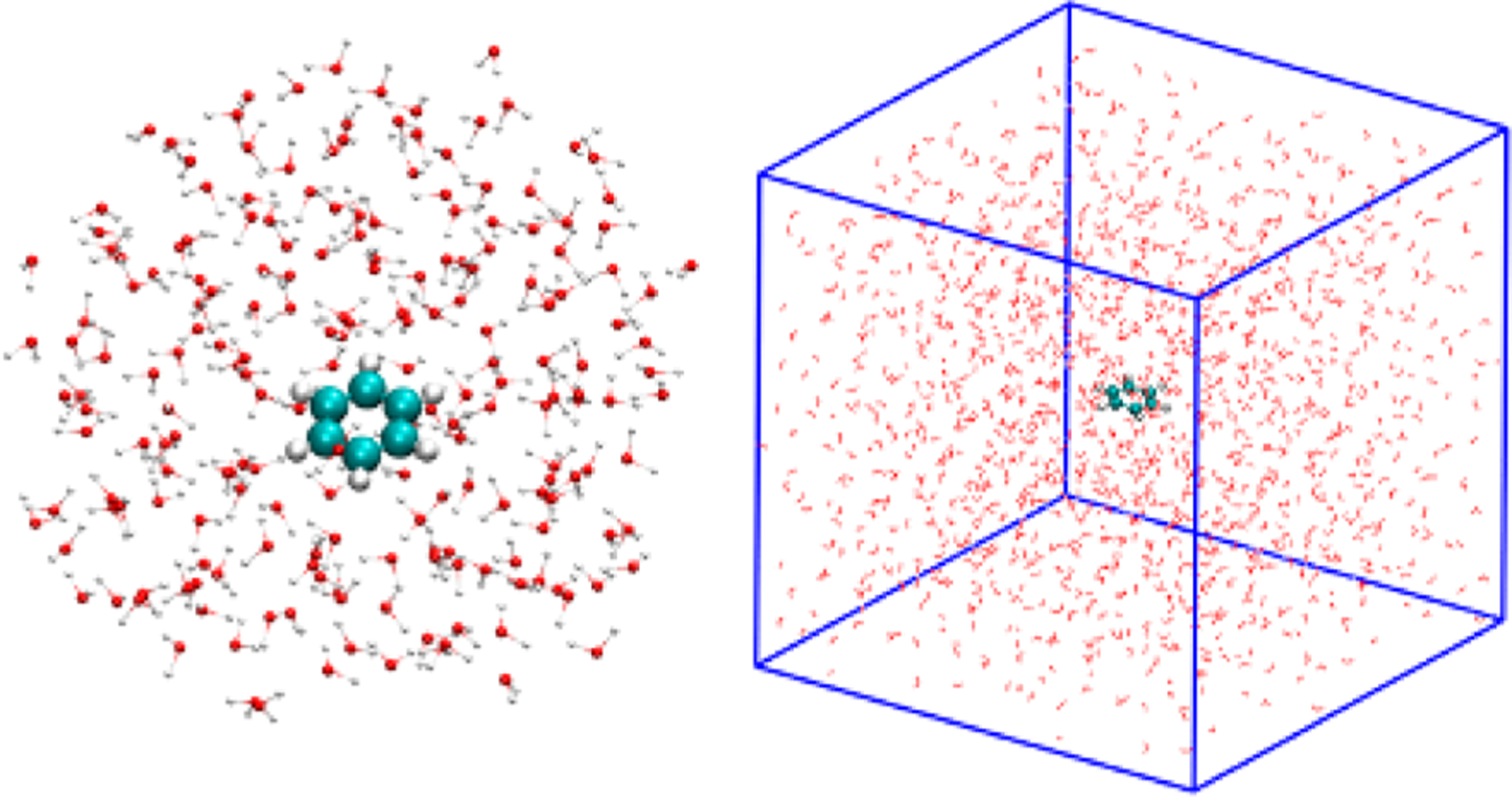
(Left) ReaxFF Benzene in a TIP3P water droplet with a total of 627 atoms, (right) ReaxFF Benzene in a TIP3P water box with a total of 4398 atoms.
For both simulations (nonperiodic and periodic), the systems are first energy-minimized and then heated to 300 K using the Berendsen thermostat in AMBER. Finally, ReaxFF/MM NVE simulations are run using a time step of 0.25 fs to check energy conservation and charges. A relatively short time step was chosen as this is the recommended setting for ReaxFF simulations, especially in the presence of H atoms. For all simulations, the SHAKE algorithm was turned off.
As shown in Figure 3, the energy is conserved for both simulations. Figure 4 shows the carbon and hydrogen charges for Reax atoms (denoted as Reax-C and Reax-H, respectively), as well as the average across all C and H atoms in a time step (denoted as Reax-C-Avg and Reax-H-Avg, respectively). As can be seen, dynamic charges produced by ReaxFF/MM under the influence of statically charged transition region atoms are in line with the carbon and hydrogen charges given in the AMBER force field for benzene (denoted as AMBER-C and AMBER-H, respectively).
Figure 3.
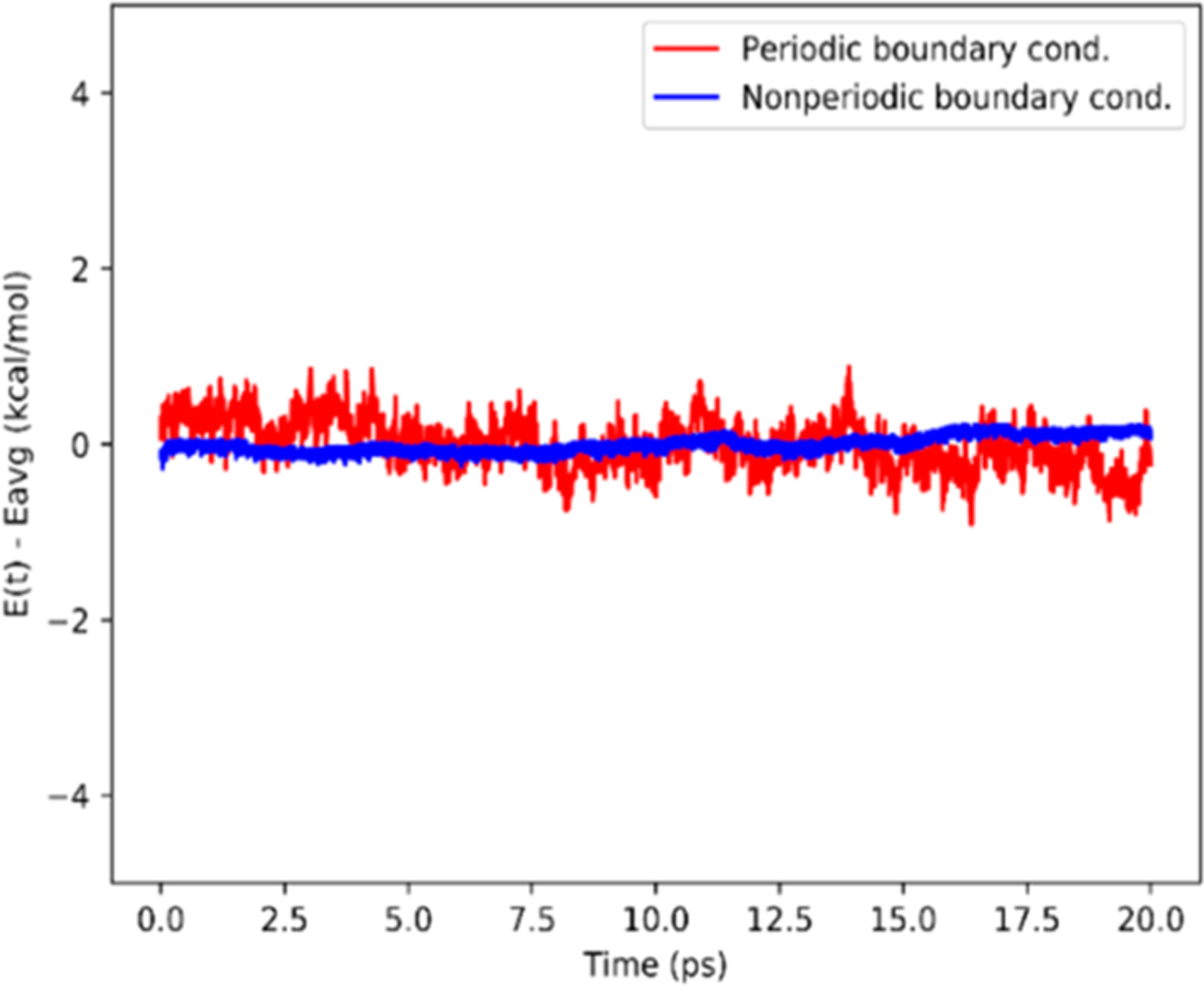
Simulation of a benzene molecule in water using the TIP3P water model and NVE ensemble. A time step of 0.25 fs was used. (Blue) Nonperiodic boundary condition with an infinite cutoff. (Red) Periodic boundary condition with a QM cutoff of 10 Å (qmcut = 10 Å) and ReaxFF/PME interaction turned off (qm_pme = 0).
Figure 4.
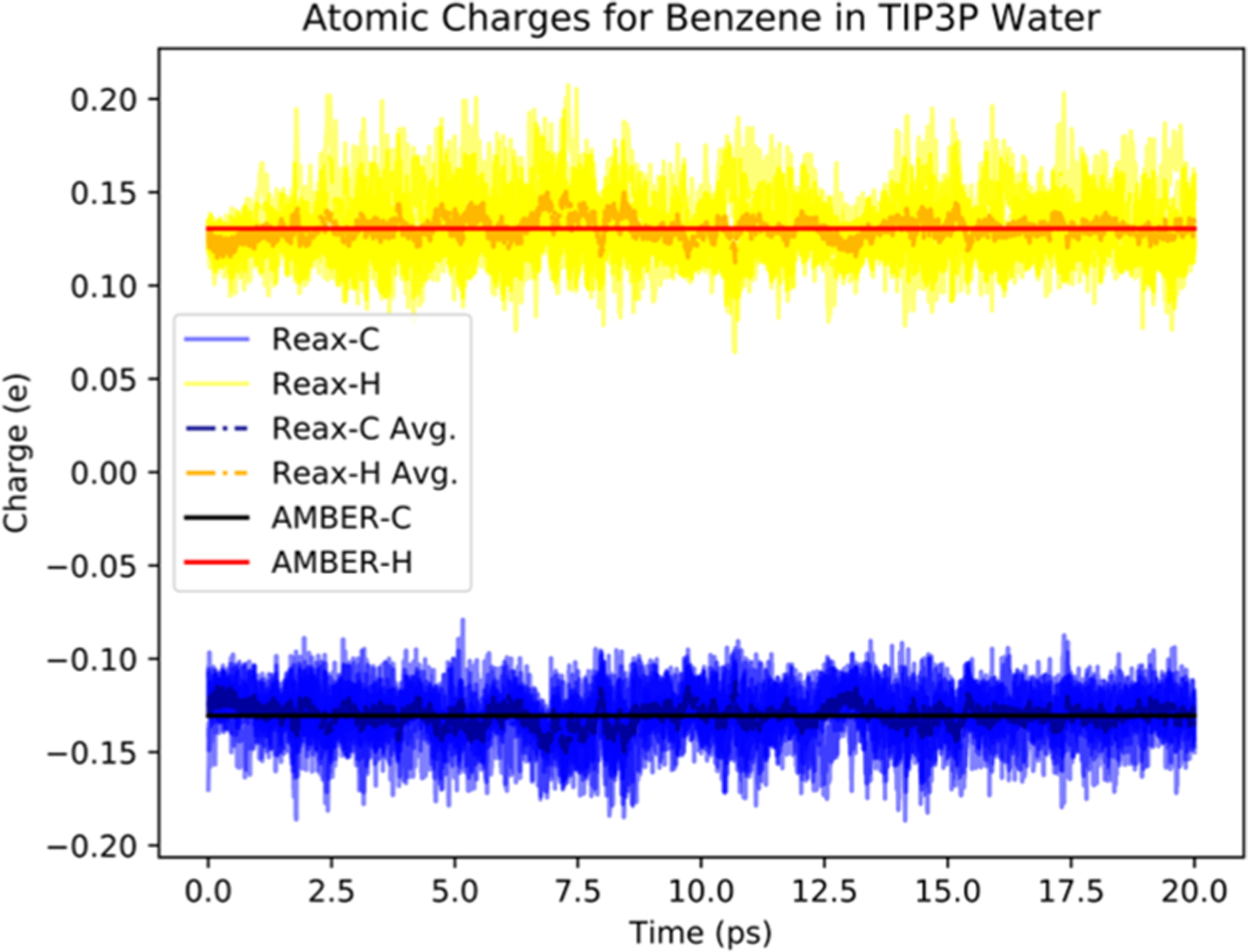
Dynamic ReaxFF charges and fixed AMBER charges with a ReaxFF/MM simulation of a benzene molecule in water with periodic boundary conditions using parameters qmcut = 10 A and qm_pme = 0
3.4. Performance Analysis.
As mentioned before, the motivation for the ReaxFF/MM method is that it can significantly reduce the computational time that would be needed by a comparable QM/MM simulation. To illustrate this, we benchmarked the computational cost of separate equilibration simulations of allyl vinyl ether (AVE) which consists of 14 atoms using ReaxFF, PuReMD, SCC-DTFB, PM3, MM, the Hartree–Fock method (HF), and density functional theory (DFT) using the B3LYP functional. The HF and DFT calculations used the 6–31G* basis set. The benchmark simulations were performed using standalone ReaxFF, PuReMD, AMBER, and the QUICK software package41 in sequential execution mode on an Intel Xeon E5–2670 v2 CPU which runs at 2.50 GHz. The benchmarked time per simulation steps are shown in Table 1.
Table 1.
Sequential Execution Time in Seconds Per Time Step and Nanoseconds Per Day for SCC-DFTB, PM3, ReaxFF, PuReMD, MM, HF, and DFT Calculationsa
| method | seconds/iteration (relative wrt MM) | time step (fs) | ns/day (relative wrt PuReMD) |
|---|---|---|---|
| SCC-DFTB | 3.088 × 10−3 (39.8) | 0.5 | 13.99 (0.2) |
| PM3 | 1.83 × 10−3 (23.6) | 0.5 | 23.61 (0.4) |
| ReaxFF | 6.25 × 10−4 (8.1) | 0.25 | 34.56 (0.6) |
| PuReMD | 3.63 × 10−4 (4.7) | 0.25 | 59.50 (1.0) |
| MM | 7.75 × 10−5 (1.0) | 1 | 1114.84 (18.7) |
| HF | 1.833 (23,651.6) | ||
| DFT | 2.762 (35,638.7) |
B3LYP functional and the 6–31G* basis set were used for the HF and DFT geometry optimization calculations.
In Table 1, PuReMD refers to a C language based efficient parallel implementation of the original ReaxFF implementation in Fortran. Time steps of 1 fs for MM, 0.5 fs for SCC-DFTB and PM3, and 0.25 fs for ReaxFF calculations are assumed for these benchmark calculations. These benchmark data show that ReaxFF method can be ~2–5 times faster than PM3 or SCC-DFTB methods, 3 orders of magnitude faster than HF or DFT methods, and ~18 times slower than conventional molecular mechanics methods. Therefore, ReaxFF can offer an alternative for QM/MM calculations to handle larger complex systems at longer time scales.
Currently, ReaxFF/AMBER software uses the original Fortran ReaxFF code through a file-based data exchange interface. We analyzed the computational performance of the ReaxFF/AMBER software with the nonperiodic benzene-in-water simulation for 1000 steps using an infinite electrostatic interaction cutoff. The timing breakdown shown in Figure 5 is averaged over the course of this simulation. Please see SI section 3 for specifications of the hardware and software used in these computational experiments.
Figure 5.
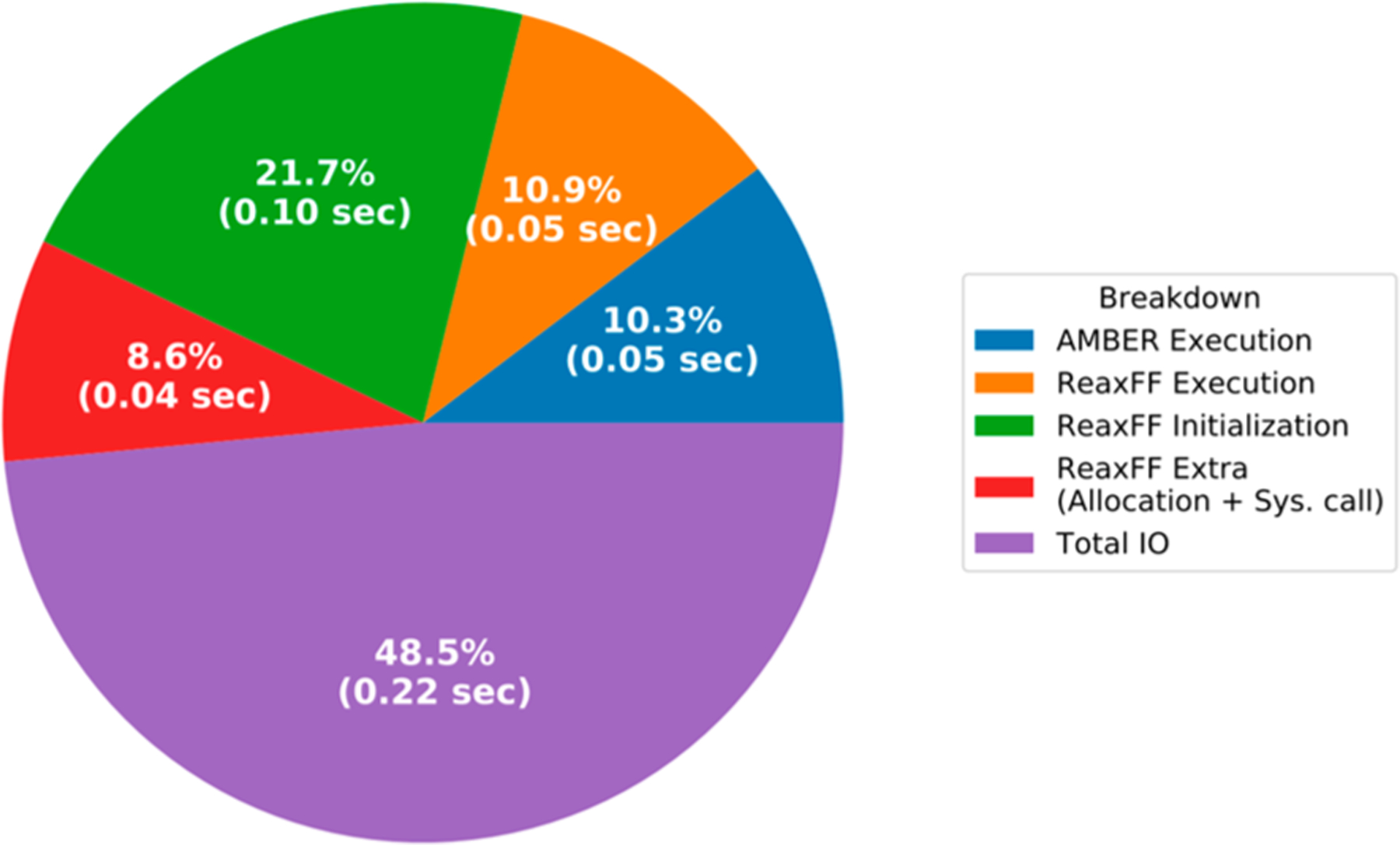
Breakdown of the total execution time of ReaxFF/AMBER software for the benzene-in-water simulation into its main components. The total time spent per step is 0.46 s.
Since the data exchange between ReaxFF and AMBER is file based, it requires the writing and reading of files at every simulation step. There are also the additional costs associated with launching the ReaxFF program as an external binary. Finally, the modifications to the standalone ReaxFF implementation is minimal and for that reason, ReaxFF allocates and initializes various data structures at every time step. Time spent on the I/O and system calls to the external program will be removed by introducing array-based data exchanges between the relevant ReaxFF and AMBER subroutines. Additionally, by keeping the data structures in memory persistently and reusing them at each time step, we could eliminate most of the time spent on the allocation and initialization parts. When all these potential updates are considered, the ReaxFF/AMBER software would be accelerated significantly beyond what is shown here because only 10.9% of the overall time is spent on the necessary ReaxFF calculations (see Figure 5).
4. CLAISEN REARRANGEMENT SIMULATIONS WITH REAXFF/AMBER
To demonstrate the capabilities of the new ReaxFF/AMBER integration, we carried out ReaxFF/MM modeling of the classic Claisen rearrangement of allyl vinyl ether (AVE) solvated in an explicit TIP3P water model42 as shown in Figure 6. Since the Claisen rearrangement is a well-studied reaction,43,44 it was chosen to evaluate the chemical accuracy of our new method. In these simulations, the solvent is treated by AMBER using the TIP3P water model and the reactant AVE is treated with ReaxFF. No covalent bonds cross the ReaxFF/AMBER boundary.
Figure 6.
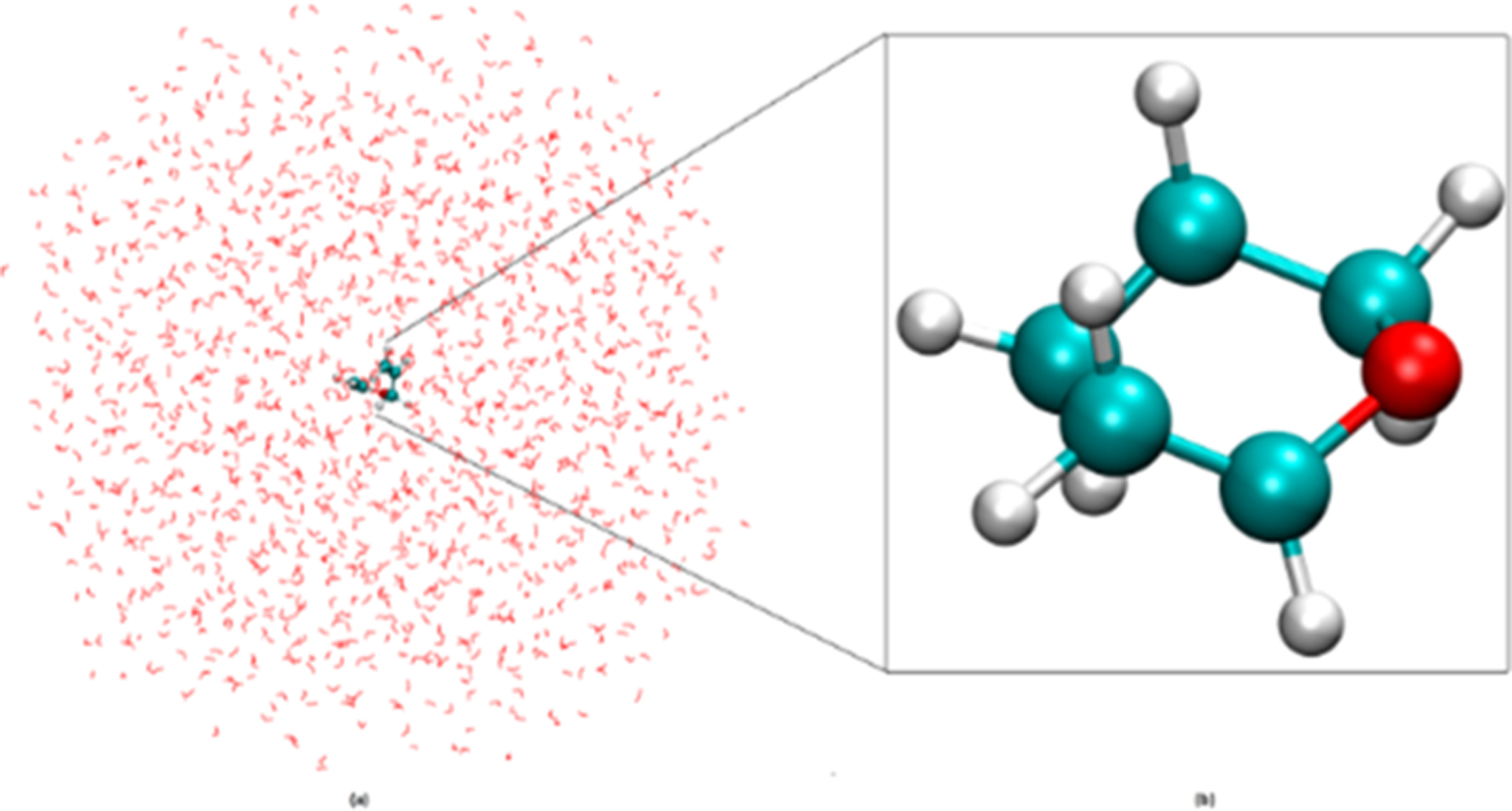
(a) Solvation of allyl vinyl ether (AVE) in octahedral TIP3P water with total number of 4319 atoms. (b) Molecular structure of AVE.
4.1. ReaxFF Parameter Optimization.
The existing ReaxFF force field45 was tested for simulating the Claisen rearrangement. The initial tests showed that the system got trapped in a local minimum after reaching the transition state (TS), and therefore a proper Claisen rearrangement could not be observed (Figure 7).
Figure 7.
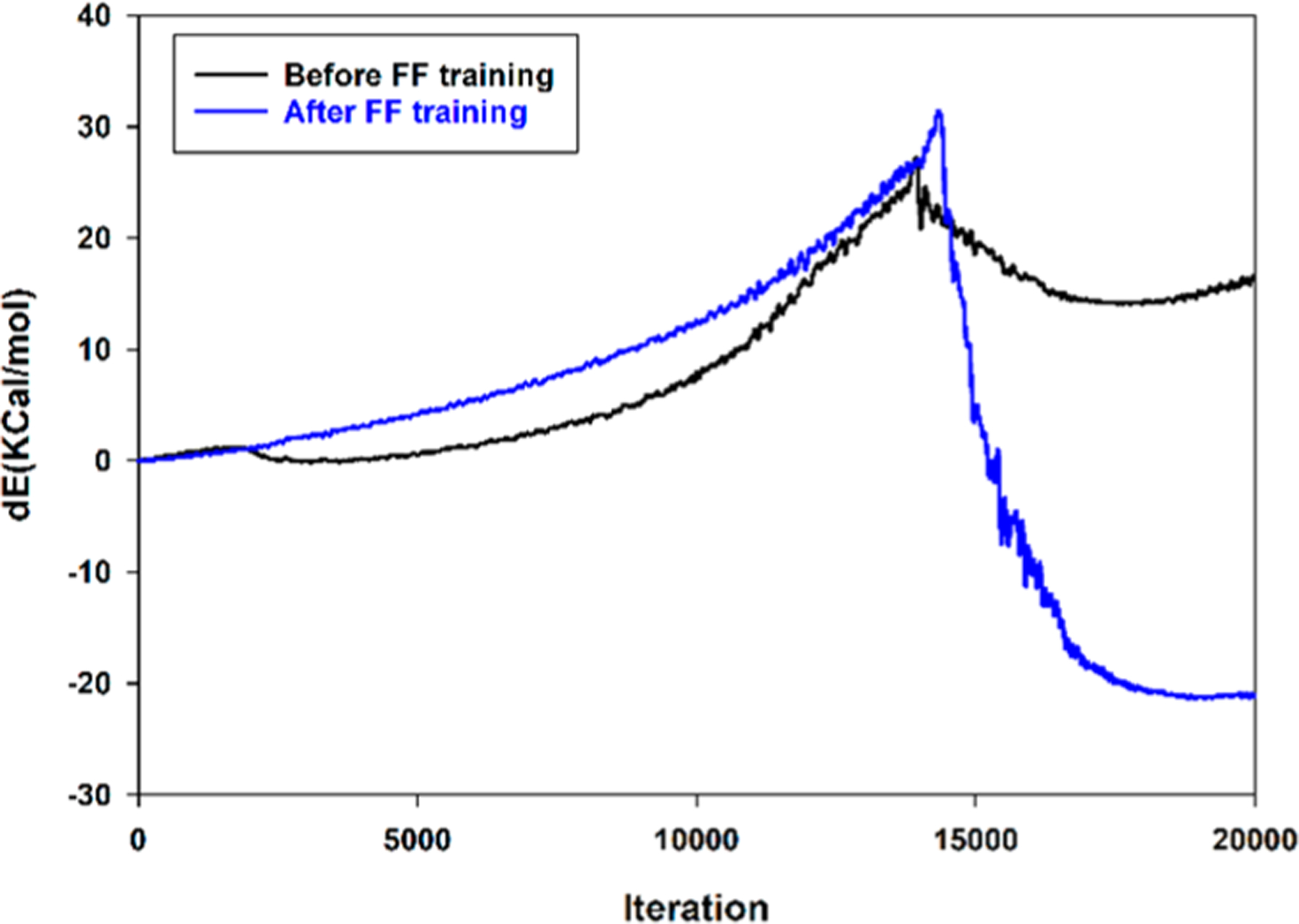
Claisen rearrangement of AVE in vacuum using original and trained ReaxFF force fields. The original force field leads to getting trapped in local minimum.
To resolve this, ab initio QM data for the Claisen rearrangement of AVE in vacuum were generated. The intrinsic reaction coordinate (IRC) method was used to obtain QM data from two different chair-like and boat-like transition states. All the optimization and IRC calculations were done with the Gaussian 16 package.46 B3LYP functional and the 6–31G* basis set were used for the calculations. Through IRC calculations, a Claisen rearrangement transition of all chair-like and boat-like configurations and the energy changes were recorded. Comparison of these QM data against the initial ReaxFF force field results are shown in Figure 8a. These initial energy differences and the failure of the initial force field in capturing the Claisen rearrangement indicated the requirement of force field training against the generated QM data. The training data used for optimizing a ReaxFF parameter set can include QM data on charges, heat of formations (kcal/mol), energy minimized geometries (in angstrom or degree), lattice cell parameters (in angstrom or degree) and relative energies (kcal/mol). All the training data are added to the training set and the force field is reparametrized to minimize the error function:
where xi,QM and xi,ReaxFF are the QM and ReaxFF values of the ith entry of the training set, respectively, and σi are weight parameters that determine the desired accuracy for individual training data items. Force field parameters which are designated to be tuned are defined in a separate input file. The ReaxFF training feature in the standalone Fortran code then uses a line search scheme to optimize each parameter to be tuned one at a time. The force field training input files and force field parameters resulting from this optimization procedure are supplied in the SI.
Figure 8.
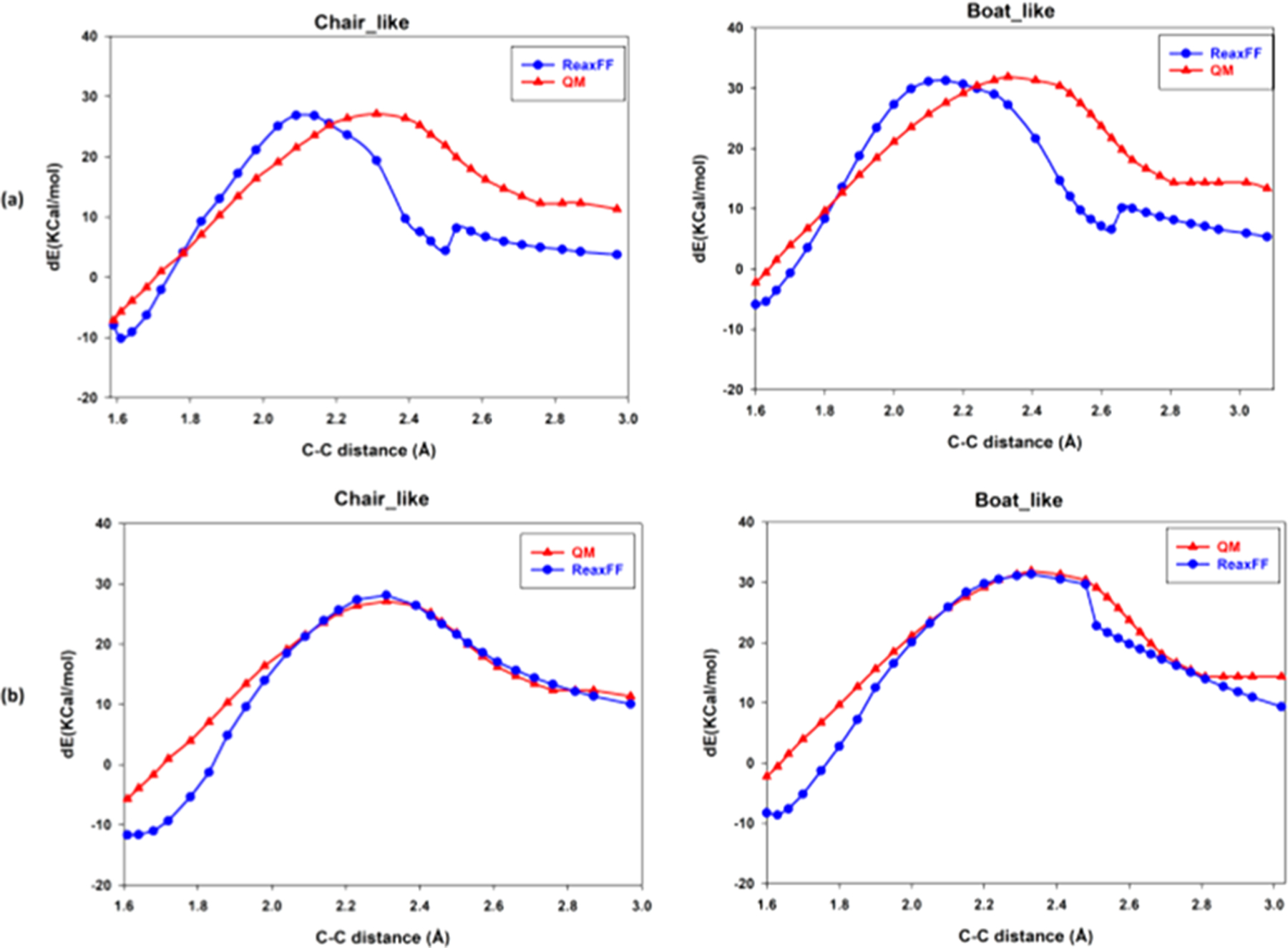
(a) QM (B3LYP/6–31G*) vs original ReaxFF force field results for the Claisen rearrangement of chair-like and boat-like structures. (b) QM (B3LYP/6–31G*) vs trained ReaxFF force field results for the Claisen rearrangement of chair-like and boat-like structures. The energies are with respect to the completely open AVE geometry optimized energy as the reference.
Figure 8b shows the results of our fitting against QM data for chair-like and boat-like transition states. Evaluation of the new force field after training showed satisfactory behavior in capturing the Claisen rearrangement in vacuum (Figure 7). Therefore, this updated ReaxFF force field was used to perform free energy calculations of the Claisen rearrangement of AVE in the presence of explicit TIP3P water using ReaxFF/AMBER.
4.2. Free Energy Calculation with Umbrella Sampling.
The MD driver in the ReaxFF/AMBER integration scheme is AMBER. Hence, we can use all of AMBER’s advanced sampling techniques. One such feature is the umbrella sampling free energy calculation technique. Using the newly optimized parameter set, AMBER’s umbrella sampling feature coupled with the weighted histogram analysis method (WHAM) was used to generate the potential of mean force (PMF) of this reaction with ReaxFF/AMBER. The reaction coordinate chosen for the umbrella sampling simulations was the distance between two terminal AVE carbon atoms referred to as the C1–C5 distance (Figure 9).
Figure 9.
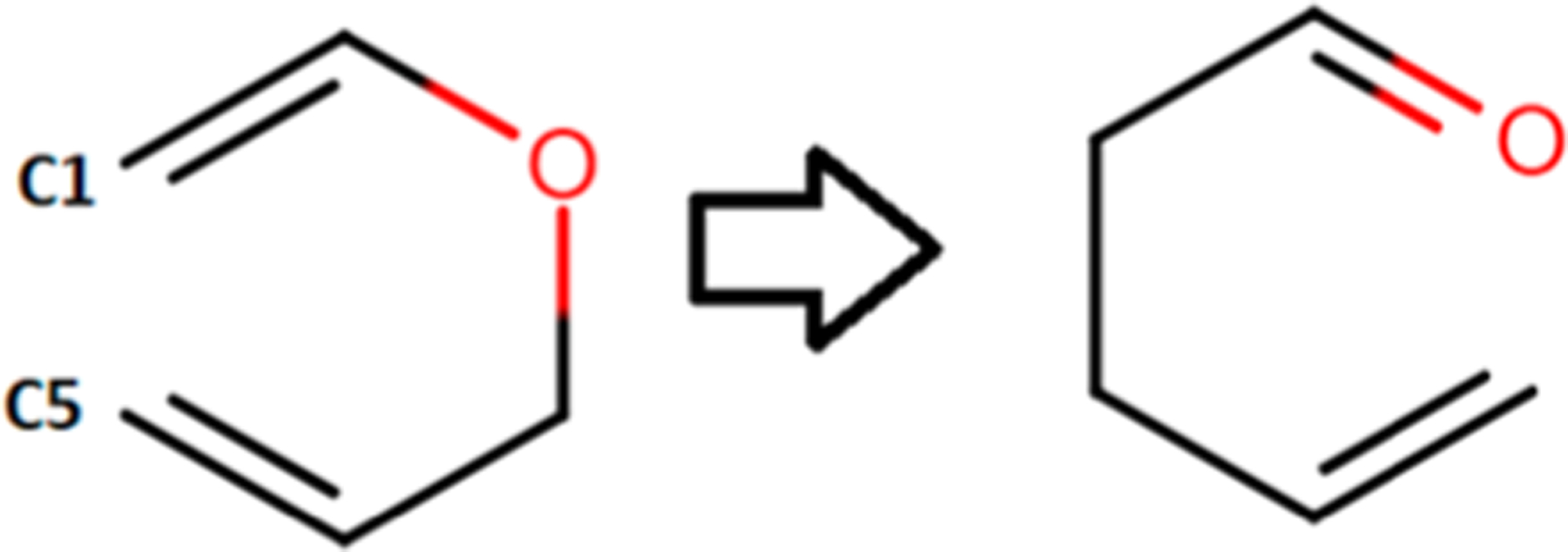
Claisen rearrangement of AVE while C1–C5 distance is changed from 3.5 to 1.6 Å.
A series of harmonic potentials were used to constrain the reaction coordinates to the defined windows. The C1–C5 distance was varied from 3.5 to1.6 Å. For the regions near the transition state (1.7–2.4 Å), 1000 kcal/mol·Å2 was used to obtain enough sampling for each window, and for the regions far from the transition state (1.6–1.7 Å and 2.4–3.5 Å) a weaker restraint (200–700 kcal/mol.Å2) was used. For the 1.6–3.0 Å range, 0.02 Å window intervals were defined and for the 3.0–3.5 Å range, 0.1 Å window intervals were defined. In total, 81 windows were created for sampling, while varying the C1–C5 distance from 3.5 to1.6 Å. All simulations were performed using the TIP3P rigid three site point charge water model. AVE was solvated in an octahedral box of TIP3P water molecules of 25 Å radius. All simulations were performed with periodic boundary conditions. The topology files for AVE were created using the general AMBER force field (GAFF).47 AMBER MM simulations using periodic boundary conditions were performed with a 10 Å cutoff for the real space nonbonded interactions, and the particle mesh Ewald (PME) algorithm was incorporated to account for long-range electrostatics beyond the cutoff.
After 2000 steps minimization in each window, we ran 25 ps NPT (constant number of atoms, constant pressure and constant temperature) equilibration using constant pressure Langevin dynamics with the Berendsen barostat at 300 K and 1 atm. The shake algorithm was enabled for these simulations in the MM region, and the time step of 0.25 fs was chosen for both ReaxFF (no shake) and AMBER regions. Data collection for umbrella sampling was started after the equilibration phase for 5 ps in each window. Umbrella sampling consisted of data collection from separate windows of the reaction coordinate simultaneously. By defining proper harmonic restraint constants in each window, we allowed neighboring windows to overlap and ensured there were enough windows to cover the entire reaction coordinate space. Data sampling were performed every 0.0125 ps of the production stage of umbrella sampling simulations. Finally, the PMF was calculated by combining the data from each window using WHAM.
4.3. Results and Discussion.
To evaluate the potential of mean force (PMF) variations as a function of the reaction coordinate defined for the Claisen rearrangement, umbrella sampling calculations were employed. As mentioned, the simulations in different windows needed to be such that we could observe convergence on sampling to complete the umbrella sampling calculations. To make sure that all the windows overlap properly before performing the WHAM calculations, the histograms of all windows were generated (Figure 10). This plot shows that there was proper overlap and no obvious gaps were observed. Using this data set, we used WHAM to construct the PMF of the Claisen rearrangement.
Figure 10.
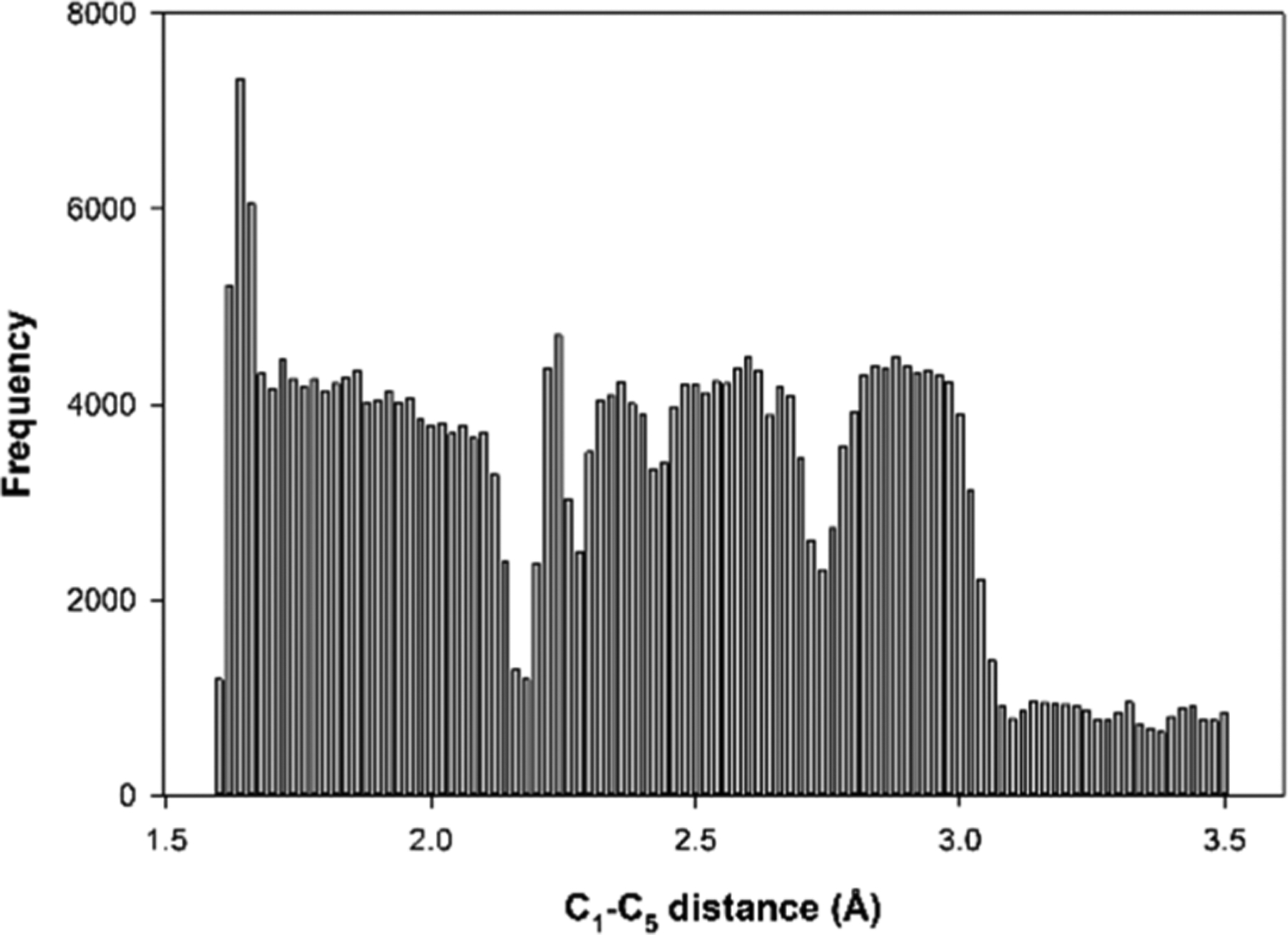
Histogram of C1–C5 distance samplings from the umbrella sampling windows. The C1–C5 distance was varied from 3.5 to 1.6 Å. For the regions far from the transition state (1.5–1.7 Å and 2.4–3.5 Å) a weaker restraint (200–700 kcal/mol·Å2) was used and for the regions near the transition state (1.7–2.4 Å) a stronger restraint (1000 kcal/mol·Å2) was used. For the 1.6–3.0 Å range, 0.02 Å interval windows were defined and for 3.0–3.5 Å windows interval of 0.1 Å were defined.
The PMF obtained from umbrella sampling calculations is shown in Figure 11. The calculated PMF can be used to evaluate the Claisen rearrangement barrier height and the transition state configuration. A barrier height of 34.8 kcal/mol was obtained from these calculations. We also utilized an implementation of the self-consistent charge density functional tight-binding (SCC-DFTB) method, which is a semiempirical method based on density functional theory (DFT),48 and also semiempirical neglect of diatomic overlap (NDDO) PM3 method49 as part of the QM/MM support in the AMBER 18 MD program to perform calculations on the Claisen rearrangement. Also, another SCC-DFTB QM/MM umbrella sampling PMF calculation using the SPC/E water model was performed to evaluate the impact of the water model on this simulation. The results of all these PMF calculations are shown in Figure 11. The transition configuration of these different methods are shown in Figure S3. ReaxFF/AMBER integration successfully captured the Claisen rearrangement reaction.
Figure 11.
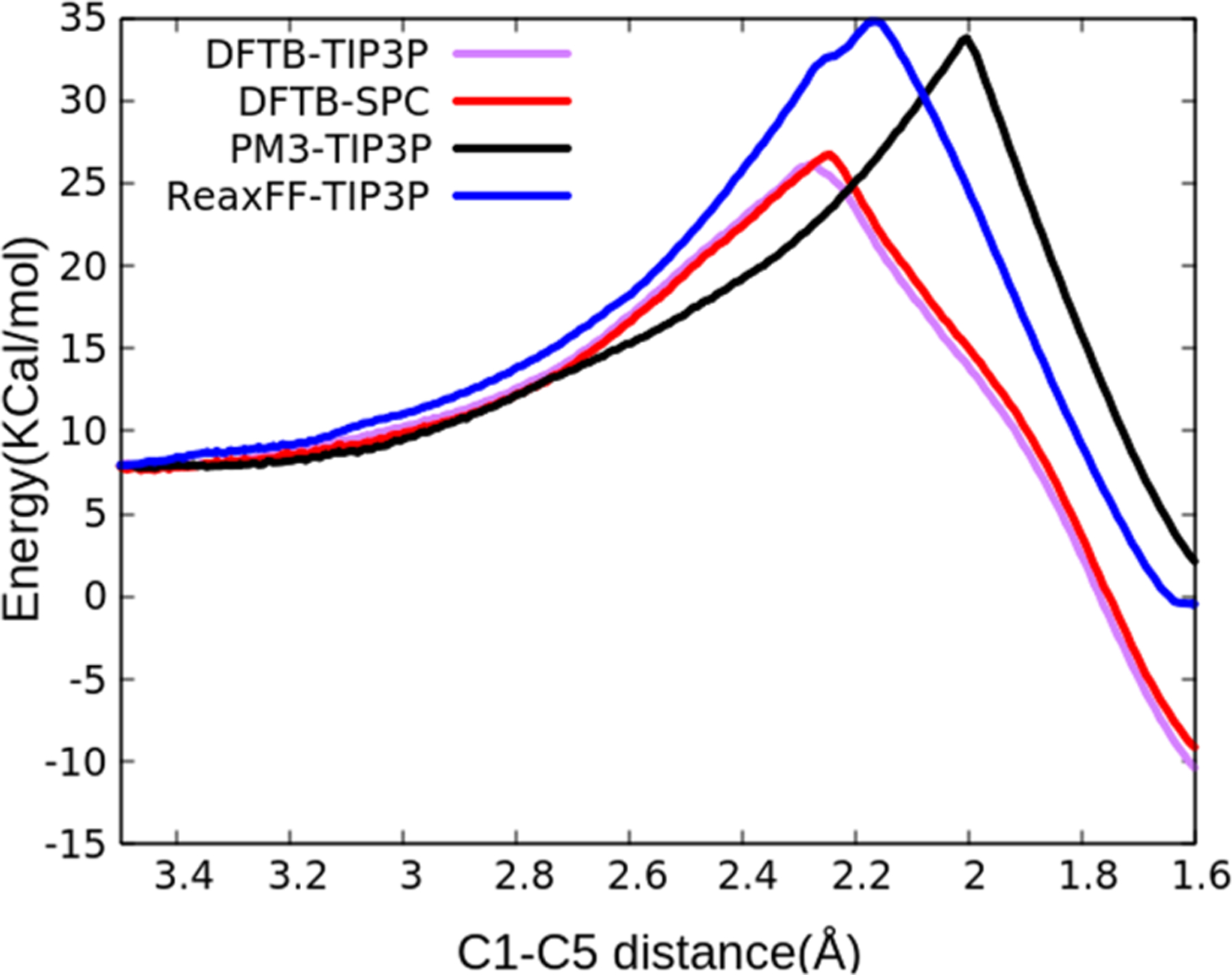
PMF of AVE Claisen rearrangement in TIP3P periodic water using combined ReaxFF/AMBER. The energies are with respect to the completely open AVE geometry optimized energy as the reference.
The first kinetic study of thermal rearrangement of AVE in the gas-phase by Schuler and Murphy reported an activation energy of 30.6 kcal/mol.50 This is consistent with other experimental reports of experimental activation energies for chair transitions.51–53 This barrier height has been reported to be lower in water solvent than the value in the gas phase and nonpolar solvents.54 Transition state bond lengths of 2.2–2.3 Å were reported using different simulation techniques.55
5. CONCLUSIONS
An AMBER/ReaxFF interface has been developed in this work that offers the capability of capturing chemical reactions as an alternative to AMBER QM/MM methods. The main objective of this development is obtaining an approach to add a reactivity feature to the classically nonreactive molecular dynamics simulations with reduced computational costs compared to QM/MM methods. This new interface will be a useful tool for modeling big biomolecular systems with local reactive regions. The initial file-based implementation of this interface was assessed by calculation of the reaction profile of Claisen rearrangement of AVE solvated in the TIP3P water model. We conducted umbrella sampling simulations by generating a series of configurations along the distance between two end carbon atoms in AVE as the reaction coordinate, ran biasing simulations, and extracted the PMF. These results showed the capability of the ReaxFF/AMBER integration in capturing a Claisen rearrangement reaction despite the small inaccuracies in the reaction barrier height which can be enhanced by more thorough training of the ReaxFF force field.
The benchmark timing data showed that the main part of the calculations time was spent on the I/O, initialization/synch in this file-based version of the integration. Therefore, we will develop array-based implementation of this integration which will lead to eliminating the I/O and initialization/synch simulation timing overheads. To further enhance the calculation speed, we will integrate PuReMD that is the C language based efficient parallel implementation of the original ReaxFF. PuReMD contains significant performance improvements over the currently used Fortran based reference ReaxFF implementations and it has shared memory, distributed memory, and GPU implementations, which will allow us to take advantage of modern massively parallel architectures. The performance of the array-based AMBER/ReaxFF (PuReMD) will be presented in the follow-up work.
Supplementary Material
ACKNOWLEDGMENTS
This work was supported in part by a NIH grant (Award No. GM130641), a NSF CDS&E grant (Award No. 1807622) and a NSF OAC grant (1835144). This work used computational resources provided by the Institute for Cyber-Enabled Research at Michigan State University.
Footnotes
Supporting Information
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.0c00874.
Modified EEM example; incorporating long range electrostatic interactions into ReaxFF; specifications of hardware and software used in computational experiments; QM Claisen rearrangement transition configurations; Reax force field training inputs used for modeling AVE Claisen rearrangement (PDF)
Complete contact information is available at: https://pubs.acs.org/10.1021/acs.jctc.0c00874
The authors declare no competing financial interest.
Contributor Information
Ali Rahnamoun, Department of Chemistry and Department of Biochemistry and Molecular Biology, Michigan State University, East Lansing, Michigan 48824-1322, United States;.
Mehmet Cagri Kaymak, Department of Computer Science and Engineering, Michigan State University, East Lansing, Michigan 48824-1322, United States.
Madushanka Manathunga, Department of Chemistry and Department of Biochemistry and Molecular Biology, Michigan State University, East Lansing, Michigan 48824-1322, United States;.
Andreas W. Götz, San Diego Supercomputer Center, University of California San Diego, La Jolla, California 92093-0505, United States;.
Adri C. T. van Duin, Department of Mechanical Engineering, Pennsylvania State University, University Park, Pennsylvania 16802, United States;.
Kenneth M. Merz, Jr., Department of Chemistry and Department of Biochemistry and Molecular Biology, Michigan State University, East Lansing, Michigan 48824-1322, United States;.
Hasan Metin Aktulga, Department of Computer Science and Engineering, Michigan State University, East Lansing, Michigan 48824-1322, United States;.
REFERENCES
- (1).Warshel A; Levitt M Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. J. Mol. Biol 1976, 103, 227–249. [DOI] [PubMed] [Google Scholar]
- (2).Lin H; Truhlar DG QM/MM: what have we learned, where are we, and where do we go from here? Theor. Chem. Acc 2007, 117, 185. [Google Scholar]
- (3).Senn HM; Thiel W QM/MM Methods for Biomolecular Systems. Angew. Chem., Int. Ed 2009, 48, 1198–1229. [DOI] [PubMed] [Google Scholar]
- (4).Friesner RA; Guallar V Ab initio quantum chemical and mixed quantum mechanics/molecular mechanics (QM/MM) methods for studying enzymatic catalysis. Annu. Rev. Phys. Chem 2005, 56, 389–427. [DOI] [PubMed] [Google Scholar]
- (5).Guallar V; Wallrapp FH QM/MM methods: Looking inside heme proteins biochemisty. Biophys. Chem 2010, 149, 1–11. [DOI] [PubMed] [Google Scholar]
- (6).Magalhães RP; Fernandes HS; Sousa SF Modelling Enzymatic Mechanisms with QM/MM Approaches: Current Status and Future Challenges. Isr. J. Chem 2020, 60, 655–666. [Google Scholar]
- (7).Lu X; Fang D; Ito S; Okamoto Y; Ovchinnikov V; Cui Q QM/MM free energy simulations: recent progress and challenges. Mol. Simul 2016, 42, 1056–1078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Pearlman DA; Case DA; Caldwell JW; Ross WS; Cheatham TE; DeBolt S; Ferguson D; Seibel G; Kollman P AMBER, a package of computer programs for applying molecular mechanics, normal mode analysis, molecular dynamics and free energy calculations to simulate the structural and energetic properties of molecules. Comput. Phys. Commun 1995, 91, 1–41. [Google Scholar]
- (9).Case DA; Cheatham TE 3rd; Darden T; Gohlke H; Luo R; Merz KM Jr.; Onufriev A; Simmerling C; Wang B; Woods RJ The Amber biomolecular simulation programs. J. Comput. Chem 2005, 26, 1668–1688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Walker R; Crowley M; Case D The implementation of a fast and accurate QM/MM potential method in AMBER. J. Comput. Chem 2008, 29, 1019–1031. [DOI] [PubMed] [Google Scholar]
- (11).Seabra G. d. M.; Walker RC; Elstner M; Case DA; Roitberg AE Implementation of the SCC-DFTB Method for Hybrid QM/MM Simulations within the Amber Molecular Dynamics Package. J. Phys. Chem. A 2007, 111, 5655–5664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Götz AW; Clark MA; Walker RC An extensible interface for QM/MM molecular dynamics simulations with AMBER. J. Comput. Chem 2014, 35, 95–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Isborn CM; Götz AW; Clark MA; Walker RC; Martínez TJ Electronic Absorption Spectra from MM and ab Initio QM/MM Molecular Dynamics: Environmental Effects on the Absorption Spectrum of Photoactive Yellow Protein. J. Chem. Theory Comput 2012, 8, 5092–5106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Kästner J Umbrella sampling. WIREs Comput. Mol. Sci 2011, 1, 932–942. [Google Scholar]
- (15).van Duin ACT; Dasgupta S; Lorant F; Goddard WA ReaxFF: A Reactive Force Field for Hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. [Google Scholar]
- (16).Rappe AK; Goddard WA Charge equilibration for molecular dynamics simulations. J. Phys. Chem 1991, 95, 3358–3363. [Google Scholar]
- (17).Mortier WJ; Ghosh SK; Shankar S Electronegativity-equalization method for the calculation of atomic charges in molecules. J. Am. Chem. Soc 1986, 108, 4315–4320. [Google Scholar]
- (18).Samieegohar M; Sha F; Clayborne AZ; Wei T ReaxFF MD Simulations of Peptide-Grafted Gold Nanoparticles. Langmuir 2019, 35, 5029–5036. [DOI] [PubMed] [Google Scholar]
- (19).Yang S; Zhao T; Zou L; Wang X; Zhang Y ReaxFF-based molecular dynamics simulation of DNA molecules destruction in cancer cells by plasma ROS. Phys. Plasmas 2019, 26, 083504. [Google Scholar]
- (20).Hubin PO; Jacquemin D; Leherte L; Vercauteren DP Parameterization of the ReaxFF reactive force field for a prolinecatalyzed aldol reaction. J. Comput. Chem 2016, 37, 2564–2572. [DOI] [PubMed] [Google Scholar]
- (21).Monti S; Jose J; Sahajan A; Kalarikkal N; Thomas S Structure and dynamics of gold nanoparticles decorated with chitosan–gentamicin conjugates: ReaxFF molecular dynamics simulations to disclose drug delivery. Phys. Chem. Chem. Phys 2019, 21, 13099–13108. [DOI] [PubMed] [Google Scholar]
- (22).Trnka T; Tvaroška I; Koča J Automated Training of ReaxFF Reactive Force Fields for Energetics of Enzymatic Reactions. J. Chem. Theory Comput 2018, 14, 291–302. [DOI] [PubMed] [Google Scholar]
- (23).Rahnamoun A; van Duin ACT Reactive Molecular Dynamics Simulation on the Disintegration of Kapton, POSS Polyimide, Amorphous Silica, and Teflon during Atomic Oxygen Impact Using the Reaxff Reactive Force-Field Method. J. Phys. Chem. A 2014, 118, 2780–2787. [DOI] [PubMed] [Google Scholar]
- (24).Raymand D; van Duin ACT; Baudin M; Hermansson K A reactive force field (ReaxFF) for zinc oxide. Surf. Sci 2008, 602, 1020–1031. [Google Scholar]
- (25).Chenoweth K; Cheung S; van Duin ACT; Goddard WA; Kober EM Simulations on the Thermal Decomposition of a Poly(dimethylsiloxane) Polymer Using the ReaxFF Reactive Force Field. J. Am. Chem. Soc 2005, 127, 7192–7202. [DOI] [PubMed] [Google Scholar]
- (26).Russo MF; Li R; Mench M; van Duin ACT Molecular dynamic simulation of aluminum–water reactions using the ReaxFF reactive force field. Int. J. Hydrogen Energy 2011, 36, 5828–5835. [Google Scholar]
- (27).Ludwig J; Vlachos DG; van Duin ACT; Goddard WA Dynamics of the Dissociation of Hydrogen on Stepped Platinum Surfaces Using the ReaxFF Reactive Force Field. J. Phys. Chem. B 2006, 110, 4274–4282. [DOI] [PubMed] [Google Scholar]
- (28).Yoon K; Rahnamoun A; Swett JL; Iberi V; Cullen DA; Vlassiouk IV; Belianinov A; Jesse S; Sang X; Ovchinnikova OS; Rondinone AJ; Unocic RR; van Duin ACT Atomistic-Scale Simulations of Defect Formation in Graphene under Noble Gas Ion Irradiation. ACS Nano 2016, 10, 8376–8384. [DOI] [PubMed] [Google Scholar]
- (29).Rahnamoun A; van Duin ACT Study of thermal conductivity of ice clusters after impact deposition on the silica surfaces using the ReaxFF reactive force field. Phys. Chem. Chem. Phys 2016, 18, 1587–1594. [DOI] [PubMed] [Google Scholar]
- (30).Zou C; Van Duin A Investigation of Complex Iron Surface Catalytic Chemistry Using the ReaxFF Reactive Force Field Method. JOM 2012, 64, 1426–1437. [Google Scholar]
- (31).Shin YK; Kwak H; Vasenkov AV; Sengupta D; van Duin ACT Development of a ReaxFF Reactive Force Field for Fe/Cr/O/S and Application to Oxidation of Butane over a Pyrite-Covered Cr2O3 Catalyst. ACS Catal 2015, 5, 7226–7236. [Google Scholar]
- (32).Senftle TP; Hong S; Islam MM; Kylasa SB; Zheng Y; Shin YK; Junkermeier C; Engel-Herbert R; Janik MJ; Aktulga HM; Verstraelen T; Grama A; van Duin ACT The ReaxFF reactive force-field: development, applications and future directions. npj Comput. Mater 2016, 2, 15011. [Google Scholar]
- (33).Aktulga HM; Fogarty JC; Pandit SA; Grama AY Parallel reactive molecular dynamics: Numerical methods and algorithmic techniques. Parallel Comput 2012, 38, 245–259. [Google Scholar]
- (34).Kylasa SB; Aktulga HM; Grama AY PuReMD-GPU: A reactive molecular dynamics simulation package for GPUs. J. Comput. Phys 2014, 272, 343–359. [Google Scholar]
- (35).Plimpton SJ; Thompson AP Computational aspects of many-body potentials. MRS Bull 2012, 37, 513–521. [Google Scholar]
- (36).Kamat AM; van Duin ACT; Yakovlev A Molecular Dynamics Simulations of Laser-Induced Incandescence of Soot Using an Extended ReaxFF Reactive Force Field. J. Phys. Chem. A 2010, 114, 12561–12572. [DOI] [PubMed] [Google Scholar]
- (37).Sanderson R An interpretation of bond lengths and a classification of bonds. Science 1951, 114, 670–672. [DOI] [PubMed] [Google Scholar]
- (38).Bultinck P; Langenaeker W; Lahorte P; De Proft F; Geerlings P; Waroquier M; Tollenaere J The electronegativity equalization method I: Parametrization and validation for atomic charge calculations. J. Phys. Chem. A 2002, 106, 7887–7894. [Google Scholar]
- (39).Darden T; York D; Pedersen L Particle mesh Ewald: An N log(N) method for Ewald sums in large systems. J. Chem. Phys 1993, 98, 10089–10092. [Google Scholar]
- (40).Chenoweth K; van Duin ACT; Goddard WA ReaxFF Reactive Force Field for Molecular Dynamics Simulations of Hydrocarbon Oxidation. J. Phys. Chem. A 2008, 112, 1040–1053. [DOI] [PubMed] [Google Scholar]
- (41).Manathunga M; Miao Y; Mu D; Götz AW; Merz KM Parallel Implementation of Density Functional Theory Methods in the Quantum Interaction Computational Kernel Program. J. Chem. Theory Comput 2020, 16, 4315–4326. [DOI] [PubMed] [Google Scholar]
- (42).Jorgensen WL; Chandrasekhar J; Madura JD; Impey RW; Klein ML Comparison of simple potential functions for simulating liquid water. J. Chem. Phys 1983, 79, 926–935. [Google Scholar]
- (43).Ganem B The Mechanism of the Claisen Rearrangement: Déjà Vu All Over Again. Angew. Chem., Int. Ed. Engl 1996, 35, 936–945. [Google Scholar]
- (44).Gao J Combined QM/MM Simulation Study of the Claisen Rearrangement of Allyl Vinyl Ether in Aqueous Solution. J. Am. Chem. Soc 1994, 116, 1563–1564. [Google Scholar]
- (45).Zhang W; van Duin A Improvement of the ReaxFF Description for Functionalized Hydrocarbon/Water Weak Interactions in the Condensed Phase. J. Phys. Chem. B 2018, 122. [DOI] [PubMed] [Google Scholar]
- (46).Frisch MJ; Trucks GW; Schlegel HB; Scuseria GE; Robb MA; Cheeseman JR; Scalmani G; Barone V; Petersson GA; Nakatsuji H; Li X; Caricato M; Marenich AV; Bloino J; Janesko BG; Gomperts R; Mennucci B; Hratchian HP; Ortiz JV; Izmaylov AF; Sonnenberg JL; Williams-Young D; Ding F; Lipparini F; Egidi F; Goings J; Peng B; Petrone A; Henderson T; Ranasinghe D; Zakrzewski VG; Gao J; Rega N; Zheng G; Liang W; Hada M; Ehara M; Toyota K; Fukuda R; Hasegawa J; Ishida M; Nakajima T; Honda Y; Kitao O; Nakai H; Vreven T; Throssell K; Montgomery JA Jr.; Peralta JE; Ogliaro F; Bearpark MJ; Heyd JJ; Brothers EN; Kudin KN; Staroverov VN; Keith TA; Kobayashi R; Normand J; Raghavachari K; Rendell AP; Burant JC; Iyengar SS; Tomasi J; Cossi M; Millam JM; Klene M; Adamo C; Cammi R; Ochterski JW; Martin RL; Morokuma K; Farkas O; Foresman JB; Fox DJ Gaussian 16 Gaussian, Inc.: Wallingford, CT, 2016. [Google Scholar]
- (47).Wang J; Wolf RM; Caldwell JW; Kollman PA; Case DA Development and testing of a general amber force field. J. Comput. Chem 2004, 25, 1157–1174. [DOI] [PubMed] [Google Scholar]
- (48).Elstner M; Porezag D; Jungnickel G; Elsner J; Haugk M; Frauenheim T; Suhai S; Seifert G Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B: Condens. Matter Mater. Phys 1998, 58, 7260–7268. [Google Scholar]
- (49).Stewart JJP Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements. J. Mol. Model 2007, 13, 1173–1213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Schuler FW; Murphy GW The Kinetics of the Rearrangement of Vinyl Allyl Ether1. J. Am. Chem. Soc 1950, 72, 3155–3159. [Google Scholar]
- (51).Gajewski JJ; Conrad ND Variable transition state structure in 3,3-sigmatropic shifts from. alpha.-secondary deuterium isotope effects. J. Am. Chem. Soc 1979, 101, 6693–6704. [Google Scholar]
- (52).Wiest O; Black KA; Houk K Density functional theory isotope effects and activation energies for the Cope and Claisen rearrangements. J. Am. Chem. Soc 1994, 116, 10336–10337. [Google Scholar]
- (53).Hiersemann M; Nubbemeyer U The Claisen rearrangement: methods and applications; John Wiley & Sons, 2007. [Google Scholar]
- (54).Zhang J; Yang YI; Yang L; Gao YQ Dynamics and Kinetics Study of “In-Water” Chemical Reactions by Enhanced Sampling of Reactive Trajectories. J. Phys. Chem. B 2015, 119, 14505–14514. [DOI] [PubMed] [Google Scholar]
- (55).Guest JM; Craw JS; Vincent MA; Hillier IH The effect of water on the Claisen rearrangement of allyl vinyl ether: theoretical methods including explicit solvent and electron correlation. J. Chem. Soc., Perkin Trans 2 1997, 71–74. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


