Changes in Allele Frequencies When Different Genomic Coancestry Matrices Are Used for Maintaining Genetic Diversity

Abstract

A main objective in conservation programs is to maintain genetic variability. This can be achieved using the Optimal Contributions (OC) method that optimizes the contributions of candidates to the next generation by minimizing the global coancestry. However, it has been argued that maintaining allele frequencies is also important. Different genomic coancestry matrices can be used on OC and the choice of the matrix will have an impact not only on the genetic variability maintained, but also on the change in allele frequencies. The objective of this study was to evaluate, through stochastic simulations, the genetic variability maintained and the trajectory of allele frequencies when using two different genomic coancestry matrices in OC to minimize the loss of diversity: (i) the matrix based on deviations of the observed number of alleles shared between two individuals from the expected numbers under Hardy–Weinberg equilibrium (θ_LH); and (ii) the matrix based on VanRaden’s genomic relationship matrix (θ_VR). The results indicate that the use of θ_LH resulted in a higher genetic variability than the use of θ_VR. However, the use of θ_VR maintained allele frequencies closer to those in the base population than the use of θ_LH.

1. Introduction

Genetic diversity is a prerequisite for populations to be able to face future environmental changes and to ensure long-term survival [1]. Thus, a common objective in genetic conservation programs is to minimize the loss of genetic variability. This can be achieved using the Optimal Contributions (OC) method that optimizes the contributions of candidates to the next generation by minimizing the global coancestry [2,3,4]. It has been demonstrated that OC maximizes genetic diversity measured as expected heterozygosity [5], which is proportional to the additive genetic variance of quantitative traits [6]. Controlling the loss of genetic diversity also keeps the inbreeding rate under control and therefore the risk of inbreeding depression.

A different objective in genetic conservation programs can be to maintain allele frequencies to preserve the uniqueness of a particular population, since current frequencies are the result not only of genetic drift, but also of previous selection processes [7,8,9]. Selection and drift can lead to a given allele responsible for a desirable trait at a high frequency. Moreover, trying to move the frequency to intermediate values to increase genetic variability would remove the uniqueness of the population. Thus, changes in the genetic composition of populations may be undesirable, particularly when dealing with ex situ conservation programs where the final aim is the reintroduction to the wild [9].

When the OC method is applied using pedigree information to compute coancestries, both objectives (maximum heterozygosity and maintenance of allele frequencies) are achieved [9], but this is not the case when coancestries are computed from molecular marker data. Previous studies have shown that using a coancestry matrix (θ) computed from large numbers of single nucleotide polymorphisms (SNPs) in OC is more efficient for maintaining diversity than using the pedigree-based coancestry matrix [10,11,12]. However, given that the highest expected heterozygosity is obtained at intermediate allele frequencies, a consequence of applying OC using a θ based on SNP genotypes is that the genetic composition of the population is modified [9,10,11,13,14].

Different genomic coancestry matrices have been proposed for being used in OC [10,11,15,16,17]. They include the matrix that describes deviations of the observed numbers of alleles shared by two individuals from the expected numbers under Hardy–Weinberg equilibrium [18], and those obtained from genomic relationship matrices currently used in genomic predictions [19,20]. In a recent study, Morales-González et al. [16] have shown that the expected heterozygosity retained through OC was higher when using the matrix proposed by Li and Horvitz [18] than when using different genomic relationship matrices (i.e., the VanRaden’s matrices based on Method 1 and 2 [19] and the Yang’s matrix [20]). However, as mentioned above, the genomic θ used in OC will have an impact not only on the diversity maintained, but also on the trajectory of the change in allele frequencies. Gómez-Romano et al. [21] suggested that while OC using a genomic coancestry matrix that simply measures the proportion of alleles shared by two individuals [22] and that correlates perfectly with Li and Horvitz’s matrix favors solutions that tend to move allele frequencies towards 0.5, OC using VanRaden’s matrices would lead to solutions that tend to keep allele frequencies closer to those in the original population (i.e., allele frequencies would tend to be unchanged). This has been recently confirmed by Meuwissen et al. [17] in the context of OC aimed at maximizing genetic gain through selection while restricting the increase in inbreeding (i.e., restricting the loss of genetic diversity).

In general, populations under conservation programs are small and genetic drift leads to a loss of diversity and changes in allele frequencies. The magnitude of these drift effects depends on the effective population size (N_e) which can be estimated from genomic coancestry. However, Toro et al. [23] have recently questioned the meaning of N_e when genomic matrices are used in OC. In particular, when optimal management is carried out using marker information, genetic diversity can increase in the initial generations implying negative estimates of N_e. Moreover, in the long term, N_e does not attain an asymptotic value, but it shows an unpredictable behavior. Their findings were based on OC using Nejati-Javaremi´s matrix [22] and it is unclear if they hold when other genomic coancestry matrices are used.

The objective of this study was to evaluate, through computer simulations, the genetic variability maintained and the trajectory of allele frequencies when different genomic coancestry matrices are used in OC. Estimates of N_e obtained from the change in heterozygosity computed from different genomic matrices were also compared.

2. Materials and Methods

Scenarios simulated involved the management of populations through the OC method using two different genomic coancestry matrices, for 50 discrete generations. Management started from a base population with family structure. The same base population was used for the 100 replicates run and it was created in two steps. Firstly, a population at mutation-drift equilibrium was generated. Secondly, the population was expanded in order to have enough individuals for sampling the 100 replicates (see below, in Section 2.1). The simulations were carried out with our own Fortran 90 codes.

2.1. Generation of the Base Population

The simulation of the base population was done in two steps to simulate a realistic amount of linkage disequilibrium and to ensure independency among the replicates. The first step was to generate a population in LD using a mutation-drift equilibrium approach. For this, 10,000 discrete generations of random mating for a population of 100 individuals (50 males and 50 females) were simulated. Using a larger population size would have generated an unrealistically low LD. Sires and dams were sampled with replacement and were mated at random. Each mating produced 2 offspring (1 of each sex). Thus, N_e was equal to 100. The genome was composed of 20 chromosomes of 1 Morgan each. Two types of biallelic loci (SNP and unobserved loci) were simulated and they differed simply in their subsequent use. SNP loci were used for computing the genomic coancestry matrices used in the management of the population that started after the base population was created. The unobserved loci were used for measuring diversity and changes of allele frequencies, and for estimating N_e across generations. Thus, the effect of different management strategies (i.e., using different genomic coancestry matrices) can be evaluated in the rest of the genome and not only on the loci used in the management (i.e., it is sometimes done using SNPs). A total of 500,000 SNPs and 500,000 unobserved loci were simulated per chromosome. At the initial generation, all loci were fixed. The mutation rate per locus and generation (μ) was 2.5 × 10⁻⁶ for all loci. The number of new mutations per generation was sampled from a Poisson distribution with mean 2N_en_cμn_l,, where n_c is the number of chromosomes (i.e., 20) and n_l is the total number of loci per chromosome (i.e., 1,000,000). Mutations were then randomly distributed across individuals, chromosomes and loci, switching allele 1 to allele 2 and vice versa. When generating the gametes, the number of crossovers per chromosome was drawn from a Poisson distribution with mean equal to 1. Crossovers were randomly distributed without interference. At the end of the process, the expected heterozygosity measured at both types of loci had stabilized (mutation-drift equilibrium). The second step consisted of expanding this population so we could sample the individuals to be used at the first generation of each replicate. The population was expanded during 4 generations with the aim of having enough individuals to sample 100 different replicates. During the 4 generations of expansion, each individual was randomly allocated to 8 different mates and each mating produced 1 offspring. In this way, the number of individuals in the population was multiplied by 4 each generation. After these 4 generations, the population was composed by 25,600 individuals and constituted the base population (t = 0). There were a total of 56,017 SNPs and 55,840 unobserved loci still segregating in t = 0. The expected heterozygosity (H_e) computed with all loci (SNPs and unobserved loci) still segregating was 0.1811 and the linkage disequilibrium (measured as r², the squared correlation between pairs of loci) between consecutive loci was 0.131.

2.2. Management Strategies

Management was performed on populations of two different sizes (N = 20 and N = 100 individuals, half of each sex) using the OC method across 50 generations. Population size was kept constant across generations. The founder individuals for each replicate were randomly sampled from the base population. Note that, given that the set of individuals sampled in t = 0 differs across replicates, the number of segregating loci can also differ. In most scenarios (see below, at the end of this section), all loci segregating in t = 0 were used for managing the population, for measuring diversity and changes of allele frequencies, and for estimating N_e.

The problem to be solved in the OC method is related to the allocation of contributions, i.e., the number of offspring each candidate should produce the next generation. The pursued strategy is to minimize the global coancestry weighted by those contributions, i.e., minimize c’θ c, where c is a N × 1 vector of proportions of offspring left by each candidate (i.e., the vector of solutions), N is the number of candidates and θ is the coancestry matrix. A restriction was imposed in the optimization such as the sum of the contributions of males and females is the same and equal to ½, i.e., Q’c = ½ 1, where Q is a (N × 2) known incidence matrix indicating the sex of the candidates with 0s and 1s, and 1 is a (2 × 1) vector of ones. The optimization problem was solved using Lagrangian multipliers [2,24]. Note that with this approach, c can contain negative values for some candidates. The contribution of candidates with c_i < 0 was then set to 0 and the optimization was repeated with the remaining candidates until all elements of c were non-negative. Finally, the contribution of individual i (c_i), which is a proportion, was converted to a number of offspring by multiplying c_i by 2N and rounding to the nearest integer but ensuring that the number of offspring of each sex equals to N/2. Each parent was randomly allocated to different mates (among the selected individuals) to produce its offspring.

Two management strategies were investigated, and they differed in the genomic coancestry matrix used in the optimization of contributions. Under strategy S_{O_LH}, the coancestry matrix used was matrix θ_LH which describes the excess in the observed number of alleles shared by two individuals relative to the expected number under Hardy–Weinberg equilibrium [18,25]. Specifically, the coancestry coefficient between individuals i and j was computed as

$$f_{LH\left(i,j\right)}=\frac{{{\displaystyle \sum }}_{k=1}^S{f}_{OBS\left(i,j\right)k}-S+2{{\displaystyle \sum }}_{k=1}^S{p}_k\left(1-p_k\right)}{2{{\displaystyle \sum }}_{k=1}^S{p}_k\left(1-p_k\right)}$$ (1)

where $f_{OBS\left(i,j\right)}$ is the proportion of alleles shared by individuals i and j, S is the number of SNPs and p_k is the frequency of the reference allele (allele B) of SNP k in t = 0. Under strategy S_{O_VR}, the coancestry matrix used was matrix θ_VR which is based on the genomic relationship matrix obtained from VanRaden’s method 2 [19]. Specifically, the coancestry coefficient between individuals i and j was computed as

$$f_{VR\left(i,j\right)}=\frac{1}{2S}{{\displaystyle \sum }}_{k=1}^S\frac{\left(x_{ki}-2p_k\right)\left(x_{kj}-2p_k\right)}{2p_k\left(1-p_k\right)}$$ (2)

where x_ki is the genotype of individual i for SNP k, coded as 0, 1 or 2 for genotypes AA, AB and BB, respectively, and $p_k$is as defined for f_LH.

In most scenarios, both coancestry matrices were computed every generation using all SNPs that were segregating in t = 0. However, we analyzed two additional scenarios where two different minor allele frequency (MAF) thresholds were imposed for the SNPs to be used to compute the coancestry matrices: (i) using only SNPs with MAF > 0.05; and (ii) using only SNPs with MAF > 0.25. The first threshold (MAF > 0.05) was considered because it is commonly applied when analyzing real data to reduce the number of potential genotyping errors. The second threshold (MAF > 0.25) was considered to explore the influence of rare alleles on the performance of the coancestry matrices investigated. It is known that with VanRaden’s method rare alleles contribute more to the coancestry coefficient than common alleles [21,26]. It is, thus, interesting to determine how the differences between management strategies S_{O_LH} and S_{O_VR} vary in the different MAF scenarios. Management in these additional scenarios was performed for 50 generations.

Furthermore, as a benchmark, we simulated a strategy (strategy S_E) where the contributions of all candidates were equalized (i.e., all individuals contributed with two offspring to the next generation). This is the simplest management strategy that has been proposed to maintain genetic diversity by increasing N_e. It should be noticed that when dealing with populations in which the relationships between individuals are homogeneous (all equally related), this strategy leads to a N_e close to 2N.

2.3. Parameters Evaluated

Management strategies were compared in terms of the genetic variability retained and the trajectory of the allele frequencies across generations for the SNPs and for the unobserved loci. Moreover, strategies were compared in terms of the number of individuals selected to produce the next generation (N_S) and the number of loci still segregating in a given generation, both for SNPs and for unobserved loci. The amount of genetic variability retained was measured as the expected heterozygosity (H_e) computed as $1-{{\displaystyle \sum }}_{k=1}^L{{\displaystyle \sum }}_{l=1}^2{p}_{kl}^2$, where L is the number of loci (SNPs or unobserved loci) and $p_{lk}$ is the frequency of allele l of locus k.

In order to evaluate the ‘distance’ between frequencies in a given generation t and frequencies in t = 0, we used the Kullback–Leibler (KL) divergence criterion, which measures how different is a particular distribution from a reference distribution [27], which here is the distribution of allele frequencies in t = 0. The KL divergence between current frequencies and frequencies in t = 0 was computed as

$$KL={\displaystyle \sum }_{k=1}^L{\displaystyle \sum }_{l=1}^2{p^{\prime }}_{kl}log\frac{{p^{\prime }}_{kl}}{p_{kl}},$$ (3)

where $p_{kl}$is the frequency of allele l of locus k in t = 0, and ${p^{\prime }}_{kl}$ is the corresponding frequency in the current generation (t > 0). The summation over alleles included only alleles with ${p^{\prime }}_{kl}$> 0.

Finally, N_e was estimated from the change in heterozygosity in SNP loci. Thus, N_e in generation t was computed as N_e = 1/2 ΔH_e, where ΔH_e equals $H_{e\left(t-1\right)}-H_{e\left(t\right)}/H_{e\left(t-1\right)}$. All results presented are averages over the 100 replicates.

3. Results

3.1. Expected Heterozygosity and Kullback–Leibler Divergence for Populations of Size N = 100

For populations of size N = 100, and using all the SNPs segregating in t = 0, strategy S_{O_LH} led to higher genetic variability (measured as H_e) than strategy S_{O_VR} (Table 1) and the difference between both strategies increased across generations. In particular, H_e was about 1%, 4% and 11% higher with S_{O_LH} than with S_{O_VR} in t = 1, 10 and 50, respectively. With S_{O_LH}, H_e even slightly increased in the initial generations while with S_{O_VR}, H_e decreased from the start. Moreover, H_e obtained with strategy S_{O_VR} was very similar to H_e obtained with strategy S_E. Table 1 also shows that S_{O_VR} maintained allele frequencies closer to those in the base population than S_{O_LH} given that the KL values for S_{O_LH} were ≥ 100% higher than for S_{O_VR}. The differences in KL between both strategies increased across generations. Moreover, at later generations, S_{O_VR} was slightly more efficient in maintaining the initial frequencies than S_E, a strategy that is expected to maximize N_e and, thus, to minimize genetic drift.

Table 1.

Expected heterozygosity (H_e, in %) and Kullback–Leibler divergence for unobserved loci (KL × 10²), number of selected candidates (N_S), and number of SNPs (S) and unobserved loci (U) segregating across generations (t) when contributions are equalized (S_E) and when they are optimized using Li and Horvitz (S_{O_LH}) and VanRaden (S_{O_VR}) coancestry matrices computed with SNPs with MAF > 0.00 in a population of 100 individuals.

	SE						SO_LH *						SO_VR *
t	He	KL	NS	S	U		He	KL	NS	S	U		He	KL	NS	S	U
1	19.17	0.06	100	51,035	50,894		+0.14	+0.14	−39	−2239	−2246		0.00	0.00	0	+8	+18
2	19.12	0.12	100	49,873	49,737		+0.21	+0.23	−36	−3206	−3229		0.00	0.00	0	−22	0
3	19.07	0.18	100	48,852	48,729		+0.28	+0.30	−35	−3792	−3847		0.00	0.00	0	−61	−52
4	19.03	0.24	100	47,946	47,828		+0.35	+0.37	−35	−4182	−4261		0.00	0.00	−1	−113	−101
5	18.98	0.30	100	47,108	47,003		+0.41	+0.43	−33	−4384	−4499		0.00	−0.01	−1	−162	−157
10	18.73	0.57	100	43,777	43,691		+0.68	+0.68	−30	−4731	−4975		0.00	−0.03	−2	−399	−401
15	18.51	0.82	100	41,311	41,217		+0.89	+0.86	−28	−4523	−4855		−0.01	−0.06	−5	−595	−587
20	18.27	1.06	100	39,313	39,229		+1.08	+0.99	−26	−4152	−4567		−0.01	−0.09	−6	−714	−720
30	17.82	1.50	100	36,231	36,140		+1.40	+1.16	−24	−3329	−3896		+0.01	−0.18	−9	−906	−899
40	17.38	1.90	100	33,854	33,759		+1.67	+1.24	−22	−2517	−3215		+0.03	−0.26	−11	−995	−970
50	16.95	2.28	100	31,940	31,848		+1.92	+1.27	−21	−1786	−2594		+0.05	−0.35	−12	−1081	−1036

* S_{O_LH} and S_{O_VR} values are those deviated from S_E. Standard errors (computed across replicates) ranged from 4.91 × 10⁻⁵ to 9.54 × 10⁻⁵ for H_e and from 0.16 × 10⁻⁵ to 7.39 × 10⁻⁵ for KL.

The use of both matrices (θ_LH and θ_VR) in OC also led to different numbers of individuals selected as parents of the next generation (N_S). In particular, with S_{O_LH}, between 10% and 30% fewer individuals were selected than with S_{O_VR} (Table 1). In fact, with the latter, almost all individuals were selected in all generations up to t = 10. The difference in N_S entailed a difference in the number of loci that remained segregating across generations that was much higher with S_{O_VR} than with S_{O_LH} (Table 1), particularly in the initial generations. As for H_e and for KL, strategies S_{O_VR} and S_E led to very similar values of N_S.

Table 2 shows the evolution across generations of the average frequency of the minor allele in t = 0. This average frequency was practically constant with S_E and slightly decreased with S_{O_VR}. However, with S_{O_LH}, it increased from ~1% in t = 1 to 16–19% in t = 50. Thus, it is clear that S_{O_LH} leads average frequencies upward (ultimately towards 0.5) and S_{O_VR} tends to maintain them. As expected, these patterns were more evident for the SNPs than for the unobserved loci.

Table 2.

Average frequency of the minor allele in generation 0 (× 10²) across generations (t) for SNPs and unobserved loci when contributions are equalized (S_E) and when they are optimized using Li and Horvitz (S_{O_LH}) and VanRaden (S_{O_VR}) coancestry matrices in a population of 100 individuals.

		SNPs				Unobserved Loci
t		SE	SO_LH	SO_VR		SE	SO_LH	SO_VR
0		13.45	13.45	13.45		13.39	13.39	13.39
1		13.44	13.68	13.45		13.39	13.60	13.40
2		13.44	13.81	13.45		13.39	13.72	13.40
3		13.44	13.94	13.45		13.38	13.82	13.39
4		13.44	14.06	13.44		13.38	13.93	13.39
5		13.44	14.17	13.44		13.38	14.02	13.39
10		13.44	14.67	13.41		13.38	14.44	13.36
15		13.45	15.08	13.37		13.39	14.77	13.33
20		13.44	15.42	13.32		13.39	15.05	13.29
30		13.44	15.96	13.23		13.39	15.46	13.23
40		13.45	16.36	13.12		13.39	15.75	13.15
50		13.45	16.67	13.01		13.40	15.98	13.07

Figure 1 and Figure 2 show the frequency (f) distribution also for minor alleles in t = 0 in this generation and after 50 generations of management, using different sets of SNPs to compute coancestries. When using all SNPs segregating in t = 0, the distributions for SNPs and unobserved loci were very similar (Figure 1a and Figure 2a). However, when using only SNPs with MAF > 0.05 or MAF > 0.25, the distribution for SNPs was greatly affected. When using SNPs with MAF > 0 or MAF > 0.05 (Figure 1a,b), a greater number of SNPs was fixed with S_{O_LH} than with S_{O_VR} across generations (see class f = 0.00). However, more loci (SNPs and unobserved loci) with low frequencies (0.00 < f ≤ 0.15) were observed with S_{O_VR} than with S_{O_LH} and more loci with higher frequencies (f > 0.4) were observed with S_{O_LH} than with S_{O_VR}. Thus, although more alleles are fixed with S_{O_LH}, those that are kept segregating increase their frequency, while with S_{O_VR} the frequencies tend to be maintained. The highest difference between SNPs and unobserved loci was found when only SNPs with MAF > 0.25 were used to estimate the coancestry matrices (Figure 1c and Figure 2c). These differences are due to the fact that no MAF filtering was done for the unobserved loci.

Figure 1.

Number of SNPs for each class of allele frequency of the allele that was minor at generation 0 (gray bars) and the frequency of this allele after 50 generations, when contributions are optimized using Li and Horvitz (S_{O_LH}, in orange) and VanRaden (S_{O_VR}, in green) coancestry matrices computed with SNPs with MAF > 0.00 (a), MAF > 0.05 (b) and MAF > 0.25 (c) in a population of 100 individuals.

Figure 2.

Number of unobserved loci for each class of allele frequency of the allele that was minor at generation 0 (gray bars) and the frequency of this allele after 50 generations, when contributions are optimized using Li and Horvitz (S_{O_LH}, in orange) and VanRaden (S_{O_VR}, in green) coancestry matrices computed with SNPs with MAF > 0.00 (a), MAF > 0.05 (b) and MAF > 0.25 (c) in a population of 100 individuals.

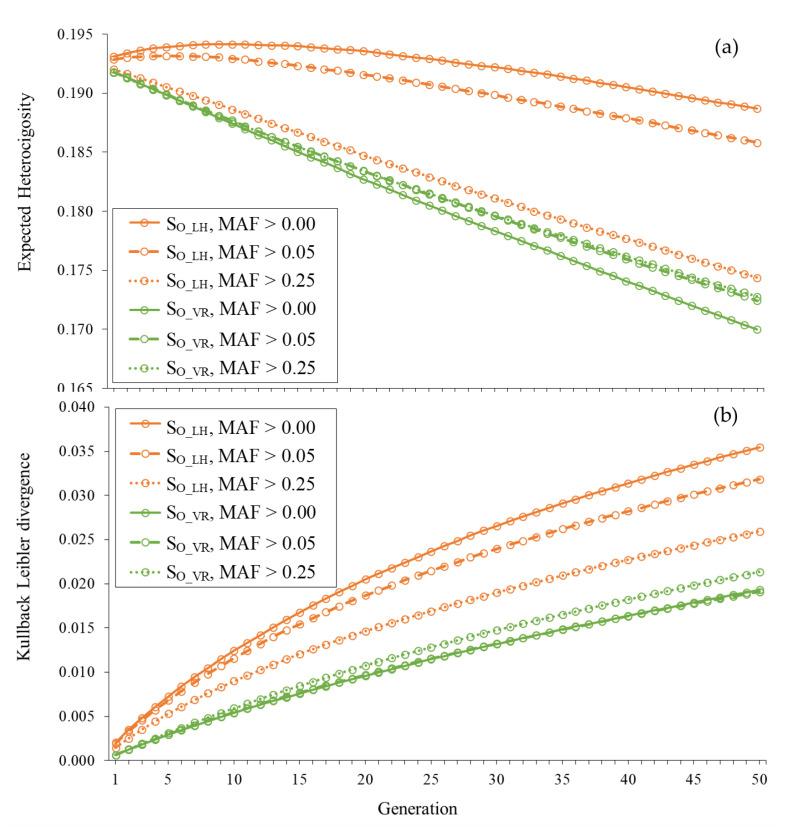
Figure 3 shows the trajectories of H_e and KL across generations for unobserved loci under strategies S_{O_LH} and S_{O_VR} using the three different sets of SNPs. The heterozygosity maintained with S_{O_LH} decreased as the MAF criterion chosen for the SNPs used to estimate coancestries becomes more restrictive given that the number of SNPs used decreased. In fact, the small increase in H_e observed in the initial generations when using all SNPs (MAF> 0.00) was not observed when using only the SNPs with MAF > 0.05 or MAF > 0.25. In parallel, the KL divergence with S_{O_LH} also decreased when increasing the severity of the restriction imposed on the SNPs used. However, with S_{O_VR}, the changes observed in H_e and KL when using a different set of SNPs were very small.

Figure 3.

Expected heterozygosity (a) and Kullback–Leibler divergence (b) for unobserved loci across generations when contributions are optimized using Li and Horvitz (S_{O_LH}) and VanRaden (S_{O_VR}) coancestry matrices computed with SNPs with MAF > 0.00, MAF > 0.05 and MAF > 0.25 in a population of 100 individuals.

3.2. Expected Heterozygosity and Kullback–Leibler Divergence for Populations of Size N = 20

Table 3 shows results from the different strategies (S_E, S_{O_LH} and S_{O_VR}) for populations of size N = 20, when all SNPs segregating in t = 0 were used in the management. Similar to the results found for populations of N = 100, (i) S_{O_LH} led to higher H_e than S_{O_VR} and S_E; and (ii) S_{O_VR} maintained allele frequencies closer to those in t = 0 than S_{O_LH}. However, differences among strategies were smaller for populations of N = 20. For instance, for N = 20, H_e in t = 10 was less than 1% higher when managing with S_{O_LH} than when managing with S_{O_VR}, while for N = 100 this percentage was about 4%. For KL, the highest difference between strategies was 0.0027 units with N = 20 and 0.0127 units with N = 100. However, with N = 20, contrary to what happened with N = 100, S_{O_LH} managed to keep frequencies closer to the initial frequencies than S_E in the last generations (t ≥ 30).

Table 3.

Expected heterozygosity (H_e, in %) and Kullback–Leibler divergence for unobserved loci (KL × 10²), number of selected candidates (N_S), and number of SNPs (S) and unobserved loci (U) segregating across generations (t) when contributions are equalized (S_E) and when they are optimized using Li and Horvitz (S_{O_LH}) and VanRaden (S_{O_VR}) coancestry matrices computed with SNPs with MAF > 0.00 in a population of 20 individuals.

	SE						SO_LH *						SO_VR *
t	He	KL	NS	S	U		He	KL	NS	S	U		He	KL	NS	S	U
1	23.35	0.27	20	38,995	38,955		+0.04	+0.05	−1	−193	−233		+0.03	0.00	0	+31	+134
2	23.06	0.52	20	37,093	37,050		+0.06	+0.07	−1	−275	−335		+0.01	0.00	0	+52	+155
3	22.76	0.76	20	35,522	35,472		+0.10	+0.09	−1	−356	−410		−0.02	+0.01	0	−12	+104
4	22.48	0.99	20	34,166	34,119		+0.07	+0.11	−1	−390	−442		−0.02	−0.01	0	−16	+94
5	22.19	1.20	20	33,016	32,978		+0.08	+0.13	−1	−456	−528		−0.03	0.00	0	−69	+37
10	20.79	2.17	20	28,782	28,692		+0.17	+0.18	−1	−533	−563		−0.07	−0.03	−1	−269	−62
15	19.52	3.00	20	25,844	25,763		+0.24	+0.17	−1	−497	−563		−0.03	−0.07	−1	−400	−206
20	18.33	3.75	20	23,512	23,434		+0.37	+0.13	−1	−336	−424		−0.01	−0.12	−1	−429	−247
30	16.02	5.13	20	19,854	19,795		+0.79	−0.02	−2	+81	−59		+0.04	−0.25	−2	−469	−337
40	14.03	6.26	20	17,044	17,002		+1.15	−0.16	−1	+545	+377		+0.18	−0.43	−2	−432	−309
50	12.32	7.23	20	14,853	14,811		+1.39	−0.27	−1	+787	+592		+0.19	−0.52	−2	−433	−322

* S_{O_LH} and S_{O_VR} values are those deviated from S_E. Standard errors (computed across replicates) ranged from 1.15 × 10⁻⁴ to 3.37 × 10⁻⁴ for H_e and from 10 × 10⁻⁴ to 1.72 × 10⁻⁴ for KL.

In populations of size N = 20, individuals are more closely related than in populations of size N = 100 and the genetic variability is smaller. Thus, most (if not all) individuals were selected to be parents of the next generation with all management strategies across generations. It should be noted that the number of loci segregating in t = 0, when management started, was substantially smaller when simulating populations of size N = 20. In order to investigate if the differences observed between N = 20 and N = 100 are a consequence of the different number of loci segregating in t = 0, a scenario with N = 100 starting with the same number of SNPs as in the scenario with N = 20 (about 40,000 SNPs) was simulated. The results indicate that the differences between scenarios with different N were due to the population size and not to the different number of loci (results not shown).

3.3. Effective Population Size

Table 4 shows estimates of N_e across generations for the different scenarios simulated. For N = 100, estimates of N_e were around 200 individuals under strategies S_E and S_{O_VR}. This is the expected value for N_e when contributions are equalized since N_e is approximately equal to 2N. However, under strategy S_{O_LH}, estimates of N_e were unreasonable as they took negative values in the initial generations. In later generations, N_e became positive but did not reach a stable value. For N = 20, estimates under strategies S_E and S_{O_VR} were around 40 individuals, as expected. Estimates of N_e under strategy S_{O_LH} were between 6% and 50% higher than under strategy S_E.

Table 4.

Effective population size (N_e) across generations (t) when contributions are equalized (S_E) and when they are optimized using Li and Horvitz (S_{O_LH}) and VanRaden (S_{O_VR}) coancestry matrices in populations of different sizes (N).

		N = 100			N = 20
t		SE	SO_LH	SO_VR	SE	SO_LH	SO_VR
1		188.21	−111.90	195.55	36.92	42.27	40.40
5		199.07	−855.78	197.46	36.78	41.24	34.31
10		191.56	−5777.32	193.05	38.54	40.81	41.77
15		203.50	1855.71	194.54	36.65	45.41	43.18
20		202.62	1033.03	201.52	40.61	47.25	40.02
25		190.44	636.00	209.85	40.20	47.08	42.02
30		193.58	670.07	209.79	36.45	53.03	38.57
35		193.30	524.97	206.03	33.41	50.28	44.62
40		204.95	601.67	212.53	36.94	47.91	49.68
45		207.44	703.31	205.00	37.52	48.50	40.09
50		206.86	481.08	213.02	41.99	46.20	38.53

4. Discussion

Using computer simulations, this study has compared two different management strategies in terms of two important criteria in genetic conservation programs, i.e., genetic diversity (H_e) maintained and changes in allele frequencies. Both strategies optimize contributions for maintaining diversity but differ in the genomic coancestry matrix used in the optimization (θ_LH in strategy S_{O_LH} and θ_VR in strategy S_{O_VR}). Moreover, as a benchmark, the simplest management strategy proposed to maintain genetic diversity that implies equalizing the contributions of all candidates (strategy S_E) was evaluated.

The changes in allele frequencies were evaluated using the KL divergence criterion. The greater the value of KL, the greater the divergence of frequencies with respect to the frequencies in the base population. When the strategies were compared using the KL criterion, it was clear that strategy S_{O_LH} gives higher values than strategy S_{O_VR}, indicating that the latter is able to maintain allele frequencies closer to the original frequencies (lower KL values). On the other hand, with strategy S_{O_LH}, the population evolves differently as it pushes frequencies towards 0.5 and thus changes the genetic composition of the population more than strategy S_{O_VR}.

Pushing frequencies towards 0.5 as strategy S_{O_LH} does leads to higher genetic variability when measured as expected heterozygosity. Thus, the hypothesis raised by Gómez-Romano et al. [21] that using matrix θ_LH in OC designed for maintaining genetic diversity better achieves the objective (i.e., higher H_e) than using matrix θ_VR, but using the latter maintains allele frequencies closer to the initial frequencies, is confirmed. This was observed both in populations with N = 20 and in populations with N = 100 although the differences between both strategies were smaller with N = 20. This is because individuals in the smaller populations are more closely related and there are less options to choose among individuals and strategies behave more similarly.

Saura et al. [9] showed that the use of the pedigree-based coancestry matrix in OC maintained allele frequencies close to those of the initial population. This is related to the high levels of N_e obtained when minimizing pedigree coancestry (close to 2N), leading to reduced drift and little departures to the original frequencies. Additionally, several studies [10,12] have shown that OC based on pedigrees leads to less maintained genetic diversity than the use of genomic coefficients based on Nejati-Javaremi´s matrix [22]. This is due to the fact that genomic data provide realized estimates of coancestry, while pedigree data provide expected values. Therefore, results under the management of populations with OC using the pedigree-based coancestry matrix would be similar to those under S_{O_VR}.

Strategy S_{O_VR} was only slightly more efficient for maintaining frequencies than strategy S_E. This strategy tends to reduce the change in allele frequencies, which implies a reduced genetic drift [17]. The magnitude of drift is minimized when N_e equals approximately 2N, and it is well known that, when managing the population using pedigree information (as said before), this is achieved by equalizing contributions [6,28]. The small advantage of S_{O_VR} in terms of maintaining frequencies over S_E arises from the fact that the former uses realized relationships and detects real differences between individuals while S_E assumes homogeneous relationships. Contrarily, S_{O_LH} does not minimize drift but maximizes H_e by shifting frequencies towards 0.5. Thus, results from S_{O_LH} are quite different to those obtained under S_E in terms of the number of selected candidates and their optimal contributions.

Given that strategy S_{O_LH} brings the frequencies towards 0.5, H_e increased in the initial generations and this led to negative estimates of N_e in the largest population (N = 100). As generations go by, N_e becomes positive but with unrealistic very high values without attaining an asymptotic value. This was also observed by Toro et al. [23] who questioned the meaning of N_e when genomic coancestry matrices are used in OC. They showed an unpredictable behavior for N_e when using the similarity genomic matrix of Nejati-Javaremi et al. [22], which has a correlation of 1 with the θ_LH matrix used here [5,16,29]. However, our results show that when using θ_VR in OC, estimates of N_e were close to the expected value when equalizing contributions (approximately 2N). As has been discussed above, the results from strategy S_{O_VR} were very similar to those from strategy S_E given that both tend to minimize drift. For the smallest population considered (N = 20), estimates of N_e were close to 2N not only with S_{O_VR} but also with S_{O_LH}. In such a small population, there are fewer options to choose among individuals and most of them are selected to contribute (Table 3). Thus, the three strategies investigated led to similar results.

Strategy S_{O_LH} led to higher H_e but also to a higher loss of segregating loci than strategy S_{O_VR}. In the largest population (N = 100), the percentage of alleles lost for unobserved loci at t = 1 was 13% and 9% with S_{O_LH} and S_{O_VR}, respectively (Table 1). The difference in both management strategies in terms of the number of alleles lost could be due to a different number of individuals selected to contribute to the next generation that was lower with S_{O_LH}. It must be emphasized that the mean coancestry of each individual with all the candidates (including the individual), i.e., the marginal of the coancestry matrix, is a useful concept for understanding the different numbers selected with both strategies. This is because the marginal of the coancestry matrix is a measure of the ‘relevance’ of each individual, in terms of the degree of genetic information shared with the rest, and the optimal solutions will depend on all relationships between candidates. Its value is the same for all candidates when considering θ_VR. Then, all candidates are equally useful and should be selected as it was observed minimizing the global coancestry through OC using θ_VR (strategy S_{O_VR}). However, when considering θ_LH, the average coancestry of individuals AA (homozygous for the minor allele) is lower than that of individuals BB (homozygous for the major allele), since individuals AA harbor genetic information that is underrepresented (i.e., they carry the rarer allele) and should be favored for selection and contributions. Therefore, OC using θ_LH minimize the objective function when selecting the same number of AA and BB candidates. This leads to an increase in the frequency of allele A (actually to 0.5 in a single generation in this example with only one locus) while frequencies stay unchanged when using θ_VR.

Fernández et al. [13] claimed that OC management using coancestry matrices based on allele sharing moves frequencies to intermediate values and reduces the probability of losing alleles. In fact, these authors observed that strategies that maximize heterozygosity, by managing contributions from parents, keep levels of allelic diversity as high as strategies that maximize allelic diversity itself. Their results were obtained when applying OC using the similarity genomic matrix of Nejati-Javaremi et al. [22], calculated with up to 40 multiallelic markers, but the same could be expected when using θ_LH given that correlation between both matrices is 1. However, we have obtained solutions which maintain genetic diversity (H_e) but result in a higher number of fixed loci and this could be due to the different numbers of markers used in both studies.

To understand these contrasting results, we carried out extra simulations to compare observed with expected values for the number of fixed loci under both management strategies (i.e., S_{O_LH} and S_{O_VR}). In this extra scenario, a population with N = 20 individuals was managed during four generations, with different numbers of SNPs used for the calculation of the coancestry matrices (20 and 1000). A single chromosome was simulated. The expected number of fixed SNPs (ES_f) was estimated using the solutions that came out of each optimization before generating the offspring, following Fernández et al. [13]. Thus, ES_f was computed as ${\displaystyle \sum }_{k=1}^2{\displaystyle \prod }_{i=1}^{N}pro{b}_{ki}$, where $pro{b}_{ki}$ is the probability of individual i not transmitting allele k. If parent i carries a unique type of allele (that is, homozygous for the h allele) and leaves descendants, $pro{b}_{ki}$ is 0 if k = h and 1 if k ≠ h. If it carries two different alleles (that is, heterozygous), the probability is $pro{b}_{ki}={\left(0.5\right)}^{c_i}$, where c_i is the number of offspring to be contributed by parent i. ES_f value can be averaged then across loci. Table 5 shows that expected and observed numbers of SNPs becoming fixed each generation were close. When using only 20 SNPs, even though only seven–eight individuals are selected with S_{O_LH}, the expected (observed) number of SNPs that become fixed is lower than with S_{O_VR}. However, when the number of SNPs used was increased, the trend reversed and the expected (and observed) number of fixed SNPs becomes lower for S_{O_VR} than for S_{O_LH}, even when the number of selected individuals increases for S_{O_LH}. The explanation for this performance could be that, with many markers, S_{O_LH} is able to find a solution with higher mean H_e by keeping loci with high MAF and allowing SNPs with rare alleles to become fixed.

Table 5.

Number of selected candidates (N_S) and expected (ES_f) and observed number of fixed SNPs (S_f) across generations (t) when contributions are optimized using Li and Horvitz’s (S_{O_LH}) and VanRaden’s (S_{O_VR}) coancestry matrices computed with two different number of SNPs (S), for a population of 20 individuals.

		SO_LH				SO_VR
t	S	NS	ESf	Sf		NS	ESf	Sf
1	20	7	0.3	0		20	0.3	0
2		7	0.7	0		13	0.8	1
3		8	0.8	0		13	1.4	1
4		8	0.9	0		12	1.7	1
1	1000	15	21.7	21		20	17.6	18
2		16	38.9	37		19	34.6	33
3		15	54.6	52		19	50.9	47
4		15	68.6	64		18	66.3	60

The results show that the differences in maintained diversity (H_e) and divergence from the original frequencies (KL) between strategies S_{O_LH} and S_{O_VR} decreased when using only SNPs with a minimum MAF (MAF > 0.05 or MAF > 0.25) for computing the coancestry matrices. As mentioned above, S_{O_LH} promotes the contribution of individuals carrying rare alleles, as their coancestries with the rest of the population are smaller, and thus increases the frequencies of rare alleles. When the minimum MAF permitted increases, the number of rare alleles decreases, and the differences between the average coancestries between pairs of individuals decrease. In such situation, S_{O_LH} does not prioritize too much the contributions from any individual and leads to solutions that imply a higher number of candidates selected. Consequently, the results are closer to those obtained with strategy S_{O_VR}. Moreover, when using only SNPs with high MAF in t = 0 (i.e., initial frequencies are close to 0.5), the performance of S_{O_VR} (i.e., keeping those initial frequencies) is similar to the performance of S_{O_LH} (moving them to intermediate values). These observations are in agreement with results from Morales-González et al. [16] and Villanueva et al. [29], who found that the correlation between VanRaden’s and Li and Horvitz’s coefficients increases with increasing the MAF of the SNPs used.

Here, we have optimized contributions of parents for minimizing the loss of variability and then changes in frequencies have been evaluated. On the other hand, Saura et al. [9] optimized contributions of parents for minimizing changes in allele frequencies and then the loss of genetic variability was evaluated. An alternative to both approaches could be to consider simultaneously the control of variability and the allele frequency changes. Similar to the OC algorithm designed for maximizing genetic gain while restricting the rate of inbreeding [2,3,24] or for maximizing the phenotypic level for a trait of interest while restricting the loss in variability when creating base populations [30], one could develop an algorithm for minimizing the loss of variability while restricting the change in frequencies or, alternatively, for minimizing frequency changes while restricting the loss of variability. The specific objective would depend on the particular interest of the managers of the program. This kind of approach was followed by Fernández et al. [31] in the context of optimizing the sampling strategy for establishing a gene bank. In particular, they developed an algorithm that simultaneously allows targeting frequencies for alleles at a particular locus while controlling the genetic diversity of other unlinked loci.

It could be also possible to combine both coancestry matrices (θ_LH and θ_VR) in the objective function when the specific objective differs across genomic regions (i.e., in some regions the interest may be to maintain diversity, and in other regions the interest may be to maintain frequencies). Maintaining diversity may be of interest for regions associated with inbreeding depression for fitness-related traits and also for regions that harbor loci involved in general resistance to diseases (e.g., the major histocompatibility complex, MHC) as a high level of genetic diversity is desirable to ensure that the population can deal with potential new disease challenges [21]. Maintaining frequencies may be of interest in regions containing loci that have been under natural or artificial selection, and one wants to keep the genetic progress obtained. Gómez-Romano et al. [21] showed that the OC method using a matrix equivalent to θ_LH is efficient in maintaining H_e in specific regions and simultaneously restricts the loss of H_e in the rest of the genome. Their approach could be extended to include the use of θ_VR for minimizing the change in allele frequencies in some genomic regions. However, it has to be kept in mind that the higher the number of different parameters to be controlled, or the more regions to be treated differently, the lower the control of each objective one can expect.

In a conservation program, the maintenance of genetic variability throughout the genome is the general aim because usually there is no information available on the relevance of each genome region and the current or future use of the genetic variability present in particular regions. Therefore, it is better to conserve as much diversity as possible because if alleles are lost in a population, they will be no longer available. However, this strategy can lead to the maintenance or even an increase in the frequency of deleterious alleles. Different methods have been proposed to avoid this when using the OC method, including (i) selection of the best sib from the group of offspring generated by the selected parents [28] and (ii) combining selection with inbred matings [14] to allow for some kind of purging. Sonesson et al. [32] also proposed a model in which they tried to eliminate a disease from a population in different scenarios by explicitly performing selection against this condition. Currently, genomics can provide information on deleterious variability and the loci determining the occurrence of the disease [33], so a strategy where selection is made against these deleterious alleles [17], while you restrict the loss of variability in the rest of the genome, could be possible.

The amount of genetic variability retained was measured as the expected heterozygosity (H_e). However, other measures such as allelic diversity can be used [13,34]. Allelic diversity is essential from an evolutionary perspective, since the limit of selection response is determined by the initial number of alleles [35,36]. It is worth noting that strategy S_{O_VR} would be more efficient than strategy S_{O_LH}, not only to maintain allele frequency but also to maintain diversity when this is measured as the number of unobserved loci segregating. It is thus clear that the coancestry matrix to be used in OC when managing a particular genetic conservation program would be case specific.

Finally, it is worth mentioning that further work is needed to explore how the relaxation of some of the assumptions implicit in our simulations could affect the results obtained. Extra work would be necessary to investigate schemes with overlapping generations, variable population size over the management time frame, and different degrees of relatedness between the founders.

5. Conclusions

When applying strategy S_{O_LH}, more H_e is maintained than when applying strategy S_{O_VR} given that S_{O_LH} moves allele frequencies towards 0.5. However, S_{O_VR} maintained allele frequencies closer to those of the initial generation and more loci segregating than S_{O_LH}. Therefore, considering that conservation programs generally aim to increase genetic diversity, but it is also important to maintain population uniqueness, the choice of which genomic coancestry matrix is used in management may depend on which of these two goals is more important for each particular case. When a subset of SNPs with MAF > 0.05 or MAF > 0.25 is used to estimate coancestry matrices, the differences between both strategies in terms of both H_e and KL were reduced. The differences between strategies were smaller for populations of smaller sizes given that in a smaller population it is more difficult to differentiate between individuals.

Author Contributions

Conceptualization, J.F., R.P.-W. and B.V.; methodology, E.M.-G., J.F. and B.V.; software, E.M.-G. and J.F.; formal analysis, E.M.-G.; writing—original draft preparation, E.M.-G., J.F. and B.V.; writing—review and editing, M.Á.T. and R.P.-W.; supervision, B.V.; project administration, J.F. All authors have read and agreed to the published version of the manuscript.

Funding

The research leading to these results has received funding from the Ministerio de Ciencia, Innovación y Universidades, Spain (grant CGL2016-75904-C2-2-P). R. Pong-Wong is funded by the European Union’s Horizon 2020 research and innovation programme under the Grant Agreement n°772787 (SMARTER) and the Biotechnology and Biological Sciences Research Council through Institute Strategic Programme Grant funding (BBS/E/D/30002275).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The codes to perform the simulations are available from the corresponding author on reasonable request.

Conflicts of Interest

The authors declare that there are no competing interests with respect to the authorship or publication of this article.