Abstract
Exciton transport and exciton–exciton interactions in molecular aggregates and polymers are of great importance in natural photosynthesis, organic electronics, and related areas of research. Both the experimental observation and theoretical description of these processes across time and length scales, including the transition from the initial wavelike motion to the following long-range exciton transport, are highly challenging. Therefore, while exciton dynamics at small scales are often treated explicitly, long-range exciton transport is typically described phenomenologically by normal diffusion. In this work, we study the transition from wavelike to diffusive motion of interacting exciton pairs in squaraine copolymers of varying length. To this end we use a combination of the recently introduced exciton–exciton-interaction two-dimensional (EEI2D) electronic spectroscopy and microscopic theoretical modelling. As we show by comparison with the model, the experimentally observed kinetics include three phases, wavelike motion dominated by immediate exciton–exciton annihilation (10–100 fs), sub-diffusive behavior (0.1–10 ps), and excitation relaxation (0.01–1 ns). We demonstrate that the key quantity for the transition from wavelike to diffusive dynamics is the exciton delocalization length relative to the length of the polymer: while in short polymers wavelike motion of rapidly annihilating excitons dominates, in long polymers the excitons become locally trapped and exhibit sub-diffusive behavior. Our findings indicate that exciton transport through conjugated systems emerging from the excitonic structure is generally not governed by normal diffusion. Instead, to characterize the material transport properties, the diffusion presence and character should be determined.
We measure excitation energy transport in conjugated polymers using direct observation of exciton pair dynamics.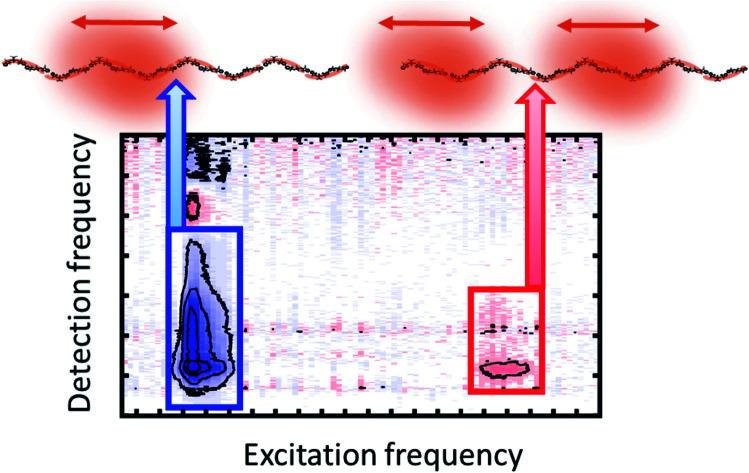
Introduction
Exciton dynamics in molecular aggregates is of interest both for natural and artificial light harvesting1–3 such as in conjugated polymers. The absorbed light energy is in both cases transported in the form of electrically neutral excitons through the light-harvesting molecules to a site where charge separation occurs.4 In photosynthesis this site is the reaction center, in organic photovoltaics the heterojunction interface. For the function of the light-harvesting devices, exciton transport and exciton–exciton interaction (EEI) are thus among the key properties.5,6 A direct observation of these processes is challenging. Ideally one needs to observe both the initial ultrafast excitation dynamics and the subsequent long-range, on average isoenergetic, energy transport.
The usual method of choice for measuring the initial dynamics is time-resolved spectroscopy of transient absorption (TA) type. There, a pump pulse triggers one-exciton dynamics, which are subsequently interrogated by the probe pulse.7 In the description of perturbation theory, this is a third-order spectroscopy with respect to the number of interactions with the laser electric field.8,9 While traditional TA spectroscopy employs one pump and one probe pulse, an extension using a pair of pump pulses is offered by coherent two-dimensional electronic spectroscopy (2DES).10–15 The resulting frequency resolution of both the pump and the probe step allows the analysis of lineshapes,16 transition couplings,17 coherent dynamics,18 state-to-state population transfer kinetics,19–21 and coupling to dark states such as charge-transfer states.22 In the double-quantum coherence variant of third-order 2DES the energetic positions and lineshapes of higher excited/biexciton states can be probed as well, though their kinetic evolution is not accessible for lack of another time variable.23
Despite the power of the technique, third-order spectroscopy is not well-suited for measurement of long-range exciton transport and exciton–exciton interaction. The reason is that, in the interpretation of the dynamics, one assumes an observed exciton to be independent of all other excitons in the sample, i.e., an interaction-free scenario. Because long-range transport of a single exciton through an extended aggregate (polymer, photosynthetic membrane, etc.) does not lead to spectral changes to the aggregate absorption, it is invisible for third-order spectroscopy. Concerning EEI, if it is observed at all, this is typically viewed to be an undesired artifact arising from too high excitation density. An exception is the biexciton decay visible in the two-exciton lineshape, as it contributes to rapid dephasing.24 However, to disentangle two-exciton kinetics from the lineshape alone is a formidable task, unfeasible for any interaction on longer timescales such as diffusive motion.
When applied carefully, studying the excitation power dependence of transient absorption can reveal valuable information about EEI.25–30 The EEI signal is, however, present merely as a power-dependent perturbation of the single-exciton time-dependent spectra. It is here that one of the key advantages of higher-order nonlinear spectroscopy comes into play. An extended nonlinear spectroscopy such as 2DES can in higher orders directly observe the biexciton dynamics in time.24,31–36
Next to power-dependent annihilation, spectroscopy methods to observe the long-range exciton transport include spatially resolved transient absorption or emission37,38 and surface or bulk quenching.39,40 Despite being powerful and widespread, all these techniques have their limitations. In transient absorption or photoluminescence microscopy, the temporal and spatial resolution are intertwined, limited by observable changes within the diffraction limit.37 Surface quenching relies on well-defined, homogeneous sample morphology, and, together with the bulk quenching, measures the average transport behavior.41
The mentioned techniques are commonly used to determine exciton transport properties such as the diffusion coefficient and diffusion length in a wide spectrum of materials.3,42 The standard procedure for evaluating the data from the various measurements is to assume normal diffusion of the excitons,43,44 often accompanied by a calculation of a (generalized) Förster radius.42 Although there is both experimental45 and theoretical46,47 evidence for occurrence of anomalous diffusion in the presence of exciton delocalization and/or energetic disorder, the normal diffusion assumption is rarely questioned in practice. In this work we challenge this assumption, observing anomalous, trapped diffusion of excitons. In the present text we employ the term “diffusion” in a general way to signify the process by which excitons move through the system as true quasiparticles, but we will then go on to show that the kinetic behavior does not, in general, follow the normal diffusion equation.
In our approach we probe the interaction of exciton pairs, using our recently developed fifth-order exciton–exciton-interaction two-dimensional (EEI2D) spectroscopy. This technique facilitates a direct observation of exciton–exciton interactions.48–50 In EEI2D, exciton–exciton annihilation is observable in the evolution of the signal amplitude as a function of population time. This technique can therefore be used not only to study EEI, but one can utilize the annihilation as a tool to probe single-exciton propagation dynamics even in the absence of spectral changes during transport.
We employ EEI2D spectroscopy to study biexciton dynamics and interactions in squaraine-based copolymers.51 Squaraine copolymers provide an excellent combination of polymer and J-aggregate properties. Previous studies have shown that these copolymers support large exciton diffusion lengths51 and can serve as efficient electron donors.52 This makes them interesting for various applications such as in heterojunction solar cells,52 thin-film transistors,53 or OLEDs.54 The optical properties of such conjugated polymers are determined by the excitonic structure.55 Locally, the exciton delocalization leads to wavelike dynamics, connected to phenomena such as supertransfer.56 On the long range, however, the exciton transport is typically described as diffusive. The current paradigm is that after photoexcitation the excitonic states are established, possibly with accompanying polaron formation.57 The excitons then diffuse by a classical random walk through the polymer.5 While separately the diffusive transport and wavelike motion have been described, how the former emerges from the latter is a subject under debate,56 typically ignored when discussing the exciton migration.2,51 Unlike in previous studies,58 we are able to systematically vary the length of the synthesized polymers. This additional degree of control enables us to study the transition from mostly wavelike to predominantly diffusive excitation dynamics.
Experimental and theoretical methods
Polymer synthesis
Synthesis of the [SQA–SQB]n copolymer was carried out via Pd-catalyzed Suzuki coupling, as described previously,59 and leads to a virtually complete consumption of monomer compounds.51 The crude polymer was subsequently partitioned into four fractions with varying molecular weight distributions by means of preparative GPC (CHCl3). Experimental procedures and characterization data of each fraction can be found in the ESI†. The important entries are displayed in Table 1. The degree of polymerization, Xn, is calculated by dividing the number average molecular weight, Mn, by the molecular weight of one [SQA–SQB] building block (1398.04 g mol−1). The labels P5, P11, P18, and P19 thus indicate the most probable number of constituting dimers for each fraction. A measure of the polymer size distribution is the polymer polydispersity, Đ, calculated by dividing the weight average molar mass Mw by the number average molar mass Mn. The smaller polymer fractions have comparably higher polydispersities. This can be explained by the presence of a relatively high amount of small oligomers and potential cyclomers, while simultaneously extending the size distribution to longer polymers.
Summary of GPC data. Mn is the number average molecular weight, Xn the degree of polymerization, and Đ the polydispersity.
| Label | M n/g mol−1 | X n | Đ |
|---|---|---|---|
| P19 | 26 200 | 19 | 1.62 |
| P18 | 24 700 | 18 | 1.54 |
| P11 | 15 200 | 11 | 2.11 |
| P5 | 7200 | 5 | 2.88 |
Spectroscopic measurements
For the presented EEI2D experiments the output of a Ti:Sa laser (Spitfire Pro, Spectra Physics, 1 kHz repetition rate, λ = 800 nm) was focused into a fused-silica hollow-core fiber (UltraFast Innovations) filled with a mixture of argon and neon in order to generate a broadband white-light continuum. The resulting broadband pulses were compressed using a chirped-mirror compressor. The compressed pulses were split into two parts serving as the probe and the pump. The probe beam, broadband with a spectrum extending from 650 nm to 850 nm (see Fig. S12 in the ESI†), was delayed by a motorized delay line (M-IMS600LM, Newport) and was focused into the sample. The other fraction of the light was used as the pump beam and received additional pre-compensation of pulse-shaper dispersion with a grism compressor. Next, the beam was guided through an acousto-optical programmable dispersive filter (DAZZLER, Fastlite), which was used to select a spectral region out of the continuum such that nearly-bandwidth-limited pulses of 14 fs duration were created after optimized DAZZLER pulse compression. The pump pulse was characterized via a collinear FROG measurement. Both beams were focused and spatially overlapped in a 200 μm cuvette under a small angle of 2°. The polarization of the beams was set to the magic-angle condition. As a signal, the spectrum of the probe beam was measured after passing the sample. For the measurement of 2D spectra of the different polymers the DAZZLER was used to split the pump pulse into two phase-locked time-delayed replicas whose time delay was varied from 0 fs to 66.78 fs in a step size of 0.42 fs. The chosen scanning range determined the resolution of the excitation axis to 249.7 cm−1. The resolution of the probe axis is fixed by the detector (ActonSpectraPro 2558i assembled with camera Pixis 2K, Princeton Instruments) and is 20 cm−1. In order to extract the desired 2D signal, pump and probe beams were both chopped, by two different choppers (MC2000, Thorlabs) with frequencies of 200 Hz (probe) and 100 Hz (pump). Four different combinations of pump and probe interactions were isolated: a background with both pump and probe blocked, a scattering contribution with the probe blocked and the pump open, the pumped probe spectrum with both beams open, and the reference of the probe with only the pump blocked. All contributions were integrated over 5 ms, i.e., five laser pulses. For the spectroscopic measurements the squaraine copolymers were dissolved in toluene.
Theoretical simulation
To simulate the measured fifth-order spectra, we used the nonlinear response-function formalism.8,9 This approach allows for detailed analysis of the excitonic structure, and for explicit treatment of effects such as wavelike exciton motion and annihilation. The calculation consists of considering all fifth-order Liouville-space pathways of the system density matrix interacting with the sequence of the laser pulses. Thanks to spectral integration in the analysis of experimental results as will be explained below, it is sufficient to calculate the amplitudes of the pathways and it is not necessary to evaluate the individual lineshapes for the fifth-order spectra kinetics. This enables us to describe extended systems, such as up to the 38-chromophore-long P19 polymer, explicitly.
The system was described by a Frenkel exciton model. Each squaraine molecule was represented by a three-level system with one ground state, one first excited state, and one higher excited state. We considered electronic coupling only between transitions of neighboring chromophores, both within and between the dimers. The resulting Hamiltonian of N dimers was diagonalized (see Section S1 in the ESI† for the full procedure and Fig. S1† for an overview of the assumed couplings and the resulting energy structure), yielding 2N one-quantum states (i.e., one-exciton states (|e〉)), 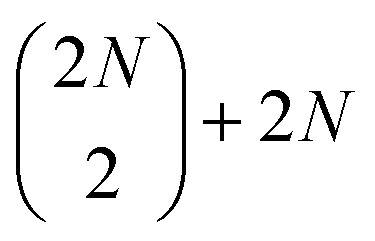 two-quantum states (i.e.,
two-quantum states (i.e., 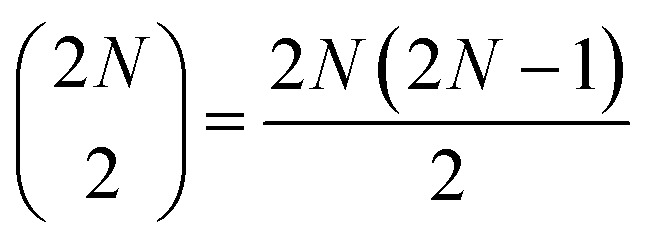 two-exciton states (|ee〉), mixed with 2N higher-excited molecular states (|f〉)), and
two-exciton states (|ee〉), mixed with 2N higher-excited molecular states (|f〉)), and 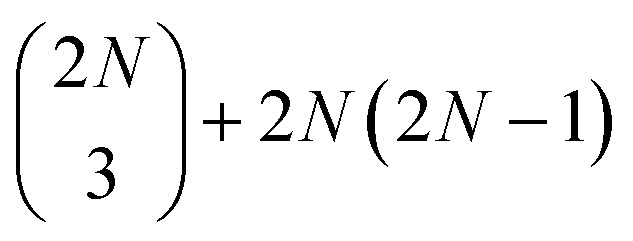 three-quantum states (i.e.,
three-quantum states (i.e., 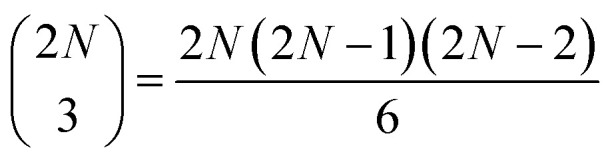 three-exciton states (|eee〉) mixed with 2N(2N − 1) combined higher- and one-exciton states (|fe〉)). The strength of the transitions between the state manifolds was obtained by transforming the transition dipole-moment operator into the eigenstate basis. The exciton delocalization length was calculated in the standard way from the inverse participation ratio as
three-exciton states (|eee〉) mixed with 2N(2N − 1) combined higher- and one-exciton states (|fe〉)). The strength of the transitions between the state manifolds was obtained by transforming the transition dipole-moment operator into the eigenstate basis. The exciton delocalization length was calculated in the standard way from the inverse participation ratio as 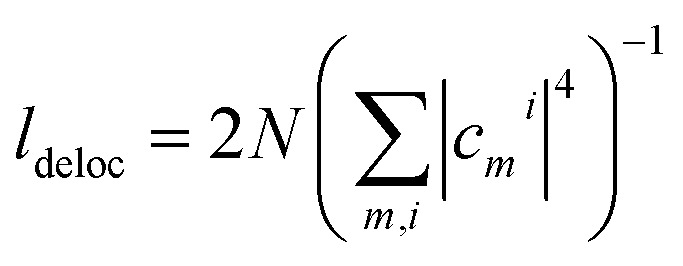 , where the cmi are coefficients of the transformation from the site (index m) to the excitonic (index i) basis and N is the polymer length. The system environment was described as a weakly interacting vibrational bath. The vibrations consisted of a continuum of low-frequency modes and one underdamped, intramolecular mode at 1280 cm−1. This relatively pronounced vibrational mode is visible in the absorption spectra and contributes to the energy transfer, as its frequency is close to the energy gap between the squaraine A and squaraine B transitions (1200 cm−1). The one- and two-quantum state dynamics were described by Redfield theory, while the relaxation from two-quantum to one-quantum states was described within a Lindblad formalism.9 All the equations used for the calculations can be found in the ESI.†
, where the cmi are coefficients of the transformation from the site (index m) to the excitonic (index i) basis and N is the polymer length. The system environment was described as a weakly interacting vibrational bath. The vibrations consisted of a continuum of low-frequency modes and one underdamped, intramolecular mode at 1280 cm−1. This relatively pronounced vibrational mode is visible in the absorption spectra and contributes to the energy transfer, as its frequency is close to the energy gap between the squaraine A and squaraine B transitions (1200 cm−1). The one- and two-quantum state dynamics were described by Redfield theory, while the relaxation from two-quantum to one-quantum states was described within a Lindblad formalism.9 All the equations used for the calculations can be found in the ESI.†
Exciton–exciton annihilation occurs between spatially overlapping excitons via mixing with and transfer to the higher excited states and subsequent relaxation to the one-exciton manifold. This avoids the commonly used phenomenological description of using an effective annihilation rate for overlapping excitons. All of the calculated quantities were averaged over a disorder in the chromophore energies, where for simplicity we assumed independent Gaussian disorder of all chromophore transition energies. The parameters used for the calculation are presented in the Theory section in the ESI.† There we also describe how we determined the parameters and discuss the robustness of our results against reasonable parameter variation. All the parameters used for the calculations (Table S1 in the ESI†) are well in the range used in previous work on squaraine dimers and copolymers.27,51,60
Results and discussion
Linear spectra
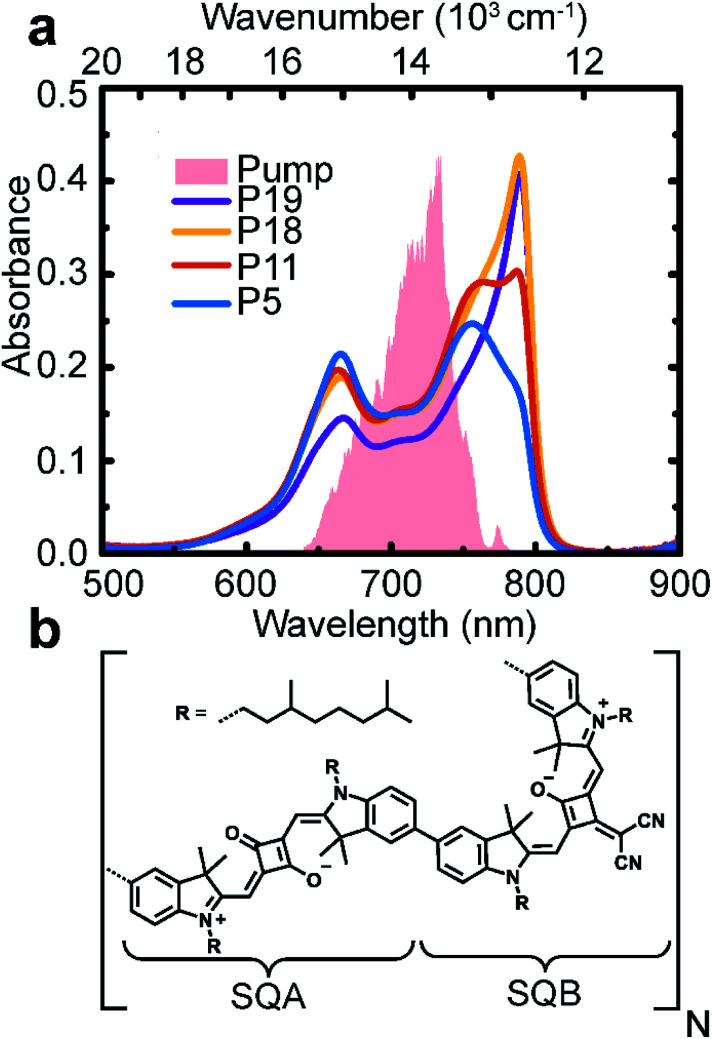
First, we characterized the polymers by their linear absorption and fluorescence spectra. The absorption spectra show two main peaks (Fig. 1a). These originate from the SQA and SQB states (dimer unit structural formula shown in Fig. 1b), further split by excitonic interaction into two bands of excitonic states. The fluorescence then occurs from the excitonic states occupied with quasi-thermal-equilibrium probability distribution. In Fig. S6 in ESI† we show both the absorption and fluorescence spectra, compared to theoretical simulations.
Fig. 1. Polymers of varying length. (a) Absorption spectra of polymers in toluene solution of length 5 (blue), 11 (red), 18 (yellow), and 19 (violet) SQA–SQB dimers. The pump pulse spectrum is given as a shaded area. (b) Chemical structure of the polymer with one SQA–SQB dimer unit.
From the absorption spectral shape, a significant disorder and heterogeneity is apparent, which is largely not present in the fluorescence spectra. From the comparison with theory, it is clear that this additional heterogeneity is not a feature of our excitonic model. A possible explanation is an increased and/or non-Gaussian disorder in the polymer ground state. As we are interested in the excited-state dynamics, this feature is not crucial. The peak splitting and oscillator-strength redistribution are characteristic of excitonic splitting; the small Stokes shift and narrow peak width indicate weak interaction with the environment, justifying the concept of delocalized excitons.
Two-dimensional electronic spectroscopy
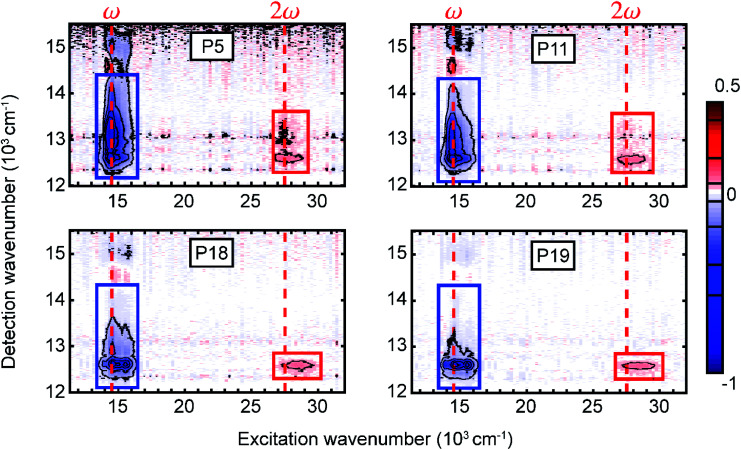
The measured 2D electronic spectra are presented in Fig. 2, acquired at a waiting time of 991 fs. On the excitation axis, we can clearly distinguish the conventional absorptive 2D spectrum around the pump central frequency (denoted ω) and the fifth-order EEI2D spectrum around double the pump central frequency (denoted 2ω). The peak position on the excitation axis is given by the overlap of the absorption spectrum with the pump spectrum (Fig. 1a, shaded area). The position of the 2D spectra is shifted along the detection axis away from the diagonal position (for which excitation and detection wavenumber would be the same) to smaller detection wavenumbers. This is due to the excitonic energy relaxation and the usage of a broader probe spectrum (compared to the pump spectrum) that allows us to cover the lowest-energy parts of the sample absorption. With increasing polymer length, the peak narrowing and red-shift become more apparent, in agreement with the increased J-aggregate character as already visible in the linear absorption spectrum. The horizontal peak-shape elongation along the excitation axis seems characteristic for the fifth-order measurements.48 Due to the lack of pronounced spectral features and large computational effort in corresponding simulations, we do not attempt to analyze the spectral shapes in detail. Instead, we integrate the fifth-order peak region and focus on the dynamics of the signal amplitude as a function of population time. This provides direct information about the exciton dynamics and exciton–exciton annihilation.
Fig. 2. Measured two-dimensional electronic spectra for the four copolymers in toluene solution at population time T = 991 fs. We distinguish the conventional absorptive 2D (blue rectangle) and fifth-order EEI2D (red rectangle) spectra arising around the fundamental pump wavenumber or its double, respectively (red dashed lines). The rectangles indicate regions of interest for calculating integrated signals that are further analyzed as a function of the population time.
Polymer length dependence
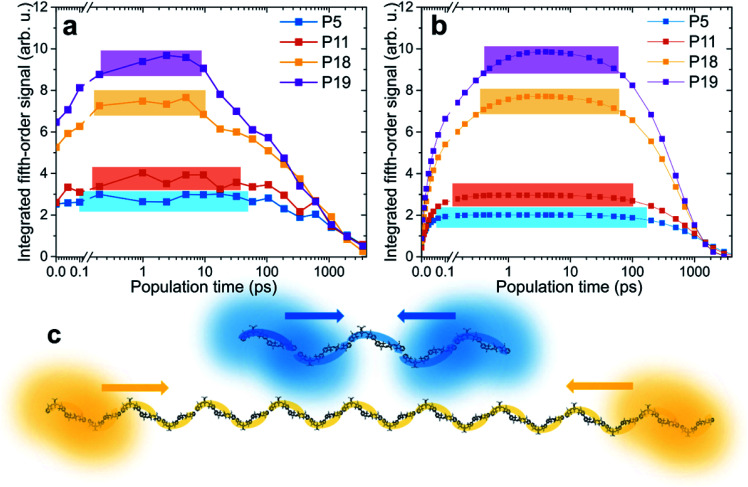
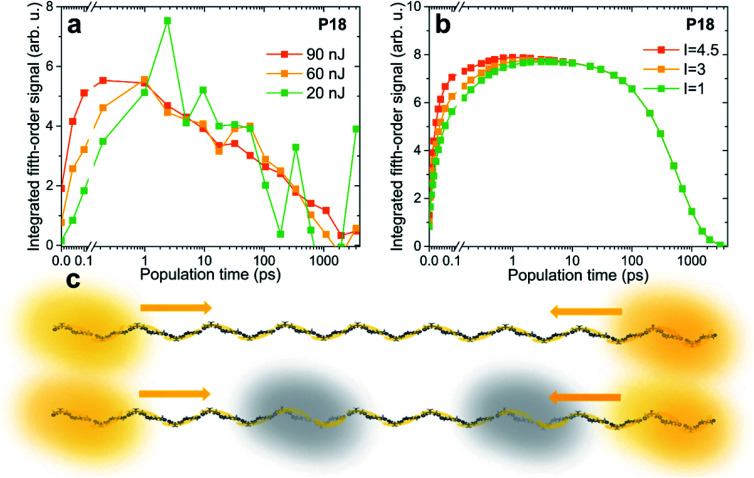
In Fig. 3 the amplitude of the fifth-order signal can be followed in population time across five orders of magnitude from fs to ps to ns, with Fig. 3a containing the experimental and Fig. 3b the theoretical traces. Starting from an initial value, the dynamics can be separated into three phases. First, we find a rapid rise due to the annihilation of excitons delocalized over the same chromophores. In principle, also a signal directly from the higher chromophore excited states contributes in this phase. However, as we verified by our calculations, for the system of our size and parameters, the contribution directly from higher states is negligible (see Fig. S7 in the ESI†). This also means that, in a simplified way, the signal can be viewed as originating from annihilated excitons at the given time. In the second phase of the kinetics, the signal rises slowly, reaching a plateau. This part is dominated by exciton transport along the polymer chain. As we will show by comparison with theoretical calculations, the transport has sub-diffusive character. Finally, the signal decays with the exciton lifetime. The lifetime decreases with polymer length as a result of increased probability of formation of a quenching defect.40 This dependence is approximately linear in the studied range (see Fig. S8 in the ESI†). The colored rectangles in Fig. 3 mark regions for which the signal reaches its maximum plateau (the amplitude threshold is calculated as 90% of the maximum value, obtained by fitting the signal peak, for details see Fig. S9 in the ESI†).
Fig. 3. Time-dependent results from EEI2D spectroscopy. (a) Measured and (b) calculated evolution of integrated fifth-order signals as a function of population time. The colors indicate the varying length of the polymers. The rectangles determine the regions within which the signal exceeds 90% of its maximum (see text for details). The data were normalized on the decaying tail. (c) Exemplary illustration of excitons in P5 and P18 polymers. The excitons are delocalized over a significantly larger fraction of the polymer in P5 than in P18 and therefore interact sooner after photoexcitation.
Unlike our previous pump–probe and third-order 2D spectroscopy study on squaraine homopolymers, this work does not investigate in detail the initial ultrafast local exciton relaxation, which occurs within the first 100 fs.58 Instead, we follow the transport of the excitons along the polymer across time scales. Let us focus on the changes with varying polymer length. For the shortest polymer, P5, the signal rises very fast, basically starting from the plateau, stays constant from 0.1 to 100 ps, and then decays. In contrast, with increasing polymer length, the exciton diffusion phase becomes increasingly prominent and the signal reaches its maximum at later times. When assessing the magnitude of the observed changes, one has to bear in mind the logarithmic scale of the time axis. The calculated traces agree very well with experimental ones, indicating that our model captures the exciton dynamics and interaction well. The source of the small deviations, mostly apparent at the initial times, is possibly the ensemble distribution of the polymer length (see ESI for details†). Another possibility are the higher-order effects of high excitation intensity, which we include and discuss below. Finally, the comparison of experiment and theory at the earliest times is made harder by the fact that the pump spectrum does not cover fully both absorption bands, which results in a difference in the initial exciton population. We especially emphasize the same trend in both experiment and theory, in that the plateau is reached at later times and the signal plateau is shorter for longer polymer chains (see systematic “nested” behavior of rectangular colored regions).
Based on our Frenkel-exciton model, the delocalization length of the excitons is found to be around 3.8 chromophores, that is, about 1.9 dimeric units (see Fig. 4 and its discussion below for exact values). The time scale of annihilation of two excitons localized on the same dimer is ultrafast (30 fs, see Table S1†). We have confirmed this value independently in another measurement, using SQA–SQB dimers, by evaluating the annihilation seen in fluorescence-detected 2DES for high excitation power (see Fig. S4 in the ESI†). While this represents the maximum annihilation rate found in the system, for any pair of excitons the rate will be effectively weighted by their co-localization. In other words, distant excitons do not interact, but once they meet, they annihilate very efficiently. In Fig. 3c, initially separated excitons are depicted exemplarily in the P5 and P18 polymers. In the short polymers, any two excitons have a larger probability, compared to long polymers, to be partially co-localized, and thus they interact practically immediately. In contrast, in the long polymers any exciton pair has a larger chance of being spatially separated, making exciton transport necessary prior to interaction. The key factor determining the biexciton dynamics is thus the exciton size (i.e., delocalization length) compared to the length of the polymer.
Fig. 4. The role of relative exciton delocalization length. (a) Calculated absolute (black) and relative (red) delocalization length as a function of polymer length (squares). Vertical lines indicate the studied polymers. Circles on the P11 line indicate the more and less disordered polymer variations of P11 studied in (b). (b) Calculated time dependence of the integrated fifth-order EEI2D signal for varying relative exciton delocalization. The effect is analogous to the varying length observed in Fig. 3. (c) Exemplary cartoon illustrating excitons with relative delocalization length of 9% (more disordered case, top) and 34% (more ordered case, bottom). The more delocalized excitons will meet and interact sooner after photoexcitation than the localized ones.
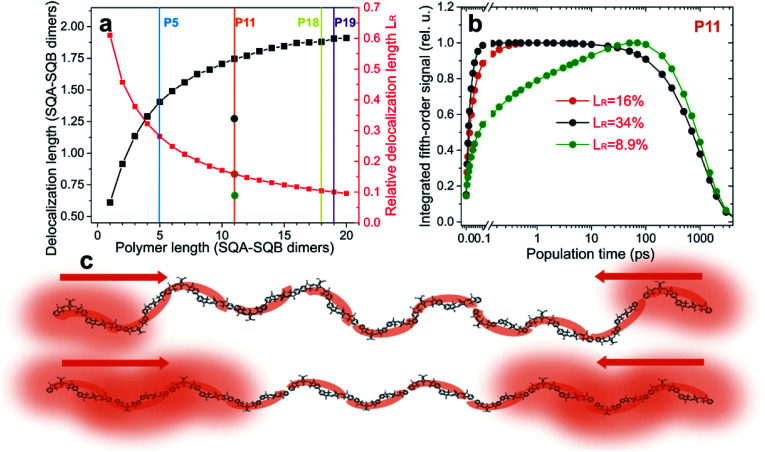
Relative exciton delocalization length
In Fig. 4a the calculated absolute (black) and relative (red) exciton delocalization length can be found as a function of polymer size, as determined from the model that successfully describes the EEI2D data. The increase of delocalization length with the chain length is an effect known from J-aggregates, where it was described in detail by Spano and others.61–63 While the absolute delocalization length increases with the polymer length, the relative exciton delocalization length decreases, in accordance with the trends observed in the amplitude traces of Fig. 3. To test the hypothesis that the key parameter for the observed annihilation kinetics is the relative exciton delocalization length, we altered in the model the polymer disorder. This leads to a change in the exciton delocalization (gray and green circles on the P11 line in Fig. 4a). In Fig. 4b, the corresponding simulated fifth-order signal dynamics are shown for polymer P11 with a relative exciton delocalization length of 8.9% (green, with a four times broader energetic disorder as compared to the model assumed for Fig. 3b and 4a), 16% (orange, normal disorder as assumed in the model), and 34% (gray, energetic disorder reduced to a quarter of the normal model). Clearly the transition in the kinetics is analogous to the one observed with varying polymer length, in that for large relative delocalization the annihilation occurs rapidly, while for relatively localized excitons the signal rises more slowly. In Fig. 4c the effect of relative delocalization length is depicted in a cartoon. Exciton–exciton annihilation will be fast whenever the excitons are, with appreciable probability, close to each other. This happens when they are larger compared to the size of the polymer (more ordered case, bottom) versus when they are smaller (more disordered case, top).
Excitation power dependence
An experimental parameter that has influence on the exciton density is the pump pulse intensity. We have conducted EEI2D measurements with varying pump power, the kinetics of which are compared in Fig. 5a. Clearly with higher excitation power the initial signal rise, attributed to exciton–exciton annihilation, gets faster, while the rest of the kinetics, i.e., the decay time, are unchanged within the noise level. While this might seem intuitive, the explanation is subtle. In third-order spectroscopy, such as pump–probe transient absorption, the temporal signal amplitude scales globally and proportionally to the excitation intensity as long as one is in the lowest order in the perturbative regime. Only when the intensity is high enough so that higher-order contributions are of importance, the kinetics (i.e., time constants and the shape of the transient) also change. In a pump–probe transient absorption experiment, such changes in the shape are typically viewed as an artifact of too high an intensity, leading to the unwanted presence of exciton–exciton annihilation. The same logic applies to the fifth-order EEI2D spectroscopy used here. As long as we are in the lowest respective perturbation order, only the signal amplitude of the EEI2D signal should increase with increasing excitation intensity, but the kinetics (including biexciton contributions) and thus the shape of the integrated transient shown in Fig. 5a should remain unchanged. The observed change in the curve shape can be explained by assuming that other excitons, not directly probed in the fifth-order signal, contribute to the annihilation rate. The dominant influence of these additional excitons is, similar to the situation in third-order pump–probe transients, the effect of annihilation of the observed excitons.
Fig. 5. Power dependence of the integrated EEI2D signal. Comparison of (a) measured and (b) calculated traces for excitation pulse energies of 20 nJ (green), 60 nJ (yellow), and 90 nJ (orange). (c) Larger excitation power leads to faster signal rise due to prompt annihilation by a population of excitons that are not directly probed, depicted in this cartoon in gray.
We can therefore modify our model to incorporate such additional excitons that are not observed directly but that influence the measured signal. In Fig. 5b the kinetics are calculated with the presence of such excitons, and the rise of the signal due to exciton–exciton annihilation is increasingly pronounced for larger excitation intensity, in agreement with the experimental data. In the model correction the quantity which directly scales with the excitation intensity is the population of the additional excitons, for details see the ESI.† While for weak intensity (green curve) there are practically no such excitons, for larger intensities (3 times larger in yellow and 4.5 times larger in orange), their presence becomes more probable. The cartoon in Fig. 5c illustrates the directly observed excitons in yellow and the additional ones in gray. At high excitation powers the excitons have a large chance to encounter one of these “dark” excitons and suffer annihilation. One could say that higher-order effects (i.e., higher than fifth order) effectively increase the exciton–exciton annihilation rate.
Explicit excitonic structure and dynamics
In this work, we use a microscopic quantum Frenkel-exciton model for the exciton structure and their annihilation. As a result, any effective behavior does not have to be postulated because the effects emerge naturally from the model. For instance, in each differently disordered polymer the structure of excitonic states is different. Moreover, the transition strength between ground state and one-exciton states differs from the transition between the one- and two-quantum manifold. Consequently, in each polymer the initially populated one- and two-exciton states have non-uniform probability of localization on the chromophores along the length of the polymer. This effect influences the rapid initial annihilation kinetics. While in our previous work we have attempted to take this effect into account effectively,48 here it arises implicitly from the excitonic structure. Exciton–exciton annihilation is typically described phenomenologically, by an annihilation rate dependent (often in a binary fashion) on the exciton overlap (co-localization). In our case the annihilation appears as a result of the coupling of the two-exciton states to the higher-lying states. The annihilation process is a result of the state mixing, population transfer, and internal conversion. As only neighboring chromophores are coupled, the annihilation rate becomes effectively weighted by the co-localization of the respective excitons. The exciton motion is not described by a phenomenological diffusion model here, but considered explicitly within the framework of Redfield theory. In our description the excitons relax down the ladder of energy eigenstates (to the local energy minima), and move in space in a wavelike fashion. We emphasize here that, as the polymers are composed of identical SQA–SQB dimer units, the one- and two-exciton probability will on average uniformly span the whole polymer chain. However, as the average of the kinetics over the disorder realizations is not equivalent to the kinetics on the average polymer chain, the explicit excitonic structure plays a role.
Crucially, as the effects just described emerge from a single microscopic description, they are not independent. Take for example the exciton–exciton annihilation, which depends on the mixing of the two-exciton and higher excited states, and also on the state coupling to the environmental vibrations. There are fixed relations between the transition couplings, transition strengths, and couplings to the bath vibrations for the one-exciton, two-exciton and higher excited states (see Table S1 in the ESI†). This leads to a firm connection between the initial contribution of higher excited states, exciton dynamics, spectral peak shapes and positions, and exciton–exciton annihilation. These inner constraints give us confidence that our theoretical description captures the physics correctly since it corresponds to experimental observations.
Exciton (sub-)diffusion
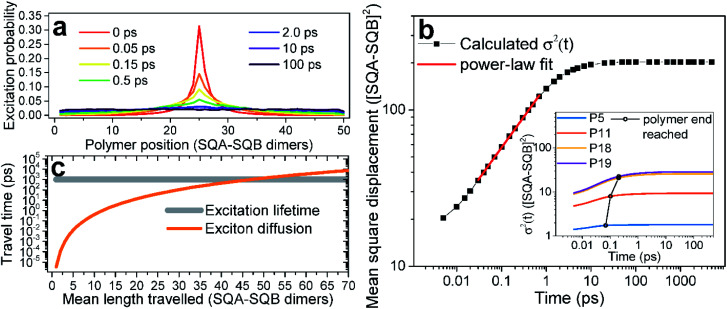
With a reliable model of the excitonic properties and their dynamics of the squaraine copolymers now established, we proceed to theoretically investigate the long-range exciton transport explicitly. To this end we consider a (hypothetical) very long polymer (P50), place an exciton in the middle of the chain (in the simulation, by making only the middle dimer absorb), and follow the dynamics of the excitation density. The spatial exciton probability distribution is depicted in Fig. 6a as a function of time (different colors). In Fig. 6b the excitation probability spreading is described by the mean square displacement of the excitation, 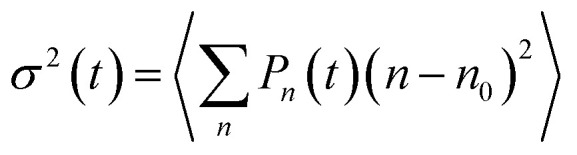 , where Pn(t) is the excitation probability of the n-th chromophore at time t and n0 is the initial mean position of the excitation (in the middle of the polymer), and angular brackets denote averaging over energetic disorder. After the initial ultrafast local exciton equilibration, a long period following a power dependence (linear in the logarithmic scale) is seen. This part can be effectively described by an anomalous exciton diffusion along the polymer. Finally, the displacement growth saturates when the exciton reaches the end of the polymer at long times. Similar curve shapes have been calculated in previous works modeling exciton dynamics in disordered systems such as polymers.46,47 To our knowledge this is the first time the transition from wavelike to (sub)-diffusive dynamics is explicitly tested experimentally, by direct comparison of the measured and calculated kinetics. In the inset of Fig. 6b, we see that the exciton spreads more with increasing size of the polymer (different colors), and also the exciton requires a longer time to reach the ends. This trend is indicated with a black line connecting those times at which the excitation reached the polymer ends and the free diffusion has thus ended.
, where Pn(t) is the excitation probability of the n-th chromophore at time t and n0 is the initial mean position of the excitation (in the middle of the polymer), and angular brackets denote averaging over energetic disorder. After the initial ultrafast local exciton equilibration, a long period following a power dependence (linear in the logarithmic scale) is seen. This part can be effectively described by an anomalous exciton diffusion along the polymer. Finally, the displacement growth saturates when the exciton reaches the end of the polymer at long times. Similar curve shapes have been calculated in previous works modeling exciton dynamics in disordered systems such as polymers.46,47 To our knowledge this is the first time the transition from wavelike to (sub)-diffusive dynamics is explicitly tested experimentally, by direct comparison of the measured and calculated kinetics. In the inset of Fig. 6b, we see that the exciton spreads more with increasing size of the polymer (different colors), and also the exciton requires a longer time to reach the ends. This trend is indicated with a black line connecting those times at which the excitation reached the polymer ends and the free diffusion has thus ended.
Fig. 6. Anomalous exciton diffusion. (a) Explicitly simulated spatial exciton probability distribution as a function of time for a hypothetical P50 polymer. The cusp shape is characteristic for sub-diffusive behavior. (b) Dynamics of the mean square displacement σ2(t) (black squares). Note the double-logarithmic scale. The red line indicates a power-dependence fit with a nonlinear coefficient of α = 0.4. The inset contains the mean square displacement for the shorter P5, P11, P18, P19 polymers, investigated experimentally. The black line connects the points where the exciton reaches the polymer ends, as determined by taking the first derivative of the σ2(t) and looking where it drops to half its maximum value. (c) The time it takes the exciton to travel a given mean path (orange). The point where the curve intersects the exciton lifetime (indicated in gray) determines the exciton diffusion length, which is in our polymers about 44 SQA–SQB dimers.
In the linear range we can fit the time dependence of the mean-square displacement with a power dependence, σ2(t) = Dtα. We obtain a coefficient of α = 0.4, signifying sub-diffusive dynamics of the disorder-trapped excitons, whereas conventional diffusion would correspond to α = 1. Coming back to the excitation probability distribution, Fig. 6a, sub-diffusive (trapped) diffusion character can be seen from the characteristic cusp shape.64 The generalized diffusion coefficient, also obtained from the fit, is D = 140([SQA − SQB])2 ps−0.4.This time-dependent diffusion coefficient contrasts with the commonly reported normal diffusion coefficients, used to determine the exciton diffusion length.42 From the fitted sub-diffusion equation, we can determine (Fig. 6c) the exciton diffusion length by asking how far the exciton could travel (orange curve) within its typical lifetime of 1 ns (gray line). By this we obtain a diffusion length of about 44 dimeric units, which corresponds to roughly 130 nm. This is in line with the previously reported diffusion length in these polymers,27 signifying their excellent transport properties, as this value is much higher than many comparable materials.42
Reporting a value for the diffusion length facilitates comparison with other materials known from the literature. Comparing directly the diffusion constant is not feasible due to the unconventional physical units of length2 time−0.4 in our case that is different from studies in which normal diffusion is assumed a priori. The main point of the present study, however, is not simply to report a value of diffusion length, but to identify the nature of exciton propagation. As shown above, the transport has a sub-diffusive, trapped character and differs substantially from the commonly assumed normal diffusion. Mathematically, in the absence of disorder-induced traps in the long-time (i.e., long-distance) limit the propagation behavior on an infinite polymer will converge to normal diffusion.46,47,65 This transition, however, depends on the system parameters. We have theoretically tested this transition by systematically varying the system parameters, see section “Transition from anomalous to normal diffusion” in the ESI.† Our findings indicate that in realistic, finite-length polymers the trapped excitons might never reach the normal diffusion regime within their lifetime. Contrary to the common assumption, the anomalous diffusion then determines the exciton transport properties.
Conclusions
We have used fifth-order exciton–exciton-interaction two-dimensional (EEI2D) electronic spectroscopy to observe exciton dynamics via exciton–exciton annihilation in squaraine copolymers as a function of the chain length. The observed kinetics include three phases: (i) initial delocalized motion, dominated by rapid annihilation of co-localized excitons, (ii) a long period of (sub-)diffusive motion of the excitons along the polymer chain, and (iii) signal decay due to the exciton lifetime. To explain the experimental results, we have developed a microscopic quantum model describing the excitonic structure and dynamics, including annihilation. From the comparison between the theory and experiment, we have found that the key property determining the observed transition from wavelike motion of delocalized excitons to the (sub-)diffusive transport is the exciton delocalization length relative to the length of the polymer. The delocalization length, about 1.9 dimeric units in our longer copolymers, is determined by the interchromophore coupling and polymer disorder. In short polymers the exciton is delocalized over a significant fraction of the polymer, and the exciton dynamics are strongly influenced by the finite size of the chain. The excitons quickly equilibrate and interact practically immediately. This is reminiscent of small excitonic antennas such as the LH2 light-harvesting complex of purple bacteria.26 In longer polymers the polymer disorder produces local exciton trapping, which leads to anomalous exciton diffusion (α = 0.4). The resulting picture of exciton transport comprises locally trapped excitons, localized over about two dimeric units, (sub-)diffusing along the polymer and annihilating whenever they meet. On a long polymer, in our model the exciton diffusion length reaches 44 dimeric units, that is about 130 nm. While these values already represent excellent exciton transport capability, at the same time the trapped diffusion, as evidenced by the current work, points to the polymer disorder as a target for improving the functional potential of these copolymers even further.
In a broader sense, our results show how phenomena such as exciton (anomalous) diffusion and annihilation, often treated phenomenologically, emerge from a microscopic excitonic structure. Perhaps surprisingly, in the developed description of the studied polymers the diffusion that emerges is of anomalous character, known from diverse other natural phenomena.66 This is in contrast to the commonly used normal diffusion. Future experimental and theoretical work will determine the generality and scope of the trapped, anomalous diffusion regime. This insight into the microscopic nature of exciton transport was made possible by applying the newly developed method of fifth-order EEI2D spectroscopy together with microscopic modeling. This approach is applicable to a wide class of other material systems, including natural and artificial light-harvesting materials. We expect it to become a key tool in future studies of exciton transport.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
We acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Grant No. 423942615 (T. B.) and 207601309 (T. B., C. L.), the European Research Council (ERC) – Grant No. 614623 (T. B.), and the Bavarian State Ministry of Science, Research, and the Arts – Collaborative Research Network “Solar Technologies Go Hybrid” (T. B. and C. L.).
Electronic supplementary information (ESI) available: Detailed theoretical description, sample characterization, synthesis. See DOI: 10.1039/c9sc04367e
Notes and references
- van Amerongen H., Valkunas L. and van Grondelle R., Photosynthetic Excitons, World Scientific Publishing Co. Pte. Ltd., 2000 [Google Scholar]
- Kippelen B. Brédas J.-L. Energy Environ. Sci. 2009;2:251. doi: 10.1039/B812502N. [DOI] [Google Scholar]
- Bardeen C. J. Annu. Rev. Phys. Chem. 2014;65:127–148. doi: 10.1146/annurev-physchem-040513-103654. [DOI] [PubMed] [Google Scholar]
- Scholes G. D. Fleming G. R. Olaya-Castro A. van Grondelle R. Nat. Chem. 2011;3:763–774. doi: 10.1038/nchem.1145. [DOI] [PubMed] [Google Scholar]
- Brédas J.-L. Norton J. E. Cornil J. Coropceanu V. Acc. Chem. Res. 2009;42:1691–1699. doi: 10.1021/ar900099h. [DOI] [PubMed] [Google Scholar]
- Mayer A. C. Scully S. R. Hardin B. E. Rowell M. W. McGehee M. D. Mater. Today. 2007;10:28–33. doi: 10.1016/S1369-7021(07)70276-6. [DOI] [Google Scholar]
- Berera R. van Grondelle R. Kennis J. T. M. Photosynth. Res. 2009;101:105–118. doi: 10.1007/s11120-009-9454-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukamel S., Principles of nonlinear optical spectroscopy, Oxford University Press, New York, 1st edn, 1995 [Google Scholar]
- Valkunas L., Abramavicius D. and Mančal T., Molecular Excitation Dynamics and Relaxation, WILEY-VCH, Weinheim, 1st edn, 2013 [Google Scholar]
- Jonas D. M. Annu. Rev. Phys. Chem. 2003;54:425–463. doi: 10.1146/annurev.physchem.54.011002.103907. [DOI] [PubMed] [Google Scholar]
- Hochstrasser R. M. Proc. Natl. Acad. Sci. U. S. A. 2007;104:14190–14196. doi: 10.1073/pnas.0704079104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeon J., Park S. and Cho M., in Encyclopedia of Analytical Chemistry, ed. R. A. Meyers, John Wiley & Sons, Ltd, Chichester, UK, 2010 [Google Scholar]
- Fuller F. D. Ogilvie J. P. Annu. Rev. Phys. Chem. 2015;66:667–690. doi: 10.1146/annurev-physchem-040513-103623. [DOI] [PubMed] [Google Scholar]
- Cundiff S. T. Mukamel S. Phys. Today. 2013;66:44–49. doi: 10.1063/PT.3.2047. [DOI] [Google Scholar]
- Ginsberg N. S. Cheng Y.-C. Fleming G. R. Acc. Chem. Res. 2009;42:1352–1363. doi: 10.1021/ar9001075. [DOI] [PubMed] [Google Scholar]
- Šanda F. Perlík V. Lincoln C. N. Hauer J. J. Phys. Chem. A. 2015;119:10893–10909. doi: 10.1021/acs.jpca.5b08909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brixner T. Stenger J. Vaswani H. M. Cho M. Blankenship R. E. Fleming G. R. Nature. 2005;434:625–628. doi: 10.1038/nature03429. [DOI] [PubMed] [Google Scholar]
- Turner D. B. Wilk K. E. Curmi P. M. G. Scholes G. D. J. Phys. Chem. Lett. 2011;2:1904–1911. doi: 10.1021/jz200811p. [DOI] [Google Scholar]
- Dostál J. Pšenčík J. Zigmantas D. Nat. Chem. 2016;8:705–710. doi: 10.1038/nchem.2525. [DOI] [PubMed] [Google Scholar]
- Dostál J. Benešová B. Brixner T. J. Chem. Phys. 2016;145:124312. doi: 10.1063/1.4962577. [DOI] [PubMed] [Google Scholar]
- Zhang Z. Wells K. L. Seidel M. T. Tan H.-S. J. Phys. Chem. B. 2013;117:15369–15385. doi: 10.1021/jp4046403. [DOI] [PubMed] [Google Scholar]
- Bixner O. Lukeš V. Mančal T. Hauer J. Milota F. Fischer M. Pugliesi I. Bradler M. Schmid W. Riedle E. Kauffmann H. F. Christensson N. J. Chem. Phys. 2012;136:204503. doi: 10.1063/1.4720492. [DOI] [PubMed] [Google Scholar]
- Christensson N. Milota F. Nemeth A. Sperling J. Kauffmann H. F. Pullerits T. Hauer J. J. Phys. Chem. B. 2009;113:16409–16419. doi: 10.1021/jp906604j. [DOI] [PubMed] [Google Scholar]
- Stone K. W. Gundogdu K. Turner D. B. Li X. Cundiff S. T. Nelson K. A. Science. 2009;324:1169–1173. doi: 10.1126/science.1170274. [DOI] [PubMed] [Google Scholar]
- Brüggemann B. May V. J. Chem. Phys. 2003;118:746–759. doi: 10.1063/1.1523392. [DOI] [Google Scholar]
- Brüggemann B. May V. J. Chem. Phys. 2004;120:2325–2336. doi: 10.1063/1.1637585. [DOI] [PubMed] [Google Scholar]
- Hader K. May V. Lambert C. Engel V. Phys. Chem. Chem. Phys. 2016;18:13368–13374. doi: 10.1039/C6CP01780K. [DOI] [PubMed] [Google Scholar]
- Engel E. Leo K. Hoffmann M. Chem. Phys. 2006;325:170–177. doi: 10.1016/j.chemphys.2005.09.004. [DOI] [Google Scholar]
- Marciniak H. Li X.-Q. Würthner F. Lochbrunner S. J. Phys. Chem. A. 2011;115:648–654. doi: 10.1021/jp107407p. [DOI] [PubMed] [Google Scholar]
- Sundström V. Gillbro T. Gadonas R. A. Piskarskas A. J. Chem. Phys. 1988;89:2754–2762. doi: 10.1063/1.455027. [DOI] [Google Scholar]
- Bakulin A. A. Morgan S. E. Kehoe T. B. Wilson M. W. B. Chin A. W. Zigmantas D. Egorova D. Rao A. Nat. Chem. 2016;8:16–23. doi: 10.1038/nchem.2371. [DOI] [PubMed] [Google Scholar]
- Brüggemann B. Pullerits T. New J. Phys. 2011;13:025024. doi: 10.1088/1367-2630/13/2/025024. [DOI] [Google Scholar]
- Cundiff S. T. Phys. Chem. Chem. Phys. 2014;16:8193–8200. doi: 10.1039/C4CP00176A. [DOI] [PubMed] [Google Scholar]
- Sahu K. Wu H. Berg M. A. J. Phys. Chem. B. 2013;117:15257–15271. doi: 10.1021/jp405785a. [DOI] [PubMed] [Google Scholar]
- Malevich P. Heshmatpour C. Lincoln C. N. Ceymann H. Schreck M. H. Hauer J. EPJ Web Conf. 2019;205:06013. doi: 10.1051/epjconf/201920506013. [DOI] [Google Scholar]
- Heshmatpour C. Hauer J. Šanda F. Chem. Phys. 2019:110433. doi: 10.1063/5.0081053. [DOI] [PubMed] [Google Scholar]
- Akselrod G. M. Deotare P. B. Thompson N. J. Lee J. Tisdale W. A. Baldo M. A. Menon V. M. Bulović V. Nat. Commun. 2014;5:3646. doi: 10.1038/ncomms4646. [DOI] [PubMed] [Google Scholar]
- Zhu T. Snaider J. M. Yuan L. Huang L. Annu. Rev. Phys. Chem. 2019;70:219–244. doi: 10.1146/annurev-physchem-042018-052605. [DOI] [PubMed] [Google Scholar]
- Topczak A. K. Roller T. Engels B. Brütting W. Pflaum J. Phys. Rev. B: Condens. Matter Mater. Phys. 2014;89:201203. doi: 10.1103/PhysRevB.89.201203. [DOI] [Google Scholar]
- Tamai Y. Ohkita H. Benten H. Ito S. J. Phys. Chem. Lett. 2015;6:3417–3428. doi: 10.1021/acs.jpclett.5b01147. [DOI] [PubMed] [Google Scholar]
- Menke S. M. Holmes R. J. Energy Environ. Sci. 2014;7:499–512. doi: 10.1039/C3EE42444H. [DOI] [Google Scholar]
- Mikhnenko O. V. Blom P. W. M. Nguyen T.-Q. Energy Environ. Sci. 2015;8:1867–1888. doi: 10.1039/C5EE00925A. [DOI] [Google Scholar]
- Jin X.-H. Price M. B. Finnegan J. R. Boott C. E. Richter J. M. Rao A. Menke S. M. Friend R. H. Whittell G. R. Manners I. Science. 2018;360:897–900. doi: 10.1126/science.aar8104. [DOI] [PubMed] [Google Scholar]
- Lin J. D. A. Mikhnenko O. V. Chen J. Masri Z. Ruseckas A. Mikhailovsky A. Raab R. P. Liu J. Blom P. W. M. Loi M. A. García-Cervera C. J. Samuel I. D. W. Nguyen T.-Q. Mater. Horiz. 2014;1:280–285. doi: 10.1039/C3MH00089C. [DOI] [Google Scholar]
- Gaab K. M. Bardeen C. J. J. Phys. Chem. A. 2004;108:10801–10806. doi: 10.1021/jp0464472. [DOI] [Google Scholar]
- Dutta R. Bagchi B. J. Chem. Phys. 2016;145:164907. doi: 10.1063/1.4966035. [DOI] [PubMed] [Google Scholar]
- Barford W. Duffy C. D. P. Phys. Rev. B: Condens. Matter Mater. Phys. 2006;74:075207. doi: 10.1103/PhysRevB.74.075207. [DOI] [Google Scholar]
- Dostál J. Fennel F. Koch F. Herbst S. Würthner F. Brixner T. Nat. Commun. 2018;9:2466. doi: 10.1038/s41467-018-04884-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Süβ J. Wehner J. Dostál J. Brixner T. Engel V. J. Chem. Phys. 2019;150:104304. doi: 10.1063/1.5086151. [DOI] [PubMed] [Google Scholar]
- Kriete B. Lüttig J. Kunsel T. Malý P. Jansen T. L. C. Knoester J. Brixner T. Pshenichnikov M. S. Nat. Commun. 2019;10:4615. doi: 10.1038/s41467-019-12345-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Völker S. F. Schmiedel A. Holzapfel M. Renziehausen K. Engel V. Lambert C. J. Phys. Chem. C. 2014;118:17467–17482. doi: 10.1021/jp5055809. [DOI] [Google Scholar]
- Völker S. F. Uemura S. Limpinsel M. Mingebach M. Deibel C. Dyakonov V. Lambert C. Macromol. Chem. Phys. 2010;211:1098–1108. doi: 10.1002/macp.200900670. [DOI] [Google Scholar]
- Gsänger M. Kirchner E. Stolte M. Burschka C. Stepanenko V. Pflaum J. Würthner F. J. Am. Chem. Soc. 2014;136:2351–2362. doi: 10.1021/ja409496r. [DOI] [PubMed] [Google Scholar]
- Stender B. Völker S. F. Lambert C. Pflaum J. Adv. Mater. 2013;25:2943–2947. doi: 10.1002/adma.201204938. [DOI] [PubMed] [Google Scholar]
- Brixner T. Hildner R. Köhler J. Lambert C. Würthner F. Adv. Energy Mater. 2017;7:1700236. doi: 10.1002/aenm.201700236. [DOI] [Google Scholar]
- Abasto D. F. Mohseni M. Lloyd S. Zanardi P. Philos. Trans. R. Soc., A. 2012;370:3750–3770. doi: 10.1098/rsta.2011.0213. [DOI] [PubMed] [Google Scholar]
- Chorošajev V. Gelzinis A. Valkunas L. Abramavicius D. J. Chem. Phys. 2014;140:244108. doi: 10.1063/1.4884275. [DOI] [PubMed] [Google Scholar]
- Lambert C. Koch F. Völker S. F. Schmiedel A. Holzapfel M. Humeniuk A. Röhr M. I. S. Mitric R. Brixner T. J. Am. Chem. Soc. 2015;137:7851–7861. doi: 10.1021/jacs.5b03644. [DOI] [PubMed] [Google Scholar]
- Völker S. F. Dellermann T. Ceymann H. Holzapfel M. Lambert C. J. Polym. Sci., Part A: Polym. Chem. 2014;52:890–911. doi: 10.1002/pola.27073. [DOI] [Google Scholar]
- Röhr M. I. S. Marciniak H. Hoche J. Schreck M. H. Ceymann H. Mitric R. Lambert C. J. Phys. Chem. C. 2018;122:8082–8093. doi: 10.1021/acs.jpcc.8b00847. [DOI] [Google Scholar]
- Yamagata H. Spano F. C. J. Phys. Chem. Lett. 2014;5:622–632. doi: 10.1021/jz402450m. [DOI] [PubMed] [Google Scholar]
- Hestand N. J. Spano F. C. Chem. Rev. 2018;118:7069–7163. doi: 10.1021/acs.chemrev.7b00581. [DOI] [PubMed] [Google Scholar]
- Scholes G. D. Faraday Discuss. 2019 doi: 10.1039/c9fd00064j. [DOI] [PubMed] [Google Scholar]
- Metzler R. Klafter J. Phys. Rep. 2000;339:1–77. doi: 10.1016/S0370-1573(00)00070-3. [DOI] [Google Scholar]
- Moix J. M. Khasin M. Cao J. New J. Phys. 2013;15:085010. doi: 10.1088/1367-2630/15/8/085010. [DOI] [Google Scholar]
- Klafter J. Sokolov I. M. Phys. World. 2005;18:29–32. doi: 10.1088/2058-7058/18/8/33. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.