Szanto et al. use heavy water and Shaker-IR K+ channel mutants to establish that structural water molecules contribute to the inactivation of the selectivity filter of the channel. Their experimental evidence supports previous predictions stemming from molecular dynamics simulations.
Abstract
It has been reported earlier that the slow (C-type) inactivated conformation in Kv channels is stabilized by a multipoint hydrogen-bond network behind the selectivity filter. Furthermore, MD simulations revealed that structural water molecules are also involved in the formation of this network locking the selectivity filter in its inactive conformation. We found that the application of an extracellular, but not intracellular, solution based on heavy water (D2O) dramatically slowed entry into the slow inactivated state in Shaker-IR mutants (T449A, T449A/I470A, and T449K/I470C, displaying a wide range of inactivation kinetics), consistent with the proposed effect of the dynamics of structural water molecules on the conformational stability of the selectivity filter. Alternative hypotheses capable of explaining the observed effects of D2O were examined. Increased viscosity of the external solution mimicked by the addition of glycerol had a negligible effect on the rate of inactivation. In addition, the inactivation time constants of K+ currents in the outward and the inward directions in asymmetric solutions were not affected by a H2O/D2O exchange, negating an indirect effect of D2O on the rate of K+ rehydration. The elimination of the nonspecific effects of D2O on our macroscopic current measurements supports the hypothesis that the rate of structural water exchange at the region behind the selectivity filter determines the rate of slow inactivation, as proposed by molecular modeling.
Introduction
Voltage-gated ion channels play an essential role in a variety of physiological processes in both excitable (neurons, skeletal, and cardiac muscle) and nonexcitable cells. The activity of these channels regulates the permeability of the membrane for specific ions, thereby influencing the resting potential of cells, the frequency and duration of action potentials in excitable tissues (Dodson and Forsythe, 2004), or membrane potential–driven processes of nonexcitable cells, such as antigen-dependent activation of T lymphocytes (Panyi et al., 2004; Varga et al., 2007). Based on x-ray crystallography and various functional (electrophysiological) data, the essential structural elements that are responsible for voltage-gated potassium (Kv) channel function were identified almost two decades ago (Yellen, 2002). Kv channels in the Shaker subfamily have three well-studied gates: an activation gate (referred to here as the A-gate) and two types of inactivation gates (Fig. 1). The A-gate is formed by the crossing of the S6 helices of each of the four subunits at the cytoplasmic end of the pore (Liu et al., 1997; del Camino et al., 2000; Yellen, 2001), which opens upon depolarization of the membrane. During prolonged membrane depolarization, most voltage-gated ion channels undergo inactivation that limits the K+ current following the activation of the channels. The N- and C-type inactivations that are most common in Kv channels have been studied in detail and reviewed extensively (Kurata and Fedida, 2006). N-type inactivation is better understood and occurs via the “ball-and-chain” mechanism (Hoshi et al., 1990; Zagotta et al., 1990) originally proposed for Na+ channel inactivation (Bezanilla and Armstrong, 1977). In the absence of N-terminal inactivating particles, several types of potassium channels become nonconductive through a process known as C-type inactivation (Hoshi et al., 1991). Although the molecular mechanism of C-type inactivation is not well understood, experimental, computational, and structural investigations favor the hypothesis that C-type inactivation is linked to rearrangements at the selectivity filter and the extracellular entrance to the pore that result in a constricted, nonconducting permeation pathway (López-Barneo et al., 1993; Yellen et al., 1994; Yellen, 2002; Cordero-Morales et al., 2006a; Cordero-Morales et al., 2006b; Chakrapani et al., 2007; Cordero-Morales et al., 2007; Hoshi and Armstrong, 2013). It is generally accepted that this slow inactivation is the result of a cooperative mechanism of the four K+ channel subunits (Panyi et al., 1995; Kiss and Korn, 1998; Loots and Isacoff, 2000).
Figure 1.
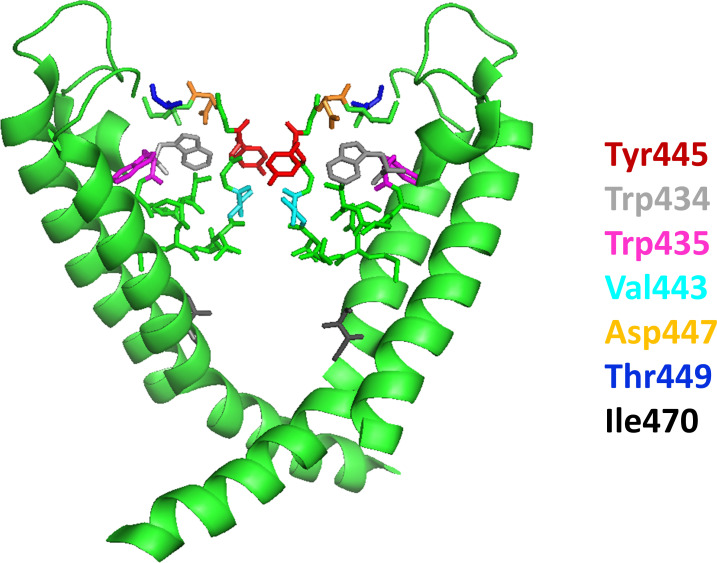
Structure of the pore region of Kv1.2. The S6 segments of two diagonally opposed subunits are shown as ribbon representations with front and rear subunits removed for clarity. The pore domain consists of the selectivity filter at the top, the water-filled cavity below, and the activation gate at the bottom. The latter is formed by the crossing of the S6 helices of each of the four subunits at the intracellular end of the pore (bundle crossing). Residues that are involved in the stabilization of the inactivated conformation of the selectivity filter region (Val443, Tyr445, and Asp447) are illustrated in stick format along with other residues important for the study (Trp434, Trp435, Thr449, and Ile470).
Several pieces of evidence support the idea that an extensive network of interactions behind the selectivity filter is important for C-type inactivation (Cordero-Morales et al., 2006a; Cordero-Morales et al., 2006b; Cordero-Morales et al., 2007; Cuello et al., 2010a; Cuello et al., 2010b; Cordero-Morales et al., 2011; Pless et al., 2013; Cuello et al., 2017; Li et al., 2018). A multipoint hydrogen-bond network between appropriate residues in the pore helix and the external vestibule adjacent to the selectivity filter has been first demonstrated in the bacterial KcsA channel+, in which the C-type inactivation gating is governed by the triad of W67–E71–D80 (equivalents to W434, V438, and D447 in Shaker-IR). Later, the role of this hydrogen-bond network was confirmed by specific mutations; the lack of at least one of these interactions favors the conductive conformation of the selectivity filter (Cordero-Morales et al., 2007).
Shaker-like K+ channels have almost identical sequences in these regions, which are involved in activation and inactivation. The formation of a hydrogen-bond network likely serves as a basis for C-type inactivation in Shaker as well. In particular, an interaction between W434 and D447 modulates the inactivation process, suggesting that these residues participate in the inactivation gating of K channels (Cordero-Morales et al., 2011). MD simulations indicated that the network of interacting residues mentioned above is affecting the distribution of structural water molecules buried behind the channel’s selectivity filter (Ostmeyer et al., 2013; Labro et al., 2018; Li et al., 2018). These buried waters are stabilized by a network of water–water and water–protein hydrogen bonds, and thus they become an integral part of the protein structure when the selectivity filter is in the inactivated conformation (Cuello et al., 2017; Li et al., 2018). The presence of these buried waters indicates that the filter is locked into the pinched nonconducting state, and the structural water prevents a spontaneous transition toward the conducting state (Ostmeyer et al., 2013).
Recent studies in KcsA showed that water access to the inactivation cavity becomes a critical factor controlling the rate and magnitude of C-type inactivation, since water molecules can diffuse into the inactivation cavity by a conduit (Cuello et al., 2017). The entrance to this conduit is guarded by Y82 (449T in Shaker-IR, gatekeeper position). A reduction in the volume and/or hydrophobicity of this residue can maximize the diffusion of water molecules into the inactivation cavity, thereby increasing the rate and magnitude of C-type inactivation. In contrast, smaller or less hydrophobic amino acid residues not only create a septum or a channel, possibly enhancing the diffusion of water molecules into it, but also allow the solvation of the inactivation cavity entryway, as evidenced by the additional crystallographic water molecules detected at this region (Cuello et al., 2017; Li et al., 2018). The access of water molecules to this cavity was shown to be altered by toxin binding to Shaker (Karbat et al., 2019).
We designed experiments to test the critical role of these buried “structural water” molecules in the conformational stability of the selectivity filter by taking advantage of the physicochemical differences between light water (protium oxide [H2O]) and heavy water (deuterium oxide [D2O]). The properties of liquid H2O and D2O as solvents are different (“solvent isotope effect”). The viscosity of D2O is 25% greater than that of H2O, and the conductivity of H+ in H2O is 1.4–1.5 times that of D+ in D2O. Moreover, D2O has a greater dielectric constant and a lower diffusion coefficient compared with H2O (by ∼20%; Weingärtner, 1984; Karbat et al., 2019). These are presumably because networks of D2O molecules have a higher degree of structural order than do H2O molecules owing to stronger intermolecular hydrogen bonding. Moreover, D+ is bound more tightly than H+ in D3O+ and many other compounds (Scheiner and Čuma, 1996). Primary and secondary kinetic isotope effects, on the other hand, occur when H atoms of compounds are exchanged with D atoms, in this case, H2O versus D2O. Of these, the primary kinetic isotope effect, which occurs when H or D is involved in a bond that is broken in the rate-limiting step of a reaction, might drastically influence the hydrogen-bond network involved in the regulation of inactivation kinetics. Isotope effects on the kinetics of inactivation gating may provide clues for the presence of water molecules that have been proposed to play an essential role in channel gating. Therefore, we addressed two questions. (1) Does D2O affect the inactivation gating of Shaker-IR channels? (2) If so, can these changes be attributed to the nonspecific effects of D2O, such as increased viscosity or slower exit rate of K+ from the site controlling inactivation related to altered hydration/dehydration of K+ ions in D2O? To address these questions, we characterized the gating transitions, particularly the C-type inactivation kinetics, in Shaker-IR T449A, T449A/I470A, and T449K/I470C constructs in the absence or presence of D2O in the extra- or intracellular solutions. Mutations at T449 and I470 modulate the rate of C-type inactivation in Shaker without changing the nature of the inactivation mechanism (Cuello et al., 2010a; Peters et al., 2013; Kratochvil et al., 2017; see Discussion), and suitable mutations result in inactivation kinetics appropriate to study the molecular details of inactivation (Panyi and Deutsch, 2006, 2007). Moreover, position 449 is the gatekeeper for water access to the inactivation cavity behind the selectivity filter, and thus, different amino acid residues in these positions may exaggerate the physicochemical differences between D2O and H2O (Cuello et al., 2017).
We found that the inactivation kinetics of various Shaker mutants, having inactivation kinetics over a wide range (between ∼60 ms and ∼150 ms), was slower if H2O was substituted for D2O selectively in the extracellular solution. Neither the increased viscosity nor nonspecific effects on the selectivity of the channel for K+ or ion occupancy in the pore could explain the slower inactivation kinetics in D2O. We propose that the reduction in the rate of inactivation upon H2O/D2O exchange is due to the isotope effects, which may manifest at either a slower rate of the formation of the hydrogen-bond network characteristic of the inactivated state or an altered rate of water transport into the inactivation cavity. These results confirm the importance of a hydrogen-bond network for the conformational stability of the inactivated state and provide experimental evidence for the presence of buried structural water molecules proposed by MD simulations.
Materials and methods
Cell culture
Human embryonic kidney cells transformed with SV40 large T antigen (tsA201) were grown in high-glucose Dulbecco’s modified Eagle’s medium supplemented with 10% FBS, 2 mM L-glutamine, 100 U/ml penicillin-g, and 100 µg/ml streptomycin (Invitrogen) at 37°C in a 5% CO2 and 95% air humidified atmosphere. Cells were passaged twice per week following a 7-min incubation in PBS containing 0.2 g EDTA/liter (Invitrogen).
DNA clones and site-directed mutagenesis
Modified Shaker-IR channels in a GW1-cytomegalovirus mammalian expression plasmid under the control of a highly expressing Kozak consensus promoter sequence (Kozak, 1991) was provided by R. Horn (Thomas Jefferson University, Philadelphia, PA; Ding and Horn, 2002). All mutations were introduced by PCR mutagenesis into Shaker-IR, including the deletion between residues 6 and 46 to eliminate N-type inactivation (Hoshi et al., 1990). Amino acid substitutions at position 449 (T449A and T449K, respectively) and 470 (I470A and I470C, respectively) were introduced using a site-directed mutagenesis kit (QuikChange; Stratagene). A Calcium Phosphate Transfection Kit (Invitrogen) was used to cotransfect a GFP plasmid vector along with the Shaker-IR construct using 10 µg Shaker-IR DNA and 1 µg GFP DNA. Transfected cells were replated onto 35-mm polystyrene cell culture dishes (Cellstar; Greiner Bio-One) pretreated with poly-L-ornithine (Sigma-Aldrich) to improve cell adhesion for excising patches. Channels were transiently expressed in tsA201 cells 12–48 h after transfection. The GFP-positive transfectants were identified by a Nikon TS-100 fluorescence microscope using bandpass filters of 455–495 nm and 515–555 nm for excitation and emission, respectively. More than 60% of the GFP-positive cells expressed the cotransfected ion channels.
Solutions
For inside-out experiments, the standard intracellular (bath) solution contained (in mM) 105 KF, 35 KCl, and 10 HEPES titrated to pH 7.36–7.38 with KOH for a final concentration of 160–165 mM K+ and an osmolarity of 285–295 mOsm, while the standard extracellular (pipette) solution was (in mM) 150 NaCl, 2 KCl, 1.5 CaCl2, 1 MgCl2, and 10 HEPES at pH 7.36–7.38. For outside-out experiments, identical solutions were prepared, but the pipette was filled with the standard intracellular solution having high [K+]. Glycerol and sucrose (Sigma-Aldrich) were dissolved in the extracellular solution, and the viscosity of the resulting solutions was determined experimentally using an Ostwald viscometer. In D2O experiments, internal and/or external solutions were prepared with 99.6% D2O (Sigma-Aldrich). pD in D2O solutions was corrected by adding 0.4 units to the nominal reading of the pH meter (Glasoe and Long, 1960). For experiments in which the K+ gradient was reversed, the external solution contained (in mM) 100 NaCl, 50 KCl, 1.5 CaCl2, 1 MgCl2, and 10 HEPES at pH 7.36–7.38 and the internal solutions contained (in mM) 105 KF, 35 KCl, and 10 HEPES or 10.5 KF, 94.5 NaF, 3.5 KCl, 31.5 NaCl, and 10 HEPES, respectively. A Warner Instruments SF-77A Perfusion Fast-Step system with three-barrel square glass (700 µM internal diameter) was used for rapid solution exchange. This system had a 10–90% exchange time for inside-out patches between 20 and 30 ms. The patches were perfused with solutions at a rate of 0.5 ml/min. The solution exchange protocol and sample data have been described previously (Panyi and Deutsch, 2006).
Electrophysiology
Standard methods (Hamill et al., 1981) were used to record currents either in inside-out or outside-out patches. Typical current amplitudes were 300–2,000 pA at +50 mV test potential, allowing the recording of macroscopic currents. Only those cells with a steady-state current <5% of the peak current were in the experiments. Micropipettes were pulled in four stages using a Flaming Brown automatic pipette puller (Sutter Instruments) from Borosilicate Standard Wall with Filament aluminum-silicate glass (Harvard Apparatus) with tip diameters between 0.5 and 1 µm and heat polished to a tip resistance typically ranging from 2 to 8 MΩ. All measurements were performed by using an Axopatch 200B amplifier connected to a personal computer using Axon Digidata 1550A data acquisition hardware, respectively (Molecular Devices). In general, the holding potential was −120 mV. Records were discarded when leak at the holding potential was >10% of the peak current at the test potential. Experiments were done at room temperature (ranging between 20°C and 24°C). Data were analyzed using the pClamp10.5 software package (Molecular Devices). Before analysis, current traces were digitally filtered with a three-point boxcar smoothing filter. Reported errors are SEM.
Data analysis
The direction of K+ currents and the voltage protocols are presented according to general conventions, except in Fig. 2 A and Fig. S1. To study activation kinetics of Shaker-IR mutants, cells were depolarized to +50 mV for 15 ms from a holding potential of −120 mV. Potassium current traces were fitted with a single-exponential function rising to the maximum according to the Hodgkin–Huxley model, I(t) = Ia × [1 − exp(−t/τact)]4 + C, where Ia is the amplitude of the activating curve component, τact is the activation time constant of the current, and C is the amplitude of the nonactivating current component. The τact for a particular cell was defined as the average of τact values obtained for at least three depolarizing pulses repeated at every 15 s in a sequence. We recorded n ≥ 4 cells of a given Shaker-IR mutant, and the average of the activation time constants was used to demonstrate the activation kinetics. To study channel inactivation, 2-s-long step pulses to +50 mV were applied from a holding potential of −120 mV. The rapid activation of outward current is followed by a decay of current corresponding to the C-type inactivation of the channels. The decaying part of the current traces was fitted with a single-exponential function, I(t) = I0 × exp(−t/τinact) + C, where I0 is the amplitude of the inactivating component of the current, τinact is the inactivation time constant for Shaker channels, and C is the steady-state current at the end of the depolarizing pulse, to obtain τinact, the time constant characterizing the inactivation kinetics. The characteristic τinact for a given cell was determined as detailed for obtaining τact. To determine the voltage dependence of steady-state activation of the current, the cells were held at −120 mV and depolarized to test potentials ranging from −80 to +70 mV in steps of 10 mV every 30 s. Peak conductance (G(V)) at each test potential was calculated from the peak current (Ipeak) at a test potential Em and the K+ reversal potential (EK) using G(V) = Ipeak/(Em − EK). The G(V) values were normalized for the maximum conductance (Gnorm) and plotted as a function of test potential along with the best-fit Boltzmann function (Gnorm = 1 / {1 + exp[−(V − V1/2) / k]}, where Gnorm is the normalized conductance, V is the test potential, V1/2 is the midpoint voltage, and k is the slope factor of the function. To study the kinetics of recovery from inactivation, pairs of depolarizing pulses were delivered from the holding potential of −120 to +50 mV for 400 ms. The duration of the first step, used to inactivate channels and measure initial peak current amplitude (I1), was at least fivefold longer than the τinact for the given channel. After a recovery period, defined as the interpulse interval (ipi) at −120 mV, the second identical voltage step was applied, and peak recovered current amplitude (I2) was measured. The ipi at −120 mV varied between 0 and 45 s. The fractional recovery (FR) was calculated as FR = (I2 − Iss1) / (I1 − Iss1), where I2 and I1 are the peak currents during the second and first pulses, respectively, and Iss1 is the steady-state current at the end of the first depolarizing pulse. The FR versus ipi plot was fit with an exponential function containing a single term, FR(t) = 1 − exp −t/τrec, or a sum of two exponential terms, FR(t) = Afast[1 − exp(−t/τfast)] + (1 − Afast)[1 − exp(−t/τslow)] to give the time constant of recovery from inactivation, τrec, or the time constants and relative amplitudes of the fast and slow components of the recovery, respectively. Prior to analysis, current traces were corrected for ohmic leak. Nonlinear least-squares fits were done using the Levenberg–Marquardt algorithm. Data are expressed as mean ± SEM. For pairwise comparisons, Student’s t test or Mann–Whitney rank sum test (nonnormal distribution population) was applied. For multiple comparisons, one-way or two-way ANOVA with post hoc Holm–Sidak tests were used. Statistical significance is shown as *, P < 0.05; **, P < 0.001; and ****, P < 0.0001.
Figure 2.
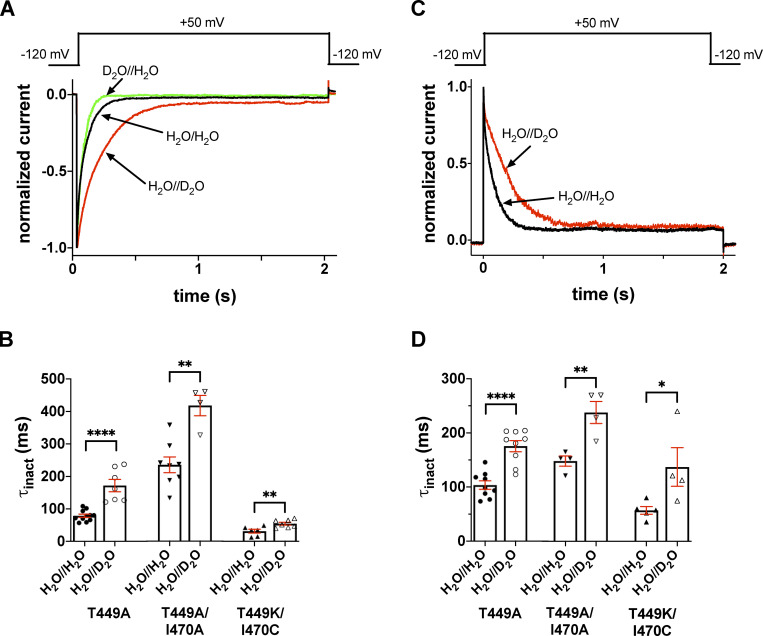
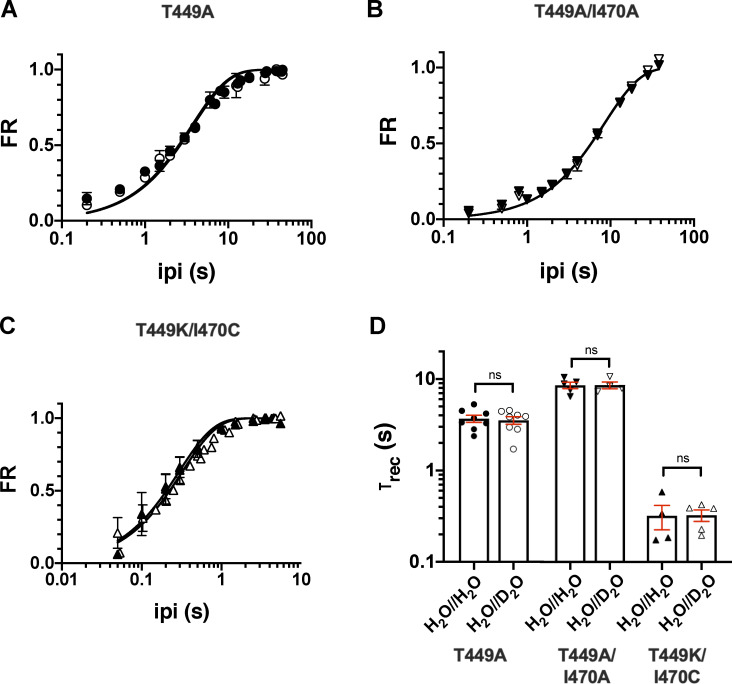
Extracellular D2O slows the inactivation kinetics of T449A, T449A/I470A, and T449K/I470C Shaker-IR mutants. (A and C) Macroscopic currents were measured in voltage-clamped inside-out (A) and outside-out patches (C) excised from tsA201 cells expressing the T449A Shaker-IR mutant. Displayed current traces were normalized to the respective peak currents. (A) Normalized inside-out patch currents obtained in different patches are displayed. The holding potential was −120 mV, and patches were repeatedly depolarized to +50 mV for 2.0 s every 45 s to measure currents. Control current was recorded in symmetric H2O//H2O (intra/extracellular, black trace); traces obtained in extracellular D2O, intracellular H2O (H2O//D2O, red trace), and intracellular D2O and extracellular H2O (D2O//H2O, green trace) are also displayed. (B) Inactivation time constants (τinact) measured at +50 mV in inside-out patches for the indicated mutants in the absence (H2O//H2O, filled symbols) or presence of extracellular D2O (H2O//D2O, empty symbols). The intracellular solution was H2O based. (C) Outside-out patches were repeatedly depolarized from a holding potential of −120 mV to obtain the currents. The first depolarization was in a H2O-based extracellular solution, followed by 60-s-long period at −120 mV, which was sufficient to ensure full recovery of the inactivated channels. Thereafter, another 2.0-s-long depolarizing pulse was applied in the presence of D2O; the solution exchange was initiated 1 s before the start of the depolarization. The voltage pulse protocol is shown above the corresponding normalized current traces; the color coding is the same as in A. For the composition of solutions, see Materials and methods. (D) The same data as in B, except that currents were recorded in outside-out configuration. Bars and error bars represent mean ± SEM for n ≥ 4 independent experiments (B and D). Symbols indicate individual data points (circles, T449A; down triangles, T449A/I470A; up triangles, T449K/I470C). Differences were considered significant (*, P < 0.05; **, P < 0.01; ****, P < 0.0001) compared with control (H2O//H2O).
Figure S1.
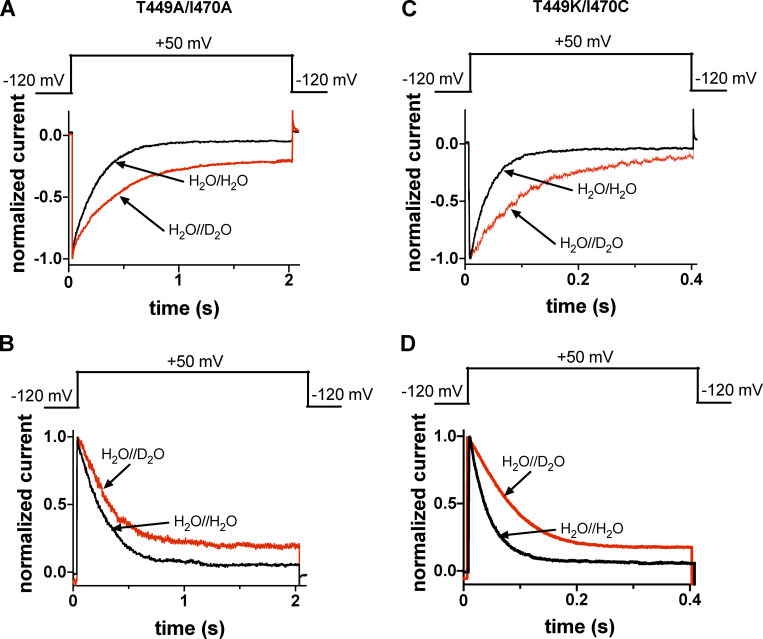
Extracellular D2O slows the inactivation kinetics of T449A/I470A and T449K/I470C Shaker-IR constructs. (A and C) Macroscopic currents were measured in voltage-clamped inside-out patches excised from tsA201-expressing T449A/I470A (A) and T449K/I470C (C) Shaker-IR constructs, and displayed records were normalized to the respective peak currents. Control currents were recorded in symmetric H2O//H2O (intra/extracellular, black traces) and extracellular D2O and intracellular H2O (H2O//D2O, red traces). For the composition of solutions, see Materials and methods. The holding potential was −120 mV, and currents were evoked using 2.0-s-long (T449A/I470A) or 400-ms-long (T449K/I470C) test pulses to +50 mV every 60 s. The inactivation time constant of the currents at +50 mV was determined by fitting a single-exponential function to the decaying part of the currents. The analysis of the inactivation time constants is presented in Fig. 2 B. (B and D) Outside-out patches were repeatedly depolarized from a holding potential of −120 mV using the pulse protocols shown above the corresponding normalized current traces. The first depolarization was in a H2O-based extracellular solution, followed by 60-s-long period at −120 mV, which was sufficient to ensure full recovery of the inactivated channels. Thereafter, another 2.0-s-long depolarizing pulse was applied in the presence of D2O, and the solution exchange was initiated 1 s before the start of the depolarization. Inactivation time constant (τinact) of the current at +50 mV was determined by fitting a single-exponential function to the decaying part of the currents; analysis of the inactivation time constants is presented in Fig. 2 D.
MD simulations
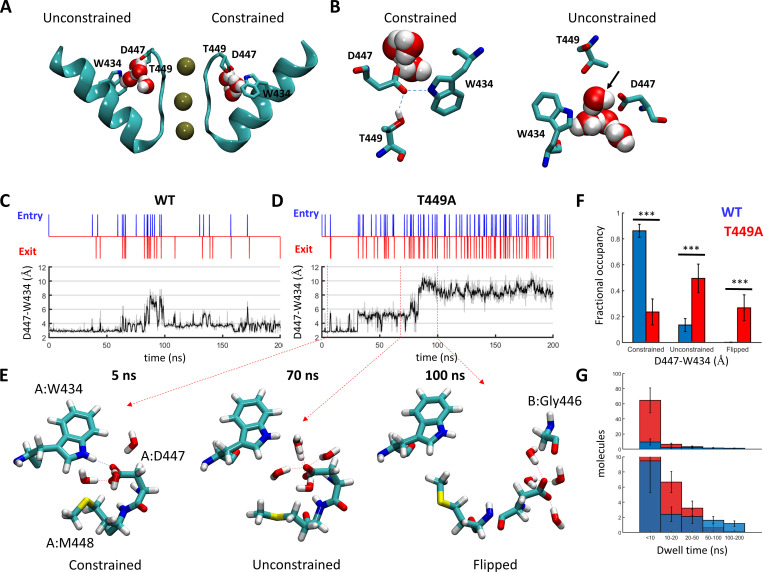
A structural model of the Shaker pore domain (residues K376-D488) was constructed based on the published crystal structure of the Kv1.2–Kv2.1 paddle chimera (PDB accession no. 2R9R, 86% identity, 94% similarity) using MODELLER (Webb and Sali, 2017). Two K+ ions and two water molecules were explicitly placed at sites S1–S4 of the selectivity filter. The system was assembled using the Charmm-GUI membrane-builder automated web service (Wu et al., 2014) and embedded in a lipid bilayer of roughly 90 × 90 Å2 of a 3:1 mixture of POPC/POPG monomers. K+ and Cl− ions were positioned using the replacement method to a final solute concentration of 150 mM. For the T449A simulations, the substitution was introduced in either all subunits or two opposing channel subunits during system assembly. The Charmm36m parameter set was used for the proteins, lipids, and ions, and Tip3p was used to describe the water molecules. The Charmm-GUI default equilibration protocol was applied, consisting of six short steps in which NVT dynamics was used for the first two, and NPT was used for the rest of the simulation with gradually decreasing restraints. System equilibration was finalized by a 20-ns unconstrained run. Simulations were run on GPU using RTX2080Ti or Tesla V100 units controlled by NAMD v2.13. Production runs were performed under NPT conditions at 303°K and 1 atm. Periodic boundary conditions and electrostatic interactions were treated using the particle mesh Ewald method with 1-Å grid size and a 12-Å cutoff distance. A time step of 2 fs was used, and bonds involving hydrogen atoms were fixed using the SHAKE algorithm. For the experiments described in Fig. S6, T449A substitutions were introduced in chains B and D of a snapshot taken at the end of a WT production run (Table S1, run 1) using the rotamers plugin of UCSF Chimera (Pettersen et al., 2004). The system was minimized by 5,000 steps of conjugated gradient and line search algorithm and then allowed to freely evolve for additional 150 ns. For the experiments described in Fig. S6, C and D (Table S1, trajectories 13–16), a D447:Oδ-W434:Nε constant distance (d) of 2.8 Å was maintained in each subunit by harmonic restraint of 5 kcal/mol/Å2. Trajectory data, including gate openings and water dynamics, were analyzed using a custom-written MATLAB code, as previously described (Karbat et al., 2019). The constrained, unconstrained, and flipped D-W gate conformations were empirically defined as d < 4 Å, 4 Å < d < 8 Å, and d > 8 Å, respectively.
Figure S6.
Introduction of T449A affects the behavior of the D-W gates and water transport through the peripheral pockets of Shaker. (A and B) Following a 200-ns unconstrained MD run of a WT Shaker tetramer, T449A substitutions were introduced in subunits B and D, and the system was allowed to evolve for additional 150 ns. (A) Time-series plots depicting water-exchange events (top) versus D447:W434 gate openings (bottom) at subunit C during the mixed trajectory. The 150 ns following the T449A substitutions are shaded in gray. (B) Top view depicting the state of the D447:W434 gates at t = 300 ns. Gate residues are depicted in sticks; pocket water molecules are represented by spheres and are color coded by the domain (A, red; B, green; C, blue; and D, yellow). (C and D) Locking the D-W gates in a constrained conformation prevents the excess water flow induced by T449A substitution. (C) Water traffic through the peripheral pockets of a T449A tetramer in which the D447:Oδ1-W434: Nε1 distances were restrained to 2.8 Å throughout the trajectory. (D) Dwell-time distributions of water molecules within the peripheral pockets compared between the T449A runs with constrained (Table S1; trajectories 13–16, blue) and unconstrained (red) D-W gates. The lower panel is a zoomed-in version of the top panel. The difference between the two distributions is statistically significant (two-sample Kolmogorov–Smirnov test, P = 0.04).
Online supplemental material
Fig. S1 shows raw current traces corresponding to the analysis in Fig. 2, B and D, for the Shaker-IR T449A/I470A and T449K/I470C constructs. Fig. S2 shows the analysis of the deactivation kinetics of Shaker-IR T449A, T449A/I470A, and T449K/I470C in H2O//H2O and H2O//D2O conditions. Fig. S3 shows the fits, using the sum of two exponential terms, to the kinetics of recovery from inactivation for Shaker-IR T449A, T449A/I470A, and T449K/I470C in H2O//H2O and H2O//D2O conditions, along with the statistical analysis of the time constants. Fig. S4 shows current–voltage relationships for T449A/I470A Shaker-IR mutant channels at various [K+] combinations in H2O//H2O and H2O//D2O conditions. Fig. S5 shows inward and outward K+ currents in H2O- or D2O-based extracellular solutions in the T449A/I470A Shaker-IR construct along with the analysis of the inactivation kinetics in these conditions at −20 mV, −10 mV, and 0 mV test potentials. Fig. S6 demonstrates, using MD simulation, the consequences of the introduction of T449A on the D-W gates and H2O transport through the peripheral pockets of Shaker. Table S1 summarizes the properties of the trajectories in Fig. 10 and Fig. S6. Video 1 demonstrates the dynamics of the D447:W434 hydrogen-bond and D447:T449 hydrogen-bond and the water traffic through the upper barrier in WT Shaker. Video 2 depicts the initial 100 ns of the trajectory in which the D-W gate in subunit C undergoes transition from constrained to unconstrained to flipped conformation in Shaker, with chain B and D bearing the T449A substitution.
Figure S2.
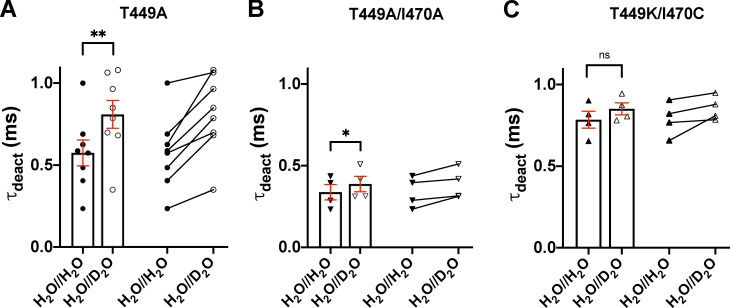
Effect of extracellular D2O substitution on the deactivation kinetics of Shaker-IR channels. (A–C) Deactivation kinetics of T449A (A), T449A/I470A (B), and T449K/I470C (C) Shaker-IR channels, expressed in tsA201 cells, was analyzed in the presence (H2O//D2O) and absence (H2O//H2O) of extracelular D2O. The cells were depolarized to +50 mV from a holding potential of −120 mV for 15 ms in outside-out configuration. Tail currents (Itail) were evoked by stepping the test potential back to −120 mV at the end of the 15-ms-long depolarization (see Fig. 3). The deactivation time constant (τdeact) was determined by fitting a single-exponential function to the decaying tail currents: where A is the tail current amplitude (pA), t is time (ms), τdeact is the deactivation time constant (ms), and C is the y offset. The deactivation time constant for a particular cell was defined as the average of time constants obtained for at least three repolarizing pulses repeated at every 15 s in a sequence. Bars and error bars indicate mean ± SEM (n ≥ 4) of τdeact for the indicated clones in H2O//H2O (filled symbols) and H2O//D2O (empty symbols). Symbols indicate individual data points (circles, T449A; down triangles, T449A/I470A; up triangles, T449K/I470C). Paired data are shown on the right part of each panel. Asterisks indicate significant differences (*, P < 0.05; **, P < 0.01).
Figure S3.
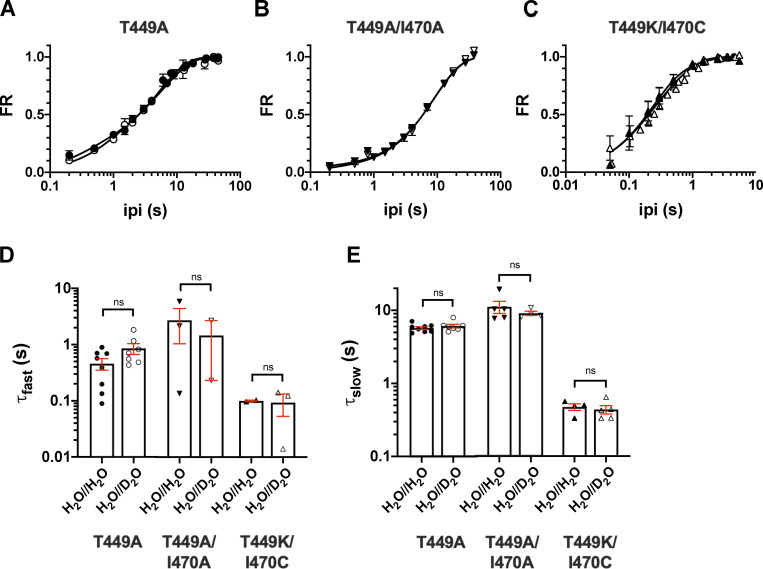
Analysis of the recovery from inactivation kinetics using the sum of two exponentials terms. (A–C) The time course of recovery from inactivation of the K+ current of Shaker-IR constructs was studied by means of a double-pulse protocol with increasing interpulse time (ipi; see text for details) for T449A (A), T449A/I470A (B), and T449K/I470C (C). Data points are presented as FR = (I2 − ISS1) / (I1 − ISS1), where I2 and I1 are the peak currents during the second and the first pulse and ISS1 is the steady-state current at the end of the first depolarization, respectively, and plotted as a function of ipi in control conditions (H2O//H2O, filled symbols) and external D2O (H2O//D2O, open symbols). Error bars indicate the SEM. The time constants of recovery were determined by fitting the averaged data points with a sum of two exponential terms, and solid lines show the best fit. (D and E) Time constants characterizing the fast (τfast; D) and slow components (τslow; E) of the recovery from inactivation were determined for each cell in control (H2O//H2O, filled symbols) and heavy water–based extracellular solution (H2O//D2O, empty symbols); the mean ± SEM and individual data points are shown for the indicated constructs (circles, T449A; down triangles, T449A/I470A; up triangles, T449K/I470C). The small number of data points for the τfast and τslow in case of the T449A/I470A and T449K/I470C mutants indicate the failure of the fit with a sum of two exponential terms; the recovery kinetics was basically single exponential for these mutants (Fig. 6).
Figure S4.
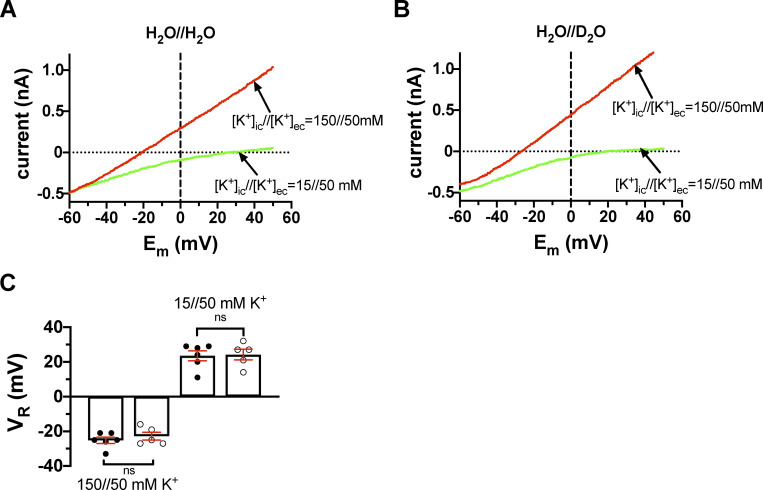
Current–voltage relationships for T449A/I470A Shaker-IR mutant channels at various [K+] combinations in inside-out patches. (A) The inside-out patch was held at a holding potential of −120 mV and depolarized to +50 mV for 5 ms to fully activate the channels (not shown). This step is followed by a fast voltage ramp to −120 mV in 25 ms. The currents corresponding to the membrane potential range of +50 mV to −60 mV are shown for clarity. The extracellular solution contained 50 mM K+ prepared in H2O (H2O//H2O). The patch was perfused with an intracellular solution containing 150 mM K+ (red trace) or 15 mM K+ (green trace). The horizontal dotted line indicates the 0-pA current, and the vertical dashed lane drawn at 0 mV indicates that the current is inward at [K+]in//[K+]ex = 15//50 mM (green trace) and outward at [K+]in//[K+]ex = 150//50 mM (red trace). (B) The same set of experiments as in A, except that the pipette-filling extracellular solution containing 50 mM K+ was prepared in D2O (H2O//D2O). All others (e.g., [K+] and labels) are the same as in A. (C) Current reversal potential (VR) was determined from the traces shown in A and B as the membrane potential at which the current crosses the 0-pA reference line (dotted). Bars and error bars indicate the mean ± SEM (n = 5–6) of the VR values, and symbols (filled and empty circles) indicate individual data points obtained in H2O//H2O solution (filled symbols) and extracellular D2O (H2O//D2O, empty symbols).
Figure S5.
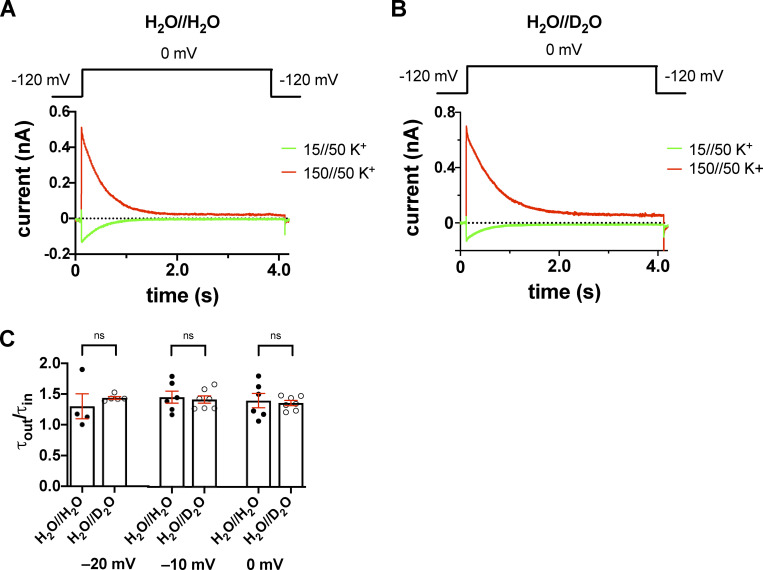
Inward and outward K+ currents in H2O- or D2O-based extracellular solutions in the T449A/I470A Shaker-IR construct. (A and B) Macroscopic currents were measured in voltage-clamped inside-out patches excised from tsA201 cells and normalized to their respective peak currents. The extracellular (pipette-filling) solution contained 50 mM K+ in H2O (A) or D2O (B), and the intracellular (bath) solution contained 150 mM K+ (red traces) or 15 mM K+ (green traces). The holding potential was −120 mV; 1.0-s-long depolarizing pulses to 0 mV were applied to activate the channels and record inward K+ current (green curves) or outward K+ current (red curves). The voltage protocol is shown above the corresponding raw current traces. (C) Inactivation time constants of the currents were determined by fitting a single-exponential function to the decaying part of the currents. The symbols indicate the ratio of the inactivation time constants measured for the outward and inward currents (τout/τin) at −20 mV, −10 mV, and 0 mV test potentials in H2O-based (H2O//H2O, filled circles) and D2O-based (H2O//D2O, empty circles) extracellular solutions. Bars represent mean ± SEM (n = 4–7).
Figure 10.
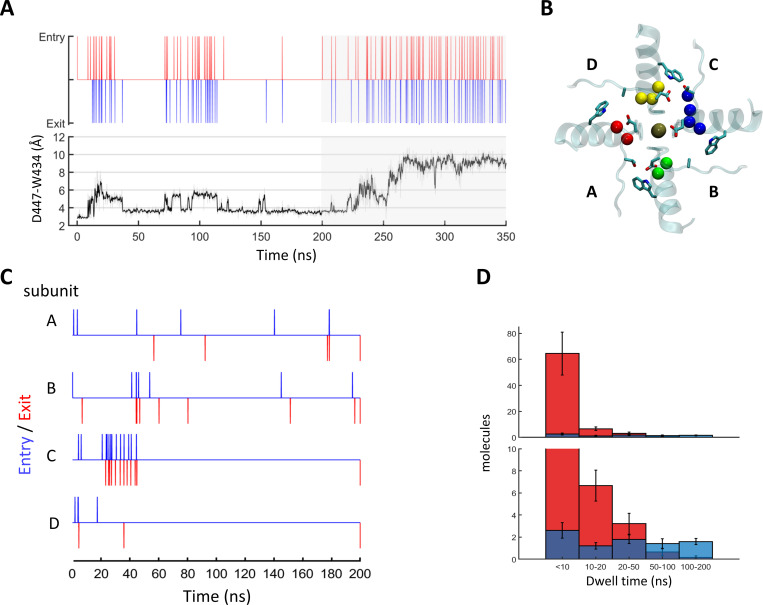
Regulation of water exchange in the peripheral pockets of Shaker by the amino acid at position 449. (A and B) Snapshot of the Shaker channel depicting the peripheral water pockets at open and closed states. (A) Side view of a cross section through the channel pore region depicting the selectivity filter and the pore helix of two opposing subunits. Bound K+ ions and structural water molecules behind the selectivity filter are depicted. Upper-barrier gate residues are indicated. (B) Top views of the peripheral pockets depicted in A. Dashed lines indicate hydrogen bonds; a water molecule passing through an open gate is marked by an arrow. (C and D) Time-series plots depicting water-exchange events (top) versus D447:W434 gate openings (bottom) during a 200-ns MD time series of WT Shaker (left) versus the T449A mutant (right). Unsmoothed data are represented as a gray shade of the smoothed trace. (E) Snapshots along a time series of Shaker T449A, depicting the spatial disposition of the upper-barrier residues of channel subunit A in a constrained (5 ns), unconstrained (70 ns), and flipped (100 ns) conformations. Water molecules within a hydrogen-bond distance from D447 are shown. (F) Dwell-time distributions of the D447:W434 gate at the constrained/unconstrained/flipped conformations averaged over six independent trajectories of WT Shaker (Table S1; trajectories 1–6, blue) or Shaker T449A (trajectories 7–12, red). Statistical significance was determined using the Wilcoxon rank sum test. (G) Dwell-time distributions of water molecules within the peripheral pockets compared between the WT (blue) and T449A (red) runs. The top panel displays the total numbers of molecules counted at the indicated bins averaged over the six runs (blue, WT; red, T449A). The lower panel is a zoomed-in version of the top panel. The bias of the T449A distribution toward shorter dwell times was statistically significant (two-sample Kolmogorov–Smirnov test, P = 0.03).
Video 1.
A link between the dynamics of the D447:W434 hydrogen-bond and D447:T449 hydrogen-bond and the water traffic through the upper barrier. The movie depicts the dynamics of the upper-barrier residues of a single WT channel subunit during a 100-ns MD run. Water molecules that come into a hydrogen-bond distance (<4 Å) from the side chain of D447 are shown. The time-series plots to the right depicts the diameter of the D-W gate (top), the D447:T449 distance (middle), and the water traffic (bottom).
Video 2.
Top view of the Shaker with chain B and D bearing the T449A substitution (chain A and C are WT). The side chains of W434, D447, and T/A 449 are rendered in sticks. Pore-resident K+ ions are rendered as spheres. The oxygen atoms of water molecules that reside in the peripheral pockets are rendered as spheres and color coded in red, green, blue, and yellow for chains A, B, C, and D, respectively. The movie depicts the initial 100 ns of the trajectory, in which the D-W gate in subunit C undergoes the transition from a constrained to unconstrained to flipped conformation.
Results
Extracellular, but not intracellular, heavy water slows the inactivation kinetics of Shaker-IR mutants displaying slow inactivation
We studied the effects of substituting H2O-based extracellular solution for a D2O-based one on various gating transitions in Shaker-IR channels having the following mutations and allowing slow inactivation at various rates: T449A, T449A/I470A, and T449K/I470C (Fig. 2). Mutations in position 449 and 470 modify C-type inactivation kinetics rather than affect the nature of C-type inactivation, and thus, these mutants are suitable to study inactivation kinetics under different experimental conditions (Cuello et al., 2010a; Peters et al., 2013; Kratochvil et al., 2017). The currents were recorded in both inside-out (Fig. 2 A, T449A) and outside-out (Fig. 2 C, T449A) patches excised from tsA201 cells in the absence or presence of D2O. Channels were held closed at −120 mV, and their activity was monitored using 2-s-long depolarizing pulses to +50 mV every 45 s by measuring the current through the channels. A step to +50 mV ensures that all channels open quickly, and the open probability at this voltage is maximal or close to maximal (Figs. 3 and 4). Fig. 2 shows that the 2-s duration of the depolarizing pulse is sufficient to induce complete inactivation in both inside-out and outside-out patch recordings. The exposure of the patches to D2O versus H2O-based solutions is indicated as intracellular solution//extracellular solution (e.g., D2O//H2O means a D2O-based cytosolic and H2O-based extracellular solution combination). The currents were normalized to their respective peaks in order to facilitate visual comparison of the D2O effects on the kinetics (Fig. 2, A and C). Normalization was also necessary, since currents recorded on different patches had to be compared—the H2O//H2O to H2O//D2O transition was impossible in inside-out configuration by changing the pipette-filling solution from an H2O-based to a D2O-based one.
Figure 3.
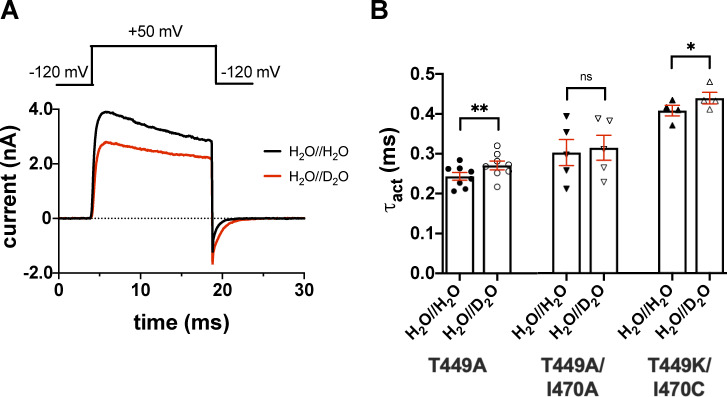
Effect of extracellular D2O substitution on the activation kinetics of Shaker-IR. (A) The tsA201 cell expressing T449A Shaker-IR channels was repeatedly depolarized to +50 mV from a holding potential of −120 mV for 15 ms in outside-out configuration in the absence (black) or the presence of extracellular D2O (red). The outward K+ current traces were fitted with a single-exponential function rising to a maximum according to the Hodgkin–Huxley n4 model (see Materials and methods). The activation time constant (τact) for a particular cell was defined as the average of time constants obtained for at least three depolarizing pulses repeated every 15 s in a sequence. (B) Bars and error bars indicate the mean ± SEM (n ≥ 4) of τact for the indicated clones. Symbols indicate individual data points (circles, T449A; down triangles, T449A/I470A; up triangles, T449K/I470C) obtained in H2O//H2O (filled symbols) and H2O//D2O (empty symbols). Asterisks indicate significant differences (*, P < 0.05; **, P < 0.01).
Figure 4.
Extracellular D2O does not alter the midpoint of the voltage dependence of steady-state activation of Shaker-IR mutant channels expressed in tsA201 cells. (A–C) Cells were held at −120 mV and depolarized to gradually increasing test potentials ranging from −100 to +70 mV in steps of 10 mV in every 45 s. The duration of the depolarizing pulses was 150 ms. G–V curves were constructed from current–voltage relationships using G(V) = Ipeak/(Vtest − EK) with the following parameters: peak current (Ipeak) at a test potential of Vtest and a K+ reversal potential of EK = −85 mV. The conductance values were normalized to the maximum (G/G0) and plotted as a function of the test potential (Em). The voltage dependencies of steady-state activation curves were determined in the absence (filled symbols, H2O//H2O condition) or presence of extracellular D2O (empty symbols, H2O//D2O condition). The superimposed solid lines show the best-fit Boltzmann functions to the averaged data points. (D) Bars and error bars indicate the mean ± SEM (n ≥ 4) of the midpoint voltages (V1/2) of steady-state activation obtained for the indicated clones. Symbols indicate individual data points (circles, T449A; down triangles, T449A/I470A; up triangles, T449K/I470C) obtained in H2O//H2O (filled symbols) and H2O//D2O (empty symbols).
Inactivation time constant (τinact) of the current at +50 mV was determined by fitting a single-exponential function to the decaying part of the currents. The time constants for inactivation (τinact) for the T449A, T449A/I470A, and T449K/I470C mutants were 79 ± 5 ms (n = 11), 235 ± 24 ms (n = 8), and 31 ± 6 ms (n = 6), respectively (Fig. 2 B and Fig. S1) measured at +50 mV depolarization in inside-out configuration in H2O//H2O (control). τinact in H2O//D2O increased significantly as compared with H2O//H2O in inside-out patch recordings regardless of the inactivation kinetics of the current in the H2O//H2O setting. The τinact values in the H2O//D2O setting were 172 ± 19 ms (n = 7, P < 0.0001), 418 ± 31 ms (n = 4, P = 0.0012), and 54 ± 4 ms (n = 7, P = 0.0093) for T449A, T449A/I470A, and T449K/I470C, respectively (Fig. 2 B and Fig. S1). Inactivation kinetics, however, was insensitive to intracellular D2O exposure (D2O//H2O setting, green trace in Fig. 2 A) The inactivation time constant for the T449A mutant in D2O//H2O in inside-out configuration was 85 ± 12 ms (n = 5, P = 0.59, as compared with data in H2O//H2O); similar results were obtained for the T449A/I470A construct as well (τinact = 211 ± 37 ms, P = 0.58, as compared with data in H2O//H2O). For outside-out patch experiments, the effect of D2O was measured using the voltage-step protocol described above, except pulses were delivered repeatedly every 45 s and the extracellular solution was switched back and forth from H2O based to D2O based between two pulses. D2O application was initiated 1 s before the start of the depolarization. Similar to our findings in inside-out configuration, the rate of inactivation was decreased in the presence of extracellular D2O (Fig. 2 D and Fig. S1), and the time constants were 103 ± 8 ms (in H2O//H2O) and 176 ± 10 ms (in H2O//D2O) for T449A (n = 9, P < 0.0001), 148 ± 9 ms (in H2O//H2O) and 237 ± 20 ms (in H2O//D2O) for T449A/I470A (n = 4, P = 0.0054), and 56 ± 7 ms (in H2O//H2O) and 136 ± 35 ms (in H2O//D2O) for T449K/I470C (n = 4, P = 0.0427), respectively. Data are given as mean ± SEM.
Activation kinetics and the steady-state parameters of gating in extracellular D2O
The effect of extracellular D2O on the activation kinetics of the three Shaker mutants introduced above was measured in outside-out patch configuration (Fig. 3). To determine the activation time constant, we used a 15-ms-long depolarizing pulse from a holding potential of −120 mV to +50 mV. The 15-ms duration of the depolarizing pulse is sufficient to completely activate channels but is too short to induce significant inactivation. Current traces were fitted with a single-exponential function rising to a maximum according to the Hodgkin–Huxley n4 model (see Materials and methods) to give the time constant for activation kinetics, τact, which was used to characterize the activation kinetics of the currents. In H2O//D2O the current magnitude is clearly reduced (Fig. 3 A). τact was minimally but significantly affected in H2O//D2O (Fig. 3 B) for the T449A and the T449K/I470C mutants: 0.24 ± 0.01 ms (in H2O//H2O) and 0.27 ± 0.01 ms (in H2O//D2O) for T449A (n = 8, P = 0.0034), 0.30 ± 0.03 ms (in H2O//H2O) and 0.31 ± 0.03 ms (in H2O//D2O) for T449A/I470A (n = 5, P = 0.7679), and 0.41 ± 0.01 ms (in H2O//H2O) and 0.44 ± 0.01 (in H2O//D2O) for T449K/I470C (n = 4, P = 0.0201), respectively. Data are given as mean ± SEM. The deactivation kinetics of the current was also slower in the D2O-based extracellular solution for the T449A (Fig. 3 A and Fig. S2) and T449A/I470A mutants, whereas the tail current kinetics was insensitive to extracellular D2O exposure in the T449K/I470C mutant (Fig. S2).
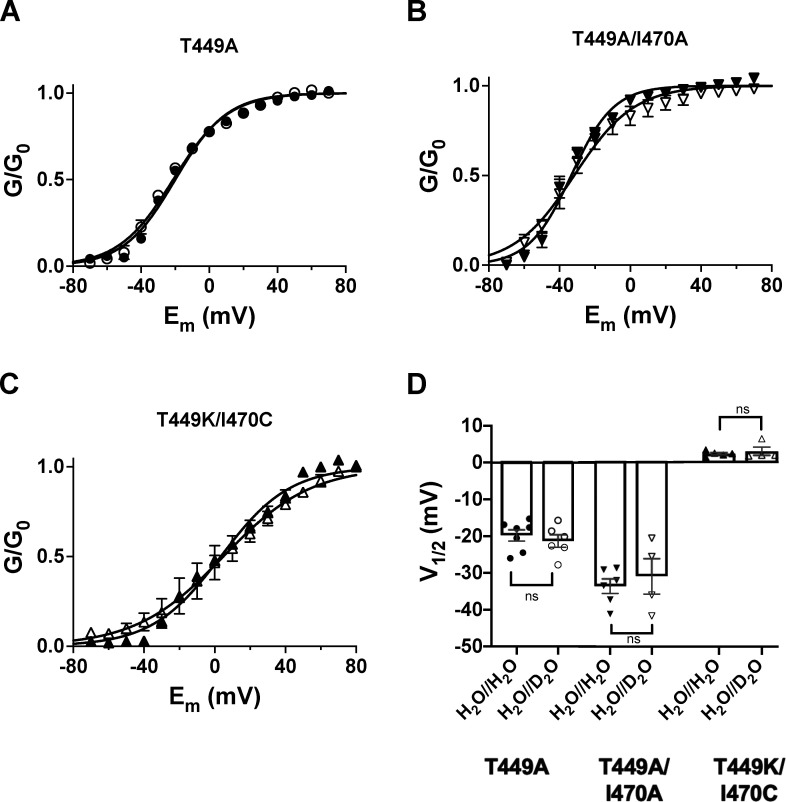
To assess the effect of external D2O on the voltage dependence of steady-state activation, we measured K+ currents in response to various depolarizations and calculated the conductances at each test potential (G(V)). The G(V) values were normalized for the maximal conductance (G0) and plotted as a function of the test potential in Fig. 4 for the three clones studies (Fig. 4, A–C). The superimposed solid lines show the best-fit Boltzmann functions in the absence (H2O//H2O) or presence of external D2O (H2O//D2O). Although the midpoint voltages (V1/2) of the G–V relationships of the different mutants ranged from approximately −40 mV to +7 mV (Fig. 4 D), changing the extracellular solution to a D2O-based one did not affect the midpoint voltages: −19.8 ± 1.5 mV (in H2O//H2O, n = 7) and −21.3 ± 1.7 mV (in H2O//D2O, n = 6) for T449A (P = 0.5234), −33.6 ± 1.9 mV (in H2O//H2O, n = 6) and −31.0 ± 4.8 mV (in H2O//D2O, n = 4) for T449A/I470A (P = 0.5739), and 2.3 ± 0.4 mV (in H2O//H2O, n = 5) and 2.9 ± 1.3 (in H2O//D2O, n = 4) for T449K/I470C (P = 0.5358), respectively (Fig. 4 D).
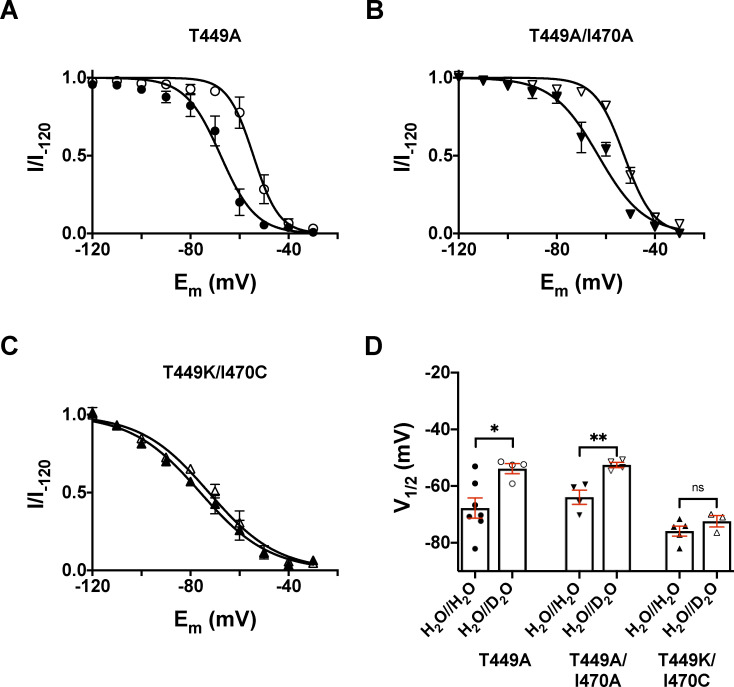
To assess the effect of external D2O on the voltage dependence of steady-state inactivation (h∞), we applied 3-s prepulse potentials from −120 to −20 mV in 10-mV increments before stepping to the test potential of +50 mV for 5 ms to measure the currents in inside-out patches. The fraction of noninactivated channels at each voltage was calculated as I/I−120, where I is the peak current evoked by 5-ms depolarization to +50 mV from a given prepulse potential, whereas I−120 is the peak current evoked by identical depolarization from the holding potential of −120 mV. The I/I−120 values were plotted as a function of the prepulse potential in Fig. 5 for the three clones studies (Fig. 5, A–C). The superimposed solid lines show the best-fit Boltzmann function in the absence (H2O//H2O) or presence of extracellular D2O (H2O//D2O). Similar to the midpoints of the G–V relationships, the midpoints of the h∞ curves also depended on the mutant in control conditions (H2O//H2O; Fig. 5 D). Moreover, the application of the D2O-based extracellular solution caused a depolarizing shift in the h∞ curves for T449A and T449A/I470A mutant (Fig. 5 D). The V1/2 parameters characterizing the midpoint of the voltage dependence of steady-state inactivation were V1/2 = −67.8 ± 3.6 mV (in H2O//H2O, n = 7) and −53.8 ± 1.8 mV (in H2O//D2O, n = 4) for T449A (P = 0.0215), V1/2 = −63.9 ± 2.5 mV (in H2O//H2O, n = 4) and −52.5 ± 0.9 mV (in H2O//D2O, n = 4) for T449A/I470A (P = 0.0052), and V1/2 = −75.8 ± 1.8 mV (in H2O//H2O, n = 5) and −72.4 ± 2.0 mV (in H2O//D2O, n = 3) for T449K/I470C (P = 0.2618), respectively (Fig. 5 D).
Figure 5.
Effect of extracellular D2O substitution on the voltage dependence of steady-state inactivation. (A–C) Steady-state inactivation of Shaker-IR mutants was determined by depolarizing inside-out patches at +50 mV for 5 ms from a holding potential of −120 mV to elicit potassium currents (I−120) and then applying a series of 3-s conditioning prepulse potentials ranging from −120 mV to −30 mV in 10-mV increments, with each voltage step followed by a constant 5-ms test pulse to +50 mV to determine I. Potassium currents recorded at each prepulse potential were normalized to their respective maximal values (I/I−120), averaged, and plotted as a function of the prepulse potential in control conditions (H2O//H2O, filled symbols) and extracellular D2O (H2O//D2O, empty symbols) for T449A (A), T449A/I470A (B), and T449K/I470C (C), respectively. (D) Bars and error bars indicate the mean ± SEM (n ≥ 3) of the midpoint voltages (V1/2) of the voltage dependence of steady-state inactivation obtained for the indicated clones. Symbols indicate individual data points (circles, T449A; down triangles, T449A/I470A; up triangles, T449K/I470C) obtained in H2O//H2O (filled symbols) as control and H2O//D2O (empty symbols). Asterisks indicate significant differences (*, P < 0.05; **, P < 0.01).
To measure the effect of D2O on the kinetics of recovery from inactivation, a standard two-step voltage protocol was used (Levy and Deutsch, 1996a). The first step, used to inactivate channels and measure initial peak current amplitude (I1), was at least fivefold longer than the channel’s time constant for inactivation. This was followed by the recovery period, defined as the time between the end of the first pulse and the beginning of the second pulse (ipi) at −120 mV. Then, the second voltage step was applied, and peak recovered current amplitude (I2) was measured. FR was calculated as (I2 − Iss1) / (I1 − Iss1), with Iss1 representing the steady-state current at the end of the first depolarization. To characterize the time course of recovery from inactivation of Shaker-IR mutants, ipi was varied between 0 and 45 s (Fig. 6). A single-exponential function (see Materials and methods) was fit to the FR versus ipi plot to give the time constant of recovery from inactivation (τrec). The data were reasonably well fit with this simple model regardless of the channel mutant in the absence (H2O//H2O) or presence of D2O (H2O//D2O) in the extracellular solution; however, the sum of two exponential terms gave better fit for the recovery kinetics of T449A (Fig. S3). The comparison of the τrec values shows that the inactivation kinetics of the currents correlates with the recovery kinetics (i.e., faster inactivation leads to faster recovery) and that the extracellular D2O does not modify the rate of recovery from inactivation in any of the mutants studied. The time constants for recovery from inactivation were τrec = 3.7 ± 0.3 s (in H2O//H2O, n = 8) and 3.5 ± 0.3 s (in H2O//D2O, n = 8, P = 0.75) for the T449A mutant. The τrec values obtained in the presence and absence of extracellular D2O were 8.5 ± 0.7 s in H2O//H2O (n = 5) versus 8.7 ± 0.7 s in H2O//D2O (n = 4, P = 0.92) for T449A/I470A; and 0.32 ± 0.09 s in H2O//H2O (n = 4) versus 0.32 ± 0.05 s in H2O//D2O (n = 5, P = 0.99) for T449K/I470C. The results were essentially the same when a biphasic recovery from inactivation model was fit to the data points (Fig. S3).
Figure 6.
Effect of extracellular D2O substitution on the kinetics of recovery from inactivation at −120 mV. (A–C) The time course of recovery from inactivation of the K+ current of Shaker-IR mutants was studied by means of a two-pulse protocol with increasing interpulse time (ipi from 0.5 to 60 s; see Materials and methods for details) between the pulses for T449A (A), T449A/I470A (B), and T449K/I470C (C). Data points presented as FR = (I2 − ISS1) / (I1 − ISS1), where I2 and I1 are the peak currents during the second and the first pulse and ISS1 is the steady-state current at the end of the first depolarization, respectively, and plotted as a function of ipi in control conditions (H2O//H2O, filled symbols) and external D2O (H2O//D2O, open symbols). The time constants of recovery (τrec) were determined by fitting the averaged data points with a single-exponential function (see Materials and methods); the superimposed solid lines show the best fits in all panels. (D) Bars and error bars indicate the mean ± SEM (n ≥ 4) of the τrec values obtained for the indicated clones. Symbols indicate individual data points (circles, T449A; down triangles, T449A/I470A; up triangles, T449K/I470C) obtained in H2O//H2O (filled symbols) and H2O//D2O (empty symbols).
Inactivation kinetics in extracellular solutions with increased viscosity
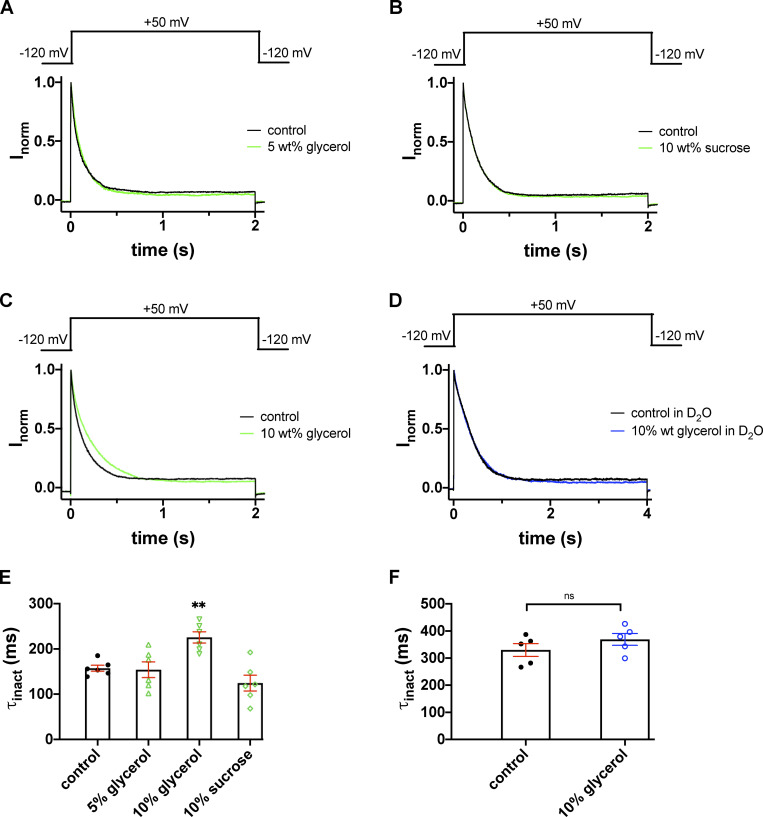
As noted in Fig. 2, extracellular D2O has a substantial impact on the time course of slow inactivation. One possible explanation for the reduced rate in inactivation may be an increase in the viscosity of the medium, in which the diffusion of K+ ions is consequently slower. We mimicked the increased viscosity by adding glycerol or sucrose to the extracellular solution, one at a time, and measured the inactivation time course for each Shaker-IR mutant. The viscosity of the solutions, measured by an Ostwald viscometer, was 1.171 mPa⋅s for 5 wt% glycerol, 1.310 mPa⋅s for 10 wt% glycerol, and 1.336 mPa⋅s for 10 wt% sucrose, respectively. These values are very close to the viscosity of D2O (1.245 mPa⋅s) but are significantly larger than that of H2O (1.002 mPa⋅s). The effect of increased viscosity on the inactivated Shaker-IR T449A single-mutant channels was determined using a pulse sequences that consisted of two consecutive 2-s-long depolarizations to +50 mV. The first of these depolarizations is in control solution to obtain the maximum current, followed by a 45-s-long period at −120 mV, which was sufficient to ensure full recovery of the inactivated channels. The effect of solutions with increased viscosities (i.e., in the presence of 5 wt% glycerol, 10 wt% glycerol and 10 wt% sucrose, respectively) was assessed during the second depolarizing pulse. Perfusion with any of these solutions was started 1 s before the second depolarizing pulse and stopped 500 ms after the end of the second depolarizing pulse. The inactivation kinetics of the current at +50 mV was single exponential regardless of the extracellular solution used (Fig. 7, A–D). The inactivation of the currents was complete and proceeded with a time constant of 157.3 ± 6.6 ms (n = 6) in control (black traces in Fig. 7, A–C), 154.1 ± 17.4 ms (n = 6, P = 0.3) in 5 wt% glycerol (green trace in Fig. 7 A) and 124.5 ± 17.4 ms (n = 6, P = 0.061) in 10 wt% sucrose (green trace in Fig. 7 B), respectively. We observed a significant decrease in the rate of inactivation in the presence of 10 wt% glycerol (time constant of inactivation was 225.4 ± 12.5 ms, n = 6, P = 0.0012; Fig. 7 C). We next examined the effects of extracellular glycerol on Shaker-IR channels in outside-out patches in D2O. The K+ current was first recorded in D2O-based extracellular solution (H2O//D2O, Fig. 7 D, black trace) and then in 10 wt% glycerol in D2O (Fig. 7 D, blue trace). Single-exponential fits to the current traces at +50 mV yielded time constants of 330.1 ± 23.6 ms (n = 5) in H2O//D2O as control and 369.0 ± 22.0 ms (n = 5) in 10 wt% glycerol dissolved in D2O (H2O//D2O), suggesting that an increase in viscosity does not give further contribution to the effect of D2O (P = 0.26). Time constants are summarized in Fig. 7, E and F, for H2O-based and D2O-based extracellular solutions, respectively. To summarize the effects of viscosity on inactivation kinetics, we propose that the slowing of the inactivation kinetics in D2O is not the consequence of the increased viscosity of the D2O solution.
Figure 7.
Inactivation kinetics of the T449A Shaker-IR current in glycerol- and sucrose-supplemented extracellular solutions. (A–C) K+ currents were recorded in outside-out patch configuration with repeated 2.0-s depolarizations from a holding potential of −120 mV to +50 mV. Test pulses were applied every 45 s. During the first depolarizing pulse the patches were perfused with standard extracellular bath solutions (solid black lines). The second depolarizing pulse was applied in the presence of 5 wt% glycerol (A), 10 wt% sucrose (B), and 10 wt% glycerol (C), respectively (solid green lines). The traces recorded after washout are omitted for clarity. (D) The time course of inactivation of outside-out patch currents was determined in an extracellular bath solution prepared in D2O (solid black line) and a solution with 10 wt% glycerol dissolved in the D2O-based external solution (solid blue line). (E and F) Inactivation time constants (τinact) at +50 mV were determined by fitting a single-exponential function to the decaying parts of the current traces and averaged for n = 5–6 cells. (E) Bars and error bars indicate the mean ± SEM of τinact values, symbols indicate individual data points obtained in H2O-based extracellular solution (H2O//H2O) in the control condition (filled circles, no glycerol or sucrose supplementation) or the glycerol- or sucrose-supplemented, H2O-based extracellular solution (as indicated, empty green symbols; up triangles, 5 wt% glycerol; down triangles, 10 wt% glycerol; diamonds, 10 wt% sucrose). (F) The same data representation as in E, except that data are from D2O-based extracellular solution (H2O//D2O) in the control condition (filled circles, no glycerol supplementation) or the 10% glycerol-supplemented, D2O-based extracellular solution (open blue circles). Asterisks indicate a statistically significant difference (**, P < 0.01).
The effect of D2O on the inactivation kinetics is independent of the direction of the K+ current
As K+ ions pass through the selectivity filter, they are dehydrated upon entry and rehydrated upon exit from the filter. Given that dehydration and rehydration are different energetically and kinetically in H2O and D2O (see Discussion), one may hypothesize that the slowing of the inactivation kinetics in D2O-based extracellular solution may simply be the consequence of altered hydration in D2O and the consequent residency time of K+ in the selectivity filter.
To test this, we constructed experimental conditions where at constant extracellular K+ concentration ([K+]ex = 50 mM), we recorded outward and inward K+ currents by manipulating the K+ concentration of the intracellular solution ([K+]in) in inside-out patches. Thus, K+ is either entering from an H2O-based solution the pore and exiting to a D2O-based extracellular one (outward current) or entering the pore from a D2O-based extracellular solution and exiting to an H2O based one (inward current).
[K+]ex was maintained at 50 mM, and [K+]in was set to 15 mM or 150 mM. The K+ equilibrium potentials (EK) from the Nernst equation were calculated as −28.2 mV ([K+]in = 150 mM) and +30.9 mV ([K+]in = 15 mM). The reversal potentials (VR) of the K+ currents were determined experimentally using the following step-ramp protocol.
The initial step in the step-ramp protocol was to depolarize the inside-out patches to +50 mV for 5 ms to open all channels (open probability is approximately maximal) but avoid inactivation. This step is followed by a fast repolarizing ramp of 6.8 mV/ms rate (6.8 V/s) to −120 mV. This fast “reverse” ramp is suitable to determine the reversal potential of the current (Levy and Deutsch, 1996b).
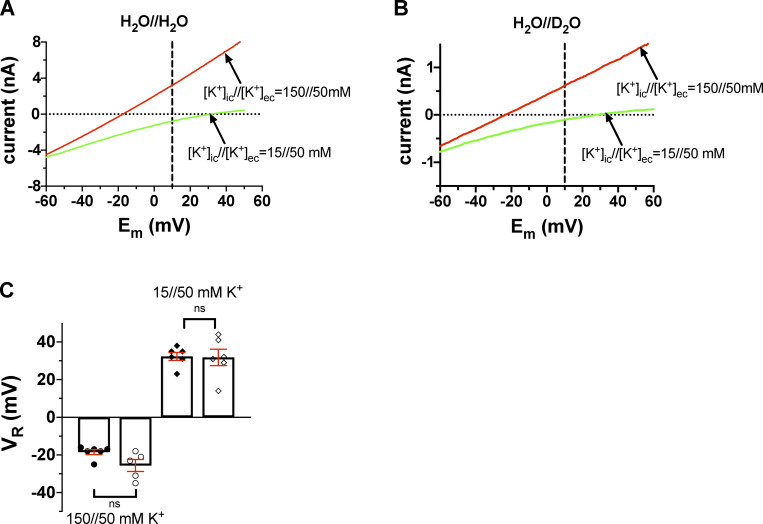
Data in Fig. 8, A and C, show that the experimentally determined VR values are in good agreement with the theoretical values for the Shaker 449A mutant. Moreover, Fig. 8, B and C, show that the reversal potentials are insensitive to the presence of D2O in the extracellular solution. At [K+]in = 150 mM, VR was −18.5 ± 1.3 mV in control solution (H2O//H2O, n = 6) and −25.6 ± 3.2 mV (H2O//D2O, n = 5; P = 0.056). At [K+]in = 15 mM, the relevant data were +31.8 ± 4.3 mV (H2O//H2O, n = 6) and +32.3 ± 2.1 mV (H2O//D2O, n = 6, P = 0.92), respectively. The experiments were repeated with the T449A/I470A mutant as well, resulting in similar observations to T449A (Fig. S4). At [K+]in = 150 mM, VR = −25.2 ± 1.8 mV (H2O//H2O, n = 6) and VR = −22.8 ± 2.2 mV (H2O//D2O, n = 5, P = 0.43) were obtained; at [K+]in = 15 mM, VR = +23.5 ± 2.9 mV (H2O//H2O, n = 6) and VR = +24.2 ± 3.0 mV (H2O//D2O, n = 5, P = 0.87) were determined. This means that the nature of the extracellular solution (i.e., H2O or D2O based) does not affect the selectivity of the pore for K+.
Figure 8.
Current–voltage relationships for T449A Shaker-IR mutant channels at various [K+] combinations in inside-out patches. (A) The inside-out patch was held at a holding potential of −120 mV and depolarized to +50 mV for 5 ms to fully activate the channels (not shown). This step is followed by a fast voltage ramp to −120 mV in 25 ms. The currents corresponding to membrane potentials at the range of +50 mV to –60 mV are shown for clarity. The extracellular solution contained 50 mM K+ prepared in H2O (H2O//H2O). The patch was perfused with an intracellular solution containing 150 mM K+ (red trace) or 15 mM K+ (green trace). The horizontal dotted line indicates the 0 pA current, the vertical dashed line drawn at +10 mV indicates that the current is inward at [K+]in//[K+]ex = 15//50 mM (green trace) and outward at [K+]in//[K+]ex = 150//50 mM (red trace). (B) The same set of experiments as in A, except that the pipette-filling extracellular solution containing 50 mM K+ was prepared in D2O (H2O//D2O). All others (e.g., [K+] and labels) are the same as in A. (C) Current reversal potential (VR) was determined from the traces shown in A and B as the membrane potential at which the current crosses the 0-pA reference line (dotted). Bars and error bars indicate the mean ± SEM of the VR values (n = 6), and symbols indicate individual data points (circles, 150//50 mM K+; diamonds, 15//50 mM K+) obtained in H2O//H2O solution (filled symbols) and extracellular D2O (H2O//D2O, empty symbols).
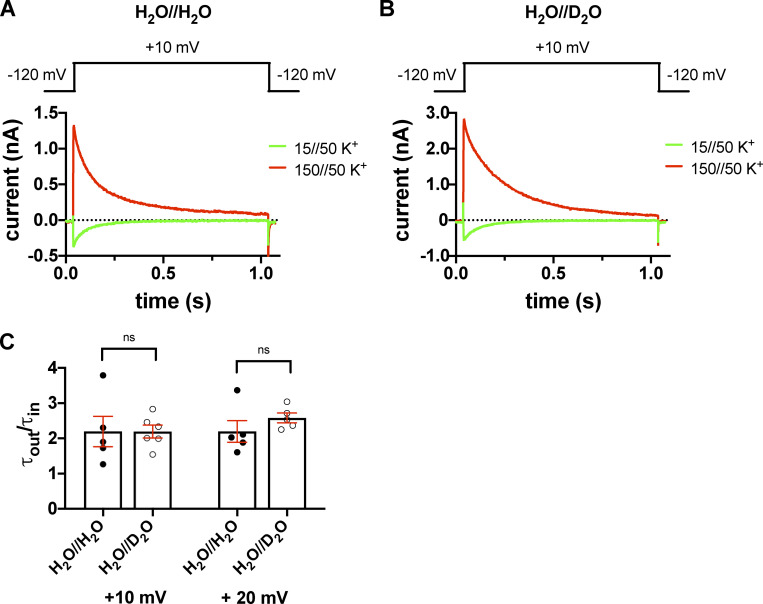
The K+ gradients and the membrane potential combinations were worked out to allow the recording of both inward and outward currents at the same membrane potentials (where channels open quickly) in inside-out patch configuration. Inside-out patches were held at the holding potential of −120 mV and then depolarized to the test potentials for 1 s under control conditions or in the presence of extracellular heavy water, which was in this case in the pipette-filling solution. The currents were recorded at different test potentials ranging from −20 mV to +20 mV in 10-mV increments. The τinact values at each test potential were determined for both outward and inward currents by fitting a single-exponential function to the current decay. Fig. 9 shows that the rate of inactivation is accelerated when the K+ current was inward (green) as compared with the outward one (red). For outward currents, the τinact of the T449A current at +10 mV was τout = 178.5 ± 9.2 ms (H2O//H2O, n = 6) and τout = 286.7 ± 15.2 ms (H2O//D2O, n = 7), and for inward K+ currents, τin = 85.4 ± 13.4 ms (H2O//H2O, n = 5) and τin = 124.9 ± 9.3 ms (H2O//D2O, n = 7) were obtained. The τout to τin ratios were 2.19 ± 0.43 (H2O//H2O, n = 5) and 2.19 ± 0.2 (H2O//D2O, n = 6, P = 0.99; Fig. 9 C). At +20 mV, the corresponding results were 177.5 ± 10.9 ms (H2O//H2O, n = 6) and 253.6 ± 14.4 ms (H2O//D2O, n = 5) for the outward current and 83.1 ± 5.5 ms (H2O//H2O, n = 5) and 109.5 ± 6.7 ms (H2O//D2O, n = 5) for the inward current with ratios of 2.19 ± 0.3 (H2O//H2O, n = 5) and 2.57 ± 0.14 (H2O//D2O, n = 5, P = 0.29; Fig. 9 C). The ratios obtained at different test potentials confirmed that the effect of D2O does not show voltage dependence. Moreover, we repeated the experiments on the double mutant T449A/I470A that resulted in similar observations; the relevant ratios were 1.40 ± 0.1 (H2O//H2O, n = 6) and 1.36 ± 0.04 (H2O//D2O, n = 7, P = 0.74) at 0 mV, 1.45 ± 0.1 (H2O//H2O, n = 6) and 1.42 ± 0.06 (H2O//D2O, n = 7, P = 0.74) at −10 mV, and 1.30 ± 0.2 (H2O//H2O, n = 4) and 1.44 ± 0.02 (H2O//D2O, n = 5, P = 0.47) at −20 mV (Fig. S5), showing that D2O has comparable effect on inactivation gating of the three mutants studied in this paper. The comparison of the ratios of the inactivation time constants for outward to inward currents showed that the ratios are practically equal in H2O and D2O.
Figure 9.
Inward and outward K+ currents in H2O- or D2O-based extracellular solutions in the T449A Shaker-IR mutant. (A and B) Macroscopic currents were measured in voltage-clamped inside-out patches excised from tsA201 cells and normalized to their respective peak currents. The extracellular (pipette-filling) solution contained 50 mM K+ in H2O (A) or D2O (B), and the intracellular (bath) solution contained 150 mM K+ (red traces) or 15 mM K+ (green traces). The holding potential was −120 mV; 1.0-s-long depolarizing pulses to +10 mV were applied to activate the channels and record inward K+ current (green curves) or outward K+ current (red curves). The voltage protocols are shown above the corresponding raw current traces. (C) Inactivation time constants of the currents were determined by fitting a single-exponential function to the decaying part of the currents. Bars and error bars indicate the mean ± SEM of the ratio of the inactivation time constants measured for the outward and inward currents (τout/τin) at +10 mV and +20 mV test potentials in H2O//H2O solution (filled circles) and extracellular D2O (H2O//D2O, empty circles). Symbols indicate the individual data points (n = 4–6).
Shaker T449 modulates the rate of water exchange at the peripheral pockets
The rate of C-type inactivation in K+ channels is affected by the spatial distribution of structural water molecules buried inside well-defined cavities that surround the central pore (inactivation cavity; Fig. 10 A; Ostmeyer et al., 2013; Li et al., 2018; Karbat et al., 2019). In Shaker-IR, the side chains of D447, M448, and W434 from one channel subunit and T449 from a neighboring subunit form a barrier (D-W gate) that limits the exchange of water molecules between these cavities and the extracellular bulk solution. In particular, the hydrogen bonds formed between the D447:Oδ and W434:Nε atoms serve as gates (D-W gates) that govern the rate of water traffic around the channel pore (Fig. 10, A and B; Pless et al., 2013; Lueck et al., 2016; Karbat et al., 2019).
During MD simulations of the WT Shaker channel, the D-W gate behaved as a two-state device, assuming a constrained conformation (D447:Oδ-W434:Nε < 4 Å) for an average fraction of 0.86 ± 0.13 of the run and an unconstrained (4–8 Å) conformation at the remaining time (Fig. 10, C and F). In most cases, the formation of the hydrogen bond between D447:Oδ and W434:Nε of one channel subunit was accompanied by the formation of an additional hydrogen-bond between D447:Oδ and the Oγ atom of the T449 residue from the adjacent channel subunit (Video 1). Consistent with this observation, MD simulations of the T449A channel mutant revealed a strong impact of this substitution on the state distribution of the D-W gates. The average dwell time at the constrained conformation was reduced to 0.24 ± 0.1, the unconstrained conformation was populated 0.5 ± 0.11 of the time, and a third conformation, characterized by wider gate diameters (flipped conformation at D447, 8–10 Å) was apparent at the remaining time (Fig. 10, D and E). While the D-W gates of WT Shaker-IR channels typically exhibited bursts of short durations in the unconstrained conformation interspersed by longer periods of the constrained conformation, the flipped conformation of the T449A subunits typically persisted for a significant fraction of the run (Fig. 10 D) before reverting to an unconstrained or a constrained conformation. As a result, the water flux behind the pore of Shaker T449A was nearly fivefold higher compared with the WT (38 ± 11 versus 8.5 ± 3 water molecules per 100 ns; Fig.10 G). Few lines of evidence suggest that the elevated water flux observed during the T449A simulations captures a specific effect of this substitution brought about by the destabilization of the D-W gates. First, the effect typically occurred within one or two subunits out of the four and was reversible. Second, to negate a possible link between the observed behavior and the particular way the system was assembled, we have conducted control runs in which a WT tetramer was allowed to freely develop for 200 ns, and subsequently, T449A substitutions were introduced in two of the four subunits (Fig. S6 and Video 2). In these simulations, we observed a sequential development of a flipped D447 conformation in one of the two substituted subunits (Fig. S6). Third, we carried control runs of T449A tetramers in which the constrained conformation of the D-W gates was maintained by harmonic restrains. In these runs, water flow behind the selectivity filter was nearly abolished (Fig. S6, C and D). This observation is consistent with the proposed stabilizing effect of T449 on the constrained conformation of the D-W gate and negates an increased water flow due to possible nonspecific effects of the mutation.
Discussion
In this study, we exploited the physicochemical differences between H2O and D2O to gain insight into the molecular interactions leading to C-type inactivation of Shaker-IR K+ channels. The role of H2O in stabilizing the inactivated conformation of the selectivity filter via a hydrogen-bond network (Ostmeyer et al., 2013; Cuello et al., 2017; Labro et al., 2018; Li et al., 2018; Karbat et al., 2019; Xu and McDermott, 2019) and/or regulating the K+ occupancy of the coordination site controlling C-type inactivation has been proposed based on x-ray crystallography and MD simulation in KcsA and more recently in Shaker. This hypothetical role of H2O has been experimentally addressed in this study using D2O as a tool. We found that substitution of H2O by D2O in the extracellular, but not intracellular, compartment slows the inactivation kinetics of Shaker-IR. We concluded that H2O and D2O act as structural water molecules controlling inactivation and that the slower inactivation kinetics in D2O can be attributed to the difference in the specific interactions of D2O and H2O with the inactivation machinery. We support our conclusion using indirect evidence, i.e., by excluding potential nonspecific effects of the D2O substitution, such as what follows here. (1) An increase in the viscosity of the external solution that mimics the viscosity of the D2O-based solution does not affect the inactivation kinetics of the current. The viscosity of the H2O-based solution was increased by either sucrose or glycerol, and the lack of the effect of increased viscosity on the inactivation kinetics was shown in three mutants (T449A, T449A/I470A, and T449K/I470C) displaying C-type inactivation at various rates. (2) The G–V relationships obtained in H2O and D2O were superimposable for all three Shaker mutants tested. This indicates that slowing of the inactivation kinetics in D2O cannot be explained by altered equilibrium and a consequent modulation of the rate of the C→O→I transition. Consistent with this, we showed that the activation and deactivation kinetics of the currents are minimally affected by the application of a D2O-based extracellular solution. (3) Substitution of H2O for D2O did not alter the K+ selectivity of the pore as measured by the reversal potential of the current. This implies the lack of gross structural changes in the selectivity filter upon H2O/D2O substitution. (4) The slowing of the inactivation kinetics by extracellular D2O was similar when K+ was transported from H2O- to D2O-based (outward current) solutions or from D2O- to H2O-based (inward current) solutions. This result suggests that neither the kinetics nor the energetics of dehydration/rehydration and consequently the exit rate of K+ from the site controlling C-type inactivation is influenced by D2O in the extracellular solution. (5) MD simulations showed that H2O indeed enters the inactivation cavity located behind the selectivity filter, and the access is affected by the amino acid in position 449. Combined, these observations provide experimental evidence for the role of structural H2O molecules in controlling C-type inactivation.
We have studied the kinetics of C-type inactivation in three Shaker-IR mutants having inactivation kinetics ranging from ∼60 ms to ∼150 ms. All three mutants contain a mutation at position 449 that is known to modify rather than disrupt C-type inactivation (López-Barneo et al., 1993; Cordero-Morales et al., 2006b; Hoshi and Armstrong, 2013; Cuello et al., 2017), possibly by regulating the access of inactivating water molecules into the cavity located behind the selectivity filter (Cuello et al., 2017; Karbat et al., 2019). Introduction of a cysteine at position 470 inhibits C-type inactivation (Holmgren et al., 1997), most likely by modulating the allosteric communication between activation and inactivation gates, as reported for mutations in equivalent positions in KcsA (Cuello et al., 2010a; Peters et al., 2013; Kratochvil et al., 2016) and Kv1.2 (Cuello et al., 2010a). In combination with 449K mutation, the 449K/470C mutant was successfully used previously to tailor the kinetics of C-type inactivation, modulate the intracellular TEA+ binding site, and blocker trapping (Panyi and Deutsch, 2007). These findings indicate that the mutants used in our study are suitable to study C-type inactivation. The mutants modify the inactivation rate rather than the principle inactivation mechanism (e.g., directly alter the conformational changes responsible for C-type inactivation). In addition, we found that extracellular D2O slows inactivation kinetics in a similar manner regardless of the specific channel mutants and their inactivation rates.
The mutants used in this study, however, display a positive shift in the voltage dependence of steady-state activation of the currents as compared with the Shaker-IR channel (V1/2 = −28.3 ± 2.8 mV, k = 4.9 ± 0.4 mV, n = 8; Martinez-Morales et al., 2014). We did not investigate the mechanism of this shift; however, it is known that several substitutions change the midpoint (V1/2), slope factor (k), or both of various Shaker-IR mutants (Hackos et al., 2002; Soler-Llavina et al., 2006). The analysis of the G–V relationships was used to define a voltage range (≥50 mV) where currents quickly and fully activate, and C-type inactivation can be studied in isolation (i.e., the rate of inactivation is determined by the O→I rather than the C→O transition). Similarly, the voltage dependence of steady-state inactivation and the kinetics of recovery from inactivation showed variability among the double mutants at positions 449 and 470, but we have not observed fundamentally altered gating properties of the channels.
The effect of D2O substitution has been studied previously on a variety of biophysical properties of ion channels in different systems (Schauf and Bullock, 1980, 1982; Alicata et al., 1990; DeCoursey and Cherny, 1997). The substitution of H2O to 99.8% D2O both externally and internally decreased the maximum Na+ and K+ conductances in squid (Conti and Palmieri, 1968; Meves, 1974) and Myxicola infundibulum giant axon (Schauf and Bullock, 1979). The effect on the conductances was comparable to the corresponding reduction in ion mobilities in D2O versus H2O (Schauf and Bullock, 1980). Our results agree well with these studies. The substitution of extracellular H2O for D2O did not induce a significant shift in G–V relationships of the Shaker mutants in this study, and the K+ conductance was reduced in the D2O-based extracellular solution (e.g., Fig. 3). A recent study of a very rapidly inactivating Shaker mutant (K427D/M448K) reported a small depolarizing shift in the G–V upon exposure to D2O-based extracellular solution (Karbat et al., 2019). However, to our knowledge, our paper is the first to address the effect of D2O substitution on the inactivation kinetics of a Kv channel.
Our principal finding is that extracellular substitution D2O for H2O slowed C-type inactivation, the relative increase in the inactivation time constants obtained in H2O//H2O versus H2O//D2O was similar in all Shaker mutants studied here. The substitution of D2O for H2O in the intracellular solution (D2O//H2O) did not affect the kinetics of C-type inactivation (Fig. 2). This finding and recent literature pointing to the importance of transport of inactivating water molecules into the cavity behind the selectivity filter (Ostmeyer et al., 2013; Cuello et al., 2017; Li et al., 2018; Karbat et al., 2019) led us to hypothesize that extracellular D2O effects might be related to D2O acting as structural water. This hypothesis cannot be tested directly using conventional electrophysiological tools. To overcome this limitation, we designed experiments to exclude all alternative effects of D2O substitution on the inactivation kinetics to reach the conclusion that D2O acts specifically on the inactivation machinery of Shaker. Of the alternative explanations, the most straightforward one is the difference in the viscosity of the D2O- and H2O-based solutions. The increased viscosity was mimicked by adding either glycerol or sucrose to the control, sodium-based extracellular solution. Our finding that neither 5 wt% glycerol (1.171 mPa⋅s) nor 10 wt% sucrose (1.336 mPa⋅s) solutions affected inactivation kinetics suggests that an increase in viscosity comparable to the D2O-based solution (1.245 mPa⋅s) does not affect inactivation kinetics, thereby excluding a viscosity-mediated effect in the H2O//D2O recording condition. 10 wt% glycerol (1.310 mPa⋅s), on the other hand, slowed C-type inactivation. We do not attribute this effect of 10 wt% glycerol to increased viscosity, since 10 wt% sucrose, having larger viscosity than 10 wt% glycerol, had no effect on inactivation. Besides, the rate of inactivation was insensitive to 10 wt% glycerol when applied in combination with D2O substitution; a simple viscosity-based effect of 10 wt% glycerol would be expected to influence inactivation kinetics in a D2O-based solution as well. Glycerol at 10 wt% concentration may directly influence protein hydration (Hirai et al., 2018), which may account for our observation, but was not investigated further.
A drastic increase in the extracellular viscosity/osmolarity using 2 M sucrose solution, which translates to ∼68 wt%, was reported to speed up the kinetics of recovery from inactivation (Ostmeyer et al., 2013) of KcsA. However, 2 M sucrose concentration may cause structural changes in proteins (Stanley et al., 2008; Tatebayashi et al., 2015) and may contribute to the observed effects. We cannot confirm the effect of increased viscosity in general, as the kinetics of recovery from inactivation was the same for all three mutants in D2O- and H2O-based solutions, albeit at a modest increase in the viscosity of the D2O-based solution that corresponds to <10 wt% sucrose. Karbat et al., on the other hand, found a slower kinetics of recovery from inactivation for a very rapidly inactivating Shaker mutant (K427D/M448K) in extracellular D2O (Karbat et al., 2019). In this construct, the K427D mutation is in the turret adjacent the pore helix, whereas M448K is part of the D-W gate controlling water movement between the peripheral cavities and the extracellular bulk solution. The combination of the altered D-W gate and the presence of D2O may additively result in the decreased recovery rate observed for 427D/M448K in the presence of D2O. Regardless of the differences above, data are consistent with the role of the structural H2O network in regulating the inactivation machinery of the channels. On the other hand, the kinetics of recovery from inactivation is sensitive to, among others, the ionic composition (Levy and Deutsch, 1996a), [K+]ex and pH (Levy and Deutsch, 1996b) of the extracellular solution, and the holding potential (Levy and Deutsch, 1996b), and it also displays large variability among the K+ channels and mutants (Levy and Deutsch, 1996b; Rasmusson et al., 1998; Fedida et al., 1999; Bett and Rasmusson, 2004; Kurata et al., 2005; Ray and Deutsch, 2006; Phan et al., 2017; Suárez-Delgado et al., 2020). For example, biphasic recovery kinetics of Kv1.3 was revealed only at increased [K+]ex in combination with −130 mV holding potential during recovery (Levy and Deutsch, 1996b). These factors may also contribute to the interpretation of the data.
Slowing of the C→O transition can reduce the apparent rate of the O→I transition in a C→O→I gating scheme characteristic of Shaker (Szanto et al., 2020). At a given test potential, slowing of the C→O can be anticipated by a depolarizing shift in the G–V relationship in the presence of extracellular D2O. This scenario was excluded by showing that D2O did not alter the G–V relationship of any of the clones (see above; Fig. 4). The activation kinetics of the T449A/I470A mutant was not affected by the H2O→D2O substitution; however, the activation time constants were minimally but significantly greater for the T449A and T449K/I470C mutants in H2O//D2O than in H2O//H2O. This slowing, in our interpretation, has no biological relevance in regulating C-type inactivation, as the increased τact is still three orders of magnitude smaller than τinact (Figs. 2 and 3). Similarly, the deactivation kinetics of the current was also minimally but significantly affected by H2O→D2O substitution for the T449A and T449A/I470A clones. The D2O-induced changes in the deactivation kinetics produce time constants that are at least 60-fold faster than the inactivation kinetics. Moreover, sufficient lag (at least 500 ms) was implemented into the solution exchange protocols to allow complete deactivation before switching between H2O- and D2O-based extracellular solutions. Thus, we conclude that these minimal changes in the activation and deactivation kinetics cannot account for the slowing of the inactivation kinetics upon D2O exposure and do not interfere with the interpretation of our experiments regarding the inactivation kinetics.
The K+ occupancy in the selectivity filter, most importantly that of the S2 K+ binding site, regulates inactivation gating (Zhou and MacKinnon, 2004; Cuello et al., 2017; Karbat et al., 2019; Renart et al., 2019). Exposure to D2O is known to alter the conformational dynamics of proteins (e.g., superoxide dismutase; Cioni and Strambini, 2002), which may, in turn, affect the interaction of the selectivity filter with K+. This scenario, however, was not supported by our experiments, as the reversal potential of the K+ current was the same either in H2O or D2O in the extracellular solution (Fig. 8). Moreover, the selectivity filter is accessible from both the extracellular and intracellular solutions, but the effect of D2O is restricted to extracellular application. Thus, from these experiments, we do not predict large-scale distortions in the selectivity filter in a D2O-based extracellular solution.
When an outward K+ current is conducted, hydrated potassium ions enter the water-filled cavity located below the selectivity filter. Potassium ions shed their water coat immediately before entering the selectivity filter (Doyle et al., 1998; Morais-Cabral et al., 2001; Zhou et al., 2001; Jiang et al., 2003; McCoy and Nimigean, 2012; Cuello et al., 2017) and become rehydrated on its extracellular side. Although it is believed that the structure of the ion–water complex does not change with deuteration (Born–Oppenheimer approximation), the rate of dehydration and rehydration steps must be sensitive to H2O or D2O being in the solutions. K+ faces a larger energy barrier for rehydration in D2O due to the primary kinetic isotope effect (Thomas and Jennings, 1999), which predicts a slower rate of hydrate shell formation. This may reduce the exit rate of the K+ ion from the site controlling C-type inactivation (Baukrowitz and Yellen, 1996) or result in an increased occupancy in the S2 defined by structural biology (Matulef et al., 2016; Heer et al., 2017; Renart et al., 2019; Tilegenova et al., 2019). In addition, diffusion of K+ is slower in a D2O environment, thereby providing an additional mechanism for the slowing of the inactivation kinetics. So, the inactivation kinetics of outward currents in extracellular D2O should be slower than that of the inward currents. Comparison of the inactivation kinetics of the inward and outward currents required specific conditions. [K+]ex must be kept constant to avoid the effects of varying [K+]ex on the inactivation kinetics (López-Barneo et al., 1993; Baukrowitz and Yellen, 1996; Kiss and Korn, 1998). To do this, inside-out patches were used with constant 50 mM [K+]ex either in H2O or D2O, and the cytosolic surface was perfused with different [K+]in solutions, keeping in mind the deteriorating effect of K+ deprivation on the K+ channels (Olcese et al., 1997; Melishchuk et al., 1998; Loboda et al., 2001). The two K+ concentrations were 15 mM and 150 mM K+ in H2O, with reversal potentials of approximately +30 mV and −25 mV, respectively. Furthermore, inward and outward currents had to be recorded at the same depolarized test potentials to avoid any voltage-dependent effects on channel gating (i.e., the voltage dependence of the activation kinetics). Under these experimental conditions, we found that the ratio of the inactivation time constants was insensitive to the presence of D2O in the extracellular solution regardless of the channel mutant used. This means that the effect of the kinetics of dehydration and rehydration (although it might be at different rates in H2O and D2O, with a consequent effect on K+ residency) is not large enough to be reflected in the inactivation kinetics. Alternatively, the electrostatic repulsion among K+ ions (“hard” or “soft” knock-on effects; Tilegenova et al., 2019) of the K+ ions interacting in the selectivity filter may overcome the effect of rehydration/dehydration in D2O-based extracellular solutions. Regardless, the slowing of the inactivation kinetics cannot be explained by altered occupancy of the K+ modulatory site of inactivation in extracellular D2O.
Having excluded the alternative explanations above, we propose that the effect of D2O in the extracellular solution should be specific for the inactivation machinery of the Shaker K+ channels. Hydrogen bonds within D2O are stronger than those in H2O, since the length of the hydrogen bond is shorter (Ubbelohde and Gallagher, 1955). Furthermore, in D2O, the more restricted atomic vibrations and, consequently, the difference in relative energies of H and D bonds, result in a decrease in the zero-point vibrational energy and slower kinetics of H(D)-bond formation (Scheiner and Čuma, 1996).
The pore region of Kv channels is surrounded proteinaceous cavities (“peripheral cavities”) to which water molecules may enter through a conduit guarded by the side chains of T449, D447, M448, and W434 (D-W gate) in Shaker (Cuello et al., 2017; Karbat et al., 2019). The network of structural water molecules at the peripheral cavities was proposed to stabilize the collapsed conformation of the selectivity filter (Ostmeyer et al., 2013; Li et al., 2018). We have recently shown that pore-modulating toxins may exert their blocking effect by engaging the above residues and modifying the rates of water exchange at the peripheral cavities. Imbalanced water flow behind the selectivity filter, observed in MD simulations conducted with a bound toxin, resulted in a flip of the aromatic side chain of Y445 of the selectivity filter and a breach at the aromatic-cuff barrier, allowing water molecules to invade the central pore and displace the ion bound at S2. These events finally lead to the collapse of the pore into an asymmetric nonconducting state (Karbat et al., 2019). Flipped backbone carbonyls were captured in the crystal structures of inactivated ion channels (Cordero-Morales et al., 2006b). Cryo-EM structures of Kv11.1 channel and its noninactivating S631A mutant highlight the association between a compromised hydrophobic cuff barrier and the inactivated state of the channel (Wang and MacKinnon, 2017). Mutations in this region were shown to impair slow inactivation in Kv1.2, Kv1.5, and KcsA and alter the arrangement of inactivating water molecules behind the selectivity filter of crystalized KcsA mutants (Labro et al., 2018).
MD simulations conducted herein showed a fivefold increase in the flux of water molecules through the D-W gates of the T449A Shaker mutant, consistent with its accelerated slow-inactivation kinetics. Notably, during our 200-ns simulation windows, the open-pore conformation of the T449A mutant remained intact, contrasting with previous simulation studies in which an irregular water flow behind the selectivity filter was induced by toxins (Karbat et al., 2019), chemical modifications (Li et al., 2017), or mutations that trigger open-channel conformations (Li et al., 2018). It is interesting to note, however, that simulation studies conducted with a Shaker channel bearing a chemically modified W434 revealed flipping of D447 in three out of four trajectories and an increased occupancy of water behind the selectivity filter (Lueck et al., 2016). While this chemical modification was reported to greatly accelerate channel inactivation, the authors did not report a collapse of the pore during their 500-ns simulation windows. In this regard, we note that the effects of the T449A substitution or chemical modification of W434 are milder compared with that of toxin binding or a direct chemical modification of the SF and that inactivation of T449A takes place within hundreds of milliseconds, well outside the time scope that is currently addressable by conventional all-atom MD simulations. Nevertheless, based on previous studies, one can easily conceive how the irregular water flow behind the selectivity filter alongside the comparably long dwell times of the D-W gates in the flipped conformation may, in the long run, breach the aromatic-cuff barrier of the T449A channel mutant and collapse its pore. Additionally, the lower diffusion coefficient of D2O may slow water permeation through the D-W gates into the peripheral cavities and thus contribute to the lower inactivation kinetics measured in D2O-based extracellular solutions. Moreover, the primary kinetic isotope effect may also differentially influence the interaction of H2O and D2O molecules with the surrounding amino acid side chains along the pathway from the extracellular solution to the selectivity filter through the D-W gate, inactivation cavity, and aromatic barrier.
Interestingly, the kinetics of recovery from inactivation was not modified significantly by extracellular D2O. During prolonged depolarizations, the selectivity filter undergoes structural changes that involve a distortion of the S3 and S4 sites as a consequence of a pinch at G77 and a backbone carbonyl flip at V76 that creates a barrier to the movement of ions through the filter in KcsA (Cuello et al., 2010b; Matulef et al., 2016; Li et al., 2018). This may mean that the rate-limiting step for recovery is different from that of the inactivation kinetics and that the sensitivity of the structural rearrangements controlling recovery from inactivation is not influenced by D2O substitution. Alternatively, the isotope effects of D2O might not be large enough to influence the recovery kinetics in the T449A, T449A/I70A, and T449K/I470C mutants. On the other hand, the voltage dependence of steady-state inactivation was shifted to depolarized potentials in the presence of extracellular D2O for two out of three mutants (Fig. 5). This is consistent with our recent results (Szanto et al., 2020), where we showed that the onset of slow inactivation in the Shaker-IR channel occurs through the open state at both negative and positive voltages. Thus, gating transitions at negative membrane potentials, where steady-state inactivation develops (C→O→OI→CI), can also be affected by extracellular D2O. In addition, extracellular D2O may also affect the voltage dependence of activation gating and, as a consequence, steady-state inactivation, since the voltage sensors are surrounded by water and displacing water molecules as they translocate (Díaz-Franulic et al., 2018). These may, on the other hand, be substantial only at negative membrane potentials, as we did not see an effect of D2O substitution on the G–V relationship (Fig. 4).
In summary, our results support the idea that the dynamics of structural water molecules at the peripheral cavities behind the selectivity filter shape the rate and magnitude of slow inactivation in Kv channels and provide fine details on the contribution of residues that modulate water access to these areas to the slow-inactivation gating of Shaker.
Supplementary Material
lists MD simulations carried in the frame of the current study.
Acknowledgments
Christopher J. Lingle served as editor.
The authors are grateful to Michael E. Green (City College of New York, New York, NY) for the valuable discussions on the physicochemistry of D2O. The authors thank Cecilia Nagy and Adrienn Bagosi for expert technical assistance.
This work was supported by the Hungarian Academy of Sciences projects KTIA_NAP_13-2-2015-0009 and KTIA_NAP_13-2-2017-0013 (Z. Varga). The following grants also supported this work: National Research Development and Innovation Office, Hungary, grants OTKA K132906 (Z. Varga) and OTKA K119417 (G. Panyi); Ministry of Human Capacities, Hungary, grant EFOP-3.6.2-16-2017-00006 (G. Panyi); and Ministry of Finance, Hungary, grant GINOP-2.3.2-15-2016-00044 (G. Panyi). This study was supported in part by the Israel Science Foundation (grant 1248/15), the Minerva Foundation, and the Willner Family Fund (to E. Reuveny) and the European Cooperation in Science and Technology (COST Action MB1406 to E. Reuveny and G. Panyi). E. Reuveny is the incumbent of the Charles H. Hollenberg Professorial Chair.
The authors declare no competing financial interests.
Author contributions: T.G. Szanto contributed to conceptualization, investigation, formal analysis, and writing of the original draft. S. Gaal contributed to investigation and formal analysis. I. Karbat contributed to conceptualization, investigation, formal analysis, writing of the original draft, and manuscript review and editing. Z. Varga contributed to conceptualization and manuscript review and editing. E. Reuveny contributed to conceptualization, manuscript review and editing, and funding acquisition. G. Panyi contributed to conceptualization, writing of the original draft, manuscript review and editing, funding acquisition, and methodology.
References
- Alicata, D.A., Rayner M.D., and Starkus J.G.. 1990. Sodium channel activation mechanisms. Insights from deuterium oxide substitution. Biophys. J. 57:745–758. 10.1016/S0006-3495(90)82595-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baukrowitz, T., and Yellen G.. 1996. Two functionally distinct subsites for the binding of internal blockers to the pore of voltage-activated K+ channels. Proc. Natl. Acad. Sci. USA. 93:13357–13361. 10.1073/pnas.93.23.13357 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bett, G.C.L., and Rasmusson R.L.. 2004. Inactivation and recovery in Kv1.4 K+ channels: lipophilic interactions at the intracellular mouth of the pore. J. Physiol. 556:109–120. 10.1113/jphysiol.2003.055012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezanilla, F., and Armstrong C.M.. 1977. Inactivation of the sodium channel. I. Sodium current experiments. J. Gen. Physiol. 70:549–566. 10.1085/jgp.70.5.549 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chakrapani, S., Cordero-Morales J.F., and Perozo E.. 2007. A quantitative description of KcsA gating I: macroscopic currents. J. Gen. Physiol. 130:465–478. 10.1085/jgp.200709843 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cioni, P., and Strambini G.B.. 2002. Effect of heavy water on protein flexibility. Biophys. J. 82:3246–3253. 10.1016/S0006-3495(02)75666-X [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conti, F., and Palmieri G.. 1968. Nerve fiber behaviour in heavy water under voltage-clamp. Biophysik. 5:71–77. 10.1007/BF01388134 [DOI] [PubMed] [Google Scholar]
- Cordero-Morales, J.F., Cuello L.G., and Perozo E.. 2006a. Voltage-dependent gating at the KcsA selectivity filter. Nat. Struct. Mol. Biol. 13:319–322. 10.1038/nsmb1070 [DOI] [PubMed] [Google Scholar]
- Cordero-Morales, J.F., Cuello L.G., Zhao Y., Jogini V., Cortes D.M., Roux B., and Perozo E.. 2006b. Molecular determinants of gating at the potassium-channel selectivity filter. Nat. Struct. Mol. Biol. 13:311–318. 10.1038/nsmb1069 [DOI] [PubMed] [Google Scholar]
- Cordero-Morales, J.F., Jogini V., Lewis A., Vásquez V., Cortes D.M., Roux B., and Perozo E.. 2007. Molecular driving forces determining potassium channel slow inactivation. Nat. Struct. Mol. Biol. 14:1062–1069. 10.1038/nsmb1309 [DOI] [PubMed] [Google Scholar]
- Cordero-Morales, J.F., Jogini V., Chakrapani S., and Perozo E.. 2011. A multipoint hydrogen-bond network underlying KcsA C-type inactivation. Biophys. J. 100:2387–2393. 10.1016/j.bpj.2011.01.073 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuello, L.G., Jogini V., Cortes D.M., Pan A.C., Gagnon D.G., Dalmas O., Cordero-Morales J.F., Chakrapani S., Roux B., and Perozo E.. 2010a. Structural basis for the coupling between activation and inactivation gates in K(+) channels. Nature. 466:272–275. 10.1038/nature09136 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuello, L.G., Jogini V., Cortes D.M., and Perozo E.. 2010b. Structural mechanism of C-type inactivation in K(+) channels. Nature. 466:203–208. 10.1038/nature09153 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuello, L.G., Cortes D.M., and Perozo E.. 2017. The gating cycle of a K+ channel at atomic resolution. eLife. 6:e28032. 10.7554/eLife.28032 [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeCoursey, T.E., and Cherny V.V.. 1997. Deuterium isotope effects on permeation and gating of proton channels in rat alveolar epithelium. J. Gen. Physiol. 109:415–434. 10.1085/jgp.109.4.415 [DOI] [PMC free article] [PubMed] [Google Scholar]
- del Camino, D., Holmgren M., Liu Y., and Yellen G.. 2000. Blocker protection in the pore of a voltage-gated K+ channel and its structural implications. Nature. 403:321–325. 10.1038/35002099 [DOI] [PubMed] [Google Scholar]
- Díaz-Franulic, I., González-Pérez V., Moldenhauer H., Navarro-Quezada N., and Naranjo D.. 2018. Gating-induced large aqueous volumetric remodeling and aspartate tolerance in the voltage sensor domain of Shaker K+ channels. Proc. Natl. Acad. Sci. USA. 115:8203–8208. 10.1073/pnas.1806578115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding, S., and Horn R.. 2002. Tail end of the s6 segment: role in permeation in shaker potassium channels. J. Gen. Physiol. 120:87–97. 10.1085/jgp.20028611 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dodson, P.D., and Forsythe I.D.. 2004. Presynaptic K+ channels: electrifying regulators of synaptic terminal excitability. Trends Neurosci. 27:210–217. 10.1016/j.tins.2004.02.012 [DOI] [PubMed] [Google Scholar]
- Doyle, D.A., Morais Cabral J., Pfuetzner R.A., Kuo A., Gulbis J.M., Cohen S.L., Chait B.T., and MacKinnon R.. 1998. The structure of the potassium channel: molecular basis of K+ conduction and selectivity. Science. 280:69–77. 10.1126/science.280.5360.69 [DOI] [PubMed] [Google Scholar]
- Fedida, D., Maruoka N.D., and Lin S.. 1999. Modulation of slow inactivation in human cardiac Kv1.5 channels by extra- and intracellular permeant cations. J. Physiol. 515:315–329. 10.1111/j.1469-7793.1999.315ac.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasoe, P.K., and Long F.A.. 1960. Use of Glass Electrodes to Measure Acidities in Deuterium Oxide1,2. J. Phys. Chem. 64:188–190. 10.1021/j100830a521 [DOI] [Google Scholar]
- Hackos, D.H., Chang T.-H., and Swartz K.J.. 2002. Scanning the intracellular S6 activation gate in the shaker K+ channel. J. Gen. Physiol. 119:521–532. 10.1085/jgp.20028569 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamill, O.P., Marty A., Neher E., Sakmann B., and Sigworth F.J.. 1981. Improved patch-clamp techniques for high-resolution current recording from cells and cell-free membrane patches. Pflugers Arch. 391:85–100. 10.1007/BF00656997 [DOI] [PubMed] [Google Scholar]
- Heer, F.T., Posson D.J., Wojtas-Niziurski W., Nimigean C.M., and Bernèche S.. 2017. Mechanism of activation at the selectivity filter of the KcsA K+ channel. eLife. 6:e25844. 10.7554/eLife.25844 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirai, M., Ajito S., Sugiyama M., Iwase H., Takata S.I., Shimizu N., Igarashi N., Martel A., and Porcar L.. 2018. Direct Evidence for the Effect of Glycerol on Protein Hydration and Thermal Structural Transition. Biophys. J. 115:313–327. 10.1016/j.bpj.2018.06.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmgren, M., Smith P.L., and Yellen G.. 1997. Trapping of organic blockers by closing of voltage-dependent K+ channels: evidence for a trap door mechanism of activation gating. J. Gen. Physiol. 109:527–535. 10.1085/jgp.109.5.527 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoshi, T., and Armstrong C.M.. 2013. C-type inactivation of voltage-gated K+ channels: pore constriction or dilation? J. Gen. Physiol. 141:151–160. 10.1085/jgp.201210888 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoshi, T., Zagotta W.N., and Aldrich R.W.. 1990. Biophysical and molecular mechanisms of Shaker potassium channel inactivation. Science. 250:533–538. 10.1126/science.2122519 [DOI] [PubMed] [Google Scholar]
- Hoshi, T., Zagotta W.N., and Aldrich R.W.. 1991. Two types of inactivation in Shaker K+ channels: effects of alterations in the carboxy-terminal region. Neuron. 7:547–556. 10.1016/0896-6273(91)90367-9 [DOI] [PubMed] [Google Scholar]
- Jiang, Y., Lee A., Chen J., Ruta V., Cadene M., Chait B.T., and MacKinnon R.. 2003. X-ray structure of a voltage-dependent K+ channel. Nature. 423:33–41. 10.1038/nature01580 [DOI] [PubMed] [Google Scholar]
- Karbat, I., Altman-Gueta H., Fine S., Szanto T., Hamer-Rogotner S., Dym O., Frolow F., Gordon D., Panyi G., Gurevitz M., and Reuveny E.. 2019. Pore-modulating toxins exploit inherent slow inactivation to block K+ channels. Proc. Natl. Acad. Sci. USA. 116:18700–18709. 10.1073/pnas.1908903116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiss, L., and Korn S.J.. 1998. Modulation of C-type inactivation by K+ at the potassium channel selectivity filter. Biophys. J. 74:1840–1849. 10.1016/S0006-3495(98)77894-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozak, M. 1991. Structural features in eukaryotic mRNAs that modulate the initiation of translation. J. Biol. Chem. 266:19867–19870. 10.1016/S0021-9258(18)54860-2 [DOI] [PubMed] [Google Scholar]
- Kratochvil, H.T., Carr J.K., Matulef K., Annen A.W., Li H., Maj M., Ostmeyer J., Serrano A.L., Raghuraman H., Moran S.D., et al. 2016. Instantaneous ion configurations in the K+ ion channel selectivity filter revealed by 2D IR spectroscopy. Science. 353:1040–1044. 10.1126/science.aag1447 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kratochvil, H.T., Maj M., Matulef K., Annen A.W., Ostmeyer J., Perozo E., Roux B., Valiyaveetil F.I., and Zanni M.T.. 2017. Probing the Effects of Gating on the Ion Occupancy of the K+ Channel Selectivity Filter Using Two-Dimensional Infrared Spectroscopy. J. Am. Chem. Soc. 139:8837–8845. 10.1021/jacs.7b01594 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurata, H.T., and Fedida D.. 2006. A structural interpretation of voltage-gated potassium channel inactivation. Prog. Biophys. Mol. Biol. 92:185–208. 10.1016/j.pbiomolbio.2005.10.001 [DOI] [PubMed] [Google Scholar]
- Kurata, H.T., Doerksen K.W., Eldstrom J.R., Rezazadeh S., and Fedida D.. 2005. Separation of P/C- and U-type inactivation pathways in Kv1.5 potassium channels. J. Physiol. 568:31–46. 10.1113/jphysiol.2005.087148 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Labro, A.J., Cortes D.M., Tilegenova C., and Cuello L.G.. 2018. Inverted allosteric coupling between activation and inactivation gates in K+ channels. Proc. Natl. Acad. Sci. USA. 115:5426–5431. 10.1073/pnas.1800559115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy, D.I., and Deutsch C.. 1996a. Recovery from C-type inactivation is modulated by extracellular potassium. Biophys. J. 70:798–805. 10.1016/S0006-3495(96)79619-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy, D.I., and Deutsch C.. 1996b. A voltage-dependent role for K+ in recovery from C-type inactivation. Biophys. J. 71:3157–3166. 10.1016/S0006-3495(96)79509-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, J., Ostmeyer J., Boulanger E., Rui H., Perozo E., and Roux B.. 2017. Chemical substitutions in the selectivity filter of potassium channels do not rule out constricted-like conformations for C-type inactivation. Proc. Natl. Acad. Sci. USA. 114:11145–11150. 10.1073/pnas.1706983114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, J., Ostmeyer J., Cuello L.G., Perozo E., and Roux B.. 2018. Rapid constriction of the selectivity filter underlies C-type inactivation in the KcsA potassium channel. J. Gen. Physiol. 150:1408–1420. 10.1085/jgp.201812082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, Y., Holmgren M., Jurman M.E., and Yellen G.. 1997. Gated access to the pore of a voltage-dependent K+ channel. Neuron. 19:175–184. 10.1016/S0896-6273(00)80357-8 [DOI] [PubMed] [Google Scholar]
- Loboda, A., Melishchuk A., and Armstrong C.. 2001. Dilated and defunct K channels in the absence of K+. Biophys. J. 80:2704–2714. 10.1016/S0006-3495(01)76239-X [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loots, E., and Isacoff E.Y.. 2000. Molecular coupling of S4 to a K(+) channel’s slow inactivation gate. J. Gen. Physiol. 116:623–636. 10.1085/jgp.116.5.623 [DOI] [PMC free article] [PubMed] [Google Scholar]
- López-Barneo, J., Hoshi T., Heinemann S.H., and Aldrich R.W.. 1993. Effects of external cations and mutations in the pore region on C-type inactivation of Shaker potassium channels. Receptors Channels. 1:61–71. [PubMed] [Google Scholar]
- Lueck, J.D., Mackey A.L., Infield D.T., Galpin J.D., Li J., Roux B., and Ahern C.A.. 2016. Atomic mutagenesis in ion channels with engineered stoichiometry. eLife. 5:e18976. 10.7554/eLife.18976 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martinez-Morales, E., Snyders D.J., and Labro A.J.. 2014. Mutations in the S6 gate isolate a late step in the activation pathway and reduce 4-AP sensitivity in shaker K(v) channel. Biophys. J. 106:134–144. 10.1016/j.bpj.2013.11.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matulef, K., Annen A.W., Nix J.C., and Valiyaveetil F.I.. 2016. Individual Ion Binding Sites in the K(+) Channel Play Distinct Roles in C-type Inactivation and in Recovery from Inactivation. Structure. 24:750–761. 10.1016/j.str.2016.02.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCoy, J.G., and Nimigean C.M.. 2012. Structural correlates of selectivity and inactivation in potassium channels. Biochim. Biophys. Acta. 1818:272–285. 10.1016/j.bbamem.2011.09.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melishchuk, A., Loboda A., and Armstrong C.M.. 1998. Loss of shaker K channel conductance in 0 K+ solutions: role of the voltage sensor. Biophys. J. 75:1828–1835. 10.1016/S0006-3495(98)77624-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meves, H. 1974. The effect of holding potential on the asymmetry currents in squid gaint axons. J. Physiol. 243:847–867. 10.1113/jphysiol.1974.sp010780 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morais-Cabral, J.H., Zhou Y., and MacKinnon R.. 2001. Energetic optimization of ion conduction rate by the K+ selectivity filter. Nature. 414:37–42. 10.1038/35102000 [DOI] [PubMed] [Google Scholar]
- Olcese, R., Latorre R., Toro L., Bezanilla F., and Stefani E.. 1997. Correlation between charge movement and ionic current during slow inactivation in Shaker K+ channels. J. Gen. Physiol. 110:579–589. 10.1085/jgp.110.5.579 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ostmeyer, J., Chakrapani S., Pan A.C., Perozo E., and Roux B.. 2013. Recovery from slow inactivation in K+ channels is controlled by water molecules. Nature. 501:121–124. 10.1038/nature12395 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panyi, G., and Deutsch C.. 2006. Cross talk between activation and slow inactivation gates of Shaker potassium channels. J. Gen. Physiol. 128:547–559. 10.1085/jgp.200609644 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panyi, G., and Deutsch C.. 2007. Probing the cavity of the slow inactivated conformation of shaker potassium channels. J. Gen. Physiol. 129:403–418. 10.1085/jgp.200709758 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panyi, G., Sheng Z., and Deutsch C.. 1995. C-type inactivation of a voltage-gated K+ channel occurs by a cooperative mechanism. Biophys. J. 69:896–903. 10.1016/S0006-3495(95)79963-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panyi, G., Varga Z., and Gáspár R.. 2004. Ion channels and lymphocyte activation. Immunol. Lett. 92:55–66. 10.1016/j.imlet.2003.11.020 [DOI] [PubMed] [Google Scholar]
- Peters, C.J., Fedida D., and Accili E.A.. 2013. Allosteric coupling of the inner activation gate to the outer pore of a potassium channel. Sci. Rep. 3:3025. 10.1038/srep03025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pettersen, E.F., Goddard T.D., Huang C.C., Couch G.S., Greenblatt D.M., Meng E.C., and Ferrin T.E.. 2004. UCSF Chimera--a visualization system for exploratory research and analysis. J. Comput. Chem. 25:1605–1612. 10.1002/jcc.20084 [DOI] [PubMed] [Google Scholar]
- Phan, K., Ng C.A., David E., Shishmarev D., Kuchel P.W., Vandenberg J.I., and Perry M.D.. 2017. The S1 helix critically regulates the finely tuned gating of Kv11.1 channels. J. Biol. Chem. 292:7688–7705. 10.1074/jbc.M117.779298 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pless, S.A., Galpin J.D., Niciforovic A.P., Kurata H.T., and Ahern C.A.. 2013. Hydrogen bonds as molecular timers for slow inactivation in voltage-gated potassium channels. eLife. 2:e01289. 10.7554/eLife.01289 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasmusson, R.L., Morales M.J., Wang S., Liu S., Campbell D.L., Brahmajothi M.V., and Strauss H.C.. 1998. Inactivation of voltage-gated cardiac K+ channels. Circ. Res. 82:739–750. 10.1161/01.RES.82.7.739 [DOI] [PubMed] [Google Scholar]
- Ray, E.C., and Deutsch C.. 2006. A trapped intracellular cation modulates K+ channel recovery from slow inactivation. J. Gen. Physiol. 128:203–217. 10.1085/jgp.200609561 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renart, M.L., Giudici A.M., Poveda J.A., Fedorov A., Berberan-Santos M.N., Prieto M., Díaz-García C., González-Ros J.M., and Coutinho A.. 2019. Conformational plasticity in the KcsA potassium channel pore helix revealed by homo-FRET studies. Sci. Rep. 9:6215. 10.1038/s41598-019-42405-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schauf, C.L., and Bullock J.O.. 1979. Modifications of sodium channel gating in Myxicola giant axons by deuterium oxide, temperature, and internal cations. Biophys. J. 27:193–208. 10.1016/S0006-3495(79)85211-X [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schauf, C.L., and Bullock J.O.. 1980. Solvent substitution as a probe of channel gating in Myxicola. Differential effects of D2O on some components of membrane conductance. Biophys. J. 30:295–305. 10.1016/S0006-3495(80)85095-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schauf, C.L., and Bullock J.O.. 1982. Solvent substitution as a probe of channel gating in Myxicola. Effects of D2O on kinetic properties of drugs that occlude channels. Biophys. J. 37:441–452. 10.1016/S0006-3495(82)84690-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheiner, S., and Čuma M.. 1996. Relative Stability of Hydrogen and Deuterium Bonds. J. Am. Chem. Soc. 118:1511–1521. 10.1021/ja9530376 [DOI] [Google Scholar]
- Soler-Llavina, G.J., Chang T.-H., and Swartz K.J.. 2006. Functional interactions at the interface between voltage-sensing and pore domains in the Shaker K(v) channel. Neuron. 52:623–634. 10.1016/j.neuron.2006.10.005 [DOI] [PubMed] [Google Scholar]
- Stanley, C., Krueger S., Parsegian V.A., and Rau D.C.. 2008. Protein structure and hydration probed by SANS and osmotic stress. Biophys. J. 94:2777–2789. 10.1529/biophysj.107.122697 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suárez-Delgado, E., Rangel-Sandín T.G., Ishida I.G., Rangel-Yescas G.E., Rosenbaum T., and Islas L.D.. 2020. KV1.2 channels inactivate through a mechanism similar to C-type inactivation. J. Gen. Physiol. 152:e201912499. 10.1085/jgp.201912499 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szanto, T.G., Zakany F., Papp F., Varga Z., Deutsch C.J., and Panyi G.. 2020. The activation gate controls steady-state inactivation and recovery from inactivation in Shaker. J. Gen. Physiol. 152:e202012591. 10.1085/jgp.202012591 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tatebayashi, K., Yamamoto K., Nagoya M., Takayama T., Nishimura A., Sakurai M., Momma T., and Saito H.. 2015. Osmosensing and scaffolding functions of the oligomeric four-transmembrane domain osmosensor Sho1. Nat. Commun. 6:6975. 10.1038/ncomms7975 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas, J.J., and Jennings H.M.. 1999. Effects of D2O and Mixing on the Early Hydration Kinetics of Tricalcium Silicate. Chem. Mater. 11:1907–1914. 10.1021/cm9900857 [DOI] [Google Scholar]
- Tilegenova, C., Cortes D.M., Jahovic N., Hardy E., Hariharan P., Guan L., and Cuello L.G.. 2019. Structure, function, and ion-binding properties of a K+ channel stabilized in the 2,4-ion-bound configuration. Proc. Natl. Acad. Sci. USA. 116:16829–16834. 10.1073/pnas.1901888116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ubbelohde, A.R., and Gallagher K.J.. 1955. Acid-base effects in hydrogen bonds in crystals. Acta Crystallogr. 8:71–83. 10.1107/S0365110X55000340 [DOI] [Google Scholar]
- Varga, Z., Hajdu P., Panyi G., Gáspár R., and Krasznai Z.. 2007. Involvement of membrane channels in autoimmune disorders. Curr. Pharm. Des. 13:2456–2468. 10.2174/138161207781368576 [DOI] [PubMed] [Google Scholar]
- Wang, W., and MacKinnon R.. 2017. Cryo-EM Structure of the Open Human Ether-à-go-go-Related K+ Channel hERG. Cell. 169:422–430.e10. 10.1016/j.cell.2017.03.048 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Webb, B., and Sali A.. 2017. Protein Structure Modeling with MODELLER. In Functional Genomics: Methods and Protocols. M. Kaufmann, C. Klinger, and A. Savelsbergh, eds. Springer, New York. 39–54. 10.1007/978-1-4939-7231-9_4 [DOI] [Google Scholar]
- Weingärtner, H. 1984. Diffusion in Liquid Mixtures of Light and Heavy Water. Ber. Bunsenges. Phys. Chem. 88:47–50. 10.1002/bbpc.19840880112 [DOI] [Google Scholar]
- Wu, E.L., Cheng X., Jo S., Rui H., Song K.C., Dávila-Contreras E.M., Qi Y., Lee J., Monje-Galvan V., Venable R.M., et al. 2014. CHARMM-GUI Membrane Builder toward realistic biological membrane simulations. J. Comput. Chem. 35:1997–2004. 10.1002/jcc.23702 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu, Y., and McDermott A.E.. 2019. Inactivation in the potassium channel KcsA. J Struct Biol X. 3:100009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yellen, G. 2001. Keeping K+ completely comfortable. Nat. Struct. Biol. 8:1011–1013. 10.1038/nsb1201-1011 [DOI] [PubMed] [Google Scholar]
- Yellen, G. 2002. The voltage-gated potassium channels and their relatives. Nature. 419:35–42. 10.1038/nature00978 [DOI] [PubMed] [Google Scholar]
- Yellen, G., Sodickson D., Chen T.Y., and Jurman M.E.. 1994. An engineered cysteine in the external mouth of a K+ channel allows inactivation to be modulated by metal binding. Biophys. J. 66:1068–1075. 10.1016/S0006-3495(94)80888-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zagotta, W.N., Hoshi T., and Aldrich R.W.. 1990. Restoration of inactivation in mutants of Shaker potassium channels by a peptide derived from ShB. Science. 250:568–571. 10.1126/science.2122520 [DOI] [PubMed] [Google Scholar]
- Zhou, M., and MacKinnon R.. 2004. A mutant KcsA K(+) channel with altered conduction properties and selectivity filter ion distribution. J. Mol. Biol. 338:839–846. 10.1016/j.jmb.2004.03.020 [DOI] [PubMed] [Google Scholar]
- Zhou, Y., Morais-Cabral J.H., Kaufman A., and MacKinnon R.. 2001. Chemistry of ion coordination and hydration revealed by a K+ channel-Fab complex at 2.0 A resolution. Nature. 414:43–48. 10.1038/35102009 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
lists MD simulations carried in the frame of the current study.