Abstract
The electrochemical reduction of CO2 offers an elegant solution to the current energy crisis and carbon emission issues, but the catalytic efficiency for CO2 reduction is seriously restricted by the inherent scaling relations between the adsorption energies of intermediates. Herein, by combining the concept of single-atom catalysts and multiple active sites, we design heteronuclear dual-atom catalysts to break through the stubborn restriction of scaling relations on catalytic activity. Twenty-one kinds of heteronuclear transition-metal dimers are embedded in monolayer C2N as potential dual-atom catalysts. First-principles calculations reveal that by adjusting the components of dimers, the two metal atoms play the role of carbon adsorption sites and oxygen adsorption sites respectively, which results in the decoupling of adsorption energies of key intermediates. Free energy profiles demonstrate that CO2 can be efficiently reduced to CH4 on CuCr/C2N and CuMn/C2N with low limiting potentials of −0.37 V and −0.32 V, respectively. This study suggests that the introduction of multiple active sites into porous two-dimensional materials would provide a great possibility for breaking scaling relations to achieve efficient multi-intermediate electrocatalytic reactions.
Monolayer C2N supported heteronuclear dual-atom catalysts are designed for efficient CO2 electrochemical reduction.
Introduction
Single-atom catalysts (SACs), providing the maximum utilization of active atoms, have been unleashing their powerful potential in heterogeneous catalysis.1–3 Great progress has been made in developing SACs for one-intermediate electrochemical reactions, i.e. the hydrogen evolution reaction.4–7 Recently, the electrochemical applications of SACs have been generalized toward multi-intermediate electrochemical reactions, such as the oxygen reduction reaction (ORR),8–10 CO2 reduction reaction (CO2RR),11–13 and N2 reduction reaction (NRR).14–16 However, any ambition to achieve optimal catalytic activity for multi-intermediate reactions by SACs seems to be in vain. As is well known, the essence of optimizing the catalytic activity is to adjust the adsorption strength of the reaction intermediates to the surface of the catalysts.17,18 For SACs with only one type of isolated active site, it is easy to adjust the binding strength of a single intermediate for one-intermediate reactions, but the binding strength optimization of all intermediates at the same time for multi-intermediate reactions is almost impossible. There are even linear scaling relations between the adsorption strength of reaction intermediates.19,20 As a fundamental issue for both traditional metal catalysts and emerging SACs, scaling relations limit the catalytic activity by forbidding the adsorption energy of a certain intermediate from being freely tuned.
Toward the electrocatalytic CO2RR, it is difficult to attain a low overpotential because of the adsorbate (particularly, *COOH, *CO and *CHO) scaling relations.21,22 For example, on Cu electrodes, the hydrogenation of *CO is the potential determining step of the reaction pathway toward CH4 with the highest free energy change.23 Although the hydrogenation of *CO to *COH or *CHO is determined by the electrode surface structure, electrode potential, level of acid or alkali, etc.,24–28 the common strategy to reduce the free energy change of this step is to strengthen the binding strength of *CHO (or *COH) and weaken the binding strength of *CO. However, according to the scaling relations, the enhancement of *CO adsorption is always accompanied by stronger binding of *CHO (or *COH). These scaling relations suggest that the rate-determining step always requires a high limiting potential.21–23 By breaking the above scaling relations, the optimal conversion of CO2 with the lowest limiting potential can be achieved by tuning the free energy change of each elementary reaction to minimum.29–32 Some advances have been made through introducing p states,30,32 reducing metal coordination numbers,33,34 tethering active ligands,35,36 alloying metal catalysts,37,38 and designing dual functional sites.39
Should the SACs be subject to the isolated single-atom active site and be powerless against the scaling relations in multi-intermediate reactions (such as the electrocatalytic CO2RR)? Taking inspiration from bimetallic alloy catalysts, two metal species can provide C-affinity and O-affinity sites that strengthen the binding of *COOH or *CHO while hardly affecting that of *CO. Herein, extending the dual-site strategy to single-atom catalysts, we show that by employing heteronuclear transition-metal dimers embedded in monolayer C2N as dual active centers, the binding energies of the key reduction intermediates are completely decoupled so that the limitation of overpotential no longer exists. The two different metal atoms act as *C binding sites and *O binding sites, respectively, resulting in a deviation from transition-metal scaling relations. By evaluating the stability, activity and selectivity, CuCr/C2N and CuMn/C2N are selected out from the 21 concept catalysts as very promising catalysts for the electrochemical reduction of CO2.
Results and discussion
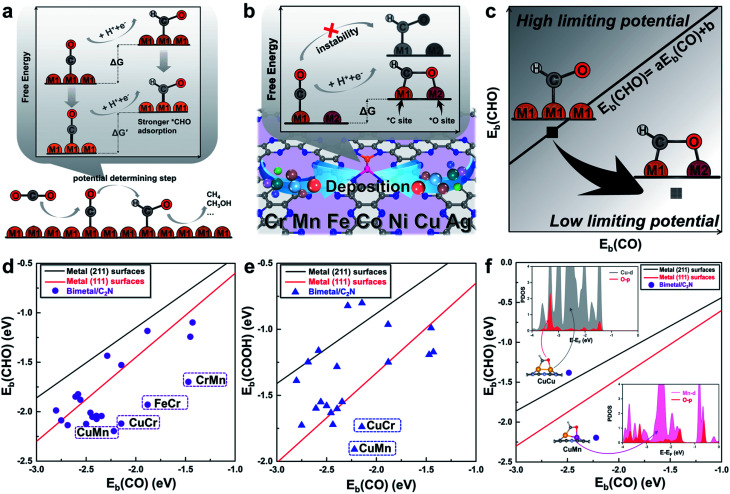
Monolayer C2N has been recently synthesized as a newcomer in the two-dimensional atomic-layered material family.40 The stable porous structure of monolayer C2N with abundant and uniform pyridine-like nitrogen provides high-density anchoring sites for SACs.41 Particularly, the 0.83 nm sized holes terminated by sp2-bonded nitrogen atoms provide the conditions for anchoring two transition-metal atoms, which offers the opportunity for construction of multiple active sites.42,43 Alloying different metal species is a general strategy to achieve multiple active sites tuning the binding strength of the targeted intermediates.42–45 With regard to the CO2RR, in order to reduce the high free energy change of the potential determining step (Fig. 1a), additional O-binding sites are required to stabilize the oxygen-containing intermediates. Considering the size of holes in monolayer C2N and the differences in C-affinity and O-affinity of the metal atoms, 21 kinds of dual-atom catalysts (two of Cr, Mn, Fe, Co, Ni, Cu and Ag are combined into heteronuclear dimers, i.e. AgCu, AgNi, AgCo, AgFe, AgMn, AgCr, CuNi, CuCo, CuFe, CuMn, CuCr, NiCo, NiFe, NiMn, NiCr, CoFe, CoMn, CoCr, FeMn, FeCr and MnCr) are embedded in monolayer C2N and anchored by N-coordination sites of cavities (Fig. 1b). Construction of dual active sites is expected to break the traditional scaling relations and achieve dramatic reduction in the limiting potential (Fig. 1c).
Fig. 1. (a) Schematic illustration of the high free energy change caused by the scaling relations between *CO and *CHO. (b) Design concept of monolayer C2N supported heteronuclear transition-metal dimers to reduce the free energy change by stabilizing *CHO. (c) Simplified schematic of decoupling the scaling relations between adsorption energies of *CHO and *CO to achieve low limiting potential. Relationship between binding energies (d) Eb(CHO) and Eb(CO), (e) Eb(COOH) and Eb(CO) of the C2N supported metal dimers and transition-metal surface. (f) Relationship between binding energies Eb(CHO) and Eb(CO) of the C2N supported CuCu and CuMn dimers. Insets show the adsorption configuration and partial density of states. The linear scaling relations between adsorbates are generated using calculated Ni, Cu, Ag, Pd, Au, Pt and Rh data.22.
Generally, the potential-limiting step of CO2 reduction is the hydrogenation of *COOH to *CO or the hydrogenation of *CO to *CHO, so the overall catalytic efficiency is determined by the binding energies of *COOH (Eb(COOH)), *CO (Eb(CO)), and *CHO (Eb(CHO)).21,22 Therefore, we first study *CHO, *COOH and *CO adsorption on C2N-supported metal dimers. The detailed adsorption configurations are shown in Fig. S1 in the ESI.† As shown in Fig. 1d and e, the scaling relations of the heteronuclear metal dimers are totally different from those of pure metal surfaces. Some of the metal dimers (CuMn, CuCr, FeCr and MnCr) with small differences between Eb(CHO) and Eb(CO) or Eb(COOH) and Eb(CO) approach the desired low overpotential region. An analysis of the underlying electronic structures can help us understand the advantage of heteronuclear dimers. As shown in Fig. 1f, the Eb(CO) of the homonuclear CuCu dimer is close to that of the heteronuclear CuMn dimer, but the Eb(CHO) of the CuMn dimer is more negative than that of the CuCu dimer. Although the adsorption configurations of *CHO on the CuCu dimer and CuMn dimer are similar, the calculated partial density of states (PDOS) shows obviously different hybridization of O-2p states and metal-3d states (Cu-3d and Mn-3d, Fig. 1f, for more details see Fig. S3 in the ESI†). The more apparent hybridization on CuMn/C2N indicates that the very negative value of Eb(CHO) stems from the strong binding strength of the O–Mn bond. The adsorption of *COOH on the CuMn dimer also shows the strong hybridization of O-2p states and Mn-3d states (Fig. S3 in the ESI†). The two heteronuclear metal atoms act as the *C binding sites and *O binding sites, respectively, thus “pulling” the adsorption relations out of the traditional region. Hence, the C2N-supported CuMn, CuCr, FeCr and MnCr dimers are promising candidates to reduce the overpotential and improve selectivity toward deep reduction products.
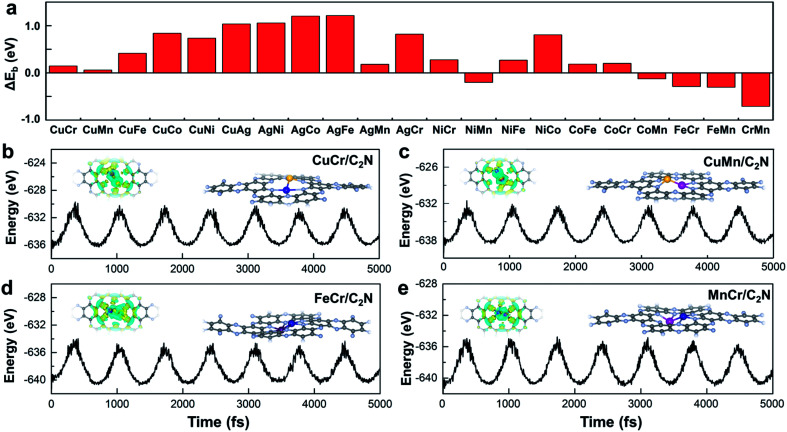
Stability is another crucial property to select the catalysts. To assess the stability of C2N-supported metal dimers, we calculate the energy difference (ΔEb) between the adsorption energy (Eb) of metal dimers on C2N and the cohesive energy (Ecoh) of metal atoms in their crystals (Ecoh), ΔEb = Eb − Ecoh. The small value of ΔEb means that the uniform distribution of metal dimers embedded in C2N is energetically more favorable than forming the metal bulk. Therefore, the issue that isolated metal dimers aggregate into clusters will not exist in the four promising candidates (i.e. C2N-supported CuMn, CuCr, FeCr and MnCr dimers) with small ΔEb (Fig. 2a). The dissolution potentials are calculated to evaluate the electrochemical stability (Fig. S4a in the ESI†). As the applied overpotential to drive the CO2RR is very negative, almost all metal dimers on C2N could be stable under electrochemical conditions. The particularly positive dissolution potentials of CuCr/C2N and FeCr/C2N indicate that the dissolution of metal atoms can be completely avoided. The stabilities of these four candidates are further evaluated by performing ab initio molecular dynamics (AIMD) simulations. As shown in Fig. 2b to d, the structures are maintained well, suggesting that they can tolerate the thermal conditions of the CO2RR. Moreover, in acidic aqueous solution, the structures of the four candidates are still maintained, showing strong dissolution resistance (Fig. S4b in the ESI†). The good dispersibility and stability result from the strong covalent bonds between metal dimers and C2N, which can be verified by the difference of charge densities of M1M2/C2N. As clearly seen in Fig. S5 in the ESI,† the electron transfers from the metal dimers to the neighboring pyridinic nitrogen atoms, and the Bader charge analysis suggests that the metal dimers are positively charged by about 1.5e loss, indicating the formation of strongly polarized covalent bonds.
Fig. 2. (a) Energy difference between adsorption energy of TM atoms on C2N and the cohesive energy of TM atoms. Energy fluctuations of (b) CuCr/C2N, (c) CuMn/C2N, (d) FeCr/C2N, and (e) MnCr/C2N against the time in AIMD simulations at 400 K. Insets show snapshots of the atomic configuration and charge density difference. Charge depletion and accumulation are displayed in cyan and yellow, respectively.
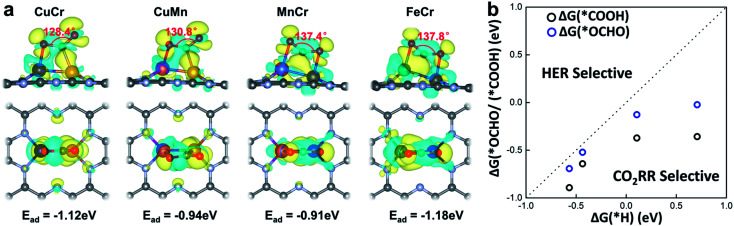
The activation of CO2 onto the surface of the catalysts is always the first step of the electrocatalytic CO2 reduction. CO2 can be activated by electron injection into the antibonding 2πu orbitals and the activation is always accompanied by the decrease of the O–C–O bond angle.46Fig. 3a illustrates the structures of CO2 adsorbed M1M2/C2N (M1M2 = CuCr, CuMn, FeCr, and MnCr). The binding strength between CO2 and M1M2/C2N is very strong with adsorption energies of −1.12, −0.94, −0.91 and −1.18 eV for CuCr/C2N, CuMn/C2N, MnCr/C2N and FeCr/C2N, respectively. The bond angle of adsorbed CO2 is significantly reduced by about 50°. The charge density difference of M1M2/C2N with the adsorption of CO2 is shown in Fig. 3a. Significant charge transfer between the anchored metal dimers and CO2 can be observed. All these demonstrate that CO2 molecules can be activated by metal dimers embedded in C2N.
Fig. 3. (a) Side and top views of the charge density difference for CO2 adsorbed on M1M2/C2N (M1M2 = CuCr, CuMn, FeCr, and MnCr). Charge depletion and accumulation are displayed in cyan and yellow, respectively. (b) Comparison between hydrogen adsorption free energy ΔG(*H) and carbon dioxide hydrogenation free energy ΔG(*COOH)/ΔG(*OCHO).
In the process of electrochemical CO2 reduction in aqueous solution, hydrogen evolution is always competitive with CO2 reduction.47 The selectivity between CO2 reduction and hydrogen evolution is evaluated by calculating the free energy change of the first hydrogenation step.48 Typically, for CO2 reduction and hydrogen evolution, the intermediates of the first hydrogenation step are *COOH (or *OCHO) and *H, respectively. The free energy changes of the formation of *COOH (or *OCHO) (ΔG(*COOH)/ΔG(*OCHO)) and *H (ΔG(*H)) for CuCr/C2N, CuMn/C2N, FeCr/C2N, and MnCr/C2N are shown in Fig. 3b. Based on Brønsted–Evans–Polanyi (BEP) relations,49 the small reaction free energy change is always accompanied by a low reaction barrier. Thus, for all four candidates, as the free energy changes of the formation of *COOH are smaller than those of *H, CO2 reduction is favorable in the competition with hydrogen evolution.
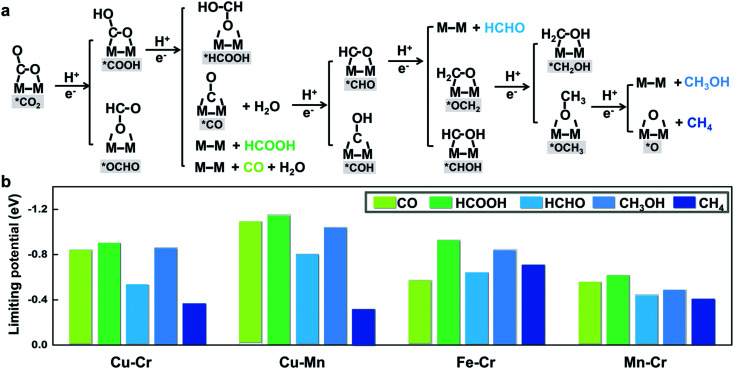
To further illustrate that breaking scaling relations is an effective approach to lower the limiting potential, we assess the catalytic performance of M1M2/C2N (M1M2 = CuCr, CuMn, FeCr, and MnCr) for the CO2RR by calculating the free energy profiles of the entire pathways toward C1 products, namely, CO, HCOOH, HCHO, CH3OH, and CH4. The reaction pathways of the four candidates are the same (Fig. 4a). The detailed free energy diagrams are shown in Fig. S6 in the ESI.† The production of CO occurs through the path CO2 → *COOH → CO. However, desorption of CO is found to be difficult because of the strong adsorption. In the reaction pathway to HCOOH, CO2 is hydrogenated by a proton–electron pair forming *COOH, and then a second proton–electron pair transfers to *COOH, generating HCOOH. The rate limiting step is the desorption of HCOOH. The key step in the formation of deep reduction products (HCHO, CH3OH and CH4) with more than 2e− reduction is the hydrogenation of the *CO to form *CHO. However, due to the breaking of *CO–*CHO scaling relations, the hydrogenation of *CO is not always the rate limiting step. For FeCr/C2N and MnCr/C2N, the hydrogenation of *CO is very easy with a free energy increase close to 0 eV, but the excessive binding strength between the intermediates and metal dimers leads to higher potentials for the desorption of products.
Fig. 4. (a) Schematic depiction of the CO2 reduction pathways toward a variety of C1 products (CO, HCOOH, HCHO, CH3OH and CH4) on M1M2/C2N (M1M2 = CuCr, CuMn, FeCr, and MnCr). (b) Thermodynamic limiting potentials toward C1 products (CO, HCOOH, HCHO, CH3OH and CH4) on CuCr/C2N, CuMn/C2N, FeCr/C2N, and MnCr/C2N.
The thermodynamic limiting potentials toward C1 products, including CO, HCOOH, HCHO, CH3OH and CH4, are summarized in Fig. 4b. The CuCr and CuMn dimers exhibit much lower required potential toward CH4 and higher potential toward other C1 productions, indicating higher efficiency and selectivity in generating CH4. The limiting potential toward all C1 products on the FeCr dimer is relatively high. Meanwhile, the MnCr dimer shows significantly low limiting potential toward all C1 products, but the similar limiting potentials toward different products suggest bad selectivity. The competition between the HER and CO2RR is further analyzed using the difference in the limiting potentials for CO2 reduction and H2 evolution, UL(CO2) − UL(H2). The higher the UL(CO2) − UL(H2) difference, the higher the selectivity for CO2 reduction over H2 evolution.29 The plot of UL(CO2) − UL(H2) for M1M2/C2N is shown in Fig. S7 in the ESI.† The CuCr, CuMn and MnCr dimers with higher UL(CO2) − UL(H2) show more selectivity for the CO2RR against the HER. These findings suggest that CuCr/C2N and CuMn/C2N are the most selective and active among all candidates.
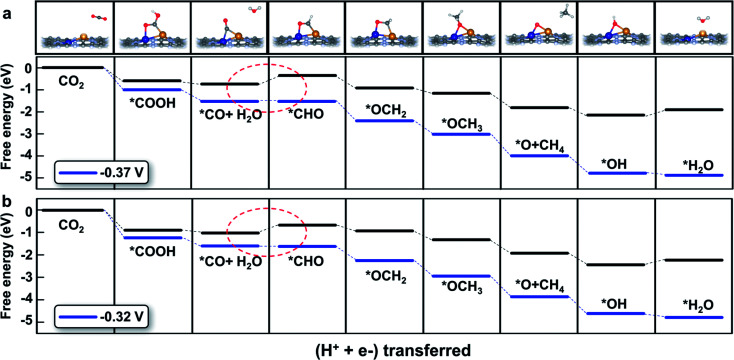
The detailed free energy diagrams for the reduction of CO2 to CH4 on CuCr/C2N and CuMn/C2N are shown in Fig. 5. Because the bimetallic active centers break the *CO–*CHO scaling relation significantly, the free energies are uphill by 0.37 eV (CuCr/C2N) and 0.32 eV (CuMn/C2N), respectively. This step is the potential-limiting step and the corresponding overpotentials are only 0.54 V (CuCr/C2N) and 0.49 V (CuMn/C2N), which are much lower than those of pure transition-metal surfaces (such as the Cu surface with a theoretical overpotential of 0.91 V).23 In the subsequent elementary reactions, *CHO is hydrogenated forming *OCH2 (*CHO + H+ + e− → *OCH2). Then, in the reaction,*OCH2 + H+ + e− → *OCH3, the C atom becomes saturated and the C–Cu bond is dissociated with the O atom directly adsorbed at the bridge site of the metal dimer. The next proton–electron transfer results in the dissociation of the C–O bond and production of CH4. The introduction of CuCr and CuMn dimer dual sites successfully lowers the free energy change (ΔG) of *CO hydrogenation without increasing the ΔG of other elementary reactions. Therefore, finding the scaling relations between the key intermediates and designing multiple active sites for breaking the scaling relations could be a universal strategy for catalyst development.
Fig. 5. Free energy diagram of the CO2 reduction pathway toward CH4 on (a) CuCr/C2N and (b) CuMn/C2N at different applied potentials. The potential-limiting steps are marked by red dotted circles.
Conclusion
To summarize, we have proposed the concept of dual-atom catalysts by extending a dual-site strategy to single-atom catalysis to achieve highly efficient CO2 reduction. The idea is to utilize the differences in carbophilicity and oxophilicity of metal atoms to form oxophilic and carbophilic dual active sites, respectively. By embedding heteronuclear transition-metal dimers into porous monolayer C2N, the dual-atom sites lead to significant deviations from linear scaling relations. Through prescreening M1M2/C2N based on the analysis of adsorption relations of key intermediates, four of the stable candidates are selected for electrocatalytic CO2 reduction and CuCr/C2N and CuMn/C2N exhibit the best performance with very low limiting potentials (−0.37 V and −0.32 V, respectively) toward deeply reduced CH4 production. The design of multiple active centers composed of different single atoms could also be applied to other multi-intermediate electrocatalytic reactions, such as the nitrogen reduction reaction and oxygen reduction/evolution reactions. Although the precise control of multiple active centers is more challenging than that of SACs, some progress has been made, such as N-doped carbon supported Fe–Co dual sites,50 Ni–Fe dual sites,51 and Co–Pt dual sites.52 Our study sheds light on the rational design of multiple active sites composed of SACs for multi-intermediate electrochemical reactions.
Methods
All density functional theory calculations were carried out using the Vienna Ab initio simulation package (VASP)53,54 with the spin-polarized Perdew–Burke–Ernzerhof (PBE)55 exchange–correlation functional used. In structural relaxation, the total energy and the force on each relaxed atom were converged to 10−4 eV and 0.02 eV Å−1, respectively. The cut-off energy was 400 eV. The density functional dispersion correction, DFT-D3, was used to describe the van der Waals interactions.56 In the standard molecular dynamics simulations, the temperature was controlled at 400 K using the Nose–Hoover thermostat approach. Partial charges of the adsorbed metal dimer were calculated using Bader charge analysis.57 The computational hydrogen electrode model58,59 was used to calculate Gibbs free energy change (ΔG) for each elemental step. The limiting potential (UL), UL = −ΔGmax/e, where ΔGmax is the maximum free energy change among all elementary steps. The theoretical overpotential (η) was the difference between the equilibrium potential (U0) and limiting potential, η = U0 − UL. Further calculation details are given in the ESI.†
Conflicts of interest
The authors declare no competing financial interests.
Supplementary Material
Acknowledgments
This work is supported by the National Natural Science Foundation of China (Grant No. 21525311, 21773027), the Scientific Research Foundation of Graduate School of Southeast University (YBJJ1772), and the China Scholarship Council (CSC, 201806090132). The authors acknowledge the computational resources from the Big Data Center of Southeast University and National Supercomputing Center of Tianjin.
Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc05236d
References
- Yang X.-F. Wang A. Qiao B. Li J. Liu J. Zhang T. Acc. Chem. Res. 2013;46:1740–1748. doi: 10.1021/ar300361m. [DOI] [PubMed] [Google Scholar]
- Chen Y. Ji S. Chen C. Peng Q. Wang D. Li Y. Joule. 2018;2:1242–1264. doi: 10.1016/j.joule.2018.06.019. [DOI] [Google Scholar]
- Wang Y. Mao J. Meng X. Yu L. Deng D. Bao X. Chem. Rev. 2019;119:1806–1854. doi: 10.1021/acs.chemrev.8b00501. [DOI] [PubMed] [Google Scholar]
- Chen W. Pei J. He C.-T. Wan J. Ren H. Zhu Y. Wang Y. Dong J. Tian S. Cheong W.-C. Lu S. Zheng L. Zheng X. Yan W. Zhuang Z. Chen C. Peng Q. Wang D. Li Y. Angew. Chem., Int. Ed. 2017;129:16302–16306. doi: 10.1002/ange.201710599. [DOI] [Google Scholar]
- Fei H. Dong J. Arellano-Jimenez M. J. Ye G. Dong Kim N. Samuel E. L. Peng Z. Zhu Z. Qin F. Bao J. Nat. Commun. 2015;6:8668. doi: 10.1038/ncomms9668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo Z. Ouyang Y. Zhang H. Xiao M. Ge J. Jiang Z. Wang J. Tang D. Cao X. Liu C. Nat. Commun. 2018;9:2120. doi: 10.1038/s41467-018-04501-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H. An P. Zhou W. Guan B. Y. Zhang P. Dong J. Lou X. W. D. Sci. Adv. 2018;4:eaao6657. doi: 10.1126/sciadv.aao6657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han Y. Wang Y. G. Chen W. Xu R. Zheng L. Zhang J. Luo J. Shen R. A. Zhu Y. Cheong W. C. Chen C. Peng Q. Wang D. J. Am. Chem. Soc. 2017;139:17269–17272. doi: 10.1021/jacs.7b10194. [DOI] [PubMed] [Google Scholar]
- Chung H. T. Cullen D. A. Higgins D. Sneed B. T. Holby E. F. More K. L. Zelenay P. Science. 2017;357:479–484. doi: 10.1126/science.aan2255. [DOI] [PubMed] [Google Scholar]
- Yang L. Cheng D. Xu H. Zeng X. Wan X. Shui J. Xiang Z. Cao D. Proc. Natl. Acad. Sci. U. S. A. 2018;115:6626–6631. doi: 10.1073/pnas.1800771115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao C. Dai X. Yao T. Chen W. Wang X. Wang J. Yang J. Wei S. Wu Y. Li Y. J. Am. Chem. Soc. 2017;139:8078–8081. doi: 10.1021/jacs.7b02736. [DOI] [PubMed] [Google Scholar]
- Li X. Bi W. Chen M. Sun Y. Ju H. Yan W. Zhu J. Wu X. Chu W. Wu C. J. Am. Chem. Soc. 2017;139:14889–14892. doi: 10.1021/jacs.7b09074. [DOI] [PubMed] [Google Scholar]
- Yang H. B. Hung S.-F. Liu S. Yuan K. Miao S. Zhang L. Huang X. Wang H.-Y. Cai W. Chen R. Gao J. Yang X. Chen W. Huang Y. Chen H. M. Li C. M. Zhang T. Liu B. Atomically Dispersed Ni(i) as the Active Site for Electrochemical CO2 Reduction. Nat. Energy. 2018;3:140–147. doi: 10.1038/s41560-017-0078-8. [DOI] [Google Scholar]
- Han L. Liu X. Chen J. Lin R. Liu H. Lu F. Bak S. Liang Z. Zhao S. Stavitski E. Luo J. Adzic R. R. Xin R. H. Angew. Chem., Int. Ed. 2019;58:2321–2325. doi: 10.1002/anie.201811728. [DOI] [PubMed] [Google Scholar]
- Geng Z. Liu Y. Kong X. Li P. Li K. Liu Z. Du J. Shu M. Si R. Zeng J. Adv. Mater. 2018;30:1803498. doi: 10.1002/adma.201803498. [DOI] [PubMed] [Google Scholar]
- Ling C. Ouyang Y. Li Q. Bai X. Mao X. Du A. Wang J. Small Methods. 2019;3:1800376. doi: 10.1002/smtd.201800376. [DOI] [Google Scholar]
- Man I. C. Su H.-Y. Calle-Vallejo F. Hansen H. A. Martínez J. I. Inoglu N. G. Kitchin J. Jaramillo T. F. Nørskov J. K. Rossmeisl J. ChemCatChem. 2011;3:1159–1165. doi: 10.1002/cctc.201000397. [DOI] [Google Scholar]
- Nørskov J. K. Bligaard T. Rossmeisl J. Christensen C. H. Nat. Chem. 2009;1:37–46. doi: 10.1038/nchem.121. [DOI] [PubMed] [Google Scholar]
- Abild-Pedersen F. Greeley J. Studt F. Rossmeisl J. Munter T. R. Moses P. G. Skúlason E. Bligaard T. Nørskov J. K. Phys. Rev. Lett. 2007;99:016105. doi: 10.1103/PhysRevLett.99.016105. [DOI] [PubMed] [Google Scholar]
- Calle-Vallejo F. Loffreda D. Koper M. T. M. Sautet P. Nat. Chem. 2015;7:403–410. doi: 10.1038/nchem.2226. [DOI] [PubMed] [Google Scholar]
- Peterson A. A. Nørskov J. K. J. Phys. Chem. Lett. 2012;3:251–258. doi: 10.1021/jz201461p. [DOI] [Google Scholar]
- Shi C. Hansen H. A. Lausche A. C. Nørskov J. K. Phys. Chem. Chem. Phys. 2014;16:4720–4727. doi: 10.1039/C3CP54822H. [DOI] [PubMed] [Google Scholar]
- Li Y. Sun Q. Adv. Energy Mater. 2016;6:1600463. doi: 10.1002/aenm.201600463. [DOI] [Google Scholar]
- Nie X. Esopi M. R. Janik M. J. Asthagiri A. Angew. Chem., Int. Ed. 2013;52:2459–2462. doi: 10.1002/anie.201208320. [DOI] [PubMed] [Google Scholar]
- Cheng T. Xiao H. Goddard W. A. J. Phys. Chem. Lett. 2015;6:4767–4773. doi: 10.1021/acs.jpclett.5b02247. [DOI] [PubMed] [Google Scholar]
- Hussain J. Jonsson H. Skulason E. ACS Catal. 2018;8:5240–5249. doi: 10.1021/acscatal.7b03308. [DOI] [Google Scholar]
- Cheng T. Xiao H. Goddard W. A. Proc. Natl. Acad. Sci. U. S. A. 2017;114:1795–1800. doi: 10.1073/pnas.1612106114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nie X. Luo W. Janik M. J. Asthagiri A. J. Catal. 2014;312:108–122. doi: 10.1016/j.jcat.2014.01.013. [DOI] [Google Scholar]
- Chan K. Tsai C. Hansen H. A. Nørskov J. K. ChemCatChem. 2014;6:1899–1905. doi: 10.1002/cctc.201402128. [DOI] [Google Scholar]
- Hong X. Chan K. Tsai C. Nørskov J. K. ACS Catal. 2016;6:4428–4437. doi: 10.1021/acscatal.6b00619. [DOI] [Google Scholar]
- Vasileff A. Xu C. Jiao Y. Zheng Y. Qiao S. Z. Chem. 2018;4:1809–1831. [Google Scholar]
- Lim H. K. Shin H. Goddard W. A. Hwang Y. J. Min B. K. Kim H. J. Am. Chem. Soc. 2014;136:11355–11361. doi: 10.1021/ja503782w. [DOI] [PubMed] [Google Scholar]
- Mistry H. Reske R. Zeng Z. Zhao Z.-J. Greeley J. Strasser P. Cuenya B. R. J. Am. Chem. Soc. 2014;136:16473–16476. doi: 10.1021/ja508879j. [DOI] [PubMed] [Google Scholar]
- Zhu W. Zhang Y. J. Zhang H. Lv H. Li Q. Michalsky R. Peterson A. A. Sun S. J. Am. Chem. Soc. 2014;136:16132–16135. doi: 10.1021/ja5095099. [DOI] [PubMed] [Google Scholar]
- Xie M. S. Xia B. Y. Li Y. W. Yan Y. Yang Y. H. Sun Q. Chan S. H. Fisher A. Wang X. Energy Environ. Sci. 2016;9:1687–1695. doi: 10.1039/C5EE03694A. [DOI] [Google Scholar]
- Kim C. Jeon H. S. Eom T. Jee M. S. Kim H. Friend C. M. Min B. K. Hwang Y. J. J. Am. Chem. Soc. 2015;137:13844–13850. doi: 10.1021/jacs.5b06568. [DOI] [PubMed] [Google Scholar]
- Ma S. Sadakiyo M. Heima M. Luo R. Haasch R. T. Gold J. I. Yamauchi M. Kenis P. J. J. Am. Chem. Soc. 2017;139:47–50. doi: 10.1021/jacs.6b10740. [DOI] [PubMed] [Google Scholar]
- Kim D. Xie C. Becknell N. Yu Y. Karamad M. Chan K. Crumlin E. J. Norskov J. K. Yang P. J. Am. Chem. Soc. 2017;139:8329–8336. doi: 10.1021/jacs.7b03516. [DOI] [PubMed] [Google Scholar]
- Hansen H. A. Varley J. B. Peterson A. A. Nørskov J. K. J. Phys. Chem. Lett. 2013;4:388–392. doi: 10.1021/jz3021155. [DOI] [PubMed] [Google Scholar]
- Mahmood J. Lee E. K. Jung M. Shin D. Jeon I. Y. Jung S. M. Choi H. J. Seo J. M. Bae S. Y. Sohn S. D. Park N. Oh J. H. Shin H. J. Baek J. B. Nat. Commun. 2015;6:6486. doi: 10.1038/ncomms7486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahmood J. Li F. Jung S.-M. Okyay M. S. Ahmad I. Kim S.-J. Park N. Jeong H. Baek J.-B. Nat. Nanotechnol. 2017;12:441–446. doi: 10.1038/nnano.2016.304. [DOI] [PubMed] [Google Scholar]
- Chen Z. W. Yan J.-M. Jiang Q. Small Methods. 2018;3:1800291. doi: 10.1002/smtd.201800291. [DOI] [Google Scholar]
- Li F. Liu X. Chen Z. Small Methods. 2019;3:1800480. doi: 10.1002/smtd.201800480. [DOI] [Google Scholar]
- Shen H. Li Y. Sun Q. J. Phys. Chem. C. 2017;121:3963–3969. doi: 10.1021/acs.jpcc.7b00317. [DOI] [Google Scholar]
- Li Y. Su H. Chan S. H. Sun Q. ACS Catal. 2015;5:6658–6664. doi: 10.1021/acscatal.5b01165. [DOI] [Google Scholar]
- Freund H.-J. Roberts M. W. Surf. Sci. Rep. 1996;25:225–273. doi: 10.1016/S0167-5729(96)00007-6. [DOI] [Google Scholar]
- Zhang Y.-J. Sethuraman V. Michalsky R. Peterson A. A. ACS Catal. 2014;4:3742–3748. doi: 10.1021/cs5012298. [DOI] [Google Scholar]
- Back S. Lim J. Kim N.-Y. Kimb Y.-H. Jung Y. Chem. Sci. 2017;8:1090–1096. doi: 10.1039/C6SC03911A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bligaard T. Nørskov J. K. Dahl S. Matthiesen J. Christensen C. H. Sehested J. J. Catal. 2004;224:206–217. doi: 10.1016/j.jcat.2004.02.034. [DOI] [Google Scholar]
- Wang J. Huang Z. Liu W. Chang C. Tang H. Li Z. Chen W. Jia C. Yao T. Wei S. J. Am. Chem. Soc. 2017;139:17281–17284. doi: 10.1021/jacs.7b10385. [DOI] [PubMed] [Google Scholar]
- Ren W. Tan X. Yang W. Jia C. Xu S. Wang K. Smith S. C. Zhao C. Angew. Chem., Int. Ed. 2019;58:1–6. doi: 10.1002/anie.201813481. [DOI] [PubMed] [Google Scholar]
- Zhang L. Fischer J. Jia Y. Yan X. Xu W. Wang X. Chen J. Yang D. Liu H. Zhuang L. Hankel M. Searles D. J. Huang K. Feng S. Brown C. L. Yao X. J. Am. Chem. Soc. 2018;140:10757–10763. doi: 10.1021/jacs.8b04647. [DOI] [PubMed] [Google Scholar]
- Kresse G. Hafner J. Phys. Rev. B: Condens. Matter Mater. Phys. 1993;47:558–561. doi: 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
- Kresse G. Furthmuller J. Phys. Rev. B: Condens. Matter Mater. Phys. 1996;54:11169–11185. doi: 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
- Perdew J. P. Burke K. Ernzerhof M. Phys. Rev. Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- Grimme S. Antony J. Ehrlich S. Krieg H. J. Chem. Phys. 2010;132:154104. doi: 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- Tang W. Sanville E. Henkelman G. J. Phys.: Condens. Matter. 2009;21:084204. doi: 10.1088/0953-8984/21/8/084204. [DOI] [PubMed] [Google Scholar]
- Nørskov J. K. Rossmeisl J. Logadottir A. Lindqvist L. Kitchin J. R. Bligaard T. Jónsson H. J. Phys. Chem. B. 2004;108:17886–17892. doi: 10.1021/jp047349j. [DOI] [Google Scholar]
- Peterson A. A. Abild-Pedersen F. Studt F. Rossmeisl J. Nørskov J. K. Energy Environ. Sci. 2010;3:1311–1315. doi: 10.1039/C0EE00071J. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.