Comparison of Microvascular Permeability Measurements, K^trans, Determined with Conventional Steady-State T1-Weighted and First-Pass T2*-Weighted MR Imaging Methods in Gliomas and Meningiomas

Abstract

BACKGROUND AND PURPOSE: The widely accepted MR method for quantitating brain tumor microvascular permeability, K^trans, is the steady-state T1-weighted gradient-echo method (ssT1). Recently the first-pass T2*-weighted (fpT2*) method has been used to derive both relative cerebral blood volume (rCBV) and K^trans. We hypothesized that K^trans derived from the ssT1 and the fpT2* methods will correlate differently in gliomas and meningiomas because of the unique differences in morphologic and functional status of each tumor vascular network.

METHODS: Before surgery, 27 patients with newly diagnosed gliomas (WHO grade I–IV; n = 20) or meningiomas (n = 7) underwent conventional anatomic MR imaging and 12 dynamic ssT1 acquisitions followed by 60 dynamic fpT2* images before and after gadopentate dimeglumine administration. The 3 hemodynamic variables—fpT2* rCBV, fpT2* K^trans, and ssT1 K^trans—were calculated in anatomically identical locations and correlated with glioma grade. The fpT2* K^trans values were compared with ssT1 K^trans for gliomas and meningiomas.

RESULTS: All 3 hemodynamic variables displayed distinct distributions among grades 2, 3, and 4 gliomas by using the Kruskal-Wallis test. Only K^trans values, and not rCBV, could differentiate between grade 4 and lower-grade gliomas by using the Wilcoxon rank sum test. The fpT2* K^trans was highly predictive of ssT1 K^trans for gliomas, with an estimated regression coefficient of 0.49 (P < .001). For meningiomas, however, fpT2* K^trans values correlated poorly with ssT1 K^trans values (r = 0.26; P = .74).

CONCLUSION: Compared with rCBV, K^trans values derived from either ssT1 or fpT2* were more predictive of glioma grade. The fpT2* K^trans was highly correlated with ssT1 K^trans in gliomas but not in meningiomas.

Endothelial permeability of vessels in brain tumors provides valuable information about blood-brain barrier (BBB) integrity, vascular morphology, and the nature of neovascularization, as well as tumor pathophysiology and prognosis.1–4 Several recent studies have shown that quantitative estimates of microvascular permeability correlate with brain tumor grade.1,5–7 Current and potential clinical uses for a noninvasive method to characterize microvascular permeability in brain tumors include guiding a surgeon to the most malignant spot for biopsy, monitoring the efficacy of chemotherapy or new treatments such as antiangiogenic drugs, manipulating the BBB for improved drug delivery, and differentiating radiation necrosis or postsurgical scar from recurring tumor.

The degree of endothelial permeability by MR imaging is typically represented by the endothelial permeability surface area product or the transfer coefficient, K^trans, a variable that is estimated on the basis of analysis of temporarily acquired dynamic contrast-enhanced (DCE) MR imaging data by using a series of assumptions and model system derived from pharmacokinetics of contrast agent distribution.8 In addition to permeability, K^trans also depends on several other factors, including vascular surface area and flow. Therefore, K^trans is an indirect measure of physiologic parameters that vary with vascular attenuation and angiogenic activity.9,10 Analysis methods described by Tofts and Kermode10 have been widely used to determine K^trans by DCE MR by using a steady-state T1-weighted 3D spoiled gradient-recalled acquisition sequence (ssT1 method) after the intravenous administration of gadopentetate dimeglumine (Gd-DTPA). Although the ssT1 approach affords high spatial resolution and is resistant to susceptibility artifact, 3 published models of data analysis method may lead to systematic overestimation of K^trans, and the values may differ profoundly based on the specific model chosen to fit the data.11

A recently published method for quantifying K^trans uses T2*-weighted gradient-echo echo-planar imaging during the first pass of Gd-DTPA (fpT2* method).4,12 In this approach, the dynamic data are converted to contrast agent concentration values in 2 compartments acquired during the first pass, and pharmacokinetic modeling is applied to T2*-weighted images of the first pass of a tracer bolus. There are several theoretical differences, as well as practical strengths and weaknesses, associated with the ssT1 and the fpT2* methods. First, whereas the contrast agent concentration-time curve in the ssT1 method fits a biexponential decay curve, the fpT2* curve is fitted to a gamma-variate function. The ssT1 method assumes negligible or minimal contribution from intravascular contrast agent within the tumor, whereas fpT2* method is entirely based on the behavior of contrast agent in the intravascular compartment. Moreover, the rate of contrast agent movement from the intravascular to the extravascular space within a single voxel of tissue is assumed to be faster in the fpT2* analysis than in the ssT1 analysis. By comparison with the ssT1 method, the fpT2* method is faster, easier to implement, affords higher temporal resolution, and allows simultaneous determination of relative cerebral blood volume (rCBV), a widely used hemodynamic variable to assess tumor vascularity and grade.

Gliomas and meningiomas are the 2 most common primary brain tumor types, and they exhibit very different vascular properties.13 Meningiomas are the most common extra-axial brain tumors that are usually highly vascular with tumor capillaries that completely lack BBB, and tumor supply most commonly derived from dural vessels.14 On the other hand, gliomas, the most common intra-axial primary brain tumor, have variable degree of neovascularity and BBB alteration depending on the grade and histologic subtype. In fact, the lower-grade gliomas may not exhibit any evidence of angiogenesis or BBB disruption.15 Therefore, the degree of capillary permeability in meningiomas is likely to be greater than that of gliomas, and hence the contrast agent behavior during DCE MR imaging is likely to differ vastly between the 2 tumor types and between the ssT1 and the fpT2* methods.

In this study, we assessed the validity of the fpT2* K^trans values by first performing a 3-way comparison among K^trans values derived from ssT1 and fpT2* methods and fpT2* rCBV values by correlating with glioma grade. In addition, we investigated how closely the fpT2* K^trans approximates the ssT1 K^trans for gliomas (intra-axial) and meningiomas (extra-axial). We hypothesized that K^trans derived from the ssT1 method and the fpT2* method would correlate better for gliomas than for meningiomas, because the latter contain much leakier tumor capillaries and earlier arrival contrast agent within tumor vasculature, hence complicating K^trans calculation in both methods.

Methods

Patients

Twenty-seven patients with treatment-naive brain tumors—20 gliomas and 7 meningiomas—were recruited for the study before surgery. Fifteen patients were men and 12 were women; the average age was 47 years, with a standard error of 15.5 years and range of 16–79 years. All patients underwent gross total or subtotal resection of tumor within 2 days after the MR examination. Our institutional review board approved this study, and informed consent was obtained from all patients.

Histologic Examination

All tumor specimens were obtained during surgery, stained with hematoxylin-eosin, and then graded qualitatively by a pathologist (T.T.), who was blinded to the imaging findings. None of the tissue samples were obtained by stereotactic biopsy. The gliomas were classified into 4 WHO groups (grades I–IV) and the meningiomas into 2 groups (typical and atypical). Histologic evaluation revealed one grade 1 glioma (juvenile pilocytic astrocytoma), 5 grade II gliomas (3 astrocytomas, one oligoastrocytoma, and one oligodendroglioma), 4 grade III gliomas (2 anaplastic astrocytomas, one anaplastic oligoastrocytoma, and one oligodendroglioma), 10 grade IV gliomas (glioblastoma multiforme [GBM]), 5 typical meningiomas, one atypical meningioma, and one hemangiopericytoma. Henceforce in this study, “meningiomas” will refer to the 6 meningiomas and one hemangiopericytoma. None of the meningioma or grade I, II, or III glioma patients received steroids immediately before or during surgery. Of the 10 patients with GBM, none received steroids at the time of MR imaging, but 5 patients received oral steroids for 2–3 weeks before imaging for a maximum of 7 days.

MR Imaging

MR examinations were performed with a 1.5T clinical system (Signa; GE Medical Systems; Milwaukee, Wis) with the following imaging protocol: 3-plane localizer, sagittal T1-weighted, axial fluid-attenuated inversion recovery (FLAIR) sequences. A gadolinium-enhanced (Gd-DTPA, 0.1 mmol/kg, Omniscan, GE Medical Systems) dynamic MR permeability sequence was performed by administering the contrast material with a power injector (Medrad, Indianola, Pa) at a rate of 2 mL/s. Axial 3D T1-weighted imaging with spoiled gradient-recalled acquisition in the steady state (SPGR) was then performed with the following parameters: 6.5/1.24/1 (TR/TE/excitations); flip angle, 30°; matrix, 128 × 128; section thickness, 3 mm; field of view, 26 cm; acquisition time, 6 minutes 35 seconds. A total of 12 dynamic acquisitions were obtained with a 40-second injection delay in each dataset.

A second injection of Gd-DTPA was performed 15 minutes after the 3D SPGR sequence (to ensure that the initial contrast bolus clears from the intravascular phase before the bolus tracking T2* acquisition), and a dynamic contrast-enhanced T2*-weighted MR perfusion sequence was performed with the following parameters: 1250/54.0/1 (TR/TE/excitations); flip angle, 35°; bandwidth, 62.5; matrix, 128 × 128; number of sections, 7–8; section thickness, 2–5 mm with spacing of 0 mm; field of view, 26 cm; acquisition time, 1 minute 18 seconds. A series of 60 dynamic acquisitions were obtained before (10 image sets), during, and after a bolus injection of Gd-DTPA at 4 mL/s, followed by a saline flush at the same rate. The gradient-echo echo-planar images were acquired at 1-second intervals during the first pass of a bolus of Gd-DTPA. Anatomic imaging—which included T1-weighted SPGR, T2-weighted, and FLAIR sequences—was performed in the 15 minutes between the steady-state T1-weighted SPGR (ssT1) and the fpT2* perfusion sequences. Twelve acquisitions were performed for each dataset. All 27 patients underwent both ssT1 and fpT2* imaging in addition to routine anatomic MR imaging.

Data Analysis

For each tumor, uniform-sized (5-mm diameter) regions of interest were drawn within a solid contrast-enhancing region on only the postcontrast injection 3D SPGR images that were resampled with the T2* perfusion dataset to ensure that the same region of interest was used for both T1 and T2* data. One reader (A.L.) drew all regions of interest blinded to histology, avoiding vessels and CSF to minimize volume averaging, and distinguishing between gray and white matter. These regions of interest were then coregistered onto the ssT1 and fpT2* image dataset. Signal intensity values measured over time in regions of interest in normal vessel (superior sagittal sinus), and tumor tissue (the enhancing portion of the tumor) were analyzed by using MRVision software (MRVision Co., Menlo Park, Calif) on a UNIX workstation. Blood data from normal vessel were usually measured from the superior sagittal sinus; however, if the mass effect of the tumor compressed the sinus, another relatively large vascular reference such as transverse sinus was chosen. In nonenhancing tumors, the most solid-appearing portion was used for analysis. The steady-state T1 kinetic analysis was based on the 2-compartment pharmacokinetic model of Tofts and Kermode10 and performed as described by Roberts et al.6 Nonlinear regression analysis (Kaleidagraph, Synergy Software, Reading, Pa) yielded fit-value estimates of k₁, which reflects efflux rate (permeability) from plasma to interstitium. Microvascular permeability, K^trans, was computed from k₁, corrected for hematocrit, and appropriately scaled. Figure 1 demonstrates a dynamic series of ssT1 images through one anatomic location before, during, and after the administration of intravenous Gd-DTPA in a patient with grade 3 gliomas where tumor enhancement lags behind normal vascular enhancement. Figure 2 is an example of a dynamic ssT1 image set in multiple locations in a patient with hemangiopericytoma, showing simultaneous enhancement of normal vessels and tumor during the early phase of Gd-DTPA injection.

Fig 1.

Right frontal anaplastic oligoastrocytoma (WHO grade III) in a 43-year-old man. A dynamic series of ssT1 SPGR images through one anatomic location before, during, and after the administration of intravenous Gd-DTPA demonstrate earlier enhancement of normal vessels followed by delayed and persistent enhancement of the right frontal high-grade glioma.

Fig 2.

Left cavernous sinus hemangiopericytoma in a 30-year-old woman. A dynamic series of ssT1 SPGR images through multiple anatomic locations before (top row), during (middle 2 rows), and after (bottom row) the administration of intravenous Gd-DTPA demonstrate simultaneous contrast agent arrival within the normal vessels (second row, horizontal arrows) and within this highly vascular extra-axial brain tumor (slanted arrow).

The fpT2* analysis was based on 5-mm regions of interest in locations anatomically identical to those of ssT1 images. This algorithm assumed that contrast material exists in 2 interchanging compartments (plasma and extravascular extracellular space) and used an exact expression for the total tissue contrast material concentration by also accounting for the residual blood concentration of contrast material after the bolus had dispersed.12 The T2*-weighted echo-planar images were transferred to a UltraSPARC 10 workstation (Sun Computer, Mountain View, Calif) for processing. The K^trans value was derived by estimating vascular contrast material concentration from normal white matter and fitting it to the expression for the tissue contrast material concentration. All 27 tumors were subject to both ssT1 and fpT2* K^trans analysis. The theoretical and practical difference between the 2 methods is illustrated in Table 1.

Table 1:

Comparison between the ssT1 and fpT2* methods: theoretical and practical considerations

	ssT1 Method	fpT2* Method
Theoretical considerations
Shape of contrast agent concentration time curve	Bi-exponential decay	Gamma-variate
Concentration of intravascular contrast agent	Lower	Higher
Ktrans for normal brain tissue	Zero	Negligible or very small, but not zero
Rate of contrast agent movement from intravascular to extravascular space within a single voxel of tissue	Slower	Faster
Practical considerations
Spatial resolution	Higher	Lower
Subjectivity to susceptibility artifact	No	Yes
Imaging time	Longer (>6 min)	Shorter (<1.5 min)
Postprocessing algorithm complexity	Higher	Lower

For both gliomas and meningiomas, the linear relationship between K^trans determined with the ssT1 method and that determined with the fpT2* method was estimated by using Pearson correlation, and the corresponding confidence intervals (CI) were obtained based on the Fisher Z transformation. In addition, a simple linear regression model was fitted for K^trans determined by the ssT1 method, by using K^trans determined by the fpT2* method as the only predictor for gliomas and meningiomas, respectively. Furthermore, for gliomas only, nonparametric Kruskal-Wallis rank sum test was used to evaluate whether the mean maximum rCBV, ssT1 K^trans, and fpT2* K^trans were the same for grades II, III, and IV. A P value ≤.05 from the Kruskal-Wallis test indicated a statistically significant difference in the means among grades II, III, and IV. For a significant Kruskal-Wallis test, 3 additional nonparametric Wilcoxon rank sum tests for 2 sample data were carried out to compare the means between different grades. The conservative Bonferroni adjustment was used for the multiple comparisons. The Cochran-Armitage trend test, which is based on the hypothesis that the higher the tumor grade the leakier the tumor vessels, was applied to determine whether the proportion of enhancement increases when the grade advances in gliomas.

Results

Anatomic MR Imaging

Gadolinium-enhanced T1-weighted SPGR imaging demonstrated enhancement in 10 of 10 grade IV gliomas, 3 of 4 grade III gliomas, 3 of 5 grade II gliomas, and the single grade 1 glioma. All high-grade contrast-enhancing gliomas showed a surrounding area of nonenhancing T2 abnormality consistent with edema. Figures 3 and 4 demonstrate examples of anatomic imaging features of typical grade IV and III gliomas, respectively. Excluding the single grade 1 glioma, the small left-sided P value (.0193) for the Cochran-Armitage trend test indicated that the probability of enhancement increases as the grade increases in gliomas.

Fig 3.

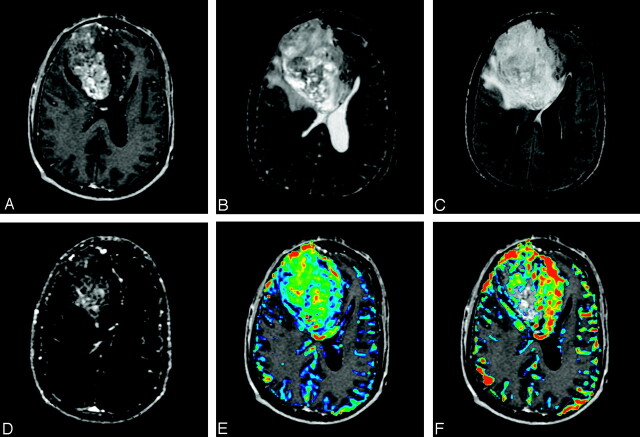
Left thalamic/posterior frontal GBM (WHO grade IV) in a 63-year-old man. Upper panel, Left, Transaxial contrast-enhanced SPGR image demonstrates an enhancing left dorsolateral thalamic and posterior frontal lobe tumor (arrow). Middle and Right, Transaxial T2-weighted image (middle) and FLAIR (right) show moderate degree of surrounding edema (arrowheads). Lower panel, Left, Transaxial ssT1 K^trans map demonstrates a rim of increased permeability (arrow). Middle, Transaxial fpT2* K^trans color map overlayed onto SPGR image also shows a rim of increased permeability. Right, Transaxial fpT2* rCBV color map overlayed onto SPGR image demonstrates similar rim shape of increased blood volume but more focused on the medial aspect of the tumor (arrow).

Fig 4.

Right frontal anaplastic oligoastrocytoma (WHO grade III) in a 43-year-old man. Upper panel, Left, Transaxial contrast-enhanced SPGR image demonstrates a large heterogeneously right frontal lobe tumor. Middle and Right, Transaxial T2-weighted image (middle) and FLAIR (right) show moderate degree of surrounding edema. Lower panel, Left, Transaxial ssT1 K^trans map demonstrates a large central area of increased permeability. Middle, Transaxial fpT2* K^trans color map overlayed onto SPGR image also shows global increase in permeability throughout the tumor. Right, Transaxial fpT2* rCBV color map overlayed onto SPGR image demonstrates increased blood volume mostly involving the medial aspect of the tumor.

Microvascular Permeability Differentiates between Glioma Grade Better Than Cerebral Blood Volume

Although no monotone increase was noted in K^trans values as the grade increased from 2 to 4 for either the ssT1 or the fpT2* method (Fig 5), the mean ± SE of the K^trans values for grade 4 gliomas determined by using either the ssT1 method (0.095 ± 0.097 minutes⁻¹) or the fpT2* method (0.194 ± 0.183 minutes⁻¹) were greater than the mean of the K^trans values for either grades II or III gliomas. For fpT2*, the Kruskal-Wallis test indicated that the average K^trans values were not the same among grades II, III, and IV (P = .003). Additional Wilcoxon rank sum tests (Table 2) indicated that a significant difference existed in K^trans values between non-GBM and GBM tumor, but no significant difference was noted between grades II and III. For ssT1, the Wilcoxon rank sum test suggested that the average K^trans values are different among grades II, III, and IV (P = .006). Additional Wilcoxon rank sum tests suggested a significant difference existed in K^trans values between grade III and GBM tumors, but no difference was noted in K^trans values between grades II and III. For rCBV values, the Kruskal-Wallis test indicated that the mean maximal rCBV values were not the same among grades II, III, and IV. The degree of difference among grades, however, was not as strong for maximum rCBV (P = .03) values as for K^trans values determined by using either fpT2*(P = .003) or ssT1 (P = .006) methods. In addition, the Wilcoxon rank sum test showed that only a marginal significant difference existed in maximum rCBV values between grade II and GBM tumors and no significant difference between grade III and GBM tumors.

Fig 5.

Box plots of fpT2* rCBV maximum, ssT1- and fpT2*-derived K^trans values (in minutes⁻¹) for grades I, II, III, and IV gliomas. Box plots of fpT2* rCBV maximum, ssT1- and fpT2*-derived K^trans values (in minutes⁻¹) for grades I, II, III, and IV gliomas. The red box extends from the first quartile to the third quartile of the data, with the white line marking the median. The black lines with end brackets represent the most extreme observations in the data that are not more than 1.5 times the height of the box beyond either quartile. All points outside this range are presented by a circle and are considered to be outliers. There was only one patient with grade I gliomas (pilocytic astrocytoma), and the value was presented as horizontal [I] bar in the plots.

Table 2:

P values from the Kruskal-Wallis test of overall equality of all three grades for rCBV max, ssT1-, and fpT2*-derived K^trans

	rCBV max	ssT1-Derived Ktrans	fpT2*-Derived Ktrans
Kruskal-Wallis test	.03*	.006*	.003*
Grade II vs III	.11	>.5	>0.5
Grade II vs IV	.019	.017	.005†
Grade III vs IV	.19	.009†	.002†

^*For significant Kruskal-Wallis test, P values from 3 Wilcoxon rank sum tests for 2 sample data were listed with Bonferroni adjustment for multiple comparisons.

^†Difference was statistically significant after Bonferroni adjustment for multiple comparisons

The fpT2* K^trans Linearly Correlates with the ssT1 K^trans

On the basis of regions of interest drawn within tumors in anatomically identical positions on ssT1 and fpT2* images, K^trans maps and rCBV maps were calculated (Fig 3 and 4). For gliomas, ssT1-derived K^trans values ranged from 0 to 0.31 minutes⁻¹, with a mean ± standard error (SE) of 0.055 ± 0.079 minutes⁻¹, whereas fpT2*-derived K^trans values ranged from 0 to 0.61 minutes⁻¹, with a mean ± SE of 0.111 ± 0.153 minutes⁻¹. For meningiomas, ssT1 K^trans values ranged from 0.04 to 1.4 minutes⁻¹, with a mean ± SE of 0.47 ± 0.51 minutes⁻¹, whereas fpT2* K^trans values ranged from 0.0023 to 0.98 minutes⁻¹, with a mean ± SE of 0.47 ± 0.31 minutes⁻¹. Figures 3 and 4 clearly demonstrate different spatial distribution of abnormality in maximal K^trans and maximal rCBV in high-grade gliomas.

Figure 6 shows ssT1-derived K^trans values plotted against fpT2*-derived K^trans values and the fitted linear regression line for gliomas and meningiomas, respectively. For gliomas, the estimated Pearson correlation coefficient between ssT1 and fpT2* K^trans was 0.95, with a 95% CI from 0.89 to 0.98. In addition, fpT2* was highly predictive of ssT1 K^trans values, with 1-unit increase of fpT2* K^trans value corresponding to approximately 0.5-unit increase of ssT1 K^trans value. For meningiomas, however, no linear correlation existed between ssT1 and fpT2* K^trans values, with an estimated Pearson correlation coefficient of 0.16 and a 95% CI ranging from 0.68 to 0.81. Furthermore, the regression coefficient of fpT2*-derived K^trans was estimated to be 0.26, which is not significantly different from 0 (P = .74).

Fig 6.

Scatter plots and fitted regression line of ssT1-derived K^trans on fpT2*-derived K^trans. The Pearson correlation coefficient for gliomas is high and estimated to be 0.95 (95% CI [0.89, 0.98]); however, no linear correlation exists between fpT2* and ssT1 K^trans values for meningiomas, with the Pearson correlation coefficient estimated to be 0.16 (95% CI [−0.68, 0.81]).

Discussion

During the past 2 decades, tremendous progress has been made toward designing a robust method to noninvasively quantify microvascular permeability for clinical use. The recent addition of pharmaceutical agents that curtail vascular proliferation and permeability to the anticancer armamentarium increases the urgency for implementing such a method.16–18 Although many techniques have been described for this purpose, none is ideal. The most widely applied and accepted MR standard to measure permeability is the dynamic contrast-enhanced ssT1 method, which is based on the pharmacokinetic model of Tofts and Kermode.10 This method fits a triexponential enhancement curve to a theoretic model based on compartmental analysis after a standard dose of gadolinium-based contrast agent. The transfer constant, or permeability surface area product, derived from this method has been applied in many clinical settings and shown to be useful in assessing the different stages of demyelinating plaques,19 glioma grade,20 and treatment response.21,22 There is clear advantage to using the ssT1 method, because it offers finer spatial resolution, is resistant to susceptibility artifact, and allows reasonable imaging time. A recently published report suggests, however, the uncertainty in the analysis of ssT1 DCE dataset where the use of commonly accepted models led to systematic overestimation of K^trans and potentially large underestimates of the blood plasma volume fraction.11 This raises the concern whether ssT1 analysis methods with modeling system specific to a certain tumor type can be generalized and applied to other brain tumor types. As can be seen in Fig 2, the temporal separation of early normal vascular phase and delayed tumor phase of contrast agent compartmentalization does not apply in highly vascular extra-axial tumors and hence complicates the calculation of K^trans by using both methods.

Our results showed a clear linear correlation between K^trans derived from the ssT1 method and the fpT2* method for gliomas. To the best of our knowledge, this is the first study that systematically compares K^trans determined by the ssT1 method with that determined by the fpT2* method. When compared with previously published estimates of maximum K^trans within gliomas with use of either a T1 or T2* method, our results are in reasonable agreement.5,6,12,23 For example, our mean K^trans value for grade 4 gliomas determined with the ssT1 method was very similar to the mean for these tumors reported by Roberts et al.6 In addition, their collective mean for 22 gliomas was nearly identical to our mean for 20 gliomas by using the ssT1 method. Li et al23 used an approximate T1 method to determine K^trans in 2 grade IV and 3 grade III gliomas and found values similar to our ssT1 estimates. Previous studies by using the fpT2* method reported means for 10 WHO grade IV gliomas12 and 31 Ringertz grade I, 16 grade II, and 26 grade IV gliomas5 (analogous to WHO grades II, III, and IV) that were similar to our fpT2* mean K^trans values for equivalent tumor groups.

We observed that there was no linear correlation for extra-axial tumors (meningiomas) even though the mean ssT1 and mean fpT2* K^trans estimates were coincidentally both 0.47 minutes⁻¹. The lower correlation in GBMs and meningiomas is in part due to the extreme leakiness of vessels within these tumors. Meningiomas are highly vascular tumors that lack a BBB. In GBMs, the BBB is partially destroyed in preexistent vessels, and the BBBs in angiogenic vessels form imperfectly. As a result, contrast agent arrives in these tumor parenchyma almost simultaneously with their arrival in the tumor vessels. In other words, the tumor phase of contrast agent may not lag behind the vascular phase in these tumors. Because the ssT1 K^trans model assumes that the rise in contrast agent concentration within a vessel is earlier and greater than within the tumor tissue or normal brain tissue, the theory behind the 3 compartment model of ssT1 is likely violated in such tumors. In addition, the fpT2* algorithm assumes that relaxation rate is independent of tracer distribution (intra- vs extravascular, normal white matter vs tumor). Because susceptibility-induced T2* losses do depend on tracer distribution, a leaky tumor will result in a more uniform tracer distribution, produce less relaxation, and therefore underestimate K^trans.

To further test the physiologic significance of parameters derived by the fpT2* algorithm, we correlated the fpT2* K^trans with glioma grade and compared with results from ssT1 K^trans correlation with glioma grade. Although our mean K^trans values determined by the fpT2* or ssT1 method did not progressively increase with glioma grade as previously reported for the ssT1 method, the significant correlation we observed between our fpT2*-derived K^trans values and glioma grade further validates the fpT2* technique for estimating K^trans. Although the standard perfusion measurement, rCBV, also displayed distinct distributions for glioma grades II–IV, our rCBV values were unable to differentiate between GBM and non-GBM gliomas with significance. This finding is consistent with previous studies that were also unable to discriminate between GBM and anaplastic astrocytoma.24,25 At least 2 studies have shown that low-grade oligodendrogliomas can have unusually high rCBV values.26,27 Because our study had only a single case of grade 1 gliomas (pilocytic astrocytoma), it is impossible to draw any conclusion on this tumor type. Inclusion of low-grade (WHO grade II) oligodendrogliomas in our study likely contributed to the poor correlation seen between our rCBV values and glioma grade. Our finding that the grade IV gliomas had the highest ssT1 and fpT2* K^trans values is consistent with previous studies showing that vascular endothelial growth factor expression is highest in more malignant gliomas.28,29 Although no significant difference was noted between K^trans values derived by either method for each individual glioma grade in our study, K^trans values determined by using both methods were able to distinguish between lower-grade and higher-grade tumors, as has been shown previously for both methods. For the above reasons, the ssT1 and fpT2* techniques may be complementary methods for providing information about the vascular status of brain tumors.

The fpT2* method for determining K^trans used in this study has several advantages over more conventional multicompartmental approaches. This fpT2* method, which is highly sensitive to changes in magnetic susceptibility, offers higher temporal resolution and broader section coverage than do T1 methods because echo-planar imaging sequences are much faster than T1-weighted sequences. For example, we can sample as many as 10 sections with 1-second temporal resolution, and our first-pass algorithm requires only first-pass data, which can be acquired in about 1 minute. In addition, our fpT2* postprocessing algorithm allows efficient determination of K^trans in about 5 minutes, compared with conventional postprocessing of ssT1 data, which can take as long as 20 minutes. Furthermore, the ssT1 method used by Li et al23 ignores backflow from tissue to plasma during bolus passage and suffers from disadvantages of T1-based methods. Zhu et al30 and Barbier et al31 combined T1- and T2*-weighted imaging to determine vascular leakage, requiring 2 injections of contrast material (determination of our fpT2* estimates of K^trans alone would not require 2 contrast material injections).

There are several limitations in this study. First, the sample size of lower-grade gliomas is small. In previous studies that showed good correlation between ssT1 K^trans and glioma grade, there were at least 8–9 grade II gliomas and 7–14 grade III gliomas. Because our patient population included only 5 grade II and 4 grade III gliomas, it is possible that a larger number of grades II and III gliomas may improve the correlation between K^trans determined by either method and grade. Second, the maximal permeability may not necessarily be at the site of maximal enhancement where the regions of interest were drawn in this study. An alternative method that has been used to obtain the maximal K^trans for tumors is derived from the site of maximal decrease in signal intensity at 25 seconds after passage of the contrast material bolus (SD25). However, as pointed out by the authors of this technique, this method is also subject to error because factors such as cardiac output and dose of contrast agent also affect the value of SD25.

The most obvious limitation of the fpT2* method is its inability to enable accurate determination of K^trans for leaky tumors such as meningiomas. Even though this method does not assume that leakage of contrast material into intercellular space during the first pass of a contrast bolus is negligible, K^trans may be underestimated because the assumption that relaxation rate is independent of tracer distribution may not be true for extremely leaky tumors (see above). Thus, the fpT2* method can underestimate K^trans for meningiomas. It is also possible that the fpT2* algorithm overestimates K^trans for leaky tumors, because this method is susceptible to the “pseudopermeability” effect (the artificial elevation of K^trans by the presence of intravascular contrast material) even though the high-temporal-resolution data allow separation of the contribution of the intravascular and extravascular contrast material to the signal intensity. An additional disadvantage of methods based on T2* studies is the poor signal intensity–to-noise ratio when the intra- and extravascular contributions are of similar magnitude as in leaky tumors. Furthermore, in tumors with extremely low vascular permeability, the extravascular tracer concentration may continue to rise after the bolus passage. In such tumors, delayed T1-weighted sequences would more accurately estimate K^trans, in light of the longer acquisition time of the steady-state T1-weighted sequence.

Although a linear correlation existed between fpT2* and ssT1 estimates of K^trans for gliomas, we noted that the fpT2* estimates were larger than the ssT1 estimates in all 20 gliomas and for 3 of the 7 meningiomas. Thus, our fpT2* method may not allow absolute quantitation of microvascular permeability if the ssT1 values are considered the reference standard. Because the ssT1 method likely overestimates true microvascular permeability, the fpT2* values may be an even grosser overestimation of K^trans. However, because a linear correlation exists for gliomas, the “accurate” K^trans values (assuming ssT1 values are the reference standard) can be easily determined from the T2* estimate by using the equation of the line that best fits the data points.

Our data suggest that the maximum microvascular permeability in different tumors determined by using the fpT2* method correlates with tumor grade. Because tumor grade has been assigned based on pathologic examination, it is imperative to show that regions within a tumor that have the highest fpT2* K^trans values actually correlate with the highest grade on the basis of pathologic findings before this method can be implemented to guide tumor biopsy for tumor grading. In addition, K^trans has been used to follow the effects of interventions32 and may prove to be a reliable method for assessing the effectiveness of antiangiogenesis drugs in the future. Incorporation of K^trans determinations into therapeutic trials or clinical routine requires a standardized approach for K^trans measurements. Thus, in addition to validating fpT2* K^trans values by measuring vascular permeability in specimens obtained by image-guided biopsy, it will be important to refine and optimize this method for routine clinical use and then determine whether this technique is reproducible over several days for individual observers and also between observers. Because K^trans is only one of many vascular descriptors, determination of K^trans along with plasma volume, extravascular extracellular space volume, flux rate, vascular tortuosity or morphology, vessel size, and other vascular characteristics ideally by using, at most, a few sequences may provide a more reliable method of predicting tumor grade. Because vascularity is only one aspect of tumor malignancy, combining insight into vascular changes with changes in cellularity (diffusion) and metabolites (spectroscopy) in the context of anatomic maps has the potential of being tremendously useful to physicians and researchers alike. Finally, we are very interested in assessing the validity of this method for characterizing microvascular permeability in other intra- and extra-axial tumors, correlating K^trans with survival, and translating this method into applications at the higher field strength MR scanners.

In summary, K^trans as determined by the fpT2* method can provide a reasonable estimate of microvascular permeability for gliomas but not for meningiomas. In addition, this method can provide estimates of K^trans that correlate well with glioma grade. The fpT2* method for estimating K^trans has the potential to be used routinely to determine areas of abnormal tumor vasculature for biopsy, to noninvasively grade gliomas, and as a surrogate marker for antiangiogenic drug activity.

Conclusion

Our study demonstrates that the microvascular permeability measurements, K^trans, derived from ssT1 and fpT2* methods were more predictive of glioma grade than rCBV derived from fpT2* method. The fpT2* K^trans was highly correlated with ssT1 K^trans in gliomas but not in meningiomas, likely because of extremely leaky vessels in meningiomas, which complicate K^trans calculation by using both methods.