Stock price reaction to the drug development setbacks in the pharmaceutical industry

Abstract

Background

Investments in pharmaceutical companies remain challenging due to the inherent uncertainties of risk assessment.

Objectives

Our paper aims to assess the impact of the drug development setbacks (DDS) on the stock price of pharmaceutical companies while taking into account the company’s financial situation, pipeline size and trend of the stock price before the DDS.

Methods

The model-based clustering based on finite Gaussian mixture modeling was employed to identify the clusters of pharmaceutical companies with homogenous parameters. An artificial neural network was constructed to aid the prediction of the positive mean rate of return 120 days after the DDS.

Results

Our results reveal that a higher pipeline size and a lower rate of return before the DDS, as well as a lower ratio of the market value of the equity and the book value of the total liabilities, are associated with a positive mean rate of return 120 days after the DDS.

Conclusion

In general, the DDS have a negative impact on the company’s stock price, but this risk can be minimized by investors choosing the companies that satisfy certain criteria.

Graphical abstract.

The higher pipeline size(spip) and lower rate of return before (srr) the drug development setback (DDS) and the Market Value of Equity/Book Value of Total Liabilities ratio (sx4) are associated with a positive mean rate of return 120 days after the DDS.

Electronic supplementary material

The online version of this article (10.1007/s40199-020-00349-6) contains supplementary material, which is available to authorized users.

Introduction

Investments in pharmaceutical companies remain challenging due to the inherent uncertainties of risk assessment. The risks that these companies face may be classified to idiosyncratic (pertaining to their drug pipelines) and systematic (pertaining to the general economic environment) risks [1]. The stocks of pharmaceutical companies are well known to be volatile. Companies in this branch have become more profitable since the 2000s [1]. However, in terms of the risk-adjusted return, the pharmaceutical industry still does not outperform comparator industries (e.g., automotive manufacturing industry), likely due to higher business/operational risks [2].

The analysis of the drug pipeline is an important factor to consider when estimating the idiosyncratic risk or business risk. The drug pipeline (a set of drug candidates in the pre-approval stage) can be classified into the phases of development. In each phase of the development [ranging from the proof of concept studies to phase III clinical trials], an executive decision regarding further development of a drug must be made. The drug pipeline ought to be optimized, i.e., it should not contain too many molecular entities and should be prioritized and have adequate funding [3]. The greatest challenge for the drug-to-be and the pharmaceutical company’s market valuation is the late termination of development after a failed phase III trial [3, 4]; this may also affect the market value of such a company [4, 5].

The financial risk assessment based on the analysis of the financial data often plays a role in the overall risk assessment. It has been shown that companies that suffer financial distress seem to earn lower returns to investors [6, 7], even though it would seem that the assumed higher risk by the investor should lead to greater returns as a compensation [7].

Rothenstein et al. have analyzed the impact of the public announcements of 59 clinical trials’ results and 50 Food and Drug Administration (FDA) decisions and have concluded that trends of the company stock price before the first public announcement differ for the companies that report positive vs. negative trials and that FDA regulatory decisions do not seem to influence the company stock price [4]. Such findings seem to be interesting, because a failure to obtain the FDA’s positive decision is an important factor for a company.

A literature review reveals that the prediction of the stock price is mainly performed based on financial or technical indicators [8]. We aimed to develop a pharmaceutical industry-specific model that takes into account the financial and nonfinancial variables. This research focuses specifically on the drug development setbacks (DDS), i.e., failure to obtain marketing authorization from the European Medicines Agency (EMA) or other negative drug development events. This research aimed to find out how the DDS influence the company stock price, adjusted by the pipeline size, financial risk and trend of the stock price before the DDS.

This research is important for regulators and pharmaceutical company managers to see changes in the company market value after the drug development setbacks. It is also helpful for investors who seek to minimize the risk of their investments.

Materials and methods

Data collection

The main data set consists of the pharmaceutical companies that withdrew the application of marketing authorization application (MAA) from the EMA in the period of 2017–2018 (see Supplementary material, Appendix 1, Table 1.1). This information was acquired from the EMA website. This data set is further referred to as Set 1. The dataset was expanded by the world’s leading pharmaceutical companies, which were selected according to the most valuable R&D projects, ranked by the net present value (NPV), that have suffered the drug development setbacks (DDS, disappointing clinical trial results or failed phase II or III clinical trials) in the period of 2017–2018 (see Supplementary material, Appendix 1, Table 1.2). This dataset was formed based on the data presented in EvaluatePharma’s World Preview [9–11] and is further referred to as Set 2.

Table 1.

The main characteristics of Set 1 and Set 2

Company	Pipeline	z-score	Chow test for structural difference with respect to dummy							RR−120	RR+120
			const	t	pt-1	dummy	dummy*t	dummy* pt-1	p value
Set 1 - European companies
Allergan Pharmaceuticals International Limited	38	0.78	16.2972**	−0.0296*	0.9092***	0.1336	0.1126***	−0.0662	0.0161	0.9994	1.0022
Kamada BioPharma Limited at Fieldfisher LLP	22	2.76	1.84309***	0.0023**	0.7282***	−1.2372**	−0.0027*	0.1546*	0.0000	1.0012	0.9971
MolMed SpA	5	3.64	26.7316**	0.0277	0.8734***	36.2649	−0.1323***	−0.1051	0.0097	1.0007	0.9946
Janssen-Cilag International NV	93	5.14	7.4563	0.0108	0.9414***	1.5070	−0.0204**	0.0019	0.2340	0.9997	0.9989
Sunesis Europe Ltd	3	−19.45	0.3072*	−0.0012**	0.9333***	1.0487**	−0.0030**	−0.2408**	0.1807	1.0007	0.9989
Sandoz GmbH	200	−1.91	1.4926	0.0025	0.9335***	−0.7590	−0.0025	−0.0686	0.0002	0.9969	0.9959
Pfizer Europe MA EEIG	77	2.65	8.0471***	0.0069*	0.8079***	8.7537	−0.0260**	−0.1569	0.0168	1.0030	0.9817
Bristol-Myers Squibb Pharma EEIG	38	5.49	0.5608	0.0042	0.9843***	−2.8697	−0.0195**	0.0864*	0.0029	0.9975	0.9986
Astra Zeneca AB	150	1.67	3.5372**	−0.0009	0.8988***	−1.7370	0.0029	0.0460	0.4028	1.0009	1.0014
Amgen Europe B.V.	60	2.64	21.4534**	0.0287*	0.8731***	−12.7674	−0.0205	0.0727	0.3189	1.0002	1.0002
Gilead Sciences Ireland UC	56	2.92	−2.0606	0.01808***	1.0179***	24.7539***	−0.0632***	−0.2479***	0.0001	1.0008	0.9967
Merck Sharp & Dohme B.V.	127	3.3	4.3931	0.0010	0.9306***	−1.3776	0.0021	0.0088	0.0788	1.0002	0.9983
Roche	185	7.41	4.0389	−0.0144	0.9754***	4.4963	0.0069	−0.0439	0.7503	1.0018	0.9987
Melinta Therapeutics Inc	12	−3.05	1.5531	−0.0066	0.9342***	1.6295	0.0160	−0.1490	0.7013	0.9944	1.0009
Radius International Ltd	4	−0.45	2.9625**	0.0056	0.9090***	3.4113	−0.0192*	−0.0612	0.3268	1.0031	0.9974
Average	71.3333	3.4909								1.0000	0.9974
Set 2 - The largest global companies
AbbVie	96	2.40	17.2255***	0.0591**	0.8175***	−*.8797	−7.0492*	−5.0006	0.0023	1.0022	0.9973
Celgene	51	4.20	9.1031*	−0.0136	0.9158***	11.4732	−7.0195	−4.1120	0.2672	0.9994	0.9975
Incyte	44	17.17	19.8815***	0.0029	0.8457***	4.4437	−4.0497	−1.0219	0.0339	1.0017	0.9964
Johnson & Johnson	214	5.72	10.5382*	0.0134	0.9146***	0.0330	−0.0019	−8.0027	0.5955	1.0007	1.0006
AstraZeneca	150	1.67	3.8965**	−*.0003	0.8890***	−*.7401	0.0034	0.0427	0.4627	1.0007	1.0010
Roche	30	6.16	34.4092***	0.0554***	0.6740***	−**.9742	0.0497	0.1211	0.0039	1.0012	1.0041
Eli Lilly	83	3.74	7.6021*	−0.0063	0.9063***	11.7512**	0.1068***	−*.3242***	0.0000	0.9991	1.0013
Ophthotech	2	−3.67	0.3755**	−*.0001	0.8581***	−*.2135	0.0002	0.0803	0.7052	0.9983	1.0015
Merck & Co	37	3.09	3.7289	0.0024	0.9394***	3.7680	−6.00430	−0.0535	0.5422	1.0000	1.0000
AbbVie	96	2.57	4.4921*	0.0038	0.9265***	−*.6938	−7.0033	0.0333	0.6359	1.0003	1.0012
Celgene	51	3.89	12.7339	0.0102	0.9039***	9.6206	−7.0195	−4.1116	0.0000	1.0004	0.9957
Average	77.6364	5.0610								1.0004	1.0000

* p < 0.1; ** p < 0.05; *** p < 0.01

The information about product pipelines was taken from the official websites of the companies. The financial data of the companies was obtained from the website of Morningstar (http://financials.morningstar.com) via the application programming interface. Stock prices were taken from Yahoo finance. The analysis was performed with the R Studio.

Calculation of indicators

The stock data were retrieved as time series of 120 calendar days before the DDS (marketing authorization application withdrawal, negative opinion or failed phase III clinical trial) and 120 calendar days after the DDS, including only the workdays. The mean rates of return [12, 13] 120 days before (RR₋₁₂₀) and after (RR₊₁₂₀) the drug development setbacks (DDS) were calculated. The mean rate of return 120 days after the DDS was also encoded as a binary variable termed the positive mean rate of return. The presence of the mean positive rate of return after the event was coded as “1”, and the negative rate of return was coded as “0”. The financial situation of the company was assessed using the Altman z-score bankruptcy prediction model [13] (see Supplementary material, Appendix 2).

Gaussian finite mixture model (GFMM)

The model-based clustering based on finite Gaussian mixture modeling was employed to find the clusters of companies and to identify the typical values of the Altman z-score, drug pipeline size and rate of return before the event and after it for each cluster. This algorithm has two key advantages. First, it is much more flexible in terms of cluster covariance than k-means, i.e., the clusters can take on any ellipse shape, rather than being restricted to circles. Second, the Gaussian finite mixture models use probabilities and can have multiple clusters per data point (i.e., it supports mixed membership). The model-based clustering is an iterative method to group a set of data into clusters by optimizing the distributions of data sets in clusters. The finite mixture model is a well-known model-based clustering method based on probabilities. It assumes that the data are generated by drawing from a finite set of exchangeable mixture components, where each mixture component corresponds to one specific data cluster [14–16]. The models are estimated by the expectation-maximization (EM) algorithm to find the most likely model components and the number of clusters while meeting two requirements: low inter-class similarity and high intra-class similarity.

The model-based clustering assumes that data come from a distribution that is a mixture of two or more clusters. Each cluster k is modeled by the normal distribution, which is characterized by three parameters: mean vector, covariance matrix and a probability of belonging to each cluster. In this research, the classification is performed using the mclust package. It is a contributed R package for model-based clustering, classification, and density estimation based on finite normal mixture modeling [16]. The mclust package offers several model options, i.e., EII, VII, EEI, VEI, EVI, VVI, EEE, EEV, VEV and VVV. The first identifier defines the volume, the second indicates the shape and the third defines the orientation. Letters are interpreted as follows: E – equal, V – variable, and I – coordinate axes. The optimal model is selected according to the Bayesian information criterion (BIC). The model with the largest BIC score is preferred. The detailed prescription of the method can be found in Melnykov and Maitra’s as well as in Malsiner-Walli et al.’s papers [14, 15]. The variables were standardized before performing the cluster analysis.

Artificial neural network

An artificial neural network (ANN) was developed to explore the relationship between the pipeline size, the rate of return, the financial health and the likelihood of the mean positive rate of return after the drug development setback. The ANN can be defined as a classification technique that consists of several layers of neurons [17]. The Neuralnet package [18] was used to construct a multilayer perceptron to model the functional relationships between analyzed variables. A simple multilayer perceptron, consisting of an input layer with n covariates and an output layer with one output neuron, can be represented as a function:

$$o\left(x\right)=f\left(w_0+\sum _{i=1}^n{w}_i{x}_i\right)=f\left(w_0+w^{T}x\right),$$ 1

where w₀ denotes the intercept, w = (w₁,. ..,w_n) is the vector consisting of all synaptic weights without the intercept, and x = (x₁,. .., x_n) is the vector of all covariates [18] and can be expanded to include additional hidden layers with J hidden neurons:

$$o\left(x\right)=f\left(w_0+\sum _{j=1}^J{w}_j·f\left(w_{0j}+\sum _{i=1}^n{w}_{\mathit{ij}}{x}_i\right)\right)=f\left(w_0+\sum _{j=1}^J{w}_j·f\left(w_{0j}+w_j^{T}x\right)\right),$$ 2

where w₀ denotes the intercept of the output neuron, the w_0j the intercept of the jth hidden neuron, w_j is the synaptic weight corresponding to the synapse starting at the jth hidden neuron, leading to the output neuron, w_j = (w_1j, . . .,w_nj) is the vector of all synaptic weights corresponding to the synapses leading to the jth hidden neuron, and x = (x₁, . . ., x_n) is the vector with covariates [18]. The hidden neurons and output neurons estimate an output f (g(z₀, z₁, . . ., z_k)) = f (g(z)), where z₀, z₁, . . ., z_k are the outputs of preceding neurons, g: R^k + 1 →R representing the integration function [usually g(z) = w₀ + w^Tz] and f: R → R is the activation function (as in our case the logistic function $\frac{1}{1+e^{-u}}$) [18]. The ANN was fitted with the supervised learning procedure with the minimization of the squared error function with the resilient backpropagation on the standardized predictor variables (the binary outcome variable was not standardized) [18]. The main ANN design problems are the identification of the optimal network topology (finding the optimal number of hidden layers and neurons in each layer) [17] and description of the relationships among variables in fitted models [19]. The NeuralNetTools package was employed [19] for better visualization of the aforementioned relationships and for gaining more insight into how the predictor variables influence the rate of return 120 days after the event.

Results

The pharmaceutical companies that withdrew the application of marketing authorization from the EMA (Set 1, n = 32) in the period of 2017–2018 were selected for the analysis (see Supplementary material, Appendix 1, Table 1.1). The most common reason for the negative preliminary EMA opinion was insufficient evidence to assess the risk-benefit ratio (n = 21). Only the publicly traded companies were selected for further analysis. An additional 10 global publicly-traded pharmaceutical companies (or Set 2) that faced drug development setbacks in 2017–2018 were also selected (see Supplementary material, Appendix 1, Table 1.2). The Celgene, as well as AbbVie companies, were included twice in this set because these companies experienced withdrawal twice (once in each year of 2017–2018). The main characteristics of both datasets are presented in Table 1. Set 1 and Set 2 were merged and the joint data set was analyzed to increase the sample size.

To test if the DDS has a significant influence on stock price (p_t), the Chow test was used. It tests for the presence of a structural break in a trend at a certain time moment (day of the DDS). The first-order autoregressive model AR(1) including time component (t) was created:

$${\mathrm{p}}_{\mathrm{t}}={\mathrm{b}}_0+{\mathrm{b}}_1\mathrm{t}+{\mathrm{b}}_2{\mathrm{p}}_{\mathrm{t}-1}+{\mathrm{e}}_{\mathrm{t}}.$$

The stationarity condition of the AR(1) model was satisfied in all cases, i.e., | b₂| < 1 (Table 1).

The Chow test for the structural difference concerning the dummy (dummy variable is equal to 0 before the DDS and 1 after the DDS) showed a significant structural break in the trend (p values <0.05) for 12 cases of 26. The significant structural break was specific to companies with a lower pipeline size (the average pipeline size of companies, for which the structural break is significant, is 62, while the average pipeline size of the companies, for which the structural break is insignificant, is 85), a higher z-score (4.14 and 0.77 on average in the case of the significant break and the insignificant structural break, respectively) and a higher growth of the stock price before the DDS (the average daily growth rate of the stock price before the DDS is 1.000342 and 1.000029 in the case of the significant break and the insignificant break, respectively).

The model-based clustering based on finite Gaussian mixture modeling was employed to identify the clusters of companies with typical standardized values of the Altman z-score, drug pipeline size and rate of return before and after the drug development setbacks. The model-based clustering revealed that the EEV (ellipsoidal, equal shape and volume) model with 3 components provided the best fit. The BIC value for this model was −260.16, df = 38, log.likelihood = − 68.18 (Fig. 1a and 2a, Table 2).

Fig. 1.

BIC values of different models with a different amount of clusters in the primary analysis (a) and final analysis (b)

Fig. 2.

Model-based EEV (ellipsoidal, equal shape and volume) classification plot (a) and model-based (ellipsoidal, equal shape) classification plot (b). The plot shows classification results of standardized variables to 2 clusters. Stpip – standardized pipeline size, stz – standardized z-score, strr1 – standardized mean rate of return 120 before the event, prr – binary outcome variable (1 if positive mean rate of return after the event exists and 0 otherwise), stx4 – standardized X4 (the market value of equity / book value of total liabilities)

Table 2.

The main characteristics of the clusters of the EEV model in the primary and final analysis

	Primary analysis			Final analysis
	Cluster 1	Cluster 2	Cluster 3	Cluster 1	Cluster 2
Standardized pipeline	−0.45	−0.10	0.40	0.09	−0.07
Standardized z-score	−0.17	0.18	−0.04
Standardized X4				0.08	−0.06
Standardized mean rate of return (120 days before the event)	−0.27	0.21	0.01	−0.03	0.02
Positive mean rate of return (120 days after the event)	1	0	0.29	0.91	0.00
Mixing probabilities	0.27	0.35	0.38	0.42	0.58
Number of observations	7	9	10	11	15

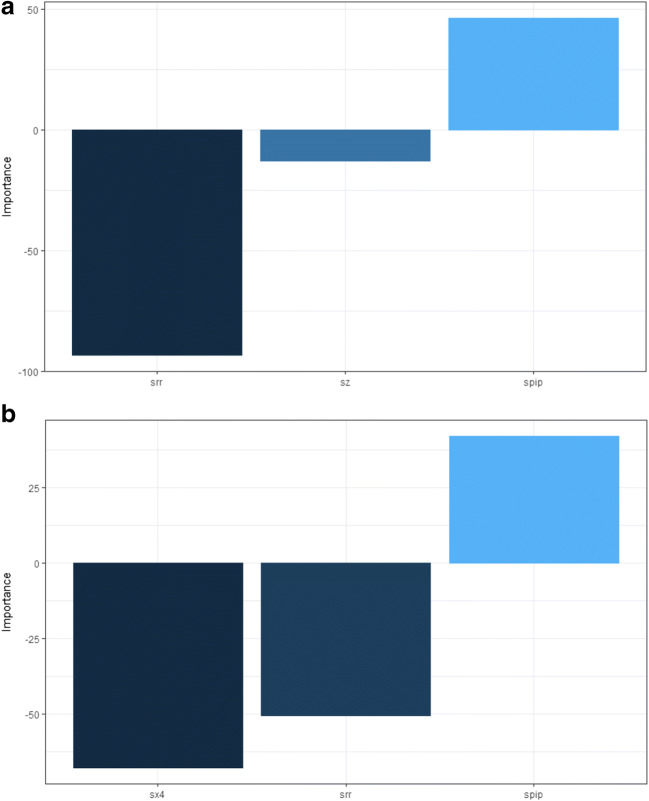
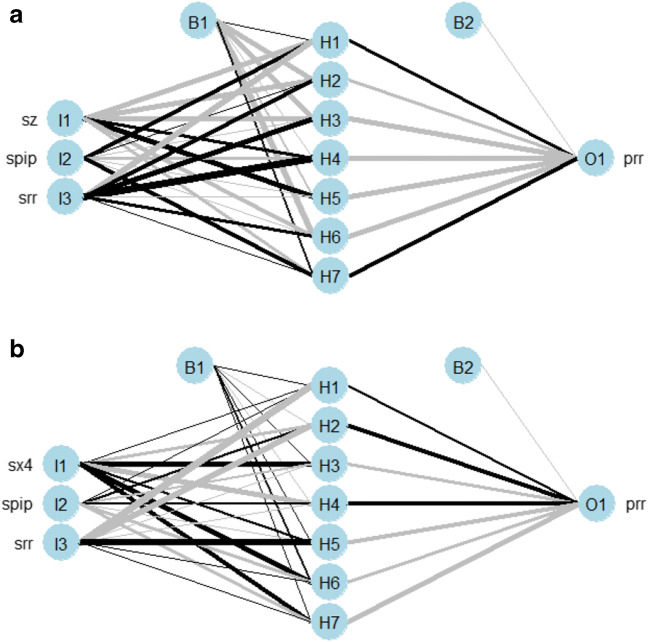
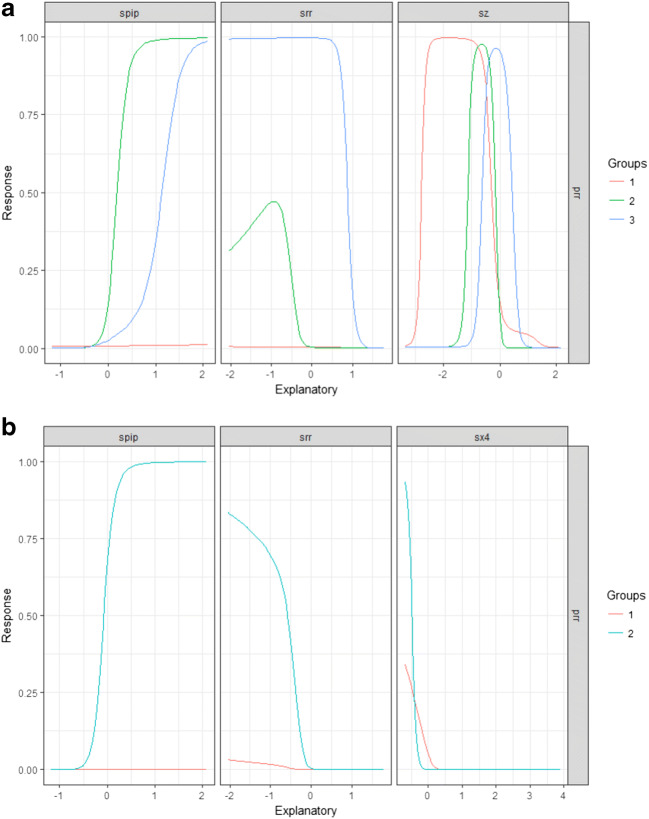
The artificial neural network (ANN) with one layer of neurons was constructed (see Supplementary material, Appendix 4). The final model had error 0.54 and mean square error 0.16 (Fig. 3a). The NeuralNetTools package was employed [19] to elucidate the relationships between the variables. The variable importance was assessed with the Olden function (Fig. 4a), which computes the importance of variables as the summed product of the raw input-hidden and output-hidden connection weights between each input and output node while keeping the magnitude and the sign of the relative contributions of each connections’ weights [20, 21]. The ANN was also represented as a neural interpretation diagram (Fig. 5a), where the positive weights between layers are shown as black lines and negative weights are shown as gray lines with thickness proportional to the absolute magnitude of each weight [19]. The sensitivity analysis was also conducted using the Lek profile method (Fig. 6a). The Lek profile function was used to evaluate the effects of predictors by plotting the model predictions across the range of values for each variable, with other explanatory variables held constant, stratified by natural groupings defined by the data. The number of groups was established as 3, based on the results of the Gaussian finite mixture model.

Fig. 3.

Artificial neural network structure in the primary analysis (a) and in the final analysis (b). Spip – standardized pipeline size, srr – standardized mean rate of return 120 before the event, sz – standardized Altman z-score, sx4 – standardized X4 (the market value of equity / book value of total liabilities), prr – binary outcome variable (1 if positive mean rate of return after the event exists and 0 otherwise)

Fig. 4.

Variable importance evaluation with the Olden function in the primary analysis (a) and in the final analysis (b). Spip – standardized pipeline size, srr – standardized mean rate of return 120 before the event, sz – standardized Altman z-score, sx4 – standardized X4 (the market value of equity / book value of total liabilities)

Fig. 5.

Neural interpretation diagram in the primary analysis (a) and in the final analysis (b). Labels outside of the nodes represent variable names and labels within the nodes indicate the layer and node (I: input, H: hidden, O: output, B: bias). Spip – standardized pipeline size, srr – standardized mean rate of return 120 before the event, sz – standardized Altman z-score, sx4 – standardized X4 (the market value of equity / book value of total liabilities), prr – binary outcome variable (1 if positive mean rate of return after the event exists and 0 otherwise)

Fig. 6.

Lek profile method assessing the effects of independent variables in the primary analysis (a) and in the final analysis (b). Spip – standardized pipeline size, srr – standardized mean rate of return 120 before the event, sz – standardized Altman z-score, sx4 – standardized X4 (the market value of equity / book value of total liabilities), prr – binary outcome variable (1 if positive mean rate of return after the event exists and 0 otherwise)

The Lek profile in the best fitting ANN showed that a greater rate of return before the DDS was more indicative of the negative rate of return after the DDS, while a higher pipeline size seemed to be associated with the mean positive rate of return after the DDS. The z-score had an uncertain impact. To improve the model, the Altman z-score estimate and its components were reanalyzed. The Spearman correlation (see Supplementary material, Appendix 3) showed that only the X4 was correlated with the mean positive rate of return after the DDS (Table 3), and it was, therefore, kept in the final model.

Table 3.

Altman z-score component analysis

	Mean	Median	St. Deviation	Coefficient of variation %	Correlation with positive mean rate of return (after standardization)
X1	0.30	0.28	0.25	84.58	insignificant
X2	−0.65	0.13	2.86	442.13	insignificant
X3	−0.07	0.08	0.35	475.83	insignificant
X4	4.55	3.36	5.46	120.01	Spearman ρ = −0.453 p = 0.020
X5	0.39	0.40	0.21	53.54	insignificant

The final cluster analysis revealed that the EEV (ellipsoidal, equal volume and shape) model with 2 components provided the best fit (BIC = −191.87, df = 25, log.likelihood = −55.21 (Fig. 2b, Table 2). The identified clusters showed that a higher pipeline size, a higher X4 ratio and a lower rate of return before the DDS were associated with a mean positive rate of return 120 days after the DDS. The ANN analysis was repeated (Fig. 3b, 4b, and 5b). The Lek profile method showed (Fig. 6b) that an increase in the pipeline size and a decrease in the rate of return before the DDS led to the mean positive rate of return after the DDS. The finding of ANN that the lower X4 ratio was associated with the mean positive rate of return after the DDS conflicted with the findings in cluster analysis. Thus, additional analysis was performed and revealed (see Supplementary material, Appendix 4), that the standardized X4 was highly variable when resampled (see Supplementary material, Appendix 4, Fig. 4.1) and had a negative correlation with the mean positive rate of return after the DDS. The relationships between the predictor variables were also explored with the variance–covariance matrix (see Supplementary material, Appendix 4, Table 4.2 and Table 4.3) to reinforce the ANN findings. The direction of the association between the predictors and the response variable was identical in the variance–covariance matrix and the ANN. Thus, we conclude that the final ANN appropriately represents the relationship among the variables.

Discussion

In our study, we constructed the ANN showing that a higher pipeline size, a lower rate of return and a lower ratio of the market value of equity and the book value of total liabilities were associated with the mean positive rate of return 120 days after the drug development setback. The Gaussian finite mixture model clustering (an unsupervised learning method) helped cluster the data to the groups of homogeneous observations; however, the clustering provided somewhat conflicting results, when compared with the results of the supervised machine learning algorithm, the ANN. This may have occurred as a result of the Gaussian finite mixture model (GFMM) being restrictive in terms of the assumption about the underlying data distribution [21]. On the other hand, patterns not belonging to any known classes may be wrongly classified into one of the clusters with the GFMM [22]. The variance-covariance matrix (showing the direction of association (covariance) between the variables, clearly reflected and supported the final ANN model) along with the Lek profile method and the Olden function helped to diagnose the developed ANN.

Previous research indicated that stock prices of companies with positive clinical trial (CT) results tend to increase, whereas stock prices of companies with negative CT results tend to decrease. However, no impact of FDA decisions on the stock price was identified [4]. In contrast, we show that the drug development setbacks lead to negative mean rates of return 120 days after the DDS in many cases, i.e., EMA decisions have an impact on the stock price of pharmaceutical companies. This is not surprising, as EMA opinion reflects the evidence of the benefit/risk ratio of a pharmaceutical product [23].

Previous literature reveals different conclusions about the impact of the financial situation of the company on its stock price [24, 25]. We show that the Z score confuses the results and only the X4 ratio (market value of equity/book value of total liabilities [26]) was included in the final ANN model. The lower market value of equity to total liabilities (a leverage variable, reflecting the relative amount of debt and other obligations of the firm) has been associated with a default risk [27]. Higher leverage is negatively associated with stock returns [24] and this is explained by the debt overhang theory of Myers [25, 28]. Our findings seem to reflect the optimal capital structure hypothesis. The optimal amount of debt may improve the company’s profitability [29].

It should be kept in mind that attempts to forecast the stock price may have inherent shortcomings. The efficient market hypothesis (EMH) states that the price is an unbiased estimate of the true value of the security and that a price change occurs due to random oscillation and is unpredictable [30]. At the same time, in an ideally efficient market, the current price is the best estimate of the price that can occur in the future, with the prices following martingales (it is the mathematical description of a fair game: the expected net gain or loss from further play, independent of the history, is 0) [30].

However, the authors of this research exhibit a different view than the followers of EMH and believe that an agnostic stance towards the predictability of stock price movements may not be the best approach and data related with the activity of the pharmaceutical companies should be considered. There may also be an issue of insider trading and an increasing influence of hedge funds on the pharmaceutical stock prices nowadays [31]. We also acknowledge that psychological and behavioral elements may play a role in stock-price determination, but these aspects are left outside the scope of this research [32].

Conclusion

The research reveals that, in general, the setbacks in drug development (e.g., failure of phase III clinical trial, failure to obtain a marketing authorization) have a negative impact on the company’s stock price. However, the stock price of companies with a higher pipeline size and a lower rate of return before the DDS, as well as the lower ratio of the market value of equity and the book value of total liabilities, is less vulnerable by the DDS. These results let investors minimize investment risk.

Authors’ contributions

conceptualization, S.A., L.M., M.V. and E.S.; methodology, S.A., M.V. and A.S.; software, S.A., M.V.; validation, S.A. and A.S.; formal analysis, L.M. and E.S.; investigation, S.S. and A.S.; resources, M.V., S.A.; preparation of paper, M.V., E.S.; paper review and editing, A.S.; visualization, A.S.; supervision, S.A.

Compliance with ethical standards

Conflict of interest

The authors declare that they have no conflict of interest.