Coordination of gene expression noise with cell size: analytical results for agent-based models of growing cell populations

Abstract

The chemical master equation and the Gillespie algorithm are widely used to model the reaction kinetics inside living cells. It is thereby assumed that cell growth and division can be modelled through effective dilution reactions and extrinsic noise sources. We here re-examine these paradigms through developing an analytical agent-based framework of growing and dividing cells accompanied by an exact simulation algorithm, which allows us to quantify the dynamics of virtually any intracellular reaction network affected by stochastic cell size control and division noise. We find that the solution of the chemical master equation—including static extrinsic noise—exactly agrees with the agent-based formulation when the network under study exhibits stochastic concentration homeostasis, a novel condition that generalizes concentration homeostasis in deterministic systems to higher order moments and distributions. We illustrate stochastic concentration homeostasis for a range of common gene expression networks. When this condition is not met, we demonstrate by extending the linear noise approximation to agent-based models that the dependence of gene expression noise on cell size can qualitatively deviate from the chemical master equation. Surprisingly, the total noise of the agent-based approach can still be well approximated by extrinsic noise models.

1. Introduction

Cells must continuously synthesize molecules to grow and divide. At a single-cell level, gene expression and cell size are coordinated but heterogeneous which can drive phenotypic variability and decision making in cell populations [1–5]. The interplay between these sources of cell-to-cell variability is not well understood since they have traditionally been studied separately. A general stochastic theory integrating size-dependent biochemical reactions with the dynamics of growing and dividing cells is hence still missing.

Many models of noisy gene expression and its regulation are based on the chemical master equation that describes the stochastic dynamics of biochemical reactions in a fixed reaction volume [6–8]. The small scale of compartmental sizes of cells implies that a small number of molecules is present at any time leading to large variability of reaction rates from cell to cell, commonly referred to as gene expression noise [9–11]. Another factor contributing to gene expression noise is that cells are continuously growing and dividing causing molecule numbers to (approximately) double over the course of a growth-division cycle. A common approach to account for cell growth is to include extra degradation reactions that describe dilution of gene expression levels due to cell growth [9–13] akin to what is done in deterministic rate equation models [14,15]. We will refer to this approach as the effective dilution model (EDM, figure 1a). However, little is known of how well this approach represents the dependence of gene expression noise on cell size observed in a growing population.

Figure 1.

Modelling approaches for cell size dependence of gene expression. (a) The effective dilution model describes cells at constant size with intracellular reactions coupled to effective dilution reactions. (b) The extrinsic noise model incorporates static cell size variability as a source of extrinsic noise coupled with effective dilution models. (c) The agent-based approach models intracellular reactions occurring across a growing and dividing cell population without the need for effective dilution reactions.

Cells achieve concentration homeostasis through coupling reaction rates to cell size via highly abundant upstream factors like cell cycle regulators, polymerases or ribosomes that approximately double over the division cycle [3,16,17]. Cell size fluctuates in single cells, however, providing a source of extrinsic noise in reaction rates that can be identified via noise decompositions [18,19]. A few studies combined EDMs with static cell size variations as an explanatory source of extrinsic noise [20–22]. In brief, the total noise in these models amounts to intrinsic fluctuations due to gene expression and dilution, and extrinsic variation across cell sizes in the population. We refer to this class of models as extrinsic noise models (ENMs, figure 1b). Yet it remains unclear how reliably these effective models describe cells that continuously synthesize molecules, grow and divide.

An increasing number of studies are investing efforts towards quantifying the dependence of gene expression noise on cell cycle progression and growth, either experimentally via ergodic principles or pseudo-time [23,24] and time-lapse imaging [22,25,26] or theoretically through noise decomposition [27–29], master equations including cell cycle dynamics [4,17,30–35] and agent-based approaches including age-structure of growing populations [35–40]. The essence of agent-based models (ABMs) is that each cell in a population is represented by an agent whose physiological state is tracked along with their molecular reaction networks. In principle, these models are able to predict gene expression distributions of cells progressing through well-defined cell cycle states as measured by time-lapse microscopy and snapshots of heterogeneous populations. The unprecedented detail of these models must cast doubt on the predictions of master equation models (EDMs and ENMs) in which growth and division are modelled by effective dilution reactions. Yet it is presently unclear why these effective models have fared reasonably well in predicting gene expression noise reported by single-cell experiments [10,17,41].

Nevertheless, most ABMs still ignore cell size, a major physiological factor affecting both intracellular reactions and cell division dynamics alike. Since cell size varies at least twofold as required by size homeostasis in a growing population, and it scales some reaction rates as required by concentration homeostasis, it is expected that cell size must significantly contribute to gene expression variation across a population. In this article, we bridge the gap between the chemical master equation and agent-based approaches by integrating cell size dynamics with the stochastic kinetics of molecular reaction networks.

The outline of the paper is as follows. First, we explain the analytical framework for EDMs, ENMs and ABMs (§2). Then we introduce the concept of stochastic concentration homeostasis (SCH), a rigorous condition under which the chemical master equations of the EDM and ENM agree exactly with the ABM (§3.1). This new condition is met by some but not all common models of gene expression. We show that when these conditions are not met, the effective models agree with the ABM only on average (§3.2). To address this problem, we propose a comprehensive theoretical framework extending the linear noise approximation to agent-based dynamics with which we quantify cell size scaling of gene expression in growing cells (§3.3). Our findings indicate that the EDM can qualitatively fail to predict this dependence but our novel approximation method accurately describes gene expression noise in the presence of cell size control variations and division errors. We further show that ENMs present surprisingly accurate approximations for the total noise statistics (§3.4).

2. Methods

We consider a biochemical reaction network of N molecular species S = (S₁, S₂, …, S_N)^T embedded in a cell of size s. The network then has the general form:

$$\sum _{i=1}^N{\nu }_{ir}^{-}{S}_i\stackrel{k_r}{⟶}\sum _{i=1}^N{\nu }_{ir}^{+}{S}_i,r=1,\dots ,R,$$ 2.1

where ${\nu }_r^{\pm }={({\nu }_{1r}^{\pm },{\nu }_{2r}^{\pm },\dots ,{\nu }_{Nr}^{\pm })}^T$ are the stoichiometric coefficients and k_r is the reaction rate constant of the rth reaction. In the following, we outline deterministic, effective dilution and extrinsic noise models and develop a new agent-based approach coupling stochastic reaction dynamics to cell size in growing and dividing cells (figure 1).

2.1. Effective dilution models, extrinsic noise models and the chemical master equation

2.1.1. Rate equation models and concentration homeostasis

Deterministically, the vector of molecular concentrations $\overline{X}={({\overline{X}}_1,{\overline{X}}_2,\dots ,{\overline{X}}_N)}^T$ is governed by rate equation models in balanced growth conditions. The balanced growth condition states that there exists a steady state between reaction and dilution rates

$$\alpha \overline{X}=\sum _{r=1}^R({\nu }_r^{+}-{\nu }_r^{-})f_r(\overline{X}).$$ 2.2

Here, $f_r(\overline{X})$ are macroscopic reaction-rate functions and α is the exponential growth rate of cells determining the dilution rate due to growth. Since these quantities are independent of cell size, the balanced growth condition (2.2) implies concentration homeostasis in rate equation models.

2.1.2. Effective dilution model

The chemical master equation [6] and equivalently the stochastic simulation algorithm [7] are state-of-the-art stochastic models of reaction kinetics inside cells. Although well-established, they are strictly valid only when describing cellular fluctuations at constant cell size s. A straightforward approach to circumvent this limitation is to supplement (2.1) by additional degradation reactions of rate α that model dilution of molecules due to cell growth:

$$S_i\stackrel{\alpha }{⟶}\text{Ø},i=1,2,\dots ,N,$$ 2.3

akin to what is traditionally for reaction rate equations (2.2). The chemical master equation of this EDM then takes the familiar form

$$0=\frac{\mathrm{\partial }{\mathit{\Pi }}_{\mathrm{EDM}}(x|s)}{\mathrm{\partial }t}=[\mathbb{Q}(s)+\alpha \mathbb{D}]{\mathit{\Pi }}_{\mathrm{EDM}}(x|s),$$ 2.4

governing the conditional probability of molecule numbers x = (x₁, x₂, …, x_N)^T of the species S in a cell of size s and where

$${\mathbb{Q}}_{x,x^{\prime }}(s)=\sum _{r=1}^R{w}_r(x^{\prime },s)({\delta }_{x,x^{\prime }+{\nu }_r^{+}-{\nu }_r^{-}}-{\delta }_{x,x^{\prime }}),$$ 2.5

are the elements of the transition matrix of the molecular reactions (2.1) and we included the extra dilution reactions (2.3) via ${\mathbb{D}}_{x,x^{\prime }}(s)=\sum _{i=1}^N{x}_i^{\prime }({\delta }_{x_i,x_i^{\prime }-1}-{\delta }_{x_i,x_i^{\prime }})$. We are here interested in the stationary solution and hence set the time-derivative in equation (2.4) to zero. Such effective models are motivated through the fact [6,42] that when the microscopic propensities w_r are linked to the macroscopic rate functions f_r of the rate equation models via mass-action kinetics

$$w_r(x,s)\approx s{f}_r(X),$$ 2.6

where X = x/s is the concentration, the mean concentrations of EDMs follow the concentrations $\overline{X}$ of the rate equations (2.2) (see §2.1.4).

2.1.3. Extrinsic noise model

A common way to incorporate static size variability between cells in the model is to consider cell size s to be distributed across cells according to a cell size distribution $\mathit{\Pi }(s)$. We will refer to this approach as the ENM, which leads to a mixture model of concentrations X = x/s,

$${\mathit{\Pi }}_{\mathrm{ENM}}(X)={\int }_0^{\mathrm{\infty }}\mathrm{d}s\hspace{0.17em}{\mathit{\Pi }}_{\mathrm{EDM}}(x=Xs|s)\mathit{\Pi }(s),$$ 2.7

and analogous expressions for the molecule number distributions.

2.1.4. Analytical solutions and noise decomposition

The advantage of the EDM and ENM is that its noise statistics can be approximated in closed-form using the linear noise approximation [6,43,44]. In this approximation, the mean concentrations are approximated by the solution $\overline{X}$ of the rate equations (2.2) and the probability distribution ${\mathit{\Pi }}_{\mathrm{EDM}}(x|s)$ is approximated by a Gaussian. In the same limit, the covariance matrix ${\mathit{\Sigma }}_Y$ can be decomposed into intrinsic and extrinsic components, ${\mathit{\Sigma }}_Y^{\mathrm{int}}$ and ${\mathit{\Sigma }}_Y^{\mathrm{ext}}$, using the law of total variance [18,19]

$${\mathit{\Sigma }}_Y=\underset{\mathrm{gene}\hspace{0.17em}\mathrm{expression}}{\underbrace{{\mathit{\Sigma }}_Y^{\mathrm{int}}}}+\underset{\mathrm{cell}\hspace{0.17em}\mathrm{size}\hspace{0.17em}\mathrm{variation}}{\underbrace{{\mathit{\Sigma }}_Y^{\mathrm{ext}}}},$$ 2.8

which correspond to molecular fluctuations due to gene expression and cell size variation, respectively, for Y ∈ {EDM, ENM}. Specifically, for molecule numbers x, we have ${\mathit{\Sigma }}_Y^{\mathrm{int}}=E_{\mathit{\Pi }}[{\mathrm{Cov}}_{{\mathit{\Pi }}_Y}[x|s]]$ and ${\mathit{\Sigma }}_Y^{\mathrm{ext}}={\mathrm{Cov}}_{\mathit{\Pi }}[E_{{\mathit{\Pi }}_Y}[x|s]]$, where $E_{\mathit{\Pi }}$ denotes the expectation value with respect to the distribution $\mathit{\Pi }$, and analogously for concentrations. The intrinsic components ${\mathit{\Sigma }}_Y^{\mathrm{int}}$ satisfy a Lyapunov equation called the linear noise approximation:

$$0={\mathcal{J}}_d{\mathit{\Sigma }}_Y^{\mathrm{int}}+{\mathit{\Sigma }}_Y^{\mathrm{int}}{\mathcal{J}}_d^T+{\mathit{\Omega }}_Y^{-1}{\mathcal{D}}_d(\overline{X}),$$ 2.9

where ${\mathit{\Omega }}_Y$ has to be chosen depending on whether concentration or number covariances are of interest:

2.10

The matrix ${\mathcal{J}}_d$ is the Jacobian of the rate equations (2.2) and ${\mathcal{D}}_d$ denotes the diffusion matrix obeying

$${\mathcal{J}}_d(\overline{X})=\mathcal{J}(\overline{X})-\alpha \underset{\_}{1},{\mathcal{D}}_d(\overline{X})=\mathcal{D}(\overline{X})+\alpha \hspace{0.17em}\mathrm{diag}(\overline{X}),$$ 2.11

where $\mathcal{J}(\overline{X})=\sum _{r=1}^R({\nu }_r^{+}-{\nu }_r^{-}){\mathrm{\nabla }}_{\overline{X}}^T{f}_r(\overline{X})$ and $\mathcal{D}(\overline{X})=\sum _{r=1}^R{f}_r(\overline{X})$ $({\nu }_r^{+}-{\nu }_r^{-}){({\nu }_r^{+}-{\nu }_r^{-})}^T$. The extrinsic components ${\mathit{\Sigma }}_Y^{\mathrm{ext}}$ follow from the dependence of the mean on cell size, which features only in the molecule number variance of the ENM:

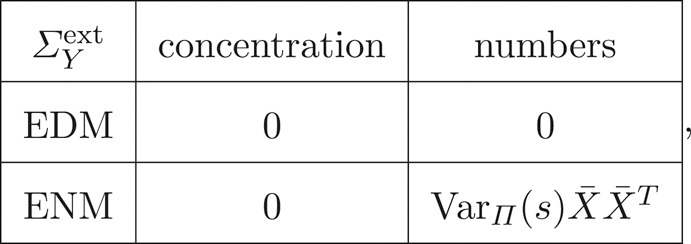2.12

where the last cell follows from ${\mathit{\Sigma }}_{\mathrm{ENM}}^{\mathrm{ext}}={\mathrm{Cov}}_{\mathit{\Pi }}[E_{\mathit{\Pi }}[x|s]]$ with $E_{\mathit{\Pi }}[x|s]=s\overline{X}$.

As a concrete example, we consider transcription of mRNAs with a size-dependent transcription rate that are translated into stable proteins:

$$\text{Ø}\stackrel{k_{0}s}{⟶}M\stackrel{k_{\mathrm{dm}}}{⟶}\text{Ø},M\stackrel{k_{\mathrm{tl}}}{⟶}M+P.$$ 2.13

We then account for dilution through the additional reactions

$$M\stackrel{\alpha }{⟶}\text{Ø},P\stackrel{\alpha }{⟶}\text{Ø}.$$ 2.14

The mean protein concentration is given by $\overline{P}=k_{0}b/\alpha$ and the coefficient of variation predicted by the EDM and ENM follow the familiar expression [10]

$${\mathrm{CV}}_{\mathrm{Y}}^2=\frac{1}{{\mathit{\Omega }}_Y\overline{P}}(1+b\frac{\delta }{1+\delta })+\frac{{\mathit{\Sigma }}_Y^{\mathrm{ext}}}{{\overline{P}}^2},$$ 2.15

where we account for size variability via ${\mathit{\Omega }}_Y$ and ${\mathit{\Sigma }}_Y^{\mathrm{ext}}$ given by equations (2.10) and (2.12), respectively, and the parameters

$$\delta =1+\frac{k_{\mathrm{dm}}}{\alpha }\mathrm{and}b=\frac{k_{\mathrm{tl}}}{k_{\mathrm{dm}}+\alpha },$$ 2.16

correspond to the ratio of mRNA and protein degradation/dilution rates and the translational burst size, respectively. From equations (2.15) with (2.10) and (2.12), it is clear that size variation acts on the intrinsic noise component of molecule concentrations (via $E_{\mathit{\Pi }}[s^{-1}]\approx E_{\mathit{\Pi }}{[s]}^{-1}(1+{\mathrm{CV}}_{\mathit{\Pi }}^2[s])$) but the extrinsic noise component of molecule numbers (via ${\mathit{\Sigma }}_Y^{\mathrm{ext}}$ (2.12)).

2.2. Agent-based modelling

Little is known about the accuracy of EDMs and ENMs in predicting cellular noise in growing populations. In the following, we introduce an agent-based modelling approach that serves as a gold standard to assess the validity of these effective models. The ABM represents cells as agents that progressively synthesize molecules via intracellular reactions (2.1), grow in size and undergo cell division. Every division gives rise to two daughter cells of varying birth sizes, each of which inherits a proportion of molecules from the mother cell via stochastic size-dependent partitioning at division.

The ABM simulation algorithm is given in box 1, which combines the First-Division algorithm, previously introduced for agent-based cell populations [38], with the Extrande method adapted to simulate reaction networks embedded in a growing cell [48]. In the following, we describe the exact analytical framework with which we characterize the snapshot distributions that underlie such a population of agents.

Box 1. First-Division Algorithm for agent-based simulations of size-dependent gene regulatory networks.

Exact simulation algorithm of general stochastic reaction networks within growing cells (agents) undergoing binary cell division according to cell size control rules [45–47]. The algorithm combines the Extrande method [48] for simulating reaction networks embedded in a growing cell and the First-Division algorithm [38] for the population dynamics. The state of each cell is given by birth time t₀, birth size s₀, present cell size s and the vector of molecule numbers x.

2.2.1. Master equation for agent-based populations

We consider the number of cells n(τ, s, x, t) with age τ (time since the last division), cell size s and molecule counts x in a snapshot at time t, which evolves as

$$\begin{array}{cc}\hspace{0.17em}& \underset{\mathrm{growth}}{\underbrace{(\frac{\mathrm{\partial }}{\mathrm{\partial }t}+\frac{\mathrm{\partial }}{\mathrm{\partial }\tau }+\frac{\mathrm{\partial }}{\mathrm{\partial }s}\alpha s+\overline{\gamma }(s,\tau ))}}n(\tau ,s,x,t)=\underset{\mathrm{stochastic}\hspace{0.17em}\mathrm{reactions}}{\underbrace{\mathbb{Q}(s)n(\tau ,s,x,t)}},\\ \hspace{0.17em}\hspace{0.17em}& \underset{\mathrm{no}.\hspace{0.17em}\mathrm{newborn}\hspace{0.17em}\mathrm{cells}}{\underbrace{n(0,s,x,t)}}=2{\int }_0^{\mathrm{\infty }}\mathrm{d}{\tau }^{\prime }{\int }_0^{\mathrm{\infty }}\mathrm{d}{s}^{\prime }\underset{\mathrm{division}\hspace{0.17em}\mathrm{error}}{\underbrace{B(s|s^{\prime })}}\\ \hspace{0.17em}& \times \sum _{x^{\prime }}\underset{\mathrm{partitioning}\hspace{0.17em}\mathrm{of}\hspace{0.17em}\mathrm{molecules}}{\underbrace{B(x|x^{\prime },s/s^{\prime })}}\underset{\mathrm{no}.\hspace{0.17em}\mathrm{dividing}\hspace{0.17em}\mathrm{cells}}{\underbrace{\overline{\gamma }(s^{\prime },{\tau }^{\prime })n({\tau }^{\prime },s^{\prime },x^{\prime },t)}}\end{array}\}$$ 2.17

and describes cell growth, stochastic reaction kinetics and a boundary condition for cell division that ensures that the number of newborn cells is twice the number of dividing cells after partitioning their size and molecular contents. These evolution equations have been derived in [38,39] for age-dependent snapshots but here we extend such ABMs to include also cell size dynamics and size-dependent reaction dynamics. We allow for the following generalizations: (i) size increases exponentially in single cells, (ii) cells divide with rate $\overline{\gamma }(s,\tau )$ that is both size- and age-dependent, (iii) the transition matrix $\mathbb{Q}(s)$ of the molecular reactions depends on cell size s via the propensities (see definition after equation (2.4)), and (iv) the molecular partitioning kernel B(x|x′, s/s′) depends on the inherited size fraction s/s′ of a daughter cell. We now describe in detail how we model the individual noise sources associated with cell size control, division errors, and molecule partitioning.

Cell size control fluctuations. Recent studies [45,49] have shown that the distribution of sizes with which cells divide does not explicitly depend on cell age but on the birth size s₀. Assuming that $\overline{\gamma }(s,\tau )=\alpha s\gamma (s,s^{-\alpha \tau })$, where γ(s, s₀) is the division rate per unit size (see also [50,51]), the division-size distribution is given by

$$\phi (s_d|s_0)=\gamma (s_d,s_0)\hspace{0.17em}{\mathrm{e}}^{-{\int }_{s_0}^{s_d}\mathrm{d}s\gamma (s,s_0)}.$$ 2.18

As a concrete example of (2.18), we consider a model where the division size is linearly related to birth size [46,51,52]

$$s_d=a{s}_0+\mathrm{\Delta }.$$ 2.19

The division rate can be calculated from the distribution $\tilde{\phi }(\mathrm{\Delta })$ of the noise term Δ in (2.19) via $\tilde{\gamma }(\mathrm{\Delta })=\tilde{\phi }(\mathrm{\Delta })/({\int }_{\mathrm{\Delta }}^{\mathrm{\infty }}\mathrm{d}u\tilde{\phi }(u))$ and setting $\gamma (s,s_0)=\tilde{\gamma }(s-a{s}_0)$, which gives the correct division-size distribution $\phi (s_d|s_0)=\tilde{\phi }(s_d-a{s}_0)$ as expected. The model generalizes the sizer (a = 0) to concerted cell size controls such as the adder (a = 1) and timer-like (2 > a > 1) models [45,47,49]. In the following, we will refer to CV_φ[Δ] as the size-control noise.

Division errors. After division, size is partitioned between cells and the birth size of the two daughter cells is obtained from s₀′ = θs_d and s₀″ = (1 − θ)s_d where θ is the inherited size fraction, a random variable between 0 and 1 with distribution $\overline{\pi }(\theta )$ (see box 1). This can be modelled using the division kernel

$$B(s_0|s^{\prime })={\int }_0^1\mathrm{d}\theta \hspace{0.17em}\pi (\theta )\delta (\theta -\frac{s_0}{s^{\prime }}),$$

where $\pi (\theta )=(1/2)\overline{\pi }(\theta )+(1/2)\overline{\pi }(1-\theta )$ including the case of asymmetric division. We will refer to ${\mathrm{CV}}_{\pi }[\theta ]$ as the division error about the centre $E_{\pi }[\theta ]=1/2$.

Molecule partitioning at cell division. The partitioning kernel B(x|x′, θ) denotes the probability that a cell inherits x molecules from a total of x′ molecules from its mother and this probability depends on the daughter’s inherited size fraction θ. We assume that cells are sufficiently well mixed and each molecule is partitioned independently with probability θ such that the division kernel is binomial

$$B(x|x^{\prime },\theta )=\prod _{i=1}^N\left(\begin{array}{r}{x}_i^{\mathrm{\prime }}\\ x_i\end{array}\right){\theta }^{x_i}{(1-\theta )}^{x_i^{\prime }-x_i}.$$ 2.20

To make analytical progress, we assume that the population establishes a long-term stationary distribution $\mathit{\Pi }(s,s_0,x)$ characterizing the fraction of cells with molecule numbers x, cell size s and birth size s₀ that is invariant in time. To this end, we let $n(\tau ,s,x,t)\propto {\mathrm{e}}^{\alpha t}\mathit{\Pi }(s,\tau ,x)$ and change variables from cell age τ to birth size s₀ such that $\mathit{\Pi }(s,s_0,x)={(\alpha s)}^{-1}\mathit{\Pi }(s,\tau =\ln (s/s_0)/\alpha ,x)$. We find that this transformation reduces the PDE (2.17) to an integro-ODE:

$$(\alpha +\frac{\mathrm{\partial }}{\mathrm{\partial }s}\alpha s+\alpha s\gamma (s,s_0))\mathit{\Pi }(s,s_0,x)=\mathbb{Q}(s)\mathit{\Pi }(s,s_0,x)$$ 2.21a

and

$$\begin{array}{rl}\hspace{0.17em}& s_0\mathit{\Pi }(s_0,s_0,x)\\ \hspace{0.17em}& =2\sum _{x^{\prime }}{\int }_0^{\mathrm{\infty }}\mathrm{d}{s}^{\prime }{\int }_0^{s^{\prime }}\mathrm{d}{s}_0^{\prime }\hspace{0.17em}B(x|x^{\prime },s_0/s^{\prime })B(s_0|s^{\prime })s^{\prime }\gamma (s^{\prime },s_0^{\prime })\mathit{\Pi }(s^{\prime },s_0^{\prime },x^{\prime }).\end{array}$$ 2.21b

We finally characterize the marginal cell size distribution $\mathit{\Pi }(s,s_0)$ and the conditional molecule number distribution $\mathit{\Pi }(x|s,s_0)$ via Bayes’ formula

$$\mathit{\Pi }(s,s_0)=\sum _x\mathit{\Pi }(s,s_0,x),\mathit{\Pi }(x|s,s_0)=\frac{\mathit{\Pi }(s,s_0,x)}{\mathit{\Pi }(s,s_0)},$$ 2.22

which together provide the full information about the population snapshot.

2.2.2. Cell size distribution

The evolution of the size distribution $\mathit{\Pi }(s,s_0)$ is obtained by summing equations (2.21) over all possible x, which yields:

$$(\alpha +\frac{\mathrm{\partial }}{\mathrm{\partial }s}\alpha s+\alpha s\gamma (s,s_0))\mathit{\Pi }(s,s_0)=0$$ 2.23a

and

$$s_0\mathit{\Pi }(s_0,s_0)=2{\int }_0^{\mathrm{\infty }}\mathrm{d}{s}^{\prime }{\int }_0^{s^{\prime }}\mathrm{d}{s}_0^{\prime }\hspace{0.17em}B(s_0|s^{\prime })s^{\prime }\gamma (s^{\prime },s_0^{\prime })\mathit{\Pi }(s^{\prime },s_0^{\prime }).$$ 2.23b

Equations (2.23) can be solved analytically

$$\mathit{\Pi }(s,s_0)=\frac{2}{Z}{\psi }_{\mathrm{bw}}(s_0)\mathit{\Phi }(s|s_0)\frac{1}{s^2},$$ 2.24

where ψ_bw(s₀) is the birth size distribution in a backward lineage (see [50] for details), $\mathit{\Phi }(s|s_0)=\exp (-{\int }_{s_0}^s\mathrm{d}{s}^{\prime }\gamma (s^{\prime },s_0))$ is the probability that a cell born at size s₀ has not divided before reaching size s, and $Z=E_{{\psi }_{\mathrm{bw}}}[s_0^{-1}]$ is a normalizing constant.

2.2.3. Molecule number distributions for cells of a certain size

The conditional molecule number distribution $\mathit{\Pi }(x|s,s_0)$ gives the probability to find the molecule numbers x in a cell of size s that was born at size s₀ and satisfies

$$\alpha s\frac{\mathrm{\partial }}{\mathrm{\partial }s}\mathit{\Pi }(x|s,s_0)=\mathbb{Q}(s)\mathit{\Pi }(x|s,s_0)$$ 2.25a

and

$$\mathit{\Pi }(x|s_0,s_0)=\sum _{x^{\prime }}{\int }_0^{\mathrm{\infty }}\mathrm{d}{s}^{\prime }{\int }_0^{s^{\prime }}\mathrm{d}{s}_0^{\prime }\hspace{0.17em}B(x|x^{\prime },\frac{s_0}{s^{\prime }})\rho (s^{\prime },s_0^{\prime }|s_0)\mathit{\Pi }(x^{\prime }|s^{\prime },s_0^{\prime }).$$ 2.25b

Equations (2.25) follow directly from substituting equation (2.22) into (2.21) and using (2.18) and (2.23). The solution of these equations depends implicitly on the ancestral cell size distribution ρ,

$$\rho (s^{\prime },s_0^{\prime }|s_0)=\frac{1}{{\psi }_{\mathrm{bw}}(s_0)}\frac{s_0}{s^{\prime }}\hspace{0.17em}B(s_0|s^{\prime })\phi (s^{\prime }|s_0^{\prime }){\psi }_{\mathrm{bw}}(s_0^{\prime }),$$ 2.25c

that gives the probability of a cell born at size s₀ having an ancestor with division size s′ and birth size s₀′. The main difference between the molecule number distributions of the ABM and the EDM/ENM is the boundary condition at cell division, which as we shall see can have a significant effect on the reaction dynamics.

3. Results

We here introduce the concept of SCH as a generalization of concentration homeostasis in deterministic systems (see §2.1.1) to higher moments and distributions in stochastic reaction networks. SCH is a homeostatic condition for the distribution p(x|s) of a size-dependent stochastic process to be expressed as a mixture of Poisson random variables drawn from an underlying continuous stochastic concentration vector κ = (κ₁, κ₂, …, κ_N)^T that is statistically independent of s:

$$p(x|s)={\int }_{\mathcal{K}}\mathrm{d}\kappa \hspace{0.17em}\chi (\kappa )\prod _{i=1}^N\frac{{({\kappa }_{i}s)}^{x_i}}{x_i!}\hspace{0.17em}{\mathrm{e}}^{-s{\kappa }_i}.$$ 3.1

The fact that κ and its density χ(κ) are independent of s ensures concentration homeostasis in the stochastic sense.

3.1. The effective dilution model is valid for reaction networks with stochastic concentration homeostasis

Theorem A.2 (appendix A) is a central result of our analysis and it states that if the EDM (2.4) satisfies SCH, i.e. equation (3.1) holds for ${\mathit{\Pi }}_{\mathrm{EDM}}(x|s)$, then its stationary solution is also a solution of the ABM (2.25):

$$\mathit{\Pi }(x|s,s_0)={\mathit{\Pi }}_{\mathrm{EDM}}(x|s),$$ 3.2

and the solution is independent of the birth size s₀. Equivalently (appendix A), we can say that the EDM/ABM satisfies SCH if the factorial-moment generating function is of the form

$$G_{\mathrm{EDM}}(z|s)=\sum _x\prod _{i=1}^N{z}_i^{x_i}{\mathit{\Pi }}_{\mathrm{EDM}}(x|s)=F(s(z-1)),$$ 3.3

where $F(t)=E_{\chi }[{\mathrm{e}}^{\sum _{i=1}^N{t}_i{\kappa }_i}]$, the moment-generating function of the concentration vector, is cell-size (s) independent. An interesting observation is that SCH implies that the mean numbers and coefficients of variation for cells of the same size s are given by

$$E_{\mathit{\Pi }}[x|s]=s{E}_{\chi }[\kappa ],{\mathrm{CV}}_{\mathit{\Pi }}^2(x|s)=\frac{1}{s{E}_{\chi }[\kappa ]}+{\mathrm{CV}}_{\chi }^2(\kappa ).$$ 3.4

Since κ is independent of s, SCH implies homeostasis of the mean concentrations in (3.4) but concentration homeostasis on average does not necessarily imply SCH. The coefficients of variation coincide both for concentrations and molecule numbers and have size-dependent and size-independent components. In the following, we provide examples of reaction networks for which SCH holds for all values of the rate constants and demonstrate the validity of the EDM by comparing its distribution solutions to ABM simulations.

It can be seen from (3.1) and (3.4) that when the EDM’s stationary distribution is Poissonian with deterministic concentration vector κ, this distribution satisfies SCH and hence is also a solution of the ABM. More generally, SCH can be checked without solving for G_EDM(z|s) (or ${\mathit{\Pi }}_{\mathrm{EDM}}(x|s)$). Assuming mass-action kinetics (2.6), for example, a sufficient condition for SCH is that the network consists entirely of mono-molecular reactions (see appendix A) of the form:

$$\begin{array}{cc}\hspace{0.17em}& \text{Ø}\stackrel{D(t)s}{⟶}{S}_1,\mathrm{or}\hspace{0.17em}\text{Ø}\stackrel{D(t)}{⟶}{m}_s\times S_1,\\ \mathrm{or}& \text{Ø}\stackrel{s}{⟶}{S}_1,\mathrm{or}\hspace{0.17em}{S}_1\to \hspace{0.17em}\text{Ø},\mathrm{or}\hspace{0.17em}{S}_1\to \hspace{0.17em}{S}_2,\end{array}\}$$ 3.5

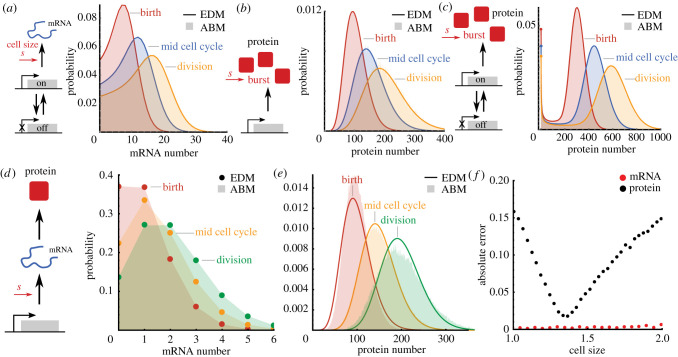
where S₁ and S₂ denote any pair of species that are partitioned at cell division and D(t) is a exogenous stationary stochastic process modelling a genetic state which is copied but not partitioned at cell division and does not scale with cell size. The propensities of zero-order reactions in SCH networks must either be proportional to cell size or include size-dependent random bursts m_s whose burst distribution satisfies SCH itself. We illustrate the predictive power of this result by demonstrating SCH for common gene expression models involving reactions of the form (3.5) and show that the analytical solution of the chemical master equations agrees exactly with the ABMs (figure 2a–c).

Figure 2.

Distributions of CME and agent-based models agree for reaction networks with stochastic concentration homeostasis. (a–c) The EDM (solid lines, analytical solution [53,54]) agrees with agent-based simulations (shaded areas) for a range of gene expression models. Panels show (a) bursty transcription [53] with transcription rate proportional to cell size, (b) bursty translation [54], and (c) bursty transcription and translation [54] with geometrically distributed bursts m_s whose average is proportional to cell size s (see main text for details). (d) mRNA distributions simulated using the ABM (shaded areas) are shown for cells of sizes s = s₀ (red), s = 1.5s₀ (orange) and s = 2s₀ (green), which agree with the effective dilution model (dots, Poisson distribution). (e) Simulated protein distributions (shaded areas) disagree with the effective dilution model (solid lines, solution in [55]). (f) Absolute error (ℓ₁) of the effective dilution model as a function of cell size for mRNA (teal) and protein (red) distributions. ABM simulations were obtained using the First-Division Algorithm (box 1) assuming an adder model (a = 1) and parameters k₀ = 10, k_dm = 9, k_tl = 100, α = 1. Cell cycle noise assumes gamma distribution $\tilde{\phi }(\mathrm{\Delta })$ with unit mean and CV_φ[Δ] = 0.1, while division noise assumes symmetric beta distribution with ${\mathrm{CV}}_{\pi }[\theta ]=0.01$.

mRNA expression involving a two-state promoter [53] (figure 2a),

$$D_{\mathrm{off}}\underset{k_{\mathrm{off}}}{\overset{k_{\mathrm{on}}}{\rightleftharpoons }}{D}_{\mathrm{on}}\stackrel{s{k}_0}{⟶}{D}_{\mathrm{on}}+M,M\stackrel{k_{\mathrm{dm}}}{⟶}\text{Ø}$$

satisfies SCH for all parameter values since the network is of the form (3.5) whenever the transcription rate is proportional to cell size. The stochastic concentration variable is distributed as κ ∼ (k₀/(k_dm + α))Beta(k_on/(k_dm + α), k_off/(k_dm + α)).

Bursty protein expression (figure 2b) of a stable (non-degrading) protein arising from a two-stage model of gene expression can be modelled using stochastic bursts:

$$\text{Ø}\stackrel{k_0}{⟶}{m}_s\times P.$$

According to (3.5) the model satisfies SCH for all parameter values when the burst distribution obeys SCH. This is the case for geometrically distributed bursts m_s whose mean is proportional to cell size, E[m_s|s] = bs. It can be shown that the stochastic concentration variable follows κ ∼ Gamma(k₀/α, b).

Similarly, bursty protein expression from a two-state promoter arising from a three-stage gene expression model [54,56] (figure 2c),

$$D_{\mathrm{off}}\underset{k_{\mathrm{off}}}{\overset{k_{\mathrm{on}}}{\rightleftharpoons }}{D}_{\mathrm{on}}\stackrel{k_0}{⟶}{D}_{\mathrm{on}}+m_s\times P,$$

also satisfies SCH for geometrically distributed bursts (with mean bs) but the concentration variable is doubly stochastic¹ κ ∼ Gamma((a₋/α), br), r ∼ Beta(a₋/α, (a₊ + k_on + k_off)/α) where $a_{\pm }=k_{\mathrm{off}}+k_{\mathrm{on}}+k_0\pm \sqrt{(k_{\mathrm{off}}+k_{\mathrm{on}}+k_0){\hspace{0.17em}}^2-4k_0{k}_{\mathrm{on}}}$. We observe excellent numerical agreement between the ABM simulations and analytical EDM solutions in all these cases validating our theoretical predictions (figure 2a–c).

A complex example of the reactions (3.5) that obeys SCH for all parameter values but yet defies analytical solution is

$$\begin{array}{rl}\hspace{0.17em}& D_i\stackrel{g_{ij}}{⟶}{D}_{\hspace{0.17em}j}\mathrm{\forall }\hspace{0.17em}i,j=1,\dots ,N_D\\ \hspace{0.17em}& D_i\stackrel{s{t}_i}{⟶}{D}_i+M_1,\mathrm{\forall }\hspace{0.17em}i=1,\dots ,N_D\\ \hspace{0.17em}& M_1\stackrel{k_1}{⟶}{M}_2\stackrel{k_2}{⟶}\dots \stackrel{k_S}{⟶}{M}_S,\\ \hspace{0.17em}& M_i\stackrel{{\delta }_i}{⟶}\text{Ø}\mathrm{\forall }\hspace{0.17em}i=1,\dots ,N_M\end{array}$$

where the exogenous genetic states D_i undergo switching with rates g_ij and are copied but not partitioned at cell division, transcription rates s t_i are assumed to be proportional to cell size s, and processing of transcripts M_i follows a multi-step process with rates k_i and degradation with rates δ_i. For example, it can be checked that for N_M = 1 we recover the 2^m-multistate model [57] as a special case whose EDM has a factorial-moment generating function (compare eqn (7) in [57] with (3.3)) satisfies SCH precisely when the transcription rates are proportional to cell size.

On the other hand, discrepancies between the EDM and ABM solutions will be apparent when reactions do not obey SCH. To illustrate this point, we return to the gene expression model with transcriptional size-scaling and explicit protein translation reaction (2.13). Note that in the EDM extra reactions are being added for the dilution of mRNAs and proteins, while for the ABM proteins are diluted through growth and divisions. Using our condition (3.3), it is straight-forward to verify that the Poissonian mRNA distributions of the EDM coincide exactly with the distributions of the ABM (figure 2d). However, this condition is not met for the protein distribution since the translation reaction is not a monomolecular reaction of the form (3.5). To demonstrate the breakdown of the EDM, we compare the analytical steady-state distributions obtained by Bokes et al. [55] against ABM simulations at various cell sizes (figure 2e). We observe that the error of the EDM (as quantified by the ℓ₁-distance of the two distributions, figure 2f) is pronounced both for newborn and dividing cells. The remainder of this article is dedicated to investigate the sources and consequences of these discrepancies.

3.2. The EDM approximates the mean concentrations of ABMs lacking SCH

SCH provides a general criterion with which to probe the validity of the EDM probability distributions. In practice, however, approximate agreement of the first few moments, e.g. mean and variances, often suffices. Here, we establish that under the mass-action scaling assumption (2.6) the mean concentrations of the ABM and EDM agree approximately, and they satisfy concentration homeostasis on average. This can be seen by multiplying equation (2.25) by x and averaging, which yields ODEs for the mean numbers:

$$\alpha s\frac{\mathrm{\partial }}{\mathrm{\partial }s}{E}_{\mathit{\Pi }}[x|s,s_0]=\sum _{r=1}^R({\nu }_r^{+}-{\nu }_r^{-})E_{\mathit{\Pi }}[w_r(x)|s,s_0],$$ 3.6a

and the boundary conditions

$$E_{\mathit{\Pi }}[x|s_0,s_0]=E_{\rho }[\frac{s_0}{s^{\prime }}{E}_{\mathit{\Pi }}[x|s^{\prime },s_0^{\prime }]|s_0].$$ 3.6b

Unfortunately, equations (3.6) are not necessarily closed since the equation for the mean may involve higher order moments when w_r(x) depends nonlinearly on x and we need to resort to approximations. Analogously to the linear noise approximation, we set $E[x|s,s_0]=s\overline{X}$ and $E_{\mathit{\Pi }}[w_r(x)|s,s_0]\approx s{f}_r(\overline{X})$ and insert the resulting expression into equations (3.6). It follows that $\overline{X}$ is independent of size and satisfies the rate equations (2.2). We conclude that, for mass-action kinetics, the EDM agrees exactly with the ABM on average for networks with linear propensities and approximately for large cell size for nonlinear reaction networks.

3.3. Scaling of fluctuations with size in individual cells manifests the breakdown of the EDM lacking SCH

Next we investigate the scaling of fluctuations with cell size. Under the linear noise approximation the covariance matrix $\mathit{\Sigma }(s,s_0)={\mathrm{Cov}}_{\mathit{\Pi }}[x|s,s_0]$ evolves according to

$$\alpha s\frac{\mathrm{\partial }}{\mathrm{\partial }s}\mathit{\Sigma }(s,s_0)=\mathcal{J}\mathit{\Sigma }(s,s_0)+\mathit{\Sigma }(s,s_0){\mathcal{J}}^T+s\mathcal{D}(\overline{X}),$$ 3.7a

where $\mathcal{J}(\overline{X})$ and $\mathcal{D}(\overline{X})$ are the Jacobian and diffusion matrices defined after equation (2.11). To make analytical progress, we assume for now that cell division is deterministic (${\mathrm{CV}}_{\phi }[\mathrm{\Delta }]={\mathrm{CV}}_{\pi }[\theta ]=0$), which implies the following boundary condition

$$4\mathit{\Sigma }(s_0,s_0)=2s_0\mathrm{diag}(\overline{X})+\mathit{\Sigma }(2s_0,s_0).$$ 3.7b

The first term is due to binomial partitioning of molecules and the second stems from gene expression noise at division. It is implicit in the deterministic division assumption (${\mathrm{CV}}_{\phi }[\mathrm{\Delta }]={\mathrm{CV}}_{\pi }[\theta ]=0$) that the birth size s₀ across cells is fixed and that the size distribution in equation (2.24) reduces to

$$\mathit{\Pi }(s)=\mathit{\Pi }(s|s_0)=\frac{2s_0}{s^2}$$ 3.8

for s₀ ≤ s ≤ 2s₀ and zero otherwise, in agreement with previous results [58,59]. Similarly, the ancestral distribution (2.25c) reduces to ρ(s′, s₀′|s₀) = δ(s′ − 2s₀)δ(s₀′ − s₀).

Equations (3.7) can be solved in closed form using the eigendecomposition of the Jacobian $\mathcal{J}$. The solution to (3.7a) that respects the boundary condition (3.7b) is (appendix D)

$$\begin{array}{rl}\hspace{0.17em}& \mathit{\Sigma }(s,s_0)=\sum _{ij}\frac{s\hspace{0.17em}{\hat{u}}_i{\hat{u}}_{\hspace{0.17em}j}^{†}}{(\alpha -{\lambda }_i-{\lambda }_{\hspace{0.17em}j}^{\ast })}\\ \hspace{0.17em}& \times [{\tilde{\mathcal{D}}}_{ij}+\frac{{\tilde{\mathcal{D}}}_{ij}+{\tilde{X}}_{ij}({\lambda }_i+{\lambda }_{\hspace{0.17em}j}^{\ast }-\alpha )}{2^{(({\lambda }_i+{\lambda }_{\hspace{0.17em}j}^{\ast })/\alpha )-1}-2}{\left(\frac{s_0}{s}\right)}^{1-({\lambda }_i+{\lambda }_{\hspace{0.17em}j}^{\ast })/\alpha }],\end{array}$$ 3.9

where ^† denotes the conjugate-transpose and we defined the matrices $\tilde{\mathcal{D}}=U^{-1}\mathcal{D}{U}^{-†}$, $\tilde{X}=U^{-1}\mathrm{diag}(\overline{X})U^{-†}$ and $U=({\hat{u}}_1,\dots ,{\hat{u}}_N)$ whose columns are the eigenvectors of $\mathcal{J}$ such that $U^{-1}\mathcal{J}U=\mathrm{diag}(\lambda )$.

We demonstrate the implications of this result using the gene expression example with transcriptional size-scaling and explicit translation reaction (2.13). The mean of mRNA numbers m and protein numbers p are

$$E_{\mathit{\Pi }}[m|s]=s\frac{k_0}{\alpha \delta },E_{\mathit{\Pi }}[p|s]=s\frac{b{k}_0}{\alpha },$$ 3.10

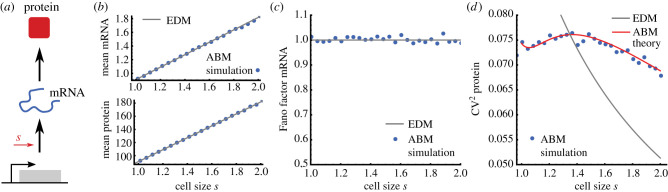
where the constants are defined in equation (2.16). These expressions hold both for the EDM and the ABM, and they exhibit concentration homeostasis on average as shown in the previous section. The exact agreement between EDM and ABM is also confirmed by ABM simulations (figure 3b).

Figure 3.

Comparing the statistics of the effective dilution and agent-based models. (a) Simple model of mRNA transcription and protein translation transcriptional size-scaling (2.13). (b) Mean mRNA (top) and protein levels (bottom) agree with the EDM (solid grey lines) and ABM simulations (blue dots). (c) mRNA statistics display unit Fano factor indicating Poisson statistics in agreement with EDM. (d) ABM simulations (dots, box 1) display non-monotonic cell size scaling of protein noise, which are predicted by the agent-based theory (solid red) but not by the EDM (solid grey). Parameters are k₀ = 10, k_dm = 10, k_tl = 100, α = 1. Cell size control parameters are as in figure 2.

Using equation (3.7), we find that the cell size-dependent fluctuations satisfy

$$\begin{array}{cc}\hspace{0.17em}& {\mathrm{Var}}_{\mathit{\Pi }}[m|s,s_0]=E_{\mathit{\Pi }}[m|s],\\ \hspace{0.17em}& {\mathrm{Cov}}_{\mathit{\Pi }}[m,p|s,s_0]=\frac{sb{k}_0}{\alpha \delta }(1+{\left(\frac{s_0}{s}\right)}^{\delta }\frac{2^{\delta }}{1-2^{\delta +1}}),\\ \hspace{0.17em}& {\mathrm{Var}}_{\mathit{\Pi }}[p|s,s_0]=E_{\mathit{\Pi }}[p|s]\\ \hspace{0.17em}& \times (1+2b-\frac{s_0}{s}\frac{4b\delta }{3(\delta -1)}+{\left(\frac{s_0}{s}\right)}^{\delta }\frac{b}{\delta -1}\frac{2^{\delta +1}}{(2^{\delta +1}-1)}).\end{array}\}$$ 3.11

We note that the mRNA variance of the ABM agrees precisely with the EDM (figure 3c). The agreement is a direct consequence of SCH exhibited by the mRNA transcription and degradation reactions (cf. (3.5)). However, the expressions for the predicted mRNA–protein covariance and protein variance disagree with their EDM counterpart since the reactions involving the protein violate SCH. To explore this dependence, we compare the corresponding coefficients of variation of both models (figure 3d). The EDM overestimates cell-to-cell variation of small cells but underestimates it for large cells. Moreover, the EDM’s coefficient of variation decreases monotonically with cell size, but this is not the case for the ABM.

Strikingly, the coefficient of variation peaks as cells progress through the cell cycle (figure 3d, solid red line), which is in excellent agreement with the ABM simulations (blue dots) but is not seen in the EDM (solid grey). This can be seen directly from equation (3.11) for which protein fluctuations can be approximated in the limit of fast mRNA degradation (δ ≫ 1) as

$${\mathrm{CV}}_{\mathrm{ABM}}^2[p|s,s_0]\approx \frac{1}{E_{\mathit{\Pi }}[p|s]}(1+b(2-\frac{s_0}{s}\frac{4}{3})),$$ 3.12

which has a maximum at a cell size of s = s₀ 8b/(3(2b + 1)) as confirmed by agent-based simulations (figure 3d). Depending on the burst size b, the peak shifts from s = s₀ for b = 3/2 to s = 4/3 s₀ for b ≫ 1. The qualitative difference between the scalings of gene expression noise with cell size of EDMs and ABMs manifests the breakdown of the EDM, which is observed both for concentrations and molecule numbers since their coefficients of variation coincide when considering cells of the same size.

3.3.1. Effect of cell size control on gene expression dynamics

Next, we ask how fluctuations in the cell size control affect gene expression noise. It may be intuitively expected that noise in cell size control and division errors cause variable birth sizes, variable division times and hence noisy expression levels. mRNA fluctuations in the gene expression model with transcriptional size-scaling (2.13) obey SCH and hence are unaffected by these noise sources. The effect on protein noise remains yet to be elucidated.

To this end, we assume small birth-size variations and approximate the actual birth size with an averaged estimate $E_{\mathit{\Pi }}[s_0|s]$ of the retrospective birth size for a cell of size s. The covariance matrix (or any other moment) can then be approximated as

$$\mathit{\Sigma }(s)=E_{\mathit{\Pi }}[\mathit{\Sigma }(s,s_0)|s]\approx \mathit{\Sigma }(s,E_{\mathit{\Pi }}[s_0|s])).$$ 3.13a

This simplification can formally be justified through a saddle-point approximation as the joint distribution $\mathit{\Pi }(s,s_0)$ has a maximum at $\mathit{\Pi }(s,E_{\mathit{\Pi }}[s_0|s])$). Generally no analytical expression of $E_{\mathit{\Pi }}[s_0|s]$ can be derived from equation (2.24) in the presence of cell size control fluctuations, however, and we approximate $E_{\mathit{\Pi }}[s_0|s]$ by a matched asymptotic expansion (appendix C):

$$E_{\mathit{\Pi }}[s_0|s]\approx {\overline{s}}_0-\underset{\mathrm{small}\hspace{0.17em}\mathrm{cells}}{\underbrace{\sigma \frac{\sqrt{2/\pi }\hspace{0.17em}{\mathrm{e}}^{-({(s-{\overline{s}}_0)}^2/2{\sigma }^2)}}{1+\mathrm{erf}((s-{\overline{s}}_0)/\sqrt{2}\sigma )}}}+\underset{\mathrm{large}\hspace{0.17em}\mathrm{cells}}{\underbrace{2a{\sigma }^2\gamma (s-a{\overline{s}}_0)}},$$ 3.13b

which holds for the linear cell size control model (2.19). The first term is the average birth size in the absence of cell size control fluctuations, the second term denotes the contributions from small cells, while the third term stems from large cells. The interpretation of this conditional expectation is that small cells were born with sizes smaller than average while larger cells were born with sizes above average depending on their size control (figure 6 in appendix C). The parameters in equation (3.13b) are given by the mean birth size ${\overline{s}}_0$ and variance σ² in a backward lineage tracing the ancestors of a random cell in the population (see [50] for details):

$$\begin{array}{cc}\hspace{0.17em}& {\overline{s}}_0=\frac{(2-a)(1+{\mathrm{CV}}_{\theta }^2)}{2-a(1+{\mathrm{CV}}_{\theta }^2)},\\ & {\sigma }^2={\overline{s}}_0^2\frac{{\mathrm{CV}}_{\mathrm{\Delta }}^2(1+3{\mathrm{CV}}_{\theta }^2){(2-a(1+{\mathrm{CV}}_{\theta }^2))}^2+4{\mathrm{CV}}_{\theta }^2(1-{\mathrm{CV}}_{\theta }^2)}{{({\mathrm{CV}}_{\theta }^2+1)}^2(4-a^2(1+3{\mathrm{CV}}_{\theta }^2))}.\end{array}\}$$ 3.13c

Equation (3.13) provide a closed-form approximation of the cell size dependence of any given moment accurate to order O(σ³).

Figure 6.

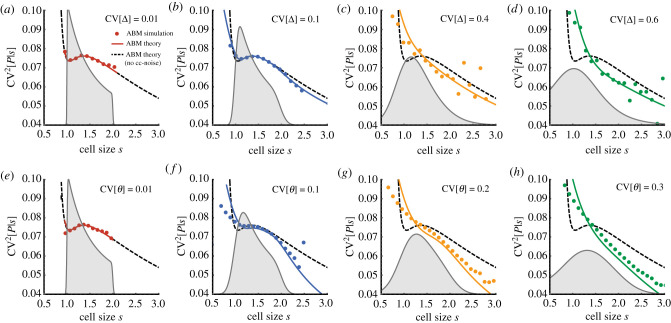
Retrospective averages of birth size. Matched asymptotic expansions of $E_{\mathit{\Pi }}[s_0|s]$ (equation (3.13b), lines) for the adder size control (a = 1, s₀ = 1) and agent-based simulations (dots) for (a) varying size control noise CV[Δ] and (b) division errors CV[θ].

To verify the accuracy of proposed approximation, we test the theory for various strengths of size control noise and division errors (figure 4). We observe that increasing cell size noise results in the monotonic decrease of gene expression noise with cell size (figure 4a–d) in good agreement with ABM simulations, even for large cell size fluctuations. We further ask about the effects of partitioning noise, which shows a similar dependence but agrees less well with the ABM simulations for cells smaller than the mean birth size (figure 4e–h), presumably since the effect of large variability in birth sizes is not captured in our approximation. Nevertheless, the present approximation qualitatively captures the overall cell size dependence of the ABM simulations (figure 4). Our findings confirm that birth size variation contributes significantly to the cell size dependence of gene expression noise of networks lacking SCH.

Figure 4.

Effect of noise in cell size control and division on gene expression noise in single cells. (a–d) Protein noise as a function of cell size s for various noise levels in added size CV[Δ]. For comparison, the prediction without cell cycle noise (dashed black line, equation (3.11)) and the cell size distributions (shaded grey) are shown. (e–h) Same as (a–d) but with division noise affecting the inherited size fraction CV[θ]. Analytical predictions (solid lines, equation (3.13a) with (3.11) and (3.13b)) and ABM simulations (dots) using the First-Division Algorithm (box 1) are shown. Gene expression model and all other parameters are as given in figure 3. Added size Δ assumes a gamma distribution with unit mean and CV[Δ] = 0.01 (e,f) while division errors θ followed a symmetric beta distribution with CV[θ] = 0.01 (a–d).

3.4. ENMs provide surprisingly accurate approximations of total noise in ABMs lacking SCH

We go on to compare the ENM introduced in §2.1 with the ABM. In contrast to the EDM, the ENM predicts the total noise statistics including the variability introduced by the cell size distribution. It is clear that the ENM agrees exactly with the ABM whenever the network obeys SCH. In particular, the marginal factorial-moment generating function of the ABM’s molecule numbers $G(z)=E_{\mathit{\Pi }}[\prod _{i=1}^N{z}_i^{x_i}]$ (irrespective of cell size) follows from equation (3.1) as

$$G(z)=E_{\chi }[\prod _{i=1}^{N}K({\kappa }_i(z_i-1))],$$ 3.14

when the concentration distribution χ has been identified (as we did for the models in §3.1) and the moment-generating function $K(t)=E_{\mathit{\Pi }}[{\mathrm{e}}^{ts}]$ of the cell size distribution (2.24) is known. When SCH does not hold, the ABM statistics can in principle be obtained through integrating equation (3.9) against the size distribution $\mathit{\Pi }(s,s_0)$. Specifically, denoting molecule numbers by x and concentrations by X = x/s, as before, we have

$$\begin{array}{cc}\hspace{0.17em}& {\mathrm{Cov}}_{\mathit{\Pi }}[X]=E_{\mathit{\Pi }}\left[\frac{\mathit{\Sigma }(s,s_0)}{s^2}\right],\\ \hspace{0.17em}& {\mathrm{Cov}}_{\mathit{\Pi }}[x]=E_{\mathit{\Pi }}[\mathit{\Sigma }(s,s_0)]+{\mathrm{Var}}_{\mathit{\Pi }}(s)\overline{X}{\overline{X}}^T,\end{array}\}$$ 3.15

where $\mathit{\Sigma }(s,s_0)$ is the size-dependent covariance matrix discussed in §3.3.

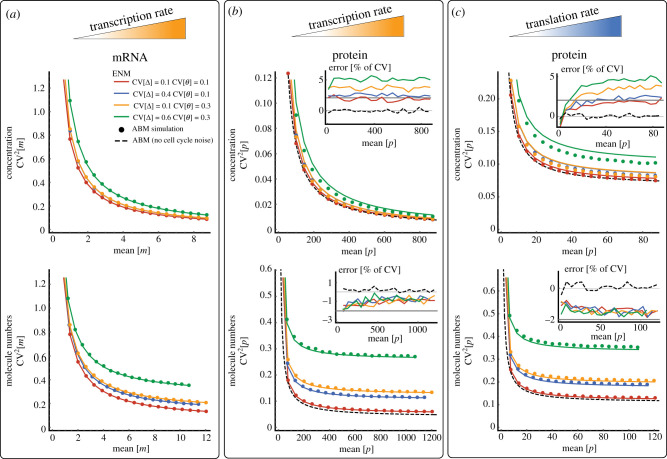
To illustrate this dependence, we consider the gene expression model with transcriptional size-scaling (2.13) and integrate equation (3.11) numerically against the size distribution (2.24). We observe that the mRNA noise-mean relationship of the ABM follows exactly the ENM predictions when the mean varies through the transcription rate (figure 5a). This agreement is confirmed for various strengths of cell size control fluctuations and division errors, both for mRNA concentrations and numbers, which validates our theoretical predictions that the mRNA distribution satisfies SCH and hence the ENM is exact.

Figure 5.

The extrinsic noise model approximates gene expression noise with size control and division errors. (a) Scaling of mRNA concentration noise with mean concentrations for various noise levels in added size CV[Δ] and partition noise CV[θ] when the transcription rate k₀ is varied (top). Corresponding scaling is shown for mRNA numbers (bottom). Analytical predictions of the ENM (solid lines, equation (2.8) with (2.10) and (2.12)) and ABM simulations using the First-Division Algorithm (dots, box 1) are shown. The inset shows the relative error in CV of the EDM compared to ABM simulations $[100\text{\%}\times ({\mathrm{CV}}_{\mathrm{ENM}}/{\mathrm{CV}}_{\mathrm{ABM}}-1)]$. (b) Scaling of protein noise with mean protein concentration (top) and numbers (bottom) when the translation rate k_tl is varied. (c) Same as (b) but varying the transcription rate k_tl. For comparison, the ABM predictions without cell cycle noise are shown (dashed black lines, equation (3.16)) and the error bounds of $2\text{\%}$ predicted by the theory (solid grey). See caption of figure 3 for the remaining parameters.

However, the protein noise–mean relationships of the ABM and ENM differ (figure 5b). The discrepancy, albeit small, exists even for deterministic divisions (${\mathrm{CV}}_{\phi }[\mathrm{\Delta }]={\mathrm{CV}}_{\pi }[\theta ]=0$) for which the averages (3.15) over the size distribution can be carried out analytically and result in:

$$\begin{array}{cc}\hspace{0.17em}& {\mathrm{CV}}_{\mathrm{ABM}}^2[P]=\frac{1}{{\mathit{\Omega }}_P\overline{P}}[1+\frac{2b(12-(24(2^{\delta -1}-1))/((2^{\delta +1}-1)(\delta -1))+13\delta )}{27(\delta +2)}],\\ \hspace{0.17em}& {\mathrm{CV}}_{\mathrm{ABM}}^2[p]={\mathrm{CV}}_{\mathit{\Pi }}^2[s]\\ \hspace{0.17em}& +\frac{1}{{\mathit{\Omega }}_{\hspace{0.17em}p}\overline{P}}[1+\frac{2b((2(2^{\delta -1}-1)/((2^{\delta +1}-1)(\delta -1)))+\delta (\ln (8)-1)-1)}{3\delta \ln (2)}],\end{array}\}$$ 3.16

where ${\mathit{\Omega }}_P=E_{\mathit{\Pi }}{[s^{-1}]}^{-1}$ and ${\mathit{\Omega }}_{\hspace{0.17em}p}=E_{\mathit{\Pi }}[s]$ and δ, b are defined as in equation (2.16). It can be verified by optimizing (3.16) over δ that the ENM underestimates ABM noise of protein numbers by at most $2\text{\%}$, while it overestimates noise in protein concentrations by the same amount. The difference between the ENM and ABM predictions increases with cell size control noise for concentration measures but appears to be practically independent of cell size control noise for protein number fluctuations (figure 5b, insets). The protein number noise, but not concentration noise, exhibits an extrinsic noise floor (${\mathrm{CV}}_{\mathit{\Pi }}^2[s]$ in (3.16)) for large mean numbers due to extrinsic cell size variability across the population and this noise floor increases with noise in size control (CV_φ[Δ]) and division errors (${\mathrm{CV}}_{\pi }[\theta ]$) as it is also predicted by the ENM (figure 5b).

Similar conclusions hold for the noise–mean relationship when the mean is varied through translation rate (figure 5c) but there appears an additional intrinsic noise floor due to stochastic bursting (figure 5c and equation (3.16)) that is present both in the protein concentration and number noise. This phenomenon is in qualitative agreement with previous findings [27,35,40] and similarly predicted by the ENM (2.15). Presumably, the better quantitative agreement for molecule numbers as compared to concentrations (figure 5b,c) is due the fact that the ENM and ABM predictions are dominated by extrinsic noise, which has the same effect in both models. Our observations suggest that, surprisingly, the ENM provides much more accurate approximations of the ABM statistics than the EDM.

4. Discussion

We presented an agent-based framework to study gene expression noise coupled to cell size dynamics across growing and dividing cell populations. The framework consists of an exact algorithm for simulating the stochastic dynamics of dividing cells (box 1), which generalizes previous algorithms for isolated lineages [4,17,32,60–62] towards growing cell populations, and a master equation framework (§2) that exactly characterizes the snapshot-distribution of gene expression and cell size across such a agent-based population.

Our theory shows that the newly defined SCH (cf. §3.1 and theorem A.2) provides a necessary and sufficient condition for the stationary distributions of the chemical master equation (EDMs and ENMs) to agree exactly with the snapshot distributions of detailed ABMs. A broad class of gene networks (3.5), involving mono-molecular reactions, multi-state promoters and bursting, satisfy SCH irrespective of network parameters when the reaction rates scale with cell size according to the law of mass-action. SCH is however not restricted to this particular class of network and can generally be checked on a case-by-case basis using the generating function equations, which can be accomplished without solving the chemical master equation analytically (see appendix A).

SCH guarantees that gene expression distributions for cells of a given size are entirely independent of extrinsic noise sources affecting birth size such as cell size control and division noise. They thus reveal whether a network embedded in a growing cell can be insulated against such noise sources, an important feature that can guide the design of synthetic circuits.

Nevertheless, most gene regulatory networks of interest do not obey SCH. To address this issue, we developed the linear noise approximation for ABMs lacking SCH embedded in growing and dividing cells. The theory provides ODEs for the mean molecule numbers (3.6) and their covariances (3.7), which—unlike the conventional linear noise approximation describing EDMs [6,43]—describe their evolution across sizes and features a boundary condition describing the stochastic partitioning of molecules at cell division. We showed that, when the reactions follow mass-action size-scaling, the mean concentrations of EDMs and ABMs agree, because they exhibit concentration homeostasis (§3.2). The theory further provides closed-form analytical expressions for the covariance matrix of gene expression fluctuations in the absence of SCH. We note that like the conventional linear noise approximation, the linear noise approximation for ABMs is exact for linear reaction networks but represents an approximation for nonlinear reaction networks (§3.3).

While the EDM always predicts birth-size-independent noise, the ABM’s covariance matrices generally depend on it (§3.3.1), both for concentrations and molecule numbers. This means that, unlike in SCH conditions, size-control noise and division errors can propagate to gene expression levels, and we unveiled quantitative and qualitative differences between EDMs and ABMs regarding the dependence of expression noise on cell size. Such differences prevail even for relatively simple gene networks involving protein expression (see (2.13)) for which our linear noise approximation readily provides exact expressions for mean and noise statistics.

Despite these discrepancies, we found that the ENM of these simple gene expression models provides surprisingly accurate total noise estimates (§3.4). In fact, we showed analytically that the ENM (and EDM) of bursty production with translational size-scaling agrees exactly with the ABM since it obeys SCH. For transcriptional size-scaling, which implies the absence of SCH, the ENM deviates at most a few per cent from ABM’s total protein noise prediction. To resolve such small differences experimentally, one would need to probe on the order of 10 000 cells for measuring the squared coefficient of variation accurate to three leading digits (assuming sampling errors inversely proportional to cell number), which is achievable only with high-throughput techniques.

An outstanding question is whether the good agreement we observed is specific to the particular model or parameter values we have chosen or whether the ENM is more generally valid. We have made an initial step in this direction by providing closed-form expressions for the ABM’s linear noise approximation of any single-species reaction network with deterministic size-distribution (appendix D). These results demonstrate that the ENM overestimates the ABM’s coefficient of variation of concentrations by at most $8\text{\%}$ but underestimates it by at most $2\text{\%}$, and vice versa for molecule numbers, and these bounds hold independently of the choice of parameters. This suggests that ENMs could be surprisingly accurate approximation of ABMs. Other effective models of bursty protein production without any size-scaling as proposed in [63] cannot obey SCH since they ignore cell size and generally produce larger errors than the ENM even for deterministic cell cycles.

A limitation of our study is that we assumed the validity of the linear noise approximation for the noise statistics of networks lacking SCH. Mean and covariance of the linear noise approximation are exact for linear reaction networks, as those we have studied here, but it represents an approximation for networks with nonlinear propensities valid in the limit of large molecule numbers. To improve the estimates of our theory, one could consider higher-order terms in the system size expansion [44], resort to moment-closure approximations [64] or to compute moment bounds [65] for nonlinear reaction networks.

Another limitation is that we neglected growth rate variability, which is a significant source of noise at the single-cell level [49]. It would be interesting to include these features in our ABMs, compare them to the effective models, and investigate whether SCH can be generalized to this case. Previous studies [3] have investigated the dependence of gene expression noise on growth rate dynamics in isolated lineages using small noise approximations similar to the one used here. Nevertheless, it may be expected that selection plays a pronounced role in populations where cells compete for growth unlike in isolated lineages, which in turn may lead to significant deviations of ENMs from ABMs [38,66,67] that we have not studied here.

In summary, we proposed SCH as a general condition for exactness of EDMs. In the absence of SCH, we found that despite qualitative differences in the predictions of EDMs, ENMs closely approximate the total noise statistics of ABMs. Our results reinstate the validity of effective models as approximations of the agent-based dynamics, and thus they significantly extend the scope of state-of-the-art master equation methods to a broad range of single-cell analyses in growing cell populations.

Appendix A. Stochastic concentration homeostasis and the validity of EDMs and ENMs

Appendices A and B use multi-index notation. In brief, a multi-index is a N-tuple α = (α₁, α₂, …, α_N). One defines powers of a vector x via $x^{\alpha }=x_1^{{\alpha }_1}{x}_2^{{\alpha }_2}\dots x_N^{{\alpha }_N}$, derivatives ${\mathrm{\partial }}_x^{\alpha }=\frac{{\mathrm{\partial }}^{{\alpha }_1}}{\mathrm{\partial }{x}^{{\alpha }_1}}\frac{{\mathrm{\partial }}^{{\alpha }_2}}{\mathrm{\partial }{x}^{{\alpha }_2}}\dots \frac{{\mathrm{\partial }}^{{\alpha }_N}}{\mathrm{\partial }{x}^{{\alpha }_N}}$, sum of components |α| = α₁ + α₂ + · · · + α_N, and the factorials α! = α₁! · α₂! · · · α_N! and analogously $(\left(\genfrac{}{}{0em}{}{\alpha }{\beta }\right))=\alpha !/\beta !(\alpha -\beta )!$.

Definition A.1 (Stochastic concentration homeostasis). —

A probability mass function $\mathit{\Pi }(x|s)$ with state space $\mathcal{X}$ obeys SCH if for all s ∈ [0, ∞) there exists a random variable κ on $\mathcal{K}$ with density χ(κ) satisfying:

$$\mathit{\Pi }(x|s)={\int }_{\mathcal{K}}\mathrm{d}\kappa \chi (\kappa )\frac{{(\kappa s)}^x}{x!}\hspace{0.17em}{\mathrm{e}}^{-s|\kappa |},\mathrm{\forall }\hspace{0.17em}x\in \mathcal{X}.$$ A 1

Definition A 1 implies that if κ has a moment-generating function $F(t)=E_{\chi }[{\mathrm{e}}^{t^T\kappa }]$ then using (A 1) one finds the factorial-moment generating function

$$\begin{array}{rl}{E}_{\mathit{\Pi }}[z^x|s]& =\sum _{x\in \mathcal{X}}{z}^x\mathit{\Pi }(x|s)={\int }_{\mathcal{K}}\mathrm{d}\kappa \chi (\kappa )\hspace{0.17em}{\mathrm{e}}^{-s|\kappa |}\sum _{x\in \mathcal{X}}{z}^x\frac{{(\kappa s)}^x}{x!}\\ \hspace{0.17em}& =E_{\chi }[{\mathrm{e}}^{s{(z-1)}^T\kappa }]=F(s(z-1))\end{array}$$ A 2

and similarly the factorial moments

$${\mu }_n(s)=E_{\mathrm{\Pi }}[\frac{x!}{(x-n)!}|s]={({\mathrm{\partial }}_z^n{E}_{\mathit{\Pi }}[z^x|s])}_{z=1}=s^{|n|}{E}_{\chi }[{\kappa }^n].$$ A 3

for a multi-index n. Since the factorial-moment generating function uniquely determines the distribution, equations (A 2) and (A 3) may equivalently serve as definitions of SCH. Furthermore, when {x(s)}_s∈[0,∞) is interpreted as a point processes along the size coordinate s, SCH emphasizes the fact that it is mixed Poisson process with stationary concentration vector κ.

Theorem A.2. —

Assume that the partitioning kernel B(x|x′, θ) is binomial with probability θ given by the ratio of daughter birth size and mother division size. A stationary solution of the EDM (2.4), if it exists, is also a solution of the ABM (2.25):

$$\mathit{\Pi }(x|s,s_0)={\mathit{\Pi }}_{\mathrm{EDM}}(x|s),$$ A 4

if and only if the EDM’s solution (2.4) obeys SCH.

The utility of the theorem is that SCH can be checked without solving the chemical master equation. We demonstrate this aspect for a general reaction network of the form (2.1) with mass-action propensities $w_r(x,s)=s^{1-|{\nu }_r^{-}|}{k}_r(x!/(x-{\nu }_r^{-})!)$, whose factorial-moment generating function (see ch. 7 in [68]) obeys:

$$\alpha s\frac{\mathrm{\partial }}{\mathrm{\partial }s}G(z|s,s_0)=\sum _{r=1}^R{k}_r{s}^{1-|{\nu }_r^{-}|}(z^{{\nu }_r^{+}}-z^{{\nu }_r^{-}}){\mathrm{\partial }}_z^{{\nu }_r^{-}}G(z|s,s_0)$$ A 5

Substituting G(z|s, s₀) = F(s(z − 1)) and x = s(z − 1) gives

$$\alpha x\cdot \mathrm{\nabla }F(x)=\sum _{r=1}^R{k}_{r}s({(x+s)}^{{\nu }_r^{+}}{s}^{-|{\nu }_r^{+}|}-{(x+s)}^{{\nu }_r^{-}}{s}^{-|{\nu }_r^{-}|}){\mathrm{\partial }}_x^{{\nu }_r^{-}}F(x).$$

It can now be seen that the right-hand side of the above equation is independent of s if either (i) $|{\nu }_r^{-}|=0$ and $|{\nu }_r^{+}|=1$, (ii) $|{\nu }_r^{-}|=1$ and $|{\nu }_r^{+}|=0$, or (iii) $|{\nu }_r^{-}|=|{\nu }_r^{+}|=1$. Thus, the EDM and the ABM solutions coincide for mass-action reaction networks (2.1) when they comprise only the mono-molecular reactions given in (3.5).

Similarly, we check that adding bursty reactions of the form $\text{Ø}\stackrel{k}{⟶}{m}_s\times X$ leads to a generating function equation

$$\alpha s\frac{\mathrm{\partial }}{\mathrm{\partial }s}G(z|s,s_0)=k[g(z|s)-1]G(z|s,s_0)+\cdots ,$$ A 6

where $g(z|s)=E[z^{m_s}|s]$ is the factorial-moment generating function of the burst distribution. Equation (A 6) transforms to $\alpha x\cdot \mathrm{\nabla }F(x)=k[g(x/s+1|s)-1]F(x)$ after substituting G(z|s, s₀) = F(s(z − 1)) and x = s(z − 1). Hence, bursty reactions obey SCH if and only if the burst distribution obeys SCH, i.e. if there exist a moment-generating function f satisfying f(x) = g(x/s + 1|s) as in (A 2).

Appendix B. Proof of theorem A.2

The proof of theorem A.2 is divided in three steps. The first step shows that a general condition (B 1) guarantees snapshot distributions that are independent of birth size. We then show that (B 1) satisfies the effective dilution model and reduces to SCH for binomial partitioning at cell division. The proof also clarifies that the assumption of binomial partitioning cannot be removed under biological constraints conserving the total number of molecule numbers at cell division. General conditions for the existence of the EDM’s stationary distributions have been discussed in [69].

B.1. Step 1: Distributions invariant of birth size

The conditional distribution $\mathit{\Pi }(x|s,s_0)$ is independent of birth size s₀ if and only if

$$\mathit{\Pi }(x|\theta s,s_0)=\sum _{x^{\prime }}B(x|x^{\prime },\theta )\mathit{\Pi }(x^{\prime }|s,s_0),$$ B 1

where B(x|x′, θ) is the partitioning kernel in equation (2.25b) that depends only the inherited size fraction θ = s₀/s′. This fact can be verified using (B 1) in the boundary condition (2.25b), which leads to

$$\mathit{\Pi }(x|s_0,s_0)={\int }_0^{\mathrm{\infty }}\mathrm{d}{s}^{\prime }{\int }_0^{s^{\prime }}\mathrm{d}{s}_0^{\prime }\hspace{0.17em}\rho (s^{\prime },s_0^{\prime }|s_0)\mathit{\Pi }(x|s_0,s_0^{\prime }).$$

This implies that $\mathit{\Pi }(x|s,s_0)$ must be independent of birth size

$$\mathit{\Pi }(x|s,s_0)=\mathit{\Pi }(x|s).$$

In the following, we show that under condition (B 1) $\mathit{\Pi }(x|s)$ coincides with the EDM solution.

B.2. Step 2: Transformation into an effective dilution model

Let us denote the factorial-moment generating function of the partitioning kernel by $G_B(z|x^{\prime },\theta )=\sum _x{z}^{x}B(x|x^{\prime },\theta )$ such that the invariance condition (B 1) becomes

$$G(z|\theta s)=\sum _{x^{\prime }}{G}_B(z|x^{\prime },\theta )\mathit{\Pi }(x^{\prime }|s).$$ B 2

Assume that additionally

$$\theta {\mathrm{\partial }}_{\theta }{G}_B(z|x^{\prime },\theta )=\sum _{i=1}^N(z_i-1){\mathrm{\partial }}_{z_i}{G}_B(z|x^{\prime },\theta ),$$ B 3

which holds for the binomial partition kernel G_B(z|x′, θ) = (1 − θ + θz)^x′. Differentiating equation (B 2) with respect to θ then gives

$$\begin{array}{rl}\theta {\mathrm{\partial }}_{\theta }G(z|\theta s)& =\sum _{x^{\prime }}\theta {\mathrm{\partial }}_{\theta }{G}_B(z|x^{\prime },\theta )\mathit{\Pi }(x^{\prime }|s)\\ \hspace{0.17em}& =\sum _{i=1}^N(z_i-1){\mathrm{\partial }}_{z_i}G(z|\theta s),\end{array}$$ B 4

where in the last line we used assumption (B 3). Changing variables (θs → s) in (B 4) yields

$$s{\mathrm{\partial }}_{s}G(z|s)=\sum _{i=1}^N(z_i-1)\frac{\mathrm{\partial }}{\mathrm{\partial }{z}_i}G(z|s),$$

or equivalently the EDM

$$\begin{array}{rl}\hspace{0.17em}& \left(\alpha s\frac{\mathrm{\partial }}{\mathrm{\partial }s}\right)\mathit{\Pi }(x|s)\\ \hspace{0.17em}& =-\alpha \sum _{i=1}^N[(x_i+1)\mathit{\Pi }(x_1,\dots ,x_i+1,\dots ,x_N|s)-x_i\mathit{\Pi }(x|s)]\\ \hspace{0.17em}& =-\mathbb{D}\mathit{\Pi }(x|s).\end{array}$$ B 5

Using the above relation, we see that (2.25a) coincides with (2.4) and (A 4) follows.

B.3. Step 3: SCH and the necessity of binomial partitioning

Finally, we show that condition (B 3) required for the validity of the EDM implies independent binomial partitioning of molecules. (B 3) is a linear PDE that can be solved using the method of characteristics, which leads to

$$\theta \frac{\mathrm{\partial }{z}_i}{\mathrm{\partial }\theta }=(1-z_i),\theta \frac{\mathrm{\partial }{G}_B}{\mathrm{\partial }\theta }=0.$$

The general solution is G_B(z|x′, θ) = J(1 − θ + θz) where the function J is fixed by the condition that for θ = 1 all molecules are partitioned deterministically, i.e. J(z) = z^x′. Hence, we obtain

$$G_B(z|x^{\prime },\theta )={(1-\theta +\theta z)}^{x^{\prime }},$$

which corresponds to independent binomial partitioning of molecules in (2.20). It then follows that (B 2) (and (B 1)) are equivalent to

$$G(z|\theta s)=G((1-\theta )+\theta z|s).$$ B 6

Finally, we show that (B 6) is equivalent to G(z|s) = F(s(z − 1)) for binomial partitioning. Expanding (B 6) around z = 1 and identifying the series coefficients with the factorial moments ${\mu }_n(s)$ in (A 3), we find that the factorial moments are homogeneous functions of order $|n|=\sum _i{n}_i$: μ_n(θs) = θ^|n|μ_n(s). Then by Euler’s homogeneous function theorem, it follows that the factorial moments with index n, satisfy s(∂/∂s)μ_n(s) = |n|μ_n(s) and hence μ_n(s) = s^|n|μ_n(1). This implies that the factorial-moment generating function is

$$G(z|s)=\sum _n{s}^{|n|}{\mu }_n(1)\frac{{(z-1)}^n}{n!}=F(s(z-1)),$$

with $F(x)=\sum _n{x}^n{\mu }_n(1)/n!$. It remains to be shown that F is indeed a moment-generating function. To this end, we note that $\frac{{\mathrm{\partial }}^{k}G(z|s)}{\mathrm{\partial }{z}^k}=s^{|k|}{F}^{(k)}(s(z-1))\ge 0$ for z ∈ (1, −∞) and hence F(− x) is a completely monotone function on x ∈ (0, ∞), which implies that there exists a distribution χ for which $F(-x)=E_{\chi }[{\mathrm{e}}^{-sx}]$ is a Laplace transform, which concludes the proof of theorem A.2.

Appendix C. Approximation of birth size moments

We here derive an analytical approximation (3.13b) for the conditional birth size moments. We start by rewriting $E_{\mathit{\Pi }}[s_0|s]$ in terms of the backward lineage distribution ψ_bw using equation (2.24):

$$\begin{array}{rl}{E}_{\mathit{\Pi }}[s_0|s]& ={\int }_0^s\mathrm{d}{s}_0\hspace{0.17em}{s}_0\mathit{\Pi }(s_0|s)\\ \hspace{0.17em}& =\frac{{\int }_0^s\mathrm{d}{s}_0\hspace{0.17em}{s}_0\mathit{\Pi }(s_0,s)}{{\int }_0^s\mathrm{d}{s}_0\hspace{0.17em}\mathit{\Pi }(s_0,s)}=\frac{E_{\psi }[s_0\mathit{\Phi }(s|s_0)1_{s_0\le s}]}{E_{\psi }[\mathit{\Phi }(s|s_0)1_{s_0\le s}]}.\end{array}$$ C 1

We now apply matched asymptotic expansion to this expression.

C.1. Large cell asymptotics

For large cells s ≫ s₀, we can extend the range of integration in equation (C 1) and compute the expectation value as follows

$$\begin{array}{rl}\hspace{0.17em}& E_{\psi }[f(s_0,s)]={\int }_0^{\mathrm{\infty }}\mathrm{d}{s}_0{\psi }_{bw}(s_0)f(s_0,s)\\ \hspace{0.17em}& ={\int }_0^{\mathrm{\infty }}\mathrm{d}{s}_0{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\mathrm{d}k}{2\pi }\hspace{0.17em}{\mathrm{e}}^{-\mathrm{i}k(s_0-{\overline{s}}_0)}(1-\frac{k^2{\sigma }^2}{2})f(s_0,s)+O({\sigma }^3)\\ \hspace{0.17em}& =f({\overline{s}}_0,s)+\frac{{\sigma }^2}{2}\frac{{\mathrm{\partial }}^{2}f({\overline{s}}_0,s)}{\mathrm{\partial }{\overline{s}}_0^2}+O({\sigma }^3).\end{array}$$

Using $f(s_0,s)=s_0\mathit{\Phi }(s|s_0)$ and $f(s_0,s)=\mathit{\Phi }(s|s_0)$ in equation (C 1), the conditional moments of birth size can be approximated by

$$\begin{array}{rl}{E}_{\mathit{\Pi }}^{\mathrm{large}}[s_0|s]& ={\overline{s}}_0(1+\frac{2{\sigma }^2}{{\overline{s}}_0}\frac{\mathrm{\partial }\ln \mathit{\Phi }(s|{\overline{s}}_0)}{\mathrm{\partial }{\overline{s}}_0})+O({\sigma }^3)\\ \hspace{0.17em}& =({\overline{s}}_0+2a{\sigma }^2\gamma (s-a{\overline{s}}_0))+O({\sigma }^3),\end{array}$$

where the last equality follows from γ(s, s₀) = γ(s − as₀) for the linear cell size control model (2.19), and ${\overline{s}}_0$ and σ are the mean and standard deviation of the backward lineage distribution ψ_bw given by equations (3.13c).

C.2. Small cell asymptotics

Next we consider small cells by noting that $\mathit{\Phi }(s|s_0)$ is practically constant when s ≈ s₀, the integral in (C 1) can be approximated by

$$E_{\mathit{\Pi }}[s_0|s]\approx \frac{E_{\psi }[s_0{1}_{s_0\le s}]}{E_{\psi }[1_{s_0\le s}]}.$$ C 2

Assuming that ψ, is approximately Gaussian with mean ${\overline{s}}_0$ and variance σ², we find that near $s\approx {\overline{s}}_0$, we have

$$\begin{array}{cc}\hspace{0.17em}& E_{\psi }[s_0{1}_{s_0\le s}]\approx \frac{1}{2}{\overline{s}}_0(1+\mathrm{erf}\left(\frac{s-{\overline{s}}_0}{\sqrt{2}\sigma }\right))-\frac{\sigma \hspace{0.17em}{\mathrm{e}}^{-({(s-{\overline{s}}_0)}^2)/2{\sigma }^2}}{\sqrt{2\pi }}\\ \mathrm{ann}& E_{\psi }[1_{{\overline{s}}_0\le s}]\approx \frac{1}{2}(1+\mathrm{erf}\left(\frac{s-{\overline{s}}_0}{\sqrt{2}\sigma }\right))\end{array}\}(\mathrm{C}\hspace{0.17em}3)$$ C 3

and hence

$$E_{\mathit{\Pi }}^{\mathrm{small}}[s_0|s]={\overline{s}}_0-\frac{\sqrt{2/\pi }\sigma \hspace{0.17em}{\mathrm{e}}^{-({(s-{\overline{s}}_0)}^2)/2{\sigma }^2}}{1+\mathrm{erf}((s-{\overline{s}}_0)/\sqrt{2}\sigma )}+O({\sigma }^3),$$

which is accurate to order σ³.

C.3. Global asymptotics

The two asymptotic solutions can be matched at the boundary layer. Since

$$\underset{s\to \mathrm{\infty }}{lim}{E}_{\mathit{\Pi }}^{\mathrm{small}}[s_0|s]=\underset{s\to s_0}{lim}{E}_{\mathit{\Pi }}^{\mathrm{large}}[s_0|s]={\overline{s}}_0,$$

the uniformly valid matched asymptotic expansion is

$$E_{\mathit{\Pi }}[s_0|s]\approx E_{\mathit{\Pi }}^{\mathrm{small}}[s_0|s]+E_{\mathit{\Pi }}^{\mathrm{large}}[s_0|s]-{\overline{s}}_0,$$

which gives equation (3.13b) (figure 6).

Appendix D. Analytical solutions and error bounds using the linear noise approximation for deterministic cell division

We begin by outlining the solution of (3.7). Defining $\tilde{\mathit{\Sigma }}(s,s_0)=U^{-1}\mathit{\Sigma }(s,s_0)U^{-†}$, equation (3.7) of the main text becomes

$$\alpha s{\mathrm{\partial }}_s{\tilde{\mathit{\Sigma }}}_{ij}=({\lambda }_i+{\lambda }_{\hspace{0.17em}j}^{\ast }){\tilde{\mathit{\Sigma }}}_{ij}+s{\tilde{\mathcal{D}}}_{ij}$$ D 1

and

$$4{\tilde{\mathit{\Sigma }}}_{ij}(s_0,s_0)={\tilde{\mathit{\Sigma }}}_{ij}(2s_0,s_0)+2s_0{\tilde{X}}_{ij}.$$ D 2

Equation (D 1) has the solution

$${\tilde{\mathit{\Sigma }}}_{ij}(s,s_0)=c_{ij}\hspace{0.17em}{s}^{({\lambda }_i+{\lambda }_{\hspace{0.17em}j}^{\ast })/\alpha }+\frac{{\tilde{\mathcal{D}}}_{ij}s}{\alpha (1-({\lambda }_i+{\lambda }_{\hspace{0.17em}j}^{\ast })/\alpha )},$$ D 3

where the constants c_ij are fixed using the boundary condition (D 2) which gives the solution of the EDM, equation (3.9) of the main text.

Using equation (3.15) and averaging (D 3) over the deterministic size distribution (3.8), we find the covariance matrix of concentrations X,

$$\begin{array}{rl}{\mathrm{Cov}}_{\mathit{\Pi }}[X]& =\frac{1}{\mathit{\Omega }}\sum _{i,j=1}^N{\hat{u}}_i{\hat{u}}_{\hspace{0.17em}j}^{†}\frac{{\beta }_{ij}(\coth ((1/2){\beta }_{ij}\ln 2)+3)}{3({\beta }_{ij}+1)}\frac{\alpha {\tilde{X}}_{ij}}{{\xi }_{ij}}\\ \hspace{0.17em}& +\frac{{\beta }_{ij}(3{\beta }_{ij}-\text{c}oth((1/2){\beta }_{ij}\ln 2))}{3({\beta }_{ij}^2-1)}\frac{{\tilde{\mathcal{D}}}_{ij}}{{\xi }_{ij}},\end{array}$$ D 4

where ${\xi }_{ij}=2\alpha -{\lambda }_i-{\lambda }_{\hspace{0.17em}j}^{\ast }$, β_ij = ξ_ij/α, ${\mathit{\Omega }}^{-1}=E_{\mathit{\Pi }}[s^{-1}]=(3/4)1/s_0$, and ${\hat{u}}_i$ are the eigenvectors of the Jacobian $\mathcal{J}$ introduced before equation (3.9). Similarly, considering molecule numbers x, we have ${\mathrm{Cov}}_{\mathit{\Pi }}[x]={\mathit{\Sigma }}_{\mathrm{ABM}}^{\mathrm{int}}+{\mathrm{Var}}_{\mathit{\Pi }}(s)\overline{X}{\overline{X}}^T$ where the intrinsic noise contribution is given by

$$\begin{array}{rl}{\mathit{\Sigma }}_{\mathrm{ABM}}^{\mathrm{int}}& =\mathit{\Omega }\sum _{i,j=1}^N{\hat{u}}_i{\hat{u}}_{\hspace{0.17em}j}^{†}[\frac{(2^{{\beta }_{ij}}-2){\beta }_{ij}}{(2^{{\beta }_{ij}}-1)({\beta }_{ij}-1)\ln 4}\frac{\alpha {\tilde{X}}_{ij}}{{\xi }_{ij}}\\ \hspace{0.17em}& +\frac{{\beta }_{ij}((2^{{\beta }_{ij}}-1){\beta }_{ij}\ln 4-2^{{\beta }_{ij}}(1+\ln 4)+2+\ln 4)}{(2^{{\beta }_{ij}}-1){({\beta }_{ij}-1)}^2\ln 4}\frac{{\tilde{\mathcal{D}}}_{ij}}{{\xi }_{ij}}],\end{array}$$ D 5

with $\mathit{\Omega }=E_{\mathit{\Pi }}[s]=s_0\ln 4$.

The expressions greatly simplify for a single species since $\hat{u}={\hat{u}}_i$, β = β_ij and ξ = ξ_ij. We note that in this case (D 4) increases monotonically with β while (D 5) decreases monotonically with β. Using the limits β → 0 and β → ∞, we find that the ABM’s coefficients of variation can be bounded by the EDM’s coefficients:

$$\frac{6}{7}\le \frac{{\mathrm{CV}}_{\mathrm{ENM}}^2[X]}{{\mathrm{CV}}_{\mathrm{ABM}}^2[X]}\le \frac{3}{2}\ln 2,$$ D 6

and

$$2{\ln }^2(2)\le \frac{{\mathrm{CV}}_{\mathrm{ENM}}^2[x]}{{\mathrm{CV}}_{\mathrm{ABM}}^2[x]}\le \frac{4\ln 2}{1+\ln 4},$$ D 7

where we have used the fact that $\mathcal{D}(\overline{X})\ge \alpha \overline{X}$ and the ENM solution of (2.9) is ${\mathit{\Sigma }}_{\mathrm{ENM}}^{\mathrm{int}}=\alpha \overline{X}/\mathit{\Omega }\xi +(\mathcal{D}/\mathit{\Omega }\xi )$. The result implies that the ENM overestimates the ABM’s coefficient of variation of concentrations by at most $8\text{\%}$ but underestimates it by at most $2\text{\%}$, and vice versa for molecule numbers.

Data accessibility

An implementation of the First-Division Algorithm (box 1) in Julia is available at github.com/pthomaslab/fda.

Authors' contributions

P.T. and V.S. designed the study and interpreted the results. P.T. developed the theory and analysed the data.

Competing interests

We declare we have no competing interests.

Funding

This work has been supported by a UKRI Future Leaders Fellowship (grant no. MR/T018429/1) to P.T. and the EPSRC Centre for Mathematics of Precision Healthcare (grant no. EP/N014529/1).