Host–pathogen immune feedbacks can explain widely divergent outcomes from similar infections

Abstract

A long-standing question in infection biology is why two very similar individuals, with very similar pathogen exposures, may have very different outcomes. Recent experiments have found that even isogenic Drosophila melanogaster hosts, given identical inoculations of some bacterial pathogens at suitable doses, can experience very similar initial bacteria proliferation but then diverge to either a lethal infection or a sustained chronic infection with much lower pathogen load. We hypothesized that divergent infection outcomes are a natural result of mutual negative feedbacks between pathogens and the host immune response. Here, we test this hypothesis in silico by constructing process-based dynamic models for bacterial population growth, host immune induction and the feedbacks between them, based on common mechanisms of immune system response. Mathematical analysis of a minimal conceptual model confirms our qualitative hypothesis that mutual negative feedbacks can magnify small differences among hosts into life-or-death differences in outcome. However, explaining observed features of chronic infections requires an extension of the model to include induced pathogen modifications that shield themselves from host immune responses at the cost of reduced proliferation rate. Our analysis thus generates new, testable predictions about the mechanisms underlying bimodal infection outcomes.

1. Introduction

Despite more than a century of infectious disease research, we still do not understand why two similar individuals exposed to nearly identical bacterial infections may experience dramatically different outcomes, with some dying while others mount a successful defence and survive. It is routine to define the LD₅₀ of a given pathogen as the infectious dose at which half the infected hosts will die. But why do half die while the other half survive? Analogously, we have very little understanding of why some individuals develop severe infections while others remain safe and healthy after similar exposures to opportunistic pathogens. Widely divergent outcomes, even when controlling for genotype and environment, give the appearance that the outcome is random or arbitrary.

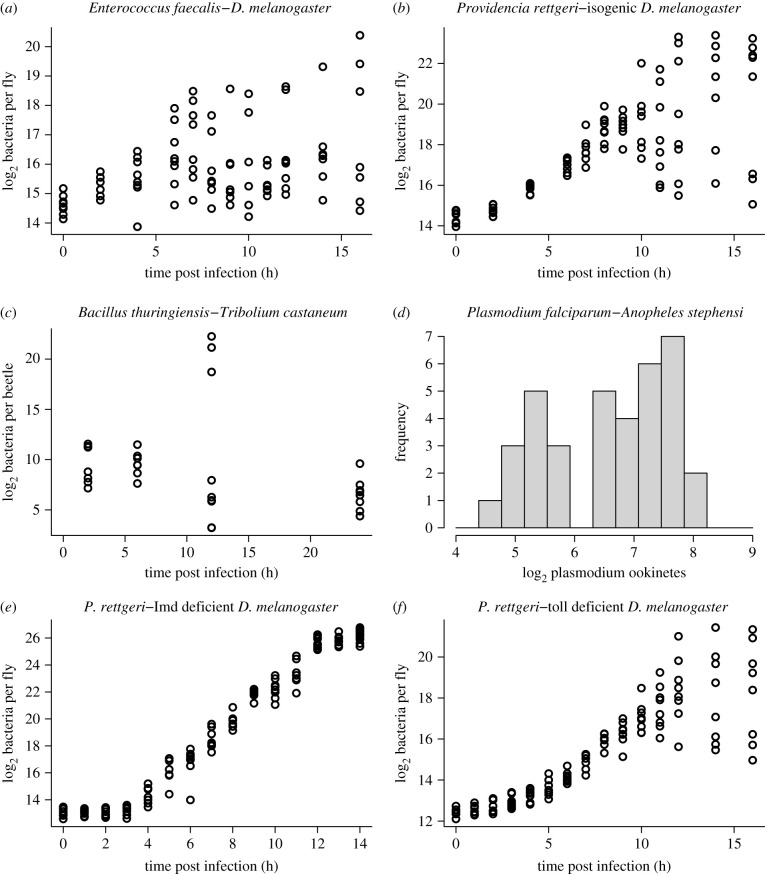
We have recently found that Drosophila melanogaster reared in a common controlled environment experience biphasic outcomes after identical injections (insofar as experimentally possible) of an opportunistic pathogen [1]. Some hosts die from acute infection with a high pathogen burden, others survive infection but sustain a lifelong chronic bacterial burden at much lower density (figure 1a). That pattern occurs even when the hosts are isogenic (figure 1b). Very similar patterns are seen in Drosophila infected with other bacteria [4,5], flour beetles (Tribolium castaneum) infected with Bacillus thuringiensis (with higher survival among offspring of immune-primed mothers; figure 1c; data from [2], fig. 1D), virus-infected flies [6] and Plasmodium-infected mosquitos (figure 1d; data from [3], fig. 2a).

Figure 1.

(a,b,e,f) Some experimental results from Duneau et al. [1] in which flies D. melanogaster were given uniform injections of opportunistic pathogens but infection outcomes could be highly variable. Each data point represents a fly that was sacrificed some time after infection to assay its total bacterial load. (c) Experimental results from [2] in which flour beetles Tribolium castaneum were experimentally infected with Bacillus thuringensis. The data plotted are unprimed beetles from Experiment 1 of that paper. The high bacterial load beetles at 12 h post infection were described as ‘moribund’ [2]. (d) Experimental results from Bian et al. ([3], fig. 2a) in which mosquitos Anopheles stephensi were experimentally infected with Plasmodium falciparum. The plotted data are Plasmodium ookinetes per midgut lumen in the LBT mosquito strain. Figure made by script Figure1.R.

Production of anti-microbial peptides (AMP) is a principal defence against invading bacteria in Drosophila and many other insects [7]. AMP production following pathogen invasion may be upregulated primarily through the Imd or Toll signalling pathways (or both in combination), depending on the structure of the peptidoglycan in the bacterial cell wall [8]. Response to Providencia rettgeri primarily involves the Imd pathway. Flies deficient in Imd-dependent immune response all experienced lethally high pathogen burdens following inoculation with P. rettgeri (figure 1e), while bimodal infection outcomes persisted in Toll-deficient mutants (figure 1f) and in phagocytosis-deficient mutants [1].

In attempting to explain the observed bimodal outcomes, Duneau et al. [1] therefore tested whether flies vary in the speed and magnitude of Imd pathway induction. They found substantial variation in mRNA levels of the Diptericin gene, a readout of Imd pathway activity, 4 h after pathogen injection. At that time, which is prior to the divergence in outcomes, Imd activity was more variable than bacterial load. Thus, the Imd variability presumably reflects intrinsic variability among the flies (despite their genetic homogeneity and common rearing), rather than being a side-effect of differences in bacterial population growth. Based on that finding, Duneau et al. [1] presented a phenomenological model positing that a fly either succeeds or completely fails to control the infection, depending on whether Imd upregulation occurs before or after bacterial density crosses some threshold. Bimodality of outcomes is thus an assumption of their model, not an outcome.

Our goal here is to develop a general mechanistic explanation for outcome bimodalities like those in figure 1 as an emergent property of interactions between the pathogen and host immune responses. Van Leeuwen et al. [9] have recently presented an explanation specifically for intestinal parasites, based on nutritional interactions between parasite and host (e.g. [10,11]). The mechanism in their model, parameterized for a nematode parasite of mouse, is competition for energy and nutrients: a larger pathogen population is increasingly able to divert the resources ingested by the host from the host to itself. The pathogen thus benefits from increased abundance (an Allee effect), potentially resulting in bimodal outcomes where infection duration is long or short depending on whether the initial pathogen abundance is above or below a threshold.

Here, we propose an alternative, broadly applicable explanation, that bimodal infection outcomes are a natural result of two negative feedbacks: hosts mount an immune response to eradicate the pathogen, while pathogens attempt to counteract or squelch the immune responses so they can proliferate at the expense of the host. Then, depending on the balance between host immune response and pathogen counter-response, the outcome can be bistable dynamics in which similar initial states lead to widely divergent outcomes in which the host either fends off or succumbs to the pathogen. A simple analogy is the well-known ‘toggle switch’ model for two genes that mutually repress each other’s activity levels. For suitable parameter values, this results in two stable equilibria (each with one gene ‘on’ and the other ‘off’), separated by an unstable saddle equilibrium. Two trajectories with very similar initial conditions near the origin, but on opposite sides of a separatrix (the stable manifold of the saddle) follow similar paths initially but then separate and eventually converge to different stable equilibria. Continuous variation in initial conditions spanning the separatrix produces discrete variation in outcomes.

We first present a minimal conceptual model for our hypothesis based on the Drosophila experimental system. We posit that flies respond to a bacterial infection by producing bactericidal AMPs, while bacteria can inactivate AMPs by sequestration and produce proteases that degrade AMPs [12]. In addition, bacteria can produce effectors that interfere with AMP production (e.g. [13]). A slow–fast approximation to this model produces a two-dimensional system, and phase plane analysis of that system verifies our hypothesis that bimodality is a robust outcome of the mutual negative feedbacks.

Importantly, we do not merely confirm that the ‘toggle switch’ mechanism for bistability can be made to operate in a host–pathogen interaction. Our analysis shows that bistability occurs in our model across a wide range of biologically plausible parameter values, and it identifies several specific scenarios in which small between-host differences can be amplified into widely divergent outcomes.

However, analysis of the minimal model shows that for biologically reasonable parameter values, the ‘toggle switch’ mechanism does not provide a complete explanation for the experimental observations. Specifically, it cannot explain the common observation (as in figure 1 examples) that in the infection outcome with lower pathogen abundance, the pathogen is not entirely, or almost entirely, eliminated. Rather, there is a non-lethal chronic infection held in check by sustained immune system activation [14]. In our Drosophila system, the chronic infection can break out into an active infection if the host immune response is subsequently eliminated (J. J. McIntyre & B. P. Lazzaro 2019, unpublished data). To explain these features of chronic infections, we therefore extend the model by allowing bacteria to enter a ‘protected’ state where they are partially shielded from immune response. Several such mechanisms for bacterial defence against AMPs are known, including biofilm formation and various cell envelope modifications [12]. The conditions for stable chronic infection in the extended model lead to new, testable predictions about the mechanisms that account for chronic infection rather than complete or near-complete elimination of the pathogen.

Finally, we develop a detailed model for the Imd signalling pathway, to show that our minimal model’s ‘cartoon’ description of immune system activation dynamics, and how it varies among individuals, can be realized in a completely mechanistic model for a defence activation pathway.

2. Conceptual model

Our conceptual model tracks a bacterial population B growing within an invertebrate host, suffering mortality caused by host-produced AMPs A, and producing proteases R that degrade AMPs:

$$\begin{array}{rl}\frac{\mathrm{d}B}{\mathrm{d}t}& =rB(1-\frac{B}{K})-cAB\\ \frac{\mathrm{d}A}{dt}& =f(B)-{\delta }_{A}A-hAR-cAB\\ \frac{\mathrm{d}R}{\mathrm{d}t}& =gB-{\delta }_{R}R\\ \mathrm{and}\text{where }f(B)& =\frac{Q_{A}B}{S_A+B}\end{array}\}$$ 2.1

and all parameters are positive. In the absence of AMPs, bacteria have logistic population growth with maximum per capita growth rate r and ‘carrying capacity’ K. The carrying capacity corresponds to pathogen growth ceasing because the host is completely consumed, so any model solution where B gets close to K is interpreted as pathogen killing the host. cAB is bacteria mortality due to AMPs. AMP production rate f is a function of bacteria abundance, monotonic increasing from f(0) = 0 and saturating at maximum rate Q_A. S_A is the bacterial abundance at which AMP production rate reaches half its maximum value. In our model, AMPs are lost three ways: natural degradation at rate δ_A A, degradation by protease at rate hAR and sequestration (i.e. each ‘kill’ of a bacterium binds and thus inactivates the A molecules involved). We take the unit of AMP to be the amount required to kill one bacterium, so that each bacterial death is matched by losing one unit of AMP. Over the time scale of interest AMPs are very stable molecules, so δ_A ≪ 1 [15,16]. However, AMPs can be produced quickly enough to create a lethal within-host environment for the pathogen [8]. Proteases R are produced by bacteria at constant per capita rate g and degrade naturally at rate δ_R R, which is not necessarily very small. Protease is not consumed in the process of promoting AMP degradation, so the hAR term is not replicated in the dR/dt equation.

To keep this ‘proof of concept’ model as simple as possible, we have omitted two potential features of the host–pathogen interaction: a constitutive immune response (i.e. production of AMPs in the absence of bacteria [17]), and bacterial production of effectors that interfere with the host mounting an immune response (e.g. [13]) rather than acting through AMP degradation and sequestration. In electronic supplementary material, S.2, we present an extended model that adds those features to the basic model presented here. We show that the only qualitative effect of the extensions is to add one more scenario (described at the end of this section) where small individual differences in host immune induction can produce bimodal outcomes.

Before analysis we re-scale the model, setting $\tilde{B}=B/S_A$, $\hspace{0.17em}\hspace{0.17em}\tilde{A}=A/S_A$, $\tilde{R}=hR$ and $\tilde{t}=rt$. For the sake of visualization and analysis, we reduce the dimension of the model by assuming that R is a ‘fast’ variable (i.e. g and δ_R are large) that remains close to its steady state conditional on the other variables, R = mB where m = g/δ_R. The calculations are carried out in Maxima script RescaleBAR.max. Then (dropping the tildes on rescaled variables and parameters for clarity), the model we consider is

$$\begin{array}{rl}\frac{\mathrm{d}B}{\mathrm{d}t}& =B(1-\frac{B}{K})-cAB\\ \frac{\mathrm{d}A}{\mathrm{d}t}& =f(B)-{\delta }_{A}A-(c+m)AB\\ \mathrm{and}\text{where }f(B)& =\frac{Q_{A}B}{1+B}.\end{array}\}$$ 2.2

Note that equilibria $(\overline{A},\overline{B})$ of the reduced model (2.2) are in 1-to-1 correspondence with equilibria $(\overline{A},\overline{B},m\overline{B})$ of the full system (2.1). Because bacterial abundance is now scaled relative to the half-saturation abundance for immune response, and immune response is triggered when bacteria are far below a lethal abundance, we can assume that K ≫ 1. Time is scaled so that bacteria that are unhindered by resource shortage or immune response would double in log 2 ≈ 0.7 time units. Observed doubling times are typically on the order of 1 h in real time [1], so we can still assume that δ_A is a small parameter in the rescaled model.

Equilibria occur at intersections of the B and A nullclines (the sets of (B, A) values at which dB/dt = 0 and dA/dt = 0, respectively). The B nullcline consists of the axis B = 0 and the line A = c⁻¹(1 − B/K); the A nullcline is the curve

$$A=\frac{Q_{A}B}{(1+B)({\delta }_A+(c+m)B)}.$$ 2.3

The infection-absent state (B = A = 0, open diamond) is always an equilibrium. Analysis of the model (in electronic supplementary material, S.1) shows that this equilibrium is always unstable: a small inoculum of bacteria initially increases. Other equilibria and their stability depend on the configuration of the B and A nullclines in the interior of the first quadrant. There are three possibilities, shown in figure 2a. Model behaviour in each of these cases is analysed in electronic supplementary material, S.1. When host immune response is very strong (large Q_A, dotted green curve), there is only one nullcline intersection giving a stable equilibrium at B ≈ 0 and A ≈ 1/c. Model solutions starting anywhere except B = A = 0 converge to that equilibrium: immune response always holds the infection in check. When host immune response is very weak (small Q_A, dashed green curve) there is again only one possible outcome: the stable equilibrium near B = K, A = 0, representing a pathogen that has overcome the host’s immune defences. In between these extremes (solid green curve), there are three interior equilibria, one unstable and two locally stable, at widely differing pathogen densities.

Figure 2.

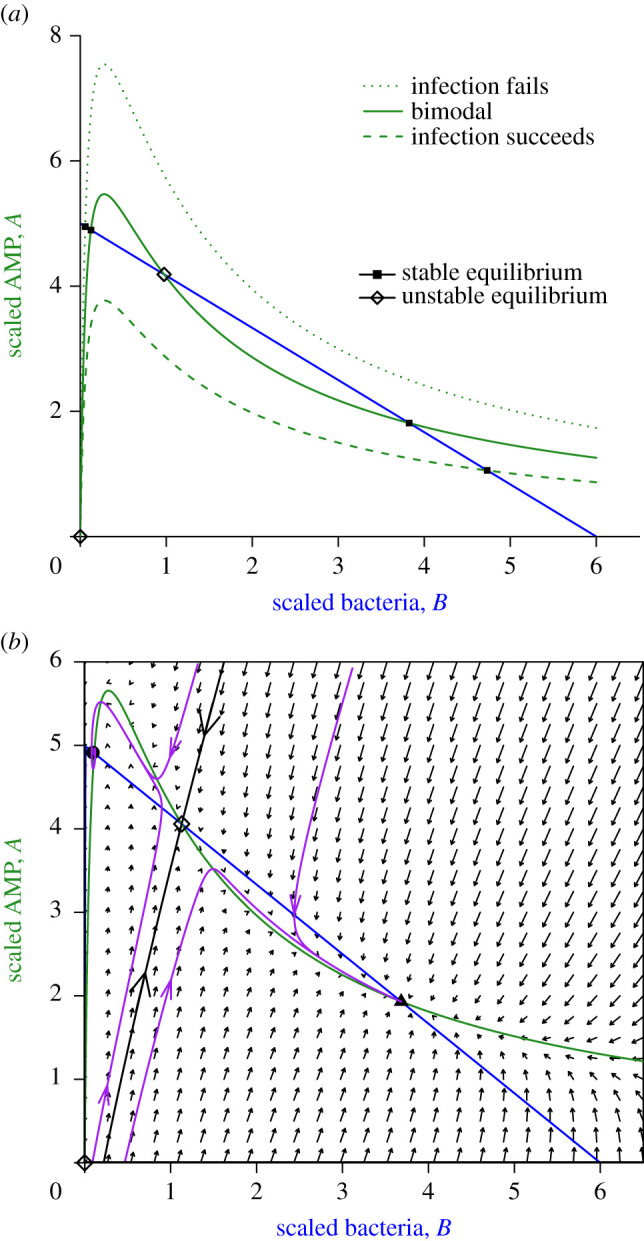
Phase-plane diagrams of the conceptual model. (a) Possible nullcline configurations. The blue line is the B nullcline, the three green curves are the A nullcline for three different values of Q_A (4, 5.8 and 8) from lowest to highest, with K = 6, δ_A = 0.05, c = 0.2, m = 0.45. Equilibria (where nullclines intersect) can be stable (solid square) or unstable (open diamond). (b) Phase portrait in the bistable case. Black curve is the stable manifold of the interior unstable equilibrium, which is a saddle. Solution trajectories (purple curves) converge to one or the other stable equilibia, depending on the location of their starting point, approaching along the unstable manifold of the saddle (not drawn). Figures were created by script files BAnullclinesPlot.R, BAModel.R. (Online version in colour.)

Figure 2b illustrates how, in the three-equilibria case, small differences in initial conditions can produce large differences in the infection outcome. Unlike the extended model in electronic supplementary material, S.2, the basic model omits constitutive production of AMPs, so initial conditions are exactly on the B axis, and different initial conditions correspond to different pathogen numbers when production of AMPs in response to the infection begins. In the extended model, initial conditions with small positive A values are also possible. The unstable manifold of the middle interior equilibrium consists of two solution trajectories having exactly the right initial conditions so that solutions converge to the middle equilibrium. Initial conditions off the stable manifold lead to infection dynamics that first approach the middle equilibrium, but then veer off to one of the stable interior equilibria, depending on which side of the stable manifold they started. The right-most equilibrium is always a node, but the left-most can be a spiral (as in this example), if it occurs where the A nullcline is very steep.

In electronic supplementary material, S.1, we derive the following approximate condition for occurrence of bistability in the scaled model:

$$1<\frac{Q_{A}c}{c+m}<\frac{(K+1{)}^2}{4K}.$$ 2.4

Although equation (2.4) is approximate, we have found numerically that bistability occurs when neither inequality is close to being violated. This condition can be interpreted biologically, showing that the requirements for bistability will often be satisfied. In the scaled model, K is the pathogen carrying capacity relative to the half-saturation constant for immune system upregulation. Thus, K is large, and the right-most term will be large, so long as the host responds strongly to a bacterial infection when it is still far below the level at which the host’s survival is threatened. The middle term can be written as Q_A/(1 + m/c). Q_A determines how quickly the host can produce AMPs to ward off a pathogen attack, and m/c is a measure of how effectively the pathogen can counter the host by degrading AMPs, relative to the lethality of the host response. The middle term is thus a measure of the ‘balance of forces’ between host and pathogen—if either antagonist is too strong or too weak, there is only one possible outcome. Condition (2.4) thus says that if the pathogen is a sufficient threat that the host responds to its presence in low numbers, bistability will occur across a wide range of values for the ‘balance of forces’ between host and pathogen.

The location of the stable manifold depends on parameter values. Here, parameter values were such that small differences in initial bacterial density produce radically different outcomes. In the Duneau et al. [1] experiments, where flies differed in the time required for immune activation, the ‘initial bacterial density’ would be the bacterial density at the time of immune activation, with higher bacterial density after a longer delay. The dynamics in figure 2b thus provide a qualitative explanation for observed bimodality in outcomes from very similar inoculations of very similar flies.

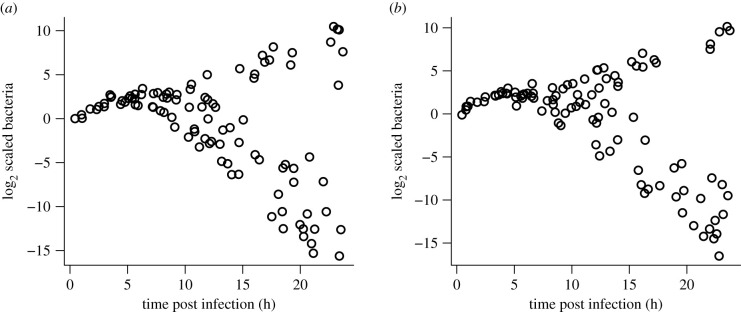
Figure 3 shows simulations of experiments like those in figure 1 using the minimal model. We assumed that host individuals varied randomly in their pattern of immune system activation, as was observed [1]. This variability could have several different biological causes, including host resource or energetic limitations, but at the level of our model, all that matters is the temporal pattern. In all hosts, following the pathogen inoculation, the AMP production rate term f(B) was multiplied by a three-piece function representing immune system activation: a delay period during which AMP production rate is zero; a linear ramp-up from zero to one; and thereafter constant at 1. The duration (in hours) of the delay period was chosen from a uniform [1.5, 2.5] distribution, and the time required for the ramp-up was chosen from a uniform [1,2] distribution. If the ramp-up were instantaneous, the variable delay period would be equivalent to random variation in the initial bacteria abundance in 2b, which shows the dynamics after the immune ramp-up. Each plotted point represents one simulated host that was ‘sacrificed’ at a random time, and Gaussian ‘measurement error’ with σ = 0.35 was added to log₂(B). These simulations show that our conceptual model provides a potential mechanistic basis for the hypothesis of Duneau et al. [1] that small variations in the speed of immune system activation can produce drastic, bimodal variation in outcomes. In electronic supplementary material, S.4, we develop a detailed mechanistic model for the Imd signalling pathway leading to AMP production, and confirm that among-individual variation in kinetic parameters of the pathway can produce a wide range of temporal patterns for immune activation (electronic supplementary material, figure S.5).

Figure 3.

Two replicates of a simulated experiment with 100 host individuals each in the minimal model equation (2.2), with parameter values Q_A = 10, δ_A = 0.02, c = 0.1, m = 0.2, K = 1000. For comparison with experimental results, time was not scaled; bacteria had intrinsic growth rate r = 0.5 multiplying the logistic growth term. Each plotted point represents ‘data’ on one host individual. Hosts vary in the delay period and ramp-up speed to full immune response, as described in the main text. Hosts were ‘sacrificed’ at a random time between 0.25 and 24 h, and Gaussian ‘measurement error’ with σ = 0.35 was added to log₂(B). Figure made by script Split_Outcomes_BA.R.

At other parameter values, the lower-left branch of the unstable manifold approaches the A axis, rather than the B axis. In our extended model that includes constitutive defence (see electronic supplementary material, S.2) this situation creates another way for small between-host differences to produce bimodal outcomes. Constitutive defence moves the pathogen-free equilibrium from the origin to a point (0, α) on the A axis. The location of this equilibrium relative to the stable manifold determines whether a small invading pathogen population sparks a lethal infection, or is driven down by the host immune response (electronic supplementary material, figure S.2b,c). This scenario can produce bimodal outcomes from small variance among hosts in their constitutive defence levels.

3. Chronic infection and protected pathogens

The minimal model can explain bimodal outcomes and it makes two other predictions that are confirmed experimentally in our Drosophila system. First, a high enough initial dose of bacteria (producing initial conditions with A ≈ 0 and B sufficiently large) always results in uncontrolled infection and host death ([1], fig. 2 supplement 1). Second, immune priming (producing initial conditions with B small and A large) can eliminate uncontrolled infections ([1], fig. 7A).

However, it cannot explain another important experimental observation: that the alternative to uncontrolled infection may be a chronic infection where bacteria remain present at substantial but non-lethal levels, and the host immune response is never fully downregulated [1,14]. At the low-B equilibrium in figure 2, the pathogen density is extremely low. This is not just a feature of the particular parameters in that figure. The slope of the A nullcline (green curve) at B = 0 is Q_A/δ_A, so it rises very steeply, and the peak of the nullcline occurs at $B=\sqrt{{\delta }_A/(c+m)}$. So under the biologically relevant assumption that δ_A is small, and host and pathogen interact strongly (so c and m are not small), the low-B equilibrium will always occur at very low B. At the parameters used in figure 3, the low-B equilibrium is very near zero even though δ_A is not greatly smaller than c or m. In our extended model (electronic supplementary material, S.2), the low-B equilibrium can be at B = 0 when hosts have constitutive AMP production. However, empirical observation is that substantial bacterial loads can persist for the duration of life in hosts that survive the initial infection [1], engendering only a mild reduction in lifespan [18]. Moreover, as bacterial abundance has been scaled in the model so that S_A = 1, the rate of AMP production at the low-B equilibrium is below the maximally upregulated rate by a factor B/(1 + B) < B. So simply from the fact that B ≪ 1, we can conclude that at the low-B equilibrium the immune system is almost completely downregulated, which is also out of line with the experimental observations.

The path to chronic infections involves pathogens switching from expansion to decline, suggesting that chronic infection may result from some change in the host–pathogen interaction. For example, the pathogen might evolve in ways that allow it to persist in a chronic infection, or the host might modify its immune response to tolerate chronic infection rather than clear it. However, the pathogen evolution hypothesis has been disproved experimentally in our Drosophila system. Bacteria taken from flies with either outcome (infection succeeds, or chronic infection), and then re-injected into uninfected flies, again produce the same bimodal infection outcomes [1]. We are not aware of any experimental evidence, in any system, that motivates the second hypothesis. Moreover, it cannot occur simply through changes in our model’s parameter values; it would require a qualitative change in how AMP production rate modulates in response to pathogen abundance (see electronic supplementary material, S.3).

Therefore, to explain chronic infection outcomes we add to our model the ability of pathogens to achieve some degree of protection from the host immune response, at the cost of reducing their division rate. We chose to model the protection hypothesis because several mechanisms are known that can produce this effect [12]. One is for cells to enter a ‘tolerant’ or ‘persister’ state, analogous to known mechanisms of antibiotic tolerance [19] involving either physiological changes (such as cell wall reduction or loss) or a reduction in metabolic rate (dormancy [20]). A second is for pathogens to invade some tissue that is protected from the host immune response. For example, intracellular pathogens such as Mycobacterium tuberculosis (the causative agent of tuberculosis) and Listeria monocytogenes do this by allowing themselves to be phagocytosed, then living inside the macrophage while being protected from host immune responses [21]. Any tissue isolated from the host immune system could play the same function. A final possibility is for cells to form a structure such as a biofilm that protects most cells against host immune response, and allows them to safely remain metabolically active to some extent, while not changing dramatically in numbers [12]. For our purposes, we need not distinguish between these possible mechanisms; we can just posit that cells can activate some mechanism affording protection at the cost of reduced proliferation rate.

We thus extend the model to distinguish between ‘normal’ bacteria N, and ‘protected’ bacteria P. For a minimally complex proof of concept model, we assume that protected cells are completely invulnerable to AMPs (without specifying how this is achieved), but have a lower intrinsic division rate and protease production rate than normal bacterial (by a factor η < 1), and a lower carrying capacity L (lower carrying capacity is a necessary assumption in this model, as slower division would otherwise simply delay the progression to a high lethal pathogen burden, but host defences could also limit protected bacterial growth if the assumption of complete invulnerability is relaxed). We assume that the per capita conversion rate from N to P states is a sigmoid increasing function p(A) of AMP concentration. Because our focus is on modelling chronic infection states where the immune system remains activated, we omit back-conversion from P to N states that might occur at low AMP concentrations. However, we do assume that division of P cells produces both a fraction ν of N cells. When AMP concentrations are low, these N cells could proliferate and potentially re-seed a growing infection.

The model is then

$$\begin{array}{rl}\frac{\mathrm{d}N}{\mathrm{d}t}& =rN(1-\frac{N}{K})+\nu \eta rP(1-\frac{P}{L})-cAN-p(A)N\\ \frac{\mathrm{d}P}{\mathrm{d}t}& =(1-\nu )\eta rP(1-\frac{P}{L})+p(A)N-{\delta }_{P}P\\ \frac{\mathrm{d}A}{\mathrm{d}t}& =f(N)-{\delta }_{A}A-hAR-cAN\\ \frac{\mathrm{d}R}{\mathrm{d}t}& =g(N+\eta P)-{\delta }_{R}R\\ \mathrm{and}\\ \text{where }f(N)& =\frac{Q_{A}N}{1+N}.\end{array}\}$$ 3.1

For this section, we again scale state variables so that S_A = h = 1, but leave time unscaled for the sake of comparisons with experimental results. A doubling time of 1–2 h (r = 0.35 − 0.7) can be taken as typical for the Drosophila pathogens shown to exhibit bimodal infection outcomes [1].

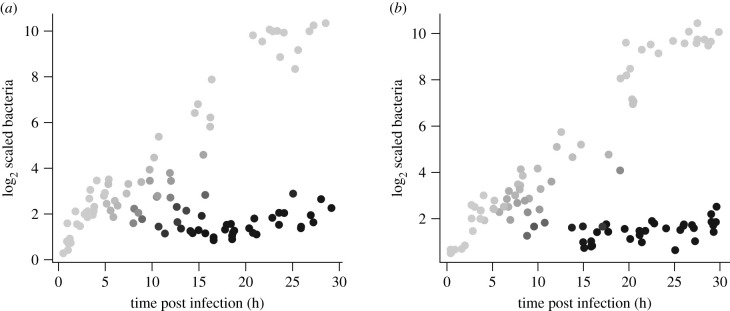
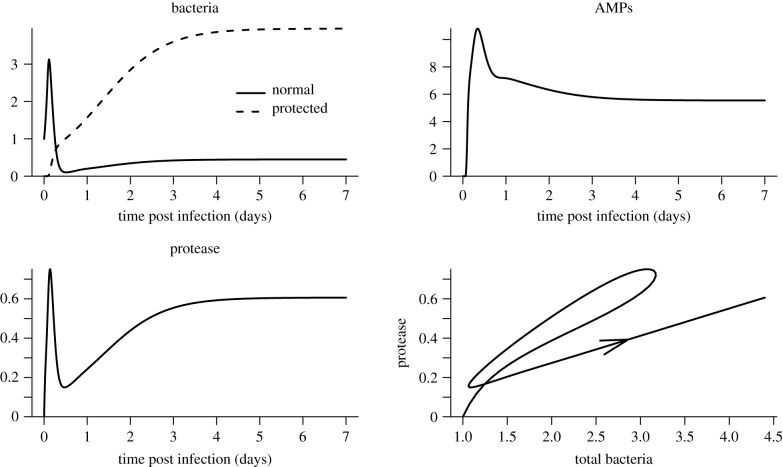
The extended model readily produces bimodal outcomes in which the pathogen is never reduced to extremely low levels (figure 4). Simulations where the pathogen is held in check (figure 5) confirm that the model can capture the known qualitative features of chronic infections: the outcome is a stalemate, converging to a stable equilibrium where a small bacterial population that continues to undergo cell divisions is held down by host immune responses. The ratio of protease to bacteria eventually drops to the lower level reflecting the slower protease production by protected bacteria. For these parameters, there are enough N-state bacteria, sustained by division of P-state cells, to keep AMP production induced to roughly 30% of its maximum rate. However, sustained AMP production could also result, in theory, if protected bacteria do not divide but nonetheless produce metabolic products that induce a host immune response (having little or no effect on them).

Figure 4.

As in figure 3, for the extended model equation (3.1) with normal and protected bacteria. Points are shaded according to the fraction of Protected bacteria running from 0 (lightest) to $\approx 90\text{\%}$ (darkest). Parameter values r = 0.5; Q_A = 12; δ_A = 0.02; c = 0.1; K = 1000; m = 0.25; δ_R = 2; g = 0.5; η = 0.25; ν = 0.5; L = 5; δ_P = 0.02. Conversion rate from N to P was given by the logit function $p(A)=\alpha \mathit{\Phi }(A|\mu =A_P,\sigma ={\sigma }_P)$, where $\mathit{\Phi }$ is the cumulative distribution function of a Gaussian distribution with mean μ and standard deviation σ, with α = 0.1, A_P = 5; σ_P = 2. Figure made by script Split_Outcomes_NPAR.R.

Figure 5.

Infection dynamics in the extended model, for a host with fast immune induction so that the outcome is a chronic infection. Parameter values are the same as in figure 4. Note, the bottom-right panel is a two-dimensional projection of a four-dimensional model trajectory. Figure made by script Split_Outcomes_NPAR.R.

Any observed chronic infection load (those in our Drosophila experiments are roughly 10⁴ − 10⁵ per host) can be matched in model (3.1) through a ‘protected tissue’ scenario where protected bacteria remain near their carrying capacity L. But even in this simple model there are multiple ways to achieve any desired equilibrium for P as the balance between cell divisions and killing by AMPs.

The outcomes in figures 4 and 5 are not the only possibility. In particular, the split into lethal or chronic infections can be transient (electronic supplementary material, figure S.2). With a larger carrying capacity L for the protected pathogens, and sufficiently high conversion rate, a large protected population can become established while the normal, unprotected cells are being driven down by the host immune response. The normal daughters of protected parents can then give the normal population enough of a ‘boost’ that they rebound from near-elimination, and increase to a lethal infection.

4. Discussion

The models presented here provide a proof of concept for our general negative feedbacks hypothesis. Hosts mounting a bactericidal immune response, and pathogens responding through mechanisms that degrade the bacteriocides or impede their production, is a simple but very general recipe for dynamics where small differences in initial conditions, or small differences between individuals in the values of key parameters, lead to dramatically different outcomes in different individuals. The effects of these differences occur within the first few hours of infection but the ultimate outcome may not be apparent until several days later.

When we additionally allow bacteria to enter a protected state at the cost of reduced ability to proliferate, the model can generate outcomes very much like those observed experimentally. The protected state could be a literal safe haven (e.g. a host tissue where they are shielded from immune responses), or a physiological or metabolic state with reduced sensitivity for the immune response.

Our model for protected pathogens assumed strictly one-way conversion (normal $\to$ protected) because that is sufficient to explain chronic infections. Allowing back-conversion would increase the theoretical potential for a suppressed bacteria population to rebound after an initially strong immune response has abated, provoking a second round of immune response. In theory, this might lead to cyclical rise and fall of infection, or to a series of infection-suppression-rebound events that grow in magnitude and eventually overwhelm the host. However, we are not aware of any empirical evidence for these scenarios in bacterial infections.

Being able to fit previously collected data is not a strong test of a model, especially when information that would constrain model assumptions and parameter values is limited. However, explaining previous observations has produced some new predictions that can be tested experimentally:

• 1. Chronic infections are dominated by a sub-population of protected pathogens.
• 2. Protected pathogens are not merely inert and invulnerable—they are doing something that provokes a sustained host immune response. In our models that ‘something’ is that some daughter cells have the normal, unprotected phenotype, but other mechanisms (such as host sensing of metabolic by-products) could have the same effect.

The models here are built from causal links (e.g. pathogens evoke a host immune response whose strength depends on pathogen abundance) without specifying the underlying ‘machinery’ (e.g. signalling pathways). This is valuable because it means that model predictions are not dependent on those details. However, it does not allow us to test our hypothesis more rigorously by predicting in advance what happens if we experimentally monkey with the machinery. To do that, our phenomenological model of the initial activation of host immune responses (a linear ramp from onset to completion) needs to be replaced by a detailed ‘systems biology’ model for the kinetic pathways leading to immune system activation, primarily the Imd signalling pathway. The actual nature of protected pathogens needs to be identified, and state transitions modelled mechanistically rather than specifying the outcomes at the level of population parameters (birth, death and state transition rates). Such models will also help us identify exactly what processes generate the variation among genetically homogeneous hosts, raised in a common environment, that can be amplified into divergent infection outcomes.

The models here and in [9] produce the same key dynamic property—widely divergent outcomes from similar initial states—from completely different biological mechanisms. In [9], the pathogen counters immune attack by diverting resources from the host to itself, thus diminishing the host’s capacity for immune response. In our model, the pathogen has its own chemical weapons that either degrade the host’s or slow their production. As a result, the two models produce two different pairs of outcomes: in [9], the pair are sustained infection contained by ongoing immune response, versus transient infection that is cleared completely. In our model, the pair are chronic and uncontrolled infection—the pathogen is never completely cleared. But these differences are less important than the similarity at the level of dynamic mechanism—a double-negative feedback loop between host and pathogen—suggesting that host–pathogen mutual antagonisms of many different types could be the common dynamic feature driving the common observation of bimodal infection outcomes in a variety of different systems.

Data accessibility

No original data are presented in this paper. The previously published data used here (in figure 1), and computer code to replicate all results in the paper, are available on figshare at https://doi.org/10.6084/m9.figshare.14502249.v1.

Authors' contributions

All authors contributed to conceiving the study, formulating hypotheses, developing models, and writing the paper. S.P.E. wrote computer scripts, performed mathematical analyses and authored the first draft. All authors gave final approval to submit the paper for publication and agree to be held accountable for the work performed therein.

Competing interests

We declare we have no competing interests.

Funding

This research was not specifically supported by any research grant. The authors receive research funding from the US National Science Foundation and National Institutes of Health.