Spatial connectivity in mosquito-borne disease models: a systematic review of methods and assumptions

Abstract

Spatial connectivity plays an important role in mosquito-borne disease transmission. Connectivity can arise for many reasons, including shared environments, vector ecology and human movement. This systematic review synthesizes the spatial methods used to model mosquito-borne diseases, their spatial connectivity assumptions and the data used to inform spatial model components. We identified 248 papers eligible for inclusion. Most used statistical models (84.2%), although mechanistic are increasingly used. We identified 17 spatial models which used one of four methods (spatial covariates, local regression, random effects/fields and movement matrices). Over 80% of studies assumed that connectivity was distance-based despite this approach ignoring distant connections and potentially oversimplifying the process of transmission. Studies were more likely to assume connectivity was driven by human movement if the disease was transmitted by an Aedes mosquito. Connectivity arising from human movement was more commonly assumed in studies using a mechanistic model, likely influenced by a lack of statistical models able to account for these connections. Although models have been increasing in complexity, it is important to select the most appropriate, parsimonious model available based on the research question, disease transmission process, the spatial scale and availability of data, and the way spatial connectivity is assumed to occur.

1. Introduction

The World Health Organization (WHO) estimates that over 80% of the world's population is now at risk of one or more vector-borne disease, accounting for 17% of the global burden of communicable diseases [1]. The past 50 years has seen an unprecedented emergence of mosquito-borne diseases, in particular dengue fever, chikungunya and Zika, linked to urbanization, globalization, international mobility and climate change [2,3]. Increased connectivity between geographical regions due to international air travel has led to these diseases invading previously naive populations where competent vectors exist, as seen in the introduction of chikungunya to Latin America and the Caribbean [4], and sporadic outbreaks of dengue fever in parts of Southern Europe [5]. Conversely, the global incidence of malaria has decreased over the past 20 years, with an increasing number of countries working towards eradication, although this trend has slowed in the past 5 years [6]. Spatial connectivity arising from human movement may pose a risk of re-introducing a pathogen into indigenous populations. Failure to account for this in modelling studies may negatively impact control and eradication campaigns [7].

The inclusion of space within infectious disease epidemiology is not a new phenomenon; however, the introduction of Geographical Information Systems, improvements in computational power, and availability of spatial data have made spatial modelling more accessible [8]. Despite this, Reiner et al. [9] found that spatial modelling methods were underrepresented in their review of mathematical models for mosquito-borne diseases, and spatial connectivity was not explored in the majority of studies. Tobler's first law of geography states that ‘everything is related to everything else, but near things are more related than distant things’ [10]. However, when studying mosquito-borne diseases, long-distance movement of hosts and vectors may create connections between distant regions. Connectivity between geographical areas and observations can arise for a number of reasons, for example, shared characteristics such as human behaviour, vector-control programmes, levels of immunity within communities and human and vector movement. Although these issues are common among diseases, their impact and the assumption about how connectivity arises may differ due to mosquito behaviours and different geographical settings.

Spatial connectivity is an important driver of mosquito-borne disease, but to our knowledge, there are no systematic reviews of spatial modelling techniques that include statistical, machine learning and mechanistic frameworks. These three approaches are used to address different objectives and require different types of information. Mechanistic models are less dependent on extensive training datasets than statistical or machine learning approaches and can be parameterized using previous experiments. However, this requires an in-depth understanding of the underlying disease process and incorrect parameterization could lead to invalid inference [11]. Mechanistic models are useful for studying (re-)emerging diseases, where few data exist, and comparing potential control strategies [12]. By contrast, machine learning models are able to make predictions about complex biological processes, without prior knowledge of the underlying process, using algorithms that learn from rich, complex data [13]. Statistical models are able to explore relationships between variables, test hypotheses about the underlying transmission process and make predictions about an outcome of interest where adequate data are available.

This systematic review aims to identify spatial models used to investigate the transmission of mosquito-borne disease to humans, the assumptions made about how spatial connectivity arises and the data used to inform the spatial models. We provide detailed explanations of these methods, their assumptions, how they were used, and discuss their advantages and disadvantages.

2. Methods

2.1. Search strategy

The PRISMA guidelines for systematic reviews and meta-analyses were followed for this review [14]. Five online bibliographic databases were searched: Ovid/Medline, Web of Science, Embase, Global Health and Scopus. The final search was completed on 14 December 2020. The search strategy included relevant keywords and Medical Subject Headings (MeSH) related to mosquito-borne diseases and the mosquito species that transmit them, mathematical models used to model infectious diseases and spatial connectivity. Full details of the search strategy are provided in table 1. Mosquito-borne diseases listed on WHO and European Centre for Disease Prevention and Control websites were considered: dengue fever, Zika, chikungunya, malaria, yellow fever, West Nile fever, Rift Valley fever, sindbis fever and Japanese encephalitis [15,16].

Table 1.

Search terms used to search Medline, Embase, Global Health and Web of Science related to mosquito-borne diseases, modelling and spatial connectivity.

mosquito-borne diseases	modelling	connectivity
mosquitoa,b diseaseb	(mathb OR statisticb)a modelb	(spatib OR cluster)a analysis
chikungunya	(gravity OR radiation)a modelb	autocorrelb OR neighbb OR hierarchb OR adjacenb OR proximity OR network OR commutb OR connectb
dengue	(spatib OR Bayesb)a modelb	randoma effectb
‘Japanese encephalitis’	(ecologb OR environmentb)a modelb	(BYM OR ‘Besagb Yorke and Mollie’)a modelb
malaria	(dynamic OR stochastic OR deterministb OR mechanb OR compartmentb)a modelb	‘conditional autoregressb’ OR CAR
(Rift Valley)a (fever OR virus)	(regression OR generalb)a modelb	humana (mobility OR movement OR travel)
sindbis	(SIR OR SEIR)a modelb	spatba dependb
(‘West Nile’)a (fever OR diseaseb or virus)	patcha modelb	metapopulation
‘yellow fever’	(empirical OR correlb OR movement)a modelb	spatiba (structure OR matrix)
Zika
Aedes
Anopheles
Culex

^aProximity searching was used, search terms had to be within three words of each other. ADJ3 was used for Embase, Medline and Global Health, NEAR/3 was used for Web of Science.

^bDenotes truncation. MeSH terms related to terms above were also searched.

Results from database searches were combined and stored using EndNote referencing software; duplicates were removed manually. The titles and abstracts were screened and irrelevant articles excluded. Two reviewers screened full texts independently and disagreements were resolved by consensus. After relevant papers were identified, their references were screened to identify other relevant studies.

2.2. Inclusion and exclusion criteria

The inclusion criteria are as follows: articles must be peer-reviewed, published in English and contain a spatial model that investigates the transmission of mosquito-borne disease to humans. Spatial models are defined as those that explicitly account for connections between geographical areas or observations. There were no geographical or publishing date restrictions applied. Articles were excluded if they only modelled transmission to vectors or non-human hosts as these were outside the scope of this review and may require different assumptions of connectivity. Theoretical modelling studies that were fitted using simulated data were excluded unless they were validated using real data. Conference and workshop proceedings were excluded, as were review articles.

2.3. Data analysis

The following variables were extracted from eligible papers: title, first author, year of publication, disease studied, country/region studied, the spatial scale of the data, spatial model used, the spatial method used to account for connectivity, connectivity assumptions and the data used to inform the spatial element of the model.

Spatial models were classified as either statistical, machine learning or mechanistic. Statistical models assume that the data are a realization of a pre-specified probability distribution. These probability distributions are defined by a set of parameters which are estimated from the data using estimation, inference and sampling techniques, such as maximum likelihood, Markov chain Monte-Carlo and bootstrapping. The association between an outcome of interest and a set of covariates is determined by how these affect the probability distribution of the outcome. Statistical models were also classified as either fixed effect, where all parameters are treated as fixed, non-random values or mixed effect, which contain both fixed parameters and random parameters that account for unobserved heterogeneity or clustering within the data. Machine learning methods use algorithms to learn patterns from observed data without the need to specify a data model prior to analysis. This makes them a useful alternative to mechanistic or statistical models where underlying biological processes are not known [13]. Mechanistic models, sometimes referred to as mathematical models, aim to replicate the process of disease transmission through a population across time based on a simplified mathematical formulation of the underlying disease mechanisms. These models often simulate the movement of individuals through infectious stages, or compartments, known as compartmental models [11]. Mechanistic models can be parameterized using a combination of data, when available, and results from previous studies. This makes them particularly useful for studying novel pathogens where there are few empirical data or when comparing potential control measures [12]. Spatial assumptions were compared between diseases and mosquito species.

Analysis of the data and visualizations were carried out using R [17]. Data extracted from the studies included in this systematic review and code used to create figures and tables are available from https://github.com/sophie-a-lee/mbd_connectivity_review and archived in a permanent repository [18]. This study is registered with PROSPERO, CRD42019135872.

3. Results

3.1. General characteristics

We identified 248 studies published between 1999 and 2020 that were eligible for inclusion (figure 1). These studies used data from 164 countries across six continents (electronic supplementary material, figure S1). Almost half (n = 118, 47.6%) of the studies modelled malaria transmission, 99 (39.9%) modelled dengue fever (including two modelling dengue haemorrhagic fever, two which also modelled Zika, one that also modelled chikungunya and one that modelled dengue, chikungunya and Zika), 11 (4.4%) modelled just Zika and five (2%) just chikungunya, one modelled both. Seven (2.8%) modelled West Nile fever, five (2%) Japanese encephalitis, 1 (0.4%) Rift Valley fever and one (0.4%) yellow fever. No spatial modelling studies were identified for sindbis fever. The number of spatial modelling studies published has increased over time, with an average of one study published per year in 1999–2005, 5.8 per year 2006–2010, 14.2 per year 2011–2015 and 28.2 per year 2016–2020. The diversity of diseases studied using spatial modelling has also increased; until 2005, only malaria studies were identified whereas there have been six different diseases studied using these methods published in 2020 (electronic supplementary material, figure S2). Most studies (n = 218, 87.9%) used aggregated data to fit models, most often aggregated to administrative district- or country-level (n = 169, 68.1%) or clusters based on surveys or shared characteristics (n = 25, 10.1%). The remaining papers either separated their study area into a grid and aggregated data to these patches (n = 24, 9.7%) or fit data to individuals (n = 30, 12.1%). A full summary of data extracted from studies by disease is given in electronic supplementary material, table S1.

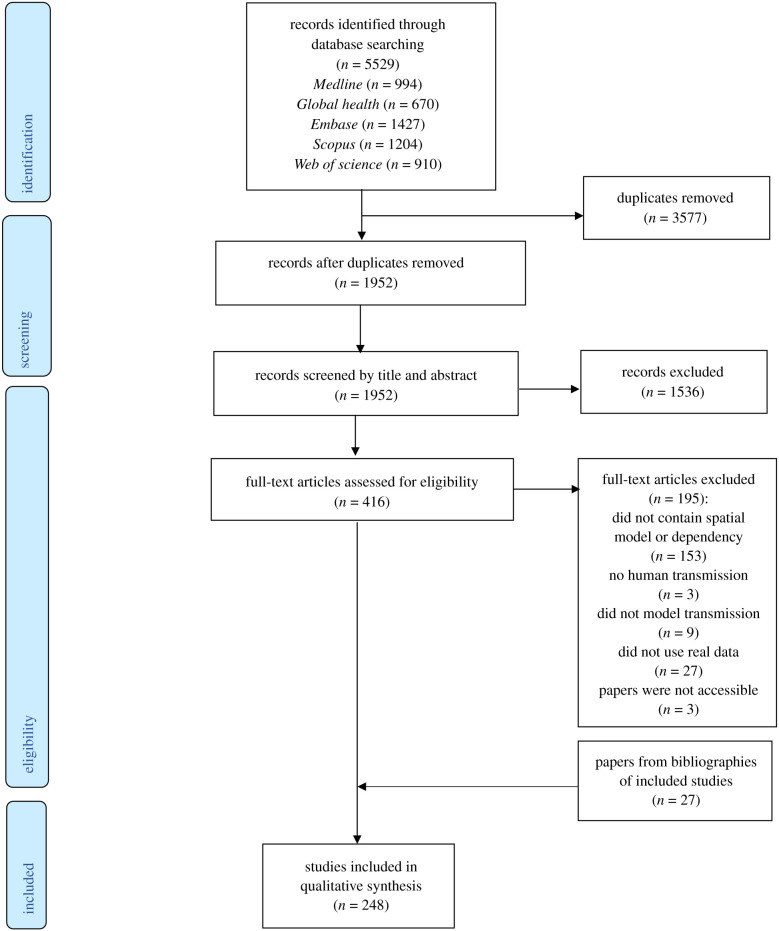
Figure 1.

PRISMA flow diagram of the search and exclusion process.

3.2. Spatial modelling methods

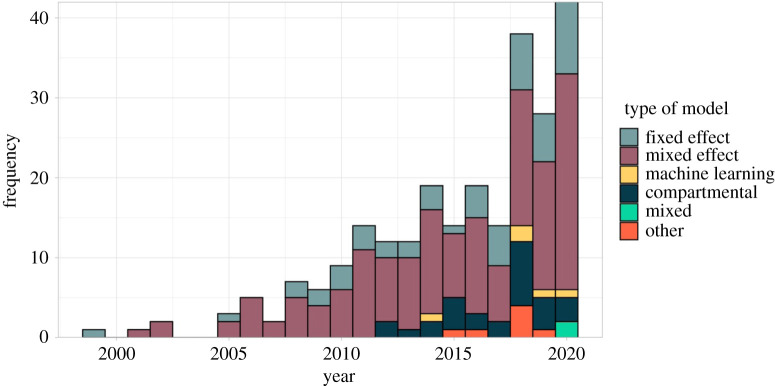
Most (n = 209, 84.2%) studies used a statistical modelling framework, in particular mixed effect models (n = 155, 62.5%). The first mechanistic model included in this review was published in 2012; mechanistic models are becoming more common with over half of those studies published since 2018 (figure 2). Newly emerging diseases (Zika and chikungunya) were more often modelled using mechanistic models rather than statistical, which were more commonly used for established diseases (e.g. malaria and dengue) (electronic supplementary material, table S1). There were two studies published in 2020 that used a combination of methods: one compared a mechanistic and machine learning approach to predicting dengue transmission [19], another used both a machine learning and statistical approaches to explore the relationship between risk factors and dengue outbreaks [20].

Figure 2.

Number of spatial modelling studies published per year by model type. Statistical models were classified as a fixed effect if parameters were treated as fixed, non-random values or mixed effect if they also included random parameters to account for unobserved heterogeneity or clustering (also known as hierarchical or multilevel models). Machine learning models used algorithms to learn patterns from the data. Compartmental models were mechanistic models that simulated the movement of hosts and/or vectors through disease compartments. Models classified as 'other' did not fall into any of these categories, this included mechanistic models that did not explicitly model movement through compartments, or bespoke statistical models.

We identified 17 distinct models that incorporated spatial connectivity into their framework: nine statistical, four machine learning and four mechanistic models. Full descriptions of the 17 models identified in this review, including model structure, the method and data used to account for spatial connectivity, and a discussion about the advantages and disadvantages of each model are given in electronic supplementary material, technical appendix. Some models were specifically designed for spatial analysis, whereas others have been adapted or extended to incorporate this connectivity. This section gives an overview of the methods used to account for spatial connectivity for each type of model. Details and best practices are summarized in table 2.

Table 2.

The advantages, disadvantages and uses of spatial modelling methods.

model type	spatial method	description	advantages	disadvantages	application
statistical or machine learning	spatial covariate	inclusion of a covariate that aims to describe spatial connectivity within a regression model. For example, incidence of surrounding regions, distance between observations, or number of people moving between regions. The covariate is treated as a fixed effect and included into a model as any other covariate	compatible with all statistical or machine learning methods relatively quick and simple to fit allows human and vector movement to be included interpretation of coefficients is often simpler than other methods allows models to 'borrow strength' from connected regions, improving precision	models assume that the relationship between the outcome and spatial covariates is stationary and isotropic inclusion of a large number of spatial covariates increases risk of overfitting and multicollinearity within a model user must specify which regions/observations are connected prior to model fitting which does not allow other connections to be explored	exploratory tool for statistical or machine learning studies carried out on a small scale where few spatial connections are expected. Statistical or machine learning modelling studies where spatial connectivity is assumed to arise from human movement
statistical	local regression models	local regression models are fitted to each region using data from nearby regions, weighted by distance. Also known as GWR. Coefficients are calculated separately for each regression model	relatively simple to carry out and interpret useful exploratory tool to understand how the relationship between covariates and the outcome differ across space does not assume these relationships are stationary	does not provide a global model to make interpretations about a region as a whole only allows distance-based spatial connectivity to be included	exploratory tool to generate hypotheses about how relationships differ across space. Cannot be used to make inferences about regions as a whole. Only appropriate when studying areal data
statistical	random effects and fields	random effects or fields with a spatially structured covariance function are included in a regression model to account for additional correlation or heterogeneity arising from spatial connectivity. Users must choose an appropriate spatial structure before fitting the model, usually assuming that regions are connected if and only if they are adjacent (areal data) or that connections decay exponentially as the distance between them increases (individual-level data)	relatively easy to obtain connectivity data (if using structure based on adjacency or distance) does not assume stationarity in the model allows connections between a large number of observations without issues of overfitting associated with other statistical methods increasing number of methods and software developed to make model-fitting process simpler	more complex to fit and interpret models than other statistical models random effects require an appropriate spatial structure defined before model is fitted structures identified in this review only allow models to account for connectivity between neighbours or close regions, other connectivity has not been explored	statistical models where spatial connectivity is expected to exist between nearby regions. Can be carried out in small- or large-scale studies. Recommended for established diseases rather than a newly emerging setting as requires large amounts of data for precise estimates
machine learning	movement matrix	movement matrices reflecting the movement of humans around a network used to weight connections between hidden layers of a neural network	allows complex, dynamic connectivity structures to be explored allows human movement to be included in a machine learning framework	requires human movement data (or a representative proxy) to create which can be difficult to obtain inclusion of the matrix in the hidden layer of neural networks means the impact of this movement is difficult to observe computationally intensive	inclusion in a neural network where human mobility is known to drive transmission. Studies that require accurate predictions based on a large amount of data but quantifying this process is not the focus
mechanistic	spatial parameter	spatial parameters are included in mechanistic model equations, either to take account for a spatial process or to update populations within each disease compartment of the model. Examples include diffusion parameters allowing hosts and vectors to move across a region or mosquito abundance that borrows information from connected regions	models can be fitted with few data and used to make causal inferences parameters can borrow information from other regions about processes to take account of shared characteristics less computationally intensive to fit than other mechanistic approaches can be used within any mechanistic model	requires knowledge and information regarding the underlying process of transmission parameters assume that the impact of spatial coefficients on transmission is stationary within a compartmental model making them inappropriate on a large scale	models aiming to make causal inferences about the underlying process of transmission. Able to fit models where few data are available making it useful for newly emerging diseases or areas with low transmission. More appropriate in small-scale studies where stationarity can be assumed
mechanistic	movement matrix	movement matrices that reflect the movement of hosts and/or vectors around a network are included within a mechanistic model. These allow interaction between hosts and vectors in different locations and update the population at each node of the network	allows complex, dynamic connectivity structures to be explored results can be extrapolated beyond the data used to fit them and causal inferences can be made provides a more 'realistic' reflection of human and vector behaviour models can be fit with relatively few data	adequate movement data are difficult to obtain the complex nature of these models means computation can be difficult and time consuming inferences can only be made about the setting the model is parameterized to reflect requires the population being studied to be split into nodes in networks	models taking account of human and/or vector movement or other complex connectivity structures. Able to fit models where few data exist as well as large amounts, useful for newly emerging diseases. Able to study the process of transmission or causal structures. Works well with agent-based or metapopulation mechanistic models where the population is described using a network

3.2.1. Statistical models

All statistical models identified within this review were extensions of generalized linear or additive models (GLM/GAM). These models assume that all observations are independent after adjusting for the covariates, which is not always appropriate when considering spatial data. Although there were nine distinct statistical models, all of them used one of three methods to account for spatial connectivity: inclusion of spatial covariates as fixed effects, localized regression models or the inclusion of a spatially structured random effect or random field.

3.2.1.1. Spatial covariates

Of the 209 papers using statistical models, 25 (12%) included spatial covariates to account for spatial connectivity in the data. Spatial covariates are entered into the model in the same way as nonspatial covariates, but aim to account for connectivity within the model. Spatial covariates included the observed incidence in connected regions [21–30], the number of people moving between regions [20,31–35], the distance between regions [31,35–37], coordinates of the centroid of a region [38–40], the number of time spent commuting between regions [41] and spatial eigenvectors created using spatial filtering [42–44]. Spatial filtering creates spatial covariates by decomposing Moran's I (a measure of spatial correlation) into an eigenvector per region/observation [45]. Two studies applied a smoothing function to the spatial covariates within a GAM, allowing for a nonlinear relationship between the outcome and measure of connectivity [24,37]. Another study included spatial kernels, exponentially decaying correlation functions of the distance between cases' home and work addresses, estimated from public transport journeys, as spatial covariates when estimating the probability of cases being linked [46].

Spatial covariates are compatible with all statistical models identified in this review. If adequate data are available, this is a simple and efficient way to include connectivity information into a statistical model. Using information from connected regions also allows the model to ‘borrow strength’ from other parts of the data to increase the precision of estimates. Spatial covariates were the only method that allowed human movement data to be included in statistical models identified in this review; all other methods relied on a function of distance. However, the inclusion of a large number of spatial covariates risks overfitting the model to the data, meaning the model reflects the sample data too closely and is unable to make prediction or inferences about the wider population, or introducing multicollinearity. Most spatial covariates require ‘connectivity’ to be defined prior to model fitting, introducing a subjective element into the model and potentially oversimplifying the spatial structure. For example, models that included incidence from connected regions defined these as regions that share borders; this ignores potential dependency between distant regions which could still invalidate the independence assumption. The inclusion of spatial covariates as fixed effects assumes that the relationship between them and the outcome is stationary (the same across the whole spatial area) and linear which may not be appropriate across large areas.

3.2.1.2. Local regression models

Twenty papers used a geographically weighted regression (GWR) model [47–65] which fits local regression models to each observation or region rather than a single global model [66]. Each local model has different coefficients, estimated using information from connected observations that are weighted by a function of distance, such as the one shown in figure 3c. As with spatial covariates, GWR is a fairly simple and efficient method to account for connectivity and a useful exploratory tool to investigate how relationships differ across space. Estimating a different coefficient for each model overcomes the issue of stationarity which is present when using spatial covariates. GWR is not suitable for making inferences or predictions about the study area as a whole.

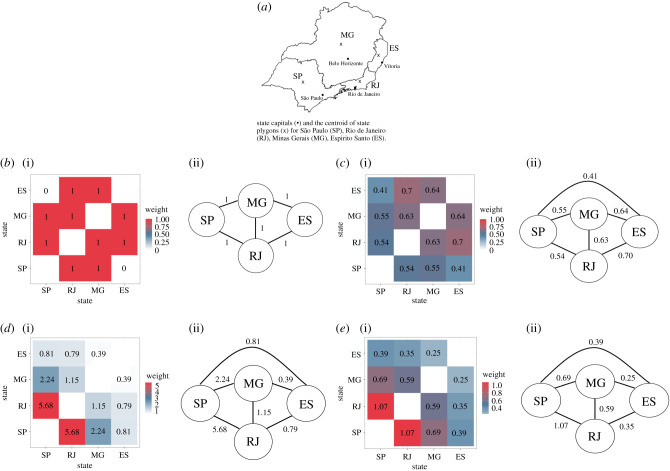
Figure 3.

Comparison of spatial connectivity using different data sources and assumptions. The level of connectivity between regions represented in models can differ substantially depending on the assumptions made about how connectivity arises, and the data used to weight connections. The heat plots and connectivity matrices show the strength of connectivity between states in Southeast Brazil (a), represented by nodes in the matrices, using assumptions and methods identified in this review. Numbers within the heat plot and along edges of the connectivity matrix represent the weight of connections. These techniques were used to weight observations in GWR models, to structure random effects and random fields, or to weight movement matrices in neural networks, metapopulation models, and agent-based models. (b) Neighbourhood based: assumes states are connected if and only if they share a border. Application: to structure random effects in a CAR model. (c) Distance-based: assumes connectivity between states decays exponentially as distance between centroids (denoted x on the map) increases, where weight = exp(dij /1000) and dij is the distance between states i and j. Application: used to weight observations from neighbouring regions in a GWR model. (d) Human movement data: assumes connectivity between states arises due to human movement. In this case, based on the number of air travel passengers moving between capital cities of each state. Application: to weight hidden layers within a neural network. (e) Movement model: assumes connectivity between states arises due to human movement, estimated using a movement model (in this case, a gravity model). Application: used to weight movement between nodes in a metapopulation model.

3.2.1.3. Spatially structured random effects and random fields

The final, and most common, method used to account for spatial connectivity in statistical methods was the inclusion of a spatially structured random effect or random field. Fixed effect statistical models assume that there is a true parameter value and that the only variation within the data, after accounting for covariates, is sampling error. Random effects and random fields explicitly allow additional spatial variation and/or correlation in the data to be incorporated directly into the model structure. The structure of the random effects or random fields must be specified prior to model fitting and should be informed by the spatial connectivity assumption. Most models identified in this review used a Gaussian process which assumes the spatial process at fixed locations follows a multivariate normal distribution, with a mean of 0 and a covariance structure based on distance or, when dealing with areal data, adjacency.

We identified 150 studies (150/209, 71.8%) that used a spatially structured random effect within their statistical model, 95 assumed a Markov random field structure based on adjacency [29,40,42,64,67–156] and 57 used a distance-based structure [141,157–212] (one used both [141]). A commonly used Markov random field is known as the conditional autoregressive (CAR) model, which assumes that regions are connected if and only if they are neighbours [213], i.e. regions that share a border or, in one case, regions within a fixed distance [140]. The weighting matrix used to formulate this Markov random field is shown in figure 3b. Distance-based approaches identified in this review used the Matérn correlation function [214] to define the random effect covariance. This assumes that connectivity between points decays exponentially as the distance between them increases, as shown in figure 3c. There were 15 studies that included a spatially structured random field, a bi-dimensional smooth function in space over the coordinates of observations or the centroid of a region [40,215–227]. Bi-dimensional smooth functions are a type of Gaussian process, with a covariance structure defined by the distance between observations, for which connectivity is expected to decrease exponentially as distance increases [228] (figure 3c). One spatial model included a random field, estimated using a Markov random field [229], similarly to the CAR models above, assuming connectivity exists between neighbouring regions [228]. One study used an alternative way of accounting for residual spatial autocorrelation by fitting a separate regression model to the error terms of a non-spatial model. The observed outcomes from previous time points were included in the residual model as covariates. This model was fitted using an iterative process and was referred to as a vectorial autoregressive model [230]. Further details are given in electronic supplementary material, technical appendix.

Although random effects and random fields are more computationally intensive than the other statistical approaches, there are a number of statistical methods and programs built to fit these types of models which aim to overcome computational issues [228,231,232]. These models are able to account for dependency between a large number of regions or observations without overfitting or introducing multicollinearity that causes issues when using spatial covariates. The structure of random effects and random fields must be determined before the model-fitting process, potentially introducing subjectivity into the model-fitting process, although they can be visualized which can help generate hypotheses and identify additional factors that may not have been accounted for within the original model. Within this review, we only identified two spatial structures that were used within these models: distance based and neighbourhood based. These structures are adequate if spatial connectivity exists between close observations but we did not identify structures that would allow for other assumptions, such as long-distance movement of hosts and vectors, to be incorporated into a statistical model.

3.2.2. Machine learning methods

We identified two methods that were used to account for spatial connectivity within machine learning models: the inclusion of spatial covariates, and the development of movement matrices that aim to replicate human movement behaviour.

3.2.2.1. Spatial covariates

Five papers included spatial covariates as inputs for their machine learning algorithms. These spatial covariates included cases from neighbouring regions [233–235], the number of people travelling between regions based on air travel [234], public transportation networks [20] or a gravity model that aimed to replicate human commuting behaviour [236], and the distance between countries [236]. The inclusion of spatial covariates as inputs is compatible with all machine learning models and, if the data are available, does not require any additional computation.

3.2.2.2. Movement matrices

We identified two papers that constructed a matrix reflecting the movement of people between districts using public transportation data [19,237]. Both papers used this matrix, similar to the one shown in figure 3d, to weight layers within a neural network model, allowing the algorithm to predict the number of dengue cases across the study area while accounting for connectivity arising from human mobility. Although both studies used public transportation information to create their matrices, they could be constructed using movement models that aim to replicate human commuting behaviour, such as gravity or radiation models [238] (figure 3e), or other proxies such as distance-based functions where data are not available (figure 3c).

3.2.3. Mechanistic models

There were two methods used to account for spatial connectivity in mechanistic models identified by this review: movement matrices and spatial parameters.

3.2.3.1. Movement matrices

There were 21 studies (21/34, 61.8%) included in the review that used a movement matrix within a mechanistic model to account for spatial connectivity [19,32,239–257]; all these studies assumed that connectivity arose from either host or vector movement. These models treated subgroups of the host and/or vector populations as nodes in a network with values of the matrix reflecting movement between those nodes. Examples of these matrices constructed using different assumptions and data are given in figure 3. Matrices were constructed using human movement data from Twitter [32,251,256], air travel [239,249,250] or public transportation [19], using movement models that aimed to replicate human commuting behaviour [32,241,243,244,246,248,254,255,257], distance [242] or using a fixed value based on the type of neighbourhood [252,253]. Two studies estimated people's home and work addresses using mobile phone data and simulated movement between those [245,247], and two simulated the short flight distance of mosquitoes by allowing movement into neighbouring cells [240,245].

3.2.3.2. Spatial parameters

Thirteen studies (13/34, 38.2%) included spatial parameters within the model equations that aimed to account for connectivity [67,258–269]. Unlike movement matrices, these were directly incorporated into the model equations to update the population within a given compartment, or as a proxy for another process. Spatial parameters included the force of infection calculated using a distance-based kernel [259,260] and mosquito abundance estimated using a GAM containing a spatial random field [258]. Some models updated the population within compartments based on spatial parameters, either using a fixed-distance dispersion value [264–266], or calculating the proportion leaving regions using mobile phone records [263], air travel [262] or movement models [262,269]. One study used a mechanistic model but estimated the number of infected people using a CAR model [67].

3.3. Spatial connectivity assumptions

We collected details on the assumptions that authors made about how spatial connectivity arises within the data, regardless of the model type or method used. Although the exact assumptions differed between studies, all could be grouped into one or more of the following categories:

• 1. distance based,
• 2. human movement,
• 3. vector movement.

This section presents the advantages, disadvantages and methods used to implement these assumptions. A summary of these points with guidance on their ideal uses are provided in table 3.

Table 3.

The advantages, disadvantages and application of connectivity assumptions.

connectivity assumption	advantages	disadvantages	application
distance based	easy to obtain data can be incorporated into all types of model can be used as a proxy for shared characteristics that cannot be observed	oversimplifies process of transmission misses connectivity between distant regions difficult to define how ‘close’ regions should be to be considered connected	small-scale studies where unobservable processes, such as shared behaviours, create spatial connectivity. Not appropriate where long-distance connections are expected to exist due to travel. Basis of most statistical approaches identified in this review, e.g. GWR and mixed effect models
human movement	shown to be an important part of disease transmission for mosquito-borne diseases can account for connectivity between distant observations as well as close	difficult to quantify and obtain data, often requiring a proxy such as distance to be used data often have a number of biases may not be necessary for malaria studies in small-scale studies of endemic areas	Aedes or Culex-borne diseases in endemic settings where commuting leads to increased exposure, studies in areas that are disease-naive or nearing elimination at risk of (re-)introduction from long-distance movement such as immigration. More popular in mechanistic approaches such as metapopulation or agent-based models that allow complex movement matrices to incorporated. Only spatial covariates were able to reflect this connectivity in statistical methods
vector movement	an important part of the disease transmission process for all mosquito-borne diseases	difficult or impossible to obtain data due to the short flight distances of most mosquitoes, would not be necessary if considering a large area or a short-term study	small-scale studies or long-term forecasts, particularly malaria studies where transmission generally occurs at night. Due to a lack of data, a proxy must be used such as distance based on known flight distances of mosquitoes. May be included to account for differences in exposure levels across space

3.3.1. Distance based

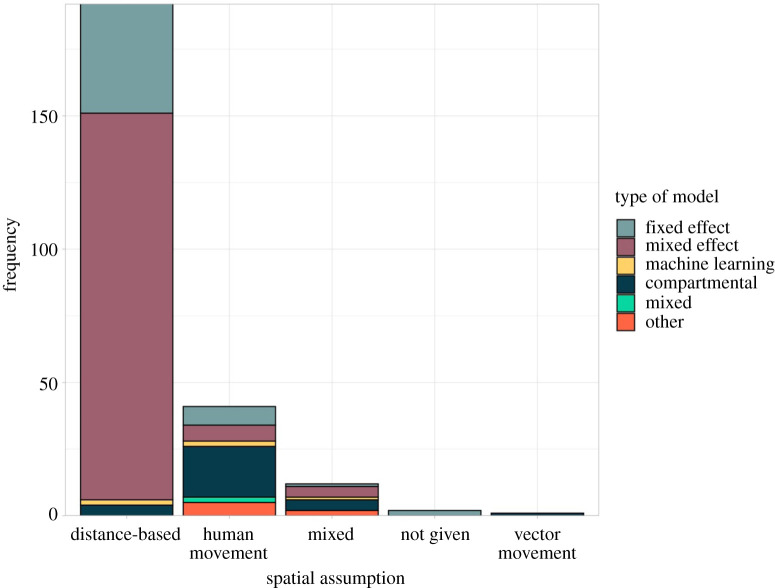
There were 200 (200/248, 80.6%) studies that assumed connectivity existed between observations or regions if and only if they were close. Although this was by far the most common assumption observed in this review, it was not explicitly stated in many of the studies. Twenty-two studies stated that they used a distance-based assumption as close regions were more likely to share characteristics such as climate systems, protective behaviours (e.g. bed net use), socioeconomic and demographic factors, vector ecology and land use type.

The majority of studies making a distance-based assumption of connectivity used a statistical model, only five studies used a mechanistic model and three used machine learning. The most common method for including distance-based connectivity within a model was the inclusion of a random effect or random field with a covariance structure defined by distance or neighbours (n = 162). Other methods included using spatial covariates (n = 16), such as the incidence rate in neighbouring regions or distance between observations, and local regression models fitted using data from nearby regions, weighted by distance (n = 20).

One of the main advantages of making a distance-based assumption of connectivity is that measures of connectivity (either distance or contiguity) are easy to obtain from geographical data. Contiguity is usually defined with chess analogies: rook contiguity defines neighbours as those sharing a common edge or border, whereas queen contiguity also includes regions sharing a common vertex. Another advantage of using one of these approaches is that there are a number of well-established models (particularly in statistical analysis) that were designed or adapted to incorporate this information, such as GWR and CAR models.

The main drawback of assuming connectivity is solely based on distance is that it may oversimplify the process, particularly for mosquito-borne diseases which require interaction between a susceptible host and an infectious vector. One of the most common models based on the assumption that connectivity exists between neighbouring regions, the Besag, Yorke and Mollié model (one example of a CAR model), states that these assumptions are reasonable if the disease is non-contagious and rare, which is not the case for mosquito-borne diseases [273]. Although regions are more likely to share characteristics with close regions, it is hard to define where this ‘closeness’ ends and how similar places should be before they are considered connected. Most studies assumed that characteristics were shared between neighbours or within a set distance; however, applying the same rule for all shared characteristics may miss some heterogeneity or exaggerate connectivity.

3.3.2. Human movement

We identified 50 studies that assumed spatial connectivity was related to human movement; most used mechanistic models (n = 28, figure 4) which are able to include complex mobility matrices (see metapopulation and agent-based models in electronic supplementary material, technical appendix, and figure 3 for more details). Other methods used to account for human movement within models included spatial covariates based on the number of people moving between regions, random effects which assumed people were more likely to travel to neighbouring regions, and a bespoke statistical model which simulated home and work addresses based on public transport journeys [46].

Figure 4.

Connectivity assumption by model type. The number of spatial modelling studies that assumed connectivity is based on distance, human movement or vector movement (bars) separated by model type. The vast majority of statistical models (fixed and mixed effect models) assumed that connectivity was based on distance, whereas compartmental models were more likely to assume human movement drives connectivity.

Studies were more likely to assume spatial connectivity arose through human mobility if the disease was transmitted by a mosquito of the Aedes genus (figure 5); this included dengue fever, chikungunya, yellow fever and Zika. Aedes mosquitoes are most active during the day, meaning interaction between host and vector is influenced by commuting behaviour [274], whereas Anopheles mosquitoes are night-biters and are more likely associated with vector movement or migration [275,276]. Less than half (n = 22) of the studies in this group used human mobility data to inform the spatial component of the model. Human mobility datasets included mobile phone GPS data, geo-located tweets, air travel information, public transportation networks and surveys. Other studies used a proxy such as distance or movement models, which replicate human commuting behaviours. The most common movement models were the gravity and radiation models. Both models assume that the movement of people is related to the population at each location and the distance between them; the radiation model also takes account of the population between locations under the assumption that people are less likely to commute to distant places when opportunities exist closer to home [238].

Figure 5.

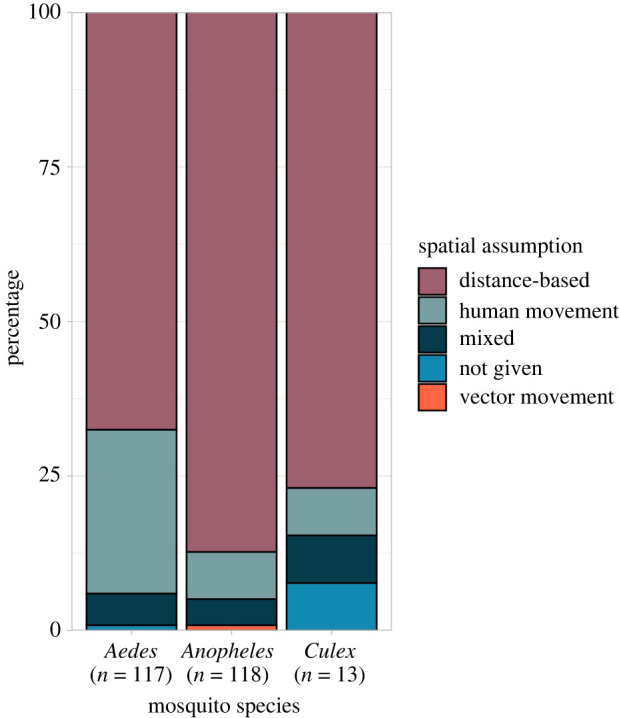
Connectivity assumptions by mosquito species. The percentage of studies modelling a disease transmitted by each mosquito species that assumed spatial connectivity is related to the distance between regions or observations (using a distance-based function or a neighbourhood structure), human movement or vector movement. Dengue fever, chikungunya, yellow fever and Zika were transmitted by mosquitoes of the Aedes genus; malaria was transmitted by mosquitoes of the Anopheles genus, and Japanese encephalitis, Rift Valley fever and West Nile fever were transmitted by mosquitoes of the Culex genus.

Unlike distance-based methods, the human mobility assumption allows for long-distance connections which may be important to the disease process, particularly in the region at risk of (re-)introduction of disease from imported cases. Prior studies have identified the importance of human mobility in the transmission of mosquito-borne diseases and found that failure to adequately account for this can lead to biased or invalid inferences [7,32,247,263,272,274,277]. However, human movement data can be difficult to obtain and may not be representative of all demographic and socioeconomic groups [272].

3.3.3. Vector movement

We identified 10 studies that explicitly stated they assumed spatial connectivity arose from vector movement; all these studies used a fixed distance or adjacency as a proxy for vector movement as adequate movement data was not available. One model included wind speed to account for vector movement as this extended the potential flight distance of mosquitoes, another weighted vector movement to adjacent tiles making this more likely if adjacent tiles contained humans or breeding grounds. There was only one study in this review that assumed all connectivity arose from vector movement, all others included other assumptions.

4. Discussion

This review provides the first comprehensive overview of spatial models, of any type, used to investigate the transmission of mosquito-borne pathogens, and the connectivity assumptions that underpin them. The last 10 years have seen a rapid increase in the number of spatial modelling studies of mosquito-borne diseases and the variety of approaches used. We identified 17 distinct spatial models that were used to explore the transmission of mosquito-borne pathogens to humans. These were classified as either statistical, machine learning or mechanistic; the choice of model should depend on the aim of the study, the type of data available and the information required from the modelling output. Statistical models are able to explore relationships between variables when sufficient data are available and can be used to make predictions or inferences about an outcome of interest. Unlike mechanistic models, they do not require an in-depth knowledge of the underlying biological process of the disease, although this can be used to improve the model. However, statistical models require a large amount of data to provide precise estimates, making them more suited to well-established diseases. They are able to make predictions within the scope of the data used to fit them but are not recommended for causal investigations or extrapolation well beyond the data. Mechanistic models are more able to make causal inferences as they model the disease transmission process rather than the data itself; however, they are only able to do this within the specific setting for which they have been parameterized. Parameters can be taken from previous experiments where data are not available, making them particularly useful in settings where data are sparse or for newly (re-)emerging diseases. An example of this can be found in Zhang et al. [239] where parameters were 'borrowed' from other settings. Care should be taken when parameterizing mechanistic models in this way as processes may differ in ways that are not apparent at the model-fitting stage. By contrast, machine learning methods require a large amount of data but use flexible algorithms that allow them to learn patterns from rich, complex data. Although machine learning can be used to make inferences about data, most algorithms focus on making the most accurate predictions possible from available data rather than understanding underlying associations [270]. As with statistical models, they are inappropriate where there is a lack of data and are not recommended for making predictions or causal inferences well outside the range of data used to fit them [271].

Connectivity assumptions differed between mosquito species, indicating that authors consider mosquito behaviour and biting patterns when deciding which spatial model and assumptions are most appropriate. For example, dengue fever is transmitted by day-biting Aedes mosquitoes and is influenced by local movement or commuting [274], whereas Anopheles-borne malaria is transmitted by vectors most active between dusk and dawn so is influenced by proximity to vector breeding grounds and bed net use [275,276]. Anopheles-borne pathogens were more likely to be modelled assuming connectivity was driven by distance, potentially a proxy for vector movement because of the short flight span of vectors. Aedes- and Culex-borne pathogens were more likely modelled assuming human movement or proximity drives connectivity as this accounts for people commuting or moving to nearby regions/cities (figure 3). An alternative explanation could be that Aedes-borne emerging diseases (e.g. chikungunya and Zika) were more likely to be modelled using a mechanistic framework, allowing for the inclusion of complex movement matrices. The majority of statistical models within this review included a random effect to account for spatial connectivity, all of which used either a distance- or neighbourhood-based covariance structure. There were no random effect model structures that explicitly adjusted for connectivity arising from human movement.

Many studies included in this review did not explicitly state the assumptions they made about how connectivity arises. Often, assumptions had to be deduced from the data and spatial methods used in the studies. Although the vast majority of studies appeared to assume that regions were connected to neighbours or based on the distance between them, it is possible some used this as a proxy for another assumption, such as shared characteristics or human movement, where data were not available. Prior studies have discussed the difficulty of quantifying human behaviour when modelling infectious diseases [272]. Where mobility data are not available, movement models that aim to replicate commuting patterns, such as gravity and radiation models, were found to give similar results when modelling the spread of dengue fever compared to actual human movement data from geo-located Tweets [278]. These may help to avoid some of the issues surrounding privacy and bias when using a mobile phone or social media data to inform models, and where certain sections of the population, such as children and older adults, may be under represented. Some studies have suggested that radiation models are more accurate at representing commuting networks than mobile phone GPS data when compared to official census surveys in central locations [279].

This review provides a synthesis of the modelling approaches and spatial connectivity assumptions used to research mosquito-borne disease transmission to humans, but does not comment on the quality of these approaches. It is important to remember that more complex methods are not necessarily better and care should be taken to identify the most parsimonious method to address a studies' aim. Choice of the model should depend on the research question, the disease studied, the spatial scale and availability of the data and the way in which spatial connectivity is assumed to occur.

Data accessibility

Data extracted from the studies included in this systematic review are available from https://github.com/sophie-a-lee/mbd_connectivity_review and archived in a permanent repository on Zenodo (http://doi.org/10.5281/zenodo.4706866) [280].

Authors' contributions

All authors were involved in defining the search strategy. S.A.L. and C.I.J. performed the search and screening of articles. S.A.L. drafted the article with feedback, input and guidance from C.I.J., T.E. and R.L. All authors read and approved the final manuscript.

Competing interests

The authors declare no conflicts of interest.

Funding

S.A.L. was supported by a Royal Society Research Grant for Research Fellows. C.I.J. receives funding from the Global Challenges Research Fund (GCRF) project ‘RECAP’ managed through RCUK and ESRC (ES/P010873/1). R.L. was supported by a Royal Society Dorothy Hodgkin Fellowship.