Physics-based computational and theoretical approaches to Intrinsically Disordered Proteins

Abstract

Intrinsically disordered proteins (IDPs) are an important class of proteins that do not fold to a well-defined three-dimensional shape but rather adopt an ensemble of inter-converting conformations. This feature makes their experimental characterization challenging and invites a theoretical and computational approach to complement experimental studies. In this review, we highlight the recent progress in developing new computational and theoretical approaches to study the structure and dynamics of monomeric and order higher assemblies of IDPs, with a particular emphasis on their phase separation into protein-rich condensates.

Introduction

Intrinsically disordered proteins (IDPs) - those which do not adopt a folded structure in isolation - are now recognized to play key roles in cellular signaling and transcription.[1] An important feature of IDPs is their ability to self-assemble into solid fibrillar structures (a process often linked to pathological outcomes for the cell) as well as liquid assemblies formed through the process of liquid-liquid phase separation. Several recent reviews have extensively covered the process of fibril formation, and we focus here on IDP monomers and liquid-liquid phase separated assemblies [2,3].

Computational and theoretical methods have proven extremely valuable in understanding the structure and function of intrinsically disordered proteins: firstly, they help to resolve details that would be difficult to tease out from experiment alone, owing to the disordered nature of these proteins, and secondly they can provide a framework for understanding the properties of IDPs and their relation to protein sequence. Building upon fundamental work on IDP structure and function using a variety of computational and theoretical tools, rapid progress has been made in the last few years spurred by the role of IDPs in the formation of membraneless organelles (MLOs) via liquid-liquid phase separation (LLPS) [4,5]. Transferable physics-based models, which have been parameterized or/and tested against experimental data, can not only help interpret experimental data but can also provide detailed predictive information on important scientific questions [6,7]. Most importantly, because they are defined by the protein sequence, such models do not require any modifications to the potential parameters based on available knowledge from experiment, before being applied to a specific protein system of interest. We note that this does not preclude subsequent integration of experimental data to improve the accuracy of the generated ensemble [8–10]. Here, we restrict our review primarily to transferable physics-based models.

We start by reviewing recent developments in simulation models for IDPs, ranging from coarse-grained to all-atom simulation methods. We then describe recent methodological developments enabling the determination of phase equilibria for liquid-liquid phase separation directly from molecular simulations. We conclude by describing newly developed theoretical approaches for single chain IDPs and formation of IDP complexes.

All-atom simulations

All-atom explicit solvent simulations have the in principle the highest resolution and accuracy, considering recent improvements in protein force fields [11] [12–14] and can capture highly specific interactions that would be averaged out in coarse graining. IDPs have served as an essential benchmark for improving the accuracy and transferability of such models to study conformational and dynamical properties of proteins. As discussed in recent work [13,15], all-atom models can now provide a rather accurate atomic view of global and local properties of IDPs, although there remain deficiencies such as their low cooperativity relative to experiment [13]. The extensive application of some of these models (Amber03ws/Amber99SBws, Amber99SB-disp) to IDPs has highlighted the remarkable accuracy with which experimental observables based on nuclear magnetic resonance (NMR)[16], small-angle X-ray scattering (SAXS)[17,18], and single-molecular Förster resonance energy transfer (smFRET)[18] can be computed from the simulated ensembles [19]. The physics-based models provide a natural path to study the dynamical relaxation properties of IDPs as opposed to the ensemble refinement methods, which are most easily applied to average structural/thermodynamic properties. There is emerging evidence that the helical propensity for IDPs (especially low-complexity prion-like domains) is not entirely consistent with NMR-derived data, which may be related to the presence of specific residues in large proportion within these sequences thereby requiring residue-level fine-tuning of parameters [14]. One should note that most algorithms used to compute experimental observables (such as chemical shifts) from the simulated ensemble were parameterized using data for folded proteins [20]. More work is needed to test and refine these empirical methods to derive experimental measurables.

One approach to reducing the computational cost of all-atom protein simulations is the use of implicit solvent. By integrating out only solvent degrees of freedom, the atomistic chemical detail is retained, but a large fraction of the computational cost is saved. Although many implicit solvent models are not appropriate for IDPs, being too collapsed, the one that has shown the most promise at the time of writing is the ABSINTH model[21], which has recently been updated to improve backbone conformational preferences [22].

However, even with implicit solvent, it is challenging to use atomistic models for studying LLPS [23–25], as system sizes and sampling requirements to study phase coexistence are computationally prohibitive with current state-of-the-art computer hardware. But such methods can be used in conjunction with coarse-grained (CG) models to obtain essential insights into the atomic-level details of inter-residue interactions [26,27]. Currently, CG models for IDPs provide the most direct path to understanding sequence-determinants of LLPS and to identifying molecular interactions responsible for self-assembly.

Coarse-grained models

Coarse-grained models have been utilized with great success in understanding protein folding, protein aggregation, and macromolecular crowding, as well as many applications in polymer physics [28,29]. There is significant flexibility in the level of detail included in a CG model; it can range from one-bead-per-protein to several-beads-per-residue. Several CG IDP models have been proposed recently that differ in terms of how bonded and nonbonded interactions are represented, which is ultimately dictated by the computational efficiency and the intended application of the model. The models used to study monomer properties are more complex and are meant to capture additional molecular details accurately [30]. On the other hand, the models intended to explore the large-scale assembly of IDPs are much simpler and mostly rely on modeling proteins as bead-spring polymers with a particular emphasis on parameterizing nonbonded interactions between CG beads meant to represent different amino acids.

A recent CG framework in this spirit has emerged as a useful computational tool to study sequence-specific changes in the phase behavior of disordered proteins [31]. Due to the simplicity of the model, it can be easily extended to represent small structural motifs or large folded domains [19], post-translational modifications [32], thermoresponsive behavior [33], and even interactions with nucleic acids [34,35] that are quite relevant for the function of MLOs. It is useful to note that most current CG models either lack or have not been tested well for partial secondary structure propensities in IDPs. The prevalence of secondary structure elements in the heterogeneous ensemble of IDPs is considered functionally important for their binding mechanism as well as the LLPS propensity. We believe this to be an important future direction of research in the physics-based CG modeling of IDPs [36]. An additional direction for improvement may be the use of more than a single bead per residue, thus allowing backbone and side-chain interactions to be distinguished [37].

Despite the simplicity of a CG model, it is almost impossible to sample the thermodynamic phase diagram of IDPs undergoing LLPS using standard sampling techniques employed in computational biophysics research such as parallel tempering. Dignon et al. proposed to use a coexistence sampling method that was previously applied successfully to sample phase behavior of short homopolymers by Howard et al. [38], and which has now become the de facto standard for computing the LLPS phase diagrams of IDPs [39]. We note that other methods that rely on the protein density differences between the two phases are also being used, most often in the context of highly simplified patchy particle models of proteins or for on-lattice systems [40,41]. We believe that this is an area of opportunity to identify suitable existing methodologies in soft matter and polymer simulations or develop new techniques that are computationally more efficient. This is especially important in the case of multicomponent assemblies of disordered proteins due to the expansion of the parameter space in terms of the relative composition of different components [42].

We note that there is an inherent limitation with the use of simplified models concerning the mapping of simulation temperature and timescales to laboratory conditions. Therefore, appropriate additional validation steps should be taken before applying these models to study issues that are typically outside the scope of the initial parameterization.

Theoretical approaches

Theoretical approaches based on polymer physics principles have provided essential insights into the behavior of monomeric IDPs. An important contribution of such methods has been the identification of low-dimensional order parameters based on relevant sequence descriptors. While earlier mean field theories of protein collapse[43] and phase separation[44] characterized proteins in terms of average sequence properties, effects of sequence order are now being included. For example, sequence charge decoration (SCD) [45] or κ [46], which are highly similar parameters to describe sequence patterning effects[47], can faithfully describe global conformational properties (such as R_g) of IDPs with predominantly polyelectrolytic or polyampholytic sequences nearly quantitatively. Recently, it was shown that one could complement SCD with an additional order parameter based on sequence hydropathy decoration (SHD), which can account for the presence of uncharged residues, to describe the conformational properties of a large number of IDPs simulated using a simple CG model [48] (Figure 1A). It has also been shown that using a similar theoretical approach one can describe the average inter-residue distances within an IDP, giving qualitative agreement with all-atom simulation results (Figure 1B) [49]. Chan and co-workers have also recently developed a parameter similar to SCD to describe association of oppositely charged chains [50].

Figure 1.

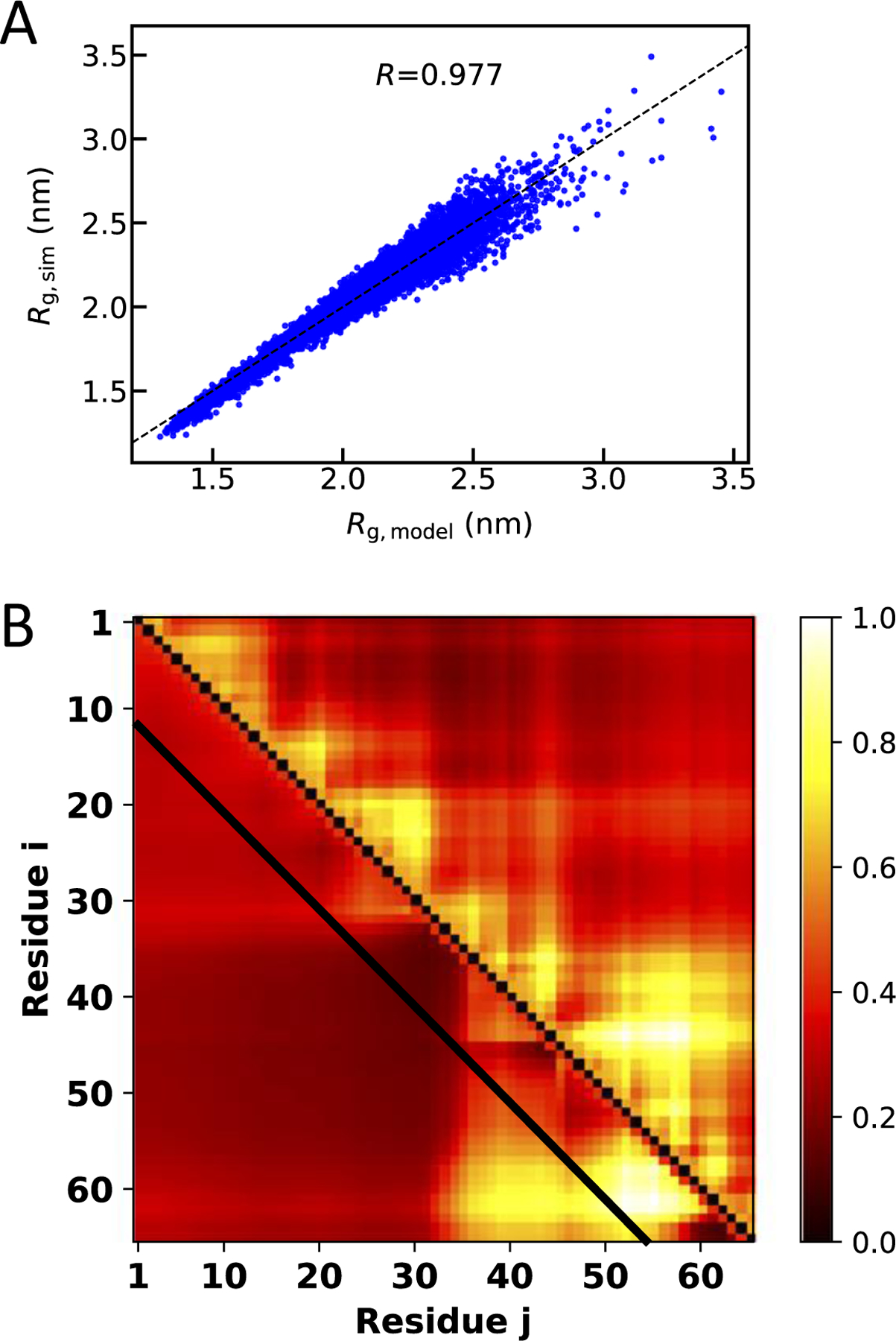
Comparison of analytical prediction of single-chain properties with simulation. (A) Radius of gyration computed from a combination of hydrophobic and charge patterning [48] compared with coarse-grained simulations. (B) Mean residue-residue distances (normalized to a [0,1] scale) from heteropolymer theory (lower left) compared with all-atom simulations [49].

Going beyond single chain properties and the association of pairs of chains, it is clearly of interest to obtain predictive theoretical models to describe phase separation. Towards this end, it was found in a recent study that the correlation between single-chain collapse transition temperature (T_θ) and critical temperature of LLPS (T_c) expected for homopolymers of infinite length could also apply to the behavior of heteropolymeric IDPs of the order of 100 residues in length (Figure 2) [51]. It is important to note that these results were preceded by Lin and Chan’s study on the dependence of protein R_g and T_c for IDPs of fixed chain lengths[52]. These theories and empirical models can be used to infer properties of IDPs in a high-throughput manner, which can potentially be used for the design of synthetic IDPs with tunable properties and associated assembly behavior, see e.g., recent work on predicting the thermoresponsive behavior of IDPs (Dignon, 2019, 10.1021/acscentsci.9b00102).

Figure 2.

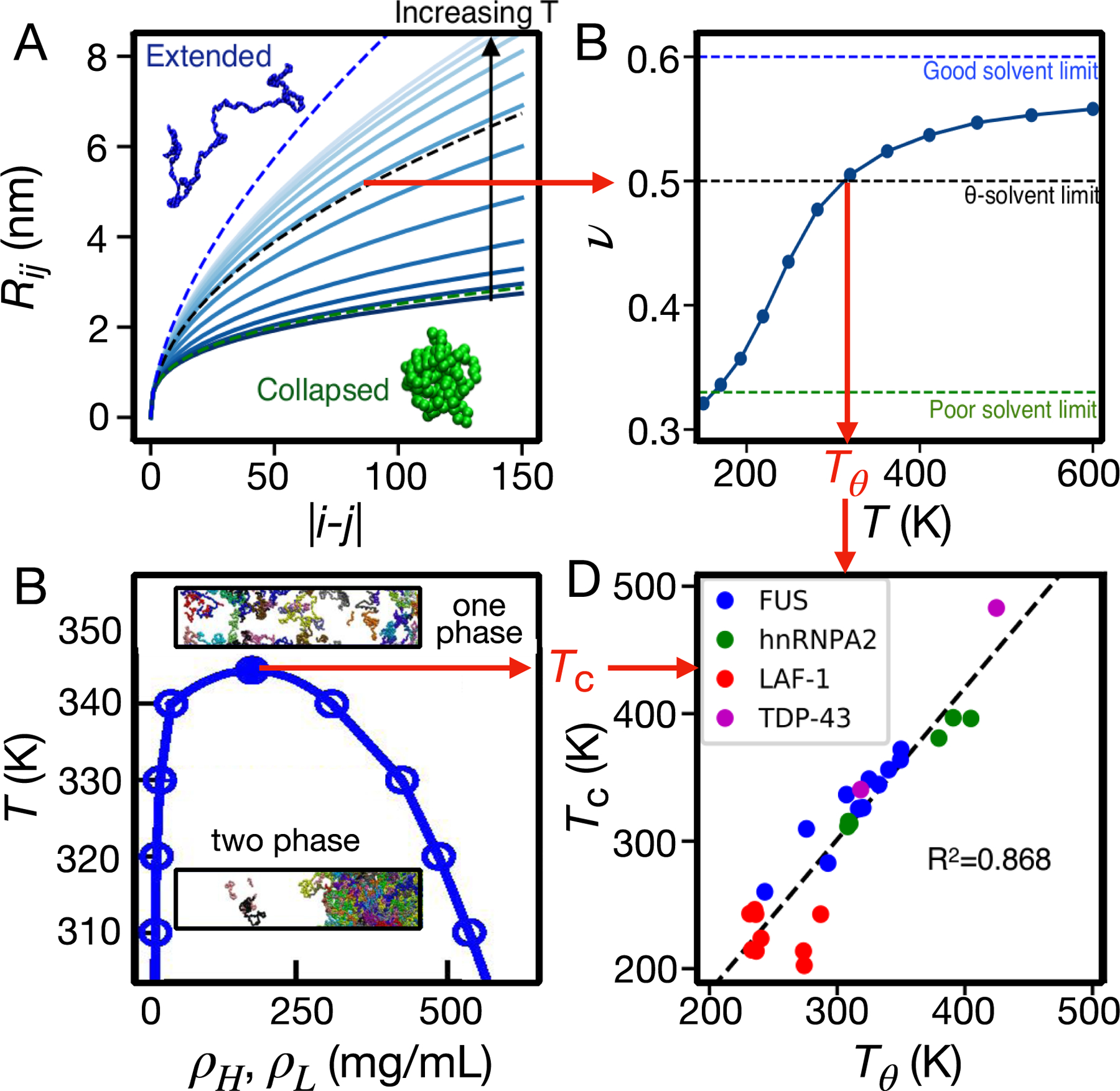
Relating single chain properties to phase separation. (A) Internal distance scaling for a single protein chain yields an effective scaling exponent ν as a function of temperature (B) – T_θ is the temperature at which v = 1/2. (C) Slab simulations (shown as insets) as a function of temperature establish the one-phase and two-phase regions of the phase diagram and an estimate of the critical temperature T_c. (D) T_c is remarkably well correlated with T_θ for a range of different sequences [51].

An important contribution of theory-based approaches has been to study the LLPS behavior of IDPs at much lower computational cost than molecular simulations of LLPS to provide important biophysical insights. Proto-models, including field theory, scaling theory, and ion release models, described in a recent review by Sing [53] in the context of complex coacervation of polyampholytes and polyelectrolytes, and that themselves build on earlier work in the context of polymer melts [54,55], are prime for extension and application to IDPs. We focus here on analytical and computational implementations of the polymer field theory model, as this is the most developed of the proto-models to date for IDP LLPS. In particular, field theoretic simulations with Complex Langevin sampling (FTS-CL) offers a computational efficient protocol as it considers a single IDP in the field of other IDPs rather than embedding many-body interactions. FTS begin with a particle-based model, and the particle-based canonical partition function is converted through a Hubbard-Stratonovich transformation into a field-theoretic partition function, in which the excluded volume and electrostatic interactions are decoupled through auxiliary fields [56]. The Hamiltonian of the system, expressed in terms of fluctuating chemical (ω) and electrostatic (φ) potential fields and the partition function Q[ω,φ] of a single chain in the complex-valued conjugate fields, is then sampled numerically using complex Langevin Dynamics. Phase diagrams for IDP LLPS can be readily obtained from FTS-CL, as detailed in references [57,58]. An alternate approach to FTS to obtain phase diagrams is to turn to analytical approaches. One of the most successful approaches has been the Random Phase Approximation (RPA), an theory initially developed by polymer physicists De Gennes [59] and Erukhimovich [60]in the context of polyelectrolytes, and recently applied to IDP coacervation [61]. This method considers Gaussian fluctuations of the chemical and electrostatic fields (as opposed to full compositions fluctuations as was the case with FTS). This approach rivals FTS simulations at a fraction of the computational cost at high densities, but the Gaussian approximation renders this analytical approach less accurate than FTS at low densities where charge and density fluctuations are magnified. Both RPA and FTS models have been able to shed insight into how sequence patterning affects the ability of peptides to LLPS. In particular, a study of peptides consisting of the amino acids E and K revealed that a blocky sequences phase separate with greater ease than scrambled sequences. Coupling the RPA/FTS results with coarse-grained simulations indicate that in this model, the interactions that drive LLPS are the same interactions that drive the collapse of an individual protein [58]. Of note is a recent improvement in the RPA formalism developed by Chan and Ghosh that combines the traditional RPA model with a renormalized Gaussian-chain formulation [62]. This combination (termed rG-RPA) gives a better representation of the conformational heterogeneity that arises when multiple chains interact and it seeks to account for pH, salt, and sequence effects. Both rG-RPA and FTS-CL are emerging as leading methodologies for efficient generation of phase diagrams for IDP LLPS, but as with all theoretical models, they will need further validation against experimental data. FTS applied to IDP is still in its infancy and restricted to date to implicit solvent representations of the polymer chain, with a limited amino acid library. Nonetheless, this approach has been successful in modeling the LLPS behavior of the Tau protein in the presence of RNA, predicting phase diagrams and identifying which segments of Tau are responsible for phase separation (Figure 3) [63,64]. On-going research involves building in explicit solvent into the FTS model and including additional sequence-specific details, and importantly extending the studies to a larger set of IDP proteins and validating results using experiment.

Figure 3.

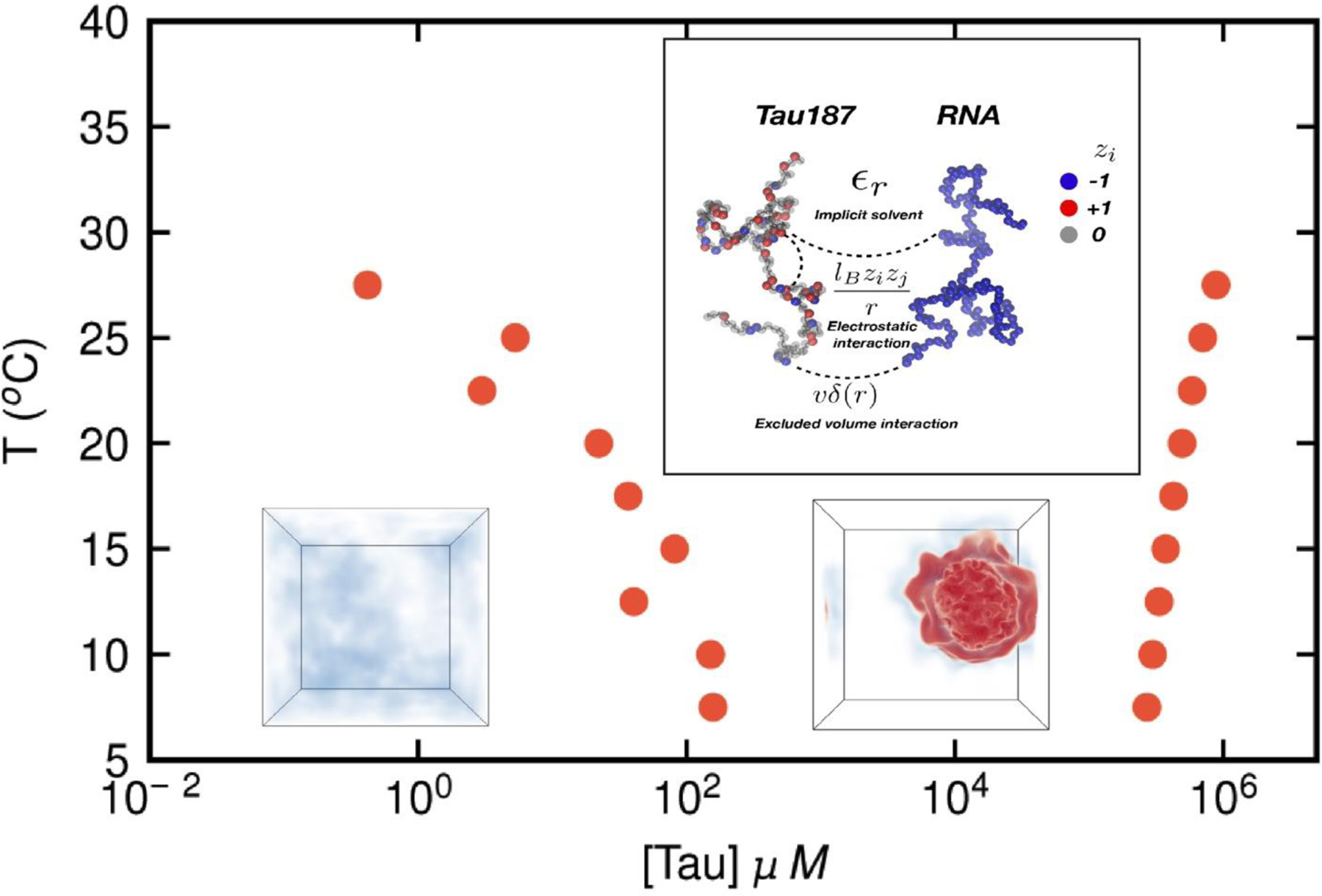
Field Theoretic Simulations of the LLPS of the Tau protein. The upper inset panel shows the coarse-grained models of Tau and RNA that serve as the input for the FTS-CL simulations. The red circles correspond to the boundaries of the phase diagram. The inner envelope corresponds to the phase separated state (shown by the red density in the FTS-CL snapshot) [63].

Conclusions

IDPs are involved in crucial biological functions and their experimental characterization is singularly challenging. Computer simulations have become an indispensable complement to experiment, as they are uniquely positioned to provide molecular mechanistic insights into the behavior of individual IDPs as well as IDP complexes. The last two years have seen tremendous progress in the development of accurate atomistic force fields, a novel framework for coarse-grained simulations of IDPs and LLPS, and powerful analytical and field theoretic models for LLPS. We are at a particularly exciting juncture in terms of the development of novel computational and theoretical tools for IDPs, and we anticipate that simulation and theory will play an essential part in coming years in unraveling the many mysteries that still surround the unique biopolymers that are IDPs.