3D segmentation of lungs with juxta-pleural tumor using the improved active shape model approach

Abstract

BACKGROUND AND OBJECTIVE:

At present, there are many methods for pathological lung segmentation. However, there are still two unresolved problems. (1) The search steps in traditional ASM is a least square optimization method, which is sensitive to outlier marker points, and it makes the profile update to the transition area in the middle of normal lung tissue and tumor rather than a true lung contour. (2) If the noise images exist in the training dataset, the corrected shape model cannot be constructed.

METHODS:

To solve the first problem, we proposed a new ASM algorithm. Firstly, we detected these outlier marker points by a distance method, and then the different searching functions to the abnormal and normal marker points are applied. To solve the second problem, robust principal component analysis (RPCA) of low rank theory can remove noise, so the proposed method combines RPCA instead of PCA with ASM to solve this problem. Low rank decompose for marker points matrix of training dataset and covariance matrix of PCA will be done before segmentation using ASM.

RESULTS:

Using the proposed method to segment 122 lung images with juxta-pleural tumors of EMPIRE10 database, got the overlap rate with the gold standard as 94.5%. While the accuracy of ASM based on PCA is only 69.5%.

CONCLUSIONS:

The results showed that when the noise sample is contained in the training sample set, a good segmentation result for the lungs with juxta-pleural tumors can be obtained by the ASM based on RPCA.

1. Introduction

Pulmonary parenchyma segmentation is the first step in computer-aided diagnosis of lung cancer. The segmentation methods of pulmonary parenchyma which includes normal and pathological can be divided into three categories, that is based on visual appearance [1], the location relationship of shape [2] and hybrid [3]. The first kind of methods mostly considers that the gray value of lung area is lower than that of other surrounding tissues, so the pathological lung (especially including interstitial lung disease) is segmented by classifier based on gray and texture features. However, such methods are only suitable for the pulmonary segmentation of no juxta-pleural tumor, because the small different of gray value between pleura and tumor, as shown in Fig. 1. The second kind of methods mainly introduces the anatomical relationship between lung and heart, liver, spleen, rib. But this method still cannot solve the problem that is juxta-pleural tumor is excluded into the pulmonary parenchyma. The third kind of methods establishes shape model and evolves lung contour according to the surface features. Sun et al. [4] used Active Shape Model (ASM) to obtain the initial lung contour, and then used local surface features to drive the evolution of contour. Anthimopoulos et al. [5] used 15 lung image sequences to construct probability map of normal lung regions, and used registration method to segment pathological lung. Alam et al. [6] used marker points on ribs and spines to initialize the shape model, and then combined with deformable models to segment lung regions with large tumors. The above literatures can achieve better segmentation results without noise samples in training set, however they all do not consider the problem of noise samples in training set during the construction process of the training shape model. Noise samples are the images in training dataset which have incorrect contours, such as Fig. 1.

Figure 1.

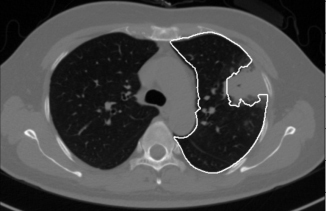
Lung segmentation result is marked by white contour. This lung with a large juxta-pleural tumor is segmented by the traditional method.

When the juxta-pleural tumor’s diameter is less than 3 cm, they can be filled by morphological or curved surface fitting methods. However, when the juxta-pleural tumor’s diameter is larger than 3 cm, it needs a segmentation algorithm which can consider both the prior shape and the features of the image to be segmented. ASM is such a segmentation algorithm [7].

ASM expresses the shape model based on point distribution model (PDM). The shape model uses principal component analysis (PCA) to learn the average shape and deformation range according to the training set. And then ASM establishes the local feature appearance model according to the training set. Finally, ASM evolves the contour of the test image based on local feature appearance model and the shape model. However, PCA used in ASM can only remove the influence of noise samples which obey Gaussian distribution. That is to say, when there are other type noise samples in the training set, ASM cannot train the correct shape model. Moreover, the segmentation effect of ASM is also affected by abnormal marker points that located on pseudo-edges [8].

In recent years, scholars have applied low rank theory to image shape processing, including alignment and segmentation. In the study by Zhou et al. [9], the low rank theory is applied to the non-rigid alignment of image sets. Ahmedtl et al. [10] propose a fixed deformable face set alignment algorithm, which combines low rank theory and piecewise affine transformation into the alignment model. Li et al. [11] combined low rank and Active Appearance Model. Hu et al. [12] and Zhang et al. [13] proposed sparse shape composition (SSC) based on sparse theory and applied it to liver shape modeling. The above literatures had solved the problem of non-Gaussian noise sensitivity in shape model and all achieved good results. However, the low rank theory has not yet been applied to the ASM model.

Scholars have also done a lot of research in abnormal marker point detection. If the updated distance offset of a marker point is bigger than other marker points, the marker point is an abnormal marker point. Shi et al. and Shao et al. [14, 15] randomly divides the set of marker points into several subsets. If the shape reconstructed by the subset of marker points is different from the shape reconstructed by the corresponding marker points according to the training model, it shows that this subset contains abnormal marker points.

The shapes of training sample set have low rank attribute because the lung anatomical shape of different human is roughly same. Robust principal component analysis (RPCA) in low rank theory is more robust to noise samples. Therefore, this paper combined RPCA with ASM to solve the problem that the correct shape model cannot be obtained because of the noise samples in the training set. In the process of evolving lung boundary contour, some marker points called abnormal marker points cannot be updated to the real edge, so it is necessary to identify these abnormal marker points first. In this paper an abnormal marker point recognition method based on distance threshold is designed and assigns different searching functions to abnormal and normal marker points. For abnormal marker points, only the prior shape model is considered in searching functions while for normal marker point local low level features appearance model and shape model should also be considered together.

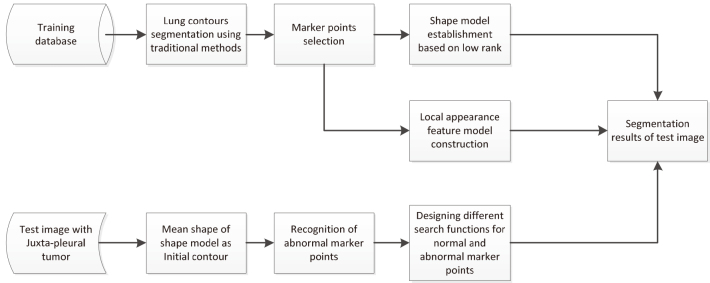
The flowchart of the proposed algorithm is shown in Fig. 2, including training and testing phase. In the training phase first use traditional segmentation methods to obtain lung contours of training data set. Then select marker points on the segmented lung contour. At last construct two models: shape model based on low rank and local appearance feature model. In the testing phase, mean shape of training data set’s shape model is considered as the initial contour of ASM. Then use traditional segmentation methods to obtain the pseudo-contour which always excludes juxta-pleural tumor. Select marker points on the pseudo-contour. Distinguish normal and abnormal marker points. Design different searching functions for normal and abnormal marker points. Subsequently, the initial shape is iteratively deformed and refined by different searching functions under training dataset’s shape model and local appearance feature model.

Figure 2.

The flow chart of the proposed algorithm.

2. Lung with juxta-pleural tumor segmentation method

2.1. Marker points extraction

First, the traditional method is used to segment the pulmonary region of the samples in training set and obtained lung boundary contour. The segmentation steps include extra-pulmonary region exclusion by iteration threshold and region growing segmentation methods, trachea elimination, internal cavity filling, liver exclusion and left and right lungs separation [16].

Second, extract marker points on left or right lung boundary contour, respectively according to Shenshen et al. [17]. In this way, there are 5 main marker points and 90 marker points in the left or right lung boundary (as shown in Fig. 3).

Figure 3.

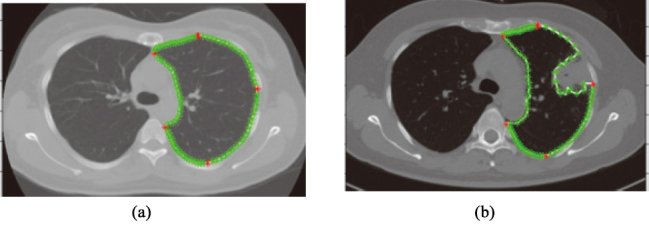
Extracted marker points. Main marker points are shown in red; other marker points are shown in green. (a) normal lung (b) pathological lungs with juxta-pleural tumor.

2.2. Shape model established

Aligned lung boundaries in training sample dataset by procrustes analysis method. In order to remove the influence of the noise contours such as Fig. 3b, PCA is replaced by RPCA.

The boundary contours of images in the training data set is $d_1,d_2,\mathrm{\dots },d_n$, represented in vector form as $D={(d_1,d_2,\mathrm{\dots },d_n)}^T$. $d_i={({(x_{i0},\mathrm{\dots },x_{ij}\mathrm{\dots },x_{im})}^T,{(y_{i0},\mathrm{\dots },y_{ij},\mathrm{\dots },y_{im})}^T)}^T$ is marker points’ coordinate, in which, $(x_{ij},y_{ij})$ is the coordinates of the $j$ marker point of the $ith$ image in the training data set.

Firstly, $D$ is processed by low rank.

$$\underset{X,E}{min}\mathit{\text{rank(X)}}+\lambda {||E||}_0$$

(1)

$$s.t.D=X+E$$

where $X$ is the decomposed low rank component and $E$ is the sparse component. Equation (2.2) is a non-convex function with no unique solution. So in order to let Eq. (2.2) be a convex function,  rank(X) is replaced by the kernel norm and the L0 norm is replaced by the L1 norm.

$$\underset{X,E}{min}{||X||}_{\ast }+\lambda {||E||}_1$$

(2)

$$s.t.{||D-X-E||}_F⩽\delta$$

where $\lambda$ is a regularized parameter which is greater than 0, and $\delta$ is a very small positive number. $|||{|}_F$ is Frobenius norm. Equation (2.2) can be written in the form of Eq. (3) by Lagrange multiplier method.

$$L_{\mu }(X,E)={||X||}_{\ast }+\lambda {||E||}_1+{\displaystyle \frac{\mu }{2}}{\parallel D-X-E\parallel }_F^2$$ (3)

where $\mu$ is a small positive number. The accelerated approximation gradient [18] is used to solve Eq. (3). Then, the mean vector and covariance matrix of $X$ are obtained. The mean vector is $m_x=E\{X\}$. Covariance matrix is $\mathrm{\Sigma }=E\{\left(X-m_x\right){\left(X-m_x\right)}^T\}$. Secondly, the covariance matrix $\mathrm{\Sigma }$ is decomposed by low rank.

$$\underset{\mathrm{\Sigma },\gamma }{min}\text{𝑟𝑎𝑛𝑘}(\mathrm{\Phi })+\lambda {\parallel \gamma \parallel }_0$$

(4)

$$s.t.\mathrm{\Sigma }=\mathrm{\Phi }+\gamma$$

where $\mathrm{\Phi }$ is the decomposed low rank component and $\gamma$ is the sparse component. Equation (2.2) is a non-convex function with no unique solution. So in order to let Eq. (2.2) be a convex function, rank(X) is replaced by the kernel norm, and the L0 norm is replaced by the L1 norm.

$$\underset{\mathrm{\Phi },\gamma }{min}{\parallel \mathrm{\Phi }\parallel }_{\ast }+\lambda {\parallel \gamma \parallel }_1$$

(5)

$$s.t.{\parallel \mathrm{\Sigma }-\mathrm{\Phi }-\gamma \parallel }_F⩽\delta$$

Equation (2.2) can be written in the form of Eq. (6). The accelerated approximation gradient [18] is used to solve Eq. (6).

$$L_{\mu }(\mathrm{\Phi },\gamma )={\parallel \mathrm{\Phi }\parallel }_{\ast }+\lambda {\parallel \gamma \parallel }_1+{\displaystyle \frac{\mu }{2}}{\parallel \mathrm{\Sigma }-\mathrm{\Phi }-\gamma \parallel }_F^2$$ (6)

Calculating the eigenvalues of $\mathrm{\Phi }$, and arranged them in descending order and the eigenvectors $p={[p_1;p_2;\mathrm{\dots };p_t]}^T$ corresponding to top-rank $t$, $t$ is set 6 in this paper, eigenvalues $b=[b_1,b_2,\mathrm{\dots },b_t]$ are selected to construct the shape model $X=m_x+pb$, where $m_x$ is the mean shape vector. The shape model is shown in Fig. 4. Figure 4a is the shape expressed $X$ by $p={\left[p_1\right]}^T$, Fig. 4b is the shape expressed $X$ by $p={[p_1;p_2]}^T$, Fig. 4c is the shape expressed $X$ by $p={[p_1;p_2;p_3]}^T$, Fig. 4d is the shape expressed $X$ by $p={[p_1;p_2;p_3;p_4]}^T$.

Figure 4.

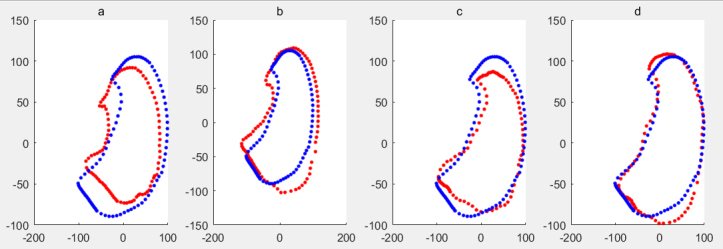
The mean shape $m_x$ of training sample set including noise samples is shown in blue, the deformed shape generated by the shape model based on RPCA of ASM is shown in red.

2.3. Model solution

The accelerated approximation gradient [18] is used to solve Eq. (2.2).

1: Input: $D\in R^{m\ast n}$, $\lambda$ is a weight parameter.

2: ${𝑿}_0,{𝑿}_{-1}\leftarrow 0,{𝑬}_0,{𝑬}_{-1}\leftarrow 0,t_0,t_{-1}\leftarrow 0,{\mu }_0\leftarrow .99{\parallel D\parallel }_{2,2},\overline{\mu }\leftarrow {10}^{-5}{\mu }_0$,

3: While no convergence

4: ${\widetilde{𝑿}}_k\leftarrow {𝑿}_k+\frac{t_{k-1}}{t_k}({𝑿}_k-{𝑿}_{k-1})$

5: ${\widetilde{𝑬}}_k\leftarrow {𝑬}_k+\frac{t_{k-1}}{t_k}({𝑬}_k-{𝑬}_{k-1})$

6: ${𝒀}_k^A\leftarrow {\widetilde{𝑿}}_k-\frac{1}{2}({\widetilde{𝑿}}_k+{\widetilde{𝑬}}_k-D)$

7: $(U,S,V)\leftarrow \text{svd}({𝒀}_k^A)$

8: ${𝑿}_{k+1}\leftarrow 𝑼{[𝑺-\frac{\mu }{2}𝑰]}_{+}{𝑽}^{\ast }$

9: ${𝒀}_k^E\leftarrow {\widetilde{𝑬}}_k-\frac{1}{2}({\widetilde{𝑿}}_k+{\widetilde{𝑬}}_k-D)$

10: ${𝑬}_{k+1}\leftarrow \text{𝑠𝑖𝑔𝑛}[{𝒀}_k^E]\circ {\left[\left|{𝒀}_k^E-\frac{\lambda \mu }{2}{11}^{\ast }\right|\right]}_{+}{t}_{k+1}\leftarrow \frac{1+\sqrt{1+4t_k^2}}{2},\mu \leftarrow \max (.9\mu ,\overline{\mu }),$

11: End while

12: Output:$X$, $E$.

The accelerated approximation gradient [18] is used to solve Eq. (2.5.2).

1: Input:$\mathrm{\Sigma }\in {ℝ}^{m\ast n}\lambda$ is weight parameter.

2: ${𝚽}_0,{𝚽}_{-1}<-0,{𝑬}_0,{𝑬}_{-1}<-0,t_0,{t_{-1}<-0,{\mu }_0\leftarrow .99\parallel 𝑫\parallel }_{2,2,}\overline{\mu }\leftarrow {10}^{-5}{\mu }_0$

3: While not convergence

4:  ${\widetilde{𝚽}}_k\leftarrow {𝑿}_k+\frac{t_{k-1}}{t_k}({𝚽}_k-{𝚽}_{k-1})$

5:  ${\widetilde{𝑬}}_k\leftarrow {𝑬}_k+\frac{t_{k-1}}{t_k}({𝑬}_k-{𝑬}_{k-1})$

6:  ${𝒀}_k^A\leftarrow {𝚽}_k-\frac{1}{2}({\widetilde{𝚽}}_k+{\widetilde{𝑬}}_k-D)$

7:  $(U,S,V)\leftarrow \text{svd}({𝒀}_k^A)$

8:  ${𝚽}_{k+1}\leftarrow 𝑼{[𝑺-\frac{\mu }{2}𝑰]}_{+}{𝑽}^{\ast }$

9: ${𝒀}_k^E\leftarrow {\widetilde{𝑬}}_k-\frac{1}{2}({\widetilde{𝑿}}_k+{\widetilde{𝑬}}_k-D)$

10:   ${𝑬}_{k+1}\leftarrow \text{𝑠𝑖𝑔𝑛}[{𝒀}_k^E]\circ {\left[\left|{𝒀}_k^E-\frac{\lambda \mu }{2}{11}^{\ast }\right|\right]}_{+}{t}_{k+1}\leftarrow \frac{1+\sqrt{1+4t_k^2}}{2},\mu \leftarrow \max (.9\mu ,\overline{\mu }),$

11: End while

12: Output: $𝚽,𝑬$.

2.4. Local appearance feature model construction

In this paper, a local appearance feature model is established based on PCA using gray features. The gray-level appearance model that describes the typical image structure around each marker point is obtained from pixel profiles, sampled (using linear interpolation) around each marker point, perpendicular to the boundary contour. On either side $k$ pixels are sampled (step size $=$ 1), which gives profiles of length $2k+1$, in this paper, $k=8$.

For each marker point $j$ ($j\in [1,95]$), gray values of the sampled points $i(i\in [1,17])$ which is on the profile perpendicular to the contours of every images in the training data set constitutes the local appearance gray feature matrix $g_j$. The PCA model of local appearance gray feature matrix $g_j$ corresponding to each landmark is established. The eigenvectors $g_j.\text{𝐸𝑣𝑒𝑐𝑡𝑜𝑟}$, eigenvalues $g_j.\text{𝐸𝑣𝑒𝑐𝑡𝑜𝑟𝑠}$ and mean vectors $g_j.\text{𝐸𝑚𝑒𝑎𝑛}$ of the PCA model are calculated.

2.5. Target contour search

2.5.1. Recognition of abnormal marker point

Because of the adhesion between tumor and chest wall, concave lung contour is obtained based on the traditional ASM method, as shown in Fig. 5 in blue. The marker points on the contour notch are the abnormal marker points. These abnormal marker points are updated to the boundary between lung parenchyma and tumor. Therefore, the different search function of abnormal marker points should be given for abnormal marker points.

Figure 5.

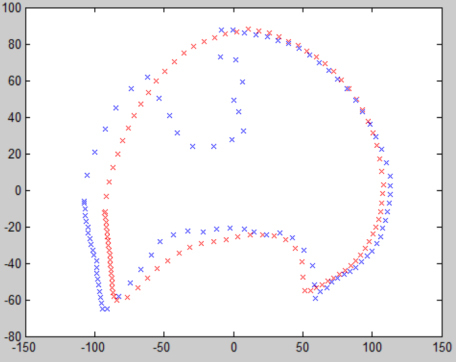
Align the mean contour of the training samples which is shown in red and lung contour with juxta-pleural tumor which is shown in blue.

Firstly, lung contour with juxta-pleural tumor ${\text{𝑆ℎ𝑎𝑝𝑒}}_1(x_1,y_1,\mathrm{\dots }{x}_k,y_k)$ is aligned based on marker points and the mean contour of training samples ${\text{𝑆ℎ𝑎𝑝𝑒}}_2(w_1,z_1,\mathrm{\dots }{w}_k,z_k)$. The alignment steps are: translation components deletion, scaling and rotation transformation. The formula for deleting translation components is following: $(X_1-{\sum }_{i=1}^k{X}_i/K,y_1-{\sum }_{i=1}^k{y}_i/k)$. The scaling scale formula is: $((x-\overline{x})/s,(y-\overline{y})/s)$, where, $s=\text{𝑠𝑞𝑟𝑡}(({(x_1-\overline{x})}^2+{(y_1-\overline{y})}^2+\mathrm{\dots })/k)$. The formula of rotation angle in rotation transformation is as follows:

$$\theta =\arctan {\displaystyle \frac{{\sum }_{i=1}^k(w_i{y}_i-x_i{z}_i)}{{\sum }_{i=1}^k(w_i{x}_i+y_i{z}_i)}},$$

the alignment results are shown in Fig. 5.

If the distance of the corresponding marker point between the lung contour with juxta-pleural tumor and the mean contour of the training samples is bigger than the threshold value $\epsilon$, then the marker point is an abnormal marker point, which is shown in Fig. 6.

Figure 6.

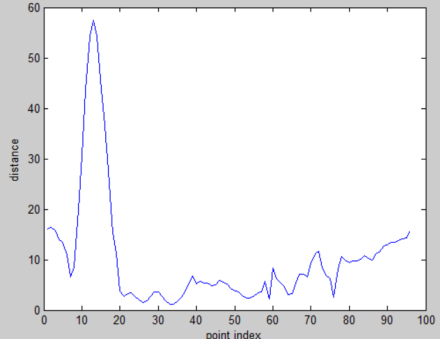
The corresponding points distance between the lung contour with juxta-pleural tumor and the mean contour of the training samples.

2.5.2. Search the targeted contour

The initial searching curve is the mean contour. Then defines the searching rule by piecewise function. For abnormal marker point, should only make b in the range of $-3\sqrt{\lambda }<b<+3\sqrt{\lambda }$ and $b=p^T(x-\overline{x})$, where $p$ is the eigenvectors and $\lambda$ is the corresponding eigenvalues. $\overline{x}$ is the mean contour of the training data set and $x$ is current contour. For non-abnormal landmark, local gray appearance model should also be considered besides the shape model. For each landmark $j(j\in [1,95])$ on the contour of the test image, the match degree $f(i,j)$ is calculated for the gray value $g_i$ of the sampling point $i(i\in [1,17])$ on the profile perpendicular to the contour on the local appearance feature model, and the most suitable point is selected as the update position of this landmark.

$$bc=g_j.\text{𝐸𝑣𝑒𝑐𝑡𝑜𝑟𝑠}{}^{\prime }\ast (g_i-g_j.\text{𝐸𝑚𝑒𝑎𝑛})$$

$$bc=bc./(\text{𝑠𝑞𝑟𝑡}(g_j.\text{𝐸𝑣𝑎𝑙𝑢𝑒𝑠}))$$ (7)

$$f(i,j)=\text{𝑠𝑢𝑚}(bc\wedge 2)$$

3. Experiment

3.1. Experiment data set

First, the training dataset is established. The training dataset consists of 135 multi-slice spiral CT lung scan images collected from the First Affiliated Hospital of Guangzhou Medical University. And among them, sixteen scans are included juxta-pleural tumor on the left side and fourteen scans are included juxta-pleural tumor on the right side. The size of the lung scan images is 512*512*100 $\sim$ 200 layers, and their thickness is 0.6 mm*0.6 mm*2 mm (or 3 mm). The test dataset consists of 122 scans from EMPIRE 10 and LIDC-IDRI [19]. It had the gold standard of lung contour and among them, 52 scans are included juxta-pleural tumor on the left side, 30 scans are included juxta-pleural tumor on the right side. Figure 7 is three scans from training dataset. Figure 7a is CT scan without any tumor on the lung wall. Figure 7b and c are scans which include juxta-pleural tumors. The juxta-pleural tumor in Fig. 7b is located in the upper lobe and the juxta-pleural tumor in Fig. 7c is located in the lower lobe. Figure 7b and c can be regarded as noise samples in the training data set, because their lung contours described in green lines are different from those in Fig. 7a.

Figure 7.

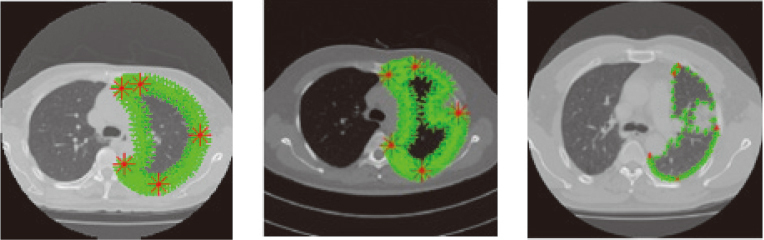
Training samples including noise samples, the five main marking points are red, the marking points are green. (a) marker points in lung contour with no juxta-pleural tumor. (b) and (c) marker points in lung contour with juxta-pleural tumor.

3.2. Parameter setting

In low rank algorithm, $\lambda =$ 0.129, $\delta =$ 0.9. Maximum number of iterations is 10000. Tolerance for stopping criterion is ${10}^{-7}$. In PCA algorithm, number of searching iterations is 500. Number of contour points interpolated between the major landmarks is 20.

3.3. Comparisons of generated shape models

The shape model is shown in Fig. 8 using ASM of RPCA for the training data set with noise samples. It can be seen that the larger t is, the more similar the shape obtained is to the average shape. And the code of low rank was also used [20]. The shape model is shown in Fig. 10 using ASM of PCA for the training data set without noise samples. When $t=$ 1, the shape is represented only by the eigenvector corresponding to the maximum eigenvalue. It can be seen that Fig. 8a is most similar to the mean shape and Fig. 10a is more similar to the mean shape, while Fig. 9a is least similar to the mean shape. When $t=$ 2, the shape is represented by the eigenvectors corresponding to the first two eigenvalues. It can be seen that Fig. 7b and Fig. 9b are more similar to the mean shape, while Fig. 8b is the least similar to the mean shape. When $t=$ 4, the shape is represented by the eigenvectors corresponding to the first two eigenvalues. It can be seen that Fig. 7b and 9b are similar to the mean shape, while Fig. 8b is the least similar to the mean shape. The red shapes of (a), (b), (c) in Fig. 8 which is the trained shape model are no longer within the normal lung shape range, while the red shapes of Figs 7 and 10 have been within the normal lung shape range. It is shown that the shape model established in Fig. 8 is affected by noise samples. Because of the application of RPCA, the shape model established in Fig. 7 is not affected by the noise samples, which is basically the same as the shape model established in training data set without noise samples in Fig. 10. It can be seen that, to a certain degree, RPCA can eliminate the influence of noise samples on the shape model.

Figure 8.

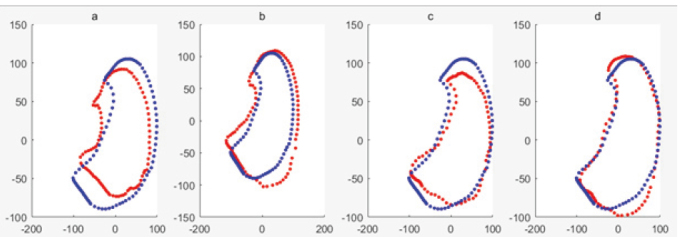
Mean shape of training sample set including noise samples is shown in blue, the deformed shape based on RPCA of ASM is shown in red, when $t=1\sim 4$ respectively. The shape model is shown in Fig. 9 using ASM of PCA for the training data set with noise samples. The code of traditional ASM was used [7].

Figure 10.

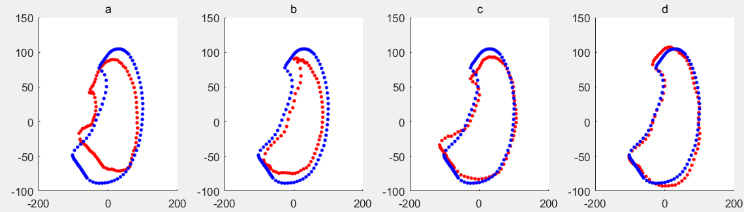
Mean shape of training sample set without noise samples is shown in blue, the deformed shape based on PCA of ASM is shown in red, when $t=1\sim 4$ respectively.

Figure 9.

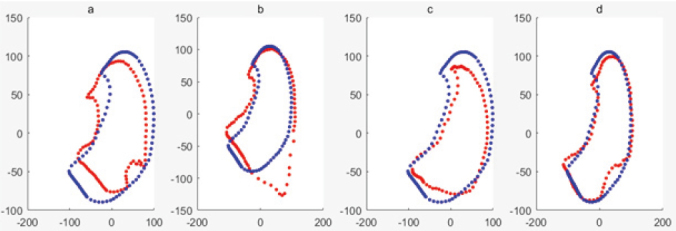
Mean shape of training sample set including noise samples is shown in blue, the deformed shape based on PCA of ASM is shown in red, when $t=1\sim 4$ respectively.

3.4. Evaluation of segmentation results

The contour containment region obtained by the segmentation algorithm is compared with the contour containment region manually drawn by the doctor (as the golden standard), and the coverage degree overlap is calculated.

$$\text{𝑂𝑣𝑒𝑟𝑙𝑎𝑝}={\displaystyle \frac{R_{\text{𝑔𝑜𝑙𝑑}}\cap R_{\text{𝑛𝑒𝑤}}}{R_{\text{𝑔𝑜𝑙𝑑}}\cup R_{\text{𝑛𝑒𝑤}}}}\ast 100\%$$ (8)

While $R_{\text{𝑔𝑜𝑙𝑑}}$ and $R_{\text{𝑛𝑒𝑤}}$ refer to the gold standard pixel set and the pixel set obtained by segmentation algorithm respectively. When the training sample set contains noise samples, 122 lung images of the test set are segmented. The results are as follows: the average overlap degree of lung region segmentation based on RPCA ASM is 94.5%, while that of traditional ASM [4] is 69.5%. Compared with the method of Shao et al. [15], the average rate of segmentation overlap is 85% because the influence of training set noise samples is not considered, as shown in the Fig. 11. The traditional ASM [4] is compared with the RPCA based ASM segmentation effect for juxta-pleural tumor lung, as shown in Fig. 12. That is because traditional ASM give the same search function to all marker points, while RPCA give different search functions to the marker points which locate in the place of tumor and pleura connection.

Figure 11.

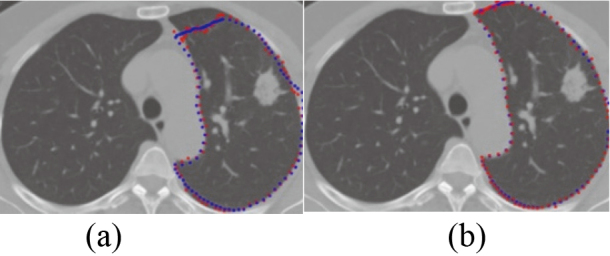
The result of lung segmentation. (a) [15]’s method (b) ASM based on RPCA.

Figure 12.

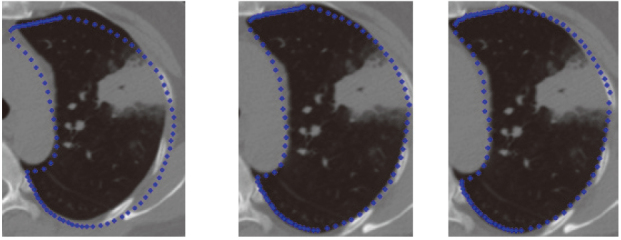
Lung segmentation processing with juxta-pleural tumor by the ASM based on RPCA.

The segmentation results were compared with the ground truth according to TPF (true positive fraction) under three situations, shown as Table 1. The first situation is the train dataset doesn’t contain noise samples and using traditional ASM; the second situation is the train dataset includes noise samples and using traditional ASM; the third situation is the train dataset includes noise samples and using RPCA-based ASM. From Table 1, it can be seen that RPCA-based ASM is largely unaffected by the training set noise images. The relationship between noise samples’ number in the training dataset and segmentation accuracy for RPCA-based ASM is shown in Table 2. It can be seen that with the increase of the number of noise samples, the accuracy of segmentation is decreasing. Figure 12 shows the initial position, middle position and final position of the lung contour searching process by the proposed method. Figure 13 compares the ASM based on RPCA and traditional ASM method in lung segmentation with juxta-pleural tumor. It can be seen that the proposed method is also useful for large juxta-pleural tumors. Figure 14 shows the effect of the lung segmentation with tumor by the ASM based on RPCA. Figure 15 shows 3D visualization results of ASM based on PCA and ASM based on RPCA. In 3D visualization results, ASM based on PCA cannot include juxta-pleural tumors into the lung parenchyma, so a hole is shown.

Table 1.

TPF of three situations comparison

	ASM $+$ PCA no noise (%)	ASM $+$ PCA noise (%)	ASM $+$ RPCA noise (%)
Left lung	97.79	76.79	95.00
Rightlung	96.89	78.60	93.54

Table 2.

Relationship between noise samples’ number and accuracy for RPCA

	4	8	12	14/16
Left lung	97.54%	97.12%	96.68%	95.03%
Rightlung	96.12%	95.73%	94.69%	93.54%

Figure 13.

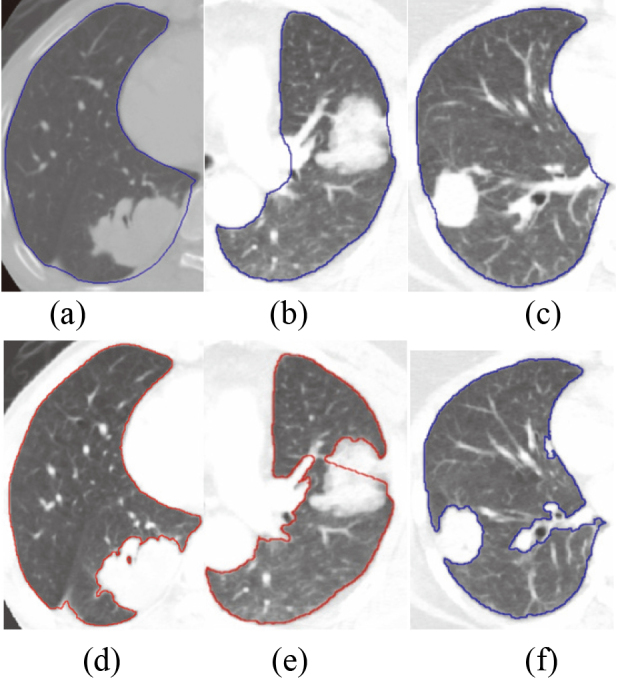
Compares the lung segmentation results with juxta-pleural tumor based on ASM based on PCA and ASM based on RPCA; (a) $\sim$ (c) the segmentation results of ASM based on RPCA; (d) $\sim$ (f) to the segmentation results of traditional methods.

Figure 14.

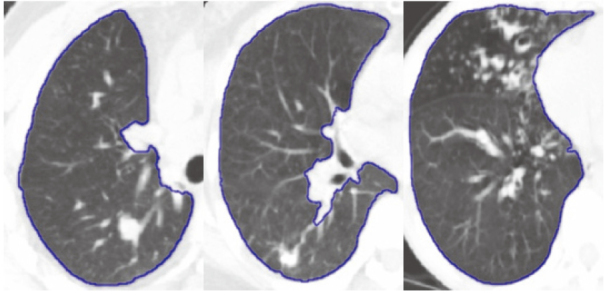
Lung segmentation result with tumor by ASM based on RPCA.

Figure 15.

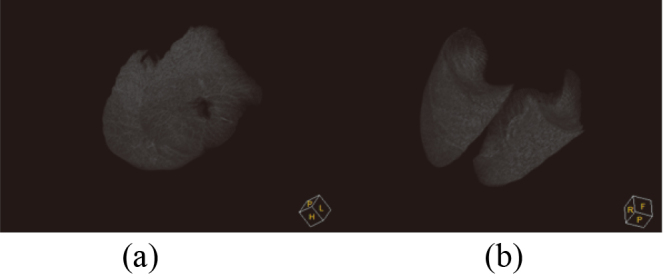
3D visualization results. (a) ASM based on PCA; (b) ASM based on RPCA.

3.5. Computer time

The proposed algorithm was implemented in C++ and Matlab Lib and test on a PC with Intel i7-8550U CPU and 8GB of RAM. The average computing time of the algorithm was 5 $\pm$ 29 s.

4. Conclusion

When using ASM based on PCA to segment lung region, the correct shape model cannot be obtained under the training data set with noise samples. In this paper, we combined the RPCA based on the low rank theory which can remove the influence of noise samples on the shape model. The average overlap degree of ASM segmentation based on RPCA is 94.5%, while the average overlap degree of traditional ASM segmentation based on PCA is 69.5%, under the training data set with the noise samples. Experiments show that ASM based on RPCA can achieve better segmentation results than traditional ASM.

The search step of traditional ASM is a least square optimization method, which is sensitive to outlier marker points. Because the CT gray value of the juxta-pleural tumor is similar to lung wall, some marker points are likely to be updated to the transition region of normal lung tissues and tumor rather than the real lung border in the searching process, so it is necessary to identify these abnormal markers firstly. A new abnormal marker identification method is proposed and give different searching function for normal markers and abnormal markers. Experiments show the improved ASM method can get better results than the traditional one. With the results obtained in this work, future endeavor will research the different type pathological lung segmentation framework into a lung CAD system.

Conflict of interest

None to report.