Skip to main content
PMC home page
Chemical Science logoLink to Chemical Science
. 2020 Mar 24;11(15):3914–3922. doi: 10.1039/c9sc05768d

The role of an interface in stabilizing reaction intermediates for hydrogen evolution in aprotic electrolytes†

Ivano E Castelli 1,2,✉, Milena Zorko 3, Thomas M Østergaard 1, Pedro F B D Martins 3, Pietro P Lopes 3, Byron K Antonopoulos 4, Filippo Maglia 4,5, Nenad M Markovic 3, Dusan Strmcnik 3,✉, Jan Rossmeisl 1,✉
PMCID: PMC8152617  PMID: 34122861

Abstract

By combining idealized experiments with realistic quantum mechanical simulations of an interface, we investigate electro-reduction reactions of HF, water and methanesulfonic acid (MSA) on the single crystal (111) facets of Au, Pt, Ir and Cu in organic aprotic electrolytes, 1 M LiPF6 in EC/EMC 3:7W (LP57), the aprotic electrolyte commonly used in Li-ion batteries, 1 M LiClO4 in EC/EMC 3:7W and 0.2 M TBAPF6 in 3 : 7 EC/EMC. In our previous work, we have established that LiF formation, accompanied by H2 evolution, is caused by a reduction of HF impurities and requires the presence of Li at the interface, which catalyzes the HF dissociation. In the present paper, we find that the measured potential of the electrochemical response for these reduction reactions correlates with the work function of the electrode surfaces and that the work function determines the potential for Li+ adsorption. The reaction path is investigated further by electrochemical simulations suggesting that the overpotential of the reaction is related to stabilizing the active structure of the interface having adsorbed Li+. Li+ is needed to facilitate the dissociation of HF which is the source of protons. Further experiments on other proton sources, water and methanesulfonic acid, show that if the hydrogen evolution involves negatively charged intermediates, F− or HO−, a cation at the interface can stabilize them and facilitate the reaction kinetics. When the proton source is already significantly dissociated (in the case of a strong acid), there is no negatively charged intermediate and thus the hydrogen evolution can proceed at much lower overpotentials. This reveals a situation where the overpotential for electrocatalysis is related to stabilizing the active structure of the interface, facilitating the reaction rather than providing the reaction energy.

By combining idealized experiments with realistic quantum mechanical simulations of an interface, we investigate electroreduction reactions of HF, water and methanesulfonic acid on the single crystal (111) facets of Au, Pt, Ir and Cu in a variety of aprotic electrolytes.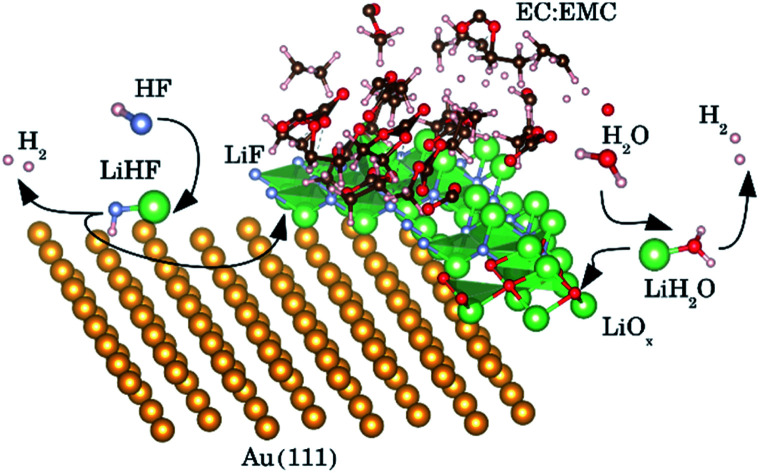graphic file with name c9sc05768d-ga.jpg

Introduction

Electrocatalytic reactions are important for technologies such as batteries, fuel cells and electrolyzers. These reactions take place at the interface between an electrode and an electrolyte. Despite its importance, only little is understood regarding the relationship between reactions and interfaces at the atomic scale. This is to a large extent due to the high complexity of the electrochemical interface which is very difficult to characterize experimentally and to model computationally.1–6 The reactions taking place at the interface can be influenced by the atomic and electronic structure of the electrode surface, by the electrolyte structure and electrostatic properties. It is known that the presence of covalently or non-covalently bonded species at the interface can in some cases influence its electrochemical properties.2,7–9 An understanding of these effects can help in designing more active and more stable materials for energy storage and conversion devices.

One of the devices that could benefit from the in-depth understanding of the electrochemical interface is the Li-ion battery (LIB). Even though the performance and safety of LIBs is linked to the formation of a solid electrolyte interphase (SEI) layer on the graphite anode, a complete understanding of the nature of the SEI at the atomic scale is still missing and thus the development of electrolytes and electrodes is often a matter of chemical intuition and trial and error.10–15 The SEI layer contains various organic and inorganic phases and encompasses different length and time scales from the initial granulation to the growth and the aging mechanism. In addition, during its formation, gasses like H2 and C2H2 are evolved from the reduction of the electrolyte and impurities. The biggest challenge for more fundamental studies seems to be the high complexity of real systems, where we encounter many undefined components of the electrochemical interface, including defects on the electrode material, impurities in the electrolyte, and purposefully added components that ensure appropriate electrical and mechanical properties of the device. In the simulations, on the other hand, it is a challenge just to include the most essential parts of the interface. Thus, there is a huge gap between the ‘ideal’ conditions modeled in simulations and the ‘real’ conditions in experiments. We aim to reduce this gap by combining experiments under idealized conditions with density functional theory (DFT) simulations under conditions as realistic as possible to understand interface reactions at the atomic level.

In the present work, we investigate the hydrogen evolution reaction (HER) from different proton donors on single crystal metal surfaces in aprotic electrolytes consisting of a binary solvent mixture of ethylene carbonate (EC) and ethyl methyl carbonate (EMC) with LiPF6 (commonly used in Li-ion batteries), LiClO4 or TBAPF6. As we focus on the understanding of the reactions that occur during the initial potential scan, we can model clean metal surfaces without possible complications that arise in instances where a deposit is formed on the electrodes during the said potential scan. Although single crystal metal surfaces are far from the electrodes used in real energy storage and conversion devices, they are ideal for this study because they provide a very well-defined, clean interface and allow us to decouple the effects of the interface from the presence of impurities and defects, which are common in conventional electrodes. The results reported here point to a previously undiscussed phenomenon which may be found in other aqueous or non-aqueous interfaces and, although common graphitic anodes work at a much lower potential compared to the metals investigated here, may have applicability for electrochemical interfaces in Li-ion batteries as well as other energy conversion and storage devices.

We employ state of the art density functional theory (DFT) simulations, to gain insight into the reduction reaction mechanisms. We use a recently developed methodology (called the generalized computational electrode) combined with ab initio molecular dynamics (AIMD) to simulate the interface as an open system, in equilibrium with the electrochemical environment and at constant potentials relative to a computational reversible lithium electrode. The output of these simulations are phase diagrams for the stable structure of the interface as a function of the potential, the structure of the electrode surface and the composition of the electrolyte.16,17 The stable structures are then used to investigate trends in the reduction reactions. All calculations are carried out using the DFT code GPAW18,19 and the Atomistic Simulation Environment (ASE)34 to handle the structures and run the molecular dynamics. All the computational data presented here are stored in an open source database available at the address: https://nano.ku.dk/english/research/theoretical-electrocatalysis/katladb/. The computational and experimental details are reported in the ESI.† Presently, there is no standard methodology to investigate interfaces in electrochemistry. This paper aims to define a pre-state-of-the-art for modeling interfaces, including the anode/electrolyte interface in Li-ion batteries.

Firstly, we investigate trends in the catalytic activity of different surfaces for hydrogen evolution with HF as a proton source in an aprotic solvent. Recently, we have described the role of H2O and HF impurities in the formation of LiF, which is one of the main SEI components,20–22 and hydrogen evolution at the interface for different surfaces, from model (111) single crystals (Cu, Au, Pt, and Ir) to more realistic carbon systems (graphite and graphene). We have shown that the formation of LiF is caused by the electro-reduction of impurity HF, according to the reaction:

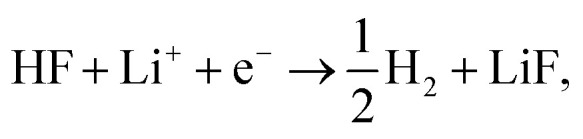graphic file with name c9sc05768d-t1.jpg 1

which is an exergonic reaction by more than 4 eV at U = 0 versus Li/Li+.14

Based on the simulations we find that the trends in the measured overpotentials, i.e. the energy required to start the reaction, are related to stabilizing the activated complex at the interface. This suggests that the ions of the electrolyte play a direct role in splitting the HF molecule.

Finally, we study the trends as the proton source is changed from HF to a weak (H2O) or to a strong (methanesulfonic, MSA) acid on Pt and Au. The experiments and simulations conclude that when the proton donor is poorly dissociated (F− for HF and OH− for water), the presence of Li+ at the interface is needed to facilitate the dissociation of HF or water. If free protons are available, hydrogen is evolved at much lower overpotentials. These results indicate that the role of the electrochemical potential is to build an interface that enables the reduction reactions, rather than providing the activation energy to run the reactions.

Results and discussion

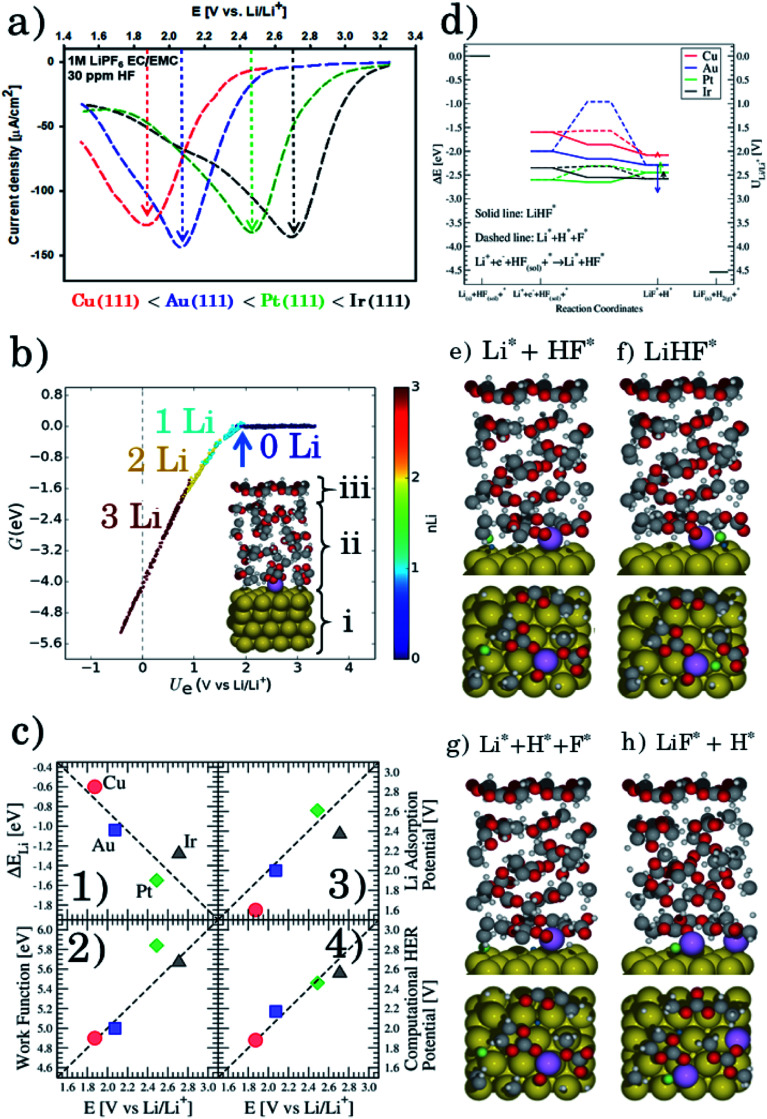
Fig. 1a shows the voltammograms (CVs) in 1 M LiPF6 in EC/EMC 3:7W (LP57), at a scan rate of 50 mV s−1, of different single crystal FCC(111) surfaces, namely Cu, Au, Ir, and Pt.14 Two additional surfaces, namely the (100) and (110) terminations for Au, are added in the ESI (Fig. S1†). Note that the shape of the CVs, which display an initial exponential current increase, followed by a sharp decrease towards 0, indicates a passivation process, consistent with our previous findings that the impurity HF in the electrolyte is reduced to a passive LiF film and hydrogen according to reaction (1). In contrast voltammograms in a HF free electrolyte (1 M LiClO4) are shown in Fig. S2.† The activity for this reaction decreases in the order Ir(111) > Pt(111) ≫ Au(111) > Cu(111).

Fig. 1. (a) Measured electrochemical response in LP57 under stagnant conditions. (b) Phase diagram of Li in LP57 on Au111. The coverage of Li atoms is obtained by dividing nLi by 16, which is the number of surface atoms. The adsorption potential of Li is indicated with an arrow. Inset shows the structure of the simulations: H atoms are represented in white, C in gray, O in red, Au in gold, and Li in purple. Different configurations of Li (at the interface as shown here and dissolved in the electrolyte) have been considered. The arrow indicates the Li adsorption potential. (c) Correlations between the first electrochemical response (arrows in Fig. 1a) and the calculated adsorption energy of Li (Fig. 1c1, ΔELi, calculated versus slab + electrolyte and Li bulk), the work function of the clean metal slabs (Fig. 1c2), the adsorption potential of Li, i.e. the potential where Li starts to be non-specifically adsorbed (Fig. 1c3, arrows from Fig. 1b), and the computational HER potential (Fig. 1c4). (d) Reaction paths for the splitting of HF and the formation of LiF. The structures of the reaction paths are shown in (e)–(h) where only the bottom layer of the electrolyte has been let free to relax, while the top three layers were kept frozen (Au atoms are represented in gold, H in gray (except the one participating in the reaction that is shown in blue), O in red, F in green, and Li in purple).

Fig. 1

Open in a new tab

Descriptors for the electrochemical response

To get a hint of the reaction mechanism we correlate the potential for the measured activity with different quantities which are easily calculated. The aim is to identify possible descriptors for the measured electrochemical response, which may suggest parts of the reaction path by means of easy to calculate quantities. We define the measured electrochemical response as the potential of maximum current, see Fig. 1a (we take the potential of the most prominent feature of the voltammograms, i.e. the peak potential, as the qualitative measure of the electrochemical activity of individual electrode surfaces). We consider the species that are involved in the reaction (1), namely H*, Li*, F*, and HF* and the work function of the electrode surface. The adsorption energies are calculated for the surface in a vacuum, i.e. without the influence of the solvent, and relative to neutral reference molecules or solids, e.g. for Li it is the energy of:

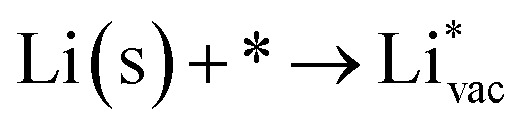graphic file with name c9sc05768d-t2.jpg 2

where vac stands for vacuum and * represents the surface. The correlation between the possible descriptors (y-axis) and the measurements (x-axis) is shown in Fig. 1c.

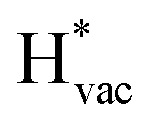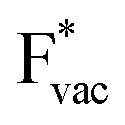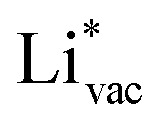The adsorption energies of the species involved in the HF dissociation and the LiF formation are very different in nature. Inline graphic adsorbs as a neutral species and forms a covalent bond with the metal slab while Inline graphic and Inline graphic absorb as F− and Li+, respectively, and form bonds which have a prevalent ionic character (we would like to point out that a covalent contribution, however small, is still present and it has an effect on the energetics of the reduction reactions). The trends for the adsorption are thus also different. The adsorption energy of 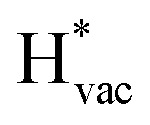Inline graphic shows no-correlation with the experimental overpotential, as shown in more detail in Fig. S3.† This may be counter intuitive as it is known that the H adsorption energy is a good descriptor for the HER under acidic conditions.23,24 In Fig. 1c it is found that both the adsorption energy of 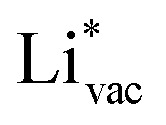Inline graphic (Fig. 1c1) and the work function (Fig. 1c2) are good descriptors for the reactions, suggesting that there is a strong correlation between the two. 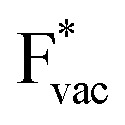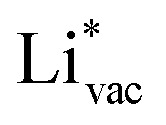The work function seems to determine the adsorption energies of the ions Inline graphic and Inline graphic. For the positively charged 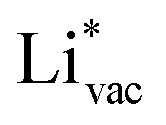Inline graphic ion, the larger the work function, the stronger the adsorption. The opposite trend holds for the adsorption of the negative 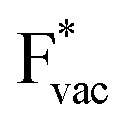Inline graphic ions (Fig. S3†). 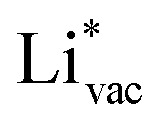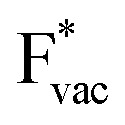This reflects that Inline graphic and Inline graphic adsorb as ions, whereas 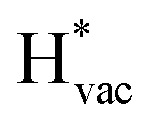Inline graphic adsorbs as a neutral and polarizable intermediate having only little interaction with the field. The potential for the electrochemical response measured in experiments is one-to-one correlated with the adsorption energy of 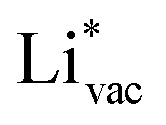Inline graphic and thereby to the work function of the metal and anti-correlated with the adsorption energy of 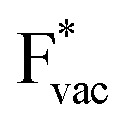Inline graphic. This suggest that 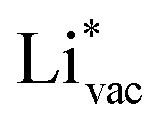Inline graphic is important for the hydrogen evolution reaction. We would like to note that the adsorption of 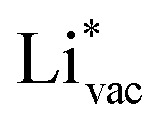Inline graphic is different from the underpotential deposition of Li (Li UPD). At low coverages, Li is adsorbed as a positive ion, and thus the adsorption energy correlates with the work function. Once the coverage is increased, Li will adsorb as metal, the correlation is broken, and the adsorption is now independent of the electric field. The situation is different from the adsorption of H, which at low coverage adsorbs as a neutral atom (H0), while only a higher coverage adsorbs as a proton (H+), with a charge transfer between the adsorbate and the surface. We will come back to this point in the next section.

Electrolyte simulations

The electrolyte has a significant effect on the nature of the adsorbed 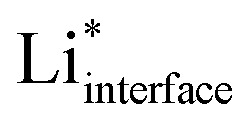Inline graphic, which is partly solvated at the surface (for simplicity, we will omit the subscript interface and indicate 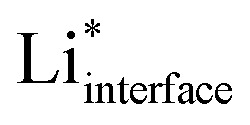Inline graphic as Li*). We therefore include the electrolyte explicitly in the calculations, in the way described in the Computational methods section and in ref. 14 and 17 (for the case of water). The phase diagram of Li* in LP57 obtained using the generalized computational electrode (GCE) combined with AIMD is shown in Fig. 1b. Li* is not present at the interface at a large potential, but the coverage increases going towards lower potentials, where Li* is found non-specifically adsorbed in the double layer. The presence of Li* ions is necessary to screen a change in the potential in combination with a reorientation of the dipoles of the electrolyte molecules. The situation in EC/EMC is somewhat different from liquid water as the water molecules are more mobile and have larger dipoles.25 On the other hand, the situation is also different from solid oxide electrolytes, where the potential is screened only by vacancies and oxygen ions.26

As shown with an arrow in Fig. 1b, the adsorption potential of Li* is the potential of the phase transition between 0 and 1 Li* per unit cell at the interface, corresponding to a coverage of 1/16. This is the potential where

Li+ + e− + * ↔ Li* 3

is in equilibrium. The adsorption of Li* is mostly electrostatic; therefore it depends on the potential set up by the slab at the interface. As for the case of adsorption of Li in a vacuum, Li here is present as a Li+ ion. Note that this electrostatic adsorption occurs at significantly higher potentials that the UPD adsorption which requires a charge transfer. For example, it has been reported that Li UPD on Au(111) is seen only at a potential of around 0.9 V vs. Li/Li+, compared to the estimated adsorption potential of Li* of approximately 2 V.27,28 The adsorption potential for Li* differs from the adsorption energy in vacuum calculations as the electrolyte, potential and electrochemical environment are included in the former, but not in the latter. The Li* is stabilized by approximately ∼1 eV, due to the interaction with the electrolyte. However, due to a similar interaction with the electrodes, these two quantities are closely related and therefore it is expected that the adsorption potential for Li* also should correlate with the experiments.

The diagonal in Fig. 1c3 corresponds to the perfect agreement between the measured potential and the calculated potential for Li+ adsorption (the phase diagrams for all the four metal surfaces are shown in Fig. S4†). There is a slight constant offset of ∼0.2 V for Ir, Au and Cu. Pt is the only material above the diagonal. The offset is related to where we read off the experimental potential on the polarization curve (we have chosen the potential of maximum current), so a perfect quantitative agreement cannot in general be expected; however, in this case the agreement is remarkable. We will later return to Pt, which in this context is slightly out of the trend. However, the good correlation strongly indicates that the presence of Li* at the interface is required to run the electrochemical charge transfer reactions performed in the experiments. To qualify how Li* can participate in the reaction, the possible reaction mechanisms have to be addressed and to compare reaction paths the potential should be kept constant. In practice in the simulations, this is done by choosing different structures of the electrolyte compensating for the change in the species adsorbed and their position. The rigorous way to deal with this is to use a GCE and run AIMD simulations for the different adsorbate fragments in the proposed reaction paths and obtain a Boltzmann weighted average of structures of the electrolyte. Due to the heavy computational load of this method, a lighter version has been chosen here, for which the reaction paths have been calculated for a set of different initial structures of the electrolyte at the adsorption potential of Li keeping the work function close to constant.

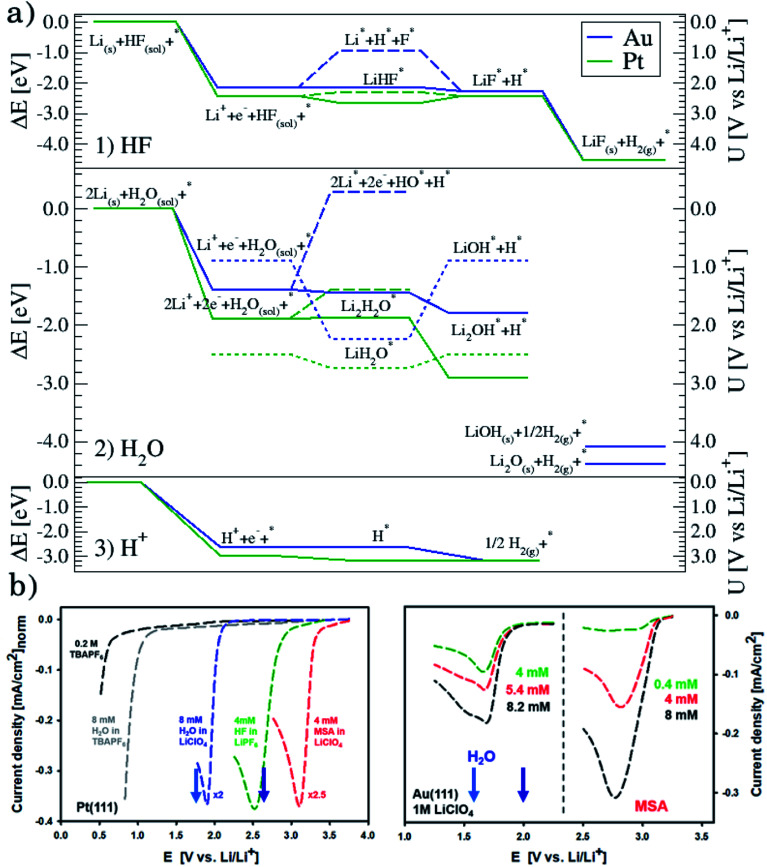
Fig. 1d shows the calculated energetics of possible reaction paths for the formation of LiF and H2 molecules. To the left the reference state Li(s), HF(sol) and the clean slab, *, are shown. This state corresponds to potential 0 V versus Li/Li+. The next state is Li+ + e− + HF(sol) + * at the adsorption potential of Li* for the different surfaces. Here, we assume that HF(sol) is in equilibrium with HF* and, as we are at the adsorption potential of Li, Li+ is in equilibrium with Li*. This is the initial state of the reaction. For the first two states, the potential vs. Li/Li+ can be read off at the y-axis to the right.

When Li and HF are adsorbed, Li* + HF*, two different paths can be followed: in one case, HF dissociates alone (indicated with a dashed line as Li* + H* + F−*) and this is always up-hill in energy compared to the previous step in the reaction path. In the other case, HF* first adsorbs together with Li*, forming a LiHF complex (solid line, LiHF*) at the surface and HF dissociates later. For all surface Li* speeds up the HF dissociation reaction, as the solid lines are below the dashed lines (Fig. 1d). After HF dissociation there is a LiF* molecule at the interface and H* adsorbed on the surface. The last step of the reaction corresponds to the formation of H2(g) and LiF(s) in the rock salt structure.

Although the descriptors in Fig. 1c, namely the adsorption energy of Li* (Fig. 1c1), the work function of the clean slab (Fig. 1c2), and the Li adsorption potential (Fig. 1c3) are quantities that describe the LiF formation process, they do not reproduce the full picture. The activity of the surface towards the Hydrogen Evolution Reaction (HER) is not taken into account. To do this, we consider that the energy of the initial state, Li+ + e− + HF(sol), must be high enough to overcome all the steps for LiF formation and the HER (as shown in Fig. 2a1). By increasing (decreasing) the overpotential, the energy of the initial state moves up (down) towards smaller potentials versus Li/Li+. For all of the surface the LiHF* complex forms spontaneously at the potential for Li adsorption suggesting that, in the presence of HF close to the surface, Li+ is adsorbed at smaller overpotentials. This potential is probably closer to the experiments. For all the surfaces except Pt, the overpotential is determined by the presence of LiHF* at the interface. However, for Pt, the overpotential has to be increased slightly beyond the Li+ adsorption potential to overcome the energy of the dissociated state. This is due to relatively weak hydrogen adsorption and strong Li+ adsorption (Fig. S3†). This to some extent explains why Pt is off trend when using simple descriptors such as the work function. Comparing the calculated HER potential, i.e. the potential where all the reaction steps are exergonic, with experiments shows a very clear correlation, see Fig. 1c4, and as mentioned before absolute agreement between experiments and simulations could not be expected, but we note that the trends are captured perfectly in the simulations and that Pt shows that if the hydrogen binding is weak and the work function is large and the adsorption of H* rather than the formation of the LiHF* intermediate becomes the potential determining step. A brief discussion on this point and how it can be used to identify the potential determining steps in future anode materials is included in the ESI and in Fig. S6.† With respect to the other quantities in Fig. 1c, the computational HER potential (Fig. 1c4) is not a good descriptor since it can be obtained only through full simulations of the reaction paths and intermediates explicitly including the electrolyte obtained from AIMD simulations. Although this gives the most precise picture of the process, it is complicated and tedious to calculate and it cannot be used to screen anode materials and interfaces.

Fig. 2. (a) Reaction paths for the three reactions considered on Au(111), in blue, and Pt(111), in green: H2 formation from HF (1) and from H2O (2), and the structures of the interface are shown in Fig. S5† and from protons (3). (b) Voltammograms in various electrolytes with different concentrations of water and MSA under stagnant conditions: 1 M LiClO4, for both Pt(111) and Au(111) and, only for Pt(111), 0.2 M TBAPF6 (no Li+ cations and water, and HF impurities below 5 ppm), 0.2 M TBAPF6 with added 8 mM water, and 1 M LiPF6, which is included for completeness. Note that for clarity, on Pt(111), the currents are normalized to the value obtained for HF electroreduction. The two arrows in each plot indicate the adsorption potential for 1 and 2 Li (darker and lighter blue, respectively) as calculated from the AIMD simulations. It shows a good correlation between the two response peaks and these values.

Fig. 2

Open in a new tab

In conclusion, setting up an active interface is therefore a necessity to allow for the reaction to run. This means that the role of the electrochemical potential is to create the interface with adsorbed Li* present, as indicated by the phase diagram in Fig. 2b, rather than providing the energy to overcome the reaction barriers. In other words, the electrochemical response that measures the production of H2 molecules occurs at a potential corresponding to the adsorption potential of Li* in the presence of HF. At lower overpotentials, the barrier for HF splitting, leaving a F− ion at the interface, is too high. The reaction runs much faster if Li* is present at the interface stabilizing the F− ion by forming the LiHF* intermediate.

To investigate if this effect is a prerogative of Li+, we have conducted experiments where the LiPF6 salt has been substituted with the NaPF6 salt on Au(111) and Pt(111). The experiments show only a small constant decrease in terms of overpotential for Na compared to Li, and thus Na* plays a similar role to Li* for the SEI layer and H2 formation, as reported in Fig. S7.† The small decrease in overpotential is consistent with the slightly lower overpotential needed for the adsorption of Na* compared to Li*, as indicated by the simulations. This is probably related to the different solvation shells of Li+ compared to Na+ (ref. 29) and thus that Na* can keep more of the solvation at the interface than Li* can.

Trends for other proton sources

The reaction above suggests that the stabilization of the anion by Li* close to the negatively charged electrode surface is crucial for understanding the trend. However, this also suggests that the reaction is anion specific and that the Li* may not be needed if the proton donor is more dissociated and there are more free protons available in the electrolyte.

We consider two different proton sources added to the electrolyte: water and methanesulfonic acid. Note that in order to avoid interference from HF, which is present in LiPF6 based electrolytes, the electrolyte chosen for these experiments was 1 M LiClO4. In the case of water, the general reactions that we consider are

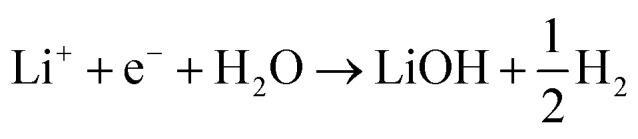graphic file with name c9sc05768d-t21.jpg 4

and

2Li+ + 2e− + H2O → Li2O + H2 5

This can run via different pathways as shown in Fig. 2a2. Similar to the case of LiF formation (reported in Fig. 2a1 for completeness) there is one pathway for the dissociation of water not involving the presence of Li*, i.e. H2O + e− + * → HO− + H*. This is up-hill in energy by around 1.5 eV. In the most favorable pathway, instead, water adsorbs in a bridge position between two Li atoms, after which, one H is transferred to the surface. H2 is formed when this process is repeated. In the cyclic-voltammetry experiment, reported in Fig. 2b, the electrochemical response corresponding to the H2 formation from water impurities occurs at a higher overpotential than the H2 formation from HF (1.8 V vs. 2.6 V on the Li/Li+ scale on Pt(111) respectively). A single Li* is insufficient to dissociate water. Two Li*s are needed to from a Li2H2O complex from which the water can easily dissociate. The formation of the Li2H2O complex occurs at a lower potential than the formation of LiHF. Therefore, just as for HF, the presence of cations at the interface facilitates the dissociation of water. A similar observation has been in our previous work in an alkaline aqueous electrolyte, where the presence of the cation in the activated complex lowered the energy barrier for water dissociation.9 In the aqueous case, however, the cation was constrained to the surface by Ni(OH)2 clusters, deposited on the Pt surface. Consistent with previous reports,7 there are multiple types of noncovalent interactions possible in the double layer, e.g. hydrogen bonding, van der Waals and electrostatic forces, which can bind a species to the electrode surface. Herein, we report for the first time to our knowledge that the potential induced electrostatic interaction can, in fact, drive the formation of an activated complex. We further strengthen our claims by performing experiments in a 0.2 M TBAPF6 electrolyte, where both HF impurities and Li+ are absent. TBA is a bulky cation and therefore very unlikely to get close to the surface or to interact with the anion of the proton donor. As shown in Fig. 2b the water electroreduction is now observed at 1 V more negative potential. In addition, similar to the hydrogen evolution reaction in alkaline electrolytes, no passivation of the electrode surface as well as much higher currents are observed. For clarity, the scans were limited to similar current densities as observed in other electrolytes. Similar to the results shown in Fig. 2b, the presence of Li+ (or Na+) has been reported to generate a large cathodic current for water reduction in acetonitrile, while no current was measured in the presence of tetrabutylammonium (TBA+) cations.30 The measured potential for the HER from water correlates now with the adsorption potential of Li+ ions together with water (Li2H2O) (light blue arrows in Fig. 2b) for both the investigated surfaces. The formation of LiOH and Li2O has already been discussed in the literature.31 On the other side, our XPS experiments do not show a precipitate (and this is why we do not connect the energy levels of LiOH and Li2O to the intermediates in Fig. 2a). This could be caused by either the fact that the formed LiOH gets washed off during the electrode preparation for the XPS analysis or the LiOH fragments further react with the electrolyte.

The situation is again different when free protons from a strong acid are added to the electrolyte and this corresponds to the acidic hydrogen evolution reaction in LP57 (Fig. 2a3). In this case, the reaction is simply:

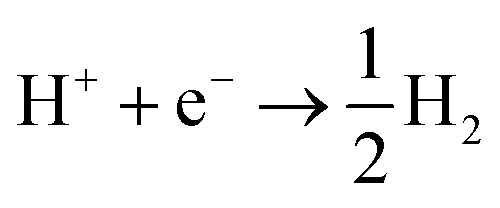graphic file with name c9sc05768d-t22.jpg 6

The evolution of H2 does not depend on the Li* coverage and occurs at a potential close to the hydrogen evolution from acid under aqueous conditions. Fig. 2b shows the polarizations curves obtained in experiments for Au(111) and Pt(111), where we use the potential measured for H(sol) on Pt(111) as the equilibrium potential for the HER. The measured difference between Au and Pt in this case corresponds to the difference in hydrogen adsorption energy, just as has been suggested for understanding trends in HER activity in acidic aqueous solutions.32–34 We note that a catalyst that cannot catalyze the HER in an acid cannot work in alkaline solution either, as all reaction paths involve the H* intermediate, so the descriptor in acid is a minimal requirement for catalysts.35 The two additional reactions from water and acid confirm our reaction model. In fact, when protons are already present in the electrolyte no specific structure of the interface is needed. In the case of HF and H2O proton sources, an overpotential is needed to obtain the active structure of the interface, to dissociate the proton source. Once HF and H2O are dissociated the hydrogen evolution is downhill in free energy. These findings are in agreement with previous studies reporting the effects of cations and the presence of water in other organic electrolytes,36,37 where the rate of concerted proton–electron transfer strongly depended on the source of the protons.38

Conclusion

The hydrogen evolution and the formation of LiF and LiOx fragments in an aprotic, organic carbonate-based electrolyte are found to be related to the formation of an active structure of the interface. The anions which are reaction intermediates need to be stabilized by nearby cations (Li) before the proton source can dissociate near the negatively charged electrode surface. The potential for adsorbing cations directly depends on the work function of the electrode surface, which correlates with the Li adsorption energy, and both can be useful descriptors to explain the trends in interfacial electrochemistry in the presence of cations. This makes the electrocatalytic processes very different from the HER catalysis in acidic aqueous environments, where the adsorption energy plays a much more pronounced role as a descriptor. The acidic trends can be obtained by adding a stronger acid to the electrolyte, and in that case the surface catalysis determines the overpotential as there are no anions as intermediates.

For the first time, we have shown that the main role of the electrochemical potential, in the case of non-dissociated HF and H2O, is to enable the adsorption of Li+, which allows the formation of the transition complex. This is in contrast to a more common situation, where the potential provides the activation energy to drive the reaction. Although we have demonstrated it for a typical battery process, these findings can be generalized for other electrocatalytic reactions.

We have used experiments made as ideal as possible, with very clean electrolytes and single crystal, single facet metal surfaces. The simulations on the other hand have been made as realistic as possible including the electrolyte, ions and potential using the generalized hydrogen electrode and ab initio molecular dynamics. We show that with this combination it is possible to bridge the gap between experiments and simulations and obtain comparisons which are close to not only qualitative but also quantitative analysis. We speculate that the effect of creating an optimal structure of the interface is general for electrocatalytic reactions where charged intermediates need to be stabilized by nearby counter ions.

Conflicts of interest

There are no conflicts to declare.

Supplementary Material

SC-011-C9SC05768D-s001

Acknowledgments

This project has been financially supported by the BMW Group. The theoretical work was done at the Department of Chemistry, University of Copenhagen and at the Department of Energy Conversion and Storage, Technical University of Denmark. The experimental work was done at the Argonne National Laboratory which is operated for the DOE Office of Science by UChicago Argonne, LLC, under contract number DE-AC02-06CH11357. The research efforts on single crystalline systems were supported by the Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division. We thank BMW Technology Corporation for sponsoring this research effort. F.M. acknowledges the support of the Technical University of Munich – Institute for Advanced Study.

†

Electronic supplementary information (ESI) available: Additional details about the computational and experimental methods, cyclic voltammetry, descriptors for the electrochemical response, phase diagrams on all the considered metals, crystal structures used to investigate the reaction paths, descriptor for the prediction of the potential determining step, and voltammetry and phase diagrams in LiPF6 and NaPF6. See DOI: 10.1039/c9sc05768d.

References

  1. Holze R. Structure of Electrified Interfaces. Herausgegeben von J. Lipkowski und P. N. Ross. VCH Verlagsgesellschaft, Weinheim/VCH Publishers, New York, 1993. 406, S., geb. 196.00 DM/125.00 $. — ISBN 3-527-28787-6/0-89573-787-6. Angew. Chem. 1994;106:2067–2068. doi: 10.1002/ange.19941061930. [DOI] [Google Scholar]
  2. Stamenkovic V. R. Strmcnik D. Lopes P. P. Markovic N. M. Energy and fuels from electrochemical interfaces. Nat. Mater. 2016;16:57. doi: 10.1038/nmat4738. [DOI] [PubMed] [Google Scholar]
  3. Nørskov J. K. Bligaard T. Rossmeisl J. Christensen C. H. Towards the computational design of solid catalysts. Nat. Chem. 2009;1:37. doi: 10.1038/nchem.121. [DOI] [PubMed] [Google Scholar]
  4. Schnur S. Groß A. Challenges in the first-principles description of reactions in electrocatalysis. Catal. Today. 2011;165:129–137. doi: 10.1016/j.cattod.2010.11.071. [DOI] [Google Scholar]
  5. Taylor C. D. Wasileski S. A. Filhol J. S. Neurock M. First principles reaction modeling of the electrochemical interface: Consideration and calculation of a tunable surface potential from atomic and electronic structure. Phys. Rev. B: Condens. Matter Mater. Phys. 2006;73:1–16. [Google Scholar]
  6. Antonopoulos B. K. Maglia F. Schmidt-Stein F. Schmidt J. P. Hoster H. E. Formation of the Solid Electrolyte Interphase at Constant Potentials: a Model Study on Highly Oriented Pyrolytic Graphite. Batteries Supercaps. 2018:1–13. [Google Scholar]
  7. Strmcnik D. Kodama K. van der Vliet D. Greeley J. Stamenkovic V. R. Marković N. M. Markovic N. M. The role of non-covalent interactions in electrocatalytic fuel-cell reactions on platinum. Nat. Chem. 2009;1:466–472. doi: 10.1038/nchem.330. [DOI] [PubMed] [Google Scholar]
  8. McCrum I. T. Janik M. J. pH and Alkali Cation Effects on the Pt Cyclic Voltammogram Explained Using Density Functional Theory. J. Phys. Chem. C. 2016;120:457–471. doi: 10.1021/acs.jpcc.5b10979. [DOI] [Google Scholar]
  9. Subbaraman R. Tripkovic D. Strmcnik D. Chang K.-C. Uchimura M. Paulikas a P. Stamenkovic V. Markovic N. M. Enhancing Hydrogen Evolution Activity in Water Splitting by Tailoring Li+-Ni(OH)2-Pt Interfaces. Science. 2011;334:1256–1260. doi: 10.1126/science.1211934. [DOI] [PubMed] [Google Scholar]
  10. An S. J. Li J. Daniel C. Mohanty D. Nagpure S. Wood D. L. The state of understanding of the lithium-ion-battery graphite solid electrolyte interphase (SEI) and its relationship to formation cycling. Carbon. 2016;105:52–76. doi: 10.1016/j.carbon.2016.04.008. [DOI] [Google Scholar]
  11. Peled E. Menkin S. Review—SEI: Past, Present and Future. J. Electrochem. Soc. 2017;164:A1703–A1719. doi: 10.1149/2.1441707jes. [DOI] [Google Scholar]
  12. Wang A. Kadam S. Li H. Shi S. Qi Y. Review on modeling of the anode solid electrolyte interphase (SEI) for lithium-ion batteries. npj Comput. Mater. 2018;4:15. doi: 10.1038/s41524-018-0064-0. [DOI] [Google Scholar]
  13. Blomgren G. E. The Development and Future of Lithium Ion Batteries. J. Electrochem. Soc. 2017;164:A5019–A5025. doi: 10.1149/2.0251701jes. [DOI] [Google Scholar]
  14. Strmcnik D. Castelli I. E. Connell J. G. Haering D. Zorko M. Martins P. Lopes P. P. Genorio B. Østergaard T. Gasteiger H. A. Maglia F. Antonopoulos B. K. Stamenkovic V. R. Rossmeisl J. Markovic N. M. Electrocatalytic transformation of HF impurity to H2 and LiF in lithium-ion batteries. Nat. Catal. 2018;1:255–262. doi: 10.1038/s41929-018-0047-z. [DOI] [Google Scholar]
  15. Antonopoulos B. K. Stock C. Maglia F. Hoster H. E. Solid electrolyte interphase: Can faster formation at lower potentials yield better performance? Electrochim. Acta. 2018;269:331–339. doi: 10.1016/j.electacta.2018.03.007. [DOI] [Google Scholar]
  16. Rossmeisl J. Chan K. Ahmed R. Tripković V. Björketun M. E. pH in atomic scale simulations of electrochemical interfaces. Phys. Chem. Chem. Phys. 2013;15:10321–10325. doi: 10.1039/C3CP51083B. [DOI] [PubMed] [Google Scholar]
  17. Hansen M. H. Rossmeisl J. pH in Grand Canonical Statistics of an Electrochemical Interface. J. Phys. Chem. C. 2016;120:29135–29143. doi: 10.1021/acs.jpcc.6b09019. [DOI] [Google Scholar]
  18. Mortensen J. J. Hansen L. B. Jacobsen K. W. Real-space grid implementation of the projector augmented wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 2005;71:035109. doi: 10.1103/PhysRevB.71.035109. [DOI] [Google Scholar]
  19. Enkovaara J. Rostgaard C. Mortensen J. J. Chen J. Dułak M. Ferrighi L. Gavnholt J. Glinsvad C. Haikola V. Hansen H. A. Kristoffersen H. H. Kuisma M. Larsen A. H. Lehtovaara L. Ljungberg M. Lopez-Acevedo O. Moses P. G. Ojanen J. Olsen T. Petzold V. Romero N. A. Stausholm-Møller J. Strange M. Tritsaris G. A. Vanin M. Walter M. Hammer B. Häkkinen H. Madsen G. K. H. Nieminen R. M. Nørskov J. K. Puska M. Rantala T. T. Schiøtz J. Thygesen K. S. Jacobsen K. W. Electronic structure calculations with GPAW: a real-space implementation of the projector augmented-wave method. J. Phys.: Condens. Matter. 2010;22:253202. doi: 10.1088/0953-8984/22/25/253202. [DOI] [PubMed] [Google Scholar]
  20. Verma P. Maire P. Novák P. A review of the features and analyses of the solid electrolyte interphase in Li-ion batteries. Electrochim. Acta. 2010;55:6332–6341. doi: 10.1016/j.electacta.2010.05.072. [DOI] [Google Scholar]
  21. Edström K. Herstedt M. Abraham D. P. A new look at the solid electrolyte interphase on graphite anodes in Li-ion batteries. J. Power Sources. 2006;153:380–384. doi: 10.1016/j.jpowsour.2005.05.062. [DOI] [Google Scholar]
  22. Aurbach D. Review of selected electrode-solution interactions which determine the performance of Li and Li ion batteries. J. Power Sources. 2000;89:206–218. doi: 10.1016/S0378-7753(00)00431-6. [DOI] [Google Scholar]
  23. Nørskov J. K. Bligaard T. Logadottir A. Kitchin J. R. Chen J. G. Pandelov S. Stimming U. Trends in the Exchange Current for Hydrogen Evolution. J. Electrochem. Soc. 2005;152:J23. doi: 10.1149/1.1856988. [DOI] [Google Scholar]
  24. Skúlason E. Tripkovic V. Björketun M. E. Gudmundsdóttir S. Karlberg G. Rossmeisl J. Bligaard T. Jónsson H. Nørskov J. K. Modeling the electrochemical hydrogen oxidation and evolution reactions on the basis of density functional theory calculations. J. Phys. Chem. C. 2010;114:18182–18197. doi: 10.1021/jp1048887. [DOI] [Google Scholar]
  25. Xu K. Nonaqueous liquid electrolytes for lithium-based rechargeable batteries. Chem. Rev. 2004;104:4303–4417. doi: 10.1021/cr030203g. [DOI] [PubMed] [Google Scholar]
  26. Zeng Z. Hansen M. H. Greeley J. P. Rossmeisl J. Björketun M. E. Ab Initio Thermodynamic Modeling of Electrified Metal–Oxide Interfaces: Consistent Treatment of Electronic and Ionic Chemical Potentials. J. Phys. Chem. C. 2014;118:22663–22671. doi: 10.1021/jp507519a. [DOI] [Google Scholar]
  27. Saito T. Uosaki K. Surface Film Formation and Lithium Underpotential Deposition on Au(111) Surfaces in Propylene Carbonate. J. Electrochem. Soc. 2003;150:A532. doi: 10.1149/1.1557966. [DOI] [Google Scholar]
  28. Paddon C. A. Compton R. G. Underpotential Deposition of Lithium on Platinum Single Crystal Electrodes in Tetrahydrofuran. J. Phys. Chem. C. 2007;111:9016–9018. doi: 10.1021/jp073304h. [DOI] [Google Scholar]
  29. Cresce A. V. Russell S. M. Borodin O. Allen J. A. Schroeder M. A. Dai M. Peng J. Gobet M. P. Greenbaum S. G. Rogers R. E. Xu K. Solvation behavior of carbonate-based electrolytes in sodium ion batteries. Phys. Chem. Chem. Phys. 2017;19:574–586. doi: 10.1039/C6CP07215A. [DOI] [PubMed] [Google Scholar]
  30. Dubouis N. Serva A. Salager E. Deschamps M. Salanne M. Grimaud A. The Fate of Water at the Electrochemical Interfaces: Electrochemical Behavior of Free Water Versus Coordinating Water. J. Phys. Chem. Lett. 2018;9:6683–6688. doi: 10.1021/acs.jpclett.8b03066. [DOI] [PubMed] [Google Scholar]
  31. Aurbach D. Daroux M. Faguy P. Yeager E. The electrochemistry of noble metal electrodes in aprotic organic solvents containing lithium salts. J. Electroanal. Chem. Interfacial Electrochem. 1991;297:225–244. doi: 10.1016/0022-0728(91)85370-5. [DOI] [Google Scholar]
  32. Breiter M. W. Electrochemical study of hydrogen adsorption on clean platinum metal surfaces. Ann. N. Y. Acad. Sci. 2006;101:709–721. doi: 10.1111/j.1749-6632.1963.tb54927.x. [DOI] [Google Scholar]
  33. Greeley J. Jaramillo T. F. Bonde J. Chorkendorff I. Nørskov J. K. Computational high-throughput screening of electrocatalytic materials for hydrogen evolution. Nat. Mater. 2006;5:909–913. doi: 10.1038/nmat1752. [DOI] [PubMed] [Google Scholar]
  34. Larsen A. H. Mortensen J. J. Blomqvist J. Castelli I. E. Christensen R. Dułak M. Friis J. Groves M. N. Hammer B. Hargus C. Hermes E. D. Jennings P. C. Jensen P. B. Kermode J. Kitchin J. R. Kolsbjerg E. L. Kubal J. Kaasbjerg K. Lysgaard S. Maronsson J. B. Maxson T. Olsen T. Pastewka L. Peterson A. Rostgaard C. Schiøtz J. Schütt O. Strange M. Thygesen K. S. Vegge T. Vilhelmsen L. Walter M. Zeng Z. Jacobsen K. W. The Atomic Simulation Environment—A Python library for working with atoms. J. Phys.: Condens. Matter. 2017;29:273002. doi: 10.1088/1361-648X/aa680e. [DOI] [PubMed] [Google Scholar]
  35. Sheng W. Myint M. Chen J. G. Yan Y. Correlating the hydrogen evolution reaction activity in alkaline electrolytes with the hydrogen binding energy on monometallic surfaces. Energy Environ. Sci. 2013;6:1509–1512. doi: 10.1039/C3EE00045A. [DOI] [Google Scholar]
  36. Ledezma-Yanez I. Díaz-Morales O. Figueiredo M. C. Koper M. T. M. Hydrogen Oxidation and Hydrogen Evolution on a Platinum Electrode in Acetonitrile. ChemElectroChem. 2015;2:1612–1622. doi: 10.1002/celc.201500341. [DOI] [Google Scholar]
  37. Suárez-Herrera M. F. Costa-Figueiredo M. Feliu J. M. Voltammetry of Basal Plane Platinum Electrodes in Acetonitrile Electrolytes: Effect of the Presence of Water. Langmuir. 2012;28:5286–5294. doi: 10.1021/la205097p. [DOI] [PubMed] [Google Scholar]
  38. Jackson M. N. Surendranath Y. Donor-Dependent Kinetics of Interfacial Proton-Coupled Electron Transfer. J. Am. Chem. Soc. 2016;138:3228–3234. doi: 10.1021/jacs.6b00167. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

SC-011-C9SC05768D-s001
SC-011-C9SC05768D-s001.pdf (1.2MB, pdf)

Articles from Chemical Science are provided here courtesy of Royal Society of Chemistry

RESOURCES