Probing competing relaxation pathways in malonaldehyde with transient X-ray absorption spectroscopy

Abstract

Excited-state intramolecular hydrogen transfer (ESIHT) is a fundamental reaction relevant to chemistry and biology. Malonaldehyde is the simplest example of ESIHT, yet only little is known experimentally about its excited-state dynamics. Several competing relaxation pathways have been proposed, including internal conversion mediated by ESIHT and C C torsional motion as well as intersystem crossing. We perform an in silico transient X-ray absorption spectroscopy (TRXAS) experiment at the oxygen K-edge to investigate its potential to monitor the proposed ultrafast decay pathways in malonaldehyde upon photoexcitation to its bright S₂(ππ*) state. We employ both restricted active space perturbation theory and algebraic-diagrammatic construction for the polarization propagator along interpolated reaction coordinates as well as representative trajectories from ab initio multiple spawning simulations to compute the TRXAS signals from the lowest valence states. Our study suggests that oxygen K-edge TRXAS can distinctly fingerprint the passage through the H-transfer intersection and the concomitant population transfer to the S₁(nπ*) state. Potential intersystem crossing to T₁(ππ*) is detectable from reappearance of the double pre-edge signature and reversed intensities. Moreover, the torsional deactivation pathway induces transient charge redistribution from the enol side towards the central C-atom and manifests itself as substantial shifts of the pre-edge features. Given the continuous advances in X-ray light sources, our study proposes an experimental route to disentangle ultrafast excited-state decay channels in this prototypical ESIHT system and provides a pathway-specific mapping of the TRXAS signal to facilitate the interpretation of future experiments.

Resolving competing hydrogen-transfer mediated internal conversion and relaxation processes in a prototype ESIHT-system with transient X-ray absorption.

Introduction

The ultrashort (from few hundreds of femtoseconds down to sub-femtosecond^1–3), tunable and intense X-ray pulses made available by X-ray free-electron lasers are revolutionizing our ability to probe photoinduced processes in matter as they unfold on the length and time scale of nuclear and electronic motion.⁴ The electronic and structural changes induced by a coherent pump source, typically in the optical region, can be followed by probing transient structures in time-domain implementations of X-ray diffraction/scattering⁵ and spectroscopies.⁶ Resonant X-ray spectroscopies exploit the localized nature of electronic transitions involving core orbitals to achieve high spatial resolution.⁷ Since the core levels of different elements have distinct resonance energies that are sensitive to the nearby chemical environment, electronic and geometric changes induced by the pump can be monitored from the viewpoint of individual atoms in the molecule.

Transient X-ray absorption spectroscopy (TRXAS), especially in the near-edge region (NEXAFS), has proven to be a powerful method to monitor light-induced processes in molecular systems.^8–13 Its use has been further spurred by the recent extension of high-harmonic generation technology into the soft X-ray region,^14–16 enabling TRXAS measurements into the water-window.^10,17 As a consequence of the valence hole created by the pump, the pre-edge features provide information about the resulting singly-occupied molecular orbital (SOMO). In particular, the signal intensity depends on the spatial overlap between the involved core and valence orbitals, and as such, provides a sensitive probe of the transient electronic character. Of particular interest is the ability to fingerprint conical intersections that lead to population transfer and coherences between electronic states. Previous oxygen K-edge TRXAS experiments on thymine have demonstrated that nπ*–ππ* internal conversion can be monitored by the difference in the local density of n- and π-orbitals.¹³

Excited-state intramolecular hydrogen transfer (ESIHT) is one of the fastest chemical reactions, occurring on time scales of the order of 50 fs.^18–20 It plays a crucial role in a wide variety of light-induced biological processes^21,22 and technological applications.^23–26 Malonaldehyde is a prototype for ESIHT, being the simplest molecule to exhibit symmetric ground-state as well as excited-state H-transfer. It is the functional unit of the entire family of β-diketones²⁷ and the structural motif in larger ESIHT systems. In the gas phase, the enol form (3-hydroxy-2-propenal) is the prevalent tautomer^28,29 stabilized by electronic conjugation and the formation of a H-chelate ring via an intramolecular hydrogen bond.³⁰ The presence of oxygen lone pairs introduces an nπ* state that, in the case of malonaldehyde, lies below the optically accessible ππ* state.³¹ For experimental investigations, malonaldehyde has to be synthesized and purified on site because of its instability at room temperature.³² Together with the added complication of differentiating reactant and product of the ESIHT process in a symmetric system, this likely explains why the majority of excited-state studies have been theoretical. To our knowledge, no experimental studies on the photodynamics of isolated malonaldehyde are yet available.

A series of early computational studies on malonaldehyde proposed that the excited-state decay following photoexcitation to the S₂(ππ*) state involves two competing S₂/S₁ decay channels.^33,34 Within less than 30 fs, a portion of the population was found to proceed downhill along the H-transfer coordinate where it reaches an intersection seam with S₁(nπ*). While barrierless on S₂, many theoretical studies agree that a substantial barrier on S₁ impedes further H-transfer.^33–36 The main part of the wavepacket was predicted to move along the C C twisting coordinate towards the global minimum on S₂ which represents a minimum on the S₂/S₁/S₀ three-state intersection (3SI) seam. However, because of the reduced configuration space volume of 3SIs, the vast majority of the population was found to transfer to the ground state sequentially through two-state intersections (i.e., S₂ → S₁ followed by S₁ → S₀ internal conversion).³⁷ While the direct involvement of the low-lying 3SI is limited, its presence induces large regions of nearby S₂/S₁ and S₁/S₀ intersections, explaining the short predicted S₁ lifetime (<175 fs). A recent theoretical study predicted relaxation from S₁(nπ*) to the lowest triplet T₁(ππ*) state by spin–orbit coupling as another important decay channel.³⁸ Indeed, for the closely related acetylacetone, both carbon K-edge TRXAS¹⁰ and combined time-resolved ion/photoelectron spectroscopy³⁹ have provided experimental evidence of T₁ state formation on the picosecond (or even sub-picosecond³⁹) time scale and intersystem crossing as an important deactivation process. While keeping in mind that caging effects can significantly impact photodynamical behavior, infrared spectroscopic measurements of photoproducts of malonaldehyde in cryogenic rare-gas matrices did not provide indications of triplet manifold involvement nor of fragmentation,⁴⁰ in contrast to analogous experiments on acetylacetone.⁴¹

In this work, we investigate theoretically the sensitivity of TRXAS at the oxygen K-edge to track the structural and electronic changes involved in the relaxation of malonaldehyde upon photoexcitation to its bright S₂(ππ*) state. Our aim is three-fold. First, the prediction of spectral fingerprints prior to experiment allows us to show whether TRXAS can resolve the proposed competing non-radiative pathways and provide insight into the photodynamics of this prototypical ESIHT system. Second, a decomposition of the predicted TRXAS signal provides the necessary foundation for interpreting future oxygen K-edge TRXAS experiments on malonaldehyde. Third, analysis of the structural and electronic changes underlying the predicted TRXAS signals enables us to rationalize the origin of the sensitivity of TRXAS to the coupled electron-nuclear dynamics in malonaldehyde. As shown below, our results show that TRXAS can differentiate between the proposed pathways. By direct computation of as-yet unmeasured TRXAS signals, our work serves as both a benchmark for the predictive abilities of theory and also a guide to the interpretation of future TRXAS experiments on this molecule.

A variety of theoretical methods for the calculation of steady-state X-ray spectroscopies have been devised over the past decade and recently reviewed.⁴² Increasing effort is being devoted towards enabling theoretical support for transient X-ray spectroscopies both in terms of accurate calculations of valence-to-core-excited state spectroscopic signals and inclusion of coupled electron-nuclear dynamics. Currently available methods for simulating TRXAS include density functional theory (DFT),^10,43–46 restricted active space self-consistent field without (RASSCF)^47,48 and with second-order perturbation correction (RASPT2),^46,49 algebraic-diagrammatic construction (ADC),^50–52 coupled cluster^13,53–55 and combined DFT/multireference configuration interaction.⁵⁶ Effects of nuclear dynamics, and in particular non-adiabatic transitions, have been treated at varying degrees of complexity and accuracy using full-dimensionality trajectory-^10,48 and Gaussian wavepacket-based^46,51,57 dynamics as well as reduced-dimensionality quantum dynamics.^44,45,54

We employ both RASPT2 ^58,59 and ADC^60,61 to simulate the oxygen K-edge TRXAS signals of the proposed photoexcited decay pathways in malonaldehyde, including internal conversion mediated by ESIHT and C C torsional motion as well as singlet-triplet intersystem crossing. We provide a link between spectroscopic signatures and underlying electron and nuclear dynamics by analyzing initial valence and final core-excited states along interpolated reaction coordinates. To investigate dynamical aspects, we further compute TRXAS signals along representative trajectories taken from ab initio multiple spawning^62,63 (AIMS) simulations where the potential energy surfaces and couplings are computed with extended multistate complete active space second-order perturbation theory (XMS-CASPT2).⁶⁴

Computational details

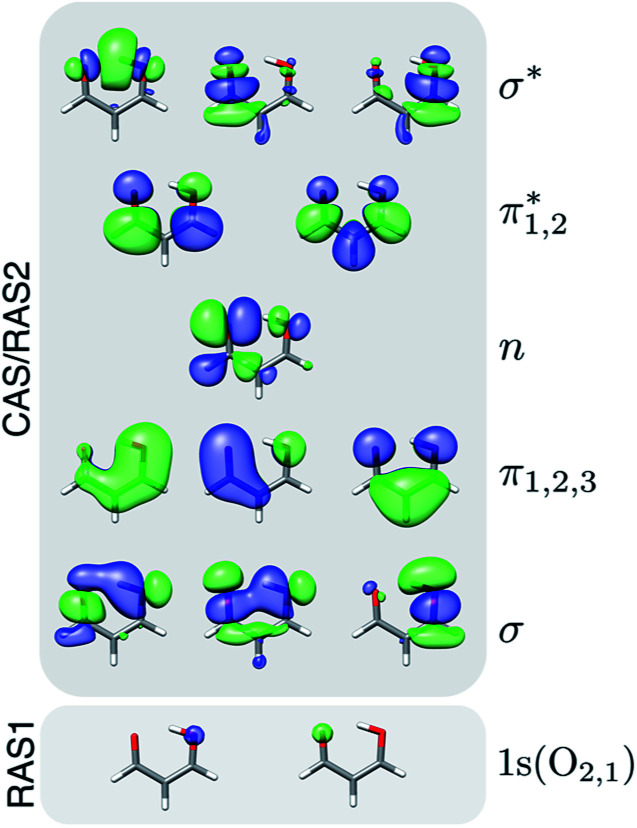
Geometry optimization and minimum energy conical intersection (MECI) searches were performed with XMS-CASPT2 using the Bagel program package.^6,65 Paths connecting the critical points were obtained using geodesic interpolation.⁶⁶ The cc-pVDZ⁶⁷ basis set was used together with its corresponding density-fitted basis set (cc-pVDZ-jkfit). A level shift of 0.3 a.u. was applied. The active space for malonaldehyde consisted of 14 electrons in 12 orbitals, i.e., XMS-CASPT2(14,12). Fig. 1 shows the active space orbitals. For geometries of singlet states, the state-averaging (SA) was performed over the three lowest singlet states with equal weights, whereas a two-state averaging over the two lowest triplet states was used to obtain the T₁ minimum geometry. Mulliken charges were computed from the relaxed one-particle density matrices in a locally modified version of Bagel.

Fig. 1. Active space orbitals used in the XMS-CASPT2(14,12) geometry optimizations and in the RASPT2 spectral calculations. Isovalue: 0.03 a.u.

Two levels of theory were employed for computing the NEXAFS spectra: (i) RASPT2, and (ii) ADC for the polarization propagator of second order in its strict and extended variants, ADC(2)(-x). The RASPT2 calculations used extended multi- and single-state (XMS and SS, respectively) formulations for valence and core states, respectively, including the two O 1s orbitals in the RAS1 space (with a zero- or one-hole constraint, respectively) in addition to the aforementioned active space (RAS2, see Fig. 1), i.e., XMS/SS-RASPT2(18,0/1,0;2,12,0) using the notation (n,l,m;i,j,k), where n is the number of active electrons, l the maximum numbers of holes in RAS1, and m the maximum number of electrons allowed in RAS3, while i, j, k are the number of active orbitals in RAS1-3, respectively. The cc-pVDZ basis set was retained in the spectral calculations since augmentation with diffuse functions did not lead to significant spectral changes (Fig. S2†). The highly-excited state procedure⁶⁸ was employed to target the oxygen K-edge, and an imaginary shift of 0.3 a.u. was applied to avoid intruder states. Cholesky decomposition of the two-electron repulsion integrals was employed.⁶⁹ The 10 lowest singlet (or triplet) states were included in the state-averaging in the core-excited state calculations. To prevent undesired orbital rotations, the 1s O orbitals were kept frozen at their valence-state RASSCF solutions. Approximate RASPT2 oscillator strengths were computed using the restricted active space state interaction (RASSI⁷⁰) module on the basis of the CASSCF wave functions and the zeroth-order XMS basis for valence states, and vertical excitation energies obtained at the RASPT2 level. RASPT2 calculations were performed using OpenMolcas.^71,72 Natural transition orbital (NTO) and natural difference orbital analyses for valence and core transitions were performed with the interface between the LIBWFA library⁷³ and OpenMolcas.⁷⁴ As a metric for the single-electron excitation character of a transition, we used the occupation numbers of the NTO pairs.^75,76 In contrast to the one-electron picture obtained from the NTO analysis, the difference density matrix includes many-electron effects like double excitations and orbital relaxation. We used the promotion number (p_AD), i.e., the integrals over the attachment and detachment densities, that counts the number of electrons that are rearranged in the transitions, as a metric for these effects. To characterize the unpaired electron distribution, we used the nonlinear metric (n_ue) based on the one-electron density matrix.^77,78

For the ADC calculations, valence-excited states were computed with ADC(2) and core-excited states with ADC(2)-x using the core-valence separation (CVS⁷⁹) approximation, i.e., CVS-ADC(2)-x.⁸⁰ Among the CVS-ADC schemes available, the extended variant⁸⁰ has been shown to yield the most reliable results, and compared with full excitation-space calculations, core excitation energies are within 0.2–0.4 eV (see ref. 81 and Section S1 of the ESI†). The 6-311++G** basis set^82,83 was used along the interpolated paths as it provides a good compromise between accuracy and computational cost.^80,84 The smaller 6-31+G* basis set retains all important spectral features (see Fig. S3†) and was therefore used for simulating TRXAS along the AIMS dynamics. CVS-ADC is a well-established approach to compute steady-state core-level spectroscopies at the Franck–Condon (FC) point.⁸⁴ Since ADC is based on a second-order Møller–Plesset perturbation (MP2) ground state, it is most appropriate at geometries with a ground state of single-reference character. Further, the different treatments of the ground and excited states mean that the topology of S₁/S₀ branching planes is incorrectly described.^85,86 While these may be serious difficulties in the context of non-adiabatic dynamics simulations, the method is nevertheless acceptable for the present purpose of static calculations, as will be shown by comparison to RASPT2. Transition dipole moments between valence- and core-excited states were computed as detailed in Section S1.† We used the procedure proposed by Stanton and Gauss⁸⁷ to estimate the lowest K-shell ionization thresholds at the FC geometry: a single diffuse s-type primitive Gaussian orbital with exponent 10⁻²⁰a₀⁻² was added at the center of mass of malonaldehyde and the ionization potential was identified among the core transitions as obtained with CVS-ADC(2)-x/6-311++G**. Calculations at the ADC level were performed using a development version of the Q-Chem package.⁸⁸

For the purpose of investigating the dynamical effects, we computed the contributions to the TRXAS signal along representative AIMS dynamics from two initial parent trajectory basis functions (TBFs), aiming to study the proposed pathways. The initial conditions (ICs) were taken from a 0 K vibrational ground-state Wigner distribution. To this end, we interfaced Bagel with AIMS to enable non-adiabatic dynamics simulations using XMS-CASPT2 energies, gradients,^89,90 and non-adiabatic couplings.⁹¹ The cheaper SA4-XMS-CASPT2(4,5)/6-31G* level of theory reproduces the potential energy profiles with the larger active space (Fig. S4 and S6†) and was used to expedite the dynamics. While the present AIMS/Bagel interface does not leverage the possible parallelization over TBFs, this is in progress and will enable a future full XMS-CASPT2 AIMS dynamics study. Similar to the approach of Neville et al.,⁵¹ we assumed a fully incoherent approximation such that the TRXAS signal reduces to a diagonal sum of contributions from each TBF (at the position of their centroid), weighted by its population. The spectroscopic calculations were performed at 1 fs intervals at the ADC(2)(valence)/CVS-ADC(2)-x(core)/6-31+G* level. A high degree of parallelity and similarity in electronic character of the XMS-CASPT2 and ADC(2) valence-state PESs (Fig. S6†) allowed us to use a simple state-matching approach in the TRXAS simulations. All stick spectra have been convolved with a Gaussian line shape, with a full-width-at-half-maximum (FWHM) specified in the relevant figures, and converted to cross sections by multiplication with a factor of 2π²/c.

Results and discussion

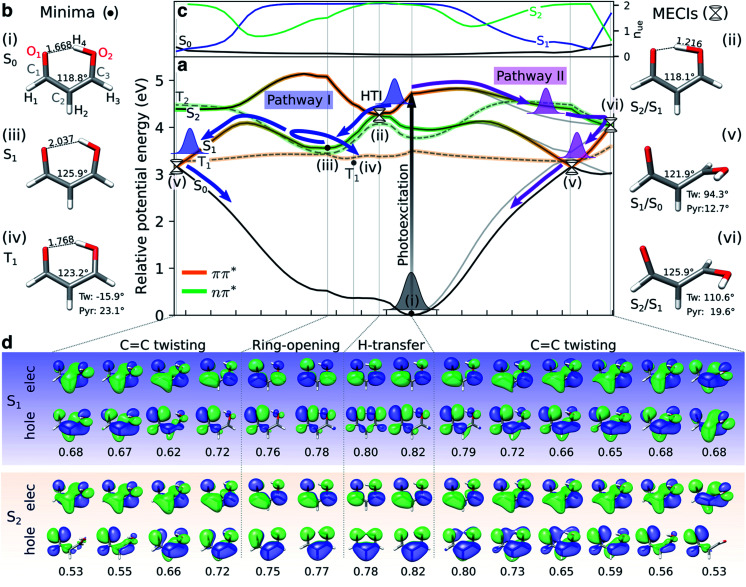
As introduced above, previous theoretical studies have implicated the relevance of two different internal conversion mechanisms for the excited-state dynamics of malonaldehyde, dominated by motion along either H-transfer or C C torsion, respectively.^{33–35,37,38} Sapunar et al. have further suggested intersystem crossing to the triplet manifold as an additional important route in the non-radiative decay.³⁸ Our potential energy profiles are consistent with this picture, and hence, we only provide a brief outline before proceeding to the TRXAS analysis.

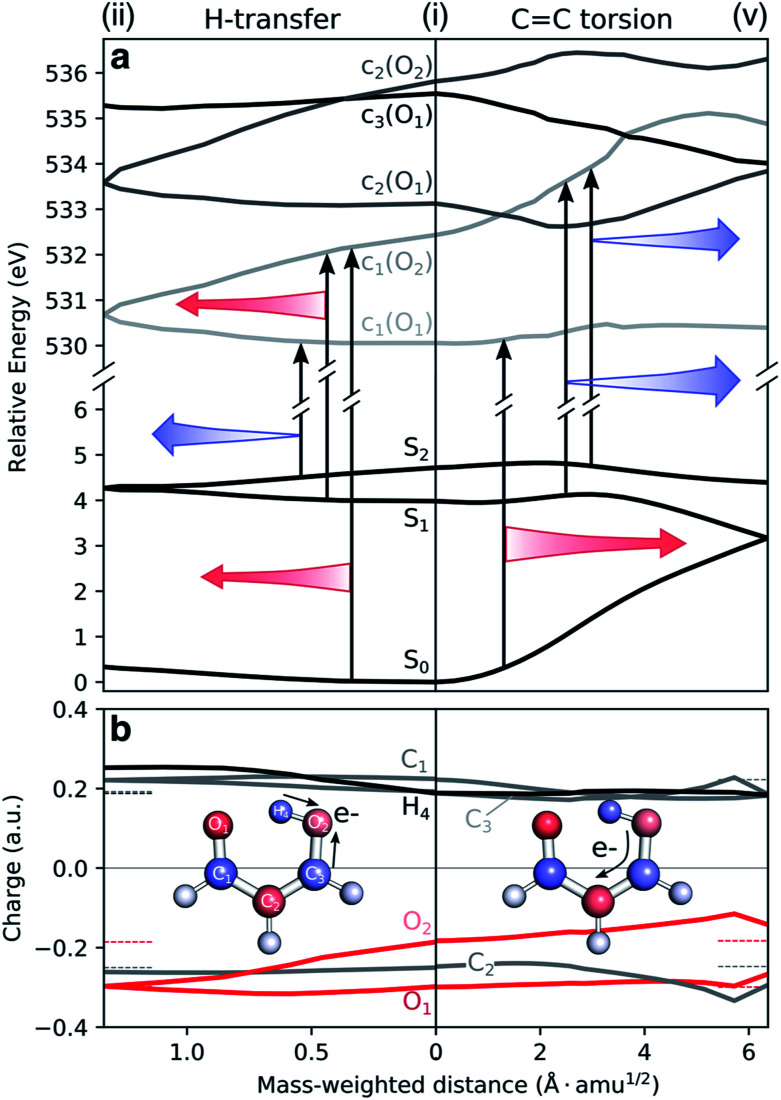
Fig. 2a shows XMS-CASPT2 energy profiles for the ground and lowest valence-excited states of malonaldehyde along geodesic interpolated paths between geometries (i–vi), expected to be important for its ultrafast radiationless excited-state decay. Since these are interpolated paths, estimated barrier heights are upper bounds to the true barriers. Geometric parameters of the critical points and their energies are provided in Fig. 2b/S7 and Table S1,† respectively. The corresponding energy profiles at the MP2/ADC(2) levels are compared in Fig. S4† (oscillator strengths in Fig. S5†) and show good agreement with XMS-CASPT2 both in terms of parallelity and electronic character. In particular, they remain well-behaved even close to the S₁/S₀ minimum energy conical intersection (MECI).

Fig. 2. Overview of proposed deactivation mechanisms for malonaldehyde upon S₂ excitation. (a) Ground and valence-excited state potential energy surfaces for malonaldehyde along geodesic interpolation paths⁶⁶ connecting minima (solid circles) and MECIs (cones). The x-axis is given in mass-weighted distance (1 Å amu^1/2 per tick) with indication of the dominant modes along each path. The experimental transition wavelength for S₂ is 4.71 eV,⁹⁴ and the adiabatic S₀–S₁ transition energy is 3.50 eV.⁹² As schematically illustrated by the thick arrows, there are two competing non-radiative decay channels from S₂. ESIHT is barrierless on S₂ (pathway I) while out-of-plane C C torsional motion (pathway II) may be associated with a barrier. While being higher in energy, the HTI is geometrically closer to the FC point and hence competes with the lower-lying C C twisted intersection. As indicated by the branching of pathway I, the population transferred to S₁via the HTI may undergo C C twist-mediated internal conversion or intersystem crossing to T₁ according to the El-Sayed rules. The parts of the surfaces dominated by ππ* (nπ*) character are marked in orange (green), as gauged by the character of the NTOs, see (d). Torsion around the C C bond leads to a gradual interchange of the electronic character of the S₁ and S₂ states. (b) Critical point geometries with key geometric parameters highlighted. Tw: ∠C₁C₂C₃O₂ dihedral angle, and Pyr: pyramidalization angle of C₃, as defined in Fig. S7.† Critical points were computed at the SA3-XMS-CASPT2(14,12)/cc-pVDZ level of theory. (c) Evolution of the effective number of unpaired electrons, n_ue, for each singlet valence state along the interpolated paths. To avoid ambiguity due to arbitrary wavefunction mixing at MECIs, n_ue-values were computed by linear interpolation between the previous point on the path and an extrapolated point obtained by displacing along the projection of the previous displacement vector onto the branching plane. (d) NTOs for the singlet valence excitations at selected points. The corresponding NTO pair weight is listed below each pair. A single NTO pair dominates each transition across all geometries with weights ranging between 0.53 (twisted) and 0.82 (planar). Isovalue: 0.03 a.u.

Upon photoexcitation to the bright S₂(ππ*) state, the excited nuclear wavepacket can proceed along two competing S₂/S₁ deactivation pathways (as shown in Fig. 2a): (1) along the H-transfer coordinate (pathway I), and (2) along the C C torsional coordinate (pathway II). Motion along the former is strongly gradient-driven,³⁵ directing the wavepacket downhill toward a minimum energy H-transfer intersection (HTI, geometry (ii) in Fig. 2a), of approximate C_2v symmetry, with the dark S₁(nπ*) state. Being geometrically close to the FC region, the early dynamics can be expected to sample regions in proximity to the HTI seam (pathway I) with concomitant ultrafast population transfer to S₁(nπ*) and possible ESIHT. For population transferred to S₁ at planar geometries, a substantial H-transfer barrier and opening of the H-chelate ring will significantly impede further motion towards the HTI seam. As discussed below, some degree of thermalization near the planar S₁ minimum can be expected because of the barrier to torsion on S₁. The S₂ depletion via pathway I competes with deactivation through torsional pathway II. Progression along the C C torsional mode (pathway II) is facilitated by a weakening of the double bond in the S₂(ππ*) state. A twisted MECI (vi) is reached upon modest pyramidalization of the enolic C-atom. While this twisted MECI (vi) is energetically below the HTI, the interpolated path suggests the presence of a small intervening barrier (∼0.1 eV) that may reduce the efficiency of the deplanarization deactivation pathway. Motion along the C C torsional coordinate further destabilizes the ground state, reducing the S₁–S₀ energy gap. The portion of the wavepacket reaching S₁ along the torsional mode is therefore geometrically close to a twisted S₁/S₀ MECI (v) and can proceed via internal conversion to the ground state. While the twisted S₁/S₀ MECI lies energetically below the planar S₁ minimum, the energy profile suggests a C C rotation barrier (∼0.54 eV from the interpolated path) on S₁ resulting from the presence of an avoided crossing between S₂ and S₁. This is in line with the experimental estimate of 5000 cm⁻¹ (∼0.6 eV) based on the span of the vibronic progressions from the origin of the S₁ absorption band.⁹² Hence, depending on the initial deactivation path from S₂ to S₁ and subsequent redistribution of kinetic energy among vibrational modes, this indicates internal conversion back to the ground state at twisted geometries with a remaining population possibly residing on S₁ for longer times.

Sapunar et al.³⁸ found that the S₁(nπ*), T₁(ππ*) and T₂(nπ*) states are energetically very closely spaced at the planar S₁(nπ*) minimum. We obtain a similar picture, although we note that the T₁ minimum geometry obtained in this work is significantly less twisted (∼16°) compared to their reported T₁ minimum geometry³⁸ (∼50°, computed at the MS-CASPT2(10,10)/cc-pVDZ level of theory). A Mulliken population analysis of the unpaired electron density matrix at the present level of theory (using the zeroth-order XMS basis) showed that the radical character is more delocalized towards the O atoms, in particular from the central C₂ atom to the keto O₁, in our geometry whereas the structure reported by Sapunar et al. displays a more localized C C biradical character (see Table S3†). Both active spaces predict a nearly flat potential energy surface for T₁(ππ*). According to the El-Sayed rules⁹³ and in analogy to the closely related acetylacetone, this indicates participation of the triplet manifold in the excited-state decay of malonaldehyde with intersystem crossing from S₁(nπ*) to T₁(ππ*) as a possible non-radiative decay channel. On the basis of CASSCF surface-hopping dynamics, Sapunar et al. predicted a splitting of the nuclear wavepacket on S₁, with a portion (40%) repopulating the ground state on the sub-picosecond time scale through twisted structures and a similarly sized portion undergoing intersystem crossing to T₁ with the residual population remaining trapped on S₁ on a longer time scale (∼1 ps). In other words, the part of the wavepacket transferred to S₁ near planar geometries (pathway I) may undergo intersystem crossing to T₁ or gradually reach the ground state via internal conversion at twisted geometries following vibrational energy redistribution. Gas-phase experiments with sensitivity to the coupled electronic and nuclear dynamics induced by the optical pump are needed to shed light on the time scales and pathways that govern the excited-state decay in malonaldehyde. In the following, we will investigate the ability of X-ray absorption spectroscopy at the oxygen K-edge to resolve the proposed competing decay channels, involving ESIHT and torsion-mediated internal conversion as well as intersystem crossing, as summarized in Fig. 2.

Steady-state X-ray absorption

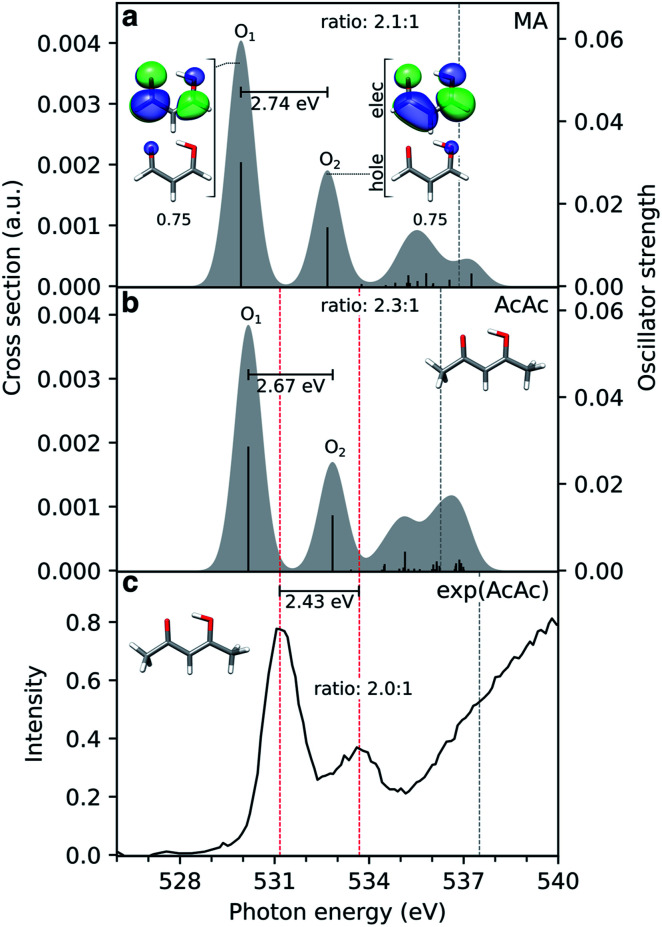
The simulated steady-state oxygen K-edge NEXAFS spectrum, computed using CVS-ADC(2)-x, is displayed in Fig. 3a. The corresponding RASPT2 spectrum is similar and will be discussed below (Fig. 4b). The experimental spectrum has not been measured yet, but is expected to bear strong resemblance to that of acetylacetone (AcAc).⁹⁵ For comparison, we therefore include the NEXAFS spectrum of acetylacetone together with its simulated counterpart. We find good agreement both in terms of relative intensities (∼2 : 1) and splitting (∼2.6 eV) of the two dominant peaks. The errors in absolute excitation energies relative to experimental absorption maxima are in the order of +1.0 eV. The neglect of scalar relativistic effects is expected to be associated with a red-shift of ∼0.3–0.4 eV.⁹⁶ Similar close agreement in shape was recently reported by Faber et al. for acetylacetone at the CVS-EOM-CCSD level of theory,⁵⁵ although the overall shift is smaller in the present study. The methyl substituents in AcAc lead to a blue-shift of both pre-edge peaks of ∼0.2 eV compared to malonaldehyde. Analysis of the NTOs (insets in Fig. 3a) shows that the lower-energy peak at ∼529.9 eV corresponds to a transition from the keto 1s(O₁) orbital into the delocalized orbital, whereas the second peak at ∼532.7 eV is assigned to the excitation out of the enol 1s(O₂) orbital. Such a large chemical shift can in part be attributed to σ and π charge redistribution from the enol towards the keto O-atom, facilitated by H-bonding and π-conjugation, increasing the screening of the keto 1s(O₁) relative to the enol 1s(O₂).^30,97,98 Another contributing factor to the splitting is the difference in valence orbital composition of the 1s(O₁)π* and 1s(O₂)π* core-excited states (also labeled c₁(O₁) and c₁(O₂), respectively), as seen by comparing the electron NTOs. Given the single-electron excitation character of both pre-edge features, their relative intensities can be explained in terms of the difference in spatial overlap between the respective core and valence orbitals being probed. The orbital is biased towards the keto O₁ atom, hence giving a more intense 1s(O₁)π* peak.

Fig. 3. Comparison of simulated and experimental oxygen K-edge NEXAFS spectra from the electronic ground state of (a) malonaldehyde (MA) and (b) acetylacetone (AcAc), as obtained at the CVS-ADC(2)-x/6-311++G** level (unshifted). The underlying NTOs for malonaldehyde are shown as insets. The lowest vertical core-ionization energies are indicated by grey dashed lines. The stick spectra were convolved with a Gaussian line shape (FWHM: 1.0 eV). A broader linewidth than the core-hole lifetime (∼0.15 eV (ref. 101)) was used to represent vibronic effects as to better align with the experiment. (c) The experimental spectrum for gas-phase AcAc was taken from ref. 95 with pre-edge maxima (531.17 and 533.6 eV) and first ionization potential (ref. 99) indicated by red and grey dashed lines, respectively. The experimental pre-edge ratio was estimated (2.0 : 1) by fitting the pre-edge features to Gaussians, using XAS viewer in Larch.¹⁰².

Fig. 4. Comparison of oxygen K-edge NEXAFS spectra at the RASPT2 and ADC level for the lowest valence singlet states (S₀: black, S₁: blue, S₂: green) at the FC point. (a) CVS-ADC(2)-x/6-311++G**, and (b) RASPT2(18,0/1,0; 2,12,0)/cc-pVDZ. The latter have been uniformly shifted by −4.254 eV to align with the steady-state spectrum at the ADC level. The lowest vertical core-ionization energies, corresponding to a 1s(O₁) hole, are indicated by dashed lines. The stick spectra were convolved with a Gaussian line shape (FWHM: 0.25 eV). (c) Dominant configurations (weight > 0.1) to the five lowest core-excited states ordered by weight from the RASPT2 calculation. Orbitals are state-averaged natural orbitals from the core-excited state calculation.

An alternative explanation for distinct 1s O signals was suggested by Feyer et al. in the context of X-ray photoelectron spectroscopy (XPS) of AcAc.⁹⁹ Rather than a ground-state chemical shift argument, they found, on the basis of a one-dimensional model for proton tunneling, the double peaks to be a consequence of asymmetric final state potentials combined with a strongly delocalized proton in the electronic ground state. In particular, their model was able to account for the observed intensity reduction in the valley between the double peaks in the XPS spectrum upon deuteration. In this picture, the relative intensities of the two peaks in the NEXAFS spectrum result from differences in FC overlap between the initial symmetric and final asymmetric double wells. Consistent with previous calculations,³⁵ we obtain an estimate of the ground-state H-transfer barrier of ∼0.164 eV (3.8 kcal mol⁻¹), similar to that of acetylacetone, 0.158 eV (3.65 kcal mol⁻¹).¹⁰⁰ Although similar impact of nuclear quantum effects might therefore be expected for malonaldehyde, we do not address quantum effects beyond non-adiabatic transitions in the present study.

Fingerprints of electronic character

Before considering the transient oxygen K-edge signals along the interpolated paths, we examine the spectra corresponding to core transitions from the valence-excited states. Fig. 4a and b compare the NEXAFS spectra of the ground state, S₁(nπ*) and S₂(ππ*) excited states at the FC point as obtained at the ADC and RASPT2 levels of theory, respectively. The dominant configurations of the lowest five final core-excited states with RASPT2 are summarized in Fig. 4c, and natural transition and difference density analyses are provided in Table S4 and Fig. S8.†

We first note the overall good agreement between the two methods for the two pre-edge peaks (peaks 1 and 2) in terms of character, splitting and relative intensities. At the RASPT2 level, the peak splitting is smaller by ∼0.4 eV, and the use of the smaller basis set is the main reason for a blue-shift of 4.25 eV for the ground-state spectrum with respect to ADC. The two pre-edge features from the lowest valence-excited states are dominated by the promotion of an electron into the vacancy of the SOMOs created by the pump, i.e., the n- and π-orbitals for S₁ and S₂, respectively. As such, the final core-excited states underlying the two pre-edge features are the same across all valence states, namely 1s(O_1/2)π*. Accordingly, the spectral shifts between the pre-edge peaks for different valence states reflect their vertical energy gaps at the specific geometry. For S₂(ππ*), which is populated upon photoexcitation, this leads to red-shifts at the FC geometry of ∼4.5 eV and ∼1 eV relative to S₀ and S₁, respectively. The change in electronic state is also apparent from a reversed intensity pattern (pre-edge ratio of ∼1 : 2–4), which is a consequence of the bias in the density of the π-orbital towards the enol O-atom (see valence NTO pairs in Fig. 2d). We note the overall reduction in the intensity of the pre-edge features from the S₂ state with respect to the ground-state spectrum. In a simplified frozen-orbital picture, this can be explained as an intensity redistribution in the excited-state NEXAFS to transitions involving core-excited states of double-excitation character with respect to the ground state but single-excitation character relative to S₂. The strong preferential localization of the n-orbital around the keto O-atom leads to a significant intensity gain (∼9 : 1) of the c₁(O₁) peak in the spectrum for S₁(nπ*).

Additional features appear in the higher-energy region of the RASPT2 NEXAFS spectra, in particular for S₂. As seen in Fig. 4c, these originate from transitions which, in addition to contributions from single-excitations involving the 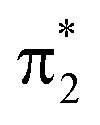-orbital, display significant double-excitation character relative to the ground-state configuration; keeping in mind the substantial orbital relaxation effects associated with core transitions, as evident from the appearance of the detachment and attachment densities. This is evident from the decrease in the sum of NTO weights for the ground-state to c_2/3(O₁) and c₂(O₂) transitions (Table S4†). For instance, the intense c₃(O₁) peak in the excited-state absorption from S₂ (green, peak 4) is dominated by a transition to a doubly-excited configuration with respect to the ground state, and hence, is not adequately described by the first-order treatment of the double-excitation block in CVS-ADC(2)-x. On the other hand, the shake-up type configurations relative to S₂ (second configuration for states c_2/3(O₁) and c₂(O₂) in Fig. 4c) involving the 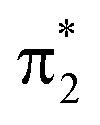-orbital are well-described.

As in the case of thymine,¹³ such distinct spectroscopic fingerprints of the valence states should allow monitoring of the electronic character of the wavepacket during the excited-state decay. We further note that the relative intensities of the two pre-edge features in the S₁(nπ*) and S₂(ππ*) spectra, i.e., the ππ*/nπ* pre-edge ratios, are ∼6 : 1 and 1 : 3 at the FC point, respectively. While a ππ*/nπ* pre-edge ratio of ∼1 : 40 in thymine was insufficient (within the signal-to-noise of the experiment) to track both electronic states,³ the comparable magnitudes of the ππ*/nπ* pre-edge features in malonaldehyde may allow the transient populations in both the S₂(ππ*) and S₁(nπ*) states to be followed.

Signatures of competing decay pathways

To gauge the ability of TRXAS to resolve the suggested competing decay mechanisms in photoexcited malonaldehyde, we performed spectral calculations along the interpolated pathways in Fig. 2a. This approach was recently proposed as an inexpensive and practical way to predict TRXAS signals.^47,49,50 In this work, it provides a simplified picture that allows us to rationalize the spectral changes associated with key geometric distortions.

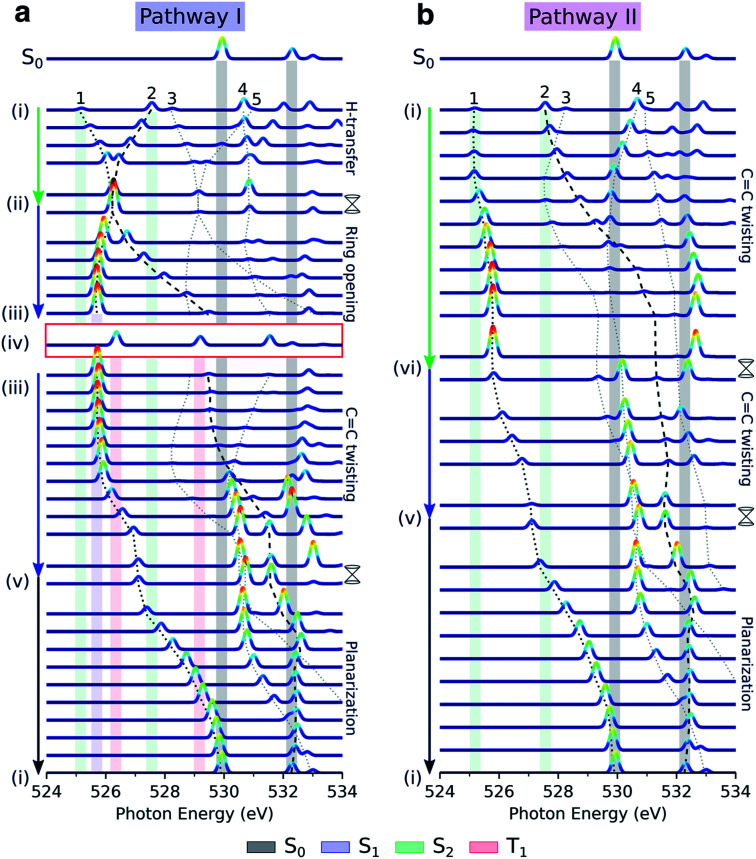
Fig. 5 displays the transient oxygen K-edge signals along the H-transfer and C C torsion-driven decay pathways (Fig. 2a; pathways I and II, respectively) obtained at the RASPT2 level. Dashed lines trace the behavior of the transitions to the five lowest core-excited states (peaks 1–5), highlighted in Fig. 4. Corresponding spectral evolutions at the ADC level are provided in Fig. S9.† The overall pre-edge trends are the same at both levels of theory, although a larger blue-shift of the c₁(O₁) state is observed at the ADC level along the C C torsion coordinate. Upon photoexcitation to S₂, motion along the H-transfer coordinate will direct the wavepacket towards the HTI seam (Fig. 2a). The approximate C_2v symmetry of the HTI imposes near chemical equivalence of the O-atoms, and accordingly, the two previously distinct pre-edge peaks coalesce at the HTI. As such, the oxygen K-edge signal should provide a characteristic fingerprint of the HTI. Due to the localization of the n-orbital on the keto O₁ atom, a concurrent symmetry breaking and change in the intensity profile towards the c₁(O₁) peak (labeled 1) provides a clear spectral signature of population transfer from S₂(ππ*) to the dark S₁(nπ*) state through the HTI. Trapping on S₁(nπ*) leads to a substantial blue-shift of the c₁(O₂) peak (labeled peak 2) and a strongly biased pre-edge ratio of ∼27 : 1 due to the increased lone-pair localization induced by H-chelate ring opening and elongation of the CO bonds. Assuming a pump excitation percentage of ∼10% of the population,¹³ the c₁(O₂) peak is likely to be obscured by its weak intensity and proximity to ground-state absorption features. Subsequent intersystem crossing to T₁(ππ*) should be evident from a ∼0.5 eV blue-shift and decreased intensity of the c₁(O₁) peak as the molecule deplanarizes on the T₁ state. The reappearance of the c₁(O₂) peak provides an additional fingerprint of the triplet state (Fig. S10† compiles the NEXAFS spectra from the S₁(nπ*) and T₁(ππ*) states at their respective minimum). Together with anticipated differences in decay time scales of the S₁(nπ*) and T₁(ππ*) states, our calculations suggest that TRXAS at the oxygen K-edge should be able to fingerprint intersystem crossing, although we may expect considerable broadening in the T₁(ππ*) fingerprints as a consequence of vibrational dynamics along its flat PES (Fig. 2a) and stronger geometric sensitivity of the core-excited states (vide infra).

Fig. 5. Simulated oxygen K-edge fingerprints along the decay pathways in malonaldehyde given in Fig. 2a: (a) H-transfer mediated pathway I, and (b) C C torsion mediated pathway II. The black dotted and dashed traces mark the spectral position of peaks 1 and 2 (labeled according to final states in Fig. 4c), while peaks 3–5 are indicated by gray dotted lines. The colored shadings indicate spectral features at minima along the pathway with geometry and electronic state indicated by Roman numbering (Fig. 2a and b) and the color coding, respectively. Signatures of intersystem crossing to T₁ are highlighted by the red rectangle. The top spectra illustrate the ground-state NEXAFS spectrum at the FC point, geometry (i). To avoid ambiguity due to arbitrary wavefunction mixing at points of degeneracy, the NEXAFS intensities at the MECIs were computed by linear interpolation between the two neighboring non-degenerate points along the pathway. Stick spectra were obtained at the RASPT2 level and convolved with a Gaussian line shape (FWHM: 0.25 eV) and were uniformly shifted by −4.254 eV.

As shown in Fig. 5b, the departure from the FC region along the competing torsional pathway leads to a significant blue-shift of the c₁(O₂) peak (>3 eV) such that it is raised beyond the previously higher-lying excitations originating from the keto 1s(O₁). This is accompanied by a decrease in its signal intensity and a substantial gain of the c₁(O₁) peak. The opposite intensity pattern is seen in the NEXAFS spectrum from S₁ upon rotation ((iii)–(v), pathway I, Fig. 2a). As follows from the number of unpaired electrons and NTO analyses in Fig. 2c and d, respectively, this is a result of the change in electronic configuration of the S₁ and S₂ states along the torsional coordinate: S₂ gains nπ* character, while S₁ acquire mixed ππ*/π² character and hence increased closed-shell character. 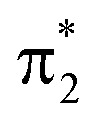In addition, the previously higher-lying peaks acquire intensity upon C C torsion as a consequence of the increasing degree of localization of the and orbitals on the enol and keto side of the molecule, respectively.

To understand the origin of the TRXAS spectral shifts along the key modes, we consider the geometry-sensitivity of both valence and core-excited states. Fig. 6a shows the underlying RASPT2 potential energy profiles along the interpolation paths dominated by (1) the H-transfer coordinate, connecting the FC point and the HTI, and (2) the torsional coordinate, connecting the FC point with the twisted S₁/S₀ MECI. We use this path rather than the twisted S₂/S₁ MECI counterpart because it is closer to a pure rotation. While the c₁(O₂) state is significantly destabilized and stabilized along (i)–(v) and (i)–(ii), respectively, the c₁(O₁) state is comparably weakly dependent on nuclear configuration. The core-excited state energies are related to the corresponding O 1s binding energies that, in turn, depend on the atomic charge distribution.^103,104 As shown by the ground-state Mulliken charge analysis in Fig. 6b, the decoupling of the enol and keto subsystems upon C C rotation induces, due to differences in electron affinities, an electronic charge redistribution from the enolic side (O₂ and C₃ atoms) towards the central C₂ and the keto C₁ atom. This decreases the electronic screening of the 1s(O₂) and leads to an increase in its binding energy, and hence a stabilization of the c₁(O₂) state. A similar NEXAFS spectral sensitivity to C C rotation has been reported for ethylene at its Tw–Py conical intersection where a transient charge separation is induced across the C-atoms upon pyramidalization due to the differences in electronegativity of sp² and sp³ hybridized C-atoms.^51,52 In other words, the observed shifts in transition energies of valence-to-c₁(O₂) transitions are a result of the combined effect of the torsional dependence of the valence and core-excited states. On the other hand, the charge of the keto O₁ atom is barely changed, hence shifts in transitions to the c₁(O₁) state will primarily be associated with the initial valence state. For example, the blue-shift in the c₁(O₁) peak in the S₁ and S₂ NEXAFS spectra along the torsional coordinate is a consequence of the stabilization of the antibonding orbital and hence of S₁ and S₂.

Fig. 6. Geometric dependence of valence to oxygen K-edge transitions. (a) Valence and core-excited state potential energy surfaces along H-transfer (left) and torsion (right) coordinates as obtained at the XMS-CASPT2/cc-pVDZ level. Core-excited state potential energies have been shifted by −4.254 eV. Note the different scaling of the x-axes of the left and right sides of the FC point. Colored arrows highlight the trends in valence-core excitation energy shifts for the most sensitive transitions (red: red-shifting and blue: blue-shifting in the direction of the arrow). (b) Mulliken charges of the ground state along the same coordinates. Horizontal dashed lines indicate the corresponding charge at the origin. To avoid ambiguity due to arbitrary wavefunction mixing at geometry (v), the charges were computed by linear interpolation between the previous point on the path and an extrapolated point obtained by displacing along the projection of the previous displacement vector onto the branching plane.

It is also interesting to note the potential energy profiles along the H-transfer coordinate, as represented by composite H-transfer and bond-length alternation (BLA). The behaviors of S₂ and S₁ are opposite, as are the profiles of the c₁(O₁) and c₁(O₂) states. Creation of a core-hole on the keto O₁ atom disfavors it as an acceptor, introducing a barrier to H-transfer. The opposite holds for c₁(O₂). Accordingly, we have an approximate valence/core-excited state pair-wise parallelity, although not quite for the S₂ and c₁(O₂) states due to the larger positive curvature for the latter. Both pre-edge features are therefore expected to be sensitive to S₂(ππ*) dynamics along the H-transfer coordinate, while only the peak from c₁(O₂) will be from the S₁(ππ*) state.

Our calculations suggest that TRXAS at the oxygen K-edge provides a distinct spectral signature of the formation of the H-chelate ring due to the indistinguishability of the O-atoms that occurs uniquely at the HTI, and as such, provides a direct way of probing the passage through the HTI. Furthermore, the sensitivity to the electronic character enables tracking of associated population transfer from S₂(ππ*) to S₁(nπ*). The symmetry of malonaldehyde, however, prevents quantification of the extent of ESIHT. A steady and intense c₁(O₁) feature at ∼526.0 eV is an evident signature of trapping on S₁ while intersystem crossing to T₁ should appear as re-emergence of two steady pre-edge features. Progress along the torsional pathway is associated with steady blue-shifts of the pre-edge features, especially the c₁(O₂) peak, and intensity changes. Population transfer will appear as a gradual reversal of the intensity pattern and with an increased complexity in the part of the spectrum overlapping with ground-state absorption.

Time-resolved X-ray absorption

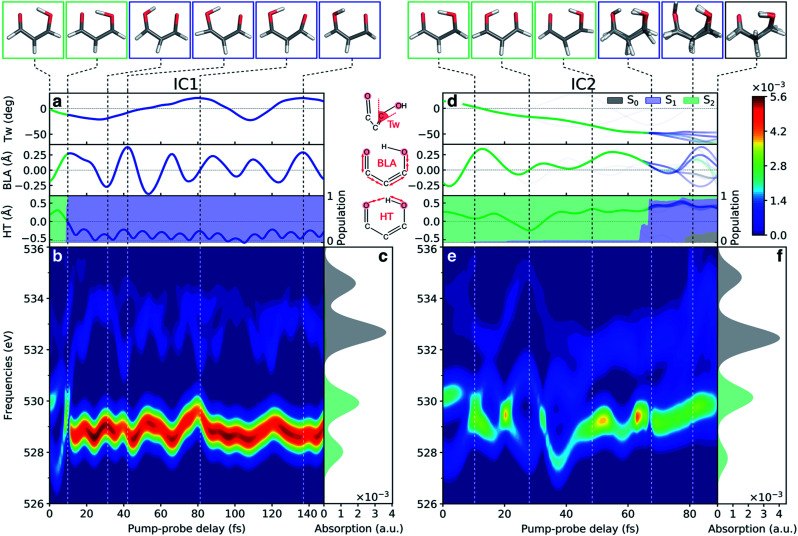
After discussing the sensitivity of the NEXAFS spectra along interpolated paths, we consider the first steps towards TRXAS. While a comprehensive excited-state dynamics study remains a task for future work, requiring non-adiabatic dynamics simulations including dynamical electron correlation and spin–orbit coupling, we here present simulated TRXAS signals for two initial conditions (IC1 and IC2) corresponding to internal conversion along the two proposed pathways. IC1 proceeds via the H-transfer decay mechanism and is trapped on S₁, whereas IC2 evolves through the twisted deactivation pathway towards the electronic ground state. This provides insight into the time scales involved and what vibrational modes are activated during the dynamics, although caution of course must be exercised since features visible for single ICs may be blurred or invisible in the complete wavepacket description.

Contributions from IC1 and IC2 to the time-resolved NEXAFS spectrum are presented in Fig. 7 together with the time evolution of key geometric parameters. In both cases, the two pre-edge signals of the vertically excited molecule near the FC point rapidly (within 10 fs) come together as a result of the contraction of the H-chelate ring, dominated by an extension of the O–H bond and inversion of the BLA coordinate. This apparent concerted motion of the H-transfer and BLA coordinates may be expected from the barrierless ESIHT on S₂, and differs from the mechanism in many related systems, where skeletal motion (including BLA inversion) precedes H-transfer and hence dictates the time scale of ESIHT.^20,105 Motion along the ring contraction mode leads to significant energetic shifts, in particular of the c₁(O₁) peak (∼1 eV). Their opposite curvature along the H-transfer coordinate explains the significant increase in energy gap between the S₂(ππ*) and c₁(O₁) states (Fig. 6a). For IC1, the internal conversion to S₁(nπ*) is very efficient and all the population is essentially transferred to S₁ within 10 fs with a concomitant transfer of the H-atom. The ESIHT is imprinted as a larger amplitude motion along the BLA coordinate. Quenching to S₁ diverts the wavepacket away from the HTI. This is immediately reflected in an intensity increase of the c₁(O₁) peak and a sweep to higher energies of the now very weak c₁(O₂) peak, as indicative of the S₁ state at planar geometries (geometry (iii), Fig. 5 and S10†). Interestingly, the BLA motion on S₁ is not apparent in the spectrum. This can be attributed to the similarity in curvature of the S₁ and the spectrally dominant c₁(O₁) states, leading to an insensitivity to BLA motion.

Fig. 7. Analysis of the oxygen K-edge TRXAS signatures for malonaldehyde along the non-radiative decay pathway of two initial conditions. (a–c) IC1 and (d–f) IC2. (a and d) Time evolution of key geometric parameters and adiabatic state populations. Line color indicates the adiabatic state while the transparency is proportional to the squared amplitude of the given TBF. (b and e) TRXAS contributions from IC1 that decays directly to S₁via the HTI seam and remains trapped near the S₁ minimum, and from IC2 that evolves to the twisted intersection seam and deactivates via S₁ to the ground state. The colormap shows the NEXAFS cross section (in a.u.). The oscillatory changes during the first ∼40 fs in (e) follow the evolution in the BLA and H-transfer (HT) parameters, where HT = R_O1H4 − R_O2H4. (c and f) NEXAFS spectra of S₀ and S₂, respectively, at the initial geometry. Insets at the top show the centroids of the TBFs representing the AIMS nuclear wavepacket on a given adiabatic state. The stick spectra were only convolved in the energy domain with a Gaussian line shape function (FWHM: 1.0 eV). Spectra were computed at the ADC(2)/CVS-ADC(2)-x level using the 6-31+G* basis set and have been shifted −2.625 eV (cf. Fig. S3†).

During the early IC2 dynamics, on the other hand, the HTI is approached several times without any significant population transfer to S₁. The oscillatory motion in the plane of the H-chelate ring clearly manifests as extensive oscillations in the spectral signatures, as expected from the analysis in Fig. 6, during the first ∼40 fs. The oscillatory behavior is followed by a gradual blue-shifting of the pre-edge peaks, especially for c₁(O₂), and an increase in intensity of the c₁(O₁) peak. These changes are concomitant with significant deplanarization of the H-chelate ring, as described by an increase in the C C twisting angle (∼50°, Fig. 7b). While a complete wavepacket picture is necessary to draw conclusions, this behavior suggests that an initial aborted passage through the HTI might open the torsional pathway. A following decrease in intensity appearing at ∼70 fs coincides with a significant population transfer to the S₁ state (∼90%). As discussed above, this can be expected from the interchange in electronic character of the S₁ and S₂ states along this mode. It is also worth noting that the generally weaker TRXAS signatures of IC2 compared to IC1, as opposed to the interpolated picture in Fig. 5, is a result of the population being transferred at geometries significantly less twisted than the MECIs. Finally, at around 80 fs, continued progression along the C C torsion facilitates population transfer from S₁ to the ground state. This appears as a blue-shift of the c₁(O₂) peak.

The simulated TRXAS signals for the two ICs provide clear signatures that enable fingerprinting the competing internal conversion channels, including population transfer mediated by the HTI. While time-resolved K-edge absorption has previously been used to discriminate reactant and product of photo-induced tautomerization using a synchrotron source (time resolution of ∼70 ps),¹⁰⁶ high temporal resolution is key in the present case.

Conclusions

We have investigated the ability of time-resolved X-ray absorption spectroscopy at the oxygen K-edge to resolve competing non-radiative decay channels in malonaldehyde upon photoexcitation to its bright S₂(ππ*) state. With a combination of spectral simulations along interpolated reaction paths and trajectories from non-adiabatic dynamics simulations, we have analyzed how competing relaxation pathways manifest themselves in the spectra. We have demonstrated that the oxygen K-edge provides an unambiguous probe of the passage through the HTI as the coalescence of the pre-edge features and a clear signature of concomitant electronic population transfer to the optically dark S₁(nπ*) state. The dynamics simulations indicate an ultrafast ESIHT process occurring within ∼10 fs. The nπ*/ππ* sensitivity of oxygen K-edge TRXAS should further enable the potential identification of intersystem crossing to T₁(ππ*) which may be assisted by the separation of time scales. Interestingly, progress along the C C torsional mode is also encoded in the oxygen K-edge TRXAS. The origin of this sensitivity was attributed a transient electronic charge redistribution from the enol O-atom towards the central C-atom caused by the rotation, leading to reduced electronic screening of the enol 1s O orbital. While we found no distinct fingerprint of the twisted conical intersections, our simulations indicate that the longer time scale of the torsional motion, gradual blue-shifting and reversed intensity pattern following population transfer at twisted geometries should be visible in the spectrum.

Given a sufficiently high temporal resolution of the pump and probe pulses, our results suggest an experimental route to sensitively probe the competing relaxation channels in malonaldehyde, involving internal conversion mediated by H-transfer and torsional motion as well as intersystem crossing to the triplet manifold. In combination with accurate non-adiabatic dynamics simulations, including dynamical electron correlation and spin–orbit coupling, and the present pathway-specific mapping of the TRXAS signal, this should provide detailed insight into the relative importance of the proposed competing pathways in this prototypical ESIHT system. We hope that the present work will provide impetus for such studies in the future.

Conflicts of interest

There are no conflicts to declare.