Metachronal μ-Cilia for On-Chip Integrated Pumps and Climbing Robots

Abstract

Biological cilia often perform metachronal motion, that is, neighboring cilia move out of phase creating a travelling wave, which enables highly efficient fluid pumping and body locomotion. Current methods for creating metachronal artificial cilia suffer from the complex design and sophisticated actuation schemes. This paper demonstrates a simple method to realize metachronal microscopic magnetic artificial cilia (μMAC) through control over the paramagnetic particle distribution within the μMAC based on their tendency to align with an applied magnetic field. Actuated by a 2D rotating uniform magnetic field, the metachronal μMAC enable strong microfluidic pumping and soft robot locomotion. The metachronal μMAC induce twice the pumping efficiency and 3 times the locomotion speed of synchronously moving μMAC. The ciliated soft robots show an unprecedented slope climbing ability (0 to 180°), and they display strong cargo-carrying capacity (>10 times their own weight) in both dry and wet conditions. These findings advance the design of on-chip integrated pumps and versatile soft robots, among others.

1. Introduction

Stimuli-responsive materials have drawn extensive attention in various applications including industrial soft robots,¹ small-scale biomedical robots,²⁻⁴ implantable and wearable devices,⁵ sensors,⁶ droplet and particle manipulators,⁷ self-cleaning and anti-fouling surfaces,^8,9 and on-chip integrated liquid mixers and pumps.¹⁰ Magnetically responsive materials, among other materials such as light-driven,¹¹ pH-driven,¹² pressure-driven,¹ and electric field-driven materials,¹³ enable the integration of such merits as a fast and reversible response and remote activation without the need for physical connections to an external actuation setup. Moreover, magnetic fields can easily and harmlessly penetrate most biological and synthetic materials.¹⁴ These advantages boost the research on magnetic artificial cilia (MAC), a type of magnetic-responsive structures inspired by nature, for applications including fluid pumping,^10,15 liquid mixing,¹⁶ particle manipulation,¹⁷ as well as soft robots.^18,19 Fluid pumping is one of the paramount functions in lab-on-a-chip devices where biological analyses and chemical syntheses are performed in small volumes (typically from 10^–4 to 10^–8 L).²⁰ Nevertheless, current methods for fluid pumping suffer from the need for large peripherals such as syringe pumps and tubing connections, which makes the platform cumbersome and nonportable. Recent advances in the study of using artificial cilia as a means of fluid pumping pave the way for the design and fabrication of on-chip integrated pumps.²¹⁻²⁴ In terms of pumping capability, metachronal cilia, where neighboring cilia move slightly out-of-phase creating a travelling wave, can lead to a 3-fold increase in propulsion velocity and a 10-fold increase in efficiency compared to synchronous cilia.²⁵ This has shifted the focus of researchers from the design and fabrication of synchronous cilia to metachronal cilia. The mechanism of creating metachronal cilia can be summarized into two categories: (i) applying different forces to each cilium within an array of cilia^23,26,27 and (ii) designing an array of cilia with different responses to a uniformly applied stimulus such as a uniform magnetic field.^19,27−30 The latter is beneficial due to its much simpler actuation method. The fabrication approaches presented in previous papers, however, are either time-consuming because complex assembly steps are needed^28,29 or they are based on expensive raw materials, costly processes, or complex actuation devices.^19,27,28,30 Moreover, the relatively large size of the reported metachronal cilia, typically several millimeters or larger,^19,28−30 render them difficult to be integrated in common microfluidic devices. Two of these previous publications demonstrated fluid flow induced by the metachronal artificial cilia.^19,28

In nature, metachronal wave motion of biological cilia enables propulsion and locomotion of many creatures,^19,31 in addition to egg cell transportation,³² mucus clearance in the human respiration system,³³ feeding assistance,³⁴ and self-cleaning and antifouling.³⁵ Locomotion is a fundamental function desired for future biomedical robots that has been shown to potentially enable capabilities such as minimally invasive surgery, targeted therapeutics and diagnostics, tissue engineering, and single-cell analysis.^36,37 Due to the diverse, dynamic, and complex nature of tissues, biomedical robots should possess a high degree of mobility and be able to overcome different obstacles with different slope angles in order to navigate in hard-to-reach regions of the human body. A few studies have demonstrated the obstacle-crossing capability of soft robots, such as crossing a small hill¹⁸ and a small tunnel,² as well as transiting at the air–liquid interface.² However, in these demonstrations either the reported actuation method is sophisticated or the design of the robots is complex, limiting their common application.

Here, we demonstrate a facile way to create metachronal microscopic MAC (μMAC) by controlling the paramagnetic particle distribution within the cilia array. Specifically, the metachronal μMAC are fabricated using a micromolding process, during which the distribution of the paramagnetic particles in the μMAC is precisely controlled by placing a rod-shaped magnet array, arranged to have an alternating dipole orientation between consecutive magnets, underneath the mold. Because the paramagnetic particles tend to align with the applied magnetic field, neighboring cilia will assume different paramagnetic particle distributions, and they will, therefore, have different magnetic properties. Consequently, the geometrically identical μMAC exhibit nonidentical bending behaviors in a static uniform magnetic field and perform a metachronal motion in a 2D rotating uniform magnetic field. The metachronal μMAC show excellent microfluidic pumping capacity and a promising capability to realize versatile climbing robots. Our metachronal μMAC outperform most previously reported μMAC in terms of the fluid pumping efficiency characterized by a normalized global flow speed. We also show that the metachronal μMAC enable superior climbing soft robots that can carry cargos 10 times their own weight, functioning in both dry and wet conditions. Moreover, the ciliated robots are able to climb slopes with angles ranging from 0 to 180°. Compared to the previously reported metachronal cilia with spatially controlled magnetic anisotropy, our metachronal μMAC provide a number of key advantages: (i) the ease of fabrication that allows for the replication of artificial cilia in large numbers, (ii) the need for only a simple actuation scheme, (iii) the excellent fluid pumping capacity, and (iv) the creation of versatile climbing soft robots. In addition, our metachronal μMAC are smaller in size than the previously reported metachronal magnetic cilia which facilitates their real applications in diverse fields including on-chip integrated micropumps and particle manipulation. The capability to create versatile climbing soft robots creates new options to realize biomedical robots.

2. Results and Discussion

2.1. Microscopic MAC (μMAC)

The polydimethylsiloxane (PDMS)- and paramagnetic carbonyl iron powder (CIP)-based μMAC are fabricated using a highly reproducible micromolding process (Figure 1A, details are available in the Experimental Section). Based on the fact that the paramagnetic particles tend to form chains that are aligned with the direction of the applied magnetic field, we placed an array of rod-shaped magnets, which are organized to have an alternating dipole orientation between consecutive magnets, underneath the mold (Figure 1A(v)). In this way, a nonuniform but periodic magnetic field is generated (Figure 1B) such that the paramagnetic particle chains are expected to have different orientations in neighboring cilia (Figure 1A(vi)). Movie S1 shows the alignment process of the paramagnetic particles when the mold is approached by the rod-shaped magnet array. In all experiments reported in this paper, the fabricated μMAC are arranged in a rectangular grid (Figure 1C), and each cilium has a cylindrical shape with a diameter of 50 μm and a height of 350 μm (Figure 1D), standing on a transparent nonmagnetic PDMS substrate. As the rod-shaped magnets have a diameter of 4 mm, the period of the generated magnetic field is also 4 mm (Figure 1B). The length of the μMAC array was chosen approximately equal to the magnetic field period, that is, 4 mm, and the width was chosen to always have 10 cilia. Thus, for the μMAC array with a pitches of 350, 450, and 550 μm between adjacent cilia, there are 12 × 10 = 120 cilia, 9 × 10 = 90 cilia, and 8 × 10 = 80 cilia, respectively. Note that the period of the μMAC array can be tuned by using magnets with different diameters, and the width can be reduced to minimally 2 cilia (∼400 μm).

Figure 1.

Magnetic field-assisted fabrication of metachronal μMAC. (A) Micromolding process of the metachronal μMAC, during which the paramagnetic particle distribution can be programmed by placing a magnet-array underneath the mold in the sample curing step. See Movie S1. (B) Snapshot of a COMSOL simulation of the magnetic flux density B induced by the rod-shaped magnet-array that is arranged with an alternating dipole orientation between adjacent magnets. The horizontal white line indicates the central position of the μMAC array, that is, 0.7 mm above the top surface of the magnet array. The red arrows indicate both the direction and the magnitude of B at the locations of each cilium, with a pitch of 350 μm. See Figure S1 for more details about the generated magnetic field. (C,D) Top-view and side-view SEM images of the fabricated μMAC array showing the arrangement in a rectangular grid and their cylindrical shape. The cylindrical μMAC have a diameter, a height, and a pitch of 50, 350, and 350 μm, respectively. (E) Schematic drawing of the alignment direction of the paramagnetic particles (black line segments) in one row of μMAC (pitch = 350 μm) according to the COMSOL simulation in panel (B), by assuming that the particle chain direction is in the same the direction as the magnetic field. The middle of the μMAC array is assumed to be placed at x = 0 in panel (B). The theoretically predicted acute angle (θ) between the magnetic particle chain and the vertical direction is shown above the corresponding cilium. See Figure S1 for results of other configurations of the magnet array. Illustration is not to scale. (F) Side-view optical microscopy image of one row of μMAC (pitch = 350 μm) showing the experimentally obtained acute angle (θ) between the magnetic particle chain and the vertical direction.

The red arrows shown in Figure 1B indicate the magnetic flux density B applied on the central part of the μMAC array, which is approximately 700 μm (half of the cilia height, ∼175 μm, plus the thickness of the silicon wafer, ∼525 μm) above the surface of the magnet array. The details of the magnetic field are available in Figure S1, which also shows a comparison between different magnet array configurations. According to the simulated direction of B, the expected alignment of the paramagnetic particles in one row of the μMAC array with a pitch of 350 μm is depicted in Figure 1E, where the acute angle θ between the expected direction of the paramagnetic particle chain and the normal direction to the PDMS substrate is shown above the corresponding cilium. The experimental results of the μMAC array made of the PDMS/CIP composite with a weight ratio of PDMS/CIP = 2:1 are shown in Figure 1F, showing good agreement with the simulation results. Thanks to the well-controlled concentration of paramagnetic particles, the difference in the CIP chain orientation is expected to result in a difference in magnetic properties of neighboring cilia and is the basis for the metachronal behavior of the μMAC array. Note the difference in the distribution of paramagnetic particles between the cilia at symmetric positions, as shown in Figure 1F, which is probably the result of a slight misalignment of the magnet array.

2.2. Magnetic Particle Distribution and μMAC Bending Behavior

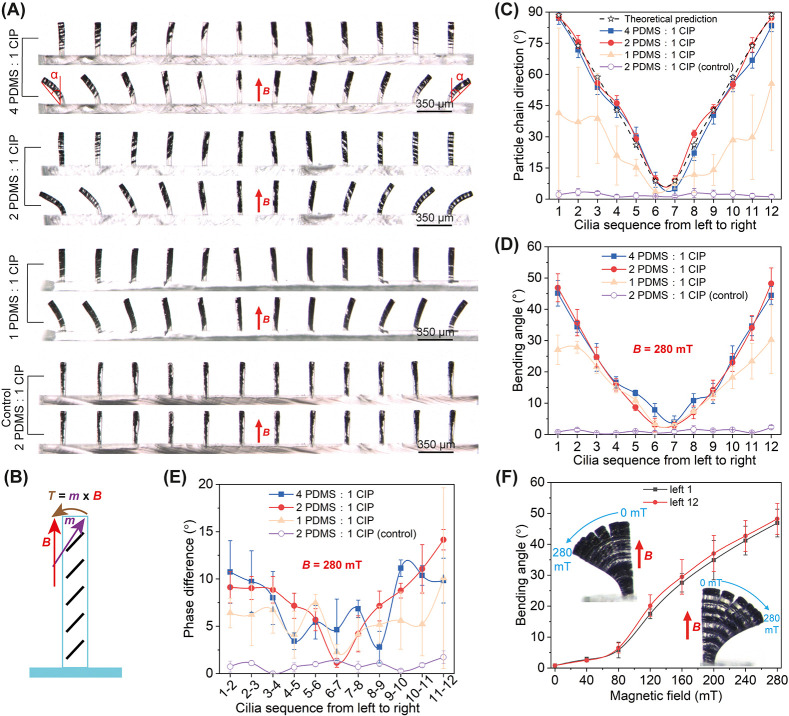
Figure 2A shows the magnetic particle distribution at different concentrations and the corresponding μMAC bending behavior in a static vertical uniform magnetic field of 280 mT generated by the electromagnetic setup reported by Wang et al.³⁸ The control μMAC, which have a unique paramagnetic particle distribution which is along the long axis of the cilia, are fabricated using the micromolding method reported in our earlier work.³⁹ In contrast to the control μMAC that do not bend at all, the μMAC fabricated using the process, as shown in Figure 1A, display bending angle differences between neighboring cilia for all three magnetic particle concentrations. This is due to the fact that the magnetization direction of each cilium is close to the magnetic particle alignment direction: the magnetic anisotropy of the μMAC is caused by both the shape anisotropy of the cilium itself and the anisotropy of the magnetic particle alignment, with the latter anisotropy dominating in our case.⁴⁰ Consequently, due to the induced magnetic torque in a uniform magnetic field, a cilium tends to bend so as to align its magnetic particle chain direction with the applied magnetic field (Figure 2B); the extent of the bending depends on the direction and magnitude of the magnetization as well as the cilia stiffness. Because of the difference in the magnetic particle alignment between adjacent cilia, the μMAC in an array exhibit different bending behaviors, which is needed to generate metachronal behavior in a uniform magnetic field. The bending is smallest for the highest particle concentration (PDMS/CIP = 1:1) because the level of particle alignment anisotropy is the smallest, and the stiffness is the highest.

Figure 2.

Magnetic particle distribution and μMAC (pitch = 350 μm) bending behavior in a static uniform vertical magnetic field. (A) Optical microscopy images of μMAC arrays made with different magnetic particle concentrations, showing the particle distribution and cilia bending behavior in a static uniform magnetic field of 280 mT. (B) Schematic drawing of the mechanism behind the cilia bending, where B is the applied magnetic field, m is the magnetization of the cilia, and T is the resulting magnetic torque acting on the cilia. Illustration is not to scale. (C,D) Quantitative results of the magnetic particle distribution and the bending angle [α in panel (A)] of the μMAC arrays. The particle chain direction in panel (C) represents θ in Figure 1F. The bending angle is denoted by the angle between the substrate normal and the straight line connecting the tip and the bottom of each μMAC. (E) Phase difference deducted from the bending angle differences between the neighboring cilia calculated from the results shown in panel (D). (F) Bending angle of the cilia at the two ends of the μMAC array (2 PDMS/1 CIP) as a function of the magnitude of the static vertical magnetic field (see Movie S2). Each experimental data point was obtained by averaging the results of at least five identical but independent experiments.

The quantitative results of the particle alignment are shown in Figure 2C. The particle chain direction is characterized by the acute angle θ to the substrate normal, as shown in Figure 1F. Clearly, the particle alignment agrees well with the theoretical prediction, as shown in Figure 1E, for the two arrays with PDMS to CIP weight ratios of 4:1 and 2:1. For the cilia array with a PDMS to CIP weight ratio of 1:1, the particle alignment shows quite some variation for cilia in the same column as is evident from the large error bars. This is probably because the high particle concentration results in an unwanted particle chain connection along the long axis of the cilia. For the control μMAC, on the contrary, the particle chain direction is almost perfectly oriented along the long axis of the cilia as expected. The bending angle (α in Figure 2A) of these μMAC arrays in an uniform vertical magnetic field of 280 mT is depicted in Figure 2D. The results show a similar trend to that in Figure 2C, while μMAC made using our new method with a PDMS to CIP weight ratio of 2:1 show the smoothest transition in the bending angle, which is the most promising for generating metachrony. Note that a relatively low magnetic particle concentration renders not only a smaller magnetization but also a lower stiffness, which is why the μMAC made of PDMS to CIP weight ratios of 2:1 and 4:1 show a similar bending behavior. In order to confirm that a weight ratio of 2:1 between PDMS and CIP results in the most promising μMAC for generating a controlled metachronal motion, we calculated the bending angle difference (i.e., phase difference) between neighboring cilia based on the results shown in Figure 2D and plotted the results in Figure 2E. Indeed, the phase difference of the μMAC made of a PDMS to CIP weight ratio of 2:1 is the smoothest, although there is some perturbation. The large variation for the μMAC made of a PDMS to CIP weight ratio of 4:1 is mostly due to the inhomogeneity of the magnetic mixture, which results in a relatively large variation in the magnetic properties of the μMAC in the same column. Note that the angle differences between the neighboring cilia is largely consistent during continuous actuation using a rotating magnetic field (see the following section), resulting in a stable phase difference for the metachronal movement.

Based on the above results, we choose μMAC made with a PDMS to CIP weight ratio of 2:1 for the following experiments. Figure 2F shows the bending behavior of the cilia at the two ultimate sides of one row of μMAC as a function of the magnitude of the applied vertical magnetic field. As expected, the two cilia exhibit a symmetrical response. Their bending angle initially increases slowly up to 80 mT, then increases steeper between 80 and 120 mT, and moderately increases along with the applied magnetic field above 120 mT. This behavior is the result of the competition between the elastic stiffness of the cilium and the magnetic torque acting on the cilium. Note that the magnetization of the paramagnetic particles has a nonlinear relationship with an applied magnetic field.⁴⁰ The bending behavior of the whole row of μMAC at different magnetic fields can be found in Movie S2.

2.3. Metachronal μMAC Motion in a 2D Rotating Magnetic Field and Fluid Pumping Capability

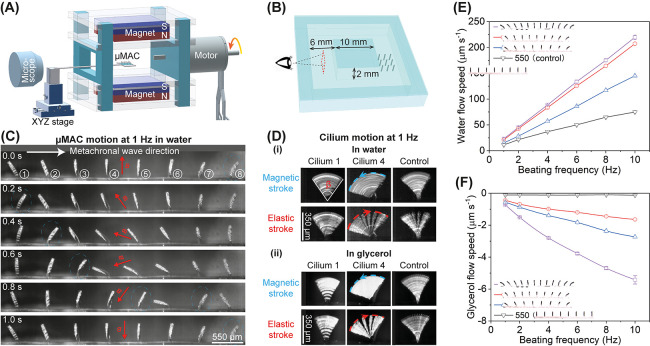
As shown above, the deformation of adjacent μMAC in an array exhibits an angle difference in a static uniform magnetic field. Here, we investigate whether this leads to metachronal motion in a uniform rotating field. Therefore, we built a setup consisting of two permanent magnets (50 × 50 × 12.5 mm³) with their opposing magnetic poles facing each other at a distance of 50 mm (Figure 3A). The magnets are mounted in a frame driven by an electric motor. In this way, a 2D rotating quasi-uniform magnetic field of approximately 150 mT is generated at the central space between the two magnets (see Figure S2 for details), where the μMAC array (PDMS/CIP = 2:1) is located. The μMAC array is covered with a microfluidic chip (Figure 3B) and is positioned within a square circulatory channel with a rectangular cross section (height 2 mm and width of 6 mm). A camera mounted on a microscope is used to observe the motion of the μMAC array in the 2D rotating uniform magnetic field and the generated liquid flow from the side (Figure 3A). Unless otherwise specified, the rotating direction of the motor is counterclockwise as seen from the microscope for the experiments reported in this section.

Figure 3.

Metachronal μMAC motion in a 2D rotating uniform magnetic field and the fluid pumping capability. (A) Schematic diagram of the magnetic actuation setup for creating a 2D rotating magnetic field. The details of the generated magnetic field are available in Figure S2. Illustration is not to scale. (B) Schematic drawing of the square microfluidic chip including the μMAC, indicating the observation area of the generated flow. Illustration is not to scale. (C) Snapshots of the metachronal motion of one row of μMAC with a pitch of 550 μm during one beating cycle at 1 Hz in water (see Movie S3). The electric motor rotates counterclockwise. The white arrow indicates the traveling direction of the metachronal wave. The red arrows indicate the direction of the applied magnetic field. The encircled numbers indicate the sequence of the μMAC for reference in later analyses. (D) Side-view time-lapse images of cilium motion at 1 Hz in both water and glycerol, showing a 2D symmetric motion. β represents the opening angle of the cilium motion. The blue dashed line and the red dashed line indicate the tip trajectory during the magnetic stroke and elastic stroke, respectively. The motion of cilium 4 during the elastic stroke in both water and glycerol is available in Movie S6. The motion of the whole μMAC array in both water and glycerol can be found in Figure S3. Note the difference in the recording speed for the metachronal μMAC and the control μMAC, as well as for in water and in glycerol. See Experimental Section for details. (E,F) Generated flow speed of water (E) and glycerol (F) as a function of the beating frequency of the metachronal μMAC array with pitches of 350, 450, and 550 μm, respectively, as well as the control μMAC array with a pitch of 550 μm. A positive result represents a flow above the ciliated area in the same direction as the metachronal wave traveling direction. The trajectories of the tracer particles in both water and glycerol can be found in Figure S4. The corresponding volumetric flow rate and pressure drop are available in Figure S5. Each data point was obtained by averaging the results of at least ten measurements.

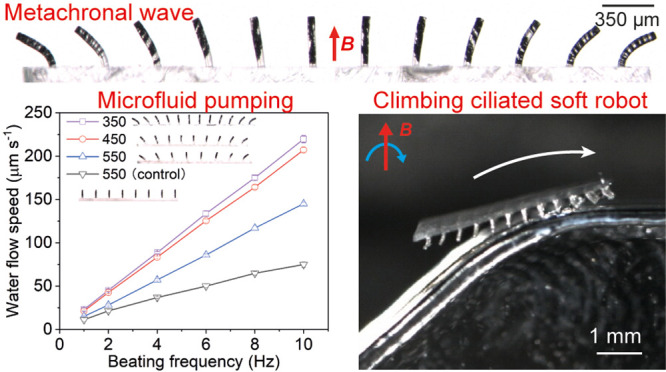
Figure 3C shows the motion of one row of μMAC (pitch = 550 μm) in the 2D rotating uniform magnetic field at a beating frequency of 1 Hz in water (see also Movie S3). Note that the μMAC beating frequency is 2 times the rotating frequency of the electric motor due to the symmetry of the generated magnetic field in the first and the second halves of one rotating cycle of the motor. Even though the directions of the magnetic fields are opposite to each other in the two different cycle halves, this has no effect on the bending behavior of the μMAC. It is clearly shown in Figure 3C that the μMAC array performs a wave-like motion, and thus indeed exhibits metachrony. The metachronal wave traveling direction is to the right as seen from the microscope. In contrast, Movie S4 shows that the control μMAC perform a 2D synchronous motion. We chose the μMAC array with a pitch of 550 μm instead of 350 μm because the neighboring cilia are too close to move freely for 350 μm pitch, touching each other (see Movie S5). Figure 3D shows that each cilium performs a 2D symmetric whip-like motion in the vertical plane consisting of two strokes: (i) a magnetic stroke when the cilium mostly follows the applied magnetic field and bends to the left, thereby accumulating elastic energy (indicated by the blue dashed line), and (ii) an elastic stroke when the cilium tip starts to move upward and whips back to its original position by releasing the accumulated elastic energy (indicated by the red dashed line). A high-speed video of the elastic stroke part of the 2D symmetric motion of cilium 4 in both water and glycerol is available in Movie S6. This movie shows that the cilium vibrates for a certain amount of time at the end of the elastic stroke before it reaches its equilibrium state in water but not in glycerol. This is a result of the competition between the elastic forces, magnetic forces, and the fluidic viscous drag, the latter being around 1000 times larger in glycerol based on Stokes’ law. The motion of the whole μMAC array can be seen in Figure S3. It shows that neighboring cilia exhibit motions with different opening angles. Specially, the motion of cilia 4, 5, and 6 has a larger opening angle than that of the others; this is caused by the fact that cilia at the central part of the μMAC array (cilia 4, 5, and 6) contain longer magnetic particle chains and thus stronger magnetization than the cilia at both ends (cilia 1, 2, 3, 7, and 8). Also, the left part of the μMAC array performs almost exactly the same motion as the right part of the μMAC array, that is, the behavior is symmetric with respect to the center of the array. This is because cilia at opposing positions contain similar magnetic particle distribution. It is important to stress that the 2D symmetric whip-like motion shown in this article is similar to that we recently reported,²⁶ but not exactly the same because the motion shown in the current work does not contain the so-called sliding stroke, and thus, it is a symmetric motion (see Figure 4 for details). Metachrony is termed symplectic, antiplectic, and laeoplectic when the metachronal wave travels in the same, opposite, and perpendicular directions as the effective stroke, respectively.⁴¹ The effective stroke is conventionally defined as the stroke during which one cilium moves more straight and thus sweeps a larger area than during the backward/recovery stroke, when the cilium performs an asymmetric motion. This definition, however, cannot be applied to our current results as our μMAC perform a symmetric motion, as seen in Figure 3D, and therefore, the common definition of symplectic or antiplectic metachrony cannot be applied here as well. In our experiments, the metachronal wave always travels in the same direction as the fast elastic stroke, which is to the right in Figure 3.

Figure 4.

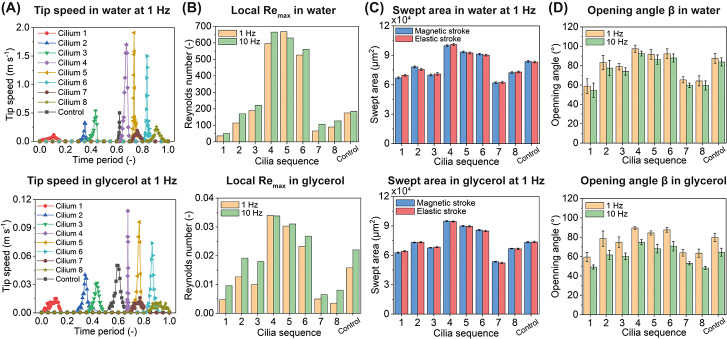
Quantitative analyses of the μMAC motion in both water and glycerol. (A) Tip speed of the μMAC array with a pitch of 550 μm during one beating cycle at 1 Hz. T = 0 corresponds to t = 0 s as shown in Figure 3A. The peak of the tip speed occurs during the elastic stroke of each cilium, and the time difference between these peaks represents the phase difference of the μMAC motion. (B) Calculated local maximum Reynolds number at 1 and 10 Hz based on the maximum tip speed in panel A and Figure S6A. See S7 for details about the calculation. (C) Swept area by the μMAC during the magnetic stroke and the elastic stroke at 1 Hz, respectively, showing that there is no difference in the swept area during the two strokes, indicating that the μMAC motion is symmetric. (D) Opening angle (β in Figure 3D) of the μMAC motion at 1 and 10 Hz. The tip speed and swept area of the μMAC motion at 10 Hz in both water and glycerol can be found in Figure S6. Each data point in panel (C,D) was obtained by averaging the results of at least three measurements.

Despite the symmetry of the metachronal μMAC motion, they can generate substantial water flow (Figure 3E) and glycerol flow (Figure 3F) in the aforementioned microfluidic chip (Figure 3B). Here, the positive results indicate that the flow direction above the ciliated area is in the same direction as the metachronal wave traveling direction, and the negative results indicate that the flow direction above the ciliated area is in the opposite direction to the metachronal wave traveling direction. In other words, the metachronal μMAC induce water flow and glycerol flow with opposite directions even though they perform the same metachronal motion. Figure S4 shows the time-lapse images of the used tracer particles over a specific period in both water and glycerol, indicating the flow speed and direction. Note that due to the cyclic nature of the cilia motions, cyclically pulsating flow may be expected to occur. However, we did not observe the pulsating flow of either water or glycerol at the recording frame rates of 10 and 0.1 fps, respectively. This is likely due to the fact that our recording frame rate is not high enough to detect the pulsating flow. The maximum water flow velocity is 220 μm s^–1, which is generated by the metachronal μMAC with a pitch of 350 μm at 10 Hz (the limit of our actuation setup). This corresponds to a volumetric flow rate of 85 μL min^–1 and a local pressure drop of 0.027 Pa in our microfluidic channel (see S5 for details). The maximal glycerol flow velocity is 5.5 μm s^–1 generated by the same μMAC array with a pitch of 350 μm at 10 Hz, which corresponds to a volumetric flow rate of 2.1 μL min^–1 and a local pressure drop of 1 Pa in our channel (see S5 for details). Due to the ease of control over the rotation of the electric motor, versatile flows can be generated in principle, for example, with time-varying flow rates, just as we reported before.^26,40

Several observations can be made from Figure 3E,F: (1) the generated water flow is in the same direction as the metachronal wave traveling direction and the elastic stroke direction as well, while the glycerol flow is in the direction opposite to the metachronal wave traveling direction; (2) the control μMAC cannot induce any significant flow in glycerol; (3) the μMAC array with a smaller pitch, thus containing more cilia, generates a higher water flow, but does not always generate a higher glycerol flow; (4) the water speed increases linearly with the beating frequency of the μMAC, and the glycerol speed has a slightly less than linear relationship with the cilia beating frequency; and (5) the metachronal μMAC generates a water flow of approximately twice that generated by the control μMAC. The mechanisms underlying these observed phenomena are similar to what we recently reported,²⁶ namely, inertial effects, asymmetric motions, and metachrony. As shown in Figure 4A, the maximum cilia tip speed during the elastic stroke in water is in the order of m s^–1, which leads to a maximum local Reynolds number (Re_max) in the order of hundreds, independent of the beating frequency (Figure 4B, see S7 for details about the calculation). Note that the average Re during the magnetic stroke in water is around 0.1 and 1 at 1 and 10 Hz, respectively. This means that inertial effects dominate over viscous effects in water during the elastic stroke but not during the magnetic stroke. In glycerol on the other hand, the cilia move much slower, and Re_max is much smaller than 1 during the whole cycle, and thus viscous effects prevail. Note that in Figure 4A, the beginning of the x axis corresponds to t = 0 s, as shown in Figure 3C, when the magnetic field is perpendicular to the cilia substrate and that the phase difference between the peaks of the tip speed also represents the phase difference of the μMAC motion. Figure 4C shows that each cilium sweeps the same area during the magnetic stroke as that during the elastic stroke, which means that the μMAC motion is a symmetric motion, both in water and in glycerol.

Based on these analyses, the explanations of the direction of the water flow and the glycerol flow [observation (1)] are as follows. In glycerol, only metachrony works, and the out-of-phase motion of the μMAC array creates a net pressure gradient, which results in a unidirectional glycerol flow whose direction is opposite to the direction of the metachronal wave. Detailed discussion of the relationship between the directions of the glycerol flow and metachrony can be found in ref (42). Therefore, we conclude that the metachrony of our μMAC array generates a flow in the opposite direction to the metachronal wave traveling direction in glycerol. Next, the explanation for the water flow direction is the following. In water, in addition to the metachrony, inertial effects operate which induce a flow in the elastic stroke direction (i.e., metachronal wave travelling direction) as observed. The contribution of metachrony remains unclear, however. Based on the glycerol results, inertia and metachrony could potentially counteract each other, and this means that the resulting water flow could be a competition between these two mechanisms with the inertial effects dominant over metachrony in water. This suggests that it might be beneficial to design a μMAC array whose elastic stroke direction is opposite to the metachrony traveling direction to further improve pumping efficiency in low viscosity liquids. However, the metachronal motion may well enhance the inertially driven flow, as can be deduced from earlier numerical studies;⁴² this is supported by observation (5) but needs to be studied in more detail using advanced numerical modeling in the future. Observation (2) confirms from another angle that the metachronal wave does contribute to the pumping efficiency in the low Re regime in glycerol. As for the relationship between the flow speed and the number of cilia [observation (3)], we believe it is a result of the competition between the pumping efficiency of each cilium and the dependency of the pumping efficiency of the metachrony on the cilia pitch. Detailed discussions can be found in refs,^25,43 and.⁴⁴ Note that inertia plays an important role in water but not in glycerol. This indicates that the optimal μMAC configuration for pumping efficiency can be different for liquids with different viscosities. As for observation (4), the relationship between the flow speed and the beating frequency of the μMAC is due to the fact that the net water flow induced by the μMAC array per beating cycle is almost constant as the μMAC motion is almost independent of the beating frequency, while the net glycerol flow induced by the μMAC array per beating cycle decreases as the μMAC motion diminishes at a higher beating frequency in glycerol (Figure 4D). The change in the μMAC motion results from the competition between the elasticity of the μMAC and the viscous drag, with viscous drag dominating in glycerol at high beating frequencies.²⁶ Observation (5) does not contradict observation (1) because the enhanced water flow is not necessarily because of the metachrony but could also result from the difference in the magnetic properties of the metachronal μMAC and the control μMAC due to their difference in the magnetic particle arrangement, which can be seen from the tip speed (Figure 4A) and the motion opening angle (Figure 4D). This asks for more in-depth numerical analysis as mentioned. In any case, observation (5) does underline that the pumping efficiency can be substantially enhanced by tuning the magnetic particle distribution within the μMAC.

2.4. Ciliated Soft Robots

Soft robots have shown remarkable potential for applications ranging from bioengineering to minimally invasive surgery.^36,45 Magnetic programmable robots offer potential to become the next generation of microsystems with advanced locomotion and manipulation capabilities.¹⁴ Here, we demonstrate the superior mobility of ciliated soft robots enabled by the metachronal motion of the μMAC on flat surfaces and slopes with angles ranging from 0 to 180° in air. We also show their remarkable cargo carrying capability in both air and liquid. The ciliated soft robots reported here are inverted μMAC arrays with a pitch of 350 μm consisting of 12 × 10 = 120 cilia; thus, the robots are approximately 4 mm long and 3.5 mm wide. For easy referencing, we name the ciliated robots made from the metachronal μMAC “metachronal robots”, and the ciliated robots made from the synchronously moving μMAC “control robots”.

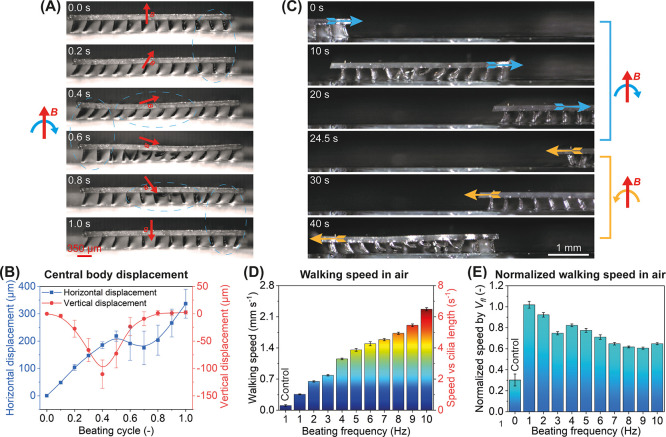
The high-speed locomotion of one metachronal robot in air during one beating cycle at 1 Hz is shown in Figure 5A (see also Movie S7 for the high-speed free μMAC motion in air and the locomotion of the metachronal robot). Note that all surfaces mentioned here are made of glass coated with a thin layer of lubricant oil in order to tune the adhesion between the μMAC and the surface (see Experimental Section). For too low adhesion (resulting from too much lubricant oil), the ciliated robot will remain stuck to the surface showing no forward movement; for too high adhesion (resulting from no or too little lubricant oil), the robot will not be able to move at all. Figure 5B quantifies the displacement of the central point of the robot body in both horizontal and vertical directions. Initially (t = 0 s), the applied magnetic field is perpendicular to the glass surface and the μMAC bend in a direction that depends on their location in the array with the center of the body as the mirror plane, to the left on the left side, and to the right on the right side. When the magnetic field starts to rotate clockwise due to the rotation of the electric motor (0–0.2 s), the front μMAC (on the right) tend to bend to the left (corresponding to the magnetic stroke, as shown in Figure 3D, see Movie S7). Due to the adhesion between the cilia and the surface, this motion causes the body of the metachronal soft robots (150 μm thick) to move forward. Meanwhile, the back μMAC tend to move to the right (corresponding to the elastic stroke in Figure 3D), but due to the cilia surface friction, they remain to be bent more toward the left and move forward together with the robot body. When the magnetic field rotates further (0.2–0.6 s), the central part of the robot body moves downward along with the bending of the μMAC at the middle part of the array (corresponding to the magnetic stroke in Figure 3D). This pushes the robot forward further. Later on (0.6–0.8 s), the μMAC array bends to the right (corresponding to the elastic stroke in Figure 3D) in a metachronal fashion, which lifts the robot upward and pushes the robot slightly backward as a result of the competition between the frictional and adhesive forces acting on the front μMAC and the back μMAC, respectively. Lastly (0.8–1 s), the front μMAC return to their original orientation and drive the robot forward further. As a result, the metachronal robot has moved ahead by a distance of approximately one cilia length, that is, 0.35 mm. Due to the symmetry of the μMAC array in terms of the particle distribution, the ciliated robot can walk in the opposite direction when the rotating direction of the magnetic field is reversed (Figure 5C, see also Movie S8), demonstrating bi-directional locomotion capability.

Figure 5.

Locomotion of ciliated soft robots in air. (A) Snapshots of the locomotion of the metachronal robot in air during one beating cycle at 1 Hz when the magnetic field rotates clockwise. See Movie S7. (B) Central body displacement along both the horizontal (blue square line) and vertical (red circle line) directions during one beating cycle at 1 Hz. The data points are connected by the B-Spline function in Origin. The trajectory of the central body over five beating cycles can be found in Movie S7. (C) Demonstration of bi-directional walking capability of the metachronal robot by reversing the rotating direction of the magnetic field. See Movie S8. (D) Walking speed of the metachronal robot in air as a function of the beating frequency, including the walking speed of the control robot at 1 Hz as a reference. Note the two y axes, with the left y axis indicating the absolute value of the walking speed and the right y axis indicating the speed relative to the cilia length. (E) Normalized walking speed by dimensionless number V_fl, representing the locomotion distance per beating cycle relative to the cilia length. Each data point was obtained by averaging the results of at least five identical but independent experiments.

Figure 5D shows that the metachronal robot moves 3 times faster than the control robot. The locomotion of the control robot can be found in Movie S9, which shows that the control robot vibrates as a whole in the rotating magnetic field due to the synchronous motion of the μMAC array. Also, its body remains straight in contrast to that of the metachronal robots of which the body performs a wave-like deformation, as can be seen in Figure 5A,B, as well as in Movie S7. This suggests that the more efficient locomotion of the metachronal robot may be partly explained by this effect, in addition to the metachronal motion of the cilia. In fact, previous studies have demonstrated magnetic soft robots shaped as rectangular thin films (without cilia or legs) that exhibit net motion precisely due to the undulating wavy deformation of the soft body.^2,30 However, the locomotion speed of our ciliated metachronal robot is substantially larger than that of the film-shaped robot demonstrated by Shinoda et al.,³⁰ as detailed in Section S9. This suggests that the contribution of the wavy deformation to the total locomotion is minor relative to the effect of the metachronal motion of the cilia, acting as the robot’s legs. Nevertheless, the efficient locomotion of the metachronal robots might benefit from the soft nature of the robot body, which can be investigated in the future by varying the body’s stiffness.

The walking speed of our metachronal robot scales slightly less than linear with the beating frequency of the μMAC, as can be seen in Figure 5D. The maximum walking speed is approximately 2.3 mm/s at 10 Hz, corresponding to almost 7 times the cilia length per second, a proportion similar to humans at running speed.¹⁸ Note that the maximum walking speed is limited by our actuation setup and can potentially be increased using an actuation setup that can generate a faster magnetic field rotation. We also quantified the walking speed of our metachronal robots using a dimensionless number V_fl, that is, the walking distance per beating cycle relative to the cilia length (Figure 5E). It shows clearly that the walking efficiency of the metachronal robot slightly drops with the increasing beating frequency. On average, the metachronal robot moves at a speed of approximately 0.75 cilia length per beating cycle, which is 3 times better than the control robot. The decrease in the walking efficiency at a higher beating frequency is probably due to an increased slip of the μMAC on the surface especially during the magnetic stroke, which renders the μMAC not being able to fully push the robot body forward sufficiently during a single beating cycle.

Obstacle-crossing and cargo-carrying capabilities are essential for biomedical robots. Our metachronal robots possess such capabilities (Figure 6). Note that all surfaces used here are made of polymethyl methacrylate (PMMA) coated with a thin lubricant layer (see Experimental Section). Note also that the beating frequency of the μMAC array is 2 Hz. Figure 6A shows that the metachronal robot is able to climb across a small hill with a slope of 45° in air (see Movie S10). The metachronal robot struggles at the corners of the hill (40–90 and 100–130 s, respectively). This is mainly because only part of the μMAC array can touch the surface at those locations, resulting in reduced work from the μMAC array per beating cycle. Consequently, the moving speed is slower than when the whole μMAC array can touch the surface. This suggests an interesting topic of study on the contribution of different parts of the μMAC array to the moving speed of the ciliated robots. This is, however, out of the scope of the current proof-of-principle work.

Figure 6.

Demonstration of the versatility of the ciliated metachronal robots. (A) Snapshots of the metachronal robot climbing across a PMMA hill at 2 Hz in air. See Movie S10. (B) Normalized climbing speed of the metachronal robots in air by V_fl on PMMA slopes with an angle ranging from 0 to 180°. See Movie S11. Each data point was obtained by averaging the results of at least five identical but independent experiments. (C) Demonstration of cargo (>10 own weight) carrying capability of the metachronal robot in both air and liquid. The cargo is a cubic glass grain of 3 × 3 × 1 mm³. The liquid is pure ethanol. See Movie S12.

To demonstrate the versatility of our metachronal robots further, we performed experiments using slopes at different angles and experiments with an extra weight placed on top of the metachronal robot in both dry and wet conditions. The results shown in Figure 6B demonstrate that our metachronal robots are capable of climbing slopes with angles ranging from 0 to 180° in air, which is unprecedented (see Movie S11). The remarkable climbing capability, especially on 90° (i.e., vertical) and 180° (upside down) slopes, is possible due to the cilia-surface adhesion overcoming gravity, while preserving continuous contact between the metachronal μMAC and the surface, which is unachievable by the control robots. The climbing speed initially decreases with the sloping angle, from a maximum speed of 0.7 cilia lengths per cycle on a horizontal surface to a minimum speed of 0.25 cilia lengths per cycle on a 45° slope. Increasing the slope further results in an increase in the speed to 0.55 cilia lengths per cycle on a 90° slope. This behavior is probably caused by the combined effects of adhesion, gravity, and friction. The adhesive forces that drive the locomotion remain similar for all slopes. As the slope increases from 0 to 90°, the gravity component along the surface that counteracts the robot motion increases, slowing down the motion. However, at the same time, the gravity component normal to the surface decreases, which leads to a decrease in the frictional force that also counteracts the locomotion of the robot, speeding up the motion. These two effects cross over at a slope of 45°, resulting in the observed behavior. Figure 6C shows that a metachronal robot of 2 mg can carry a glass grain of 25 mg (3 × 3 × 1 mm³), which is more than 10 times heavier than its own weight, in both air and ethanol at speeds of 0.2 and 0.3 cilia lengths per beating cycle, respectively (see Movie S12). This is substantially slower than the speed without cargo (which is 0.9 cilia lengths per beating cycle in air at 2 Hz, see Figure 5E), showing that the cargo weight reduces the locomotion speed. The slightly faster speed in ethanol is probably attributed to the reduced forces on the metachronal robots due to the buoyance of the glass grain. Ethanol instead of water was chosen in order to maintain the lubricant layer intact, as the lubricant layer would float in water.

3. Conclusions and Perspective

Metachronal μMAC arrays, actuated with a uniform magnetic field, have been successfully created using a facile and repeatable fabrication method that induces programmable magnetic anisotropy. Specifically, the paramagnetic particle distribution in the μMAC array is well controlled by placing a rod-shaped magnet array arranged with an alternating dipole orientation between neighboring magnets underneath the mold during the sample curing step. The working principle is based on the fact that the paramagnetic particles form structures that tend to align with the applied magnetic field. This mechanism also enables the design of a variety of smart stimulus-responsive structures and micromachines.⁴⁵ Owing to the difference in the magnetic particle arrangement between adjacent μMAC, neighboring μMAC in the array exhibit a phase-shifted deformation when actuated in a uniform magnetic field, while the amplitude of the μMAC bending varies with varying magnetic field magnitudes, see Figure 2 and Movie S2. This behavior of the μMAC arrays in a uniform magnetic field offers an alternative solution for creating reversible adhesion,⁴⁶ switchable wettability,⁴⁷ particle and droplet manipulation,⁴⁸ controlled liquid spreading,⁴⁹ cell/tissue stimulation by applying stretching and/or squeezing forces on cells, as well as microgrippers.¹⁷ Note that the concentration of the magnetic particles has an important impact on the μMAC behavior and that the bending angle of the μMAC scales nonlinearly with the applied magnetic field.

When the μMAC are placed in a 2D rotating magnetic field, a metachronal wave is observed to travel along the μMAC array. This metachronal wave enables superior fluid pumping and locomotion capability compared with the synchronous motion. Specifically, in terms of pumping efficiency, the metachronal μMAC exhibit twice the pumping efficiency than the synchronously moving control μMAC in water. In glycerol, with a viscosity 1000 times larger than that of water, the control μMAC cannot induce a flow, while the metachronal μMAC are still able to generate significant flow. The individual μMAC exhibit a 2D whip-like motion consisting of two strokes (a magnetic stroke and an elastic stroke), with no noticeable shape asymmetry but with different timescales. Hence, depending on the precise conditions (magnetic field rotation frequency, fluid viscosity), the generated flow is caused by the combination of inertial effects (in water) and metachrony (in water and in glycerol). For the previously reported artificial cilia with controlled anisotropic magnetic properties, the individual cilia motion is different: these exhibit 3D asymmetric motion,¹⁹ curved film oscillation,²⁷ 2D rotational buckling,²⁸ or rotation,²⁹ and therefore, the mechanism of the fluid flow generation of our cilia is different. A quantitative comparison with the flows reported by two studies of cilia with controlled anisotropic magnetization^19,28 shows that our metachronal μMAC generate similar or larger global flow in a microchannel, and the normalized flow speed has the same order of magnitude for all studies (see Table S1).

Concerning the locomotion capability of the ciliated robots based on inverted μMAC arrays, the metachronal robots move at a speed of approximately 0.7 cilia length per beating cycle, which is 3 times faster than the control robots. Due to the continuous contact between the metachronal μMAC and the surface, the metachronal robots show an unprecedented slope climbing ability (0 to 180°). The metachronal robots also exhibit heavy cargo carrying capacity (over 10 times its own weight) in both dry and wet conditions. We quantitatively compare the performance of our ciliated soft microrobot to that of a similar robot presented previously.¹⁹ Apart from our ciliated robot being substantially smaller, the locomotion speed is much larger (up to 2 mm/s vs 0.1 mm/s) due to the higher actuation frequency used, and the maximal normalized walking speed is larger as well, namely, at least 1 versus 0.5 (see Figure 5E). This is due to the differences in individual cilia motion as mentioned above and differences in adhesive and frictional interactions between the cilia and the surface.

The demonstrated abilities of the metachronal μMAC facilitate the design of on-chip integrated pumps as well as advanced versatile soft robots. Compared to previously reported metachronal cilia with spatially controlled magnetic anisotropy, our metachronal μMAC provide a number of key advantages, including (i) the ease of fabrication, (ii) the need for only a simple actuation scheme, (iii) the relatively small size that is compatible with common microfluidic chips, (iv) excellent fluid pumping capacity, and (iv) the capability to create versatile climbing soft robots.

While scaling of the programmable μMAC array is feasible in theory according to the predicted magnetic particle distribution by the COMSOL simulation, the use of the rod-shaped magnets imposes limits to the design of more complex and sophisticated structures because of their specific periodical magnetic field. More systematic studies need to be done in order to find the best magnetic particle arrangement in terms of pumping and locomotion efficiency. Besides the magnetic properties of the μMAC array, the cilia surface adhesion also has an impact on the locomotion efficiency of the metachronal soft robots. Therefore, a theoretical-numerical model is needed to calculate the bending performance of the metachronal μMAC in a given magnetic field both in a liquid and in contact with a solid surface and to predict the corresponding fluid pumping and locomotion efficiency. The pumping efficiency of our metachronal μMAC outperforms most reported artificial cilia (Table S1 and Figure S7),^{19,21−23,26,38,40} and is competitive with that of most of the existing microfluidic pumping methods including electrohydrodynamic, piezoelectric, electroosmotic, and electrostatic micropumps (Figure S8),^50,51 while the proposed concept requires no physical connection to peripheral equipment, reduces the usage of reagents by minimizing “dead volumes”, avoids undesirable electrical effects, and accommodates a wide range of different fluids. However, to create fully integrated on-chip pumps, more work needs to be done including standardizing the geometry of the μMAC and the microfluidic chips, building a benchmark database for the corresponding pumping capability, and creating a portable magnetic actuation setup. To move toward the real applications of the metachronal soft robots, more studies need to be performed, for example, on the effect of surface roughness on the robot locomotion and on biocompatibility for biomedical applications. Furthermore, we have shown that the metachronal robots can move both in air and in liquid, however, to obtain fully amphibious robots requires them to be able to transit through the liquid–air interface, which we have not been able to demonstrate. This may require surface modification or multimodal locomotion capacities including strong global body deformations.^2,3 In some cases, a biodegradable robot body may be preferred.

4. Experimental Section

4.1. Fabrication of the μMAC

The fabrication process of the metachronal μMAC is modified from the micromolding method of the control μMAC.³⁹ Briefly, it consists of 6 steps, as shown in Figure 1A: (1) A 350 μm thick SU-8 mold, featured with an array of microwells with a diameter of 50 μm arranged in a rectangular grid, was fabricated using standard photolithography. (2) A uniform magnetic precursor mixture of PDMS (Sylgard 184, Dow Corning, Base to Curing Agent weight ratio is 10:1) and paramagnetic microparticles (CIP, 99.5%, Sigma-Aldrich) was casted onto the mold, followed by a degassing procedure. The weight ratio between PDMS and CIP was varied from 4:1, 2:1 to 1:1. The details of the mixture preparation are available in ref (40). (3) The excess magnetic mixture outside the microwells was removed. (4) Pure PDMS (base to curing agent weight ratio = 10:1) was poured onto the mold. After degassing the pure PDMS layer was reduced to a thickness of 150 μm by spin-coating at a rotating speed of 500 rpm for 30 s. (5) A rod-shaped magnet array arranged with an alternating dipole orientation between adjacent magnets was placed underneath the mold in order to align the paramagnetic particles within the mold (see Movie S1). After 1 min at room temperature, the sample together with the magnet array was left in an oven at 80 °C for 3 h to cure the mixture. The rod magnets have a diameter of 4 mm and a length of 10 mm, and a remnant flux density of 1.2 T (S-04-10-DN, Supermagnete, Germany). (6) The cured pure PDMS layer with PDMS/CIP micropillars was peeled off the mold. Finally, the μMAC with the same spatial arrangement (Figure 1B) and the same geometry (Figure 1C) as the microwells were obtained, “standing” on a transparent PDMS base substrate. The cilia pitch was varied from 350, 450 ,to 550 μm, respectively.

4.2. Characterization of the Paramagnetic Particle Alignment and μMAC Bending Behavior

The alignment of the paramagnetic particles in the μMAC was captured using a CMOS camera (DFK 33UX252, Imaging Source Europe GmbH) mounted on a stereo microscope (Olympus SZ61) connected with a 2× auxiliary lens (110AL2X-2 Auxiliary objective) resulting in a 90× magnification. The particle alignment was then measured using ImageJ. The bending behavior of the μMAC array in a uniform magnetic field generated with an electromagnetic setup³⁸ was recorded from the side with the same microscopy setup. The bending angle (α in Figure 2A) of each cilium was measured using ImageJ.

4.3. Characterization of the μMAC Motion in a 2D Rotating Magnetic Field

The 2D rotating magnetic field was generated by a home-made setup (Figure 3A), which consists of a pair of permanent magnets (50 × 50 × 12.5 mm³, remnant flux density of 1.2 T, Q-50-50-12.5-N, Supermagnete, Germany) with their opposing magnetic poles facing each other at a distance of 50 mm supported by a PMMA frame. The frame with the magnets was driven by an electric motor that can be controlled with an in-house program through a commercial software (Escon Studio). The μMAC array, supported by a glass plate fixed on a manual XYZ stage, was placed at the central position between the magnets where the magnetic field is quasi-uniform. A high-speed camera (Phantom V9) mounted on the stereo microscope was used to capture the motion of the μMAC array from the side (Figure 3A). The recording frequency of the motion of a single metachronal cilium and the control cilium in water was 20,000 and 5000 frame per second (fps), respectively. For glycerol experiments, the recording frequency was 1000 fps for all cilia. The recording frequency for the motion of one row of μMAC was 20 times the beating frequency of the μMAC. The recorded μMAC motions were analyzed with ImageJ to study the trajectory and quantify the speed of the μMAC tip, the swept area, and the opening angle of the motion.

4.4. Characterization of the Flow Generated by the μMAC

The flow generated by the μMAC in the square microfluidic chip is characterized at the opposite location to the μMAC, indicated by the red dashed square shown in Figure 3B. The used liquids were deionized water and pure glycerol, respectively, and the flow speed was visualized by seeding the liquids with 10 μm polystyrene tracer particles (PS-Red-10.5, microParticles GmbH, Germany). The CMOS camera (DFK 33UX252) connected to the stereo microscope (Olympus SZ61) was used to record the movement of the tracer particles by taking image sequences at 10 and 0.1 fps for water and glycerol, respectively. The speed of the tracer particles in the geometrical center of the microfluidic channel (i.e., at a height of 1 mm above the channel substrate and at a distance of 3 mm to the sidewalls of the channel, where the flow speed is the highest) was measured by a Manual Tracking addon in ImageJ. To obtain the data shown in Figure 3E,F, at least ten independent measurements were done, of which the mean and standard deviation were determined.

4.5. Characterization of the Locomotion of the Ciliated Soft Robots

For all the experiments of the ciliated soft robots, in order to reduce the adhesion between the μMAC and the glass/PMMA surface, a thin layer of lubricant oil (Sewing-machine Oil, Kroon-oil) was applied on the surface by sliding a flat glass plate against the surface smoothly. In addition to, or instead of, the use of lubricant oil, surface treatment to the cilia and/or the surface may also be employed to tune the cilia surface adhesion. A ciliated robot was placed on the surface with a sharp tweezer. Then, the sample is placed on the XYZ stage, as shown in Figure 3A, located at the central part of the space between the two magnets (within 10 mm from the central axis, where the magnetic field is quasi-uniform, as shown in Figure S2). The high-speed locomotion of the ciliated robots, as shown in Figure 5A and Movie S7, was recorded using a high-speed camera (Phantom V9) mounted on the stereo microscope (Olympus SZ61) from the side (Figure 3A) at a recording speed of 100 fps. The displacement of the central body of the metachronal robots was then analyzed using ImageJ. The recording speed was 1000 fps for the high-speed motion of the μMAC array placed on the roof in air (Movie S7). For all other experiments, the CMOS camera (DFK 33UX252) was used at a recording speed of 10 or 60 fps. The hill shown in Figure 6A and the slopes in Figure 6B were fabricated from a PMMA sheet using laser cutting (VLS 3.50, VersaLaser).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsami.1c03009.

• Paramagnetic particle distribution resulting from the different arrangements of magnets; magnetic field generated by the rotating magnets; μMAC motion in the 2D rotating magnetic field in both water and glycerol; trajectories of tracer particles in both water and glycerol; calculation of the generated volumetric flow rate and pressure drop; tip speed and swept area of μMAC motion at 10 Hz in both water and glycerol; maximum local Reynolds number (Re_max); comparison of the fluid pumping capability of our metachronal μMAC with other artificial cilia and microfluidic pumps; and estimated robot locomotion due to wave-like body deformation (PDF)

• Paramagnetic particle alignment process during μMAC fabrication (MP4)

• Bending of one row of μMAC in a uniform magnetic field varying from 0 to 280 mT (MP4)

• Motion of one row of metachronal μMAC in the 2D rotating magnetic field in both water and glycerol at 1 Hz (MP4)

• Motion of one row of control μMAC in the 2D rotating magnetic field in both water and glycerol at 1 Hz (MP4)

• Motion of one row of metachronal μMAC with a pitch of 350 μm in the 2D rotating magnetic field in water (MP4)

• Motion of cilium 4 at 1 Hz in the 2D rotating magnetic field during the elastic stroke in both water and glycerol (MP4)

• Locomotion of the metachronal robot and the free motion of one row of metachronal μMAC in air in the 2D rotating magnetic field (MP4)

• Bi-directional locomotion of the metachronal robot in the 2D rotating magnetic field (MP4)

• Locomotion of the control robot in the 2D rotating magnetic field (MP4)

• Metachronal robot climbing across a hill (MP4)

• Metachronal robot climbing slopes at an angle ranging from 0 to 180° (MP4)

• Metachronal robot carrying cargo in both air and liquid (MP4)

Author Present Address

^§ Physical Intelligence Department, Max Planck Institute for Intelligent Systems, Stuttgart 70569, Germany.

Author Contributions

S.Z. conceived and designed the research; S.Z. and Z.C. performed the COMSOL simulation; S.Z. performed the experiments and analyzed the data; S.Z. drafted the manuscript; Z.C., Y.W., and J.d.T. revised the manuscript; and J.d.T. supervised the project.

The authors declare no competing financial interest.