The Geometry of Incompatibility in Growing Soft Tissues: Theory and Numerical Characterization

Abstract

Tissues in vivo are not stress-free. As we grow, our tissues adapt to different physiological and disease conditions through growth and remodeling. This adaptation occurs at the microscopic scale, where cells control the microstructure of their immediate extracellular environment to achieve homeostasis. The local and heterogeneous nature of this process is the source of residual stresses. At the macroscopic scale, growth and remodeling can be accurately captured with the finite volume growth framework within continuum mechanics, which is akin to plasticity. The multiplicative split of the deformation gradient into growth and elastic contributions brings about the notion of incompatibility as a plausible description for the origin of residual stress. Here we define the geometric features that characterize incompatibility in biological materials. We introduce the geometric incompatibility tensor for different growth types, showing that the constraints associated with growth lead to specific patterns of the incompatibility metrics. To numerically investigate the distribution of incompatibility measures, we implement the analysis within a finite element framework. Simple, illustrative examples are shown first to explain the main concepts. Then, numerical characterization of incompatibility and residual stress is performed on three biomedical applications: brain atrophy, skin expansion, and cortical folding. Our analysis provides new insights into the role of growth in the development of tissue defects and residual stresses. Thus, we anticipate that our work will further motivate additional research to characterize residual stresses in living tissue and their role in development, disease, and clinical intervention.

1. Introduction

It is well known that soft tissues in their physiological environment are not stress-free [1]. For instance, skin has been shown to have pre-strain in vivo [2]. This is also observed in the heart and heart valves [3, 4]. It has been hypothesized that the state of pre-stress of different organs yields specific physiological function [5]. For example, residual stresses in arteries actually reduce the peak stresses during systole [1]. Experimentally, the opening angle experiment of arteries was the first method introduced to measure residual deformation [6]. Thick slices of whole hearts have been dissected and then cut to measure the opening angle of these slices and, by extension, the residual stress of the heart [7, 8]. Heart valves have been measured in vivo and ex vivo to quantify their overall pre-strain [9]. Such approaches have further cemented the existence of pre-strain in vivo, but they are incomplete because they reduce the residual strain field to a homogeneous indicator like the scalar opening angle. The true state of residual deformation is more complex [10]. Indeed, there is evidence that tissues develop heterogeneous patterns of residual deformation during growth [11]. In response to skin expansion, for instance, the residual deformation of skin varies across the entire expanded region [12]. Even restricting the attention to the opening angle measurement, significant variation of this pre-strain metric varies along the length of an artery [13]. Thus, although numerous previous studies have confirmed the existence of pre-strain in living tissue, the precise features of this field are still poorly understood. Increasing our understanding of the basic mechanisms that can drive the development of residual strain in soft tissues has significant implications: it would allow estimation of the true reference configuration, the true mechanical behavior of tissues with respect to a stress-free state, and the way in which residual strain contributes to the tissue mechanical function in vivo [14, 15].

Residual stresses are not just a feature that emerges from tissue growth and remodeling. The opposite question is equally relevant: Does residual strain and stress guide the growth and remodeling process itself, and if so, how? Advances in mechanobiology have helped elucidate the way in which cells can sense mechanical cues. Yet, it is not clear how these cues can be coordinated during growth and remodeling to achieve a desired homeostatic state that is not stress-free [16]. Work on Dropsohpila wing disc development has brought up residual stress as a key regulator to explain embryo development patterns that are not explained by morphogen gradients alone [17, 18]. In [19], the authors propose a formulation of tissue growth and remodeling by considering a residual stress field directly as a target for tissue homeostasis. Beyond animal tissues, work in plant development has also characterized mismatch in growth rates between adjacent regions of the plant as a source of tissue conflicts that guide plant morphogenesis [20, 21].

Among different theoretical frameworks of growth and remodeling, a phenomenological description adopted from the theory of plasticity has been particularly successful [22, 23, 24]. In finite deformation plasticity, the deformation gradient is multiplicatively split into elastic and inelastic deformations [25]. Instead of a plastic deformation, the corresponding tensor in biomechanics is termed the growth deformation tensor [26, 27], and captures addition of mass by changes in volume [28]. The decomposition of the deformation gradient tensor plays a key role in understanding the origin of residual stresses observed at the macroscopic scale. The multiplicative split in fact introduces a geometric origin for the residual stress [29]. Growth and elastic deformations are in general incompatible fields, which means that they cannot be obtained from a displacement field [30]. If the growth deformation is incompatible, an incompatible elastic deformation is required to ensure compatibility of the total deformation. In turn, the necessary incompatibility of the elastic deformation is the source of the residual stress field [31]. Thus, quantifying the incompatibility of growth fields is intimately linked to the understanding of residual strains.

The notion of incompatibility arising from the multiplicative split of the deformation gradient is common between plasticity and growth, but the physical mechanisms leading to incompatibility and residual stresses are different between the two. In crystals, it is universally acknowledged that plastic deformation occurs through the movement of a dislocation, which is the most important line defect in crystals [29]. Mismatch in the deformation between adjacent regions in the crystal results in the disruption of the lattice structure [32, 33]. The defect in the lattice at the atomic scale is captured at the macroscopic scale via the plastic deformation tensor. Defects or imperfections of the lattice accommodated by the dislocation are connected to the storage of additional energy and, hence, residual stress [34, 35, 36]. Other types of topological defects in crystals can lead to residual stresses, for instance quasi-plastic thermal expansion [33, 37, 38]. In soft tissues, on the other hand, the physical mechanism at the microscale behind the accumulation of residual stress is still unclear [14]. Hypotheses include: differences in mechanical properties between adjacent structures within the tissue [11], different growth rates leading to unequal material accumulation [39], microstructure reorganization [27, 13], surface accretion [40, 41], and multiple and evolving natural configurations for different constituents [42]. Even if the precise microscopic origin of the residual stress is still in question, the macroscopic observation captured by the framework of finite volume growth condenses the origin of the residual stress field to geometric mismatches in the soft tissue stress-free configuration due to a heterogeneous growth and remodeling field.

In this manuscript, we quantify the geometric incompatibility that arises during growth of soft tissue described by the finite volume growth framework. This geometric characterization is linked to the origin of residual stress at the continuum scale. For our analysis, we rely on some well-established tools from crystal physics, such as the reinterpretation of the Burgers vector and the geometric dislocation density tensor [43, 44]. In plasticity, the Burgers vector explains the geometry of the dislocation density [45, 46, 47]. Soft tissues do not accumulate dislocations due to growth, but we can still use similar geometric analysis to understand the type of incompatibility possible in growing tissue, and how it may be connected to the accumulation of residual stress. We derive the form of the local Burgers vector density for representative scenarios of volumetric, area, and fiber growth. Moreover, we also characterize incompatibility and the associated residual stress for relevant biomedical applications such as human brain atrophy and skin expansion. We believe that our results will provide new insights and foster discussion about the geometric incompatibility induced by growth, how it may be related to microscale phenomena, and how it is connected to the accumulation of residual stress. Moreover, we anticipate that this work will not only improve our basic understanding of tissue mechanics, but also be useful for medical interventions that trigger growth and remodeling of soft tissues leading to accumulation of residual stress that can impact tissue function.

2. Materials and Methods

2.1. Kinematics of growth

Starting from the kinematics of finite deformation, we introduce the functional relation x = ϕ(X,t) to describe the motion of a body at time t. Let $\mathbf{\text{X}}\in {\mathcal{B}}_0\in {ℝ}^3$ be a point in the reference configuration ${\mathcal{B}}_0$. Then, ϕ maps X to a point in the current configuration $\mathbf{\text{x}}\in \mathcal{B}\subset {ℝ}^3$. The map ϕ is continuously differentiable with respect to X. Thus, the local deformation is captured by the deformation gradient F = ∇₀ϕ, which is a linear transformation of points from the tangent space $\mathcal{T}{\mathcal{B}}_0$ to $\mathcal{T}\mathcal{B}$. The determinant of the deformation gradient captures the local volume change J = det(F). Growth in biological tissues can be expressed via the multiplicative split of the deformation gradient tensor F into growth and elastic components [26],

$$\mathbf{\text{F}}={\mathbf{\text{F}}}^e{\mathbf{\text{F}}}^g,$$ (1)

where F^g is the growth contribution and F^e is the elastic deformation. The tensor F^g captures the biological process of tissue adaptation and requires further constraints. In fact, the form of F^g is not just a kinematic assumption but also a constitutive one. The split in eq. (1) further implies the split of the local volume change into elastic and growth components

$$J=J^e{J}^g,$$ (2)

with J^e = det(F^e), and J^g = det(F^g). In a more general scenario, growth can mean also atrophy or shrinkage and not just addition of mass,

$$\begin{gathered} J^g>1:\text{growth}, \\ {J}^g<1:\text{Shrinkage}. \end{gathered}$$ (3)

Of course, both J^e and J^g should be positive. At the microscopic level, J^g > 1 can be interpreted, for instance, as cell migration into the tissue, cell proliferation, material deposition, or hyperplasia of cells. On the other hand, J^g < 1 can entail cell necrosis or apoptosis, or material degradation [23].

The first requirement is that F^g should not be singular; then, F^e can be recovered from eq. (1), F^e = FF^g−1. Other reasonable assumptions include that F^g should be symmetric [48, 49]. Further restrictions on F^g are related to particular biological contexts as will be seen in later sections. The split, see eq. (1), implies the presence of an intermediate configuration that is stress-free. However, the intermediate configuration is fictitious and, generally, incompatible. In other words, F^g cannot be observed in general since the deformation described by this tensor does not originate from the continuous deformation of a body. At the same time, the elastic deformation F^e = FF^g−1 is, by construction, the necessary incompatible field that renders the total deformation compatible. In turn, the need for F^e to ensure compatibility even in the absence of any external loading is the source of residual stress. Let’s further consider the polar decomposition of F^e,

$${\mathbf{\text{F}}}^e={\mathbf{\text{V}}}^e{\mathbf{\text{R}}}^e={\mathbf{\text{R}}}^e{\mathbf{\text{U}}}^e,$$ (4)

where V^e and U^e are the elastic left and right stretch tensors and R^e is the elastic rotation tensor. The stress in the current configuration is calculated based on the elastic deformation F^e. To satisfy objectivity, however, the elastic left and right Cauchy-Green tensors are used,

$${\mathbf{\text{B}}}^e={\mathbf{\text{F}}}^e{\mathbf{\text{F}}}^{e\top }={\mathbf{\text{V}}}^e{\mathbf{\text{V}}}^{e\top }\hspace{0.17em}\text{and}\hspace{0.17em}{\mathbf{\text{C}}}^e={\mathbf{\text{F}}}^{e\top }{\mathbf{\text{F}}}^e={\mathbf{\text{U}}}^{e\top }{\mathbf{\text{U}}}^e.$$ (5)

The stress in the current configuration can be derived in terms of either B^e or C^e, which are independent of the rotation R^e. This suggests that the elastic deformation field needed for compatibility does not always induce stress. If the incompatible deformation needed is a pure rotation F^e = R^e, then, the current configuration is still stress-free. In crystal plasticity, this scenario is the stress-free curvature of the crystal lattice [50, 51]. An example of this situation for growing tissue will be covered in the Results section. Note also that if F^g is actually compatible and there are no external forces acting on the body, then, the elastic deformation is a compatible field that minimizes the potential energy. The solution is the identify field F^e = I. This implies that for a compatible growth field there is no residual stress in the body when all external loading is removed.

2.2. The geometric incompatibility tensor G

As stated above, the deformation gradient tensor is compatible because it is the gradient of a vector field, while the growth and elastic contributions are not necessarily compatible [29]. The condition of compatibility can be expressed via the Curl(•) operator. For any vector field v, it is always the case that Curl (Gradv) = 0. The notation Grad(•) denotes the same operation as ∇(•). Similarly, the Curl can also be represented with the notation ∇ × (•). It is clear that for the total deformation of a body we have Curl F = 0, while Curl F^g and Curl F^e are not necessarily zero. Therefore, Curl F^g and Curl F^e are quantitative indicators for the degree of incompatibility induced by growth. The Curl of a tensor field A is another tensor field defined by

$$\left(\text{Curl}\hspace{0.17em}\mathbf{\text{A}}\right)\mathbf{\text{v}}=\text{Curl}\left({\mathbf{\text{A}}}^{\top }\mathbf{\text{v}}\right)$$ (6)

for all constant vectors v. We use the notation Curl(•) for the operation with respect to the reference configuration X, compared to curl(•) which is with respect to the current configuration x [44]. In index notation, the components of Curl A are

$${\left(\text{Curl}\hspace{0.17em}\mathbf{\text{A}}\right)}_{ij}={\epsilon }_{irs}\frac{\partial A_{js}}{\partial X_r},$$ (7)

where ϵ_irs is the permutation symbol. We remark also that our definition of the Curl is sometimes introduced as the transpose of the Curl in other references and the reader should be careful about the definition being used in different papers [44, 50]. Next, we introduce the Burgers vector, which measures the gap introduced after deforming a closed circuit on a reference surface by the tensor field F^g. With the help of Stokes’ theorem, the Burgers vector b can be written in terms of the Curl(•),

$$\mathbf{\text{b}}\left({\mathcal{S}}_0\right):={\int }_{{\mathcal{C}}_0}{\mathbf{\text{F}}}^g\text{d}\mathbf{\text{X}}={\int }_{{\mathcal{S}}_0}{\left(\text{Curl}\hspace{0.17em}{\mathbf{\text{F}}}^g\right)}^{\top }{\mathbf{\text{n}}}_0\text{d}{A}_0,$$ (8)

where ${\mathcal{C}}_0$ is the closed circuit that encloses a surface ${\mathcal{S}}_0\left({\mathcal{B}}_0\right)$, with normal n₀ in the reference configuration. The differential n₀dA₀ is the surface element in the reference configuration. If Curl F^g = 0, the growth deformation is compatible and the Burgers vector b vanishes. This is the integrability condition for there to exist a unique vector field v whose gradient is F^g [36, 50]. Failure to satisfy this integrability condition implies the contrary, that there is no vector field v whose gradient leads to F^g.

The Burgers vector in crystal physics measures the geometry of a dislocation. On the other hand, the Burgers vector in eq. (8) for growing tissues can be interpreted as a mismatch in the geometry between two adjacent surface elements that grow at different rates. For example, imagine more material is deposited in one small element compared to an adjacent microscopic volume. Upon growth, the initially closed circuit that traverses these two areas would not be closed anymore. The resulting length of the mismatch is uniquely given by the Burgers vector. Note that this picture does not capture the molecular mechanism of the incompatibility in the growing tissue. We restrict our incompatibility density measure to the continuum scale.

The Burgers vector defined over the small region ${\mathcal{S}}_0$ can be localized [44]. In addition, the Burgers vector actually lies in the intermediate configuration, but the variable of integration in eq. (8) is defined in the reference configuration. Using Nanson’s formula, we can express the localized Burgers vector completely in terms of quantities in the intermediate configuration,

$${\left(\text{Curl}\hspace{0.17em}{\mathbf{\text{F}}}^g\right)}^{\top }{\mathbf{\text{n}}}_0\text{d}{A}_0=\frac{1}{J^g}{\left(\text{Curl}\hspace{0.17em}{\mathbf{\text{F}}}^g\right)}^{\top }{\mathbf{\text{F}}}^{g^{\top }}\overline{\mathbf{\text{n}}}\hspace{0.17em}\text{d}\overline{A},$$ (9)

where $\overline{\mathbf{\text{n}}}\hspace{0.17em}\text{d}\overline{A}$ is the surface element in the intermediate configuration with normal $\overline{\mathbf{\text{n}}}$. Therefore, eq. (9) evaluates the incompatibility due to growth or shrinkage on a surface with normal $\overline{\mathbf{\text{n}}}$ at a point in the intermediate configuration. To capture the incompatibility in all possible directions, we now introduce the central geometric object in this paper: the geometric incompatibility tensor G [44],

$$\mathbf{\text{G}}=\frac{1}{J^g}{\mathbf{\text{F}}}^g\text{Curl}\hspace{0.17em}{\mathbf{\text{F}}}^g.$$ (10)

The local Burgers vector density can now be computed for any direction $\overline{\mathbf{\text{n}}}$ using G,

$$\mathbf{\text{b}}:={\mathbf{\text{G}}}^{\top }\overline{\mathbf{\text{n}}}.$$ (11)

Strikingly, it is also possible to quantify the amount of incompatibility without knowing the growth field. Consider the following thought experiment: A body in the current configuration is unloaded and broken up into smaller and smaller pieces. As constraints are released and the body is split into differential volume elements that each approach a stress-free state, we would recover the incompatible elastic deformation field F^e. Knowledge of this field alone should be sufficient to determine the residual stress in the body $\mathcal{B}$. Indeed, G can be derived solely from F^e via [45, 46]

$$\mathbf{\text{G}}=J^e{\mathbf{\text{F}}}^{e-1}\text{curl}\hspace{0.17em}{\mathbf{\text{F}}}^{e-1}.$$ (12)

The equivalence between eqs. (10) and (12) can be evaluated using eqs. (1) and (2).

2.3. Constraints on the growth field determine the geometry of incompatibility

As mentioned before, the specific form of F^g is both a kinematic and a constitutive assumption. In particular, the restrictions in the tensor F^g should reflect the connection between growth and tissue microstructure. Here we focus on three representative growth models: volume, area, and length (or fiber) growth [24]. Additionally, the tensor F^g can be expressed in terms of scalar fields directly linked to mass sources. The scalar field for growth is denoted by ϑ^g throughout this manuscript. The added structure for F^g leads to interesting properties of the geometric incompatibility tensor G which are unique to growing soft tissue.

2.3.1. Isotropic volume growth

The simplest and most natural growth model is isotropic volume growth. This corresponds, for instance, to cell proliferation or deposition of new tissue without any preferred orientation. A common example of this type of growth is tumor growth [52, 53]. We have

$${\mathbf{\text{F}}}^g:=\sqrt[3]{{\vartheta }^g}\mathbf{\text{I}},$$ (13)

where ϑ^g is a scalar field that represents local volume change due to growth, and I is the second-order identity tensor. The evolution of ϑ^g should obey a constitutive equation representing cell mechanobiology which we will define later. The Curl operation for this tensor leads to

$${\left(\text{Curl}\hspace{0.17em}{\mathbf{\text{F}}}^g\right)}_{ij}={ϵ}_{irs}\frac{\partial F_{js}^g}{\partial X_r}=\frac{\partial \sqrt[3]{{\vartheta }^g}}{\partial X_r}{ϵ}_{irs}{\delta }_{js}=\frac{\partial \sqrt[3]{{\vartheta }^g}}{\partial X_r}{ϵ}_{irj}.$$ (14)

Alternatively, in tensor notation,

$$\text{Curl}\hspace{0.17em}{\mathbf{\text{F}}}^g=\frac{1}{3\sqrt[3]{{\vartheta }^{g2}}}\star \nabla {\vartheta }^g=\frac{1}{3\sqrt[3]{{\vartheta }^{g2}}}\left(\nabla {\vartheta }^g\times {\mathbf{\text{e}}}_i\right)\otimes {\mathbf{\text{e}}}_i,$$ (15)

with $\star (•)$ denoting the Hodge star operator, and e_i the standard orthonormal basis vectors. For isotropic volume growth, using eq. (15) and recalling the definition of the geometric incompatibility tensor in eq. (10), we find that G is a skew-symmetric tensor and the matrix form in the standard Cartesian basis is

$$\mathbf{\text{G}}=\frac{1}{3\sqrt[3]{{\vartheta }^{g4}}}\left[\begin{array}{ccc}0& -{\vartheta }_{,X_3}^g& {\vartheta }_{,X_2}^g\\ {\vartheta }_{,X_3}^g& 0& -{\vartheta }_{,X_1}^g\\ -{\vartheta }_{,X_2}^g& {\vartheta }_{,X_1}^g& 0\end{array}\right],$$ (16)

where ${\vartheta }_{,X_1}^g$, ${\vartheta }_{,X_2}^g$, and ${\vartheta }_{,X_3}^g$ are the partial derivatives of ϑ^g with respect to the reference configuration coordinates.

Based on eq. (11), the local Burgers vector density for the standard basis in 3D Euclidean space is, in matrix form,

$$\begin{gathered} {\mathbf{\text{b}}}_1={\mathbf{\text{G}}}^{\top }{\mathbf{\text{e}}}_1=\frac{1}{3\sqrt[3]{{\vartheta }^{g4}}}{\left(0,-{\vartheta }_{,X_3}^g,{\vartheta }_{,X_2}^g\right)}^{\top }, \\ {\mathbf{\text{b}}}_2={\mathbf{\text{G}}}^{\top }{\mathbf{\text{e}}}_2=\frac{1}{3\sqrt[3]{{\vartheta }^{g4}}}{\left({\vartheta }_{,X_3}^g,0,-{\vartheta }_{,X_1}^g\right)}^{\top }, \\ {\mathbf{\text{b}}}_3={\mathbf{\text{G}}}^{\top }{\mathbf{\text{e}}}_3=\frac{1}{3\sqrt[3]{{\vartheta }^{g4}}}{\left(-{\vartheta }_{,X_2}^g,{\vartheta }_{,X_1}^g,0\right)}^{\top }. \end{gathered}$$ (17)

Recall that these Burgers vectors b_i measure the incompatibility on planes defined by the basis vectors e_i. Thus, here we see that for isotropic growth there is no incompatibility orthogonal to the plane of interest. In other words, for the plane defined by each of the e_i, the local Burgers vector density is restricted to that plane. Contrast this with crystals, where screw dislocations are possible and entail defects in the direction of the normal vector [54]. Another key insight from analyzing incompatibility in the context of growth and remodeling is that we have a direct connection between the gradients of growth and incompatibility. For instance, if the growth is uniform (that is, if ${\vartheta }_{,\mathbf{\text{X}}}^g=0$) then it is clear that G vanishes. Another useful example would be growth that only varies in one direction, for instance X₁. In that case, b₁ vanishes completely and there is no incompatibility in planes defined by the growth gradient. We actually explore this example further in the Results section. We also investigate a brain atrophy model [55] where shrinkage of white and gray matter leads to local growth gradients and, as a result, to residual stresses from incompatibility [56].

2.3.2. Transversely isotropic area growth

Transversely isotropic in-plane area growth is applicable for thin tissues in which there is area growth but the thickness remains unchanged [57]. An important example of area growth is that of skin in tissue expansion [58]. Computational models of skin growth based on the multiplicative split of the deformation gradient have been shown to accurately capture animal experiments and patient-specific scenarios [59, 60]. The growth deformation tensor for area growth takes the form

$${\mathbf{\text{F}}}^g:=\sqrt{{\vartheta }^g}\mathbf{\text{I}}+\left(1-\sqrt{{\vartheta }^g}\right){\mathbf{\text{N}}}_0\otimes {\mathbf{\text{N}}}_0,$$ (18)

where N₀ is the tissue normal vector in the reference configuration. eq. (18) inherently restricts volume change to permanent changes in area while keeping thickness deformations purely elastic. The determinant of eq. (18), which is the total volume of new tissue, is also the local area change. The Curl operation in this case can be expressed in tensor notation as

$$\text{Curl}\hspace{0.17em}{\mathbf{\text{F}}}^g=\frac{1}{2\sqrt{{\vartheta }^g}}\left(\nabla {\vartheta }^g\times {\mathbf{\text{e}}}_i\right)\otimes {\mathbf{\text{e}}}_i-\frac{1}{2\sqrt{{\vartheta }^g}}\left(\nabla {\vartheta }^g\times {\mathbf{\text{N}}}_0\right)\otimes {\mathbf{\text{N}}}_0.$$ (19)

The geometric incompatibility tensor for area growth can be computed from eqs. (19) and (10). For completeness, in index notation this tensor takes the form

$$G_{ij}=\left(\frac{1}{\sqrt{{\vartheta }^g}}{\delta }_{im}+\left(\frac{1}{{\vartheta }^g}-\frac{1}{\sqrt{{\vartheta }^g}}\right)N_{0i}{N}_{0m}\right){ϵ}_{mrs}\frac{\partial F_{js}^g}{\partial X_r}.$$ (20)

Similar to the isotropic case, incompatibility occurs due to gradients in the permanent area change, as is evident from eq. (19). Having an expression for G, we can determine the Burgers vector density in any direction. To that end, the most relevant plane is defined by N₀ or, more rigorously, the normal $\overline{\mathbf{\text{N}}}$ in the intermediate configuration. For this particular type of growth we have $\overline{\mathbf{\text{N}}}={\mathbf{\text{N}}}_0$ by construction. The local Burgers vector density ${\mathbf{\text{G}}}^{\top }\overline{\mathbf{\text{N}}}$ becomes

$$\mathbf{\text{b}}={\mathbf{\text{G}}}^{\top }\overline{\mathbf{\text{N}}}=\frac{1}{2\sqrt{{\vartheta }^{g3}}}\left({\mathbf{\text{s}}}_{\alpha }\otimes \left(\nabla {\vartheta }^g\times {\mathbf{\text{s}}}_{\alpha }\right)\right)\overline{\mathbf{\text{N}}},$$ (21)

where the vectors s_α, with α = {1,2}, are the local basis for the surface defined by $\overline{\mathbf{\text{N}}}$. We observe again that the Burgers vector corresponding to the plane defined by $\overline{\mathbf{\text{N}}}$ is restricted to that plane and will have only components along the s_α directions. Moreover, if the gradient is aligned with any of the surface basis vectors, then the expression can be further simplified. For instance, without loss of generality, assume that ∇ϑ^g is aligned with s₂ and denote s₁ = s. The vector s is the vector on the surface which is orthogonal to the in plane growth gradient. Then,

$$\mathbf{\text{b}}=\frac{\left|\nabla {\vartheta }^g\right|}{2\sqrt{{\vartheta }^{g3}}}\mathbf{\text{s}}.$$ (22)

This last expression condenses the key type of incompatibility of area growth. Since the local basis can always be aligned with the direction of the growth gradient, eq. (22) shows that the incompatibility is orthogonal to the growth gradient and its magnitude is proportional to the magnitude of the growth gradient scaled with respect to the amount of growth.

2.3.3. Uniaxial Fiber growth

In tissues such as muscle, growth can occur along the fiber direction [61, 62]. In addition, axons in the white matter of the brain also show lengthwise growth induced by chronic overstretch during development [63]. Cortical folding of the brain is a phenomenon that occurs in part due to mechanical instabilities triggered by this type of growth coupled to other biological factors [64]. The heart also has a unique and well-defined fiber structure along which growth can occur, especially due to volume overload. For growth along the fiber direction, F^g is defined as

$${\mathbf{\text{F}}}^g:=\mathbf{\text{I}}+\left({\vartheta }^g-1\right){\mathbf{\text{f}}}_0\otimes {\mathbf{\text{f}}}_0,$$ (23)

where f₀ is the fiber direction in the reference configuration. The determinant of eq. (23) is the volume change, which in the fiber growth scenario is also the irreversible change in length along the fiber direction. For this specific type of growth tensor, the Curl operator leads to an elegant form

$$\text{Curl}\hspace{0.17em}{\mathbf{\text{F}}}^g=\left(\nabla {\vartheta }^g\times {\mathbf{\text{f}}}_0\right)\otimes {\mathbf{\text{f}}}_0.$$ (24)

The incompatibility tensor can then be computed based on its definition G = (1/ϑ^g)F^gCurl F^g. For completeness, we write it in index notation,

$$G_{ij}=\left(\frac{1}{{\vartheta }^g}{\delta }_{im}+\left(1-\frac{1}{{\vartheta }^g}\right)f_{0i}{f}_{0m}\right){ϵ}_{mrs}\frac{\partial {\vartheta }^g}{\partial X_r}{f}_{0j}{f}_{0s}.$$ (25)

For fiber growth, the fiber direction is unchanged in the intermediate configuration, $\overline{\mathbf{\text{f}}}={\mathbf{\text{f}}}_0$. The local Burgers vector density in the plane defined by the fiber direction $\overline{\mathbf{\text{f}}}$ is

$${\mathbf{\text{G}}}^{\top }\overline{\mathbf{\text{f}}}=\frac{1}{{\vartheta }^g}{\mathbf{\text{f}}}_0\otimes \left(\nabla {\vartheta }^g\times {\mathbf{\text{f}}}_0\right)\overline{\mathbf{\text{f}}}=\text{0}.$$ (26)

Thus, in the case of fiber growth, there cannot be incompatibility in the direction of the fiber. Also from eq. (24), it can be seen that if the gradient of growth is aligned with the direction of the fiber there is also no incompatibility. We turn our attention to the planes orthogonal to the fiber direction. Consider the unit vector in the intermediate configuration $\overline{\mathbf{\text{m}}}$, which is locally orthogonal to both the growth gradient and the fiber direction. Then, the local Burgers vector density for the plane defined by $\overline{\mathbf{\text{m}}}$ is

$${\mathbf{\text{G}}}^{\top }\overline{\mathbf{\text{m}}}=\frac{\left|\nabla {\vartheta }^g\right|\sin \left(\beta \right)}{{\vartheta }^g}{\mathbf{\text{f}}}_0,$$ (27)

where β is the angle between the growth gradient and the fiber direction. Therefore, the incompatibility for fiber growth is aligned with the fiber direction, and the magnitude of the Burgers vector is proportional to the magnitude of the growth gradient and inversely proportional to the amount of growth. As stated before, if the growth gradient is aligned with the fiber direction, the Burgers vector vanishes. On the contrary, the Burgers vector will have maximum magnitude when the growth gradient is orthogonal to the fiber direction.

In the Results section, we present examples for each of the three growth types. Firstly, we illustrate the concepts derived here with simple examples of each of the growth tensors, eqs. (13), (18), and (23). Secondly, we characterize incompatibility and residual stresses for the examples of skin growth during tissue expansion, brain atrophy, and cortical folding due to axon fiber growth. Overall, the notion of the geometric incompatibility tensor G takes on specific features for growing soft tissues described with the finite growth framework. While we limit the present work to this geometric description, the characteristics of G and the Burgers vector for the different growth cases raises intriguing questions about the possible molecular origins of these phenomena.

2.4. Balance equations for growing soft tissues

Growth requires considering the thermodynamics of open systems, as carefully outlined in [48]. Under the assumption of a quasi-static process, balance equations for linear momentum akin to plasticity are derived. For completeness, we review the mass specific format of the balance equations in the Lagrangian form, similar to [65].

2.4.1. Balance of mass

Let the density of the mass element in the reference configuration be ρ₀ and its rate of change ${\dot{\rho }}_0$. We remark that ρ₀ is the current density of the material but pulled back to the reference configuration. Then the local form of balance of mass for open systems (growing tissues in our setting) implies the possible flux of mass R in the reference configuration and a possible mass source ${\mathcal{R}}_0$ term [66],

$${\dot{\rho }}_0={\nabla }_0\cdot \mathbf{\text{R}}+{\mathcal{R}}_0.$$ (28)

The flux in the reference configuration is the Piola transform of the corresponding spatial flux, and the mass source in the reference configuration is the pull-back of a corresponding source term in the spatial configuration. The mass change of growing matter can lead to changes in density, volume, or both. In the framework of finite volume growth for soft tissue, the density-preserving notion is implied [28]. As a consequence, the mass source will be linked to the time evolution of F^g, as will be seen later.

2.4.2. Balance of linear momentum

The local form of balance of linear momentum for the open systems is obtained by considering the mass change ${\dot{\rho }}_0$ in the Lagrangian equations of motion,

$${\dot{\rho }}_0\mathbf{\text{v}}+{\rho }_0\dot{\mathbf{\text{v}}}={\nabla }_0\cdot \text{P}+{\rho }_0\mathbf{\text{f}},$$ (29)

where v is the velocity vector, P is the first Piola-Kirchhoff stress, and f is the body force field. Under quasi-static conditions and neglecting the mass flux, R = 0 and $\dot{\mathbf{\text{v}}}=0$, eq. (29) can be simplified considerably,

$$\text{0}={\nabla }_0\cdot \mathbf{\text{P}}+{\rho }_0\mathbf{\text{f}}.$$ (30)

2.4.3. Balance of entropy

Local balance of entropy is enforced through the Clausius-Duhem inequality. For an open system, the local form of the dissipation inequality $\mathcal{D}$ ignoring temperature changes [60] can be stated as

$${\rho }_0\mathcal{D}=\text{S}:\dot{\mathbf{\text{E}}}-{\rho }_0\dot{\psi }-T{\rho }_0{S}_0\ge 0,$$ (31)

where S = F⁻¹P is the second Piola-Kirchhoff stress, $\dot{\mathbf{\text{E}}}$ is the rate of change of the Green-Lagrange strain tensor, Ψ= ρ₀ψ is the volume specific free energy density, T is temperature, and S₀ is an external entropy source [67]. For growing tissues, it is common to assume that added mass does not contribute to additional entropy and S₀ = 0. Hence, neglecting any dissipative mechanisms, eq. (31) reduces to the standard definition of the second Piola-Kirchhoff stress as the derivative of the strain energy with respect to its work-conjugate Green-Lagrange strain tensor E,

$$\text{S}={\rho }_0\frac{\partial \psi }{\partial \mathbf{\text{E}}}.$$ (32)

To close this section on the balance equations of growth, we establish the relationship between the mass balance in eq. (28) and the growth tensor F^g. Considering that the density in the current and intermediate configurations is constant, ρ^g = ρ = const [48], we have ρ^g = j^gρ₀ with j^g = J^g−1, then

$${\dot{\rho }}^g={\dot{j}}^g{\rho }_0+j^g{\dot{\rho }}_0=0.$$ (33)

In addition, recall that we neglect flux of mass, R = 0, an assumption that is usually employed in the description of growing soft tissues [48]. Then, eqs. (28) and (33) yield

$${\dot{\rho }}_0=-{\rho }_0{J}^g{\dot{j}}^g=-{\rho }_0{J}^g\frac{\partial j^g}{\partial {\mathbf{\text{F}}}^{g-1}}:{\dot{\mathbf{\text{F}}}}^{g-1}=-{\rho }_0{\mathbf{\text{F}}}^{g\top }:{\dot{\mathbf{\text{F}}}}^{g-1},$$ (34)

where we have introduced the growth velocity tensor ${\mathbf{\text{L}}}^g={\dot{\mathbf{\text{F}}}}^g{\mathbf{\text{F}}}^{g-1}$ [28]. Using ${\dot{\mathbf{\text{F}}}}^g{\mathbf{\text{F}}}^{g-1}=-{\mathbf{\text{F}}}^g{\dot{\mathbf{\text{F}}}}^{g-1}$ we have

$${\rho }_0\text{tr}\left({\mathbf{\text{L}}}^g\right)={\mathcal{R}}_0,$$ (35)

which is the link between the mass source field and the growth tensor field.

2.5. Constitutive model for soft tissue mechanics

We consider hyperelastic behavior, which is a common framework for modeling soft tissues. This requires the definition of the volume specific free energy density which depends only on the elastic deformation, $\mathrm{\Psi }={\rho }_0\widehat{\psi }\left({\mathbf{\text{F}}}^e,{\rho }_0\right)=\mathrm{\Psi }\left({\mathbf{\text{C}}}^e\right)$. Moreover, the strain energy can be written in terms of the invariants of ${\mathbf{\text{C}}}^e,\hspace{0.17em}\mathrm{\Psi }=\mathrm{\Psi }\left(I_1^e,I_2^e,I_3^e\right)$. Two different models are considered. First, we introduce a compressible neo-Hookean hyperelastic potential of the form

$$\mathrm{\Psi }=\frac{\mu }{2}\left(I_1^e-3-2\ln \left(J^e\right)\right)+\frac{\lambda }{2}{\ln }^2\left(J^e\right),$$ (36)

where $I_1^e=\text{tr}\left({\mathbf{\text{C}}}^e\right)=\text{tr}\left({\mathbf{\text{B}}}^e\right)$ is the first invariant of C^e and B^e, $I_3^e=\det \left({\mathbf{\text{C}}}^e\right)=\det \left({\mathbf{\text{B}}}^e\right)=J^{e2}$ is the third invariant of C^e and B^e, and µ and λ are the Lame’s parameters. The second Piola-Kirchhoff stress tensor follows from eq. (32),

$${\text{S}}^e=2\frac{\partial \mathrm{\Psi }}{\partial {\mathbf{\text{C}}}^e}=\left(\lambda \ln \left(J^e\right)-\mu \right){\mathbf{\text{C}}}^{e-1}+\mu \mathbf{\text{I}}.$$ (37)

Alternatively, the Kirchhoff stress is given by

$${\tau }^e=2{\mathbf{\text{B}}}^e\frac{\partial \mathrm{\Psi }}{\partial {\mathbf{\text{B}}}^e}=\left(\lambda \ln \left(J^e\right)-\mu \right)\mathbf{\text{i}}+\mu {\mathbf{\text{B}}}^e,$$ (38)

where i is the spatial second-order identity tensor. The rationale for introducing both the Lagrangian and the Eulerian stress tensors is that the finite element implementation can be formulated for either setting. Obviously, both expressions of the stress are equivalent.

Many soft tissues are characterized by a high degree of collagen content [68]. Collagen is the most common structural protein in mammals. It is observed in the microstructure of tissues as a fiber network [69, 70]. Mechanically, this fibrous architecture endows tissues with a characteristic exponential behavior under tensile loading [71]. Among several hyperelastic strain energy potentials that capture this response, we employ the one proposed by Gasser-Ogden-Holzapfel (GOH) [72],

$$\begin{gathered} \mathrm{\Psi }={\mathrm{\Psi }}_{\text{iso}}\left({\overline{\mathbf{\text{C}}}}^e\right)+{\mathrm{\Psi }}_{\text{aniso}}\left({\overline{\mathbf{\text{C}}}}^e,{\mathbf{\text{H}}}_{\alpha }\right)+{\mathrm{\Psi }}_{\text{vol}}\left(J^e\right)\hspace{0.17em}\text{with} \\ {\mathrm{\Psi }}_{\text{iso}}\left({\overline{\mathbf{\text{C}}}}^e\right)=\frac{\mu }{2}\left({\overline{I}}_1^e-3\right), \\ {\mathrm{\Psi }}_{\text{aniso}}\left({\overline{\mathbf{\text{C}}}}^e,{\mathbf{\text{H}}}_{\alpha }\right)=\frac{k_1}{2k_2}\left(\exp \left(k_2{\langle {\overline{E}}_{\alpha }\rangle }^2\right)-1\right),\hspace{0.17em}\text{and} \\ {\mathrm{\Psi }}_{\text{vol}}\left(J^e\right)=\frac{\lambda }{2}\left(\frac{J^{e2}-1}{2}-\ln \left(J^e\right)\right), \end{gathered}$$ (39)

where ${\overline{I}}_1^e=J^{e-\frac{2}{3}}{I}_1^e$ is the first invariant of ${\overline{\mathbf{\text{C}}}}^e$, the isochoric part of C^e, and ${\overline{E}}_{\alpha }\equiv {\overline{\mathbf{\text{C}}}}^e:{\mathbf{\text{H}}}_{\alpha }-1$ is the pseudo-invariant with respect to the symmetric generalized structure tensor ${\mathbf{\text{H}}}_{\alpha }=\kappa \mathbf{\text{I}}+\left(1-3\kappa \right){\overline{\mathbf{\text{a}}}}_{\alpha }\otimes {\overline{\mathbf{\text{a}}}}_{\alpha }$ with fiber direction ${\overline{\mathbf{\text{a}}}}_{\alpha }={\mathbf{\text{F}}}^g{\text{a}}_{0\alpha }/\left|{\mathbf{\text{F}}}^g{\text{a}}_{0\alpha }\right|$ in the intermediate configuration, a₀α in the reference configuration. The notation $\langle \cdot \rangle$ in eq. (39) denotes the Macaulay brackets. The parameters k₁, k₂, and κ capture the response of the fiber family: k₁ describes the tensile response, k₂ is dimensionless and expresses nonlinearity of the fiber response, and κ is another dimensionless parameter that indicates dispersion in the range 0 to 1/3, from perfectly anisotropic to perfectly isotropic. The second Piola-Kirchhoff stress tensor of GOH potential can be derived from the strain energy,

$$\begin{gathered} {\mathbf{\text{S}}}^e=2\frac{\partial {\mathrm{\Psi }}_{\text{iso}}}{\partial {\mathbf{\text{C}}}^e}+2\frac{\partial {\mathrm{\Psi }}_{\text{aniso}}}{\partial {\mathbf{\text{C}}}^e}+2\frac{\partial {\mathrm{\Psi }}_{\text{vol}}}{\partial {\mathbf{\text{C}}}^e} \\ \hspace{1em}=\mu \frac{\partial {\overline{I}}_1^e}{\partial {\mathbf{\text{C}}}^e}+2k_1\langle {\overline{E}}_{\alpha }\rangle \exp \left(k_2{\langle {\overline{E}}_{\alpha }\rangle }^2\right)J^{e-\frac{2}{3}}\mathbb{P}:\frac{\partial {\overline{E}}_{\alpha }}{\partial {\overline{\mathbf{\text{C}}}}^e}+\frac{\lambda }{2}\left(J^e-\frac{1}{J^e}\right)\frac{\partial J^e}{\partial {\mathbf{\text{C}}}^e}, \end{gathered}$$ (40)

where

$$\mathbb{P}=\mathbb{I}-\frac{1}{3}{\mathbf{\text{C}}}^{e-1}\otimes {\mathbf{\text{C}}}^e=\mathbb{I}-\frac{1}{3}{\overline{\mathbf{\text{C}}}}^{e-1}\otimes {\overline{\mathbf{\text{C}}}}^e,$$ (41)

is the fourth order projection tensor, with $\mathbb{I}=\frac{1}{2}\left(\mathbf{\text{I}}\overline{\otimes }\mathbf{\text{I}}+\mathbf{\text{I}}\underset{\_}{\otimes }\mathbf{\text{I}}\right)$ the fourth order identity tensor, ${\left\{•\overline{\otimes }\circ \right\}}_{ijkl}={\{•\}}_{ik}{\{\circ \}}_{jl}$ and ${\left\{•\underset{\_}{\otimes }\circ \right\}}_{ijkl}={\{•\}}_{il}{\{\circ \}}_{jk}$. The derivatives in (40) can be expanded further,

$$\frac{\partial {\overline{I}}_1^e}{\partial {\mathbf{\text{C}}}^e}=J^{e-\frac{2}{3}}\left(\mathbf{\text{I}}-\frac{1}{3}{\overline{I}}_1^e{\overline{\mathbf{\text{C}}}}^{e-1}\right),\hspace{0.17em}\hspace{0.17em}\frac{\partial {\overline{E}}_{\alpha }}{\partial {\overline{\mathbf{\text{C}}}}^e}={\mathbf{\text{H}}}_{\alpha },\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\frac{\partial J^e}{\partial {\mathbf{\text{C}}}^e}=\frac{J^e}{2}{\mathbf{\text{C}}}^{e-1}.$$ (42)

The corresponding Kirchhoff stress can be obtained by pushing-forward the second Piola-Kirchoff stress tensor,

$${\tau }^e={\mathbf{\text{F}}}^e{\mathbf{\text{S}}}^e{\mathbf{\text{F}}}^{e\top }=\mu ({\overline{\mathbf{\text{B}}}}^e-\frac{1}{3}{\overline{I}}_1^e\mathbf{\text{i}})+2k_1\langle {\overline{E}}_{\alpha }\rangle \exp (k_2{\langle {\overline{E}}_{\alpha }\rangle }^2)J^{e-\frac{2}{3}}({\overline{\mathbf{\text{h}}}}_{\alpha }-\frac{1}{3}({\overline{\mathbf{\text{C}}}}^e:{\mathbf{\text{H}}}_{\alpha })\mathbf{\text{i}})+\frac{\lambda }{4}(J^{e2}-1)\mathbf{\text{i}},$$ (43)

where ${\overline{\mathbf{\text{B}}}}^e=J^{e-\frac{2}{3}}{\mathbf{\text{B}}}^e$ is the isochoric part of B^e and ${\overline{\mathbf{\text{h}}}}_{\alpha }={\overline{\mathbf{\text{F}}}}^e{\mathbf{\text{H}}}_{\alpha }{\overline{\mathbf{\text{F}}}}^{e\top }=\kappa {\overline{\mathbf{\text{B}}}}^e+\left(1-3\kappa \right){\mathbf{\text{a}}}_{\alpha }\otimes {\mathbf{\text{a}}}_{\alpha }$ is the push-forward of the symmetric generalized structure tensor of H_α with ${\mathbf{\text{a}}}_{\alpha }={\overline{\mathbf{\text{F}}}}^e{\overline{\mathbf{\text{a}}}}_{\alpha }=J^{e-\frac{1}{3}}{\mathbf{\text{F}}}^e{\overline{\mathbf{\text{a}}}}_{\alpha }$ the fiber vector in the current configuration.

2.6. Constitutive model for growth

Continuing directly from eq. (35), the rate of change of mass dictates the change in the growth tensor F^g. Furthermore, recalling the different types of growth, the rate of change in mass can be directly linked to the evolution of the scalar field ϑ^g. The constitutive equation for the rate of change of this scalar field, ${\dot{\vartheta }}^g$, is often coupled to either mechanical cues, or to biological processes independent of mechanical input [73]. Mechanically-coupled growth is separated into stress-driven [28] or strain-driven [59] approaches,

$${\dot{\vartheta }}^g=k^g\left({\vartheta }^g,{\vartheta }^e\right){\varphi }^g\left({\mathbf{\text{M}}}^e\right)\hspace{0.17em}\text{or}\hspace{0.17em}{\dot{\vartheta }}^g=k^g\left({\vartheta }^g,{\vartheta }^e\right){\varphi }^g\left({\mathbf{\text{F}}}^e\right),$$ (44)

where M^e = C^eS^e is the Mandel stress which is the power conjugate to L^g [74], and φ^g(·) is the growth criterion that activates growth based on whether the stress or strain exceeds a certain threshold. The function k^g(ϑ^g,ϑ^e) dictates the shape of the curve. An overview of different functions for k^g(ϑ^g,ϑ^e) and φ^g(·) are available in the literature [75, 76, 60, 77]. For example, the strain-driven approach from [78] is

$$\begin{gathered} k^g\left({\vartheta }^g\right)=\frac{1}{\tau }{\left(\frac{{\vartheta }^{\max }-{\vartheta }^g}{{\vartheta }^{\max }-1}\right)}^{\gamma }\hspace{0.17em}\text{and} \\ {\varphi }^g\left({\vartheta }^e\right)=\langle {\vartheta }^e-{\vartheta }^{\text{crit}}\rangle =\langle \frac{\vartheta }{{\vartheta }^g}-{\vartheta }^{\text{crit}}\rangle , \end{gathered}$$ (45)

where τ⁻¹ adjusts the adaptation speed, ϑ^max is the upper limit of growth, γ regulates the shape of the growth curve, and ϑ^crit controls the homeostatic state [73]. We have recently proposed a growth rate curve with saturation as the input increases [77]. Using a Hill function to control the growth rate with saturation at increasing ϑ^e we have

$${\dot{\vartheta }}^g=\frac{k{\left({\vartheta }^e-{\vartheta }^{\text{crit}}\right)}^n}{K^n+{\left({\vartheta }^e-{\vartheta }^{\text{crit}}\right)}^n}$$ (46)

with biological parameters k, K, and n [77].

On the other hand, non-mechanically coupled growth is also relevant, for instance during morphogenesis or development. In these situations, the growth rate could be coupled to biological factors or cytokines [79]. Here we do not couple the growth field to other inputs but only deal with prescribed functions of growth as a function of time and location

$${\vartheta }^g=1+R\left(\mathbf{\text{X}},t\right).$$ (47)

2.7. Finite element implementation

The numerical implementation of the examples shown in the following sections was achieved by programming a user subroutine in the nonlinear finite element package Abaqus (Dassault Systems, Waltham, MA), similar to [78].

The global problem of finding the displacements incrementally is left to the Abaqus nonlinear solver. Our user subroutine is used at the integration point level. For each integration point, we keep an internal variable with the value of the growth field ϑ^g at the end of the previous converged step. The integration point subroutine takes in the current total deformation F and updates ϑ^g. For the mechanically-coupled growth problem, ${\vartheta }_{t+\Delta t}^g$ is determined by an implicit Euler backward scheme

$${\text{R}}^g={\vartheta }_{t+\Delta t}^g-{\vartheta }_t^g-{\dot{\vartheta }}^g\left({\mathbf{\text{F}}}^e\right)\Delta t,$$ (48)

where R^g is the residual of the local growth update problem, and ${\vartheta }_{t+\Delta t}^g$ and ${\vartheta }_t^g$ are the growth values at the integration point at the current and previous time steps, respectively. eq. (48) is solved via Newton-Raphson iterations [78]. Once growth has been updated, the elastic deformation is calculated from F^e = FF^g−1, and the corresponding stress is evaluated.

The global Newton-Raphson iterations carried out by the Abaqus solver require the stress tensor and the consistent tangent. Thus, our user subroutine first calculates the fourth order Eulerian tangent c by linearization of the elastic Kirchhoff stress in eqs. (38) or (43) with respect to B^e,

$$\mathbf{\text{c}}=4{\mathbf{\text{B}}}^e\frac{{\partial }^2\mathrm{\Psi }}{\partial {\mathbf{\text{B}}}^e\partial {\mathbf{\text{B}}}^e}{\mathbf{\text{B}}}^e={\mathbf{\text{c}}}^e+{\mathbf{\text{c}}}^g,$$ (49)

where c^e corresponds to the partial derivative when F^g is held constant, and it corresponds to the usual elastic constitutive moduli. In contrast, c^g is the derivative at constant F. For the non-mechanically coupled growth problem defined in eq. (47), ϑ^g is a function of the reference position and time only, and c^g = 0. For an overview of the specific form of c^g for different growth formulations, the reader is referred to [80].

The tangent c is further modified to obtain the tangent corresponding to the Jaumann stress rate used in Abaqus: ${\mathbf{\text{c}}}^{\text{abaqus}}=\left(\mathbf{\text{c}}+\frac{1}{2}\left(\tau \overline{\otimes }\mathbf{\text{i}}+\mathbf{\text{i}}\overline{\otimes }\tau \text{+}\tau \underset{\_}{\otimes }\mathbf{\text{i}}+\mathbf{\text{i}}\underset{\_}{\otimes }\tau \right)\right)/J$. The user subroutine allows us to solve for the evolving deformation of the growing body. During postprocessing, we use the shape functions to interpolate F^g and calculate the geometric incompatibility tensor G as defined in eq. (10). Code for the different examples is also attached as part of this submission.

3. Results

We first quantify the incompatibility in four illustrative examples in which the growth field is entirely prescribed, i.e., it is not coupled to any mechanical input. The growth fields for these examples are summarized in Table 1. The examples are chosen to show the features of each type of growth and also the consequences of seeing different characteristics for the gradients of growth across the body. For each of these cases we compute the metrics of incompatibility defined in the Methods section, and show the corresponding residual stress when no other external forces are applied to the body. Next, we turn our attention to mechanically-coupled growth examples which correspond to relevant biomedical applications. The first of these examples is brain atrophy which involves volume growth. The second is skin expansion where area growth is considered. The last example is cortical folding of the brain with fiber growth based on axonal orientation.

Table 1:

Kinematics of growth for non-mechanically coupled examples

Growth type	Growth tensor	Growth indicator
Isotropic volume growth (unidirectional field)	${\mathbf{\text{F}}}^g=\sqrt[3]{{\vartheta }^g}\mathbf{\text{I}}$	${\vartheta }^g=1+\frac{1}{4}{X}_{1}t$
Isotropic volume growth (multi-directional field)	${\mathbf{\text{F}}}^g=\sqrt[3]{{\vartheta }^g}\mathbf{\text{I}}$	${\vartheta }^g=1+\frac{1}{4}f\left(R\right)t$, $\hspace{0.17em}R=\sqrt{X_1^2+X_2^2+X_3^2}$
Area growth	${\mathbf{\text{F}}}^g=\sqrt{{\vartheta }^g}\mathbf{\text{I}}+\left(1-\sqrt{{\vartheta }^g}\right){\mathbf{\text{N}}}_0\otimes {\mathbf{\text{N}}}_0$	${\vartheta }^g=1+\frac{1}{4}f\left(R\right)t$, $R=\sqrt{X_1^2+X_2^2}$
Fiber growth	${\mathbf{\text{F}}}^g=\mathbf{\text{I}}+\left({\vartheta }^g-1\right){\mathbf{\text{f}}}_0\otimes {\mathbf{\text{f}}}_0$	${\vartheta }^g=1+\frac{1}{4}{X}_{2}t$

3.1. Isotropic volume growth driven by a unidirectional field

We start with the simplest example for non-mechanically coupled isotropic volume growth. The domain is a 1 × 1 × 1 mm³ cube discretized with 1,000 C3D8 elements. The growth variable ϑ^g is prescribed as a function of time and space

$${\vartheta }^g:=1+\frac{1}{4}{X}_{1}t,$$ (50)

with time t ∈ [0,1]. This function leads to a 25% volume increase across the domain (Fig. 1a). The growth field is non-uniform, showing a non-zero gradient in the direction of the X₁ coordinate. The rationale for this field is to isolate a simple pattern of growth that can be caused by a morphogen gradient for example.

Figure 1:

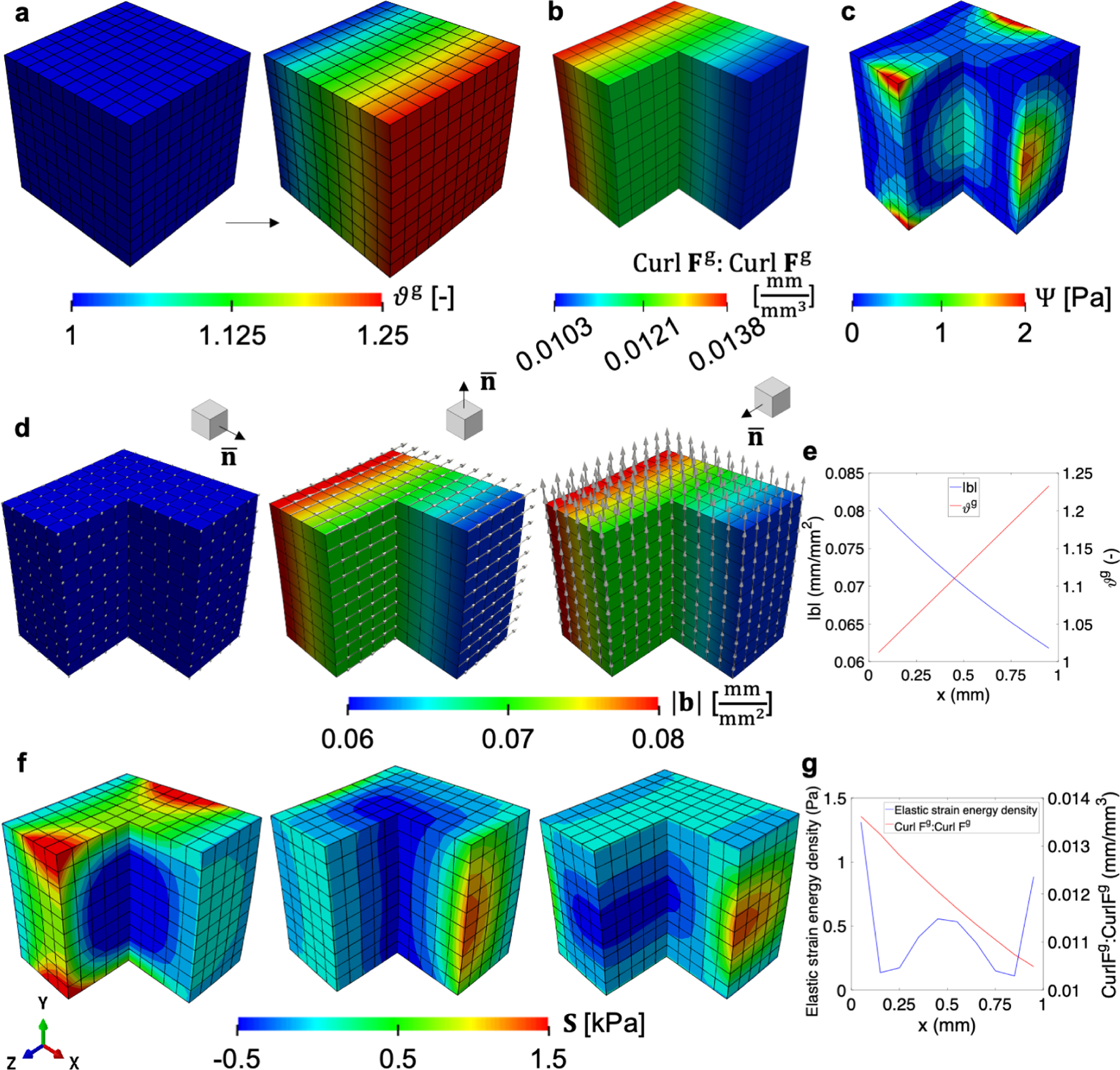
Isotropic growth guided by a unidirectional field. Finite element model of a simple cube deforms in response to a linear growth field, ϑ^g, with respect to the X₁ direction (a). Based on this growth field, the invariant of the incompatibility tensor Curl F^g : Curl F^g is obtained (b). There are only six constraints to prevent rigid body motion, but elastic free energy accumulates across the domain due to the incompatibility of the growth field (c). The local Burgers vector density b is derived with respect to the standard basis in 3D Euclidean space, $\overline{\mathbf{\text{n}}}\left(\text{d}\right)$. The arrows in (d) are scaled relative to the magnitude of |b|. For $\overline{\mathbf{\text{n}}}$ along the X₁ direction, there is no incompatibility. For the other two directions, b lies on the plane defined by $\overline{\mathbf{\text{n}}}$ and orthogonal to the growth direction. The magnitude of |b| shows an inverse trend compared to the growth value ϑ^g (e). The components of second Piola-Kirchhoff stress, S₃₃ and S₂₂, are matched with the local Burgers vector direction in (d) respectively when $\overline{\mathbf{\text{n}}}$ is not X₁ direction (second and third in f), while S₁₁ is plotted when there is no local Burgers vector (first in f). The free energy density and the invariant Curl F^g : Curl F^g are also plotted (g), showing that while incompatibility decreases along X₁, the strain energy is highest at the boundary, with another local maximum at the center of the domain.

The finite element model has 1,331 nodes and we constrain only three translations and three rotations in order to allow free deformation except for rigid body motions. Zero-traction natural boundary conditions are applied on all six boundary surfaces. For the material behavior we consider the neo-Hookean hyperelastic potential introduced before, with µ = 0.55 MPa [77] and the initial compressibility ν = 0.4. Upon growth, the cube deforms solely due to growth into the configuration depicted in Fig. 1a. The contour plot in this panel is the growth variable ϑ^g, showing the desired gradient along X₁.

The amount of incompatibility can be boiled down to the single invariant Curl F^g : Curl F^g, which is motivated by similar scalar fields in gradient plasticity related to energy stored as a consequence of crystal defects [35, 36]. While in our case the scalar field does not correspond to an energy quantity, it is an invariant field which overall relates to the degree of incompatibility and is therefore useful to visualize. The scalar Curl F^g : Curl F^g changes in the same direction of the gradient of ϑ^g (Fig. 1b), which matches the intuition that incompatibility is related to mismatch between adjacent differential volumes with different growth. Note, however, that even though the gradient of the volume change is constant, the incompatibility metric is not. This occurs because even though the volume growth increases linearly with X₁, the growth tensor is actually not a linear function of ${\vartheta }^g$. To achieve volume growth of ϑ^g, a differential volume element has to grow $\sqrt[3]{{\vartheta }^g}$ in all directions.

The local Burgers vector density b can be calculated for any plane in the intermediate configuration. We choose the standard basis in 3D Euclidean space as the normals of interest, e.g., $\overline{\mathbf{\text{n}}}={\mathbf{\text{F}}}^g{\mathbf{\text{e}}}_1/\left|{\mathbf{\text{F}}}^g{\mathbf{\text{e}}}_1\right|$ and so on for the other two directions (Fig. 1d). For the plane corresponding to the growth gradient, $\overline{\mathbf{\text{n}}}={\mathbf{\text{F}}}^g{\mathbf{\text{e}}}_1/\left|{\mathbf{\text{F}}}^g{\mathbf{\text{e}}}_1\right|$, the Burgers vector vanishes. This occurs because on the plane orthogonal to the growth gradient, growth is uniform and therefore compatible. This follows directly from the definition of Curl F^g in eq. (15). The local Burgers vector density in the other two planes is restricted to the corresponding plane. This was noted in the derivation of G for the different growth types. In the case of isotropic growth fields it is always true that ${\overline{\mathbf{\text{n}}}}^{\top }\text{G}\overline{\mathbf{\text{n}}}=0$ for any normal $\overline{\mathbf{\text{n}}}$. In this example it also becomes evident that b is orthogonal to the growth gradient. The magnitude of the local Burgers vector density |b| is also not constant over the domain (Fig. 1e). Instead, maybe albeit surprisingly, the magnitude is greater in the region with least growth, and decreases as growth increases. This can be explained by the fact that G is scaled by the determinant of the permanent volume change. Even though on one end of the cube the growth is small, the relative difference in adjacent volume elements is greater in these regions compared to the relative mismatch in size between adjacent volume elements that have undergone more substantial growth.

To visualize the consequences of nonuniform growth on the development of residual stress, the second Piola-Kirchhoff stress tensor S is represented along each of the b directions in Fig. 1d and the result is depicted in Fig. 1f. For the first panel of Fig. 1f, since the Burgers vector is not defined, we showed the first component of the second Piola-Kirchhoff stress S₁₁. There are residual stresses in all three directions. The magnitude of the stress is not necessarily aligned with the magnitude of the local Burgers vector density. To get a better understanding of how the elastic deformation is distributed, Fig. 1c shows the contours of the elastic strain energy, and Fig. 1g compares the elastic strain energy against the scalar invariant of incompatibility Curl F^g : Curl F^g.

The mechanical equilibrium problem that gives rise to F^e is not trivial. Even when no external forces are considered and the only driver for F^e is the incompatibility of F^g, the elastic deformation F^e also has to minimize Ψ (which is a nonlinear function of F^e), and satisfy the vanishing of the normal stress at the boundaries. As a result, even though the geometry of the incompatibility has the elegant and simple features expected based on the analytical derivation (16), the stress field is more intricate. Take the first component of the second Piola-Kirchhoff stress S₁₁ shown in the first column of Fig. 1f. The stress on the faces with normal e₁ or −e₁ have zero stress, as required. Along the other two directions, the stress goes from tension at the boundary to compression at the center. Similar trends are observed for the other two components, S₃₃ and S₂₂ (second and third columns of Fig. 1f).

3.2. Examples for isotropic volume growth driven by a multi-directional vector field

In the second example we consider a half sphere with radius R₀ = 1 mm discretized with 1,920 C3D8 elements and 2,300 nodes. Material properties, boundary conditions, and the range of ϑ^g are the same as in the previous example, but in this case we consider radial growth as stated in Table 1. The amount of growth is a monotonically increasing function of the variable $R=\sqrt{X_1^2+X_2^2+X_3^3}$. This example is motivated by evidence that tumors grow more at the outer layers which have more access to nutrients compared to the core of the tumor which may even be necrotic [52]. In the simplest case, we consider once again the linear increase in growth rate ${\dot{\vartheta }}^g=\frac{1}{4}R$. However, we also consider other functions of ϑ^g(R) that are nonlinear, either concave or convex (Fig. 2f). These functions are not necessarily motivated by biological phenomena, rather, they are chosen to showcase the effect of non-constant gradients of growth on the resulting incompatibility metrics. In particular, Fig. 2a shows two different growth fields; in one case growth increases slowly near the core and more rapidly near the outer surface, while in the other case we have a very rapidly increasing growth near the core compared to near the outer surface.

Figure 2:

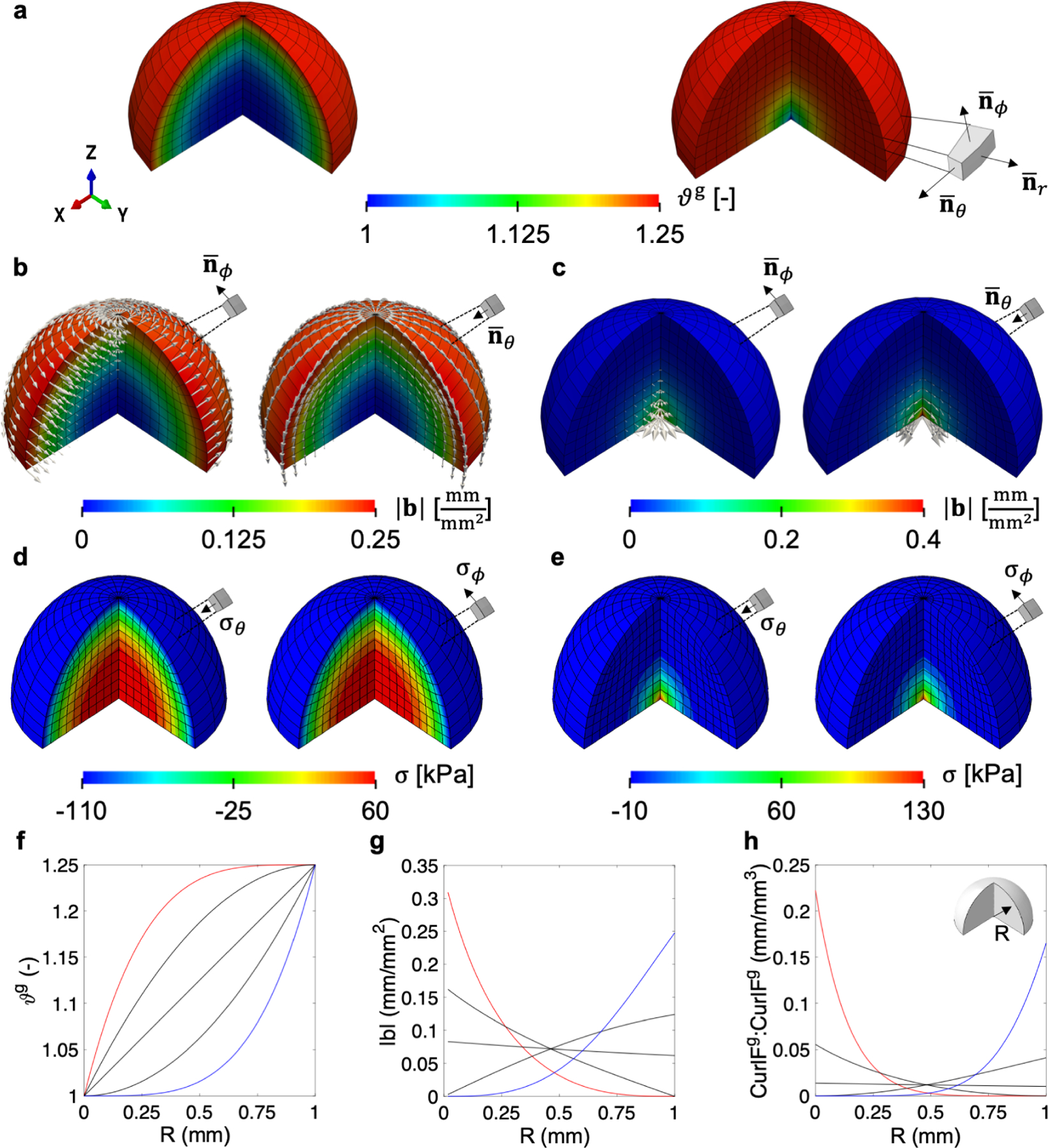
Isotropic volume growth guided by a multi-directional field with different growth distributions: an increasing gradient of ϑ^g from the inner core to the outer shell (a, left) and a case in which ϑ^g increases rapidly at the core and slowly at the outer layers (a, right). The local Burgers vector density is computed for each of the two cases and for planes defined by the spherical basis vector corresponding to meridional and circumferential directions ${\overline{\mathbf{\text{n}}}}_{\varphi }$ and ${\overline{\mathbf{\text{n}}}}_{\theta }$. (b, c) The Burgers vector vanishes for planes defined by the radial direction ${\overline{\mathbf{\text{n}}}}_r$ and are thus not shown. Stress components aligned with the direction of the Burgers vectors show similar trends to the degree of incompatibility for the two cases considered (d, e). The growth fields considered, in addition to the two cases illustrated in the top panels, are shown in f, were the blue curve is the case shown in the left column of a, and the red curve is the right column of a. The magnitude of the local Burgers vector density |b| is greater for higher growth gradients, but also greater for smaller growth values (g). The scalar metric Curl F^g : Curl F^g shows the same trends as the magnitude of the local Burgers vector density (h).

To analyze the incompatibility we focus on the spherical basis vector field ${\overline{\mathbf{\text{n}}}}_r$, ${\overline{\mathbf{\text{n}}}}_{\varphi }$ and ${\overline{\mathbf{\text{n}}}}_{\theta }$, called radial, meridional, and circumferential respectively. As can be expected based on the previous example and the derivation for Curl F^g in eq. (15), the local Burgers vector density vanishes for the planes defined by the growth gradient ${\overline{\mathbf{\text{n}}}}_r$. The growth is uniform within each concentric spherical shell forming the tumor and there is no incompatibility in the infinitesimal area elements making up these spherical shells. Incompatibility arises from the mismatch in growth between different concentric layers of the tumor. The local Burgers vector density b is shown for the other two directions of interest in Fig. 2b and c. When the plane of interest for the characterization of the Burgers vector is defined by the normal ${\overline{\mathbf{\text{n}}}}_{\varphi }\mathbf{\text{b}}$ is circumferential. For ${\overline{\mathbf{\text{n}}}}_{\varphi }$, the Burgers vector b is meridional. This observation, again, aligns with the remarks of the previous example and with the derivation of G in eq. (16).

The nonlinearity of the growth rate translates to the degree of incompatibility. In particular, the magnitude of the local Burgers vector density |b| is proportional to the magnitude of the growth gradient. Note that if the growth increases rapidly at the core compared to the outer region, the magnitude of the local Burgers vector density is higher at the core and decreases toward the outer layers as the growth gradient decreases (red curve in Fig. 2g). In contrast, when the growth shows an increasing gradient with respect to R, |b| increases with respect to R as well. Compare this to the case in which growth rate is constant across the tissue. In such case, there is still a small variation in b as a function of R because, as discussed before, the magnitude of growth also contributes to b and not just the magnitude of the growth gradient. However, the scaling of b by the growth amount is barely noticeable when compared to the effect of the nonlinear functions ϑ^g(R) with large gradients |∇₀ϑ^g| relative to the growth ϑ^g.

Residual stresses in the absence of any traction or body force align with the incompatibility as characterized by the local Burgers vector density. For instance, for the case in which growth is slower at the core compared to the outside, the circumferential and meridional components of the Cauchy stress tensor (Fig. 2d) show radial patterns aligned with the features of the b field in Fig. 2d. Similarly, residual stresses follow the observations of the local Burgers vector density for the case in which growth is faster at the core compared to the periphery (Fig. 2e). In either case, there is a transition from tension to compression along the radial direction, which has also been shown in [52].

To reduce the incompatibility characterization to a single invariant scalar field, we once again opt for Curl F^g : Curl F^g, plotted with respect to R in Fig. 2h. The trends are similar to what happens with the local Burgers vector density: higher gradients of growth lead to higher incompatibility in general, while for the same gradient higher growth leads to less incompatibility. When compared to the previous example, it is obvious that the same amount of overall growth produced by some field ϑ^g can lead to very different residual stresses depending on the gradient ∇₀ϑ^g.

3.3. Examples for transverse isotropic area growth

Thin biological membranes and epithelial tissues also undergo growth and remodeling during development and in response to environmental cues [81]. For instance, skin grows in development, in response to our body weight, and in pregnancy [82]. The knowledge that skin responds to stretch by growing has been leveraged for the clinical application of tissue expansion [83]. Computational models of skin growth within the volumetric growth framework have been shown to accurately capture the clinical scenario using a transversely isotropic in-plane area growth [59]. Before we consider a more realistic problem, we first explore the case of a disc with prescribed area growth

$${\vartheta }^g:=1+\frac{1}{4}Rt,$$ (51)

where $R=\sqrt{X_1^2+X_2^2}$ is the radial coordinate on the plane and t ∈ [0,1] is time. The corresponding growth tensor F^g for area growth is given eq. (18), and in this case the normal is simply N₀ = e₃. We partition a flat disc of radius R₀ = 1 mm and height h = 0.5 mm into 2,080 C3D8 elements and 2,808 nodes (Fig. 3). The growth contour ϑ^g is shown in (Fig. 3a). The boundary conditions, time for the simulation, and resulting range of the growth indicator ϑ^g are the same as in the previous two examples, but the constitutive model is now different. For this problem we consider the anisotropic GOH model.

Figure 3:

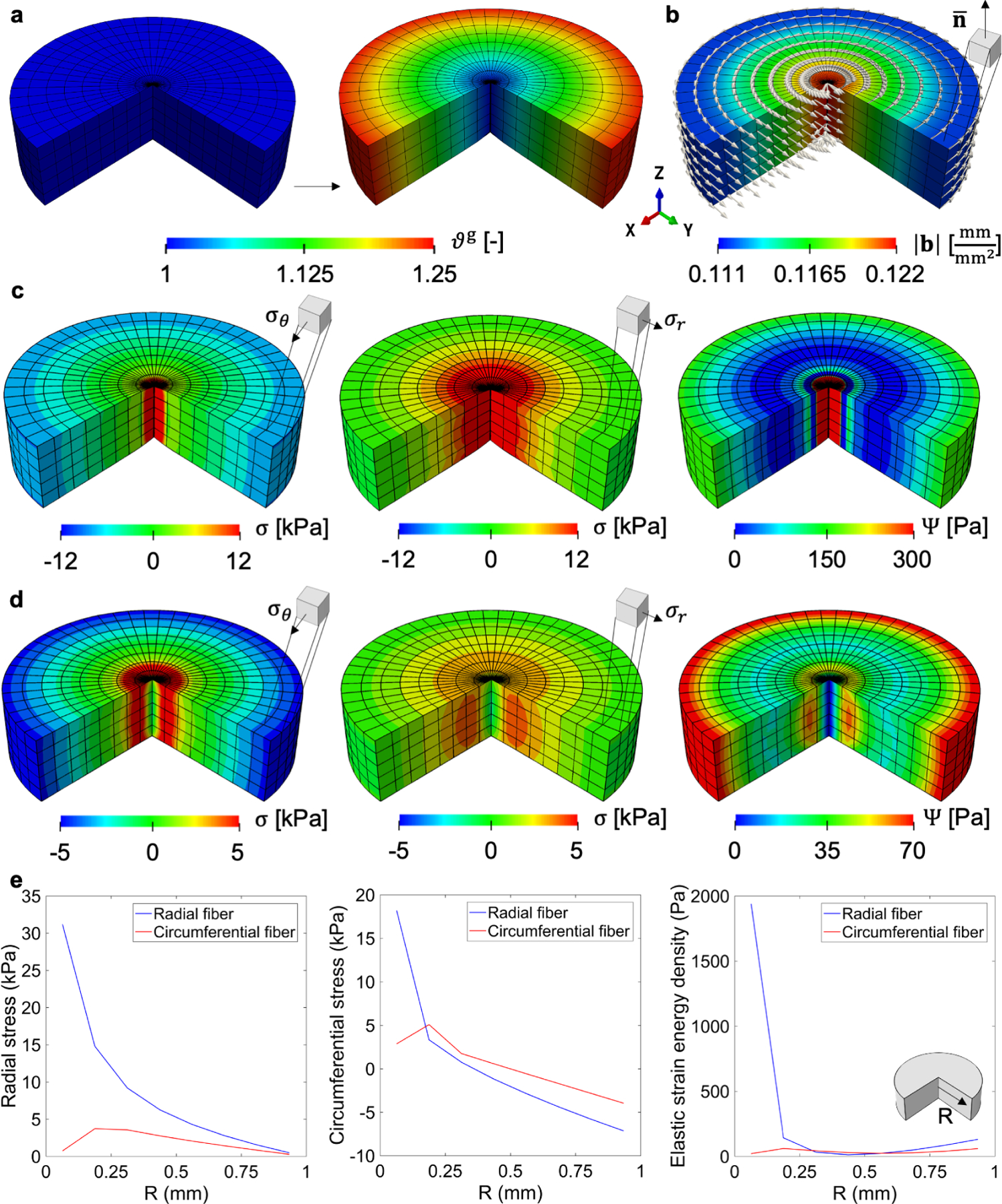
In-plane area growth: A flat disc grows in area driven by the linearly varying growth field ϑ^g along the radial direction (a). Even though the material is anisotropic, the amount of incompatibility is independent of the material behavior. The local Burgers vector density for the plane, defined by e₃ is aligned circumferentially (b). Residual stress, however, do depend on whether the direction of anisotropy is radial (c) or circumferential (d). The patterns in the elastic deformation are similar in both cases, with the circumferential component of the stress going from tension to compression from the center to the boundary of the disc. In contrast, the radial component of the stress has to satisfy a traction free boundary condition, and the stress decreases from the center to the periphery. Because the Gasser-Ogden-Holzapfel model leads to increasing stress when fibers are in tension, the overall stresses from radially aligned fibers are larger compared to circumferential fibers. Plots of σ_r, σ_θ, and Ψ with respect to R are shown in (e).

Two kinds of fiber orientation are considered, radial and circumferential. With this example we want to further illustrate that the development of residual stress is linked to both the need for an incompatible F^e that balances out the incompatibility introduced by F^g, as well the mechanical equilibrium problem, which depends on the specific constitutive model. The geometric incompatibility tensor G does not depend on the material model being used, but only on the growth field F^g. There is an alternative derivation for the geometric incompatibility tensor G in terms of the elastic deformation alone F^e (see eq. (12)), but the two are equivalent. Thus, even when G is computed from F^e, it is still independent of the mechanical equilibrium problem and the choice of material model. For our example, we compute the local Burgers vector density and observe that it is circumferentially aligned on the plane (Fig. 3b). This circumferential alignment is indeed what we expected based on the derivation for b for area growth in eq. (22).

Even though the growth field and incompatibility metrics remain the same, the residual stresses change if the GOH material is considered with a radial fiber family (Fig. 3c) or circumferential fiber family (Fig. 3d). We report the circumferential stress σ_θ, radial stress σ_r, and free energy density Ψ. When the fiber is radially distributed, stress along fiber direction is higher than the stress in the circumferential direction (Fig. 3c). The radial component of the stress is in tension and the stress is higher at the center compared to the periphery of the disk, where it vanishes because of the boundary condition. The circumferential direction follows a more similar pattern compared to the previous cases, with tension at the center and gradually transitioning to compression at the outer layers just as in the simple tumor example. If the fiber orientation is circumferential, the trends in the stress are similar but overall the stresses and strain energy are lower, particularly due to the lack of fibers in tension in the radial direction (Fig. 3d).

The residual stress patterns follow the geometric constraints of the entire body. Clearly, the outer boundary of the disk has to satisfy a zero normal stress component, and in consequence the stress in the radial direction decreases from the center to the periphery. While the pattern of deformation is similar in both cases, when the fibers are aligned radially they contribute to higher stress. For the circumferential component, the elastic deformation is similar to the previous example, with a transition from tension to compression [52]. For clarity, plots of σ_r, σ_θ, and Ψ with respect to the radial direction are shown in Fig. 3e.

3.4. Examples for uniaxial fiber growth

Anisotropy arising from fibrous microstructures is a key feature of biological materials. This is not only important for the mechanical behavior of tissues, as seen in the previous example, but also for the way they grow and remodel. For example, tissues such as muscle grow preferentially in the fiber direction [61]. Computational models of muscle growth within the finite volume growth framework have accurately captured the observations that muscles adapt to mechanical cues by growing or shrinking in length [62]. For this example we consider a cylindrical domain with cross sectional area π/4mm² and length 1 mm discretized with 960 C3D8 elements and 1,243 nodes (Fig. 4a). Only the minimum set of essential boundary conditions that prevent rigid body motion are imposed. The fiber direction in the domain is constant and aligned with the basis vector f₀ = e₁. We restrict our attention to the neo-Hookean hyperelastic potential. The prescribed growth field is

$${\vartheta }^g:=1+\frac{1}{4}{X}_{2}t.$$ (52)

Figure 4:

Fiber growth with linear field ϑ^g is modeled in a cylinder-shaped finite element model. The reference and current configurations are shown (a). The associated local Burgers vector density is calculated on the plane normal to $\overline{\mathbf{\text{n}}}={\mathbf{\text{e}}}_3$ (b). The body undergoes pure bending. The stress, however, is zero everywhere as reflected in the strain energy contour (d). In fact, the elastic deformation is a pure rotation field around e₃ (c). The scalar invariant of incompatibility Curl F^g : Curl F^g is constant and nonzero over the domain (e).

The resulting growth as time progresses in the simulation, t ∈ [0,1], is a 25% increase in length at the top of the fiber with no growth at the bottom of the fiber (Fig. 4a). Note that the gradient of growth is in the direction e₂, orthogonal with respect to the fiber direction, but keep in mind that growth actually occurs along the fiber direction. Our choice for this growth field directly follows the derivation of the geometric incompatibility tensor G for fiber growth, where we show that the magnitude of the local Burgers vector density |b| is greatest when the growth gradient is orthogonal to the fiber direction. The associated local Burgers vector density corresponding to the plane e₃ is shown in Fig. 4b. The local Burgers vector density b shows a small variation from greater values at the bottom of the fiber to smaller values at the top. This inverse trend with respect to the growth variable is the same feature from the previous examples and it is due to the scaling of the geometric incompatibility tensor by the Jacobian ϑ^g (see eq. (27)). The Burgers vector is aligned with the fiber direction as expected based on eq. (27).

In contrast to previous examples, in this case the residual stress is zero everywhere in the domain. Instead of showing the residual stress contour, we show the free energy density (Fig. 4d), and the scalar invariant of incompatibility Curl F^g : Curl F^g (Fig. 4e). Note that there is incompatibility induced by the growth field, and that the cylinder deforms due to the prescribed growth. Yet, there is no residual stress. Recall that the elastic deformation tensor should counteract the incompatibility introduced by F^g. However, the polar decomposition of F^e in eq. (4) reveals that a pure rotation field could be able to get a globally compatible F with no stress. This is in fact what is happening here. In matrix form, using the Cartesian basis, the growth tensor is

$${\mathbf{\text{F}}}^g=\left[\begin{array}{ccc}1+a{X}_2& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right],$$ (53)

for some non-zero value a. This growth field is incompatible as illustrated in Fig. 4b and e. We propose that the elastic deformation can be a rotation F^e = R^e. We suggest this solution expressed in matrix form

$${\mathbf{\text{F}}}^e=\left[\begin{array}{ccc}\cos \theta & \sin \theta & 0\\ -\sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right].$$ (54)

This rotation should be such that the total deformation F = F^gF^e is compatible. The total deformation gradient is

$$\mathbf{\text{F}}=\left[\begin{array}{ccc}\left(1+a{X}_2\right)\cos \theta & \sin \theta & 0\\ -\left(1+a{X}_2\right)\sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right].$$ (55)

To show that this is the case, all we need to do is to show that there is a vector field whose gradient leads to eq. (55). Consider the deformation map

$$\phi =\left(X_2\sin \left(a{X}_1\right)+\frac{1}{a}\sin \left(a{X}_1\right),X_2\cos \left(a{X}_1\right)+\frac{1}{a}\cos \left(a{X}_1\right),X_3\right).$$ (56)

The deformation gradient F in eq. (55) is actually the gradient of the map ϕ in eq. (56), with θ = aX₁. Furthermore, this has to be the solution of the problem since, by reducing to a rotation, F^e leads to zero stress while also satisfying mechanical equilibrium. Numerically, Fig. 4c shows that the elastic deformation F^e from our finite element solution is actually a pure rotation around e₃ that varies along X₁ as expected.

3.5. Brain atrophy

Commonly, the idea of tissue growth is associated with an increase in mass; however, as noted after introducing eq. (3), volume loss can also be considered, as in the case of tissue atrophy. A representative example is atrophy and shrinkage of the brain as a result of amyloid-β accumulation and tau protein malfunction [84]. Coupled to a nonlinear reaction-diffusion model that captures the propagation of the misfolded proteins in pyron-like diseases, brain volume loss has been modeled with a nonlinear finite element model [85, 55]. Here, we look into the incompatibility and residual stress that arise from the heterogeneous growth patterns associated with reaction-diffusion coupling. For the reader interested in details on the theory, finite element implementation, and simulations for the coupled reaction-diffusion model of brain atrophy please consult [85, 55].

One of the main features of the models in [85, 55] is the relative shrinkage rate between gray and white matter tissues. Gray matter undergoes faster volume loss than white matter [56]. From the mismatch in the growth field at the boundary between gray and white matter it is expected that residual stresses will arise.

We start by depicting the two configurations of the brain: the reference, healthy geometry; and the shrunken, atrophied configuration (Fig. 5a). The maximum volume loss is about 30%. The corresponding residual stresses from growth are heterogeneously distributed in the brain (Fig. 5b). To improve visualization, slices with normals given by the standard basis in 3D Euclidean space are presented (Fig. 5c–e).

Figure 5:

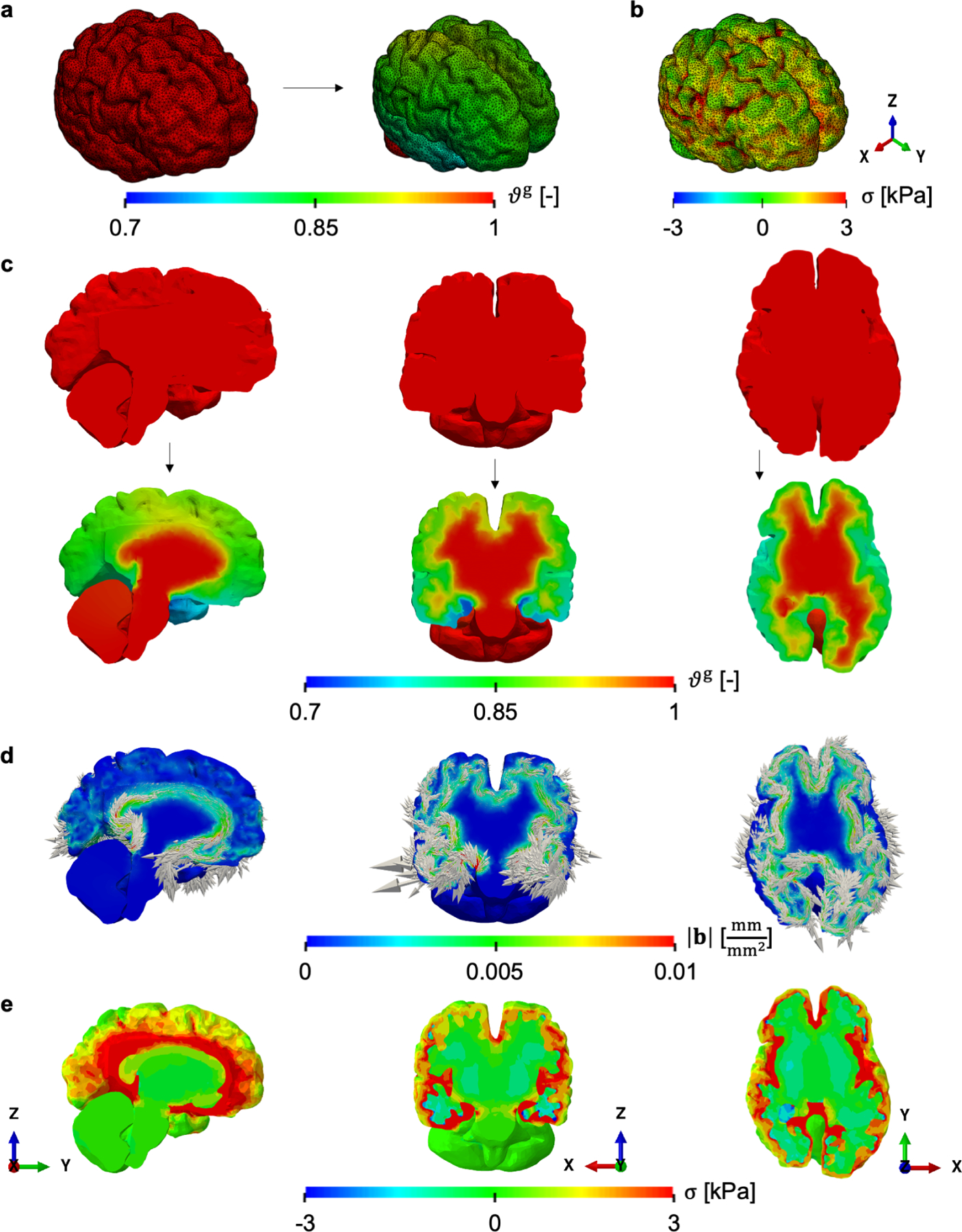
Isotropic volume shrinkage or negative growth caused by diffusion-reaction of misfolded proteins in the human brain: Growth field ϑ^g in the reference and current configuration (a) and the maximum principal stress field seen on the outer surface of the brain (b). Representative cross-sections in the sagittal, coronal, and axial direction (left to right column in c-e) show that the inner white matter undergoes almost no shrinkage while the outer gray matter has up to 30% volume loss (c). The local Burgers vector density can be calculated solely based on the growth field, showing greater incompatibility at the interface between gray and white matter because of the higher growth gradients (d). The Burgers vectors are in the plane and aligned with the interface between the two types of brain tissue (d). Maximum principal stress on the sections of interest reflects the incompatibility characterization, with greater stress at the interface between gray and white matter (e).

It can be observed from the different cross sections that atrophy takes place mostly on the outer gray matter while the inner white matter has almost no volume loss (Fig. 5c). As a result, sharp growth gradients are expected near the interface of these two tissues. Indeed, after computing the geometric incompatibility tensor G and the corresponding local Burgers vector density b for each of the planes of interest, we can observe that the degree of incompatibility characterized by the magnitude |b| is concentrated near the interface (Fig. 5d). The maximum principal stress visualized on the same planes aligns with the geometric measure of the incompatibility (Fig. 5e). Similar to |b|, stress σ localizes at the interface between gray and white matter and decreases towards the outer brain surface. Thus, in this case, the characterization of the necessary geometric incompatibility based solely on the growth field provides useful intuition regarding the resulting stress field.

3.6. Area growth induced by skin expansion

As mentioned already, skin adapts to mechanical cues via transversely isotropic growth and remodeling [86]. This knowledge has been leveraged in the clinical setting to gain skin for reconstructive purposed in tissue expansion [87, 58]. In this technique, a balloon-like device is implanted subcutaneously and dilated over a period of months to stretch skin supra-physiologically and trigger its growth [88]. Previous work by our group has resulted in computational models of skin expansion [59] as well as a porcine experimental model to better understand skin mechanobiology [89]. Some of our experimental work revealed the existence of a complex residual strain field even after releasing the skin from external loads and constraints [12]. Here we start from the model of tissue expansion that we have previously developed and quantify the geometric incompatibility tensor for representative examples.

We create finite element models of 10 × 10 cm² skin patches with thickness h = 0.3 cm discretized with 3,200 C3D8 elements and 5,043 nodes. Four different expander geometries are considered: rectangle-, circle-, square-, and crescent-shaped (Fig. 6a). The expanders are inflated to 50 cc and this volume is maintained for 7 days before deflation, analogous to an individual inflation step in the clinical setting [89]. For these simulations, the neo-Hookean model of our previous work is considered [77]. The constitutive model for growth is the one introduced in eq. (46).

Figure 6:

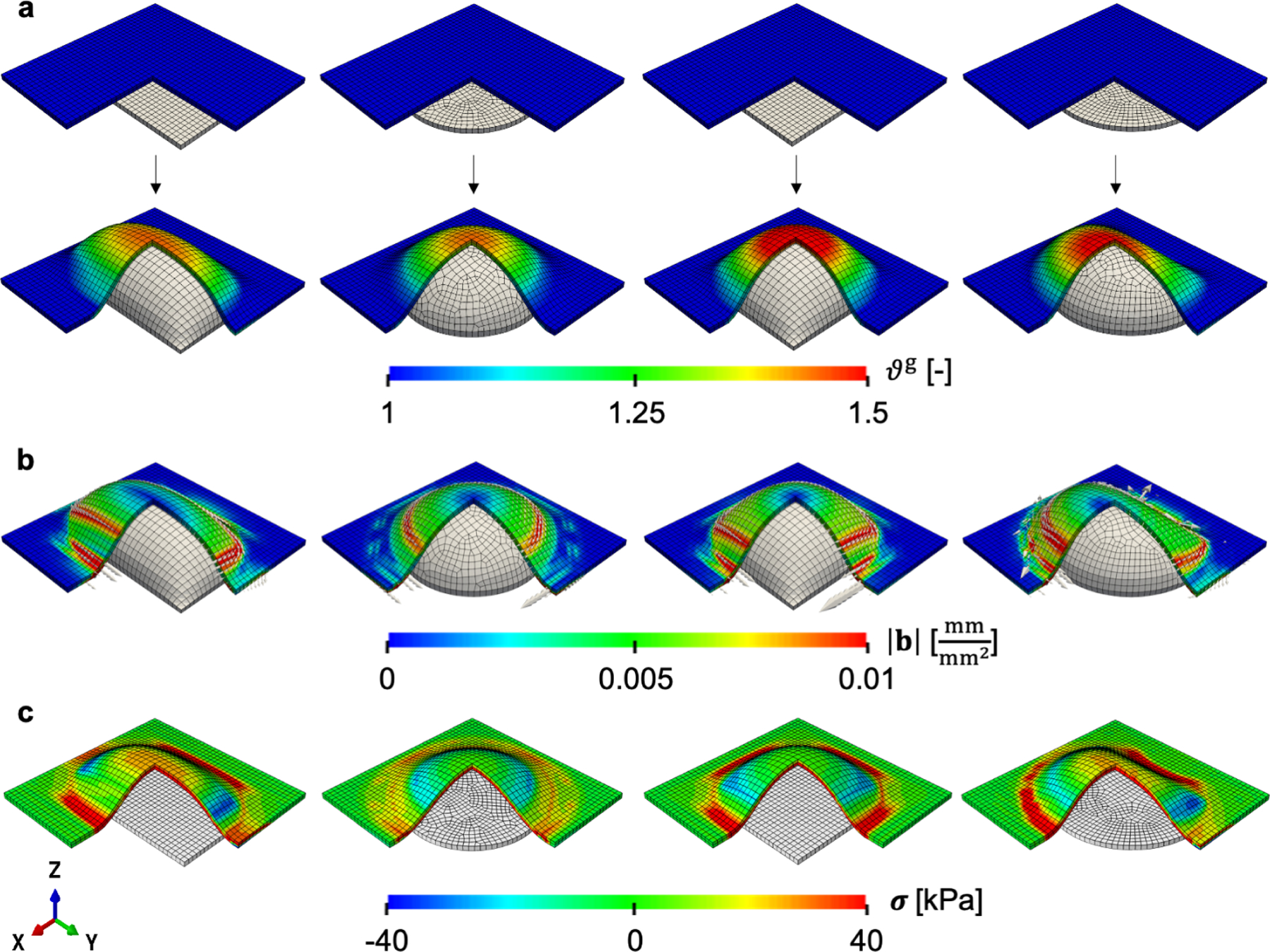
Area growth in tissue expansion: growth ϑ^g following inflation with four different expander geometries (rectangle-, circle-, square-, and crescent-shaped) shows greatest area increase at the apex compared to the periphery (a). The local Burgers vector density and its magnitude on the skin plane determined by the surface normal shows larger magnitude in regions of higher growth gradients (b). The corresponding residual stress contours from maximum principal stress also shows similar features (c).

Inflating the expanders to 50 cc induces area growth up to 50% with respect to the original area (Fig. 6a). The area increase depends on the shape of the expander. The square expander results in the largest area growth and the circular expander yields the smallest growth. In all cases, the growth field is characterized by greater area gains at the apex of the expander and gradually less toward the periphery of the expanded region. The local Burgers vector density b is calculated based on the growth field on the plane normal to $\overline{\mathbf{\text{n}}}={\mathbf{\text{e}}}_3$ (Fig. 6b). Similar to the previous example and due to the fact that the geometric incompatibility tensor G is directly linked to the gradient of ϑ^g, the magnitude of the local Burgers vector density |b| is generally greater in regions of steep growth gradient. There are other factors at play, such as the total growth as discussed in the first three examples. |b| is greater right at the base of the expander, where there is a rapid transition between regions that are not stretched and not growing to regions being affected by the expander. Another region of high growth gradient is due to the contact and the shape of the expander. The apex has the largest growth ϑ^g, but it is actually free of incompatibility. After deflation, we observe that the maximum principal stress shows similar features compared to the incompatibility metrics (Fig. 6c). Tension of about 40 kPa occurs at the base, with regions of 40 kPa compression at the zones of contact between expander and skin, which also have large incompatibility in terms of |b|.

3.7. Axon growth in brain development

The exact mechanisms of cortical folding in the brain are not yet fully understood. However, abnormal folding is associated with impaired brain function and psychological diseases [64]. Some of the theories that have been proposed to explain brain folding include the differential growth between different brain regions due to both mechanical and biological cues. Finite element and theoretical models have been developed to improve our understanding of cortical folding [64, 90]. In particular, the essential model of cortical folding is that of a bi-layered system coupled to the finite volume growth theory.

We start from the finite element model proposed in [64] which considers the role of axon orientation on the resulting instabilities of the bi-layered system. The growth tensor is that introduced in eq. (23) for fiber growth. The rectangular domain of 3 × 1 cm² with thickness 0.05 cm is discretized into 6,000 C3D8 elements and 12,462 nodes. The top layer, gray matter (cortex), has thickness of 0.05 cm, while the lower region in the domain is the white matter (subcortex). Three different axon orientations f₀ in the subcortex in the reference configuration are considered: curved outward, concentric, and straight (Fig. 7a). The cortex is allowed to grow only in the e₁ direction. Although not relevant for the incompatibility characterization, for the buckling instability patterns we note that there is a difference in the shear modulus between the cortex and subcortex µ_gray/µ_white = 3. The growth rate between the two layers also differs, with ${\dot{\vartheta }}_{\text{cortex}}^g/{\vartheta }_{\text{axon}}^g=0.1$. We simulate a time of 75 days, fixing ${\dot{\vartheta }}_{\text{.cortex}}^g$ to 0.008/hour. The growth field ${\vartheta }_{\text{cortex}}^g$ is not mechanically coupled, while the axon growth in the subcortex is stretch driven [64].

Figure 7:

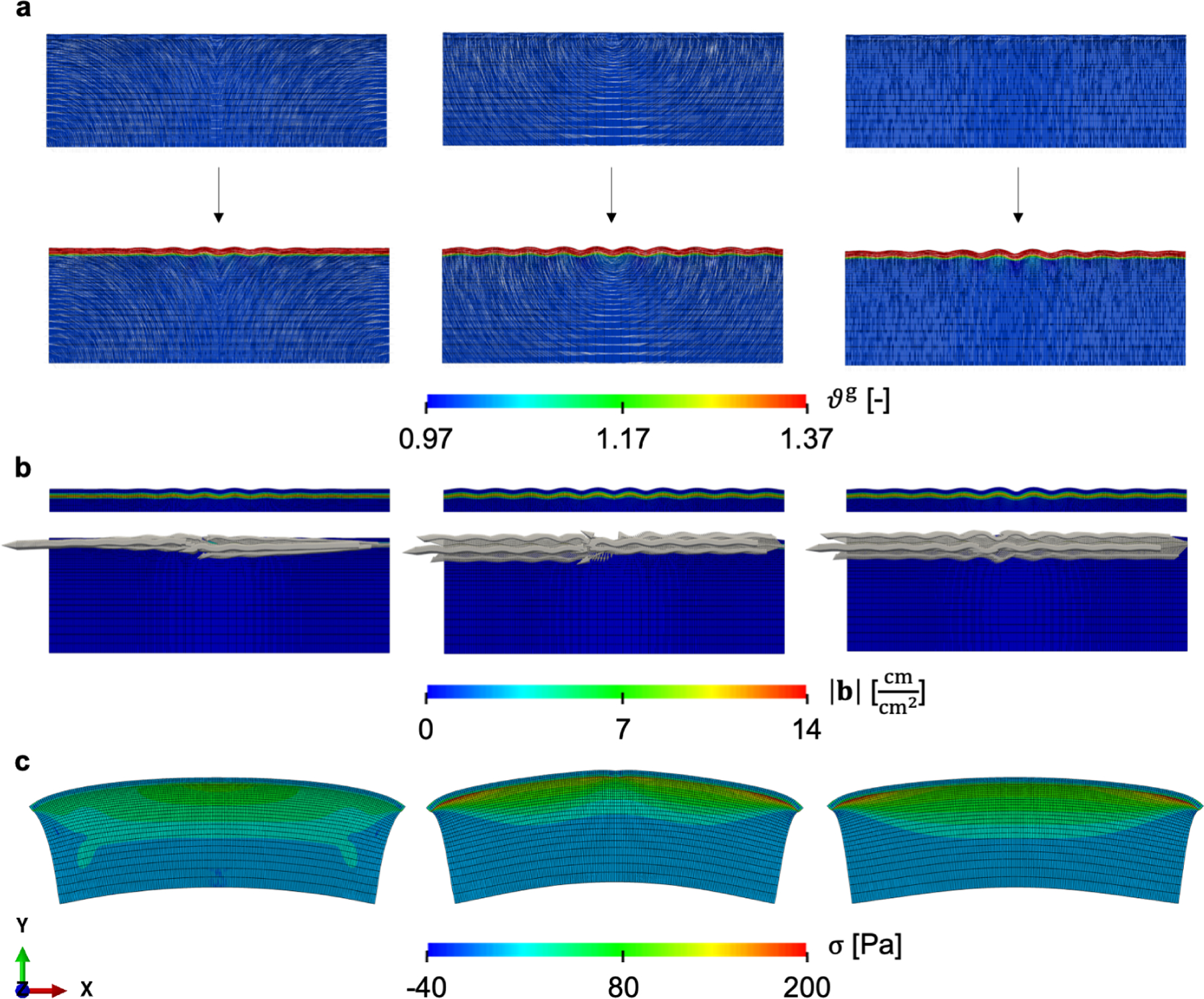
Bi-layered system to capture cortical folding taking into account the axonal fiber orientation. The top layer, the cortex, has a constant growth rate, while the bottom layer, the subcortex, shows stretch-driven fiber growth in the direction of the axons. Folding patterns emerge for three different axon orientations: curved outward, concentric, normal to the interface (a, left to right). The local Burgers vector density is calculated on the plane normal to $\overline{\mathbf{\text{n}}}={\mathbf{\text{e}}}_3$ and it shows that the incompatibility due to growth occurs mostly at the interface between cortex and subcortex (b). Removing all constraints and external forces, the only residual stress left is due to the incompatible growth field, which shows that the maximum principal stress occurs at the interface between the two layers (c).

The differential growth between the two layers and the constraints at the ends of the domain lead to the characteristic patterns of folding seen in the brain (Fig. 7a). Most of the growth is observed on the top layer of the system, but, resulting from the instability and subsequent fold formation, some growth is observed along the axon orientation in the subcortex. The greatest growth gradients are observed at the interface between the two layers of the domain. Given F^g in eq. (23), we compute the geometric incompatibility tensor G and then the local Burgers vector density b on the plane normal to $\overline{\mathbf{\text{n}}}={\mathbf{\text{e}}}_3$. The Burgers vector density has its greatest magnitude precisely at the interface between the cortex and subcortex, where the gradient of growth is sharpest. This is the expected behavior of the system. The ideal scenario in which no axon growth is considered but only differential isotropic growth between the two layers is allowed, would lead to zero incompatibility in either region. In that case, the incompatibility would be completely restricted to a singular region of non-zero incompatibility exactly at the interface. In that case, folds would still form, and the cause for residual stress would be the mismatch along the interface of the two layers [91]. In fact, an experimental confirmation is presented in [92], where two thin strips of elastomers are deformed elastically to a different extent (and therefore without any incompatibility) and then glued together. The bi-layered system shows the expected instabilities and buckling patterns, but in the end the only source of incompatibility is precisely at the interface. In our example, incorporating the axon orientation and growth leads to Burgers vectors mostly aligned with the interface (Fig. 7b). The direction of the axons does affect the pattern and magnitude of |b|, as the gradient between cortex and subcortex is greater when the axons are normal to the cortex (second and third columns in Fig. 7a), as opposed to the case in which axons approach the interface tangentially (first column in Fig. 7a).

The buckling patterns typical of the folded brain exist because of the constraints applied to the system, which is fixed at both ends. We are interested in the residual stress patterns when there are no external loads and the only constraints imposed are those that prevent rigid body motion. The residual stress field that arises solely by the incompatibility is shown in Fig. 7c. We restrict our attention to the maximum principal stress. There is peak tension at the subcortex right below the interface with the cortex. This is particularly noticeable for the cases in which the axon orientation is normal to the interface. For the case in which the axon orientation is tangential to the interface, the incompatibility is less pronounced and the residual stress is also much lower. Moving away from the interface, the stress decreases. In the cortex, stresses are actually very small. The growth in the cortex is uniform and this layer is stiffer that the subcortex. As a result, releasing all constraints on the system leads to a constant bending of the top layer. This overall bending exerts the tensile stresses at the top of the softer subcortex, with small variations corresponding to the growth field in the axon direction. Yet, as stated before, the variations in the growth field within the subcortex are small compared to near the interface with the cortex.

4. Discussion

The exact microscopic origin of residual stress in soft tissues is still an open question. However, it is generally accepted that the pre-stress field at the macroscopic level is a consequence of the constant growth and remodeling of living matter [23, 42, 11]. Growth and remodeling can be captured within a continuum mechanics framework in a manner akin to plasticity by splitting the deformation gradient into growth and elastic contributions [25, 26]. This split is linked to the idea of incompatibility [30], a notion of mismatch and discontinuity between differential volume elements at the microscopic scale. In crystal plasticity, these concepts are linked to lattice defects. Although the interpretation is not the same for soft tissues, we borrow from the concepts of crystal plasticity to describe the kinematics of incompatibility due to growth. Through this paper, we have presented the distinctive features of the geometric incompatibility tensor that exist for three general growth formulations: volume, area, and fiber growth. We also compute the geometrically necessary incompatibility for three realistic biomedical problems. Although we focus on the geometry of incompatibility, we show that some features of the residual stress field are closely related to the incompatibility field.

The primary object of the present work was to introduce the geometric incompatibility tensor G in the context of growth and remodeling. This tensor is based on the definition of the Burgers vector, which is a measure of the failure to close circuits in a surface after the application of the irreversible deformation F^g. The generalization of the Burgers vector calculation for any normal n, together with a localization argument, yields the tensor G, which is closely related to the Curl operator. In the finite volume growth theory, the tensor F^g is constrained by the biology and by the anatomy or microstructure of the tissue. Growth is also connected to the thermodynamic balance laws which connect the tensor F^g to the scalar mass source. These constraints on F^g allow us to derive specific features of G for different growth modes. The most prominent feature is that the degree and direction of incompatibility depend on the magnitude and direction of the growth gradient. There are more subtle features that were discussed for the individual growth models.

To better understand these incompatible fields we started with very simple illustrative examples. A key task in our manuscript was the numerical implementation of the different growth problems and the subsequent calculation of the incompatibility metrics within the finite element framework. To that end, we were able to compare our simulations against the analytical derivations. The finite element calculations further cemented some of the observations about G and the local Burgers vector density b. For example, the simpler problems confirmed that there is no incompatibility in the direction of the growth gradient, and that for a given plane defined by normal n the Burgers vector has to lie in that plane. In contrast, we did not devote much attention to the residual stress resulting from the incompatible growth field. The stress field is more complex because there are several factors that come into play beyond the geometry of the permanent deformation. Clearly the F^e field is generally dependent on the overall geometry and boundary conditions [52]. That being said, our numerical implementation naturally delivers the residual stresses in our simulations and allows us a side by side comparison of incompatibility patterns and the resulting stress field. The last of the representative examples allowed us to showcase that there are incompatible growth fields that do not lead to stress, something that is better understood for crystals [47]. In our fiber growth example we showed how a pure rotation F^e = R^e which is incompatible is sufficient to obtain a total deformation that is compatible but entails no residual stress.

Our idealized problems enabled us to point out the distinctive features of the geometry of incompatibility and to showcase the finite element implementation (which we make available with this manuscript). Yet, we are interested in understanding how these incompatible fields look like in realistic applications. We know that residual stress is a feature of living tissue and that it is important for function [93]. Hence, having presented our tools, we applied them to three relevant biomedical questions. In the brain, for example, we observed that the gradient of growth during development and atrophy is highest at the interface between white and gray matter, and this is the region with the highest degree of incompatibility and also residual stress. The perfect experimental analogy of an ideal system is the work by Budday et al. [92], where the compatible deformation of two layers before being glued together leads to residual stress due to the mismatch of deformation at the interface. Our numerical example in the brain adds additional complexities compared to the idealized experiment. For example, the growth of axons in the white matter can increase or decrease the degree of incompatibility depending on their orientation with respect to the interface.

From the tissue expansion simulations we also gained valuable insights. It has been discussed in previous computational models, clinical experience, and animal experiments, that there is more growth at the apex compared to the periphery [2, 87]. Here we show that, in fact, the residual stress is highest at the periphery and at the beginning of the contact region between expander and skin. These regions coincide with the sharpest gradients of growth and our incompatibility metrics.

In the illustrative examples at the beginning of the Results, and the biomedical applications that we present afterwards, we have focused on characterizing the type of geometry associated with growth and remodeling. As pointed out in the introduction, the opposite question is also of utmost interest: Can the constitutive equation for the growth rate take into account incompatibility? Residual stress has indeed been proposed as a key regulator in development of plants and animals [19, 21]. An initial exploration into this question through the lens of the incompatible configurations is presented in the Supplemental material, where we show conditions on the growth profile that can lead to constant magnitude of the Burgers vector along the growth gradient. A direct dependence on G in eq. (44) is one possible way of connecting the geometric defects due to growth to the growth process itself. Another phenomenon worth discussing is that cellular mechanobiology is most likely not a local phenomenon. Mechanobiology pathways for connective tissue include the production and diffusion of growth factors [16, 94]. Due to the presence of diffusion of these coupled fields, it is reasonable to anticipate that consideration of growth factors will impact growth gradients and, consequently, the incompatibility metrics. Such analysis is, however, beyond the scope of this paper.

This work is not without limitations. One of the open questions in this work is the precise connection between the geometry of incompatibility and the residual stress. While the metrics introduced do align in general with the development of residual stress, more work is needed to elucidate this relationship in more detail. An area of future research in this regard is to understand the effect of material properties on the development of residual stress, especially for the mechanically-coupled problems. The other main limitation is that we have fully focused on the split of the deformation gradient into growth and elastic contributions. This approach is useful in practice, describes growth and remodeling accurately, and is amenable to efficient finite element implementations [80]. However, comparison against other descriptions of growth and remodeling is our future endeavor, such as the evolution of natural configurations for individual constituents [42], or the notion of a higher-dimensional reference configuration [40, 41]. Furthermore, the multiplicative split into a single pair of growth and elastic deformations is a valid representation of the final state of residual stress in the tissue, but does not capture the dynamic process of growth as a sequence of incremental growth and elastic deformations. This last point connects to one open question that we will also continue to investigate in the near future: what is the connection between the geometry of incompatibility and the microscale remodeling for soft tissues? As we stated repeatedly in the manuscript, soft tissues do not have lattice defects or dislocations. While our analysis is useful at the continuum scale, it leaves unanswered the microscopic and molecular origin of incompatibility in living matter.

5. Conclusions

Within the finite volume growth framework, residual stress arises due to the incompatibility of the growth field. Here we explore in detail the geometric characterization of this incompatibility. We implement the calculations of growing tissues and the geometric incompatibility tensor G into a nonlinear finite element framework. We showcased idealized scenarios and also relevant biomedical applications. Therefore, we expect that this work will further our insight into the origin and characterization of residual stress in soft tissue, which can be instrumental in understanding disease and designing clinical interventions in which growth and remodeling of soft tissue plays a central role.