Abstract
The reaction kinetics of solid fuel is a critical aspect of energy production because its energy component is determined during the process. The overall fuel quality is also evaluated to account for a defined energy need. In this study, a two-step first-order reaction mechanism was used to model the rapid mass loss of pine sawdust (PSD) during torrefaction using a thermogravimetric analyzer (Q600 SDT). The kinetic analysis was carried in a MATLAB environment using MATLAB R2020b software. Five temperature regimes including 220, 240, 260, 280, and 300 °C and a retention time of 2 h were used to study the mechanism of the solid fuel reaction. Similarly, a combined demarcation time (i.e., estimating the time that demarcates the first stage and the second stage) and iteration technique was used to determine the actual kinetic parameters describing the fuel’s mass loss during the torrefaction process. The fuel’s kinetic parameters were estimated, while the developed kinetic model for the process was validated using the experimental data. The solid and gas distributions of the components in the reaction mechanism were also reported. The first stage of the degradation process was characterized by the rapid mass loss evident at the start of the torrefaction process. In contrast, the second stage was characterized by the slower mass loss phase, which follows the first stage. The activation energies for the first and second stages were 10.29 and 141.28 kJ/mol, respectively, to form the solids. The developed model was reliable in predicting the mass loss of the PSD. The biochar produced from the torrefaction process contained high amounts of the intermediate product that may benefit energy production. However, the final biochar formed at the end of the process increased with the increase in torrefaction severity (i.e., increase in temperature and time).
1. Introduction
Combustion of fossil fuels and other carbon content materials without proper control has contributed to the emission of green house gases, leading to enhanced global warming and climate change worldwide. The energy insecurity posed by the rapid depletion of fossil fuels and the environmental impact of using the fuels have motivated researchers to study biomass as an alternative fuel source for energy production.1,2
Several thermochemical conversion technologies such as pyrolysis, combustion, and gasification have been regarded as promising routes for converting waste biomass to biofuels.3 The utilization of raw biomass as against fossil fuel such as coal is faced with challenges including its low bulk energy density, grindability, hydrophobicity, and low combustion properties.4
A pretreatment technology such as torrefaction has proved to be an efficient thermal process for the improvement of the quality of raw biomass, and the application of this process will help solve the problems mentioned earlier.5−10 Torrefaction is a thermal pretreatment process whereby a known quantity of biomass is subjected to a mild temperature between 200 and 300 °C for a residence time of around 2 h. During this process, the bulk energy density of a lignocellulosic biomass increases and is accompanied by the mass loss of the fuel. Mass loss is characterized by the removal of water content, the release of volatile matter, and the depolymerization of lignocellulosic components.11−13 This technology fosters the utilization of torrefied biomass as a replacement for coal in coal-firing plants.
Several researchers including Dorde et al.,14 Acharjee et al.,15 Wang et al.,16 and Singh et al.17 have studied the effect of process conditions on the improved fuel properties of torrefied biomass. Fluidized bed reactors, batch reactors, and continuous reactors were employed for the process.18−20 Understanding the mass loss of solid fuel is necessary because it helps design a gasification or pyrolysis reactor. Mass loss is related to the degree of torrefaction and is measured by the degradation of biomass.21−24 The authors mentioned above concluded that the solid mass loss of biomass can estimate the severity of the torrefaction process.
Thermogravimetric analysis (TGA) has been the most commonly used experimental technique for studying biomass’s thermal degradation. It is also used to study the solid distribution during the torrefaction process. The thermogravimetric analyzer determines the rapid mass loss. Two main methods have been extensively used to describe the thermal degradation of biomass. These methods are the isothermal method (steady-state conditions) and the nonisothermal method (unsteady-state conditions). The main advantage of estimating kinetic parameters using the nonisothermal method (i.e., Friedman method, Kissinger–Akahira–Sunose method, Flynn–Wall–Ozawa, etc.) is that it is easier to account for the mass loss during the nonisothermal period. However, results reported by Kumar et al.,25 Yan et al.,26 and Sharma et al.27 while employing the nonisothermal method suggested that multiple reactions are present during the torrefaction and pyrolysis of biomass. Therefore, using the nonisothermal method can lead to a wrong estimation of the kinetic parameters, and based on this fact, the isothermal method is considered.
Isothermal degradation of biomass is the rate at which biomass decomposes when subjected to a fixed temperature without any heat loss or gain during the process. Modelling this process is essential because it provides relevant information for designing an efficient torrefaction reactor, estimates the fuel conversion system’s mass and energy balance, estimates and improves biochar’s fuel properties. It has been reported in the literature that torrefaction occurs within the temperature range of 200–300 °C, which is attributed to the degradation of mainly the hemicellulose component in the fuel.2
A variety of kinetic models have been employed in modelling the isothermal degradation of biomass.28,29 Over the years, two models have been proposed for studying the kinetic process, namely, the detailed model and the pseudo-components model.29,30 The detailed model considered the individual decomposition of three different biopolymer components, hemicellulose, cellulose, and lignin, in the biomass. This model was first introduced by Ranzi et al.30 and was later modified and improved by Blondeau and Jeanmart31 and Anca-Couce et al.,32 respectively. However, because of the difficulty in extending this method to various biomass species’ torrefaction, the pseudo-component model is adopted due to its simplicity. This model describes the overall anhydrous weight loss of the biomass during the reaction. It has been adopted based on a one-reaction scheme,33 several reaction steps scheme in parallel,34 as well as several reaction steps scheme in series by Peduzzi et al.35
The use of the two-step reaction mechanism requires that the fuel degradation be demarcated into two stages, namely, the first stage (i.e., characterized by a rapid mass loss rate) and the second stage (i.e., characterized by a slower mass loss rate). Several kinetic studies have been carried out employing the two-step kinetic model technique. For example, the kinetics of the isothermal degradation of pure xylan during pyrolysis was first studied by Di Blasi and Lanzetta,29 and the activation energies of the decomposition steps were found to be 76.57 kJ/mol for the first stage and 54.81 kJ/mol for the second stage.
Shang et al.36 also carried out a kinetic study on the isothermal degradation of wheat straw biomass employing the two-step reaction scheme and reported activation energies of 71 and 76.6 kJ/mol for the char formation at stage one and stage two, respectively. It was also reported that this model technique was efficient in predicting the residual mass of the biomass during torrefaction on a bench-scale batch reactor.
Edgar37 carried out a similar study on woody biomass and obtained the char’s activation energies as 104.42 and 97.60 kJ/mol for stages one and two, respectively. Bach et al.38 also studied the isothermal degradation of spruce and birch biomass using a similar reaction mechanism. Activation energies of 20.79 and 70.61 kJ/mol for spruce biomass were reported for the first and second stages. In contrast, 87.71 and 93.51 kJ/mol for birch biomass were recorded for the first and second stages.
Prins et al.39 reported the activation energies of the first and second stages of torrefaction of willow biomass using the same kinetic model technique as 76.0 and 151.7 kJ/mol, respectively. It was suggested that the first stage of the degradation process is attributed to depolymerization of hemicellulose, accompanied by the removal of free moisture content within the walls of the biomass and the removal of light compounds in the form of volatiles. The second stage of the degradation process is mainly attributed to the cellulose’s depolymerization and a fraction of the lignin. Because of the more resistive behavior of the cellulosic components than the hemicellulose, the second stage’s activation energy has been estimated to be higher than that of the first stage.
Similarly, Shang et al.18 considered the mass loss during the heating period when estimating the kinetic parameters. The study showed that it is difficult to model the nonisothermal degradation phase of the process. This difficulty was reflected by the low correlation between the estimated kinetic parameters and the Arrhenius equation. Bach et al.38 reported similar observations. Hence, while carrying out the kinetic study of the process, the nonisothermal period was not included. It was assumed that the mass at the set temperature was the initial mass. A similar procedure was employed in this study.
While estimating the kinetic parameters using the two-step reaction technique, a demarcation time must be determined to separate the two steps and estimate the reactions’ overall rate constants. However, Prins et al.39 suggested that it is difficult to identify a demarcation time as the two stages co-occur. Subsequent kinetic studies either used only the demarcation method or used previously estimated kinetic parameters as initial guesses to estimate the correct kinetic parameters using MATLAB. Based on this fact, experimental results with modelled results have not exhibited a good correlation.
Previous studies have focused on the incomplete degradation of biomass existent within the torrefaction region. In this study, the complete degradation of ash-free biomass, which allows for further degradation of biomass beyond the torrefaction region, was assumed. The demarcation time methods and the iteration methods were used to study the kinetics of isothermal degradation of pine sawdust (PSD) during the torrefaction process. Mathematical modelling of the isothermal degradation of the fuel (PSD) following the intrinsic two-step kinetic reaction scheme in series was carried out. The accuracy of the modelled results in comparison with the experimental results was improved via this approach. The study’s outcome will provide information for the development of efficient torrefaction and energy production plants based on the mechanism of the fuel reaction and its activation energy.
2. Experimental Section
2.1. Sample Preparation
Pinewood (Pinus Pinaster), obtained from Johannesburg, South Africa, was used as the feedstock for this study. Before the TGA experiments, the wood samples were air-dried for 48 h. After that, the logs of wood were reduced to chips having an average dimension of 10 mm × 15 mm × 20 mm using a Rekord SSF 520 vertical band saw. These wood chips were pulverized to a particle size of 600 μm using a ring and puck laboratory pulverizer with a capacity of 100–1000 g sample. The dried pine sawdust was sealed in an airtight bag for further analysis and experiment. Proximate analysis of PSD was carried out according to ASTM E1755-01,40 E872-82,41 and E1756-08.42 The free moisture content was reported as the mass loss after drying the PSD sample at 105 °C for 24 h. A thermogravimetric analyzer was further used to heat the PSD sample at 950 °C in a nitrogen atmosphere. The recorded mass loss was termed the volatile matter. The remainder of the biomass was combusted at 550 °C for 3 h. The remaining noncombusted solid was reported as the ash content. The fixed carbon (FC) was therefore calculated by the difference: FC = 100 – (moisture + volatile + ash).
Table 1 contains the proximate analysis of the PSD and the lignocellulosic compositional analysis of the PSD used in this study. From Table 1, it can be observed that the lignocellulosic composition of the PSD of China origin studied by Shi and Wang.43 significantly differs from the PSD of South African origin because of the geographical difference of the biomass.
Table 1. Lignocellulosic and Proximate Analysis of Air-Dried Pine Sawdust.
| lignocellulosic
composition (%) |
proximate
analysis (%) |
||||||
|---|---|---|---|---|---|---|---|
| hemicellulose | cellulose | lignin | moisture | volatile | FCa | ash | refs |
| 38.0 | 21.6 | 30.1 | 8.6 | 71.8 | 19.1 | 0.6 | this study |
| 10.5 | 48.6 | 25.3 | Shi and Wang43 | ||||
FC—fixed carbon by difference.
2.2. TGA
A thermogravimetric analyzer (Q600 SDT) was used to carry out the torrefaction of the biomass samples. For each run, an initial mass of 10 mg of each sample was loaded in the analyzer, and nitrogen gas of flow rate, 100 mL/min, was supplied for the experiment. The experiment was allowed to start at room temperature till it got to 105 °C, and it was allowed to stay for 3 min for further drying. It was then heated to preset torrefaction temperatures (220, 240, 260, 280, and 300 °C) and held isothermally for 2 h. Different but slow heating rates were used for different preset temperatures to achieve the same nonisothermal period, and 5 min was the allowable time for the temperatures to rise from 105 °C to the various preset temperatures. Because of the difficulty in modelling the nonisothermal heating period, this short heating period was set to reduce the nonisothermal period’s effect. The mass recorded when the preset temperature reached was taken as the initial mass to eliminate the complexity of modelling the nonisothermal period. The initial time was set at the time the preset temperature was reached.
2.3. Kinetic Model Formulation
A two-step reaction in series was first adopted to describe pure xylan (hemicellulose) decomposition during an isothermal pyrolysis process by Di Blasi and Lanzetta.29 The assumptions using this model are based on two things; conversion occurs purely under kinetic control and a semi-global reaction mechanism is applicable. These steps, as shown in Figure 1, indicate that during torrefaction, an initial mass of biomass when heated at a specific temperature between 200 and 300 °C from an initial time (ti) to a time (t*) produces an intermediate solid B accompanied by the first release of volatiles V1. When the intermediate solid is further heated to a final time (tf), a final solid char C is produced accompanied by the second release of volatiles V2.
Figure 1.
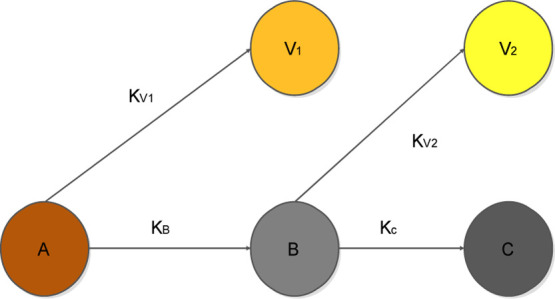
Two-step kinetic model.
A first-order kinetic reaction is assumed for the degradation of biomass.44 Based on this hypothesis and from Figure 1, differential eqs 1–5 are developed from the rate equations of the individual steps
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
Mi is the mass fraction of the pseudo-components (A, B, C, V1, and V2), and ki is the rate constant for each of the equations. As illustrated in Figure 1, the mathematical expressions for the overall rate constant for the first and second stages of the torrefaction reaction are expressed in eqs 6a and 6b and can be estimated from the relationship between the mass loss and time as shown in eqs 7 and 8.
| 6a |
| 6b |
| 7 |
| 8 |
where M0 is the initial mass of the solid, W is the mass of the solid char remaining at any time t after the torrefaction process obtained from TGA results, and MB* is the mass at the demarcation time t*. The demarcation time will be the point on the TGA graph where there is a significant mass loss indicated by a shoulder on the curve. After estimating the rate constants, the linearized Arrhenius equation plots are then used to estimate the activation energies, Ei, and the pre-exponential factors, Ai
| 9 |
2.4. Kinetic Model Solution
Integrating eqs 1–5 yields eqs10–14, with boundary conditions when time t = 0; MA(0) = M0, MB(0) = MV1(0) = MV2(0) = MC(0) = 0
| 10 |
| 11 |
| 12 |
| 13 |
| 14 |
where W/M0 is the solid char remaining after the torrefaction process, and eq 16 is obtained
| 15 |
| 16 |
However, because the ash content is unreactive during the torrefaction process, the experimental fractional mass loss is represented by eq 17
| 17 |
where m0 is the initial mass of the biomass, ms is the mass of the solid remaining, recorded by the thermogravimetric analyzer, and mash is the mass of ash contained in PSD, as shown in Table 1.
Integrating eq 3 with boundary conditions MC(0) = 0, MC(∞) = MC∞ (when there is sufficient time for the formation of final char, C) results in eqs 18 and 19.
| 18 |
| 19 |
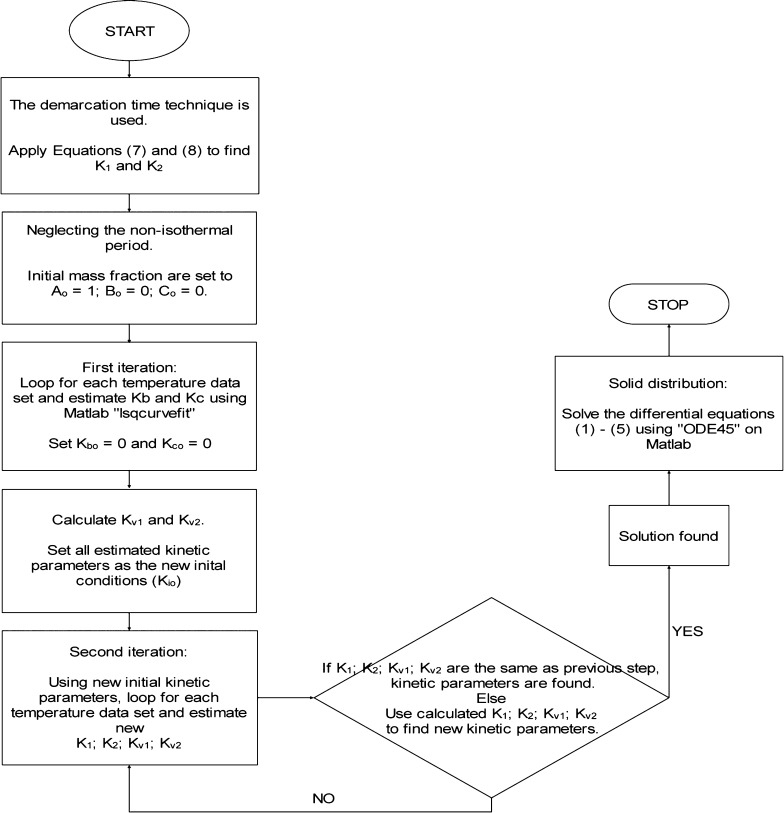
A flowchart diagram describing the MATLAB algorithm used in determining the kinetic parameters of the torrefaction of PSD while employing both demarcation time techniques and numerical solution techniques is shown in Figure 2. First of all, the demarcation time method as used by Prins et al.39 was employed to determine the kinetic parameters.
Figure 2.
Flowchart algorithm used in MATLAB for estimating the kinetic parameters and the solid distribution during the torrefaction of PSD.
It was reported that due to the inaccuracy in estimating the demarcation time, the kinetic parameters derived using this technique were unable to predict the mass loss obtained experimentally adequately. Hence, the kinetic parameters derived using the demarcation time technique were used as the initial conditions for the numerical solution method known as nonlinear optimization using MATLAB software version R2020b.
In this study, “lsqcurvefit” is used as the function. The “lsqcurvefit” function operates under the principle of Niedler–Mead optimization algorithm. It is used to minimize the residual sum of squares between the modelled and TGA data, as shown in eq 20. The “lsqcurvefit” process was therefore iterated till the initial conditions for the kinetic parameters became the estimated kinetic parameters, indicating an optimum solution.
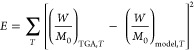 |
20 |
T indicates each isothermal temperature, (W/M0)TGA is the weight loss recorded experimentally by the TGA, and (W/M0)model is the calculated weight loss from the model.
3. Results and Discussion
3.1. Isothermal Degradation of PSD During Torrefaction in a TGA
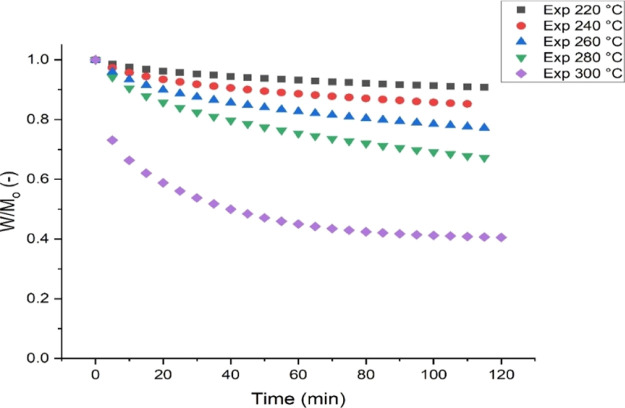
The instantaneous mass loss during pine sawdust’s torrefaction using a thermogravimetric analyzer is shown in Figure 3. Figure 3 contains a plot of the fractional mass loss of the fuel against time. The nonisothermal period (heating period) was removed by assuming the mass yield at each set temperature to be the initial mass (Ys, T °C = 1), and the time was recorded as the initial time (t = 0).
Figure 3.
Mass loss curves during the torrefaction of PSD using a thermogravimetric analyzer.
Figure 3 shows continuous mass loss as the torrefaction process’s severity (i.e. temperature and time) increased. This continuous mass loss as the severity of the process increases was also reported in investigations done by Anca-Couce et al.45 and Gajera et al.46 on the thermal degradation of biomass using a thermogravimetric analyzer. Furthermore, it can be observed that there was a drastic mass loss when the temperature was increased to 300 °C. The marginal mass loss at temperatures below 300 °C could be attributed to the removal of moisture content and the decomposition of a fraction of the hemicellulose, whereas at 300 °C, most of the hemicellulose, which account for the largest fraction of the PSD composition used in this study as shown in Table 1, is decomposed. At this temperature, the decomposition of cellulose is also evident. Similarly, Xiao et al.47 studied the thermal degradation of pine sawdust in a thermogravimetric analyzer. They observed that cellulose’s depolymerization, though overlapping with hemicellulose depolymerization, is more evident between 260 and 380 °C.
Evidently, there seem to be higher slopes within the first 10–20 min of the mass loss curves from the TGA curves, which indicate a rapid mass loss rate within the first period than the second period. Previous studies have shown that the rapid mass loss in the first stage is due to hemicellulose’s depolymerization, accompanied by water loss, light compounds, CO2, and acetic acid. The slow mass loss rate evident in the second stage is mainly caused by the difficulty in depolymerizing the cellulosic component, which happens to be a more crystalline compound than hemicellulose.4,36,38
3.2. Estimation of Kinetic Parameters
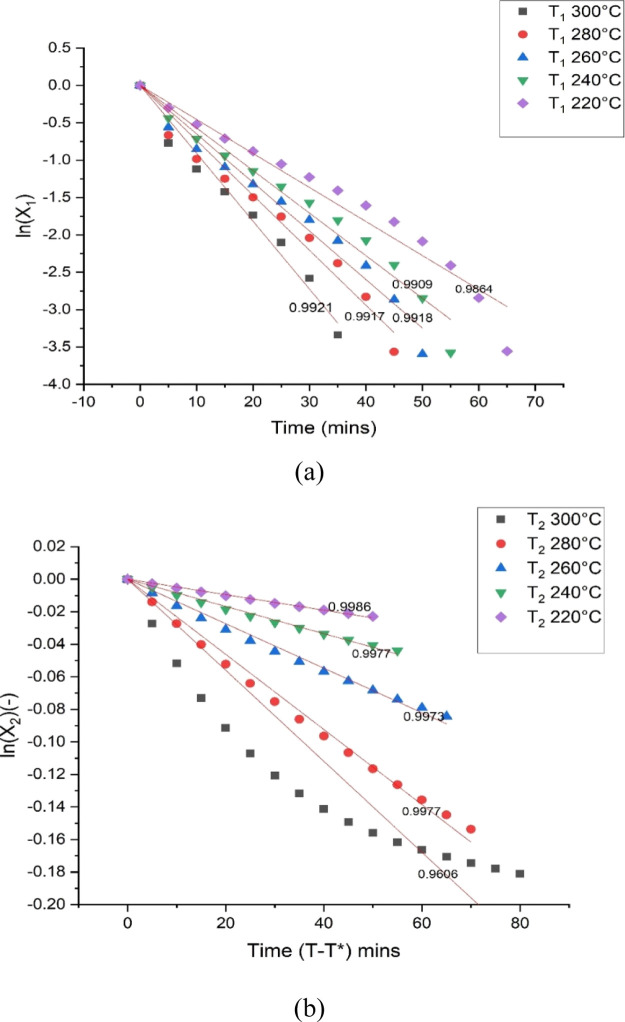
The demarcation time technique was applied to achieve the initial kinetic parameters from which the torrefaction kinetic parameters were estimated. After that, the model was validated using the experimental mass loss curves. In this study, the presence of two stages (fast and slow mass loss stages) during the isothermal degradation of PSD was determined, and a demarcation time was assumed. In this case, eqs 7 and 8 were applied. Figure 4a,b shows plots of eqs 7 and 8, respectively. The straight–line graphs’ slopes were estimated as the overall rate constants for the first and second stages of the isothermal degradation during the torrefaction process. The coefficient of determination (R2) indicated on the plots shows that the equations could explain the mass loss during the stages. The 300 °C data as shown in Figure 4b is not such a good fit because of the overlapping decomposition of both hemicellulose and cellulose, evident at higher temperature regions. As a result of this overlap, there could be the formation of more intermediate solids before the formation of the final char. Therefore, it is recommended that at higher temperatures (pyrolysis region), more than one demarcation time needs to be estimated because of the simultaneous decomposition of different lignocellulosic components. This will lead to the assumption of more intermediate solids.
Figure 4.
Logarithmic plots of the mass loss for the (a) first stage and (b) second stage.
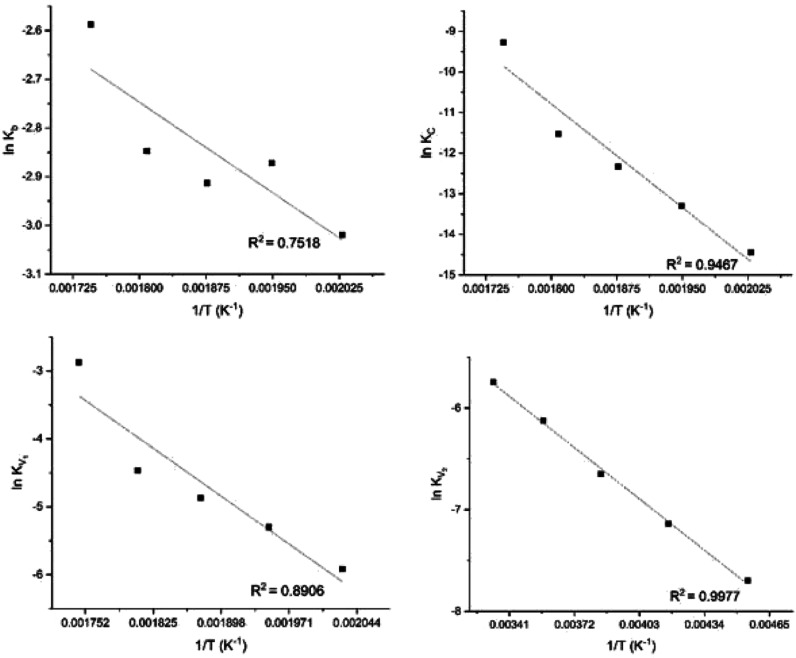
Table 2 shows the torrefaction kinetic parameter estimated in this study. It shows the activation energies and pre-exponential factors via the Arrhenius equations and explains the relationship between the rate constants and temperature for the formation of each pseudo-component. These parameters were estimated based on five torrefaction temperature regimes that were studied (220, 240, 260, 280, and 300 °C) while employing different heating rates (23, 27, 31, 35, and 39 °C/min) such that only 10 min was the allowable time for the solid to rise from room temperature to each preset temperature. As illustrated in eq 9, the Arrhenius equation was used to determine the activation energies and pre-exponential factors for each stage of the degradation process. The plots are shown in Figure 5.
Table 2. Estimated Kinetic Parameters for the Torrefaction of Pine Sawdusta.
| rate constant (min–1) | Arrhenius equations |
|---|---|
| kb | 5.954 × 10–1exp(−10292.73/RT) |
| kc | 3.96 × 108exp(−141279.8/RT) |
| kv1 | 7.19 × 105exp(−80290.79/RT) |
| kv2 | 7.086 × 10–1exp(−13736.39/RT) |
kB, kC, kV1, kV2—rate constants for the formation of intermediate char B, final char C, first volatiles V1, and second volatile V2; R = 8.314 J K–1 mol–1; T—torrefaction temperature (K).
Figure 5.
Arrhenius plots to determine the activation energies and pre-exponential factors for each pseudo-component (kB, kC, kV1, and kV2).
As shown in Figure 5, the determination coefficient (R-squares) shows that the estimated kinetic parameters follow the Arrhenius equation. As seen in Table 2, in agreement with the literature, the mass loss in the first stage occurs faster than the mass loss in the second stage. The table also shows that the activation energy required to form the intermediate solid in the first stage (Ea) is lower than the activation energy needed to form the solid char in the second stage (Eb). This low activation energy in the first stage is because less energy is required to depolymerize the hemicellulose component and remove water and light compounds in the first stage than to depolymerize cellulose in the second stage. This result is in agreement with the result of the degradation of spruce and birch wood reported by Bach et al.38 Furthermore, the activation energy required to form the first volatiles was higher than the energy required to form the second volatile. These observations are equally in agreement with the results of the degradation of pine sawdust reported by Shang et al.18
3.3. Kinetic Model Validation
The predicted mass loss was compared to the experimental plots using the model for each isothermal temperature period, as shown in Figure 6 to validate the kinetic model. The residual sum of squares (RSS), the coefficient of determination (R2), and the Pearson correlation coefficient (r) values as reported in Table 3 were used to check the goodness of fit of the model. As shown in Figure 6, the predicted mass loss using the kinetic model is close to the experimental values. It can be seen that the predicted curves overlap with the experimental curves. Likewise, the low RSS and the high coefficient of determination (R2) support the goodness of fit as seen graphically.
Figure 6.
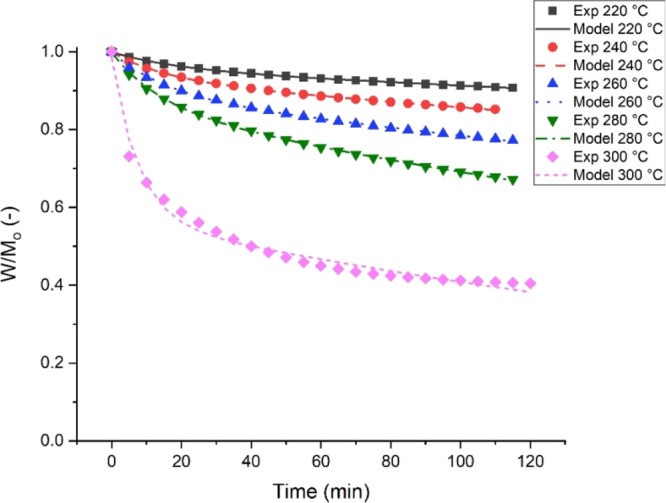
Experimental and modelled mass loss of PSD torrefaction at different temperatures.
Table 3. Statistical Test of Kinetic Models for Prediction of Massa.
| temperature (°C) | RSS | R2 | r |
|---|---|---|---|
| 220 | 0.00000676 | 0.9996 | 0.9998 |
| 240 | 0.0000253 | 0.9993 | 0.9997 |
| 260 | 0.0000607 | 0.9993 | 0.9997 |
| 280 | 0.000119 | 0.9993 | 0.9997 |
| 300 | 0.00671 | 0.9847 | 0.9923 |
RSS—residual sum of squares.
It can also be observed that the mass loss at lower temperatures had a better fit than that at higher temperatures. This observation could be because of the drastic mass loss occurring at the beginning of the isothermal period. Hence, the model tends to overestimate the mass loss at the end of the process.18 The predicted mass loss curves also suggest that there will be a continuous mass loss as the temperature and time increase. Hence, this model can be further applied to the isothermal degradation of biomass in the pyrolysis temperature region.
3.4. Predicted Solid and Gas Distribution
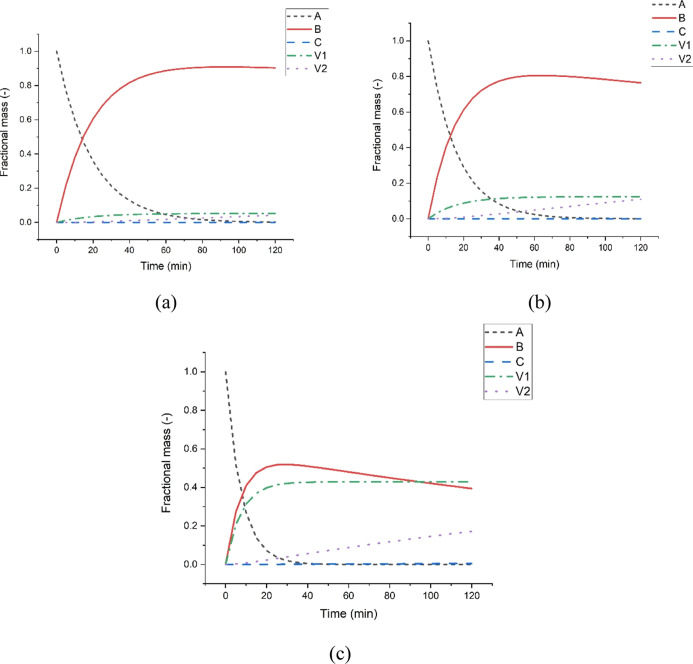
The kinetic parameters estimated from this study were used to predict the solid distribution using eqs 1–5 during pine sawdust torrefaction. Although five torrefaction temperatures were studied, three selected temperatures 220, 260, and 300 °C were presented for discussion, as shown in Figure 7a–c respectively. Figure 7 shows the conversion of the initial solid (A) into an intermediate solid (B) and finally into a solid char (C). The formation of the first and second volatiles are also presented in the figures. Figure 7 shows that the conservation of mass is obeyed such that the sum of the fractional composition of each component at any given time always equals 1.
Figure 7.
Solid and gas distributions during torrefaction of PSD at (a) 220, (b) 260, and (c) 300 °C. (A—initial biomass, B—the intermediate biochar, C—final biochar, V1—first volatiles, and V2—final volatiles).
The degradation of the initial solid biomass has been discovered to be significantly influenced by the operating temperature. In particular, it can be observed that at 220, 260, and 300 °C, it takes about 90, 80, and 40 min for the initial biomass to get converted, respectively. Similarly, the conversion of the intermediate solid (B) is also dependent on temperature. This phenomenon is observed as the intermediate solid curve decreases earlier at higher temperatures than at lower temperatures. These results agreed with the kinetic parameters reported in Table 2, indicating lower activation energy in the first stage than in the second stage of the degradation process. Figure 7 also supports the observation by Prins et al.39 that the first and second stages co-occur, hence making it difficult to establish an accurate demarcation time between the stages.
Furthermore, the formation of the final char was considerable at higher temperatures. As seen at 220 °C, the total mass loss is mainly occupied by the degradation of the initial biomass and the intermediate solid formation. Figure 8 shows the final char’s formation extracted from the solid distribution curve at different temperatures. It can be observed that the formation of the final char only becomes evident at 300 °C. In essence, after torrefaction, the char produced often contains more of the intermediate solid, little of untreated biomass, and a fraction of the final char if sufficient time is given for the process. It can also be observed that higher temperatures favour the formation of volatiles.
Figure 8.
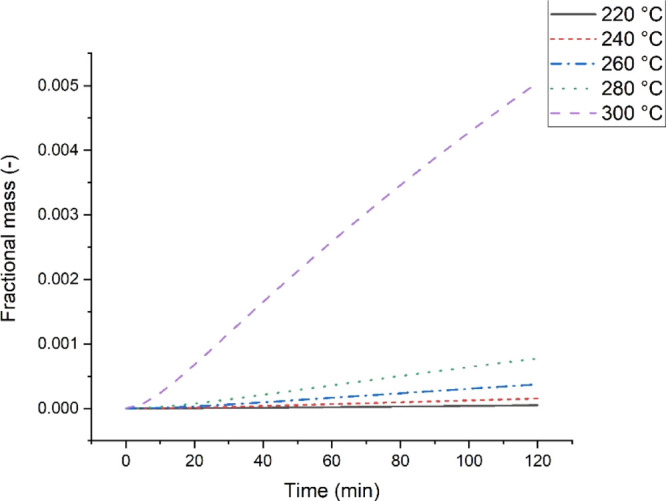
Formation of final char at different temperatures.
Furthermore, it can be seen that as the temperature increases, the fractional composition of the first volatiles significantly increases as compared to the second volatiles. Therefore, it can be said that the formation of the second volatiles is dependent on the formation of the first volatile. This observation could be responsible for the higher activation energy needed to form the first volatiles, as reported in Table 2. Conclusively, an increase in the severity of the torrefaction process fosters the final char C formation and vice versa.
While employing this two-step reaction mechanism for the isothermal degradation of different biomass types as reviewed in the literature, various estimated kinetic parameters are shown in Table 4. The kinetic parameters estimated in this study are also tabulated and compared with those in the literature.
Table 4. Kinetic Parameters for Different Types of Biomass Reported in the Literature.
| pseudo-components |
||||||
|---|---|---|---|---|---|---|
| biomass | kinetic parameters | B | C | V1 | V2 | refs |
| xylan | Ea (kJ mol–1) | 66.23 | 56.35 | 91.47 | 52.59 | Di Blasi and Lanzetta29 |
| A (s–1) | 1.74 × 104 | 3.43 × 102 | 3.31 × 106 | 58.70 | ||
| spruce | Ea (kJ mol–1) | 76.00 | 151.70 | 11.40 | 11.40 | Repellin et al.33 |
| A (s–1) | 2.47 × 104 | 1.10 × 1010 | 1.95 × 107 | 1.10 × 106 | ||
| willow | Ea (kJ mol–1) | 75.98 | 151.71 | 114.21 | 151.71 | Prins et al.39 |
| A (s–1) | 2.48 × 104 | 1.1 × 1010 | 3.23 × 107 | 1.59 × 1010 | ||
| wheat | Ea (kJ mol–1) | 41.00 | 76.57 | 139.46 | 118.62 | Shang et al.36 |
| A (s–1) | 3.48 × 103 | 4.34 × 103 | 3.91 × 1010 | 3.48 × 107 | ||
| poplar | Ea (kJ mol–1) | 104.42 | 97.60 | 125.10 | 111.57 | Edgar37 |
| A (s–1) | 4.80 × 108 | 3.2 × 106 | 9.65 × 109 | 2.75 × 107 | ||
| spruce | Ea (kJ mol–1) | 20.79 | 40.61 | 90.26 | 93.47 | Bach et al.38 |
| A (s–1) | 1.04 × 101 | 2.76 × 104 | 1.26 × 107 | 3.84 × 106 | ||
| birch | Ea (kJ mol–1) | 87.71 | 93.51 | 119.85 | 109.62 | Bach et al.38 |
| A (s–1) | 2.25 × 107 | 2.39 × 101 | 1.02 × 1010 | 1.03 × 108 | ||
| pine | Ea (kJ mol–1) | 46.85 | 6.1 × 10–6 | 122.11 | 94.40 | Shang et al.18 |
| A (s–1) | 77.14 | 1 × 10–5 | 2.68 × 108 | 5.75 × 104 | ||
| pine | Ea (kJ mol–1) | 10.29 | 141.28 | 80.29 | 13.74 | this study |
| A (s–1) | 5.95 × 10–1 | 3.96 × 108 | 7.19 × 105 | 7.09 × 10–1 | ||
As discussed early, the trends in the activation energies obtained in this study agree with those reported in the literature.33,36,38 However, the difference in parameters for different biomass types can be attributed to the different lignocellulosic structures. The kinetic parameters for pine reported by Shang et al.18 are different from those estimated in this study because the nonisothermal heating period was not considered in this study.
As a result of Shang modelling the nonisothermal period, the model reported was not accurate enough to describe the degradation process. Furthermore, in accounting for the nonisothermal period by Shang, the kinetic parameters failed to fit the Arrhenius equation. Hence, because of the difficulty in modelling the nonisothermal period, only the isothermal period should be considered while employing this reaction mechanism scheme. A similar suggestion was made by Bach et al.38
4. Conclusions
A kinetic study on the isothermal degradation of pine sawdust during torrefaction was carried out by employing a two-step first-order reaction mechanism in series. A thermogravimetric analyzer was used to carry out the torrefaction process. The demarcation technique was used to determine the initial conditions for the rate constants. After that, an iteration technique was employed to estimate the actual kinetic parameters that will efficiently predict pine sawdust’s mass loss during torrefaction. The model results obtained from this study agree with the experimental results. Different and slow heating rates were employed to reduce the nonisothermal period’s effect on the mass loss and neglect the heat transfer within the biomass sample. The activation energies of the pseudo-components (kB, kC, kV1, and kV2) obtained at different stages of the degradation process were 10.29, 141.28, 80.29, and 13.74 kJ/mol, respectively. Understanding the solid distribution of components during torrefaction via kinetics can pave the way for implementing the torrefaction process in the industry.
This study also provides relevant data for designing an optimal torrefaction reactor for different biomasses as well as evaluating the energy efficiency of torrefaction, specific to PSD. However, the kinetic data obtained from this study is peculiar to PSD because the degradation of biomass is based on its lignocellulosic composition. The effect of particle size on the torrefaction process has been reported in the literature. It is reported that a smaller particle size (larger surface area) fosters the decomposition of the lignocellulosic components of PSD. The shrinking core kinetic model has established this hypothesis. Hence, based on the results obtained from this study, the combined demarcation time and iteration technique is recommended to study the reaction kinetics of similar waste biomass using their respective TGA data. Also, the blending of different biomasses having similar lignocellulosic distribution should be considered to estimate uniform kinetic data for a range of biomasses.
Acknowledgments
The authors gratefully thank the Research and Innovation Support and Advancement in collaboration with the National Research Foundation, South Africa, (DST-NRF) for the financial support rendered to the first author (grant no: 123105). The School of Chemical and Metallurgical Engineering at the University of The Witwatersrand, Johannesburg, South Africa, supported this study by providing the experimental facilities used in this study. There is no financial or competing interest declared by the authors from this research.
The authors declare no competing financial interest.
References
- Alper K.; Tekin K.; Karagöz S.; Ragauskas A. J. Sustainable energy and fuels from biomass: A review focusing on hydrothermal biomass processing. Sustainable Energy Fuels 2020, 4, 4390–4414. 10.1039/d0se00784f. [DOI] [Google Scholar]
- Li S.-X.; Chen C.-Z.; Li M.-F.; Xiao X. Torrefaction of corncob to produce charcoal under nitrogen and carbon dioxide atmospheres. Bioresour. Technol. 2018, 249, 348–353. 10.1016/j.biortech.2017.10.026. [DOI] [PubMed] [Google Scholar]
- Okolie J. A.; Rana R.; Nanda S.; Dalai A. K.; Kozinski J. A. Supercritical water gasification of biomass: A state-of-the-art review of process parameters, reaction mechanisms and catalysis. Sustainable Energy Fuels 2019, 3, 578–598. 10.1039/c8se00565f. [DOI] [Google Scholar]
- Bates R. B.; Ghoniem A. F. Biomass torrefaction: Modeling of reaction thermochemistry. Bioresour. Technol. 2013, 134, 331–340. 10.1016/j.biortech.2013.01.158. [DOI] [PubMed] [Google Scholar]
- Nhuchhen D. R.; Afzal M. T.; Parvez A. M. Effect of torrefaction on the fuel characteristics of timothy hay. Biofuels 2018, 7269, 1–14. 10.1080/17597269.2018.1479135. [DOI] [Google Scholar]
- Chen W.-H.; Peng J.; Bi X. T. A state-of-the-art review of biomass torrefaction, densification and applications. Renew. Sustain. Energy Rev. 2015, 44, 847–866. 10.1016/j.rser.2014.12.039. [DOI] [Google Scholar]
- Van der Stelt M. J. C.; Gerhauser H.; Kiel J. H. A.; Ptasinski K. J. Biomass upgrading by torrefaction for the production of biofuels: A review. Biomass Bioenergy 2011, 35, 3748–3762. 10.1016/j.biombioe.2011.06.023. [DOI] [Google Scholar]
- Phanphanich M.; Mani S. Impact of torrefaction on the grindability and fuel characteristics of forest biomass. Bioresour. Technol. 2011, 102, 1246–1253. 10.1016/j.biortech.2010.08.028. [DOI] [PubMed] [Google Scholar]
- Gil M. V.; García R.; Pevida C.; Rubiera F. Grindability and combustion behavior of coal and torrefied biomass blends. Bioresour. Technol. 2015, 191, 205–212. 10.1016/j.biortech.2015.04.117. [DOI] [PubMed] [Google Scholar]
- Liu Q.; Chmely S. C.; Abdoulmoumine N. Biomass Treatment Strategies for Thermochemical Conversion. Energy Fuels 2017, 31, 3525–3536. 10.1021/acs.energyfuels.7b00258. [DOI] [Google Scholar]
- Barbanera M.; Muguerza I. F. Effect of the temperature on the spent coffee grounds torrefaction process in a continuous pilot-scale reactor. Fuel 2020, 262, 116493. 10.1016/j.fuel.2019.116493. [DOI] [Google Scholar]
- Cahyanti M. N.; Doddapaneni T. R. K. C.; Kikas T. Biomass torrefaction: An overview on process parameters, economic and environmental aspects and recent advancements. Bioresour. Technol. 2020, 301, 122737. 10.1016/j.biortech.2020.122737. [DOI] [PubMed] [Google Scholar]
- Jagodzińska K.; Czerep M.; Kudlek E.; Wnukowski M.; Pronobis M.; Yang W. Torrefaction of Agricultural Residues: Effect of Temperature and Residence Time on the Process Products Properties. J. Energy Resour. Technol. 2020, 142, 070912. 10.1115/1.4046275. [DOI] [Google Scholar]
- Medic D.; Darr M.; Potter B.; Shah A.. Effect of Torrefaction Process Parameters on Biomass Feedstock Upgrading. ASABE Annual International Meeting; David L., Ed.; Convention Center Pittsburgh: Pennsylvania, June 20–23, 2010.
- Acharjee T. C.; Coronella C. J.; Vasquez V. R. Effect of thermal pretreatment on equilibrium moisture content of lignocellulosic biomass. Bioresour. Technol. 2011, 102, 4849–4854. 10.1016/j.biortech.2011.01.018. [DOI] [PubMed] [Google Scholar]
- Wang Z.; Lim C. J.; Grace J. R.; Li H.; Parise M. R. Effects of temperature and particle size on biomass torrefaction in a slot-rectangular spouted bed reactor. Bioresour. Technol. 2017, 244, 281–288. 10.1016/j.biortech.2017.07.097. [DOI] [PubMed] [Google Scholar]
- Singh S.; Chakraborty J. P.; Mondal M. K. Optimization of process parameters for torrefaction of Acacia nilotica using response surface methodology and characteristics of torre fi ed biomass as upgraded fuel. Energy 2019, 186, 115865. 10.1016/j.energy.2019.115865. [DOI] [Google Scholar]
- Shang L.; Ahrenfeldt J.; Holm J. K.; Bach L. S.; Stelte W.; Henriksen U. B. Kinetic model for torrefaction of wood chips in a pilot-scale continuous reactor. J. Anal. Appl. Pyrolysis 2014, 108, 109–116. 10.1016/j.jaap.2014.05.010. [DOI] [Google Scholar]
- Severy M. A.; Chamberlin C. E.; Eggink A. J.; Jacobson A. E. Demonstration of a Pilot-Scale Plant for Biomass Torrefaction and Briquetting. Appl. Eng. Agric. 2018, 34, 85–98. 10.13031/aea.12376. [DOI] [Google Scholar]
- Brachi P.; Chirone R.; Miccio M.; Ruoppolo G. Fluidized bed torrefaction of biomass pellets: A comparison between oxidative and inert atmosphere. Powder Technol. 2019, 357, 97–107. 10.1016/j.powtec.2019.08.058. [DOI] [Google Scholar]
- Almeida G.; Brito J. O.; Perré P. Alterations in energy properties of eucalyptus wood and bark subjected to torrefaction: The potential of mass loss as a synthetic indicator. Bioresour. Technol. 2010, 101, 9778–9784. 10.1016/j.biortech.2010.07.026. [DOI] [PubMed] [Google Scholar]
- Pathomrotsakun J.; Nakason K.; Kraithong W.; Khemthong P.; Panyapinyopol B.; Pavasant P. Fuel properties of biochar from torrefaction of ground coffee residue: effect of process temperature, time, and sweeping gas. Biomass Convers. Biorefin. 2020, 10, 743–753. 10.1007/s13399-020-00632-1. [DOI] [Google Scholar]
- Rago Y. P.; Collard F.-X.; Görgens J. F.; Surroop D.; Mohee R. Torrefaction of biomass and plastic from municipal solid waste streams and their blends: Evaluation of interactive effects. Fuel 2020, 277, 118089. 10.1016/j.fuel.2020.118089. [DOI] [Google Scholar]
- Lee S. M.; Lee J.-W. Optimization of biomass torrefaction conditions by the Gain and Loss method and regression model analysis. Bioresour. Technol. 2014, 172, 438–443. 10.1016/j.biortech.2014.09.016. [DOI] [PubMed] [Google Scholar]
- Kumar M.; Shukla S. K.; Upadhyay S. N.; Mishra P. K. Analysis of thermal degradation of banana (Musa balbisiana) trunk biomass waste using iso-conversional models. Bioresour. Technol. 2020, 310, 123393. 10.1016/j.biortech.2020.123393. [DOI] [PubMed] [Google Scholar]
- Yan J.; Jiao H.; Li Z.; Lei Z.; Wang Z.; Ren S.; Shui H.; Kang s.; Yan H.; Pan C. Kinetic analysis and modeling of coal pyrolysis with model-free methods. Fuel 2019, 241, 382–391. 10.1016/j.fuel.2018.12.079. [DOI] [Google Scholar]
- Sharma P.; Pandey O. P.; Diwan P. K. Non-isothermal kinetics of pseudo-components of waste biomass. Fuel 2019, 253, 1149–1161. 10.1016/j.fuel.2019.05.093. [DOI] [Google Scholar]
- Broido A.; Nelson M. A. Char yield on pyrolysis of cellulose. Combust. Flame 1975, 24, 263–268. 10.1016/0010-2180(75)90156-x. [DOI] [Google Scholar]
- Di Blasi C.; Lanzetta M. Intrinsic kinetics of isothermal xylan degradation in inert atmosphere. J. Anal. Appl. Pyrolysis 1997, 40-41, 287–303. 10.1016/s0165-2370(97)00028-4. [DOI] [Google Scholar]
- Ranzi E.; Cuoci A.; Faravelli T.; Frassoldati A.; Migliavacca G.; Pierucci S.; Sommariva S. Chemical kinetics of biomass pyrolysis. Energy Fuels 2008, 22, 4292–4300. 10.1021/ef800551t. [DOI] [Google Scholar]
- Blondeau J.; Jeanmart H. Biomass pyrolysis at high temperatures: Prediction of gaseous species yields from an anisotropic particle. Biomass Bioenergy 2012, 41, 107–121. 10.1016/j.biombioe.2012.02.016. [DOI] [Google Scholar]
- Anca-Couce A.; Mehrabian R.; Scharler R.; Obernberger I. Kinetic scheme to predict product composition of biomass torrefaction. Chem. Eng. Trans. 2014, 37, 43–48. [Google Scholar]
- Repellin V.; Govin A.; Rolland M.; Guyonnet R. Modelling anhydrous weight loss of wood chips during torrefaction in a pilot kiln. Biomass Bioenergy 2010, 34, 602–609. 10.1016/j.biombioe.2010.01.002. [DOI] [Google Scholar]
- Ratte J.; Fardet E.; Mateos D.; Héry J.-S. Mathematical modelling of a continuous biomass torrefaction reactor: TORSPYDTM column. Biomass Bioenergy 2011, 35, 3481–3495. 10.1016/j.biombioe.2011.04.045. [DOI] [Google Scholar]
- Peduzzi E.; Boissonnet G.; Haarlemmer G.; Dupont C.; Maréchal F. Torrefaction modelling for lignocellulosic biomass conversion processes. Energy 2014, 70, 58–67. 10.1016/j.energy.2014.03.086. [DOI] [Google Scholar]
- Shang L.; Ahrenfeldt J.; Holm J. K.; Barsberg S.; Zhang R.-z.; Luo Y.-h.; Egsgaard H.; Henriksen U. B. Intrinsic kinetics and devolatilization of wheat straw during torrefaction. J. Anal. Appl. Pyrolysis 2013, 100, 145–152. 10.1016/j.jaap.2012.12.010. [DOI] [Google Scholar]
- Lin B.-J.; Silveira E. A. Prediction of higher heating values (HHVs) and energy yield during torrefaction via kinetics. Energy Procedia 2019, 158, 111–116. 10.1016/j.egypro.2019.01.054. [DOI] [Google Scholar]
- Bach Q.-V.; Chen W.-H.; Chu Y.-S.; Skreiberg Ø. Predictions of biochar yield and elemental composition during torrefaction of forest residues. Bioresour. Technol. 2016, 215, 239–246. 10.1016/j.biortech.2016.04.009. [DOI] [PubMed] [Google Scholar]
- Prins M. J.; Ptasinski K. J.; Janssen F. J. J. G. Torrefaction of wood. Part 1. Weight loss kinetics. J. Anal. Appl. Pyrolysis 2006, 77, 28–34. 10.1016/j.jaap.2006.01.002. [DOI] [Google Scholar]
- ASTM International . ASTM E1755-01, Standard Test Method for Ash in Biomass, West Conshohocken, PA, 2015. [Google Scholar]
- ASTM International . ASTM E872-82, Standard Test Method for Volatile Matter in the Analysis of Particulate Wood Fuels, West Conshohocken, PA, 2013. [Google Scholar]
- ASTM International . ASTM E1756-08, Standard Test Method for Determination of Total Solids in Biomass, West Conshohocken, PA, 2015. [Google Scholar]
- Shi X.; Wang J. A comparative investigation into the formation behaviors of char, liquids and gases during pyrolysis of pinewood and lignocellulosic components. Bioresour. Technol. 2014, 170, 262–269. 10.1016/j.biortech.2014.07.110. [DOI] [PubMed] [Google Scholar]
- Braga R. M.; Costa T. R.; Freitas J. C. O.; Barros J. M. F.; Melo D. M. A.; Melo M. A. F. Pyrolysis kinetics of elephant grass pretreated biomasses. J. Therm. Anal. Calorim. 2014, 117, 1341–1348. 10.1007/s10973-014-3884-2. [DOI] [Google Scholar]
- Anca-Couce A.; Tsekos C.; Retschitzegger S.; Zimbardi F.; Funke A.; Banks S.; Kraia T.; Marques P.; Scharler R.; de Jong W.; et al. Biomass pyrolysis TGA assessment with an international round robin. Fuel 2020, 276, 118002. 10.1016/j.fuel.2020.118002. [DOI] [Google Scholar]
- Gajera Z. R.; Verma K.; Tekade S. P.; Sawarkar A. N. Kinetics of co-gasification of rice husk biomass and high sulphur petroleum coke with oxygen as gasifying medium via TGA. Bioresour. Technol. Rep. 2020, 11, 100479. 10.1016/j.biteb.2020.100479. [DOI] [Google Scholar]
- Xiao R.; Yang W.; Cong X.; Dong K.; Xu J.; Wang D.; Yang X. Thermogravimetric analysis and reaction kinetics of lignocellulosic biomass pyrolysis. Energy 2020, 201, 117537. 10.1016/j.energy.2020.117537. [DOI] [Google Scholar]