Development of Dimensionless Parameters and Groups of Heat and Mass Transfer to Predict Wax Deposition in Crude Oil Pipelines

Abstract

A new methodology has been developed for analyzing heat and mass transfer to predict wax deposition in crude oil pipelines using the law of the wall dimensionless parameters. A set of physically meaningful dimensionless groups and parameters has laid a strong foundation behind the proposed methodology. The paper presents a discussion regarding the development of scale-up correlations from laboratory scale to field scale, considering the combination of both analytical groups and empirical correlations. Data from previous literature studies were employed for determining realistic values for the developed parameters and scale-up correlations. The utilization of new dimensionless scale-up parameters indicated that the wax deposition in crude oil pipelines is independent of the Reynolds number and the inner diameter of the pipeline. It further indicates that wax deposition in crude oil pipelines is mainly dependent on the heat transfer process and not on the shear reduction process. The dimensionless technique developed here can be utilized for determining the optimum pipe size and pigging frequencies to reduce and mitigate the effect of the wax deposition process.

1. Introduction

An increase in global energy consumption shifts hydrocarbon resource exploitation toward harsher, remote, deep and ultradeep offshore environments with the advancement of technology.¹⁻³ The production of oil and gas in this harsh environment poses several issues regarding flow assurance, such as wax deposition, hydrate formation, asphaltene deposition, corrosion, and erosion.⁴⁻⁶ Among all of these, wax deposition is a severe flow assurance issue.^7,8 Wax deposition is a severe issue not only in offshore crude oil transportation but also in various onshore regions of West Texas, Western onshore India, Indonesia, and Malaysia, to name a few.⁹⁻¹¹ The severity of wax deposition is such that it can sometimes block a crude oil pipeline, resulting in heavy economic losses over billions of dollars.¹² Remediating wax deposition in the pipeline can cost around $1 million/mile.¹³

Accurate prediction of the wax deposition process in a crude oil pipeline can help for timely planning of the pigging operation or hot oil circulation process to minimize production loss and ultimately economic losses. The predictions of the amount of wax deposition in the pipelines from available models¹⁴⁻¹⁸ do not match with the field observations. Sometimes, even these predictions fail to match the data generated in the laboratory using flow loops, as shown in Table 1.

Table 1. Literature Review of Experimental Data and Model Verification.

researcher	year	research group and facility	fluid	pipe dia. [in.]	flow regime	main experimental characteristics	model verification with experimental results
Lund19	1998	TUPDP, single-phase loop	South Pelto crude oil	1	laminar, single-phase flow	coupled behavior with the Reynolds number
						the ambient temperature was not maintained constant
						do not resemble field conditions
Matzain15	1999	TUPDP multiphase flow loop	South Pelto crude oil	1	laminar and turbulent, two-phase oil–gas flow	coupled behavior with the Reynolds number	wax deposition prediction dependent on flow pattern
						the ambient temperature was not maintained constant	experimental results are in good agreement with the Matzain model
						do not resemble field conditions
Singh20	2000	University of Michigan, flow loop	model oil	0.5	laminar, single-phase	coupled behavior with the Reynolds number	experimental results are in good agreement with the FMT model
						do not resemble field conditions
Hernandez21	2003	TUPDP, multiphase loop	South Pelto crude oil	1	turbulent, single-phase	do not resemble field conditions	FMT model overpredicts deposition and the EM model underpredicts the deposition process
Venkatesan16	2004	University of Michigan, flow loop	model oil	0.5	turbulent, single-phase	coupled behavior with the Reynolds number	FMT model failed experimental data in good agreement with Venkatesan 2004 model
						do not resemble field conditions
Lee22	2008	University of Michigan, gel-breaking facility	model oil	0.3	laminar, single-phase flow	do not resemble field conditions	new precipitation kinetics model that predicted Venkatesan 2004 and Singh 2000 experimental data were in good agreement
Dwivedi25	2010	TUPDP, small-scale facility	South Pelto crude oil	0.5	turbulent, single-phase flow	do not keep the interface temperature constant	EM model deposition was underpredicted in comparison with experimental data
				1		the data cannot be utilized to investigate scale-up and dominant parameters of wax deposition
				1.5
						interface temperature was not kept constant
						inaccurate measurement technique
						do not resemble field conditions
Karami26	2011	TUPDP, small-scale facility	Garden Banks condensate	0.5	turbulent, single-phase flow	considered constant interface temperature	EM model deposition was overpredicted in comparison with experimental data in some cases while it was underpredicted in some cases
				1		initial Reynolds number and initial shear stress were not considered constant
				1.5
						ambient temperature was not maintained constant
						inaccurate measurement technique
						experimental data obtained by all researchers
						high shear stress and high Reynolds number
						do not resemble field conditions
Panacharoensawad17	2012	TUPDP, mini flow loop	South Pelto crude oil	1	laminar and turbulent, two-phase oil–water flow	do not resemble field conditions	FMT model overpredicts deposition and the EM model underpredicts the deposition process
Singh23,24	2013	TUPDP, mini flow loop	Garden Banks condensate	1	turbulent	do not resemble field conditions	FMT model overpredicts deposition and the EM model underpredicts the deposition process
Rittirong18	2014	TUPDP, multiphase loop	Garden Banks condensate	1	laminar and turbulent multiphase flow	do not resemble field conditions	FMT model overpredicts deposition and the EM model underpredicts the deposition process
Agarwal2	2016	TUPDP, small-scale facility	model oil	0.5	turbulent	closer to field conditions	FMT model overpredicts deposition and the EM model underpredicts the deposition process
				1
				1.5

The reason for the failure is assumed to be due to either incorporating various fudge factors in the models or not using the appropriately defined parameters for scaling up the process. Both of these points are a clear indication that there exists a gap in understanding the transport process involved and its application to the wax deposition process. Besides, the bulk diffusion coefficient utilized in each model is based on the binary system. However, crude oil is a multicomponent system, and a specie diffusion coefficient based on different n-alkanes and their amount should be utilized for better prediction purposes. Thus, there is a need to investigate and understand the wax deposition process in crude oil pipelines (experimental flow loops and field pipelines) along with the verification of available predictive models¹⁴⁻¹⁸ for field pipelines.⁵ A simple predictive tool, along with upscaling parameters, is required for accurate prediction of the wax deposition process in a crude oil pipeline.⁵ Thus, the following methodology has been utilized to obtain a simple predicting tool.

• 1.Selection of experimental data for finding dimensionless scale-up parameters.
• 2.Dimensionless scale-up parameters are defined, and a dimensionless scale-up approach is proposed using the data set of ref (2).
• 3.The developed dimensionless approach is then verified using data sets of refs (17 and 23).
• 4.Based on the verified dimensionless approach, generalized correlations are obtained for scaling up flow loop data to field scale.
• 5.For a better understanding, steps for scaling up flow loop data to field scale have been showcased.

1.1. Selection of Experimental Data Sets for Scale-Up Parameters

Table 1 represents the thorough literature survey of available experimental points that was conducted to attain the objective of finding scale-up parameters. It was found that most researchers¹⁵⁻²³ have obtained experimental data using a single pipe where shear stress, the Reynolds number, and the heat transfer coefficient were coupled with each other. The coupled behavior results in unknown fudge factors and makes it difficult to obtain an upscaling parameter. Thus, to remove this coupled effect, other researchers^2,24,25 utilized the Tulsa University Paraffin Deposition, TUPDP small-scale facility loop as shown in Figure 1, which consists of three different pipe sizes (0.5, 1.0, and 1.5 in.).

Figure 1.

Small-scale facility loop of TUPDP with three different nominal pipe sizes (0.5, 1.0, and 1.5 in.).²

However, in the data set,²⁵ the interface temperature was not kept constant, and, therefore, the data cannot be utilized to investigate scale-up and dominant parameters of wax deposition. While the data set²⁶ considered constant the interface temperature, the initial Reynolds number and initial shear stress were not considered constant for all pipe sizes. Besides, both data sets^25,26 did not preserve the constant ambient temperature of the facility.

To overcome the limitations of the data set,^25,26 a unique set of experiments² were designed and conducted (Table 2) using the TUPDP small-scale facility. To closely resemble typical field conditions, experiments² were designed and conducted with low wall shear stress and a high Reynolds number based on the limitation of the facility (Table 2). To investigate the effect on wax deposition, three initial Reynolds numbers, 11 000, 7300, 4300, and two initial shear stresses, 4.5, 1.68 Pa, were considered. To understand the effect of hydrodynamics, the initial thermal driving force, ΔT_eff = 4 °F (ΔT_eff = (T_b – T_i)), was kept constant by keeping T_b = 95 °F and T_i = 91 °F for all tests. All tests were repeated for four different time durations of 2, 4, 12, and 24 h to study the aging process. Hence, data² obtained is considered more reliable as compared to data sets.^24,25 Therefore, these data points were utilized to develop upscaling parameters and to understand the dominant parameters in wax deposition.

Table 2. Test Matrix of the Data Set of Ref (2).

test number	Tb [°F]	Tambient [°F]	Ti [°F]	Qoil [m3/s]	diameter [m]	voil [m/s]	τini [Pa]	ΔTeff [°F]	Re [ ]	hoil [W/(m2/K)]	Nuoil [ ]
SSF-MO-14-01	95	88	91	0.0005	0.015	2.7	25	4	11 000	1993	209
SSF-MO-14-03		90		0.0014	0.041	1.0	3.5		11 000	830	226
SSF-MO-14-04		89.5		0.0004	0.015	1.8	12		7300	1300	136
SSF-MO-14-05		90		0.0006	0.027	1.1	4.5		7300	831	147
SSF-MO-14-06		90.5		0.0009	0.041	0.7	1.7		7300	533	146
SSF-MO-14-07		90.5		0.0002	0.015	1.1	4.8		4300	740	77
SSF-MO-14-08		90.5		0.0004	0.027	0.6	1.6		4300	444	78
SSF-MO-14-09		90		0.0005	0.041	0.4	0.7		4300	303	82

In summary, two schools of thought exist among researchers: one group considers wax deposition as only a function of heat and mass transfer, while the other considers wax deposition to be a combination of heat and mass transfer along with the shear effect. It may also be noted that the consideration of equilibrium or supersaturation inside the heat and mass transfer boundary layer is subject to debate.

There is no consensus among researchers. Besides, all models have fitting parameters with unavailable closure relationships.⁹ Therefore, there is a necessity for a better understanding of the physical parameters affecting the wax deposition process. Furthermore, the models are developed based on the laboratory data, and the scale-up parameters for the conversion of laboratory data to field conditions are unavailable.^2,5,9

All models failed to predict the wax deposition process when applied to field conditions.^23,24 Besides, to obtain the closure relationship of all of the abovementioned models, an extensive experimental data set is required, which is a very expensive and time-consuming affair. Thus, in the absence of adequate physical understanding of the wax deposition mechanism, a simple predicting tool (statistical correlation, dimensionless theory) can be the advancement to upscale the laboratory data to field conditions.^5,17,26,27

As per the observation of statistical analysis of ref (5), the statistical parameter used in the statistical tool is not dimensionless; hence, there is a need for dimensionless correlation. Thus, other scale-up parameters were established using the data sets of refs (2, 17, 23) as per the law of the wall for turbulent theory. To develop the dimensionless scale-up approach, the following steps were considered.

Dimensionless scale-up parameters are defined, and a dimensionless scale-up approach is proposed using the data set of ref (2). The developed dimensionless approach is then verified using data sets of refs (17, 23). Based on the verified dimensionless approach, generalized correlations are obtained for scaling up flow loop data to field scale. For a better understanding, steps for scaling up flow loop data to field scale have been showcased in the below section.

2. Results and Discussion

2.1. Dimensionless Scale-Up Parameters

In the wax deposition process, as the wax is deposited in the pipe, the cross-sectional area of the pipe reduces resulting in a change of dynamic parameters, such as velocity and frictional velocity of the crude oil. The change of the abovementioned dynamic parameters affects the prediction of wax deposition in the pipe. Thus, to obtain accurate prediction, it is necessary to capture varying diameter effects due to wax deposition. Thus, the varying diameter was included in formulating two dimensionless scale-up time parameters presented in eqs 1 and 2

1

2

Equation 1 is based on the pipe average velocity (v), eq 2 is based on frictional velocity (v*), t is the time, R is the inside radius of the pipe, and δ is the deposition thickness.

Here, T′ and T″ are obtained using a dynamic change of the inner diameter of the pipe (2(R – δ)), due to wax deposition in the pipe. As the diameter changes, average velocity and frictional velocity in the pipe also changes; thus, the effect of average velocity and frictional velocities have also been incorporated into T′ and T″.

To understand the effect of the changed dynamic parameters of velocity and frictional velocity on the wax deposition thickness, the dimensionless wax deposition thicknesses δ′ and δ″ are considered as the scale-up parameters. Equation 3 represents the classical dimensionless thickness used for wax deposition analysis,²⁰ and eq 4(14) defines the new dimensionless wax deposition thickness. The new dimensionless wax thickness resembles the nondimensional wall distance y⁺ for turbulent flow theory.¹⁴

3

4

5

6

Fluid properties mentioned in eqs 4–6 were obtained at bulk oil temperature. Thus, dimensionless parameters were evaluated using eqs 1–4.

Various graphs (Figures 2–22) were depicted using evaluated dimensionless parameters to understand the trends and effect of wax deposition in crude oil pipelines for selected experimental data sets of refs (2, 17, 23) as per the abovementioned reasons.

Figure 2.

Linear correlation between the two dimensionless times for ref (2).

Figure 22.

Wax deposition potential exists to attain an asymptomatic value between the dimensionless concentration (ΔC_onc) and the dimensionless time (T″) for the data set of ref (17).

Also, to understand the experimental discrepancy from the data, the uncertainty analysis was conducted, as explained by ref (27) (S2: Appendix B of the Supporting Information). Also, the abovementioned data sets for validation of available wax deposition models were utilized. The estimated uncertainty bars are incorporated in Figures 2–22 to provide deeper insight into the analysis of the selected data sets.

Figure 2 helps to understand the relationship between two dimensionless time parameters. It shows a linear relationship between both dimensionless time parameters (T′ and T″), which means that both dimensionless times show similar trends with all other parameters, i.e., δ, δ′, δ″, and the Nusselt number (Nu). Although the quantification (magnitude) of each dimensionless time may be different, the calculated time (t) from either of the proposed dimensionless times for wax deposition in the pipe should be the same. Since T″ is obtained using v*, which is a dominant parameter for turbulent flow conditions, further investigations have been conducted using T″ with the other parameters.

Similarly, Figure 3 helps to understand the relationship between two dimensionless wax thicknesses δ′ and δ″ at given constant initial Reynolds numbers of 11 000, 7300, and 4300 for three pipe sizes (0.5, 1.0, and 1.5 in.). It indicates that there is a linear relationship between δ′ and δ″ at a given constant initial Reynolds number for varying pipe sizes. Thus, it may be inferred that there is a unique linear correlation between δ′ and δ″ irrespective of the pipe size for a given Reynolds number. Thus, no general correlation can be established for estimating wax deposition using the data of all Reynolds number cases.

Figure 3.

Relationship between the two dimensionless wax deposition thicknesses for ref (2).

Figure 4 (δ′ vs T″) shows the effect of the Reynolds number on wax deposition and also indicates that the Reynolds number is the only parameter affecting the wax deposition under turbulent flow conditions irrespective of the pipe size. However, the unified general trend has not been established, and the prediction of the dimensionless wax deposition thickness with respect to Reynolds numbers has not been defined yet.

Figure 4.

Dimensionless wax deposition thickness (δ′) dependency on the Reynolds number for ref (2).

The trends of Figure 5 gave further insight into the wax deposition process, indicating that it is independent of the pipe size but mildly dependent on the Reynolds number. However, the dependency is within the uncertainty bars incorporated in Figure 5, indicating that wax deposition may be independent of the Reynolds number.

Figure 5.

Dimensionless wax deposition thickness (δ″) independency with respect to the pipe size but mild dependency on the Reynolds number for ref (2).

Similarly, a plot of the deposit wax fraction was also drawn with T″ (Figure 6), as a wax fraction of the deposit is also one of the important parameters in the wax deposition process. Figure 6 also displays the independency of the values of F_w of varying pipe sizes but mild dependency on the Reynolds number.

Figure 6.

Wax fraction (F_w) independency with respect to the pipe diameter but mild dependency on the Reynolds number for ref (2).

Now, to further appreciate the dependent nature of wax deposition (δ″, F_w) on the Reynolds number within uncertainty bars, a plot of the Nusselt number and T″ (Figure 7) is shown. The Nusselt number is defined by Nu = h_oild_p/k_oil, where h_oil is the inside heat transfer coefficient, k_oil is the thermal conductivity of oil, and d_p is the inside diameter of the pipe.

Figure 7.

Nusselt number (Nu) and the dimensionless time (T″) for ref (2).

Figure 7 clearly indicates the propagation of discrepancy in the data set of Figures 5 and 6, which is due to either an experimental error or experimental facility limitation that is also reported in refs (17, 23, 26). Thus, it describes the dependency of wax deposition (δ″, F_w) on the Reynolds number, which is merely due to uncertainties caused during experimentation. Therefore, considering this fact, it can be further inferred that a general correlation, independent of both pipe size and the Reynolds number, can be established.

In addition to this, the asymptotic behavior of Figure 5 is an indication that the interface temperature of the wax deposit has approached the bulk oil temperature. Table B-1 (S1: Appendix A of the Supporting Information) displays the interface temperature and bulk oil temperature values corresponding to asymptotic value. This means that there is no temperature or concentration gradient; therefore, further wax deposition is not possible. Thus, an equilibrium condition has been attained by the system.

The temperature gradient between the bulk oil temperature and the interface temperature of the wax deposit plays an important role. Thus, new dimensionless temperature and concentration gradients, ΔT_emp and ΔC_onc, respectively, were defined using the central difference method. They are shown below as eqs 7–10.

7

where

8

9

where

10

C_b is the wax concentration in the bulk liquid phase, C_i is the concentration of wax in the liquid phase, T_b is the bulk oil temperature [°F], T_i is the interface temperature [°F], ΔC_onc is the dimensionless concentration gradient, and ΔT_emp is the dimensionless temperature gradient.

Based on the abovementioned equations, the dimensionless temperature gradient ΔT_emp and the dimensionless concentration gradient ΔC_onc were plotted against dimensionless time T″ to investigate the asymptotic nature further. Figures 8 and 9 present these results and display a similar dependent and independent nature with the Reynolds number and the pipe size, as observed in Figures 5 and 6. Again, considering the fact of experimental errors,^17,23,26 it can be inferred that this mild dependency is absent and a general correlation, independent of both the pipe size and the Reynolds number, can be established for dimensionless temperature gradient ΔT_emp and ΔC_onc with T″.

Figure 8.

Attainment of an asymptomatic value between the dimensionless temperature (ΔT_emp) and the dimensionless time (T″) for the data set of ref (2).

Figure 9.

Attainment of an asymptomatic value between the dimensionless concentration (ΔC_onc) and the dimensionless time (T″) for the data set of ref (2).

Figures 8 and 9 show that an asymptotic value is attained when ΔT_emp and ΔC_onc approach a value of 0.1. This similar trend of attaining an asymptotic value was observed in Figures 5 and 6.

Thus, this indicates that the interface temperature of the wax deposit has approached the bulk oil temperature, and no further deposition occurs on the wax deposit surface, showing that our inference (the interface temperature of the deposit has approached the bulk oil temperature of crude oil, resulting in no further wax deposition on the wax deposit surface) seems to be true. However, to discern this effect, experiments can be conducted for an extended duration (preferably up to 48 h) as ref (2) conducted experiments for the duration of up to 24 h.

Thus, ΔT_emp and ΔC_onc can be utilized as dimensionless upscaling parameters to predict wax deposition from flow loop to field conditions. It also indicates that when ΔT_emp reaches the asymptotic value of 0.1, further wax deposition stops as the interface temperature is almost equal to the bulk oil temperature. Thus, ΔT_emp = 0.1 can be utilized to estimate the maximum deposition thickness. The above theory was verified using the experimental data sets of refs (17, 23).

2.2. Verification of the Upscaling Theory Utilizing the Data Set of Ref (17) and (23)

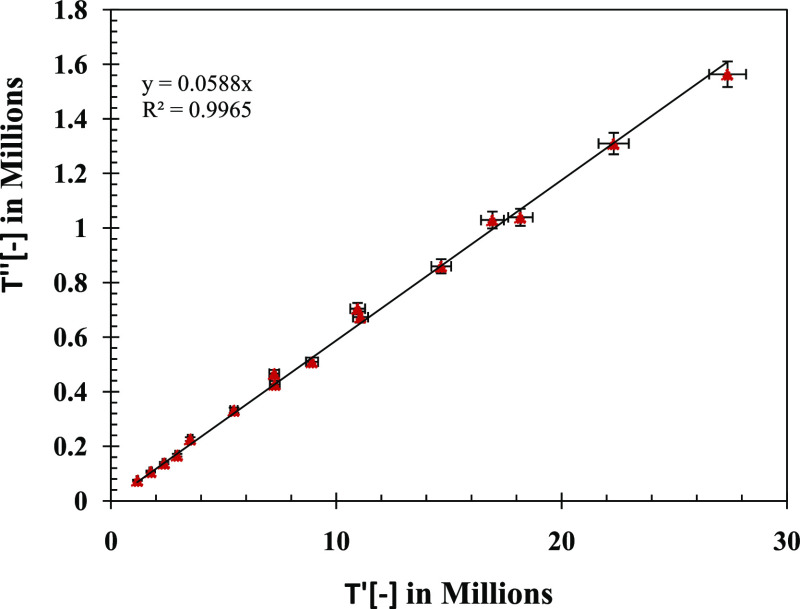
Figures 10 and 11 show the correlation between T′ and T″ parameters to understand the abovementioned observations of Figure 2. Figures 10 and 11 show a similar linear relationship between both dimensionless time parameters for the data set of refs (17 and 23), respectively, as observed in the data set of ref (2).They also display that a similar correlation of T″ = mT′ exists for all three data sets, where m is 0.0634, 0.0588, and 0.0712 for the data sets of refs (2, 23) and (17), respectively.

Figure 10.

Linear correlation between the two dimensionless times for ref (23).

Figure 11.

Linear correlation between the two dimensionless times for ref (17).

As per the values of m for refs (2, 23) data sets, it can be inferred that m can be considered to be 0.06; however, based on ref (17), where m = 0.0712, it cannot be generalized for all of the data sets.

Thus, Figure 12 is plotted with T′ and T″ values for all of the three data sets together for establishing a generalized value of m. A good linear relationship was observed between T′ and T″ for all of the data sets in Figure 12 with a general value of m = 0.0663. Therefore, it can be inferred that T″ = 0.0663T′ can be used for any data set with varying crude oil compositions and pipe sizes.

Figure 12.

Linear correlation between the two dimensionless times for refs (2, 17, 23).

Similarly, δ′ vs T″ was plotted in Figures 13 and14 for refs (17 and 23) data, respectively. Trends, similar to those of the data set of ref (2), were observed. Both data sets show that δ′ is a function of the Reynolds number and independent of the pipe size within the uncertainty range of data. The data of Re = 7000 of ref (23) in Figure 13 show a discrepancy against the decreasing trend in the wax deposition thickness as the Reynolds number increases. The reason for this discrepancy has been explained by refs (23, 26) that it may be due to uncertainty propagated by either the experimental facility or the experimental procedure.

Figure 13.

Dimensionless wax deposition thickness (δ′) dependency on the Reynolds number for the data set ref (23).

Figure 14.

Dimensionless wax deposition thickness (δ′) dependency on the Reynolds number for the data set of ref (17).

Similarly, the data set for the Re = 2700 in the data set ref (17) displayed inconsistency as compared to the well-established theory. The reason for this can be again due to uncertainty propagation or the turbulent flow correlations used for estimating the Nusselt number. Correlations for estimating the Nusselt number at the Re = 2700 (transition flow regime) are not well established. Thus, Figures 13 and 14 show that the dimensionless thickness δ′ (traditional approach) is still dependent on the Reynolds number, and it is difficult to establish a general correlation to predict wax deposition, which is independent of the pipe size and the Reynolds number.

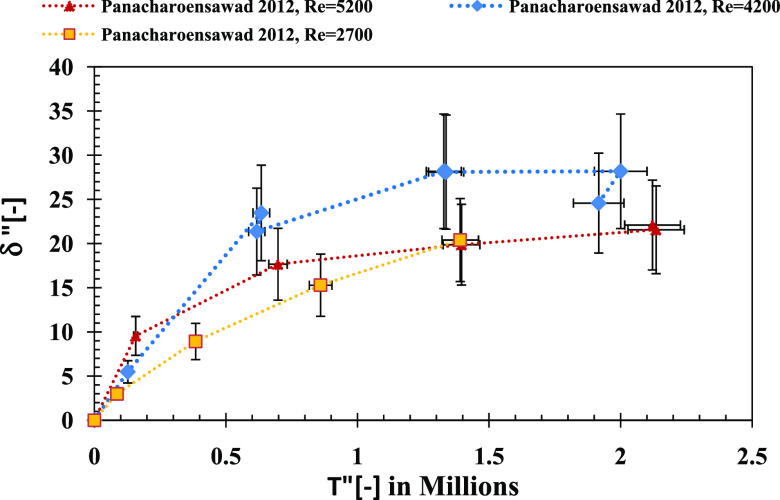
Thus, to further understand the independent nature of wax deposition with the pipe size and the Reynolds number as observed in Figure 5 for the data set of ref (2), plots of δ″ vs T″ and F_w vs T″ were drawn for the data sets of refs (17, 23) (Figures 15–18).

Figure 15.

Dimensionless wax deposition thickness (δ″) independency with respect to the pipe size if the red triangle is ignored for the data set of ref (23).

Figure 18.

Wax fraction (F_w) dependent on the pipe diameter for the data set of ref (17).

For the data set of ref (23), Figures 15 and 17 display the dependency of wax deposition (δ″, F_w) on the Reynolds number and not the pipe size. However, if Re = 7000, the data are ignored, and wax deposition (δ″, F_w) becomes independent of both the pipe size and the Reynolds number. Similarly, for the data of ref (17), Figures 16 and 18 exhibit dependency of wax deposition on the Reynolds number and not the pipe size.

Figure 17.

Wax fraction (F_w) independency with respect to the pipe diameter within the uncertainty bars for the data set of ref (23).

Figure 16.

Dimensionless wax deposition thickness (δ″) independency with respect to the pipe size within the uncertainty bars for the data set of ref (17).

As mentioned above, the reason for dependency on the Reynolds number may be due to utilization of the value of the Nusselt number based on the correlation applicable for a turbulent flow regime and not for a transition regime (Re = 2700). Also, it may be due to experimental errors, as reported in the data set of ref (17).

Thus, as per the above analysis of the data set of ref (2), if uncertainty error bars in Figure 16 are considered, then the dimensionless wax deposition thickness (δ″) becomes independent of both the Reynolds number and the pipe size for the data set of ref (17) also.

However, while considering uncertainty bars in Figure 18, they still show the dependency of wax deposition (F_w) on the Reynolds number. The reason for this inconsistency cannot be inferred due to insufficient data, and, thus, further investigation is necessary.

Furthermore, plots of ΔT_emp with T″ and ΔC_onc with T″ (Figures 19–22) for the data sets of ref (17) and (23) were drawn to compare the observations of Figures 8 and 9 for the data of ref (2) (Figure 20).

Figure 19.

Wax deposition potential exists to attain an asymptomatic value between the dimensionless concentration (ΔT_emp) and the dimensionless time (T″) for the data set of ref (23).

Figure 20.

Wax deposition potential exists to attain an asymptomatic value between the dimensionless concentration (ΔT_emp) and the dimensionless time (T″) for the data set of ref (17).

Similar trends as Figures 8 and 9 were observed in Figures 19–22. However, Figures 19–22 show that the asymptotic value of 0.1 is not reached for both data sets of refs (17 and 23). As per the data analysis of ref (2) (Figures 8 and 9), there is still potential for wax deposition until ΔT_emp and ΔC_onc = 0.1, which can be clearly observed in the data set of ref (17) and mildly in the data set of ref (23). Thus, based on all of the three data sets, it can be inferred that the value ΔT_emp and ΔC_onc = 0.1 can be utilized in the calculation of the maximum deposition thickness, where further wax deposition in the pipe stops. However, additional long-term experimental data are required for the data set of refs (17 and 23) to achieve a robust conclusion (Figure 21).

Figure 21.

Wax deposition potential exists to attain an asymptomatic value between the dimensionless concentration (ΔC_onc) and the dimensionless time (T″) for the data set of ref (23).

In summary, dimensionless thickness δ″ and T″ seem to be better scale-up parameters that should be utilized to scale up the laboratory flow loop data to field-scale data. The analysis of δ″ and T″ with the data sets of refs (2, 17, and 23) successfully showcases the independency of the Reynolds number and the pipe size from wax deposition, which was missing in traditional approaches. However, no common correlation for calculating δ″ and F_w was obtained between all three data sets. This might be due to different crude oils, MO-14, Garden Banks, and South Pelto, being utilized by refs (2, 17, and 23), respectively. Thus, data sets with different crude oils are required for incorporating the effect of crude composition in the upscaling parameter analysis.

2.3. Correlations Obtained Based on the Law of the Wall

To obtain a generalized correlation for predicting the dimensionless wax deposition thickness and a wax fraction (δ″, F_w), inconsistent data sets of refs (17 and 23) were ignored (testing condition at Re = 2700 for both data sets). Experimental inconsistency was considered for all three data sets. Figures 23–28 provide generalized correlations to predict the dimensionless wax deposition thickness and a wax fraction (δ″, F_w) for all of the three experimental data sets.

Figure 23.

Correlation between the dimensionless wax deposition thickness (δ″) and the dimensionless time (T″) for the data set of ref (2).

Figure 28.

Correlation between the wax fraction (F_w) and the dimensionless time (T″) for the data set of ref (17).

Figure 24.

Correlation between the wax fraction (F_w) and the dimensionless time (T″) for the data set of ref (2).

Figure 25.

Correlation between the dimensionless wax deposition thickness (δ″) and the dimensionless time (T″) for the data set of ref (23).

Figure 27.

Correlation between the dimensionless wax deposition thickness (δ″) and the dimensionless time (T″) for the data set of ref (17).

Based on the trends and observations of correlations obtained from Figures 23–28, generalized correlations for finding δ″ and F_w are provided in eqs 11 and 12, where values of a, b, a′, and b′ provided in Table 3 vary with the crude oil composition (Figure 26). Thus, the provided correlations can be used for the prediction of wax deposition in crude oil pipelines carrying Garden Banks, South Pelto, and MO-14 crude oil. For prediction of wax deposition of any other crude oil sample, obtaining values of a, b, a′, and b′ based on a small set of experiments is required.

11

12

Also, the discrepancy in the abovementioned constants is due to the varying crude oil composition, which might be eliminated using a multicomponent correlation to calculate the diffusion coefficient. Currently, the binary component system correlations²⁸⁻³⁰ are being used. Besides, diffusivity is calculated by estimating the viscosity based on the Newtonian behavior of the crude oil.^31,32 Also, looking at the current scenario, the utilization of artificial intelligence can be very handy in making the proposed predictive model more robust.³³⁻³⁶

Table 3. Value of Coefficients for All of the Three Crude Oil Data Sets.

coefficients	Agarwal (2016) MO-14 crude oil	Singh (2013) Garden Banks condensate	Panacharoensawad (2012) South Pelto crude oil
a′	1.088	0.165	0.008
b′	0.277	0.345	0.561
c′	0.6456	0.0283	0.0363
d′	0.2254	0.4989	0.4397

Figure 26.

Correlation between the wax fraction (F_w) and the dimensionless time (T″) for the data set of ref (23).

To verify the accuracy and precision of the abovementioned correlations in eqs 11 and 12, a statistical analysis was conducted.³⁷Table 4 displays the mean error, standard deviation, mean standard deviation, 95% confidence, and 95% precision level for all of the dimensionless parameters (δ″, F_w) predicted through correlations.

Table 4. Statistical Values of All of the Dimensionless Parameters (δ″, F_w) Predicted through Correlations.

	Agarwal (2016)		Singh (2013)		Panacharoensawad (2012)
	δ″	Fw	δ″	Fw	δ″	Fw
mean error	4.8	1.5	2.3	2.3	3.9	2.8
standard deviation	3.8	1.0	2.5	2.5	2.8	2.1
standard mean deviation	0.6	0.2	0.7	0.6	1.0	0.8
95% confidence	1.1	0.3	1.5	1.3	2.9	2.2
95% precision interval	0.2	0.04	0.4	0.3	1.1	0.8

Further, to observe the frequency of the errors obtained through the predictive tool, a percentage frequency plot was depicted for δ″ and F_w in Figures 29 and 30. Figures 29and 30 show that more than 50% of the predicted dimensionless parameters δ″ and F_w falls under the minimum error range. Thus, this indicates that the predictions from the proposed theory can be considered more accurate and reliable.

Figure 29.

Frequency plot for the dimensionless thickness δ″ showing that more than 50% of predictions made through the predictive tool falls under the minimum error range.

Figure 30.

Frequency plot for the dimensionless thickness F_w showing that more than 50% of predictions made through the predictive tool falls under the minimum error range.

3. Conclusions

The dimensionless times (T′, T″) and the dimensionless thickness δ″ were obtained by incorporating the varying diameter effect along with the law of the wall for turbulent flow conditions. A unique linear relationship between δ′ and δ″ at a given constant initial Reynolds number for different pipe sizes was obtained, which indicated independency of the pipe size and the dependency on the Reynolds number. The relationship between δ′ and T′ explained that the Reynolds number is the only parameter that affects the wax deposition process for turbulent flow conditions, while wax deposition is independent of the pipe size. However, the general correlation to predict wax deposition with varying Reynolds numbers has not yet been established. Thus, the relationship between δ″, F_w, and T″ was analyzed, which indicated the proposed general dimensionless correlation is independent of both the pipe size and the Reynolds number for all of the three data sets by considering discrepancies of experimental errors. Hence, it can be inferred that δ″ and T″ are the correct scale-up parameters that can be utilized for scaling up the laboratory data to the field. However, the analysis revealed that the coefficients in the generalized correlation are different for different oils. Therefore, this indicates that the oil effect remains and needs to be removed to make the proposed technique more universal.

The limitation of the above-proposed approaches can be due to a flaw in the calculation of the diffusivity coefficient during wax deposition in a pipe, as the correlations^29,30 are utilized for calculation of diffusivity coefficients, which are based on the binary system, while wax deposition in the pipe is a multicomponent system. Thus, it is recommended to obtain and utilize the multicomponent correlation for calculating the diffusivity coefficient as proposed by various researchers^{2−5,23,26,28} to make the correlation independent of the crude oil composition. Besides, the flaw may be rectified by estimating the viscosity based on the non-Newtonian behavior of the crude oil for the calculation of the diffusivity coefficient.^31,32 Also, looking at the current scenario, the above flaw may be rectified by the utilization of artificial intelligence to make the proposed predictive model more comprehensive.³³⁻³⁶ Further, for making more general universal correlations as mentioned in both the approaches of refs (5, 28) (statistical and turbulent theory), more experimental data in a controlled environment with varying pipe sizes and varying crude oil compositions are required. Further, to validate the above correlations, flow loop experiments should be conducted on the same crude oil whose field data are known and easily available. However, the proposed dimensionless technique can benefit the industry to decide the optimum pigging frequency and to design the optimum pipe size to mitigate the effect of the wax deposition process and save millions of dollars, provided the coefficients of the correlation are obtained at laboratory scale for the crude oil whose field data are known.

4. Computational Method

4.1. Procedure to Utilize the Dimensionless Theory

The proposed correlations and dimensionless parameters can be utilized for predicting wax deposition in pipes for particular crude-carrying pipes by generating the prescribed data and using the suggested eqs 13–14. The steps for utilization of correlations are listed below.

• 1.Gather the bulk oil temperature, oil flow rate, pipe geometry, pipe insulations, and the ambient temperature of the crude oil transportation pipeline that has a severe wax deposition issue.
• 2.Also gather crude oil samples for the experiment along with their characterized properties (density, viscosity, precipitation curve, thermal conductivity, specific heat, and pour point). An example of data collection is provided in Table 5.
• 3.Conduct the experiments for the smallest inner diameter of the pipe (0.5″) and generate graphs of δ″ vs T″, F_w vs T″, and ΔT_emp vs T″ as mentioned in Figures 5, 6, and 8, respectively.
• 4.
  Calculate T_i|_t0 based on eqs 13 and 14.²³

  13

  14

  T_i|_t0 = 90.40 °F
• 5.
  Calculate T_i|_tn based on eq 7 by keeping the value of ΔT_emp|_tn+1/2 = 0.1; this provides us with the interface temperature at which further wax deposition should not occur in the pipeline.

  15
• 6.Based on T_interface|_tn = 93.77 °F, one can predict the corresponding wax deposition thickness in the pipeline. This wax deposition thickness is the final or the maximum wax deposition thickness (δ_max) at which no further deposition occurs. δ_max can be obtained through an iterative procedure.
• 7.Let us consider the SSF-MO-14-04 condition (dark blue triangles) last point for the calculation of δ″ = 54 from Figure 5.
• 8.
  Once the value of δ″ is obtained, the value of v* can be calculated. The value of v* varies as the diameter varies; therefore, the value of v* of SSF-MO-14-04 is not the same as the value of v* of the 12″ field pipeline. Therefore, it is required to calculate v* from eq 16, where it is assumed that δ_exp= δ_max= 18 and the reduced internal pipe diameter after deposition of δ_max is 0.2688 m (10.50 in.).

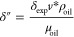
  16
• 9.Thus, the v* value for 12″ pipe is 0.01217 m/s.
• 10.
  After obtaining v*, the value of T″ can be calculated from eq 17

  17
• 11.Here, a = 1.088 and b = 0.2729 for the MO-14 crude oil for the data set of.² After substituting the values of a and b in eq 17, the obtained value of T″ = 1 264 720 s.
• 12.Now using this T″ in eq 18, the predicted field-scale time (t) for the maximum deposition thickness δ_max = 27 987 981 s = 324 days.

18

Thus, the abovementioned novel procedure successfully shows the independency of the Reynolds number and the pipe size from wax deposition, which is missing in traditional approaches, and helps to accurately predict the field-scale time for wax deposition in crude oil pipelines for a wide range of circular pipe sizes and operating conditions (different Reynolds numbers, flow rates, and temperature), provided the flow regime is turbulent, the coefficients a and b are obtained from a preliminary set of experiments, and the range of ΔT_eff is in the same region as the precipitation curve (Table 5).

Table 5. Collected Field Data.

parameters	values	parameters	values
outer pipe diameter [m]	0.311	μ [Pa·s]	0.00315
inner pipe diameter [m]	0.305	density [kg/m3]	788
Qoil [lb/min]	10 000	koil [W/(m K)]	0.1326
Toil [°F]	94.40	Cp oil[J/(kg K)]	2111.72
Tambient [°F]	89	Re	110 437
initial Tinterface [°F]	90
velocity [m/s]	1.51

Also, this procedure helps to design optimum pipe sizes and decide optimum operating conditions and pigging frequencies. However, the oil effect is still present, and more experimental data with different crude oils are required to develop a general correlation. This might be the limitation in the calculation of the diffusivity coefficient during a wax deposition process. Correlation of^29,30 utilized for the calculation of the diffusivity coefficient is based on a binary system, while wax deposition in the pipe is a multicomponent system. Thus, to remove the above limitations of the work, future attempts should be made to obtain a multicomponent system correlation for the calculation of the diffusion coefficient. It is likely that this correlation can include the varying oil composition effect and can help establish a general correlation, independent of the Reynolds number, pipe size, and the crude oil composition.

Glossary

Nomenclature Used

A_pipe

cross-sectional area of pipe [m²]

C_b

wax concentration in bulk liquid phase [kg/m³]

C_i

concentration of wax in liquid phase [kg/m³]

C_p

heat capacity of crude oil [J/(kg/K)]

dC/dT

radial concentration gradient [kg/(m³ K)]

dT/dr

radial temperature gradient

d_p

inside diameter of pipe [m]

D_wo

molecular diffusivity of wax in oil [m²/s]

f_fanning

Fanning friction factor []

f_moody

Moody friction factor []

F_w

solid weight fraction of deposit []

h_oil

inside heat transfer coefficient [W/(m² K)]

h_c

heat transfer coefficient for glycol [W/(m² K)]

J_exp

experimental wax mass flux [kg/(m²s)]

J_in

incoming wax mass flux [kg/(m² s)]

J_wax

wax mass flux [kg/(m² s)]

k_coating

thermal conductivity of coating [W/(m K)]

k_exp

experimental mass transfer coefficient [m/s]

k_l

mass transfer coefficient [m/s]

k_oil

thermal conductivity of oil [W/(m K)]

k_pipe

thermal conductivity of pipe [W/(m K)]

k_soil

thermal conductivity of soil [W/(m K)]

k_theoretical

theoretical mass transfer coefficient [m/s]

k_wax

thermal conductivity of deposit [W/(m K)]

L

length of pipeline [m]

Q_oil

hot side mass flow rate [kg/min]

r

inside radius of pipe which changes as deposition occurs [m]

R

inside radius of pipe [m]

R_o

outside radius of pipe [m]

t

time [s]

T_ambient

ambient temperature [°F]

T_b

bulk oil temperature [°F]

T_i

interface temperature [°F]

T

residence time [s]

T′

dimensionless time based on average velocity []

T″

dimensionless time based on frictional velocity []

U_eff

overall heat transfer coefficient [W/(m² K)]

U_env

heat transfer coefficient of the environment [W/(m² K)]

U_o

heat transfer coefficient of oil [W/(m² K)]

U_soil

heat transfer coefficient of soil [W/(m² K)]

U_Wax

heat transfer coefficient of wax [W/(m² K)]

v

average fluid velocity in pipeline [m/s]

v*

frictional fluid velocity in pipeline [m/s]

Glossary

Greek Symbol

ΔC_onc

dimensionless concentration gradient []

ΔT_eff

temperature difference [°F]

ΔT_emp

dimensionless temperature gradient []

δ

deposition thickness [m]

δ_exp

experimental deposition thickness [mm]

δ_max

maximum deposition thickness [mm]

δ′

dimensionless thickness based on average velocity []

δ″

dimensionless thickness based on frictional velocity []

μ_oil

viscosity of crude oil [cP]

ρ_oil

density of oil [kg/m³]

ρ_wax

density of deposit [kg/m³]

τ_max

maximum shear stress [Pa]

τ_r

shear stress at a given point, as wax deposition occurs [Pa]

Glossary

Dimensionless Numbers

Nu

Nusselt number of heat transfer

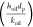
Pr

Prandtl number

Re

Reynolds number

Re_ini

initial Reynolds number

Sc

Schimdt number

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c05966.

• Appendix A, temperature data (Table S1); and Appendix B, uncertainty analysis (S2) (PDF)

The authors declare no competing financial interest.