Abstract
The design and optimization of solvent extraction processes for metal separations are challenging tasks due to the large number of adjustable parameters. A quantitative predictive solvent extraction model could help to determine the optimal parameters for solvent extraction flow sheets, but such predictive models are not available yet. The main difficulties for such models are the large deviations from ideal thermodynamic behavior in both the aqueous and organic phases due to high solute concentrations. We constructed a molecular thermodynamic model for the extraction of CoCl2 from different chloride salts by 0.2 mol L–1 trioctylmethylammonium chloride in toluene using the OLI mixed-solvent electrolyte (OLI-MSE) framework. This was accomplished by analyzing the water and hydrochloric acid content of the organic phase, measuring the water activity of the system, and using metal complex speciation and solvent extraction data. The full extractant concentration range cannot be modeled by the OLI-MSE framework as this framework lacks a description for reversed micelle formation. Nevertheless, salting effects and the behavior of hydrochloric acid can be accurately described with the presented extraction model, without determining specific Co(II)–salt cation interaction parameters. The resulting model shows that the salting effects originate from indirect salt cation–solvent interactions that influence the availability of water in the aqueous and organic phases.
1. Introduction
Solvent extraction (SX or liquid–liquid extraction) is a technique often applied to separate and purify metals on an industrial scale. In a solvent extraction process, the separation of metal ions is based on the differential distribution of solutes between two immiscible liquid phases. It is a scalable technology that allows to process large quantities in a controllable manner, but it also requires the optimization of several operational parameters.1 Traditionally, several experiments should be performed to determine the best conditions for each solvent extraction step in a separation flow sheet. Understanding the chemistry on a qualitative basis will already help to determine the direction of the experiments, but a quantitative predictive model seems necessary to significantly reduce the amount of experimental work. Quantitative models can be generated by fitting solvent extraction data with purely mathematical expressions, but this strictly empirical approach has little predictive power.2−4
The predictive power of a model increases when the model describes the underlying chemical phenomena better. As most solvent extraction systems are used at thermodynamic equilibrium, it suffices to use a thermodynamic model. Nevertheless, there are solvent extraction systems where kinetics plays an important role. For these systems, a time-dependent model is necessary.5 In a first step to produce a predictive thermodynamic model, chemical species, reactions, and equilibrium constants can be used.6 However, in the absence of activity corrections, this approach can overestimate the number of chemical species necessary to describe the system due to the absence of activity corrections. Some of the species in the model have no real chemical basis, which limits the predictive power of the model. The issue of too many chemical species can be resolved by calculating activity coefficients. Several activity models are capable of this.7−9 However, these models mainly use solvent extraction data to fit the model parameters that describe the activity coefficients. Restriction to the use of such data to describe a chemically complicated process might result in a set of parameters that does not represent the correct underlying chemistry.1 This also limits the predictive capabilities of such models.
Completely different from these empirical models are the more fundamental formulations of solvent extractions. These formulations try to incorporate the complex structure of the organic phase on a nanoscale. Recently, it has become evident that the organic phase of an extraction system is not just simply an extractant solvated by a diluent. The extractants often resemble surfactants and thus have surfactant-like properties, such as self-assembly in reverse aggregates.10,11 Quantum mechanical calculations and molecular dynamics simulations can be used to describe the organic phase. However, these techniques are computationally very demanding and difficult to implement in a thermodynamic model that can accessibly describe a complete solvent system. Nevertheless, concepts start to emerge that try to tackle this problem.12−14
A middle ground should be found to get a predictive solvent extraction model that can describe the whole extraction process and can even be the basis for flow sheet modeling. A predictive model can be constructed starting from the thermodynamics of solvent extraction, but it should also correct for the non-ideal behavior via an excess Gibbs energy (GEX). The GEX can be described using semiempirical molecular thermodynamics.15,16 Herein, a thermodynamic description of the solution is combined with accessible experimental data. The experimental data should describe the fundamental chemistry of the extraction process to get a correct expression for GEX. A mixed-solvent electrolyte molecular thermodynamic model is necessary to account for the non-ideal behavior in aqueous and organic phases that contain electrolytes. In this class, both the electrolyte non-random two-liquid (eNRTL) and the OLI mixed-solvent electrolyte (OLI-MSE) frameworks are promising.17−20
To create a predictive quantitative solvent extraction model, we translated the chemistry behind the extraction of cobalt(II) from chloride media by a basic extractant in the OLI-MSE framework. The basic extractant of choice was trioctylmethylammonium chloride (TOMAC) as this is the pure form of the well-known commercially available extractant Aliquat 336. Aliquat 336 is a mixture of quaternary ammonium chlorides with different alkyl chain lengths and impurities that derive from the starting materials.21 The use of a pure extractant simplifies the thermodynamic model as only one molecule should be added to describe the extractant system. The CoCl2–TOMAC extraction system is well suited as an example to construct a thermodynamic model of basis extractant systems. The commercial equivalent (Aliquat 336) is commonly used in several metal separation schemes,22−24 and it is specifically used for Co(II) purification in chloride media.1 Also, Co(II) forms complexes by coordinating chloride anions, which can be easily spectroscopically quantified. This is invaluable to get a full chemical description of the extraction system that is necessary for accurate thermodynamic modeling. The OLI-MSE framework was selected as it uses interaction parameters for individual ions, rather than interaction parameters for ion pairs used in the eNRTL model.
To construct the model, first, hydration effects in the organic phase were investigated. Then, a quantitative description of the aqueous phase in the MSE-OLI framework was created. Finally, the organic phase in the OLI-MSE framework was reconstructed and the complete solvent extraction model was created by forming a Co(II)–TOMAC complex in the organic phase. This paper shows that the OLI-MSE framework can be used to describe salting-out effects in solvent extraction systems with basic extractants, but it is less suited to describe the full TOMAC concentration range from diluted solutions to pure extractants.
2. Results and Discussion
2.1. Water Uptake by TOMAC
Previous studies showed that the extraction of transition-metal ions to basic extractants for a given extractant and its concentration is mainly determined by the metal ion hydration.25−28 These studies focused mainly on the effects of a changing aqueous phase composition on the aqueous phase itself. However, it seems logical to assume that the organic phase is also influenced by changes in the aqueous phase. Thus, it is necessary to further investigate the organic phase before a quantitative chemistry-based extraction model can be constructed.
As hydration effects are crucial for the solvent extraction process, the water content in the organic phases of TOMAC in toluene was measured as a function of the TOMAC concentration after equilibrating with a 0.1 mol L–1 LiCl aqueous phase (Figure 1). The last data point at an initial TOMAC concentration of 2.14 mol L–1 is for pure TOMAC. Also, the water activity aw of all samples was measured and converted to a mole-fraction-based activity coefficient (γw,org) using the equilibrium mole fraction of water in the organic phase (Figure 1).
Figure 1.
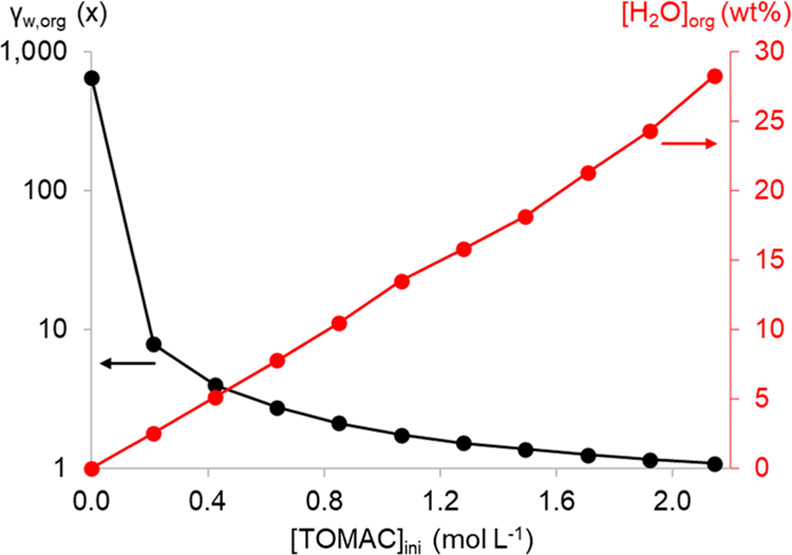
Water content of the organic phase and mole-fraction-based activity coefficients of water in the organic phase as a function of the initial (ini) TOMAC molarity in toluene after equilibration with a 0.1 mol L–1 LiCl aqueous solution.
The densities of the water-saturated organic phases were also measured to convert the mass-based results of the organic phase to molarities (Table 1). This conversion allows for easier comparison with other solvent extraction literature values that are most often reported in molarities. The small amount of LiCl (0.1 mol L–1) was added to the aqueous phase to improve phase separation after mixing.29 This only slightly lowers the water activity of the aqueous phase before the two-phase experiments to 0.996. On the x-axis of Figure 1, the initial TOMAC concentration is given, but the TOMAC concentration at equilibrium is significantly lower due to the large amount of water taken up in the organic phase. Therefore, the relation between the initial molarity of TOMAC and the equilibrium molarity (i.e., the water-saturated TOMAC solution) is given in Table 1. The equilibrium TOMAC molarities were calculated as follows
with n(x) being the number of moles of x, m(x) being the mass of x, and ρ being the density. The subscripts ini and org stand for initial phase and organic phase, respectively.
Table 1. Relation between Initial (ini) and Water-Saturated (eq) TOMAC Molarity in Toluene after Equilibration with 0.1 mol L–1 LiCla.
| [TOMAC]ini (mol L–1) | [TOMAC]eq (mol L–1) | densityorg,eq (g mL–1) |
|---|---|---|
| 0.21 | 0.21 | 0.868 |
| 0.43 | 0.41 | 0.874 |
| 0.64 | 0.60 | 0.880 |
| 0.85 | 0.78 | 0.886 |
| 1.06 | 0.94 | 0.891 |
| 1.28 | 1.11 | 0.897 |
| 1.49 | 1.26 | 0.902 |
| 1.71 | 1.39 | 0.907 |
| 1.92 | 1.51 | 0.912 |
| 2.14 | 1.60 | 0.918 |
The equilibrium TOMAC concentration is significantly reduced by the presence of large amounts of water in the organic phase. In addition, the density of the organic phase at 25 °C at equilibrium is given.
As expected, the water content of the organic phase significantly increased with increasing TOMAC concentration. At higher TOMAC concentrations, significant volume changes of the aqueous and organic phases occurred when fresh TOMAC was used. Therefore, it is advised to saturate the organic phase with water prior to the actual solvent extraction experiments in order to minimize volume changes. Also, the equilibrium TOMAC concentration should be used when analyzing solvent extractions with TOMAC as using the initial TOMAC concentration will result in significant errors in, for example, organic metal loading calculations. Together with an increase in water content of the organic phase, the γw,org is significantly lowered to almost 1. At high TOMAC concentrations, the water activity is close to unity so that the water in the organic phase almost behaves as pure water.
The unusually high water content of the organic phase and the corresponding low γw,org can be explained by considering how water is present in the organic phase, the large concentration of which is determined by the surfactant properties of TOMAC. Surfactant molecules tend to organize themselves in micellar structures, and this occurs already at concentrations as low as 10–4 to 10–3 mol L–1 TOMAC in the aqueous phase.30,31 This critical micelle concentration (CMC) is in the same order as the solubility of TOMAC in water.32 In the organic phase, reversed micelles can be formed.33−38 In these reversed micelles, the hydrophobic alkyl chains of TOMAC are directed toward the bulk organic phase and the charged headgroup forms the outer layer of an aqueous pocket. In biological and biochemical studies, these reversed micelles of TOMAC are used for separation purposes after addition of an alcohol as a cosurfactant.33,35,38 This cosurfactant is added to increase the packing parameter P above 1. This packing parameter is defined as P = v/(al), where v is the volume of the hydrophobic tail, a is the headgroup area, and l is the effective tail length. When P > 1, a spontaneous radius of curvature would be obtained that promotes the formation of reversed micelles.39
However, the formation of micellar structures depends on many parameters, and there is no clear indication that the presence of a cosurfactant is necessary to form reverse micelles in these biological and biochemical studies. On the contrary, experimental evidence is available that indicates the formation of TOMAC reversed micelles in organic solvents without the addition of a cosurfactant.34,36,37,40 This evidence includes a breakpoint in the absorption maxima and specific conductivity as a function of TOMAC concentration in dichloroethane,34 transmission electron microscopy observations of reversed micelles of TOMAC in trichloroethylene,36,37 and the formation of TOMAC reversed micelles in dichloromethane.40 The CMC for TOMAC reversed micelles in dichloromethane is 0.06 mol L–1, according to Berkovich and Garti, and this value is far below the concentration used in our study.34
These aqueous pockets in the organic phase are structurally very different from the bulk organic phase and most likely result in a different local behavior of salts and extractable metal complexes.12−14 If the contents of reversed micelles appear almost identical to the aqueous phase, a similar explanation for the solubility of salts and extractable complexes can be given. Thus, solutes that preferably reside in the aqueous phase might also preferably distribute to the reversed micelles compared to the bulk of the organic phase. Such solutes are, for instance, salting agents or strongly hydrated metal complexes. On the other hand, solutes are extracted efficiently when they are weakly hydrated and when they associate easily with TOMAC. Under these conditions, these solutes will not receive significant extra stabilization from the aqueous pockets in the organic phase. However, it is very difficult to quantify the influence of reversed micelles on the overall extraction of metal complexes as the extraction is the sum of different processes and effects. Nevertheless, it might still be possible to quantify the overall extraction process with a thermodynamic model that incorporates all the different processes and effects of an extraction.
2.2. Salting Effects in the Organic Phase
The water content of the organic phase is influenced not only by the TOMAC concentration but also by the composition of the aqueous phase. For instance, this was observed directly in the case of extraction of rare-earth chlorides by basic extractants. Vander Hoogerstraete et al. determined the speciation of the extracted metal complex as a function of the water content of the aqueous phase and found that the speciation changes the number of water molecules directly coordinated to the extracted rare-earth ion and thus the water content of the organic phase.41
Figure 2 shows the water content of the organic phase after equilibrating 0.2 mol L–1 TOMAC with aqueous phases containing different chloride salts or HCl. The water content of the organic phase decreases with increasing salt or HCl concentration because a higher salt or HCl concentration lowers aw in the two-phase system.42,43
Figure 2.
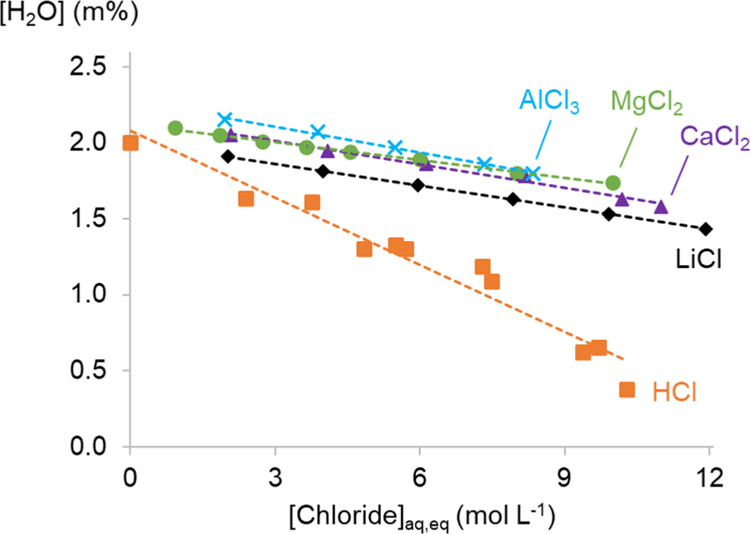
Water content of the organic phase comprising 0.2 mol L–1 TOMAC in toluene for different chloride salts in the aqueous phase. The x-axis shows the total chloride concentration at equilibrium in the aqueous phase. Linear fits were added to increase the readability.
The water content of the organic phase is very similar when different salts are used, but there is a trend related to the charge of the salt cation. Salts with higher charged cations result in an organic phase with a slightly higher water content, but it is not clear whether these two phenomena are causally related. The water activity aw of a LiCl solution is slightly lower than that of a CaCl2, MgCl2, or AlCl3 solution with the same total aqueous chloride concentration.42,43 This can be the cause of a slightly lower water content of the organic phase. The aw values of CaCl2, MgCl2, or AlCl3 solutions with the same chloride concentration are comparable, which is also reflected by an almost identical water content of the organic phase in contact with the aqueous phases.
The water content of the organic phase of the systems with HCl decreases more rapidly with increasing acid concentration compared to the salt systems. This is most likely due to the presence of significant amounts of HCl in the organic phase. Literature reports show that HCl is extracted to the organic phase by quaternary ammonium chlorides and attribute the HCl extraction to the formation of a TOMA–HCl2 complex.44,45 This could also explain the often observed decrease in metal extraction efficiency at high HCl concentrations. However, our previous studies showed that the decrease in metal extraction at high HCl concentrations is not related to competition effects.25,26 HCl in the organic phase does not seem to remove free TOMAC molecules from the system by forming a TOMA–HCl2 complex. Nevertheless, HCl is present in the organic phase and seems to replace some of the water molecules in the reversed micelles. Apart from the effects of HCl on the properties of the organic phase, HCl might also influence the stability of metal complexes in the aqueous phase differently due to the more covalent character of the H–Cl bond and the formation of a covalently bonded H–H2O network.46−48 Further investigation on the role of HCl in the extraction system will be discussed in the text below, when the overall extraction system is discussed with thermodynamic modeling.
2.3. Water Activity of Aqueous Co(II) Solutions
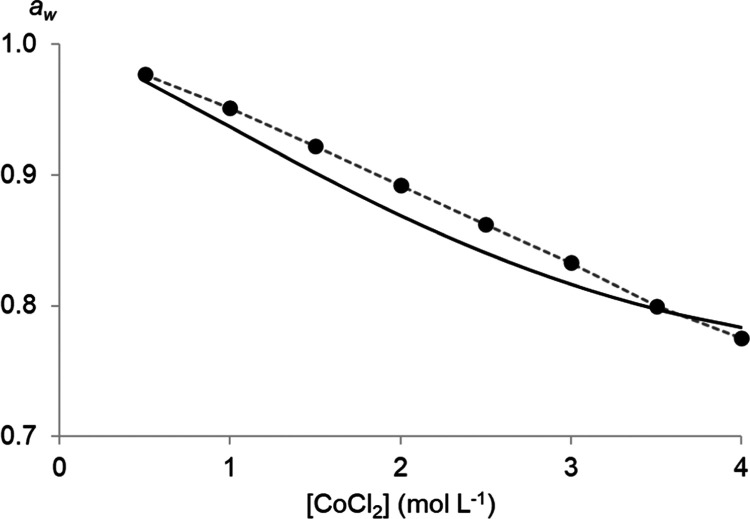
The water activity aw of an aqueous solution has been proven useful to investigate hydration effects in an aqueous solution on solvent extractions.26,27 Understanding these effects helps to explain and calculate the extraction of metal ions by basic extractants. To quantify the change in hydration of the extractable metal complexes, the aw values of salt solutions were subtracted from that of Co(II)-containing solutions (0.085 mol L–1 CoCl2) with the same amount of salt. This results in Δaw (eq 7) that accounts only for the measurable hydration effects of the addition of CoCl2 to a salt solution (Figure 3). Using Δaw instead of the aw of the salt solutions with CoCl2 is specifically useful to visualize the tiny effects on the aw that arise from the addition of a small amount of CoCl2to the salt solutions. Note that Δaw of HCl solutions could only be determined for HCl concentrations up to 4 mol L–1 because of too much interference by the HCl vapor in the water activity meter above 4 mol L–1 HCl.
Figure 3.
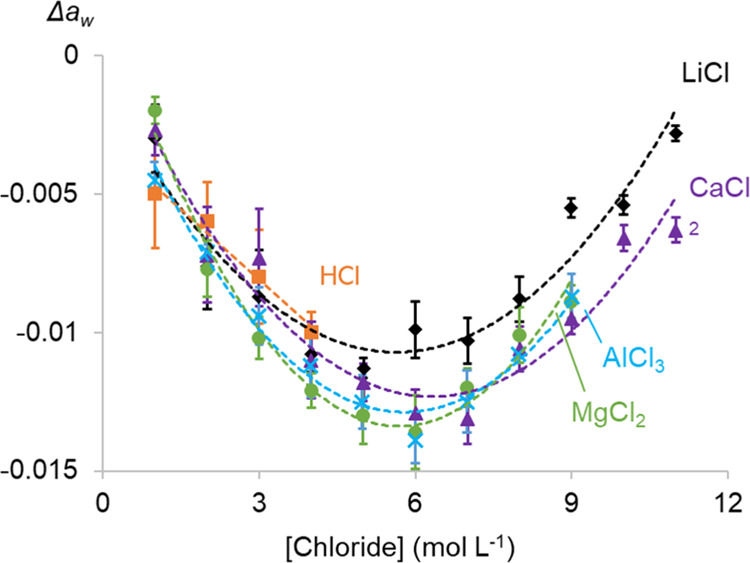
Difference in the water activity (Δaw) of salt solutions with and without 0.085 mol L–1 CoCl2 as a function of the total chloride concentration. Error bars are based on triplicate measurements, and quadratic fits were added to increase the readability.
The Δaw value is minuscule compared to the individual aw values (range: 0.2274–0.9788), which results in significant errors on the Δaw values. For this reason, error bars have also been added to the graph. A comparison between the Δaw in different salt solutions is difficult due to this significant error, but a general trend for all salt solutions can be observed. All Δaw curves go through a minimum at a chloride concentration of about 6 mol L–1.
It is not possible to directly relate the measured Δaw values to the hydration of Co(II) for two reasons. First, it is impossible to experimentally measure the effect of hydration of a single ion or charged complex directly in solution because counterions are always present for maintaining charge neutrality. For instance, Co(II) is added as CoCl2, and complexation between Co(II) and chloride ions influences the free chloride concentration
| 1 |
The contribution of Co(II) to the measured aw can be extracted in two ways: (1) by determining the contribution of the counterion (e.g., chlorides) using computational techniques, but this works properly only under standard conditions,49 and (2) by constructing a thermodynamic model that incorporates activity coefficients to allow working at high ionic strengths. The second reason that the measured Δaw values cannot be related directly to the hydration of Co(II) is that the changes in hydration of all species in a solution influence aw. The addition of CoCl2 also influences the speciation and/or hydration of the salting agent, and this will also affect aw. Such interactions/reactions in LiCl and CoCl2 solutions could be represented by eqs 2 and 3
| 2 |
| 3 |
To account for all interactions of solutes with each other and with the solvent on aw of the solution, a complete thermodynamic model is required.
2.4. Model for Co(II) Extraction from Different Salting Agents
To get a predictive quantitative model, it is necessary to combine all known chemical data of a solvent extraction system in one model, including activity data. Otherwise, it can be expected that the determined interaction parameters will not correctly represent the underlying chemistry.50 The OLI-MSE framework was selected because it is one of the most advanced thermodynamic models available and it also allows to start from an extended database of chemical thermodynamic data.19,20 The OLI-MSE thermodynamic framework can accurately model electrolytes in both aqueous and organic solutions, and the already available data in the database will increase the thermodynamic accuracy of the new solvent extraction model. For instance, the activity of aqueous salting agents and the chemistry of the binary water–toluene system are already validated by OLI.
However, there is one major drawback. The OLI-MSE framework describes every phase homogeneously, but the organic TOMAC phase has two markedly different regions. There is not only the bulk hydrophobic organic phase with mainly a diluent but also aqueous pockets enclosed by TOMAC reversed micelles. Therefore, it was not possible to model the whole concentration region from dilute TOMAC to the pure extractant, where different structures and/or sizes of reversed micelles are formed. Instead, it was decided to limit the modeled TOMAC concentration range to only 0.2 mol L–1 TOMAC in toluene because all other extraction data were available at this concentration. Generally, short-range (SR) UNIQUAC parameters are sufficient to model the two-phase behavior of neutral species, but the presence of inversed micelles also necessitates the use of the mid-range (MR) interaction parameters. Of course, the use of the OLI-MSE framework to model a system with micelles will result in somewhat deformed H2O–TOMAC interaction parameters.
First, a summary of the extraction mechanism of TOMAC is given before explaining the extraction model. The extraction of a metal ion is determined by the stabilization of its metal complexes in the aqueous and organic phases. In the organic phase, most transition-metal ions are present as anionic complexes by coordination with anions such as chlorides. These anionic complexes associate with the TOMA cation, and this interaction stabilizes them in the organic phase.25 Therefore, metal ions that easily form complexes with a certain anion are overall more efficiently extracted in that anion system. In the aqueous phase, the stabilization of a metal ion is determined by its degree of hydration. This hydration can be lowered by lowering the charge density of the metal ion or by removing free water from the system.26,27 The charge density of a metal ion in a certain anion system can be lowered by coordinating the right number of anions. The free water content of the aqueous phase can be lowered by increasing the salt concentration and by increasing the Gibbs free energy of hydration of the salt cation, while taking self-association of the cation and the anion of the salt into account.26
In the aqueous phase, the Co(II) speciation and aw are the most important properties for a correct solvent extraction model. Therefore, the speciation of CoCl2 in HCl and different salt solutions was calculated using UV–visible (UV–vis) absorption spectra of Co(II) reported in our previous papers using the three Co(II) species determined by Uchikoshi et al.(25,26,51) The activity of the CoCl2 solutions was modeled with aw of CoCl2 as a function of the CoCl2 concentration based on data from Goldberg and using the Δaw data presented above (Figure 3).52 All these data could be modeled using only the standard-state formation Gibbs free energies (ΔGf0) of Co2+, CoCl+, and CoCl42– and MR interaction parameters between the Co(II) species and chloride ions (Figures 4, 5, and 6). The ΔGf of Co2+ was taken from the OLI database, the ΔGf0 of CoCl+ was estimated via a group contribution method and further optimized to represent the experimental data, and the ΔGf of CoCl42– was taken from a literature report and slightly optimized for an improved fit to the data.53 The optimization of ΔGf0 was performed together with the interaction parameter regressions with the OLI ESP 9.6 regression tool. An overview of all optimized thermodynamic data and interaction parameters can be found in Tables 2 and 3.
Figure 4.
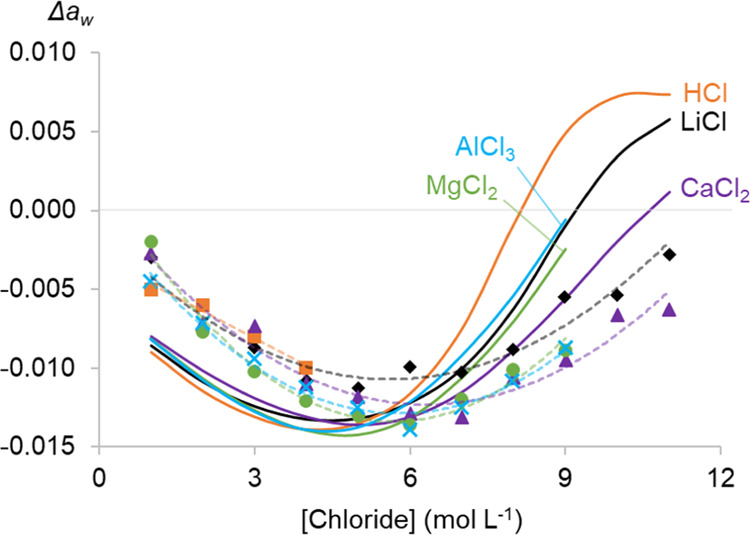
Δaw of 0.085 mol L–1 CoCl2 solutions as a function of the total chloride concentration. The full lines represent the fitted model calculations, while the points are experimental data. The dotted quadratic lines have been added and experimental error bars have been omitted to increase the readability of the experimental results.
Figure 5.
Water activity aw of aqueous CoCl2 solutions as a function of CoCl2 concentration. The full line represents the model calculations, and the points represent the experimental data reported by Goldberg.52
Figure 6.
Speciation of Co(II) in different aqueous chloride solutions expressed as the mole ratio (x) of each species to the total Co(II) content. The x-axis shows the total chloride concentration. The full lines represent the model calculations, while the points are experimental data from our previous papers.25,26
Table 2. Optimized Standard-State Thermodynamic Properties and the UNIQUAC Surface and Size Parameters of All Species Necessary for the Co(II) Chloride Solvent Extraction Model with TOMAC in Toluene.
| species | ΔGf0 (kJ mol–1) | υ0a(L mol–1) | qb | rc |
|---|---|---|---|---|
| Co2+ | –54.39 | |||
| CoCl+ | –176.89 | |||
| CoCl42+ | –538.65 | |||
| TOMAC | 218.15 | 0.444 | 12.27 | 16.50 |
| Q2CoCl4 | 139.65 | 1.031 | 27.34 | 34.84 |
Molar volume of the pure liquid.
UNIQUAC surface parameter.
UNIQUAC size parameter.
Table 3. Optimized UNIQUAC and MIDRANGE Binary Interaction Parameters for the Co(II) Chloride Solvent Extraction Model with TOMAC in Toluene at 298 K.
| system | UNIQUAC | MIDRANGEa | MIDRANGE densityb |
|---|---|---|---|
| b0(Cl–,Co2+) = 54.96 | |||
| aqueous phase: | c0(Cl–,Co2+) = −89.56 | ||
| Water | b0(Cl–,CoCl+) = 32.37 | ||
| CoCl2 | c0(Cl–,CoCl+) = 60.02 | ||
| HCl, LiCl | |||
| CaCl2, MgCl2 | b0(Cl–,CoCl42–) = 23.88 | ||
| AlCl3 | c0(Cl–,CoCl42–) = −45.38 | ||
| b0(Cl–,Li+) = 194.0 | d1(H2O,Li+) = 1.95 × 10–3 | ||
| c0(Cl–,Li+) = 10.36 | |||
| b0(Cl–,Al3+) = −902.1 | |||
| c0(Cl–,Al3+) = 1268 | |||
| a(H2O,QCl) = 1.239 × 105 | b0(H2O,QCl) = 30.32 | d1(H2O,QCl) = −6.99 × 10–3 | |
| a(QCl,H2O) = −3239 | c0(H2O,QCl) = 6.506 | d2(H2O,QCl) = −1.54 × 10–2 | |
| d4(H2O,QCl) = −1.54 × 10–6 | |||
| a(HCl,QCl) = −5970 | b0(HCl,QCl) = 7.738 | d1(HCl,QCl) = −0.207 | |
| organic phase: | a(QCl,HCl) = −1.720 × 104 | c0(HCl,QCl) = −114.1 | d2(HCl,QCl) = −0.195 |
| TOMAC (QCl) | |||
| toluene (Tol) | a(Tol,QCl) = 6510 | b0(Tol,QCl) = 23.48 | d1(H2O,Tol) = −3.38 × 10–4 |
| Water | a(Tol,H2O) = −4082 | d2(H2O,Tol) = −3.08 × 10–4 | |
| HCl | |||
| Q2CoCl4 | a(Tol,Q2CoCl4) = 651.4 | d1(HCl,Tol) = 4.51 × 10–3 | |
| a(Q2CoCl4,Tol) = −2492 | d2(HCl,Tol) = 8.08 × 10–3 | ||
| a(H2O,Q2CoCl4) = −664.4 | |||
| a(Q2CoCl4,H2O) = 5.296 × 106 |
MIDRANGE ionic strength independent (b) and dependent (c) parameters.19
MIDRANGE binary density interaction
parameters in the OLI-MSE framework according to the equation 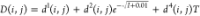 .
.
No specific salt cation–Co(II) interaction parameters were necessary. This further supports our hypothesis that the hydration and stability of Co(II) chloride complexes in the aqueous phase are governed by ion–solvent interactions, which are accounted for in the general OLI public database by the single salt systems.19,26 The agreement between the experimental and fitted Δaw of Co(II) in LiCl, CaCl2, MgCl2, and AlCl3 is reasonably good (Figure 4). The shape and range of the experimental and calculated curves are similar, and minima for all curves are found at a chloride concentration of about 5–6 mol L–1. The differences between the experimental and calculated results can be explained most likely by the very small values of Δaw and the relatively large error on the experimental measurements. The Δaw of Co(II) in HCl solutions was also calculated over the whole chloride concentration range, but comparison with experimental data is possible only for a chloride concentration up to 4 mol L–1. The calculated speciation of Co(II) agrees quite well with experimental results (Figure 6). Only the amount of CoCl+ in HCl seems to be overestimated by the calculations or underestimated by the statistical analysis of the UV–vis absorption data. The latter might be true as the shapes of the absorption spectra of Co2+ and CoCl+ are quite similar.51 The shift in formation of CoCl+ and CoCl42– to higher chloride concentrations in CaCl2, MgCl2, and AlCl3 media can be explained by a lower free chloride concentration due to ion-pair formation between those salt cations and chloride.26
When looking at the organic phase, first, the TOMAC species should be defined in the MSE-OLI model. The ΔGf0 of TOMAC was not available in the literature. Therefore, it was determined using a group contribution method based on the ΔHf and Sf0 of trioctylamine and chloromethane (Table 2).54−56 The UNIQUAC surface (q) and size (r) parameters of TOMAC were taken from Carneiro et al. (Table 2).57 The ΔGf, q, and r of TOMAC were kept constant during the optimization of the UNIQUAC and MR interaction parameters between TOMAC, the solvents, and HCl.
To extract Co(II), a single-phase extraction equation was written using TOMAC and the aqueous Co(II) chemistry, as is required for the MSE-OLI model
| 4 |
where QCl is TOMAC. Only one organic Co(II)–TOMAC complex is obtained.58,59 Note that it is not important which aqueous Co(II) species is chosen for the reaction equation. Equation 4 can be rewritten for every other aqueous Co(II) speciation using Hess’s law and the aqueous Co(II)–chloride coordination reactions, which results in the same outcome of the thermodynamic calculations. Initial values for ΔGf0, q, and r of Q2CoCl4 were all determined with group contributions methods as no data could be found in the literature (Table 2). The obtained ΔGf value was later optimized during the regression, while q and r were kept constant. In a next step, the Co(II)–TOMAC complex is distributed between the aqueous and organic phases using the UNIQUAC interaction parameters.
The interaction parameters and ΔGf0 values of Q2CoCl4, TOMAC, and Co(II)–chloride species were optimized together to produce a model that resembles the correct chemistry for the whole Co(II) chloride extraction system at 0.2 mol L–1 TOMAC. All available experimental data were used during this parameter optimization. The first set of experimental data was the two-phase behavior of a water–TOMAC–toluene system as a function of the type and concentration of the salting agent used, as described above. This also includes the distribution of HCl to the organic phase. The second data set comprised the solvent extraction data of Co(II) from different salting agents taken from previous publications.25,26 The last data set was the aqueous phase chemistry of Co(II). The last data set was already used to optimize the Co(II) speciation and aw in chloride media. It seems that only the combination of the experimental data from all these subsystems describes the conditional range necessary to accurately determine all standard-state thermodynamic values and interaction parameters (Tables 2 and 3).
Both UNIQUAC and MIDRANGE interaction parameters between H2O–TOMAC, HCl–TOMAC, and toluene–TOMAC were found to be necessary to calculate the water and HCl content of the organic phase (Figure 7). The fitted water content of the organic phase follows the experimental HCl system for all salt solutions. This results in a good calculation of the water content of the organic phase in the HCl system but substantially deviates for the other systems. The cause of this discrepancy might be found in the MSE-OLI framework itself. As explained above, the framework cannot account for the reversed micelles in the organic phase that greatly determine the water content of the organic phase. This discrepancy is not found in the HCl system, but this organic phase also has a significant amount of HCl. HCl in the organic phase greatly impacts the structure of the organic phase to a point where the MSE-OLI framework can correctly account for the water and HCl content in the organic phase. However, it is not possible to distill the structural causes for this observation from a thermodynamic calculation.
Figure 7.
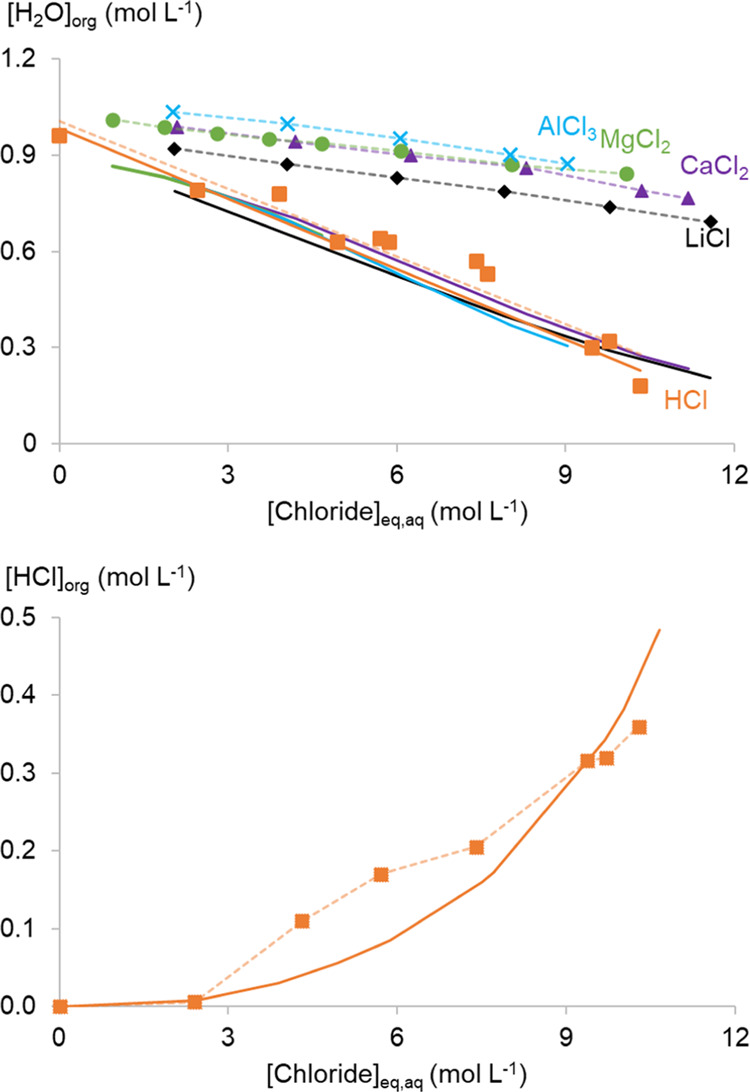
Top: water content of the organic phase comprising 0.2 mol L–1 TOMAC in toluene at equilibrium with different aqueous chloride salt/HCl solutions. Bottom: a similar graph with the HCl concentration of an organic phase in equilibrium with HCl solutions. The full lines represent the model calculations, while the points are experimental data.
Solvent extraction data of Co(II) by 0.2 mol L–1 TOMAC in toluene in HCl, LiCl, CaCl2, MgCl2, and AlCl3 systems were taken from previous publications to create the Co(II) extraction model.25,26 The distribution of the formed Q2CoCl4 complex between the two phases was modeled using UNIQUAC interaction parameters between Q2CoCl4–H2O and Q2CoCl4–toluene (Figure 8). No Q2CoCl4–TOMAC interaction parameters were optimized as no TOMAC concentration-dependent data were used. Note that these parameters should be determined to extend the applicability of the solvent extraction model to significantly different TOMAC concentrations. As explained above, the reversed micelle formation by TOMAC should then also be incorporated in the thermodynamic framework.
Figure 8.
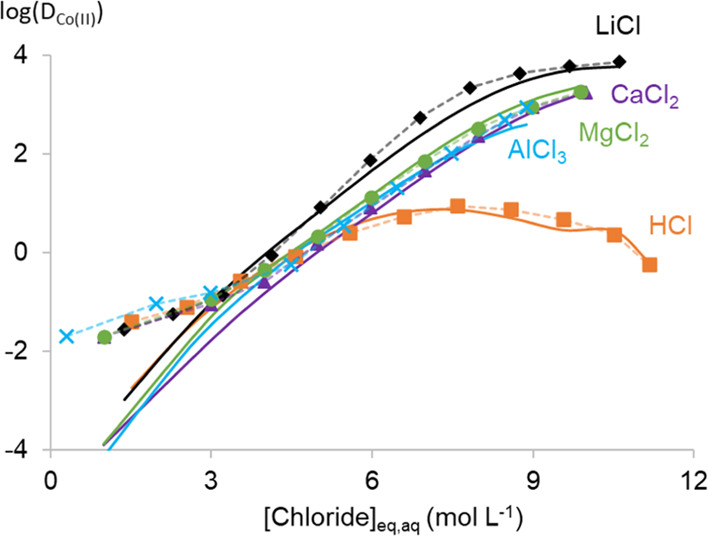
Logarithm of the distribution ratio of 0.015 mol L–1 Co(II) (log(DCo(II))) as a function of the total aqueous chloride concentration of different salting agents. The organic phase consisted of 0.2 mol L–1 TOMAC in toluene. The full lines represent the model calculations, while the points are experimental data from our previous papers.25,26
The distribution ratios of Co(II) (DCo(II)) calculated with the optimized MSE-OLI extraction model follow the experimental data very well. The DCo(II) is defined as the ratio between the total Co(II) molarity in the organic and aqueous phases at equilibrium. Only at the lowest chloride concentrations, the calculated DCo(II) was underestimated. However, it is more likely that the experimental data at these low chloride concentrations are inaccurate; the deflection in the experimental curve is probably related to the difficulty of measuring very low Co(II) concentration differences in the aqueous phase before and after extraction. This might be further complicated by small volume changes of both phases, even though the organic phase was pre-equilibrated with the corresponding salt solutions. Therefore, the importance of the solvent extraction data points at the lowest chloride concentrations was lowered by decreasing their weight during the parameter optimization. In addition, a small bump can be observed at the end of the DCo(II) curve in HCl media, but this could not be averted. It might be related to the fundamentals of the MSE-OLI thermodynamic framework and its inability to take reversed micelle behavior into account. When looking at the HCl content in the organic phase (Figure 7 bottom), a clear exponential trend is observed for the calculated curve, while this is much less pronounced for the experimental data. This might be related to the small bump in DCo(II) from HCl media.
A complete Co(II) solvent extraction model can be created without the need for interaction parameters between the salting agent and aqueous or organic Co(II) complexes. In addition, no salt parameters with TOMAC itself are necessary to create a model that correctly calculates the solvent extraction of Co(II) by TOMAC. All differences in extraction efficiency of Co(II) in different salting agents are obtained by indirect interactions of the salting agents with water and by differences in aqueous transition-metal ion speciation. Both phenomena change the hydration of Co(II), with the first by changing aw and thus the number of available water molecules and the latter by changing the hydration energy of Co(II) itself.
In the aqueous phase, all hydration and stabilization effects on Co(II) might be visualized by the activity coefficient of Co(II)aq (γCo(II),aq, Figure 9) according to eq 5
| 5 |
Figure 9.
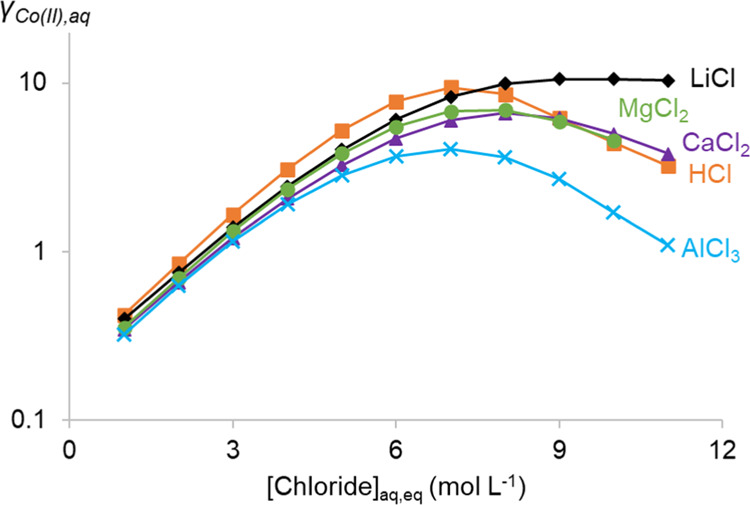
Total mole-fraction-based activity coefficient for all Co(II) complexes in aqueous solution (γCo(II)) determined using the OLI-MSE framework.
A higher γCo(II),aq value corresponds to more active Co(II), thus less stabilized in the aqueous phase. Some resemblance can be found between the γCo(II),aq and the trends in DCo(II) as depicted in Figure 8. The γCo(II),aq value increases in all solutions until a certain point. Then, a maximum is observed in all solutions except for LiCl solutions. For HCl solutions, this maximum is found close to the maximum in DCo(II), while for the other solutions, no maximum DCo(II) is observed. Furthermore, the γCo(II),aq in HCl solutions is higher than would be expected based on the DCo(II) from HCl. Both observations show that not only the hydration and the speciation in the aqueous phase should be considered. It seems that the decreasing water content in the organic phase at higher chloride concentrations increases the DCo(II). Less water in the organic phase results in an organic phase that is compositionally less similar to the aqueous phase. This enlarges the stability differences of the extractable metal complexes in both phases and increases the DCo(II). This would explain the shift from maxima in the γCo(II),aq curves in CaCl2, MgCl2, and AlCl3 to increasing DCo(II) curves. The reduced DCo(II) from HCl compared to the γCo(II),aq value might then be explained by the presence of HCl in the organic phase. Both water and HCl in the organic phase make the organic phase more similar to the aqueous phase. This decreases the stability difference of Co(II) between both phases and thus decreases DCo(II).
Two important remarks could still be made. First, the solution densities should be calculated correctly to properly convert molar concentrations and volumes in mole fractions and moles. This was accomplished by determining the standard-state pure liquid volumes (υ0) of TOMAC and Q2CoCl4 based on the density of TOMAC (Table 2). In more complex solutions, specific MIDRANGE density interaction parameters were necessary to correctly calculate the aqueous and organic densities (Table 3). These parameters were determined during the regression procedure. Second, aw of water–LiCl and water–AlCl3 mixtures [without Co(II)] calculated by OLI systems with the already available interaction parameters did not completely match with the literature and own experiments.42,43 Therefore, it was necessary to update the MIDRANGE Li+–Cl– and Al3+–Cl– interaction and density parameters (Table 3).
3. Conclusions
A thermodynamic model was constructed with the OLI-MSE thermodynamic framework to describe the solvent extraction of CoCl2 from different salting agents by 0.2 mol L–1 TOMAC in toluene. This model can accurately describe the salting effects of different chloride salting agents on the extraction of Co(II) by TOMAC without the need for specific Co(II)–salt cation interaction parameters. This further supports our hypothesis that the salting effect in these systems is governed by indirect solute–solvent interactions. Therefore, the water activity of a system is an easily accessible property to qualitatively access the salting effect on extraction of transition-metal ions by basic extractants. To obtain a complete description of the salting effects, the changes in hydration in the organic phase and the distribution of the acid between the aqueous and organic phases should be included as well. The decrease in water content in the organic phase at higher salt concentrations seem to enhance the extraction of Co(II) by enlarging the stabilization differences of Co(II) in both phases. A similar effect is not observed in the HCl system as HCl replaces water in the organic phase. A complete quantitative extraction model can then be constructed by further including the speciation of the extractable metal in both phases and its association with the basic extractant. However, a description for the formation of inverse micelles should be added to the thermodynamic framework to describe the extraction of transition-metal ions to surfactant-like extractants if one wants to perform calculations over the whole extractant concentration range.
4. Experimental Section
4.1. Chemicals
HNO3 (65 wt %), NaCl (99.99%), LiCl (99.9%), HCl (∼37 wt %), AlCl3·6H2O (>99%), CaCl2·2H2O (>99%), and toluene (>99.8%) were purchased from VWR (Leuven, Belgium). The aqueous cobalt and scandium standards (1000 mg L–1 in 3–5% HNO3), CoCl2·6H2O (>98%), and MgCl2·6H2O (>99%) were obtained from Chem Lab (Zedelgem, Belgium). Methyltrioctylammonium chloride (TOMAC, 98%) was purchased from J&K Scientific (Lommel, Belgium). 1-Octylimidazole (>98%) was purchased from IoLiTec (Germany). Water was always of ultrapure quality, deionized to a conductivity of less than 0.055 μS cm–1 (298.15 K) with a Merck Millipore Milli-Q Reference A+ system. All chemicals were used as received, without any further purification.
4.2. Water and HCl Distribution Experiments
Solvent extraction experiments were performed without the addition of an extractable metal ion with 5.0 mL of the aqueous phase and 5.0 mL of the organic phase in 20 mL glass vials to determine the water uptake in the organic phase, the water activity, the HCl uptake by the organic phase, and the density. The vials were shaken for 1 h at 200 rpm at a controlled temperature of 25 °C with a Thermoshake THL 500/1 from C. Gerhardt Analytical Systems. The phases were first allowed to separate by gravity in the Thermoshake at 25 °C for 15 min to keep the temperature constant as long as possible. Subsequently, the phases were further separated by centrifugation for 5 min at 2500 rpm in an Eppendorf 5804 centrifuge.
In one series, the mole fraction x of TOMAC in toluene was varied from 0 to 1. The exact TOMAC concentrations were obtained by mixing the correct masses of TOMAC and toluene. This series of organic solutions were contacted with an equal volume of 0.1 mol L–1 aqueous LiCl. In another series, the composition of the organic phase was kept constant (0.2 mol L–1 TOMAC in toluene) and the organic phase was contacted with different concentrations of different salting agents. The aqueous phases contained 0–10.7 mol L–1 HCl, 2.0–12.0 mol L–1 LiCl, 1.0–5.6 mol L–1 CaCl2, 0.46–5.0 mol L–1 MgCl2, or 0.67–3.0 mol L–1 AlCl3. These aqueous feed solutions were prepared by taking an aliquot of highly concentrated salt or acid stock solutions and diluting it to a fixed volume with ultrapure water. The exact salt concentrations were calculated based on the densities of the highly concentrated salt or acid stock solutions to avoid weighing errors due to the uptake of water by the hygroscopic salts.
The water content in the organic phases was measured using a Mettler–Toledo V30S volumetric Karl Fischer titrator. Acids like HCl are not tolerated in samples to be measured by the Karl Fischer method. Therefore, HCl in the organic phase was neutralized with 1-octylimidazole prior to the Karl Fischer titration. This was done by adding an excess of 1-octylimidazole (0.6 mL) to 2 g of the sample. 1-Octylimidazole was chosen as the base as its reaction product with HCl is soluble in toluene. Experimental errors were calculated based on triplicate measurements. These errors were found to be less than 1% of the measured values. For the Karl Fischer measurements of the solutions that contained HCl, the errors were slightly higher due to the neutralization step with the organic base. In addition, the water content of pure 1-octylimidazole was determined to calculate the correct water content in the samples. Error bars were omitted in the related figures because of the low errors and to increase the readability of the figures. Densities of the solutions were measured with an Anton Paar DMA 4500M densitometer.
4.3. Water Activities
The water activity (aw) of the aqueous phases was determined using a water activity meter (AQUALAB TDL of METER). The aw measured in the aqueous phase also reflects aw in the organic phase as this is the same at equilibrium. This can be seen from the general expression of a multiphase equilibrium, where the chemical potential of a species i (μi) is the same in all phases in equilibrium. The expression of μw in both phases can be converted to
| 6 |
where γw is the mole-fraction-based activity coefficient of water, xw is the mole fraction of water, and α and β are two phases in equilibrium.20
The aw of different aqueous salt solutions was determined with and without 0.085 mol L–1 CoCl2. The salt solutions were 1.0–10.7 mol L–1 LiCl, 0.5–5.4 mol L–1 CaCl2, 0.5–4.9 mol L–1 MgCl2, and 0.32–2.9 mol L–1. These aqueous phases were created by taking an aliquot of highly concentrated salt stock solutions, adding 0.5 mL of ultrapure water or 0.5 mL of a 1.7 mol L–1 CoCl2 solution, and diluting it to a fixed volume of 10 mL with ultrapure water. The exact salt concentrations were calculated based on the densities of the highly concentrated salt stock solutions to avoid weighing errors due to the uptake of water by the hygroscopic salts. By measuring both the solution with Co(II) and its corresponding solutions without Co(II), Δaw (eq 7) could be calculated that reflects the effect of adding CoCl2 on the water activity
| 7 |
4.4. Thermodynamic Modeling with OLI-MSE
The proprietary software packages OLI ESP 9.6 and OLI Studio 9.6.3 were used to create the solvent extraction model (OLI Systems Inc., Parsippany NJ). The thermodynamic data for complexes not present in the original OLI database were added on top of the chemistry available in the OLI public database revision 9.6.3. The use of the extensive OLI database reduces the calculation costs, especially in the aqueous phase where a vast collection of chemistry is already covered by OLI Systems.19,60,61 In addition, toluene is already available in the OLI database. This also improves the thermodynamic accuracy of the new extraction model of TOMAC as it also uses parameters already extensively verified by OLI Systems.
Over the years, the OLI-MSE thermodynamic framework has been extended to a speciation-based mixed-solvent electrolyte model.19,20 The speciation in every phase is determined by chemical equilibria and standard thermodynamic properties. The excess Gibbs energy (GEX) is expressed as a sum of long-range (LR) electrostatic interactions and MR and SR intermolecular interactions
| 8 |
The LR interactions are represented by a mole-fraction-based symmetrically normalized Pitzer–Debye–Hückel expression. It uses charge, ionic strengths, molar densities, and solvent dielectric constants to determine the LR contribution to GEX and does not require the determination of specific interaction parameters. SR interactions are described by the UNIQUAC equation using the size and surface parameters for a single species and interaction parameters between two species. MR interaction parameters are then used to describe mainly ionic interactions that are not accounted for by the LR contribution. The whole thermodynamic framework for GEX was designed to obtain a uniform mole-fraction-based, symmetrically-normalized reference state for all equations. This reference state is then converted to an unsymmetrical reference state to make the GEX calculations consistent with the standard-state thermodynamic properties, which are defined at infinite dilution in water.
Liquid–liquid equilibria (LLE) are obtained by constraining the activity coefficient model parameters to obtain the Gibbs energy of transfer of a species (i) from water (R) to another solvent (S)
| 9 |
where Mx is the molar mass of the solvent X (R or S) and γi*,X is the mole-fraction-based unsymmetrical activity coefficient of i in solvent X. At equilibrium, the chemical potential of each species should be equal over all equilibrated phases, which results in eq 6 as a further LLE criterion.20 The symmetrical reference state of the MSE-OLI GEX model should ensure the thermodynamic consistency of the LLE calculations. Thus, a species in solution is defined by its standard-state properties to calculate its thermodynamic behavior in an infinitely dilute aqueous phase. The distribution of the species to other equilibrated phases is then determined by the activity of the species in the other phase. This activity is influenced by LR, MR, and SR interactions with the solvent and solutes of the other phase.
The Co(II) speciation in aqueous and organic phases and the Co(II) extraction data from different salt solutions by 0.2 mol L–1 TOMAC in toluene were taken from our previous papers and further literature analysis.25,26,51 Other experimental data were determined within this work. Standard-state thermodynamic data were taken from the literature.53−56 When appropriate values were not available, they were estimated based on a group contribution method and further optimized while determining the interaction parameters for the model.62 Experimental data on the mutual solubility, water activity, aqueous Co(II) speciation from UV–vis absorption spectra, HCl distribution, and Co(II) extraction toward 0.2 mol L–1 TOMAC in toluene were used to determine the interaction parameters.
Acknowledgments
The authors thank the FWO Flanders (project G0B6918N) for financial support. The research was supported by the European Research Council (ERC) under the European Union’s Horizon 2020 Research and Innovation Programme: Grant Agreement 694078—Solvometallurgy for Critical Metals (SOLCRIMET). The contents of this publication are the sole responsibility of the authors and do not necessarily reflect the opinion of the European Union.
Author Contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
The authors declare no competing financial interest.
References
- Rydberg J.Solvent Extraction Principles and Practice, Revised and Expanded, 2nd ed.; Marcel Dekker: New York, 2004. [Google Scholar]
- Bourget C.; Soderstrom M.; Jakovljevic B.; Morrison J. Optimization of the Design Parameters of a CYANEX 272 Circuit for Recovery of Nickel and Cobalt. Solvent Extr. Ion Exch. 2011, 29, 823–836. 10.1080/07366299.2011.595640. [DOI] [Google Scholar]
- Cohen L.; McCallum T.; Tinkler O.; Szolga W.. Technological Advances, Challenges and Opportunities in Solvent Extraction from Energy Storage Applications. Extraction 2018; The Minerals, Metals & Materials Series, 2018; pp 2033–2045. [Google Scholar]
- Dash S.; Mohanty S. Mathematical Modeling Aspect in Solvent Extraction of Metals. Sep. Purif. Rev. 2021, 50, 74–95. 10.1080/15422119.2019.1648294. [DOI] [Google Scholar]
- Frey K.; Krebs J. F.; Pereira C. Time-Dependent Implementation of Argonne’s Model for Universal Solvent Extraction. Ind. Eng. Chem. Res. 2012, 51, 13219–13226. 10.1021/ie301421d. [DOI] [Google Scholar]
- Chagnes A. Simulation of Solvent Extraction Flowsheets by a Global Model Combining Physicochemical and Engineering Approaches—Application to Cobalt(II) Extraction by D2EHPA. Solvent Extr. Ion Exch. 2020, 38, 3–13. 10.1080/07366299.2019.1691135. [DOI] [Google Scholar]
- Bisson J.; Dinh B.; Huron P.; Huel C. PAREX, A Numerical Code in the Service of La Hague Plant Operations. Procedia Chem. 2016, 21, 117–124. 10.1016/j.proche.2016.10.017. [DOI] [Google Scholar]
- Moyer B. A.; Baes C. F.; Case F. I.; Driver J. L. Liquid–Liquid Equilibrium Analysis in Perspective Ii. Complete Model of Water, Nitric Acid, and Uranyl Nitrate Extraction by Di-2-Ethylhexyl Sulfoxide in Dodecane. Solvent Extr. Ion Exch. 2001, 19, 757–790. 10.1081/sei-100107024. [DOI] [Google Scholar]
- Baes C. F. Jr. Modeling Solvent Extraction Systems with Sxfit. Solvent Extr. Ion Exch. 2001, 19, 193–213. 10.1081/sei-100102691. [DOI] [Google Scholar]
- Ibrahim T. H. An Overview of the Physiochemical Nature of Metal-Extractant Species in Organic Solvent/Acidic Organophosphorus Extraction Systems. Sep. Sci. Technol. 2011, 46, 2157–2166. 10.1080/01496395.2011.594478. [DOI] [Google Scholar]
- Bley M.; Siboulet B.; Karmakar A.; Zemb T.; Dufrêche J.-F. A Predictive Model of Reverse Micelles Solubilizing Water for Solvent Extraction. J. Colloid Interface Sci. 2016, 479, 106–114. 10.1016/j.jcis.2016.06.044. [DOI] [PubMed] [Google Scholar]
- Špadina M.; Bohinc K.; Zemb T.; Dufrêche J.-F. Multicomponent Model for the Prediction of Nuclear Waste/Rare-Earth Extraction Processes. Langmuir 2018, 34, 10434–10447. 10.1021/acs.langmuir.8b01759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Špadina M.; Bohinc K.; Zemb T.; Dufrêche J.-F. Colloidal Model for the Prediction of the Extraction of Rare Earths Assisted by the Acidic Extractant. Langmuir 2019, 35, 3215–3230. 10.1021/acs.langmuir.8b03846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Špadina M.; Bohinc K. Multiscale Modeling of Solvent Extraction and the Choice of Reference State: Mesoscopic Modeling as a Bridge between Nanoscale and Chemical Engineering. Curr. Opin. Colloid Interface Sci. 2020, 46, 94–113. 10.1016/j.cocis.2020.03.011. [DOI] [Google Scholar]
- Prausnitz J. M. Molecular Thermodynamics: Opportunities and Responsibilities. Fluid Phase Equilib. 1996, 116, 12–26. 10.1016/0378-3812(95)02868-4. [DOI] [Google Scholar]
- Prausnitz J.; Lichtenthaler R.; de Azevedo E. G.. Molecular Thermodynamics of Fluid-Phase Equilibria, 3rd ed.; Pearson: Upper Saddle River, N.J, 1998. [Google Scholar]
- Chen C.-C.; Bokis C. P.; Mathias P. Segment-based excess Gibbs energy model for aqueous organic electrolytes. AIChE J. 2001, 47, 2593–2602. 10.1002/aic.690471122. [DOI] [Google Scholar]
- Chen C.-C. Toward Development of Activity Coefficient Models for Process and Product Design of Complex Chemical Systems. Fluid Phase Equilib. 2006, 241, 103–112. 10.1016/j.fluid.2006.01.006. [DOI] [Google Scholar]
- Wang P.; Anderko A.; Young R. D. A Speciation-Based Model for Mixed-Solvent Electrolyte Systems. Fluid Phase Equilib. 2002, 203, 141–176. 10.1016/s0378-3812(02)00178-4. [DOI] [Google Scholar]
- Wang P.; Anderko A.; Springer R. D.; Young R. D. Modeling Phase Equilibria and Speciation in Mixed-Solvent Electrolyte Systems: II. Liquid–Liquid Equilibria and Properties of Associating Electrolyte Solutions. J. Mol. Liq. 2006, 125, 37–44. 10.1016/j.molliq.2005.11.030. [DOI] [Google Scholar]
- Lee G. L.; Cattrall R. W.; Daud H.; Smith J. F.; Hamilton I. C. The Analysis of Aliquat-336 by Gas Chromatography. Anal. Chim. Acta 1981, 123, 213–220. 10.1016/s0003-2670(01)83173-1. [DOI] [Google Scholar]
- Qi D.Chapter 2-Extractants Used in Solvent Extraction-Separation of Rare Earths: Extraction Mechanism, Properties, and Features. In Hydrometallurgy of Rare Earths; Qi D., Ed.; Elsevier, 2018; pp 187–389. [Google Scholar]
- Jha M. K.; Kumari A.; Panda R.; Rajesh Kumar J.; Yoo K.; Lee J. Y. Review on Hydrometallurgical Recovery of Rare Earth Metals. Hydrometallurgy 2016, 165, 2–26. 10.1016/j.hydromet.2016.01.035. [DOI] [Google Scholar]
- Jha M. K.; Kumar V.; Singh R. J. Solvent Extraction of Zinc from Chloride Solutions. Solvent Extr. Ion Exch. 2002, 20, 389–405. 10.1081/sei-120004812. [DOI] [Google Scholar]
- Lommelen R.; Vander Hoogerstraete T.; Onghena B.; Billard I.; Binnemans K. Model for Metal Extraction from Chloride Media with Basic Extractants: A Coordination Chemistry Approach. Inorg. Chem. 2019, 58, 12289–12301. 10.1021/acs.inorgchem.9b01782. [DOI] [PubMed] [Google Scholar]
- Lommelen R.; Onghena B.; Binnemans K. Cation Effect of Chloride Salting Agents on Transition Metal Ion Hydration and Solvent Extraction by the Basic Extractant Methyltrioctylammonium Chloride. Inorg. Chem. 2020, 59, 13442–13452. 10.1021/acs.inorgchem.0c01821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moyer B. A.; Sun Y.. Principles of Solvent Extraction of Alkali Metal Ions: Understanding Factors Leading to Cesium Selectivity in Extraction by Solvation. Ion Exchange and Solvent Extraction; Marcel Dekker, Inc.: New York, 1997; Vol. 13, pp 295–391. [Google Scholar]
- Narbutt J.Chapter 4-Fundamentals of Solvent Extraction of Metal Ions. In Liquid-Phase Extraction; Poole C. F., Ed.; Handbooks in Separation Science; Elsevier, 2020; pp 121–155. [Google Scholar]
- Pfennig A.Thermodynamik der Gemische; Springer: Berlin Heidelberg, 2004. [Google Scholar]
- Zhang W.; Jiang S.; Qin T.; Sun J.; Dong C.; Hu Q. Effect of Ionic Liquid Surfactants on Coal Oxidation and Structure. J. Anal. Methods Chem. 2019, 2019, 1868265. 10.1155/2019/1868265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuchs-Godec R. The Adsorption, CMC Determination and Corrosion Inhibition of Some N-Alkyl Quaternary Ammonium Salts on Carbon Steel Surface in 2M H2SO4. Colloids Surf., A 2006, 280, 130–139. 10.1016/j.colsurfa.2006.01.046. [DOI] [Google Scholar]
- Xu J.; Paimin R.; Shen W.; Wang X. An Investigation of Solubility of Aliquat 336 in Different Extracted Solutions. Fibers Polym. 2003, 4, 27–31. 10.1007/bf02899326. [DOI] [Google Scholar]
- Cardoso M. M.; Viegas R. M. C.; Crespo J. P. S. G. Extraction and Re-Extraction of Phenylalanine by Cationic Reversed Micelles in Hollow Fibre Contactors. J. Membr. Sci. 1999, 156, 303–319. 10.1016/s0376-7388(98)00357-3. [DOI] [Google Scholar]
- Berkovich Y.; Garti N. Catalytic Colloidal Pd Dispersions in Water-Organic Solutions of Quaternary Ammonium Salt. Colloids Surf., A 1997, 128, 91–99. 10.1016/s0927-7757(96)03911-8. [DOI] [Google Scholar]
- Hilhorst R.; Sergeeva M.; Heering D.; Rietveld P.; Fijneman P.; Wolbert R. B. G.; Dekker M.; Bijsterbosch B. H. Protein Extration from an Aqueous Phase into a Reversed Micellar Phase: Effect of Water Content and Reversed Micellar Composition. Biotechnol. Bioeng. 1995, 46, 375–387. 10.1002/bit.260460411. [DOI] [PubMed] [Google Scholar]
- Reddy T. R.; Meeravali N. N.; Reddy A. V. R. Reverse Micelle Mediated Bulk Liquid Membrane Separation of Platinum Gold and Silver From Real Samples. Sep. Sci. Technol. 2013, 48, 1859–1866. 10.1080/01496395.2013.763708. [DOI] [Google Scholar]
- Reddy T. R.; Meeravali N. N.; Reddy A. V. R. Novel Reverse Mixed Micelle Mediated Transport of Platinum and Palladium through a Bulk Liquid Membrane from Real Samples. Sep. Purif. Technol. 2013, 103, 71–77. 10.1016/j.seppur.2012.10.025. [DOI] [Google Scholar]
- Streitner N.; Voß C.; Flaschel E. Reverse Micellar Extraction Systems for the Purification of Pharmaceutical Grade Plasmid DNA. J. Biotechnol. 2007, 131, 188–196. 10.1016/j.jbiotec.2007.06.011. [DOI] [PubMed] [Google Scholar]
- Warr G. G.; Sen R.; Evans D. F.; Trend J. E. Microemulsion Formation and Phase Behavior of Dialkydimethylammonium Bromide Surfactants. J. Phys. Chem. 1988, 92, 774–783. 10.1021/j100314a037. [DOI] [Google Scholar]
- Bressler E.; Braun S. Separation Mechanisms of Citric and Itaconic Acids by Water-Immiscible Amines. J. Chem. Technol. Biotechnol. 1999, 74, 891–896. . [DOI] [Google Scholar]
- Vander Hoogerstraete T.; Souza E. R.; Onghena B.; Banerjee D.; Binnemans K. Mechanism for Solvent Extraction of Lanthanides from Chloride Media by Basic Extractants. J. Solution Chem. 2018, 47, 1351–1372. 10.1007/s10953-018-0782-4. [DOI] [Google Scholar]
- Guendouzi M. E.; Dinane A.; Mounir A. Water Activities, Osmotic and Activity Coefficients in Aqueous Chloride Solutions at T= 298.15 K by the Hygrometric Method. J. Chem. Thermodyn. 2001, 33, 1059–1072. 10.1006/jcht.2000.0815. [DOI] [Google Scholar]
- Richter U.; Brand P.; Bohmhammel K.; Könnecke T. Thermodynamic Investigations of Aqueous Solutions of Aluminium Chloride. J. Chem. Thermodyn. 2000, 32, 145–154. 10.1006/jcht.1999.0557. [DOI] [Google Scholar]
- Sato T.; Watanabe H.; Kikuchi S. Extraction of Some Mineral Acids by High Molecular Weight Quaternary Ammonium Chloride. J. Appl. Chem. Biotechnol. 1975, 25, 63–72. 10.1002/jctb.5020250107. [DOI] [Google Scholar]
- du Preez J. G. H. Recent Advances in Amines as Separating Agents for Metal Ions. Solvent Extr. Ion Exch. 2000, 18, 679–701. 10.1080/07366290008934703. [DOI] [Google Scholar]
- Pethes I. The Structure of Aqueous Lithium Chloride Solutions at High Concentrations as Revealed by a Comparison of Classical Interatomic Potential Models. J. Mol. Liq. 2018, 264, 179–197. 10.1016/j.molliq.2018.05.044. [DOI] [Google Scholar]
- Fulton J. L.; Balasubramanian M. Structure of Hydronium (H3O+)/Chloride (Cl–) Contact Ion Pairs in Aqueous Hydrochloric Acid Solution: A Zundel-like Local Configuration. J. Am. Chem. Soc. 2010, 132, 12597–12604. 10.1021/ja1014458. [DOI] [PubMed] [Google Scholar]
- Jiang J.-C.; Wang Y.-S.; Chang H.-C.; Lin S. H.; Lee Y. T.; Niedner-Schatteburg G.; Chang H.-C. Infrared Spectra of H+(H2O)5-8 Clusters: Evidence for Symmetric Proton Hydration. J. Am. Chem. Soc. 2000, 122, 1398–1410. 10.1021/ja990033i. [DOI] [Google Scholar]
- Vlcek L.; Chialvo A. A. Single-Ion Hydration Thermodynamics from Clusters to Bulk Solutions: Recent Insights from Molecular Modeling. Fluid Phase Equilib. 2016, 407, 58–75. 10.1016/j.fluid.2015.05.048. [DOI] [Google Scholar]
- Li Z.; Smith K. H.; Mumford K. A.; Wang Y.; Stevens G. W. Regression of NRTL Parameters from Ternary Liquid–Liquid Equilibria Using Particle Swarm Optimization and Discussions. Fluid Phase Equilib. 2015, 398, 36–45. 10.1016/j.fluid.2015.04.006. [DOI] [Google Scholar]
- Uchikoshi M.; Shinoda K. Determination of Structures of Cobalt(II)-Chloro Complexes in Hydrochloric Acid Solutions by X-Ray Absorption Spectroscopy at 298 K. Struct. Chem. 2019, 30, 945. 10.1007/s11224-018-1245-7. [DOI] [Google Scholar]
- Goldberg R. N.; Nuttall R. L.; Staples B. R. Evaluated Activity and Osmotic Coefficients for Aqueous Solutions: Iron Chloride and the Bi-univalent Compounds of Nickel and Cobalt. J. Phys. Chem. Ref. Data 1979, 8, 923–1004. 10.1063/1.555615. [DOI] [Google Scholar]
- DeGrand M. J.; Abrams M. L.; Jenkins J. L.; Welch L. E. Gibbs Energy Changes during Cobalt Complexation: A Thermodynamics Experiment for the General Chemistry Laboratory. J. Chem. Educ. 2011, 88, 634–636. 10.1021/ed100833x. [DOI] [Google Scholar]
- Steele W. V.; Chirico R. D.; Knipmeyer S. E.; Nguyen A.; Smith N. K.; Tasker I. R. Thermodynamic Properties and Ideal-Gas Enthalpies of Formation for Cyclohexene, Phthalan (2,5-Dihydrobenzo-3,4-Furan), Isoxazole, Octylamine, Dioctylamine, Trioctylamine, Phenyl Isocyanate, and 1,4,5,6-Tetrahydropyrimidine. J. Chem. Eng. Data 1996, 41, 1269–1284. 10.1021/je960093t. [DOI] [Google Scholar]
- Manion J. A. Evaluated Enthalpies of Formation of the Stable Closed Shell C1 and C2 Chlorinated Hydrocarbons. J. Phys. Chem. Ref. Data 2002, 31, 123–172. 10.1063/1.1420703. [DOI] [Google Scholar]
- Messerly G. H.; Aston J. G. The Heat Capacity and Entropy, Heats of Fusion and Vaporization and the Vapor Pressure of Methyl Chloride1. J. Am. Chem. Soc. 1940, 62, 886–890. 10.1021/ja01861a048. [DOI] [Google Scholar]
- Carneiro A. P.; Rodríguez O.; Macedo E. A. Solubility of Xylitol and Sorbitol in Ionic Liquids – Experimental Data and Modeling. J. Chem. Thermodyn. 2012, 55, 184–192. 10.1016/j.jct.2012.05.020. [DOI] [Google Scholar]
- Sato T. The Extraction of Cobalt (II) from Hydrochloric Acid Solution by Tri-n-Octylamine. J. Inorg. Nucl. Chem. 1967, 29, 547–553. 10.1016/0022-1902(67)80060-5. [DOI] [Google Scholar]
- Wellens S.; Thijs B.; Binnemans K. An Environmentally Friendlier Approach to Hydrometallurgy: Highly Selective Separation of Cobalt from Nickel by Solvent Extraction with Undiluted Phosphonium Ionic Liquids. Green Chem. 2012, 14, 1657–1665. 10.1039/c2gc35246j. [DOI] [Google Scholar]
- Kosinski J. J.; Wang P.; Springer R. D.; Anderko A. Modeling Acid–Base Equilibria and Phase Behavior in Mixed-Solvent Electrolyte Systems. Fluid Phase Equilib. 2007, 256, 34–41. 10.1016/j.fluid.2006.11.018. [DOI] [Google Scholar]
- Wang P.; Anderko A.; Springer R. D.; Kosinski J. J.; Lencka M. M. Modeling Chemical and Phase Equilibria in Geochemical Systems Using a Speciation-Based Model. J. Geochem. Explor. 2010, 106, 219–225. 10.1016/j.gexplo.2009.09.003. [DOI] [Google Scholar]
- Fredenslund A.; Jones R. L.; Prausnitz J. M. Group-Contribution Estimation of Activity Coefficients in Nonideal Liquid Mixtures. AIChE J. 1975, 21, 1086–1099. 10.1002/aic.690210607. [DOI] [Google Scholar]