Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2021 Apr 14;6(16):11083–11085. doi: 10.1021/acsomega.1c01208

Can CP Be Less Than CV?

Yingbin Ge 1,*, Samuel L Montgomery 1, Gabriel L Borrello 1
PMCID: PMC8153929  PMID: 34056262

Abstract

graphic file with name ao1c01208_0002.jpg

Can CP be less than CV? This is a fundamental question in physics, chemistry, chemical engineering, and mechanical engineering. This question hangs in the minds of many students, instructors, and researchers. The first instinct is to answer “Yes, for water between 0 and 4 °C” if one knows that water expands as temperature decreases in this temperature range. The same question is asked in several Physical Chemistry and Physics textbooks. Students are supposed to answer that water contracts when heated at below 4 °C in an isobaric process. Because work is done to the contracting water, less heat is required to increase the water temperature in an isobaric process than in an isochoric process. Therefore, CP is less than CV. However, this answer is fundamentally flawed because it assumes, implicitly and incorrectly, that the internal energy change of water depends solely on its temperature change. Neglecting the variation of the internal energy with volume (internal pressure) will invalidate the Clausius inequality and violate the second law of thermodynamics. Once the internal pressure is properly taken into account, it becomes clear that CP cannot be less than CV for any substance at any temperature regardless of the sign of the thermal expansion coefficient of the substance.

Introduction

“The heat capacity CP,m is less than CV,m for H2O(l) near 4 °C. Explain this result”. This is one of the concept problems in Chapter 3 of Physical Chemistry (3rd ed.) by Engel and Reid.1 Students are supposed to explain that liquid water contracts when heated at below 4 °C in an isobaric process. Because work is done to the contracting water, less heat is required to increase its temperature in an isobaric process than in an isochoric process. The above explanation is flawed because it assumes, implicitly and incorrectly, that the internal energy change of water in an isobaric process is the same as in an isochoric process. As a result of the flawed assumption, CP,m is less than CV,m for H2O(l) near 4 °C. The same flawed assumption also appears on page 252 of Physical Chemistry by Cooksy:2 “Why should CP be different from CV? Briefly, because if the volume can change, some of the heat added to the system is used to do work by expansion, leaving less to raise the temperature of the sample”. This seemingly small mistake is beyond just a trivial omission of the variation of the internal energy with volume; it results in the violation of the second law of thermodynamics and thereby destroys the foundation of thermodynamics. Unfortunately, this severe error might have been infused into thousands of chemistry students and perhaps physics students as well. In University Physics by Ling, Sanny, and Moebs,3 Conceptual Question 3.13 asks: “Most materials expand when heated. One notable exception is water between 0 and 4 °C, which actually decreases in volume with the increase in temperature. Which is greater for water in this temperature region, CP or CV?” The answer key is provided in this textbook: “Typically CP is greater than CV because when expansion occurs under constant pressure, it does work on the surroundings. Therefore, heat can go into internal energy and work. Under constant volume, all heat goes into internal energy. In this example, water contracts upon heating, so if we add heat at constant pressure, work is done on the water by surroundings and therefore, CP is less than CV”. In University Physics by Young and Freedman,4 Q19.10 asks “There are a few materials that contract when their temperature is increased, such as water between 0 and 4 °C. Would you expect CP for such materials to be greater or less than CV? Explain?” The key is not provided but this question alone may be misleading. And this error has affected not only classrooms: a research article published in the Journal of Chemical Physics claims that CP can be less than CV for silicon at low temperatures.5 There seems to be a widespread misunderstanding about the difference between CP and CV in academia, which originates from the improper omission of the variation of the internal energy with volume and results in the violation of the second law of thermodynamics.

Results and Discussion

CP cannot be less than CV because this violates the second law of thermodynamics. Our proof starts with the following equation that is rigorous for all matters1,6−8

graphic file with name ao1c01208_m001.jpg

where α is the isobaric thermal expansion coefficient and κ is the isothermal compressibility

graphic file with name ao1c01208_m002.jpg
graphic file with name ao1c01208_m003.jpg

Because T and V are always positive and α2 is non-negative, κ will have to be negative if CP is less than CV. Experimentally, the value of κ of liquid water was found to be always positive.9−12 Specifically, under 1 atm pressure, the κ value for liquid water is 5.1 × 10–10 Pa–1 at 0 °C or 4.5 × 10–10 Pa–1 at 25 °C.12 The value of κ must also be positive between 0 °C and 25 °C because the κ vs T curve must be continuous for liquid water within this temperature range. A single negative value of κ would result in κ having to be equal to zero at two different temperatures between 0 and 25 °C. The difference between CP and CV would then have to be infinity at one of these two temperatures using the Inline graphic equation because α is zero only at one temperature near 4 °C. Hereafter, we will prove in a more rigorous yet still concise manner that a negative κ for any substance would invalidate the Clausius inequality and consequently violate the second law of thermodynamics.

First, we prove that a negative κ would invalidate the Clausius inequality (TdS > dqirreversible). The infinitesimal change to the state of a system, from (P, V, T, S) to (P + dP, V + dV, T + dT, S + dS), can be made via a reversible process or an irreversible process. In the reversible process, dU = TdS – PdV. In the irreversible process, dU = dqirreversible + dwirreversible. Because U is a state function, we have TdS – PdV = dqirreversible – Pexternal dV. Therefore, TdS – dqirreversible = (P – Pexternal)dV. If κ is negative,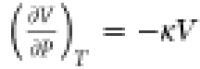Inline graphic must be positive. In this case, when Pexternal is greater than P, the system expands as its system pressure increases to match with Pexternal. Because (P – Pexternal) is negative and dV is positive, the Clausius inequality is invalidated: TdS – dqirreversible < 0. This further violates the second law of thermodynamics:

graphic file with name ao1c01208_m006.jpg

We have proved that a negative κ would violate the second law of thermodynamics and thus 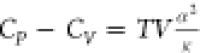Inline graphic cannot be negative.

It is well known that α can be zero, e.g., for water at ∼4 °C. In this case, CP equals CV. Can κ be zero too? No. If any substance had a zero κ, its α value would have to be zero to avoid the difference between CP and CV approaching infinity. The volume of such a substance under such conditions would then be independent of pressure and temperature as dV = VαdT – VκdP = 0. This is apparently unphysical. Therefore, we conclude that κ must be positive for all substances.

The above rigorous proof is supported by numerical calculations for water at 0–4 °C. The α value of liquid water under 1 atm pressure is −6.8 × 10–5 K–1 at 0 °C or 2.57 × 10–4 K–1 at 25 °C.12 Its κ value under 1 atm pressure is 5.1 × 10–10 Pa–1 at 0 °C or 4.5 × 10–10 Pa–1 at 25 °C.12 Using the 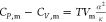Inline graphic equation, we find that CP,m is greater than CV,m by 0.04 J mol–1 K–1 at 0 °C or 0.8 J mol–1 K–1 at 25 °C. CP,m – CV,m is positive at both 0 and 25 °C (and in between). The difference, however, is much smaller than the CP,m (75.3 J mol–1 K–1) of water at 25 °C and 1 atm pressure. Therefore, when we refer to the heat capacity of liquid water or many other liquids or solids, there is often no need to specify the isobaric or isochoric condition. Is it always true that CP,m is close to CV,m for liquids and solids or at least for liquids that are similar to water such as methanol? No. Methanol has a similar molecular structure as water but the difference between CP,m and CV,m of methanol is expected to be much greater than that of water. This is because its isobaric thermal expansibility (1.49 × 10–3 K–1) is ∼6 times that of water under the standard condition, while its isothermal compressibility (1.2 × 10–9 Pa–1) is only ∼3 times that of water at 25 °C.1 Moreover, the molar volume of methanol (40.7 mL mol–1) is more than twice that of water due to its greater molar mass (32 g mol–1) and lower density (0.787 g mL–1)13 at 25 °C. The result is that the calculated difference (ca. 22 J mol–1 K–1) between CP,m (81 J mol–1 K–1)1 and CV,m for methanol is much greater than that of water at 25 °C and even greater than the ideal gas constant. The CV,m for methanol is thus estimated to be 81–22 = 59 J mol–1 K–1 at 25 °C and 1 atm. At the room temperature, the experimental data of CV,m for methanol is unavailable at 1 atm; it is 72 J mol–1 K–1 under 137 atm.14 Another example of CP,m being much larger than CV,m is liquid benzene. The values of CP,m and CV,m of benzene are 136 and 95 J mol–1 K–1, respectively, at room temperature and under ∼0.14 atm of saturated benzene vapor.15 For benzene, CP,m is 41 J mol–1 K–1 greater than CV,m. This vast difference between CP,m and CV,m of benzene is due to its very large molar volume (90 mL mol–1) and significant thermal expansibility (1.14 × 10–3 K–1).1

There are caveats associated with the above analysis of the difference between CP and CV. One caveat is that 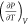Inline graphic must be negative for water between 0 and 4 °C because Inline graphic is negative in Inline graphic. This seems counterintuitive, but, when temperature decreases between 0 and 4 °C, the pressure of liquid water does increase because water at lower temperatures resembles more like ice and thus needs to occupy more space when the pressure is held constant or exerts (and feels) higher pressure when the volume is held constant. 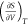Another explanation is that Inline graphic is negative. The entropy of liquid water decreases when its volume increases because, given more space, water can form a more ordered structure (to reduce energy) that resembles the crystalline structure of ice. One may ask, if Inline graphic is negative for water, wouldn’t the entropy of the universe decrease as the water volume increases while the volume of its surroundings decreases? No. While water expands at a constant temperature between 0 and 4 °C, its internal energy decreases because the hydrogen bonding between water molecules, given more space, becomes more significant. This internal energy decrease becomes heat that flows into the surroundings and consequently increases the entropy of the surroundings. Overall, the entropy increase of the surroundings would be large enough to compensate the entropy loss of the expanding water; the second law of thermodynamics is not in jeopardy. A second caveat is that some materials such as NaNH2BH3 may expand along one or two (out of three) dimensions under compression.16−21 In these cases, the overall three-dimensional volume of such a material must decrease, dictated by the second law of thermodynamics.

Conclusions

When the temperature is held constant, no substance can expand against higher pressures because this would invalidate the Clausius inequality and violate the second law of thermodynamics. Consequently, CP can never be less than CV, even for water at temperatures between 0 and 4 °C.

Acknowledgments

This work is partially supported by the Central Washington University CBA Faculty Development Fund. Y.G. also thanks his 2019–2020 physical chemistry students for their feedback on the manuscript.

The authors declare no competing financial interest.

References

  1. Engel T.; Reid P.. Physical Chemistry, 3rd ed.; Pearson: Boston, 2012. [Google Scholar]
  2. Cooksy A.Physical Chemistry: Thermodynamics, Statistical Mechanics, & Kinetics; Pearson: Boston, 2014. [Google Scholar]
  3. Ling S. J.; Sanny J.; Moebs W.. University Physics; Rice University, 2018; Vol. 2. [Google Scholar]
  4. Young H. D.; Freedman R. A.. University Physics with Modern Physics, 14th ed.; Pearson: Boston, 2016. [Google Scholar]
  5. Fine M. E. Cp–Cv in Silicon and Germanium. J. Chem. Phys. 1953, 21, 1427. 10.1063/1.1699272. [DOI] [Google Scholar]
  6. Smith N. O. The Difference between Cp and Cv for Liquids and Solids. J. Chem. Educ. 1965, 42, 654–655. 10.1021/ed042p654. [DOI] [Google Scholar]
  7. McQuarrie D. A.; Simon J. D.. Physical Chemistry: A Molecular Approach; University Science Books: Sausalito, CA, 1997. [Google Scholar]
  8. Levine I. N.Physical Chemistry, 3rd ed.; McGraw-Hill: New York, 1988. [Google Scholar]
  9. Millero F. J.; Curry R. W.; Drost-Hansen W. Isothermal Compressibility of Water at Various Temperatures. J. Chem. Eng. Data 1969, 14, 422–425. 10.1021/je60043a018. [DOI] [Google Scholar]
  10. Fine R. A.; Millero F. J. Compressibility of Water as a Function of Temperature and Pressure. J. Chem. Phys. 1973, 59, 5529–5536. 10.1063/1.1679903. [DOI] [Google Scholar]
  11. Bradshaw A.; Schleicher K. Compressibility of Distilled Water and Seawater. Deep-Sea Res. Oceanogr. Abstr. 1976, 23, 583–593. 10.1016/0011-7471(76)90002-4. [DOI] [Google Scholar]
  12. Kell G. S. Density Thermal Expansivity, and Compressibility of Liquid Water from 0. OC to 150. OC. Correlations and Tables for Atmospheric Pressure and Saturation Reviewed and Expressed on 1968 Temperature Scale. J. Chem. Eng. Data 1975, 20, 97–105. 10.1021/je60064a005.. [DOI] [Google Scholar]
  13. Wei I. C.; Rowley R. L. Binary Liquid Mixture Viscosities and Densities. J. Chem. Eng. Data 1984, 29, 332–335. 10.1021/je00037a032. [DOI] [Google Scholar]
  14. Kuroki T.; Kagawa N.; Endo H.; Tsuruno S.; Magee J. W. Specific Heat Capacity at Constant Volume for Water, Methanol, and Their Mixtures at Temperatures from 300 K to 400 K and Pressures to 20 MPa. J. Chem. Eng. Data 2001, 46, 1101–1106. 10.1021/je0002437. [DOI] [Google Scholar]
  15. CRC Handbook of Chemistry and Physics, 97th ed.; Haynes W. M., Ed.; CRC Press, 2016. [Google Scholar]
  16. Cairns A. B.; Goodwin A. L. Negative Linear Compressibility. Phys. Chem. Chem. Phys. 2015, 17, 20449–20465. 10.1039/C5CP00442J. [DOI] [PubMed] [Google Scholar]
  17. Magos-Palasyuk E.; Fijalkowski K. J.; Palasyuk T. Chemically Driven Negative Linear Compressibility in Sodium Amidoborane, Na(NH2BH3). Sci. Rep. 2016, 6, 28745 10.1038/srep28745. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Serra-Crespo P.; Dikhtiarenko A.; Stavitski E.; Juan-Alcañiz J.; Kapteijn F.; Coudert F.-X.; Gascon J. Experimental Evidence of Negative Linear Compressibility in the MIL-53 Metal–Organic Framework Family. CrystEngComm 2015, 17, 276–280. 10.1039/C4CE00436A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Cairns A. B.; Catafesta J.; Levelut C.; Rouquette J.; van der Lee A.; Peters L.; Thompson A. L.; Dmitriev V.; Haines J.; Goodwin A. L. Giant Negative Linear Compressibility in Zinc Dicyanoaurate. Nat. Mater. 2013, 12, 212–216. 10.1038/nmat3551. [DOI] [PubMed] [Google Scholar]
  20. Li W.; Probert M. R.; Kosa M.; Bennett T. D.; Thirumurugan A.; Burwood R. P.; Parinello M.; Howard J. A. K.; Cheetham A. K. Negative Linear Compressibility of a Metal–Organic Framework. J. Am. Chem. Soc. 2012, 134, 11940–11943. 10.1021/ja305196u. [DOI] [PubMed] [Google Scholar]
  21. Cai W.; Katrusiak A. Giant Negative Linear Compression Positively Coupled to Massive Thermal Expansion in a Metal–Organic Framework. Nat. Commun. 2014, 5, 4337 10.1038/ncomms5337. [DOI] [PubMed] [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES