Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2021 Apr 20;6(17):11209–11222. doi: 10.1021/acsomega.0c06232

Distinct Modes of Tissue Expansion in Free Versus Earlier-Confined Boundaries for More Physiological Modeling of Wound Healing, Cancer Metastasis, and Tissue Formation

Abhimanyu Kiran †,*, Navin Kumar †, Vishwajeet Mehandia ‡,*
PMCID: PMC8153934  PMID: 34056276

Abstract

graphic file with name ao0c06232_0013.jpg

Collective cell migration is often seen in many biological processes like embryogenesis, cancer metastasis, and wound healing. Despite extensive experimental and theoretical research, the unified mechanism responsible for collective cell migration is not well known. Most of the studies have investigated artificial model wound to study the collective cell migration in an epithelial monolayer. These artificial model wounds possess a high cell number density compared to the physiological scenarios like wound healing (cell damage due to applied cut) and cancer metastasis (smaller cell clusters). Therefore, both systems may not completely relate to each other, and further investigation is needed to understand the collective cell migration in physiological scenarios. In an effort to fill this existing knowledge gap, we investigated the freely expanding monolayer that closely represented the physiological scenarios and compared it with the artificially created model wound. In the present work, we report the effect of initial boundary conditions (free and confined) on the collective cell migration of the epithelial cell monolayer. The expansion and migration aspects of the freely expanding and earlier-confined monolayer were investigated at the tissue and cellular levels. The freely expanding monolayer showed significantly higher expansion and lower migration in comparison to the earlier-confined monolayer. The expansion and migration rate of the monolayer exhibited a strong negative correlation. The study highlights the importance of initial boundary conditions in the collective cell migration of the expanding tissue and provides useful insights that might be helpful in the future to tune the collective cell migration in wound healing, cancer metastasis, and tissue formation.

Introduction

Collective cell migration is a fundamental multicellular activity involved in several biological processes such as embryonic development, tissue regeneration, wound healing, and cancer metastasis.1−4 Therefore, it is important to understand the mechanism responsible for collective cell migration. However, the mechanism of single-cell migration is well known, where a cell migrates by forming new focal adhesion in the front, followed by the retraction and detachment of the focal adhesion from the rear end. However, the mechanism of collective cell migration cannot be explained as a large number of single cells migrate in a similar direction with a constant rate, without considering the intercellular interactions.5 These intercellular interactions occur due to the physical connectivity between the cells via cell–cell junctions and the actin cytoskeleton.6 Thereby, the motion of each cell is affected by its neighboring cell.7,8 Despite being caged, the collective cell migration is more efficient than single-cell migration due to their intercellular forces.6 This indicates the vital role of intercellular forces in collective cell migration.9

Earlier, it was assumed that the monolayer migrates due to the active pulling generated by the leader cells located at the margin, and follower cells passively follow them.10−13 Contrary to the earlier assumption, the measurement of intercellular forces showed that the leader cell generates a pull of ∼100 nN, which is insufficient to pull the complete monolayer.5,14 Hence, the leader cells need the assistance of the follower cells. Later, many studies have indicated the active role of follower cells in collective cell migration.15−19 These studies experimentally demonstrated the presence of the significant amount of traction force up to ∼10 cell rows from the leading edge,15 propagation of slow mechanical wave via monolayer,16 presence of correlated velocity field up to ∼10 to 15 cell rows,17 strong alignment of principle stress with velocity field,18 and mechanical interaction among the follower cells cause the emergence of leader cells.19 Apart from these studies, the presence of “cryptic” cell groups in the submarginal region has also been reported.20 The lamellipodia of these cryptic cells penetrate the basal region of their front cells. It was assumed that these groups of cryptic cells might contribute to the collective cell migration.20 Despite such extensive research on collective cell migration, the underlying mechanism through which a large number of cells move together as a sheet is not well understood.

Most of the experimental studies done on collective cell migration use artificial model wound,12,17,19,21,22 where the cells were grown inside a culture insert of a fixed shape and the insert was removed after the formation of a fully confluent monolayer. The removal of this insert or physical barrier provides the free space, enough to trigger the collective cell migration.12 Thereby, the cells migrate rapidly toward the newly available free space.12,19,22,23 Moreover, it has been experimentally demonstrated that cell number density determines the velocity of the cells in the monolayer.22 Therefore, high collective cell migration observed in earlier-confined monolayers could be due to their initial high cell number density. However, in physiological scenarios like free tissue expansion, wound repair, or cancer metastasis, the cell number density is relatively less compared to the artificially formed (or earlier-confined) monolayer. This implies that both types of monolayer may have distinct properties. Therefore, further investigation is needed to understand the similarity and differences between both types of monolayers.

Hence, we compared the leading site of the freely expanding and earlier-confined confluent Madin-Darby Canine Kidney (MDCK) cell monolayer. The freely expanding and earlier-confined monolayers were formed using free and fixed boundary conditions, respectively. For both types of the monolayer, the expansion and migration aspects were compared at the tissue and cellular level. Here, we report that cells of the submarginal region of the freely expanding monolayer expand at a higher rate and migrate at a slower rate than the earlier-confined monolayer. It was observed that most of the cells of the freely expanding monolayer grow or expand in their area. Therefore, these types of monolayers were referred to as the growth-dominant monolayer (GDM). In contrast, the majority of cells of the earlier-confined monolayers prefer to migrate. Thereby, these monolayers were referred to as the migration-dominant monolayer (MDM). The MDM is the artificial model wound discussed in the literature.12,17,19,21,22 Finally, we aimed to decipher the mechanism by which the leader and follower cells coordinate to achieve collective cell migration. To the best of our knowledge, this work has not been reported earlier.

Result and Discussion

In this work, the monolayer has been classified into two categories depending on the characteristics of its constituent cells. The first type is GDM (Figure 1A), which contains the majority of cells that prefer to expand (or grow) in the area. The second is MDM (Figure 1B), which consists of the majority of cells that prefer to migrate. The leading site of the GDM and MDM was compared to find the basic difference between their mode of expansion and migration.

Figure 1.

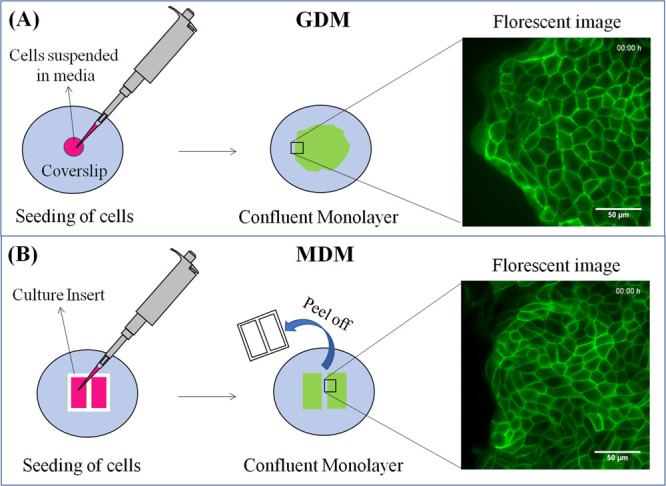
Figure 1

Open in a new tab

Schematic representation of the monolayer formation. (A) GDM, (B) MDM.

Temporal Area Expansion

The area of the monolayer was calculated by adding the area of all the cells of the leading site that remained in the frame throughout the observation. Since it was found that many cells randomly expand with time resulting in the expansion of the monolayer, this monolayer expansion was measured by subtracting the final area of the monolayer from its initial area. Further, the expansion rate was obtained by dividing the monolayer expansion with its original area and the time during which expansion took place. The expansion rate for GDM decreased slowly with time (Figure 2A). It suggests that initially, more cells were expanding, but this number later decreased with time. Bindschadler and McGrath25 showed that the cell divisions significantly reduce with the increase in the confluency of the monolayer. We assumed that the cell number density of the confluent monolayer almost remains constant during the observation. It implies that the rate of cell expansion remains much greater than the rate of cell division. Since the randomly growing cells of GDM expand at different rates and for different durations, we assumed that many of these cells might not grow further after achieving a certain area. Thereby, the number of growing cells may decrease with time. As a result, the expansion rate of GDM reduces with time.

Figure 2.

Figure 2

Open in a new tab

Comparing the expansion of GDM and MDM. (A) Average expansion rate versus time, (B) average number of cells, (C) average cell area versus time, (D) representation of the number of cells with respect to change in their effective cell radius. Note: The black asterisk in (A–C) represents statistical significance obtained by applying an unpaired t-test between corresponding rows of GDM and MDM. The red asterisk in (A) represents statistical significance obtained by applying a paired t-test between the expansion rates of the same monolayer at a different time point. The black asterisk in (D) represents statistical significance obtained by applying an unpaired t-test between the similar effective cell radius of GDM and MDM. Standard errors plotted here are obtained from 5 independent experiments. The significant differences were determined by p-values, where *, **, and *** represents the significance level of p < 0.05, p < 0.01, and p < 0.001, respectively.

For MDM, the expansion rate decreased rapidly from 1st to 3rd hour (Figure 2A) that may be attributed to high cell number density. Analyzing step by step, the expansion rate for the 1st hour of MDM was more than that of GDM (Figure 2A). It implies that the cells of MDM initially expanded more as compared to the GDM. Later, the expansion rate fell sharply from the 2nd to 3rd hour (Figure 2A). The negative expansion rate was recorded in this duration, suggesting that many cells started to shrink in their area. The plausible mechanism to explain the negative expansion is that the high initial expansion rate observed in the 1st hour due to expansion of submarginal cells may apply the necessary push toward the marginal cells, resulting in the transformation of few marginal cells into leader cells. These newly formed leader cells invade the free space and start pulling densely packed follower cells. As a result, the submarginal cells shrink in their size by minimizing the number of focal adhesion in order to rapidly migrate toward the leader cells and relieve the stress in the submarginal region associated with their dense packing. Therefore, the difference in the expansion rate with time for GDM and MDM could be attributed to the difference in their cell number density per unit area.

The t-test showed that the expansion rate of the 2nd hour was statistically significant (p = 0.0012) to the expansion rate of the 3rd hour (marked by the red asterisk in Figure 2A). The t-test applied between the GDM and MDM at the corresponding time interval showed that their expansion rate was statistically significant (p = 0.0055) at the 3rd hour (marked by the black asterisk in Figure 2A). Further, the expansion rate of MDM increased from 3rd to 4th hour. It suggests that many cells of the leading site started to expand in this duration. It may happen because the initial effect of high cell number density is over or earlier recruited leader cells stopped working, and submarginal cells start to expand again to push and recruit new leader cells. The t-test also showed that the expansion rate of GDM and MDM was statistically significant (p = 0.0357) at the 4th hour. Taking the time average of five independent experiments, the expansion rates of GDM and MDM were 0.058 ± 0.005 and 0.036 ± 0.006 μm2/h, respectively (Figure S1A). The expansion rate of GDM showed a statistically significant (p = 0.0285) difference from MDM.

The GDM and MDM contained 81 ± 7 cells and 110 ± 15 cells at their leading site, respectively (Figure 2B). The number of cells at the leading site for GDM and MDM were significantly different (p = 0.0090). It implies that the average area of GDM should be more than that of MDM. It was found that throughout the experimental observation, the average cell area of GDM remained higher than that of MDM. At each time point, the average cell area of GDM was statistically significant (p < 0.05) to the MDM. The average cell area of GDM keeps on increasing with time (Figure 2C). It suggests that the majority of cells of GDM increased in their area with time, whereas the average area of the MDM increased up to 2 h, followed by the decrease and so on (Figure 2C). It suggests that the cells may expand and shrink at a different time interval. The expansion rate of MDM exhibited the wave pattern that could be seen as an indicator of collective cell migration.

Then, the change in the effective radius (ΔRE) was measured for all the cells with time.

graphic file with name ao0c06232_m001.jpg 1

where ΔRE is the change in the cell effective radius and AF and AI represents the final and initial cell area, respectively.

For GDM and MDM, the number of cells exhibited a change in their cell effective radius, as shown by the bar graph (Figure 2D). It was found that 67% of GDM and 89% of MDM cells had undergone a small change in their effective radius (ΔRE < 1.5). However, the remaining 33% of GDM and 11% of MDM cells had undergone a large change in their effective radius (ΔRE > 1.5). It shows that many cells of GDM can undergo a huge change in their effective cell radius compared to the cells of the MDM.

Migration of GDM and MDM with Time

At the leading site of the monolayer, the GDM and MDM have a cell number density of ∼3094 and ∼4055 cells/mm2, respectively. For GDM and MDM, cell migration analysis was done by tracking the cell center with time. The coordinates of the cell geometric center stored in the excel sheet were imported in a MATLAB code to mark the cell center (red dot) in the image sequence (Figure 3A,B). Then, the MTrackJ plug-in of ImageJ was used to track the center for each cell throughout the image sequence. The trajectory of cell centers exhibited directed migration toward the leading edge (Figure 3A,B). However, within the same time span, the trajectories of cell centers for GDM (Figure 3A) were smaller than the MDM (Figure 3B). It indicates that the cells of GDM migrated less than the MDM. Similarly, the velocity field obtained by the change in the cell’s geometric coordinates showed that the cells of GDM (Figure 3C) exhibited less coordinated motion compared to MDM (Figure 3D). The above results confirm that less and highly coordinated collective cell migration was found in GDM and MDM, respectively (Movie S1). The high cell number density of the MDM could be responsible for its highly coordinated collective cell migration. Further, the mean square displacement (MSD) was obtained from the geometric coordinates of the cells and plotted against time. The slope of the MSD versus time for the monolayer was greater than 1, which implies that cells at the leading site exhibit superdiffusive behavior. Nava-Sedeño et al.26 also demonstrated that for the directed cell trajectory, the MSD versus time graph shows the superdiffusive trend. Since the trajectories of the vertices for the GDM were less directed and shorter (Figure 3A) as compared to MDM (Figure 3B), therefore, the GDM exhibited a less superdiffusive trend compared to MDM (Figure 3E).

Figure 3.

Figure 3

Open in a new tab

Comparison of migration between GDM and MDM. (A) Tracking of the cell center in GDM, (B) tracking of the cell center in MDM, (C) velocity field of GDM, (D) velocity field of MDM, (E) MSD as a function of time for GDM and MDM, (F) average migration rate versus time for GDM and MDM. Note: MSD vs time plot in (E) and standard errors in (F) are obtained from 5 independent experiments. The black asterisk represents statistical significance obtained by applying an unpaired t-test between corresponding rows of GDM and MDM. The significant differences were determined by p-values, where * and ** represent the significance level of p < 0.05 and p < 0.01, respectively.

The migration rate or velocities of the cells were measured by dividing the change in the cell geometric center by the time in which the change has occurred. The migration rate of the monolayer was calculated by taking the spatial average of the migration rate of cells present at the leading site. It was observed that at every time step, the migration rate of MDM was more than that of GDM (Figure 3F). The migration rate of the MDM was statistically significant (p < 0.05) to GDM throughout the experimental observation. Tlili et al.22 experimentally demonstrated that cell number density determines the velocity of the cell in the monolayer since the cell number density of the MDM was more than that of GDM. Thereby, the MDM exhibited more migration rate (or velocity) than GDM (Figure 3F). The migration rate of GDM remained almost constant.

In contrast, the migration rate of MDM increased sharply from 1st hour to 3rd hour and afterward decreased slowly. It was observed that the migration rate (Figure 3F) of MDM exhibited the opposite trend as that of its expansion rate (Figure 2A). Comparing the expansion and migration rate of MDM step by step, the initial value of the expansion rate for 1st hour was high (Figure 2A), and the migration rate was low (Figure 3F). Then, the expansion rate fell (Figure 2A), and the migration rate increased (Figure 3F) rapidly from the 1st hour to the 3rd hour. Further, the expansion rate (Figure 2A) increased, and the migration rate (Figure 3F) decreased from 3rd to 4th hour. By taking the temporal average of the experiments, the average migration rate of GDM and MDM was 2.4 ± 0.4 and 5.8 ± 0.8 μm/h, respectively (Figure S1B). The average migration rate of GDM was statistically significant (p = 0.0201) to the MDM.

Cell Competition Approach to Analyze Cells of GDM and MDM

There are two types of cell populations observed among the cell monolayer: (1) Winner cells and (2) Loser cells. The winner cells gain, and loser cells decrease in their area as a result of “Cell Competition.” As per the literature, the cells having the winner phenotype are strong, adaptive, fast-growing, and more fit,27−33 whereas cells having loser phenotype are weak, less active, senescence-like, slow-growing, and less fit.27−33 Therefore, the winner cells have a relatively more fit phenotype compared to the loser cells.27−32,34,35 In our analysis, the cells that grew more than or equal to 20% of their original area in 4 h were considered a winner cell. Whereas the cells that grew less than 20% of their original area after 4 h were considered a loser cell.

At the leading site of GDM, only 39% of cells were the winner (Figure 4A), but they contributed to 71% in the overall expansion of the monolayer (Figure 4B). Whereas the remaining 61% of cells were losers (Figure 4A), and they only contributed to 29% in the overall expansion of the monolayer (Figure 4B). Similarly, at the leading site of the MDM, only 21% of cells was the winner (Figure 4C), but they contributed to 53% in the overall expansion of the monolayer (Figure 4D), whereas the remaining 79% of cells were losers (Figure 4C), and they only contributed to 47% in the overall expansion of the monolayer (Figure 4D). In both types of monolayers, winner cells, despite being less in number than that of loser cells, majorly contributed to the overall expansion of the monolayer.

Figure 4.

Figure 4

Open in a new tab

Distribution of population and contribution of winner and loser cells in the overall expansion. (A) Percentage distribution of winner and loser cells in the overall population of the GDM, (B) percentage contribution of the winner and loser cells in the overall expansion of the GDM, (C) percentage distribution of winner and loser cells in the overall population of MDM, (D) percentage contribution of winner and loser cells in the overall expansion of MDM.

For GDM, the net gain in the area by winner and loser cells in 4 h was 3746 ± 444 and 1465 ± 131 μm2, respectively (Figure 5A). The collective expansion of winner and loser cells was statistically significant (p = 0.0087), shown by the red asterisk in Figure 5A. Whereas, for MDM, the net gain in the area by winner and loser cells in 4 h was 1626 ± 445 and 1225 ± 83 μm2, respectively (Figure 5A). The t-test showed that for MDM, the net expansion of winner cells was not statistically significant (p = 0.4773) to the loser cells. However, the net expansion of winner cells of GDM and MDM was statistically significant (p = 0.0098), shown by the black asterisk in Figure 5A. The changes in the average cell area of winner and loser cells were observed with time (Figure 5B). In both types of the monolayer (GDM and MDM), the average area of the loser cell was initially more than the winner cell. However, with time, the winner cells expanded at a higher rate than the loser cells. Thereby, during the experiments, the average cell area of the winner exceeded the loser cells (Figure 5B). Further, the expansion rates of winner and loser cells were compared for both the monolayer. It was found that throughout the experimental observation, the expansion rate of the winner cells remained higher than that of the loser cells (Figure 5C,D). For GDM, the expansion rate of winner and loser cells exhibited a mirror opposite or out-of-phase trend (Figure 5C). The t-test showed that at all time points, the expansion rate of the winner cells remained statistically significant (p < 0.05) to the loser cells. However, for MDM, the expansion rate of the winner and loser cells exhibited a similar or in-phase trend (Figure 5D). It indicates that in the case of MDM, both winner and loser cells were expanding in a synchronized way.

Figure 5.

Figure 5

Open in a new tab

Comparison of expansion between winner and loser cells of GDM and MDM. (A) Net gain in the area by winner and loser cells, (B) average cell area versus time, (C) expansion rate of winner and loser cells of GDM, (D) expansion rate of winner and loser cells of MDM. Note: Standard error bars shown here are obtained from 5 independent experiments. The significance of paired and unpaired t-test was shown by the red and black asterisk, respectively. The significant differences were determined by p-values, where *, **, and *** represents the significance level of p < 0.05, p < 0.01, and p < 0.001, respectively.

The migration aspects of winner and loser cells were analyzed for both types of the monolayer. The velocity fields of winner and loser cells were highlighted with a different color to identify the difference between their magnitude and direction. The winner cells were shown with yellow vectors, and loser cells were marked by red vectors (Figure 6A,B). Unfortunately, we observed no visual difference between the velocity vectors of winner and loser cells in both types of the monolayer. Therefore, to understand the difference between the migration of winner and loser cells, their MSD was plotted as a function of time. For GDM, the loser cells exhibited more displacement compared to the winner cells (Figure 6C). Whereas for MDM, both winner and loser cells displaced at the same rate (Figure 6D). Later, for both the cases (GDM and MDM), the average migration rates of winner and loser cells were plotted as a function of time. In both cases, the value of the migration rate of winner and loser cells was found in the same range (Figure 6E). Finally, the time average of the migration rate of winner and loser cells was taken for both cases. By applying the t-test between the migration rate of winner and loser cells, no statistical significance (p > 0.05) was obtained for both the cases (Figure 6F). Although for GDM, the loser cells displaced more than winner cells (Figure 6C) there was no significant difference (p > 0.05) between their temporal average migration rates (Figure 6F). The possible reason for this may be the physical connectivity of winner and loser cells.

Figure 6.

Figure 6

Open in a new tab

Migration of winner and loser cells for GDM and MDM. (A) Velocity field of the winner (yellow vectors) and loser cells (red vectors) in GDM, (B) velocity field of the winner (yellow vectors) and loser cells (red vectors) in MDM, (C) MSD vs time graph for the winner and loser cells of GDM, (D) MSD vs time graph for winner and loser cells of MDM, (E) migration rate as a function of time for winner and loser cells of GDM and MDM, (F) temporal average migration rate of winner and loser cells of GDM and MDM.

Row Wise Comparison between GDM and MDM

The spatial comparison of the cell rows can indicate the hidden mechanism responsible for the collective cell migration. Here, the cells of the monolayer were categorized based on their position from the leading edge. The first cell row includes all the border cells present at the leading edge, and the second cell row includes cells that were directly attached to the first cell row and so on. The first row cells were smaller in height and sometimes traveled out of the fixed imaging window. Since the cells of the first row were difficult to track, they were excluded from our study. Since we intended to analyze the monolayer as a function of space, the temporal averages of cells of the monolayer were computed for each row. It was found that the average cell area of the monolayer increased along the cell row (Figure 7A). The average area of GDM remained greater than that of MDM (Figure 7A). The t-test applied between the corresponding cell rows of GDM and MDM showed that for all cell rows, the average cell area of GDM was statistically significant (p < 0.05) to the MDM, shown by the black asterisk in Figure 7A.

Figure 7.

Figure 7

Open in a new tab

Spatial comparison between GDM and MDM. (A) Average cell area vs cell rows, (B) average cell expansion rate vs cell rows, (C) average migration rate vs cell rows, (D) average expansion and migration rate of GDM as a function of cell rows, (E) average expansion and migration rate of MDM as a function of cell rows. Note: Standard error bars shown here were obtained from 5 independent experiments. The unpaired t-test was applied between the corresponding rows of GDM and MDM. The statistical significance of the unpaired t-test is shown by the black asterisk. The significant differences were determined by p-values, where *, **, and *** represents the significance level of p < 0.05, p < 0.01, and p < 0.001, respectively.

Further, the average expansion rate of the different cell rows of the monolayer was measured. The average expansion rate of GDM and MDM was plotted as a function of cell rows. It was observed that the expansion rate exhibited the wave nature (Figure 7B). The wave nature may indicate the presence of long-range cell–cell communication along the cell rows. For the GDM, a high expansion rate was observed in the 2nd row. Although we have excluded the first row from our analysis, however, to explain the high growth rate observed in the 2nd row, it is assumed that the pull generated by the leader cells found in the 1st row causes the stretching of the cells of the 2nd row (Figure S3). Whereas moving along the cell row, there was a dip in the expansion rate of the 3rd cell row and a rise from the 3rd to 5th cell row (Figure 7B). It indicates that cells of the 4th and 5th rows expanded more than the cells of the 3rd row. The higher expansion maybe since the 4th and 5th row together contained the maximum number of growing cells. As the expansion rate of the 4th and 5th row was more than the 3rd row, it suggests that the expansion of the cells of these rows was not driven by the pull generated by leader cells, since the cells of the 4th and 5th row expanded in the sub-marginal region. Thereby, they may have preferred to expand toward the less cell number density (or toward the leading edge). We hypothesized that the cells expanding in the submarginal region apply a considerable push toward the leader cells. Further, there was a dip in the 6th row followed by a higher expansion rate for the 7th and 8th cell rows. The trend of expansion rate suggests that the random expansion of the submarginal cells could be responsible for the expansion of the GDM. For MDM, large error bars indicate no change in the expansion rate along the cell rows (Figure 7B). Unlike GDM, there was not much variation of the expansion rate along the cell rows.

The average migration rates of the cell rows were measured. The average migration rate of the GDM and MDM were plotted as a function of the cell rows (Figure 7C). It was found that the migration rate (or velocity) of the monolayer decay along the cell rows and is consistent with the reported literature.17,36,37 However, the migration rate of the MDM was higher than the migration rate of GDM (Figure 7C). The high cell number density may be responsible for the high migration rate observed in the MDM. The t-test was applied between the corresponding cell rows of GDM, and MDM showed that the average migration rate of front cell rows (2nd to 5th) of GDM was statistically significant (p < 0.05) to the MDM (Figure 7C). Then, we checked for the existence of an opposite trend for expansion (Figure 2A) and migration rate (Figure 3F) across the rows, as observed for the MDM with time. Hence, for both types of the monolayer, the expansion and migration rates were compared. Interestingly, the expansion and migration rate from 3rd to 7th cell rows exhibited a mirror-opposite trend (Figure 7D,E). The expansion rate decreased with the increase in the migration rate and vice versa. It suggests that the row that expands more also migrates less and vice versa. The reason for excluding the 2nd row from the analysis was that it might have undergone the stretching due to the pull generated by the leader cells (Figure S3). Whereas, the reason for neglecting the values of the 8th row is because in many experiments of GDM, very few cells of the 8th row were tracked. Finally, to establish the relation between the expansion and migration rates, the Pearson’s correlation coefficient was calculated. It was found that a strong negative correlation existed between the expansion rate and the migration rate. For GDM and MDM, the value of correlation was −0.98 and −0.77, respectively. The strong negative correlation indicates that the expansion rate and migration rate exhibit the opposite trend. It supports the earlier statement that the row that expands more migrate less and vice versa.

Cell Morphology Variation along the Cell Rows

The cell morphology can be used to predict its elasticity, fluidity, polarity, and intercellular interaction with its neighbors. The cells being active in nature can change their morphology in real-time. It was observed that within same duration, cells of the GDM undergo minute changes, but cells of MDM undergo huge transformation in their morphology (Figure 8A). Here, we have analyzed two parameters, namely shape index (SI) and aspect ratio (AR), to check the change in the cell morphology along the cell rows. The first parameter was SI, which is a dimensionless parameter used to quantify the elastic or fluid-like behavior of the cells. It is measured by dividing the parameters of the cell by the square root of its area (eq 2). If the SI > 3.81, the cell–cell adhesion dominates over cortical tension. Hence, cells exhibit fluid-like behavior.38 Here, we found that cells at the leading site of the monolayer exhibit fluid-like behavior (SI > 3.81). The SI of cells reduces along the cell row (Figure 8B). The cells of the MDM were more fluid-like as compared to the GDM. The t-test showed that the SI of the 6th and 7th row of GDM was statistically significant to the 6th and 7th row of MDM, respectively.

graphic file with name ao0c06232_m002.jpg 2

where P is the cell parameter and A is the cell area.

Figure 8.

Figure 8

Open in a new tab

Morphological analysis of GDM and MDM. (A) Change in the cell shape with time, (B) SI as a function of the cell rows, (C) AR as a function of the cell rows. Note: The standard error bars shown here were obtained from 5 independent experiments. The unpaired t-test was applied between the corresponding rows of GDM and MDM. The statistical significance is shown by the black asterisk. The significant differences were determined by the p-values, where * and ** represent the significance level of p < 0.05 and p < 0.01, respectively.

Similarly, the second parameter was AR, and it is also a dimensionless parameter used to quantify the cell shape. The ‘Fit ellipse’ was selected from the “Set Measurements” in ImageJ. It measures the major and minor axis of the best fitting ellipse to the cell. The major to the minor axis ratio was computed to obtain the AR (eq 3). The AR indicates the polarity of the cell that can be linked to its motility. For GDM, the AR decreased along the cell row. However, for MDM, the AR remained constant from the 2nd to the 4th cell row and decreased afterward. Upon comparing the corresponding cell rows, the AR of GDM remains lower than that of MDM. The t-test showed that the AR of the 5th and 6th cell row of GDM was statistically significant to the AR of the 5th and 6th cell row of MDM. In summary, both SI and AR indicated that cells of the MDM were more fluid-like and motile compared to GDM.

graphic file with name ao0c06232_m003.jpg 3

Modes of Collective Cell Migration

The collectively expanding cell groups were found at the leading site of the monolayer. The procedure of identification of these groups has been discussed in the materials and methods section. These groups were referred to as dynamic growing cell colonies because they can change their shape with time. Moreover, these groups can emerge at different locations with time. To understand the function of these dynamically growing cell colonies, these colonies were converted into static growing cell colonies (Material and Methods section) and then analyzed. We assumed that the dynamically growing cell colonies also perform the same function for a short time span as discussed here for static growing cell colonies.

In order to understand the physiological meaning of the growth for these collectively growing cell colonies, the z-stack (Figure S2A) image analysis was performed. In this analysis, the 3D interpretations of the 2D images were made. The static growing cell colonies were considered for this analysis. The final image of the experiment was selected as the reference image. All the cells of the static growing colonies were marked by blue circles. It was found that the remaining cells either shrink or fluctuate in the area with time. Contrary to the expanding or growing cells, the shrinking cell reduced in their area by the end of the experiment. Whereas the fluctuating cell increase in area from the beginning and after a while their area decrease till the end of the experiment (such that the net change in its area was less than 20% of its original area). The shrinking and the fluctuating cells were also marked in the reference image by red and yellow circles. The regions of interest (ROI) were marked in the reference image as “B,” “C,” and “D.” The ROI “B” and ROI “C” contained the majority of collectively growing cells. It was found that at t = 0 h, the growing cells of these ROIs were focused on both the top and bottom plane (Figure 9B,C). However, at t = 4 h, the growing cells remained focused on the bottom plane and went out of focus from the top plane (Figure 9B,C). It suggests that the growing cells reduced in their height (Figure S2B). It implies that these growing (or expanding) cells were spreading with time as they expanded in their area and reduced their height. The collective expansion of these growing cells must push their neighboring cells. Therefore, ROI “D” was selected to evaluate the interface of growing cells and their neighboring cells to find the trace of the push. The final image at t = 4 h was selected to compare the change in height and area of the growing cells with their neighboring cells (Figure 9D). It was found that on the top plane, the growing cells were out of focus, and neighboring cells were focused (Figure 9D). As we know that growing cells were out of focus from the top plane because they reduced in height. Thereby, the neighboring cells have more height as compared to growing cells. Interestingly, the neighboring cells either shrink or fluctuate in their area. Therefore, we assumed that the push applied by the expansion of the growing cells might be responsible for the shrinkage or fluctuation of the neighboring cells (Figure S2C). So, we hypothesized that the cells of the collectively growing cell colonies spread to push their neighboring cells toward the leading edge. This hypothesis was used to explain the collective cell migration of the monolayer.

Figure 9.

Figure 9

Open in a new tab

3D interpretation of the 2D images. (A) Final image of the experiment is used as a reference image. The growing, shrinking, and fluctuating cells are represented by blue, red, and yellow circles, respectively. The ROIs “B”, “C” and “D” are marked in the reference image, (B) zoom-in of ROI “B,” and (C) zoom-in of ROI “C” contains the majority of growing cells. At t = 0 h, cells are focused on both planes. However, at t = 4 h, cells remained focused on the bottom plane and went out of focus on the top plane. Therefore, growing cells spread in the area by reducing in height and expanding in the area, (D) zoom-in of ROI “D”, the growing cells were out of focus in the top plane, whereas their neighboring cells (shrinking and fluctuating) remained in focus. It means that neighboring cells have more height than the growing cells. As these neighboring cells shrink or fluctuate with time, it may result from the push applied by the collectively growing or spreading cell colonies.

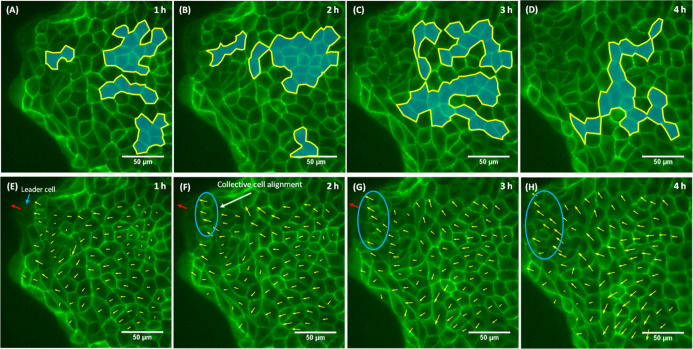
In GDM, the growing cell colonies found in the submarginal region expand at a higher rate compared to its neighboring cells. Thereby, the differential growth rate causes the formation of localized mechanical stress in the tissue.39 We assumed that some of the marginal cells get recruited as leader cells (Figure S3A) to relieve this localized mechanical stress. The leader cells start to pull their immediate follower cells of the 2nd row attached to it and cause them to stretch. Thereby, the cells of the 2nd row connected to the leader cells rapidly increase in their area with time (Figure S3B). It may be the reason for the high expansion rate observed in the 2nd row of the GDM (Figure 7B). Toward the monolayer center, a less expansion rate was observed in the cells of the 3rd row. However, a high expansion rate was observed in the 4th and 5th cell rows, as these rows contained the maximum number of growing cells. Since the expansion rate of the 4th and 5th row was higher than the 3rd row, it also indicates that the cells of the growing colonies were spreading by themselves and not getting stretched by the pull applied by the leader cells. As discussed earlier, we assumed that these growing cell colonies push and displace their front cell rows toward the leader cells. Thereby, high collective cell alignment was observed in the front cell rows (Figure S4A). Superimposing the initial and final location of growing cell colonies showed that the growing cell colonies prefer to expand toward the leader cells (Figure S4B). Therefore, we assumed that the push applied by the growing cell colonies act in the same direction in which the leader cells were pulling their immediate cell rows. Hence, both the forces work together to displace the front cell rows toward the leader cells. As these dynamically growing cell colonies emerge at different locations with time (Figure 10A–D), they can efficiently support the migration of the leader cell to regulate the expansion of the tissue. For GDM, the velocity field of the cells moved in the outward direction (Figure 10E–H). However, highly aligned velocity vectors were spotted just behind the leader cells (Figures 10F–H, and S4A, shown by the blue color ellipse).

Figure 10.

Figure 10

Open in a new tab

Dynamically growing cell colonies and the velocity field of GDM. The growing cell colonies found in (A) 1st h, (B) 2nd h, (C) 3rd h, and (D) 4th h. The velocity field of (E) 1st h, (F) 2nd h, (G) 3rd h, and (H) 4th h. Note: The growing cell colonies are represented by blue color and yellow outline. The blue ellipse shows the region of high collective cell alignment, and the red arrow represents the direction of motion of the leader cell.

In the case of MDM, it was formed by the growing large number of cells in a finite space by placing a physical barrier. The removal of the physical barrier leads to the availability of free space, and the cells of the monolayer exhibit collective motility toward the free space.12,19,22,23 Vishwakarma et al.19 showed in their study that the first leader cell emerged after 3 h. In our case, the experiment was performed after 2 h of removal of the culture insert. The large growing cell colonies were observed in the 1st hour (Figure 11A), since we assumed that the growing (or winner) cells expand more and migrate less. Therefore, in the 1st hour, very small magnitudes of velocity vectors were observed behind the front cell rows (the region indicated with an orange ellipse, Figure 11E), supporting the hypothesis that the push generated by the growing cell colonies might recruit some of the marginal cells as leader cells. Then, these newly formed leader cells begin to pull the follower cells. Due to the presence of high cell number density, the cells begin to exhibit collective cell migration, region indicated by a blue ellipse (Figure 11F,G), and growing cell colonies start to disappear (Figure 11B,C) from the 1st hour to the 3rd hour. It may be the reason for the decrease in expansion rate (Figure 2A) and an increase in the migration rate (Figure 3F) from 1st to 3rd hour. Petitjean et al.17 also showed that after 4 h of removing the physical barrier, the migration rate increases with time. Tlili et al.22 claimed that the velocity of the cells of the monolayer depends upon cell number density and is independent of its distance from the leading edge. Later, in our experiments, the growing cell colonies emerge again in the 4th hour (Figure 11D) maybe because the initial effect of high cell number density reduce or old leader cells become ineffective and newly formed growing cell colonies push the front cell rows to recruit new leader cell to maintain the collective cell migration of the monolayer (Figure 11H).

Figure 11.

Figure 11

Open in a new tab

Dynamically growing cell colonies and velocity field in MDM. The growing cell colonies in (A) 1st h, (B) 2nd h, (C) 3rd h, and (D) 4th hr. The velocity field in (E) 1st h, (F) 2nd h, (G) 3rd h, and (H) 4th hr. Note: The growing cell colonies are represented by blue color and yellow outline. The orange ellipse in (E) encloses the region having small magnitude vectors. The blue ellipse in (F–H) encloses the region showing high collective cell migration.

The distinct modes of collective cell migration observed in this work can be possibly explained by considering intercellular social interactions such as local alignment (LA) and contact inhibiting locomotion (CIL). Recent studies showed that the trade-off between LA and CIL could be responsible for modes of collective cell migration.40−42 The coordination between LA and CIL may dictate giant density fluctuation, leading to phase separation in the monolayer.40,41,43 In our study, the cells of the colonies grow at a higher rate compared to their surrounding tissue. It can be considered as phase separation. The literature suggests that translation motion occurs when LA dominates the CIL and cage-relative motion when CIL dominates LA.40,41 The high MSD observed for the surrounding tissue compared to the colonies (Figure 6C) in our study may be possibly attributed to CIL dominance in colonies and LA in the surrounding tissue, suggesting cage-relative motion of cells in colonies and translational motion of cells in the surrounding tissue. For GDM, the colonies were observed throughout the experiment, suggesting that the combined effects of the cage-relative motion and translation motion might be responsible for a less degree of collective cell migration (Figure 10). Whereas in MDM, the colonies were present initially (1st hour), and a less degree of collective cell migration was observed in that duration (Figure 11A,E). However, after the formation of the leader cells, this monolayer behaved differently to GDM, which might be associated with the difference in their cell number density. In this case (MDM), the shrinking of submarginal cells was observed from the 2nd to 3rd hour, which might have helped the cells migrate effectively by minimizing their focal adhesions and resulting in the disappearance of colonies in this duration (Figure 11B,C). Therefore, the phase separation may cease to exist at this stage, and LA began to dominate in the monolayer. This may be the possible reason for the synchronized and directional motion of the submarginal cells toward the free space resulting in rapid collective cell migration (Figure 11F,G). It may ease the effect of high cell number density at later stages, and colonies start to appear again with time (Figure 11D).

Conclusions

In the present work, we investigated two types of monolayer formed by using initially free (GDM) and confined (MDM) boundary conditions. A distinct mode of tissue expansion and collective cell migration was observed in the MDM and GDM. The GDM showed significantly more expansion compared to the MDM. The winner and loser population was identified in both the monolayer. Despite being less in number, winner cells majorly contributed to the expansion of the monolayer, indicating the relatively fit phenotype of the winner cells. The opposite trends of the expansion rate for winner and loser cells suggested that the idea of cell competition was more relevant in the case of GDM. In contrast, the similar trends of the expansion rate and identical slopes of MSD versus time for the winner and loser cells can be linked to the high collective cell migration observed in MDM. It has been shown that the GDM having less cell number density exhibited slow and less aligned collective cell migration, whereas rapid and highly aligned collective cell migration was observed in MDM having high cell number density, revealing a fundamental link between the cell number density and collective cell migration of the expanding monolayer. In physiological scenarios such as wound healing and cancer metastasis, the cell number density is relatively low compared to the extensively investigated artificial wound model (MDM). Therefore, GDM closely resembles these physiological scenarios. This study provides useful insights into the collective cell migration in physiological conditions that are expected to be used in the future to design a better system that can tune the collective cell migration in wounds, cancer metastasis, and other biological processes.

Materials and Methods

Cell Culture Protocol

The live-cell experiments were performed with MDCK II cells, stably transfected with Green Florescent Protein E-Cadherin. The cells were cultured in Dulbecco’s modified Eagle medium supplemented with 10% fetal bovine serum (FBS) and 1% penicillin–streptomycin in humidified conditions with 5% CO2 at 37 °C. The ∼70% confluent cells were harvested by treating with the trypsin–EDTA solution for the experiments.

Formation of GDM

The GDM was formed by seeding the cells (100 μL, 1,000,000 cells/mL) at the center of the 25 mm glass coverslip (Figure 1A) placed inside the 35 mm tissue culture-treated polystyrene Petri dish and kept in the incubator (37 °C and 5% CO2). After 2 h, 2 mL of complete media was added to the Petri dish. The cells were incubated for 48 h inside the incubator and analyzed under the microscope. If a confluent cell monolayer was formed, then, the coverslip was rinsed with PBS and fixed in the Attofluor cell chamber (coverslip holder). Then, the image acquisition media (2 mL, Leibovitz-15 supplemented with 10% FBS and 1% antibiotics) was added to it. The imaging of cells was done by using a motorized inverted microscope (Leica DMI 6000B) integrated with a cage incubator maintained at 37 °C. After 2 h, the live-cell imaging with z-stacking was performed at the selected location at the leading site (∼8–10 cell rows from the leading edge) by using Leica’s LAS X software, which automatically captured the images after a fixed interval up to 4 h. The z-stack images were merged by using the average intensity projection method available in the software.

Formation of MDM

It was formed by seeding the cells (50 μL, 1,000,000 cells/mL) inside each well of the culture insert (from ibidi) fixed on the top of the glass coverslip (Figure 1B) and placed inside the 35 mm tissue culture-treated polystyrene Petri dish. The cells were incubated and regularly analyzed under the microscope after 48 h. When a confluent cell monolayer was formed, the culture insert was peeled off, and the coverslip was fixed in the coverslip holder. Then, 2 mL of image acquisition was added to it, and the holder was taken under the microscope-integrated with a cage incubator. At last, the desired location was selected at the leading site of the monolayer formed after the removal of the physical barrier. After 2 h, the live-cell imaging with z-stacking was performed at this location for 4 h. The average intensity projection method of the software was employed to merge the z-stack images.

Image Analysis

Skeletonization and Cell Tracking

The time-lapse image sequences were converted into the skeletonized image with the help of ImageJ. The image sequence was imported in ImageJ (File > Import > Image Sequence) and converted into 8-bit images (Image > Type > 8-bit). Then, the bandpass fast Fourier transform (FFT) filter (Process > FFT > Bandpass Filter) was applied to the image sequence. Further, the image sequence was converted into a binary format (Process > Binary > Make Binary) by selecting the “Percentile” method and “Dark” background. Finally, the binary images were skeletonized (Process > Binary > Skeletonize). The cell area tracking was manually performed by using the “Wand (tracing) tool” of ImageJ on skeletonized images. For the cells that were not segmented properly, their area was measured manually using the “Polygon selection tool” of ImageJ on the raw fluorescent images. The change in the cell area and geometric center with time was measured for all cells. These measurements were stored in excel sheets.

Identification of Collectively Growing Cell Colonies

The Pearson correlation coefficient was employed to identify the group of cells expanding or growing together with time. It establishes a direct relationship between two parameters (i.e., change in the area of cell a and cell b with time). For any two connected cells (a and b), if 70% of the time they are changing their area in the same way (may increase, decrease, or fluctuate), then, the value of correlation becomes 0.7, representing a strong positive correlation.

graphic file with name ao0c06232_m004.jpg 4

Where aab denotes the Pearson correlation coefficient between the change in the area of the cell a and cell b, n represent the number of time frame, and ai and bi represent the area of a and b at the ith frame, respectively.

Initially, all cells of the leading site were randomly assigned with a number as their identity. Then, the initial area (at t = 0 h) and final area (at t = 1 h) of the same cell were compared. If the cell expands more than 5% of the initial area, it was considered a growing cell. All growing cells were marked in the reference image (at t = 0 h). Then, the area of each cell was individually compared to its neighboring cells for previous 1 h images. All the cells exhibiting a strong positive correlation (aab > 0.7), their common edges were marked in a reference image (at t = 0 h). Finally, the growing cells exhibiting strong positive correlation were enclosed together and referred to as “Dynamically Growing cell colonies.” Similarly, the colonies were obtained after each hour, up to 4 h. These colonies were referred to as dynamic as the different shapes of colonies emerged at different hours. However, the dynamic colonies were converted into static colonies for the ease of analysis by considering previous 4 h images for analysis (covering the entire experimental span). For static colonies, all the cells that expand more than 20% of their initial area were considered as growing cells and all the growing cells that exhibited a positive correlation (aab > 0.7) were enclosed to form such a colony. Since it covers the entire experimental span of 4 h, therefore, these colonies have a fixed shape. Thereby, these colonies were named “static growing cell colonies.”

The growth criteria (5% for dynamic and 20% for static cell colonies) were selected because Zehnder et al.24 reported that the cell area fluctuates by ± 20% in 4 h. Therefore, cells that grow more than 20% in 4 h were considered as growing cells during the identification of static colonies. Accordingly, 5% growth criteria were selected during the identification of dynamic colonies obtained from 1 h images. These growth criteria effectively reduced the chances of cell area fluctuations to be considered growth.

MATLAB Codes

The MSD versus time was plotted by importing the geometric coordinates of the cells in a self-written MATLAB code.

Statistical Analysis

The normality of data was tested by visual inspection of the histogram, normal Q–Q plots, values of kurtosis, and skewness, before applying the t-test. The paired and unpaired t-tests were applied as suitable. The significant differences were determined by p-values, where *, **, and *** represents the significance level of p < 0.05, p < 0.01, and p < 0.001, respectively. The statistical analysis was performed using Microsoft Excel (2007).

Acknowledgments

The authors acknowledge W. J. Nelson for sending the MDCK cell lines. The authors also acknowledge the Department of Mechanical Engineering and the Department of Chemical Engineering for providing the necessary instruments and consumables. A.K. is thankful to IIT Ropar for the institute fellowship.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c06232.

  • Comparison of velocity field between GDM and MDM (AVI)

  • Expansion and migration rates of the GDM and MDM; schematic representation of the procedure used for z-stack image analysis; leader cell pulls to stretch the cells of the 2nd row; and expansion of static cell clusters (PDF)

Author Contributions

The manuscript was written through the contributions of all authors, and they have given their approval to the final version of the manuscript.

The financial support for this work was provided by IIT Ropar, Punjab, India.

The authors declare no competing financial interest.

Supplementary Material

ao0c06232_si_001.avi (2.6MB, avi)
ao0c06232_si_002.pdf (768.9KB, pdf)

References

  1. Friedl P.; Hegerfeldt Y.; Tusch M. Collective Cell Migration in Morphogenesis and Cancer. Int. J. Dev. Biol. 2004, 48, 441–449. 10.1387/ijdb.041821pf. [DOI] [PubMed] [Google Scholar]
  2. Martin P.; Parkhurst S. M. Parallels between Tissue Repair and Embryo Morphogenesis. Development 2004, 131, 3021–3034. 10.1242/dev.01253. [DOI] [PubMed] [Google Scholar]
  3. Lecaudey V.; Gilmour D. Organizing Moving Groups during Morphogenesis. Curr. Opin. Cell Biol. 2006, 18, 102–107. 10.1016/j.ceb.2005.12.001. [DOI] [PubMed] [Google Scholar]
  4. Friedl P. Prespecification and Plasticity: Shifting Mechanisms of Cell Migration. Curr. Opin. Cell Biol. 2004, 16, 14–23. 10.1016/j.ceb.2003.11.001. [DOI] [PubMed] [Google Scholar]
  5. De Pascalis C.; Etienne-Manneville S. Single and Collective Cell Migration: The Mechanics of Adhesions. Mol. Biol. Cell 2017, 28, 1833–1846. 10.1091/mbc.e17-03-0134. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Mayor R.; Etienne-Manneville S. The Front and Rear of Collective Cell Migration. Nat. Rev. Mol. Cell Biol. 2016, 17, 97. 10.1038/nrm.2015.14. [DOI] [PubMed] [Google Scholar]
  7. Vicsek T.; Czirók A.; Ben-Jacob E.; Cohen I.; Shochet O. Novel Type of Phase Transition in a System of Self-Driven Particles. Phys. Rev. Lett. 1995, 75, 1226. 10.1103/physrevlett.75.1226. [DOI] [PubMed] [Google Scholar]
  8. Szabó B.; Szöllösi G. J.; Gönci B.; Jurányi Z.; Selmeczi D.; Vicsek T. Phase Transition in the Collective Migration of Tissue Cells: Experiment and Model. Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. 2006, 74, 061908. 10.1103/physreve.74.061908. [DOI] [PubMed] [Google Scholar]
  9. Ladoux B. Biophysics: Cells Guided on Their Journey. Nat. Phys. 2009, 5, 377. 10.1038/nphys1281. [DOI] [Google Scholar]
  10. Du Roure O.; Saez A.; Buguin A.; Austin R. H.; Chavrier P.; Silberzan P.; Ladoux B. Force Mapping in Epithelial Cell Migration. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 2390–2395. 10.1073/pnas.0408482102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Vitorino P.; Meyer T. Modular Control of Endothelial Sheet Migration. Genes Dev. 2008, 22, 3268–3281. 10.1101/gad.1725808. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Poujade M.; Grasland-Mongrain E.; Hertzog A.; Jouanneau J.; Chavrier P.; Ladoux B.; Buguin A.; Silberzan P. Collective Migration of an Epithelial Monolayer in Response to a Model Wound. Proc. Natl. Acad. Sci. U.S.A. 2007, 104, 15988–15993. 10.1073/pnas.0705062104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Gov N. S. Collective Cell Migration Patterns: Follow the Leader. Proc. Natl. Acad. Sci. U.S.A. 2007, 104, 15970–15971. 10.1073/pnas.0708037104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Reffay M.; Parrini M. C.; Cochet-Escartin O.; Ladoux B.; Buguin A.; Coscoy S.; Amblard F.; Camonis J.; Silberzan P. Interplay of RhoA and Mechanical Forces in Collective Cell Migration Driven by Leader Cells. Nat. Cell Biol. 2014, 16, 217. 10.1038/ncb2917. [DOI] [PubMed] [Google Scholar]
  15. Trepat X.; Wasserman M. R.; Angelini T. E.; Millet E.; Weitz D. A.; Butler J. P.; Fredberg J. J. Physical Forces during Collective Cell Migration. Nat. Phys. 2009, 5, 426–430. 10.1038/nphys1269. [DOI] [Google Scholar]
  16. Serra-Picamal X.; Conte V.; Vincent R.; Anon E.; Tambe D. T.; Bazellieres E.; Butler J. P.; Fredberg J. J.; Trepat X. Mechanical Waves during Tissue Expansion. Nat. Phys. 2012, 8, 628. 10.1038/nphys2355. [DOI] [Google Scholar]
  17. Petitjean L.; Reffay M.; Grasland-Mongrain E.; Poujade M.; Ladoux B.; Buguin A.; Silberzan P. Velocity Fields in a Collectively Migrating Epithelium. Biophys. J. 2010, 98, 1790–1800. 10.1016/j.bpj.2010.01.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Tambe D. T.; Corey Hardin C.; Angelini T. E.; Rajendran K.; Park C. Y.; Serra-Picamal X.; Zhou E. H.; Zaman M. H.; Butler J. P.; Weitz D. A.; et al. Collective Cell Guidance by Cooperative Intercellular Forces. Nat. Mater. 2011, 10, 469. 10.1038/nmat3025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Vishwakarma M.; Di Russo J.; Probst D.; Schwarz U. S.; Das T.; Spatz J. P. Mechanical Interactions among Followers Determine the Emergence of Leaders in Migrating Epithelial Cell Collectives. Nat. Commun. 2018, 9, 3469. 10.1038/s41467-018-05927-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Farooqui R.; Fenteany G. Multiple Rows of Cells behind an Epithelial Wound Edge Extend Cryptic Lamellipodia to Collectively Drive Cell-Sheet Movement. J. Cell Sci. 2005, 118, 51–63. 10.1242/jcs.01577. [DOI] [PubMed] [Google Scholar]
  21. Zorn M. L.; Marel A.-K.; Segerer F. J.; Rädler J. O. Phenomenological Approaches to Collective Behavior in Epithelial Cell Migration. Biochim. Biophys. Acta, Mol. Cell Res. 2015, 1853, 3143–3152. 10.1016/j.bbamcr.2015.05.021. [DOI] [PubMed] [Google Scholar]
  22. Gauquelin E.; Tlili S.; Gay C.; Peyret G.; Mège R.-M.; Fardin M. A.; Ladoux B. Influence of Proliferation on the Motions of Epithelial Monolayers Invading Adherent Strips. Soft Matter 2019, 15, 2798–2810. 10.1039/c9sm00105k. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Murrell M.; Kamm R.; Matsudaira P. Tension, Free Space, and Cell Damage in a Microfluidic Wound Healing Assay. PLoS One 2011, 6, e24283 10.1371/journal.pone.0024283. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Zehnder S. M.; Suaris M.; Bellaire M. M.; Angelini T. E. Cell Volume Fluctuations in MDCK Monolayers. Biophys. J. 2015, 108, 247–250. 10.1016/j.bpj.2014.11.1856. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Bindschadler M.; McGrath J. L. Sheet Migration by Wounded Monolayers as an Emergent Property of Single-Cell Dynamics. J. Cell Sci. 2007, 120, 876–884. 10.1242/jcs.03395. [DOI] [PubMed] [Google Scholar]
  26. Nava-Sedeño J. M.; Hatzikirou H.; Klages R.; Deutsch A. Cellular Automaton Models for Time-Correlated Random Walks: Derivation and Analysis. Sci. Rep. 2017, 7, 16952. 10.1038/s41598-017-17317-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Bowling S.; Lawlor K.; Rodríguez T. A. Cell Competition: The Winners and Losers of Fitness Selection. Development 2019, 146, dev167486. 10.1242/dev.167486. [DOI] [PubMed] [Google Scholar]
  28. Lawlor K.; Pérez-Montero S.; Lima A.; Rodríguez T. A. Transcriptional versus Metabolic Control of Cell Fitness during Cell Competition. Semin. Cancer Biol. 2020, 63, 36–43. 10.1016/j.semcancer.2019.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Madan E.; Gogna R.; Moreno E. Cell Competition in Development: Information from Flies and Vertebrates. Curr. Opin. Cell Biol. 2018, 55, 150–157. 10.1016/j.ceb.2018.08.002. [DOI] [PubMed] [Google Scholar]
  30. Gogna R.; Shee K.; Moreno E. Cell Competition during Growth and Regeneration. Annu. Rev. Genet. 2015, 49, 697–718. 10.1146/annurev-genet-112414-055214. [DOI] [PubMed] [Google Scholar]
  31. Marongiu F.; Laconi E. Cell Competition in Liver Carcinogenesis. World J. Hepatol. 2020, 12, 475. 10.4254/wjh.v12.i8.475. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Amoyel M.; Bach E. A. Cell Competition: How to Eliminate Your Neighbours. Development 2014, 141, 988–1000. 10.1242/dev.079129. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Casas-Tinto S.; Torres M.; Moreno E. The Flower Code and Cancer Development. Clin. Transl. Oncol. 2011, 13, 5–9. 10.1007/s12094-011-0610-4. [DOI] [PubMed] [Google Scholar]
  34. Tamori Y.; Deng W.-M. Cell Competition and Its Implications for Development and Cancer. J. Genet. Genomics 2011, 38, 483–495. 10.1016/j.jgg.2011.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. de la Cova C.; Senoo-Matsuda N.; Ziosi M.; Wu D. C.; Bellosta P.; Quinzii C. M.; Johnston L. A. Supercompetitor Status of Drosophila Myc Cells Requires P53 as a Fitness Sensor to Reprogram Metabolism and Promote Viability. Cell Metab. 2014, 19, 470–483. 10.1016/j.cmet.2014.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Kondo Y.; Aoki K.; Ishii S. Inverse Tissue Mechanics of Cell Monolayer Expansion. PLoS Comput. Biol. 2018, 14, e1006029 10.1371/journal.pcbi.1006029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Vedula S. R. K.; Leong M. C.; Lai T. L.; Hersen P.; Kabla A. J.; Lim C. T.; Ladoux B. Emerging Modes of Collective Cell Migration Induced by Geometrical Constraints. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, 12974–12979. 10.1073/pnas.1119313109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Bi D.; Yang X.; Marchetti M. C.; Manning M. L. Motility-Driven Glass and Jamming Transitions in Biological Tissues. Phys. Rev. X 2016, 6, 021011. 10.1103/physrevx.6.021011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Shraiman B. I. Mechanical Feedback as a Possible Regulator of Tissue Growth. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 3318–3323. 10.1073/pnas.0404782102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Lin S.-Z.; Ye S.; Xu G.-K.; Li B.; Feng X.-Q. Dynamic Migration Modes of Collective Cells. Biophys. J. 2018, 115, 1826–1835. 10.1016/j.bpj.2018.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Lin S.-Z.; Bi D.; Li B.; Feng X.-Q. Dynamic Instability and Migration Modes of Collective Cells in Channels. J. R. Soc., Interface 2019, 16, 20190258. 10.1098/rsif.2019.0258. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Barton D. L.; Henkes S.; Weijer C. J.; Sknepnek R. Active Vertex Model for Cell-Resolution Description of Epithelial Tissue Mechanics. PLoS Comput. Biol. 2017, 13, e1005569 10.1371/journal.pcbi.1005569. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Smeets B.; Alert R.; Pešek J.; Pagonabarraga I.; Ramon H.; Vincent R. Emergent Structures and Dynamics of Cell Colonies by Contact Inhibition of Locomotion. Proc. Natl. Acad. Sci. U.S.A. 2016, 113, 14621–14626. 10.1073/pnas.1521151113. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao0c06232_si_001.avi (2.6MB, avi)
ao0c06232_si_002.pdf (768.9KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES