Abstract
Two Bromodomain-Containing proteins BAZ2A and BAZ2B are responsible for remodeling chromatin and regulating noncoding RNAs. As for our current studies, integration of multiple short molecular dynamics simulations (MSMDSs) with molecular mechanics generalized Born surface area (MM-GBSA) method is adopted for insights into binding selectivity of three small molecules D8Q, D9T and UO1 to BAZ2A against BAZ2B. The calculations of MM-GBSA unveil that selectivity of inhibitors toward BAZ2A and BAZ2B highly depends on the enthalpy changes and the details uncover that D8Q has better selectivity toward BAZ2A than BAZ2B, D9T more favorably bind to BAZ2B than BAZ2A, and UO1 does not show obvious selectivity toward these two proteins. The analysis of interaction network between residues and inhibitors indicates that seven residues are mainly responsible for the selectivity of D8Q, six residues for D9T and four residues provide significant contributions to associations of UO1 with two proteins. Moreover the analysis of interaction network not only reveals warm spots of inhibitor bindings to BAZ2A and BAZ2B but also unveils that common residue pairs, including (W1816, W1887), (P1817, P1888), (F1818, F1889), (V1822, V1893), (N1823, N1894),(L1826, L1897), (V1827, V1898), (F1872, F1943), (N1873, N1944) and (V1879, I1950) belonging to (BAZ2A, BAZ2B), induce mainly binding differences of inhibitors to BAZ2A and BAZ2B. Hence, insights from our current studies offer useful dynamics information relating with conformational alterations and structure-affinity relationship at atomistic levels for novel therapeutic strategies toward BAZ2A and BAZ2B.
1. Introduction
Bromodomains (BRDs), regarded as evolutionarily conserved protein interaction modules, can specifically identify acetylated lysine (Kac)1,2 residues in histone tails and other substrates, which promotes the roles in regulating gene transcription. By now, the most of different bromodomain-containing proteins encoded by human genome have been potential targets used as treatments of cancer, inflammation, and neurological disease.3,4 The bromodomains (BDs) located at the bromo- and extra-terminal domain (BET)5,6 have been intensively researched in recent years. According to structural topology, four members BRD2, BRD3, BRD4 and BRDT of human BET family share a wider pocket identify diacetylated peptides.7−9 Inhibition of BET BDs’ activity through potent and selective inhibitors, such as IBET and JQ1, has been thought to be an effective therapeutic strategy on inflammatory, cardiovascular disease and cancers.10−12 However, the physiological role of some bromodomains remains rarely understood and a large portion of them lack any selective inhibitors that can reveal their individual functions. Amongst these, the two homologous bromodomains (BAZ2A and BAZ2B) situated near the zinc finger domain protein 2A and 2B share sequence identity of 57%8 and these two proteins also have an unusual binding pocket that rationally accommodates Kac. Consequently, BAZ2A and BAZ2B are regarded as drugable bromodomains13,14 and have been significant targets of drug design toward treatment of various diseases.
Based on structural information, 110 amino acids of BAZ2A and BAZ2B (BAZ2A/B) form four α-helices αA, αB, αC and αZ, moreover a distinct binding cranny appears between two featured loops ZA loop and BC loop in Figure 1A. The work of Gu et al. suggested that epigenetic mutations of BAZ2A is involved in prostate cancers, furthermore overexpression of BAZ2A is detected in patients of various diseases.15 Spiliotopoulos et al. recognized an inhibitor that efficiently suppresses the activity of BAZ2A though theoretical and experimental methods and seven molecules used as potential Kac-competitive binders were also determined with the NMR spectroscopy.16 Arking et al. also revealed that the BAZ2B locus is related with the mortality worldwide in the light of their meta-analysis of genome-wide associations on 1283 Sudden cardiac death reports.17 Ferguson et al. investigated interactions of the BAZ2B with H3K14ac acetylated peptides through NMR spectroscopy method and their studies indicated that both the Kac binding sites and BC loop are recognized as the hot spots of this interaction.18 Moreover, the structural information on fragment binders to BAZ2B obtained by Marchand et al. suggested that the derivatives of 3-Amino-2methylpyridine can be utilized to design inhibitors of the BAZ2B through silico discovery and crystal validation.19 Furthermore, several small molecules such as BAZ2-ICR20 and GSK280121 are currently used as potent and selective inhibitors toward the BAZ2A/B. Unfortunately, insufficiency of molecular mechanisms determining binding differences of inhibitors to BAZ2A/B potentially hinders developing process of effective inhibitors keeping down the activity of BAZ2A/B. Therefore, atomistic-level clarification of molecular mechanism and conformational changes related to binding diversity of inhibitors to BAZ2A/B can play vital roles in design of highly selective inhibitors toward BAZ2A over BAZ2B.
Figure 1.
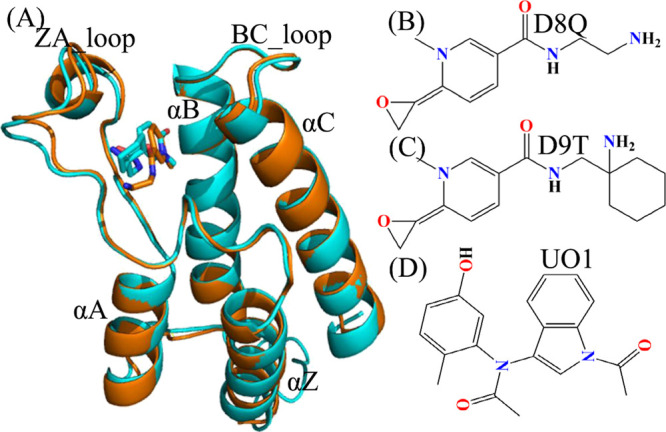
Structures of molecules: (A) Structural alignment between inhibitor-BAZ2A and inhibitor-BAZ2B, in which BAZ2A is exhibited in orange and BAZ2B in cyan; (B), (C) and(D) respectively corresponding to structures of D8Q, D9T and UO1. The blue and red letters suggest the polar atoms. BAZ2A and BAZ2B are depicted in cartoon modes and inhibitors in stick or line modes. The crystal structures of ID code 6FG6 and 6FGT in PDB are utilized to respectively display the structural topology of inhibitor-BAZ2A and inhibitor-BAZ2B.
With rapid development of calculational technology and computer hardware, classical molecular dynamics (cMD) simulations22−35 and binding affinity computations36−45 increasingly play significant roles in unveiling molecular mechanism and conformational transformations of receptors. In calculations of binding affinity, the entropic computation is highly changing, Duan et al. proposed a more efficient method of entropic calculations, namely interaction entropy, which not only obtains rational results but also saves computational time.33,46 Moreover, various works have been involved in successful insights into binding selectivity of small compounds toward homologous receptors with very similar sequence.47−52 However, the conformations of receptors sampled by cMD simulations are possibly trapped at a local minimum energy well,53 which will generate an insufficient structural ensemble and affect statistical rationality. To relieve this sampling issue in cMD simulations, multiple short molecular dynamics simulations (MSMDSs) with various initial conformations are proposed so as to obtain better sampling efficiency than a single long trajectory.54,55 Recently, different works verify that MSMDSs can indeed obtain rational conformational samplings of receptors, moreover MSMDSs have been extensively applied to uncover conformational transformations of receptors, binding selectivity, drug resistance, etc.56−67 In the present work, three inhibitors, namely D8Q, D9T, and UO1 were chosen to study their binding selectivity toward BAZ2A/B and decipher selectivity-dependent molecular mechanism. The structures of D8Q, D9T, and UO1 were displayed in Figure 1B–D. As shown in Figure 1B–D, three inhibitors D8Q, D9T and UO1 have obvious structural difference and different binding ability, thus it is requisite for design of clinically available inhibitors toward BAZ2A/B to explore atomic-level molecular mechanism depending on binding selectivity. To realize our aims, MSMDSs, principal component (PC) analysis,68−71 binding free energy prediction and free energy landscapes were coupled together to realize this current aim. Furthermore, this study is also expected to supply valuable dynamics information at the atomistic levels for design of powerfully selective inhibitors toward BAZ2A/B.
2. Materials and Methods
2.1. Construction of Simulated Systems
The starting structures of six simulated systems were obtained from the Protein Data Bank (PDB): 6FG6, 6FGV, and 6FGL respectively related to the D8Q-, D9T-, and UO1-BAZ2A complexes, while 6FH6, 6FGT, and 5E73 are separately connected to the D8Q-, D9T-, and UO1-BAZ2B compounds.72 Due to the variance in the length of residues from N-terminals of BAZ2A and BAZ2B, the residues 1798–1894 in BAZ2A and the residues 1869–1965 in BAZ2B were adopted for the constructions of six simulated systems. The program PROPKA73,74 was wielded to examine and allocate the rational protonated states to residues in BAZ2A and BAZ2B. The force field parameters of BAZ2A and BAZ2B and water molecules were yielded by employing the ff14SB75,76 and TIP3P model,77 separately. The structural optimization of three inhibitors D8Q, D9T, and UO1 was implemented at a semiempirical AM1 level, and then the BCC charges were allocated to every atom of inhibitors through the Antechamber module in Amber 18.78,79 The force field parameters of three ligands were yielded by utilizing the general amber force field (GAFF).80 Each complex was solvated in a truncated octahedral periodic box of TIP3P water molecules (buffer: 12.0 Å) consisting of ∼11,000 water molecules, which reflects the solvent environment. Eight sodium ions (Na+) were added around the protein-ligand system to neutralize the charges of the inhibitors-BAZ2A/B complexes.
2.2. Multiple Short Molecular Dynamics Simulations
Removing bad interatomic contacts and highly repulsive orientations between protein and solvent caused by system initialization plays an important role in stability of systems through MSMDSs. Based on this importance, all systems must endure energetic minimizations composed of 2500-steepest descent minimization and 2500-step conjugate gradient minimization. Subsequently, each system was heated from 0 to 300 K within 2 ns at constant volume by using a softly procedure. And then, further 2 ns equilibrium simulations were executed on each system at 300 K level. Finally, 100 ns of cMD simulations was carried out on these six systems at 300 K and a constant pressure of 1 bar through periodic boundary terms and the particle mesh Ewald (PME) approach.81,82 Nine new conformations randomly selected from the previous 100 ns MD simulations were utilized as the start coordinates for subsequent MSMDSs by randomly assigning initial atomic velocities of each protein conformations with Maxwell distribution. Therefore MSMDSs of 10 replicas (Figure S1) were realized to improve protein conformational samplings of the inhibitor-BA2ZA/B complexes. The equilibrated parts of 10 cMD simulations were integrated into a single connected MSMD trajectory convenient for the post-processing computational analysis. During all MSMDSs, the SHAKE algorithm was adopted to restrain the hydrogen-heavy atomic chemical bonds83 with a time interval of 2 fs. The temperature of the current six systems is regulated through the Langevin thermostat84 with a collision frequency of 2.0 ps–1. MSMDSs were run by using the tool pememd.cuda in Amber 18.85−87 The software VMD88 and PyMOL (www.pymol.org.) were employed to analyze the single joined trajectory and draw pictures.
2.3. Principal Component Analysis
In general, the conformational alterations of receptors are investigated with principal component (PC) analysis on the basis of the structural ensembles stemming from the experiments and molecular simulations. For our current work, PC analysis is implemented on the single joined MSMD trajectory of six simulated systems to investigate the difference in conformational changes of BAZ2A and BAZ2B, which relates to the diagonalization of a covariance matrix formed by utilizing the Cα atomic coordinates kept at the MSMD trajectory. The concerted motion direction and strength of the domains in BAZ2A/B are individually characterized by means of the eigenvectors and eigenvalues, stemming from PC analysis. Functional concerted motions of the domains in BAZ2A/B are efficiently unveiled by the first few eigenvectors with bigger eigenvalues arising from PC analysis. Meanwhile, cross-correlation analysis89−92 is also employed to understand the alterations in motion characters of BAZ2A and BAZ2B and the details concerning cross-correlation analysis (CCA) has been introduced in our previous work.28 In this study, two current analyses can be achieved by an efficient tool CPPTRAJ93 inlayed in Amber 18 and the obtained data can be visualized by the software VMD.
2.4. Calculations of MM-GBSA
Among different approaches of binding free energy predictions, molecular mechanics Poisson-Boltzmann surface area (MM-PBSA) and MM-GBSA are two efficient methods to fast measure binding strength of ligands to receptors.46,94−96 From the assessing on the performance of these two methods from Hou’s group, MM-GBSA approach,97,98 indicated in the eq 1, can obtain more rational results than MM-PBSA. Therefore, MM-GBSA method was utilized to evaluate binding strength of three inhibitors D8Q, D9T, and UO1 to BAZ2A/B and determine binding selectivity of these inhibitors to BAZ2A VS BAZ2B.
| 1 |
where ΔGcomp,ΔGpro, and ΔGinh indicate the free energies of the complex, BAZ2A/BAZ2B, as well as inhibitors D8Q, D9T, and UO1, respectively. Moreover, ΔEele and ΔEvdW represent the electrostatic and van der Waals interactions of D8Q, D9T and UO1 with BAZ2A/B in the gas phase, independently, which in general come from estimation of molecular mechanics. The terms ΔGgb and ΔGnonpol denote the polar and nonpolar solvation free energies of the inhibitor-BAZ2A/B complexes, independently. ΔGgb is estimated with the GB model proposed by Onufriev et al.99 and ΔGnonpol is computed with an empirical equation as below
| 2 |
in which the parameter γ and ΔSASA respectively characterize the surface tension and the difference in the solvent accessible surface areas because of inhibitor bindings. As for our current study, the values of 0.0072 kcal · mol · Å–2 and 0 kcal · mol–1 are assigned to two empirical parameters γ and β, individually.100,101 And hence, the sum of ΔEele,ΔEvdW, ΔGgb, and ΔGnonpol forms the enthalpy changes (ΔH) of the binding complexes. The term −TΔS represents the contribution of the entropy changes to inhibitor bindings and this component is derived through the mmpbsa_py_nabnmode program.102
3. Results and Discussion
3.1. Structural Fluctuation and Flexibilities of BAZ2A and BAZ2B
In order to obtain reasonable and sufficient conformational sampling of BAZ2A and BAZ2B, MSMDSs with a total simulated time of 1 microsecond (μs), consisting of 100-ns cMD simulations of 10 replicas, were implemented on six inhibitor-BAZ2A compounds and inhibitor-BAZ2B ones. The evolution of root-mean-square-deviations (RMSDs) of atoms C, CA, O and N in BAZ2A and BAZ2B as the simulated time were computed to measure the stability of MSMDSs and the initial optimized structures are used as the reference frames in this calculation (Supporting Information Figure S1). The RMSDs of all replicas verify that six simulated systems display relatively stable structural fluctuations after 40 ns of MSMDSs, implying that all current systems fundamentally situate at the equilibrium phases. Hence, the 40–100 ns parts from MSMD trajectories (MSMDTs) of 10 replicas were joined into a single trajectory of 600 ns to execute all post-process analyses.
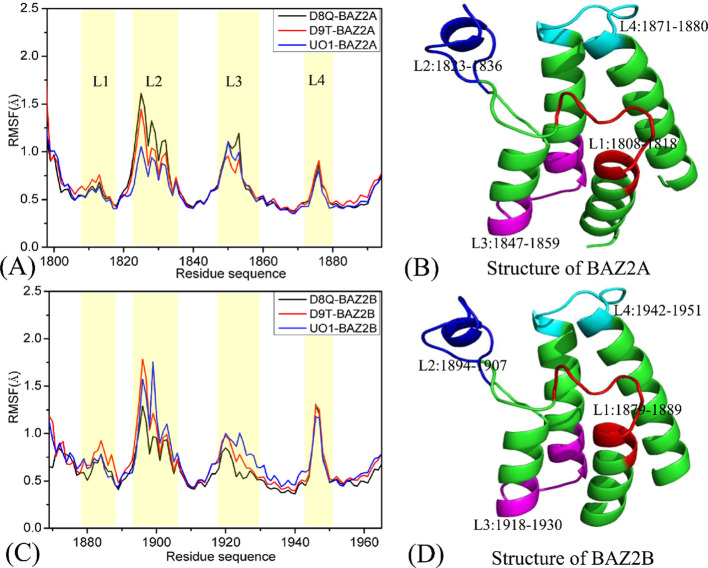
To estimate and uncover the changes in local structures of BAZ2A and BAZ2B, root-mean-square fluctuations (RMSFs) of the Cα atoms in BAZ2A and BAZ2B were calculated by using the single joined MSMDTs (Figure 2). On the whole, BAZ2A and BAZ2B yield similar tendencies of local structural fluctuations, demonstrating that BAZ2A and BAZ2B should share similar flexible or rigid regions. The high flexible structures of the inhibitor-BAZ2A and inhibitor-BAZ2B compounds are mainly located at four regions, including L1 (residues 1808–1818 for BAZ2A and 1878–1888 for BAZ2B), L2 (residues 1822–1836 for BAZ2A and 1892–1906 for BAZ2B), L3 (residues 1847–1859 for BAZ2A and 1917–1929 for BAZ2B) and L4 (residues 1872–1881 for BAZ2A and 1942–1951 for BAZ2B), which signify that some residues arising from the aforementioned regions should be situated in warm spots of inhibitor bindings. In the case of BAZ2A, inhibitor associations induce apparent changes in the RMSF values in the regions L2 and L3, while inhibitor binding to BAZ2B exert significant influences on three regions L1, L2, and L3. The results indicate that the structural flexibilities of the L4 loop in BAZ2B are higher than that in BAZ2A. The D8Q-BAZ2A binding produces smaller flexibility of the L2 and L3 loops compared to the D8Q-BAZ2B complex, the presence of the two inhibitors D9T and UO1 in BAZ2B makes the bigger flexibility of the L2 and L3 loops than BAZ2A. The aforementioned domains not only display different internal dynamics behavior but also imply hot spots of the inhibitor-BAZ2A/B bindings.
Figure 2.
Root-mean-square fluctuations (RMSFs) of the Cα atoms in two proteins BAZ2A and BAZ2B: (A) for BAZ2A complexed with three inhibitors D8Q, D9T and UO1, (B) the structure of BAZ2A,(C) for BAZ2B complexed with three inhibitors D8Q, D9T and UO1, (D) the structure of BAZ2B.
3.2. Internal Dynamics of BAZ2A and BAZ2B
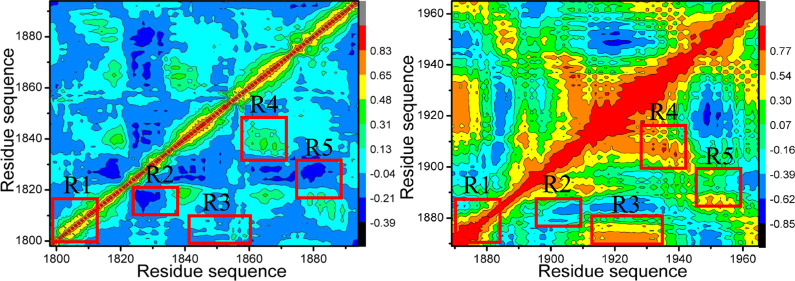
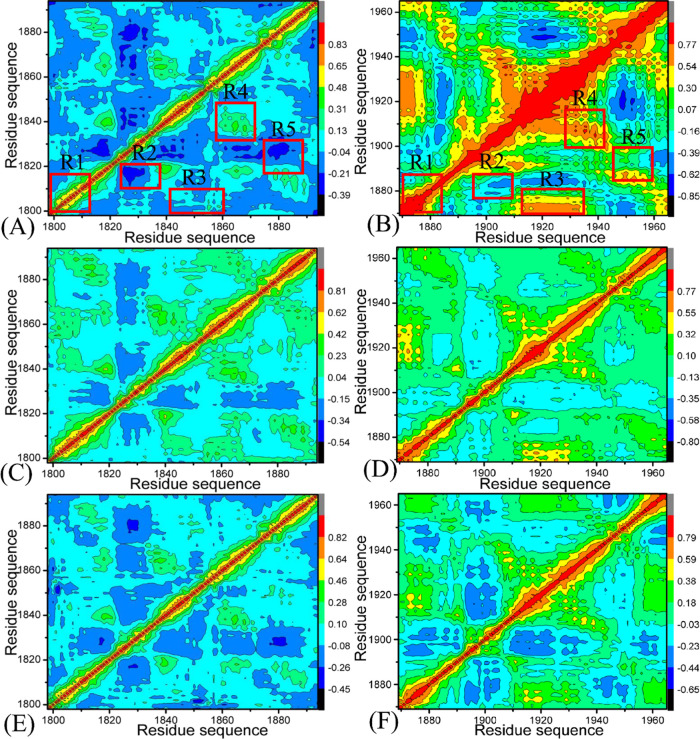
Exploring the alterations in internal dynamics of BAZ2A and BAZ2B due to inhibitor associations is requisite for drug design toward BAZ2A/B.103,104 To further probe the internal dynamic-dependent differences of BAZ2A and BAZ2B caused by inhibitor bindings, CCA is run by means of the Cα atomic coordinates extracted from the single joined MSMDTs, and the results are depicted in Figure 3. The correlated movement of a certain region relative to itself is characterized by the diagonal regions of Figure 3, while the relative motion between different regions is indicated by the off-diagonal regions. The color-coded styles are adopted to reflect the extent of correlated motions between structural regions. Two different motion pattern (strongly positive correlated motions and anticorrelated ones) are represented by the red or yellow parts and the blue or dark blue ones, separately. In the light of Figure 3, inhibitor associations produce a vital impact on structural dynamics of BA2ZA and BAZ2B.
Figure 3.
Cross-correlation metric computed with the Cα atomic coordinates saved the MSMDTs: (A), (C), and (E) respectively indicating BAZ2A with D8Q, D9T, and UO1; (B), (D), and (F) separately representing to BAZ2B with D8Q, D9T, and UO1.
For BAZ2A complexed with D8Q, D9T, and UO1 (Figure 3A,C,E), the structural domains R1 and R4 yield slightly positive correlated movements, while the structural regions R2, and R5 generate apparently anticorrelated motions (dark blue) ant the region R3 produces slightly anticorrelated movement. Compared with the D8Q-BAZ2A compound (Figure 3A), the binding of D8Q to BAZ2B extremely strengthens the positive correlated motions of the structural domains R1, R3, and R4 and slightly weakens the anticorrelated motions in the structural region R2. Meanwhile, the presence of D8Q in BAZ2B weakens the anticorrelated motion in the region R5 but strengthens the positively correlated movement of this structural domain (Figure 3B). By comparison with the D9T-BAZ2A complex (Figure 3C), the binding of D9T to BAZ2B slightly enhances the positively correlated motions of the structural domains R1, R3 and R4 from BAZ2B, but slightly weakens the anticorrelated motions of the structural domains R2 and R5 in BAZ2B (Figure 3D). By referencing the UO1-bound BAZ2A (Figure 3E), the binding of UO1 to BAZ2B strengthens the correlated motion in the structural domain R1, but weakens the anticorrelated motion of R2, R3, and R5 (Figure 3F). Hence, it is concluded that associations of the same inhibitors lead to apparent alterations in dynamics behavior of BAZ2A relative to BAZ2B and residues situated at the structural domains R1-R5 of BAZ2A and BAZ2B may generate different interaction intensity with D8Q, D9T, and UO1. The changes in inhibitor-residues interactions are responsible for binding selectivity of D8Q, D9T, and UO1 to BAZ2A/B.
3.3. Conformational Transformations of BAZ2A and BAZ2B Probed by Principal Component Analysis
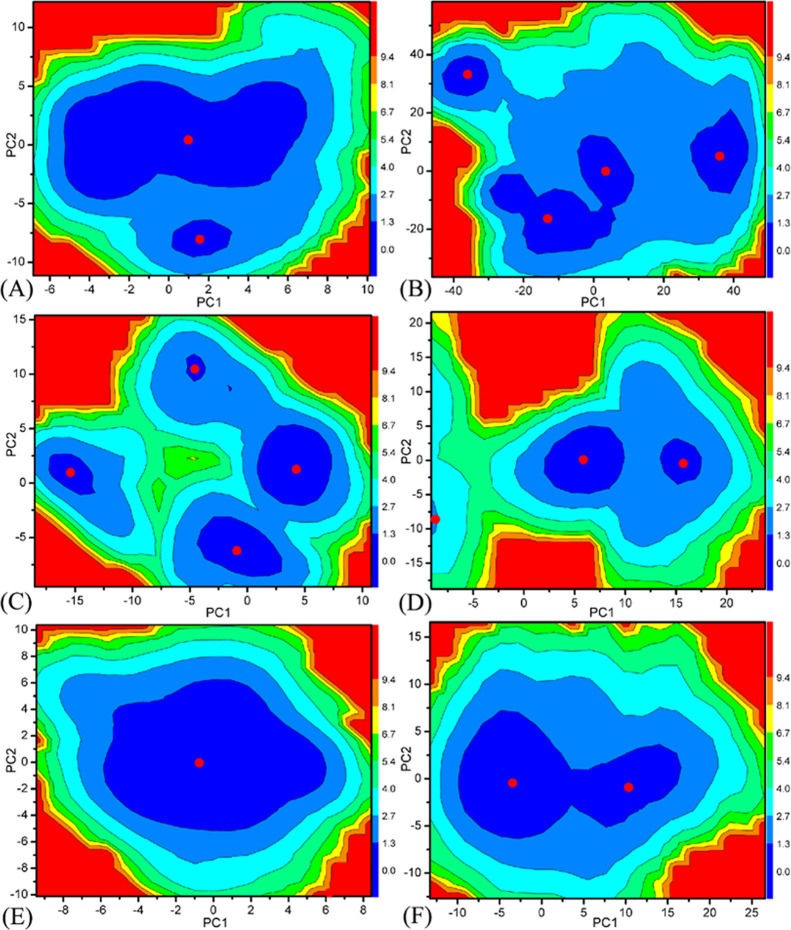
PC analysis is a vital method to study conformational alterations of proteins.105,106 As for our current study, PC analysis is implemented on the single joined MSMDTs to investigate binding selectivity of D8Q, D9T, and UO1 to BAZ2A and BAZ2B and the details are as following: (1) a covariance matrix is yielded based on the Cα atomic coordinates extracted from the single joined MSMDTs, (2) the diagonalization of this covariance matrix is carried out to derive the eigenvalues and eigenvectors that independently describe motions strength and direction of the structural domains in BAZ2A and BAZ2B (Figure S2), (3) the eigenvectors are depicted with the aid of molecular graphics program VMD and the molecular structure of BAZ2A and BAZ2B (Figure S3), (4) free energy landscapes are generated through the reaction coordinates stemming from the projections of the MSMDTs on the eigenvectors PC1 and PC2 (Figure 4).
Figure 4.
Free energy landscapes yielded with projections of the MSMDTs on PC1 and PC2: (A) D8Q-BAZ2A, (B) D8Q-BAZ2B, (C) D9T-BAZ2A, (D) D9T-BAZ2B, (E) UO1-BAZ2A and (F) UO1-BAZ2B.
In accordance with Figure S2, significant concerted motions of BAZ2A and BAZ2B represented by the first eigenvalues fast abated in amplitude into a number of constrained and more localized motions. The first six PCs account for 61.42, 73.42, and 54.88% of the observed motions in MSMDSs of the D8Q-, D9T-, and UO1-BAZ2A, respectively, while that account for 59.85, 81.00, and 68.91% of the total movements from the MSMDSs of the D8Q-, D9T-, and UO1-BAZ2B, individually. Compared to the BAZ2A with inhibitors, the first few eigenvalues of BAZ2B with inhibitors are extremely enhanced by inhibitor bindings, demonstrating that the same inhibitors in BAZ2A and BAZ2B produce distinct impacts on the total motion strength of BAZ2A and BAZ2B.
Figure S3 depicts motion directions of structural domains in BAZ2A along the first eigenvector. Figure S3A, C and E display the concerted motions of different structural domains of BAZ2A with D8Q, D9T, and UO1, independently, while Figure S3B, D and F indicate the concerted motions of different structural domains with D8Q-, D9T-, and UO1-BAZ2B, separately. By comparison to BAZ2B, bindings of D8Q, D9T, and UO1 not only alter the motion direction of two significant featured loops ZA and BC loops in BAZ2A, but also affect the strengthen the motion of these two loops in BAZ2A. Furthermore, the helix αA in the D8Q-BAZ2A complex moves toward right (Figure S3A), while the motion direction of αA in the D8Q-BAZ2B complex is changed toward the left and moves outward (Figure 3B). The helix αZ in the D8Q-BAZ2B complex moves toward the right and down (Figure S3B). Figure S3E exhibits that the ZA_loop of the UO1-BAZ2A complex moves toward left, while the motion direction of ZA_loop of the UO1-BAZ2B complex is changed toward up and right (Figure S3F). These results demonstrate that the differences in dynamics behavior between BAZ2A and BAZ2B revealed by MSMDSs may be a possibility for inducing binding selectivity of D8Q, D9T, and UO1 toward BAZ2A and BAZ2B.
To deeply reveal molecular basis affecting conformational variation of proteins caused by inhibitor bindings, the conformational spaces of BAZ2A and BAZ2B were reflected by free energy landscapes to dedicate significant information (Figure 4). An interesting redistribution of conformations in BAZ2A and BAZ2B is observed, which indicates conformational alterations of BAZ2A/B because of inhibitor bindings. In the case of the D8Q-BAZ2A complex, two energetic basins are detected, while the D8Q binding makes the conformation of BAZ2B focus on four subspaces (Figure 4A,B). The presence of inhibitor D9T in BAZ2A produces four energy basins (Figure 4C), but the D9T-BAZ2B binding only induces two conformational spaces (Figure 4D). The presence of inhibitor UO1 in BAZ2A only generates an energy basin (Figure 4E), which leads to a conformational convergence of BAZ2A however the UO1-BAZ2B binding induces two different conformational subspaces (Figure 4F). The above analyses show that inhibitor bindings can result in the conformational rearrangements of two proteins BAZ2A and BAZ2B.
3.4. Binding Variation of Inhibitors to BAZ2A and BAZ2B
To better evaluate free energy-dependent selectivity of inhibitors on BAZ2A against BAZ2B, MM-GBSA method was used to compute binding affinity of D8Q, D9T, and UO1 to BAZ2A and BAZ2B by using 300 structural frames extracted from the 600-ns MSMDT with a time interval of 2 ns and the results are listed in Table 1. Due to the expensive time in entropy calculations, only 100 ones coming from the above 300 frames were used to estimate the entropy changes. Because of the differences in the number of snapshots used to calculate binding enthalpy and entropy, we do not provide the standard errors of binding free energy in Table 1. The energetic components with negative values provide favorable forces for inhibitor bindings, and yet the positive energetic components contribute unfavorable factors to inhibitor associations. Despite lack of the experimental IC50 values of the D9T-BAZ2A and D9T-BAZ2B, the rank of our predicated binding free energies agree well with that of the available experimental IC50 data, which implies the rationality of our current study.
Table 1. Binding Affinities of Inhibitors to BAZ2A and BAZ2B Calculated with MM-GBSA Methoda.
| D8Q-BAZ2A |
D8Q-BAZ2B |
D9T-BAZ2A |
D9T-BAZ2B |
UO1-BAZ2A |
UO1-BAZ2B |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| terms | mean | bsem | mean | bsem | mean | bsem | mean | bsem | mean | bsem | mean | bsem |
| ΔEele | –28.11 | 0.35 | –8.74 | 0.36 | –10.03 | 0.20 | –20.10 | 0.29 | –23.76 | 0.17 | –24.40 | 0.29 |
| ΔEvdW | –24.07 | 0.14 | –16.69 | 0.56 | –24.23 | 0.13 | –28.64 | 0.22 | –33.09 | 0.16 | –32.53 | 0.14 |
| ΔGgb | 35.44 | 0.32 | 14.32 | 0.50 | 18.12 | 0.19 | 28.61 | 0.25 | 34.46 | 0.15 | 34.32 | 0.26 |
| ΔGnonpol | –2.50 | 0.01 | –1.74 | 0.06 | –2.43 | 0.01 | –2.77 | 0.02 | –3.02 | 0.01 | –2.98 | 0.01 |
| cΔGele + gb | 7.33 | 0.33 | 5.58 | 0.43 | 8.09 | 0.19 | 8.51 | 0.27 | 10.70 | 0.16 | 9.92 | 0.28 |
| dΔGvdW + nonpol | –26.57 | 0.08 | –18.43 | 0.31 | –26.66 | 0.07 | –31.41 | 0.12 | –36.11 | 0.09 | –35.51 | 0.07 |
| ΔH | –19.24 | 0.18 | –12.85 | 0.44 | –18.57 | 0.13 | –22.90 | 0.21 | –25.41 | 0.13 | –25.59 | 0.14 |
| -TΔS | 14.99 | 0.63 | 11.56 | 0.97 | 15.38 | 0.68 | 17.37 | 0.77 | 17.41 | 0.77 | 17.50 | 0.68 |
| ΔGbind | –4.25 | –1.29 | –3.19 | –5.53 | –8.00 | –8.09 | ||||||
| IC50(μM) | >820 | >1000 | e | e | 24 | 8 | ||||||
| fΔGexp | –4.22 | –4.10 | –6.32 | –6.97 | ||||||||
All components of free energies are in kcal/mol.
Standard errors of means.
ΔGele + gb = ΔEele + ΔGgb.
ΔGvdW + nonpol = ΔEvdW + ΔGnonpol.
The experimental binding data is not available,
The experimental values were generated from the experimental IC50 values in reference using the equation ΔGexp = – RT ln IC50.
According to Table 1 and Figure S4, for the present six systems, electrostatic interaction energies (ΔEele) in the gas space generate profitable contributions for associations of D8Q, D9T, and UO1, but adverse solvation free energies (ΔGgb) produce complete offset on this beneficial term to induce the balance between ΔEele and ΔGgb and further result in a disadvantageous polar interactions (ΔGele + gb) for bindings of D8Q, D9T, and UO1 to BAZ2A/B. The entropy components (−TΔS) are also detrimental factors weakening binding strength of D8Q, D9T, and UO1 to BAZ2A and BAZ2B. ΔEvdW and ΔGnonpol, separately representing van der Waals interactions and nonpolar solvation energies, provide beneficial contributions for inhibitor bindings and leads to hydrophobic interactions (ΔGvdW + nonpol) of D8Q, D9T, and UO1 with BAZ2A/BAZ2B. According to Table 1, two components ΔGele + gb and ΔGvdW + nonpol of the D8Q-BAZ2A complex are improved by 1.75 and 8.14 kcal/mol relative to the D8Q-BAZ2B, which brings a total enhancement of 6.39 kcal/mol in the binding enthalpy (ΔH) of the D8Q-BAZ2A complex in contrast to the D8Q-BAZ2B one. Moreover the binding entropy ( – TΔS) of D8Q to BAZ2A is improved by 3.43 kcal/mol in comparison to that of D8Q to BAZ2B. On the whole, the binding free energy of D8Q to BAZ2A is raised by 2.96 kcal/mol, demonstrating that D8Q possesses more favorable selectivity on BAZ2A than BAZ2B. With regard to D9T, an improvement of 4.75 kcal/mol in hydrophobic interactions of D9T with BAZ2B in contrast to that of D9T with BAZ2A are mainly responsible for the enhancement of the binding enthalpy of D9T to BAZ2B in comparison to that of D9T to BAZ2A. Furthermore, the binding entropy of D9T to BAZ2B is enhanced by 1.99 kcal/mol compared with that of D9T to BAZ2A. Based on the above two reasons, binding affinity of D9T to BAZ2B is improved by 2.34 kcal/mol by contrast to that of D9T to BAZ2A, signifying that D9T prefers associating with BAZ2B to binding to BAZ2A. With respect to UO1, the unfavorable component ΔGele + gb for the UO1-BAZ2A complex is elevated by 0.78 kcal/mol in comparison to the UO1-BAZ2B one, while the favorable component ΔGvdW + nonpol of the UO1-BAZ2A complex is strengthened by 0.60 kcal/mol compared to the UO1-BAZ2B one. These two changes result in a reduction of 0.18 kcal/mol in the binding enthalpy of UO1 to BAZ2A relative to that of UO1 to BAZ2B, and the binding entropy of UO1 to BAZ2A is reduced by 0.09 kcal/mol relative to that of UO1 to BAZ2B, which finally leads to a reduced of 0.09 kcal/mol in binding affinity of UO1 to BAZ2A relative to that of UO1 to BAZ2B. Therefore, UO1 does not show obvious selectivity toward BAZ2A and BAZ2B.
3.5. Selectivity Uncovered by Inhibitor-Residue Interaction Analyses
To investigate binding selectivity of D8Q, D9T, and UO1 toward BAZ2A and BAZ2B, interactions of inhibitors with single residue in BAZ2A/B were computed by using the MM-GBSA tool inlayed in Amber 18 (Figure 5). Table 2 shows the contributions of van der Waals energy, electrostatic energy and solvation energy to interactions of inhibitors with important residues in BAZ2A and BAZ2B. Meanwhile van der Waals interactions of per residue with D8Q, D9T, and UO1 were further decomposed into contributions from backbone and sidechain of residues. Key residues of BAZ2A and BAZ2B that form important interactions with three inhibitors were depicted in Figure 6. In addition, the CPPTRAJ tool in Amber 18 was yielded to identify hydrogen bonding interactions (HBIs) of D8Q, D9T, and UO1 with BAZ2A and BAZ2B (Table 3). The lowest energy structure obtained from MSMDSs is utilized to depict geometric positions of D8Q, D9T, and UO1 relative to significant residues around the active sites of BAZ2A and BAZ2B in Figures 6 and 7.
Figure 5.
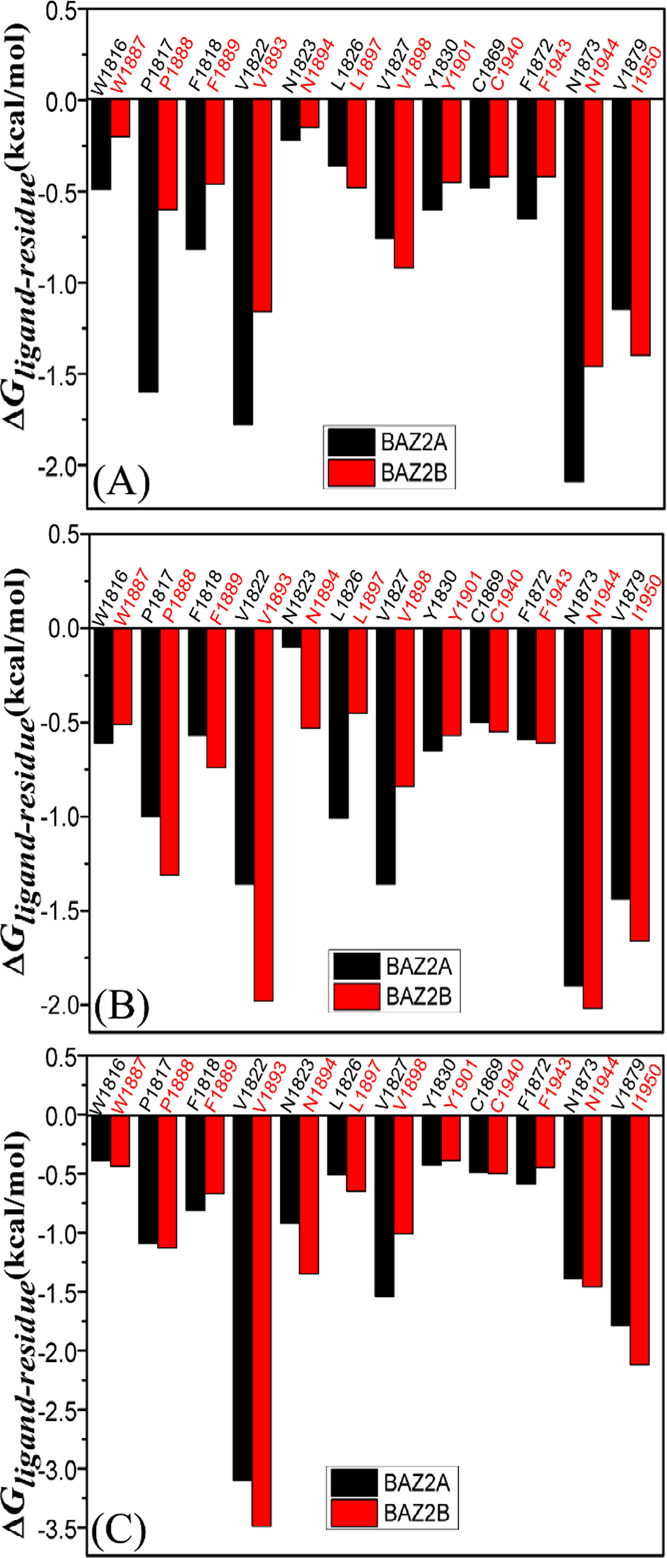
Comparisons between ΔGligand – residue of BAZ2A and BAZ2B, (A) D8Q, (B) D9T and (C) UO1.
Table 2. Energy Contributions of BAZ2A and BAZ2B Residues to the Binding of Ligandsa.
| BAZ2s | residue | D8Q | D9T | UO1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SvdW | BvdW | Tele | Tsolv | SvdW | BvdW | Tele | Tsolv | SvdW | BvdW | Tele | Tsolv | ||
| BAZ2A | W1816 | –0.64 | –0.28 | –0.72 | 1.14 | –0.83 | –0.12 | 0.33 | 0.01 | –0.55 | –0.38 | –0.13 | 0.67 |
| BAZ2B | W1887 | –0.27 | –0.05 | 0.17 | –0.05 | –0.82 | –0.35 | –0.49 | 1.15 | –0.76 | –0.33 | –0.82 | 1.47 |
| BAZ2A | P1817 | –1.17 | –0.65 | –2.89 | 3.11 | –0.95 | –0.45 | –1.29 | 1.69 | –1.21 | –0.75 | –1.50 | 2.37 |
| BAZ2B | P1888 | –0.59 | –0.32 | –0.81 | 1.11 | –1.07 | –0.74 | –2.08 | 2.58 | –1.05 | –1.00 | –1.13 | 2.03 |
| BAZ2A | F1818 | –0.57 | –0.23 | –0.23 | 0.21 | –0.51 | –0.12 | –0.08 | 0.14 | –0.57 | –0.23 | –0.18 | 0.16 |
| BAZ2B | F1889 | –0.40 | –0.09 | –0.10 | 0.13 | –0.56 | –0.21 | –0.24 | 0.26 | –0.54 | –0.24 | –0.02 | 0.12 |
| BAZ2A | V1822 | –1.45 | –0.24 | –0.20 | 0.11 | –1.17 | –0.13 | –0.20 | 0.14 | –2.26 | –0.43 | –1.10 | 0.69 |
| BAZ2B | V1893 | –0.95 | –0.11 | –0.22 | 0.11 | –1.57 | –0.34 | –0.29 | 0.22 | –2.14 | –0.60 | –1.96 | 1.21 |
| BAZ2A | N1823 | –0.12 | –0.10 | –0.07 | 0.07 | –0.13 | –0.11 | –0.30 | 0.44 | –0.45 | –0.46 | –0.83 | 0.82 |
| BAZ2B | N1894 | –0.11 | –0.09 | –0.44 | 0.49 | –0.39 | –0.25 | –0.22 | 0.33 | –0.62 | –0.15 | –1.13 | 0.55 |
| BAZ2A | L1826 | –0.31 | –0.05 | –0.06 | 0.06 | –0.91 | –0.31 | –0.54 | 0.75 | –0.41 | –0.11 | –0.30 | 0.31 |
| BAZ2B | L1897 | –0.44 | –0.11 | –0.16 | 0.23 | –0.40 | –0.05 | –0.03 | 0.04 | –0.51 | –0.07 | –0.41 | 0.33 |
| BAZ2A | V1827 | –0.69 | –0.05 | –0.01 | –0.02 | –1.16 | –0.14 | 0.09 | –0.15 | –1.29 | –0.12 | –0.11 | –0.02 |
| BAZ2B | V1898 | –0.78 | –0.07 | 0.12 | –0.18 | –0.76 | –0.06 | –0.02 | –0.00 | –0.88 | –0.08 | –0.11 | 0.06 |
| BAZ2A | Y1830 | –0.86 | –0.02 | –0.73 | 1.01 | –0.77 | –0.02 | –0.88 | 1.03 | –0.73 | –0.02 | –0.34 | 0.66 |
| BAZ2B | Y1901 | –0.56 | –0.01 | –0.54 | 0.65 | –0.70 | –0.02 | –0.88 | 1.03 | –0.63 | –0.02 | –0.59 | 0.85 |
| BAZ2A | C1869 | –0.33 | –0.15 | 0.47 | –0.47 | –0.31 | –0.14 | 0.20 | –0.24 | –0.34 | –0.14 | 0.32 | –0.33 |
| BAZ2B | C1940 | –0.26 | –0.12 | 0.12 | –0.17 | –0.35 | –0.15 | 0.30 | –0.36 | –0.35 | –0.13 | 0.32 | –0.34 |
| BAZ2A | F1872 | –0.66 | –0.06 | –0.55 | 0.61 | –0.68 | –0.06 | –0.51 | 0.66 | –0.77 | –0.07 | –0.33 | 0.58 |
| BAZ2B | F1943 | –0.48 | –0.05 | –0.38 | 0.49 | –0.66 | –0.06 | –0.53 | 0.63 | –0.64 | –0.06 | –0.28 | 0.54 |
| BAZ2A | N1873 | –0.14 | –0.04 | –3.52 | 1.61 | –0.32 | –0.05 | –3.84 | 2.30 | –0.50 | –0.05 | –2.59 | 1.76 |
| BAZ2B | N1944 | –0.25 | –0.04 | –2.88 | 1.70 | –0.26 | –0.05 | –3.54 | 1.83 | –0.48 | –0.05 | –2.55 | 1.62 |
| BAZ2A | V1879 | –1.04 | –0.08 | –0.20 | 0.17 | –1.30 | –0.10 | 0.07 | –0.11 | –1.56 | –0.11 | –0.25 | 0.13 |
| BAZ2B | I1950 | –1.24 | –0.06 | 0.04 | –0.14 | –1.49 | –0.08 | –0.19 | 0.10 | –1.90 | –0.09 | –0.28 | 0.16 |
All components of free energies are in kcal/mol. SvdW: van der Walls energy of side chain atoms, BvdW: van der Waals energy of backbone atoms, Tele: electrostatic energy of residue, Tsolv: solvation energy of residue.
Figure 6.
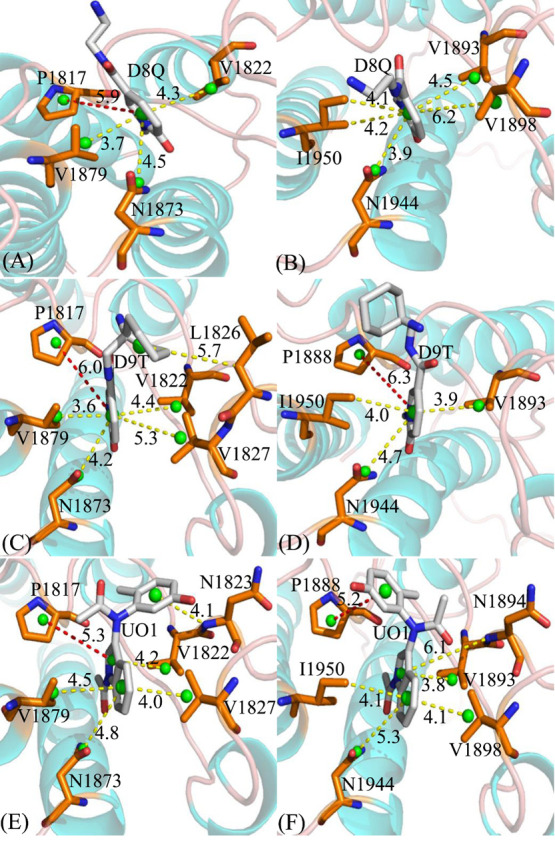
Relative positions of D8T, D9Q, and UO1 to vital residues: (A) D8Q-BAZ2A, (B) D8Q-BAZ2B, (C) D9T-BAZ2A, (D) D9T-BAZ2B, (E) UO1-BAZ2A and (F) UO1-BAZ2B. The red dash lines indicate the π-π interactions and the yellow ones represent the CH-π interactions. The green balls indicate the pseudoatoms located at the mass center of atoms forming the interactions between residues and inhibitors.
Table 3. Hydrogen Bonds Yielded between D8T, D9Q, and UO1 and BAZ2A/B.
| complexes | hydrogen bonds | distance/( Å)a | angle/(°)a | occupancy/(%)b |
|---|---|---|---|---|
| D8Q-BAZ2A DBRD | Asn1873-ND2-HD21···D8Q-O08 | 2.91 | 162.53 | 99.01 |
| Pro1817-O···D8Q-N11-H11 | 3.22 | 148.23 | 46.91 | |
| Glu1820-O···D8Q-N14-H12 | 3.03 | 143.50 | 20.46 | |
| D8Q-BAZ2B | Asn1944-ND2-HD21···D8Q-O08 | 2.93 | 161.33 | 74.20 |
| D9T-BAZ2A | Asn1873-ND2-HD21···D9T-O08 | 2.94 | 161.97 | 99.39 |
| D9T-BAZ2B | Asn1944-ND2-HD21···D9T-O08 | 2.92 | 161.52 | 99.43 |
| Asn1894-N-H···D9T-N14 | 3.17 | 154.23 | 19.86 | |
| Pro1888-O···D9T-N11-H19 | 3.30 | 153.73 | 24.48 | |
| UO1-BAZ2A | Asn1873-ND2-HD21···UO1-O03 | 2.98 | 161.02 | 99.14 |
| Asn1823-N-H···UO1-O18 | 3.25 | 155.77 | 70.53 | |
| UO1-BAZ2B | Asn1944-ND2-HD21···UO1-O03 | 2.97 | 160.02 | 99.09 |
| Asn1894-N-H···UO1-O10 | 2.98 | 164.16 | 94.04 |
Standard of Hydrogen bonds: the acceptor-donor atom distance of <3.5 Å and acceptor-H-donor angle of >120°.
Occupancy (%) is determined as the percentage of the time a specific hydrogen bond existing accounting for the total simulation time.
The full lines represent chemical bonds, and the dotted lines indicate hydrogen bonding interactions.
Figure 7.
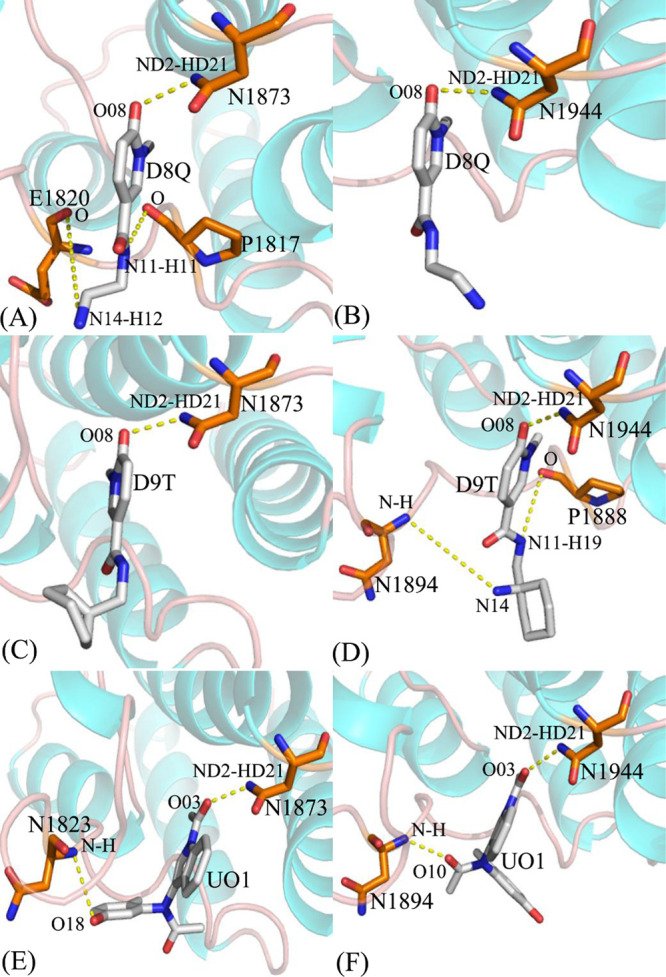
Hydrogen bonds between residues of BAZ2A or BAZ2B and three inhibitors: (A) D8Q-BAZ2A, (B) D8Q-BAZ2B, (C) D9T-BAZ2A, (D) D9T-BAZ2B, (E) UO1-BAZ2A and (F) UO1-BAZ2B.
Binding of D8Q to BAZ2A against BAZ2B. Binding selectivity of D8Q to BAZ2A and BAZ2B are mainly from seven residues (W1816, W1887), (P1817, P1888), (F1818, F1889), (V1822, V1893), (F1872, F1943), (N1873, N1944) and (V1879, I1950) in (BAZ2A, BAZ2B) due to the difference greater than 0.2 kcal/mol in interactions of D8Q with key residues in BAZ2A and BAZ2B (Figure 5A). The hydrophobic interactions of D8Q with four residues P1817, V1822, N1873, and V1879 in BAZ2A are stronger than −1.0 kcal/mol (Figure S5A and Table 2) and these interactions are mainly devoted by the π – π interactions of the rings of P1817 with that of D8Q and the CH−π interactions of the alkyls of V1822, N1873, and V1879 with the ring of D8Q (Figure 6A). The interaction energies of D8Q with four residues V1893, V1898, N1944, and I1950 in BAZ2B are also higher than −1.0 kcal/mol (Figure 5B), which is mostly dedicated by the CH−π interactions between the hydrophobic ring of D8Q and the CH groups of these four residues in BAZ2B (Figure 6B). In the meantime, D8Q forms three HBIs with BAZ2A, including Asn1873-ND2-HD21···D8Q-O08, Pro1817-O···D8Q-N11-H11, and Glu1820-O···D8Q-N14-H12 with the occupancies 99.01, 46.91, and 20.46%, respectively (Table 3 and Figure 7A). However, for the D8Q-BAZ2B complex, there is only one HBI formed between the atom O08 of D8Q and the ND2-HD21 of Asn1944 (Table 3 and Figure 7B). The binding energies of D8Q to P1817, V1822 and N1873 in BAZ2A are much stronger than that of D8Q with the corresponding residues V1893, V1822 and N1944 in BAZ2B (Figure 5A, Figures S5A, S5B and Table 2). Therefore, residues P1817, V1822, N1873 in BAZ2A and residues V1893, V1822 and N1944 in BAZ2B devote key forces to selectivity of D8Q to BAZ2A over BAZ2B.
Binding of D9T to BAZ2A over BAZ2B. According to Figure 5B, the binding difference of D9T to six residue pairs (P1817, P1888), (V1822, V1893), (N1823, N1894),(L1826, L1897),(V1827, V1898), and(V1879, I1950) in (BAZ2A, BAZ2B) is greater than 0.2 kcal/mol, signifying that these residues dedicate special forces to binding selectivity of D9T to BAZ2A over BAZ2B. Among these residues, (V822, V1893), (L1286, L1897) and (V1827, V1898) in (BAZ2A, BAZ2B) show extremely obvious difference. Furthermore, the hydrophobic interactions of D9T with the six aforementioned residues in BAZ2A are stronger than −1.0 kcal/mol, including P1817, V1822, L1826, V1827, N1873, and V1879 (Figure S5C and Table 2) and these interactions are in good agreement with the π – π interactions and the CH−π interactions of the hydrophobic ring of D9T with that of P1817 and the alkyls of V1822, L1826, V1827, N1873, and V1879 (Figure 6C). With regard to the D9T-BAZ2B complex, four residues P1888, V1893, N1944 and I1950 are involved in the interactions higher than 1.0 kcal/mol with D9T (Figure S5D and Table 2), which is mostly dedicated by from the π-π interactions and the CH-π interactions of the hydrophobic ring of D9T with that of P1888 and the CH groups of V1893, N1944 and I1950 (Figure 6D). For the D9T-BAZ2A complex, the atoms O08 of the D9T form a HBI with the ND2-HD21 of Asn1873 (Asn1873-ND2-HD21···D9T-O08) with an occupancy of 99.39% (Table 3 and Figure 7C). However D9T forms three HBIs with BAZ2B, including Asn1944-ND2-HD21···D9T-O08, Asn1894-N-H···D9T-N14, and Pro1888-O···D9T-N11-H19 (Table 3 and Figure 7D). Based on the current analyses, residues (V822, V1893), (L1286, L1897) and (V1827, V1898) in (BAZ2A, BAZ2B) as well as Pro1888 and Asn1894 are mostly devote key factors for binding selectivity of D9T to BAZ2A VS BAZ2B.
Binding of UO1 to BAZ2A VS BAZ2B. Although four residues (V1822, V1893), (N1823, N1894), (V1827, V1898), and (V1879, I1950) corresponding to (BAZ2A, BAZ2B) produce the energy differences greater than 0.2 kcal/mol, these differences reach compensation each other and do not provide obvious binding selectivity of UO1 to BAZ2A and BAZ2B. Moreover, six residues P1817, V1822, N1823, V1827, N1873, and V1879 in BAZ2A produce the interactions stronger than −1.0 kcal/mol (Figure S5E and Table 2) with UO1, which is primarily devoted by the π – π and CH-π interactions of the hydrophobic ring of UO1 with that of P1817 and the alkyls of V1822, N1823, V1827, N1873, and V1879 (Figure 6E). According to Table 2, Figures 5C and 6F, the corresponding residues in BAZ2B also produce similar interactions to the UO1-BAZ2A complex. In addition, UO1 forms two HBIs with BAZ2A, including Asn1873-ND2-HD21···UO1-O03 and Asn1823-N-H···UO1-O18 with the occupancies 99.14 and 70.53% (Table 3 and Figure 7E), respectively. Similar to the UO1-BAZ2A complex, UO1 also produces two HBIs Asn1944-ND2-HD21···UO1-O03 and Asn1894-N-H···UO1-O10 with BAZ2B and their occupancies are 99.09 and 94.04% (Table 3 and Figure 7F). Therefore, although the above mentioned residues hardly lead to the selectivity of UO1 toward BAZ2A and BAZ2B, these residues can be employed as target sites of drug design toward two proteins.
In the light of analysis on interaction networks of D8Q, D9T, and UO1 with BAZ2A/B, three conclusions are draw as below: (1) the CH-π and π-π interactions play special parts in binding selectivity of D8Q and D9T to BAZ2A and BAZ2B, (2) HBIs of D8Q, D9T, and UO1 with residues (Asn1873, Asn1944) in (BAZ2A, BAZ2B) contribute significant force to the stabilization of the inhibitor-BAZ2A/BAZ2B complexes and (3) for this work, D8Q shows better selectivity toward BAZ2A than BAZ2B, D9T has stronger binding ability to BAZ2B than BAZ2A and UO1 does not displays obvious selectivity toward these two proteins. How to optimize the CH-π, π-π and HBIs will key factors for successful design of efficient inhibitors targeting BAZ2A and BAZ2B.
4. Conclusions
Unveiling molecular mechanisms concerning binding differences of three D8Q, D9T, and UO1 to BAZ2A and BAZ2B bromodomains will be requisite for design of highly selective inhibitors targeting BAZ2A against BAZ2B. As for our current study, MSMDSs of ten 100-ns replicas with the time evolution of 1 μs and the MM-GBSA estimations were carried out for exploring selectivity of D8T, D9Q, and UO1 toward BAZ2A and BAZ2B. The RMSF analysis and CCA were executed with the Cα atomic coordinates of BAZ2A/B kept in the MSMDTs and the results verify that the presence of D8Q, D9T, and UO1 evidently affects structural flexibility and motion modes of BAZ2A/B. Binding affinities of D8Q, D9T, and UO1 to BAZ2A and BAZ2B calculated by MM-GBSA approach hint that D8Q shows better selectivity toward BAZ2A than BAZ2B, D9T has stronger binding ability to BAZ2B than BAZ2A and UO1 does not display obvious selectivity toward these two proteins. Moreover, residue-based free energy decomposition calculations also denote that residues (W1816, W1887), (P1817, P1888), (F1818, F1889), (V1822, V1893), (N1823, N1894), (L1826, L1897), (V1827, V1898), (F1872, F1943), (N1873, N1944) and (V1879, I1950) in (BAZ2A, BAZ2B) induce certain binding variances of inhibitors to BAZ2A and BAZ2B, demonstrating that these residues play different roles in binding selectivity of inhibitors towards BAZ2A and BAZ2B. With our expectation, this current study are able to devote useful dynamics data as well as structure-affinity relationship for development of effective inhibitors targeting BAZ2A and BAZ2B.
Acknowledgments
This work is supported by the National Natural Science Foundation of China (nos. 21863003 and 61762048). The authors sincerely thank Prof. Jianzhong Chen (School of Science, Shandong Jiaotong University, Jinan 250357, China) for useful discussions and invaluable comments.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c00687.
Root-mean-square deviations (RMSDs) of backbone atoms in BAZ2A and BAZ2B (Figure S1M); The function of eigenvalues versus eigenvector index (Figure S2); Collective motions corresponding to the first component PC1 (Figure S3); Comparisons between binding free energy terms (Figure S4); and Inhibitor-residue interactions (Figure S5) (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Owen D. J.; Ornaghi P.; Yang J.-C.; Lowe N.; Evans P. R.; Ballario P.; Neuhaus D.; Filetici P.; Travers A. A. The structural basis for the recognition of acetylated histone H4 by the bromodomain of histone acetyltransferase Gcn5p. EMBO J. 2000, 19, 6141–6149. 10.1093/emboj/19.22.6141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchand J.-R.; Caflisch A. Binding Mode of Acetylated Histones to Bromodomains: Variations on a Common Motif. Chem. Med. Chem. 2015, 10, 1327–1333. 10.1002/cmdc.201500141. [DOI] [PubMed] [Google Scholar]
- Muller S.; Filippakopoulos P.; Knapp S. Bromodomains as therapeutic targets. Expert Rev. Mol. Med. 2011, 13, e29 10.1017/S1462399411001992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbieri I.; Cannizzaro E.; Dawson M. A. Bromodomains as therapeutic targets in cancer. Brief. Funct. Genomics 2013, 12, 219–230. 10.1093/bfgp/elt007. [DOI] [PubMed] [Google Scholar]
- Delmore J. E.; Issa G. C.; Lemieux M. E.; Rahl P. B.; Shi J.; Jacobs H. M.; Kastritis E.; Gilpatrick T.; Paranal R. M.; Qi J.; Chesi M.; Schinzel A. C.; McKeown M. R.; Heffernan T. P.; Vakoc C. R.; Bergsagel P. L.; Ghobrial I. M.; Richardson P. G.; Young R. A.; Hahn W. C.; Anderson K. C.; Kung A. L.; Bradner J. E.; Mitsiades C. S. BET Bromodomain Inhibition as a Therapeutic Strategy to Target c-Myc. Cell 2011, 146, 904–917. 10.1016/j.cell.2011.08.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mietton F.; Ferri E.; Champleboux M.; Zala N.; Maubon D.; Zhou Y.; Harbut M.; Spittler D.; Garnaud C.; Courçon M.; Chauvel M.; d’Enfert C.; Kashemirov B. A.; Hull M.; Cornet M.; McKenna C. E.; Govin J.; Petosa C. Selective BET bromodomain inhibition as an antifungal therapeutic strategy. Nat. Commun. 2017, 8, 15482 10.1038/ncomms15482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morinière J.; Rousseaux S.; Steuerwald U.; Soler-López M.; Curtet S.; Vitte A. L.; Govin J.; Gaucher J.; Sadoul K.; Hart D. J.; Krijgsveld J.; Khochbin S.; Müller C. W.; Petosa C. Cooperative binding of two acetylation marks on a histone tail by a single bromodomain. Nature 2009, 461, 664–668. 10.1038/nature08397. [DOI] [PubMed] [Google Scholar]
- Filippakopoulos P.; Picaud S.; Mangos M.; Keates T.; Lambert J.-P.; Barsyte-Lovejoy D.; Felletar I.; Volkmer R.; Müller S.; Pawson T.; Gingras A.-C.; Arrowsmith C. H.; Knapp S. Histone Recognition and Large-Scale Structural Analysis of the Human Bromodomain Family. Cell 2012, 149, 214–231. 10.1016/j.cell.2012.02.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y.; Wu S.; Wang L.; Yang Z.; Zhao J.; Zhang L. Binding selectivity of inhibitors toward the first over the second bromodomain of BRD4: theoretical insights from free energy calculations and multiple short molecular dynamics simulations. RSC Adv. 2021, 11, 745–759. 10.1039/D0RA09469B. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Filippakopoulos P.; Knapp S. Targeting bromodomains: epigenetic readers of lysine acetylation. Nat. Rev. Drug Discov. 2014, 13, 337–356. 10.1038/nrd4286. [DOI] [PubMed] [Google Scholar]
- Romero F. A.; Taylor A. M.; Crawford T. D.; Tsui V.; Côté A.; Magnuson S. Disrupting Acetyl-Lysine Recognition: Progress in the Development of Bromodomain Inhibitors. J. Med. Chem. 2016, 59, 1271–1298. 10.1021/acs.jmedchem.5b01514. [DOI] [PubMed] [Google Scholar]
- Wang C. Y.; Filippakopoulos P. Beating the odds: BETs in disease. Trends Biochem. Sci. 2015, 40, 468–479. 10.1016/j.tibs.2015.06.002. [DOI] [PubMed] [Google Scholar]
- Ferguson F. M.; Fedorov O.; Chaikuad A.; Philpott M.; Muniz J. R. C.; Felletar I.; von Delft F.; Heightman T.; Knapp S.; Abell C.; Ciulli A. Targeting Low-Druggability Bromodomains: Fragment Based Screening and Inhibitor Design against the BAZ2B Bromodomain. J. Med. Chem. 2013, 56, 10183–10187. 10.1021/jm401582c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vidler L. R.; Brown N.; Knapp S.; Hoelder S. Druggability analysis and structural classification of bromodomain acetyl-lysine binding sites. J. Med. Chem. 2012, 55, 7346–7359. 10.1021/jm300346w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu L.; Frommel S. C.; Oakes C. C.; Simon R.; Grupp K.; Gerig C. Y.; Bär D.; Robinson M. D.; Baer C.; Weiss M.; Gu Z.; Schapira M.; Kuner R.; Sültmann H.; Provenzano M.; Yaspo M.-L.; Brors B.; Korbel J.; Schlomm T.; Sauter G.; Eils R.; Plass C.; Santoro R.; BAZ2A (TIP5) is involved in epigenetic alterations in prostate cancer and its overexpression predicts disease recurrence. Nat. Genet. 2015, 47, 22–30. 10.1038/ng.3165. [DOI] [PubMed] [Google Scholar]
- Spiliotopoulos D.; Wamhoff E. C.; Lolli G.; Rademacher C.; Caflisch A. Discovery of BAZ2A bromodomain ligands. Eur. J. Med. Chem. 2017, 139, 564–572. 10.1016/j.ejmech.2017.08.028. [DOI] [PubMed] [Google Scholar]
- Arking D. E.; Junttila M. J.; Goyette P.; Huertas-Vazquez A.; Eijgelsheim M.; Blom M. T.; Newton-Cheh C.; Reinier K.; Teodorescu C.; Uy-Evanado A.; Carter-Monroe N.; Kaikkonen K. S.; Kortelainen M. L.; Boucher G.; Lagacé C.; Moes A.; Zhao X.; Kolodgie F.; Rivadeneira F.; Hofman A.; Witteman J. C.; Uitterlinden A. G.; Marsman R. F.; Pazoki R.; Bardai A.; Koster R. W.; Dehghan A.; Hwang S. J.; Bhatnagar P.; Post W.; Hilton G.; Prineas R. J.; Li M.; Köttgen A.; Ehret G.; Boerwinkle E.; Coresh J.; Kao W. H.; Psaty B. M.; Tomaselli G. F.; Sotoodehnia N.; Siscovick D. S.; Burke G. L.; Marbán E.; Spooner P. M.; Cupples L. A.; Jui J.; Gunson K.; Kesäniemi Y. A.; Wilde A. A.; Tardif J. C.; O’Donnell C. J.; Bezzina C. R.; Virmani R.; Stricker B. H.; Tan H. L.; Albert C. M.; Chakravarti A.; Rioux J. D.; Huikuri H. V.; Chugh S. S. Identification of a sudden cardiac death susceptibility locus at 2q24.2 through genome-wide association in European ancestry individuals. PLoS Genet. 2011, 7, e1002158 10.1371/journal.pgen.1002158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferguson F. M.; Dias D. M.; Rodrigues J. P.; Wienk H.; Boelens R.; Bonvin A. M.; Abell C.; Ciulli A. Binding hotspots of BAZ2B bromodomain: Histone interaction revealed by solution NMR driven docking. Biochemistry 2014, 53, 6706–6716. 10.1021/bi500909d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchand J. R.; Lolli G.; Caflisch A. Derivatives of 3-Amino-2-methylpyridine as BAZ2B Bromodomain Ligands: In Silico Discovery and in Crystallo Validation. J. Med. Chem. 2016, 59, 9919–9927. 10.1021/acs.jmedchem.6b01258. [DOI] [PubMed] [Google Scholar]
- Drouin L.; McGrath S.; Vidler L. R.; Chaikuad A.; Monteiro O.; Tallant C.; Philpott M.; Rogers C.; Fedorov O.; Liu M.; Akhtar W.; Hayes A.; Raynaud F.; Müller S.; Knapp S.; Hoelder S. Structure Enabled Design of BAZ2-ICR, A Chemical Probe Targeting the Bromodomains of BAZ2A and BAZ2B. J. Med. Chem. 2015, 58, 2553–2559. 10.1021/jm501963e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen P.; Chaikuad A.; Bamborough P.; Bantscheff M.; Bountra C.; Chung C. W.; Fedorov O.; Grandi P.; Jung D.; Lesniak R.; Lindon M.; Müller S.; Philpott M.; Prinjha R.; Rogers C.; Selenski C.; Tallant C.; Werner T.; Willson T. M.; Knapp S.; Drewry D. H. Discovery and Characterization of GSK2801, a Selective Chemical Probe for the Bromodomains BAZ2A and BAZ2B. J. Med. Chem. 2016, 59, 1410–1424. 10.1021/acs.jmedchem.5b00209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu G.; Li H.; Xu S.; Wang J. Ligand Binding Mechanism and Its Relationship with Conformational Changes in Adenine Riboswitch. Int. J. Mol. Sci. 2020, 21, 1926 10.3390/ijms21061926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hou T.; McLaughlin W. A.; Wang W. Evaluating the potency of HIV-1 protease drugs to combat resistance. Proteins 2008, 71, 1163–1174. 10.1002/prot.21808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang M.; Zhang X.; Han K. Molecular dynamics simulation of SRP GTPases: Towards an understanding of the complex formation from equilibrium fluctuations. Proteins 2010, 78, 2222–2237. 10.1002/prot.22734. [DOI] [PubMed] [Google Scholar]
- Bao L.; Wang J.; Xiao Y. Dynamics of metal ions around an RNA molecule. Phys. Rev. E 2019, 99, 012420 10.1103/PhysRevE.99.012420. [DOI] [PubMed] [Google Scholar]
- Yang M.-J.; Pang X.-Q.; Zhang X.; Han K.-L. Molecular dynamics simulation reveals preorganization of the chloroplast FtsY towards complex formation induced by GTP binding. J. Struct. Biol. 2011, 173, 57–66. 10.1016/j.jsb.2010.07.013. [DOI] [PubMed] [Google Scholar]
- Khan M. T.; Rehaman A. U.; Junaid M.; Malik S. I.; Wei D.-Q. Insight into novel clinical mutants of Rps A-S324F, E325K, and G341R of Mycobacterium tuberculosis associated with pyrazinamide resistance. Comput. Struct. Biotechnol. J. 2018, 16, 379–387. 10.1016/j.csbj.2018.09.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L.; Wang Y.; Sun H.; Zhao J.; Wang Q. Theoretical insight into molecular mechanisms of inhibitor bindings to bromodomain-containing protein 4 using molecular dynamics simulations and calculations of binding free energies. Chem. Phys. Lett. 2019, 736, 136785 10.1016/j.cplett.2019.136785. [DOI] [Google Scholar]
- Prieto-Martínez F. D.; Medina-Franco J. L. Current advances on the development of BET inhibitors: insights from computational methods. Adv. Protein Chem. Str. 2020, 122, 127–180. 10.1016/bs.apcsb.2020.06.002. [DOI] [PubMed] [Google Scholar]
- Chen J.; Wang X.; Zhang J. Z. H.; Zhu T. Effect of Substituents in Different Positions of Aminothiazole Hinge-Binding Scaffolds on Inhibitor–CDK2 Association Probed by Interaction Entropy Method. ACS Omega 2018, 3, 18052–18064. 10.1021/acsomega.8b02354. [DOI] [Google Scholar]
- Gao Y.; Zhu T.; Chen J. Exploring drug-resistant mechanisms of I84V mutation in HIV-1 protease toward different inhibitors by thermodynamics integration and solvated interaction energy method. Chem. Phys. Lett. 2018, 706, 400–408. 10.1016/j.cplett.2018.06.040. [DOI] [Google Scholar]
- Mamontov E.; Cheng Y.; Daemen L. L.; Keum J. K.; Kolesnikov A. I.; Pajerowski D.; Podlesnyak A.; Ramirez-Cuesta A. J.; Ryder M. R.; Stone M. B. Effect of Hydration on the Molecular Dynamics of Hydroxychloroquine Sulfate. ACS Omega 2020, 5, 21231–21240. 10.1021/acsomega.0c03091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cong Y.; Huang K.; Li Y.; Zhong S.; Zhang J. Z. H.; Duan L. Entropic effect and residue specific entropic contribution to the cooperativity in streptavidin–biotin binding. Nanoscale 2020, 12, 7134–7145. 10.1039/C9NR08380D. [DOI] [PubMed] [Google Scholar]
- Li G.; Shen H.; Zhang D.; Li Y.; Wang H. Coarse-Grained Modeling of Nucleic Acids Using Anisotropic Gay–Berne and Electric Multipole Potentials. J. Chem. Theory Comput. 2016, 12, 676–693. 10.1021/acs.jctc.5b00903. [DOI] [PubMed] [Google Scholar]
- Dong S.; Luo S.; Huang K.; Zhao X.; Duan L.; Li H. Insights into four helical proteins folding via self-guided Langevin dynamics simulation. Mol. Phys. 2021, 119, e1874558 10.1080/00268976.2021.1874558. [DOI] [Google Scholar]
- Ni D.; Liu D.; Zhang J.; Lu S. Computational Insights into the Interactions between Calmodulin and the c/nSH2 Domains of p85α Regulatory Subunit of PI3Kα: Implication for PI3Kα Activation by Calmodulin. Int. J. Mol. Sci. 2018, 19, 151. 10.3390/ijms19010151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng G.; Yang F.; Fu T.; Tu G.; Chen Y.; Yao X.; Xue W.; Zhu F. Computational characterization of the selective inhibition of human norepinephrine and serotonin transporters by an escitalopram scaffold. Phys. Chem. Chem. Phys. 2018, 20, 29513–29527. 10.1039/C8CP06232C. [DOI] [PubMed] [Google Scholar]
- Hu G.; Ma A.; Wang J. Ligand Selectivity Mechanism and Conformational Changes in Guanine Riboswitch by Molecular Dynamics Simulations and Free Energy Calculations. J. Chem. Inf. Model. 2017, 57, 918–928. 10.1021/acs.jcim.7b00139. [DOI] [PubMed] [Google Scholar]
- Chen J.; Wang X.; Pang L.; Zhang J. Z. H.; Zhu T. Effect of mutations on binding of ligands to guanine riboswitch probed by free energy perturbation and molecular dynamics simulations. Nucleic Acids Res. 2019, 47, 6618–6631. 10.1093/nar/gkz499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu E. L.; Han K.; Zhang J. Z. H. Selectivity of Neutral/Weakly Basic P1 Group Inhibitors of Thrombin and Trypsin by a Molecular Dynamics Study. Chem. – Eur. J. 2008, 14, 8704–8714. 10.1002/chem.200800277. [DOI] [PubMed] [Google Scholar]
- Hou T.; Zhang W.; Wang J.; Wang W. Predicting drug resistance of the HIV-1 protease using molecular interaction energy components. Proteins 2009, 74, 837–846. 10.1002/prot.22192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jia X.; Wang M.; Shao Y.; König G.; Brooks B. R.; Zhang J. Z. H.; Mei Y. Calculations of Solvation Free Energy through Energy Reweighting from Molecular Mechanics to Quantum Mechanics. J. Chem. Theory Comput. 2016, 12, 499–511. 10.1021/acs.jctc.5b00920. [DOI] [PubMed] [Google Scholar]
- Duan L.; Liu X.; Zhang J. Z. H. Interaction Entropy: A New Paradigm for Highly Efficient and Reliable Computation of Protein–Ligand Binding Free Energy. J. Am. Chem. Soc. 2016, 138, 5722–5728. 10.1021/jacs.6b02682. [DOI] [PubMed] [Google Scholar]
- Chen J.; Wang X.; Zhu T.; Zhang Q.; Zhang J. Z. H. A Comparative Insight into Amprenavir Resistance of Mutations V32I, G48V, I50V, I54V, and I84V in HIV-1 Protease Based on Thermodynamic Integration and MM-PBSA Methods. J. Chem. Inf. Model. 2015, 55, 1903–1913. 10.1021/acs.jcim.5b00173. [DOI] [PubMed] [Google Scholar]
- Yan F.; Liu X.; Zhang S.; Su J.; Zhang Q.; Chen J. Effect of double mutations T790M/L858R on conformation and drug-resistant mechanism of epidermal growth factor receptor explored by molecular dynamics simulations. RSC Adv. 2018, 8, 39797–39810. 10.1039/C8RA06844E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang K.; Luo S.; Cong Y.; Zhong S.; Zhang J. Z. H.; Duan L. An accurate free energy estimator: based on MM/PBSA combined with interaction entropy for protein–ligand binding affinity. Nanoscale 2020, 12, 10737–10750. 10.1039/C9NR10638C. [DOI] [PubMed] [Google Scholar]
- Aldeghi M.; Heifetz A.; Bodkin M. J.; Knapp S.; Biggin P. C. Predictions of Ligand Selectivity from Absolute Binding Free Energy Calculations. J. Am. Chem. Soc. 2017, 139, 946–957. 10.1021/jacs.6b11467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi D.; Bai Q.; Zhou S.; Liu X.; Liu H.; Yao X. Molecular dynamics simulation, binding free energy calculation and unbinding pathway analysis on selectivity difference between FKBP51 and FKBP52: Insight into the molecular mechanism of isoform selectivity. Proteins 2018, 86, 43–56. 10.1002/prot.25401. [DOI] [PubMed] [Google Scholar]
- Tian S.; Zeng J.; Liu X.; Chen J.; Zhang J. Z. H.; Zhu T. Understanding the selectivity of inhibitors toward PI4KIIIα and PI4KIIIβ based molecular modeling. Phys. Chem. Chem. Phys. 2019, 21, 22103–22112. 10.1039/C9CP03598B. [DOI] [PubMed] [Google Scholar]
- Chen J.; Wang J.; Yin B.; Pang L.; Wang W.; Zhu W. Molecular Mechanism of Binding Selectivity of Inhibitors toward BACE1 and BACE2 Revealed by Multiple Short Molecular Dynamics Simulations and Free-Energy Predictions. ACS Chem. Neurosci. 2019, 10, 4303–4318. 10.1021/acschemneuro.9b00348. [DOI] [PubMed] [Google Scholar]
- Su J.; Liu X.; Zhang S.; Yan F.; Zhang Q.; Chen J. A theoretical insight into selectivity of inhibitors toward two domains of bromodomain-containing protein 4 using molecular dynamics simulations. Chem. Biol. Drug Des. 2018, 91, 828–840. 10.1111/cbdd.13148. [DOI] [PubMed] [Google Scholar]
- Su J.; Liu X.; Zhang S.; Yan F.; Zhang Q.; Chen J. Insight into selective mechanism of class of I-BRD9 inhibitors toward BRD9 based on molecular dynamics simulations. Chem. Biol. Drug Des. 2019, 93, 163–176. 10.1111/cbdd.13398. [DOI] [PubMed] [Google Scholar]
- Chen J.; Wang J.; Pang L.; Zhu W. Inhibiting mechanism of small molecule toward the p53-MDM2 interaction: A molecular dynamic exploration. Chem. Biol. Drug Des. 2018, 92, 1763–1777. 10.1111/cbdd.13345. [DOI] [PubMed] [Google Scholar]
- Elofsson A.; Nilsson L. How Consistent are Molecular Dynamics Simulations?: Comparing Structure and Dynamics in Reduced and Oxidized Escherichia coli Thioredoxin. J. Mol. Biol. 1993, 233, 766–780. 10.1006/jmbi.1993.1551. [DOI] [PubMed] [Google Scholar]
- Knapp B.; Ospina L.; Deane C. M. Avoiding False Positive Conclusions in Molecular Simulation: The Importance of Replicas. J. Chem. Theory Comput. 2018, 14, 6127–6138. 10.1021/acs.jctc.8b00391. [DOI] [PubMed] [Google Scholar]
- Auffinger P.; Westhof E. RNA hydration: three nanoseconds of multiple molecular dynamics simulations of the solvated tRNAAsp anticodon hairpin11Edited by J. Karn. J. Mol. Biol. 1997, 269, 326–341. 10.1006/jmbi.1997.1022. [DOI] [PubMed] [Google Scholar]
- Caves L. S. D.; Evanseck J. D.; Karplus M. Locally accessible conformations of proteins: Multiple molecular dynamics simulations of crambin. Protein Sci. 1998, 7, 649–666. 10.1002/pro.5560070314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang L.-Q.; Sang P.; Zhang R. P.; Liu S. Q. Substrate-induced changes in dynamics and molecular motions of cuticle-degrading serine protease PL646: a molecular dynamics study. RSC Adv. 2017, 7, 42094–42104. 10.1039/C7RA07797A. [DOI] [Google Scholar]
- Chen J.; Wang W.; Sun H.; Pang L.; Yin B. Mutation-mediated influences on binding of anaplastic lymphoma kinase to crizotinib decoded by multiple replica Gaussian accelerated molecular dynamics. J. Comput. Aided. Mol. Des. 2020, 34, 1289–1305. 10.1007/s10822-020-00355-5. [DOI] [PubMed] [Google Scholar]
- Chen J.; Yin B.; Wang W.; Sun H. Effects of Disulfide Bonds on Binding of Inhibitors to β-Amyloid Cleaving Enzyme 1 Decoded by Multiple Replica Accelerated Molecular Dynamics Simulations. ACS Chem. Neurosci. 2020, 11, 1811–1826. 10.1021/acschemneuro.0c00234. [DOI] [PubMed] [Google Scholar]
- Wang L. F.; Wang Y.; Yang Z. Y.; Zhao J.; Sun H. B.; Wu S. L. Revealing binding selectivity of inhibitors toward bromodomain-containing proteins 2 and 4 using multiple short molecular dynamics simulations and free energy analyses. SAR QSAR Environ. Res. 2020, 31, 373–398. 10.1080/1062936X.2020.1748107. [DOI] [PubMed] [Google Scholar]
- Chen J.; Liu X.; Zhang S.; Chen J.; Sun H.; Zhang L.; Zhang Q. Molecular mechanism with regard to the binding selectivity of inhibitors toward FABP5 and FABP7 explored by multiple short molecular dynamics simulations and free energy analyses. Phys. Chem. Chem. Phys. 2020, 22, 2262–2275. 10.1039/C9CP05704H. [DOI] [PubMed] [Google Scholar]
- Wang J.; Miao Y. Peptide Gaussian accelerated molecular dynamics (Pep-GaMD): Enhanced sampling and free energy and kinetics calculations of peptide binding. J. Chem. Phys. 2020, 153, 154109. 10.1063/5.0021399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J.; Miao Y. Mechanistic Insights into Specific G Protein Interactions with Adenosine Receptors. J. Phys. Chem. B 2019, 123, 6462–6473. 10.1021/acs.jpcb.9b04867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y.; Wang L. F.; Zhang L. L.; Sun H. B.; Zhao J. Molecular mechanism of inhibitor bindings to bromodomain-containing protein 9 explored based on molecular dynamics simulations and calculations of binding free energies. SAR QSAR Environ. Res. 2020, 31, 149–170. 10.1080/1062936X.2019.1701075. [DOI] [PubMed] [Google Scholar]
- Huang K.-F.; Dong S.-H.; Zhong S.-S.; Li H.; Duan L.-L. Study on the Amyloid Aβ42 with Accelerated Molecular Dynamics Simulations. Commun. Theor. Phys. 2019, 71, 1121. 10.1088/0253-6102/71/9/1121. [DOI] [Google Scholar]
- Zhao J.; Sun H.; Wang W.; Zhang L.; Chen J. Theoretical insights into mutation-mediated conformational changes of the GNP-bound H-RAS. Chem. Phys. Lett. 2020, 759, 138042 10.1016/j.cplett.2020.138042. [DOI] [Google Scholar]
- Amadei A.; Linssen A. B. M.; Berendsen H. J. C. Essential dynamics of proteins. Proteins 1993, 17, 412–425. 10.1002/prot.340170408. [DOI] [PubMed] [Google Scholar]
- Hayward S.; Kitao A.; Go̅ N. Harmonicity and anharmonicity in protein dynamics: A normal mode analysis and principal component analysis. Proteins 1995, 23, 177–186. 10.1002/prot.340230207. [DOI] [PubMed] [Google Scholar]
- Balsera M. A.; Wriggers W.; Oono Y.; Schulten K. Principal Component Analysis and Long Time Protein Dynamics. J. Phys. Chem. 1996, 100, 2567–2572. 10.1021/jp9536920. [DOI] [Google Scholar]
- Chen J.; Wang W.; Pang L.; Zhu W. Unveiling conformational dynamics changes of H-Ras induced by mutations based on accelerated molecular dynamics. Phys. Chem. Chem. Phys. 2020, 22, 21238–21250. 10.1039/D0CP03766D. [DOI] [PubMed] [Google Scholar]
- Dalle Vedove A.; Spiliotopoulos D.; D’Agostino V. G.; Marchand J.-R.; Unzue A.; Nevado C.; Lolli G.; Caflisch A. Structural Analysis of Small-Molecule Binding to the BAZ2A and BAZ2B Bromodomains. Chem. Med. Chem. 2018, 13, 1479–1487. 10.1002/cmdc.201800234. [DOI] [PubMed] [Google Scholar]
- Li H.; Robertson A. D.; Jensen J. H. Very fast empirical prediction and rationalization of protein pKa values. Proteins 2005, 61, 704–721. 10.1002/prot.20660. [DOI] [PubMed] [Google Scholar]
- Bas D. C.; Rogers D. M.; Jensen J. H. Very fast prediction and rationalization of pKa values for protein–ligand complexes. Proteins 2008, 73, 765–783. 10.1002/prot.22102. [DOI] [PubMed] [Google Scholar]
- Song D.; Luo R.; Chen H.-F. The IDP-Specific Force Field ff14IDPSFF Improves the Conformer Sampling of Intrinsically Disordered Proteins. J. Chem. Inf. Model. 2017, 57, 1166–1178. 10.1021/acs.jcim.7b00135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maier J. A.; Martinez C.; Kasavajhala K.; Wickstrom L.; Hauser K. E.; Simmerling C. ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. 10.1021/acs.jctc.5b00255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
- Jakalian A.; Bush B. L.; Jack D. B.; Bayly C. I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: I. Method. J. Comput. Chem. 2000, 21, 132–146. . [DOI] [PubMed] [Google Scholar]
- Jakalian A.; Jack D. B.; Bayly C. I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J. Comput. Chem. 2002, 23, 1623–1641. 10.1002/jcc.10128. [DOI] [PubMed] [Google Scholar]
- Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- Darden T.; York D.; Pedersen L. Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
- Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
- Ryckaert J.-P.; Ciccotti G.; Berendsen H. J. C. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
- Izaguirre J. A.; Catarello D. P.; Wozniak J. M.; Skeel R. D. Langevin stabilization of molecular dynamics. J. Chem. Phys. 2001, 114, 2090–2098. 10.1063/1.1332996. [DOI] [Google Scholar]
- Le Grand S.; Götz A. W.; Walker R. C. SPFP: Speed without compromise—A mixed precision model for GPU accelerated molecular dynamics simulations. Comput. Phys. Commun. 2013, 184, 374–380. 10.1016/j.cpc.2012.09.022. [DOI] [Google Scholar]
- Salomon-Ferrer R.; Götz A. W.; Poole D.; Le Grand S.; Walker R. C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 2. Explicit Solvent Particle Mesh Ewald. J. Chem. Theory Comput. 2013, 9, 3878–3888. 10.1021/ct400314y. [DOI] [PubMed] [Google Scholar]
- Götz A. W.; Williamson M. J.; Xu D.; Poole D.; Le Grand S.; Walker R. C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 1. Generalized Born. J. Chem. Theory Comput. 2012, 8, 1542–1555. 10.1021/ct200909j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey W.; Dalke A.; Schulten K. VMD: Visual Molecular Dynamics. J. Mol. Graphics 1996, 16, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- Ichiye T.; Karplus M. Collective motions in proteins: A covariance analysis of atomic fluctuations in molecular dynamics and normal mode simulations. Proteins 1991, 11, 205–217. 10.1002/prot.340110305. [DOI] [PubMed] [Google Scholar]
- Zhao J.; Yin B.; Sun H.; Pang L.; Chen J. Identifying hot spots of inhibitor-CDK2 bindings by computational alanine scanning. Chem. Phys. Lett. 2020, 747, 137329 10.1016/j.cplett.2020.137329. [DOI] [Google Scholar]
- Chen J.; Wang J.; Lai F.; Wang W.; Pang L.; Zhu W. Dynamics revelation of conformational changes and binding modes of heat shock protein 90 induced by inhibitor associations. RSC Adv. 2018, 8, 25456–25467. 10.1039/C8RA05042B. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J.; Zhang S.; Wang W.; Pang L.; Zhang Q.; Liu X. Mutation-Induced Impacts on the Switch Transformations of the GDP- and GTP-Bound K-Ras: Insights from Multiple Replica Gaussian Accelerated Molecular Dynamics and Free Energy Analysis. J. Chem. Inf. Model. 2021, 61, 1954–1969. 10.1021/acs.jcim.0c01470. [DOI] [PubMed] [Google Scholar]
- Roe D. R.; Cheatham T. E. PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data. J. Chem. Theory Comput. 2013, 9, 3084–3095. 10.1021/ct400341p. [DOI] [PubMed] [Google Scholar]
- Wang W.; Kollman P. A. Free energy calculations on dimer stability of the HIV protease using molecular dynamics and a continuum solvent model11Edited by B. Honig. J. Mol. Biol. 2000, 303, 567–582. 10.1006/jmbi.2000.4057. [DOI] [PubMed] [Google Scholar]
- Wang W.; Kollman P. A. Computational study of protein specificity: The molecular basis of HIV-1 protease drug resistance. Proc. Natl. Acad. Sci. 2001, 98, 14937–14942. 10.1073/pnas.251265598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J.; Morin P.; Wang W.; Kollman P. A. Use of MM-PBSA in Reproducing the Binding Free Energies to HIV-1 RT of TIBO Derivatives and Predicting the Binding Mode to HIV-1 RT of Efavirenz by Docking and MM-PBSA. J. Am. Chem. Soc. 2001, 123, 5221–5230. 10.1021/ja003834q. [DOI] [PubMed] [Google Scholar]
- Sun H.; Li Y.; Shen M.; Tian S.; Xu L.; Pan P.; Guan Y.; Hou T. Assessing the performance of MM/PBSA and MM/GBSA methods. 5. Improved docking performance using high solute dielectric constant MM/GBSA and MM/PBSA rescoring. Phys. Chem. Chem. Phys. 2014, 16, 22035–22045. 10.1039/C4CP03179B. [DOI] [PubMed] [Google Scholar]
- Sun H.; Li Y.; Tian S.; Xu L.; Hou T. Assessing the performance of MM/PBSA and MM/GBSA methods. 4. Accuracies of MM/PBSA and MM/GBSA methodologies evaluated by various simulation protocols using PDBbind data set. Phys. Chem. Chem. Phys. 2014, 16, 16719–16729. 10.1039/C4CP01388C. [DOI] [PubMed] [Google Scholar]
- Onufriev A.; Bashford D.; Case D. A. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins 2004, 55, 383–394. 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
- Gohlke H.; Kiel C.; Case D. A. Insights into Protein–Protein Binding by Binding Free Energy Calculation and Free Energy Decomposition for the Ras–Raf and Ras–RalGDS Complexes. J. Mol. Biol. 2003, 330, 891–913. 10.1016/S0022-2836(03)00610-7. [DOI] [PubMed] [Google Scholar]
- Li Y.; Cong Y.; Feng G.; Zhong S.; Zhang J. Z. H.; Sun H.; Duan L. The impact of interior dielectric constant and entropic change on HIV-1 complex binding free energy prediction. Struct. Dynam. 2018, 5, 064101 10.1063/1.5058172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller B. R.; McGee T. D.; Swails J. M.; Homeyer N.; Gohlke H.; Roitberg A. E. MMPBSA.py: An Efficient Program for End-State Free Energy Calculations. J. Chem. Theory Comput. 2012, 8, 3314–3321. 10.1021/ct300418h. [DOI] [PubMed] [Google Scholar]
- Zaware N.; Zhou M.-M. Bromodomain biology and drug discovery. Nat. Struct. Mol. Biol. 2019, 26, 870–879. 10.1038/s41594-019-0309-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linhares B. M.; Grembecka J.; Cierpicki T. Targeting epigenetic protein–protein interactions with small-molecule inhibitors. Future Med. Chem. 2020, 12, 1305–1326. 10.4155/fmc-2020-0082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu M.; Wang L.; Sun X.; Zhao X. Investigating the Impact of Asp181 Point Mutations on Interactions between PTP1B and Phosphotyrosine Substrate. Sci. Rep. 2014, 4, 5095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wan H.; Hu J.-P.; Tian X.-H.; Chang S. Molecular dynamics simulations of wild type and mutants of human complement receptor 2 complexed with C3d. Phys. Chem. Chem. Phys. 2013, 15, 1241–1251. 10.1039/C2CP41388D. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.